Журнал вычислительной математики и математической физики, 2019, T. 59, № 1, стр. 3-20

ВВЕДЕНИЕ

Для успешного контроля погрешности численных решений гарантированная апостериорная оценка погрешности должна удовлетворять условиям достаточной точности и быстродействия, то есть близости к оптимальной по вычислительной работе. Естественно ожидать, в частности, что вычислительная стоимость оценки погрешности не превышает стоимости численного решения задачи. К числу распространенных относятся апостериорные оценки энергетической нормы погрешности, содержащие в правой части два основных слагаемых, одно из которых есть ${{L}_{2}}$-норма невязки, вычисляемая с помощью приближенного решения и некоторого тестирующего потока. Для определенности в качестве достаточно характерного примера приближенных решений будем рассматривать решения метода конечных элементов. Для эллиптических уравнений второго порядка, как правило, применяют МКЭ класса $C$ с решениями из конечномерного подпространства пространства $C(\Omega ) \cap {{H}^{1}}(\Omega )$. Вторые производные таких приближенных решений, как и первые производные от соответствующих им компонент потоков, нужные для вычисления невязки, не определены. Поэтому для вычисления оценок погрешности используют более гладкие тестирующие потоки, которые находят по потокам МКЭ посредством специальных процедур. Их называют процедурами восстановления потоков, от них существенно зависит точность и вычислительная сложность апостериорной оценки.

Таким образом, развитие многочисленных в настоящее время процедур восстановления потоков было мотивировано необходимостью повышения гладкости потоков без потери точности. Если ${{\mathbb{V}}_{h}}(\Omega )$ – пространство конечно-элементных функций и ${{u}_{{{\text{fem}}}}}$ – решение МКЭ, ${{u}_{{{\text{fem}}}}} \in {{\mathbb{V}}_{h}}(\Omega )$, то для вычислимости невязочного слагаемого апостериорной оценки достаточно определить тестирующую вектор-функцию потока ${\mathbf{y}},{{{\mathbf{y}}}^{ \top }} = ({{y}_{1}},{{y}_{2}},\; \ldots ,\;{{y}_{m}})$, как элемент пространства ${{{\mathbf{V}}}_{h}}(\Omega ) = {{({{\mathbb{V}}_{h}}(\Omega ))}^{m}}$, где $m$ – размерность области $\Omega $, $h$ – размер сетки, или конечномерного подпространства пространства ${\mathbf{H}}(\Omega ,{\text{div}})$. Можно, например, в качестве ${\mathbf{y}}$ взять ортогональную ${{L}_{2}}$-проекцию потока МКЭ на ${{{\mathbf{V}}}_{h}}(\Omega )$. Такой алгоритм достаточно прост, его вычислительная стоимость во многих случаях линейна, так как он требует решения системы алгебраических уравнений с малозаполненной матрицей, имеющей при использовании, например, квазиоднородных сеток равномерное по $h$ диагональное преобладание. Значительное внимание уделялось процедурам, в которых нахождение сглаженного потока сводится к решению вспомогательных локальных задач аппроксимации, нередко с одновременным удовлетворением уравнений баланса или уравнений равновесия для задач механики твердого тела. Совершенствованию этих процедур посвящена весьма обширная литература (см., в частности, [1]–[8]).

Процедуры восстановления потоков получают, исходя из трех требований:

$\alpha $) сохранения порядков точности в энергетической и других нормах, одинаковых с потоком, определяемым приближенным решением краевой задачи;

$\beta $) получения сбалансированных, т.е. удовлетворяющих уравнениям баланса, см. (6), или частично сбалансированных восстановленных потоков, обеспечивающих поэлементные равенства нулю или достаточную малость невязки;

$\gamma $) линейной или почти линейной вычислительной сложности.

В статье термин апостериорная мажоранта используется для правой части апостериорной оценки. Очевидно, что требование $\beta $) усложняет процедуры вычисления оценок, делает их менее универсальными, более зависимыми от свойств краевых задач. Однако за счет его выполнения удается обнулить слагаемое в апостериорной мажоранте, содержащее норму невязки, или уменьшить ее до величины, сопоставимой по порядку малости с оцениваемой нормой погрешности приближенного решения. Примером последовательной реализации такого подхода является работа [8] и предшествующие ей работы [2], [9].

Термин согласованная апостериорная оценка погрешности в настоящей работе имеет отношение к степени точности оценок. Он применяется к апостериорным оценкам, которые на тестирующих потоках, удовлетворяющих требованиям $\alpha $), $\gamma $), имеют порядки точности, совпадющие с порядками точности соответствующих априорных оценок погрешности. Очевидно, согласованная апостериорная оценка погрешности неулучшаема по порядку точности, если в этом смысле неулучшаема априорная оценка погрешности численного метода. Заметим, что в зарубежной литературе параллельный термин “consistency” понимается часто в более слабом смысле как обращение мажоранты в ноль при подстановке в нее точного решения задачи.

Мажоранты энергетической нормы погрешности, как правило, содержат в качестве слагаемого ${{L}_{2}}$-норму невязки, умноженную на $1{\text{/}}\sqrt \sigma $, где $\sigma $ – коэффициент реакции в уравнении реакции-диффузии. Для случая $\sigma \equiv 0$ известны также апостериорные мажоранты погрешности, в которых множитель перед указанной нормой является константой. Как легко убедиться, на тестовых потоках, удовлетворяющих только требованиям $\alpha $) и $\gamma $), мажоранты обоих указанных типов могут завышать оценку мажорируемой нормы погрешности в ${{h}^{{ - 1}}}$ раз и более. Это говорит о том, что такие мажоранты, примеры которых приведены в разд. 1, не являются согласованными. Как отмечалось, применение тестовых потоков, учитывающих все требования $\alpha $)–$\gamma $), способно выправить положение, однако известные эффективные способы сглаживания потоков с одновременным удовлетворением уравнениям баланса и сохранением порядков точности не являются простыми. Кроме того, они, как правило, получены для уравнений конкретного вида и схем их решения первого порядка точности, то есть не являются универсальными. В то же время есть другая возможность повышения точности, позволяющая одновременно упростить процедуры восстановления потоков. В данной работе с использованием новых приемов вывода, кратко изложенных в работах [10]–[12], доказываются согласованные апостериорные оценки. В них перед упомянутой выше ${{L}_{2}}$-нормой невязки появляется множитель $h$. Это не только на порядок повышает точность апостериорной оценки, но и устраняет необходимость, чтобы тестирующий поток удовлетворял уравнениям баланса.

У работы есть и другой мотив. Ряд популярных в настоящее время апостериорных оценок для уравнения реакции-диффузии имеет описанную выше структуру правой части, которая обязана своим появлением Обэну [13]. Его оценка эффективна при больших $\sigma $, но в ней присутствует упоминавшееся слагаемое с ${{L}_{2}}$-нормой невязки, умноженной на $1{\text{/}}\sqrt \sigma $, в связи с чем точность оценки падает при $\sigma \to 0$ и при $\sigma = 0$ она теряет смысл. Попытки усовершенствовать мажоранту Обэна в лучшем случае приводили к мажорантам, определенным для всех $\sigma \geqslant 0$, но, тем не менее, при относительно небольших коэффициентах реакции не обеспечивающим порядок точности, гарантированный известными априорными оценками. Мажоранты, предлагаемые в данной работе, определены для всех $\sigma \geqslant 0$, при $\sigma \geqslant c{{h}^{{ - 2}}}$, $c = {\text{const}}$, совпадают с мажорантой Обэна, при $0 \leqslant \sigma \leqslant c{{h}^{{ - 2}}}$ не теряют точность и являются согласованными с неулучшаемыми по порядку априорными оценками.

Востребованность апостериорных оценок погрешности вычислительной практикой зависит от простоты вычисления входящих в них постоянных. В связи с этим для погрешности решений метода конечных элементов в работе получены согласованные апостериорные оценки двух типов, отличающихся способами определения постоянных. В оценках одного из них постоянные зависят от свойств области и постоянных в оценках аппроксимации в ${{H}^{1}}(\Omega )$ функций из пространства ${{H}^{2}}(\Omega )$ конечно-элементными функциями. В оценках другого типа постоянные зависят только от локальных свойств аппроксимации в ${{L}_{2}}(\Omega )$ и устойчивости в ${{H}^{1}}(\Omega )$ проекционного оператора ${{H}^{1}}(\Omega ) \to {{\mathbb{V}}_{h}}(\Omega )$, в качестве которого используется квазиинтерполяционный оператор [14]. Подчеркнем, что предлагаемые оценки являются гибкими в том смысле, что они остаются гарантированными апостериорными оценками и при грубых значениях постоянных.

Неулучшаемость по порядку точности полученных апостериорных оценок погрешности решений метода конечных элементов подтверждается в работе доказательством их согласованности с неулучшаемыми априорными оценками, а также оценкой, которую можно назвать почти обратной. Обратной является оценка апостериорной мажоранты погрешности энергетической нормой погрешности, под почти обратной понимается оценка, отличающаяся от обратной присутствием в правой части дополнительного малого члена.

Работа организована следующим образом. Раздел 1 является вводным. В нем формулируется краевая задача реакции-диффузии, кратко обсуждаются известные апостериорные оценки энергетической нормы погрешности, близкие по структуре рассматриваемым в данной работе, но не всегда согласованные. В разд. 2 предлагается новая апостериорная оценка погрешности приближения точного решения краевой задачи произвольной достаточно гладкой функцией $\text{v}$, удовлетворяющей главным краевым условиям. Ее можно рассматривать как усовершенствованную оценку работы [13], с которой она совпадает при $\sigma $, превосходящем некоторое критическое значение ${{\sigma }_{ * }}$. Соответствующая мажоранта представлена в нескольких вариантах, с разными способами определения ${{\sigma }_{ * }}$. Наиболее простой способ отвечает варианту, применимому к приближенным решениям $\text{v}$ методом Галеркина с координатными функциями из пространства ${{H}^{2}}(\Omega )$. Этот вариант имеет непосредственное отношение к изогеометрическому анализу, (см. [15]), в котором применяются координатные функции повышенной гладкости. Мажоранты разд. 2 являются достаточно общими, в них не учитываются специальные свойства приближенных методов, кроме гладкости приближенных решений. Апостериорным оценкам погрешности решений МКЭ посвящены разд. 3 и 4. В первом из них доказываются две оценки, см. теоремы 5 и 6, различающиеся значениями двух основных постоянных. При этом постоянные оценки теоремы 6 определяются только аппроксимационными свойствами конечно-элементных функций. В случаях использования линейных треугольных и тетраэдральных конечных элеменов они выражаются через постоянные в оценках аппроксимации посредством квазиинтерполяционного проекционного оператора работы [14]. В разд. 4 обсуждаются свойства полученных апостериорных оценок. Устанавливается их согласованность с априорными оценками погрешности, для МКЭ первого порядка получена почти обратная оценка. Указываются некоторые возможные обобщения.

В дальнейшем 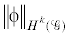– норма в соболевском пространстве ${{H}^{k}}(\mathcal{G})$ на области $\mathcal{G}$

где и $q = ({{q}_{1}},{{q}_{2}},\; \ldots ,\;{{q}_{m}})$, ${{q}_{k}} \geqslant 0$, $\left| q \right| = {{q}_{1}} + {{q}_{2}} + \ldots + {{q}_{m}}$. Если $\mathcal{G} = \Omega $, для ${{\left\| {\, \cdot \,} \right\|}_{{{{L}_{2}}(\Omega )}}}$, ${{\left\| {\, \cdot \,} \right\|}_{{{{H}^{k}}(\Omega )}}}$ и ${{\left| {\, \cdot \,} \right|}_{{{{H}^{k}}(\Omega )}}}$ будут использоваться также более простые обозначения ${{\left\| {\, \cdot \,} \right\|}_{0}}$, ${{\left\| {\, \cdot \,} \right\|}_{k}}$ и ${{\left| {\, \cdot \,} \right|}_{k}}$ соответственно. Если на всей границе $\partial \Omega $ или ее части ${{\Gamma }_{D}}$ поставлено однородное краевое условие Дирихле, то для соответствующих подпространств функций из пространства ${{H}^{1}}(\Omega )$ используются обозначения $ \circ {{H}^{1}}(\Omega ): = \left\{ {\text{v} \in {{H}^{1}}(\Omega ):{{\text{v}}_{{\partial \Omega }}} = 0} \right\}$ и $ \circ H_{{{{\Gamma }_{D}}}}^{1}(\Omega ): = \left\{ {\text{v} \in {{H}^{1}}(\Omega ):{{\text{v}}_{{{{\Gamma }_{D}}}}} = 0} \right\}$. Нам понадобятся также пространства $ \circ {{H}^{1}}(\Omega ,\Delta ) = \left\{ {\text{v} \in \circ {{H}^{1}}(\Omega ):\Delta \text{v} \in {{L}_{2}}(\Omega )} \right\}$, и пространство ${{H}^{{ - 1}}}(\Omega )$, определение которого можно найти, например, в [4], [16], [17].

Под $ \circ {{\mathbb{V}}_{h}}(\Omega )$ имеется в виду подпространство $ \circ {{\mathbb{V}}_{h}}(\Omega ) = \left\{ {\text{v} \in } \right.{{\mathbb{V}}_{h}}(\Omega ):\text{v} = 0\;{\text{н а }}\;\left. {\partial \Omega } \right\}$.

Везде ниже предполагается, что на $\Omega \subset {{\mathbb{R}}^{m}}$, $m = 2,\;3$, задан комплекс геометрически совместных, вообще говоря, криволинейных конечных элементов, занимающих области ${{\tau }_{r}}$, $r = 1,\;2,\; \ldots ,\;\mathcal{R}$. Конечные элементы определяются посредством неособенных достаточно гладких отображений $x = {{\mathcal{X}}^{{(r)}}}(\xi ){\text{:}}\;{{\tau }_{\Delta }} \to {{\tau }_{r}}$ базисного конечного элемента, заданного на стандартном треугольнике или тетраэдре ${{\tau }_{\Delta }}$. Пространство, натянутое на координатные функции базисного элемента, есть пространство полиномов степени не выше $p \in {{\mathbb{N}}^{ + }}$. При $p > 1$ для конечно-элементного пространства иногда используется также обозначение ${{\mathbb{V}}_{h}}(\Omega ) = {{\mathbb{V}}_{{h,p}}}(\Omega )$. Если упоминания других условий нет, всегда предполагается, что отображения удовлетворяют обобщенным условиям квазиоднородности с параметром сетки $h > 0$. При этом $h$ можно понимать как максимальный из диаметров конечных элементов. Условия квазиоднородности отображений (конечно-элементной сетки), как и обобщенные условия однородности формы, для МКЭ с криволинейными конечными элементами можно найти, например, в [18, разд. 3.2]. Вид постоянных апостериорных оценок существенно упрощается, если выполнено используемое нами в некоторых случаях условие:

$\mathcal{A}$) $\Omega $ – полигональная область $\Omega \in {{\mathbb{R}}^{m}}$, $m = 2,\;3$, ${{\tau }_{r}}$ – совместные $m$-мерные симплексы (с плоскими гранями и соответственно прямолинейными ребрами, сторонами), образующие триангуляцию области $\Omega $ и удовлетворяющие условиям квазиоднородности.

В приложениях и далее, как правило, ${{\mathbb{V}}_{h}}(\Omega ) \subset C(\Omega ) \cap {{H}^{1}}(\Omega )$. В то же время в изогеометрическом анализе применяются вычислительные схемы решения эллиптических уравнений 2-го порядка, основанные на более гладких конечномерных пространствах ${{\mathbb{V}}_{h}}(\Omega ) = \mathbb{V}_{h}^{1}(\Omega ) \subset {{C}^{1}}(\Omega ) \cap $ $ \cap \;{{H}^{2}}(\Omega )$, см., например, [15]. Верхний индекс в обозначении $\mathbb{V}_{{h,p}}^{l}(\Omega )$ соответствует включению $\mathbb{V}_{{h,p}}^{l}(\Omega ) \subset {{C}^{l}}(\Omega ) \cap {{H}^{{l + 1}}}(\Omega )$.

1. МОДЕЛЬНАЯ КРАЕВАЯ ЗАДАЧА, ПРИМЕРЫ МАЖОРАНТ

Одними из наиболее ранних являются апостериорные мажоранты погрешности работы Обэна [13]. Проиллюстрируем одну из них на модельной задаче

где ${{\Gamma }_{D}}$, ${{\Gamma }_{N}}$ – непересекающиеся, для простоты односвязные, части границы $\partial \Omega = {{\Gamma }_{D}} \cup {{\Gamma }_{N}}$, $\operatorname{mes} {{\Gamma }_{D}} > 0$, ${\mathbf{\nu }}$ – внутренняя нормаль к границе, ${\mathbf{A}}$ – симметричная $m \times m$ матрица, удовлетворяющая неравенствам при любых $x \in \Omega $ и ${\mathbf{\xi }} \in {{\mathbb{R}}^{m}}$. Коэффициент реакции $\sigma \geqslant 0$ считаем постоянным и в некоторых случаях кусочно-постоянным ${{\left. \sigma \right|}_{{{{\tau }_{r}}}}} = {{\sigma }_{r}} = {\text{const}},\;r = 1,2,\; \ldots ,\;\mathcal{R}$. Границу области $\Omega $, коэффициенты матрицы ${\mathbf{A}}$ и правую часть $f$ всегда предполагаем достаточно гладкими и, по крайней мере, $f \in {{L}_{2}}(\Omega )$, если требования к их гладкости не конкретизированы.

Прежде всего представляют интерес оценки погрешности в энергетической норме

Для векторов ${\mathbf{y}} \in {{\mathbb{R}}^{m}}$ введем также пространства ${{{\mathbf{L}}}^{2}}(\Omega ) = {{({{L}_{2}}(\Omega ))}^{m}}$, ${\mathbf{H}}(\Omega ,\operatorname{div} ) = \left\{ {{\mathbf{y}} \in {{{\mathbf{L}}}^{2}}(\Omega ){\text{:}}\;\operatorname{div} {\mathbf{y}} \in } \right.$ $\left. { \in \;L_{2}^{{}}(\Omega )} \right\}$ и норму ${{\left] {\left| y \right|} \right[}_{{{{{\mathbf{A}}}^{{ - 1}}}}}} = {{\left( {\int_\Omega {{{\mathbf{A}}}^{{ - 1}}}{\mathbf{y}} \cdot {\mathbf{y}}} \right)}^{{1/2}}}$.

Теорема 1 (Aubin, 1975). Пусть $f \in {{L}_{2}}(\Omega )$, $0 < \sigma = {\text{const}}$, ${{\psi }_{D}} \in {{H}^{1}}(\Omega )$, ${{\psi }_{N}} \in {{L}_{2}}({{\Gamma }_{N}})$, $u$ – решение краевой задачи (1), $u \in {{H}^{1}}(\Omega )$, $\text{v}$ – любая функция из ${{H}^{1}}(\Omega )$, удовлетворяющая краевому условию на ${{\Gamma }_{D}}$. Тогда для любого ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$, удовлетворяющего на ${{\Gamma }_{N}}$ краевому условию ${\mathbf{z}} \cdot {\mathbf{\nu }} = {{\psi }_{N}}$, имеем

Доказательство. Оценка (4) – частный случай результатов [13], см., например, Теорему 22 Введения и Теоремы 1.2, 1.4, 1.6 гл. 10.

Очевидно, при $\sigma \to 0$ оценка (4) Обэна теряет точность и при $\sigma = 0$ утрачивает смысл. При $\sigma = 0$ можно использовать мажоранту Репина и Фролова [19]. Пусть для простоты ${{\Gamma }_{D}} = \partial \Omega $, ${{\psi }_{D}} \equiv 0$, ${\mathbf{A}} = {\mathbf{I}}$, где ${\mathbf{I}}$ – единичная матрица, и $\sigma \equiv 0$. Тогда

где $\text{v}$ и ${\mathbf{z}}$ – произвольные фукция и вектор-функция из $ \circ {{H}^{1}}(\Omega )$ и ${\mathbf{H}}(\Omega ,{\text{div}})$ соответственно, а ${{c}_{\Omega }}$ – постоянная из неравенства Фридрихса.

Апостериорную оценку $\left\| {\left| {\text{v} - u} \right|} \right\||| \leqslant \left\| {{\mathbf{A}}\nabla {{u}_{{{\text{fem}}}}} + {\mathbf{\tau }}} \right\|_{{{{{\mathbf{A}}}^{{ - 1}}}}}^{2}$, которая содержит вектор-функцию потока $\tau $, удовлетворяющую уравнению баланса

можно найти у Михлина [20]. При $\sigma = 0$ существуют простые способы построения вектор-функций ${\mathbf{\tau }}$ и коррекции произвольных вектор-функций ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$ до вектор-функций ${\mathbf{\tau }}$, удовлетворяющих уравнению баланса. Ряд таких способов был предложен в работах [21], [22], где рассмотрены также приемы коррекции вектор-фунций конечно-элементных потоков $ - \nabla {{u}_{{{\text{fem}}}}} = {{{\mathbf{z}}}_{{{\text{fem}}}}}$ до ${\mathbf{\tau }} = {\mathbf{\tau }}({{{\mathbf{z}}}_{{{\text{fem}}}}})$ для решений $\text{v} = {{u}_{{{\text{fem}}}}}$ МКЭ, как и для приближенных решений другими методами. Они позволяют, кроме того, получить апостериорные оценки погрешности со свободной вектор-функцией ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$ в правой части. Ограничимся, как и выше, однородной задачей Дирихле для уравнения Пуассона, предположив дополнительно, что область выпуклая, и пусть ${{T}_{k}}$ – проекции области $\Omega $ на оси ${{x}_{{3 - k}}}$, а уравнения левой и нижней частей границы имеют вид ${{x}_{k}} = {{a}_{k}}({{x}_{{3 - k}}})$, ${{x}_{{3 - k}}} \in {{T}_{k}}$. Если ${{\beta }_{k}}$ – произвольные ограниченные функции, для которых ${{\beta }_{1}} + {{\beta }_{2}} \equiv 1$, то согласно [21], [22]

То, что в (7) справа под знаком норм стоит не невязка, а интегралы от нее, может повысить точность мажоранты. Кроме того, имеется дополнительная свободная функция, ${{\beta }_{1}}$ или ${{\beta }_{2}}$, ее правильный выбор (например, с использованием найденного приближенного решения $\text{v}$) тоже может способствовать минимизации правой части по ${\mathbf{z}}$. Оценивая одномерные интегралы под знаком ${{L}_{2}}$-нормы, приходим к оценке (5) с несколько превосходящей ${{c}_{\Omega }}$ постоянной.

Рядом авторов предпринимались попытки модифицировать мажоранту (4) с целью обеспечения приемлемой точности при всех $\sigma \geqslant 0$ (см., например, [23], [24]). Мажоранта [24] для $\forall \sigma = {\text{const}} \geqslant 0$ имеет вид

В эффективной для МКЭ апостериорной оценке работы [8] применяются сбалансированные тестирующие потоки, вычисляемые посредством предложенного в ней алгоритма линейной сложности. Для записи ее понадобятся обозначения: ${{h}_{r}}$ – диаметр области ${{\tau }_{r}}$, $\Pi _{r}^{p}{\text{:}}\;{{L}_{2}}({{\tau }_{r}}) \to {{\mathcal{P}}_{p}}({{\tau }_{r}})$ – оператор ортогонального проектирования в ${{L}_{2}}({{\tau }_{r}})$, ${{\left] {\left| {\, \cdot \,} \right|} \right[}_{{{{\tau }_{r}},{{{\mathbf{A}}}^{{ - 1}}}}}}$ – норма ${{\left] {\left| {\, \cdot \,} \right|} \right[}_{{{{{\mathbf{A}}}^{{ - 1}}}}}}$ для области $\Omega = {{\tau }_{r}}$.

Ниже, в Теоремах 2 и 3, для простоты считаем ${{\Gamma }_{D}} = \partial \Omega $, ${{\psi }_{D}} \equiv 0$ и условие $\mathcal{A})$ выполненным.

Теорема 2 (Ainsworth and Vejchodsky, 2015). Пусть $u \in \circ {{H}^{1}}(\Omega )$ – слабое решение задачи, $x,\xi \in S$ – решение МКЭ. Тогда существует $z \in {\mathbf{V}}(\Omega ) \subset {{[{{\mathbb{V}}_{{h,2}}}(\Omega )]}^{m}}$ со следующими свойствами:

i) ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$ вычисляется посредством локальных процедур, имеет линейную вычислительную сложность,

ii) для всех $x \in {{\tau }_{r}}$ и удовлеворяет уравнениям

iii) для индикатора ${{\eta }_{{{{\tau }_{r}}}}}({\mathbf{z}})$ ошибки ${{e}_{{{\text{fem}}}}} = u - {{u}_{{{\text{fem}}}}}$, определяемого выражениями

справедливы оценки где ${\text{os}}{{{\text{c}}}_{{{{\tau }_{r}}}}}(f) = min\left\{ {\tfrac{{{{h}_{r}}}}{\pi },\frac{1}{r}} \right\}{{\left\| {f - \Pi _{r}^{1}f} \right\|}_{{{{L}_{2}}({{\tau }_{r}})}}}$.

Доказательство. Теорема – один из результатов Эйнсворта и Вейходского, см. [8], [9]. Заметим, что в этих работах оценки (11), (12) получены при несколько более общих условиях. В частности, ${{\Gamma }_{N}} \ne \not {0}$, а оценка (12) дана также в локальном варианте.

Приведем еще одну мажоранту, полученную Чеддади и др. в [6] для приближенных решений задачи реакции-диффузии методом центрированных конечных объемов. В ней условие (9) поточечного удовлетворения уравнениям равновесия заменено более слабым. Введем обозначения: – двойственное по отношению к ${{\mathcal{T}}_{h}}$ подразделение области $\Omega $; – мелкая симплициальная сетка, индуцированная разбиением 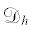; $D$ – многогранник с центром в вершине триангуляции ${{\mathcal{T}}_{h}}$ и содержащий все симплексы мелкой сетки с этой вершиной, ${{h}_{D}}$ – его диаметр; 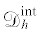– множество, включающее все многранники $D$, для которых $\partial D \cap \partial \Omega = \not {0}$. За дополнительной информацией относительно этих обозначений отсылаем к [6].

Теорема 3 (Cheddadi et al., 2011). Пусть ${{u}_{h}}$ – решение методом центрированных конечных объемов, ${{e}_{h}} = u - {{u}_{h}}$, вектор-функция ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$ удовлетворяет уравнениям

и ${{\theta }_{D}} = {\text{min}}({{C}_{D}}h_{D}^{2},\sigma _{D}^{{ - 1}})$, где ${{C}_{D}}$ – постоянная из неравенства Пуанкаре для многогранника $\mathcal{D}$. Тогда

Доказательство. См. [6].

Мажоранты (5)–(8) имеют известные достоинства, но при применении к решениям МКЭ и других сеточных методов не являются согласованными. Воспользуемся (5), наиболее простой и универсальной из них, для решения МКЭ $\text{v} = {{u}_{{{\text{fem}}}}}$ задачи (1) при ${{\Gamma }_{D}} = \partial \Omega $, ${{\psi }_{D}} \equiv 0$, ${\mathbf{A}} = {\mathbf{I}}$, и $\sigma = 0$. Для установления несогласованности достаточно рассмотреть решения МКЭ повышенной гладкости, например, принадлежащие пространству ${{\mathbb{V}}_{h}}(\Omega ) \subset {{C}^{1}}(\Omega ) \cap {{H}^{2}}(\Omega )$. Допустим, $u \in {{H}^{l}}(\Omega )$, тогда для $k = 0,\;1,\;2$ справедливы априорные оценки

В частности, если $f \in {{L}_{2}}(\Omega )$ и, следовательно, $u \in {{H}^{2}}(\Omega )$, см. ниже (39), то согласно (15) левая часть (5) оценивается сверху как $\mathcal{O}({{h}^{2}})$. В то же время при выборе ${\mathbf{z}} = \nabla \text{v}$ первое слагаемое правой части обращается в ноль, но слагаемое ${{c}_{\Omega }}\left( {1 + \tfrac{1}{\epsilon }} \right)\left\| {\nabla \cdot {\mathbf{z}} - f} \right\|_{{{{L}_{2}}(\Omega )}}^{2}$ $\forall \epsilon > 0$, оценивается сверху только постоянной. Оценки (15) неулучшаемы по порядку на пространстве $u \in {{H}^{2}}(\Omega )$. Для двумерных областей $\Omega \in {{\mathbb{R}}^{2}}$ это подтверждено, например, оценками работы [25] соответствующих поперечников Колмогорова. Отсюда следует существование функций $f \in {{L}_{2}}(\Omega )$, для которых $u \in {{H}^{2}}(\Omega )$, а второе слагаемое правой части (5) оценивается снизу постоянной. То есть порядки малости левой и правой частей апостериорной оценки различны и величина $\mathcal{O}({{h}^{2}})$, стоящая слева, оценивается мажорантой с порядком единицы. Если $l > 2$, то левая и правая части оцениваются с несогласованными порядками $\mathcal{O}({{h}^{{2(l - k)}}})$ и $\mathcal{O}({{h}^{{2(l - k - 1)}}})$ соответственно. Несогласованность апостериорной мажоранты (8) при $\sigma \leqslant c{{h}^{{ - \alpha }}}$, $0 \leqslant \alpha < 2$, $c = {\text{const}}$, с априорными оценками устанавливается так же. Мажоранта (7) в общем случае также является несогласованной.

Несогласованность, очевидно, сохраняется, если применяются конечные элементы класса $C$, а тестовый поток находится посредством какой-либо процедуры восстановления потока, удовлетворяющей только требованиям $\alpha $), $\gamma $).

Оценки (11), (14) можно назвать условно согласованными. Они доказаны только в случае выполнения для тестовых вектор-функций ${\mathbf{z}}$ уравнений (9), (13), отвечающих требованию $\beta )$. Процедуры восстановления таких потоков ${\mathbf{z}}$ не всегда относятся к простым и не являются универсальными, так как для других задач (например, с другими коэффициентами в старших членах уравнения) и других схем МКЭ, например, более высоких порядков точности, их надо конструировать заново.

2. СОГЛАСОВАННАЯ АПОСТЕРИОРНАЯ МАЖОРАНТА ПОГРЕШНОСТИ

Ниже будет получена гарантированная, надежная (см. определения терминов в [8]) робастная апостериорная оценка погрешности, вычисляемая и сохраняющая точность при $\forall \sigma \in [0,\infty )$. Более того, будет показано, что при $\sigma \in [0,{{\sigma }_{ * }}]$ она является согласованной для приближенных решений задач с достаточно гладкими данными, получаемых с помощью квазиоднородных МКЭ, где ${{\sigma }_{ * }}$ есть некоторое критическое значение коэффициента реакции. Для точного решения $u$ краевой задачи (1) и любого приближения $\text{v}$ из $ \circ H_{{{{\Gamma }_{D}}}}^{1}(\Omega )$ определим ${{\sigma }_{ * }}$ посредством неравенства

Если $\text{v} = {{u}_{G}}$ есть решение методом Галеркина из подпространства $\mathcal{V}(\Omega ) \subset \circ H_{{{{\Gamma }_{D}}}}^{1}(\Omega ,\Delta )$, то условие (16) может быть ослаблено: где $Q$ – оператор ортогонального проектирования в ${{L}_{2}}(\Omega )$ на $\mathcal{V}(\Omega )$, т.е. такой, что для любой $\phi \in {{L}_{2}}(\Omega )$ имеем Значение ${{\sigma }_{ * }}$ может определяться неравенством (17) и при $\text{v}$ из произвольного подпространства $\mathcal{V}(\Omega ) \subset \circ H_{{{{\Gamma }_{D}}}}^{1}(\Omega )$, но возникают дополнительные требования к тестирующему потоку ${\mathbf{z}}$. Например, достаточно, чтобы он удовлетворял равенствам (33).

Положим $\hat {f}(x) = \prod\nolimits_r^1 f $ при $x \in {{\tau }_{r}}$, $r = 1,2,\; \ldots ,\;\mathcal{R}$. В теореме, формулируемой ниже, области ${{\tau }_{r}}$ можно считать произвольными выпуклыми липшицевыми подобластями декомпозиции области

для которых выполняются неравенства Пуанкаре, см. [26],

Теорема 4. Пусть ${{\Gamma }_{D}} = \partial \Omega $, выполнены условия теоремы 1 и ${{\sigma }_{ * }}$ удовлетворяет неравенству (16). Тогда

гдеипри $\kappa = \sigma {\text{/}}{{\sigma }_{ * }}$. Также для $\sigma \in [0,{{\sigma }_{ * }}]$ и $\sigma \geqslant {{\sigma }_{ * }}$, соответственно, справедливы оценки в которыхиЕсли $\text{v} = {{u}_{G}}$ – решение метода Галеркина из подпространства $\mathcal{V}(\Omega ) \subset \circ H_{{{{\Gamma }_{D}}}}^{1}(\Omega ,\Delta )$, то оценка (18)–(20) справедлива при ${{\sigma }_{ * }}$, удовлетворяющем неравенству (17) и ${\mathbf{z}} = {{{\mathbf{z}}}_{G}}: = - {\mathbf{A}}\nabla {{u}_{G}}$, то есть

Доказательство. Очевидно, при $\sigma \geqslant {{\sigma }_{ * }}$ мажоранта (18)–(20) совпадает с мажорантой (4), в то время как для $\sigma \in [0,{{\sigma }_{ * }}]$ мажоранты (18)–(20) и (4) существенно различны. Поэтому нужно рассмотреть только случай $\sigma < {{\sigma }_{ * }}$.

Чтобы не загромождать доказательство второстепенными деталями, считаем ${\mathbf{A}} = {\mathbf{I}}$ и ${{\psi }_{D}} \equiv 0$. Для решения задачи $u$, произвольных функции $\text{v} \in \circ {{H}^{1}}(\Omega )$ и вектор-функции ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$ имеем

Интегрируя по частям второе слагаемое правой части и применяя неравенство найдем, что Неравенство (16) при любом $\beta \in (0,1]$ позволяет преобразовать второй множитель в правой части (26) к виду Выбор $\beta = 1{\text{/}}(1 + \kappa )$ делает отношение множителей перед второй и первой нормой в правой части (27) равным $\sigma $. Подстановка такого $\beta $ в (27) и затем (27) в (26) приводит к неравенству эквивалентному (18) при ${\mathbf{A}} = {\mathbf{I}}$.

Для доказательства оценки (21) преобразуем (24) к виду

Интеграл от последнего слагаемого в правой части (29) разобьем на интегралы по ${{\tau }_{r}}$, $r = 1,2,\; \ldots ,\;\mathcal{R}$, и каждый из них оценим с помощью неравенства Пуанкаре: Чтобы получить (21), достаточно теперь подставить (30) в (29), применить к правой части неравенство Коши-Буняковского и при оценке правой части воспользоваться неравенством (27), выбрав $\beta $ из условия $\sigma \left[ {1 + \varepsilon + ({{\sigma }_{ * }} - \sigma )\tfrac{\beta }{{{{\sigma }_{ * }}}}} \right] = (1 - \beta )({{\sigma }_{ * }} - \sigma ) + \sigma $.

Если принять

неравенство (22) следует из оценок вторая из которых есть следствие неравенства (16).

Перейдем к доказательству оценки (23). Для $e = \text{v} - u$ и ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$ имеем

Предположим, ${\mathbf{z}}$ удовлетворяет тождеству на конечно-элементном пространстве $\mathcal{V}(\Omega )$. Если $\text{v} \in \mathcal{V}(\Omega )$, то для фукции ${{e}_{ \circ }} = (Qu - u)$ имеем и Подставив (34) в (32), применив неравенство Коши и неравество (17), получим

Выбор $\beta = (1 - \kappa ){\text{/}}(1 + \kappa )$ приводит к оценке, совпадающей по виду с (18)–(20), но при ${{\sigma }_{ * }}$, удовлетворяющим неравенству (17). Заметим теперь, что при $\mathcal{V}(\Omega ) \subset \circ H_{{{{\Gamma }_{D}}}}^{1}(\Omega ,\Delta )$ тождество (33) имеет место. Кроме того, при ${\mathbf{z}} = - {\mathbf{A}}\nabla {{u}_{G}}$ норма ${{\left] {\left| {{\mathbf{A}}\nabla \text{v} + {\mathbf{z}}} \right|} \right[}_{{{{{\mathbf{A}}}^{{ - 1}}}}}}$ равна нулю, что доказывает оценку (23).

Замечание 1. Есть другие способы получения мажорант (18)–(20) и мажоранты (21), (22). Для простоты положим ${\mathbf{A}} \equiv {\mathbf{I}}$ и ${{\Gamma }_{D}} = \partial \Omega $. Можно рассмотреть вспомогательную задачу

с произвольным $\Bbbk \geqslant {{\sigma }_{ * }}$ и ${{f}_{{\lambda ,\sigma }}} = f + (\Bbbk - \sigma )u$, решение которой совпадает с решением задачи (1) при указанных ${\mathbf{A}}$ и ${{\Gamma }_{D}}$. Воспользуемся мажорантой Обэна для аппроксимаций решения задачи (36), в качестве которых можно взять аппроксимации $\text{v}$ решений задачи (1). После подстановки в оценку Обэна правой части ${{f}_{{\lambda ,\sigma }}} = f + (\Bbbk - \sigma )u$, воспользовавшись неравенством Коши с $\varepsilon $, неравенством (16) и выполнив несложные манипуляции, получим вспомогательную мажоранту. Минимизируя ее по $\mathbb{K}$ и параметрам типа $\beta $ и $\varepsilon $, придем к мажорантам теоремы 2, но с несколько отличающимися значениями $\Theta $ и $\theta $. Изменяя выбор $\beta $, $\varepsilon $, можно управлять весами перед первой и второй нормами в правой части.

3. МАЖОРАНТЫ ПОГРЕШНОСТИ ДЛЯ РЕШЕНИЙ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ

Для конкретных классов приближенных решений и, в частности, для решений МКЭ критические значения ${{\sigma }_{ * }}$ коэффициента реакции в полученных мажорантах погрешности могут быть уточнены.

Лемма 1. Пусть ${{\Gamma }_{D}} = \partial \Omega $, $\sigma \equiv {\text{const}}$, ${{\psi }_{D}} \equiv 0$, $u \in \circ {{H}^{1}}(\Omega )$, $f \in {{H}^{{ - 1}}}(\Omega )$, конечно-элементный комплекс порождает пространство ${{\mathbb{V}}_{{h,p}}}(\Omega )$, $p \geqslant 1$, и ${{e}_{{{\text{fem}}}}} = {{u}_{{{\text{fem}}}}} - u$. Тогда справедлива оценка

с постоянными ${{c}_{{\text{o}}}},$ ${{c}_{{{\text{ap}}}}}$, определенными ниже, см. (39), (46).

Доказательство. Рассмотрим задачу нахождения решения $\chi \in \circ {{H}^{1}}(\Omega )$ интегрального тождества

в котором ${{a}_{\Omega }}(\text{v},w) = \int_\Omega \nabla \text{v} \cdot {\mathbf{A}}\nabla wdx$. Если область $\Omega $ достаточно гладкая и $\sigma \geqslant 0$, то при любой $F \in {{L}_{2}}(\Omega )$. Действительно, для $\sigma \leqslant 1$ неравенство выполняется [27]. В случае $\sigma \geqslant 1$, очевидно, и, применив (39) для задачи найдем Осталось только переобозначить постоянную в (39).

Введем обозначения ${{u}_{{\text{o}}}}$, ${{u}_{{\text{1}}}}$ и ${{u}_{s}}$ для функций, минимизирующих $\left\| {u - \phi } \right\|_{0}^{2},$ $\left\| {u - \phi } \right\|_{{\mathbf{A}}}^{2}$, и ${{h}^{{ - 2}}}\left\| {u - \phi } \right\|_{{0,\Omega }}^{2} + \left\| {u - \phi } \right\|_{{\mathbf{A}}}^{2}$ соответственно среди всех и обозначения для соответствующих погрешностей ${{e}_{{\text{o}}}} = {{u}_{{\text{o}}}} - u$, ${{u}_{{{\text{fe}}}}} = {{u}_{{{\text{fe}}}}} - u$ и ${{e}_{s}} = {{u}_{s}} - u$. Так как ${{u}_{{{\text{fem}}}}}$ минимизирует ${{\left\| {\left| {u - \phi } \right|} \right\|}^{2}}$, 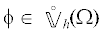, то

где $\tilde {u}$ может быть любой из функций $\tilde {u} = {{u}_{{\text{o}}}},{{u}_{{{\text{fe}}}}},{{u}_{s}}$. Если принять во внимание неравенства ${{\left\| {{{e}_{{{\text{fem}}}}}} \right\|}_{0}} \geqslant {{\left\| {{{e}_{{\text{o}}}}} \right\|}_{0}}$ и ${{\left\| {{{e}_{{{\text{fem}}}}}} \right\|}_{{\mathbf{A}}}} \geqslant {{\left\| {{{e}_{{{\text{fe}}}}}} \right\|}_{{\mathbf{A}}}}$, вытекающие из определения функций ${{u}_{{\text{o}}}}$ и ${{u}_{{{\text{fe}}}}}$, то из (43) следует

Пусть $\phi \in \circ {{H}_{1}}(\Omega )$ – решение краевой задачи

Очевидно, ${{e}_{{{\text{fe}}}}} \in {{L}_{2}}(\Omega )$ и, как следствие (39), и симметричности билинейной формы ${{a}_{\Omega }}( \cdot , \cdot )$, имеем $\phi \in {{H}^{2}}(\Omega )$ и Аппроксимируем $\phi $ какой-либо функцией ${{\phi }_{{{\text{ap}}}}} \in \circ {{\mathbb{V}}_{{h,p}}}(\Omega )$. Можно использовать функцию ${{\phi }_{{{\text{ap}}}}} \in \circ {{\mathbb{V}}_{{h,1}}}(\Omega ) \subset \circ {{\mathbb{V}}_{{h,p}}}(\Omega )$, которую в случае выполнения условия $\mathcal{A})$ получаем посредством квазиинтерполяционного оператора Скотта-Жанга [14]. В общем случае можно также понимать ${{\phi }_{{{\text{ap}}}}}$ как решение МКЭ, или ${{L}_{2}}$-проекцию или интерполяцию из $ \circ {{\mathbb{V}}_{{h,1}}}(\Omega )$ или $ \circ {{\mathbb{V}}_{{h,p}}}(\Omega )$. Заметим, что так как в лемме используется только значение постоянной ${{c}_{{{\text{ap}}}}}$ в оценке а не сама функция ${{\phi }_{{{\text{ap}}}}}$, то под ${{\phi }_{{{\text{ap}}}}}$ можно иметь в виду ту из перечисленных аппроксимаций, которая позволяет найти лучшее значение постоянной.

Оценивая ${{\left\| {{{e}_{{{\text{fe}}}}}} \right\|}_{0}}$ посредством приема Обэна-Нитше [13] для задачи (45) и оценки (46), получаем

что вместe с первым неравенством (44) и определениями функций ${{e}_{{{\text{fe}}}}}$, ${{e}_{{{\text{fem}}}}}$ приводит к оценке (37).

Теорема 5. Пусть ${{\Gamma }_{D}} = \partial \Omega $, ${{\psi }_{D}} \equiv 0$, $0 \leqslant \sigma \leqslant {{\sigma }_{ * }} = 1{\text{/}}{{({{c}_{\dag }}h)}^{2}}$, где ${{c}_{\dag }} = \tfrac{{\sqrt {{{\mu }_{2}}} }}{{{{\mu }_{1}}}}{{c}_{{\text{o}}}}{{c}_{{{\text{ap}}}}}$, и $u \in \circ {{H}_{1}}(\Omega ,\Delta )$. Пусть также конечно-элементный комплекс порождает пространство , $p \geqslant 1$, и ${{u}_{{{\text{fem}}}}}$ – решение метода конечных элементов. Тогда для любого ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$

Если конечно-элементный комплекс удовлетворяет условию $\mathcal{A}$), то при $\sigma \leqslant {{\sigma }_{ * }}{\text{/}}(1 + \varepsilon )$ справедлива также оценка

Доказательство. Так как $\mathcal{M}_{{{\text{fem}}}}^{{(1)}}(\sigma ,f,{\mathbf{z}}) = \mathcal{M}(\sigma ,{{\sigma }_{ * }},f,\text{v},{\mathbf{z}})$, теорема есть прямое сдедствие теоремы 4 и леммы 1.

Отметим, что оценки (48), (49), как и более общие оценки теоремы 4, удобны для практического использования, в частности, потому что они остаются гарантированными апостериорными оценками при грубых оценках величины ${{\sigma }_{ * }}$. Оценки (18)–(20) и (21) справедливы при любом $\sigma \in [1{\text{/}}{{c}_{\Omega }},\;1{\text{/}}{{({{c}_{\dag }}h)}^{2}}]$, где ${{c}_{\Omega }}$ – постоянная в неравенстве Фридрихса $\left\| \phi \right\|_{0}^{2} \leqslant {{c}_{\Omega }}\left| \phi \right|_{1}^{2}\,\;\forall \phi \in \circ {{H}^{1}}(\Omega )$. При наихудших значениях $\Theta = 2$ и $\theta = {{c}_{\Omega }}$, соответствующих $\sigma = 0$ и ${{\sigma }_{ * }} = 1{\text{/}}{{c}_{\Omega }}$, оценка (18)–(20) совпадает с (5) при $\epsilon = 1$. При $\sigma > 0$ и более точном выборе ${{\sigma }_{ * }}$ коэффициенты $\Theta $ и $\theta $ улучшаются, а в условиях теоремы 5 оценки (18)–(20) и (21) превращаются в (48) и (49).

Сравнение с (11), (12) и (14) затрудняется тем, что тестирующий поток ${\mathbf{z}}$ в (11), (12) фиксирован, а в (14) удовлетворяет условиям (13). Предположим для простоты, что в (11)–(12) $\sigma = {\text{const}}$. Аналогичный $\Theta $ коэффициент в (11) равен 2, а коэффициент $\theta $ равен нулю. Однако оценка (11), (12) получена только для решения МКЭ ${{u}_{{{\text{fem}}}}} \in \circ \mathbb{V}_{{h,1}}^{0}(\Omega )$ и построенного по нему фиксированного потока ${\mathbf{z}}$. Для таких ${{u}_{{{\text{fem}}}}}$ и ${\mathbf{z}}$ соответствующее слагаемое в (21) тоже обращается в ноль. В то же время ${\mathbf{z}}$ – свободная вектор-функция в оценках Теорем 4 и 5, что дает возможность дополнительной минимизации правой части по ${\mathbf{z}}$.

Использованный в лемме способ нахождения постоянной ${{c}_{\dag }}$ является достаточно общим и практически без изменений переносится на аналогичные апостериорные оценки погрешности решений МКЭ для эллиптических уравнений порядка $2n,$ $n \geqslant 1$, см. Корнеев [12]. При этом наиболее сложной является оценка постоянной ${{c}_{{\text{o}}}}$. Однако во многих ситуациях такая оценка известна. Например, если $\Omega $ – выпуклая область, то ${{\left| \text{v} \right|}_{2}} \leqslant {{\left\| {\Delta \text{v}} \right\|}_{0}}$ (см. [17], (6.5) гл. II), и, следовательно, при ${\mathbf{A}} = {\mathbf{I}}$ и $\sigma \equiv 0$ имеем ${{c}_{{\text{o}}}} \leqslant 1$, а в общем случае $\sigma \geqslant 0$ на основании (42) заключаем, что ${{c}_{{\text{o}}}} \leqslant 2$. Необходимость нахождения постоянной ${{c}_{{\text{o}}}}$ накладывает известные условия на гладкость границы и коэффицентов задачи. В то же время, если имеется квазиинтерполяционный оператор для получения аппроксимаций функций из ${{H}^{1}}(\Omega )$, удовлетворяющий определенным требованиям, то можно убедиться в том, что постоянные в апостериорных оценках погрешности зависят только от аппроксимационных свойств конечно-элементного пространства. Например, таким требованиям удовлетворяет квазиинтерполяционный оператор работы [14], который используем ниже для иллюстрации этого утверждения. Сначала опишем сам оператор.

Пусть $\Omega \subset {{\mathbb{R}}^{m}},$ $m \geqslant 2,$ – ограниченная липшицева область, на которой задана квазиоднородная триангуляция 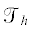с вершинами ${{x}^{{(i)}}},$ $i = 1,2,\; \ldots ,\;I$, и симплексами ${{\tau }_{r}}$, диаметр которых не превышает $h$. Ради простоты предполагаем грани симплексов плоскими, записав условия квазиоднородности триангуляции в виде

где ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } }_{r}}$ и ${{h}_{r}}$ – радиус наибольшей вписанной сферы и диаметр симплекса ${{\tau }_{r}}$. Каждой вершине ${{x}^{{(i)}}}$ сопоставим $(m - 1)$-мерный симплекс $\tau _{i}^{{(m - 1)}}$, который является гранью одного из симплексов ${{\tau }_{r}}$ с вершиной ${{x}^{{(i)}}}$. Для $m$ вершин симплекса $\tau _{i}^{{(m - 1)}}$ используем также обозначения $z_{l}^{{(i)}},$ $l = 1,2,\; \ldots ,\;m,$ считая для определенности, что $z_{1}^{{(i)}} = {{x}^{{(i)}}}$. Очевидно, выбор грани $\tau _{i}^{{(m - 1)}}$ не единствен. Для ${{x}^{{(i)}}} \in \partial \Omega $ всегда выбираем одну из граней $\tau _{i}^{{(m - 1)}} \subset \partial \Omega $. В формулировке результата Скотта Жанга используем также более простые обозначения ${{\mathbb{V}}_{\Delta }}(\Omega )$, $ \circ {{\mathbb{V}}_{\Delta }}(\Omega )$ и ${{\mathcal{V}}_{{{\text{tr}}}}}(\partial \Omega )$ для пространства непрерывных кусочно-линейных функций $\mathbb{V}_{{h,1}}^{0}(\Omega )$, его подпространства функций, равных нулю на границе, и его ограничения на $\partial \Omega $ соответственно.

Определим функции ${{\theta }_{i}} \in {{\mathcal{P}}_{1}}\left( {\tau _{i}^{{(m - 1)}}} \right)$, удовлетворяющие уравнениям

где $\lambda _{l}^{{(i)}}$ – барицентрические координаты в $\tau _{i}^{{(m - 1)}}$, соответствующие вершинам $z_{l}^{{(i)}}$, и ${{\delta }_{{i,l}}}$ – символ Кронекера. Если ${{\phi }_{i}} \in {{\mathbb{V}}_{\Delta }}(\Omega )$ – базисные функции в ${{\mathbb{V}}_{\Delta }}(\Omega )$, определяемые равенствами ${{\phi }_{i}}({{x}_{j}}) = {{\delta }_{{i,j}}},\;i,j = 1,2,\; \ldots ,\;I,$ то для любой $\text{v} \in {{H}^{1}}(\Omega )$ квазиинтерполяция ${{\mathcal{I}}_{h}}\text{v}$ есть функция

Лемма 2. Квазиинтерполяционный оператор ${{\mathcal{I}}_{h}}:{{H}^{1}}(\Omega ) \to {{\mathbb{V}}_{\Delta }}(\Omega )$ является проекционным и имеет следующие свойства:

a) ${{\mathcal{I}}_{h}}\text{v}:{{H}^{1}}(\Omega ) \mapsto {{\mathbb{V}}_{\Delta }}(\Omega )$ и, если $\text{v} \in {{\mathbb{V}}_{\Delta }}(\Omega )$, то ${{\mathcal{I}}_{h}}\text{v} = \text{v}$,

b) $(\text{v} - {{\mathcal{I}}_{h}}\text{v}) \in \circ {{H}^{1}}(\Omega ),$ если ${{\left. \text{v} \right|}_{{\partial \Omega }}} \in {{\mathcal{V}}_{{{\text{tr}}}}}(\partial \Omega )$,

c) ${{\left\| {\text{v} - {{\mathcal{I}}_{h}}\text{v}} \right\|}_{{t,\Omega }}} \leqslant {{c}_{{{\text{sz}}}}}{\text{(}}t,s){{h}^{{s - t}}}{{\left\| \text{v} \right\|}_{{s,\Omega }}}$ для $t = 0,\;1,$ $s = 1,\;2$ и $\forall \text{v} \in {{H}^{s}}(\Omega )$,

d) ${{\left| {{{\mathcal{I}}_{h}}\text{v}} \right|}_{{1,\Omega }}} \leqslant {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{c} }_{{{\text{cs}}}}}{{\left| \text{v} \right|}_{{1,\Omega }}}$ и ${{\left\| {{{\mathcal{I}}_{h}}\text{v}} \right\|}_{{1,\Omega }}} \leqslant {{\hat {c}}_{{{\text{cz}}}}}{{\left\| \text{v} \right\|}_{{1,\Omega }}}$ $\forall \text{v} \in {{H}^{1}}(\Omega )$,

где ${{c}_{{{\text{sz}}}}}(s,t),$ ${{\hat {c}}_{{{\text{cz}}}}}$ и $\hat {c}$ – положительные постоянные, зависящие от ${{c}_{\Delta }}$.

Доказательство. Лемма в более общей форме была доказана Скоттом и Жангом [14], в приведенной форме ее можно найти в [28].

Теорема 6. Пусть ${{\Gamma }_{D}} = \partial \Omega $, ${{\psi }_{D}} \equiv 0$, $u \in \circ {{H}^{1}}(\Omega ,\Delta )$, конечно-элементный комплекс удовлетворяет условию $\mathcal{A}$) и порождает пространство $ \circ {{\mathbb{V}}_{\Delta }}(\Omega ) \subset \circ {{H}^{1}}(\Omega )$ и ${\mathbf{z}} \in {\mathbf{H}}(\Omega ,{\text{div}})$. Тогда при $\sigma \in \left[ {0,\;1{\text{/}}{{{({{c}_{{{\text{sz}}}}}(0,\;1)h)}}^{2}}} \right]$ для $\text{v} = {{u}_{{{\text{fem}}}}}$ выполняется оценкa

в которойи $\tilde {c}_{{{\text{sz}}}}^{2}(1,1)$ – постоянная, зависящая только от $c$ и ${{\hat {\alpha }}^{{(1)}}}$, см. (58).

Доказательство. При любой $w \in \circ {{\mathbb{V}}_{\Delta }}(\Omega )$ имеет место равенство

Интегрируя по частям второе слагаемое под знаком интеграла в правой части и применяя неравенство Коши, при любом $\epsilon > 0$ получаем

Согласно лемме 2 и определению оператора $Q$ ${{L}_{2}}$-проекции на $ \circ {{\mathbb{V}}_{\Delta }}(\Omega )$ для разности $\phi - Q\phi $ при любой $\phi \in {{H}^{1}}(\Omega )$ выполняются неравенства

где постоянная ${{\tilde {c}}_{{{\text{cz}}}}}(1,1)$ зависит только от $c$ и ${{\hat {\alpha }}^{{(1)}}}$. Доказательства требует только последнее неравенство. Оно вытекает из соотношений в которых ${{c}_{{1,0}}}$ – постоянная в обратном неравенстве ${{\left\| {\nabla ({{\mathcal{I}}_{h}}\phi - Q\phi )} \right\|}_{0}} \leqslant {{c}_{{1,0}}}{{h}^{{ - 1}}}{{\left\| {{{\mathcal{I}}_{h}}\phi - Q\phi } \right\|}_{0}}$. Таким образом,

Заметим, что третье неравенство (57), свидетельствующее об устойчивости в ${{H}^{1}}(\Omega )$ ${{L}_{2}}$-проекции, было получено в [29] другим путем соответственно с другим способом вычисления постоянной ${{\tilde {c}}_{{{\text{sz}}}}}(1,1)$. Он основан на локальных ${{L}_{2}}$-проекциях ${{Q}_{{{{\tau }_{r}}}}}{\text{:}}\;{{L}_{2}}({{\tau }_{r}}) \to {{\mathcal{P}}_{1}}$.

Так как $w = Q{{e}_{{{\text{fem}}}}} \in \circ {{\mathbb{V}}_{\Delta }}(\Omega )$, то можно принять $w = Q{{e}_{{{\text{fem}}}}}$. Если также использовать (57) и положить $\epsilon = {{\sigma }_{{{\text{sz}}}}}: = {{({{c}_{{{\text{sz}}}}}(0,1)h)}^{{ - 2}}}$, то придем к оценке

На основании (59) заключаем, что где $\kappa = \sigma {\text{/}}{{\sigma }_{{{\text{sz}}}}}$. Из (56) и (60) следует утверждение теоремы.

Замечание 2. Квазиинтерполяционный оператор ${{\mathcal{I}}_{h}}$ определен в [28] на триангуляциях, удовлетворяющих условиям квазиоднородности формы $0 < {{c}_{\Delta }} \leqslant {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } }_{r}}{\text{/}}{{h}_{r}},\quad {{h}_{r}} \leqslant h$, с сохранением свойств a), b) и свойствами с), d), принимающими вид

где ${{c}_{{{\text{sz}}}}}(t,s) = {\text{const}}$, ${{\delta }_{r}} = {\text{interior}}\left\{ {{{ \cup }_{\varkappa }}{{{\bar {\tau }}}_{\varkappa }}:{{{\bar {\tau }}}_{\varkappa }} \cap {{{\bar {\tau }}}_{r}} \ne \emptyset } \right\}$ и $r = 1,2,\; \ldots ,\;\mathcal{R}$. Более того, там же получены интерполяционные операторы ${{\mathcal{I}}_{{h,p}}}:{{H}^{1}}(\Omega ) \to {{\mathbb{V}}_{{h,p}}}(\Omega )$, для которых также сохраняются свойства a), b), а в (61) $s = 1,2,\; \ldots ,\;p + 1$. Эти факты ведут к ряду обобщений. Одно из них – распространение оценки (53)–(54) на конечно-элементные решения из пространств ${{\mathbb{V}}_{{h,p}}}(\Omega ),$ $p > 1$. При этом в (53), (54) постоянные для оператора ${{\Im }_{h}}$ заменяются постоянными для оператора ${{\mathcal{I}}_{{h,p}}}$. Появляется также возможность обобщения (53), (54) на случай кусочно-постоянного коэффициента реакции ${{\left. \sigma \right|}_{{{{\tau }_{r}}}}} = {{\sigma }_{r}} = {\text{const}} \geqslant 0$ при некоторых ограничениях на величины скачков, например, $\left| {{{\sigma }_{r}} - {{\sigma }_{\varkappa }}} \right| \leqslant cmin({{\sigma }_{r}},{{\sigma }_{\varkappa }}),$ $c = {\text{const}} \leqslant 1{\text{/}}2$, для любой пары конечных элементов ${{\tau }_{r}}$, ${{\tau }_{\varkappa }}$, имеющих общие вершины. Для каждого конечного элемента получаем локальные значения ${{\Theta }_{{{\text{sz}}}}} = \Theta _{{{\text{sz}}}}^{{(r)}}$ и ${{\theta }_{{{\text{sz}}}}} = \theta _{{{\text{sz}}}}^{{(r)}}$.

Замечание 3. Имеются различные способы вывода апостериорных оценок рассматриваемого класса, приводящие к различным значениям ${{\sigma }_{ * }}$ и весов перед нормами в правых частях оценок. В частности, можно ожидать, что значение ${{\sigma }_{{{\text{sz}}}}}$ будет больше ${{\sigma }_{ * }}$ в лемме 1, а значение ${{\theta }_{{{\text{sz}}}}}$ в (54) меньше $\theta = 1{\text{/}}{{\sigma }_{ * }}$ в теореме 5. В то же время ${{\Theta }_{{{\text{sz}}}}}$ в (54) превосходит $\Theta $ в оценках теоремы 5. Дополнительно к возможностям, указанным в замечании 1, изменять ${{\Theta }_{{{\text{sz}}}}}$ и ${{\theta }_{{{\text{sz}}}}}$ в (53), (54) можно посредством выбора $\epsilon = \gamma {{\sigma }_{{{\text{sz}}}}},\;\gamma \in (0,1)$.

4. СОГЛАСОВАННОСТЬ С АПРИОРНЫМИ ОЦЕНКАМИ, ПОЧТИ ОБРАТНОЕ НЕРАВЕНСТВО

В этом разделе установим некоторые важные свойства полученных апостериорных оценок погрешности.