Журнал вычислительной математики и математической физики, 2019, T. 59, № 1, стр. 143-157
Моделирование течений вязкой несжимаемой жидкости на графических процессорах при помощи схемы расщепления и многосеточного методаК. Н. Волков, В. Н. Емельянов, А. Г. Карпенко, И. В. Тетерина
К. Н. Волков 1, *, В. Н. Емельянов 1, А. Г. Карпенко 2, **, И. В. Тетерина 1
1 БГТУ
190005 С.-Петербург, ул.1-я Красноармейская, 1, Россия
2 СПбГУ
199034 С.-Петербург, Университетская наб., 7–9, Россия
* E-mail: dsci@mail.com
** E-mail: aspera.2003.ru@mail.ru
Поступила в редакцию 05.02.2018
После доработки 12.03.2018
Аннотация
Обсуждаются возможности использования графических процессоров общего назначения для численного решения задач динамики вязкой несжимаемой жидкости. Рассматриваются особенности параллельной реализации схемы расщепления (метод проекции). Система разностных уравнений, порожденная дискретизацией уравнения Пуассона для давления, решается многосеточным методом. Приводится решение ряда модельных задач на графических процессорах, и обсуждаются подходы к оптимизации программного кода, связанные с использованием различных типов памяти. Сравнивается ускорение счета на графических процессорах по отношению к расчетам на центральном процессоре при использовании сеток различной разрешающей способности и различных способах разбиения исходных данных на блоки. Библ. 20. Фиг. 12. Табл. 2.
ВВЕДЕНИЕ
Увеличение вычислительной мощности одноядерных процессоров за счет повышения их тактовой частоты и архитектурных усовершенствований представляется нерентабельным. Производители микропроцессоров переходят на разработку многоядерных процессоров с новой архитектурой, обеспечивающей распараллеливание обработки данных (см. [1], [2]). Среди многоядерных процессоров с параллельной архитектурой наиболее известными являются центральные процессоры (Central Processor Unit, CPU) и графические процессоры (Graphics Processor Unit, GPU). Графические процессоры общего назначения обладают собственной динамической памятью и содержат множество мультипроцессоров, которые управляют высокоскоростной памятью, что делает их использование эффективным как для графических, так и для неграфических вычислений (см. [2], [3]).
Структурные отличия CPU и GPU приводят к тому, что теоретическая производительность ГПУ, измеряемая количеством арифметических и логических операций в единицу времени, значительно превосходит теоретическую производительность CPU. У современных CPU имеется небольшое количество арифметически-логических устройств (АЛУ), контроллер управления, отвечающий за передачу следующей машинной инструкции АЛУ и ряд других функций, контроллер доступа к внешней памяти и внешняя память. Каждое АЛУ содержит набор регистров и свой сопроцессор для расчета сложных функций. Структура и организация памяти GPU является более сложной, чем CPU. В GPU находится большое количество АЛУ, несколько контроллеров управления и внешняя память. В отличие от CPU, где имеется один тип памяти с несколькими уровнями кэширования в самом процессоре, GPU обладает более сложной организацией памяти. Часть памяти располагается непосредственно в каждом из потоковых мультипроцессоров (регистровая и разделяемая памяти), а часть памяти размещается в запоминающем устройстве (локальная, глобальная, константная и текстурная памяти).
Для GPU требуется разработка алгоритмов, имеющих высокую степень параллелизма на уровне данных. При этом одна операция выполняется над всеми элементами массива данных (под элементом массива понимается структура данных или несколько чисел, хранящихся во внешней памяти). Из-за того, что пропускная способность канала передачи данных между АЛУ и внешней памятью является ограниченной, наиболее продуктивными оказываются алгоритмы, в которых минимизируется число обращений к внешней памяти, а отношение количества операций над данными к количеству обращений к внешней памяти является максимальным.
Программный код состоит из CPU-кода и ядра, которое исполняется в несколько нитей с локальными переменными. Ядра являются относительно небольшими операциями, обрабатывающими элементы данных и обменивающимися данными при помощи нитей. Каждой нити, выполняющей ядро, дается уникальный идентификатор, доступный внутри ядра через встроенную переменную. На каждом шаге ядро берет по одному элементу данных из каждой входной нити, выполняет обработку данных и подает один или несколько элементов данных на выход.
В имеющихся публикациях обсуждаются вопросы, связанные с производительностью вычислений на GPU и реализацией конкретных вычислительных задач (см. [1]–[4]). Прирост производительности вычислений на GPU по сравнению с вычислениями на CPU отличается в существенной степени, изменяясь от десятков до сотен раз (см. [1]–[3], [5], [6]). Возможности использования блочно-структурированных и неструктурированных сеток, а также особенности распараллеливания вычислительной процедуры и отдельных подзадач обсуждаются в работах [7]–[9].
Модельные уравнения математической физики на структурированных сетках при использовании шаблонов различного типа и различных методов решения системы разностных уравнений рассматриваются в работах [10], [11]. Расчеты проводятся с использованием разностного шаблона, содержащего 7 и 27 узлов, а для реализации граничных условий применяется подход, связанный с введением фиктивных узлов, находящихся за пределами расчетной области. В работе [10] для ускорения вычислений предлагается новый подход к распределению данных на блоки и копированию данных из глобальной памяти в локальную. На платформе Tesla C2050 производительность вычислений на шаблоне, содержащем 7 узлов, составляет 98 и 52 ГФлопс при использовании вычислений с одинарной и двойной точностью, а на шаблоне из 27 узлов – 72 и 38 ГФлопс соответственно.
Моделирование течений вязкой несжимаемой жидкости в приближении Буссинеска на кластерах GPU проводится в работе [12]. В качестве примеров рассчитываются двумерные течения в квадратной каверне с подвижной стенкой и свободная конвекция в квадратной каверне. Обсуждаются различные стратегии декомпозиции расчетной области и особенности реализации подзадач. Исследуются эффективность и масштабируемость программного кода при использовании до 256 узлов кластера и сеток, содержащих 17.2 миллионов ячеек. Особенности применения разностных схем высокой разрешающей способности обсуждаются в работе [9], а расчет сжимаемых течений в работе [13].
Несмотря на то что потенциальные возможности GPU при решении широкого круга прикладных задач не подлежат сомнению, технологические вопросы реализации вычислительных задач на GPU общего назначения требуют дальнейшего развития.
Для поддержки неграфических приложений на GPU компании NVIDIA используется унифицированная архитектура компьютерных вычислений CUDA (Compute Unified Device Architecture), основанная на расширении языка C и позволяющая получить доступ к набору инструкций GPU для управления его памятью (см. [2], [3]). При этом GPU рассматривается как вычислительное устройство, способное поддерживать параллельное исполнение большого числа нитей или потоковых программ.
В данной работе обсуждается применение схемы расщепления для решения задач, связанных с моделированием течений вязкой несжимаемой жидкости. Рассматриваются особенности реализации программного кода на GPU и ряд вопросов, связанных с его оптимизацией. Приводятся детали реализации ряда частных подзадач, сравнивается ускорение решения задачи на GPU по сравнению с расчетами на CPU при использовании сеток различной разрешающей способности и различных способах разбиения исходных данных на блоки.
1. СХЕМА РЕШЕНИЯ ЗАДАЧИ
Модель программирования CUDA предполагает, что вычислительные потоки (thread) выполняются на отдельном физическом устройстве (device), которое работает в качестве сопроцессора центрального процессора (CPU). С центрального процессора запускается программа на языке CUDA-С, называемая ядром (kernel), для каждого из вычислительных потоков. Конфигурация потоков задается на CPU перед вызовом функции ядра. Для удобства и наилучшей производительности вычислительные потоки объединяются в блоки (block), а блоки – в сетку (grid).
Потоки обращаются к данным, которые находятся в различных видах памяти. Каждый поток имеет видимую только ему локальную память (local memory) и разделяемую память (shared memory), видимую для всех потоков в блоке, которому он принадлежит. Все потоки имеют доступ к глобальной памяти (global memory). Помимо этого, еще существуют константная (constant memory) и текстурная память (texture memory). Контроль работы с памятью и выбор нужного типа памяти в зависимости от особенностей решаемой задачи лежат на программисте.
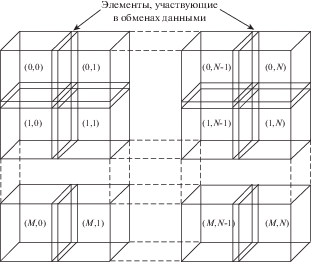
Для реализации параллельных вычислений на GPU массив входных данных (например, массив, содержащий значения искомой функции в узлах сетки) разбивается на ряд блоков (фиг. 1). Блоки образуют сетку, которая имеет размер $M \times N$. Для обеспечения корректности вычислений имеется пересечение между соседними блоками, что позволяет осуществлять обмен граничными данными между блоками.
Обмен данными обычно производится при помощи использования разделяемой памяти (использования разделяемой памяти удается избежать в том случае, когда одна нить обрабатывает данные в одной ячейке сетки).
При использовании метода конечных разностей или метода конечных объемов решение дифференциальных уравнений в частных производных реализуется по схеме, показанной на фиг. 2. Подготовка исходных данных (координаты узлов сетки, граничные условия, структуры данных для хранения топологии неструктурированной сетки) производится на CPU. Осуществляются копирование данных в глобальную память GPU и инициализация соответствующих переменных. На GPU производятся расчет невязких и вязких потоков, продвижение решения во времени и решение системы разностных уравнений тем или иным итерационным методом. Расчеты во внутренних и граничных узлах проводятся на GPU при помощи различных ядер (по разным правилам). Проверка сходимости численного решения производится на CPU. Синхронизация между CPU и GPU требуется при проверке условия сходимости, когда норма невязки копируется в память CPU. При выполнении условия сходимости переменные переносятся из GPU в память CPU.
Для проверки выполнения условия Куранта–Фридрихса–Леви (условие устойчивости) на каждом шаге по времени используется метод редукционного суммирования и его модификации (см. [2]).
2. СХЕМА РАСЩЕПЛЕНИЯ
Для решения уравнений Навье–Стокса, описывающих нестационарное течение вязкой несжимаемой жидкости, используются схема расщепления (см. [14], [15]) (метод проекции) и метод конечных объемов (см. [16]).
Уравнения, описывающие нестационарное течение вязкой несжимаемой жидкости, имеют следующий вид:
(2)
$\frac{{\partial {\mathbf{v}}}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{v}} = - \frac{1}{\rho }\nabla p + \nu \Delta {\mathbf{v}} + {\mathbf{f}}.$Пусть в момент времени ${{t}_{n}}$ известны поле скорости ${\mathbf{v}}$ и поле давления $p$. Тогда для расчета неизвестных функций в момент времени ${{t}_{{n + 1}}}$ используется следующая схема расщепления (см. [14], [15]).
На этапе 1 предполагается, что перенос количества движения осуществляется только за счет конвекции и диффузии
(3)
$\frac{{{\mathbf{\tilde {v}}} - {{{\mathbf{v}}}^{n}}}}{{\Delta t}} = - \left( {{{{\mathbf{v}}}^{n}} \cdot \nabla } \right){{{\mathbf{v}}}^{n}} + \nu \Delta {{{\mathbf{v}}}^{n}} + {{{\mathbf{f}}}^{n}}.$На этапе 2 по найденному промежуточному полю скорости ${\mathbf{\tilde {v}}}$ с учетом соленоидальности вектора скорости ${{{\mathbf{v}}}^{{n + 1}}}$ рассчитывается поле давления
Для решения уравнения Пуассона (4) на каждом шаге по времени используются либо итерационные, либо прямые методы.На этапе 3 предполагается, что перенос количества движения осуществляется только за счет градиента давления (конвекция и диффузия отсутствуют)
(5)
$\frac{{{{{\mathbf{v}}}^{{n + 1}}} - {\mathbf{\tilde {v}}}}}{{\Delta t}} = - \nabla {{p}^{{n + 1}}}.$Уравнение Пуассона (4) получается путем взятия дивергенции от обеих частей равенства (5) с учетом уравнения неразрывности $\nabla {{{\mathbf{v}}}^{{n + 1}}} = 0$.
Для дискретизации уравнений (3) и (5) по времени применяется схема Адамса–Бэшворта, а для дискретизации конвективных и диффузионных потоков – противопоточные и центрированные разности 2-го порядка. Уравнение Пуассона для давления решается методом Гаусса–Зейделя с использованием красно-черной (red/black) параллелизации и многосеточным методом (multigrid method).
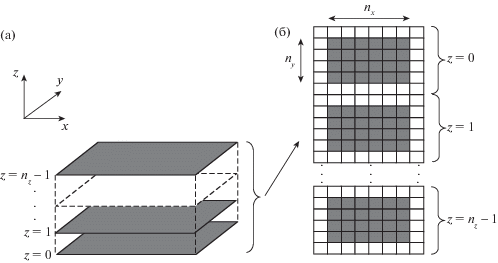
Сетка размером ${{n}_{x}} \times {{n}_{y}} \times {{n}_{z}}$ на GPU представляется в виде набора из ${{n}_{z}}$ матриц, каждая из которых имеет размер ${{n}_{x}} \times {{n}_{y}}$ (фиг. 3). Ячейки, выделенные белым цветом, являются фиктивными и используются для постановки граничных условий. Такое отображение сетки с CPU на GPU является удобным при использовании глобальной памяти.
Фиг. 3.
Представление трехмерной сетки в вычислительной области (а) в виде набора матриц на GPU (б).
Параллельный код на одном GPU, реализующий метод проекции, имеет два вложенных цикла, один из которых (внешний цикл) осуществляет продвижение решения во времени, а другой (внутренний цикл) – интегрирование уравнения Пуассона для давления итерационным методом. При использовании схемы Эйлера решение на слое $n + 1$ зависит только от значений искомых функций на слое $n$ по времени. Для хранения скорости в узлах сетки на двух смежных слоях по времени используется 6 матриц (3 матрицы на слой по времени). Обмен их значениями производится в конце каждого шага по времени. Для хранения давления на двух смежных слоях по времени используются 2 матрицы, а обмен их значениями осуществляется в конце каждой итерации.
Параллельный код на нескольких GPU имеет 6 ядер, обеспечивающих реализацию основных шагов метода проекции. Различные ядра требуются для того, чтобы обеспечить глобальную синхронизацию между блоками перед тем, как перейти к следующему слою по времени.
Для оптимизации вычислений используется разделяемая память. Блоки нитей копируют переменные из глобальной памяти в разделяемую память. Расчеты производятся нитями с использованием переменных, находящихся в разделяемой памяти. Перед выходом из ядра результаты расчета копируются из разделяемой памяти в глобальную. Для компенсации времени, затрачиваемого на обмен данными между глобальной и разделяемой памятью, увеличивается интенсивность вычислительной нагрузки, приходящейся на ядро. Один из способов состоит в том, чтобы увеличить размер подобласти, предназначающейся каждому блоку нитей.
Сравнение различных способов распределения данных, когда каждый блок нитей представляет собой матрицу $4 \times 4$, показано на фиг. 4. Ячейки, закрашенные белым цветом, используются для постановки граничных условий. На фрагменте 4а блок отображается на подобласть, содержащую $4 \times 4$ вычислительных ячеек (108 ячеек, из которых 16 являются вычислительными, а 92 ячейки – фиктивными). Для обновления переменных в вычислительных ячейках подобласть и фиктивные ячейки копируются в разделяемую память. Для расчета переменных в $4 \times 4$ ячейках требуется скопировать в разделяемую память $6 \times 6 \times 3$ ячеек. При этом блок нитей обновляет менее 15% разделяемой памяти. Декомпозиция, приведенная на фрагменте 4б (144 ячейки, из которых 32 являются вычислительными, а 112 ячеек – фиктивными), позволяет нитям обновить переменные в ячейках, находящихся в различных вертикальных колонках. Каждая нить обновляет переменные в двух ячейках. Нити работают с $4 \times 4 \times 2$ ячейками, а общее число ячеек, вовлеченных в расчет, составляет $6 \times 6 \times 4$. При этом ячейки, в которых обновляются значения искомых функций, составляют 22% от их общего количества. Время, затрачиваемое на обмен данными между разделяемой и глобальной памятью, компенсируется увеличением вычислительной нагрузки, приходящейся на каждую нить.
Фиг. 4.
Различные подходы к использованию разделяемой памяти при использовании блока размером $4 \times 4$.

Расчеты, проведенные в работе [17], показывают, что реализации ядер, предназначенных для расчета предварительного поля скорости и решения уравнения Пуассона для давления, оказываются наиболее критичными к использованию ресурсов разделяемой памяти. Использование разделяемой памяти позволяет получить почти двукратный выигрыш в производительности по сравнению с реализацией, использующей только глобальную память. Интенсивность вычислительной нагрузки, приходящейся на другие ядра, является сравнительно низкой.
3. МНОГОСЕТОЧНЫЙ МЕТОД
Многосеточный метод используется для решения системы разностных уравнений, порожденной конечно-разностной или конечно-объемной дискретизацией уравнения Пуассона (см. [16]).
Отображение вычислительной сетки (массива данных) размером ${{n}_{x}} \times {{n}_{y}} \times {{n}_{z}}$ на блоки GPU поясняет фиг. 5. Под $n$ понимается число уровней сетки, используемых в многосеточном методе решения системы разностных уравнений.
Каждая нить производит расчет параметров в одной ячейке и обновляет один элемент массива данных. Сетка блоков является двумерной структурой, в то время как блок нитей – трехмерной. Размерности массива в координатных направлениях $y$ и $z$ объединяются, а индекс каждой нити рассчитывается при помощи операции деления нацело.
Индексы внутренних ячеек изменяются от $(i,j,k) = (2,2,2)$ до $(i,j,k) = ({{n}_{x}} + 1,\;{{n}_{y}} + 1,\;{{n}_{z}} + 1)$. Граничные ячейки, не показанные на фигуре, располагаются вдоль плоскостей $(1,1,1)$ и $({{n}_{x}} + 2,\;{{n}_{y}} + 2,\;{{n}_{z}} + 2)$. Сетка GPU имеет размер $({{g}_{x}},{{g}_{y}},{{g}_{z}})$, а каждый блок – размер $({{b}_{x}},{{b}_{y}},{{b}_{z}})$. Размеры сетки GPU в координатных направлениях ${{g}_{x}}$ и ${{g}_{y}}$ получаются путем деления размеров расчетной сетки на размер блока, поэтому ${{g}_{x}} = {{n}_{x}}{\text{/}}{{b}_{x}}$ и ${{g}_{y}} = {{n}_{y}}{\text{/}}{{b}_{y}}$. Нить имеет трехмерный индекс, равный индексу элемента массива, с которым она работает. В направлении оси $z$ нить $(i,j)$ имеет дело со слоями расчетной сетки, обрабатывая одну ячейку в каждом слое $s = {{n}_{z}}(n){\text{/}}{{b}_{z}} - 1$. Нить обрабатывает множество ячеек в направлении изменения индекса $k$, находящихся в колонке с фиксированными индексами $(i,j)$. Нить имеет индексы $({{t}_{x}},{{t}_{y}},{{t}_{z}})$. Для расчета переменных во всех ячейках сетки внутри ядра используется цикл по всем слоям сетки (индексы $i$ и $j$ остаются фиксированными). Для постановки граничных условий используется массив, имеющий размер $({{g}_{x}},{{g}_{y}},{{g}_{z}})$.
Размер блока задается исходя из размера расчетной сетки. Имеются конфликты между размером сетки и оптимальным размером блока. Например, наиболее грубой сеткой является сетка размером $4 \times 4 \times 4$, а оптимальный размер блока составляет $32 \times 1 \times 8$ (размер блока превышает размер сетки).
Код, выполняемый на CPU, производит перебор всех сеточных уровней и осуществляет вызов ядра для фиксированного уровня сетки $n$.
Код, запускаемый на GPU, получает на вход номер обрабатываемого уровня сетки и выполняет необходимые вычисления.
Для увеличения эффективности многосеточных вычислений на GPU используется red/black параллелизация метода Гаусса–Зейделя. Для этого реализуются два ядра, осуществляющих обработку красных (red) и черных (black) узлов. Код, выполняемый на CPU, производит перебор всех сеточных уровней и вызывает ядра для обработки красных узлов и черных узлов. Код, выполняемый на GPU, реализует необходимые вычисления (ядра для красных узлов и черных узлов реализуются по схожей схеме).
4. ТЕСТОВЫЕ ЗАДАЧИ
Рассмотрим решение ряда задач, связанных с моделированием течений вязкой несжимаемой жидкости. При разработке модулей используется глобальная память. При запуске расчетов в глобальную память GPU копируются массивы, которые не меняются на протяжении вычислений. В зависимости от надобности для определенных CUDA ядер подгружаются нужные данные в глобальную или разделяемую память GPU, либо уже расчетные данные обратно на CPU. Передачи данных минимизируются для объединения запросов в одну транзакцию при доступе в глобальную память GPU.
4.1. Решение уравнения Пуассона
Рассмотрим решение уравнения Пуассона $\Delta u = f$ в трехмерной области, представляющей собой куб с единичной стороной $\Omega = {{[0,\;1]}^{3}}$. На гранях куба задаются значения искомой функции ($u = {{u}_{D}}$ при ${\mathbf{x}} \in \partial \Omega $). Краевая задача Дирихле для уравнения Пуассона описывает установившееся распределение скорости в квадратной каверне с подвижной верхней стенкой при малых числах Рейнольдса (конвективными слагаемыми пренебрегается по сравнению с вкладом вязких слагаемых) и находит применение для моделирования течений вязкой несжимаемой жидкости в переменных функция тока–вихрь скорости.
Для дискретизации уравнения Пуассона используется шаблон типа “крест”. Система разностных уравнений решается методом Гаусса–Зейделя с использованием red/black параллелизации. Отображение вычислительной области на структуру памяти GPU поясняет фиг. 6. Расчеты проводятся на сетке, содержащей imax $ \times $ jmax узлов. При этом ряд узлов используется для постановки граничных условий и не обрабатывается кодом (соответствующие ячейки выделяются белым цветом). Код осуществляет обработку imx $ \times $ jmx узлов.
Дискретизация трехмерного уравнения Пуассона в узле $(i,j,k)$ на шаблоне $3 \times 3 \times 3$ представляется в виде взвешенной суммы значений искомой функции в узле $i,j,k$ и 26 соседних узлов. В общем случае вычисления на шаблоне из 27 узлов требуют 27 умножений и 26 сложений на один узел сетки (53 операции с плавающей точкой). В случае симметричного шаблона требуется только 30 операций с плавающей точкой на один узел сетки.
Реализация кода, вызываемого на CPU, заключается в указании размера блока и размера сетки, а также в вызове ядер, запускаемых на GPU для обработки красных и черных узлов.
Код на GPU реализуется в виде следующей последовательности шагов: динамическое выделение памяти; постановка начальных и граничных условий; расчет коэффициентов разностной схемы; выделение памяти на GPU и копирование переменных с CPU на GPU; задание размеров блоков и сетки; вызов ядра для красных узлов и вызов ядра для черных узлов; копирование результатов с GPU на CPU.
Реализация кода, запускаемого на GPU, заключается в обработке узлов одного цвета (ядро для красных узлов и ядро для черных узлов реализуются по одной и той же схеме). На GPU решение хранится в виде матрицы размером $m \times n$ (в одной матрице хранятся значения искомой функции как во внутренних, так и в граничных узлах сетки). Вычисления производятся параллельно по $n{\text{/}}2$ блоков, каждый из которых содержит ($m - 2$) нитей. Каждая нить в блоке записывает по одному значению в разделяемую память, что позволяет уменьшить вероятность двух одновременных обращений к одному и тому же элементу динамической памяти и ускоряет доступ нитей к требуемым данным.
Ускорение решения уравнений Пуассона на GPU по отношению к вычислениям на CPU составляет около 20 (в расчетах используется только глобальная память). Расчеты показывают, что наибольшие затраты компьютерного времени приходятся на работу сглаживающей процедуры, которая, в зависимости от размера конечно-разностной сетки, занимает от 72 до 78% от общего времени счета. При этом реализации процедур продолжения и ограничения требуют менее 8–10% и 12–20% от общего времени счета. Производительность вычислений с использованием шаблона из 7 узлов составляет 56 ГФлопс, с использованием симметричного шаблона из 27 узлов – 126 ГФлопс, а с использованием общего шаблона из 27 узлов – 308 ГФлопс.
4.2. Течение в каверне
Задача о течении в кубической каверне с подвижной стенкой служит для тестирования и сравнения различных методов дискретизации уравнений Навье–Стокса, а основные структурные особенности течения в каверне присущи и другим отрывным течениям в более сложной геометрии (см. [19]).
Рассмотрим моделирование крупных вихрей течения вязкой несжимаемой жидкости в каверне с подвижной верхней стенкой при числе Рейнольдса ${\text{Re}} = 1000$. Для дискретизации основных уравнений используется метод проекции (см. [16]), а в качестве модели подсеточной вязкости применяется модель Смагоринского (см. [18]). Система разностных уравнений, порожденная дискретизацией уравнения Пуассона для давления, решается методами Гаусса–Зейделя и многосеточным. Сетка наилучшей разрешающей способности содержит ${{128}^{3}}$ узлов. Сетки грубого разрешения строятся путем последовательного удаления граней сетки более высокого уровня в каждом координатном направлении.
Картины растекания жидкости по стенкам каверны, полученные для различных чисел Рейнольдса, показывают наличие особых точек типа фокуса, центра и седла, а также линий стекания и растекания жидкости (фиг. 7). В соответствии с теоремой Пуанкаре–Бендиксона имеет место связь между типом и числом особых точек $\Sigma N - \Sigma S = 2$, где $N$ соответствует узлу или центру, а $S$ – седловой точке. В частности, $\Sigma S = 10$ и $\Sigma N = 12$.
Фиг. 7.
Картина растекания жидкости по стенкам каверны при ${\text{Re}} = 1000$ ($\square $ – седловая точка,  – устойчивый узел, $ \circ $ – неустойчивый узел, $\blacksquare $ – устойчивый фокус).
– устойчивый узел, $ \circ $ – неустойчивый узел, $\blacksquare $ – устойчивый фокус).

На дне каверны развитие картины растекания с ростом числа Рейнольдса сопровождается ослаблением влияния боковых стенок и превращением источника жидкости при ${\text{Re}} = 100$ в линию растекания при ${\text{Re}} = 1000$. Указанный источник образуется в результате присоединения отрывного потока в серединной части каверны к ее донной грани. Отрыв придонного потока у передней стенки каверны генерирует дополнительный источник. По мере возрастания числа Рейнольдса (при ${\text{Re}} > 1000$) источник превращается в линию растекания.
Взаимодействие потоков, истекающих от указанных источников вдоль днища каверны, происходит по линии растекания жидкости. Следствием этого взаимодействия является образование двух симметричных периферийных стоков на дне каверны. По мере роста числа Рейнольдса эти стоки перемещаются в окрестности ребер боковых граней.
Течение жидкости по грани, расположенной выше по потоку, определяется увлекающим воздействием подвижной стенки. С ростом числа Рейнольдса происходит перестройка течения, которая приводит к преобразованию источников в линии растекания, что свидетельствует о формировании квазидвумерного вихря в угловой зоне.
Движение жидкости по грани, расположенной ниже по потоку, обусловливается взаимодействием с этой стенкой сдвигового потока, сформировавшегося под влиянием движущейся с постоянной скоростью верхней крышки. Линии тока являются практически параллельными боковым стенкам на большей части рассматриваемой грани в направлении ко дну каверны. На ребре вблизи днища возникает источник, индуцированный перетеканием жидкости со дна каверны на заднюю стенку. Взаимодействие этого источника с набегающим сверху потоком происходит по линии растекания, которая с ростом числа Рейнольдса становится параллельной дну. Также интересно отметить возникновение в окрестности боковых стенок двух стоков, отодвигающихся от дна каверны по мере увеличения числа Рейнольдса.
На боковых стенках каверны реализуется закрученное течение жидкости со стоком из центральной части вихревой структуры. С ростом числа Рейнольдса вихревая структура перемещается к геометрическому центру боковой грани.
Затраты на исполнение различных участков кода показывает фиг. 8. При этом время, затрачиваемое на реализацию метода Гаусса–Зейделя с красно-черной параллелизацией (функции red_kernel и black_kernel), составляют почти 2/3 от общего времени вычислений. Следующей по затратам процессорного времени является функция adams_bashworth, реализующая дискретизацию основных уравнений по времени. Функция residp осуществляет расчет невязки уравнения Пуассона для давления. Копирование и выделение памяти под переменные производится при помощи функции memcopy. Функции coeffp_kernel и smagorinsky_kernel производят расчет коэффициентов, связанных с дискретизацией уравнения Пуассона для давления, и расчет подсеточной вязкости на основе модели Смагоринского. Для перехода к следующему шагу интегрирования по времени используются функции update_kernel и adams_bashworth_kernel. Вклад других функций (prodp, restrp, mresid_kernel, perturb_kernel, visc), выполняющих вспомогательные операции, в общее время счета сравнительно невелик.
Ускорение счета при параллельной реализации различных операций показывает фиг. 9. Цифры 1–5 соответствуют вычислительным модулям, используемым для расчета шага по времени (1), подсеточной модели (2), невязких слагаемых (3), вязких слагаемых (4) и продвижения решения по времени (5). Максимальное ускорение счета достигается при вычислении вязких потоков, которое составляет 70.2, а минимальное – при реализации процедуры продвижения решения во времени, которое равняется 12.8.
Ускорение счета при решении задачи на разных сетках с использованием различных способов разбиения области на блоки размером ${{n}_{x}} \times {{n}_{y}} \times {{n}_{z}}$ приводится в табл. 1 (время расчета указывается для 100 шагов по времени). Способ разбиения сетки на блоки оказывает существенное влияние на ускорение вычислений. На сетке, содержащей ${{128}^{3}}$ узлов, изменение способа разбиения расчетной области на блоки позволяет получить выигрыш в ускорении решения задачи в 2.8 раза по сравнению с исходным разбиением.
Таблица 1.
Течение в каверне. Время и ускорение вычислений
| Сетка | ${{n}_{x}} = {{n}_{y}} = {{n}_{z}} = 4$ | ||
|---|---|---|---|
| CPU, с | GPU, с | Ускорение | |
| 163 | 0.34 | 0.39 | 0.86 |
| 323 | 3.08 | 1.24 | 2.50 |
| 643 | 31.14 | 6.49 | 4.81 |
| 1283 | 291.05 | 50.92 | 5.72 |
| Сетка | ${{n}_{x}} = 32,\;{{n}_{y}} = 1,\;{{n}_{z}} = 8$ | ||
| CPU, с | GPU, с | Ускорение | |
| 163 | 0.34 | 0.31 | 1.11 |
| 323 | 3.08 | 0.66 | 4.73 |
| 643 | 31.14 | 2.71 | 11.51 |
| 1283 | 291.05 | 18.35 | 15.88 |
4.3. Течение в канале
Моделирование крупных вихрей турбулентного течения вязкого сжимаемого газа в канале с квадратной формой поперечного сечения в плане проводится при ${\text{R}}{{{\text{e}}}_{\tau }} = 360$ на сетке $256 \times 64 \times 64$. Отношение длины канала к ребру составляет $L{\text{/}}H = 4$. Сетка является равномерной по продольной координате, а в поперечном сечении узлы сетки сгущаются по направлению к стенкам канала (на стенке канала ${{y}^{ + }} \sim {{z}^{ + }} \sim 1$).
Расчеты проводятся на центральном процессоре Intel Core 2 Duo с тактовой частотой 3 ГГц и графической плате GeForce GTX 480. Вихревую картину течения в канале, обработанную при помощи критерия $Q$ [20], показывает фиг. 10. Ускорение счета при решении задачи на разных сетках с использованием различных способов разбиения расчетной области приводится в табл. 2 (время расчета указывается в секундах для 100 шагов).
Таблица 2.
Течение в канале. Время и ускорение вычислений
| Сетка | ${{n}_{x}} = {{n}_{y}} = {{n}_{z}} = 4$ | ||
|---|---|---|---|
| CPU | GPU | Ускорение | |
| $256 \times 64 \times 64$ | 208.09 | 34.56 | 6.02 |
| $512 \times 64 \times 64$ | 448.47 | 64.29 | 6.98 |
| Сетка | ${{n}_{x}} = 32,\;{{n}_{y}} = 1,\;{{n}_{z}} = 8$ | ||
| CPU | GPU | Ускорение | |
| $256 \times 64 \times 64$ | 208.09 | 14.32 | 14.50 |
На сетке, содержащей $256 \times 64 \times 64$ узлов, изменение способа разбиения расчетной области на блоки позволяет получить выигрыш в ускорении вычислений в 2.4 раза.
4.4. Обтекание сферы
Рассмотрим нестационарное течение вязкой несжимаемой жидкости около сферы при ${\text{Re}} = {\text{40}}0$. Расчеты проводятся на неструктурированных сетках, состоящих из ячеек различной формы. Тетраэдральная сетка содержит 27 915 контрольных объемов, шестигранная сетка – 20 736 контрольных объемов, а призматическая сетка – 40 500 контрольных объемов. Для дискретизации невязких потоков применяются разностные схемы 3 -го, 4-го, 5-го и 6-го порядка точности. Дискретизация вязких потоков проводится при помощи центрированных конечных разностей. Расчеты с двойной точностью проводятся на одном ядре центрального процессора Xeon x5670 с тактовой частотой 2.94 ГГц и платформе Tesla C2050. Ускорение вычислений оценивается путем сравнения времени, необходимого для расчета 100 шагов по времени. Вихревая картина течения около сферы показана на фиг. 11.
Фиг. 11.
Линии тока в течении около сферы. Фрагменты (а) и (б) соответствуют различным углам зрения.

Производительность и ускорение вычислений при использовании различных сеток и разностных схем показывает фиг. 12. Цифры служат для указания на вариант расчета, соответствующий неструктурированным сеткам с различной формой ячеек (1 – для тетраэдральной сетки, 2 – для шестигранной и 3 – для призматической).
Фиг. 12.
Производительность (а) и ускорение (б) вычислений при использовании разностных схем различного порядка.

Наивысшая производительность вычислений достигается на сетке с тетраэдральными ячейками и составляет 118 ГФлопс при использовании схемы 5 -го порядка, в то время как для схемы 3 -го порядка производительность вычислений составляет 60 ГФлопс (фиг. 12а). При этом производительность вычислений для сеток с шестигранными и призматическими ячейками оказывается существенно ниже, чем для сетки с тетраэдральными ячейками.
Расчеты, выполняемые на GPU, оказываются как минимум в 25 раз быстрее расчетов на CPU (фиг. 12б). Наименьшее ускорение вычислений, равное 26, достигается при использовании сетки с призматическими элементами и схемы 3 -го порядка, а наибольшее ускорение – для сеток с шестигранными и призматическими ячейками при использовании схемы 5 -го порядка (ускорение, достигнутое на этих сетках, различается слабо и составляет около 37).
Ускорение расчетов с двойной точностью на неструктурированных сетках, достигнутое в работе (см. [7]), составляет около 7.4 (расчеты проводились на процессоре Intel Core 2 и платформе Tesla 1060). В [8] достигается ускорение, равное 19.5 (расчеты проводились на процессоре Intel Core 2 Duo с тактовой частотой 3.8 ГГц и видеокарте GeForce GTX 285).
ЗАКЛЮЧЕНИЕ
Рассмотрены подходы к параллельному решению задач вязкой несжимаемой жидкости с использованием графических процессоров общего назначения.
Приведено решение ряда модельных задач, на основе которых сопоставлены ускорение счета на сетках различной разрешающей способности при использовании разных способов разбиения исходных данных на блоки. Для моделирования течений вязкой несжимаемой жидкости применяется схема расщепления по физическим процессам. Уравнение Пуассона для давления решается при помощи метода Гаусса–Зейделя и многосеточного метода. Использование GPU позволяет ускорить расчеты в 2–16 раз (в зависимости от постановки задачи и используемых вычислительных алгоритмов).
Список литературы
Owens J.D., Luebke D., Govindaraju N., Harris M., Krűger J., Lefohn A.E., Purcell T.J. A survey of general-purpose computation on graphics hardware // Computer Graphics Forum. 2007. V. 26. № 1. P. 80–113.
Боресков А.В., Харламов А. Основы работы с технологией CUDA. М.: Изд-во ДМК-Пресс, 2010.
Сандерс Дж., Кэндрот Э. Технология CUDA в примерах: введение в программирование графических процессоров. М.: Изд-во ДМК Пресс, 2011.
Волков К.Н., Дерюгин Ю.Н., Емельянов В.Н., Карпенко А.Г., Козелков А.С., Тетерина И.В. Методы ускорения газодинамических расчетов на неструктурированных сетках. М.: Физматлит, 2014.
Горобец А.В., Суков С.А., Железняков А.О., Богданов П.Б., Четверушкин Б.Н. Применение GPU в рамках гибридного двухуровневого распараллеливания MPI+OpenMP на гетерогенных вычислительных системах // Параллельные вычислительные технологии. Челябинск: Издательский центр ЮУрГУ, 2011. С. 452–460.
Волков К.Н., Емельянов В.Н., Карпенко А.Г., Смирнов П.Г., Тетерина И.В. Реализация метода конечных объемов и расчет течений вязкого сжимаемого газа на графических процессорах // Вычислительные методы и программирование. 2013. Т. 14. № 1. С. 183–194.
Corrigan A., Camelli F., Lőhner R., Wallin J. Running unstructured grid-based CFD solvers on modern graphics hardware // AIAA Paper. 2009. P. 2009–4001.
Kampolis I.C., Trompoukis X.S., Asouti V.G., Giannakoglou K.C. CFD-based analysis and two-level aerodynamic optimization on graphics processing units // Computer Methods in Applied Mechanics and Engineering. 2010. V. 199. № 9–12. P. 712–722.
Fu L., Gao Z., Xu K., Xu F. A multi-block viscous flow solver based on GPU parallel methodology // Computers and Fluids. 2014. V. 95. P. 19–39.
Krotkiewski M., Dabrowski M. Efficient 3D stencil computations using CUDA // Parallel Computing. 2013. V. 39. № 10. P. 533–548.
Meng J., Skadron K. A performance study for iterative stencil loops on GPUs with ghost zone optimizations // Int. J. Parallel Program. 2011. V. 39. № 1. P. 115–142.
Jacobsen D.A., Senocak I. Multi-level parallelism for incompressible flow computations on GPU clusters // Parallel Computing. 2013. V. 39. № 1. P. 1–20.
Tuttafesta M., Colonna G., Pascazio G. Computing unsteady compressible flows using Roe’s flux-difference splitting scheme on GPUs // Comput. Phys. Commun. 2013. V. 184. № 6. P. 1497–1510.
Chorin A.J. Numerical solution of Navier–Stokes equations // Mathematics of Computation. 1968. V. 22. № 104. P. 745–762.
Белоцерковский О.М. Численное моделирование в механике сплошных сред. М.: Физматлит, 1994.
Волков К.Н. Реализация схемы расщепления на разнесенной сетке для расчета нестационарных течений вязкой несжимаемой жидкости // Вычислительные методы и программирование. 2005. Т. 6. № 1. С. 269–282.
Thibault J.C., Senocak I. CUDA implementation of a Navier–Stokes solver on multi-GPU desktop platforms for incompressible flows // AIAA Paper. 2009. P. 2009–758.
Волков К.Н., Емельянов В.Н. Моделирование крупных вихрей в расчетах турбулентных течений. М.: Физматлит, 2008.
Управление обтеканием тел с вихревыми ячейками в приложении к летательным аппаратам интегральной компоновки (численное и физическое моделирование) / Под ред. А.В. Ермишина и С.А. Исаева. М.: Изд-во МГУ, 2001.
Волков К.Н., Емельянов В.Н., Тетерина И.В., Яковчук М.С. Визуализация вихревых течений в вычислительной газовой динамике // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 8. С. 1374–1391.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики