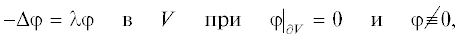Журнал вычислительной математики и математической физики, 2019, T. 59, № 10, стр. 1803-1814

О гладкой вихревой катастрофе единственности стационарных течений идеальной жидкости

О. В. Трошкин^*

ФГУ ФНЦ НИИСИ РАН
117218 Москва, Нахимовский пр-т, 36, кор. 1, Россия

Поступила в редакцию 08.11.2018
После доработки 08.11.2018
Принята к публикации 10.06.2019

DOI: 10.1134/S0044466919100132

Аннотация

Известно, что установившееся во времени и разложимое в степенной ряд по пространственным координатам, т.е. аналитическое, а значит, точно вычисляемое стационарное плоскопараллельное или осесимметричное течение идеальной несжимаемой жидкости на конечном отрезке длины плоского канала или трубы однозначно определяется заданием завихренности на участке втекания. Не вычисляемых же фантомов, т.е. бесконечно гладких, но не аналитических течений, при тех же граничных условиях, оказывается как угодно много, если в области единственного аналитического течения присутствует достаточно мощная вихревая камера, где нарушается принцип максимума для надлежащей функции тока. В работе детализируется схема получения невычисляемого вихревого фантома для гидродинамических уравнений Эйлера. Библ. 32. Фиг. 2.

Ключевые слова: cтационарная идеальная несжимаемая жидкость, конечный плоский или осесимметричный канал, завихренность на участке втекания, единственное аналитическое течение, нарушение принципа максимума, неединственность гладких неаналитических течений.

1. ВЫЧИСЛЯЕМАЯ ВИХРЕВАЯ ТРУБКА

Как и обычно, в пространстве декартовых ортогональных орт ${\mathbf{i}},{\mathbf{j}},{\mathbf{k}}$ и координатах $x,y,z$, вводимых одновременно с винтом ($ \times $), метрикой ($ \cdot $) и градиентом $\nabla $ как

${\mathbf{i}} = {\mathbf{j}} \times {\mathbf{k}},\quad {\mathbf{j}} = {\mathbf{k}} \times {\mathbf{i}},\quad {\mathbf{k}} = {\mathbf{i}} \times {\mathbf{j}},\quad {\mathbf{i}} \cdot {\mathbf{i}} = {\mathbf{j}} \cdot {\mathbf{j}} = {\mathbf{k}} \cdot {\mathbf{k}} = 1\quad {\text{и}}\quad \nabla = {\mathbf{i}}{{\partial }_{x}} + {\mathbf{j}}{{\partial }_{y}} + {\mathbf{k}}{{\partial }_{z}},$

обратимся к двумерной несжимаемой, с постоянной массовой плотностью $\rho > 0$, идеальной (невязкой) сплошной среде, частицы, или точки которой, ${\mathbf{r}} = x{\mathbf{i}} + y{\mathbf{j}}$, испытывают действие $ - \nabla p$ удельного (отнесенного к $\rho $) молекулярного давления $p\left( {x,y} \right)$. Пусть к этим точкам приложено и стационарное удельное поле массовых сил ${\mathbf{g}} = - \nabla G$, с гладким (бесконечно дифференцируемым) потенциалом $G\left( {x,y} \right)$.

Как предполагается [1]–[3], если с течением времени $t$ в такой среде и установится стационарное гладкое поле скоростей, или течение ${\mathbf{u}} = u{\mathbf{i}} + v{\mathbf{j}}$, то последнее необходимо будет эйлеровым полем, обнаруживая потенциал $p + G$ у конвективного ускорения ${\mathbf{u}} \cdot \nabla {\mathbf{u}}$, т.е. разрешая вместе с $p$ стационарные гидродинамические уравнения Эйлера,

${\mathbf{u}} \cdot \nabla {\mathbf{u}} = - \nabla \left( {p + G} \right)\quad {\text{и}}\quad \nabla \cdot {\mathbf{u}} = 0\quad ({\text{или}}\;\;~{{\rho }_{t}} + \nabla \cdot \rho {\mathbf{u}} = 0\;\;{\text{для}}\;\;\rho = 1).$

Примечательной особенностью рассматриваемой среды оказывается при этом то обстоятельство, что удельной силой другого потенциала $\gamma + G$, с интегралом Бернулли

$\gamma = p + \frac{{{\mathbf{u}} \cdot {\mathbf{u}}}}{2},$

и тождествами Громеки–Лэмба [4], [5],

${\mathbf{u}} \times \nabla \times {\mathbf{u}} = \nabla \frac{{{\mathbf{u}} \cdot {\mathbf{u}}}}{2} - {\mathbf{u}} \cdot \nabla {\mathbf{u}},$

или

$u{{u}_{x}} + v{{u}_{y}} = {{\left( {\frac{{{{u}^{2}} + {{v}^{2}}}}{2}} \right)}_{x}} - v({{v}_{x}} - {{u}_{y}})\quad {\text{и}}\quad u{{v}_{x}} + v{{v}_{y}} = {{\left( {\frac{{{{u}^{2}} + {{v}^{2}}}}{2}} \right)}_{y}} + u({{v}_{x}} - {{u}_{y}}),$

в этой среде уравновешивается и передаваемое частице ${\mathbf{r}}$ вектором завихренности

${\mathbf{\omega }} = \nabla \times {\mathbf{u}} = \omega {\mathbf{k}},\quad \omega = {{v}_{x}} - {{u}_{y}}\quad ({\mathbf{u}} = u{\mathbf{i}} + v{\mathbf{j}},\;\;{{u}_{z}} = {{v}_{z}} = 0),$

вихревое ускорение

(1)

${\mathbf{\omega }} \times {\mathbf{u}} = - \nabla (\gamma + G),\quad \nabla \times {\mathbf{u}} = {\mathbf{\omega }}\quad {\text{и}}\quad \nabla \cdot {\mathbf{u}} = 0,$

или

$ - v\omega + {{(\gamma + G)}_{x}} = u\omega + {{(\gamma + G)}_{y}} = {{v}_{x}} - {{u}_{y}} - \omega = {{u}_{x}} + {{v}_{y}} = 0\quad {\text{в}}\quad V.$

Далее, в односвязной области $V$ $x,y$-плоскости, с кусочно-гладкой границей $\partial V$ и компактным (ограниченным) замыканием $\bar {V} = V + \partial V$, где всякий цикл (или простая замкнутая кривая) стягивается в точку, с точностью до произвольной аддитивной постоянной, однозначно определен удельный секундный массовый расход $\psi $ течения ${\mathbf{u}}$ на единицу площади [6],

${\mathbf{u}} = u{\mathbf{i}} + v{\mathbf{j}} = {{\psi }_{y}}{\mathbf{i}} - {{\psi }_{x}}{\mathbf{j}}\quad {\text{в}}\quad \bar {V} = V + \partial V,$

или функция тока $\psi $ поля ${\mathbf{u}}$.

В этом случае эйлеровость (1) течения ${\mathbf{u}}$ сводится к равносильной (1) вихревой системе

(2)

$ - {{\psi }_{{xx}}} - {{\psi }_{{yy}}} = - \Delta \psi = \omega \quad {\text{в}}\quad V\quad {\text{и}}\quad {{\psi }_{y}}{{\omega }_{x}} - {{\psi }_{x}}{{\omega }_{y}} = u{{\omega }_{x}} + v{{\omega }_{y}} = 0\quad {\text{в}}\quad \bar {V},$

исключающей из рассмотрения давление $p$, но предполагающей наличие его в приведенной дифференциальной зависимости расхода $\psi $ и завихренности $\omega $. Последняя рассматривается всюду в односвязной области течения $V$, включая и ее предельные (граничные) точки, и обеспечивается функциональной зависимостью вида

$\omega = \mu \left( \psi \right),\quad a = \mathop {\min }\limits_{\partial V} \psi \leqslant \psi \leqslant \mathop {\max }\limits_{\partial V} \psi = b,$

с произвольным гладким либо единственным аналитическим продолжением последней с исходного граничного отрезка $a \leqslant \psi \leqslant b$ на все допустимые значения $ - \infty < \psi < \infty $ расхода $\psi $, называемым обычно приводимостью $\mu \left( \psi \right)$ эйлерова поля ${\mathbf{u}}$ [7].

И тогда, в силу того же основного закона (1), или (2), при сохранении в целом массы перемешиваемой жидкости и заданной единичной внешней нормали ${\mathbf{n}}$, ${\mathbf{n}} \cdot {\mathbf{n}} = 1$, на гладком участке границы $\partial V$, приводимость естественно определять втекающей, ${\mathbf{u}} \cdot {\mathbf{n}} < 0$ ($ + $), или вытекающей, ${\mathbf{u}} \cdot {\mathbf{n}} > 0$ ($ - $), завихренностью, ${{\omega }^{ + }}$ или ${{\omega }^{ - }}$, заданной в граничных точках, где начинается либо заканчивается лежащая в области течения $V$ линия тока, как в стационарной задаче о протекании [8],

(3)

${{\left. \omega \right|}_{{\partial {{V}^{{ + \left( - \right)}}}}}} = {{\omega }^{{ + \left( - \right)}}}\quad {\text{для}}\quad \partial {{V}^{ \pm }} = {{\left. {\partial V} \right|}_{{ \pm {\mathbf{u}} \cdot {\mathbf{n}} < 0}}}\quad {\text{при}}\quad \int\limits_{\partial V} { - vdx + udy} = 0.$

Простейшей аналитической приводимостью оказывается при этом тождественная постоянная ${{\omega }^{ + }}$ (или ${{\omega }^{ - }}$), заданная на единственном участке втекания $\partial {{V}^{ + }}$ (вытекания $\partial {{V}^{ - }}$), как в нижеследующей задаче о простом протекании в плоском канале $V$ конечных длины $2l$ и ширины $h$, т.е. в прямоугольнике

(4)

$V = \left\{ {\left| x \right| < l,\;0 < y < h} \right\}\quad {\text{при}}\quad {{\left. u \right|}_{{y = 0,h}}} = 0,\quad {{\left. u \right|}_{{x = \mp l}}} = U\quad {\text{и}}\quad l,h,U = {\text{const}} > 0,$

где отмеченным участком служит

(5)

$\partial {{V}^{ \pm }} = {{\left. {\partial V} \right|}_{{ \pm u > 0}}} = {{\left. {\partial V} \right|}_{{x = \mp l}}}\quad {\text{при}}\quad {{\omega }^{ \pm }} = \mu \left( \psi \right) = \Omega ,\quad - {\kern 1pt} \infty < \Omega = {\text{const}} < \infty .$

И если теперь ограничиться эйлеровыми полями, исследуемыми, вслед за первым вычислителем-гиродинамиком [1], в классе $C{\kern 1pt} * = C{\kern 1pt} {\text{*}}(\bar {V})$ точно вычисляемых, или аналитических расходов $\psi \left( {x,y} \right)$, как разложимых в сходящиеся степенные ряды, или бесконечные суммы пропорций степеней ${{\left( {x - {{x}_{0}}} \right)}^{m}}{{\left( {y - {{y}_{0}}} \right)}^{n}}$, $m,n = 0,1,2,\;...$, приращений $x - {{x}_{0}}$ и $y - {{y}_{0}}$ пространственных координат $x$ и $y$ из фиксированных окрестностей точек ${{x}_{0}},{{y}_{0}}$ замыкания $\bar {V}$, то можно утверждать, что и в общем случае [8], и в примере (4), (5) рассматриваемая в $C{\kern 1pt} {\text{*}}$ плоская стационарная задача о протекании (3) для уравнений Эйлера (1), или (2), в ограниченной односвязной области $V$ сводится к аналитической приводимости $\omega = \mu \left( \psi \right)$, $ - \infty < \psi < \infty $, однозначно определяемой втекающей или вытекающей завихренностью, с вычисляемым расходом $\psi = {{\psi }_{ * }}$, как аналитическим решением нелинейной задачи Дирихле

$ - \Delta \psi = \mu \left( \psi \right)\quad {\text{в}}\quad V\quad {\text{и}}\quad {{\left. \psi \right|}_{{\partial V}}} = {{\left. \Phi \right|}_{{\partial V}}}\quad {\text{при}}\quad \Delta \Phi = 0\quad {\text{в}}\quad V,$

получаемым простым наложением $\Phi + \varphi $ на потенциальное течение, с гармоническим расходом $\Phi \in C{\text{*}}$, вихря, с аналитическим расходом $\varphi \in C{\text{*}}$ на твердых стенках,

$ - \Delta \varphi = \mu \left( \psi \right)\quad {\text{в}}\quad V\quad {\text{и}}\quad {{\left. \varphi \right|}_{{\partial V}}} = 0\quad {\text{при}}\quad \psi = \Phi + \varphi .$

Например, в простом протекании (1), (4), (5), или (2), (4), (5), с главным фактором (aspect ratio) $\alpha = {h \mathord{\left/ {\vphantom {h l}} \right. \kern-0em} l} > 0$ и уровнем завихренности $ - \infty < \beta = {{\Omega h} \mathord{\left/ {\vphantom {{\Omega h} U}} \right. \kern-0em} U} < \infty $, искомое наложение $\psi = {{\psi }_{ * }} = \Phi + \varphi \in С{\kern 1pt} {\text{*}}$,

(6)

$ - \Delta {{\psi }_{ * }} = \mu ({{\psi }_{ * }}) = \Omega \quad {\text{в}}\quad V\quad {\text{при}}\quad {{\left. {{{\psi }_{ * }}} \right|}_{{\partial V}}} = {{\left. \Phi \right|}_{{\partial V}}}\quad {\text{и}}\quad - {\kern 1pt} \Delta \Phi = 0\quad {\text{в}}\quad V,$

слагают расходы потенциального течения $\Phi \in С{\text{*}}$ и однородного вычисляемого вихря $\varphi = {{\psi }_{ * }} - \Phi \in С{\kern 1pt} {\text{*}}$ вида

$\Phi = Yb,\quad b = Uh,\quad {\text{и}}\quad \varphi = \beta b\chi \left( {\alpha ,Y,Z} \right)\quad {\text{при}}\quad 0 \leqslant Y = \frac{y}{h} \leqslant 1\quad {\text{и}}\quad \left| {Z = \frac{x}{h}} \right| \leqslant \frac{1}{\alpha },$

для

$ - {{\chi }_{{YY}}} - {{\chi }_{{ZZ}}} = 1\quad {\text{при}}\quad 0 < Y < 1\quad {\text{и}}\quad \left| {Z = \frac{x}{h}} \right| < \frac{1}{\alpha }\quad {\text{для}}\quad {{\left. \chi \right|}_{{\left| Z \right| = \frac{1}{\alpha }}}} = {{\left. \chi \right|}_{{X = 0,1}}} = 0.$

Надлежащие топологические конструкции [8] при этом позволяют усилить и классический принцип максимума

$0 = a = \mathop {\min }\limits_{\partial V} \Phi \leqslant {{\left. \psi \right|}_{{\beta = 0}}} = \Phi \leqslant Uh = \mathop {\max }\limits_{\partial V} \Phi = b,\quad \psi = b\left( {Y + \beta \chi } \right),$

и связанную с ним лемму о нормальной производной [9],

${{\left. {{{\chi }_{Y}}} \right|}_{{Y = 0,{\text{ }}Z = 0}}} = \frac{1}{{{{\beta }_{ - }}\left( \alpha \right)}} > 0,\quad {{\left. {{{\chi }_{Y}}} \right|}_{{Y = 1,{\text{ }}Z = 0}}} = - \frac{1}{{{{\beta }_{ + }}\left( \alpha \right)}} < 0,$

доставляющую совпадающие здесь критические значения ${{\beta }_{ - }}\left( \alpha \right) = {{\beta }_{ + }}\left( \alpha \right) > 0$ параметра $\beta $, следующей выпуклостью одиночного вихря,

${{\chi }_{{YY,{\text{ }}ZZ}}}\left( {\alpha ,Y, - Z} \right) = {{\chi }_{{YY,{\text{ }}ZZ}}}\left( {\alpha ,Y,Z} \right) < 0,\quad \alpha > 0.$

Последняя приводит как к расширению вышеотмеченного принципа,

$a \leqslant \psi \leqslant b\quad {\text{для}}\quad - {\kern 1pt} {{\beta }_{ - }} \leqslant \beta \leqslant {{\beta }_{ + }}\quad {\text{или\;}}\;{\text{для}}\quad \left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) \leqslant 0,$

так и к его нарушению

$\begin{gathered} \psi \left( {0,h{{Y}_{ - }}} \right) < a\quad {\text{для}}\quad \beta < - {{\beta }_{ - }}\quad {\text{или}}\quad \psi \left( {0,h{{Y}_{ + }}} \right) > b\quad {\text{для}}\quad \beta > {{\beta }_{ + }} \\ {\text{или\;}}\;{\text{для}}\quad \left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0, \\ \end{gathered} $

т.е. к бифуркации рождения центра вихря $\left( {{{Y}_{ \mp }},0} \right)$, обеспечиваемой соотношениями

${{\left. {\frac{u}{U}} \right|}_{{y = 0,{\text{ }}x = 0}}} = {{\left. {\frac{{{{\psi }_{Y}}}}{b}} \right|}_{{Y = 0,{\text{ }}Z = 0}}} = \frac{{{{\beta }_{ - }} + \beta }}{{{{\beta }_{ - }}}}\quad {\text{и}}\quad {{\left. {{{{\left. {\frac{u}{U}} \right|}}_{{y = h,{\text{ }}x = 0}}} = \frac{{{{\psi }_{Y}}}}{b}} \right|}_{{Y = 1,{\text{ }}Z = 0}}} = \frac{{{{\beta }_{ + }} - \beta }}{{{{\beta }_{ + }}}},$

и неравенствами $\beta < - {{\beta }_{ - }}$ и $\beta > {{\beta }_{ + }}$, как на фиг. 1, сверху.

Фиг. 1.

Снизу – зеркальные отражения вычисляемых плоских вихрей.

Таким образом, единственность аналитического продолжения постоянной приводимости $\Omega $, единственность классического решения ${{\psi }_{ * }}$ задачи Дирихле (6), бифуркация рождения центра $hZ{\mathbf{i}} + h{{Y}_{ \mp }}{\mathbf{j}}$ при $Z = 0$ и третья координата $ - \infty < z < \infty $ приводят к возникновению в пространстве единственной вычисляемой вихревой трубки, как отвечающей плоскому эйлерову полю ${{{\mathbf{u}}}_{ * }}$ в классе $C{\kern 1pt} {\text{*}}$.

2. ФАНТОМЫ ВИХРЕВОЙ ТРУБКИ

Что же касается невычисляемых течений из более широкого, чем требуется механике [1]–[3], класса ${{C}^{\infty }} = {{C}^{\infty }}(\bar {V})$, к которому приводит математика [10]–[13], то бесконечно гладких, но не аналитических плоскопараллельных эйлеровых полей ${{{\mathbf{u}}}_{\# }}$, порождаемых фантомами, или расходами ${{\psi }_{\# }} \in {{C}^{\# }} = {{C}^{\infty }}{\backslash }C{\kern 1pt} {\text{*}}$, с фиксированной втекающей или вытекающей завихренностью (3), как в (4), (5), при ее значительном уровне, для $\left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0$, т.е. при наличии вихревой трубки, как на фиг. 1, в области единственного аналитического течения ${{{\mathbf{u}}}_{ * }}$, оказывается бесконечно много.

Действительно, задавшись константой ${{\lambda }_{{\min }}} > 0$ вложения Пуанкаре–Стеклова

$\left\langle {{{\varphi }^{2}}} \right\rangle = \int\limits_V {{{\varphi }^{2}}dV} \leqslant \frac{{\left\langle {\varphi _{x}^{2} + \varphi _{y}^{2}} \right\rangle }}{{{{\lambda }_{{\min }}}}}\quad {\text{при}}\quad dV = dxdy\quad {\text{для}}\quad \varphi \in C_{0}^{\infty } = \{ \varphi \in {{C}^{\infty }}:{{\left. \varphi \right|}_{{\partial V}}} = 0\} ,$

как наименьшим собственным числом $\lambda > 0$ спектральной задачи

воспользуемся компактностью Реллиха–Кондрашова [10], [11], или частичной (т.е. при обратимой замене номеров $k,m = 1,2,\;...$ на ${{n}_{k}},{{n}_{m}} \in \left\{ {1,2,\;...} \right\}$) среднеквадратичной сходимостью $\left\langle {{{{\left( {{{\varphi }_{k}} - {{\varphi }_{m}}} \right)}}^{2}}} \right\rangle \to 0$, $k,m \to \infty $, всякой сильно ограниченной, $\left\langle {{{{\left( {{{\varphi }_{n}}_{x}} \right)}}^{2}} + {{{\left( {{{\varphi }_{n}}_{y}} \right)}}^{2}}} \right\rangle \leqslant {\text{const}}$, последовательности ${{\varphi }_{n}} \in C_{0}^{\infty }$, $n = 1,2,\;...$, отыщем число ${{\lambda }_{{\min }}}$, следуя [11], как

${{\lambda }_{{\min }}} = \mathop {\inf }\limits_{\varphi \in C_{0}^{\infty },{\text{ }}\varphi \not\equiv 0} {{\left\langle {\varphi _{x}^{2} + \varphi _{y}^{2}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\varphi _{x}^{2} + \varphi _{y}^{2}} \right\rangle } {\left\langle {{{\varphi }^{2}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{\varphi }^{2}}} \right\rangle }},$

чтобы свести его в канале (4) к знакомой величине

${{\lambda }_{{\min }}} = {{\left( {\frac{\pi }{{2l}}} \right)}^{2}} + {{\left( {\frac{\pi }{h}} \right)}^{2}}\quad {\text{для}}\quad {{\varphi }_{{\min }}}\left( {x,y} \right) = \sin \frac{{\pi \left( {x + l} \right)}}{{2l}}\sin \frac{{\pi y}}{h}.$

Далее, обратимся к бесконечно гладкой срезке Соболева (cutoff) [12], или сглаживателю Фридрихса (mollifier) [13], без предположения о какой-либо симметрии, как в [14], или с симметрией вида

$W = \exp \frac{1}{{1 - {{\tau }^{2}}}} < 1,\quad \tau > 1,\quad {\text{и}}\quad W = 0,\quad 0 \leqslant \tau \leqslant 1,\quad W(\tau ) = - W( - \tau ),\quad \tau \leqslant 0,$

и производными

$0 < W{\kern 1pt} ' = \frac{{2\tau W(\tau )}}{{{{{(1 - {{\tau }^{2}})}}^{2}}}} \leqslant W_{ + }^{'} = W{\kern 1pt} '({{\tau }_{ + }}),\quad \tau > 1,\quad {\kern 1pt} {{\tau }_{ \pm }} = \sqrt {\frac{{\sqrt 7 \pm 2}}{3}} ,\quad {\kern 1pt} 0 < {{\tau }_{ + }} - 1.244421 < {{10}^{{ - 7}}},$

$W''(\tau ) = \frac{{6(\tau _{ + }^{2} - {{\tau }^{2}})(\tau _{ - }^{2} + {{\tau }^{2}})W(\tau )}}{{{{{(1 - {{\tau }^{2}})}}^{4}}}} > ( < )\;0\quad {\text{при}}\quad \tau < ( > )\;{{\tau }_{ + }}\quad ({\kern 1pt} {\text{0}} < {{\tau }_{ - }} - {\text{0}}{\text{.46395}} < {\text{1}}{{{\text{0}}}^{{ - {\text{6}}}}}).$

Относительно константы ${{\lambda }_{{\min }}} > 0$ и наибольшей производной $W_{ + }^{'}$ срезки $W$ определим требуемое ниже произвольное достаточно малое число $\varepsilon $ такое, что

(7)

$0 < \varepsilon < {{\varepsilon }_{ + }} = \frac{{(b - a){{\lambda }_{ + }}}}{{2\left| \Omega \right|{{{W'}}_{ + }}}}\quad {\text{при}}\quad 0 < {{\lambda }_{ + }} = {\text{const}} < {{\lambda }_{{\min }}}.$

Зафиксировав аналитический расход ${{\psi }_{ * }} \in C{\kern 1pt} {\text{*}}$ задачи (6), для указанного $\varepsilon $ возьмем гладкую неаналитическую приводимость

$\eta \left( \psi \right) = \mu \left( \psi \right)\left( {1 + \varepsilon W\left( {\tau \left( \psi \right)} \right)} \right),\quad \tau \left( \psi \right) = \frac{{2\psi - b - a}}{{b - a}}\quad (a = \mathop {\min }\limits_{\partial V} \psi < b = \mathop {\max }\limits_{\partial V} \psi ),$

или

(8)

$\eta \left( \psi \right) = \Omega \left( {1 + \varepsilon W\left( {\tau \left( \psi \right)} \right)} \right)\quad {\text{в}}\;{\text{случае}}\;(4),\;(5),$

которая при наличии вихря у соответствующего течения на фиг. 1, т.е. при $\left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0$, искажает его постоянную завихренность $\Omega $ как

${{\left. W \right|}_{\begin{subarray}{l} a \leqslant \psi \leqslant b \\ (\left| \tau \right| \leqslant 1) \end{subarray} }} = 0,\quad {{\left. {0 < - W} \right|}_{\begin{subarray}{l} \psi < a \\ (\tau < - 1) \end{subarray} }} = {{\left. W \right|}_{\begin{subarray}{l} \psi > b \\ (\tau > 1) \end{subarray} }} < 1,$

$0 < \left( {b - a} \right){{\left. {\left| {{{W}_{\psi }}} \right|} \right|}_{{\psi < a}}} = \left( {b - a} \right){{\left. {\left| {{{W}_{\psi }}} \right|} \right|}_{{\psi > b}}} \leqslant 2W_{ + }^{'}\quad {\text{и}}\quad a = \mathop {\min }\limits_{\partial V} \psi < b = \mathop {\max }\limits_{\partial V} \psi ,$

или как на фиг. 2.

Фиг. 2.

Численно приближаемая с произвольной точностью на любом конечном интервале, но точно невычисляемая приводимость эйлерова поля.

При таком искажении снова рассмотрим граничную задачу (4)–(6), но теперь уже для $\varsigma $ (stigma)–наложения

$\psi = {{\psi }_{ * }} + \varepsilon \Omega \varsigma ,\quad {{\psi }_{ * }} \in C{\kern 1pt} {\text{*,}}\quad \varsigma \in С_{0}^{\# } = \{ \varsigma \in {{C}^{\# }}:{{\left. \varsigma \right|}_{{\partial V}}} = 0\} ,$

вихря однородного фантома $\varepsilon \Omega \varsigma \in С_{0}^{\# }$ (принимающего значение $0$ на твердых стенках границы $\partial V$) на вычисляемое течение расхода ${{\psi }_{ * }}$, продолжив завихренность $\Omega $ с отрезка $a \leqslant \psi \leqslant b$ на прямую $ - \infty < \psi < \infty $ не постоянной зависимостью (8),

$ - \Delta \psi = \Omega + \varepsilon \Omega W\left( {\tau \left( \psi \right)} \right)\quad {\text{в}}\quad V{{\left. {\quad {\text{при}}\quad \psi } \right|}_{{\partial V}}} = {{\left. {{{\psi }_{ * }}} \right|}_{{\partial V}}}\quad {\text{и}}\quad - {\kern 1pt} \Delta {{\psi }_{ * }} = \Omega \quad {\text{в}}\quad V.$

Наконец, обратимся к соответствующей однородной задаче при закритическом уровне завихренности:

(9)

$\begin{gathered} - \Delta \varsigma = f\left( \varsigma \right) = W(\tau ({{\psi }_{ * }} + \varepsilon \Omega \varsigma )),\quad \varsigma > 0\quad {\text{в}}\quad V,\quad {{\left. \varsigma \right|}_{{\partial V}}} = 0,\quad \varsigma \in С_{0}^{\# }, \\ {\text{при}}\quad \left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0 \\ \end{gathered} $

нетривиальное решение которой,

, и доставит нам искомый фантом $\varepsilon \Omega \varsigma \in С_{0}^{\# }$ расхода ${{\psi }_{ * }} + \varepsilon \Omega \varsigma \in {{С}^{\# }}$ вычисляемого вихря ${{\psi }_{ * }}$ на фиг. 1.

Для этого, следуя теории [11], [15], получаем это решение $\varsigma $ сначала, как и обычно [14], [16], т.е. в гильбертовом пополнении выпуклого линейного множества $C_{{0 + }}^{\infty }$ неотрицательных в целом и однородных (удерживающих значение $0$ на твердых стенках) расходов $\xi $, с надлежащей нормой $\sqrt {\left\langle {\varsigma _{x}^{2} + \varsigma _{y}^{2}} \right\rangle } $ суммируемого квадрата $\left\langle {\varsigma _{x}^{2} + \varsigma _{y}^{2}} \right\rangle $ градиента $\nabla \varsigma $,

$C_{{0 + }}^{\infty } = \{ \xi \in C_{0}^{\infty }:{{\left. \xi \right|}_{{\bar {V}}}} \geqslant 0\} ,\quad C_{0}^{\infty } = \{ \xi \in {{C}^{\infty }}:{{\left. \xi \right|}_{{\partial V}}} = 0\} ,\quad \left\langle {\varsigma _{x}^{2} + \varsigma _{y}^{2}} \right\rangle < \infty $

как доставляющее минимум интегралу энергии

$E\left( \xi \right) = \frac{1}{2}\left\langle {\xi _{x}^{2} + \xi _{y}^{2}} \right\rangle - \left\langle {\int\limits_0^\xi {f\left( t \right)dt} } \right\rangle \to \mathop {\inf }\limits_{\xi \in C_{{0 + }}^{\infty }} E = {{\left. {\min E} \right|}_{{\left\langle {\xi _{x}^{2} + \xi _{y}^{2}} \right\rangle < \infty }}} = E\left( \varsigma \right),$

необходимо совпадающее здесь с критической точкой, или нулем дифференциала Фреше [16],

(10)

$\left\langle {E{\kern 1pt} '\left( \varsigma \right)\xi } \right\rangle = \left\langle {{{\xi }_{x}}{{\varsigma }_{x}} + {{\xi }_{y}}{{\varsigma }_{y}}} \right\rangle - \left\langle {\xi f\left( \varsigma \right)} \right\rangle = 0,\quad \xi \in C_{0}^{\infty }.$

Наличие минимума и обеспечивается [14], [17] выбором (7) параметра $\varepsilon $ задачи (9) и, ввиду оценки

$\left| {{{f}_{\varsigma }}} \right| = \frac{{2\varepsilon \left| \Omega \right|}}{{b - a}}\left| {W{\kern 1pt} '(\tau ({{\psi }_{ * }} + \varepsilon \Omega \varsigma ))} \right| \leqslant \frac{{2\varepsilon \left| \Omega \right|W_{ + }^{'}}}{{b - a}} = {{\lambda }_{ + }} < {{\lambda }_{{\min }}},$

строгой положительной определенностью квадратичной формы повторного дифференциала,

$\left\langle {E{\kern 1pt} ''\left( \varsigma \right){{\xi }^{2}}} \right\rangle = \left\langle {\xi _{x}^{2} + \xi _{y}^{2}} \right\rangle - \left\langle {{{f}_{\varsigma }}{{\xi }^{2}}} \right\rangle \geqslant \left\langle {\xi _{x}^{2} + \xi _{y}^{2}} \right\rangle - {{\lambda }_{ + }}\left\langle {{{\xi }^{2}}} \right\rangle \geqslant \frac{{{{\lambda }_{{\min }}} - {{\lambda }_{ + }}}}{{{{\lambda }_{{\min }}}}}\left\langle {\xi _{x}^{2} + \xi _{y}^{2}} \right\rangle .$

Приграничные оценки [18] для надлежащих норм обобщенных производных полученного нетривиального решения $\varsigma $ задачи (9) завершают рассуждения, обеспечивая требуемое включение $\varsigma $ в класс $C_{0}^{\# }$:

$\left\langle {{{\xi }_{x}}{{\varsigma }_{x}} + {{\xi }_{y}}{{\varsigma }_{y}}} \right\rangle = - \left\langle {\xi \Delta \varsigma } \right\rangle \quad {\text{при}}\quad \xi \in C_{0}^{\infty },~\quad {\text{т}}{\text{.е}}{\text{.}}\;(10)\;{\text{влечет}}\;(9).$

3. ВЫЧИСЛЯЕМОЕ ВИХРЕВОЕ КОЛЬЦО

В цилиндрических, или полярных координатах

$z,r = \sqrt {{{x}^{2}} + {{y}^{2}}} \quad {\text{и}}\quad \theta = {\text{arctg}}\frac{y}{x},\quad {\text{при}}\quad x = r\cos \theta \quad {\text{и}}\quad y = r\sin \theta ,$

и ортах ${\mathbf{k}}$,

${\mathbf{I}} = {\mathbf{I}}\left( \theta \right) = {\mathbf{i}}\cos \theta + {\mathbf{j}}\sin \theta \quad {\text{и}}\quad {\mathbf{J}} = {\mathbf{J}}\left( \theta \right) = {\mathbf{j}}\cos \theta - {\mathbf{i}}\sin \theta $

как и радиус-вектор

${\mathbf{r}} = x{\mathbf{i}} + y{\mathbf{j}} + z{\mathbf{k}} = z{\mathbf{k}} + r{\mathbf{I}}\left( \theta \right)\quad {\text{при}}\quad {{{\mathbf{I}}}_{\theta }} = {\mathbf{J}}\quad {\text{и}}\quad {{{\mathbf{J}}}_{\theta }} = - {\mathbf{I}}\quad ({{\partial }_{\theta }} = {\partial \mathord{\left/ {\vphantom {\partial {\partial \theta }}} \right. \kern-0em} {\partial \theta }}),$

зависящих от полярного угла $ - \infty < \theta < \infty $, но при этом обратимых,

${\mathbf{i}} = {\mathbf{I}}\cos \theta - {\mathbf{J}}\sin \theta \quad {\text{и}}\quad {\mathbf{j}} = {\mathbf{J}}\cos \theta + {\mathbf{I}}\sin \theta ,$

и сохраняющих свойства исходного ортогонального базиса ${\mathbf{i}},{\mathbf{j}},{\mathbf{k}}$,

${\mathbf{I}} = {\mathbf{J}} \times {\mathbf{k}},\quad {\mathbf{J}} = {\mathbf{k}} \times {\mathbf{I}},\quad {\mathbf{k}} = {\mathbf{I}} \times {\mathbf{J}}\quad {\text{и}}\quad \left| {\mathbf{I}} \right| = \left| {\mathbf{J}} \right| = \left| {\mathbf{k}} \right| = \sqrt {{\mathbf{k}} \cdot {\mathbf{k}}} = 1,$

обратимы и полярные компоненты градиента

$\nabla = {\mathbf{k}}{{\partial }_{z}} + {\mathbf{I}}{{\partial }_{r}} + {\mathbf{J}}\frac{{{{\partial }_{\theta }}}}{r},\quad {{\partial }_{r}} = \cos \theta {{\partial }_{x}} + \sin \theta {{\partial }_{y}}\quad {\text{и}}\quad \frac{{{{\partial }_{\theta }}}}{r} = \cos \theta {{\partial }_{y}} - \sin \theta {{\partial }_{y}},$

как

${{\partial }_{x}} = \cos \theta {{\partial }_{r}} - \frac{{\sin \theta }}{r}{{\partial }_{\theta }}\quad {\text{и}}\quad {{\partial }_{y}} = \sin \theta {{\partial }_{r}} + \frac{{\cos \theta }}{r}{{\partial }_{\theta }},$

и такие же составляющие винтового (swirling) течения

${\mathbf{u}} = w{\mathbf{k}} + \hat {u}{\mathbf{I}} + \hat {v}{\mathbf{J}},\quad \hat {v} = r\hat {\omega },\quad r > 0\quad {\text{и}}\quad {{{\mathbf{u}}}_{\theta }} = \hat {u}{{{\mathbf{I}}}_{\theta }} + \hat {v}{{{\mathbf{J}}}_{\theta }} = \hat {u}{\mathbf{J}} - \hat {v}{\mathbf{I}} = {\mathbf{k}} \times {\mathbf{u}}$

закручиваемого вокруг оси $r = 0$ с линейной скоростью $\hat {v} = r{{\theta }_{t}}$ и угловой скоростью $\hat {\omega }$ при осевой и радиальной линейных скоростях $w = {{z}_{t}}$ и $\hat {u} = {{r}_{t}}$, как и закрутка $\hat {v}$ (swirl), не зависящих от полярного угла $\theta $, т.е. при осевой симметрии

${{\varphi }_{\theta }} = 0\quad {\text{для}}\quad \varphi = p,\hat {u},\hat {v},w,\quad {\mathbf{g}} = - \nabla G,$

касающейся и молекулярного давления $p$, и приложенной к частице (точке) ${\mathbf{r}}$ удельной внешней (массовой) силы ${\mathbf{g}}$.

При этом лапласиан

$\Delta = \nabla \cdot \nabla = {{\partial }_{z}}{{\partial }_{z}} + {{\partial }_{x}}{{\partial }_{x}} + {{\partial }_{y}}{{\partial }_{y}},\quad {{\partial }_{\theta }} = 0,$

может принимать полярную, азимутальную и потоковую формы

$\dot {\Delta } = {{\partial }_{z}}{{\partial }_{z}} + \frac{{{{\partial }_{r}}r{{\partial }_{r}}}}{r},\quad L = {{\partial }_{z}}{{\partial }_{z}} + \frac{{{{\partial }_{r}}{{r}^{3}}{{\partial }_{r}}}}{{{{r}^{3}}}}\quad {\text{и}}\quad \Lambda = {{\partial }_{z}}{{\partial }_{z}} + r{{\partial }_{r}}\frac{{{{\partial }_{r}}}}{r},$

связанные непосредственно проверяемыми тождествами

$\frac{{\Lambda {{r}^{2}}\varphi }}{r} = rL\varphi = \frac{{\dot {\Delta }r\varphi }}{r} - \frac{\varphi }{r}.$

Тогда для интеграла Бернулли

$\gamma = p + \frac{{{\mathbf{u}} \cdot {\mathbf{u}}}}{2} = \hat {\gamma } + \frac{1}{2}{{\hat {v}}^{2}},\quad \hat {\gamma } = p + \frac{1}{2}({{w}^{2}} + {{u}^{2}}),\quad \nabla (\gamma + G) = {\mathbf{k}}{{(\gamma + G)}_{z}} + {\mathbf{I}}{{(\gamma + G)}_{r}},$

и передаваемого частице ${\mathbf{r}}$ закруткой $\hat {v}$ и азимутальной завихренностью ${{\hat {u}}_{z}} - {{w}_{r}}$, или вектором завихренности

${\mathbf{\omega }} = \nabla \times {\mathbf{u}} = \frac{{{{{\left( {r\hat {v}} \right)}}_{r}}}}{r}{\mathbf{k}} - {{\hat {v}}_{z}}{\mathbf{I}} + \omega {\mathbf{J}},\quad \omega = {{\hat {u}}_{z}} - {{w}_{r}},$

вихревого ускорения

${\mathbf{\omega }} \times {\mathbf{u}} = \left( { - {{{\hat {v}}}_{z}}\hat {v} - \omega \hat {u}} \right){\mathbf{k}} + \left( {\omega w - \frac{{{{{\left( {r\hat {v}} \right)}}_{r}}}}{r}\hat {v}} \right){\mathbf{I}} + \left( {\frac{{{{{\left( {r\hat {v}} \right)}}_{r}}}}{r}\hat {u} + {{{\hat {v}}}_{z}}w} \right){\mathbf{J}} = - \nabla \left( {\hat {\gamma } + \frac{{{{{\hat {v}}}^{2}}}}{2} + G} \right)$

динамическое равновесие (1) принимает вид

(11)

$ - \hat {u}\omega + {{\left( {\hat {\gamma } + G} \right)}_{z}} = w\omega - \frac{{{{{\hat {v}}}^{2}}}}{r} + {{\left( {\hat {\gamma } + G} \right)}_{r}} = w{{\hat {v}}_{z}} + \hat {u}\frac{{{{{\left( {r\hat {v}} \right)}}_{r}}}}{r} = {{w}_{z}} + \frac{{{{{\left( {r\hat {u}} \right)}}_{r}}}}{r} = 0.$

В односвязной области $V$ азимутальной плоскости переменных $ - \infty < z < \infty $ и $r > 0$, при отсутствии закрутки (swirl), $\hat {v} = 0$, для ядра (whorl) $\bar {\psi } = {\psi \mathord{\left/ {\vphantom {\psi {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}}$ расхода $\psi $ и вихря, или керлинга (curl) $\bar {\omega } = {\omega \mathord{\left/ {\vphantom {\omega r}} \right. \kern-0em} r}$ азимутальной завихренности $\omega $ [19], [20], т.е. при

$\hat {v} = 0,\quad r{\mathbf{u}} = {{\psi }_{r}}{\mathbf{k}} - {{\psi }_{z}}{\mathbf{I}},\quad \psi = {{r}^{2}}\bar {\psi }\quad {\text{и}}\quad \bar {\omega } = {\omega \mathord{\left/ {\vphantom {\omega r}} \right. \kern-0em} r},$

равновесие (11) сводится к потоковой форме уравнения Лапласа $\Lambda \psi = - r\omega $ для расхода $\psi $ в зависимости от радиальной пропорции $r\omega $ завихренности $\omega $, или к равносильной азимутальной форме $L\bar {\psi } = - \bar {\omega }$ для ядра $\bar {\psi }$ расхода $\psi $, и дифференциальной зависимости расхода $\psi $ и вихря $\bar {\omega }$, т.е. к уравнениям [8], [19], [20],

$ - \Lambda \psi = r\omega = {{r}^{2}}\bar {\omega } = - {{r}^{2}}L\bar {\psi }\quad {\text{и}}\quad \left[ {\psi ,\bar {\omega }} \right] = {{\psi }_{r}}\frac{{{{\omega }_{z}}}}{r} - {{\psi }_{z}}{{\left( {\frac{\omega }{r}} \right)}_{r}} = {{\left( {w\omega } \right)}_{z}} + {{\left( {\hat {u}\omega } \right)}_{r}} = 0,$

или к аналогичной (2) полярной вихревой системе

(12)

$\frac{{\Lambda \psi }}{r} + \omega = \left[ {\psi ,\bar {\omega }} \right] = \hat {v} = 0\quad {\text{при}}\quad \psi = {{r}^{2}}\bar {\psi }\quad {\text{и}}\quad \omega = r\bar {\omega }\quad {\text{в}}\quad V.$

Как и вихревая система (2), последняя тоже однозначно разрешима в классе $C{\text{*}}$ [8] при втекающей или вытекающей завихренности,

${{\left. \omega \right|}_{{\partial {{V}^{{ + \left( - \right)}}}}}} = {{\omega }^{{ + \left( - \right)}}} = r{{\bar {\omega }}^{ \pm }}\quad {\text{для}}\quad \partial {{V}^{ \pm }} = {{\left. {\partial V} \right|}_{{ \pm {\mathbf{u}} \cdot {\mathbf{n}} > 0}}}\quad {\text{при}}\quad \int\limits_{\partial V} { - r\hat {u}dz + rwdr} = 0$

в задаче о простом протекании в прямоугольнике $V$ на $z,r$-плоскости, или в трубе длины $2l$ и радиуса $h$,

(13)

$V = \left\{ {\left| z \right| < l,\;0 < r < h} \right\}\quad {\text{при}}\quad {{\left. w \right|}_{{r = 0,h}}} = 0,\quad {{\left. w \right|}_{{z = \mp l}}} = U\quad (l,h,U = {\text{const}} > 0),$

где участками втекания ($ + $) и вытекания ($ - $) служат те же отрезки задания завихренности, что и в плоской задаче (4), (5),

(14)

$\partial {{V}^{ \pm }} = {{\left. {\partial V} \right|}_{{ \pm u > 0}}} = {{\left. {\partial V} \right|}_{{z = \mp l}}}\quad {\text{при}}\quad \frac{{{{\omega }^{ \pm }}}}{r} = {{\bar {\omega }}^{ \pm }} = \mu \left( \psi \right) = \frac{\Omega }{h}\quad (r > 0,\;\Omega = {\text{const}})$

и где рассматриваемая пространственная задача об осе-симметричном протекании без закрутки (12)–(14) в ограниченной односвязной области $V$ азимутальной $z,r$-плоскости сводится к аналитической приводимости $\bar {\omega } = \mu \left( \psi \right)$, $ - \infty < \psi < \infty $, с однозначным вычисляемым расходом $\psi = {{\psi }_{ * }}$, определяемым единственным решением задачи Дирихле для лапласиана $\Lambda $ [8],

$ - \Lambda \psi = {{r}^{2}}\mu \left( \psi \right)\quad {\text{в}}\quad V\quad {\text{и}}\quad {{\left. \psi \right|}_{{\partial V}}} = {{\left. \Phi \right|}_{{\partial V}}}\quad {\text{при}}\quad \Lambda \Phi = {{\Phi }_{{zz}}} + r{{\left( {\frac{{{{\Phi }_{r}}}}{r}} \right)}_{r}} = 0\quad {\text{в}}\quad V,$

получаемым наложением $\Phi + \varphi $ на потенциальное течение, с гармоническим расходом $\Phi \in C{\kern 1pt} {\text{*}}$, вихря, с аналитическим расходом $\varphi \in C{\kern 1pt} {\text{*}}$ при непротекаемых твердых стенках,

$ - \Lambda \varphi = {{r}^{2}}\mu \left( \psi \right)\quad {\text{в}}\quad V\quad {\text{и}}\quad {{\left. \varphi \right|}_{{\partial V}}} = 0\quad {\text{для}}\quad \psi = \Phi + \varphi .$

Действительно, в простом протекании (12)–(14), с прежними главным фактором $\alpha = {h \mathord{\left/ {\vphantom {h l}} \right. \kern-0em} l} > 0$ и двукратно увеличенным уровнем завихренности $ - \infty < \beta = {{2\Omega h} \mathord{\left/ {\vphantom {{2\Omega h} U}} \right. \kern-0em} U} < \infty $, наложение

(15)

$\psi = {{\psi }_{ * }} = \Phi + \varphi \in С{\kern 1pt} {\text{*}},\quad - {\kern 1pt} \Lambda \psi = {{r}^{2}}\frac{\Omega }{h}\quad {\text{и}}\quad \Lambda \Phi = 0\quad {\text{в}}\quad V\quad {\text{при}}\quad {{\left. \psi \right|}_{{\partial V}}} = {{\left. \Phi \right|}_{{\partial V}}},$

слагают потенциальный и однородный расходы $\Phi \in С{\kern 1pt} {\text{*}}$ и $\varphi = {{\psi }_{ * }} - \Phi \in С{\kern 1pt} {\text{*}}$,

$\Phi = b{{Y}^{2}},\quad b = \frac{{U{{h}^{2}}}}{2},\quad {\text{и}}\quad \varphi = \beta b\chi \left( {\alpha ,Y,Z} \right)\quad {\text{при}}\quad 0 \leqslant Y = \frac{r}{h} \leqslant 1\quad {\text{и}}\quad \left| {Z = \frac{z}{h}} \right| \leqslant \frac{1}{\alpha }$

для

$ - {{\chi }_{{ZZ}}} - Y{{\left( {\frac{{{{\chi }_{Y}}}}{Y}} \right)}_{Y}} = {{Y}^{2}}\quad {\text{при}}\quad 0 < Y < 1,\quad \left| Z \right| < \frac{1}{\alpha }\quad {\text{и}}\quad {{\left. \chi \right|}_{{Y = 0,1}}} = {{\left. \chi \right|}_{{\left| Z \right| = \frac{1}{\alpha }}}} = 0.$

Упомянутые топологические конструкции [8] и здесь допускают требуемые уточнение принципа максимума

$0 = a = \mathop {\min }\limits_{\partial V} \Phi \leqslant {{\left. \psi \right|}_{{\beta = 0}}} = \Phi \leqslant \frac{{U{{h}^{2}}}}{{\text{2}}} = \mathop {\max }\limits_{\partial V} \Phi = b,\quad \psi = b({{Y}^{2}} + \beta \chi ),$

и усиление леммы о нормальной производной [8], [9],

$\mathop {\lim }\limits_{Y \to + 0} {{\left. {\frac{{{{\chi }_{Y}}}}{Y}} \right|}_{{Z = 0}}} = \frac{2}{{{{\beta }_{ - }}(\alpha )}} > 0\quad {\text{и}}\quad {{\left. {{{\chi }_{Y}}} \right|}_{{Y = 1,{\text{ }}Z = 0}}} = - \frac{2}{{{{\beta }_{ + }}(\alpha )}} < 0,$

по-прежнему доставляющей уже несовпадающие здесь критические значения ${{\beta }_{ \mp }}(\alpha ) > 0$ параметра $\beta $, выпуклостью одиночного вихря [8],

${{\chi }_{{YY,{\text{ }}ZZ}}}\left( {\alpha ,Y, - Z} \right) = {{\chi }_{{YY,{\text{ }}ZZ}}}\left( {\alpha ,Y,Z} \right) < 0,\quad \alpha > 0,$

снова приводящей как к расширению отмеченного принципа,

$a \leqslant \psi \leqslant b\quad {\text{для}}\quad - {\kern 1pt} {{\beta }_{ - }} \leqslant \beta \leqslant {{\beta }_{ + }},\quad {\text{или}}\;{\text{при}}\quad \left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) \leqslant 0,$

так и к его нарушению,

$\begin{gathered} \psi \left( {0,h{{Y}_{ - }}} \right) < a\quad {\text{для}}\quad \beta < - {{\beta }_{ - }}\quad {\text{или}}\quad \psi \left( {0,h{{Y}_{ + }}} \right) > b\quad {\text{для}}\quad \beta > {{\beta }_{ + }}, \\ {\text{т}}{\text{.е}}{\text{.}}\;{\text{при}}\quad \left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0, \\ \end{gathered} $

или к бифуркации рождения центра вихря $\left( {{{Y}_{ \mp }},0} \right)$, поскольку

${{\left. {\frac{w}{U}} \right|}_{{Y = Z = 0}}} = \mathop {\lim }\limits_{Y \to + 0} {{\left. {\frac{{{{\psi }_{Y}}}}{{2Yb}}} \right|}_{{Z = 0}}} = \frac{{{{\beta }_{ - }} + \beta }}{{{{\beta }_{ - }}}}\quad {\text{и}}\quad {{\left. {\frac{w}{U}} \right|}_{{y = h,{\text{ }}x = 0}}} = {{\left. {\frac{{{{\psi }_{Y}}}}{{2Yb}}} \right|}_{{Y = 1,{\text{ }}Z = 0}}} = \frac{{{{\beta }_{ + }} - \;\beta }}{{{{\beta }_{ + }}}},$

как на всей (меридиальной) плоскости фиг. 1.

4. ФАНТОМЫ ВИХРЕВОГО КОЛЬЦА

Как и в разд. 2, невычисляемых течений класса ${{C}^{\infty }} = {{C}^{\infty }}\left( {\bar {V}} \right)$, или бесконечно гладких, но не аналитических пространственных эйлеровых полей ${{{\mathbf{u}}}_{\# }}$, без закрутки, $\hat {v} = 0$, отвечающих фантомам, или расходам ${{\psi }_{\# }} \in {{C}^{\# }} = {{C}^{\infty }}{\backslash }C{\kern 1pt} {\text{*}}$ в задаче (12)–(14) о простом протекании в трубе $V$ для равносильных (1) уравнений (12), при фиксированных граничных значениях в (12)–(14) и условии $\left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0$ наличия вихревого кольца, как на меридиальной плоскости фиг. 1, в области единственного вычисляемого, или аналитического течения ${{{\mathbf{u}}}_{ * }}$, оказывается бесконечно много.

Действительно, как и выше в разд. 2, задавшись константой ${{\sigma }_{{\min }}} > 0$ полярного вложения Пуанкаре–Стеклова

$\int_V {r{{\varphi }^{2}}dV} = \left\langle {r{{\varphi }^{2}}} \right\rangle \leqslant \frac{h}{{{{\sigma }_{{\min }}}}}\left\langle {\frac{{\varphi _{z}^{2} + \varphi _{r}^{2}}}{r}} \right\rangle \quad {\text{при}}\quad dV = dzdr\quad {\text{для}}\quad \varphi \in C_{0}^{\infty },$

сравнимой с прежней постоянной ${{\lambda }_{{\min }}} > 0$ очевидной оценкой

т.е. определив наименьшее собственное число $\sigma > 0$ спектральной задачи

(как и прежде, существующее благодаря отмеченной выше компактности Реллиха–Кондрашова), далее, прежнюю срезку $W\left( \tau \right)$, затем произвольную постоянную

$0 < \varepsilon < {{\varepsilon }_{ + }} = \frac{{\left( {b - a} \right){{\sigma }_{ + }}}}{{2\left| \Omega \right|W_{ + }^{'}}}\quad {\text{при}}\quad 0 < {{\sigma }_{ + }} = {\text{const}} < {{\sigma }_{{\min }}},$

и, наконец, аналитический расход ${{\psi }_{ * }} \in C{\kern 1pt} {\text{*}}$ и гладкую неаналитическую приводимость

или

$\eta \left( \psi \right) = \frac{\Omega }{h}\left( {1 + \varepsilon W\left( {\tau \left( \psi \right)} \right)} \right)\quad {\text{для}}\quad (12{\kern 1pt} --{\kern 1pt} 14),$

которая при наличии вихря на фиг. 1, т.е. для $\left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0$, искажает постоянный вихрь ${\Omega \mathord{\left/ {\vphantom {\Omega h}} \right. \kern-0em} h}$ в (14), как на фиг. 2, снова рассмотрим граничную задачу для наложения

вихря однородного фантома $\varepsilon \Omega \varsigma \in С_{0}^{\# }$ на вычисляемое течение расхода ${{\psi }_{ * }}$, исказив при этом ${\Omega \mathord{\left/ {\vphantom {\Omega h}} \right. \kern-0em} h}$ в (15) неаналитической приводимостью,

$ - \frac{{\Lambda \psi }}{r} = r\frac{\Omega }{h} + \varepsilon r\frac{\Omega }{h}W\left( {\tau \left( \psi \right)} \right)\quad {\text{в}}\quad V\quad {\text{при}}\quad {{\left. \psi \right|}_{{\partial V}}} = {{\left. {{{\psi }_{ * }}} \right|}_{{\partial V}}}\quad {\text{и}}\quad - \frac{{\Lambda {{\psi }_{ * }}}}{r} = r\Omega \quad {\text{в}}\quad V,$

обратившись для этого к соответствующей однородной граничной задаче при закритическом уровне завихренности,

(16)

$\begin{gathered} - \frac{{\Lambda \varsigma }}{r} = rf\left( \varsigma \right) = rW\left( {\tau \left( {{{\psi }_{ * }} + \varepsilon \Omega \varsigma } \right)} \right)\quad {\text{и}}\quad \varsigma > 0\quad {\text{в}}\quad V,\quad {{\left. \varsigma \right|}_{{\partial V}}} = 0 \\ {\text{при}}\quad \left( {\beta + {{\beta }_{ - }}} \right)\left( {\beta - {{\beta }_{ + }}} \right) > 0, \\ \end{gathered} $

нетривиальное решение которой,

, снова доставит невычисляемый фантом расхода ${{\psi }_{ * }} + \varepsilon \Omega \varsigma \in {{С}^{\# }}$ вычисляемого вихря ${{\psi }_{ * }} \in С{\kern 1pt} {\text{*}}$ на фиг. 1.

И опять, следуя рассуждениям разд. 2, получим это решение $\varsigma $, сначала в замыкании выпуклого линейного множества $C_{{0 + }}^{\infty } = \{ \xi \in C_{0}^{\infty }:{{\left. \xi \right|}_{{\bar {V}}}} \geqslant 0\} $ гильбертовой нормой

$\sqrt {\left\langle {\frac{{\xi _{z}^{2} + \xi _{r}^{2}}}{r}} \right\rangle } < \infty ,$

как минимизирующее новый интеграл энергии

$E\left( \xi \right) = \frac{1}{2}\left\langle {\frac{{\xi _{z}^{2} + \xi _{r}^{2}}}{r}} \right\rangle - \left\langle {r\int\limits_0^\xi {f\left( t \right)dt} } \right\rangle \to \mathop {\inf }\limits_{\xi \in C_{{0 + }}^{\infty }} E = {{\left. {\min E} \right|}_{{\left\langle {\frac{{\xi _{z}^{2} + \xi _{r}^{2}}}{r}} \right\rangle < \infty }}} = E\left( \varsigma \right),$

и совпадающее с критической точкой, или нулем дифференциала

(17)

$\left\langle {E'\left( \varsigma \right)\xi } \right\rangle = \left\langle {\frac{{{{\xi }_{z}}{{\varsigma }_{z}} + {{\xi }_{r}}{{\varsigma }_{r}}}}{r}} \right\rangle - \left\langle {r\xi f\left( \varsigma \right)} \right\rangle = 0,\quad \xi \in C_{0}^{\infty },$

наличие которой обеспечивается, как и в [14], [17], надлежащим выбором $0 < \varepsilon < {{\varepsilon }_{ + }}$ параметра $\varepsilon $ задачи (16) и строгой положительной определенностью квадратичной формы повторного дифференциала

$\left\langle {E''\left( \varsigma \right){{\xi }^{2}}} \right\rangle = \left\langle {\frac{{\xi _{z}^{2} + \xi _{r}^{2}}}{r}} \right\rangle - \left\langle {r{{f}_{\varsigma }}{{\xi }^{2}}} \right\rangle \geqslant \frac{{{{\sigma }_{{\min }}} - {{\sigma }_{ + }}}}{{{{\sigma }_{{\min }}}}}\left\langle {\frac{{\xi _{z}^{2} + \xi _{r}^{2}}}{r}} \right\rangle .$

Приграничные оценки [18] для надлежащих норм обобщенных производных полученного решения $\varsigma $ и здесь завершают рассуждения, обеспечивая требуемое включение $\varsigma $ в класс $C_{0}^{\infty }$:

$\left\langle {\frac{{{{\xi }_{z}}{{\varsigma }_{z}} + {{\xi }_{r}}{{\varsigma }_{r}}}}{r}} \right\rangle = - \left\langle {\frac{{\xi \Lambda \varsigma }}{r}} \right\rangle \quad {\text{при}}\quad \xi \in C_{0}^{\infty },\quad {\text{т}}{\text{.е}}{\text{.}}\;(17)\;{\text{влечет}}\;(16).$

5. ЗАКЛЮЧЕНИЕ

Выделенные курсивом предложения разд. 1–4 о единственности в $C{\kern 1pt} {\text{*}}$ (разд. 1 и 3) и неединственности в ${{C}^{\infty }}$ (разд. 2 и 4) решений стационарных уравнений Эйлера (1) можно рассматривать как необходимые уточнения известных утверждений об однозначной разрешимости соответствующих нестационарных уравнений

${{{\mathbf{u}}}_{t}} + {\mathbf{\omega }} \times {\mathbf{u}} = - \nabla \left( {\gamma + G\left( {x,y} \right)} \right),\quad \nabla \times {\mathbf{u}} = {\mathbf{\omega }},\quad \nabla \cdot {\mathbf{u}} = 0\quad {\text{и}}\quad \gamma = p + {{{\mathbf{u}} \cdot {\mathbf{u}}} \mathord{\left/ {\vphantom {{{\mathbf{u}} \cdot {\mathbf{u}}} 2}} \right. \kern-0em} 2},$

исходно ориентированных на гладкие, быть может, невычисляемые течения в ограниченной односвязной области $V$ с компактным замыканием $\bar {V}$ при наличии участков втекания $\partial {{V}^{ + }}$, где фиксируется завихренность [21] или давление [22], либо с непроницаемой границей (твердыми стенками) $\partial V$ [23]–[25], либо вовсе без нее ($\partial V = \emptyset $) как на двумерном торе [26]. И тогда действительно возникает затронутая вначале задача об установлении плоского течения идеальной несжимаемой жидкости.

Однако так называемые основные (невозмущенные, стационарные), но нестационарно возмущаемые гладкие эйлеровы поля в этой задаче сводятся к простому протеканию (все линии тока начинаются на одном участке границы, $\partial {{V}^{ + }}$, и заканчиваются на другом, $\partial {{V}^{ - }}$) [27], допуская при этом даже асимптотическую устойчивость [28], но исключая вихри.

Последние все же могут рассматриваться в качестве основных течений для реальной (вязкой) жидкости Ньютона–Навье [29],

${{{\mathbf{u}}}_{t}} - \nu \Delta {\mathbf{u}} + {\mathbf{\omega }} \times {\mathbf{u}} = - \nabla \left( {\gamma + G} \right),\quad \nabla \times {\mathbf{u}} = {\mathbf{\omega }},\quad \nabla \cdot {\mathbf{u}} = 0,\quad \nu = {\text{const}} > 0,$

как в [30], либо для идеальной аналитической среды, как выше, аналогичной первой тем, что в силу теоремы о единственности аналитического продолжения все возмущения в такой среде распространяются не только вдоль траекторий движения частиц как в неаналитической среде, но и трансверсально им как при вязкой диффузии.

Что же касается живых примеров неаналитических вихрей, то простейший вихревой фантом доставляет гладкое невычисляемое возмущение покоящейся плоской среды, или вмороженный вихрь Дезина [31], с расходом

$\begin{gathered} \psi = \psi (f) = \pm \exp \frac{{{{\varepsilon }^{2}}}}{{{{f}^{2}} - {{\varepsilon }^{2}}}}\quad {\text{при}}\quad f = \sqrt {{{{\left( {x - {{x}_{0}}} \right)}}^{2}}{\kern 1pt} - {{{\left( {y - {{y}_{0}}} \right)}}^{2}}} < \varepsilon \\ {\text{и}}\quad \psi = 0\quad {\text{при}}\quad f > \varepsilon = {\text{const}} > 0. \\ \end{gathered} $

В настоящей статье в целом детализированы примыкающие к нему общие теоретико-функциональные конструкции, формально затронутые ранее в работах [8], [14], [32].

Список литературы

Эйлер Л. Общие законы движения жидкостей // Известия РАН. Механ. жидкости и газа. 1999. № 6. С. 26–54.
Бэтчелор Дж. Введение в динамику жидкости. М: Мир, 1973. 760 с.
Лойцянский Л.Г. Механика жидкостей и газов. М.: Наука, 1987. 840 с.
Громека И.С. Некоторые случаи движения несжимаемой жидкости. Казань, 1881. В собр. соч. М.: АН СССР, 1952. 296 с.
Ламб Г. Гидродинамика. М.: Гостехиздат, 1947. 827 с.
Милн-Томсон Л.M. Теоретическая гидродинамика. М.: Мир, 1964. 521 с.
Трошкин О.В. О некоторых свойствах эйлеровских полей // Дифференц. ур-ния. 1982. Т. 18. № 1. С. 138–144.
Трошкин О.В. О топологическом анализе структуры гидродинамических течений // Успехи матем. наук. 1988. Т. 43. Вып. 4(262). С. 129–158.
Ландис Е.М. Уравнения второго порядка эллиптического и параболического типов. М.: Наука, 1971. 287 с.
Rellich F. Ein Satz über mittlere Konvergenz // Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. 1930. P. 30–35.
Соболев С.Л. Некоторые применения функционального анализа в математической физике. М.: Наука, 1988. Изд. 3-е. 337 с.
Соболев С. Об одной теореме функционального анализа // Матем. сб. 1938. Т. 4(46). № 3. С. 471–497.
Friedrichs K.O. The identity of weak and strong extensions of differential operators // Trans. Amer. Math. Soc. 1944. V. 55. P. 132–151.
Трошкин О.В. Двумерная задача о протекании для стационарных уравнений Эйлера // Матем. сб. 1989. Т. 180. № 3. С. 354–374.
Канторович Л.В., Акилов Г.П. Функциональный анализ в нормированных пространствах. М.: Физматгиз, 1959. 684 с.
Экланд И., Темам Р. Выпуклый анализ и вариационные проблемы. М.: Мир, 1979. 399 с.
Трошкин О.В. Допустимость множества граничных значений в одной стационарной гидродинамической задаче // Докл. АН СССР. 1983. Т. 272. № 5. С. 1086–1090.
Агмон С., Дуглис А., Ниренберг Л. Оценки решений эллиптических уравнений вблизи границы. М.: Изд-во иностр. лит., 1962. 208 с.
Fraenkel L.E., Berger M.S. A global theory of steady vortex rings in an ideal fluid // Bulletin of the American Mathematical Society. 1973. V. 79. № 3. P. 806–810. // Acta Math. 1974. V. 132. № 1. P. 13–51.
Moffatt H.K. Generalised vortex rings with and without swirl // Fluid Dynamic Research. 1988. V. 3. P. 22–30.
Юдович В.И. Двумерная нестационарная задача протекания идеальной жидкости через заданную область // Матем. сб. 1964. Т. 64. С. 562–588.
Кажихов А.В., Рагулин В.В. О задаче протекания для уравнений идеальной жидкости // Зап. научн. сем. ЛОМИ. 1980. Т. 96. С. 84–96.
Wolibner W. On theoreme sur l’existence du movement plan d’un fluid parfait, homogene, incompressible, pendant um temps infiniment longue // Math. Z. 1933. V. 37. P. 698–726.
Kato T. On classical solutions of the two dimensional nonstationary Fuler equation // Arch. Rat. Mech. Anal. 1967. V. 25. № 3. P. 188–200.
Glass O. Existence of solutions for the two–dimensional stationary Euler system for ideal fluids with arbitrary force // Ann. I. H. Poincaré. 2003. V. 20. P. 921–946.
Arnold V.I. Sur la geometrie differentielle des groupes de Lie de dimension infinie et ses applications a l’hydrodynamique de fluids parfaits // Ann. Inst. Fourier (Grenoble). 1966. V. 16. P. 319–361.
Алексеев Г.В. О единственности и гладкости плоских вихревых течений идеальной жидкости // Динамика сплошной среды. Сб. Новосибирск. 1973. Вып. 15. С. 7–17.
Моргулис А.Б., Юдович В.И. Асимптотическая устойчивость стационарного режима протекания идеальной несжимаемой жидкости // Сибирский матем. журнал. 2002. Т.43. № 4. С. 840–857.
Navier C.L.M.H. Memoire sur les lois du mouvement des fluides // Memoires de I' Academic Royale des Sciences de I’Institut de France. 1823. T. 6. P. 389–440.
Трошкин О.В. Алгебраическая структура двумерных стационарных уравнений Навье–Стокса и нелокальные теоремы единственности // Докл. АН СССР. 1988. Т. 298. № 6. С. 1372–1376.
Дезин А.А. Об одном классе векторных полей. Комплексный анализ и его приложения (сб. статей). М.: Наука, 1978. С. 203–208.
Трошкин О.В. К устойчивости вихрей возвратного течения // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 12. С. 129–134.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал