Журнал вычислительной математики и математической физики, 2019, T. 59, № 11, стр. 1973-1997
Платежеспособность страховой компании в дуальной модели риска с учетом инвестиций: анализ и численные исследования сингулярных краевых задач
Т. А. Белкина 1, *, Н. Б. Конюхова 2, **, Б. В. Славко 3, ***
1 ЦЭМИ РАН
117418 Москва, Нахимовский пр-т, 47, Россия
2 ВЦ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия
3 Университет Сиднея
NSW 2006 Сидней, Австралия
* E-mail: tbel@cemi.rssi.ru
** E-mail: nadja@ccas.ru
*** E-mail: slavkobogdan@gmail.com
Поступила в редакцию 23.05.2019
После доработки 19.06.2019
Принята к публикации 08.07.2019
Аннотация
Рассматривается задача о вероятности неразорения для коллективной модели пенсионного страхования (так называемой дуальной модели риска) в условиях инвестирования всего резерва страховой компании (или фиксированной его доли) в рисковый актив, моделируемый геометрическим броуновским движением. Типичный договор страхования в данной модели предполагает пожизненное обеспечение страхователя в обмен на передачу права наследования его собственности в пользу страховой компании. Модель рассматривается как дуальная по отношению к классической модели Крамера–Лундберга. В структуре процесса страхового риска это выражается наличием положительных случайных скачков (составного пуассоновского процесса) и линейно убывающей детерминированной составляющей, отвечающей выплате пенсий. Для случая экспоненциального распределения размеров скачков показано, что вероятность неразорения как функция начального капитала, определенная на неотрицательной вещественной полуоси, является решением сингулярной краевой задачи для интегродифференциального уравнения c невольтерровым интегральным оператором. Приводится доказательство существования и единственности решения этой задачи, получены асимптотические представления для вероятности неразорения при малых и больших значениях начального капитала, предложен эффективный алгоритм численного нахождения решения, проведены расчеты и дана их экономическая интерпретация: показано, что в пенсионном страховании вложение средств в рисковые активы играет важную роль для увеличения платежеспособности компании при малых значениях начального капитала. Библ. 30. Фиг. 6.
ВВЕДЕНИЕ
В работе проводятся исследования влияния инвестиций на вероятность разорения (ВР) страховой компании (СК) в модели, наиболее известной под названием дуальной модели риска (см., например, [1, ch. VI, 2]). Она рассматривается как дуальная по отношению к классической модели коллективного риска – модели Крамера–Лундберга (КЛ), называемой также составной пуассоновской моделью [1]. Дуальная модель риска (ДМР) получается из модели КЛ заменой знаков на противоположные у составляющих случайного процесса, описывающего динамику рискового резерва (процесса риска). В модели КЛ указанный процесс включает детерминированную составляющую – линейно растущую функцию, отвечающую накоплению страховых премий, которые поступают с постоянной интенсивностью в СК от страхователей, и случайную составляющую – взятый с отрицательным знаком составной пуассоновский процесс, определяющий сумму страховых выплат. В результате замены знаков детерминированная составляющая в ДМР приобретает отрицательный знак, что соответствует непрерывному постоянному убыванию процесса риска, а составной пуассоновский процесс входит в уравнение динамики капитала с положительным знаком, давая тем самым положительные скачки.
Положительные скачки в суммарном процессе риска могут рассматриваться как отрицательный риск, что объясняет еще одно название ДМР – модель страхования с отрицательными рисковыми суммами (negative risk sums, см., например, [2]); в [1] она также называется составной пуассоновской моделью с отрицательными требованиями (compound Poisson model with negative claims).
С содержательной точки зрения ДМР может иметь различную интерпретацию. В [3] она представлена как коллективная модель страхования жизни, или модель пенсионного страхования (далее придерживаемся именно этой интерпретации, первоначально используемой Крамером в [4]). В [1] указывается, что ДМР может также описывать общий доход некоей венчурной компании, несущей постоянные расходы с фиксированной интенсивностью и получающей случайные доходы от инноваций, и, наконец, она может иметь применение как модель $M{\text{/}}G{\text{/}}1$ в теории массового обслуживания.
Важнейшим показателем качества работы как СК, так и пенсионного фонда является вероятность неразорения (ВНР), являющаяся традиционной характеристикой платежеспособности. Это вероятность того, что значение капитала компании не станет отрицательным, и СК будет способна выполнять свои обязательства по выплате страховых возмещений или пенсий (вероятностью дополнительного события и является ВР, о проблеме вычисления и оценки которой см., например, [1], [5] и библиографию там).
В современных условиях СК, пенсионные и другие фонды являются активными участниками финансового рынка, инвестируя свой капитал в различного вида активы. При этом возникает необходимость учета этого факта в модели динамики капитала (см., например, [6]), что ведет к усложнению проблемы оценки ВР. Первый результат в этом направлении для модели КЛ при условии вложения всего текущего капитала (ТК) или его постоянной доли в рисковый актив, моделируемый геометрическим броуновским движением, получен в [7] (в случае более общего вида премий как детерминированной функции времени – в [8]), где показано, что в случае экспоненциального распределения страховых требований и “надежного портфеля активов” (смысл этого термина уточним позже) ВР убывает как степенная функция при стремлении начального капитала (НК) к бесконечности; при “ненадежном портфеле” инвестиций разорение происходит с вероятностью единица. Аналогичный результат получен в [2] для ДМР (для более общей модели динамики цены рискового актива и других моделей см., например, [9] и цитируемую там литературу).
Содержательный вывод, полученный из результатов указанных исследований, объявлен в заголовках статей [2], [7]: “в страховом бизнесе инвестиции в рисковые активы опасны”. Он сделан на основании того, что данные асимптотические представления, характеризующие убывание ВР с ростом НК, являются намного более медленными по сравнению с экспоненциальным убыванием в моделях без инвестиций.
В то же время в [10], [11] начаты исследования проблемы оптимального управления инвестициями в модели КЛ (см. также [12], [13]), в результате которых показано, что именно использование рисковых активов позволяет минимизировать ВР при малых значениях НК. Оптимальная стратегия в этой и подобных моделях является функцией решения нелинейного уравнения, которому удовлетворяет функция Беллмана. Тогда возникают вопросы: каково влияние на ВР рисковых инвестиций при простых для реализации стратегиях (т.е. при полном вложении ТК или его постоянной доли в акции) при малых значениях НК и каким образом соответствующая вероятность может быть корректно вычислена как функция НК на всей неотрицательной вещественной полуоси.
Для модели КЛ (а также ее модификации со стохастическими премиями, в том числе в “вырожденном” случае полного отсутствия премий – модели благотворительного фонда) полный ответ на эти вопросы получен в [14]–[18]. Как уже отмечено выше, в [7] получена асимптотика ВР при больших значениях НК, что сделано на основе асимптотического анализа решения интегродифференциального уравнения (ИДУ), которому ВНР (в модели с вложением постоянной доли резерва в рисковый актив) должна удовлетворять в предположении ее дважды непрерывной дифференцируемости. Последнее свойство, характеризующее гладкость ВНР, доказано в [19], но при дополнительных искусственных ограничениях на параметры модели. Для обоснования справедливости асимптотики в [7] также использовались верхние и нижние оценки для ВР, полученные с помощью теории восстановления. Подход, применяемый в [14]–[18], позволяет провести полный анализ ВНР как решения соответствующей сингулярной задачи для ИДУ с доказательством существования решения, исследованием его глобальных свойств и асимптотических представлений как при больших, так и при малых значениях НК, не нуждаясь при этом в априорном доказательстве гладкости ВНР и получении каких-либо ее оценок. Данный подход основан на принципе достаточности [20], связанном с доказательством теорем, утверждающих, что полученное решение определяет ВНР в рассматриваемой модели. В результате такого исследования сделан вывод о положительном влиянии простых инвестиций, использующих рисковый актив, на ВНР при малых значениях НК. Причем это влияние оказывается тем больше, чем меньше так называемая нагрузка безопасности в исходной модели риска (которая может быть и отрицательной, когда в модели без инвестиций разорение неминуемо).
Основной целью данной работы является изучение ВНР как функции НК на всей неотрицательной вещественной полуоси его возможных значений в ДМР при условии применения простых инвестиционных стратегий, определяемых постоянной долей рискового актива в резерве в каждый момент времени (при этом предполагается, что оставшаяся доля инвестируется в безрисковый актив с постоянной положительной процентной ставкой). Для данного исследования применяется описанный выше подход. При этом не используется знание уже доказанного в [2] для этой модели факта дважды непрерывной дифференцируемости ВНР: при указанном подходе этот факт будет доказан независимо – косвенным путем, как и ранее для модели КЛ. Как результат исследования, предлагаются также теоретически обоснованные алгоритмы корректного вычисления ВНР. Представлены результаты численных экспериментов, которые, в частности, позволяют сделать выводы о влиянии рисковых инвестиций при малых значениях НК в данной модели. Некоторые результаты в этом направлении частично отражены в кратких публикациях [21], [22].
Заметим при этом, что в моделях с инвестициями оказывается невозможным применение описанного в [1] метода, основанного на дуальности модели КЛ и составной пуассоновской модели с отрицательными требованиями, для вывода оценок ВР во второй модели на основе известных результатов для первой. Таким образом, задача требует отдельного рассмотрения. Соответствующая сингулярная краевая задача (КрЗ) для ИДУ представляется здесь более сложной в силу наличия в ИДУ невольтеррова интегрального оператора.
Работа организована следующим образом. В разд. 1 даются описание модели и постановка задачи, а также приводятся некоторые предварительные сведения и утверждения. В разд. 2 формулируется некоторая вспомогательная сингулярная КрЗ для ИДУ и проводятся ее предварительные исследования. В частности, устанавливается связь между решением ИДУ, удовлетворяющим некоторым предельным условиям в нуле и на бесконечности, и решением исходной задачи вычисления ВНР в изучаемой модели. Далее в этом разделе приводится формулировка сингулярной задачи для обыкновенного дифференциального уравнения (ОДУ) и доказывается эквивалентность задач для ИДУ и ОДУ. Вопросы существования, единственности и асимптотических представлений решения сингулярной задачи для ОДУ исследуются в разд. 3. В разд. 4 формулируется окончательное утверждение о ВНР как решения сингулярной КрЗ для ИДУ и приводится алгоритм ее определения через решение сингулярной КрЗ для ОДУ. В разд. 5 приводятся результаты численных экспериментов и их интерпретация.
Работа является итоговой по дуальной модели риска с простыми рисковыми стратегиями инвестиций.
Далее, в частности, используются обозначения: ${\mathbf{P}}(A)$ – вероятность события $A$; ${\mathbf{E}}X$ – математическое ожидание случайной величины $X$. Остальные обозначения и сокращения будут вводиться по мере необходимости.
1. ОПИСАНИЕ МОДЕЛИ ПЕНСИОННОГО СТРАХОВАНИЯ С ПРОСТЫМИ СТРАТЕГИЯМИ ИНВЕСТИЦИЙ И ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
1.1. Исходный процесс риска для модели без инвестиций
Рассмотрим коллективную модель пенсионного страхования с непрерывным временем, в которой типичный договор устроен по принципу пожизненной ренты. Точнее, будем считать, что согласно договору страхователь предоставляет СК право наследования его собственности в обмен на пожизненное содержание. Тот факт, что модель носит коллективный характер, означает, как обычно, что каждый такой договор в отдельности не анализируется, но при этом описывается динамика суммарного капитала по всему портфелю однотипных договоров на некотором временном интервале – конечном или бесконечном. Будем также предполагать, что модель является однородной во времени: суммарные выплаты (пенсий) осуществляются с постоянной скоростью, а процесс поступления “премий” (увеличения капитала в моменты перехода к СК права распоряжаться имуществом клиента) – сложный пуассоновский с постоянной интенсивностью и одинаково распределенными скачками.
При таких предположениях динамика капитала СК (по данному портфелю договоров) описывается процессом риска вида
Здесь ${{R}_{t}}$ – размер капитала в момент времени $t$, $t \geqslant 0$; $u$ – размер НК, $0 < c$ – размер затрат на выплату пенсий в единицу времени, $N(t)$ – однородный пуассоновский процесс с интенсивностью $\lambda > 0$ (${\mathbf{E}}N(t) = \lambda t$, $N(0) = 0$), описывающий количество поступивших премий к моменту времени $t$; ${{Z}_{k}}$, $k = 1,2,\; \ldots $, – размеры премий – независимые одинаково распределенные неотрицательные случайные величины (СВ), не зависящие от процесса $N(t)$ и имеющие функцию распределения (ФР) $F(z)$ такую, что Таким образом модель без инвестиций описывается процессом риска (1.1), где $c$, $\lambda $, $m$ – положительные числа. По аналогии с классическим определением относительной “нагрузки безопасности” вводимОпределение 1. Относительной нагрузкой (коэффициентом) безопасности для процесса риска (1.1) называется величина
а условие (положительности нагрузки безопасности) отвечает положительности чистого ожидаемого дохода.Положим ${{\varphi }_{0}}(u) = {\mathbf{P}}\left( {{{R}_{t}} \geqslant 0,\;t \geqslant 0\,|\,{{R}_{0}} = u} \right)$, тогда ${{\varphi }_{0}}(u)$ определяет ВНР для процесса (1.1) на бесконечном интервале времени.
Приведенные далее утверждения для модели без инвестиций являются, в частности, следствиями результатов для более общих моделей с инвестициями, что будет ясно из дальнейшего (естественно, они могут быть доказаны независимо).
В случае положительности нагрузки безопасности, т.е. при выполнении условия (1.4) (ожидаемые поступления средств в единицу времени больше выплат за то же время), процесс (1.1) имеет положительный снос, и можно показать для соответствующей ВНР ${{\varphi }_{0}}(u)$, что, как и в классической модели КЛ (при замене неравенства (1.4) на противоположное, см., например, [3], [5]), имеет место предельное условие
Кроме того, для данной модели выполняется условие (см. далее лемму 1) Нетрудно показать, что, как и в классической модели, ВНР ${{\varphi }_{0}}(u)$ является дифференцируемой функцией, она удовлетворяет ИДУ(1.7)
$ - c\varphi _{0}^{'}(u) - \lambda {{\varphi }_{0}}(u) + \lambda \int\limits_0^\infty {{{\varphi }_{0}}(u + z)dF(z)} = 0,\quad u > 0,$(1.9)
$(c{\text{/}}m - \lambda )\varphi _{0}^{'}(u) - c\varphi _{0}^{{''}}(u) = 0,\quad {{\varphi }_{0}}(0) = 0,\quad \mathop {lim}\limits_{u \to \infty } {{\varphi }_{0}}(u) = 1.$(1.10)
${{\varphi }_{0}}(u) = 1 - exp( - (\lambda m - c)u{\text{/}}(cm)) = 1 - exp( - \rho u{\text{/}}m).$(1.11)
$0 < {{\varphi }_{0}}(u) < 1,\quad \varphi _{0}^{'}(u) > 0,\quad \varphi _{0}^{{''}}(u) < 0\quad {\text{для}}\;{\text{любого}}\;{\text{конечного}}\quad u > 0;$Мы вернемся к обоснованию приведенных формул и утверждений в дальнейшем тексте.
1.2. Модель с инвестициями
1.2.1. Описание процесса риска при простых стратегиях инвестирования. Пусть весь капитал фонда непрерывно инвестируется в рисковый актив (акции), динамика цен которого моделируется процессом геометрического броуновского движения
где ${{S}_{t}}$ – цена акции в момент времени $t$, $\mu $ – ожидаемая доходность, $\sigma $ – волатильность, ${{w}_{t}}$ – стандартное броуновское движение. В этом случае ТК компании ${{X}_{t}}$ удовлетворяет стохастическому дифференциальному уравнению (СДУ) с начальным условием ${{X}_{0}} = u$. Положим $\varphi (u) = {\mathbf{P}}\left( {{{X}_{t}} \geqslant 0,\;t \geqslant 0\,|\,{{X}_{0}} = u} \right)$, тогда $\varphi (u)$ определяет ВНР на бесконечном интервале времени.Рассматриваемая модель охватывает и более общую ситуацию, когда СК с процессом риска (1.1) непрерывно инвестирует некоторую постоянную долю $\alpha $ ($0 < \alpha \leqslant 1$) своего ТК в акции, изменение цены которых описывается СДУ (1.12), а оставшаяся доля ТК инвестируется в безрисковый актив – банковский счет при постоянной процентной ставке $r$ ($0 < r < \mu $), эволюция которого описывается ОДУ
где ${{B}_{t}}$ – величина банковского счета в момент времени $t$. Тогда динамика капитала (результирующий процесс риска) описывается начальной задачей для СДУ:(1.14)
$d{{X}_{t}} = {{X}_{t}}[\alpha \mu + (1 - \alpha )r]dt + \alpha \sigma {{X}_{t}}d{{w}_{t}} + d{{R}_{t}},\quad t \geqslant 0,\quad {{X}_{0}} = u.$(1.15)
${{\mu }_{\alpha }} = \alpha \mu + (1 - \alpha )r > 0,\quad {{\sigma }_{\alpha }} = \alpha \sigma > 0$(1.16)
$d{{X}_{t}} = {{\mu }_{\alpha }}{{X}_{t}}dt + {{\sigma }_{\alpha }}{{X}_{t}}d{{w}_{t}} + d{{R}_{t}},\quad t \geqslant 0,\quad {{X}_{0}} = u.$Процесс (1.16) может рассматриваться и при $\alpha = 0$. В этом случае ${{\mu }_{\alpha }} = {{\mu }_{0}} = r > 0$, ${{\sigma }_{\alpha }} = {{\sigma }_{0}} = 0$, что приводит к СДУ для динамики капитала в случае инвестирования всех средств в безрисковый актив: $d{{X}_{t}} = r{{X}_{t}}dt + d{{R}_{t}}$, $t \geqslant 0$, ${{X}_{0}} = u$. Случай $\alpha = 0$ коротко рассмотрен в [22], [23].
1.2.2. Предварительные утверждения о вероятности неразорения.
Лемма 1. Пусть функция $\varphi (u)$ – ВНР процесса (1.16), где ${{R}_{t}}$ определено в (1.1), параметры $c$, $\lambda $, $m$ – положительные числа, ${{\mu }_{\alpha }}$ и ${{\sigma }_{\alpha }}$ – любые числа.
Тогда $\varphi (u)$ удовлетворяет условию
т.е. при нулевом начальном состоянии разорение неминуемо (как в случае простой стратегии, так и при отсутствии инвестиций).Доказательство. Действительно, для процесса (1.16) справедливо равенство (аналог для СДУ формулы Коши для решений линейных неоднородных ОДУ)
(1.18)
${{X}_{t}} = exp({{H}_{t}})\left[ {u - c\int\limits_0^t {exp( - {{H}_{s}})ds} + \int\limits_{i = 1}^{N(t)} {{{Z}_{i}}} exp( - {{H}_{{{{\theta }_{i}}}}})} \right],\quad t \geqslant 0,$(1.19)
${{H}_{t}} = ({{\mu }_{\alpha }} - \sigma _{\alpha }^{2}{\text{/}}2)t + {{\sigma }_{\alpha }}{{w}_{t}},$Нетрудно понять, что ВНР является неубывающей функцией НК. О ее предельном значении на бесконечности ($\varphi (\infty ): = li{{m}_{{u \to \infty }}}\varphi (u)$) первоначально можно судить в соответствии с утверждением следующей леммы, доказанной в более общем случае в [24].
Лемма 2. Пусть выполнены условия леммы 1. Тогда для процесса (1.16) имеет место одно из двух соотношений: или $\varphi \equiv 0$, или $\varphi (\infty ) = 1$.
Далее в работе проводятся исследования поведения ВНР (как функции НК $u$ на всей неотрицательной вещественной полуоси его возможных значений) для процесса (1.16) при $0 < \alpha \leqslant 1$ в случае экспоненциального распределения скачков процесса (1.1). В частности, целью работы является получение асимптотических представлений ВНР не только при больших, но и при малых значениях НК, а также разработка алгоритма вычислений и проведение численных экспериментов.
В качестве средства решения указанной задачи используются корректная постановка и исследование сингулярной КрЗ для ИДУ, которой, как будет показано, удовлетворяет ВНР.
1.2.3. Инфинитезимальный оператор для процесса риска и предварительные утверждения о свойствах решений соответствующего ИДУ. Рассмотрим формально инфинитезимальный оператор, соответствующий однородному марковскому процессу ${{X}_{t}} = X_{t}^{\alpha }$, удовлетворяющему (1.16) (о понятии инфинитезимального оператора см., например, [25]). Этот оператор в данном случае имеет вид
(1.20)
$({{\mathcal{A}}^{\alpha }}f)(u) = \frac{1}{2}\sigma _{\alpha }^{2}{{u}^{2}}f{\kern 1pt} {\text{''}}(u) + f{\kern 1pt} {\text{'}}(u)({{\mu }_{\alpha }}u - c) - \lambda f(u) + \lambda \int\limits_0^\infty {f(u + z)} dF(z),\quad u > 0,$Тогда для ВНР как функции НК имеем линейное ИДУ:
(1.21)
$\frac{1}{2}\sigma _{\alpha }^{2}{{u}^{2}}\varphi {\text{''}}(u) + ({{\mu }_{\alpha }}u - c)\varphi {\text{'}}(u) - \lambda \varphi (u) + \lambda \int\limits_0^\infty \varphi (u + z)dF(z) = 0,\quad u > 0.$Для процесса (1.16) в случае экспоненциального распределения скачков вопросы дифференцируемости функции ВНР $\varphi (u)$ (а следовательно, и выполнения для нее ИДУ (1.21) при $F(z)$ вида (1.8)) и справедливости (при определенных условиях) предельного соотношения $li{{m}_{{u \to \infty }}}\varphi (u) = 1$ разрешаются в данной работе косвенным путем – через постановку и исследование некоторой априорно сформулированной сингулярной КрЗ для указанного ИДУ. Доказательство существования решения этой задачи и установление некоторых его свойств позволяют утверждать (с помощью теоремы достаточности, аналогичной доказанной в [20] для других моделей), что именно это решение определяет ВНР как функцию НК $u$. Исследование свойств этого решения и его численное нахождение дают возможность судить о поведении $\varphi (u)$ на всей положительной полуоси и, в частности, о влиянии рассматриваемой стратегии инвестиций на ВНР.
Определение 2. Под $\mathcal{K}$ будем понимать класс функций $f(u)$, принадлежащих ${{\mathcal{C}}^{2}}({{\mathbb{R}}_{ + }})$ и удовлетворяющих условиям
(1.22)
$\mathop {lim}\limits_{u \to + 0} f(u) = 0,\quad \mathop {lim}\limits_{u \to + \infty } f(u) = 1.$Справедливы следующие утверждения (в этом разделе считаем, как и при описании модели риска, что $F(z)$ – ФР неотрицательной (невырожденной) С.В. с конечным математическим ожиданием; см. (1.2)).
Лемма 3. Пусть все числовые параметры в (1.20) (за исключением, быть может, ${{\mu }_{\alpha }}$) строго положительны, и пусть ИДУ
имеет решение $f \in \mathcal{K}$.Тогда: 1) это решение единственно в $\mathcal{K}$; 2) решение $f(u)$ удовлетворяет ограничениям
3) если, кроме того, топологическим носителем распределения, определяемого ФР $F(z)$, является ${{\mathbb{R}}_{ + }}{\backslash }\{ 0\} $, а для функции $f(u)$ выполнены условия
(1.25)
$\mathop {lim}\limits_{u \to + 0} \left| {f{\kern 1pt} {\text{'}}(u)} \right| < \infty ,\quad \mathop {lim}\limits_{u \to + 0} [uf{\kern 1pt} {\text{''}}(u)] < \infty ,$Доказательство. 1. Предположим противное, т.е. в классе $\mathcal{K}$ существует еще решение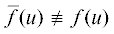 
ИДУ (1.23). Рассмотрим разность $\eta (u) = \bar {f}(u) - f(u)$. Очевидно, $\eta (u)$ удовлетворяет ИДУ (1.23) с условиями $li{{m}_{{u \to + 0}}}\eta (u) = li{{m}_{{u \to \infty }}}\eta (u) = 0$. Это означает, что существует точка максимума $u = \hat {u} > 0$ функции $\eta (u)$ (либо минимума, но в этом случае вместо $\eta (u)$ можно рассмотреть $ - \eta (u)$). Пусть также $\hat {u}$ – максимальная из всех точек максимума $\eta (u)$. Тогда выполняются условия $\eta {\text{'}}(\hat {u}) = 0$, $\eta {\text{''}}(\hat {u}) \leqslant 0$. Но из ИДУ (1.23) получаем
(1.27)
$\frac{1}{2}\sigma _{\alpha }^{2}{{\hat {u}}^{2}}\eta {\text{''}}(\hat {u}) = \lambda \left( {\eta (\hat {u}) - \int\limits_0^\infty \eta (\hat {u} + z)dF(z)} \right) > \lambda \left( {\eta (\hat {u}) - \int\limits_0^\infty \eta (\hat {u})dF(z)} \right) = 0,$2. Покажем, что $f(u) \geqslant 0$ для всех $u > 0$. Предположим противное: существует $u > 0$ такое, что $f(u) < 0$. Тогда, так как $f(u)$ удовлетворяет условиям (1.22), то существует точка минимума $u = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} > 0$, в которой выполняются условия $f{\kern 1pt} {\text{'}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} ) = 0$ и $f{\kern 1pt} {\text{''}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} ) \geqslant 0$. Пусть $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} $ – максимальная из всех таких точек минимума $f(u)$. Тогда из (1.23) получаем
3. Покажем теперь, что, по крайней мере при выполнении дополнительных требований (1.25), для производной решения выполнено неравенство (1.26). Действительно, для решения ИДУ (1.23) в классе $\mathcal{K}$, удовлетворяющего также (1.25), выполнено соотношение
Отсюда с учетом доказанного свойства неотрицательности функции $f$ с выполнением условий (1.22) для нее как функции из класса $\mathcal{K}$, условия на носитель меры и положительности $c$ заключаем, что $f{\kern 1pt} {\text{'}}( + 0) > 0$. Лемма доказана.Докажем еще две леммы, в которых $f(u)$ – некоторая функция, вообще говоря, не связанная с рассматриваемым ИДУ. Сначала заметим, что невольтерров интегральный оператор в (1.20) может быть переписан в виде
(1.29)
$\int\limits_0^\infty f (u + z)dF(z) = \int\limits_u^\infty f (s)dF(s - u),\quad u \geqslant 0.$Лемма 4. Пусть $F$ – ФР с условиями (1.2), функция $f$ непрерывно дифференцируема на $(0,\infty )$ и удовлетворяет условиям
(1.30)
$\mathop {lim}\limits_{u \to \infty } f(u) = 1,\quad \mathop {lim}\limits_{u \to \infty } f{\kern 1pt} {\text{'}}(u) = 0.$Тогда выполняется предельное условие
Доказательство. Рассмотрим левую часть выражения (1.31):
(1.32)
$\begin{gathered} \mathop {lim}\limits_{u \to + \infty } \int\limits_u^\infty f (s)dF(s - u) = \mathop {lim}\limits_{u \to + \infty } \left[ { - \int\limits_u^\infty f (s)d(1 - F(s - u))} \right] = \\ = \mathop {lim}\limits_{u \to + \infty } \left[ {f(u) + \int\limits_u^\infty g (s)(1 - F(s - u))ds} \right] = 1 + \mathop {lim}\limits_{u \to + \infty } \int\limits_u^\infty g (s)(1 - F(s - u))ds, \\ \end{gathered} $(1.33)
$\left| {\int\limits_u^\infty g (s)(1 - F(s - u))ds} \right| \leqslant \mathop {sup}\limits_{s \geqslant u} \left| {g(s)} \right|\int\limits_u^\infty {(1 - F(s - u))ds} = m\mathop {sup}\limits_{s \geqslant u} \left| {g(s)} \right|.$Лемма 5. Пусть $c$, $\lambda $, $m$ – фиксированные положительные числа, и пусть функция $f(u)$ принадлежит классу $\mathcal{K}$. Тогда соотношение (1.28) эквивалентно нелокальному соотношению
где $g(u) = f{\kern 1pt} {\text{'}}(u)$.Доказательство. Указанная эквивалентность легко проверяется интегрированием по частям в (1.28) с учетом условий (1.22).
1.2.4. Утверждение о связи вероятности неразорения с решением сингулярной задачи для ИДУ (проверочная теорема).
Теорема 1. Пусть выполнены условия леммы 3 и справедливо соотношение
Тогда для любого $u \in {{\mathbb{R}}_{ + }}$ значение $f(u)$ функции, определенной в лемме 3, является ВНР для процесса (1.16), т.е. $f(u) \equiv \varphi (u)$.Доказательство аналогично доказательству теоремы 3.1 в [20] и здесь не приводится. (Кроме того, доказательство соответствующего утверждения при $\alpha = 0$ приведено в [23], причем оно является немного более сложным в силу возможной негладкости ВНР при безрисковых инвестициях в дуальной модели риска.)
Напомним, что утверждения такого типа, как теорема 1, мы называем также теоремами достаточности [20]; они сводят задачу исследования ВНР (в частности, проблемы ее дифференцируемости) к проблеме существования решения некоторых корректно поставленных задач для ИДУ и исследования свойств решений этих задач.
Условие (1.35), обеспечивающее положительный снос процесса (1.19), в дальнейшем будем называть условием надежности портфеля активов, или надежности акций.
2. СИНГУЛЯРНАЯ КРАЕВАЯ ЗАДАЧА ДЛЯ ИДУ, СООТВЕТСТВУЮЩАЯ ИНФИНИТЕЗИМАЛЬНОМУ ОПЕРАТОРУ ПРОЦЕССА РИСКА В СЛУЧАЕ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ СКАЧКОВ
В этом разделе и последующих разд. 3, 4 опущен индекс $\alpha $ в обозначениях СДУ (1.16) и ИДУ (1.21), (1.23).
2.1. Формулировка сингулярной задачи для ИДУ второго порядка
При $F(z)$ вида (1.8) преобразование (1.29) невольтеррова интегрального оператора в (1.20) приводит его к виду сингулярного вольтеррова оператора из бесконечности:
(2.1)
$({{J}_{m}}f)(u): = \frac{1}{m}\int\limits_0^\infty f (u + z)exp( - z{\text{/}}m)dz = \frac{1}{m}\int\limits_u^\infty f (z)exp( - (z - u){\text{/}}m)dz,\quad u \geqslant 0.$С учетом (1.20), (1.8), (2.1) сформулируем (пока формально) сингулярную КрЗ для ИДУ (1.23):
(2.2)
$\frac{{{{\sigma }^{2}}}}{2}{{u}^{2}}f{\kern 1pt} {\text{''}}(u) + (\mu u - c)f{\kern 1pt} {\text{'}}(u) - \lambda f(u) + \frac{\lambda }{m}\int\limits_u^\infty f (z)exp( - (z - u){\text{/}}m)dz = 0,\quad u > 0,$(2.4)
$\mathop {lim}\limits_{u \to + 0} \left| {f{\kern 1pt} {\text{'}}(u)} \right| < \infty ,\quad \mathop {lim}\limits_{u \to + 0} [uf{\kern 1pt} {\text{''}}(u)] = 0,$(2.6)
$\mathop {{\text{lim}}}\limits_{u \to \infty } [uf{\kern 1pt} {\text{'}}(u)] = 0,\quad \mathop {{\text{lim}}}\limits_{u \to \infty } [{{u}^{2}}f{\kern 1pt} {\text{''}}(u)] = 0.$(2.7)
$ - cf{\kern 1pt} {\text{'}}( + 0) + \frac{\lambda }{m}\int\limits_0^\infty f (z)exp( - z{\text{/}}m)dz = 0,$2.2. Эквивалентная сингулярная задача для ОДУ третьего порядка
Лемма 6. Пусть в ИДУ (2.2) все параметры $c$, $m$, $\lambda $, ${{\sigma }^{2}}$, $\mu $ – фиксированные положительные числа.
Тогда сингулярная КрЗ (2.2)–(2.6) для ИДУ второго порядка эквивалентна следующей сингулярной КрЗ для ОДУ третьего порядка:
(2.9)
$\frac{1}{2}{{\sigma }^{2}}{{u}^{2}}f{\kern 1pt} {\text{'''}}(u) + \left( {\mu u + {{\sigma }^{2}}u - c - \frac{1}{{2m}}{{\sigma }^{2}}{{u}^{2}}} \right)f{\kern 1pt} {\text{''}}(u) + \left( {\mu - \lambda - \frac{{\mu u - c}}{m}} \right)f{\kern 1pt} {\text{'}}(u) = 0,\quad 0 < u < \infty ,$(2.11)
$\mathop {lim}\limits_{u \to + 0} \left| {f{\kern 1pt} {\text{'}}(u)} \right| < \infty ,\quad \mathop {lim}\limits_{u \to + 0} \left[ {uf{\kern 1pt} {\text{''}}(u)} \right] = 0,$(2.13)
$\mathop {\lim }\limits_{u \to \infty } [uf{\kern 1pt} {\text{'}}(u)] = 0,\quad \mathop {\lim }\limits_{u \to \infty } [{{u}^{2}}f{\kern 1pt} {\text{''}}(u)] = 0.$Доказательство. Пусть функция $f$ удовлетворяет ИДУ (2.2). Покажем, что она удовлетворяет также ОДУ (2.9).
Нетрудно подсчитать, что для оператора, введенного в (2.1), имеет место соотношение
Дифференцируя исходное ИДУ (2.2) с учетом (2.14), получаем(2.15)
$\frac{{{{\sigma }^{2}}}}{2}{{u}^{2}}f{\kern 1pt} {\text{'''}}(u) + {{\sigma }^{2}}uf{\kern 1pt} {\text{''}}(u) + (\mu u - c)f{\kern 1pt} {\text{''}}(u) + (\mu - \lambda )f{\kern 1pt} {\text{'}}(u) + \frac{\lambda }{m}[({{J}_{m}}f)(u) - f(u)] = 0,\quad u > 0.$Обратно, пусть функция $\hat {f}(u)$ удовлетворяет ОДУ (2.9) и условиям (2.12), (2.13) (или (2.5), (2.6), что то же). Покажем, что она удовлетворяет также ИДУ (2.2). Обозначим левую часть ИДУ (2.2) с функцией $\hat {f}(u)$ через $h(u)$. Имеем
(2.16)
$h(u) = - \lambda \hat {f}(u) + \lambda ({{J}_{m}}\hat {f})(u) + (\mu u - c)\hat {f}{\kern 1pt} {\text{'}}(u) + ({{\sigma }^{2}}{\text{/}}2){{u}^{2}}\hat {f}{\kern 1pt} {\text{''}}(u),$В силу условий (2.12), (2.13) для функции $\hat {f}(u)$ выполнены условия леммы 4 в случае экспоненциальной ФР, и, следовательно, имеет место соотношение
С учетом формулы (2.16) для $h(u)$, условий (2.12), (2.13) и соотношения (2.19) заключаем, что справедливо предельное равенство $li{{m}_{{u \to \infty }}}h(u) = 0$. Следовательно, в силу положительности $m$, константа $C$ в (2.18) равна нулю, т.е. $h(u) \equiv 0$. Тогда из (2.16) получаем, что $\hat {f}(u)$ является решением ИДУ (2.2).
Осталось заметить, что весь набор условий в рассматриваемых сингулярных задачах один и тот же, что завершает доказательство леммы.
Замечание 1. Заметим, что приведенное ранее ОДУ в (1.9) для модели без инвестиций является частным случаем ОДУ (2.9) при $\mu = {{\sigma }^{2}} = 0$.
3.3. Теорема о представлении решения сингулярной задачи для ИДУ через решение сингулярной задачи для ОДУ второго порядка
Теорема 2. Пусть в ИДУ (2.2) все параметры $c$, $m$, $\lambda $, ${{\sigma }^{2}}$, $\mu $ – фиксированные положительные числа, и пусть функция $f(u)$ является решением сингулярной задачи для ИДУ (2.2)–(2.6). Тогда
где $g(u)$ есть решение сингулярной задачи для ОДУ(2.21)
$\frac{1}{2}{{\sigma }^{2}}{{u}^{2}}g{\text{''}}(u) + \left( {\mu u + {{\sigma }^{2}}u - c - \frac{1}{{2m}}{{\sigma }^{2}}{{u}^{2}}} \right)g{\text{'}}(u) + \left( {\mu - \lambda - \frac{{\mu u - c}}{m}} \right)g(u) = 0,\quad 0 < u < \infty ,$(2.22)
$\mathop {lim}\limits_{u \to + 0} \left| {g(u)} \right| < \infty ,\quad \mathop {lim}\limits_{u \to + 0} [ug{\text{'}}(u)] = 0,$(2.23)
$\mathop {\lim }\limits_{u \to \infty } [ug(u)] = 0,\quad \mathop {\lim }\limits_{u \to \infty } [{{u}^{2}}g{\text{'}}(u)] = 0,$Доказательство. Очевидно, представление (2.20) соответствует связи $g = f{\kern 1pt} {\text{'}}$, а при условии нормировки (2.24) обеспечивает также выполнение условий (2.3) и (2.5); ОДУ (2.21) – это ОДУ (2.9), переписанное в терминах $g$, то же относится к условиям (2.22), (2.23) по сравнению с условиями (2.11), (2.13) (они же (2.4), (2.6)). Тогда, с учетом леммы 6, получаем требуемое утверждение.
Замечание 2. ОДУ (2.21) обладает иррегулярной (сильной) особенностью в нуле ранга $1$ (по поводу классификации особых точек типа полюса для систем линейных ОДУ см., например, монографии [26]–[28], дополняющие друг друга). Ниже мы увидим, что сингулярная задача (2.21), (2.22) без начальных данных имеет двухпараметрическое семейство решений, т.е. все решения ОДУ (2.21) удовлетворяют условиям (2.22). Кроме того, для решений этой задачи из требования вырождения ОДУ (2.21) при $u \to + 0$ вытекает соотношение
из которого следует, что $g{\text{'}}(u)$ на самом деле является ограниченной в нуле функцией.3. АНАЛИЗ СИНГУЛЯРНОЙ ЗАДАЧИ ДЛЯ ОДУ ВТОРОГО ПОРЯДКА
В этом разделе доказываются существование и единственность решения сингулярной задачи (2.21)–(2.24), а также исследуется асимптотическое поведение решения при малых и больших значениях аргумента. Для этих целей прежде всего изучаются сингулярные задачи в окрестностях особых точек: в окрестности точки $u = 0$ – сингулярная задача без начальных данных (2.21), (2.22); в окрестности бесконечно удаленной точки – сингулярная задача Коши (ЗК) (2.21), (2.23). Для достаточно больших значений аргумента (в окрестности бесконечно удаленной точки) используются обозначения типа ${{\tau }_{\infty }}$, ${{u}_{\infty }}$ (${{\tau }_{\infty }} \gg 1$, ${{u}_{\infty }} \gg 1$).
3.1. Поведение решений при малых значениях аргумента
Для исследования асимптотического поведения решений ОДУ (2.21) при $u \to + 0$ задачу (2.21), (2.22) перепишем в параметризованном виде, введя также новые обозначения:
(3.1)
${{u}^{3}}g{\text{''}}(u) + ({{a}_{1}} + {{a}_{2}}u + {{a}_{3}}{{u}^{2}})ug{\text{'}}(u) + ({{a}_{4}}u + {{a}_{5}}{{u}^{2}})g(u) = 0,\quad u > 0,$(3.2)
$\mathop {lim}\limits_{u \to + 0} g(u) = {{D}_{1}},\quad \mathop {lim}\limits_{u \to + 0} [ug{\text{'}}(u)] = 0,$(3.3)
$\begin{gathered} {{a}_{1}} = - 2c{\text{/}}{{\sigma }^{2}},\quad {{a}_{2}} = 2(\mu {\text{/}}{{\sigma }^{2}} + 1),\quad {{a}_{3}} = - 1{\text{/}}m, \\ {{a}_{4}} = 2(\mu - \lambda + c{\text{/}}m){\text{/}}{{\sigma }^{2}},\quad {{a}_{5}} = - 2\mu {\text{/}}(m{{\sigma }^{2}}). \\ \end{gathered} $Используя методы и подходы [28], [29] к изучению ОДУ с иррегулярными особыми точками, докажем справедливость следующего утверждения.
Лемма 7. Пусть в ОДУ (3.1), где величины ${{a}_{j}}$, $1 \leqslant j \leqslant 5$, определены в (3.3), все параметры $c$, $m$, $\lambda $, ${{\sigma }^{2}}$, $\mu $ – фиксированные положительные числа. Тогда при каждом фиксированном значении ${{D}_{1}}$ сингулярная ЗК (3.1), (3.2) обладает однопараметрическим семейством решений $g(u,{{D}_{1}},{{C}_{1}})$, и при малых $u > 0$ справедливо представление
(3.4)
$g(u,{{D}_{1}},{{C}_{1}}) = {{D}_{1}}(1 + {{\chi }_{1}}(u)) + {{C}_{1}}{{u}^{{ - 2\mu /{{\sigma }^{2}}}}}exp( - 2c{\text{/}}({{\sigma }^{2}}u))(1 + {{\chi }_{2}}(u)),$(3.5)
${{\chi }_{1}}(u) \sim \sum\limits_{k = 1}^\infty {{{D}_{{k + 1}}}} {{u}^{k}},\quad u \sim + 0,$(3.7)
${{D}_{3}} = [{{D}_{2}}(2\mu + {{\sigma }^{2}} - \lambda + c{\text{/}}m) - \mu {\text{/}}m]{\text{/}}(2c),$(3.8)
$\begin{gathered} {{D}_{{k + 1}}} = [{{D}_{k}}(k(k - 1){{\sigma }^{2}}{\text{/}}2 + \mu k - \lambda + c{\text{/}}m) - \\ - \;{{D}_{{k - 1}}}((k - 2){{\sigma }^{2}}{\text{/}}(2m) + \mu {\text{/}}m)]{\text{/}}(kc),\quad k = 3,4,\; \ldots \;. \\ \end{gathered} $Доказательство. Введем обозначения:
(3.9)
${{y}_{1}}(u) = g(u),\quad {{y}_{2}} = ug{\text{'}}(u),\quad y(u) = {{({{y}_{1}}(u),{{y}_{2}}(u))}^{{\text{т}}}}$(3.10)
${{u}^{2}}y{\kern 1pt} {\text{'}}(u) = ({{A}_{0}} + {{A}_{1}}u + {{A}_{2}}{{u}^{2}})y(u),\quad u > 0,\quad \mathop {lim}\limits_{u \to + 0} y(u) = {{({{D}_{1}},0)}^{{\text{т}}}},$Замены переменных
приводят (3.10) к ЗК на бесконечности:(3.11)
$\dot {\tilde {y}}(\tau ) = - ({{A}_{0}} + {{A}_{1}}{\text{/}}\tau + {{A}_{2}}{\text{/}}{{\tau }^{2}})\tilde {y}(\tau ),\quad \tau \geqslant {{\tau }_{\infty }},\quad \mathop {lim}\limits_{\tau \to \infty } \tilde {y}(\tau ) = {{({{D}_{1}},0)}^{{\text{т}}}}.$В силу наличия у матрицы ${{A}_{0}}$ нулевого собственного значения (СЗ), поведение решений задачи (3.11) при больших значениях $\tau $ определяется двумя матрицами ${{A}_{0}}$ и ${{A}_{1}}$, как это следует из общей теории ОДУ с иррегулярными особенностями. Тогда для изучения этого поведения достаточно осуществить асимптотическую диагонализацию матрицы ${{A}_{1}}$ с помощью преобразования переменных
где $z(\tau ) = {{({{z}_{1}}(\tau ),{{z}_{2}}(\tau ))}^{{\text{т}}}}$, $E$ – единичная $2 \times 2$-матрица, $T = ({{t}_{{ij}}})_{{i,j = 1}}^{2}$ есть $2 \times 2$-матрица, элементы которой будут определены ниже. Для $z(\tau )$ из (3.11) получим ЗК на бесконечности:(3.13)
$\dot {z}(\tau ) = {{(E + T{\text{/}}\tau )}^{{ - 1}}}[T{\text{/}}{{\tau }^{2}} - ({{A}_{0}} + {{A}_{1}}{\text{/}}\tau + {{A}_{2}}{\text{/}}{{\tau }^{2}})(E + T{\text{/}}\tau )]{\kern 1pt} z(\tau ),\quad \tau \geqslant {{\tau }_{\infty }},$Далее, выберем матрицу $T$ так, чтобы выполнялось соотношение
(3.15)
$T{\text{/}}{{\tau }^{2}} - ({{A}_{0}} + {{A}_{1}}{\text{/}}\tau + {{A}_{2}}{\text{/}}{{\tau }^{2}})(E + T{\text{/}}\tau ) = - (E + T{\text{/}}\tau )({{A}_{0}} + {{\tilde {A}}_{1}}{\text{/}}\tau + G(\tau ){\text{/}}{{\tau }^{2}}),$Приравнивая в (3.15) коэффициенты при $1{\text{/}}\tau $, получаем соотношение
которое равносильно равенству(3.17)
$\left( {\begin{array}{*{20}{c}} 0&1 \\ { - {{a}_{4}} - {{a}_{1}}{{t}_{{21}}}}&{1 - {{a}_{2}} - {{a}_{1}}{{t}_{{22}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&{ - {{a}_{1}}{{t}_{{12}}}} \\ 0&{1 - {{a}_{2}} - {{a}_{1}}{{t}_{{22}}}} \end{array}} \right).$(3.18)
$T = \left( {\begin{array}{*{20}{c}} 0&{{{\sigma }^{2}}{\text{/}}(2c)} \\ {(\mu - \lambda ){\text{/}}c + 1{\text{/}}m}&0 \end{array}} \right).$(3.19)
$\dot {z}(\tau ) = - [{{A}_{0}} + {{\tilde {A}}_{1}}{\text{/}}\tau + G(\tau ){\text{/}}{{\tau }^{2}}]{\kern 1pt} z(\tau ),\quad \tau \geqslant {{\tau }_{\infty }},$На основании теоремы 8 из [26, гл. II] получаем, что при больших $\tau $ система (3.19) асимптотически эквивалентна системе
(3.21)
$\dot {\tilde {z}}(\tau ) = - ({{A}_{0}} + {{\tilde {A}}_{1}}{\text{/}}\tau )\tilde {z}(\tau ),\quad \tau \gg 1,$(3.22)
${{\dot {\tilde {z}}}_{1}}(\tau ) = 0,\quad {{\dot {\tilde {z}}}_{2}}(\tau ) = [{{a}_{1}} + ({{a}_{2}} - 1){\text{/}}\tau ]{{\tilde {z}}_{2}}(\tau ).$Следовательно, учитывая обозначения (3.9), для семейства решений сингулярной ЗК (3.1), (3.2) получаем асимптотическое представление (3.4), где ${{\chi }_{2}}(u) = o(1)$ при $u \to + 0$. Для того чтобы проверить, что ${{\chi }_{1}}(u)$ представляется в виде (3.5), достаточно произвести непосредственную подстановку ряда (3.5) в ОДУ (3.1) и убедиться, что все его коэффициенты определяются в соответствии с формулами (3.6)–(3.8). Это также следует из общей теории линейных ОДУ с иррегулярными особыми точками, которая, кроме того, позволяет уточнить и поведение ${{\chi }_{2}}(u)$ при малых $u$: следствием поведения $G(\tau )$ в (3.19) при больших $\tau $ является представление ${{\chi }_{2}}(u)$ в (3.4) в виде асимптотического ряда по целым степеням $u$ при малых $u$. Лемма доказана.
Напомним, что параметр ${{D}_{1}}$ выбирался произвольно, так что получаем, что ОДУ (2.21) (оно же (3.1)) обладает двухпараметрическим семейством решений, удовлетворяющих условиям (3.2), т.е. все решения этого ОДУ ограничены при $u \to + 0$ и имеют интегрируемые в нуле производные. Более того, из (3.4) и доказательства леммы 7 точнее получаем, что производные этого семейства в нуле ограничены (см. также замечание 2).
3.2. Поведение решений при больших значениях аргумента
Для исследования асимптотического поведения на бесконечности решений ОДУ (2.21) (или, что то же, ОДУ (3.1)) перепишем (3.1) в виде
(3.23)
$g{\text{''}}(u) + ({{a}_{1}}{\text{/}}{{u}^{2}} + {{a}_{2}}{\text{/}}u + {{a}_{3}})g{\text{'}}(u) + ({{a}_{4}}{\text{/}}{{u}^{2}} + {{a}_{5}}{\text{/}}u)g(u) = 0,\quad u \gg 1.$Для упрощения дальнейших выкладок условия (2.23) заменим более слабыми:
(3.24)
$\mathop {lim}\limits_{u \to \infty } g(u) = 0,\quad \mathop {lim}\limits_{u \to \infty } g{\text{'}}(u) = 0.$Будем изучать ЗК (3.23), (3.24) и покажем, что при ограничении (1.35) существует однопараметрическое семейство решений этой задачи, причем все решения этого семейства (и только они) удовлетворяют условиям (2.23), так что они интегрируемы на бесконечности вместе с производными.
Лемма 8. Пусть в ОДУ (3.23), где величины ${{a}_{j}}$, $1 \leqslant j \leqslant 5$, определены в (3.3), все параметры $c$, $m$, $\lambda $, ${{\sigma }^{2}}$, $\mu $ – фиксированные положительные числа, и пусть выполняется условие
Тогда существует однопараметрическое семейство $g(u,{{C}_{2}})$ решений ЗК (3.23), (3.24), где ${{C}_{2}}$ – параметр (${{C}_{2}} \in \mathbb{R}$), причем при больших $u$ справедливо асимптотическое представлениеДоказательство. Введем обозначения: ${{y}_{1}}(u) = g(u)$, ${{y}_{2}}(u) = g{\kern 1pt} '(u)$, $y(u) = {{({{y}_{1}}(u),{{y}_{2}}(u))}^{{\text{т}}}}$. Получим из (3.23) для $y(u)$ ОДУ:
(3.27)
$y{\kern 1pt} {\text{'}}(u) = ({{B}_{0}} + {{B}_{1}}{\text{/}}u + {{B}_{2}}{\text{/}}{{u}^{2}})y(u),\quad u \geqslant {{u}_{\infty }},$(3.28)
${{B}_{0}} = \left( {\begin{array}{*{20}{c}} 0&1 \\ 0&{ - {{a}_{3}}} \end{array}} \right),\quad {{B}_{1}} = \left( {\begin{array}{*{20}{c}} 0&0 \\ { - {{a}_{5}}}&{ - {{a}_{2}}} \end{array}} \right),\quad {{B}_{2}} = \left( {\begin{array}{*{20}{c}} 0&0 \\ { - {{a}_{4}}}&{ - {{a}_{1}}} \end{array}} \right).$В силу (3.29) имеем из (3.27) ОДУ для $w(u)$:
(3.30)
$\begin{gathered} w{\kern 1pt} {\text{'}}(u) = {{(E + N{\text{/}}u)}^{{ - 1}}}M_{0}^{{ - 1}}y{\kern 1pt} {\text{'}} + {{(E + N{\text{/}}u)}^{{ - 1}}}(N{\text{/}}{{u}^{2}})w(u) = \\ = \;{{(E + N{\text{/}}u)}^{{ - 1}}}[M_{0}^{{ - 1}}({{B}_{0}} + {{B}_{1}}{\text{/}}u + {{B}_{2}}{\text{/}}{{u}^{2}}){{M}_{0}}(E + N{\text{/}}u) + N{\text{/}}{{u}^{2}}]w(u). \\ \end{gathered} $(3.31)
$w{\kern 1pt} {\text{'}}(u) = {{(E + N{\text{/}}u)}^{{ - 1}}}[({{\tilde {B}}_{0}} + {{\tilde {B}}_{1}}{\text{/}}u + {{\tilde {B}}_{2}}{\text{/}}{{u}^{2}})(E + N{\text{/}}u) + N{\text{/}}{{u}^{2}}]w(u).$(3.32)
$[{{\tilde {\tilde {B}}}_{0}} + {{\tilde {\tilde {B}}}_{1}}{\text{/}}u + {{\tilde {\tilde {B}}}_{2}}{\text{/}}{{u}^{2}}](E + N{\text{/}}u) + N{\text{/}}{{u}^{2}} = (E + N{\text{/}}u)[{{\tilde {B}}_{0}} + {{\tilde {B}}_{1}}{\text{/}}u + P(u){\text{/}}{{u}^{2}}],$Окончательно матрица $N$ имеет вид
Учитывая введенные обозначения и преобразование (3.29), для решений системы ОДУ (3.27) при больших $u$ получаем
(3.33)
$\begin{gathered} g(u,{{C}_{2}}) = {{C}_{2}}{{u}^{{ - 2\mu /{{\sigma }^{2}}}}}(1 + o(1)),\quad u \to \infty , \\ g{\text{'}}(u,{{C}_{2}}) = - (2\mu {\text{/}}{{\sigma }^{2}}){{C}_{2}}{{u}^{{ - (2\mu /{{\sigma }^{2}} + 1)}}}(1 + o(1)),\quad u \to \infty . \\ \end{gathered} $Следствие 1. В предположениях леммы 8 сингулярные ЗК (2.21), (2.23) и (3.23), (3.24) эквивалентны, так что существует однопараметрическое семейство $g(u,{{C}_{2}})$ решений ЗК (2.21), (2.23), причем для решений этого семейства справедливы асимптотические представления (3.33).
3.3. Существование и единственность решения исходной сингулярной задачи для ОДУ и его гладкость
Следствием приведенных утверждений является
Теорема 3. Пусть выполнены условия леммы 8. Тогда существует единственное решение $g(u)$ сингулярной задачи (2.21)–(2.24); это решение является бесконечно дифференцируемой функцией на ${{\mathbb{R}}_{ + }}$ и принадлежит однопараметрическому семейству $g\left( {u,{{C}_{2}}} \right)$ решений ЗК (2.21), (2.23), где постоянная ${{C}_{2}}$ однозначно определяется из условия нормировки (2.24); в окрестности нуля это решение $g(u)$ имеет представление (3.4), где постоянные ${{D}_{1}}$ и ${{C}_{1}}$, вообще говоря, не могут быть найдены методами локального анализа.
Бесконечная дифференцируемость решения $g(u)$ сингулярной задачи (2.21)–(2.24) следует из его поведения в окрестностях особых точек $u = 0$ и $u \to \infty $ и бесконечной дифференцируемости ОДУ (2.21) на любом конечном интервале ${{u}_{0}} \leqslant u \leqslant {{u}_{\infty }}$, где ${{u}_{0}} > 0$, ${{u}_{\infty }} < \infty $. Для дальнейшего достаточно непрерывной дифференцируемости на $\mathbb{R}$ функции $g(u)$.
4. ОКОНЧАТЕЛЬНОЕ УТВЕРЖДЕНИЕ О ВЕРОЯТНОСТИ НЕРАЗОРЕНИЯ В СЛУЧАЕ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ СКАЧКОВ КАК РЕШЕНИЯ СИНГУЛЯРНОЙ ЗАДАЧИ ДЛЯ ИДУ И МЕТОД ЕГО ЧИСЛЕННОГО НАХОЖДЕНИЯ
4.1. Основная теорема для вероятности неразорения
Пусть выполнены условия теоремы 3, и пусть $g(u)$ есть решение сингулярной задачи (2.21)–(2.24) для ОДУ. Тогда по теореме 2 функция $f(u)$, определенная формулой (2.20), является решением сингулярной задачи (2.2)–(2.26) для ИДУ. Следовательно, для этой функции выполнены условия леммы 3, в соответствии с которой, в частности, справедливо ограничение (1.24), а по теореме 1 для любого $u \in {{\mathbb{R}}_{ + }}$ значение $f(u)$ определяет ВНР для процесса ${{X}_{t}}(u)$, описываемого СДУ (1.13) с начальным условием ${{X}_{0}} = u$, т.е. $f \equiv \varphi $. При этом, в силу утверждения 1 леммы 3 о единственности соответствующего решения в классе $\mathcal{K}$, эта вероятность как функция $u$ с необходимостью удовлетворяет условиям (2.4) и (2.6); кроме того, выполнено неравенство $\varphi {\text{'}}( + 0) > 0$, а с учетом замечания 2, получаем, что величина $\varphi {\text{''}}( + 0)$ имеет тот же знак, что и выражение $\mu - \lambda + c{\text{/}}m$.
Таким образом, получаем, что справедлива следующая основная
Теорема 4. Пусть $F(z) = 1 - exp( - z{\text{/}}m)$, все параметры $\mu $, ${{\sigma }^{2}}$, $c$, $m$, $\lambda $ – фиксированные положительные числа, и пусть выполнено условие “надежности акций” (3.25).
Тогда следующие утверждения справедливы:
(I) ВНР $\varphi (u)$ процесса (1.13) с начальным условием ${{X}_{0}} = u$ принадлежит классу $\mathcal{K}$ и является решением сингулярной КрЗ для ИДУ (2.2), (2.3), (2.5);
(II) это решение существует и единственно в классе $\mathcal{K}$, оно удовлетворяет условиям (2.4), (2.6) и соотношениям
(III) при малых $u > 0$ для $\varphi (u)$ справедливо асимптотическое представление
(IV) при больших $u$ для ВНР $\varphi (u)$ справедливо асимптотическое представление
(4.1)
$\varphi (u) = 1 - K{{u}^{{1 - 2\mu /{{\sigma }^{2}}}}}\left( {1 + o(1)} \right),\quad u \to \infty ,$(V) при $u \to + 0$ поведение производных решения зависит от соотношения между параметрами, в частности, от знака величины ${{i}_{r}} = (\lambda - \mu )m - c$: 1) если ${{i}_{r}} \geqslant 0$, то $li{{m}_{{u \to + 0}}}\varphi {\text{''}}(u) \leqslant 0$, и решение $\varphi (u)$ вогнуто на ${{\mathbb{R}}_{ + }}$; 2) если ${{i}_{r}} < 0$, то $li{{m}_{{u \to + 0}}}\varphi {\text{''}}(u) > 0$, решение $\varphi (u)$ выпукло в некоторой окрестности нуля и имеет точку перегиба на ${{\mathbb{R}}_{ + }}$;
(VI) ВНР $\varphi (u)$ может быть найдена по формуле
где $g(u)$ – решение сингулярной задачи (2.21)–(2.24) для ОДУ.4.2. Численный метод нахождения вероятности неразорения
Проведенные математические исследования позволяют привести достаточно простой алгоритм численного нахождения ВНР в исходной модели. Для этого достаточно решить сингулярную ЗК из бесконечности (2.21), (2.23) с условием нормировки (2.24) и воспользоваться соотношением (2.20). Для практического решения сингулярной ЗК (2.21), (2.23) надо предварительно осуществить перенос предельных условий (2.23) из бесконечности в конечную точку, воспользовавшись приведенным ниже утверждением (для его обоснования см. [30]).
При этом для удобства изложения будем использовать запись ОДУ (2.21) в виде (3.23), а вместо (2.23) используем условия (3.24) (см. следствие 1 об эквивалентности ЗК (2.21), (2.23) и (3.23), (3.24)).
Утверждение 1. Пусть в ОДУ (3.23) величины ${{a}_{j}}$, $1 \leqslant j \leqslant 5$, определены по формулам (3.3), где все параметры $\mu $, ${{\sigma }^{2}}$, $c$, $m$, $\lambda $ – фиксированные положительные числа, и пусть выполнено условие (3.25).
Тогда предельные граничные условия (3.24) для решений ОДУ (3.23) для достаточно больших $u$ ($u \geqslant {{u}_{\infty }} \gg 1$) эквивалентны линейному соотношению
Здесь $\beta (u)$ есть решение сингулярной нелинейной ЗК на бесконечности:(4.4)
$\beta {\text{'}}(u) + {{\beta }^{2}}(u) + ({{a}_{1}}{\text{/}}{{u}^{2}} + {{a}_{2}}{\text{/}}u + {{a}_{3}})\beta (u) + {{a}_{4}}{\text{/}}{{u}^{2}} + {{a}_{5}}{\text{/}}u = 0,\quad u \geqslant {{u}_{\infty }},$(4.6)
$\beta (u) \sim \sum\limits_{k = 1}^\infty {{{\beta }_{k}}} {\text{/}}{{u}^{k}},\quad u \gg 1,$(4.8)
${{\beta }_{2}} = - ( - {{\beta }_{1}} + \beta _{1}^{2} + {{a}_{2}}{{\beta }_{1}} + {{a}_{4}}){\text{/}}{{a}_{3}},$(4.9)
${{\beta }_{k}} = - {{\left[ { - (k - 1){{\beta }_{{k - 1}}} + \sum\limits_{i = 1}^{k - 1} {{{\beta }_{i}}} {{\beta }_{{k - i}}} + {{a}_{1}}{{\beta }_{{k - 2}}} + {{a}_{2}}{{\beta }_{{k - 1}}}} \right]} \mathord{\left/ {\vphantom {{\left[ { - (k - 1){{\beta }_{{k - 1}}} + \sum\limits_{i = 1}^{k - 1} {{{\beta }_{i}}} {{\beta }_{{k - i}}} + {{a}_{1}}{{\beta }_{{k - 2}}} + {{a}_{2}}{{\beta }_{{k - 1}}}} \right]} {{{a}_{3}}}}} \right. \kern-0em} {{{a}_{3}}}},\quad k = 3,4,\; \ldots \;.$Приведем алгоритм численного нахождения ВНР.
АЛГОРИТМ
Шаг 1. Выбираем большое значение ${{u}_{\infty }}$, ${{u}_{\infty }} \gg 1$, и малое положительное значение ${{g}_{\infty }}$, $\varepsilon > {{g}_{\infty }} > 0$.
Шаг 2. Приближенно вычисляем $\beta ({{u}_{\infty }})$, используя разложение (4.6) и рекуррентные формулы (4.7)–(4.9). Учитывая соотношение (4.3), обозначим $g_{\infty }^{'} = \beta ({{u}_{\infty }}){{g}_{\infty }}$.
Шаг 3. От точки $u = {{u}_{\infty }}$ до близкой к нулю точки $u = {{u}_{0}} > 0$ численно решаем справа налево ЗК: ОДУ (3.23) с начальными условиями
Шаг 4. Находим ВНР $\varphi (u)$ по формуле
При этом интеграл $I(u)$ в (4.11) приближенно находим, добавив к ЗК (3.23), (4.10) связанную с ней ЗК(4.12)
${{I}_{\infty }} \approx \int\limits_{{{u}_{\infty }}}^\infty {{{C}_{2}}} {{u}^{{ - 2\mu /{{\sigma }^{2}}}}}du = {{C}_{2}}u_{\infty }^{{1 - 2\mu /{{\sigma }^{2}}}}{\text{/}}(2\mu {\text{/}}{{\sigma }^{2}} - 1) = {{g}_{\infty }}{{u}_{\infty }}{\text{/}}(2\mu {\text{/}}{{\sigma }^{2}} - 1).$Шаг 5. Чтобы в (4.11) точнее вычислить $I(0)$, не прибегая к формулам экстраполяции, исходим из соотношения $I(0) = J({{u}_{0}}) + I({{u}_{0}})$ и вычисляем величину $J({{u}_{0}}) = {{J}_{0}} = \int_0^{{{u}_{0}}} g (s)ds$. Для этого используем (3.4) для представления $g(u)$ в главном при $u \to + 0$:
5. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ИССЛЕДОВАНИЙ ВЕРОЯТНОСТИ НЕРАЗОРЕНИЯ КАК ФУНКЦИИ НАЧАЛЬНОГО КАПИТАЛА
По аналогии с [18], приведем замечание о размерности параметров модели и способе их “обезразмеривания” для последующих вычислений.
Замечание 3. В ИДУ (2.2) параметр $m$ – безразмерный (при безразмерных переменных $u$ и $\varphi $), а каждый из параметров ${{\sigma }^{2}}$, $\mu $, $c$ и $\lambda $, вообще говоря, имеет размерность $1{\text{/}}[t]$, где $[t]$ – размерность времени. Чтобы перейти к безразмерным величинам, достаточно разделить ИДУ (2.2) на какую-либо характерную положительную постоянную той же размерности: такое деление приводит задачу (2.2)–(2.6) к задаче того же вида с новыми параметрами $\mathop {\tilde {\sigma }}\nolimits^2 $, $\tilde {\mu }$, $\tilde {c}$ и $\tilde {\lambda }$. В частности, удобно в (2.2)–(2.6) в качестве параметра “обезразмеривания” выбрать $\lambda $: если положить $\lambda = 1$, то остальные параметры будут измеряться в долях $\lambda $ и при необходимости их можно пересчитать в размерном виде простым умножением на величину $\lambda > 0$. В результате, оставляя $\lambda $ в формулах, как это принято в литературе, полагаем всюду в расчетах $\lambda = 1$.
Далее для моделей с рисковыми инвестициями приводятся графики $\varphi (u)$ зависимостей ВНР от НК при разных наборах значений параметров $\mu $, ${{\sigma }^{2}}$, $c$, $\lambda $, которые указываются в безразмерном виде (параметр $m$ изначально является безразмерным), что достигается за счет фиксированного значения $\lambda = 1$ (при сохранении $\lambda $ в формулах; см. замечание 3). Для всех примеров расчетов выполняется условие надежности акций: $2\mu {\text{/}}{{\sigma }^{2}} > 1$; при $\lambda m > c$ дается сравнение результатов расчетов с аналитическим решением ${{\varphi }_{0}}(u)$ в модели без инвестиций (см. (1.10); для $\varphi _{0}^{'}(0)$ и $\varphi _{0}^{{''}}(0)$ см. соотношения (1.11)).
Следующие графики иллюстрируют утверждения теоремы 4. На численных примерах также показывается, каким образом изменение параметров рискового актива влияет на глобальное поведение ВНР.
Для всех примеров расчетов зафиксированы значения $\lambda = 1$, $m = 2$. Напомним, что под нагрузкой безопасности понимается величина $\rho $, определенная формулой (1.3).
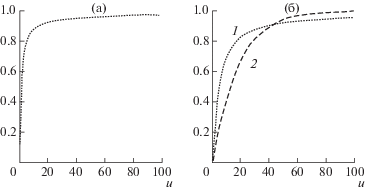
Данные к графикам на фиг. 1: $c = 1$ ($\lambda m - c = 1$), $\mu = 0.2$. Для фиг. 1а ${{\sigma }^{2}} = 0.265$, $\varphi {\text{'}}(0) = 0.458$, $\varphi {\text{''}}(0) = - 0.186$; для фиг. 1б ${{\sigma }^{2}} = 0.22$, $\varphi {\text{'}}(0) = 0.504$, $\varphi {\text{''}}(0) = - 0.2$ для графика 1 и $\mu = \sigma = 0$, $\varphi _{0}^{'}(0) = 0.5$, $\varphi _{0}^{{''}}(0) = - 0.25$ для графика 2 (модель без инвестиций).
Графики на фиг. 1б демонстрируют, в частности, повышение платежеспособности СК за счет рисковых инвестиций при значениях НК в примерном диапазоне $0 < u < 40$.
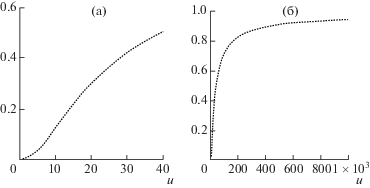
Данные к графикам на фиг. 2 (один график в разных масштабах): $c = 4$ ($\lambda m - c = - 2$), $\mu = 0.2$, ${{\sigma }^{2}} = 0.23$, $\varphi {\text{'}}(0) = 0.00449$, $\varphi {\text{''}}(0) = 0.001224$.
Графики демонстрируют, в частности, что ВНР становится положительной при всех $u > 0$ за счет рисковых инвестиций (напомним, что в случае отсутствия инвестиций при отрицательной нагрузке безопасности ВНР нулевая).
Данные к графикам на фиг. 3 с разными значениями $\mu $: $c = 4$ ($\lambda m - c = - 2$), ${{\sigma }^{2}} = 0.265$; $\mu = 0.2;\;0.3;\;0.4$ для графиков 1, 2, 3 соответственно со значениями производных в нуле: $\varphi {\text{'}}(0) \approx 0.002495;\;0.009;\;0.014$, $\varphi {\text{''}}(0) \approx 0.0010;\;0.0039;\;0.0067$.
Данные к графикам на фиг. 4 (на фиг. 4а, 4б одни и те же графики в разных масштабах) со значениями ${{i}_{r}}$ разных знаков (${{i}_{r}} = (\lambda - \mu )m - c$; ${{i}_{r}}$ меняется за счет изменения значений $\mu $): $c = 1.5$ ($\lambda m - c = 0.5$), ${{\sigma }^{2}} = 0.265$; $\mu = 0.2$ (${{i}_{r}} = 0.1$), $\mu = 0.3$ (${{i}_{r}} = - 0.1$), $\mu = 0.9$ (${{i}_{r}} = - 1.4$) для графиков 1, 2, 3 соответственно со значениями производных в нуле: $\varphi {\text{'}}(0) \approx 0.166;\;0.246;\;0.406$, $\varphi {\text{''}}(0) \approx - 0.0070;\;0.0056;\;0.194$.
Графики на фиг. 3 и 4 демонстрируют, в частности, повышение платежеспособности страховой компании за счет рисковых инвестиций при увеличении доходности акций.
Данные к графикам на фиг. 5 (графики на фиг. 5а, 5б, в одни и те же в разных масштабах) с отрицательным значением ${{i}_{r}}$ и разными значениями ${{\sigma }^{2}}$: $c = 1.95$ ($\lambda m - c = 0.05$); $\mu = 0.2$ (${{i}_{r}} = - 0.35$); ${{\sigma }^{2}} = 0.37;\;0.38$ и $\varphi {\text{'}}(0) \approx 0.017;\;0.011$, $\varphi {\text{''}}(0) \approx 0.0016;\;0.00098$ для графиков 1, 2 соответственно; $\mu = {{\sigma }^{2}} = 0$ для графика 3 – графика функции ${{\varphi }_{0}}(u)$ в модели без инвестиций, $\varphi _{0}^{'}(0) \approx 0.013$, $\varphi _{0}^{{''}}(0) \approx - 0.00016$.
Данные к графикам на фиг. 6 (графики на фиг. 6а, 6б, 6в одни и те же в разных масштабах) с положительным значением ${{i}_{r}}$ и разными значениями ${{\sigma }^{2}}$: $c = 1.5$ ($\lambda m - c = 0.5$); $\mu = 0.2$ (${{i}_{r}} = 0.1$); ${{\sigma }^{2}} = 0.26;\;0.275$ и $\varphi {\text{'}}(0) \approx 0.17;\;0.157$, $\varphi {\text{''}}(0) \approx - 0.0090;\; - {\kern 1pt} 0.0084$ для графиков 1, 2 соответственно; $\mu = {{\sigma }^{2}} = 0$ для графика 3 – графика функции ${{\varphi }_{0}}(u)$ в модели без инвестиций, $\varphi _{0}^{'}(0) \approx 0.167$, $\varphi _{0}^{{''}}(0) \approx - 0.028$.
Графики на фиг. 5, 6 демонстрируют, в частности, понижение платежеспособности СК при увеличении волатильности акций, причем, начиная с некоторого порога волатильности рисковые инвестиции дают отрицательный результат, т.е. уменьшают ВНР при всех начальных значениях капитала. Нужно также отметить, что наблюдается следующая закономерность: чем меньше нагрузка безопасности в исходной модели риска, тем больше порог волатильности, в пределах которого соответствующие рисковые инвестиции будут полезны с точки зрения увеличения ВНР при малых значениях начального капитала. Так, на фиг. 6 при нагрузке безопасности $0.5$ этот порог находится между значениями $0.26$ и $0.275$, а на фиг. 5 при нагрузке безопасности $0.05$ этот порог – между $0.37$ и $0.38$.
ЗАКЛЮЧИТЕЛЬНЫЕ ВЫВОДЫ
В заключение отметим, что в данной работе полностью решена проблема оценки влияния на ВР рисковых инвестиций при простых для реализации стратегиях (т.е. при полном вложении ТК или его постоянной доли в акции) в дуальной модели риска. Результаты численных экспериментов позволяют дополнить выводы, следующие из теоретических исследований данной модели, при этом сами численные эксперименты основаны на строго теоретически обоснованных алгоритмах вычисления ВНР как функция НК на всей неотрицательной вещественной полуоси. В частности, при положительной нагрузке безопасности (1.3) в исходной модели страхового риска в каждом конкретном случае может быть численно определен тот порог значений НК, начиная с которого рисковые инвестиции дают уменьшение значений ВНР по сравнению с ВНР в случае отсутствия каких-либо инвестиций.
В то же время применение “надежных” рисковых инвестиционных портфелей дает положительные значения ВНР при любом значении НК и произвольной нагрузке безопасности, в том числе отрицательной. Численные эксперименты показывают, что применение рисковых инвестиций (при “надежном” портфеле) может повышать ВНР в области малых значений НК, и особенно ощутимо это преимущество при отрицательной нагрузке безопасности, когда в отсутствие инвестиций наступает разорение с вероятностью единица.
Параметры $\mu $, $\sigma $, использовавшиеся как в теоретических исследованиях разд. 2–4, так и в численных расчетах, могут интерпретироваться не только как параметры акций в модели с полным вложением резерва в этот вид актива, но и как параметры ожидаемой доходности и волатильности инвестиционного портфеля, включающего также безрисковый актив с доходностью $r$ (напомним, что, начиная с разд. 3, индекс $\alpha $, обозначающий долю акций в портфеле, опущен в силу эквивалентности рассматриваемых задач для всех $\alpha \in (0,1]$). При сохранении индекса $\alpha $ в обозначениях (1.15) условие надежности портфеля имеет вид (1.35). Ясно, что при любых параметрах акций $\mu $, $\sigma $, даже если сами они не удовлетворяют требованию надежности (3.25), условие надежности портфеля (1.35) всегда может быть обеспечено за счет понижения доли $\alpha $ акций в этом портфеле; результатом этого является и снижение его волатильности, а также ожидаемой доходности (при естественном предположении $\mu > r$). Применение инвестиционных портфелей, удовлетворяющих требованию надежности, может приводить к качественно разным результатам двух типов: в первом случае такое применение повышает ВНР в области малых значений НК, во втором (если волатильность портфеля достаточно велика при фиксированной ожидаемой доходности) отсутствие инвестиций дает лучший результат. Таким образом, при заданных параметрах активов и процесса страхового риска, возможность выбора подходящего инвестиционного портфеля, с помощью которого можно повысить в достаточной мере ВНР в области небольших значений НК, определяется с помощью теоретически обоснованных численных расчетов, описанных в данной работе.
Для более полного исследования роли рисковых инвестиций в повышении платежеспособности необходимо провести сравнение ВНР, получаемой в результате применения рисковых инвестиционных портфелей, с ВНР, соответствующей применению безрисковой стратегии (т.е. с ВНР в случае, когда доля рисковых инвестиций в портфеле нулевая). Последний случай приводит к сингулярным задачам для ИДУ качественно другого вида и требует отдельного рассмотрения.
Окончательный ответ на вопрос о том, какую роль рисковые активы могут играть в увеличении ВНР, должно дать изучение задачи оптимального динамического управления портфелем активов (в предположении, что доля рискового актива может меняться со временем и зависеть, возможно, от величины резерва в текущий момент). Эта задача связана с исследованием нелинейных ИДУ и также выходит за рамки данной работы.
Авторы выражают благодарность рецензенту за внимательное отношение к работе и полезные замечания, которые способствовали улучшению статьи.
Список литературы
Asmussen S., Albrecher H. Ruin Probabilities. Advanced series on statistical science and applied probability. V. 14. Singapore: World Scientific, 2010. 602 p.
Kabanov Yu., Pergamenshchikov S. In the insurance business risky investments are dangerous: the case of negative risk sums // Finance Stochast. 2016. V. 20. № 2. P. 355–379.
Grandell J. Aspects of Risk Theory. New York: Springer, 1991. 175 p.
Cramér H. Collective Risk Theory: A Survey of the Theory from the Point of View of the Theory of Stochastic Processes. Stockholm: AbNordiska Bokhandeln, 1955. P. 1–92.
Королев В.Ю., Бенинг В.Е., Шоргин С.Я. Математические основы теории риска. М.: Физматлит, 2007. 383 с.
Paulsen J., Gjessing H.K. Ruin theory with stochastic return on investments // Adv. Appl. Probab. 1997. V. 29. № 4. P. 965–985.
Frolova A., Kabanov Yu., Pergamenshchikov S. In the insurance business risky investments are dangerous // Finance Stochast. 2002. V. 6. № 2. P. 227–235.
Pergamenshchikov S., Zeitouny O. Ruin probability in the presence of risky investments // Stochastic Process. Appl. 2006. V. 116. № 2. P. 267–278.
Paulsen J. On Cramer-like asymptotics for risk processes with stochastic return on investments // Ann. Appl. Probab. 2002. V. 12. № 4. P. 1247–1260.
Hipp C., Plum M. Optimal investment for insurers // Insurance Math. Econom. 2000. V. 27. № 2. P. 215–228.
Hipp C., Plum M. Optimal investment for investors with state dependent income, and for insurers // Finance Stochast. 2003. V. 7. № 3. P. 299–321.
Azcue P., Muler M. Optimal investment strategy to minimize the ruin probability of an insurance company under borrowing constraints // Insurance Math. Econom. 2009. V. 44. № 1. P. 26–34.
Belkina T., Hipp C., Luo S., Taksar M. Optimal constrained investment in the Cramer-Lundberg model // Scandinavian Actuarial Journal. 2014. Issue 5. P. 383–404.
Белкина Т.А., Конюхова Н.Б., Курочкин С.В. Сингулярная краевая задача для интегродифференциального уравнения в модели страхования со случайными премиями: анализ и численное решение // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 10. С. 1812–1846.
Belkina T., Konyukhova N., Kurochkin S. Singular problems for integro-differential equations in dynamic insurance models // Differential and Difference Equations with Applications / Series: Springer Proceedings in Mathematics and Statistics. 2013. V. 47. P. 27–44 (arXiv:1511.08666v1 [q-fin.RM] Nov 2015. 17 p.; Cornell University Library, e–print: http://arxiv.org/abs/1511.08666).
Белкина Т.А., Конюхова Н.Б., Курочкин С.В. Сингулярные начальные и краевые задачи для интегродифференциальных уравнений в динамических моделях страхования с учетом инвестиций // Современная математика. Фундаментальные направления. 2014. Т. 53. С. 5–29.
Belkina T.A., Konyukhova N.B., Kurochkin S.V. Singular initial-value and boundary-value problems for integrodifferential equations in dynamical insurance models with investments // Journal of Mathematical Sciences. 2016. V. 218. № 4. P. 369–394 (Springer Science+Business Media, New York; https://doi.org/10.1007/s10958-016-3037-1).
Белкина Т.А., Конюхова Н.Б., Курочкин С.В. Динамические модели страхования с учетом инвестиций: сингулярные задачи с ограничениями для интегродифференциальных уравнений // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 1. С. 47–98.
Wang G., Wu R. Distributions for the risk process with a stochastic return on investments // Stochastic Process. Appl. 2001. V. 95. P. 329–341.
Belkina T. Risky investment for insurers and sufficiency theorems for the survival pobability // Markov Processes Relat. Fields. 2014. № 20. P. 505–525.
Belkina T.A., Konyukhova N.B., Slavko B.V. Risky investments and survival in the dual risk model // VIII Moscow Intern. Conf. on Operations Research (ORM-2016; Moscow, October 17–22, 2016): Proceedings: V. I. P. 130–133. M.: MAKS Press, 2016.
Belkina T.A., Konyukhova N.B., Slavko B.V. Analytic-numerical investigations of singular problems for survival probability in the dual risk model with simple investment strategies // Analytical and Computational Methods in Probability Theory and Its Applications (V. V. Rykov et al. (Eds.)) / Series: Lecture Notes in Computer Science (LNCS). 2017. V. 10684. P. 236–250 (Springer International Publishing AG 2017; https://doi.org/10.1007/978-3-319-71504-9).
Belkina T.A., Konyukhova N.B. On sufficient conditions for survival probability in the life annuity insurance model with risk-free investment income // In: “IX Moscow International Conference on Operations Research (ORM2018; Moscow, October 22–27, 2018). Proceedings. In two volumes / Editor-in-chief F. Ereshko”. Moscow: MAKS Press, 2018. V. 1. P. 213–218.
Белкина Т.А., Кабанов Ю.М. Вязкостные решения интегродифференциальных уравнений для вероятности неразорения // Теория вероятностей и ее применения. 2015. Т. 60. № 4. С. 802–810.
Karatzas I., Shreve S.E. Brownian Motion and Stochastic Calculus. New York: Springer–Verlag, 1988. 470 p.
Беллман Р. Теория устойчивости решений дифференциальных уравнений. М.: Изд-во иностр. лит., 1954. 216 с.
Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. М.: Изд-во иностр. лит., 1958. 474 с.
Вазов В. Асимптотические разложения решений обыкновенных дифференциальных уравнений. М.: Мир, 1968. 464 с.
Конюхова Н.Б. Сингулярные задачи Коши для систем обыкновенных дифференциальных уравнений // Ж. вычисл. матем. и матем. физ. 1983. Т. 23. № 3. С. 629–645.
Биргер Е.С., Ляликова (Конюхова) Н.Б. О нахождении для некоторых систем обыкновенных дифференциальных уравнений решений с заданным условием на бесконечности // I: Ж. вычисл. матем. и матем. физ. 1965. Т. 5. № 6. С. 979–990; II: Ж. вычисл. матем. и матем. физ. 1966. Т. 6. № 3. С. 446–453.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики
Пн.-пт.: 10.00-19.00