1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 59, № 11, 2019

Журнал вычислительной математики и математической физики, 2019, T. 59, № 11, стр. 1883-1898

Уравнение типа Власова–Максвелла–Эйнштейна и переход к слаборелятивистскому приближению

В. В. Веденяпин 1, 2, *, Н. Н. Фимин 1, В. М. Чечеткин 1, 3

1 Федеральный Исследовательский Центр Институт прикладной математики им. М.В. Келдыша Российской Академии наук
125047 Москва, Миусская пл., 4, Россия

2 Российский университет дружбы народов
117198 Москва, ул. Миклухо-Маклая, 6, Россия

3 Институт автоматизации проектирования РАН
123056 Москва, 2-ая Брестcкая ул., 19/18, Россия

* E-mail: vicveden@yahoo.com

Поступила в редакцию 16.12.2018
После доработки 16.12.2018
Принята к публикации 08.07.2019

Полный текст (PDF)

Аннотация

В настоящей статье рассмотрен лагранжиан гравитации общей теории относительности совместно с лагранжианом электромагнетизма. Из него выведены уравнения типа Власова в общем, нерелятивистском и слаборелятивистском пределах. Предложены выражения для получающихся поправок в уравнении Пуассона, которые могут давать вклад в эффективное действие темной материи и темной энергии. Библ. 50. Фиг. 1.

Ключевые слова: модель Милна–МакКри, уравнение Власова–Максвелла–Эйнштейна, лагранжиан, космологическая постоянная, действие Гильберта.

1. ВВЕДЕНИЕ

Исходя из классического действия Максвелла–Эйнштейна–Гильберта [1]–[3] можно единообразным способом получить уравнения Власова–Максвелла–Эйнштейна и их нерелятивистские и слаборелятивистские аналоги. При этом вначале варьируем траектории частиц, получая уравнения движения, а потом, переходя к функции распределения, вводим уравнение Лиувилля. После этого варьируем поля, для чего предварительно переписываем действия через функции распределения (именно так получаются уравнения типа Власова при выводе их из классических лагранжианов). Мы иллюстрируем это в более простых ситуациях нерелятивизма и слабого релятивизма. При таком выводе мы получаем возможность анализа $\Lambda $-члена в уравнениях общей теории относительности (ОТО), получая выражения, которые приводят к таким же математическим выводам, как при эмпирическом введении А. Эйнштейном в полевые уравнения этого члена (использующегося для объяснения темной энергии [4], [5]). Отсюда делается вывод о совпадении: 1) темной энергии с космической плазмой, 2) “антигравитации” как атрибута темной энергии, с электростатическим отталкиванием (любое другое дальнодействующее отталкивание “фантомных полей” былo бы уже обнаруженo).

В разд. 2 настоящей статьи обсуждается модель Милна–МакKри – нерелятивистский аналог решения Фридмана, и возможность ее получения с помощью уравнения Власова–Пуассона; в разд. 3 выводится уравнение движения релятивистской частицы и уравнение Лиувилля (согласно [27]); в разд. 4 рассматривается общее релятивистское действие полей и частиц, действие для частиц переписывается через функцию распределения. Это позволяет математическую аналогию $\Lambda $-члена с другими слагаемыми действия. Выводятся уравнения Власова–Максвелла–Эйнштейна, следуя [27]. В разд. 5 предлагается нерелятивистский аналог действия, из которого получается уравнение Власова–Пуассона–Пуассона (первый Пуассон имеет отношение к электростатике, второй – к гравитации) для гравитации и электростатики (здесь мы следуем [7], [10], [12], [25], [27]). В разд. 6 получаем нерелятивистский предел действия Эйнштейна–Гильберта и уравнение Власова–Пуассона с космологическим $\Lambda $-членом. В разд. 7 учитывается электромагнетизм, при этом выписываются выражения, которые имеют с точки зрения математики то же происхождение, что и $\Lambda $-член.

2. РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ И МОДЕЛЬ МИЛНА–МАККРИ

Понятие “расширяющейся Вселенной” появилось после того, как в 1922 г. А.А. Фридман нашел точные нестационарное решения уравнений общей теории относительности А. Эйнштейна, а Э. Хаббл в 1929 г. в результате анализа астрономических наблюдений обнаружил красное смещение в спектрах галактик, подтверждающее физическую правомерность этих решений [3]. Представляется желательным обсудить результаты А.А. Фридмана с различных точек зрения и обобщить их.

Нерелятивистский аналог данных решений – самогравитирующий шар или модель Милна–МакКри [6]. В то же время они могут быть получены как точные решения уравнений Власова–Пуассона для тяготения, что мы и используем в дальнейшем для обобщений. Уравнения Власова–Пуассона для однокомпонентной системы частиц (массой $m$) имеют вид

(1)
$\frac{{\partial f}}{{\partial t}} + \left( {\frac{{\mathbf{p}}}{m},\frac{{\partial f}}{{\partial {\mathbf{x}}}}} \right) - \left( {\frac{{\partial U}}{{\partial {\mathbf{x}}}},\frac{{\partial f}}{{\partial {\mathbf{p}}}}} \right) = 0,\quad \Delta U = 4\pi m\gamma \int {f({\mathbf{x}},{\mathbf{p}},t)d{\mathbf{p}}} .$
Здесь $f({\mathbf{x}},{\mathbf{p}},t)$ – функция распределения гравитирующих объектов (например, звездных скоплений, ионов космической плазмы и т.п.) по импульсам ${\mathbf{p}} \in {{\mathbb{R}}^{3}}$ в точке пространства ${\mathbf{x}} \in {{\mathbb{R}}^{3}}$ в момент времени $t \in {{\mathbb{R}}^{1}}$. Первое уравнение в системе (1) – это уравнение сдвига функции распределения (по характеристикам) в силовом поле ${\mathbf{G}} = - \nabla U$, a второе – уравнение Пуассона, показывающее, что сила гравитации ${\mathbf{G}}$ caма зависит от функции распределения $f({\mathbf{x}},{\mathbf{p}},t)$. Решения типа Милна–МакКри могут быть найдены cледующей подстановкой (использующей лагранжевы координаты ${\mathbf{q}}$) [7]:
(2)
$f({\mathbf{x}},{\mathbf{p}},t) = \int {\delta ({\mathbf{x}} - {\mathbf{Y}}({\mathbf{q}},t))\delta ({\mathbf{p}} - {\mathbf{Q}}({\mathbf{q}},t))\rho ({\mathbf{q}})d{\mathbf{q}}} .$
Такая функция $f$ является решением системы (1), если ${\mathbf{Y}},\;{\mathbf{Q}}$ удовлетворяют соответствующим гамильтоновым уравнениям “континуума тел”:

(3)
${\mathbf{\dot {Y}}}({\mathbf{q}},t) = \frac{1}{m}{\mathbf{Q}}({\mathbf{q}},t),\quad {\mathbf{\dot {Q}}}({\mathbf{q}},t) = \gamma m\nabla \int {\frac{{{\mathbf{q}}{\kern 1pt} '\rho ({\mathbf{q}}{\kern 1pt} ')d{\mathbf{q}}{\kern 1pt} '}}{{\left| {{\mathbf{Y}}({\mathbf{q}},t) - {\mathbf{Y}}({\mathbf{q}}',t)} \right|}}} .$

Рассматриваемые решения Милна–МакКри сферически симметричны, т.e. ${\mathbf{Y}}({\mathbf{q}},t) = \mathcal{R}(r,t){\mathbf{q}}{\text{/}}\left| {\mathbf{q}} \right|$, где $r = \left| {\mathbf{q}} \right|$. Скорости частиц направлены вдоль радиус–векторов частиц, и тоже зависят только от величин $r$ и $t$. Фактически, переменная $r$ идентифицирует сферические слои, которым принадлежат частицы с координатой ${\mathbf{q}}$. Воспользуемся тем, что однородный сферический слой действует на точку во внутренней области с нулевой силой, а на точку во внешней области – аналогично точке с массой, равной массе слоя, и расположенной в геометрическом центре слоя. Получаем следующие уравнения:

(4)
$\frac{{{{\partial }^{2}}\mathcal{R}}}{{\partial {{t}^{2}}}} = - \gamma \frac{{M(r)}}{{{{\mathcal{R}}^{2}}(r,t)}},$
где $M(r)$ – масса шара с лагранжевой координатой, меньшей $r$. Интегрируя это уравнение, получаем интеграл энергии
(5)
$\frac{1}{2}{{\left( {\frac{{\partial{ \mathcal{R}}}}{{\partial t}}} \right)}^{2}} - \gamma \frac{{M(r)}}{{\mathcal{R}(r,t)}} = C.$
Случай $C > 0$ соответствует открытой модели Вселенной (бесконечное расширение), случай $C < 0$ отвечает закрытой модели (в которой расширение на определенном этапе сменяется сжатием). Преобразуем уравнение (5), разделив его на ${{\mathcal{R}}^{2}}$, следуя [6]:
$\frac{1}{2}{{\left( {\frac{{\dot {\mathcal{R}}}}{\mathcal{R}}} \right)}^{2}} \equiv \frac{1}{2}{{H}^{2}} = \gamma \frac{{M(r)}}{{{{\mathcal{R}}^{3}}}} + \frac{C}{{{{\mathcal{R}}^{2}}}}.$
Величина $H = \dot {\mathcal{R}}{\text{/}}\mathcal{R}$ называется постоянной Хаббла, она характеризует скорость разбегания галактик. Первое слагаемое в правой части пропорционально плотности $\rho = 3M{\text{/}}(4\pi {{\mathcal{R}}^{3}})$ (поскольку величина $4\pi {{\mathcal{R}}^{3}}{\text{/}}3$ есть текущий объем шара радиуса $\mathcal{R}$). Случай $C = 0$ соответствует критической плотности ${{\rho }_{c}} = 3{{H}^{2}}{\text{/}}(8\pi \gamma )$. Плотность, большая критической, дает закрытую модель, меньшая – открытую. Эта модель типа Фридмана будет давать хорошую иллюстрацию и с лямбда-членом.

3. УРАВНЕНИЕ ДВИЖЕНИЯ ЧАСТИЦ В ГРАВИТАЦИОННОМ И ЭЛЕКТРОМАГНИТНОМ ПОЛЕ И УРАВНЕНИЕ ЛИУВИЛЛЯ

Общерелятивистское действие для движущейся заряженной (c зарядом $e$) частицы массы $m$ в присутствии гравитационного и электромагнитного поля может быть записан в следующем виде:

${{S}_{1}} = - mc\int\limits_0^{{{\lambda }_{{{\text{max}}}}}} {\sqrt {{{g}_{{\mu \nu }}}({\mathbf{X}})\frac{{d{{X}^{\mu }}({\mathbf{q}},\lambda )}}{{d\lambda }}\frac{{d{{X}^{\nu }}({\mathbf{q}},\lambda )}}{{d\lambda }}} d\lambda } - \frac{e}{c}\int {{{A}_{\mu }}\frac{{d{{X}^{\mu }}}}{{d\lambda }}d\lambda } ,$
где: ${{g}_{{\mu \nu }}}({\mathbf{X}})$ – фундаментальный тензор 4-мерного пространства–времени (${\mathbf{X}} = {{\{ {{X}^{\mu }}\} }_{{\mu = 1,...,4}}}$), ${{A}_{\mu }}({\mathbf{X}}) \equiv \{ \varphi (X);A(X)\} $ – 4-потенциал электромагнитного поля, ${\mathbf{q}}$ – лагранжев параметр частицы; переменная $\lambda \in {{\mathbb{R}}^{ + }}$ – произвольный параметр.

Введем в рассмотрение также действие с модифицированным первым членом

${{S}_{2}} = - \frac{{mc}}{{2\sqrt I }}\int\limits_0^{{{\lambda }_{{{\text{max}}}}}} {{{g}_{{\mu \nu }}}({\mathbf{X}})\frac{{d{{X}^{\mu }}({\mathbf{q}},\lambda )}}{{d\lambda }}\frac{{d{{X}^{\nu }}({\mathbf{q}},\lambda )}}{{d\lambda }}d\lambda } - \frac{e}{c}\int {{{A}_{\mu }}\frac{{d{{X}^{\mu }}}}{{d\lambda }}d\lambda } .$
В литературе (cм., например, [1]–[3], [8]) подобная операция (переход к новой форме действия) производится без электромагнитного поля (второго слагаемого в действиях), и обосновывается тем, что уравнения движения частицы в гравитационном поле будут одинаковыми в обоих случаях (т.e. при использовании действий ${{S}_{1}}$ и ${{S}_{2}}$ с заменой параметра $\lambda $ на “натуральный” параметр $s$ или собственное время $\tau = s{\text{/}}c$).

Поставим вопрос обоснования эквивалентности действий по признаку совпадения уравнений Эйлера–Лагранжа. Рассмотрим два типа действий c ядрами–лагранжианами следующей общей формы:

$\begin{gathered} {{S}_{I}} = k\int {L\left( {{\mathbf{X}},\frac{{d{\mathbf{X}}}}{{d\lambda }}} \right)d\lambda } + \int {{{L}_{1}}\left( {{\mathbf{X}},\frac{{d{\mathbf{X}}}}{{d\lambda }}} \right)d\lambda } , \\ {{S}_{{II}}} = \int {h(L)d\lambda } + \int {{{L}_{1}}\left( {{\mathbf{X}},\frac{{d{\mathbf{X}}}}{{d\lambda }}} \right)d\lambda } , \\ \end{gathered} $
где $h(L)$ – некоторая (гладкая) произвольная функция своего аргумента. Сравним уравнения Эйлера–Лагранжа, получаемые из действий ${{S}_{I}}$ и ${{S}_{{II}}}$.

Лемма (об эквивалентности действий ${{S}_{I}}$ и ${{S}_{{II}}}$). Достаточные условия для эквивалентности, то есть совпадения уравнений Эйлера–Лагранжа, действий ${{S}_{I}}$ и ${{S}_{{II}}}$ таковы:

1) лагранжиан $L({\mathbf{X}},{{{\mathbf{X}}}_{\lambda }})$ должен быть интегралом движения для действия ${{S}_{I}}$;

2) коэффициент $k$ в определении ${{S}_{I}}$ должен совпадать с производной функции $h(L)$ из определения действия ${{S}_{{II}}}$: $k = dh(L){\text{/}}dL$. Если лагранжиан не равен нулю, то коэффициент $k$ определяется единственным образом.

Доказательство получается прямым варьированием действия ${{S}_{{II}}}$, генерирующего уравнения Эйлера–Лагранжа [1]–[12], [8]:

$\frac{{{{d}^{2}}h}}{{d{{L}^{2}}}}\frac{{dL}}{{d\lambda }}\frac{{\partial L}}{{\partial {{{\mathbf{X}}}_{\lambda }}}} + \frac{{dh}}{{dL}}\frac{d}{{d\lambda }}\frac{{\partial L}}{{\partial {{{\mathbf{X}}}_{\lambda }}}} + \frac{d}{{d\lambda }}\frac{{\partial {{L}_{1}}}}{{\partial {{{\mathbf{X}}}_{\lambda }}}} = \frac{{dh}}{{dL}}\frac{{\partial L}}{{\partial {\mathbf{X}}}} + \frac{{\partial {{L}_{1}}}}{{\partial {\mathbf{X}}}},$
и сравнением получающихся уравнений с соответствующими уравнениями движения для действия ${{S}_{I}}$:

$k\frac{d}{{d\lambda }}\frac{{\partial L}}{{\partial {{{\mathbf{X}}}_{\lambda }}}} + \frac{d}{{d\lambda }}\frac{{\partial {{L}_{1}}}}{{\partial {{{\mathbf{X}}}_{\lambda }}}} = k\frac{{\partial L}}{{\partial {\mathbf{X}}}} + \frac{{\partial {{L}_{1}}}}{{\partial {\mathbf{X}}}}.$

Cледствием из данной Леммы является тот факт, что ранее введенные действия ${{S}_{1}}$ и ${{S}_{2}}$ эквивалентны в смысле Леммы, то есть обладают одинаковыми уравнениями движения. Действительно, для этих действий имеем

$h(L) = - mc\sqrt L ,\quad L = {{g}_{{\mu \nu }}}\frac{{d{{X}^{\mu }}}}{{d\lambda }}\frac{{d{{X}^{\nu }}}}{{d\lambda }},\quad {{L}_{1}} = - \frac{e}{c}{{A}_{\mu }}\frac{{d{{X}^{\mu }}}}{{d\lambda }}.$
Условие 1) леммы выполнено по теореме Эйлера об однородных функциях: функция Гамильтона (интеграл движения!) для действия ${{S}_{2}}$, получаемая применением преобразования Лежандра, пропорциональна лагранжиану $L = {{g}_{{\mu \nu }}}\mathop {{{X}^{\mu }}}\nolimits_\lambda \mathop {{{X}^{\nu }}}\nolimits_\lambda $, и лагранжиан ${{L}_{1}}$ – 1-й cтепени по “скоростной” переменной $\mathop {{{X}^{\mu }}}\nolimits_\lambda $; условие 2) выполнено, поскольку коэффициент $k$ в ${{S}_{I}}$ равен в точности производной функции $h(L)$ из ${{S}_{{II}}}$: $k = dh{\text{/}}dL = - mc{\text{/}}(2\sqrt L )$ (это соотношение проясняет физический смысл величины $I$, т.е. она численно равна сохраняющейся величине лагранжиана $L$ и пропорциональна соответствующему ему гамильтониану).

Выпишем уравнения Эйлера–Лагранжа для действий ${{S}_{1}}$ или ${{S}_{2}}$ – в соответствии с леммой, они идентичны (в отличие от обычной процедуры [1]–[3] при варьировании ${{S}_{1}}$ величину интервала полагаем равной не единице, а $\sqrt I $):

(6)
$\frac{{mc}}{{\sqrt I }}\frac{d}{{d\lambda }}\left( {{{g}_{{\mu \nu }}}\frac{{d{{X}^{\nu }}}}{{d\lambda }}} \right) + \frac{e}{c}\frac{{d{{A}_{\mu }}}}{{d\lambda }} = \frac{{mc}}{{2\sqrt I }}\frac{{\partial {{g}_{{\nu \zeta }}}}}{{\partial {{X}^{\mu }}}}\frac{{d{{X}^{\nu }}}}{{d\lambda }}\frac{{d{{X}^{\zeta }}}}{{d\lambda }} + \frac{e}{c}\frac{{\partial {{A}_{\nu }}}}{{\partial {{X}^{\mu }}}}\frac{{d{{X}^{\nu }}}}{{d\lambda }}.$

Отсюда видно, что при отсутствии электромагнитного взаимодействия между частицами величинa $mc{\text{/}}\sqrt I $ cокращается, и уравнения движения могут быть равносильным образом записаны с использованием как параметра $\lambda $, так и параметра собственного интервала $s$. Однако учет электромагнитного взаимодействия приводит при использовании различных параметров к различающимся уравнениям. Хотя, как можно видеть из уравнения (6), можно в принципе перейти к аффинному параметру $s$, выразив $d\lambda $ через $ds$ и $I$: $ds = \sqrt I d\lambda $.

В многочастичных системах такая возможность отсутствует. Рассмотрим действиe, аналогичное ${{S}_{1}}$, но для системы многих частиц с различающимися массами ${{m}_{a}}$ и зарядами ${{e}_{a}}$ ($a = \overline {1,N} $):

${{S}_{{1,\Sigma }}} = - \sum\limits_a \,{{m}_{a}}c\int {\sqrt {{{g}_{{\mu \nu }}}\frac{{dX_{a}^{\mu }}}{{d\lambda }}\frac{{dX_{a}^{\nu }}}{{d\lambda }}} d\lambda } - \sum\limits_a \,\frac{{{{e}_{a}}}}{c}\int {{{A}_{\mu }}\frac{{dX_{a}^{\mu }}}{{d\lambda }}d\lambda } .$
Снова переходим к лагранжиану, квадратичному по скоростям, и получаем эквивалентное действие:
${{S}_{{2,\Sigma }}} = - \sum\limits_a \,\frac{{{{m}_{a}}c}}{{2\sqrt {{{I}_{a}}} }}\int {{{g}_{{\mu \nu }}}({{{\mathbf{X}}}_{a}})} \frac{{dX_{a}^{\mu }}}{{d\lambda }}\frac{{dX_{a}^{\nu }}}{{d\lambda }}d\lambda - \sum\limits_a \,\frac{{{{e}_{a}}}}{c}\int {{{A}_{\mu }}\frac{{dX_{a}^{\mu }}}{{d\lambda }}d\lambda } .$
Отметим здесь появление индекса $a$, нумерующего частицы, у интеграла ${{I}_{a}}$: величины этих интегралов, обозначающих величину интервала разных частиц, не обязательно одинаковы. Этим мы синхронизовали собственное время разных частиц $d{{s}_{a}} = \sqrt {{{I}_{a}}} d\lambda $ в следующем смысле: 1) установили, что невозможность синхронизации самих интервалов $d{{s}_{a}}$ связана с различными величинами интегралов ${{I}_{a}}$; 2) показали, как различные собственные времена связаны между собой: параметр $\lambda $ для всех частиц один и тот же. Отметим, что интегралы ${{I}_{a}}$ зависят от параметризации, но их отношение не зависит (${{I}_{{{{a}_{1}}}}}{\text{/}}{{I}_{{{{a}_{2}}}}} \ne \phi (\lambda )$, ${{a}_{{1,2}}} \in \{ 1,...,N\} $).

Для описания динамики многочастичной системы, ассоциированной с действиями ${{S}_{{1,\Sigma }}}$ или ${{S}_{{2,\Sigma }}}$, можно ввести стандартным образом канонические (“длинные”) [1–3] импульсы:

${{({{Q}_{a}})}_{\mu }} = \frac{{\partial L}}{{\partial V_{a}^{\mu }}} = - \frac{{{{m}_{a}}c}}{{\sqrt {{{I}_{a}}} }}{{g}_{{\mu \nu }}}({{{\mathbf{X}}}_{a}})V_{a}^{\nu } - \frac{{{{e}_{a}}}}{c}{{A}_{\mu }}({{{\mathbf{X}}}_{a}}),\quad V_{a}^{\nu } \equiv \frac{{\partial X_{a}^{\nu }}}{{\partial \lambda }}.$
Очевидным образом можно получить явное выражение скоростей через длинные импульсы:
$V_{a}^{\nu } = - \frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}{{g}^{{\mu \nu }}}({{{\mathbf{X}}}_{a}})\left( {{{{({{Q}_{a}})}}_{\mu }} + \frac{{{{e}_{a}}}}{c}{{A}_{\mu }}} \right).$
Соответственно второе уравнение гамильтоновой пары уравнений, ассоциированной с канонически сопряженными переменными $({{{\mathbf{X}}}_{a}},{{{\mathbf{Q}}}_{a}})$:
$\frac{{d{{{({{Q}_{a}})}}_{\mu }}}}{{d\lambda }} = \sum\limits_a \,\frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}\left( {{{{({{Q}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{A}_{\zeta }}({{{\mathbf{X}}}_{a}})} \right)\frac{{\partial {{g}^{{\zeta \nu }}}}}{{\partial X_{a}^{\mu }}}\left( {{{{({{Q}_{a}})}}_{\nu }} + \frac{{{{e}_{a}}}}{c}{{A}_{\nu }}({{{\mathbf{X}}}_{a}})} \right) + \frac{{{{e}_{a}}\sqrt {{{I}_{a}}} }}{{{{m}_{a}}{{c}^{2}}}}\left( {{{{({{Q}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{A}_{\zeta }}({{{\mathbf{X}}}_{a}})} \right){{g}^{{\zeta \xi }}}\frac{{\partial {{A}_{\xi }}({{{\mathbf{X}}}_{a}})}}{{\partial X_{a}^{\mu }}}.$
При этом соответствующая этим уравнениям функция Гамильтона имеет вид
$H = \sum\limits_a \,\frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}\left( {{{{({{Q}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{A}_{\zeta }}({{{\mathbf{X}}}_{a}})} \right){{g}^{{\zeta \nu }}}\left( {{{{({{Q}_{a}})}}_{\nu }} + \frac{{{{e}_{a}}}}{c}{{A}_{\nu }}({{{\mathbf{X}}}_{a}})} \right).$
Здесь интегралы $\sqrt {{{I}_{a}}} $ осуществляют синхронизацию времен, приводя к дифференцированию по одному и тому же параметру $\lambda $: соотношение $d{{s}_{a}} = \sqrt {{{I}_{a}}} d\lambda $ показывает, что получаются уравнения, где можно перейти к собственным (вообще говоря, различающимся) временам. Введем (парциальную, для типа $a$ частиц) функцию распределения ${{f}_{a}}({\mathbf{X}},{\mathbf{Q}},\lambda )$ над расширенным 9-мерным фазовым пространством (в соответствии с [9]–[12] индексы $a$ переместились от координат и импульсов к функции распределения ${{f}_{a}}$). Соответствующее уравнение Лиувилля для ${{f}_{a}}$ принимает следующую форму:
(7)
$\begin{gathered} \frac{{\partial {{f}_{a}}({\mathbf{X}},{\mathbf{Q}},\lambda )}}{{\partial \lambda }} - \frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}{{g}^{{\mu \nu }}}({{{\mathbf{X}}}_{a}})\left( {{{{({{Q}_{a}})}}_{\mu }} + \frac{e}{c}{{A}_{\mu }}} \right)\frac{{\partial {{f}_{a}}}}{{\partial {{X}^{\nu }}}} + \left( {\frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}\left( {{{{({{Q}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{A}_{\zeta }}({{{\mathbf{X}}}_{a}})} \right)\frac{{\partial {{g}^{{\zeta \nu }}}}}{{\partial X_{a}^{\mu }}}\left( {{{{({{Q}_{a}})}}_{\nu }} + \frac{{{{e}_{a}}}}{c}{{A}_{\nu }}({{{\mathbf{X}}}_{a}})} \right)} \right. + \\ \,\left. { + \frac{{{{e}_{a}}\sqrt {{{I}_{a}}} }}{{{{m}_{a}}{{c}^{2}}}}\left( {{{{({{Q}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{A}_{\zeta }}({{{\mathbf{X}}}_{a}})} \right){{g}^{{\zeta \xi }}}\frac{{\partial {{A}_{\xi }}}}{{\partial X_{a}^{\mu }}}} \right)\frac{{\partial {{f}_{a}}}}{{\partial {{P}_{\mu }}}} = 0. \\ \end{gathered} $
Уравнения зависят от индекса $a$ через массы ${{m}_{a}}$, заряды ${{e}_{a}}$ и интеграл ${{I}_{a}}$. Выпишем $\lambda $-стационарную форму этого уравнения, когда ${{f}_{a}}$ не зависит от параметра $\lambda $ (именно так обычно записывают уравнение Власова–Эйнштейна, хотя и в более упрощенном случае отсутствия электромагнитного взаимодействия [9], [13], [14]):

$\begin{gathered} - {{g}^{{\mu \nu }}}({{{\mathbf{X}}}_{a}})\left( {{{{({{Q}_{a}})}}_{\mu }} + \frac{e}{c}{{A}_{\mu }}} \right)\frac{{\partial {{f}_{a}}({\mathbf{X}},{\mathbf{P}})}}{{\partial {{X}^{\nu }}}} + \left( {\frac{{\partial {{g}^{{\zeta \nu }}}}}{{\partial X_{a}^{\mu }}}\left( {{{{({{Q}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{A}_{\zeta }}} \right)\left( {{{{({{Q}_{a}})}}_{\nu }} + \frac{{{{e}_{a}}}}{c}{{A}_{\nu }}} \right)} \right. + \\ \left. { + \;\frac{{{{e}_{a}}}}{c}{{F}_{{\mu \nu }}}({\mathbf{X}}){{g}^{{\zeta \nu }}}\left( {{{{({{Q}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{A}_{\zeta }}} \right)} \right)\frac{{\partial {{f}_{a}}}}{{\partial {{P}_{\mu }}}} = 0. \\ \end{gathered} $

Можно сравнить выписанные выше кинетические уравнения с уравнениями Лиувилля, где используются неканонические (“короткие”) импульсы с нулевыми электромагнитными полями действия ${{S}_{{1,\Sigma }}}$: ${{({{P}_{a}})}_{\mu }} = - {{m}_{a}}cI_{a}^{{ - 1/2}}{{g}_{{\mu \nu }}}({{{\mathbf{X}}}_{a}})V_{a}^{\nu }$. Получаемые при этом уравнения негамильтоновы, но бездивергентные:

(8)
$\begin{gathered} \frac{{dX_{a}^{\nu }}}{{d\lambda }} = - \frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}{{g}^{{\mu \nu }}}({\mathbf{X}}){{({{P}_{a}})}_{\mu }}, \\ \frac{{d{{{({{P}_{a}})}}_{\mu }}}}{{d\lambda }} = - \frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}\frac{{\partial {{g}^{{\nu \zeta }}}}}{{\partial {{X}^{\mu }}}}{{({{P}_{a}})}_{\nu }}{{({{P}_{a}})}_{\zeta }} + \frac{{{{e}_{a}}}}{c}\frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}{{F}_{{\mu \nu }}}({{{\mathbf{X}}}_{a}}){{g}^{{\zeta \nu }}}({{{\mathbf{X}}}_{a}}){{({{P}_{a}})}_{\zeta }}. \\ \end{gathered} $
Отметим, что и здесь такая ситуация с синхронизацией времен: собственные времена все различаются, как показывает та же формула $d{{s}_{a}} = \sqrt {{{I}_{a}}} d\lambda $.

Выпишем уравнение Лиувилля, вводя парциальные функции распределения ${{f}_{a}}({\mathbf{X}},{\mathbf{P}},\lambda )$ частиц с массами ${{m}_{a}}$ и зарядами ${{e}_{a}}$ над 9-мерным фазовым $({\mathbf{X}},{\mathbf{P}},\lambda )$-пространством:

$\frac{{\partial {{f}_{a}}({\mathbf{X}},{\mathbf{P}},\lambda )}}{{\partial \lambda }} - \frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}{{g}^{{\mu \nu }}}({\mathbf{X}}){{({{P}_{a}})}_{\mu }}\frac{{\partial {{f}_{a}}}}{{\partial {{X}^{\nu }}}} + \left( { - \frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}\frac{{\partial {{g}^{{\nu \zeta }}}}}{{\partial {{X}^{\mu }}}}{{{({{P}_{a}})}}_{\nu }}{{{({{P}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}\frac{{\sqrt {{{I}_{a}}} }}{{{{m}_{a}}c}}{{F}_{{\mu \nu }}}({\mathbf{X}}){{g}^{{\zeta \nu }}}{{{({{P}_{a}})}}_{\zeta }}} \right)\frac{{\partial {{f}_{a}}}}{{\partial {{P}_{\mu }}}} = 0.$
Это уравнение можно переписать в форме, исключающей параметр $\lambda $, заменяя его на собственный интервал фиксированной ${{a}_{0}}$-й частицы (${{a}_{0}} \in \{ 1,...,N\} $) согласно формуле $d\lambda = d{{s}_{{{{a}_{0}}}}}{\text{/}}\sqrt {{{I}_{{{{a}_{0}}}}}} $:
$\begin{gathered} \frac{{\partial {{f}_{a}}({\mathbf{X}},{\mathbf{P}},s)}}{{\partial {{s}_{{{{a}_{0}}}}}}} - \frac{1}{{{{m}_{a}}c}}\frac{{\sqrt {{{I}_{a}}} }}{{\sqrt {{{I}_{{{{a}_{0}}}}}} }}{{g}^{{\mu \nu }}}({\mathbf{X}}){{({{P}_{a}})}_{\mu }}\frac{{\partial {{f}_{a}}}}{{\partial {{X}^{\nu }}}} + \\ + \;\left( { - \frac{1}{{2{{m}_{a}}c}}\frac{{\sqrt {{{I}_{a}}} }}{{\sqrt {{{I}_{{{{a}_{0}}}}}} }}\frac{{\partial {{g}^{{\nu \zeta }}}}}{{\partial {{X}^{\mu }}}}{{{({{P}_{a}})}}_{\nu }}{{{({{P}_{a}})}}_{\zeta }} + \frac{{{{e}_{a}}}}{c}\frac{1}{{{{m}_{a}}c}}\frac{{\sqrt {{{I}_{a}}} }}{{\sqrt {{{I}_{{{{a}_{0}}}}}} }}{{F}_{{\mu \nu }}}({\mathbf{X}}){{g}^{{\zeta \nu }}}{{{({{P}_{a}})}}_{\zeta }}} \right)\frac{{\partial {{f}_{a}}}}{{\partial {{P}_{\mu }}}} = 0. \\ \end{gathered} $
При этом, как уже было отмечено выше, отношение ${{I}_{a}}{{{\text{/}}}_{{{{a}_{0}}}}}$ не зависит от $\lambda $ (а является только функцией переменной ${\mathbf{X}}$).

Приведем $\lambda $-стационарную форму уравнения Лиувилля, когда ${{f}_{a}} = {{f}_{a}}({\mathbf{X}},{\mathbf{P}})$, т.e. не зависит от параметрической переменной $\lambda $ (при этом сокращаются множители $\sqrt {{{I}_{a}}} {\text{/}}({{m}_{a}}c)$ в левой части уравнения):

$ - {{g}^{{\mu \nu }}}({\mathbf{X}}){{P}_{\mu }}\frac{{\partial {{f}_{a}}({\mathbf{X}},{\mathbf{P}})}}{{\partial {{X}^{\nu }}}} + \left( { - \frac{1}{2}\frac{{\partial {{g}^{{\nu \zeta }}}}}{{\partial {{X}^{\mu }}}}{{P}_{\nu }}{{P}_{\zeta }} + \frac{{{{e}_{a}}}}{c}{{F}_{{\mu \nu }}}({\mathbf{X}}){{g}^{{\zeta \nu }}}{{P}_{\nu }}} \right)\frac{{\partial {{f}_{a}}}}{{\partial {{P}_{\mu }}}} = 0$
(поскольку ${{X}^{0}} = ct$, последнее уравнение в общем случае $t$-нестационарно). B известной авторам литературе подобная форма (для гравитирующих заряженных частиц для функции распределения, зависящей от “короткого” импульса) уравнения Лиувилля отсутствует; c использованием канонических импульсов уравнение Лиувилля выписано – отметим, на уровне интуитивных рассуждений – в некоторых работах, см., например, [13], [14]). Для нейтральных массивных частиц одинаковой массы $m$ над фазовым $({\mathbf{X}},{\mathbf{P}})$–пространством уравнение Лиувилля записано в работах [14], [15] в следующем виде:
$\frac{{{{P}^{\mu }}}}{m}\frac{{\partial f({\mathbf{X}},{\mathbf{P}})}}{{\partial {{X}^{\mu }}}} - \frac{1}{{2m}}{{P}_{\eta }}{{P}_{\zeta }}\frac{{\partial {{g}^{{\eta \zeta }}}}}{{\partial {{X}^{\mu }}}}\frac{{\partial f}}{{\partial {{P}_{\mu }}}} = 0,$
то есть с точностью до переобозначений совпадает с введенным нами $\lambda $-независимым уравнением Лиувилля (без электромагнетизма). Следует, однако, указать на то, что в большинстве публикаций, посвященных уравнению Власова–Эйнштейна, приводится другая форма общерелятивистского уравнения Лиувилля, использующая функцию распределения, зависящую от $4$-скоростей (cм., например, [16], [17]):
${{V}^{\zeta }}\frac{{\partial f}}{{\partial {{X}^{\zeta }}}} + \left( { - \Gamma _{{\eta \mu }}^{\zeta }{{V}^{\eta }}{{V}^{\mu }} + \frac{e}{c}F_{\beta }^{\zeta }{{V}^{\beta }}} \right)\frac{{\partial f}}{{\partial {{V}^{\zeta }}}} = 0$
(практически идентичная данной форма уравнения Лиувилля рассматривается также в работах [18]–[20]).

Пример 1. Рассмотрим частный случай уравнения (6), когда метрика ${{g}_{{\mu \nu }}}$ и компоненты векторного потенциала ${{A}_{\mu }}$ не зависят от временной координаты. Тогда правая часть равенства (6) при индексе $\mu = 0$ аннулируется, и возможно аналитически проинтегрировать левую часть (индекс $a$ опускаем):

$\frac{{mc}}{{\sqrt I }}\left( {{{g}_{{0\nu }}}\frac{{d{{X}^{\nu }}}}{{d\lambda }}} \right) + \frac{e}{c}{{A}_{0}} = {{Q}_{0}}.$
Cмысл получающегося интеграла можно выяснить, взяв постгалилееву метрику
${{g}_{{\mu \nu }}} = {\text{diag}}(1 + 2U{\text{/}}{{c}^{2}}, - 1, - 1, - 1),$
где U – ньютоновcкий гравитационный потенциал (cм., например, [3]). Тогда последнее соотношение преобразуется к форме
(9)
$\frac{{mc}}{{\sqrt I }}\left( {1 + \frac{{2U}}{{{{c}^{2}}}}} \right)\frac{{d{{X}^{0}}}}{{d\lambda }} + \frac{e}{c}{{A}_{0}} = {{Q}_{0}},$
а остальные уравнения Эйлера–Лагранжа системы (6) приобретают вид

$\frac{{mc}}{{\sqrt I }}\frac{d}{{d\lambda }}\frac{{d{{X}^{j}}}}{{d\lambda }} + \frac{{d{{A}_{j}}}}{{d\lambda }} = \frac{{mc}}{{2{{c}^{2}}\sqrt I }}\frac{{\partial U}}{{\partial {{x}^{j}}}}{{\left( {\frac{{d{{X}^{0}}}}{{d\lambda }}} \right)}^{2}} + \frac{e}{c}\frac{{\partial {{A}_{\nu }}}}{{\partial {{X}^{j}}}}\frac{{d{{X}^{\nu }}}}{{d\lambda }},\quad j = 1,2,3.$

Заменяя параметр $\lambda $ из уравнения (9) на время $t$, получаем уравнения движения заряженной частицы в электростатическом поле и в гравитационном потенциале $U$:

$M\frac{{{{d}^{2}}{{x}^{j}}}}{{d{{t}^{2}}}} = M\frac{{\partial U}}{{\partial {{x}^{j}}}} + \frac{e}{c}{{F}_{{\mu j}}}\frac{{d{{X}^{\mu }}}}{{dt}},$
где
$M = ({{Q}_{0}}{\text{/}}c - e{{A}_{0}}{\text{/}}{{c}^{2}}){\text{/}}(1 + 2U{\text{/}}{{c}^{2}})$
есть эффективная масса частицы при суперпозиции полей.

Пример 2. Разберем случай полностью однородной Вселенной: метрика, гравитационное и электромагнитное поля зависят только от времени. В этом случае уравнения (6) интегрируются из общих соображений гамильтоновой механики, но интересно проследить и конкретные детали. Имеем три интеграла движения (для простоты индекс $a$ не вводится):

(10)
$\frac{{mc}}{{\sqrt I }}\left( {{{g}_{{j\nu }}}\frac{{d{{X}^{\nu }}}}{{d\lambda }}} \right) + \frac{e}{c}{{A}_{j}} = {{Q}_{j}},\quad j = 1,2,3.$
Вместо соотношения для нулевой компоненты циклического импульса воспользуемся интегралом энергии $I = {{g}_{{\mu \nu }}}X_{\lambda }^{\mu }X_{\lambda }^{\nu }$. Следовательно, пространственные компоненты “короткого” импульса определяются как функции времени из формулы (9): ${{P}_{j}} = {{p}_{j}} = eA{\text{/}}c - {{Q}_{j}}$, a нулевая (“временная”) компонента определяется как функция времени из определения $I$: ${{g}^{{\xi \mu }}}{{P}_{\mu }}{{P}_{\xi }} = {{m}^{2}}{{c}^{2}}$. Мы пришли к известному соотношению (так называемому условию массовой поверхности [17]), которое ведет к методу Гамильтона–Якоби [3], [8].

Итак, мы получаем следующие уравнения для определения всех координат:

$\frac{{d{{X}^{\mu }}}}{{d\lambda }} = - \frac{{\sqrt I }}{{mc}}{{g}^{{j\mu }}}({{X}^{0}}){{P}_{j}},\quad \mu = \overline {0,3} ;\quad j = \overline {1,3} .$
Исключая отсюда параметр $\lambda $ путем деления трех уравнений (10) (для $j = 1,2,3$) на уравнение для $\mu = 0$, получаем
$\frac{{d{{X}^{i}}}}{{d{{X}^{0}}}} = \frac{{{{g}^{{ji}}}({{X}^{0}}){{P}_{j}}({{X}^{0}})}}{{{{g}^{{0j}}}({{X}^{0}}){{P}_{j}}({{X}^{0}})}} = \frac{{{{g}^{{ji}}}({{X}^{0}})(e{{A}_{j}}{\text{/}}c - {{Q}_{j}})}}{{{{g}^{{0j}}}({{X}^{0}})(e{{A}_{j}}{\text{/}}c - {{Q}_{j}})}},\quad i = 1,2,3.$
Мы получили уравнения с заданными функциями только временной компоненты, которые просто интегрируются. Такие уравнения можно будет применить к вопросу о темной энергии и темной материи. Эти решения обобщают Вселенную де Ситтера и другие Вселенные [28].

4. ОБЩЕРЕЛЯТИВИСТСКОЕ СУММАРНОЕ ДЕЙСТВИЕ ДЛЯ СИСТЕМЫ ЧАСТИЦ С УЧЕТОМ ПОЛЕВЫХ ДЕЙСТВИЙ

Рассмотрим общее действие для материи с электромагнитным полем в гравитационном поле, представляющee собой сумму действия ${{S}_{p}}$ ($particles$), действия Максвелла ${{S}_{f}}$ для электромагнитого поля ($f$ oт $fields$) c учетом взаимодействия c частицами ${{S}_{{pf}}}$ ($particles - fields$) и действия ${{S}_{g}}$ ($gravity$) Эйнштейна–Гильберта [1]–[3]) (по повторяющимся верхним и нижним индексам идет суммирование):

(11)
$\begin{gathered} S_{4}^{L} = - \sum\limits_a \,{{m}_{a}}c\sum\limits_{\mathbf{q}} \,\int\limits_0^{{{\lambda }_{{\max }}}} \,\sqrt {{{g}_{{\mu \nu }}}\frac{{dX_{a}^{\mu }({\mathbf{q}},\lambda )}}{{d\lambda }}\frac{{dX_{a}^{\nu }({\mathbf{q}},\lambda )}}{{d\lambda }}} d\lambda - \sum\limits_a \,\frac{{{{e}_{a}}}}{c}\sum\limits_{\mathbf{q}} \,\int\limits_0^{{{\lambda }_{{\max }}}} \,{{A}_{\mu }}({{{\mathbf{X}}}_{a}}({\mathbf{q}},\lambda ))\frac{{dX_{a}^{\mu }({\mathbf{q}},\lambda )}}{{d\lambda }}d\lambda - \\ - \;\frac{1}{{16\pi c}}\int {{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}}{{{\left| g \right|}}^{{1/2}}}{{d}^{4}}X} + \mathcal{K}\int {{{{\left| g \right|}}^{{1/2}}}(R + \Lambda ){{d}^{4}}X} \equiv S_{p}^{L} + S_{{pf}}^{L} + S_{f}^{L} + S_{g}^{L},\quad \mathcal{K} = \frac{{ - {{c}^{3}}}}{{16\pi \gamma }}, \\ \end{gathered} $
где: $a$ – индекс сорта частиц с массой ${{m}_{a}}$ и зарядом ${{e}_{a}}$, $a = 1,...,{{a}_{{\max }}}$, лагранжев параметрический индекс ${\mathbf{q}}$ идентифицирует частицы (числом ${{N}_{a}}$) внутри сорта $a$, ${{{\mathbf{X}}}_{a}}({\mathbf{q}},\lambda )$ – 4-мерная координата ${\mathbf{q}}$-частицы сорта $a$ ($\mu ,\nu = 0,1,2,3$), $d\lambda = d{{s}_{a}}{\text{/}}\sqrt {{{I}_{a}}} $; ${{A}_{\mu }} = (\phi ,{\mathbf{A}})$ есть 4-мерный потенциал, ${{F}_{{\mu \nu }}} = {{A}_{{\mu ;\nu }}} - {{A}_{{\nu ;\mu }}}$ – тензор напряженности электромагнитного поля:
${{F}_{{\mu \nu }}} = \left( {\begin{array}{*{20}{c}} 0&{{{E}_{1}}}&{{{E}_{2}}}&{{{E}_{3}}} \\ { - {{E}_{1}}}&0&{ - {{H}_{3}}}&{{{H}_{2}}} \\ { - {{E}_{2}}}&{{{H}_{3}}}&0&{ - {{H}_{1}}} \\ { - {{E}_{3}}}&{ - {{H}_{2}}}&{{{H}_{1}}}&0 \end{array}} \right),\quad {{F}^{{\mu \nu }}} = {{g}^{{\mu \eta }}}{{g}^{{\nu \zeta }}}{{F}_{{\eta \zeta }}},$
где ${{g}_{{\mu \nu }}}({\mathbf{X}})$ – метрический тензор ($g = {\text{det}}{{g}_{{\mu \nu }}}$), $R$ – cкаляр Риччи.

Дальнейшее рассмотрение структуры действия $S_{4}^{L}$ может проводиться на основании двух подходов: если исключить из рассмотрения параметр $\lambda $ и пытаться исследовать соответствующие уравнения движения и кинетические уравнения, производя при необходимости определенные упрощения, и, в качестве альтернативы, принять в качестве основы 9-мерное расширенное фазовое пространство и развивать надлежащий формализм для получения уравнений типа Лиувилля и Власова.

В настоящей статье мы будем действовать в основном в соответствии с первой методикой, поскольку априори специальное внимание мы полагали уделить постньютоновскому приближению, в котором можно перейти от параметра $\lambda $ к переменной единого для всей системы времени $t$. Перепишем действие $S_{4}^{L}$, заменяя скорости $X_{\lambda }^{\mu },X_{\lambda }^{\nu }$ в первом и втором слагаемых правой части определения (11), в соответствии с результатами разд. 3 (cм. формулу (8)):

$\frac{{dX_{a}^{\mu }({\mathbf{q}})}}{{d\lambda }} \to \frac{{dX_{a}^{\mu }({\mathbf{q}})}}{{d{{t}_{a}}}}\frac{{d{{t}_{a}}}}{{d\lambda }} = c\frac{{{{g}^{{\xi \mu }}}({{{\mathbf{X}}}_{a}}({\mathbf{q}})){{{({{P}_{\xi }})}}_{a}}({\mathbf{q}})}}{{{{g}^{{0\xi }}}({{{\mathbf{X}}}_{a}}({\mathbf{q}})){{{({{P}_{\xi }})}}_{a}}({\mathbf{q}})}}\frac{{d{{t}_{a}}}}{{d\lambda }},\quad \xi ,\mu = \overline {0,3} .$
Тогда действие $S_{4}^{L}$ приобретает следующий вид:
(12)
$\begin{gathered} S_{4}^{L} = - \sum\limits_{a,{\mathbf{q}}} \,{{m}_{a}}{{c}^{2}}\int\limits_0^{{{t}_{{a,\max }}}} \,\frac{{\sqrt {{{{({{P}_{a}})}}_{\mu }}{{g}^{{\xi \mu }}}({{{\mathbf{X}}}_{a}}){{{({{P}_{a}})}}_{\xi }}} }}{{{{g}^{{\xi 0}}}({{{\mathbf{X}}}_{a}}){{{({{P}_{a}})}}_{\xi }}}}d{{t}_{a}} - \sum\limits_{a,{\mathbf{q}}} \,{{e}_{a}}\int\limits_0^{{{t}_{{a,\max }}}} \,\frac{{{{A}_{\mu }}{{g}^{{\xi \mu }}}({{{\mathbf{X}}}_{a}}){{{({{P}_{a}})}}_{\xi }}}}{{{{g}^{{\xi 0}}}({{{\mathbf{X}}}_{a}}){{{({{P}_{a}})}}_{\xi }}}}d{{t}_{a}} - \\ - \;\frac{1}{{16\pi c}}\int {{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}}{{{\left| g \right|}}^{{1/2}}}{{d}^{4}}X} + \mathcal{K}\int {{{{\left| g \right|}}^{{1/2}}}(R + \Lambda ){{d}^{4}}X} . \\ \end{gathered} $
Перейдем к континуальному пределу при суммировании по ${\mathbf{q}}$, заменяя сумму интегралом с плотностью в виде функции распределения ${{f}_{a}}({\mathbf{X}},{\mathbf{P}})$:
(13)
$\begin{gathered} S_{4}^{E} = - \sum\limits_a \,{{m}_{a}}{{c}^{2}}\iint {\frac{{\sqrt {{{P}_{\mu }}{{g}^{{\xi \mu }}}({\mathbf{X}}){{P}_{\xi }}} }}{{{{g}^{{\xi 0}}}({\mathbf{X}}){{P}_{\xi }}}}}{{f}_{a}}({\mathbf{X}},{\mathbf{P}}){{d}^{4}}X{{d}^{4}}P - \sum\limits_a \,{{e}_{a}}\smallint \frac{{{{A}_{\mu }}{{g}^{{\xi \mu }}}({\mathbf{X}}){{P}_{\xi }}}}{{{{g}^{{\xi 0}}}({\mathbf{X}}){{P}_{\xi }}}}{{f}_{a}}({\mathbf{X}},{\mathbf{P}}){{d}^{4}}X{{d}^{4}}P - \\ - \;\frac{1}{{16\pi c}}\int {{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}}{{{\left| g \right|}}^{{1/2}}}{{d}^{4}}X} + \mathcal{K}\int {{{{\left| g \right|}}^{{1/2}}}(R + \Lambda ){{d}^{4}}X} . \\ \end{gathered} $
(В $S_{4}^{E}$ верхний индекс $E$ означает эйлерово представление, а в ранее введенном $S_{4}^{L}$ индекс $L$ – лагранжево представление.) Обратный переход от действия (13) к действию (12) производится подстановкой
${{f}_{a}}({\mathbf{X}},{\mathbf{P}}) = \sum\nolimits_{\mathbf{q}} \,{{\varrho }_{a}}\delta ({\mathbf{x}} - {{{\mathbf{x}}}_{a}}({\mathbf{q}},t))\delta ({\mathbf{P}} - {{{\mathbf{P}}}_{a}}({\mathbf{q}},t)),\quad {{\varrho }_{a}} > 0\;\; - \;\;{\text{веса,}}$
что по сути является проверкой метода.

Отметим, что подстановка функции распределения в виде суммы дельта–функций хорошо известна в теории уравнения Власова, так как она приводит к точным уравнениям движения системы $N$ тел (для любого $N$), что показывает фундаментальность уравнений типа Власова, а также является основой метода частиц [7], [24].

Обратимся к рассмотрению $\Lambda $-члена. В последнее время он вновь находится под пристальным вниманием специалистов по космологии в связи с новыми экспериментальными данными по ускоренному расширению Вселенной и попытками это хоть как-то объяснить [4], [5], [34], [36].

Cравним лагранжиан, определяемый действием $S_{4}^{L}$, с действием, включающим в качестве подынтегральной функции лагранжиан Гильберта–Эйнштейна с $\Lambda $-членом:

(14)
${{S}_{{g,\Lambda }}} = \mathcal{K}\int {(R + \Lambda )} {{\left| g \right|}^{{1/2}}}{{d}^{4}}X.$
Из сравнения формул (13) и (14) видно, что в качестве формального аналога $\Lambda $-члена могут выступать первые три слагаемых в правой части формулы (13):
$\Lambda {\kern 1pt} ' = - \frac{1}{{16\pi c\mathcal{K}}}{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}} - \sum\limits_a \frac{{{{m}_{a}}{{c}^{2}}}}{{\sqrt { - g} \mathcal{K}}}\int {\frac{{\sqrt {{{P}_{\mu }}{{g}^{{\xi \mu }}}({\mathbf{X}}){{P}_{\xi }}} }}{{{{g}^{{\xi 0}}}({\mathbf{X}}){{P}_{\xi }}}}} {{f}_{a}}({\mathbf{X}},{\mathbf{P}}){{d}^{4}}P - \sum\limits_a \frac{{{{e}_{a}}}}{{\sqrt { - g} \mathcal{K}}}\int {\frac{{{{A}_{\mu }}{{g}^{{\mu \xi }}}({\mathbf{X}}){{P}_{\xi }}}}{{{{g}^{{\xi 0}}}({\mathbf{X}}){{P}_{\xi }}}}} {{f}_{a}}({\mathbf{X}},{\mathbf{P}}){{d}^{4}}P.$
Подобным же образом можно учитывать вклады любых других полей. Мы получаем шанс не вводить $\Lambda $-член априори, а получить его аналог по математике воздействия на материю из классических лагранжианов. Отметим, что в (13) интегрирование при $\Lambda = {\text{const}}$ дает бесконечность (что отмечалось многими исследователями), в то время как выражение с $\Lambda '$ вполне может быть конечным.

Уравнения Власова–Максвелла–Эйнштейна для метрики и электромагнитных полей получаются варьированием (13) по ним. Варьируем метрику, получаем полевые уравнения Эйнштейна

$\begin{gathered} \mathcal{K}\left( {{{R}_{{\mu \nu }}} - \frac{1}{2}R} \right)\sqrt { - g} = \sum\limits_a \,{{m}_{a}}{{c}^{2}}\int {\left( {\frac{1}{{2{{P}^{0}}\sqrt {{{P}^{\xi }}{{P}_{\xi }}} }} - \frac{{\sqrt {{{P}^{\xi }}{{P}_{\xi }}} }}{{{{P}_{0}}{{{({{P}^{0}})}}^{2}}}}\delta _{0}^{\nu }} \right)} {{f}_{a}}({\mathbf{X}},{\mathbf{P}}){{P}_{\mu }}{{P}_{\nu }}{{d}^{4}}P + \\ \, + \sum\limits_a \,{{e}_{a}}\int {\left( {\frac{{{{A}_{\mu }}{{P}_{\nu }} + {{A}_{\nu }}{{P}_{\mu }}}}{{2{{P}^{0}}}} - \frac{{{{A}_{\xi }}{{P}^{\xi }}}}{{{{P}_{0}}{{{({{P}^{0}})}}^{2}}}}{{P}_{\mu }}{{P}_{\nu }}\delta _{0}^{\nu }} \right)} {{f}_{a}}({\mathbf{X}},{\mathbf{P}}){{d}^{4}}P - \frac{{{{F}_{{\alpha \beta }}}{{F}^{{\alpha \beta }}}}}{{32\pi c}}\sqrt { - g} {{g}_{{\mu \nu }}}. \\ \end{gathered} $
Варьируем электромагнитные потенциалы и получаем уравнения Максвелла в гравитационном поле:

$\frac{1}{{8\pi c}}\frac{{\partial ({{F}^{{\alpha \beta }}}\sqrt { - g} )}}{{\partial {{X}^{\beta }}}} = \sum\limits_a \,{{e}_{a}}\int {\frac{{{{g}^{{\xi \alpha }}}({\mathbf{X}}){{P}_{\xi }}}}{{{{g}^{{\xi 0}}}({\mathbf{X}}){{P}_{\xi }}}}} {{f}_{a}}({\mathbf{X}},{\mathbf{P}}){{d}^{4}}P.$

Далее мы рассмотрим аналогию с $\Lambda $-членом для каждого из слагаемых (13) в нерелятивистском и слаборелятивистском пределах.

5. ВЫВОД УРАВНЕНИЯ ВЛАСОВА–ПУАССОНА–ПУАССОНА В НЕРЕЛЯТИВИСТСКОМ СЛУЧАЕ

Рассмотрим, следуя [25], нерелятивистское действие, соответствующее предельному переходу в действии (11) $c \to \infty $ (скорость света стремится к бесконечности), для электростатики с гравитацией (в лагранжевых 3-мерных координатах, причем параметр $\lambda $ заменяется на $t$, поскольку он является переменной интегрирования и инвариантен относительно замены):

$\begin{gathered} S_{5}^{L} = \sum\limits_{a,{\mathbf{q}}} \,\frac{1}{2}{{m}_{a}}\int {\mathop {{\mathbf{\dot {x}}}}\nolimits_a^2 ({\mathbf{q}},t)dt} - \sum\limits_a \,{{e}_{a}}\int {\sum\limits_{\mathbf{q}} \,\varphi ({{{\mathbf{x}}}_{a}}({\mathbf{q}},t),t)dt} - \\ \, - \sum\limits_a \,{{m}_{a}}\int {\sum\limits_{\mathbf{q}} \,U({{{\mathbf{x}}}_{a}}({\mathbf{q}},t),t))dt} + \frac{1}{{8\pi }}\int {{{{(\nabla \varphi )}}^{2}}d{\mathbf{x}}dt} - \frac{1}{{8\pi \gamma }}\int {{{{(\nabla U)}}^{2}}d{\mathbf{x}}dt} . \\ \end{gathered} $
Оно легко может быть получено из $S_{4}^{L}$ (индекс $L$ означает принадлежность к лагранжеву подходу), если в первом слагаемом правой части произвести предельный переход ${{g}_{{00}}} \to 1 + 2U{\text{/}}{{c}^{2}}$, ${{g}_{{kk}}} = - 1$ (остальные компоненты метрического тензора аннулируются). Это приближение слабого релятивизма для действия (11):
$\begin{gathered} - \sum\limits_a \,{{m}_{a}}c\int {\sqrt {{{g}_{{\mu \nu }}}\mathop {\dot {X}}\nolimits_a^\mu ({\mathbf{q}},t)\mathop {\dot {X}}\nolimits_a^\nu ({\mathbf{q}},t)} \,dt} \to - \sum\limits_a \,{{m}_{a}}{{c}^{2}}{{\int {\left( {1 - \frac{{{\mathbf{v}}_{a}^{2}}}{{{{c}^{2}}}} + \frac{{2U({{{\mathbf{x}}}_{a}}({\mathbf{q}},t),t))}}{{{{c}^{2}}}}} \right)} }^{{1/2}}}dt \approx \\ \, \approx \sum\limits_a \,{{m}_{a}}{{c}^{2}}\int {\left( { - 1 + \frac{1}{2}\frac{{{\mathbf{v}}_{a}^{2}}}{{{{c}^{2}}}} - \frac{{U({{{\mathbf{x}}}_{a}}({\mathbf{q}},t),t)}}{{{{c}^{2}}}}} \right)} \,dt, \\ \end{gathered} $
и исключить из рассмотрения постоянную $\left( { - \sum\nolimits_a \,{{m}_{a}}{{c}^{2}}} \right)$.

Покажем, что из действия $S_{5}^{L}$ получаются правильные уравнения динамики и полей. Варьируя координаты частиц в первых трех слагаемых, получаем уравнение движения

${{m}_{a}}{{{\mathbf{\ddot {x}}}}_{a}}({\mathbf{q}},t) = - {{m}_{a}}\nabla U({{{\mathbf{x}}}_{a}}({\mathbf{q}},t)) - {{e}_{a}}\nabla \varphi ({{{\mathbf{x}}}_{a}}({\mathbf{q}},t))$
(второй закон Ньютона для частицы массы ${{m}_{a}}$ c учетом гравитационного и электромагнитного взаимодействия).

Чтобы получить уравнение для функции распределения (в фазовом пространстве), перепишем уравнение движения в гамильтоновом виде:

$\frac{{d{{{\mathbf{x}}}_{a}}}}{{dt}} = \frac{{\mathbf{p}}}{{{{m}_{a}}}},\quad \frac{{d{{{\mathbf{p}}}_{a}}}}{{dt}} - {{m}_{a}}\frac{{\partial U}}{{\partial {\mathbf{x}}}} - {{e}_{a}}\frac{{\partial \varphi }}{{\partial {\mathbf{x}}}}.$
На их основании можно выписать уравнение Лиувилля для функции распределения ${{f}_{a}}({\mathbf{x}},{\mathbf{p}},t)$:

(15)
$\frac{{\partial {{f}_{a}}}}{{\partial t}} + \left( {\frac{{\mathbf{p}}}{{{{m}_{a}}}},\frac{{\partial {{f}_{a}}}}{{\partial {\mathbf{x}}}}} \right) - \left( {\left( {{{m}_{a}}\frac{{\partial U}}{{\partial {\mathbf{x}}}} + {{e}_{a}}\frac{{\partial \varphi }}{{\partial {\mathbf{x}}}}} \right),\frac{{\partial {{f}_{a}}}}{{\partial {\mathbf{p}}}}} \right) = 0.$

Чтобы написать уравнения для полей, перепишем, следуя [7], [9]–[13], действие $S_{4}^{L}$ через функцию распределения во втором и третьем слагаемых. Этот переход можно символически выразить, заменяя суммы интегралами, переходя от лагранжевых координат к эйлеровым:

$\sum\limits_{\mathbf{q}} \to \int {d{\mathbf{q}}} \to \iint {f({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}x{{d}^{3}}p}.$
Получаем в эйлеровом представлении:
$\begin{gathered} S_{4}^{E} = \sum\limits_a \,\int {\frac{{{{{\mathbf{p}}}^{2}}}}{{2{{m}_{a}}}}} {{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}x{{d}^{3}}pdt - \sum\limits_a \,{{e}_{a}}\int {\varphi ({\mathbf{x}},t){{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}x{{d}^{3}}pdt} - \\ \, - \sum\limits_a \,{{m}_{a}}\int {U({\mathbf{x}},t){{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}x{{d}^{3}}pdt} + \int {\frac{{{{{(\nabla \varphi )}}^{2}}}}{{8\pi }}{{d}^{3}}xdt} - \int {\frac{{{{{(\nabla U)}}^{2}}}}{{8\pi \gamma }}{{d}^{3}}xdt} \\ \end{gathered} $
(индекс $E$ в обозначении $S_{5}^{E}$ означает эйлеровость). Переход от действия $S_{5}^{E}$ к исходному $S_{5}^{L}$ получаем  формально  подстановкой  функции  распределения $f$ во второе и третье слагаемое правой части определения $S_{5}^{E}$ в виде суммы произведений дельта-функций:
${{f}_{a}}({\mathbf{x}},{\mathbf{p}},t) = \sum\nolimits_{\mathbf{q}} \,\delta ({\mathbf{x}} - {{{\mathbf{x}}}_{a}}({\mathbf{q}},t))\delta ({\mathbf{p}} - {{{\mathbf{p}}}_{a}}({\mathbf{q}},t));$
так мы контролируем эквивалентность действий в эйлеровом и лагранжевом представлениях.

Варьируя действие $S_{4}^{E}$ по $U$ и $\varphi $, получаем уравнения Пуассона для гравитационного и электромагнитного полей:

(16)
$\Delta U = 4\pi \gamma \sum\limits_a \,{{m}_{a}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} ,\quad \Delta \varphi = - 4\pi \sum\limits_a \,{{e}_{a}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} .$
Cистему уравнений (15), (16), рассматриваемых совместно, можно назвать системой Власова–Пуассона–Пуассона [25], [12]. Этот вывод уравнения типа Власова является, видимо, самым простым и наглядным – например, его можно сравнить с более сложными выводами И. Хуанчуна и Ф. Моррисона [31]. A в сложных ситуациях простые выводы предпочтительны.

В работе [15] было введено понятие “критической массы” ${{m}_{{cr}}} = {{m}_{e}}\sqrt {{{D}_{1}}} \approx {{10}^{{ - 12}}}$ г (${{m}_{e}}$ – масса электрона, ${{D}_{1}}$ – первая “большая” константа Дирака), связанной с доминированием во взаимодействии сил гравитации или электростатических сил. При $m \gtrsim {{m}_{{cr}}}$ преобладает гравитация, при $m \lesssim {{m}_{{cr}}}$ – преобладает, соответственно, электростатика. Из этого следует, что темная энергия должна быть связана с заряженными объектами (частицами, системами частиц) с массой $m \lesssim {{m}_{{cr}}}$, а заряженные объекты с $m \gtrsim {{m}_{{cr}}}$ и все электронейтральные объекты дают вклад только в материю (обычную или темную).

6. СЛАБОРЕЛЯТИВИСТСКИЙ ПРЕДЕЛ УРАВНЕНИЙ ЭЙНШТЕЙНА И УЧЕТ КОСМОЛОГИЧЕСКОГО ЧЛЕНА

Помимо нерелятивистского приближения, при выписывании действия для материи с электромагнитным и гравитационным полями значительный интерес представляет собой первое постньютоновское (иначе слаборелятивистское) приближение, в котором компоненты фундаментального метрического тензора раскладываются по степеням величины $1{\text{/}}c$. Предположим, следуя [1]–[3], что ненулевые компоненты метрического тензора имеют вид

${{g}_{{00}}} = 1 + \frac{{2U}}{{{{c}^{2}}}},\quad {{\left. {{{g}_{{jj}}}} \right|}_{{j = 1,2,3}}} = - \left( {1 - \frac{{2U}}{{{{c}^{2}}}}} \right).$
Если следовать методике слабого релятивизма, принятой в [3], то получаем
$\int {R{{{\left| g \right|}}^{{1/2}}}{{d}^{4}}X} = {{c}^{{ - 2}}}\int {\Delta U\sqrt {1 - 4U{\text{/}}{{c}^{2}}} {{d}^{4}}X} = \frac{2}{{{{c}^{4}}}}\int {{{{(\nabla U)}}^{2}}{{d}^{4}}X} .$
Действительно, первое слагаемое под знаком интеграла при разложении корня $\sqrt {1 - 4U{\text{/}}{{c}^{2}}} \approx 1 - 2U{\text{/}}{{c}^{2}}$ равно нулю: $\int {\Delta U{{d}^{4}}X} = 0$, a второе слагаемое $\int {( - 2U{{c}^{{ - 4}}}\Delta U){{d}^{4}}X} $ преобразуем интегрированием по частям к форме
$( - 2{{c}^{{ - 4}}})\int {Ud(\nabla U)} = ( - 2{{c}^{{ - 4}}})\left( {\left. {U\nabla U} \right|_{{ - \infty }}^{\infty } - \int {\nabla U \cdot \nabla U{{d}^{4}}X} } \right),$
после чего окончательно имеем
$\mathcal{K}\int {R{{{\left| g \right|}}^{{1/2}}}{{d}^{4}}X} \to \frac{{2\mathcal{K}}}{{{{c}^{4}}}}\int {{{{(\nabla U)}}^{2}}{{d}^{3}}xdct} .$
Cравнивая полученное выражение с последним членом правой части $S_{4}^{{L + E}}$ (cм. разд. 5), получаем $2\mathcal{K}{\text{/}}{{c}^{3}} = - 1{\text{/}}(8\pi \gamma )$, откуда $\mathcal{K} = - {{c}^{3}}{\text{/}}(16\pi \gamma )$ (этот вывод соответствует [1]–[3]).

Теперь исследуем cлучай учета $\Lambda $-члена в действии Эйнштейна–Гильберта в том же приближении:

$\int {(R + \Lambda ){{{\left| g \right|}}^{{1/2}}}{{d}^{4}}X} = \frac{2}{{{{c}^{4}}}}\int {{{{(\nabla U)}}^{2}}{{d}^{3}}xd(ct)} + \int {\Lambda {{d}^{3}}xd(ct)} - \frac{{2\Lambda }}{{{{c}^{2}}}}\int {U{{d}^{3}}xd(ct)} .$
Укажем, что $\Lambda = {\text{const}} \ne 0$ второе слагаемое в правой части стремится к бесконечности, так что правомерно предполагать, что эта величина действительно достаточно быстро убывающая функция пространственно-временных координат.

Действие для гравитации в приближении слабого релятивизма с $\Lambda $-членом имеет следующий вид (в лагранжевом представлении):

$\begin{gathered} S_{6}^{L} = \sum\limits_{a,{\mathbf{q}}} \,\int {\frac{{{{m}_{a}}}}{2}{\mathbf{\dot {x}}}_{a}^{2}({\mathbf{q}},t)dct} - \sum\limits_{a,{\mathbf{q}}} \,\int {{{m}_{a}}U({{{\mathbf{x}}}_{a}}({\mathbf{q}},t))dct} + \\ + \;\frac{{2\mathcal{K}}}{{{{c}^{4}}}}\iint {{{{(\nabla U)}}^{2}}{{d}^{3}}xdct} + \mathcal{K}\iint {\Lambda {{d}^{3}}xdct} - \frac{{2\mathcal{K}\Lambda }}{{{{c}^{2}}}}\iint {U{{d}^{3}}xdct}. \\ \end{gathered} $
Bарьируем по частицам и получаем уравнение движения в постньютоновском приближении, соответствующее вышеприведенному действию:
${{m}_{a}}{{{\mathbf{\ddot {x}}}}_{a}} = - {{m}_{a}}\nabla U({{{\mathbf{x}}}_{a}})$
(оно оказывается совпадающим по форме с уравнением классической динамики). Перепишем действие ${{S}_{5}}$ в эйлеровом представлении, вводя классическую функцию распределения (на 7-мерном расширенном фазовом пространстве):
$\begin{gathered} S_{5}^{E} = \sum\limits_a \,\frac{1}{{2{{m}_{a}}}}\int {{{{\mathbf{p}}}^{2}}{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}x{{d}^{3}}pdt} - \sum\limits_a \,\int {U({\mathbf{x}},t){{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p{{d}^{3}}xdt} + \\ + \;\frac{{2\mathcal{K}}}{{{{c}^{4}}}}\iint {{{{(\nabla U)}}^{2}}{{d}^{3}}xdt} + \mathcal{K}\iint {\Lambda {{d}^{3}}xdct} - \frac{{2\mathcal{K}\Lambda }}{{{{c}^{2}}}}\iint {U{{d}^{3}}xdt}. \\ \end{gathered} $
Oбратнoe преобразование к лагранжеву представлению может быть произведено путем подстановки
${{f}_{a}}({\mathbf{x}},{\mathbf{p}},t) = \sum\nolimits_{\mathbf{q}} \,\delta ({\mathbf{x}} - {{{\mathbf{x}}}_{a}}({\mathbf{q}},t))\delta ({\mathbf{p}} - {{{\mathbf{p}}}_{a}}({\mathbf{q}},t)).$
Проварьируем $S_{5}^{E}$ по U и получим уравнение Пуассона с $\Lambda $-членом:

(17)
$\Delta U = 4\pi \gamma \sum\limits_a \,{{m}_{a}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} - \frac{1}{2}{{c}^{2}}\Lambda .$

Что дает второе слагаемое в правой части? Наличие “эффективного” внешнего поля: решение уравнения $\Delta U = - \tfrac{1}{2}{{c}^{2}}\Lambda $ можно выбрать в простейшем виде как

$U = - \tfrac{1}{{12}}{{c}^{2}}\Lambda ({{x}^{2}} + {{y}^{2}} + {{z}^{2}}),$
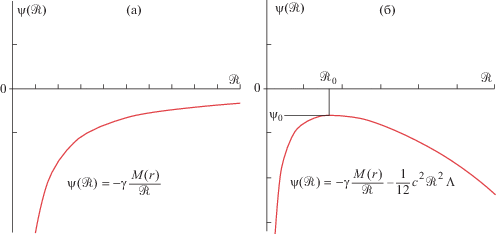
что приводит к “расталкиванию” частиц. Что дает нам это в решении типа Милна–МакКри? Из уравнения Пуассона получаем
$U = 4\pi \gamma \sum\limits_a \,{{m}_{a}}\int {\frac{{{{f}_{a}}({\mathbf{x}}{\kern 1pt} ',{\mathbf{p}},t)}}{{\left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '} \right|}}} {{d}^{3}}p{{d}^{3}}x{\kern 1pt} ' - \frac{{{{c}^{2}}\Lambda }}{{12}}({{x}^{2}} + {{y}^{2}} + {{z}^{2}}).$
Мы воспользовались тем, что решение неоднородного линейного уравнения (17) есть сумма частного решения и общего решения однородного уравнения, т.е. гармонической функции. Наш выбор частного решения однозначно диктуется требованием изотропности (инвариантности относительно вращений) решения Фридмана и Милна–МакКри.

Уравнение модели Милна (4) заменяется на

$\frac{{{{\partial }^{2}}\mathcal{R}}}{{\partial {{t}^{2}}}} = - \gamma \frac{{M(r)}}{{{{\mathcal{R}}^{2}}}} + \frac{{c\Lambda }}{6}\mathcal{R}.$
Интегрируя последнее уравнение, получаем
$\frac{1}{2}({{\dot {\mathcal{R}}}^{2}}) - \gamma \frac{{M(r)}}{\mathcal{R}} - \frac{{{{c}^{2}}{{\mathcal{R}}^{2}}\Lambda }}{{12}} = E.$
Эффективный потенциал
$\psi (\mathcal{R}) = - \gamma \tfrac{{M(r)}}{\mathcal{R}} - \tfrac{1}{{12}}{{c}^{2}}{{\mathcal{R}}^{2}}\Lambda $
имеет вид выпуклой (перевернутой) псевдопараболы с точкой максимума

$\mathcal{R} = {{\mathcal{R}}_{0}} = {{\left( {\tfrac{{12\gamma M(r)}}{{c\Lambda }}} \right)}^{{1/3}}}.$

Интересно сравнить два графика с $\Lambda = 0$ (фиг. 1а) и $\Lambda > 0$ (фиг. 1б). Интерес к $\Lambda $-члену вновь возрос в связи с общим признанием начиная с 1990-х годов понятий темной энергии и темной материи и особенно в связи с обнаружением ускоренного разбегания галактик в результате соответствующих наблюдений за космическим микроволновым фоном, интерпретация которых отмечена в 2011 г. Нобелевской премией. Наша задача – проанализировать вполне классический лагранжиан и предложить модель, рационально объясняющую действие формального $\Lambda $-члена в уравнениях Эйнштейна.

Фиг. 1.

Эффективный потенциал $\psi (\mathcal{R})$ с $\Lambda = 0$ (a) и $\Lambda > 0$ (б).

Приведем соответствующее “уравнение Власова–Пуассона с $\Lambda $-членом” (для сорта частиц $a$):

$\begin{gathered} \frac{{\partial {{f}_{a}}}}{{\partial t}} + \left( {\frac{{\mathbf{p}}}{{{{m}_{a}}}},\frac{{\partial {{f}_{a}}}}{{\partial {\mathbf{x}}}}} \right) - \left( {\nabla U,\frac{{\partial {{f}_{a}}}}{{\partial {\mathbf{p}}}}} \right) = 0, \\ \Delta U = 4\pi \gamma \sum\limits_a \,{{m}_{a}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} - \frac{1}{2}{{c}^{2}}\Lambda . \\ \end{gathered} $

Итак, мы теперь видим не только в лагранжианах, но и в уравнениях динамики, где искать аналоги $\Lambda $-члена.

Из приведенного выше выражения для $S_{6}^{E}$ вытекает математическая аналогия $\Lambda '$ и “космологического параметра” $\Lambda $ в постньютоновском приближении (в нем присутствует зависимость от координат и времени), причем интеграл в $S_{6}^{E}$ c $\Lambda '$ конечен:

$\Lambda ({\mathbf{x}},t) = {{(\mathcal{K} - 2\mathcal{K}U({\mathbf{x}},t){{c}^{{ - 2}}})}^{{ - 1}}}\left( {\sum\limits_a \,\frac{1}{{2{{m}_{a}}}}\int {{{{\mathbf{p}}}^{2}}{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} - \sum\limits_a \,U({\mathbf{x}},t){{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} \right),\quad \mathcal{K} = - \frac{{{{c}^{3}}}}{{16\pi \gamma }}.$

7. УРАВНЕНИЕ ВЛАСОВА–МАКСВЕЛЛА–ЭЙНШТЕЙНА В СЛАБОРЕЛЯТИВИСТСКОМ ПО ГРАВИТАЦИИ СЛУЧАЕ

Перейдем к анализу в слаборелятивистском приближении общего действия $S_{4}^{L}$ (c дополнительным учетом космологического $\Lambda $-члена), для чего перепишем формулу (12) (а впоследствии и (13)), заменяя члены, содержащие компоненты метрического тензора ${{g}^{{\mu \nu }}}$ и ${\text{det}}{{g}_{{\mu \nu }}} \equiv g$ их приближенными постньютоновскими выражениями, как сделано выше:

$\begin{gathered} S_{7}^{L} = \sum\limits_{a,{\mathbf{q}}} \,\int {\frac{{{{m}_{a}}}}{2}{\mathbf{\dot {x}}}_{a}^{2}({\mathbf{q}},t)dct} - \sum\limits_{a,{\mathbf{q}}} \,\int {{{m}_{a}}U({{{\mathbf{x}}}_{a}}({\mathbf{q}},t))dct} - \frac{1}{{8\pi \gamma c}}\iint {{{{(\nabla U)}}^{2}}{{d}^{3}}xdct} - \tfrac{{{{c}^{3}}}}{{16\pi \gamma }}\iint {\Lambda {{d}^{3}}xdct} + \\ + \;\tfrac{{c\Lambda }}{{8\pi \gamma }}\iint {U{{d}^{3}}xdct} - \sum\limits_a {\tfrac{{{{e}_{a}}}}{{{{c}^{2}}}}} \sum\limits_{\mathbf{q}} {\int\limits_0^T \,{{A}_{\mu }}V_{a}^{\mu }{{{\left| g \right|}}^{{1/2}}}dct} + \tfrac{1}{{16\pi c}}\int {{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}}} {{\left| g \right|}^{{1/2}}}{{d}^{4}}X, \\ \end{gathered} $
$\begin{gathered} V_{a}^{0} = - m_{a}^{{ - 1}}{{g}^{{0\zeta }}}{{({{P}_{\zeta }})}_{a}},\quad V_{a}^{j} = - m_{a}^{{ - 1}}{{g}^{{jk}}}{{({{P}_{k}})}_{a}}, \\ {{g}^{{\zeta \eta }}} \approx {\text{diag}}\left( {1 + \tfrac{{2U}}{{{{c}^{2}}}}, - \left( {1 - \tfrac{{2U}}{{{{c}^{2}}}}} \right), - \left( {1 - \tfrac{{2U}}{{{{c}^{2}}}}} \right), - \left( {1 - \tfrac{{2U}}{{{{c}^{2}}}}} \right)} \right),\quad {{\left| g \right|}^{{1/2}}} \approx 1 - \tfrac{{2U}}{{{{c}^{2}}}}. \\ \end{gathered} $
Здесь мы взяли слаборелятивистскую метрику “по Фоку” [2]. Она отличается от слаборелятивистской метрики “по Ландау” [1], [3]: ${{g}^{{\mu \nu }}} = {\text{diag}}(1 - 2U{\text{/}}{{c}^{2}}, - 1, - 1, - 1)$, где ${{\left| g \right|}^{{1/2}}} \approx 1 - U{\text{/}}{{c}^{2}}$.

Варьируя по координатам частиц, получаем уравнения движения (3-мерной динамики) в заданных полях (c точностью до ${{c}^{{ - 2}}}$):

$\frac{{d{{p}_{{ai}}}}}{{dt}}{{m}_{a}}{{({{\ddot {x}}_{a}})}_{i}} = - {{m}_{a}}\frac{{\partial U}}{{\partial x_{a}^{i}}} - \frac{{{{e}_{a}}}}{c}\left( {{{{\dot {A}}}_{i}} + c\frac{{\partial {{A}_{0}}}}{{\partial x_{a}^{i}}} + \sum\limits_j \,{{F}_{{ij}}}\dot {x}_{a}^{j}} \right).$

Переходя к функции распределения, получаем соответствующую систему уравнений Власова–Максвелла–Эйнштейна в постньютоновском (по гравитации) приближении:

(18)
$\frac{{\partial {{f}_{a}}}}{{\partial t}} + \sum\limits_i \,\left( {\frac{{{{p}_{i}}}}{{{{m}_{a}}}},\frac{{\partial {{f}_{a}}}}{{\partial {{x}^{i}}}}} \right) + \sum\limits_i \,\frac{{{{e}_{a}}}}{c}\left( {\left( { - \frac{{\partial {{A}_{i}}}}{{\partial t}} - c\frac{{\partial {{A}_{0}}}}{{\partial {{x}^{i}}}} - \sum\limits_j \,{{F}_{{ij}}}\frac{{{{p}_{j}}}}{{{{m}_{a}}}}} \right),\frac{{\partial {{f}_{a}}}}{{\partial {{p}_{i}}}}} \right) - \sum\limits_i \,\left( {\nabla {{U}_{i}},\frac{{\partial {{f}_{a}}}}{{\partial {{p}_{i}}}}} \right) = 0.$

Чтобы выписать уравнение для полей, перепишем действие $S_{6}^{L}$, переходя к эйлеровскому представлению для второго и пятого слагаемых правой части формулы, определяющей данное действие (то есть для членов, которые могут выражаться через функцию распределения частиц):

$\begin{gathered} S_{7}^{{L + E}} = \sum\limits_a \,\int {\frac{{{{{\mathbf{p}}}^{2}}}}{{2{{m}_{a}}}}} {{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}x{{d}^{3}}pdct - \sum\limits_a \,{{m}_{a}}\int {U({\mathbf{x}},t){{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}x{{d}^{3}}pdct} - \frac{{{{c}^{3}}}}{{16\pi \gamma }}\int {\Lambda {{d}^{3}}xdct} + \\ + \;\frac{{\Lambda c}}{{8\pi \gamma }}\int {U{{d}^{3}}xdct} - \sum\limits_a \,\frac{{{{e}_{a}}}}{{{{m}_{a}}{{c}^{2}}}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t)} \sum\limits_{j = 1}^3 \,{{p}_{j}}{{A}_{j}}({\mathbf{x}},t){{d}^{3}}x{{d}^{3}}pdct + \\ \end{gathered} $
$\begin{gathered} + \;\sum\limits_a \,\frac{{{{e}_{a}}}}{{{{m}_{a}}{{c}^{2}}}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t)} \left( {{{P}_{0}}\left( {1 - \frac{{4U}}{{{{c}^{2}}}}} \right)} \right)\varphi ({\mathbf{x}},t){{d}^{3}}x{{d}^{3}}pdct + \\ + \;\frac{1}{{16\pi c}}\int {{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}}} \left( {1 - \frac{{2U}}{{{{c}^{2}}}}} \right){{d}^{3}}xdct\quad ({\text{здесь}}\;\;\varphi ({\mathbf{x}},t) \equiv {{A}_{0}}({\mathbf{x}},t)). \\ \end{gathered} $
Отсюда непосредственно можно получить выражение для “космологического параметра” $\Lambda '({\mathbf{x}},t)$ в используемом приближении:

$\begin{gathered} \Lambda {\kern 1pt} ' = \left[ {\sum\limits_a \,\frac{1}{{2{{m}_{a}}}}\int {{{{\mathbf{p}}}^{2}}{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} } \right. - \sum\limits_a \,U({\mathbf{x}},t)\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} - \sum\limits_a \,\frac{{{{e}_{a}}}}{{{{m}_{a}}{{c}^{2}}}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t)} \sum\limits_{j = 1}^3 \,{{p}_{j}}{{A}_{j}}({\mathbf{x}},t){{d}^{3}}p + \\ + \;\sum\limits_a \,\frac{{{{e}_{a}}}}{{{{m}_{a}}{{c}^{2}}}}\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t)} \left( {{{P}_{0}}\left( {1 - \frac{{4U}}{{{{c}^{2}}}}} \right)} \right)\varphi ({\mathbf{x}},t){{d}^{3}}p + \left. {\frac{1}{{16\pi c}}{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}}\left( {1 - \frac{{2U}}{{{{c}^{2}}}}} \right)} \right]{{\left( {\frac{{cU}}{{8\pi \gamma }} - \frac{{{{c}^{3}}}}{{16\pi \gamma }}} \right)}^{{ - 1}}}. \\ \end{gathered} $

Отметим, что в вышеприведенных формулах мы использовали выражение скорости через импульсы в виде $V_{a}^{\zeta } = - m_{a}^{{ - 1}}{{g}^{{\zeta \eta }}}{{({{P}_{\eta }})}_{a}}$, где ${{({{P}_{\eta }})}_{a}} = \partial \mathop {\widetilde L}\nolimits_p {\text{/}}\partial V_{a}^{\eta }$, ${{\tilde {L}}_{p}} = - \tfrac{{{{m}_{a}}}}{2}{{g}_{{\eta \zeta }}}V_{a}^{\eta }V_{a}^{\zeta }$ – упрощенный лагранжиан, приводящий к тем же геодезическим, что и исходный ${{L}_{p}}$ (фактически, здесь использована возможность введения для системы частиц в постньютоновском приближении единого времени). При варьировании по $U$ получаем:

(19)
$\Delta U = 4\pi \gamma \sum\limits_a \,\int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} - \frac{{{{c}^{2}}\Lambda }}{2} + 8\pi \gamma \sum\limits_a \,{{e}_{a}}\varphi \int {{{f}_{a}}({\mathbf{x}},{\mathbf{p}},t)} \frac{{{{P}_{0}}}}{{{{m}_{a}}{{c}^{2}}}}{{d}^{3}}p - \frac{\gamma }{{2{{c}^{2}}}}{{F}_{{ik}}}{{F}^{{ik}}}.$

Уравнение Власова (18) следует рассматривать совместно с уравнением (19) для $U$ и уравнениями Максвелла для полей:

${{\partial }_{i}}{{F}^{{ji}}} = - \frac{{4\pi }}{c}\sum\limits_a \,{{e}_{a}}\int {v_{a}^{j}({\mathbf{p}}){{f}_{a}}({\mathbf{x}},{\mathbf{p}},t){{d}^{3}}p} .$

Это и есть система уравнений Власова–Максвелла–Эйнштейна в слаборелятивистском приближении. Особый интерес представляет уравнение (19): первое слагаемое в правой части, очевидно, представляет собой величину плотности вещества, состоящего из частиц сортов $a$, второе слагаемое – классический $\Lambda $-член, который в настоящее время олицетворяет темную энергию, третье слагаемое – электромагнитная энергия (которая может быть переписана в виде, пропорциональном $({{{\mathbf{E}}}^{2}} - {{{\mathbf{H}}}^{2}})$).

Итак, мы получили выражения, аналогичные $\Lambda $-члену, из принципа наименьшего действия, как в самих действиях, так и в уравнениях.

8. ЗАКЛЮЧЕНИЕ

Мы предложили способ вывода уравнений Власова–Максвелла–Эйнштейна и сравнили эти уравнения с нерелятивистскими и слаборелятивистскими аналогами, находя и проверяя константы как для действий, так и для уравнений, а также проверяя сами уравнения. Уравнения Власова–Эйнштейна ранее выписывались в разных формах [15], [23], [31], [35], поэтому их вывод из классических действий совершенно необходим. При этом выводе автоматически получались выражения, похожие на $\Lambda $-член. Анализ этих выражений, как количественный, так и качественный, представляет значительный интерес в связи с природой темной материи и темной энергии [4], [5], [49], [50]. При этом здесь должны помочь частные решения уравнений типа Власова – стационарные, гидродинамического типа и микроканонические [29], [46]. Особый интерес представляет вопрос о росте энтропии и о совпадении временных средних и экстремалей Больцмана для уравнений типа Власова, как это имеет место для уравнений Лиувилля [15], [46], [48].

Мы также в настоящей статье рассмотрели способ вывода уравнений типа Власова в слаборелятивистской форме, где такие слагаемые, отвечающие за темную материю и темную энергию, обретают явную форму. Дальнейшее исследование требует изучения частных решений, которые могут быть аналогичны рассмотренным в работах [7], [48].

Здесь представляет интерес исследовать модели фридмановского типа однородной вселенной [1], [7], стационарные [25]–[30], микроскопические [7]–[28] и гидродинамические [7], [28], [43], [45] решения. Интерес представляет вопрос об агрегации материи [42] во Вселенной, насколько эти процессы влияют на формирование темной энергии и темной материи. Интерес представляют работы по изучению автомодельных решений – насколько именно такие решения соответствуют крупномасштабным процессам во Вселенной [49], [50]. Мы предложили выражение для $\Lambda $-члена, анализ которого дает представление как о темной энергии, так и о темной материи: заряженные частицы с массой, меньшей ${{m}_{e}}\sqrt {{{D}_{1}}} $, дают вклад в темную энергию (${{m}_{e}}$ – масса электрона, ${{D}_{1}}$ – первая большая константа Дирака).

Список литературы

  1. Паули В. Теория относительности. М.: Наука, 1983.

  2. Фок В.А. Теория пространства, времени и тяготения. М.: ГИТТЛ, 1956.

  3. Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1988.

  4. Чернин А.Д. Темная энергия и всемирное антитяготение // Успехи физ. наук. 2008. Т. 178. № 3. С. 267–300.

  5. Лукаш В.Н., Рубаков В.А. Темная энергия: мифы и реальность // Успехи физ. наук. 2008. Т. 178. № 3. С. 301–308.

  6. Зельдович Я.Б., Мышкис А.Д. Элементы математической физики. M.: Наука, 1973.

  7. Веденяпин В.В. Кинетические уравнения Больцмана и Власова. М.: Физматлит, 2001.

  8. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения. М.: Наука, 1986.

  9. Власов А.А. Статистические функции распределения. М.: Наука, 1966. 356 с.

  10. Веденяпин В.В., Негматов М.А. О выводе и классификации уравнений типа Власова и МГД. Тождество Лагранжа и форма Годунова // Теор. и матем. физ. 2012. Т. 170. № 3. С. 468–480.

  11. Веденяпин В.В., Негматов М.-Б.А., Фимин Н.Н. Уравнения типа Власова и Лиувилля, их микроскопические, энергетические и гидродинамические следствия // Изв. РАН. Сер. матем. 2017. Т. 81. № 3. С. 45–82.

  12. Vedenyapin V., Sinitsyn A., Dulov E. Kinetic Boltzmann, Vlasov and related equations. Amsterdam: Elsevier Insights. 2011. 304 p.

  13. O’Neill E. Hamiltonian structure and stabilty of relativistic gravitational theories. Dissertation for degree D.Ph., University of Florida. 2000.

  14. Kandrup H.E., Morrison P.J. Hamiltonian structure of the Vlasov–Einstein system and the problem of stability for spherical relativistic star clusters // Ann. Phys. 1993. V. 225. P. 114–166.

  15. Zeldovich Ya.B., Novikov I.D. Relativistic astrophysics. Vol. 1. Chicago: Univesity of Chicago. 1971.

  16. Cercigniani C., Kremer G.M. The relativistic Boltzmann equation: theory and applications. Berlin: Birkhauser, 2002.

  17. Choquet-Bruhat Y. General relativity anf the Einstien equations. Oxford: Oxford University Press, 2009.

  18. Ehlers J. Kinetic theory of gases in general relativity theory // Lect. Notes in Physics. 1974. V. 28. P. 78–105.

  19. Droz-Vincent Ph., Hakim R. Collective motions of the relativistic gravitational gas // Ann. de l’I. H.P., section A. 1968. T. 9. № 1. P. 17–33.

  20. Lindquist R.W. Relativistic transport theory // Annals of Phys. 1966. V. 37. P. 487–518.

  21. Choquet-Bruhat Y., Damour T. Introduction to general relativity, black holes and cosmology. New York: Oxford University Press. 2015.

  22. Batt J. Global symmetric solutions of the initial value problem in steller dynamics // Journ. Diff. Eqs. 1977. V. 25. № 3. P. 342–364.

  23. Rein G., Rendall A.D. Smooth static solutions of the spherically symmetric Vlasov–Einstein system // Ann. de l’Inst. H. Poincarґe, Physique Theorique. 1993. V. 59. P. 383–397.

  24. Волков Ю.А. O решениях уравнения Власова в лагранжевых координатах // Теор. и матем. физ. 2007. Т. 151. № 1. С. 138–148.

  25. Веденяпин В.В., Фимин Н.Н., Негматов М.А. Уравнения Лиувилля и Власова. Их микроскопические и гидродинамические следствия. М.: ИПМ им. М.В. Келдыша РАН, 2016.

  26. Веденяпин В.В., Негматов М.А. О выводе и классификации уравнений типа Власова и магнитной гидродинамики. Тождество Лагранжа, форма Годунова и критическая масса // СМФН. 2013. Т. 47. С. 5–17.

  27. Веденяпин В.В. Уравнение Власова–Максвелла–Эйнштейна // Препринты ИПМ им. М.В. Келдыша РАН. 2018. № 188. 20 c. https://doi.org/10.20948/prepr-2018-188 URL: http://library.keldysh.ru/preprint.asp?id 18-188

  28. Narlikar J. V. An introduction to cosmology (3rd ed.). Cambridge: Cambridge University Press. 2002.

  29. Веденяпин В.В. О стационарных решениях уравнения Власова–Пуассона // Докл. АН СССР. 1986. Т. 290. № 4. С. 777–780.

  30. Веденяпин В.В. O классификации стационарных решений уравнения Власова на торе и граничная задача // Докл. РАН СССР. 1992. Т. 323. № 6. С. 1004–1006.

  31. Huanchun Ye, Morrison Ph. Action principles for the Vlasov equations // Phys Fluids B. 1992. V. 4. № 4. P. 771–777.

  32. Игнатьев Ю.Г. Релятивистская кинетическая теория неравновесных процессов. Казань: OOO “Фолиантъ”. 2010.

  33. Игнатьев Ю.Г. Вывод кинетических уравнений из общерелятивистской цепочки Боголюбова. Сб. Современные теоретические и экспериментальные проблемы теории относительности и гравитации. Тез. доклад. Всесоюзн. конф., Минск. 1976. С. 146–148.

  34. Munoz J.B., Loeb A. A small amount of mini-charged dark matter could cool the baryons in the early Universe // Nature. 2018. V. 557. P. 684–686.

  35. Brans C., Dicke R.H. Mach’s principle and a relativistic theory of gravitation // Phys. Rev. 1961. V. 124. P. 925.

  36. Мейерович Б.Э. Гравитационные свойства космических струн // Успехи физ. наук. 2001. Т. 171. № 10. С. 1033–1049.

  37. Kibble T.W.B. Lorentz invariance and gravitational field // J. Math. Phys. 1961. V. 2. P. 212.

  38. Choquet-Bruhat Y., Noutcheguenne N. Systeme hyperbolique pour les ґequations d’Einstein avec sources // C. R. Acad. Sci. Paris, Ser. I. 1986. V. 303. P. 259–263.

  39. Orlov Yu.N., Pavlotsky I.P. BBGKY hierarchies and Vlasov’s equations in postgalilean aproximation // Physica A. 1988. V. 151. P. 318.

  40. Скубачевский А.Л., Тсузуки Ю. Уравнения Власова–Пуассона для двухкомпонентной плазмы в полупространстве // Докл. РАН. 2016. Т. 471. № 5. С. 528–530.

  41. Веденяпин В.В., Аджиев C.З., Казанцева В.В. Энтропия по Больцмана и Пуанкаре, экстремали Больцмана и метод Гамильтона–Якоби в негамильтоновой ситуации // Совр. матем. Фундаментальные направления. 2018. Т. 64. № 1. С. 37–59.

  42. Аджиев С.З., Веденяпин В.В., Волков Ю.А., Мелихов И.В. Обобщенные уравнения типа Больцмана для агрегации в газе // Ж. вычисл. матем. и матем. физ. Т. 57. № 12. С. 2065–2078.

  43. Веденяпин В.В., Фимин Н.Н. Уравнение Лиувилля, гидродинамическая подстановка и уравнение Гамильтона-Якоби // Докл. РАН, 446:2 (2012), С. 142–144.

  44. Веденяпин В.В., Негматов М.А. О топологии гидродинамических и вихревых следствий уравнений Власова и метод Гамильтона-Якоби // Докл. РАН. 2013. Т. 449. № 5. С. 521–526.

  45. Захаров В.Е., Кузнецов Е.А. Гамильтоновский формализм для нелинейных волн // Успехи физ. наук. 1997. Т. 167. № 12. С. 1137–1167.

  46. Веденяпин В. В. Временные средние и экстремали по Больцману // Докл. РАН. 2008. Т. 422. № 2. С. 161–163.

  47. Аджиев С.З., Веденяпин В.В. Временные средние и экстремали Больцмана для марковских цепей, дискретного уравнения Лиувилля и круговой модели Каца // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 11. С. 2063–2074.

  48. Веденяпин В.В., Аджиев С.З. Энтропия по Больцману и Пуанкаре // Успехи матем. наук. 2014. Т. 69. № 6. С. 45–80.

  49. Валиев Х.Ф., Крайко А.Н. Разлет идеального газа из точки в пустоту. Новая модель большого взрыва и расширения вселенной // Прикл. матем. и механ. Т. 79. № 6. С. 793–807.

  50. Valiyev Kh., Kraiko A.N. The dispersion of an ideal gas from a point into a void. A new model of the Big Bang and the expansion of the Universe // J. of Applied Mathematics and Mechanics. 2015. V. 79. P. 556–565.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал