Журнал вычислительной математики и математической физики, 2019, T. 59, № 8, стр. 1340-1357

1. ПОСТАНОВКА ЗАДАЧИ И ФОРМУЛИРОВКА РЕЗУЛЬТАТА

Рассматривается уравнение Мэкки-Гласса

в котором $\gamma $, $\beta $, $\theta $, $\tau $ – положительные параметры, $n \geqslant 3$ – натуральное число. Уравнение (1.1) предложено в [1] в качестве математической модели изменения плотности $x(t)$ циркулирующих нейтрофилов (белых клеток крови) человека. Входящие в (1.1) параметры имеют четкий биологический смысл.

Перейдем в (1.1) к безразмерным переменным и параметрам, положив $x{\text{'}}(t) = \theta x(t)$, $t{\kern 1pt} {\text{'}} = t{\text{/}}\tau $, ${{\varepsilon }_{1}} = {{(\gamma \tau )}^{{ - 1}}}$, $\beta {\text{'}} = \beta {\text{/}}\gamma $. В результате, опустив штрих, получим уравнение

в котором по физике задачи параметр $\beta $ принимает значение порядка единицы, а $0 < {{\varepsilon }_{1}} \ll 1$.

Уравнение (1.1) изучалось в ряде работ (см. [2]–[9]), где изучались свойства решений и в основном на основе численного интегрирования отмечено существование разнообразных периодических решений, а также сложной, в том числе хаотической, динамики. В работе [8] динамика уравнения (1.1) моделируется посредством электронного устройства.

Уравнение (1.2) имеет единственное положительное состояние равновесия

устойчивость которого определяется значениями $\beta $ и $n$.

Настоящая работа дополняет работу авторов [10]. Ниже изучаются бифуркации периодических решений уравнения (1.2) из состояния равновесия (1.3) при изменении параметров уравнения, исследуется их устойчивость. Доказана теорема о структуре решений уравнения (1.2) с начальными условиями из окрестности состояния равновесия (1.3) в фазовом пространстве уравнения. Показано, что поведение решений определяется счетной системой обыкновенных нелинейных дифференциальных уравнений, которая может быть построена в некотором нормализованном виде, содержащем минимальное число возможных параметров. Анализ этой системы уравнений позволяет изучить бифуркации периодических решений и получить для них асимптотические формулы. Показана возможность одновременной бифуркации из состояния равновесия (1.3) большого числа устойчивых периодических решений, т.е. бифуркация мультистабильности. Численно показано, что бифурцирующие периодические решения при увеличении бифуркационного параметра через серию бифуркаций удвоения периода колебаний переходят в хаотические колебания. Таким образом, в уравнении (1.2) наблюдается одновременное существование различных хаотических аттракторов. Это явление можно назвать мультистабильным хаосом.

Некоторые утверждения работы [10], используемые в настоящей работе, приведены без доказательства.

2. АНАЛИЗ УСТОЙЧИВОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (3)

Выполним в уравнении (1.2) замену $x(t) = {{x}_{ * }} + y(t)$ и представим нелинейную часть уравнения (1.2) рядом Тейлора. В результате в окрестности состояния равновесия (1.3) поведение решений уравнения (1.2) будет определяться следующим уравнением:

в котором $f(y) = {{b}_{2}}{{y}^{2}} + {{b}_{3}}{{y}^{3}} + o({{y}^{3}})$ аналитическая в окрестности $y = 0$ функция,

Устойчивость нулевого решения (2.1) определяется поведением решений его линейной части

которое, в свою очередь, определяется расположением корней характеристического уравнения уравнения (2.3).

Уравнение (2.4) при фиксированном ${{b}_{1}} > 1$ и $0 < {{\varepsilon }_{1}} \leqslant {{\varepsilon }_{0}}$, где ${{\varepsilon }_{0}}$ мало, имеет корни, лежащие в правой комплексной полуплоскости, при фиксированном ${{b}_{1}} < 1$ и $0 < {{\varepsilon }_{1}} \leqslant {{\varepsilon }_{0}}$ все корни уравнения лежат в левой комплексной полуплоскости [11]. В соответствии с этим, нулевое решение уравнения (2.1) в первом случае будет неустойчиво, во втором – асимптотически устойчиво. Пограничным является случай ${{b}_{1}} = 1$. Это определяет согласно (2.2) последовательность критических значений ${{\beta }_{n}} = n{\text{/}}(n - 2)$. Положив $\beta = {{\beta }_{n}}(1 + {{\varepsilon }_{2}}{\text{/}}(n - 2 - {{\varepsilon }_{2}}))$, $\left| {{{\varepsilon }_{2}}} \right| \ll 1$, получим

а также согласно (2.2) ${{b}_{2}} = {{b}_{2}}({{\varepsilon }_{2}})$, ${{b}_{3}} = {{b}_{3}}({{\varepsilon }_{2}})$. Введем в рассмотрение функцию определенную в замкнутой области {$(w,{{\varepsilon }_{1}}): - {{x}_{0}} \leqslant {\text{Re}}\,w \leqslant {{x}_{0}}$, где ${{x}_{0}} > 0$ – малое фиксированное число, ${\text{Im}}\,w \geqslant 0$, $0 \leqslant \left| {{{\varepsilon }_{1}}} \right| \leqslant {{\varepsilon }_{0}}$}, непрерывную по совокупности переменных, аналитическую по $w$ внутри области при каждом фиксированном ${{\varepsilon }_{1}}$ и аналитическую по ${{\varepsilon }_{1}}$ при каждом фиксированном $w$.

В дальнейшем $\varepsilon = ({{\varepsilon }_{1}},{{\varepsilon }_{2}})$, $\left| \varepsilon \right| = {{(\varepsilon _{1}^{2} + \varepsilon _{2}^{2})}^{{1/2}}}$.

Теорема 1 [10]. В предположении (2.5) существует такое ${{\varepsilon }_{0}} > 0$, что при $\left| \varepsilon \right| < {{\varepsilon }_{0}}$ все множество корней уравнения (2.4) определяется формулой

Отсюда равномерно относительно $k$

Таким образом, вопрос устойчивости решений уравнения (2.3) сводится к анализу функций ${{\gamma }_{k}}(\varepsilon )$, являющихся аналитическими в точке $\varepsilon = 0$ и имеющих радиус сходимости соответствующих рядов ${{r}_{k}} = O({{k}^{{ - 1}}})$. При этом имеем

т.е. при малых $\varepsilon $ и выполнении неравенства ${{\varepsilon }_{2}} > \varepsilon _{1}^{2}{{(\pi k)}^{2}}{\text{/}}2$ $k$-й корень характеристического уравнения (2.4) имеет положительную вещественную часть.

Опишем теперь структуру решений уравнения (2.3). Фазовым пространством уравнения (2.3) является пространство непрерывных вещественнозначных функций $C[ - 1;0]$, норму в котором определим стандартным способом и обозначим ${{\left\| {\text{v}(s)} \right\|}_{C}}$. Под решением уравнения (2.3) (уравнения (2.1)), определенном при $t \geqslant {{t}_{0}}$, с начальным условием ${{y}_{0}}(s) \in C[ - 1;0]$ будем понимать функцию $y(t + s;\varepsilon )$ ($ - 1 \leqslant s \leqslant 0$), которая обращает уравнение (2.3) (уравнение (2.1)) в тождество и удовлетворяет начальному условию $y({{t}_{0}} + s;\varepsilon ) \equiv {{y}_{0}}(s)$.

Введем в рассмотрение функцию Коши $K(t;\varepsilon )$ уравнения (2.3)

Применив к (2.9) преобразование Лапласа и воспользовавшись формулой его обращения, с необходимостью будем иметь выражение

В (2.10) $\bar {x} > 0$ – некоторое фиксированное число. Отметим, что ряд (2.10) равномерно сходится на любом отрезке $0 \leqslant t \leqslant \bar {t}$.

Применив к уравнению (2.3) преобразование Лапласа и используя функцию (2.9) с учетом ее представления в виде (2.10), решение уравнения (2.3) с начальным условием ${{y}_{0}}(s)$ может быть записано в виде

Формула (2.11) определяет семейство $T(t;\varepsilon )$, $t \geqslant 0$, линейных вполне непрерывных операторов, действующих в пространстве $C[ - 1,0]$ и образующих полугруппу $T({{t}_{1}} + {{t}_{2}};\varepsilon ) = T({{t}_{1}};\varepsilon )T({{t}_{2}};\varepsilon ) = $ $ = T({{t}_{2}};\varepsilon )T({{t}_{1}};\varepsilon )$ ($T(0) = I$ – единичный оператор) класса ${{\mathbb{C}}_{0}}$ [12]. Производящий (инфинитезинальный) оператор полугруппы $T(t;\varepsilon )$ согласно (2.3), (2.11) имеет вид

с областью определения $D(A) = \{ \text{v}(s) \in {{C}^{1}}[ - 1,0],\;{{\varepsilon }_{1}}\text{v}{\kern 1pt} '(0) + \text{v}(0) + (1 + {{\varepsilon }_{2}})\text{v}( - 1) = 0\} $.

Здесь и в дальнейшем ${{C}^{k}}[ - 1,0]$ – пространство $k$-раз непрерывно дифференцируемых вещественнозначных функций, норма в которых определяется стандартным способом. Обозначим через $\tilde {C}[ - 1,0]$ комплексное расширение пространства $C[ - 1,0]$, в котором

${{\left\| {\text{v}(s)} \right\|}_{{\tilde {C}}}} = {{\left\| {{{{({{\text{v}}_{1}}{{{(s)}}^{2}} + {{\text{v}}_{2}}{{{(s)}}^{2}})}}^{{1/2}}}} \right\|}_{C}},\quad \text{v}(s) = {{\text{v}}_{1}}(s) + i{{\text{v}}_{2}}(s).$

Собственными значениями оператора $A(\varepsilon )$ являются величины ${{\lambda }_{k}} = {{\lambda }_{k}}(\varepsilon )$, а соответствующими собственными функциями будут функции ${{e}_{k}}(s;\varepsilon ) = {{e}^{{{{\lambda }_{k}}(\varepsilon )s}}}{\text{/}}P{\text{'}}({{\lambda }_{k}}(\varepsilon );\varepsilon ) = {{e}^{{{{\lambda }_{k}}(\varepsilon )s}}}{\text{/}}(1 + {{\varepsilon }_{1}} + {{\varepsilon }_{1}}{{\lambda }_{k}}(\varepsilon ))$, $k = \pm 1, \pm 3,\; \ldots $, ${{\left\| {{{e}_{k}}(s;\varepsilon )} \right\|}_{{\tilde {C}}}} \sim 1$ при $k \to \infty $.

Наряду с (2.12) введем в рассмотрение оператор

действующий в пространстве $C[0,1]$, с областью определения $D(A{\kern 1pt} {\text{*}}) = \{ h(s) \in {{C}^{1}}[0,1],$ $ - {{\varepsilon }_{1}}h{\text{'}}(0) + h(0) + (1 + {{\varepsilon }_{2}})h(1) = 0\} $. Оператор (2.13) является сопряженным с (2.12) в смысле скалярного произведения С.Н. Шиманова [13], которое для уравнения (2.3) имеет вид Заметим, что собственными значениями оператора $A{\kern 1pt} {\text{*}}(\varepsilon )$ являются величины $ - {{\bar {\lambda }}_{k}}(\varepsilon )$, а соответствующими собственными функциями будут функции ${{h}_{k}} = {{h}_{k}}(s;\varepsilon ) = {{e}^{{ - {{{\bar {\lambda }}}_{k}}(\varepsilon )s}}}$. Между функциями ${{e}_{k}}(s;\varepsilon )$ и ${{h}_{k}}(s;\varepsilon )$ выполнены следующие условия ортогональности: где ${{\delta }_{{{{k}_{1}}{{k}_{2}}}}}$ – символ Кронекера.

Выражения

определяют последовательность линейных непрерывных функционалов в пространстве $\tilde {C}[ - 1;0]$, нормы которых

Теорема 2 (см. [10]). Система функций ${{e}_{k}}(s,\varepsilon )$ полна в $C[ - 1,0]$ в следующем смысле: не существует функции $q(s) \in C[ - 1,0]$, $q(s)\not { \equiv }0$, для которой $\left\langle {q(s),{{h}_{k}}(s)} \right\rangle = 0$, $k = \pm 1, \pm 3,\; \ldots $ .

Обозначим через ${{l}_{2}}$ пространство последовательностей вида $z = ({{z}_{1}},{{z}_{{ - 1}}},{{z}_{3}},{{z}_{{ - 3}}},\; \ldots )$, ${{z}_{k}} \in C$, ${{z}_{{ - k}}} = {{\bar {z}}_{k}}$, $\left\| z \right\|_{{{{l}_{2}}}}^{2} = \sum\nolimits_{k = 1,3, \ldots } {{\left| {{{z}_{k}}} \right|}^{2}} < \infty $. Через $l_{2}^{1}$ обозначим подпространство ${{l}_{2}}$ последовательностей $z = ({{z}_{1}},{{z}_{{ - 1}}},{{z}_{3}},{{z}_{{ - 3}}},\; \ldots )$, для которых

Подпространство $C[ - 1,0]$ функций указанного вида обозначим через ${{D}_{ * }}(A)$.

Теорема 3. Любое решение $y(t + s;\varepsilon )$ уравнения (2.3) с начальным условием $y(s;\varepsilon ) = {{y}_{0}}(\varepsilon ) \in C[ - h,0]$ при $t \geqslant {{t}_{0}}$, ${{t}_{0}} \geqslant 3$, может быть представлено в виде

где $z(t;\varepsilon )$ – решение уравненияв пространстве ${{l}_{2}}$ с начальным условием $z({{t}_{0}};\varepsilon ) = ({{z}_{1}}({{t}_{0}};\varepsilon ),{{z}_{{ - 1}}}({{t}_{0}};\varepsilon ),\; \ldots )$, аОбратно, если $z(t;\varepsilon )$ при $t \geqslant {{t}_{0}}$ решение уравнения (2.18) с начальным условием $z({{t}_{0}};\varepsilon ) \in l_{2}^{1}$, то выражение (2.17) определяет при $t \geqslant {{t}_{0}}$ решение уравнения (2.3).

Доказательство. При ${{t}_{0}} \geqslant 3$ решение уравнения (2.3) $y({{t}_{0}} + s;\varepsilon ) \in {{C}^{3}}[ - 1,0]$ и ${{\varepsilon }_{1}}y{\text{'''}}({{t}_{0}}) + y{\text{''}}({{t}_{0}}) + $ $ + \;(1 + {{\varepsilon }_{2}})y{\text{''}}({{t}_{0}} - 1) = 0$. Отсюда, интегрируя по частям равенства (2.19) с учетом (2.14), (2.16) имеем

Таким образом, $z({{t}_{0}};\varepsilon ) \in l_{2}^{1}$ и ${{z}_{k}}(t,\varepsilon ) = {{e}^{{{{\lambda }_{k}}(\varepsilon )(t - {{t}_{0}})}}}{{z}_{k}}({{t}_{0}};\varepsilon )$, $k = \pm 1, \pm 3,\; \ldots $ . Подставив ${{z}_{k}}(t;\varepsilon )$ в (2.17), замечаем, что ряд и его производная по $t$ равномерно сходятся при $ - 1 \leqslant s \leqslant 0$ и удовлетворяют уравнению (2.3) при $t \geqslant {{t}_{0}}$. Обратно, если $z(t;\varepsilon )$ решение (2.18) с начальным условием $z({{t}_{0}};\varepsilon ) \in l_{2}^{1}$, то определяемая рядом (2.17) функция $y({{t}_{0}} + s) \in {{D}_{ * }}(A)$, и при $t > {{t}_{0}}$ удовлетворяет уравнению (2.3), в чем легко убедиться непосредственной подстановкой. Теорема доказана.

3. СТРУКТУРА РЕШЕНИЙ УРАВНЕНИЯ (4) В ОКРЕСТНОСТИ НУЛЕВОГО СОСТОЯНИЯ РАВНОВЕСИЯ

В предположении (2.5) ($f(y)) \equiv f(y;\varepsilon )$) изучим структуру решений $y(t + s;\varepsilon )$ уравнения (2.1) с начальными условиями , т.е. принадлежащими шару фиксированного радиуса ${{R}_{0}}$ с центром в нуле фазового пространства. При $t > {{t}_{0}},\;\,{{t}_{0}} \geqslant 3,$ $y(t + s;\varepsilon ) \in {{C}^{3}}[ - 1,0]$ и

С учетом этого и интегрируя по частям скалярное произведение (2.14) при $t \geqslant {{t}_{0}}$, имеем

В связи с тем, что то согласно (2.10), (2.16) ряд $\sum\nolimits_{k = \pm 1, \pm 3, \ldots } {\lambda _{k}^{{ - 1}}} (\varepsilon ){{e}_{k}}(s;\varepsilon )$ сходится равномерно при $ - 1 \leqslant s \leqslant 0$ и $w(t;\varepsilon ) = ({{w}_{1}}(t;\varepsilon ),{{w}_{{ - 1}}}(t;\varepsilon ),\; \ldots ,) \in l_{2}^{1}$, где ${{w}_{k}}(t;\varepsilon )$ определены в соответствии с (3.2). Отсюда следует, что при $t \geqslant {{t}_{0}}$ для решения $y(t + s;\varepsilon )$ уравнения (2.1) справедливо представление Из (3.3) при ${{\left\| {\sum\nolimits_{k = \pm 1, \pm 3, \ldots } {{{w}_{k}}} (t;\varepsilon ){{e}_{k}}(s;\varepsilon )} \right\|}_{C}} \leqslant {{r}_{0}}$, где ${{r}_{0}}$ мало, найдем Здесь $g(y;\varepsilon ) = {{g}_{2}}(\varepsilon ){{y}^{2}} + O({{y}^{2}})$ аналитическая в окрестности точки $y = 0$ функция.

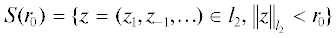Обозначим через , . Из (3.4) следует, что при $w(t;\varepsilon ) = ({{w}_{1}}(t;\varepsilon ),{{w}_{{ - 1}}}(t;\varepsilon ), \ldots ) \in {{S}^{1}}({{r}_{0}})$

Рассматривая в уравнении (2.1) $f(y(t - 1);{{\varepsilon }_{2}})$ как неоднородное слагаемое линейного уравнения (2.3), решение $y(t + s;\varepsilon )$ уравнения (2.1) при $t \geqslant {{t}_{0}}$ с начальным условием ${{y}_{0}}(s;\varepsilon ) = {{y}_{0}}({{t}_{0}} + s;\varepsilon )$ согласно (2.11) и используя функцию $K(t;\varepsilon )$ запишем в следующем виде:

Отсюда с учетом (2.9), (2.10) и (3.4), (3.5) имеем последовательность равенств

Продифференцировав равенства (3.7) по $t$, получим систему дифференциальных уравнений в пространстве ${{l}_{2}}$ вида

решением  которой при $t \geqslant {{t}_{0}}$ являются функции ${{w}_{k}}(t;\varepsilon )$,  $k = \pm 1, \pm 3,\; \ldots $, определенные в (3.2) и  имеющие соответствующие начальные условия ${{w}_{k}}({{t}_{0}};\varepsilon )$. Верно и обратное. Если $w(t;\varepsilon ) = ({{w}_{1}}(t;\varepsilon ),{{w}_{{ - 1}}}(t;\varepsilon ),\; \ldots ) \in {{S}^{1}}({{r}_{0}})$ при $t \geqslant {{t}_{0}}$ является решением системы дифференциальных уравнений (3.8), то согласно (3.4), (3.5) при $t \geqslant {{t}_{0}}$ ряд (3.3) равномерно сходится в области и с учетом (3.2) является решением (2.1).

Разрешим (3.8) относительно ${{\dot {w}}_{k}}$. Умножим (3.8) на ${{e}_{k}}( - 1;\varepsilon )$ и просуммируем по $k$. Это позволяет получить в явном виде выражение для $\sum\nolimits_{k = \pm 1, \pm 3, \ldots } {{{{\dot {w}}}_{k}}} {{e}_{k}}( - 1;\varepsilon )$. Отметим, что ${{e}_{k}}( - 1;\varepsilon ) = {{e}^{{ - {{\lambda }_{k}}(\varepsilon )}}}(1 + $ $ + \;{{\varepsilon }_{1}} + {{\varepsilon }_{1}}{{\lambda }_{k}}(\varepsilon ){{)}^{{ - 1}}} = (1 + {{\varepsilon }_{1}}{{\lambda }_{k}}(\varepsilon )){{(1 + {{\varepsilon }_{1}} + {{\varepsilon }_{1}}{{\lambda }_{k}}(\varepsilon ))}^{{ - 1}}}{{(1 + {{\varepsilon }_{2}})}^{{ - 1}}} \sim 1$ при $k \to \infty $.

В результате получим эквивалентную (3.8) систему дифференциальных уравнений:

Отметим следующее свойство функции ${{\lambda }_{k}}(\varepsilon )$.

Теорема 4 (см. [10]). Существуют такие ${{\varepsilon }_{0}} > 0$, ${{c}_{0}} > 0$, что при $0 \leqslant \left| \varepsilon \right| \leqslant {{\varepsilon }_{0}}$ равномерно относительно ${{k}_{j}} = \pm 1, \pm 3,\; \ldots $,  $j = 1,\; \ldots ,\;4$, выполнены неравенства

вторые при условии ${{k}_{1}} + {{k}_{2}} + {{k}_{3}} + {{k}_{4}} \ne 0.$

С учетом неравенств (3.10) выполним в системе уравнений (3.9) нормализующую замену переменных $w = z + {{c}_{2}}(z) + {{c}_{3}}(z):{{S}^{1}}({{r}_{0}}) \to {{S}^{1}}({{r}_{0}})$ вида

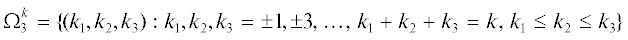где , $\tilde {\Omega }_{3}^{k} = {\{ }({{k}_{1}},{{k}_{2}},{{k}_{3}}):{{k}_{1}},{{k}_{2}},{{k}_{3}}$ = $ \pm 1, \pm 3, \ldots ,\;{{k}_{1}} + {{k}_{2}} + {{k}_{3}} \ne k,$ , приводящую ее к системе уравнения в пространстве ${{l}_{2}}$ вида в которой , гладкий по совокупности переменных оператор $Z(z;\varepsilon ) = ({{Z}_{1}}(z;\varepsilon ),{{Z}_{{ - 1}}}(z;\varepsilon ),\; \ldots )(Z(0;\varepsilon ) \equiv 0):{{S}^{1}}({{r}_{0}}) \to S({{r}_{0}})$ и ${{\left\| {Z{\kern 1pt} {\text{*}}(z;\varepsilon )} \right\|}_{{{{l}_{2}}}}} = o\left( {\left\| z \right\|_{{l_{2}^{1}}}^{3}} \right)$.

Для построения замены (3.11) и уравнений (3.12) подставим (3.11) в (3.9) с учетом (3.12) и приравняем в полученных равенствах последовательно при каждом $k = \pm 1, \pm 3,\; \ldots $ коэффициенты при одинаковых степенях ${{z}_{{{{k}_{1}}}}}{{z}_{{{{k}_{2}}}}}$, ${{z}_{{{{k}_{1}}}}}{{z}_{{{{k}_{2}}}}}{{z}_{{{{k}_{3}}}}}$, ${{k}_{1}},{{k}_{2}},{{k}_{3}} = \pm 1, \pm 3$. В результате получим рекуррентную последовательность алгебраических уравнений, из которых однозначно определяются коэффициенты $c_{{{{k}_{1}}{{k}_{2}}}}^{k}(\varepsilon )$, $c_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}^{k}(\varepsilon )$, ${{d}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}}(\varepsilon )$ с указанными свойствами. Из условий окончательных тождеств при каждом $k$ однозначно определяются функции $Z_{k}^{ * }(z;\varepsilon )$ с указанными свойствами.

Систему уравнений (3.12) назовем нормальной формой уравнения (2.1) в окрестности нулевого состояния равновесия, нормализованной до кубических слагаемых включительно.

Отметим, что нормализация уравнений (3.9) может быть выполнена до любой нечетной степени по ${{z}_{k}}$. При этом для функций ${{\lambda }_{k}}(\varepsilon )$ справедливы аналогичные (3.10) соотношения более высокого порядка, а нормализованные уравнения не будут содержать четных степеней ${{z}_{k}}$.

Подставив выражения (3.11) в (3.3) с учетом (3.4), получим окончательное представление решений уравнения (2.1) с начальными условиями из окрестности нулевого состояния равновесия, которое сформируем в виде окончательной теоремы.

Теорема 5. Существуют такие ${{R}_{0}},{{r}_{0}},{{\varepsilon }_{0}} > 0$, что при $0 < \left| \varepsilon \right| < {{\varepsilon }_{0}}$ любое решение $y(t + s;\varepsilon )$ уравнения (2.1) с начальным условием ${{y}_{0}}(s;\varepsilon ) \in S({{R}_{0}})$ при $t \geqslant {{t}_{0}}$, ${{t}_{0}} \geqslant 3$, и тех $t$, пока $y(t + s;\varepsilon ) \in S({{R}_{0}})$ может быть представлено в виде

где гладкий по совокупности переменных оператор $g(z;\varepsilon ) = ({{g}_{1}}(z;\varepsilon ),{{g}_{{ - 1}}}(z;\varepsilon ),\; \ldots )(g(0;\varepsilon ) \equiv $ $ \equiv 0):{{S}^{1}}({{r}_{0}}) \to {{S}^{1}}({{r}_{0}})$ и $\left\| {g(z;\varepsilon )} \right\| = o\left( {{{{\left\| z \right\|}}_{{l_{2}^{1}}}}} \right)$, $z(t;\varepsilon ) = ({{z}_{1}}(t;\varepsilon ),{{z}_{{ - 1}}}(t;\varepsilon ),\; \ldots ) \in {{S}^{1}}({{r}_{0}})$, а ${{z}_{k}}(t;\varepsilon )$, $k = \pm 1, \pm 3,\; \ldots $, являются решениями системы уравнений (3.12) с начальными условиями ${{z}_{k}}({{t}_{0}};\varepsilon )$, определяемыми и равенств $\left\langle {y({{t}_{0}} + s;\varepsilon ),\;{{h}_{k}}(s;\varepsilon )} \right\rangle = {{z}_{k}}({{t}_{0}};\varepsilon ) + {{g}_{k}}(z({{t}_{0}};\varepsilon );\varepsilon )$. Обратно, если $z(t;\varepsilon ) \in {{S}^{1}}({{r}_{0}})$ при $t \geqslant {{t}_{0}}$ решения системы уравнений (3.12), то функция $y(t + s;\varepsilon )$, определенная согласно (3.13) является решением уравнения (2.1).

Таким образом, вопрос бифуркации периодических решений уравнения (2.1) из нулевого состояния равновесия при изменении параметра $\varepsilon $ сводится к решению аналогичной задачи для системы уравнений (3.12).

В дальнейшем, главной частью нормальной формы (3.12) будем называть систему уравнений, содержащую в правой части слагаемые, не выше кубических по ${{z}_{k}}$.

Вычисление главной части нормальной формы (3.12) может быть выполнено непосредственно по уравнению (2.1). Перейдем для этого от уравнения (2.1) к эквивалентной начально-краевой задаче

в полосе $ - 1 \leqslant s \leqslant 0$, $t \geqslant 0$, положив $u(t,s) = y(t + s)$.

Введем в рассмотрение функцию оператор

где ${{\Omega }_{2}}$ определено в (3.11), , действующую из в $C[ - 1,0]$ и гладко зависящую от своих переменных, и главную часть нормальной формы (3.12) уравнения (2.1)

Функции ${{u}_{{{{k}_{1}}{{k}_{2}}}}}(s;\varepsilon )$, ${{u}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}}(s;\varepsilon )$, ${{d}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}}(\varepsilon )$ подлежат определению. Условие принадлежности траекторий системы уравнений (3.17) в силу (3.16) краевой задачи (3.14), (3.15) примут вид

Соотношения (3.18), (3.19) определяют тождества, которые должны равномерно по $\left| \varepsilon \right| < {{\varepsilon }_{0}}$ выполняться с точностью до величины $o\left( {\left| z \right|_{{{{l}_{2}}}}^{3}} \right)$. При первых степенях ${{z}_{k}}$ они выполняются в силу определения функций ${{e}_{k}}(s;\varepsilon )$ и ${{\lambda }_{k}}(\varepsilon )$. Соотношения (3.18), (3.19) позволяют последовательно определять функции ${{u}_{ * }}(s;\varepsilon )$ и ${{d}_{ * }}(\varepsilon )$, приравнивая коэффициенты справа и слева при одинаковых степенях ${{z}_{k}}$.

Приравняем в (3.18), (3.19) коэффициенты при ${{z}_{{{{k}_{1}}}}}{{z}_{{{{k}_{2}}}}}$. В результате получим краевую задачу

для определения ${{u}_{{{{k}_{1}}{{k}_{2}}}}}(s;\varepsilon )$. В (3.21) ${{p}_{{{{k}_{1}}{{k}_{2}}}}} = 1$ при ${{k}_{1}} = {{k}_{2}}$, и 2 при ${{k}_{1}} \ne {{k}_{2}}$. Решение (3.20), (3.21) определяется однозначно

Приравняем в (3.18), (3.19) коэффициенты при ${{z}_{{{{k}_{1}}}}}{{z}_{{{{k}_{2}}}}}{{z}_{{{{k}_{3}}}}}$. В результате получим краевую задачу

${{p}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}} = 1$, если ${{k}_{1}} = {{k}_{2}} = {{k}_{3}}$, ${{p}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}} = 3$, если ${{k}_{1}} = {{k}_{2}} \ne {{k}_{3}}$, либо ${{k}_{1}} = {{k}_{3}} \ne {{k}_{2}}$, либо ${{k}_{2}} = {{k}_{3}} \ne {{k}_{1}}$, ${{p}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}} = 6$, если ${{k}_{1}} \ne {{k}_{2}} \ne {{k}_{3}}$.

Общее решение уравнения (3.22) имеет вид

где использовано обозначение ${{\lambda }_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}}(\varepsilon ) = {{\lambda }_{{{{k}_{1}}}}}(\varepsilon ) + {{\lambda }_{{{{k}_{2}}}}}(\varepsilon ) + {{\lambda }_{{{{k}_{3}}}}}(\varepsilon )$, $c$ – произвольная постоянная. Подставив (3.24) в краевое условие (3.23), имеем Условие непрерывности функции ${{u}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}}(s{\text{;}}\;\varepsilon )$ по $\varepsilon $ при $0 \leqslant \left| \varepsilon \right| \leqslant \left| {{{\varepsilon }_{0}}} \right|$ дает $c = 0$, что однозначно ее определяет равенством (3.24).

При построении нормальной формы (3.12) до порядка $2m + 1$, где $m > 1$, соответствующего порядка берутся разложения (3.16), (3.17). Алгоритмическая часть повторяет изложенную.

4. АНАЛИЗ НОРМАЛЬНОЙ ФОРМЫ УРАВНЕНИЯ (4)

Перейдем в системе уравнений (3.12) к полярным координатам, положив ${{z}_{k}} = {{\rho }_{k}}{{e}^{{i{{\tau }_{k}}}}}$, ${{\rho }_{k}} \geqslant 0$, $0 \leqslant {{\tau }_{k}} < 2\pi $. В результате получим систему уравнений вида

в которой ${{\gamma }_{k}}(\varepsilon )$ и ${{\sigma }_{k}}(\varepsilon )$ определены в (2.70), $\rho = ({{\rho }_{1}},{{\rho }_{3}},\; \ldots ),$ $\left\| \rho \right\|_{{l_{2}^{1}}}^{2} = \sum\nolimits_{k = 1,3, \ldots } {{{k}^{2}}} \rho _{k}^{2} < \infty $, $\tau = ({{\tau }_{1}},{{\tau }_{3}}, \ldots )$, функционалы $R_{k}^{{(3)}}({\kern 1pt} \cdot {\kern 1pt} )$, $R_{k}^{{( * )}}({\kern 1pt} \cdot {\kern 1pt} )$, $T_{k}^{{(3)}}({\kern 1pt} \cdot {\kern 1pt} )$, $T_{k}^{{( * )}}({\kern 1pt} \cdot {\kern 1pt} )$ гладко  зависят  от  входящих переменных и параметров, $2\pi $-периодические по ${{\tau }_{j}}$, при этом $R_{k}^{{(3)}}({\kern 1pt} \cdot {\kern 1pt} )$ и $T_{k}^{{(3)}}({\kern 1pt} \cdot {\kern 1pt} )$ – кубические формы по $\rho $, а $\left| {R_{k}^{ * }({\kern 1pt} \cdot {\kern 1pt} )} \right|,\left| {T_{k}^{ * }({\kern 1pt} \cdot {\kern 1pt} )} \right| = o\left( {\left\| \rho \right\|_{{l_{2}^{1}}}^{3}} \right)$.

Структура системы (4.1), (4.2) позволяет ввести одну “быструю” переменную и счетное число “медленных” переменных. Как это сделать, покажем сначала на примере “усеченной” системы. Рассмотрим главную часть нормальной формы (3.17), в которой положим ${{z}_{k}} = 0$, $k = \pm 5, \pm 7, \ldots \;.$ В результате имеем систему уравнений

Уравнения для ${{z}_{{ - 1}}}$, ${{z}_{{ - 3}}}$ получаются сопряжением (4.3), (4.4) с учетом равенств ${{\bar {\lambda }}_{k}}(\varepsilon ) = {{\lambda }_{{ - k}}}(\varepsilon )$, ${{\bar {z}}_{k}}(\varepsilon ) = {{z}_{{ - k}}}(\varepsilon )$. Обозначив ${{d}_{ * }}(\varepsilon ) = {{a}_{ * }}(\varepsilon ) + i{{b}_{ * }}(\varepsilon )$, ${{A}_{ * }}(\varepsilon ) = \left| {{{d}_{ * }}(\varepsilon )} \right|$, ${{\beta }_{ * }}(\varepsilon ) = \arg {{d}_{ * }}(\varepsilon ) \in [0,2\pi )$, перейдем в (4.3), (4.4) к полярным переменным ${{\rho }_{1}}$, ${{\rho }_{3}}$, ${{\tau }_{1}}$, ${{\tau }_{3}}$. В результате получим систему уравнений Перейдем в (4.5)–(4.8) к переменным ${{\rho }_{1}},{{\rho }_{3}},{{\theta }_{1}} = - 3{{\tau }_{1}} + {{\tau }_{3}}$ и $\tau = {{\tau }_{1}}$. В результате имеем систему уравнений “медленных” переменных, где ${{\delta }_{1}}(\varepsilon ) = - 3{{\sigma }_{1}}(\varepsilon ) + {{\sigma }_{3}}(\varepsilon )$, и уравнение “быстрой” переменной Заметим, что правая часть (4.9)–(4.11) не зависит от $\tau $.

Пусть теперь в (3.17) все z$_{k}(t) \ne 0$. Ввести переменные ${{\theta }_{k}}$ можно не единственным способом, однако они все связаны между собой линейными соотношениями. В качестве одного из возможных способов введение ${{\theta }_{k}}$ может быть предложен следующий. В качестве “быстрой” переменной берем ${{\tau }_{1}}$ и рассматриваем “усеченные” конечномерные системы, последовательно полагая в (3.17) ${{z}_{k}} = 0$, $k = \pm 5, \pm 7,\; \ldots $, затем $k = \pm 7, \pm 9,\; \ldots $ и т.д. Первый случай рассмотрен выше. Во втором случае к системе (4.3), (4.4) добавляются два новых уравнения для переменных ${{z}_{5}}$ и ${{z}_{{ - 5}}}$. При этом в правой части уравнения для ${{z}_{1}}$ появляется резонансный моном ${{z}_{5}}{{z}_{{ - 3}}}{{z}_{{ - 1}}}$(в уравнении для ${{z}_{{ - 1}}}$ появляется резонансный моном ${{z}_{{ - 5}}}{{z}_{3}}{{z}_{1}}$). При переходе к полярным координатам это приводит к появлению слагаемых, зависящих от выражения ${{\tau }_{5}} - {{\tau }_{3}} - 2{{\tau }_{1}} = {{\theta }_{3}}$, которое берем в качестве новой “медленной” переменной. В результате имеем две дополнительные “медленные” переменные ${{\rho }_{5}}$, ${{\theta }_{3}}$. Система уравнений для ${{\rho }_{1}}$, ${{\rho }_{3}}$, ${{\rho }_{5}}$, ${{\theta }_{1}}$, ${{\theta }_{3}}$ будет иметь вид, аналогичный (4.9)–(4.11), правая часть которой также не будет зависеть от $\tau $. В правой части уравнения (4.12) для $\tau $ появятся новые слагаемые. При рассмотрении следующей “усеченной” системы в правой части уравнения для ${{z}_{1}}$ появится резонансный моном ${{z}_{7}}{{z}_{{ - 5}}}{{z}_{{ - 1}}}$, а при переходе к полярным координатам слагаемое, зависящее от выражения ${{\tau }_{7}} - {{\tau }_{5}} - 2{{\tau }_{1}} = {{\theta }_{5}}$. Имеем две новые “медленные” переменные ${{\rho }_{7}}$, ${{\theta }_{5}}$. В общем случае на очередном шаге, добавив уравнения для ${{z}_{{{{k}_{0}}}}}$ и ${{z}_{{ - {{k}_{0}}}}}$, получим в уравнениях для ${{z}_{1}}$ и ${{z}_{{ - 1}}}$ появление новых мономов ${{z}_{{{{k}_{0}}}}}{{z}_{{ - {{k}_{0}} + 2}}}{{z}_{{ - 1}}}$ и ${{z}_{{ - {{k}_{0}}}}}{{z}_{{{{k}_{0}} - 2}}}{{z}_{1}}$ соответственно, а при переходе к полярным координатам появятся слагаемые, зависящие от ${{\tau }_{{{{k}_{0}}}}} - {{\tau }_{{{{k}_{0}} - 2}}} - 2{{\tau }_{1}} = {{\theta }_{{{{k}_{0}} - 2}}}$. Имеем две новые “медленные” переменные ${{\rho }_{{{{k}_{0}}}}}$, ${{\theta }_{{{{k}_{0}} - 2}}}$. Продолжая этот процесс, осуществим в системе уравнений (3.17) переход к “медленным” переменным $\rho = ({{\rho }_{1}},{{\rho }_{3}},\; \ldots )$, $\theta = ({{\theta }_{1}},{{\theta }_{3}},\; \ldots )$ и “быстрой” $\tau $. Соответствующий переход к “медленным” и “быстрой” переменным в (4.1), (4.2) даст следующую систему дифференциальных уравнений для их определения

в которой функционалы ${{R}_{k}}({\kern 1pt} \cdot {\kern 1pt} )$, $R_{k}^{ * }({\kern 1pt} \cdot {\kern 1pt} )$, ${{\Theta }_{k}}({\kern 1pt} \cdot {\kern 1pt} )$, $\Theta _{k}^{ * }({\kern 1pt} \cdot {\kern 1pt} )$, $T({\kern 1pt} \cdot {\kern 1pt} )$, $T{\text{*}}({\kern 1pt} \cdot {\kern 1pt} )$ – $2\pi $-периодические по ${{\theta }_{k}}$, остальные их свойства и свойства функции ${{\delta }_{k}}(\varepsilon )({{\delta }_{k}}(0) = 0)$ определяются свойствами функций и функционалов, входящих в (4.1), (4.2).

Фазовым пространством системы уравнений (4.13)–(4.15) будет произведение пространств ${{l}_{2}} \otimes c \times R$, здесь ${{l}_{2}}\, = \,\left\{ {\mathop \rho \limits_{} } \right.\, = \,({{\rho }_{1}},{{\rho }_{3}},\; \ldots ){{\rho }_{k}}\, \geqslant \,0,$ $\left\| \rho \right\|_{{{{l}_{2}}}}^{2}\, = \,\left. {\sum\nolimits_{k = 1,3, \ldots } {\rho _{k}^{2}} \, < \,\infty } \right\}$ $c\, = \,\left\{ {\theta \, = \,({{\theta }_{1}},{{\theta }_{3}},\; \ldots ),\;{{{\left\| \theta \right\|}}_{c}}\, = \,su{{p}_{k}}\left| {{{\theta }_{k}}} \right|\, < \,\infty } \right\}$. Областью определения правой части (4.13)–(4.15) является произведение пространств $l_{2}^{1} \otimes {{c}_{0}} \times R$, здесь $l_{2}^{1} = \left\{ {\rho \in {{l}_{2}},\;{{\rho }_{k}} > 0,\;\left\| \rho \right\|_{{l_{2}^{1}}}^{2} = \sum\nolimits_{k = 1,3, \ldots } {{{k}^{2}}} \rho _{k}^{2} < \infty } \right\}$, ${{c}_{0}} = \left\{ {\theta = ({{\theta }_{1}},{{\theta }_{3}},\; \ldots )} \right. \in c,\;0 \leqslant {{\theta }_{k}} < \left. {2\pi } \right\}$.

Введем в области $\left\{ {({{\varepsilon }_{1}},{{\varepsilon }_{2}}),\;{{\varepsilon }_{1}} > 0,\;\left| \varepsilon \right| < {{\varepsilon }_{0}}} \right\}$ переменные $\zeta \geqslant 0$ и $\pi {\text{/}}2 < \psi < \pi {\text{/}}2$, положив

Подставим (4.16) в (4.13)–(4.15), нормировав также ${{\rho }_{k}} \to \zeta {{\rho }_{k}}$. В результате получим систему уравнений в которой свойства функций и функционалов определяются свойствами функций и функционалов системы уравнений (4.13)–(4.15).

Отметим, что в виду того, что согласно (2.7), (4.16) равномерно относительно $k$$\gamma (\psi ,\zeta ) = O({{\zeta }^{2}})$, ${{\delta }_{k}}(\psi ,\zeta ) = O({{\zeta }^{3}})$, уравнения (4.17), (4.18) оправдывают название уравнений “медленных”переменных, а (4.19) – уравнения “быстрой” переменной.

Рассмотрим главную часть системы уравнений “медленных” переменных (4.17), (4.18), предварительно нормировав время $t \to t{\text{/}}{{\zeta }^{2}}$. В результате имеем

где $\gamma _{k}^{ * }(\psi ,\zeta ) = {{\gamma }_{k}}(\psi ,\zeta ){\text{/}}{{\zeta }^{2}}$, $\delta _{k}^{ * }(\psi ,\zeta ) = {{\delta }_{k}}(\psi ,\zeta ){\text{/}}{{\zeta }^{2}}$ согласно (2.7), (4.16) непрерывные функции $\pi {\text{/}}2 \leqslant \psi \leqslant - \pi {\text{/}}2$, $0 \leqslant \zeta \leqslant {{\zeta }_{0}}$. При этом $\gamma _{k}^{ * }(\psi ,0) = {{\gamma }_{k}}(\psi ) = si{{n}^{2}}\psi \operatorname{sign} \psi - {{\pi }^{2}}{{k}^{2}}co{{s}^{2}}\psi {\text{/}}2$, $\delta _{k}^{ * }(\psi ,0) = 0$.

Рассмотрим в ${{l}_{2}} \otimes c$ систему нелинейных уравнений

считая $(\rho ,\theta ) \in E_{0}^{1} = l_{2}^{1} \otimes {{c}_{0}}$. В (4.22) оператор $\gamma (\psi )\rho = ({{\gamma }_{1}}(\psi ){{\rho }_{1}},{{\gamma }_{3}}(\psi ){{\rho }_{3}},\; \ldots )$ рассматривается на основании (4.20) симметрично расширенным на $l_{2}^{1}$.

Пусть $(\rho {\text{*}}(\psi ),\theta {\text{*}}(\psi )) \in l_{2}^{1} \otimes {{c}_{0}}$ – решение системы уравнений (4.22), (4.23).

Введем в рассмотрение бесконечную матрицу

вычисленную в точке $\rho {\text{*}}(\psi )$, $\theta {\text{*}}(\psi )$, где ${{\delta }_{{{{k}_{j}}}}}$ – символ Кронекера. Матрица (4.24) определяет линейный оператор ${{\left\| \text{v} \right\|}_{E}} = {{\left\| \rho \right\|}_{{{{l}_{2}}}}} + {{\left\| \theta \right\|}_{c}},\;{{\left\| \text{v} \right\|}_{{{{E}^{1}}}}} = {{\left\| \rho \right\|}_{{l_{2}^{1}}}} + {{\left\| \theta \right\|}_{c}}$.

Пусть ${{\mu }_{k}}(\psi )(B(\psi ){{\text{v}}_{k}}(\psi ) = {{\mu }_{k}}(\psi ){{\text{v}}_{k}}(\psi ))$ – собственное значение оператора (4.25). Покажем, что оператор (4.25) имеет счетное число собственных значений ${{\mu }_{k}}(\psi )$, которые могут быть пронумерованы в порядке возрастания их модулей и любой ограниченной области комплексной плоскости может принадлежать лишь конечное число собственных значений конечной кратности. Предельной может быть лишь точка бесконечность, при этом $li{{m}_{{k \to \infty }}}\operatorname{Re} {{\mu }_{k}}(\psi ) = - \infty $.

Действительно, заметим, что функции

определяют периодическое решение следующей системы дифференциальных уравнений: ($\Omega _{3}^{k}$ и ${{d}_{{{{k}_{1}}{{k}_{2}}{{k}_{3}}}}}(0)$ определены соответственно в (3.12) и (3.23)), в чем легко убедиться непосредственной подстановкой (4.26), (4.27) в (4.28), с учетом произведенных для $\rho {\text{*}}(\psi )$, $\theta {\text{*}}(\psi )$ замен и равенств (4.22), (4.23), выполненных для $\rho {\text{*}}(\psi )$, $\theta {\text{*}}(\psi )$. Система уравнений (4.28) является абстрактно параболической в комплексном пространстве ${{l}_{2}}$ с областью определения $l_{2}^{1}$. Для таких систем уравнения оператор монодромии, построенный для периодического решения (4.27), является вполне непрерывным, содержащим счетное число собственных значений (мультипликаторов) ${{\rho }_{k}}(\psi )$, $li{{m}_{{k \to \infty }}}\left| {{{\rho }_{k}}(\psi )} \right| = 0$. Оператор (4.25) определяет характеристические показатели периодического решения (4.27). Отсюда следуют все перечисленные свойства ${{\mu }_{k}}(\psi )$. Подставим $\rho {\text{*}}(\psi )$, $\theta {\text{*}}(\psi )$ в (4.19). В результате на основании (2.7), (3.25) имеем

Теорема 6. Пусть при некотором $\psi $ система уравнений (4.22), (4.23) имеет решение $(\rho {\text{*}}(\psi ),\theta {\text{*}}(\psi )) \in l_{2}^{1} \otimes {{c}_{0}}$, а построенная по этому решению матрица (4.24) определяет оператор (4.25), который не имеет собственных значений, лежащих на мнимой оси комплексной плоскости. Тогда существует такое ${{\zeta }_{0}} > 0$, что при $0 < \zeta \leqslant {{\zeta }_{0}}$ уравнение (2.1), в котором ${{\varepsilon }_{1}}$ и ${{\varepsilon }_{2}}$ определены согласно (4.16), имеет периодическое решение $y{\text{*}}(t + s;\varepsilon ) = y{\text{*}}(t + s;\psi ,\zeta )$, допускающее представление

в котором ${{b}_{2}}({{\varepsilon }_{2}})$, ${{\Omega }_{2}}$, ${{p}_{{{{k}_{1}}{{k}_{2}}}}}$, $z_{k}^{ * }(\tau ;\psi )$ и $\tau $ соответственно определены в (2.5), (3.11), (3.20), (4.27) и (4.29).

Решение $y{\kern 1pt} {\text{*}}(t + s;\psi ,\zeta )$ будет асимптотически орбитально устойчиво, если все собственные значения оператора (4.25) лежат в левой комплексной полуплоскости и неустойчиво, если $m$ корней с учетом кратностей принадлежит правой комплексной полуплоскости. В последнем случае периодическое решение имеет $m$-мерное неустойчивое инвариантное периодическое многообразие.

Доказательство. Перейдем в (4.17), (4.18) к новому времени $\tau $ согласно (4.19). В результате получим систему дифференциальных уравнений в пространстве ${{l}_{2}} \otimes c$, которую запишем в операторной форме:

Операторы $\gamma {\kern 1pt} {\text{*}}({\kern 1pt} \cdot {\kern 1pt} ) = ({{\pi }^{{ - 1}}}\gamma _{1}^{ * }({\kern 1pt} \cdot {\kern 1pt} ),{{\pi }^{{ - 1}}}\gamma _{{ - 1}}^{ * }({\kern 1pt} \cdot {\kern 1pt} ),\; \ldots )$, $\delta {\text{*}}({\kern 1pt} \cdot {\kern 1pt} ) = ({{\pi }^{{ - 1}}}\delta _{1}^{ * }({\kern 1pt} \cdot {\kern 1pt} ),{{\pi }^{{ - 1}}}\delta _{{ - 1}}^{ * }({\kern 1pt} \cdot {\kern 1pt} ),\; \ldots )$, $R({\kern 1pt} \cdot {\kern 1pt} ) = ({{\pi }^{{ - 1}}}{{R}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\pi }^{{ - 1}}}{{R}_{{ - 1}}}({\kern 1pt} \cdot {\kern 1pt} ),\; \ldots )$, $\Theta ({\kern 1pt} \cdot {\kern 1pt} ) = ({{\pi }^{{ - 1}}}{{\Theta }_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\pi }^{{ - 1}}}{{\Theta }_{{ - 1}}}({\kern 1pt} \cdot {\kern 1pt} ),\; \ldots )$, операторы ${{R}^{ \vee }}({\kern 1pt} \cdot {\kern 1pt} ) = (R_{1}^{ \vee }({\kern 1pt} \cdot {\kern 1pt} ),R_{{ - 1}}^{ \vee }({\kern 1pt} \cdot {\kern 1pt} ),\; \ldots )$, ${{\Theta }^{ \vee }}({\kern 1pt} \cdot {\kern 1pt} ) = (\Theta _{1}^{ \vee }({\kern 1pt} \cdot {\kern 1pt} ),\Theta _{{ - 1}}^{ \vee }({\kern 1pt} \cdot {\kern 1pt} ),\; \ldots )$, построены по функционалам $R_{k}^{ \vee }({\kern 1pt} \cdot {\kern 1pt} )$ и $\Theta _{k}^{ \vee }({\kern 1pt} \cdot {\kern 1pt} )$, свойства которых определяются свойствами функционалов $R_{k}^{ * }({\kern 1pt} \cdot {\kern 1pt} )$, $\Theta _{k}^{ * }({\kern 1pt} \cdot {\kern 1pt} )$, $T{\kern 1pt} {\text{*}}({\kern 1pt} \cdot {\kern 1pt} )$, $T({\kern 1pt} \cdot {\kern 1pt} )$.

Обозначим

среднее функции $R_{k}^{ \vee }( \cdot )$ и $\Theta _{k}^{ \vee }( \cdot )$ и рассмотрим в $E$ систему нелинейных операторных уравнений с областью опеределения ${{E}^{1}}$, в которой операторы ${{\bar {R}}^{ \vee }}({\kern 1pt} \cdot {\kern 1pt} )$, ${{\bar {\Theta }}^{ \vee }}({\kern 1pt} \cdot {\kern 1pt} )$ определены в соответствии с (4.33). При $\zeta = 0$ (4.34), (4.35) имеет решение $\rho {\kern 1pt} {\text{*}}(\psi )$, $\theta {\kern 1pt} {\text{*}}(\psi )$. При этом собственные значения ${{\mu }_{j}}(\psi )$ оператора (4.25), построенного по матрице частных производных (4.24), соответствующей этому решению, удовлетворяют условию $\left| {\operatorname{Re} {{\mu }_{j}}(\psi )} \right| > {{\mu }_{0}} > 0$. Следовательно, по теореме о неявной функции для операторных уравнений в банаховом пространстве (см., например, [14], с. 304) существует такое ${{\zeta }_{0}}$, что при $0 \leqslant \zeta \leqslant {{\zeta }_{0}}$ система уравнений (4.34), (4.35) имеет решение $\rho {\kern 1pt} {\text{*}}(\psi ;\zeta ),\theta {\kern 1pt} {\text{*}}(\psi ;\zeta )(\rho {\kern 1pt} {\text{*}}(\psi ;0) = \rho {\kern 1pt} {\text{*}}(\psi ),\theta {\kern 1pt} {\text{*}}(\psi ;0) = \theta {\kern 1pt} {\text{*}}(\psi ))$, гладко зависящее от параметра $\zeta $.

Линеаризуем (4.34), (4.35) на решении $\rho {\kern 1pt} {\text{*}}(\psi ;\zeta )$, $\theta {\kern 1pt} {\text{*}}(\psi ;\zeta )$. В результате получим бесконечную матрицу, аналогичную матрице (4.24) и обращающуюся в нее при $\zeta = 0$, которая определяет линейный оператор

Отметим, что собственные значения ${{\mu }_{j}}(\psi ,\zeta )({{\mu }_{j}}(\psi ,0) = {{\mu }_{j}}(\psi ))$ оператора (4.36) при $0 < \zeta < {{\zeta }_{0}}$ удовлетворяют условию $\left| {\operatorname{Re} {{\mu }_{j}}(\psi )} \right| > {{\mu }_{0}} > 0$.

Введем в рассмотрение банаховы пространства ${{C}_{{2\pi }}}$, $C_{{2\pi }}^{1}$ соответственно непрерывных и непрерывно дифференцируемых $2\pi $-периодических функций $f(\tau )$, $ - \infty < \tau < \infty $, со значениями в $E$, определив нормы ${{\left\| f \right\|}_{{{{C}_{{2\pi }}}}}} = su{{p}_{\tau }}{{\left\| {f(\tau )} \right\|}_{E}}$, ${{\left\| f \right\|}_{{C_{{2\pi }}^{1}}}} = {{\left\| f \right\|}_{{{{C}_{{2\pi }}}}}} + {{\left\| {f{\kern 1pt} {\text{'}}} \right\|}_{{{{C}_{{2\pi }}}}}}$.

Обозначим через ${{E}_{ + }}(\psi ,\zeta )$ и ${{E}_{ - }}(\psi ,\zeta )$ корневые подпространства оператора (4.36) ($\dim {{E}_{ + }}({\kern 1pt} \cdot {\kern 1pt} ) = m$), отвечающие соответственно собственным значениям с положительными и отрицательными вещественными частями, ${{E}_{ + }}(\psi ,\zeta ) \oplus {{E}_{ - }}(\psi ,\zeta ) = {{E}^{1}}$. Соответствующие проекторы обозначим $P + (\psi ,\zeta )$ и ${{P}_{ - }}(\psi ,\zeta )({{P}_{ + }}(\psi ,\zeta ) + {{P}_{ - }}(\psi ,\zeta ) = I)$, ${{P}_{ \pm }}(\psi ,\zeta )E_{ + }^{1} = {{E}_{ \pm }}(\psi ;\zeta )$.

Рассмотрим в $E$ линейное дифференциальное уравнение

Пусть $T(\tau ;\psi ,\zeta )$, $\tau \geqslant 0$, – полугруппа линейных ограниченных операторов $T({\kern 1pt} \cdot {\kern 1pt} ):{{E}^{1}} \to $ $ \to {{E}^{1}}(T({{\tau }_{1}} + {{\tau }_{2}}; \cdot ) = T({{\tau }_{1}}; \cdot )T({{\tau }_{2}}; \cdot ) = T({{\tau }_{2}}; \cdot )T({{\tau }_{1}}; \cdot ))$, определяющая решения (4.37) при $\tau \geqslant {{\tau }_{0}}$ с начальным условием ${{\text{v}}_{0}} = \text{v}({{\tau }_{0}}):\text{v}(\tau ;\psi ,\zeta ) = T(\tau ;\psi ,\zeta ){{\text{v}}_{0}}$. За непрерывным расширением $T({\kern 1pt} \cdot {\kern 1pt} )$, ${{P}_{ + }}({\kern 1pt} \cdot {\kern 1pt} )$, ${{P}_{ - }}({\kern 1pt} \cdot {\kern 1pt} )$ на $E$ (${{E}_{ + }}({\kern 1pt} \cdot {\kern 1pt} ) \oplus {{E}_{ - }}({\kern 1pt} \cdot {\kern 1pt} ) = E$) оставим прежние обозначения.

Введем определенный на $E$ оператор Грина уравнения (4.37)

В (4.38) оператор ${{T}_{ + }}({\kern 1pt} \cdot {\kern 1pt} )$ конечномерный и поэтому единственным способом продолжим на область $\tau < 0$. Справедливы также оценки

где ${{\left\| {T({\kern 1pt} \cdot {\kern 1pt} )} \right\|}_{ * }} = su{{p}_{{{{{\left\| \text{v} \right\|}}_{E}} = 1}}}{{\left\| {T({\kern 1pt} \cdot {\kern 1pt} )\text{v}} \right\|}_{E}}$.

Рассмотрим в $E$ дифференциальное уравнение

Уравнение (4.40) имеет единственное $2\pi $-периодическое решение

при этом на основании (4.39) имеем

Формула (4.41) проверяется непосредственной подстановкой в уравнение (4.40). При этом устойчивость $2\pi $-периодического решения (4.41) определяется расположением собственных значений оператора (4.36). При $m = 0$ решение (4.41) асимптотически устойчиво, при $m > 0$ решение (4.41) имеет $m$-мерное инвариантное неустойчивое многообразие.

Покажем, что система уравнений (4.31), (4.32) имеет $2\pi $-периодическое решение вида

Считая ${{\text{v}}_{1}}(\tau ) = {{\text{v}}_{1}}(\tau ; \cdot )$ в (4.42) искомой функцией (знак * опустим), подставим (4.42) в (4.31), (4.32). В результате получим уравнение для определения ${{\text{v}}_{1}}(\tau )$ следующего вида:

в котором гладко зависящие от параметров и переменных функция $f{\kern 1pt} {\text{*}}(\tau ;\psi ,\zeta ) \in {{C}_{{2\pi }}}$ и операторы $F({\kern 1pt} \cdot {\kern 1pt} )$, ${{F}^{ \vee }}({\kern 1pt} \cdot {\kern 1pt} )$ удовлетворяют условиям ${{\left\| {F({{\text{v}}_{1}};\psi ,\zeta )} \right\|}_{E}} = O\left( {\left\| {{{\text{v}}_{1}}} \right\|_{{{{E}^{1}}}}^{2}} \right)$, ${{F}^{ \vee }}(\tau ,0;\psi ,\zeta ) \equiv 0$, средние $\bar {f}{\text{*}}(\psi ;\zeta ) \equiv 0$ и ${{\bar {F}}^{ \vee }}({{\text{v}}_{1}};\psi ,\zeta ) = 0$.

Задача существования решения ${{\text{v}}_{1}}(\tau ) \in C_{{2\pi }}^{1}$ уравнения (4.44) на основании (4.40), (4.41) эквивалентна разрешимости следующего операторного уравнения:

в пространстве $C_{{2\pi }}^{1}$. На основании (4.42) к операторному уравнению (4.45) применима теорема о неявной функции для операторных уравнений в банаховом пространстве [14, с. 304]. В результате имеем решение $\text{v}_{1}^{ * }(\tau ;\psi ,\varsigma )(\text{v}(\tau ;\psi ,0) \equiv 0)$ уравнения (4.45), которое гладко зависит от входящих параметров. Выполнив обратные замены, имеем периодическое решение $y{\text{*}}(t + s;\psi ,\zeta )$. Формула (4.30) получена на основании (3.13), (3.16) (при $s = 0$), (4.19) с учетом лишь ($\rho {\kern 1pt} {\text{*}}(\psi )$, $\theta {\kern 1pt} {\text{*}}(\psi )$) – “главной части” решения (4.43). Устойчивость периодического решения $y{\kern 1pt} {\text{*}}(t + s;\psi ,\zeta )$ определяется устойчивостью периодического решения уравнения (4.40). Теорема доказана.

5. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ НОРМАЛЬНОЙ ФОРМЫ УРАВНЕНИЯ (4)

Приведем некоторые результаты численного анализа устойчивых состояний равновесия ($\rho {\kern 1pt} {\text{*}}(\psi )$, $\theta {\kern 1pt} {\text{*}}(\psi )$) системы дифференциальных уравнений (4.20), (4.21) при $\zeta = 0$, являющихся решениями системы нелинейных алгебраических уравнений (4.22), (4.23) и определяющих согласно (4.26), (4.29), (4.30) устойчивые периодические решения уравнения (1.2), бифурцирующие из состояния равновесия (1.3).

На фиг. 1 приведена картина $D$-разбиений [15] плоскости параметров (${{\varepsilon }_{1}}$, ${{\varepsilon }_{2}}$). На ней изображены кривые, на которых уравнение (2.4) имеет корни, лежащие на мнимой оси. Эти кривые являются границами областей $D$-разбиений. При значениях $\varepsilon $ из области ${{D}_{0}}$ все корни характеристического уравнения (2.4) находятся в левой комплексной полуплоскости, при $\varepsilon \in {{D}_{2}}$ одна пара комплексно-сопряженных корней находится в правой комплексной полуплоскости, а остальные – в левой, при $\varepsilon \in {{D}_{4}}$ две пары комплексно-сопряженных корней находятся в правой комплексной полуплоскости, а остальные – в левой, и т.д. Пунктирной линией обозначены границы последующих областей $D$-разбиений, аналогичные описанным выше.

Положим в (1.2) $n = 3$ и зафиксируем в (4.16) значения параметров $\psi = 1.51$. Этому значению $\psi $ на фиг. 1 соответствует кривая в области ${{D}_{8}}$, отмеченная точками. Для этого значения $\psi $ численно находились устойчивые состояния равновесия системы дифференциальных уравнений (4.20), (4.21) (при $\zeta = 0$). Вычисления проводились по следующей схеме. Рассматривалась последовательность усеченных конечномерных систем (4.20), (4.21) (при $\zeta = 0$), в которых $k = 1,3,\; \ldots ,\;N$. Конечномерная система дифференциальных уравнений численно интегрировалась при различных начальных условиях. Для численного интегрирования использовался программный комплекс [16], позволяющий одновременно строить большое число интегральных траекторий (с автоматическим выбором шага интегрирования) для случайным образом “брошенных”, например, по равномерному закону, начальных условий. Находилось устойчивое состояние равновесия ($\rho _{N}^{ * }(\psi )$, $\theta _{N}^{ * }(\psi )$). Это состояние равновесия уточнялось в системе уравнений (4.20), (4.21) (при $\zeta = 0$) при $k = 1,3,\; \ldots ,\;N + 1$ и т.д. до тех пор, пока ${{{{{\left\| {\rho _{N}^{ * }(\psi ) - \rho _{{N + 1}}^{ * }(\psi )} \right\|}}_{{l_{2}^{1}}}}} \mathord{\left/ {\vphantom {{{{{\left\| {\rho _{N}^{ * }(\psi ) - \rho _{{N + 1}}^{ * }(\psi )} \right\|}}_{{l_{2}^{1}}}}} {{{{\left\| {\rho _{N}^{ * }(\psi )} \right\|}}_{{l_{2}^{1}}}} < \Delta }}} \right. \kern-0em} {{{{\left\| {\rho _{N}^{ * }(\psi )} \right\|}}_{{l_{2}^{1}}}} < \Delta }}$ (выбиралось $\Delta = {{10}^{{ - 2}}}$).

Для указанного значения $\psi $ удалось выявить пять устойчивых состояний равновесия системы дифференциальных уравнений (4.20), (4.21) (при $\zeta = 0$). Других устойчивых установившихся решений выявлено не было. Для каждого из найденных состояний равновесия было построено периодическое решение уравнения (1.2) согласно (1.3), (4.26), (4.29), (4.30). На фиг. 2 для $\zeta = 0.1$ (на фиг. 1 – жирная точка в области ${{D}_{8}}$) приведены графики этих решений (жирная линия), и их проекции на плоскость ($x(t)$, $x(t - 1)$). На фигурах также приведены графики решений уравнения (1.2), полученные путем его численного интегрирования методом Эйлера с постоянным выбором шага, при этих же значениях параметров. Шаг интегрирования уменьшался до полной стабилизации результатов вычислений. В качестве начальных функций при интегрировании уравнения (1.2) выбирались периодические функции (решения), полученные согласно (1.3), (4.26), (4.29), (4.30).

Таким образом, для выбранного значения параметра $\psi $ при изменении параметра $\zeta > 0$ в уравнении (1.2), в котором ${{\varepsilon }_{1}}$ и $\beta $ изменяются согласно (2.2), (2.5), (4.16) наблюдается бифуркация из состояния (1.3) одновременно пяти периодических решений. Такое явление можно назвать бифуркацией мультистабильности.

Отметим, что при других значениях параметра $\psi $ система уравнений (4.20), (4.21) (при $\zeta = 0$) также имеет большое число устойчивых состояний равновесия, которым отвечают периодические решения уравнения (1.2). Так, например, при $\psi = 1.55$ было выявлено семь устойчивых состояний равновесия. Количество состояний равновесия возрастает при увеличении $\psi $.

Зафиксируем теперь значение параметра $\psi = 1.51$ и будем увеличивать $\zeta $. Этому случаю на фиг. 1 будет соответствовать точечная линия в области ${{D}_{8}}$. Рассмотрим, как будут изменяться найденные периодические решения при изменении $\zeta $. При увеличении параметра $\zeta $ каждое периодическое решение через серию бифуркаций удвоения периода колебаний переходит в нерегулярные (хаотические) колебания. Для хаотических колебаний вычислялся максимальный характеристический показатель и он оказывался положительным. При этом существует область значений параметра $\zeta $, при которых существует одновременно пять различных хаотических колебаний (аттракторов). Такое явление можно назвать хаотической мультистабильностью. Для численного интегрирования уравнения (1.2) и вычисления максимального характеристического показателя использовался программный комплекс [16]. На фиг. 3 приведены проекции фазовых портретов периодических решений на плоскость ($x(t)$, $x(t - 1)$), соответствующие переходу первых двух периодических решений, представленных на фиг. 2, от регулярных колебаний к хаотическим для значений $\zeta = 0.2,0.4,0.8$.