Журнал вычислительной математики и математической физики, 2019, T. 59, № 8, стр. 1358-1380
О задаче Томаса–Ферми и о решениях уравнения Эмдена–Фаулера
С. В. Пикулин *
ВЦ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия
* E-mail: spikulin@gmail.com
Поступила в редакцию 15.03.2019
После доработки 15.03.2019
Принята к публикации 10.04.2019
Аннотация
Рассмотрена двухточечная краевая задача для уравнения Эмдена–Фаулера – сингулярного нелинейного обыкновенного дифференциального уравнения второго порядка. При условии рациональности показателя степени в коэффициенте при нелинейном членe получены новые параметрические представления решения краевой задачи на луче и на отрезке. Для задачи на луче дана новая эффективная формула первого члена известного разложения Коулсона–Марча решения в окрестности бесконечности, получены обобщения этого представления и его аналоги для функции, обратной к решению. Для модели Томаса–Ферми многоэлектронного атома и положительно заряженного иона построены высокоэффективные вычислительные алгоритмы, позволяющие, в частности, найти решение задачи для атома (т.е. краевой задачи на луче) вместе с производной этого решения с любой заданной точностью в произвольной точке полупрямой. В основе полученных результатов лежит аналитическое свойство уравнения Абеля II рода специального вида, к которому приводится исходное уравнение Эмдена–Фаулера, а именно – свойство частичного прохождения модифицированного теста Пенлеве в узловой особой точке. Библ. 57. Фиг. 4. Табл. 2.
1. ВВЕДЕНИЕ
1.1. Модель Томаса–Ферми
Согласно модели Томаса–Ферми многоэлектронного атома или иона при нулевой абсолютной температуре (см. [1]–[3, § 70]) безразмерная пространственная плотность заряда подчиняется нелинейному уравнению
где $\Delta $ – оператор Лапласа в ${{\mathbb{R}}^{3}}$. В сферически симметричном случае с учетом естественных требований к поведению $\Phi $ на бесконечности и вблизи точечного ядра (т.е. при $\left| {\mathbf{x}} \right| \to 0$) модель (1.1) приводит к следующей краевой задаче для сингулярного обыкновенного дифференциального уравнения второго порядка:(1.2)
$\frac{{{{d}^{2}}\Psi }}{{d{{r}^{2}}}} - \frac{1}{{\sqrt r }}{{\Psi }^{{3/2}}}(r) = 0,\quad r \in (0,R),$(1.3)
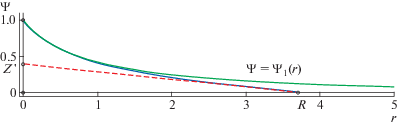
$\mathop {lim}\limits_{r \to + 0} \Psi (r) = Z,\quad \mathop {lim}\limits_{r \to R} \Psi (r) = 0,$Фиг. 1.
Графики решений задачи (1.2), (1.3) при $Z = 1$, моделирующих атом ($R = + \infty $) и положительно заряженный ион ($R < + \infty $) Томаса–Ферми.
Отметим, что базовые принципы модели Томаса–Ферми находят применение при моделировании неоднородного электронного газа в рамках так называемого метода функционала плотности (см. [4]).
1.2. Уравнение Эмдена–Фаулера и некоторые свойства его решений
Рассмотрим следующую двухточечную краевую задачу для уравнения Эмдена–Фаулера (см. [5, гл. VIII]):
(1.5)
$\frac{{{{d}^{2}}y}}{{d{{r}^{2}}}} - {{r}^{\nu }}{{y}^{{1 + \sigma }}}(r) = 0,\quad r \in (0,R),\quad R \in (0, + \infty ],\quad \nu > - 1,\quad \sigma > 0,$Известно (см. [5], [6]), что при $0 < R \leqslant + \infty $, $Z \in (0, + \infty )$ задача (1.5)–(1.7) имеет единственное классическое решение, которое является монотонно
убывающей положительной аналитической функцией на интервале $r \in (0,R)$. Известно также (см. [5, гл. VII, п. 7]), что каждое положительное решение $y(r)$ уравнения (1.5) при $\nu > - 2$, определенное на луче  , имеет асимптотический вид
, имеет асимптотический вид
(1.8)
$y(r) \sim \mathop {{{f}_{0}}}\nolimits^{1/\sigma } {{r}^{{ - \beta }}},\quad r \to + \infty ,$(1.10)
$\forall \varkappa > 0:\quad r \mapsto (\varkappa r),\quad y \mapsto ({{\varkappa }^{{ - \beta }}}y).$В частном случае задачи Томаса–Ферми (1.2), (1.3) параметры (1.9) принимают значения $\beta = 3$, ${{f}_{0}} = 12$, и формула масштабирования (1.10) позволяет (см. [2], [7]) выразить решение $\Psi (r)$ этой задачи через решение ${{\Psi }_{1}}(r)$ той же задачи при $Z = 1$ в виде
В этой связи функцию ${{\Psi }_{1}}(r)$ называют стандартным решением задачи Томаса–Ферми для нейтрального атома (см. [8, § 172]). Отметим, что для решения общей задачи (1.5)–(1.7) справедлива аналогичная формулаПри отрицательных значениях показателя $\nu \in ( - 1,0)$ левый конец $r = 0$ рассматриваемого в задаче (1.5)–(1.7) промежутка $r \in [0,R]$ является сингулярной точкой уравнения, поскольку коэффициент при нелинейном члене обращается в бесконечность. В отношении задачи (1.2), (1.3) известно (см. [9]), что при любых $R \in (0, + \infty ]$ ее решение в окрестности точки $r = 0$ представляется сходящимся рядом Пюизё по степеням $\sqrt r $:
причем решениям при фиксированном $Z$ и различных $R$ соответствуют различные значения наклона графика в нуле $\Psi {\kern 1pt} {\text{'}}(0) = {{b}_{2}} \in ( - \infty ,B]$, где $B = B(Z)$ – некоторое отрицательное число. Коэффициенты ${{b}_{k}}$, $k \geqslant 3$ определяются (см. [10]) по $Z$ и ${{b}_{2}}$ однозначно из уравнения (1.2). Решению задачи (1.2), (1.3) на полубесконечном промежутке ($R = + \infty $) соответствует в разложении (1.12) критическое значение ${{b}_{2}} = B(Z)$, которое при $Z = 1$ равно Отметим, что величина ${{b}_{2}}$ имеет в модели Томаса–Ферми следующий физический смысл: с точностью до множителя это энергия кулоновского взаимодействия электронного облака с ядром (см. [8, § 174]).Известно, что решение задачи (1.2), (1.3) при $R = + \infty $ в окрестности бесконечности может быть приближенно найдено по следующей формуле (так называемое представление Коулсона–Марча, см. [11], [12]):
(1.14)
$\Psi (r) = {{12}^{2}}{{r}^{{ - 3}}}{\kern 1pt} \sum\limits_{k = 0}^\infty {{{a}_{k}}} {{(r{{Z}^{{1/3}}})}^{{\alpha k}}},\quad \alpha = \frac{{7 - \sqrt {73} }}{2},\quad {{a}_{0}} = 1,\quad {{a}_{1}} = A: = - 13.76 \ldots ,$Отысканию численных значений критического наклона (1.13) в разложении (1.12) и константы $A$ в разложении (1.14), а также разработке методов решения задачи (1.2), (1.3) посвящена обширная литература (см. [1], [2], [7], [10]–[45 ]).
1.3. Описание результатов
Для того, чтобы сформулировать результаты настоящей работы, введем в рассмотрение константы ${{\omega }_{0}}$, $\alpha $, зависящие только от параметров $\nu $, $\sigma $ уравнения (1.5), по следующим формулам:
(1.16)
$\alpha : = - \frac{{{{\omega }_{0}} + \sqrt {\omega _{0}^{2} + 4\sigma {{f}_{0}}} }}{2} < 0,$Основной результат (теорема 1) заключается в следующем параметрическом представлении решения задачи (1.5)–(1.7), (1.17) при $R = + \infty $:
(1.18)
$r(t) = {{T}_{1}}{{t}^{{1/\alpha }}}{{(1 - t)}^{M}}\mathcal{H}(t),\quad y(t) = {{T}_{2}}{{t}^{{ - \beta /\alpha }}}{{\mathcal{H}}^{{ - \beta }}}(t),\quad t \in (0,1],$Представление (1.18) развивает известный (см. [38]–[45]) подход к построению решения задачи Томаса–Ферми в параметрическом виде. Отметим также построенный в работе [46] аналитико-численный метод решения сингулярной краевой задачи для нелинейного сингулярно возмущенного уравнения, аналогичного уравнению (1.5). Новизна подхода настоящей работы заключается в использовании обнаруженного ранее (см. [47]) аналитического свойства уравнения Абеля II рода специального вида, к которому приводится исходное уравнение Эмдена–Фаулера, а именно, свойства частичного прохождения модифицированного теста Пенлеве (см. [48]) в узловой особой точке.
Основанный на представлении (1.18) (при $M = 2$, $N = - 1$, $\beta = 3$, $\alpha = (7 - \sqrt {73} ){\text{/}}2$) метод решения задачи (1.2), (1.3) сочетает в себе высокую точность получаемого результата с относительно небольшой вычислительной трудоемкостью, что трудно достижимо в рамках предлагавшихся ранее методов. В основе такого сочетания лежит тот факт, что ряд Тейлора функции $\mathcal{H}(t)$ в точке $t = 0$ демонстрирует экспоненциально быструю сходимость на всем отрезке $t \in [0,1]$ (эмпирическое значение радиуса сходимости ≈1.2; в работе также дана теоретическая оценка снизу этого радиуса), что позволяет эффективно находить решение $\Psi (r)$ и его производную $\Psi {\text{'}}(r)$ в произвольной точке луча $r \in [0, + \infty )$ с практически любой наперед заданной точностью.
Также в работе получено (см. теорему 5) представление типа (1.18) решения двухточечной краевой задачи (1.5)–(1.7) на конечном отрезке $[0,R]$ при $R \in (0, + \infty )$, $Z \in (0, + \infty )$. Такая постановка в рамках модели Томаса–Ферми отвечает случаю положительно заряженного иона.
Следствием полученных параметрических формул (см. теорему 6) является представимость решения задачи (1.5)–(1.7) при $R \in (0, + \infty ]$, $Z > 0$ и рациональном значении $\nu $ в виде сходящегося в окрестности $r = 0$ ряда
(1.19)
$y(r) = Z + {{b}_{M}}r + {{b}_{{M + 1}}}{{r}^{{1 + 1/M}}} + {{b}_{{M + 2}}}{{r}^{{1 + 2/M}}} + \ldots $Как и в случае разложения (1.12), обобщением которого является ряд (1.19), значение коэффициента ${{b}_{M}} \in ( - \infty ,B]$ параметризует решения задачи (1.5)–(1.7) при данном $Z$ и различных $R \in (0, + \infty ]$; здесь $B = B(Z,\sigma ,\nu )$ – наклон графика в нуле решения задачи на полубесконечном интервале, т.е. при $R = + \infty $. Из (1.11) следует, что
В данной работе получена формула (см. (2.15)) для критического значения $B(1,\sigma ,\nu )$ производной решения в нулевой точке при $Z = 1$, обобщающая известную формулу Майораны (см. [40]) для величины (1.13). В этой связи отметим построенный в работах [50], [51] аналитико-численный метод нахождения константы Блазиуса, возникающей в теории погранслоя.Теорема 2 настоящей работы дает следующее представление в окрестности $r = + \infty $ решения задачи (1.5)–(1.7), $R = + \infty $, обобщающее разложение (1.14) и уточняющее асимптотику (1.8):
(1.20)
$y(r) = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } {{r}^{{ - \beta }}}{\kern 1pt} \sum\limits_{n = 0}^\infty {{{a}_{n}}} {{({{Z}^{{1/\beta }}}r)}^{{n\alpha }}},\quad {{a}_{0}} = 1,\quad {{a}_{1}} = {{a}_{1}}(\sigma ,\nu ),$Хорошо известно (см. [52]), что разложение (1.14) сходится лишь при достаточно больших значениях $r$. В теоремах 3 и 4 получены новые представления, аналогичные (1.20), (1.14), для обратной к решению $y(r)$ функции $r(y)$:
(1.21)
$r(y) = \frac{{\mathop {{{f}_{0}}}\nolimits^{1/(\nu + 2)} }}{{{{y}^{{1/\beta }}}}}\sum\limits_{n = 0}^\infty {{{A}_{n}}} {{(y{\text{/}}Z)}^{{ - n\alpha /\beta }}},$(1.22)
$r(y) = \frac{{\mathop {{{f}_{0}}}\nolimits^{1/(\nu + 2)} }}{{{{y}^{{1/\beta }}}}}\sum\limits_{n = 0}^\infty {A_{n}^{'}} {{\mathcal{Y}}^{n}},\quad \mathcal{Y}: = 1 - \sqrt[M]{{1 - {{{(y{\text{/}}Z)}}^{{ - \alpha /\beta }}}}} \in (0,1],$(1.23)
$r(\Psi ) \approx {{12}^{{2/3}}}{{\Psi }^{{ - 1/3}}}\left( {1 - {{{(\Psi {\text{/}}Z)}}^{{ - \alpha /3}}}} \right).$Аналитичность функции $\mathcal{H}(t)$ в представлении (1.18) при $t = 1$ обусловлена некоторым свойством узловой особой точки уравнения Абеля II рода – вспомогательного уравнения первого порядка, к которому приводится исходное уравнение (1.5) в результате процедуры понижения порядка. Это свойство заключается в том, что семейство решений уравнения, проходящих через его узловую точку в начале координат, может быть задано общей формулой, включающей ряд по дробным степеням переменной, причем один из коэффициентов ряда является параметром данного семейства. Как показано в работе [47], такая аналитическая структура решений уравнения Абеля II рода вблизи его узловой особой точки связана с частичным прохождением некоторой модификации теста Пенлеве для данного уравнения. Отметим, что в работах [53]–[55] с помощью указанного свойства уравнения Абеля II рода были получены новые представления квазистационарных решений нелинейных параболических уравнений типа Колмогорова–Петровского–Пискунова.
1.4. Переход к автономному уравнению второго порядка
Положим
где по определению $ln( + \infty ) = + \infty $. Пользуясь обозначениями (1.9), перейдем в задаче (1.5)–(1.7) к новым переменным(1.25)
$\psi : = \mathop {{{f}_{0}}}\nolimits^{ - 1/\sigma } {{r}^{\beta }}y(r) > 0,\quad \rho : = lnr \in I(R),$(1.26)
$\frac{{{{d}^{2}}\psi }}{{d{{\rho }^{2}}}} + {{\omega }_{0}}\frac{{d\psi }}{{d\rho }} + {{f}_{0}}\psi (1 - {{\psi }^{\sigma }}) = 0.$Зафиксируем решение $y(r)$ задачи (1.5)–(1.7) при некоторых $0 < R \leqslant + \infty $, $Z \in (0, + \infty )$ и рассмотрим поведение соответствующего решения $\psi (\rho )$ уравнения (1.26). Из формулы подстановки (1.25) и из условия (1.6) следует асимптотика
а из условия (1.7) и соотношения (1.8) вытекает равенство(1.29)
$\mathop {lim}\limits_{\rho \to lnR} \psi (\rho ) = \left\{ \begin{gathered} 0,\quad R \in (0, + \infty ), \hfill \\ 1,\quad R = + \infty . \hfill \\ \end{gathered} \right.$В силу автономности уравнения (1.26) его решение $\psi (\rho )$ при сдвиге вдоль оси $\rho $,
переходит в решение этого же уравнения. Из формул (1.25), (1.27) видно, что перенос (1.30) соответствует масштабному преобразованию (1.10) уравнения (1.5). Кроме того, трансляция (1.30) сохраняет величину которая, тем самым, является инвариантом масштабирования (1.10).Исходя из условий (1.6), (1.7), докажем от противного следующее включение:
В самом деле, из предположения $\mu > 1$ и асимптотик (1.28), (1.29) вытекает наличие у функции $\psi (\rho )$ локального максимума в некоторой точке ${{\rho }_{0}} \in I(R)$, $\psi ({{\rho }_{0}}) > 1$. Тогда в этой точке должны быть выполнены условияСледующее утверждение непосредственно вытекает из предложения 5 работы [47].
Предложение 1. Для каждого $\mu $ из полуинтервала (1.32) существует решение $\psi = {{\psi }_{\mu }}(\rho )$ задачи (1.26)–(1.29) на промежутке $I(R)$ вида (1.24) при некотором $R \in (0, + \infty ]$, имеющее заданное формулой (1.31) значение $\mu $. Функция ${{\psi }_{\mu }}(\rho )$ определена однозначно с точностью до сдвига (1.30), при этом $\mu = 1$ тогда и только тогда, когда $R = + \infty $.
Из проведенных выше рассуждений и из предложения 1 вытекает
Предложение 2. Множество решений $y(r)$ задачи (1.5)–(1.7), $Z \in (0, + \infty )$, $R \in (0, + \infty ]$ находится во взаимно однозначном соответствии с множеством решений задачи (1.26)–(1.29), (1.31), (1.32) при $\mu \in (0,1]$. Это соответствие, заданное формулами (1.25), (1.27), согласовано с преобразованиями (1.10), (1.31) так, что промежуток (1.32) параметризует классы эквивалентности решений $y(r)$ по отношению к масштабированию (1.10).
В дальнейшем нам будет удобно задавать решение $y(r)$ задачи (1.5)–(1.7), не парой $(R,Z)$, где $R \in (0, + \infty ]$, $Z \in (0, + \infty )$, а парой $(\mu ,Z)$, где $\mu \in (0,1]$, $Z \in (0, + \infty )$.
1.5. Понижение порядка уравнения и условие прохождения теста Пенлеве
Определим новую переменную $p = p(\psi )$ в виде
тогда задача (1.26), (1.28), (1.29), (1.31) при $\mu \in (0,1]$ сведется к следующей (сингулярной) задаче Коши относительно $p(\psi )$:(1.34)
$p(\psi )\frac{{dp}}{{d\psi }} + {{\omega }_{0}}p(\psi ) + {{f}_{0}}\psi (1 - {{\psi }^{\sigma }}) = 0,\quad p(\mu ) = 0.$Определим индекс Фукса для узловой точки $\psi = 0$, $p = 0$ уравнения (1.34) с учетом (1.9), (1.15) следующим образом:
(1.35)
$K: = - \frac{{{{\omega }_{0}} + 2\beta }}{{\beta \sigma }} = \frac{1}{{\sigma \beta }} = \frac{1}{{\nu + 2}}.$Введем в рассмотрение переменные $q$, $z$, связанные с $p$, $\psi $ следующим образом:
тогда относительно $q(z)$ задача (1.34) принимает вид(1.38)
$\frac{\sigma }{{2\tilde {N}}}z\frac{{d{{q}^{2}}}}{{dz}} + {{q}^{2}}(z) + {{\omega }_{0}}q(z) + {{f}_{0}}(1 - {{z}^{{\tilde {N}}}}) = 0,$Согласно предложению 1 работы [47] все траектории, представляющие решения задачи (1.34) на плоскости $(\psi ,p)$, приходят в начало координат $\psi = 0$, $p = 0$ с наклоном $\beta $ к горизонтали, а соответствующие решения задачи (1.38), (1.39) обладают свойством $q(0) = \beta $. Применяя теорему 1 той же работы [47], получаем
Предложение 3. Всякое решение $q(z)$ уравнения (1.38) с условием $q(0) = \beta $ является аналитической при $z = 0$ функцией вида
где функция $\mathcal{Q}(z)$ также аналитична при $z = 0$. Решения вида (1.40) образуют семейство, параметризованное величиной $C: = \mathcal{Q}(0)$, т.е. для каждого $C \in \mathbb{R}$ существует единственное решение $q(z)$ вида (1.40). При этом коэффициенты Тейлора функции $\mathcal{Q}(z)$ в точке $z = 0$ рационально выражаются через $\beta $, $M$, $\tilde {N}$, $C$.Решения $q = {{q}_{\mu }}(z)$ задачи (1.38), (1.39) при $\mu \in (0,1]$ принадлежат указанному семейству, и формула (1.40) определяет для каждого $\mu \in (0,1]$ функцию $\mathcal{Q} = {{\mathcal{Q}}_{\mu }}(z)$. При этом отображение
Предложение 3 утверждает, таким образом, что при выполнении условия (1.17) переход в уравнении Абеля (1.34) к переменным $z$, $\mathcal{Q}$ в определенном смысле устраняет нерегулярность этого уравнения в узловой точке $\psi = 0$, $p = 0$.
2. ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ УРАВНЕНИЯ ЭМДЕНА–ФАУЛЕРА
2.1. Решение задачи на полубесконечном промежутке
Рассмотрим задачу (1.5)–(1.7), $R = + \infty $ при некотором $Z > 0$. Согласно предложениям 1, 2 ее решение $y(r)$ выражается по формулам (1.27) через решение $\psi = {{\psi }_{1}}(\rho )$ задачи (1.26), (1.28), (1.29), (1.31) при $\mu = 1$.
2.1.1. Параметрическое представление решения и его производной. Предположим, что для показателя $\nu $ в уравнении (1.5) выполнено условие рациональности (1.17). Тогда теорема 2 работы [47] утверждает, что функция $\psi = {{\psi }_{1}}(\rho )$ имеет следующее параметрическое представление:
(2.1)
$\psi = {{(1 - t)}^{{\tilde {N}/\sigma }}},\quad \rho = Mln(1 - t) + \frac{1}{\alpha }lnt + H(t),\quad t \in (0,1),$(2.2)
$H(t) = \int\limits_0^t {h(t){\kern 1pt} {\kern 1pt} } dt,\quad h(t) = - \frac{1}{{\alpha t}} + M\mathcal{Q}(t)\frac{{{{{(1 - t)}}^{{M - 1}}}}}{{1 + {{{(1 - t)}}^{M}}\mathcal{Q}(t)}}$(2.3)
$\frac{{d\mathcal{Q}}}{{dt}} = - \,(\beta + 1)M\frac{{{{{(1 - t)}}^{{M - 1}}}{{\mathcal{Q}}^{2}}(t) - {{{(1 - t)}}^{{\tilde {N} - M - 1}}}}}{{1 + {{{(1 - t)}}^{M}}\mathcal{Q}(t)}},\quad t \in [0,1]{\kern 1pt} {\kern 1pt} ,$Подставляя параметризацию (2.1) в формулы (1.27), с учетом равенства
вытекающего из (1.35), (1.36), получаем представление (1.18), где ${{T}_{1}} = {\text{const}} > 0$,(2.9)
${{T}_{2}} = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathop {{{T}_{1}}}\nolimits^{ - \beta } .$Выберем константу ${{T}_{1}}$ в (2.1) таким образом, чтобы удовлетворить краевому условию (1.6). Вводя обозначение
подставляя $t = 1$ в (1.18) и приравнивая $Z$ полученное выражение для $y$ при $r = 0$, запишем условие (1.6) в следующем виде:(2.11)
${{T}_{1}} = \frac{{\mathop {{{f}_{0}}}\nolimits^K }}{{{{\mathcal{H}}_{e}}}}{{Z}^{{ - 1/\beta }}},\quad {{T}_{2}} = \mathcal{H}_{e}^{\beta }Z,$На основании формул (2.2), (2.8), (2.5) найдем производные функций $r(t)$, $y(t)$ в параметрическом представлении (1.18):
(2.12)
$\frac{{dy}}{{dt}} = y(t)\frac{{dlny}}{{dt}} = - \,\beta y(t)\frac{d}{{dt}}\left( {\frac{1}{\alpha }lnt + H(t)} \right) = - \,\beta \left( {\frac{1}{{\alpha t}} + h(t)} \right)y(t) = - \,\beta M\frac{{{{{(1 - t)}}^{{M - 1}}}\mathcal{Q}(t)}}{{g(t)}}y(t),$(2.13)
$\begin{gathered} \frac{{dr}}{{dt}} = r(t)\frac{{dlnr}}{{dt}} = r(t)\frac{d}{{dt}}\left( {Mln(1 - t) + \frac{1}{\alpha }lnt + H(t)} \right) = \left( { - \frac{M}{{1 - t}} + \frac{1}{{\alpha t}} + h(t)} \right)r(t) = \\ = \;\left( { - \frac{M}{{1 - t}} + M\frac{{{{{(1 - t)}}^{{M - 1}}}\mathcal{Q}(t)}}{{1 + {{{(1 - t)}}^{M}}\mathcal{Q}(t)}}} \right)r(t) = - \frac{M}{{(1 - t)g(t)}}r(t). \\ \end{gathered} $Используя полученные выражения (2.12), (2.13), вычислим производную решения $dy{\text{/}}dr$ в зависимости от параметра $t \in (0,1]$:
(2.14)
$\frac{{dy}}{{dr}} = \frac{{dy}}{{dt}}\mathop {\left( {\frac{{dr}}{{dt}}} \right)}\nolimits^{ - 1} = \beta \frac{{y(t)}}{{r(t)}}{{(1 - t)}^{M}}\mathcal{Q}(t) = \beta \frac{{{{T}_{2}}}}{{{{T}_{1}}}}{{t}^{{ - (\beta + 1)/\alpha }}}{{\mathcal{H}}^{{ - (\beta + 1)}}}(t)\mathcal{Q}(t),\quad t \in (0,1],$(2.15)
$\frac{{dy}}{{dr}}(0) = \frac{{{{T}_{2}}}}{{{{T}_{1}}}}\mathcal{H}_{e}^{{ - (\beta + 1)}}{{\mathcal{Q}}_{e}} = \mathop {{{f}_{0}}}\nolimits^{ - K} {{Z}^{{(\beta + 1)/\beta }}}{{\mathcal{Q}}_{e}},\quad {{\mathcal{Q}}_{e}}: = {{\left. {\mathcal{Q}(t)} \right|}_{{t = 1}}}.$Отметим, что в силу (2.12), (2.13), (1.18) обе производные $dy{\text{/}}dt$ и $dr{\text{/}}dt$ имеют нули порядка $(M - 1)$ при $t = 0$ и не обращаются в нуль в других точках единичного отрезка.
2.1.2. Вычисление тейлоровских коэффициентов и оценка радиуса сходимости. Найдем коэффициенты разложения введенных выше (2.2)–(2.4), (2.8) функций $\mathcal{Q}(t)$, $\mathcal{H}(t)$ по степеням переменной $t$. Используя обозначение (2.5), перепишем уравнение (2.3) в виде
(2.16)
$g(t)\frac{{d\mathcal{Q}}}{{dt}} = (\beta + 1)M\left( {{{{(1 - t)}}^{{M - 1}}}{{\mathcal{Q}}^{2}}(t) - {{{(1 - t)}}^{{\tilde {N} - M - 1}}}} \right),\quad t \in [0,1]{\kern 1pt} {\kern 1pt} ,$(2.17)
$\mathcal{Q}(t) = :\sum\limits_{n = 0}^\infty {{{\mathcal{Q}}_{n}}} {{t}^{n}},\quad {{\mathcal{Q}}_{0}} = - 1,\quad {{\mathcal{Q}}_{1}} = - \,(\alpha + 1)M,$(2.18)
$g(t) = :\sum\limits_{n = 1}^\infty {{{g}_{n}}} {{t}^{n}},\quad {{g}_{n}} = \sum\limits_{j = 0}^M {{{{( - 1)}}^{j}}} \left( {\begin{array}{*{20}{c}} M \\ j \end{array}} \right){{\mathcal{Q}}_{{n - j}}},\quad n \geqslant 1,\quad {{g}_{1}} = - \alpha M.$Приравнивая коэффициенты при ${{t}^{n}}$, $n \geqslant 2$, в обеих частях равенства (2.16), получаем
(2.19)
${{\mathcal{Q}}_{1}}{{\mathcal{Q}}_{n}} + n{{\mathcal{Q}}_{n}}{{g}_{1}} - 2(\beta + 1)M{{\mathcal{Q}}_{0}}{{\mathcal{Q}}_{n}} = {{V}_{n}},$(2.20)
$\begin{gathered} {{V}_{n}}: = (\beta + 1)M\left[ {\sum\limits_{j,k = 0}^{n - 1} {{{{( - 1)}}^{{n - j - k}}}} \left( {\begin{array}{*{20}{c}} {M - 1} \\ {n - j - k} \end{array}} \right){{\mathcal{Q}}_{j}}{{\mathcal{Q}}_{k}} + {{{( - 1)}}^{{n + 1}}}\left( {\begin{array}{*{20}{c}} {\tilde {N} - M - 1} \\ n \end{array}} \right)} \right] - \\ - \;{{\mathcal{Q}}_{1}}\sum\limits_{j = 1}^M {{{{( - 1)}}^{j}}} \left( {\begin{array}{*{20}{c}} M \\ j \end{array}} \right){{\mathcal{Q}}_{{n - j}}} - \sum\limits_{j = 2}^{n - 1} j \,{{\mathcal{Q}}_{j}}{{g}_{{n - j + 1}}} \\ \end{gathered} $(2.21)
$\begin{gathered} {{\mathcal{Q}}_{1}} + n{{g}_{1}} - 2(\beta + 1)M{{\mathcal{Q}}_{0}} = - \,(\alpha + 1)M - n\alpha M + 2(\beta + 1)M = \\ = \; - \,{\kern 1pt} \left( {\alpha (n + 1) + 1 - 2(\beta + 1)} \right)M = - \left( {(n + 1)\alpha + {{\omega }_{0}}} \right)M > 0,\quad n \geqslant 2. \\ \end{gathered} $Решая (2.19) как линейное уравнение относительно ${{\mathcal{Q}}_{n}}$ последовательно при $n = 2,3,\; \ldots $, с учетом (2.21) получаем
(2.22)
${{\mathcal{Q}}_{n}} = \frac{{{{V}_{n}}}}{{ - \left( {{{\omega }_{0}} + (n + 1){\kern 1pt} {\kern 1pt} \alpha } \right)M}},\quad n \geqslant 2.$Найдем коэффициенты ряда Тейлора
функции $h(t)$ на основании (2.2), (2.5), (2.7):(2.24)
$\begin{gathered} h(t) = - \frac{1}{{\alpha t}} + \frac{{M{{{(1 - t)}}^{{M - 1}}}\mathcal{Q}(t)}}{{g(t)}} = \frac{{M{{{(1 - t)}}^{{M - 1}}}\mathcal{Q}(t) - {{\alpha }^{{ - 1}}}{{t}^{{ - 1}}}g(t)}}{{g(t)}} = \\ = \;\frac{{{{t}^{{ - 1}}}\left( {M{{{(1 - t)}}^{{M - 1}}}\mathcal{Q}(t) - {{\alpha }^{{ - 1}}}{{t}^{{ - 1}}}g(t)} \right)}}{{{{t}^{{ - 1}}}g(t)}}. \\ \end{gathered} $(2.25)
${{G}_{n}} = - \frac{{{{g}_{{n + 2}}}}}{\alpha } + M\sum\limits_{j = 0}^{n + 1} {{{{( - 1)}}^{j}}} \left( {\begin{array}{*{20}{c}} {M - 1} \\ j \end{array}} \right){{\mathcal{Q}}_{{n + 1 - j}}},\quad n \geqslant 0,$(2.26)
${{h}_{n}} = \frac{1}{{{{g}_{1}}}}\left( {{{G}_{n}} - \sum\limits_{j = 0}^{n - 1} {{{h}_{j}}} {{g}_{{n + 1 - j}}}} \right),\quad n \geqslant 0.$Для тейлоровских коэффициентов ${{H}_{n}}$ функции
(2.27)
$H(t) = \int\limits_0^t {h(t)} {\kern 1pt} {\kern 1pt} dt = :\sum\limits_{n = 1}^\infty {{{H}_{n}}} {{t}^{n}}$Ряд Тейлора функции (2.8) получаем, раскрывая скобки и приводя подобные члены в правой части формулы
(2.29)
$\mathcal{H}(t) = expH(t) = \sum\limits_{n = 0}^\infty {\frac{{{{t}^{n}}}}{{n!}}} {{\left( {\sum\limits_{k = 0}^\infty {{{H}_{{k + 1}}}{{t}^{k}}} } \right)}^{n}},$Оценим радиус сходимости рядов (2.17), (2.18), (2.23), предполагая дополнительно, что значение параметра $\sigma $ уравнения (1.5) лежит в диапазоне
Сначала покажем, что решение $p = {{p}_{1}}(\psi )$ задачи (1.34), $\mu = 1$, является аналитической функцией в круге $\mathcal{O}: = \left\{ {\left| {\psi - 1} \right| < 1} \right\}$. Согласно предложению 4 работы [47] достаточно показать, что свободный член $F(\psi ) = {{f}_{0}}\psi (1 - {{\psi }^{\sigma }})$ этого уравнения обладает следующими свойствами: во-первых, $F(\psi )$ является голоморфной внутри круга $\mathcal{O}$ функцией, не обращающейся в этом круге в нуль нигде, кроме его центра $\psi = 1$, и, во-вторых, коэффициенты разложения функции $F(\psi ){\text{/}}\psi $ в точке $\psi = 1$ по степеням переменной $\tau : = (1 - \psi )$ образуют убывающую последовательность положительных чисел. Первое из этих условий, очевидно, выполнено; проверим второе условие:
При замене переменной $\psi $ на t при помощи подстановок (1.37), (2.6) круг $\mathcal{O}$ сходимости функции ${{p}_{1}}(\psi )$ конформно отображается на выпуклую “каплевидную” область $\mathcal{D}$ аналитичности функций $\mathcal{Q}(t)$, $q(t)$, $h(t)$, $H(t)$, $\mathcal{H}(t)$. Область $\mathcal{D}$ имеет угловую точку с раствором угла $(\pi \sigma {\text{/}}\tilde {N})$ в точке $t = 1$. Расстояние от начала координат $t = 0$ до границы $\partial{ \mathcal{D}}$ равно
Таким образом, получен следующий результат.
Предложение 4. При выполнении условия (2.30) функции $\mathcal{Q}(t)$, $q(t)$, $h(t)$, $H(t)$, $\mathcal{H}(t)$ голоморфны в области $\mathcal{D}$ и величина (2.31) ограничивает снизу радиус сходимости рядов (2.17), (2.18), (2.23).
Получив значение функции $\mathcal{Q}(t)$ в некоторой внутренней точке единичного интервала $t \in (0,1)$, можно найти в этой точке тейлоровские разложения функций $\mathcal{Q}(t)$, $g(t)$ методом неопределенных коэффициентов из уравнений (2.5), (2.16), и затем вычислить соответствующие разложения функций $h(t)$, $H(t)$, $\mathcal{H}(t)$ по формулам (2.24), (2.27)–(2.29).
Суммируем результаты, полученные в пп. 2.1.1, 2.1.2, в виде следующей теоремы.
Теорема 1. Рассмотрим задачу (1.5)–(1.7), $R = + \infty $ при $Z \in (0, + \infty )$ и при условии (1.17). Тогда для решения $y(r)$ этой задачи и его первой производной $dy{\text{/}}dr$ справедливо параметрическое представление (1.18), (2.11), (2.14), т.е.
(2.32)
$r = {{T}_{1}}{{(1 - t)}^{M}}{{t}^{{1/\alpha }}}\mathcal{H}(t),\quad t \in (0,1],\quad {{T}_{1}} = \frac{{\mathop {{{f}_{0}}}\nolimits^K }}{{{{\mathcal{H}}_{e}}}}{{Z}^{{ - 1/\beta }}},$(2.33)
$y = {{T}_{2}}{{t}^{{ - \beta /\alpha }}}{{\mathcal{H}}^{{ - \beta }}}(t),\quad {{T}_{2}} = \mathcal{H}_{e}^{\beta }Z,$(2.34)
$\frac{{dy}}{{dr}} = {{T}_{3}}{\kern 1pt} {\kern 1pt} {{t}^{{ - (\beta + 1)/\alpha }}}{{\mathcal{H}}^{{ - (\beta + 1)}}}(t)\mathcal{Q}(t),\quad {{T}_{3}} = \beta \mathop {{{f}_{0}}}\nolimits^{ - K} \mathcal{H}_{e}^{{\beta + 1}}{{Z}^{{(\beta + 1)/\beta }}},$2.1.3. Исключение параметра t. Рассмотрим решение $y(r)$ задачи (1.5)–(1.7), (1.17), $R = + \infty $ при $Z \in (0, + \infty )$ в виде (2.32), (2.33) и исключим параметр $t$ из этого представления. Возводя в степень $\sigma {\text{/}}\tilde {N}$ обе части равенства $\psi = (\mathop {{{f}_{0}}}\nolimits^{ - 1/\sigma } {{r}^{\beta }}y)$, т.е. первой формулы (1.25), запишем результат с учетом (2.1), (2.7) в следующем виде:
(2.35)
${{r}^{{1/M}}}{{y}^{{\sigma /\widetilde N}}} = \mathop {{{f}_{0}}}\nolimits^{1/\tilde {N}} (1 - t).$Выразим параметр $t$ через $r$ из равенства (2.32). Разделив обе части (2.32) на ${{T}_{1}}$ и возведя их в степень $\alpha $, введем обозначения соответственно $\tilde {r}$ и $\xi $ для преобразованных левой и правой частей:
(2.36)
$\tilde {r} = \tilde {r}(r): = \mathop {\left( {\frac{r}{{{{T}_{1}}}}} \right)}\nolimits^\alpha = {{(1 - t)}^{{M\alpha }}}t{{\mathcal{H}}^{\alpha }}(t) = :\xi (t),\quad t \in [0,1],\quad r,\tilde {r} \in [0, + \infty ],$Проверим, что $d\xi {\text{/}}dt \ne 0$ при $t \in [0,1)$. В самом деле, в силу (2.13) с учетом (2.5) имеем
Вычислим разложение функции $\xi (t)$ по степеням переменной $t$. В окрестности $t = 0$ справедливы формулы
(2.38)
$\begin{gathered} {{(1 - t)}^{{M\alpha }}} = \sum\limits_{n = 0}^\infty {{{{( - 1)}}^{n}}} \left( {\begin{array}{*{20}{c}} {M\alpha } \\ n \end{array}} \right){{t}^{n}} = 1 - M\alpha t + \ldots , \\ t{{\mathcal{H}}^{\alpha }}(t) = \sum\limits_{n = 0}^\infty {\frac{{{{t}^{{n + 1}}}}}{{n!}}} {{\left( {\alpha \sum\limits_{k = 0}^\infty {{{H}_{{k + 1}}}{{t}^{k}}} } \right)}^{n}} = t + \alpha {{H}_{1}}{{t}^{2}} + \ldots , \\ \end{gathered} $(2.40)
$\theta (\tilde {r}) = \tilde {r} + \alpha ({{H}_{1}} - M){{\tilde {r}}^{2}} + \cdots : = \sum\limits_{n = 1}^\infty {{{\theta }_{n}}} {{\tilde {r}}^{n}},$Подставляя выражение (2.37) для $t$ в формулу (2.35), получаем следующие представления функции $y = y(r)$:
(2.41)
${{y}^{{\sigma /\tilde {N}}}} = \frac{{\mathop {{{f}_{0}}}\nolimits^{1/\tilde {N}} }}{{{{r}^{{1/M}}}}}\left( {1 - \theta (\tilde {r})} \right),\quad y(r) = \frac{{\mathop {{{f}_{0}}}\nolimits^{1/\sigma } }}{{{{r}^{\beta }}}}{{\left( {1 - \theta (\tilde {r})} \right)}^{{\tilde {N}/\sigma }}},\quad \tilde {r} = \tilde {r}(r) \in (0, + \infty ),$(2.42)
$y(r) = \frac{{\mathop {{{f}_{0}}}\nolimits^{1/\sigma } }}{{{{r}^{\beta }}}}{{\left( {1 - \sum\limits_{n = 1}^\infty {{{\theta }_{n}}} {{{(r{{Z}^{{1/\beta }}}\mathop {{{f}_{0}}}\nolimits^{ - K} {{\mathcal{H}}_{e}})}}^{{n\alpha }}}} \right)}^{{\tilde {N}/\sigma }}} = :\frac{{\mathop {{{f}_{0}}}\nolimits^{1/\sigma } }}{{{{r}^{\beta }}}}\sum\limits_{n = 0}^\infty {{{a}_{n}}} {{(r{{Z}^{{1/\beta }}})}^{{n\alpha }}},$(2.43)
${{a}_{0}} = 1,\quad {{a}_{1}} = - \frac{{\tilde {N}}}{{\sigma \mathop {{{f}_{0}}}\nolimits^{\alpha K} }}\mathcal{H}_{e}^{\alpha }.$Таким образом, получена следующая
Теорема 2. В условиях теоремы 1 параметр $t \in (0,1]$ выражается через $r$ в виде (2.37). Для решения $y(r)$ задачи (1.5)–(1.7), $R = + \infty $, справедливо представление (2.41), принимающее в окрестности $r = + \infty $ вид (2.42), (2.43).
Выразим теперь параметр $t$ через $y$ из равенства (2.33). Возводя в степень $ - \alpha {\text{/}}\beta $ обе части этого равенства и вводя по аналогии с (2.36) обозначения $\tilde {y}$, $\Xi $, находим
(2.44)
$\tilde {y} = \tilde {y}(y): = \mathop {\left( {\frac{y}{{\mathcal{H}_{e}^{\beta }Z}}} \right)}\nolimits^{ - \alpha /\beta } = t{{\mathcal{H}}^{\alpha }}(t) = :\Xi (t).$Для функции $\Xi (t)$ в окрестности $t = 0$ справедливо разложение (2.38), откуда находим разложение Тейлора в точке $\tilde {y} = 0$ обратной функции:
(2.46)
$\Theta (\tilde {y}) = \tilde {y} - \alpha {{H}_{1}}{{\tilde {y}}^{2}} + \cdots = :\sum\limits_{n = 1}^\infty {{{\Theta }_{n}}} {{\tilde {y}}^{n}}.$Подставляя $t$ в виде (2.45) в формулу (2.35) и разрешая ее относительно $r$, получаем
(2.47)
${{r}^{{1/M}}} = \frac{{\mathop {{{f}_{0}}}\nolimits^{1/\tilde {N}} }}{{{{y}^{{\sigma /\tilde {N}}}}}}\left( {1 - \Theta (\tilde {y}(y))} \right),$(2.48)
$r(y) = \frac{{\mathop {{{f}_{0}}}\nolimits^K }}{{{{y}^{{1/\beta }}}}}{{\left( {1 - \sum\limits_{n = 1}^\infty {{{\Theta }_{n}}} {{{\tilde {y}}}^{n}}} \right)}^{M}} = :\frac{{\mathop {{{f}_{0}}}\nolimits^K }}{{{{y}^{{1/\beta }}}}}\sum\limits_{n = 0}^\infty {{{A}_{n}}} {{(y{\text{/}}Z)}^{{ - n\alpha /\beta }}},\quad {{A}_{0}} = 1,\quad {{A}_{1}} = - M\mathcal{H}_{e}^{\alpha }.$Таким образом, справедлива
Теорема 3. В условиях теоремы 1 параметр $t \in (0,1]$ выражается через $y$ в виде (2.45), причем функция $t = t(y)$ имеет в комплексной области $M$ – листное ветвление при $y = Z$. Для обратной к решению функции $r = r(y)$ верно представление (2.44), (2.47), принимающее вид (2.48) в окрестности $y = 0$.
Круг сходимости ряда в правой части (2.48) заведомо не покрывает точку ветвления $y = Z$ аналитической (по $y$) функции (2.45), соответствующую точке $M$ – листного ветвления $\tilde {y} = \mathcal{H}_{e}^{\alpha }$ функции $\Theta (\tilde {y})$. Устраним эту особую точку, введя, во-первых, переменную $\mathcal{Y} \in [0,1]$ по формулам
(2.49)
$\tilde {y} = :\mathcal{H}_{e}^{\alpha }\left( {1 - {{{(1 - \mathcal{Y})}}^{M}}} \right),\quad \mathcal{Y} = 1 - {{\left( {1 - \frac{{\tilde {y}}}{{\mathcal{H}_{e}^{\alpha }}}} \right)}^{{1/M}}} = 1 - {{\left( {1 - {{{(y{\text{/}}Z)}}^{{\alpha /\beta }}}} \right)}^{{1/M}}},$(2.50)
$\epsilon (\mathcal{Y}): = \Theta \left( {\tilde {y}(\mathcal{Y})} \right),\quad \frac{{d\epsilon }}{{d\mathcal{Y}}} > 0,\quad \mathcal{Y} \in [0,1],$(2.52)
$\epsilon (\mathcal{Y}) = :\sum\limits_{n = 1}^\infty {{{\epsilon }_{n}}} {{\mathcal{Y}}^{n}} = M\mathcal{H}_{e}^{\alpha }\mathcal{Y} - \left( {\frac{{M(M - 1)}}{2}\mathcal{H}_{e}^{\alpha } + \alpha {{M}^{2}}{{H}_{1}}\mathcal{H}_{e}^{{2\alpha }}} \right){{\mathcal{Y}}^{2}} + \cdots .$Подставляя (2.50) в (2.47), получаем зависимость $r$ от $y$ в виде
(2.53)
${{r}^{{1/M}}} = \frac{{\mathop {{{f}_{0}}}\nolimits^{1/\tilde {N}} }}{{{{y}^{{\sigma /\tilde {N}}}}}}(1 - \epsilon (\mathcal{Y})),\quad y \in (0,Z],\quad \mathcal{Y} = \mathcal{Y}(y) \in (0,1].$(2.54)
$r(y) = \frac{{\mathop {{{f}_{0}}}\nolimits^K }}{{{{y}^{{1/\beta }}}}}{{\left( {1 - \sum\limits_{n = 1}^\infty {{{\epsilon }_{n}}} {{\mathcal{Y}}^{n}}} \right)}^{M}} = :\frac{{\mathop {{{f}_{0}}}\nolimits^K }}{{{{y}^{{1/\beta }}}}}\sum\limits_{n = 0}^\infty {A_{n}^{'}} {{\mathcal{Y}}^{n}},\quad A_{0}^{'} = 1,\quad A_{1}^{'} = - {{M}^{2}}\mathcal{H}_{e}^{\alpha }.$Таким образом, получена
Теорема 4. В условиях теоремы 1 параметр $t \in (0,1]$ выражается через $y$ в виде (2.51), (2.49), где функция $\epsilon (\mathcal{Y})$ является аналитической функцией на замкнутом отрезке $\mathcal{Y} \in [0,1]$. Для обратной к решению $y(r)$ функции $r = r(y)$ верно представление (2.53), принимающее вид (2.54) в окрестности $y = 0$.
2.2. Решение задачи на отрезке
Получим решение задачи (1.5)–(1.7), (1.17) при $Z,R \in (0, + \infty )$ в предположении, что известно соответствующее (см. предложение 2) значение параметра $\mu \in (0,1)$.
Теорема 3 работы [47] утверждает, что решение $\psi = {{\psi }_{\mu }}(\rho )$ задачи (1.26)–(1.29), (1.31) при заданном $\mu $ допускает следующее параметрическое представление:
(2.55)
$\psi = \mu {{(1 - u)}^{{\tilde {N}/\sigma }}}{{(\tilde {N}u + 1)}^{{1/\sigma }}},\quad \rho = Mln(1 - u) + S(u),\quad u \in ({{u}_{1}},1],\quad {{u}_{1}}: = - \frac{1}{{\tilde {N}}},$(2.56)
$S(u) = \mathop \smallint \limits^u \,s(u){\kern 1pt} du,\quad s(u) = M\frac{{{{{(\tilde {N}u + 1)}}^{{1/\sigma - 1}}} + {{{(1 - u)}}^{{M - 1}}}\mathcal{P}(u)}}{{{{{(\tilde {N}u + 1)}}^{{1/\sigma }}} + {{{(1 - u)}}^{M}}\mathcal{P}(u)}}$(2.57)
$\frac{{d\mathcal{P}}}{{du}} = M(\beta + 1)\frac{{{{{(1 - u)}}^{{M - 1}}}{{\mathcal{P}}^{2}}(u) + {{{(\tilde {N}u + 1)}}^{{1/\sigma - 1}}}\mathcal{P}(u) + c(u)}}{{{{{(\tilde {N}u + 1)}}^{{1/\sigma }}} + {{{(1 - u)}}^{M}}\mathcal{P}(u)}},\quad u \in ({{u}_{1}},1],$(2.58)
$\mathcal{P}(0) = - 1,\quad \frac{{d\mathcal{P}}}{{du}}(0) = M(\beta + 1)\left( { - 1 + \sqrt {\frac{{(1 - {{\mu }^{\sigma }})(\tilde {N} + 1)}}{{M(\beta + 1)}}} } \right).$Отметим, что если справедливо включение
то уравнение (2.57) удовлетворяет условию теоремы Коши (см. [56, § 3]) при $u = - 1{\text{/}}\tilde {N} = {{u}_{1}}$, следовательно, функция $\mathcal{P}(u)$ в этом случае является аналитической на всем отрезке $u \in [{{u}_{1}},1]$, включая его левый конец.Подставляя параметризацию (2.55) в формулы (1.27) и полагая
с учетом (2.7) получаем(2.61)
$r = {{U}_{1}}{{(1 - u)}^{M}}\mathcal{S}(u),\quad {{U}_{1}} = {\text{const}} > 0,\quad u \in ({{u}_{1}},1],$(2.62)
$y = {{U}_{2}}\mathop {(\tilde {N}u + 1)}\nolimits^{1/\sigma } {{\mathcal{S}}^{{ - \beta }}}(u),\quad {{U}_{2}} = \mu \mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathop {{{U}_{1}}}\nolimits^{ - \beta } .$Значение постоянной ${{U}_{1}}$ найдем из сопоставления (2.62) и краевого условия (1.6), т.е. $y = Z$ при $u = 1$:
(2.63)
${{U}_{1}} = \frac{{\mathop {{{f}_{0}}}\nolimits^K {{\mu }^{{1/\beta }}}}}{{{{\mathcal{S}}_{e}}}}\mathop {(\tilde {N} + 1)}\nolimits^K {{Z}^{{ - 1/\beta }}},\quad {{\mathcal{S}}_{e}}: = {{\left. {\mathcal{S}(u)} \right|}_{{u = 1}}},$Вычислим производную $dy{\text{/}}dr$ как функцию параметра $u$. Из формул (2.56), (2.60)–(2.62) с учетом (2.7) находим
(2.64)
$\frac{{dlny}}{{du}} = \frac{{\tilde {N}}}{{\sigma (\tilde {N}u + 1)}} - \beta s(u) = \frac{{ - \beta M(\tilde {N} + 1)u{{{(1 - u)}}^{{M - 1}}}}}{{(\tilde {N}u + 1)\left( {{{{(\tilde {N}u + 1)}}^{{1/\sigma }}} + {{{(1 - u)}}^{M}}\mathcal{P}(u)} \right)}}\mathcal{P}(u),$(2.65)
$\frac{{dlnr}}{{du}} = - \frac{M}{{1 - u}} + s(u) = \frac{{ - M(\tilde {N} + 1)u{{{(\tilde {N}u + 1)}}^{{1/\sigma - 1}}}}}{{(1 - u)\left( {{{{(\tilde {N}u + 1)}}^{{1/\sigma }}} + {{{(1 - u)}}^{M}}\mathcal{P}(u)} \right)}},$Таким образом, доказана
Теорема 5. Решение $y(r)$ задачи (1.5)–(1.7), (1.17) при $Z,R \in (0, + \infty )$ допускает следующее параметрическое представление:
(2.66)
$r = {{U}_{1}}{{(1 - u)}^{M}}\mathcal{S}(u),\quad {{U}_{1}} = \frac{{\mathop {{{f}_{0}}}\nolimits^K {{\mu }^{{1/\beta }}}}}{{{{\mathcal{S}}_{e}}}}\mathop {(\tilde {N} + 1)}\nolimits^K {{Z}^{{ - 1/\beta }}},\quad u \in ({{u}_{1}},1],$(2.67)
$y = {{U}_{2}}\mathop {(\tilde {N}u + 1)}\nolimits^{1/\sigma } {{\mathcal{S}}^{{ - \beta }}}(u),\quad {{U}_{2}} = \frac{{\mathcal{S}_{e}^{\beta }}}{{\mathop {(\tilde {N} + 1)}\nolimits^{1/\sigma } }}Z,$(2.68)
$\frac{{dy}}{{dr}} = {{U}_{3}}{{\mathcal{S}}^{{ - (\beta + 1)}}}(u)\mathcal{P}(u),\quad {{U}_{3}} = \beta \frac{{{{U}_{2}}}}{{{{U}_{1}}}} = \frac{{\beta \mathcal{S}_{e}^{{\beta + 1}}}}{{{{\mu }^{{1/\beta }}}\mathop {{{f}_{0}}}\nolimits^K \mathop {(\tilde {N} + 1)}\nolimits^{(\beta + 1)K} }}{{Z}^{{(\beta + 1)/\beta }}},$Если выполнено условие (2.59), то функции $\mathcal{P}(u)$, $\mathcal{S}(u)$ являются аналитическими на всем отрезке $u \in [{{u}_{1}},1]$, включая его левый конец $u = {{u}_{1}}$.
Из формулы (2.68) при $u = 1$ получаем значение наклона графика решения $y(r)$ в концевой точке $r = 0$ в следующем виде, аналогичном (2.15):
(2.69)
$\frac{{dy}}{{dr}}(0) = \frac{{\beta {{Z}^{{(\beta + 1)/\beta }}}}}{{{{\mu }^{{1/\beta }}}\mathop {{{f}_{0}}}\nolimits^K \mathop {(\tilde {N} + 1)}\nolimits^{(\beta + 1)K} }}{{\mathcal{P}}_{e}},\quad {{\mathcal{P}}_{e}}: = {{\left. {\mathcal{P}(u)} \right|}_{{u = 1}}}.$Из формул (2.64), (2.65) и (2.61), (2.62) следует, что каждая из производных $dr{\text{/}}du$ и $dy{\text{/}}du$ представляется в виде произведения множителя ${{(1 - u)}^{{M - 1}}}{{(\tilde {N}u + 1)}^{{1/\sigma - 1}}}$, задающего кратность нулей в концах отрезка параметризации $u \in [{{u}_{1}},1]$, и некоторой функции, не обращающейся в нуль нигде на этом отрезке.
Тейлоровские разложения функций $\mathcal{P}(u)$, $s(u)$, $\mathcal{S}(u)$ в точке $u = 0$ и других точках промежутка $u \in ({{u}_{1}},1]$ могут быть вычислены, исходя из уравнения (2.57) по схеме, изложенной в п. 2.1.2.
2.3. Поведение решения вблизи начала координат
Покажем, что для решения $y(r)$ уравнения (1.5), (1.17), $Z \in (0, + \infty )$, с условием (1.6) справедливо разложение вида (1.19) в окрестности $r = 0$. Для этого воспользуемся параметрическим представлением этого решения с параметром $z$, определяемым подстановкой (1.37).
Из второй формулы (1.25), подстановок (1.33), (1.37) и равенства (2.7) находим
(2.70)
$\ln r = \mathop \smallint \limits^\psi \frac{{d\psi }}{{p(\psi )}} = \mathop \smallint \limits^\psi \frac{{d\psi }}{{\psi q(\psi )}} = \frac{{\tilde {N}}}{\sigma }\mathop \smallint \limits^z \frac{{dz}}{{zq(z)}} = :\frac{{\tilde {N}}}{{\sigma \beta }}\mathop \smallint \limits^z \frac{{dz}}{z} + G(z) = M\ln z + G(z),$(2.71)
$G(z) = M\mathop \smallint \limits^z \left( { - \frac{1}{z} + \frac{1}{{z\left( {1 + {{z}^{M}}\mathcal{Q}(z)} \right)}}} \right)dz = - M\mathop \smallint \limits^z \frac{{{{z}^{{M - 1}}}\mathcal{Q}(z)}}{{1 + {{z}^{M}}\mathcal{Q}(z)}}dz,$(2.72)
$r = {{z}^{M}}\mathcal{G}(z),\quad y = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } {{\mathcal{G}}^{{ - \beta }}}(z),\quad \mathcal{G}(z): = expG(z)$Используя обозначение $C: = \mathcal{Q}(0)$ (см. предложение 3), вычислим начальные члены тейлоровских разложений величин $G$, $\mathcal{G}$, ${{r}^{{1/M}}}$, $y$ по степеням $z$, исходя из формул (2.71), (2.72):
(2.73)
$\begin{gathered} G(z) = {{G}_{0}} - C{{z}^{M}} + {{G}_{{M + 1}}}{{z}^{{M + 1}}} + \ldots ,\quad {{G}_{0}},{{G}_{{M + 1}}} = {\text{const}}, \\ \mathcal{G}(z) = {{\mathcal{G}}_{0}}(1 - C{{z}^{M}} + {{\gamma }_{1}}{{z}^{{M + 1}}} + \ldots ),\quad {{\mathcal{G}}_{0}} = exp{{G}_{0}} > 0,\quad {{\gamma }_{1}} = {{G}_{{M + 1}}} + \delta _{M}^{1}\frac{{{{C}^{2}}}}{2}, \\ \end{gathered} $(2.74)
${{r}^{{1/M}}}(z) = \mathcal{G}_{0}^{{1/M}}z\left( {1 - \frac{C}{M}{{z}^{M}} + \frac{{{{\gamma }_{1}}}}{M}{{z}^{{M + 1}}} + \ldots } \right),$(2.75)
$y(z) = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathcal{G}_{0}^{{ - \beta }}(1 + \beta C{{z}^{M}} + {{\gamma }_{2}}{{z}^{{M + 1}}} + \ldots ),\quad {{\gamma }_{2}} = - \,\beta {{\gamma }_{1}} + \delta _{M}^{1}\frac{{\beta (\beta + 1)}}{2}{{C}^{2}},$(2.76)
$\mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathcal{G}_{0}^{{ - \beta }} = Z,\quad {{\mathcal{G}}_{0}} = \mathop {{{f}_{0}}}\nolimits^K {{Z}^{{ - 1/\beta }}}.$Выражая $z$ через $r$ из равенства (2.74), получаем в окрестности $r = 0$ разложения
(2.77)
$z = \mathop {\left( {\frac{r}{{{{\mathcal{G}}_{0}}}}} \right)}\nolimits^{1/M} + \frac{C}{M}\mathop {\left( {\frac{r}{{{{\mathcal{G}}_{0}}}}} \right)}\nolimits^{1 + (1/M)} + {{\gamma }_{3}}\mathop {\left( {\frac{r}{{{{\mathcal{G}}_{0}}}}} \right)}\nolimits^{1 + (2/M)} + \ldots ,\quad {{\gamma }_{3}} = - \frac{{{{\gamma }_{1}}}}{M} + \delta _{M}^{1}\frac{{M + 1}}{{{{M}^{2}}}}{{C}^{2}}$(2.78)
${{z}^{M}} = \frac{r}{{{{\mathcal{G}}_{0}}}} + C\mathop {\left( {\frac{r}{{{{\mathcal{G}}_{0}}}}} \right)}\nolimits^2 + M{{\gamma }_{3}}\mathop {\left( {\frac{r}{{{{\mathcal{G}}_{0}}}}} \right)}\nolimits^{2 + (1/M)} + \ldots ,$(2.79)
$\begin{gathered} y(r) = Z\left( {1 + \frac{{\beta C}}{{\mathop {{{f}_{0}}}\nolimits^K }}{{Z}^{{1/\beta }}}r + {{\gamma }_{4}}{{r}^{{1 + (1/M)}}} + \ldots } \right) = :\sum\limits_{n = 0}^\infty {{{b}_{n}}} {{r}^{{n/M}}}, \\ {{\gamma }_{4}} = \frac{{{{\gamma }_{2}}}}{{\mathcal{G}_{0}^{{1 + 1/M}}}} + \delta _{M}^{1}\frac{{\beta {{C}^{2}}}}{{\mathcal{G}_{0}^{2}}},\quad {{b}_{0}} = Z,\quad {{b}_{1}} = \ldots = {{b}_{{M - 1}}} = 0,\quad {{b}_{M}} = \frac{{\beta C}}{{\mathop {{{f}_{0}}}\nolimits^K }}{{Z}^{{1 + (1/\beta )}}}, \\ \end{gathered} $Решение сингулярной задачи Коши для уравнения (1.5) с условием (1.6) и заданной производной при $r = 0$ существует и единственно по теореме Каратеодори (см. [57, гл. 2, § 1]). Получаем следующее уточнение этого результата.
Теорема 6. Для всякого $b \in \mathbb{R}$ задача Коши для уравнения (1.5), (1.17) с условиями (1.6), $dy{\text{/}}dr(0) = b$ однозначным образом разрешима на некотором отрезке $[0,\varepsilon ]$, $\varepsilon > 0$, при этом ее решение $y(r)$ представимо в окрестности $r = 0$ сходящимся рядом (2.79), где ${{b}_{M}} = b$.
Коэффициенты ${{b}_{n}}$ разложения $($2.79) при заданном ${{b}_{M}} = b$ можно найти методом неопределенных коэффициентов, подставив его в уравнение (1.5). Кроме того, в силу (2.76) и указанных выше свойств коэффициентов разложений (2.77), (2.78), при каждом $n \geqslant M$ величина ${{b}_{n}}\mathop {{{f}_{0}}}\nolimits^{n/\tilde {N}} {\text{/}}{{Z}^{{1 + (\sigma n/\tilde {N})}}}$ рационально выражается через $\beta $, $M$, $\tilde {N}$ и $C = {{b}_{M}}\mathop {{{f}_{0}}}\nolimits^K {\text{/}}(\beta {{Z}^{{1 + (1/\beta )}}})$.
3. ЗАДАЧА ТОМАСА–ФЕРМИ
Показатель $\nu $ = –1/2 в уравнении Томаса–Ферми (1.2) удовлетворяет условию рациональности (1.17), следовательно, к задаче (1.2), (1.3) применимы доказанные в разд. 2 теоремы 1–6. Введенные выше числовые параметры (в частности, (1.9), (1.15)–(1.17), (1.36)) имеют следующие значения:
3.1. Решение задачи Томаса–Ферми на луче
Представление (2.32)–(2.34) решения $\Psi (r)$ задачи (1.2), (1.3) при $R = + \infty $ имеет вид
(3.1)
$\begin{gathered} r = {{T}_{1}}{{(1 - t)}^{2}}{{t}^{{1/\alpha }}}\mathcal{H}(t),\quad \Psi = {{T}_{2}}{{t}^{{ - 3/\alpha }}}{{\mathcal{H}}^{{ - 3}}}(t),\quad \frac{{d\Psi }}{{dr}} = \frac{{{{T}_{3}}}}{{{{t}^{{4/\alpha }}}{{\mathcal{H}}^{4}}(t)}}\mathcal{Q}(t),\quad t \in (0,1], \\ {{T}_{1}} = \frac{{\mathop {12}\nolimits^{2/3} }}{{{{\mathcal{H}}_{e}}}}{{Z}^{{ - 1/{\text{3}}}}},\quad {{T}_{2}} = \mathcal{H}_{e}^{3}Z,\quad {{T}_{3}} = \frac{{3\mathcal{H}_{e}^{4}}}{{\mathop {12}\nolimits^{2/3} }}{{Z}^{{4/3}}},\quad {{\mathcal{H}}_{e}} = {{\left. {\mathcal{H}(t)} \right|}_{{t = 1}}}, \\ \end{gathered} $(3.2)
$\frac{{d\mathcal{Q}}}{{dt}} = 8\frac{{(1 - t){{\mathcal{Q}}^{2}}(t) - 1}}{{1 + {{{(1 - t)}}^{2}}\mathcal{Q}(t)}},\quad \mathcal{Q}(0) = {{\mathcal{Q}}_{0}}: = - 1,\quad \frac{{d\mathcal{Q}}}{{dt}}(0) = {{\mathcal{Q}}_{1}}: = - 2(\alpha + 1),$Разложения функций $\mathcal{Q}(t)$ и $\mathcal{H}(t)$ в ряды Тейлора в окрестности $t = 0$ могут быть вычислены по формулам (2.17), (2.18), (2.20), (2.22) и (2.25)–(2.29) соответственно, т.е.
(3.3)
${{h}_{n}} = - \frac{1}{{2\alpha }}\left( { - \frac{{{{g}_{{n + 2}}}}}{\alpha } + 2({{\mathcal{Q}}_{{n + 1}}} - {{\mathcal{Q}}_{n}}) - \sum\limits_{j = 0}^{n - 1} {{{h}_{j}}} {{g}_{{n + 1 - j}}}} \right),\quad {{H}_{{n + 1}}} = \frac{{{{h}_{n}}}}{n},\quad n \geqslant 0,$Представление (2.54) обратной к решению функции принимает вид
(3.4)
$r(\Psi ) = \frac{{\mathop {12}\nolimits^{2/3} }}{{{{\Psi }^{{1/3}}}}}{{\left( {1 - \sum\limits_{n = 1}^\infty {{{\epsilon }_{n}}} {{{\tilde {\Psi }}}^{n}}} \right)}^{2}} = :\frac{{\mathop {12}\nolimits^{2/3} }}{{{{\Psi }^{{1/3}}}}}\sum\limits_{n = 0}^\infty {A_{n}^{'}} {{\tilde {\Psi }}^{n}},\quad \mathcal{Y} = \tilde {\Psi }: = 1 - \sqrt {1 - {{{(\Psi {\text{/}}Z)}}^{{ - \alpha /3}}}} ,$Таблица 1.
Коэффициенты рядов Тейлора при $t = 0$ функций $\mathcal{Q}(t)$, $H(t) = ln\mathcal{H}(t)$, $\epsilon (\tilde {\Psi })$; см. (3.3), (3.4)
| n | ${{\mathcal{Q}}_{n}}$ | ${{H}_{n}}$ | ${{\epsilon }_{n}}$ |
|---|---|---|---|
| 0 | –1 | 0 | 0 |
| 1 | 0.4559963 | 0.37541199 | 1.231293471269155 |
| 2 | –0.3044551 | 0.11680513 | –1.762572651223578E–01 |
| 3 | –0.2221798 | 0.05301555 | –3.586264513410257E–02 |
| 4 | –0.1682126 | 0.02866072 | –1.188294019140811E–02 |
| 5 | –0.1298041 | 0.01715679 | –4.527629495209355E–03 |
| 6 | –0.1013002 | 0.01096849 | –1.786511681720532E–03 |
| 7 | –0.0796352 | 0.00733582 | –6.888630288626336E–04 |
| 8 | –0.0629230 | 0.00506758 | –2.446296099146174E–04 |
| 9 | –0.0499053 | 0.00358590 | –7.102100665478879E–05 |
| 10 | –0.0396962 | 0.00258466 | –9.114850026654934E–06 |
| 11 | –0.0316498 | 0.00189023 | 8.628385118260053E–06 |
| 12 | –0.0252839 | 0.00139865 | 1.055443881972420E–05 |
| 13 | –0.0202322 | 0.00104492 | 7.992270000062715E–06 |
| 14 | –0.0162136 | 0.00078697 | 5.020985928867133E–06 |
| 15 | –0.0130101 | 0.00059677 | 2.790922739565175E–06 |
| 16 | –0.0104518 | 0.00045523 | 1.390873927946046E–06 |
| 17 | –0.0084056 | 0.00034904 | 6.107369113157270E–07 |
| 18 | –0.0067666 | 0.00026885 | 2.202119071036909E–07 |
| 19 | –0.0054522 | 0.00020791 | 4.755499195027076E–08 |
| 20 | –0.0043968 | 0.00016137 | –1.546319759284382E–08 |
| 21 | –0.0035485 | 0.00012565 | –2.963705543713770E–08 |
| 22 | –0.0028660 | 0.00009813 | –2.574541382040214E–08 |
| 23 | –0.0023164 | 0.00007684 | –1.761541125892188E–08 |
| 24 | –0.0018734 | 0.00006032 | –1.043404093568663E–08 |
| 25 | –0.0015161 | 0.00004746 | –5.471632131286884E–09 |
| 26 | –0.0012277 | 0.00003742 | –2.507170177006865E–09 |
| 27 | –0.0009947 | 0.00002956 | –9.383306761822078E–10 |
| 28 | –0.0008064 | 0.00002339 | –2.107653561459858E–10 |
| 29 | –0.0006540 | 0.00001854 | 6.735556420063704E–11 |
| 30 | –0.0005307 | 0.00001472 | 1.344897961831818E–10 |
| 31 | –0.0004309 | 0.00001170 | 1.192816857741852E–10 |
| 32 | –0.0003500 | 0.00000932 | 8.286855224853180E–11 |
| 33 | –0.0002844 | 0.00000743 | 4.959995317512788E–11 |
| 34 | –0.0002312 | 0.00000593 | 2.612434022331377E–11 |
| 35 | –0.0001880 | 0.00000474 | 1.189884390936907E–11 |
| 36 | –0.0001530 | 0.00000379 | 4.309774068847392E–12 |
| 37 | –0.0001245 | 0.00000304 | 7.936738883378811E–13 |
| 38 | –0.0001014 | 0.00000243 | –5.214790707757887E–13 |
| 39 | –0.0000825 | 0.00000195 | –7.998120745465573E–13 |
| 40 | –0.0000673 | 0.00000157 | –6.785731610539916E–13 |
Фиг. 2.
Поведение абсолютных величин тейлоровских коэффициентов функций a – для $\mathcal{Q}(t)$; b – для $\mathcal{H}(t)$; c – для $\epsilon (\tilde {\Psi })$; см. (3.3), (3.4).

Представление (2.42) принимает вид (1.14) с константой $A$, заданной формулой (2.43):
(3.5)
$A = - \frac{{6\mathcal{H}_{e}^{\alpha }}}{{\mathop {12}\nolimits^{2\alpha /3} }} = - 13.270973848026935153531683853762148437493478662432830 \ldots ,$(3.6)
${{\mathcal{H}}_{e}} = exp\left\{ {\sum\limits_{n = 1}^\infty {{{H}_{n}}} } \right\} = 1.874501926556901049744114038434817246829720167631 \ldots \;.$Сформулируем полученный результат.
Теорема 7. Решение $\Psi (r)$ задачи (1.2), (1.3) при $R = + \infty $ допускает параметрическое представление (3.1). Коэффициенты Тейлора входящих в него функций $\mathcal{H}(t)$, $\mathcal{Q}(t)$ могут быть вычислены по формулам (3.3), (2.8). Обратная к решению функция $r = r(\Psi )$ допускает представление (3.4), где ряды в правой части сходятся в окрестности $\tilde {\Psi } = \Psi = 0$. Для константы $A$ в разложении (1.14) справедлива формула (3.5).
Подчеркнем отличие формул (3.5), (3.6), основанных на суммировании экспоненциально сходящегося числового ряда, каждый член которого вычисляется явно за конечное число операций из соотношений рекуррентного типа (3.3), от аналогичной формулы (см. [42, § 2.12]), опирающейся на параметризацию вида (2.72) и требующей численного разрешения неопределенности вида $(0 \cdot \infty )$, где бесконечно большой множитель является результатом численного интегрирования неограниченно растущей функции.
Отметим, что выражение для константы (1.13), даваемое формулой (2.15) при $Z = 1$,
Вычислить решение $\Psi (r)$ и его производную $d\Psi {\text{/}}dr$ в заданной точке ${{r}_{0}} \in (0, + \infty )$ с помощью представления (3.1) можно, найдя соответствующее значение параметра $t = {{t}_{0}}$ и подставив его в формулу $\Psi = \Psi ({{t}_{0}})$. Для обращения функции $r = r(t)$ методом Ньютона нужно учесть, что в силу формулы (2.13) эта функция имеет кратный нуль порядка $M = 2$ при $t = 1$, и ее производная не обращается в нуль более нигде на отрезке $t \in [0,1]$. Таким образом, эффективность метода Ньютона обеспечена для задачи обращения не самой функции $r(t)$, а функции $\sqrt {r(t)} $ (или функции ${{r}^{{1/M}}}(t)$ в общем случае представления (2.32)), при этом начальное приближение для ${{t}_{0}}$ можно выбрать на отрезке $[0,1]$ произвольно.
Принимая в (3.4) приближение $\epsilon (\tilde {\Psi }) \approx \tilde {\Psi }$, получаем формулу (1.23). Аппроксимируя функции $\epsilon (\tilde {\Psi })$, $\mathcal{Q}(t)$, $\mathcal{H}(t)$ тем или иным способом, можно получить из представлений (3.1), (3.4) другие эффективные формулы приближенного решения задачи в явном аналитическом виде.
3.2. Решение задачи Томаса–Ферми на отрезке
Представление (2.66)–(2.68) решения $\Psi (r)$ задачи (1.2), (1.3) при $Z,R \in (0, + \infty )$ имеет вид
(3.7)
$\begin{gathered} r = {{U}_{1}}{{(1 - u)}^{2}}\mathcal{S}(u),\quad \Psi = {{U}_{2}}\mathop {(3u + 1)}\nolimits^2 {{\mathcal{S}}^{{ - 3}}}(u),\quad \frac{{d\Psi }}{{dr}} = {{U}_{3}}{{\mathcal{S}}^{{ - 4}}}(u)\mathcal{P}(u),\quad u \in ({{u}_{1}},1], \\ {{U}_{1}} = \frac{{4 \cdot \mathop {(36\mu )}\nolimits^{1/3} }}{{{{\mathcal{S}}_{e}}}}{{Z}^{{ - 1/3}}},\quad {{U}_{2}} = \frac{{\mathcal{S}_{e}^{3}}}{{16}}Z,\quad {{U}_{3}} = \frac{{3\mathcal{S}_{e}^{4}}}{{64\mathop {(36\mu )}\nolimits^{1/3} }}{{Z}^{{ - 4/3}}},\quad {{\mathcal{S}}_{e}} = \mathcal{S}(1),\quad {{u}_{1}} = - \frac{1}{3}, \\ \end{gathered} $(3.8)
$\begin{gathered} \frac{{d\mathcal{P}}}{{du}} = 8\frac{{(1 - u){{\mathcal{P}}^{2}}(u) + (3u + 1)\mathcal{P}(u) - 4\sqrt \mu {\kern 1pt} {\kern 1pt} u{{{(3u + 1)}}^{4}}}}{{{{{(3u + 1)}}^{2}} + {{{(1 - u)}}^{2}}\mathcal{P}(u)}},\quad u \in ({{u}_{1}},1], \\ \mathcal{P}(0) = - 1,\quad \frac{{d\mathcal{P}}}{{du}}(0) = 8\left( { - 1 + \sqrt {\frac{{1 - \sqrt \mu }}{2}} } \right), \\ \end{gathered} $(3.9)
$S(u) = 2\int\limits_0^u {\frac{{(3u + 1) + (1 - u)\mathcal{P}(u)}}{{{{{(3u + 1)}}^{2}} + {{{(1 - u)}}^{2}}\mathcal{P}(u)}}{\kern 1pt} {\kern 1pt} } du,\quad \mathcal{S}(u) = expS(u).$Численное решение $\Psi (r)$ задачи (1.2), (1.3) при $R,Z \in (0,\infty )$ с помощью представления (3.7) проводится аналогично случаю $R = + \infty $, рассмотренному в п. 3.1. Круг сходимости ряда Тейлора функции $S(u)$ с центром $u = 0$ может не покрывать всего отрезка изменения параметра $u \in [ - 1{\text{/}}3,1]$ – в этом случае можно построить тейлоровские разложения функций $\mathcal{P}(u)$, $S(u)$ в нескольких других точках этого отрезка с помощью уравнения (3.8).
Значение параметра $\mu $, соответствующее заданным $R,Z \in (0, + \infty )$, может быть приблизительно установлено c помощью интерполяции согласно табл. 2 (вычисления проведены на основе формул (3.7)–(3.9), (2.69)).
Таблица 2.
Числовые характеристики (нормированные по Z) решений задачи Томаса–Ферми (1.2), (1.3) при различных значениях параметра $\mu $: 1) производная в нуле, см. (1.12), (2.69); 2) размер иона, $R = r({{u}_{1}})$ в (3.7); 3) степень ионизации, см. (1.4)
| μ | ${{Z}^{{ - 4/3}}}\Psi _{r}^{'}(0)$ | ${{Z}^{{ - 1/3}}}R$ | $1 - Z{\kern 1pt} {\text{'/}}Z$ |
|---|---|---|---|
| 0.0001 | –2.5864080 | 0.53 | 9.30E–01 |
| 0.02 | –1.5938269 | 4.17 | 3.68E–01 |
| 0.1 | –1.5881541 | 10.84 | 1.02E–01 |
| 0.2 | –1.5880743 | 19.49 | 3.42E–02 |
| 0.3 | –1.5880712 | 30.74 | 1.28E–02 |
| 0.4 | B – 1.39E–08 | 46.65 | 4.81E–03 |
| 0.5 | B – 8.16E–10 | 70.85 | 1.68E–03 |
| 0.6 | B – 3.42E–11 | 111.14 | 5.14E–04 |
| 0.7 | B – 7.67E–13 | 187.62 | 1.22E–04 |
| 0.8 | B – 4.98E–15 | 369.34 | 1.79E–05 |
| 0.9 | B – 1.41E–18 | 1082.77 | 7.83E–07 |
| 0.999 | B – 6.59E–41 | 824 236.00 | 1.91E–15 |
| 0.9999 | B – 5.62E–52 | 21 893 653.21 | 1.02E–19 |
| 1.0 | B | +∞ | 0 |
Список литературы
Fermi E. Un metodo statistico per la determinazione di alcune prioprieta dell’atomo // Rend. Accad. Naz. Lincei 6. 1927. P. 602–607.
Thomas L.H. The calculations of atomic fields // Proc. Cambridge Philos. Soc. 1927. № 23. P. 542–598.
Ландау Л.Д., Лившиц Е.М. Теоретическая физика. Квантовая механика (нерелятивистская теория). М.: Наука, 1989.
March N.H. The Fermi–Thomas theory // Theory of the inhomogeneous electron gas / Ed. by S. Lunqvist, N.H. March. New York, London: Plenum Press, 1983. P. 9–85.
Беллман Р. Теория устойчивости решений дифференциальных уравнений. М.: Изд-во иностр. лит., 1954.
Сансоне Д. Обыкновенные дифференциальные уравнения. Т. 2. М.: Изд-во иностр. лит., 1954.
Sommerfeld A. Integrazione asintotica dell’equazione differenziale di Fermi–Thomas // Rend. R. Accademia dei Lincei 15. 1932. P. 293–308.
Флюгге 3. Задачи по квантовой механике. М.: Мир, 1974. Т. 2.
Hille E. Some aspects of the Fermi–Thomas equation // J. Anal. Math. 1970. V. 23. P. 147–170.
Baker E.B. The application of the Fermi–Thomas statistical model to the calculation of potential distribution in positive ions // Phys. Rev. 1930. V. 36. P. 630–647.
Coulson C.A., March N.H. Momenta in atoms using the Fermi–Thomas method // Proc. Phys. Soc. Sect. A. 1950. V. 63. № 4. P. 367–367.
Дышко А.Л., Карпентьер М.П., Конюхова Н.Б., Лима П.М. О сингулярных задачах для нелинейных обыкновенных дифференциальных уравнений второго порядка типа Эмдена–Фаулера // Ж. вычисл. матем. и матем. физ. 2001. Т. 41. № 4. С. 595–619.
Bush V., Caldwell S.H. Fermi–Thomas equation solution by the differential analyzer // Phys. Rev. 1931. V. 38. № 10. P. 1898–1902.
Miranda C. Teoremi e metodi per l’integrazione numerica dell’ equazione differenziale di Fermi // Mem. della R. Acc. ltalia. 1934. № 5. P. 285–322.
Slater J.C., Krutter H.M. The Fermi–Thomas method for metals // Phys. Rev. 1935. V. 47. № 7. P. 559–568.
Feynman R.P., Metropolis N., Teller E. Equations of state of elements based on the generalized Fermi–Thomas theory // Phys. Rev. 1949. V. 75. № 10. P. 1561–1573.
Kobayashi S., Matsukuma T., Nagai S., Umeda K. Accurate value of the initial slope of the ordinary TF function // J. Phys. Soc. Jpn. 1955. V. 10. P. 759–762.
Krutter H. Numerical integration of the Thomas–Fermi equation from zero to infinity // J. Comput. Phys. 1982. V. 47. № 2. P. 308–312.
Bellman R. Dynamic programming and the variational solution of the Fermi–Thomas equation // J. Phys. Soc. Jpn. 1957. V. 12. P. 1049.
Ikebe T., Kato T. Application of variational method to the Fermi–Thomas equation // J. Phys. Soc. Jpn. 1957. V. 12. № 2. P. 201–203.
Ramnath R.V. A new analytical approximation for the Fermi–Thomas model in atomic physics // J. Math. Analys. and Appl. 1970. V. 31. № 2. P. 285–296.
Torrens I.M. Interatomic Potentials. New York: Academic, 1972.
Anderson N., Arthurs A.M. Variational solutions of the Fermi–Thomas equation // Quart. Appl. Math. 1981/82. V. 39. P. 127–129.
Desaix M., Anderson D., Lisak M. Variational approach to the Fermi–Thomas equation // Eur. J. Phys. 2004. V. 25. P. 699–705.
Oulne M. Variation and series approach to the Fermi–Thomas equation // Appl. Math. and Comput. 2011. V. 218. № 2. P. 303–307.
Flagg R.C., Luning C.D., Perry W.L. Implementation of new iterative techniques for solutions of Thomas–Fermi and Emden–Fowler equations // J. Comput. Phys. 1980. V. 38. P. 396–405.
Bender C.M., Milton K.A., Pinsky S.S., Simmons L.M. A new perturbative approach to nonlinear problems // J. Math. Phys. 1989. V. 30. № 7. P. 1447–1455.
Tu K. Analytic solution to the Fermi–Thomas and Fermi–Thomas–Dirac–Weizsäcker equations // J. Math. Phys. 1991. V. 32. P. 2250–2253.
Zaitsev N.A., Matyushkin I.V., Shamonov D.V. Numerical solution of the Fermi–Thomas equation for the centrally symmetric atom // Russ. Microelectron. 2004. V. 33. № 5. P. 303–309.
MacLeod A.J. Chebyshev series solution of the Fermi–Thomas equation // Computer Phys. Commun. 1992. V. 67. № 3. P. 389–391.
Parand K., Shahini M. Rational Chebyshev pseudospectral approach for solving Fermi–Thomas equation // Phys. Lett. A. 2009. V. 373. № 2. P. 210–213.
Parand K., Rabiei K., Delkhosh M. An efficient numerical method for solving nonlinear Thomas–Fermi equation // Acta Universitatis Sapientiae, Mathematica. 2018. V. 10. № 1. P. 134–151.
Boyd J.P. Rational Chebyshev series for the Fermi–Thomas function: Endpoint singularities and spectral methods // J. Comput. and Appl. Math. 2013. V. 244. P. 90–101.
Mason J.C. Rational approximations to the ordinary Fermi–Thomas function and its derivative // Proc. Phys. Soc. 1964. V. 84. № 3. P. 357.
Abbasbandy S., Bervillier C. Analytic continuation of Taylor series and the boundary value problems of some nonlinear ordinary differential equations // Appl. Math. Comput. 2011. V. 218. P. 2178–2199.
Epele L.N., Fanchiotti H., Canal C.A. García, Ponciano J.A. Padé approximant approach to the Fermi–Thomas problem // Phys. Rev. A. 1999. V. 60. P. 280–283.
Liao S. An explicit analytic solution to the Fermi–Thomas equation // Appl. Math. and Comput. 2003. V. 144. P. 495–506.
Plindov G.I., Pogrebnaya S.K. The analytical solution of the Fermi–Thomas equation for a neutral atom // J. Phys. B. 1987. V. 20. P. 547–550.
Fernández F.M., Ogilvie J.F. Approximate solutions to the Fermi–Thomas equation // Phys. Rev. A. 1990. V. 42. № 1. P. 149–154.
Esposito S. Majorana solution of the Fermi–Thomas equation // Am. J. Phys. 2002. V. 70. № 8. P. 852–856.
Esposito S. Majorana transformation for differential equations // Int. J. Theor. Phys. 2002. V. 41. № 12. P. 2417–2426.
Finch S.R. Mathematical Constants II. Encyclopedia of Mathematics and its Applications. Cambridge: Cambridge University Press, 2018.
Panayotounakos D.E., Kravvaritisb D.C. Exact analytic solutions of the Abel, Emden–Fowler and generalized Emden–Fowler nonlinear ODEs // Nonlinear Analysis: Real World Applications. 2006. V. 7. № 4. P. 634–650.
Panayotounakos D.E., Sotiropoulos N. Exact analytic solutions of unsolvable classes of first- and second-order nonlinear ODEs (Part II: Emden–Fowler and relative equations) // Appl. Math. Lett. 2005. V. 18. № 4. P. 367–374.
Theotokoglou E.E., Zarmpoutis T.I., Stampouloglou I.H. Closed-form solutions of the Fermi–Thomas in heavy atoms and the Langmuir–Blodgett in current flow ODEs in mathematical physics // Math. Problems in Engng. 2015. V. 2015, Article ID 721637.
Безродных С.И., Власов В.И. Краевая задача для моделирования физических полей в полупроводниковом диоде // Ж. вычисл. матем. и матем. физ. 2004. Т. 44. № 12. С. 2112–2142.
Пикулин С.В. О поведении решений уравнения Абеля II рода специального вида вблизи узловой особой точки // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 12. С. 2074–2095.
Conte R.M., Musette M. The Painlevé Handbook. Dordrecht: Springer Science + Business Media B.V., 2008.
Hille E. Ordinary Differential Equations in the Complex Domain. New York, London, Sydney, Toronto: John Willey and Sons, 1976.
Varin V.P. A solution of the Blasius problem // Comput. Math. Math. Phys. 2014. V. 54. № 6. P. 1025–1036.
Варин В.П. Асимптотическое разложение решения Крокко и константа Блазиуса // Ж. вычисл. матем. и матем. физ. 2018. V. 58. № 4. P. 530–540.
Bender C.M., Orszag S.A. Advanced Mathematical Methods for Scientists and Engineers. New York: McGraw-Hill book company, 1978.
Пикулин С.В. О решениях типа бегущей волны уравнения Колмогорова–Петровского–Пискунова // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 2. С. 244–252.
Пикулин С.В. О промежуточных асимптотических режимах в некоторых моделях теории горения // Таврический вестник информатики и математики. 2017. Т. 3. № 36. С. 55–72.
Пикулин С.В. О решениях типа бегущей волны для нелинейного параболического уравнения // Вестник СамГУ. Естественнонаучная серия. 2015. Т. 6. № 128. С. 110–116.
Голубев В.В. Курс аналитической теории дифференциальных уравнений. М.: Гостехтеориздат, 1950.
Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. М.: Изд-во иностр. лит., 1958.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики







