Журнал вычислительной математики и математической физики, 2019, T. 59, № 8, стр. 1314-1330
Методы неотрицательной матричной факторизации на основе крестовых малоранговых приближений
Е. Е. Тыртышников 1, *, Е. М. Щербакова 2, **
1 ИВМ РАН
119333 Москва, ул. Губкина 8, Россия
2 МГУ
119991 Москва, Ленинские горы 1, Россия
* E-mail: eugene.tyrtyshnikov@gmail.com
** E-mail: lena19592@mail.ru
Поступила в редакцию 13.03.2019
После доработки 13.03.2019
Принята к публикации 10.04.2019
Аннотация
Известные на данный момент методы для решения задачи неотрицательной матричной факторизации предполагают использование всех элементов исходной матрицы размера $m \times n$ и сложность их не меньше $O(mn)$, что при больших объемах данных делает их слишком ресурсоемкими. Поэтому естественным образом возникает вопрос: можно ли построить неотрицательную факторизацию матрицы, зная ее неотрицательный ранг, используя лишь несколько ее строк и столбцов? В данной работе предлагаются методы решения этой задачи для определенных классов матриц: неотрицательных сепарабельных матриц – тех, для которых существует конус, натянутый на несколько столбцов исходной матрицы и содержащий все ее столбцы; неотрицательных сепарабельных матриц с возмущениями; неотрицательных матриц ранга 2. На практике предложенные алгоритмы используют число операций и объем памяти, линейно зависящие от $m + n$. Библ. 24. Фиг. 7. Табл. 2.
1. ВВЕДЕНИЕ
Задача неотрицательной матричной факторизации (задача NMF) ранга $r \leqslant min(m,n)$ формулируется следующим образом: для заданной матрицы $M$ с неотрицательными элементами требуется найти разложение $M = WH$, где $W$ и $H$ имеют $r$ столбцов и $r$ строк соответственно и все их элементы неотрицательны. Число $r$ считается заданным.
Матрицу с неотрицательными элементами принято называть неотрицательной, сам факт неотрицательности матрицы $M$ записывается в виде неравенства $M \geqslant 0$, а множество всех неотрицательных матриц размера $m \times n$ обозначается через $\mathbb{R}_{ + }^{{m \times n}}$. Наименьшее число $r$ в разложениях вида
называется неотрицательным рангом матрицы $M$.В общем случае задача неотрицательной матричной факторизации минимального ранга является NP-трудной даже при условии, что неотрицательный ранг матрицы известен (см. [1]). То же самое можно сказать о сложности поиска самого неотрицательного ранга матрицы. Заметим также, что если факторизация $M = WH$ ранга $r$ существует, то она заведомо не единственная, так как $M = (WD)({{D}^{{ - 1}}}H)$ для любой невырожденной матрицы $D$: $WD \geqslant 0$, ${{D}^{{ - 1}}}H \geqslant 0$.
Известные на данный момент методы неотрицательной матричной факторизации предполагают использование всех элементов исходной матрицы, и сложность их как минимум линейно зависит от общего числа элементов матрицы. Однако на практике матрица часто задается не как массив всех ее элементов, а с помощью некоторой процедуры, вычисляющей любой элемент по требованию. В таких ситуациях при построении факторизаций хотелось бы избежать вычисления и хранения всех элементов матрицы. В случае скелетных разложений без ограничений неотрицательности такая возможность предоставляется крестовыми методами [2]–[5], в которых вычисляются лишь порядка $(m + n)r$ элементов исходной матрицы. Наша цель – исследовать аналогичную возможность при построении неотрицательных факторизаций. В данной статье дается решение этой задачи для определенных классов матриц. Прежде всего, это так называемые сепарабельные матрицы (разд. 2) и возмущенные сепарабельные матрицы (разд. 3). Кроме того, отдельно рассматривается класс неотрицательных матриц ранга 2 (разд. 5).
Впервые условие сепарабельности было исследовано в [6] в контексте единственности неотрицательного матричного разложения. Для решения задачи неотрицательной факторизации сепарабельных матриц в [7] авторы предложили метод, требующий решения $n$ задач линейного программирования с $O(n)$ переменными ($n$ – число столбцов исходной матрицы), что не очень подходит для больших матриц. В [8] рассматривается выпуклая модель с ${{n}^{2}}$ переменными, но вычислительная сложность является очень высокой. В [9] авторы описали метод, основанный на решении единственной выпуклой оптимизационной задачи с ${{n}^{2}}$ переменными. В 2014 г. Гиллис и Вавасис (Gillis, Vavasis) в [10] предложили алгоритм, сложность которого они оценили как $O(mnr)$. Это далеко не все методы для решения неотрицательной факторизации сепарабельных матриц, но одни из самых известных, сложность их не меньше $O(mn)$. В данной работе предлагается алгоритм, позволяющий решить данную задачу за время, линейно зависящее от суммы размеров матрицы. Основная идея – построить крестовое разложение исходной матрицы и преобразовать факторы так, чтобы метод из [10] был применим к одному из них, в итоге ведется работа над задачей меньшего размера. Дополнительно рассмотрен еще один вариант применения алгоритма. В ряде приложений (см. [11], [12]) возникают матрицы, допускающие симметричную неотрицательную факторизацию. Для подкласса таких матриц, а именно симметричных неотрицательных матриц ранга $r$, содержащих диагональную главную подматрицу того же ранга, в 2012 г. был предложен в [13] метод, строящий их неотрицательную симметричную факторизацию. В разд. 4 мы демонстрируем, как, используя наш алгоритм, можно решить эту задачу эффективнее.
Исследован случай возмущенных сепарабельных матриц. В частности, выведены теоретические оценки точности работы алгоритма в зависимости от возмущения. Проведены численные эксперименты (разд. 6), включая сравнение с результатами работы [10]. На практике предложенный алгоритм использует число операций и объем памяти, линейно зависящие от суммы размеров исходной матрицы.
Хотя уже было известно, что если ранг неотрицательной матрицы равен двум, то всегда можно построить неотрицательную факторизацию ранга 2 (см. [14]), ранее никто не приводил конкретного метода для решения данной задачи, используя на практике лишь $O(m + n)$ операций и элементов исходной матрицы (разд. 5).
2. СЕПАРАБЕЛЬНЫЕ МАТРИЦЫ
Определение 1. Матрица $M \in {{R}^{{m \times n}}}$ называется $r$-сепарабельной, если все ее столбцы принадлежат конусу, натянутому на некоторые $r$ столбцов той же матрицы. Соответствующая система столбцов называется определяющей.
Очевидно, что с помощью перестановки определяющими можно сделать первые $r$ столбцов. Тогда матрица $M$ представляется в виде
где $W \in {{R}^{{m \times r}}}$, $H \in R_{ + }^{{r \times n}}$, ${{I}_{r}}$ – единичная матрица порядка $r$. Ранг $r$-сепарабельной матрицы в общем случае необязательно равен $r$.Условие сепарабельности с первого взгляда может показаться несколько искусственным, однако существуют приложения, где оно является естественным и логичным. Например, это условие широко распространено при работе с гиперспектральными изображениями. В данном случае каждый столбец матрицы $M$ интерпретируется как “спектральная подпись” смеси материалов, соответствующей одному элементу изображения, а условие сепарабельности означает, что для всякого материала существует элемент изображения, содержащий только его. При работе с текстами столбцы $M$ могут описывать слова. Тогда условие сепарабельности означает, что для каждой темы найдется слово, относящееся исключительно к ней.
В дальнейшем нам нужны некоторые дополнительные предположения о матрицах $W$ и $H$.
Во-первых, будем считать, что столбцы матрицы $W \in {{R}^{{m \times r}}}$ линейно независимы. Тогда $W$ и $H$ определены единственным образом с точностью до перестановки и масштабирования столбцов. Другими словами, пусть матрицы $W$ и $\tilde {W}$ имеют по $r$ линейно независимых столбцов и каждая из матриц $H$ и $\tilde {H}$ содержит единичную подматрицу порядка $r$. Тогда, если невырожденная матрица $Q$ обеспечивает равенства
то она обязана быть мономиальной – так называются квадратные матрицы, которые в каждой строке и каждом столбце имеют ровно один ненулевой элемент. При сделанных предположениях матрицы $Q$ и ${{Q}^{{ - 1}}}$ обе должны быть неотрицательными и очевидным образом доказывается, что такие матрицы являются мономиальными. Более тонкие вопросы единственности неотрицательных разложений обсуждаются в [10], [15].Во-вторых, предположим, что сумма элементов в каждом столбце матрицы $H$ $ \in R_{ + }^{{r \times n}}$ не превышает 1. Такую матрицу будем называть нормированной $r$-сепарабельной. В случае неотрицательных сепарабельных матриц этого можно легко добиться с помощью нормировки, делающей сумму элементов каждого ненулевого столбца равной 1. В самом деле,
где матрица ${{D}_{X}}$ определяется как диагональная матрица, в которой $i$-й элемент диагонали равен сумме элементов $i$-го столбца матрицы $X$, если он ненулевой, а в противном случае этот элемент равен 1. Суммы элементов в ненулевых столбцах матриц $MD_{M}^{{ - 1}}$ и $WD_{W}^{{ - 1}}$ равны 1, а позиции нулевых столбцов соответствуют нулевым столбцам матрицы $M$. То же верно для матрицы ${{D}_{W}}HD_{M}^{{ - 1}}$, при этом все ее элементы будут неотрицательными. Заметим однако, что нормировка требует просмотра всех $mn$ элементов матрицы $M$.Предлагаемый нами алгоритм представляет собой модификацию алгоритма Гиллиса–Вавасиса (Gillis–Vavasis), которая работает с некоторой факторизацией исходной матрицы без предположения о неотрицательности факторов. Таким образом, полный массив элементов исходной матрицы не требуется и за счет этого наш алгоритм обладает существенно меньшей вычислительной сложностью. Прежде чем описывать новый алгоритм, поясним идеи, лежащие в основе метода Гиллиса–Вавасиса.
Задача алгоритма – найти определяющую систему столбцов неотрицательной $r$-сепарабельной матрицы $M$. Мы предполагаем, что матрица $M$ нормирована так, как было указано выше. В этом случае столбец максимальной длины заведомо входит в определяющую систему столбцов.
Последнее вытекает из следующего общего наблюдения. Пусть имеются векторы ${{w}_{1}},\; \ldots ,\;{{w}_{r}}$, среди них есть хотя бы один ненулевой вектор и все ненулевые векторы попарно различны. Пусть числа ${{\alpha }_{1}},\; \ldots ,\;{{\alpha }_{r}}$ неотрицательны, их сумма не больше 1 и ни одно из них не равно 1. Тогда
Итак, столбец максимальной длины матрицы $M$ входит в искомую определяющую систему. Чтобы получить остальные столбцы, вычтем из каждого столбца его ортогональную проекцию на линейную оболочку найденного вектора. Преобразованная таким образом матрица, обозначим ее через $M{\text{'}}$, в общем случае уже не будет неотрицательной. Но она останется $r$-сепарабельной матрицей с разложением вида $M{\text{'}} = W{\text{'}}H$, в котором один из столбцов матрицы $W{\text{'}}$ нулевой, а остальные линейно независимы. Действительно, пусть $j$-й столбец матрицы $M$ равен
и для каждого столбца ${{w}_{i}}$ записано разложение ${{w}_{i}} = {{u}_{i}} + {{\text{v}}_{i}}$ по одной и той же паре ортогональных подпространств. Тогда в аналогичном разложении вектора ${{m}_{j}} = {{z}_{j}} + {{p}_{j}}$ получаемЗаметим, что номера определяющих столбцов матрицы $M{\text{'}}$ те же, что и для матрицы $M$. При этом уже найденный нами определяющий столбец матрицы $M$ соответствует нулевому столбцу матрицы $M{\text{'}}$. Если $r \geqslant 2$, то столбец максимальной длины в матрице $M{\text{'}}$ не может быть нулевым. Но мы знаем, что он входит в определяющую систему для $M{\text{'}}$, а значит, и в определяющую систему для $M$. Таким образом, мы имеем уже два определяющих столбца матрицы $M$. Продолжая в том же духе, найдем все столбцы искомой определяющей системы.
Краткое формальное описание изложенных преобразований приводится ниже в виде псевдокода. Это и есть алгоритм Гиллиса–Вавасиса [10]. На его вход подается произвольная нормированная $r$-сепарабельная матрица ранга $r$, ее неотрицательность не требуется. Выше мы уже видели, что в случае неотрицательной матрицы необходимую нормировку можно выполнить достаточно просто. Это должно быть сделано перед применением алгоритма.
Алгоритм 1. Алгоритм Гиллиса–Вавасиса [10]
| Дано:M – нормированная r-сепарабельная $m \times n$-матрица ранга r. | ||
| Найти: Множество J, содержащее номера столбцов определяющей системы матрицы M. | ||
| 1 | $R = M,\;J = {\{ \} },\;j = 1;$ | |
| 2 | while$R \ne 0\;{\& }\;j \leqslant r$do | |
| 3 | $j{\kern 1pt} {\text{*}} = argma{{x}_{j}}\left\| {{{R}_{{:j}}}} \right\|_{2}^{2};$ | |
| 4 | ${{u}_{j}} = {{R}_{{:{{j}^{ * }}}}};$ | |
| 5 | $R \leftarrow \left( {I - \tfrac{{{{u}_{j}}u_{j}^{{\text{т }}}}}{{\left\| {{{u}_{j}}} \right\|_{2}^{2}}}} \right)R;$ | |
| 6 |  |
|
| 7 | $j = j + 1$; | |
| 8 | end | |
В алгоритме Гиллиса–Вавасиса выполняется $O(mnr)$ арифметических операций. В работах [2]–[5] было показано, что для матриц ранга $r$ скелетные разложения могут быть построены с использованием специально выбранных $r$ столбцов и $r$ строк заданной матрицы. Соответствующие методы обычно называются крестовыми. В них для получения разложений достаточно памяти для хранения порядка $(m + n)r$ чисел, и в случае $m = n$ сложность зависит от $n$ линейно, а не квадратично. Более точно вычислительные затраты составляют порядка $(m + n){{r}^{2}}$ операций.
Будем считать, что у нас уже есть разложение вида $M = UV$, где матрицы $U$ и $V$ имеют $r$ столбцов и $r$ строк соответственно, но в этих матрицах допускается наличие отрицательных элементов. Получив $U$ и $V$ и далее используя только их, мы предлагаем редуцированный алгоритм вычисления неотрицательной факторизации матрицы $M$ существенно меньшей сложности, чем алгоритм Гиллиса–Вавасиса.
Пусть мы знаем, что произведение $M = UV$ является неотрицательной $r$-сепарабельной матрицей ранга $r$. Тогда вектор-строка
содержит $n$ элементов и может быть найдена с затратой $2(m + n)r$ арифметических операций (сначала вычисляем строку $eU$, а затем умножаем результат на матрицу $V$). Очевидно, что ${{d}_{j}}$ есть сумма элементов $j$-го столбца матрицы $M$. Составим из них диагональную матрицу порядка $n$ и каждый нулевой элемент главной диагонали, если таковые есть, заменим на 1. Полученную диагональную матрицу обозначим через $D$. Очевидно, матрица $\tilde {M} = M{{D}^{{ - 1}}}$ будет нормированной $r$-сепарабельной.Лемма 1. Если $M$ является неотрицательной $r$-сепарабельной матрицей ранга $r$, то $\tilde {V} = V{{D}^{{ - 1}}}$ также будет нормированной $r$-сепарабельной матрицей ранга $r$.
Доказательство. Для матрицы $\tilde {M} = M{{D}^{{ - 1}}}$ имеет место разложение $WH$, где матрица $W$ имеет $r$ линейно независимых столбцов, а матрица $H$ содержит единичную подматрицу порядка $r$, все ее элементы неотрицательны и сумма элементов в каждом столбце не больше 1. Из равенства $U\tilde {V} = WH$ получаем $\tilde {V} = \tilde {W}H$, где $\tilde {W} = {{({{U}^{{\text{т }}}}U)}^{{ - 1}}}{{U}^{{\text{т }}}}W$.
Лемма 2. Определяющие столбцы матрицы $\tilde {V}$ соответствуют определяющим столбцам матрицы $M$.
Доказательство. Достаточно принять во внимание, что нормировка никак не влияет на порядок столбцов, поэтому у $M$ и $\tilde {M} = M{{D}^{{ - 1}}}$ совпадают множества индексов определяющих столбцов. Остается заметить, что из равенств $\tilde {M} = U\tilde {V}$ и $\tilde {V} = \tilde {W}H$ сразу же следует, что $\tilde {M} = (U\tilde {W})H$.
Объединяя наши рассуждения, можно сформулировать следующую теорему.
Теорема 1. Пусть матрица $M$ является неотрицательной сепарабельной матрицей ранга $r$. Если известно некоторое разложение $M = UV$, $U \in {{R}^{{m \times r}}}$, $V \in {{R}^{{n \times r}}}$, то число действий для построения неотрицательной матричной факторизации будет линейно зависеть от размеров матрицы.
Доказательство. Из лемм 1 и 2 следует, что матрица $\tilde {V} = V{{D}^{{ - 1}}}$ является нормированной $r$-сепарабельной матрицей ранга $r$, причем ее определяющие столбцы соответствуют определяющим столбцам матрицы $M$. Значит, чтобы найти определяющие столбцы матрицы $M$, достаточно применить алгоритм 1 не к исходной матрице размера $m \times n$, а к $\tilde {V} = V{{D}^{{ - 1}}}$, у которой $r \times n$ элементов. Число требуемых арифметических операций оценивается как $O({{r}^{2}}n)$.
Ранее обсуждалось, как найти матрицу $D$, а точнее вектор-строку $d$ на ее диагонали, за $2(m + n)r$ операций. Чтобы вычислить $\tilde {V} = V{{D}^{{ - 1}}}$, нужно поделить каждый столбец $V$ на соответствующий элемент $d$, что потребует еще $rn$ арифметических операций. В итоге, просуммировав число действий на поиск определяющих столбцов $M$, мы получим линейную зависимость от суммы размеров матрицы.
Ниже представлен предлагаемый нами редуцированный алгоритм.
Алгоритм 2. Редуцированный алгоритм
| Дано: Вещественные матрицы $U$ и $V$ размеров $m \times r$ и $n \times r$ соответственно. Предполагается известным, что произведение $M = UV$ является неотрицательной $r$-сепарабельной матрицей ранга $r$. | |||
| Найти: Множество индексов $J$, соответствующих определяющей системе $M$. | |||
| 1 | $d = eU,\;e = [1,\; \ldots ,\;1]$ | ||
| 2 | $d = dV$ | ||
| 3 | for ($j = 1$; $j \leqslant n$; $i = i + 1$) { | ||
| 4 | for ($i = 1$; $i \leqslant r$; $i = i + 1$) { | ||
| 5 | $\mathop {\tilde {v}}\nolimits_{ij} = {{\text{v}}_{{ij}}}{\text{/}}{{d}_{j}}$ | ||
| 6 | } | ||
| 7 | } | ||
| 8 | Алгоритм 1 применяется к матрице $\tilde {V}$. | ||
При работе с большими объемами данных имеет смысл использовать описанный метод в целях ускорения вычислений, его преимущество по сравнению с алгоритмом 1 наглядно продемонстрировано в разд. 6, посвященном численным экспериментам.
3. ВОЗМУЩЕННЫЕ СЕПАРАБЕЛЬНЫЕ МАТРИЦЫ
Пусть $A$ – нормированная сепарабельная матрица ранга $r$, а предложенный нами редуцированный алгоритм применяется к факторизации возмущенной матрицы $\tilde {A} = A + E$, где евклидова длина каждого столбца матрицы $E$ не выше $\varepsilon > 0$. Очевидно, что при достаточно малых возмущениях алгоритм Гиллиса–Вавасиса найдет возмущенные векторы определяющей системы исходной матрицы $M$. Существенно более трудный вопрос – выяснить, насколько малыми должны быть возмущения и как именно зависит от них точность приближений. В [10] получены некоторые конкретные, хотя и завышенные оценки в ситуации, когда максимизируется не длина, а произвольно взятая сильно выпуклая функция вектора. Практического смысла в таком обобщении, как признают сами авторы, им выявить не удалось. В этом разделе мы дадим более простой вывод оценок того же типа в случае максимизации именно длины и применим их для анализа нашего редуцированного алгоритма в условиях возмущений.
Прежде всего нам нужно исследовать ситуацию, когда при поиске вектора наибольшей длины в возмущенной матрице будет выбран столбец, соответствующий нетривиальной выпуклой комбинации определяющих столбцов исходной (невозмущенной) сепарабельной матрицы. При некотором ограничении на возмущение мы покажем, что найденный столбец будет, тем не менее, близок к какому-то из столбцов определяющей системы исходной матрицы. Чтобы это сделать, мы будем опираться на следующую лемму.
Лемма 3. Для произвольных векторов ${{a}_{1}},\; \ldots ,\;{{a}_{k}}$ и их выпуклой комбинации с коэффициентами ${{\alpha }_{1}},\; \ldots ,\;{{\alpha }_{k}}$ справедливо тождество
Доказательство. При $k = 2$ получаем легко проверяемое равенство
Следствие 1. Для произвольной выпуклой комбинации заданных векторов имеет место неравенство
Отметим еще одно интересное следствие, которое в данной работе не используется, но может быть полезно при работе с сильно выпуклыми функциями. Так называются выпуклые функции $f$, для которых выполняется неравенство
Следствие 2. Для произвольной сильно выпуклой функции $f$ с параметром сильной выпуклости $\gamma $ и произвольной выпуклой комбинации векторов ${{a}_{1}},\; \ldots ,\;{{a}_{k}}$ имеет место неравенство
Доказательство проводится по индукции в полной аналогии с доказательством леммы 3 и с использованием установленного в ней тождества. В литературе нами было найдено эквивалентное данному неравенство только для случая, когда ${{a}_{1}},\; \ldots ,\;{{a}_{k}}$ – вещественные числа (см. [16]).
Для вывода оценок нам нужны некоторые величины, связанные с системой столбцов ${{a}_{1}},\; \ldots ,\;{{a}_{k}}$ или составленной из них матрицы $A$:
Лемма 4. Предположим, что в $\varepsilon $-окрестности вектора $b$ имеется вектор, длина которого не меньше $\mu $, и пусть ${{a}_{j}}$ – вектор с наибольшим коэффициентом ${{\alpha }_{j}}$. Тогда для всех достаточно малых $\varepsilon $ справедливы оценки
(2)
$\left\| {b - {{a}_{j}}} \right\| = O\left( {\frac{{{{\mu }^{2}}}}{{{{\omega }^{2}}}}\varepsilon } \right).$Доказательство. Если ${{\alpha }_{j}} = 1$, то утверждение очевидно. Полагаем далее, что ${{\alpha }_{j}} < 1$. Пусть вектор $e$ имеет длину $\left\| e \right\| \leqslant \varepsilon \leqslant \mu $ и при этом $\left\| {b + e} \right\| \geqslant \mu $. Тогда, согласно следствию 1, имеем
(3)
${{\alpha }_{j}} \geqslant \frac{{1 + \sqrt {1 - 4c\varepsilon } }}{2} \geqslant 1 - 2c\varepsilon $(4)
${{\alpha }_{j}} \leqslant \frac{{1 - \sqrt {1 - 4c\varepsilon } }}{2} \leqslant 2c\varepsilon .$Замечание. Условие малости $\varepsilon $ можно записать в виде $\varepsilon \leqslant min\left\{ {{{c}_{1}}\tfrac{{\sigma _{r}^{2}}}{{r\mu }},\mu } \right\}$, а его следствие – в виде неравенства $\left\| {b - {{a}_{j}}} \right\| \leqslant {{c}_{2}}\tfrac{{{{\mu }^{2}}}}{{{{\omega }^{2}}}}\varepsilon $, если взять, например, ${{c}_{1}} = \tfrac{1}{{12}}$ и ${{c}_{2}} = 12$.
Следующая теорема – это ключевой результат анализа возмущений. Его прототипом служит теорема из [10], полученная там для алгоритма, в котором на каждом шаге выбирается столбец, максимизирующий заданную сильно выпуклую функцию. В частности, такой функцией является квадрат длины вектора.
Теорема 2. Пусть $A \in {{\mathbb{R}}^{{m \times n}}}$ – нормированная сепарабельная матрица ранга $r$, и предположим, что алгоритм Гиллиса–Вавасиса применяется к возмущенной матрице $\tilde {A} = A + E$, где длина каждого столбца матрицы $E$ не превышает $\varepsilon $, и находит столбцы $\mathop {\tilde {a}}\nolimits_{{{i}_{1}}} ,\; \ldots ,\;\mathop {\tilde {a}}\nolimits_{{{i}_{r}}} $. Тогда определяющие столбцы матрицы $A$ можно занумеровать таким образом, что при всех достаточно малых $\varepsilon $ имеют место неравенства
Доказательство. Пусть $W = [{{w}_{1}},\; \ldots ,\;{{w}_{r}}]$ – матрица, составленная из определяющих столбцов матрицы $A$, и ${{\sigma }_{r}}$ – ее минимальное сингулярное число. Тогда $\left\| {Wx} \right\| \geqslant {{\sigma }_{r}}\left\| x \right\|$ для любого $x \in {{\mathbb{R}}^{r}}$ и, следовательно,
После выбора вектора ${{\tilde {a}}_{{{{i}_{1}}}}}$ из каждого столбца матрицы $\tilde {A}$ вычитается ортогональная проекция на выбранный столбец. В результате получается матрица
Очевидно, что $\mu ({{W}_{1}}) \leqslant \mu = \mu (W)$. Для определенности будем считать, что ${{w}_{1}} = {{a}_{{{{j}_{1}}}}}$, и рассмотрим подматрицу $\hat {W} = [{{w}_{2}},\; \ldots ,\;{{w}_{r}}]$ в $W$ и соответствующую ей подматрицу ${{\hat {W}}_{1}} = {{Q}_{1}}\hat {W}$ в матрице ${{W}_{1}}$. Первый столбец матрицы ${{W}_{1}}$ равен ${{Q}_{1}}{{a}_{{{{j}_{1}}}}} \approx {{Q}_{1}}{{\tilde {a}}_{{{{i}_{1}}}}} = 0$ и, следовательно, его длина достаточно мала при малых $\varepsilon $. Значит, при достаточно малых $\varepsilon $ находим
В следующей теореме исследуется применение редуцированного алгоритма к факторизации, полученной каким-либо вариантом крестового метода [3]. Ниже используется норма Фробениуса ${{\left\| E \right\|}_{F}}$, определяемая как корень квадратный из суммы квадратов всех элементов матрицы.
Теорема 3. Пусть $A \in {{\mathbb{R}}^{{m \times n}}}$ – нормированная сепарабельная матрица ранга $r$ и рассматривается возмущенная матрица $\tilde {A} = A + E$, где ${{\left\| E \right\|}_{F}} \leqslant \varepsilon $. Тогда существуют такие $r$ столбцов $C$ и $r$ строк $R$ матрицы $\tilde {A}$, дающие в пересечении $r \times r$-матрицу $G$, что применение редуцированного алгоритма к факторизации $C{{G}^{{ - 1}}}R$ находит столбцы ${{\tilde {a}}_{{{{i}_{1}}}}},\; \ldots ,\;{{\tilde {a}}_{{{{i}_{r}}}}}$, которые при некоторой нумерации определяющих столбцов матрицы $A$ при всех достаточно малых $\varepsilon $ удовлетворяют неравенствам
Доказательство. В работе [18] доказано существование $r$ столбцов и $r$ строк, гарантирующих неравенство ${{\left\| {C{{G}^{{ - 1}}}R - \tilde {A}} \right\|}_{F}} \leqslant (r + 1)\varepsilon $. Остается принять во внимание оценки теоремы 2.
Заметим также, что аппроксимации ранга $r$ могут строиться на основе большего, чем $r$, числа столбцов и строк (см. [19], [20]). Выбирая, например, $2r$ столбцов и строк, мы можем гарантировать поэлементную оценку погрешности, в которой уже нет зависимости от $r$.
Интересным представляется вопрос, насколько точны полученные теоретические оценки и какова вероятность, что алгоритм выберет на некотором шаге вектор не из определяющей системы. Мы провели следующий эксперимент. Были сгенерированы матрицы $W \in {{R}^{{10 \times 2}}}$ и $H \in {{R}^{{2 \times 10000}}}$, элементы которых – равномерно распределенные на отрезке $[0;1]$ числа. Затем столбцы матрицы $H$ были нормированы, чтобы сумма каждого была равна 1. Далее было подсчитано, как указано в замечании к 4, максимальное значение $\varepsilon $. После этого были рассмотрены 100 значений $\tilde {\varepsilon }$ от 0 до $\varepsilon $, к каждому столбцу $M = WH$ прибавлялся вектор $\tfrac{{\tilde {\varepsilon }}}{{\sqrt n }}e$, норма которого равна $\tilde {\varepsilon }$. Мы считали, сколько векторов в возмущенной матрице $M = WH$ по норме превзошли $\mu (W)$. Результаты представлены на фиг. 1. Даже при максимальном возмущении доля нетривиальных выпуклых комбинаций определяющих векторов, норма которых при возмущении больше $\mu (W)$, меньше 1.5%.
4. РЕДУЦИРОВАННЫЙ АЛГОРИТМ ДЛЯ СИММЕТРИЧНОЙ НЕОТРИЦАТЕЛЬНОЙ ФАКТОРИЗАЦИИ
В [13] предложен метод построения симметричной неотрицательной факторизации $M = W{{W}^{{\text{т }}}}$ для симметричных неотрицательных матриц $M \in {{\mathbb{R}}^{{m \times m}}}$ ранга $r$, содержащих диагональную главную подматрицу ранга $r$. Напомним, что главная подматрица получается вычеркиванием строк и столбцов с общими номерами. Матрица $W$ определяется однозначно с точностью до перестановки столбцов (см. [13]). Время работы алгоритма, названного авторами IREVA (Identification and Rotation of Extreme Vectors Algorithm), оценивается ими как $O({{m}^{2}}r)$ для неразреженных матриц.
Однако эту задачу можно решить гораздо быстрее. Для этого нужно заметить, что симметричные неотрицательные матрицы ранга $r$ с диагональной главной подматрицей того же ранга принадлежат классу сепарабельных матриц. Если главную диагональную подматрицу обозначить $D$, а содержащие ее столбцы $S$, то справедливо разложение $M = S{{D}^{{ - 1}}}{{S}^{{\text{т }}}} = S({{D}^{{ - 1}}}{{S}^{{\text{т }}}}).$ Очевидно, матрица ${{D}^{{ - 1}}}{{S}^{{\text{т }}}}$ неотрицательна и содержит единичную подматрицу порядка $r$. Таким образом, $M$ сепарабельна, а $S$ состоит из ее определяющих столбцов. Чтобы их найти, можно применить алгоритм крестовой аппроксимации, а затем редуцированный алгоритм 2. Вместо $O({{m}^{2}}r)$ потребуется всего $O(m{{r}^{2}})$ операций.
5. МАТРИЦЫ РАНГА 2
Очевидно, что для произвольной неотрицательной $m \times n$-матрицы имеют место неравенства ${\text{rank}}(A) \leqslant {\text{ran}}{{{\text{k}}}_{ + }}(A) \leqslant min(m,n)$. Как показано в [14], если ${\text{rank}}(A) \leqslant 2$, то ${\text{ran}}{{{\text{k}}}_{ + }}(A) = {\text{rank}}(A)$.
Теорема 4. Любая неотрицательная матрица ранга не выше 2 является сепарабельной матрицей того же ранга.
Доказательство. Если ${\text{rank}}(A) = 1$, то $A = u{{\text{v}}^{{\text{т }}}} = (\gamma \left| u \right|){{({{\gamma }^{{ - 1}}}\left| \text{v} \right|)}^{{\text{т }}}}$, где $\gamma = \mathop {max}\limits_{1 \leqslant j \leqslant n} \left| {{{\text{v}}_{j}}} \right|$, а $\left| u \right|$ и $\left| \text{v} \right|$ обозначают векторы, координаты которых равны абсолютным величинам координат векторов $u$ и $\text{v}$. Если ${\text{rank}}(A) = 2$, то, разделив каждый столбец матрицы $A$ на сумму его элементов, получим стохастическую матрицу с тем же неотрицательным рангом. Поэтому без ограничения общности можно считать $A$ стохастической матрицей. Если $a$ и $b$ – какие-то линейно независимые столбцы, то $j$-й столбец записывается в виде линейной комбинации ${{a}_{j}} = {{\alpha }_{j}}a + {{\beta }_{j}}b$, где в силу стохастичности ${{\alpha }_{j}} + {{\beta }_{j}} = 1$. Пусть ${{\beta }_{k}}$ и ${{\beta }_{l}}$ – минимальное и максимальное среди чисел ${{\beta }_{1}},\; \ldots ,\;{{\beta }_{n}}$. Тогда, поскольку ${{\beta }_{k}} \leqslant {{\beta }_{j}} \leqslant {{\beta }_{l}}$, можно найти числа ${{\delta }_{j}}$ такие, что
Следствие 3. Если $A \geqslant 0$ и ${\text{ran}}{{{\text{k}}}_{ + }}(A) \leqslant 3$, то ${\text{ran}}{{{\text{k}}}_{ + }}(A) = {\text{rank}}(A)$.
Доказательство. Пусть ${\text{ran}}{{{\text{k}}}_{ + }}(A) = 3$. Как установлено выше, если ${\text{rank}}(A) \leqslant 2$, то ${\text{ran}}{{{\text{k}}}_{ + }}(A) = {\text{rank}}(A)$. Следовательно, ${\text{rank}}(A) = 3.$ Остальные случаи разбираются аналогично.
Теорема 5. Если для неотрицательной $m \times n$-матрицы $A$ ранга 2 известно скелетное разложение $A = UV$, где $U \in {{R}^{{m \times 2}}}$ и $V \in {{R}^{{2 \times n}}}$, то для получения неотрицательной факторизации ранга 2 достаточно выполнить число операций, линейно зависящее от суммы размеров матрицы $A$.
Доказательство. Линейного числа операций достаточно для того, чтобы получить разложение $A = UV$, в котором $V$ содержит единичную матрицу порядка 2. Тогда $U = [a,b]$ состоит из двух линейно независимых столбцов матрицы $A$. Матрицы $A$, $U$, $V$ можно считать стохастическими (чтобы провести соответствующую нормировку, достаточно линейного числа операций). Пусть ${{\beta }_{1}},\; \ldots ,\;{{\beta }_{n}}$ – элементы второй строки матрицы $V$. Согласно описанным выше построениям, найдем среди них минимальный ${{\beta }_{{{{j}_{ * }}}}}$ и максимальный ${{\beta }_{{{{j}^{ * }}}}}$. Тогда пара столбцов матрицы $A$ с номерами ${{j}_{ * }}$ и $j{\text{*}}$ составляют $W$, для определения $H$ можно воспользоваться крестовым разложением, достаточно найти в $W$ невырожденную подматрицу размера $2 \times 2$. Все эти действия требуют линейного числа операций.
Ниже приведен алгоритм для построения факторизации матриц ранга 2. Напомним, что ${{D}_{X}}$ – диагональная матрица, в которой $i$-й элемент диагонали равен сумме элементов $i$-го столбца матрицы $X$, если он ненулевой, а в противном случае этот элемент равен 1.
Алгоритм 3. Неотрицательная факторизация матриц ранга 2
| Дано:$A \in R_{ + }^{{m \times n}}$, ${\text{rank}}(A) = 2.$ | |
| Найти: Матрицы $W \in R_{{ \geqslant 0}}^{{m \times 2}}$, $H \in R_{{ \geqslant 0}}^{{2 \times n}}$: $A = WH$. | |
| 1 | Строится крестовое разложение $A$: $A = UV$. |
| 2 | $\tilde {V} = {{D}_{U}}V$ |
| 3 | $\tilde {V} = \tilde {V}D_{{\tilde {V}}}^{{ - 1}}$ |
| 4 | ${{i}_{ * }} = i:{{\tilde {v}}_{{2i}}} = mi{{n}_{{1 \leqslant i \leqslant n}}}{{\tilde {v}}_{{2i}}}$ |
| 5 | $i* = i:{{\tilde {v}}_{{2i}}} = ma{{x}_{{1 \leqslant i \leqslant n}}}{{\tilde {v}}_{{2i}}}$ |
| 6 | $W = [{{a}_{{{{i}_{ * }}}}}{{a}_{{{{i}^{ * }}}}}]$ |
| 7 | Найти в $W$ строки $p$ и $s$: подматрица $\left[ {\begin{array}{*{20}{c}} {{{w}_{{p1}}}}&{{{w}_{{p2}}}} \\ {{{w}_{{s1}}}}&{{{w}_{{s2}}}} \end{array}} \right]$ невырожденная. |
| 8 | $H = \mathop {\left[ {\begin{array}{*{20}{c}} {{{w}_{{p1}}}}&{{{w}_{{p2}}}} \\ {{{w}_{{s1}}}}&{{{w}_{{s2}}}} \end{array}} \right]}\nolimits^{ - 1} \left[ {\begin{array}{*{20}{c}} {{{a}_{{p1}}}}& \ldots &{{{a}_{{pn}}}} \\ {{{a}_{{s1}}}}& \ldots &{{{a}_{{sn}}}} \end{array}} \right]$ |
6. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
Проведем сравнение алгоритма Гиллиса–Вавасиса (1) и предложенного нами метода, когда сначала строится крестовое разложение матрицы, которое затем подается на вход редуцированному алгоритму 2. Такой двухэтапный метод будем называть алгоритмом 2+. Весь код для проведения численных экспериментов был написан в Matlab. При построении крестового разложения использовались функции из библиотеки ”TT-Toolbox” (см. [21]).
Для численных экспериментов сепарабельные матрицы $M \in R_{ + }^{{n \times n}}$ ранга $r$ генерировались следующим образом. Сначала матрицы $W \in {{R}^{{n \times r}}}$ и $H{\text{'}} \in {{R}^{{r \times (n - r)}}}$ заполняются модулями нормально распределенных чисел, $H = [{{I}_{r}}H{\text{'}}]$, при этом столбцы $H$ нормируются так, чтобы сумма элементов в каждом была равна $1$, и случайным образом перемешиваются. Итоговая матрица $M$ равна произведению $W$ и $H$.
Рассматривались $n$ от $100$ до $10\,000$ с шагом $100$, для каждого $n$ строились $100$ матриц $M$, которые подавались на вход алгоритмам 1 и 2+. На фиг. 2 приведены графики зависимости времени работы от $n$ при фиксированных $r$. Программная реализация алгоритма 1 была взята из [22].
Во всех случаях оба алгоритма верно определили столбцы $W$. График времени работы нового метода демонстрирует линейную зависимость от размера, алгоритм 1 – квадратичную.
Фиг. 3.
Сравнение времени работы алгоритмов 1+, 3 и метода из [23] в зависимости от размера матрицы ранга 2.

Для случая неотрицательной матричной факторизации ранга 2 было проведено сравнение работы трех алгоритмов: алгоритма 3; алгоритма 1 при $r = 2$, матрица $H$ затем находилась так же, как в алгоритме 3 (назовем такой двухэтапный метод алгоритмом 1+); метода, описанного в [23] (исходный код взят из [24]).
Матрицы для экспериментов строились так же, как было описано выше, $r = 2$. На графике 3 демонстрируется время работы каждого из заявленных трех алгоритмов при изменении $n$ от $100$ до $2000$ с шагом, равным $100$. При этом для каждого $n$ было проведено $100$ экспериментов, результаты затем усреднялись.
Было получено, что алгоритмы 1+ и 3 верно построили разложение исходной матрицы, в то время как метод из [23] дает ошибку, увеличивающуюся с ростом $n$. Таким образом, приходим к выводу, что метод из [23] проигрывает остальным двум и в точности, и в быстроте.
Сравним, как изменяется время работы алгоритмов 1+ и 3 с изменением $n$ от $100$ до $10\,000$ с шагом, равным $100$. Результаты представлены на фиг. 4. Как видно, у алгоритма 1+ наблюдается квадратичная зависимость времени работы от размера матрицы, а у алгоритма 3 – линейная, что полностью подтверждает теоретические выкладки.
Как обсуждалось в секции 4, алгоритм 2+ можно применять для построения симметричной неотрицательной факторизации симметричных неотрицательных матриц ранга $r$, содержащих диагональную главную подматрицу того же ранга. Сравним время его работы и метода IREVA (см. [13]).
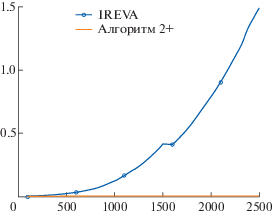
Фиг. 5.
Сравнение времени работы алгоритмов 2+ и IREVA (см. [13]) в зависимости от размера матрицы, $r = 3$.
Фиг. 6.
Сравнение алгоритмов 1 и 2+ для возмущенных сепарабельных матриц. Зависимость доли верно найденных столбцов определяющей системы от $\delta $. (а) эксперимент 1; (б) эксперимент 2.

Фиг. 7.
Сравнение алгоритмов 1 и 2+ для возмущенных сепарабельных матриц. Зависимость доли верно найденных столбцов определяющей системы от $\delta $. (а) эксперимент 3; (б) эксперимент 4.

Для тестирования генерировались неотрицательные симметричные матрицы $M \in R_{{ \geqslant 0}}^{{n \times n}} = W{{W}^{{\text{т }}}}$ ранга $r$ c диагональной главной подматрицей того же ранга. Матрицы ${{W}^{{\text{т }}}} \in {{R}^{{r \times n}}} = [{{I}_{r}}W{\text{'}}]$, где $W{\kern 1pt} {\text{'}} \in {{R}^{{r \times (n - r)}}}$ заполняются модулями нормально распределенных чисел, при этом столбцы $W{\text{'}}$ нормируются так, чтобы сумма элементов в каждом была равна $1$, и случайным образом перемешиваются.
Алгоритм IREVA можно условно поделить на 2 части. В первой вычисляется матрица $V \in {{\mathbb{R}}^{{n \times r}}}$: $M = V{{V}^{{\text{т }}}}$, у которой первый столбец состоит только из положительных чисел. При реализации метода мы воспользовались предложением из [13] и для построения $V$ использовали комбинацию формулы понижения ранга и разложения Холецкого. Во второй части алгоритма вычисляется ортогональная матрица $R \in {{\mathbb{R}}^{{r \times r}}}$, чтобы перевести столбцы $V$ в $\mathbb{R}_{ + }^{r}$.
Рассматривались $n$ от $100$ до $2500$ с шагом $100$, для каждого $n$ строились $100$ матриц $M$, которые подавались на вход доработанному алгоритму 2+ и методу IREVA (см. [13]). Ниже приведен график 5 зависимости времени работы от значения $n$ при фиксированном $r = 3$. Как видно, у алгоритма IREVA наблюдается квадратичная зависимость времени работы от размера матрицы, а у алгоритма 2+ – линейная, что согласуется с нашими рассуждениями.
Далее проверим работу алгоритма 2+ для возмущенных сепарабельных матриц. Будем строить матрицы для экспериментов так же, как в [10].
1. Матрица $W$ будет генерироваться двумя способами:
(а) Равномерное распределение. Элементы $W \in {{R}^{{200 \times 20}}}$ – равномерно распределенные на отрезке $[0;1]$ случайные числа (функция rand() в MATLAB).
(б) Плохо обусловленная. Сперва генерируем $W{\kern 1pt} {\text{'}} \in {{R}^{{200 \times 20}}}$, как описано в предыдущем пункте. Затем находится SVD представление: $W{\kern 1pt} {\text{'}} = U\Sigma {{V}^{{\text{т }}}}$, $U \in {{R}^{{200 \times 20}}}$, $\Sigma \in {{R}^{{20 \times 20}}}$, $V \in {{R}^{{20 \times 20}}}$. Тогда $W = US{{V}^{{\text{т }}}}$, где $S$ – диагональная матрица, у которой элементы на диагонали равны ${{\alpha }^{{i - 1}}}$, $i = 1,2,\; \ldots ,\;20$, а ${{\alpha }^{{19}}} = {{10}^{{ - 3}}}$.
2. Матрицы $H$, $N$ тоже будут генерироваться двумя способами:
(в) Средние точки. Пусть $H = [{{I}_{{20}}},H{\text{'}}] \in {{R}^{{20 \times 210}}}$, где столбцы $H{\text{'}}$ содержат все возможные комбинации 2 ненулевых элементов, равных $0.5$, в разных позициях. Поэтому у $H{\text{'}}$ $C_{{20}}^{2} = 190$ столбцов. Таким образом, первые 20 столбцов $W$ совпадают со столбцами $M$, в то время как оставшиеся 190 являются средним каких-то двух столбцов $M$. Первые 20 столбцов $M$ не изменяются, а к остальным добавляется шум – ${{n}_{i}} = \delta ({{m}_{i}} - \bar {w})$, $21 \leqslant i \leqslant 210$, $\delta \geqslant 0$, где $\bar {w}$ – среднее столбцов $W$.
(г) Распределения Дирихле и Гаусса. Пусть $H = [{{I}_{{20}}},{{I}_{{20}}},H{\text{'}}] \in {{R}^{{20 \times 240}}}$, где столбцы $H{\text{'}}$ получены из распределения Дирихле с $r$ параметрами, выбранными равномерно на $[0,1]$, т.е. сумма элементов в каждом столбце $H{\text{'}}$ равна 1. Значения матрицы шума $N$ – нормально распределенные случайные числа: ${{n}_{{ki}}} \sim \delta N(0,1)$, $1 \leqslant k \leqslant 200$, $1 \leqslant i \leqslant 240$.
В итоге возмущенная сепарабельная матрица $M{\text{'}} = WH + N$ может быть получена четырьмя различными способами путем комбинации $W$, $H$ и $N$, построенных как описано выше.
Ниже приведены две таблицы. В табл. 1 указаны измеренные значения параметров исходных матриц, усредненные для всех экспериментов. Они практически полностью совпали с теми, что были получены в [10]: максимальное абсолютное отклонение составляет 0.01. Далее проанализировано, при каком наибольшем $\delta $ алгоритмы 1 ([10]) и 2+ способны правильно идентифицировать столбцы, входящие в $W$. Результаты представлены в табл. 2. Заметим, что в экспериментах 1–3 максимальные значения $\delta $ для алгоритма 2+ больше. Единственный случай, когда алгоритм 2+ несколько уступил алгоритму 1 в случае возмущенной сепарабельной матрицы – эксперимент 4. Однако отметим, что при этом разница между максимальными $\delta $ очень мала, т.е. отличие представляется несущественным.
Таблица 1.
Средние значения параметров для различных экспериментов при генерации зашумленных сепарабельных матриц
| Параметр | Эксперимент | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| $W$ | (а) | (а) | (б) | (б) |
| $N$ и $H$ | (в) | (г) | (в) | (г) |
| $\tfrac{{{{\sigma }_{1}}(W)}}{{{{\sigma }_{r}}(W)}}$ | 10.84 | 10.84 | 1000 | 1000 |
| $\mu (W)$ | 8.64 | 8.64 | 0.41 | 0.41 |
| ${{\sigma }_{r}}(W)$ | 2.95 | 2.95 | ${{10}^{{ - 3}}}$ | ${{10}^{{ - 3}}}$ |
| Среднее $ma{{x}_{i}}\left\| {{{n}_{i}}} \right\|{{\delta }^{{ - 1}}}$ | 3.06 | 16.15 | 0.30 | 16.15 |
Таблица 2.
Максимальные значения $\delta $ для верного определения столбцов $W$ алгоритмом
| Алгоритм | Эксперимент | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| 1 | 0.24 | 0.23 | 0.01 | $20 \times {{10}^{{ - 4}}}$ |
| 2+ | 0.39 | 0.25 | 0.38 | $1 \times {{10}^{{ - 4}}}$ |
Итак, в случае возмущенных сепарабельных матриц алгоритм 2+ в большинстве случаев по качеству не уступает исходному алгоритму 1, имея при этом явное преимущество в скорости работы.
7. ЗАКЛЮЧЕНИЕ
В данной работе предложен быстрый метод решения задачи неотрицательной матричной факторизации для неотрицательных сепарабельных матриц, у которых совпадают неотрицательный и обычный ранги. Изучена его работа с неотрицательными возмущенными матрицами и доказано, что он позволяет значительно сократить число операций и затраты памяти, поскольку все другие известные алгоритмы предполагают сложность не меньше $O(mn)$. Также рассмотрена применимость метода для симметричной неотрицательной факторизации симметричных неотрицательных матриц ранга $r$, содержащих диагональную главную подматрицу того же ранга. Алгоритм 2+ по теоретическим оценкам не сильно уступает исходному методу в случае возмущенных сепарабельных матриц, а численные эксперименты показали, что на практике отличие в точности является очень незначительным.
Также представлен отдельный метод для неотрицательных матриц ранга 2, решающий на практике задачу неотрицательной факторизации за время, линейно зависящее от $m$ и $n$. Численные эксперименты полностью подтвердили наши теоретические оценки и продемонстрировали преимущество алгоритма 3 перед другими методами как в точности, так и по скорости работы.
В дальнейшем мы планируем продолжить работу над задачей неотрицательной матричной факторизации, когда известен неотрицательный ранг и разрешается использовать лишь несколько столбцов и строк исходной матрицы, чтобы предложить методы ее решения для более широких классов матриц.
Список литературы
Vavasis S.A. On the complexity of nonnegative matrix factorization // SIAM J. Optim. 2008. V. 20. № 3. P. 1364–1377.
Goreinov S.A., Tyrtyshnikov E.E., Zamarashkin N.L. A theory of pseudo-skeleton approximations // Linear Algebra Appl. 1997. V. 261. P. 1–21.
Tyrtyshnikov E.E. Incomplete cross approximation in the mosaic-skeleton method // Computing. 2000. V. 64. № 4. P. 367–380.
Goreinov S.A., Tyrtyshnikov E.E. The maximal-volume concept in approximation by low-rank matrices // Contemporary Mathematics. 2001. V. 208. P. 47–51.
Goreinov S., Oseledets I., Savostyanov D., Tyrtyshnikov E., Zamarashkin N. How to find a good submatrix // Matrix Methods: Theory, Algorithms and Applications. 2010. P. 247–256.
Donoho D., Stodden V. When does non-negative matrix factorization give a correct decomposition into parts? // INIPS. 2003.
Arora S., Ge R., Kannan R., Moitra A. Computing a nonnegative matrix factorization – provably // CoRR. 2011.
Esser E., Moller M., Osher S., Sapiro G., Xin J. A convex model for nonnegative matrix factorization and dimensionality reduction on physical space // IEEE Transactions on Image Proc. 2012. V. 21. № 7. P. 3239–3252.
Bittorf V., Recht B., Ré C., Tropp J. Factoring nonnegative matrices with linear programs // NIPS 2012. 2012. P. 1223–1231.
Gillis N., Vavasis S.A. Fast and robust recursive algorithms for separable nonnegative matrix factorization // IEEE Trans. on Pattern Analysis and Machine Intelligence. 2014. V. 36. P. 698–714.
Ding C., He X., Simon H.D. On the equivalence of nonnegative matrix factorization and spectral clustering // Proc. of the SIAM Internat. Conference on Data Mining (SDM’05). 2005. P. 606–610.
Vandendorpe A., Ho H.N., Vanduffel S., Dooren, P.V. On the parameterization of the creditrisk-plus model for estimating credit portfolio risk // Insurance: Mathematics and Economics. 2008. V. 42. № 2. P. 736–745.
Kalofolias V., Gallopoulos E. Computing symmetric nonnegative rank factorizations // Linear Algebra Appl. 2012. V. 436. № 2. P. 421–435.
Cohen J., Rothblum U. Nonnegative ranks, decompositions and factorizations of nonnegative matrices // Linear Algebra and its Applications. 1993. V. 190. P. 149–168.
Gillis N. Sparse and unique nonnegative matrix factorization through data preprocessing // J. Machine Learning Res. 2012. V. 13. P. 3349–3386.
Bakula M.K. Jensen–Steffensen inequality for strongly convex functions // M. J. Inequal Appl. 2018. V. 306. P. 1–12.
Тыртышников Е.Е. Методы численного анализа. М.: Издательский центр “Академия”, 2007.
Замарашкин Н.Л., Осинский А.И. О существовании близкой к оптимальной скелетной аппроксимации матрицы во фробениусовой норме // Докл. АН. 2018. Т. 479. № 5. С. 489–492.
Zamarashkin N.L., Osinsky A.I. New accuracy estimates for pseudoskeleton approximations of matrices // Dokl. Math. 2016. V. 94. № 3. P. 643–645.
Osinsky A., Zamarashkin N. Pseudo-skeleton approximations with better accuracy estimates // Linear Algebra and its Applicat. 2018. V. 537. P. 221–249.
Oseledets I. et al. TT-Toolbox 2.2, Institute of Numerical Mathematics, Moscow, Russia. 2009–2013. https://github.com/oseledets/TT-Toolbox.
Gillis N. Fast and robust recursive algorithm for separable NMF [Source code], https://sites.google.com/site/nicolasgillis/code.
Kuang D., Park H. Fast rank-2 nonnegative matrix factorization for hierarchical document clustering // The 19th ACM SIGKDD International Conference on Knowledge, Discovery, and Data Mining (KDD’13). 2013. P. 739–747.
Kuang D. Hierarchical rank-2 NMF for document clustering and topic modeling with visualization [Source code], https://github.com/dakuang/hiernmf2.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики





