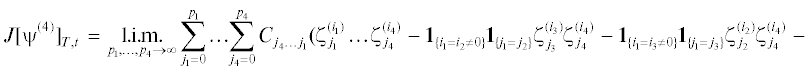Журнал вычислительной математики и математической физики, 2019, T. 59, № 8, стр. 1299-1313

Сравнительный анализ эффективности применения полиномов Лежандра и тригонометрических функций к численному интегрированию стохастических дифференциальных уравнений Ито

Д. Ф. Кузнецов^*

С.-Пб. Политехнический ун-т Петра Великого
195251 С.-Петербург, ул. Политехническая, 29, Россия

Поступила в редакцию 15.01.2019
После доработки 15.01.2019
Принята к публикации 10.04.2019

DOI: 10.1134/S0044466919080118

Аннотация

Статья посвящена сравнительному анализу эффективности применения полиномов Лежандра и тригонометрических функций к численному интегрированию стохастических дифференциальных уравнений Ито в рамках метода аппроксимации повторных стохастических интегралов Ито и Стратоновича, основанного на обобщенных кратных рядах Фурье. На примере повторных стохастических интегралов кратностей 1–3, входящих в разложение Тейлора–Ито, показано, что их разложения, полученные с помощью кратных рядов Фурье–Лежандра, существенно проще и требуют значительно меньших вычислительных затрат в сравнении со своими аналогами, полученными на основе кратных тригонометрических рядов Фурье. Результаты статьи могут быть полезны для построения и реализации сильных численных методов для стохастических дифференциальных уравнений Ито с многомерным и нелинейным шумом. Библ. 20. Табл. 7.

Ключевые слова: кратный ряд Фурье, полином Лежандра, повторный стохастический интеграл, стохастический интеграл Ито, стохастический интеграл Стратоновича, разложение Тейлора–Ито, стохастическое дифференциальное уравнение Ито, численное интегрирование, среднеквадратическая сходимость.

1. ВВЕДЕНИЕ

Пусть задано фиксированное вероятностное пространство ($\Omega $, ${\text{F}}$, ${\text{P}}$), неубывающая совокупность $\sigma $-алгебр 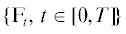на нем и ${{{\text{F}}}_{t}}$-измеримый при всех $t \in [0,T]$ $m$-мерный стандартный винеровский процесс ${{{\mathbf{f}}}_{t}}$ с независимыми компонентами ${\mathbf{f}}_{t}^{{(i)}};$ $i = 1,\; \ldots ,\;m$.

Рассмотрим стохастическое дифференциальное уравнение (СДУ) Ито

(1)

${{{\mathbf{x}}}_{t}} = {{{\mathbf{x}}}_{0}} + \int\limits_0^t \,{\mathbf{a}}({{{\mathbf{x}}}_{\tau }},\tau )d\tau + \int\limits_0^t \,B({{{\mathbf{x}}}_{\tau }},\tau )d{{{\mathbf{f}}}_{\tau }},\quad {{{\mathbf{x}}}_{0}} = {\mathbf{x}}(0,\omega ),\quad \omega \in \Omega ,$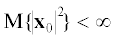

где ${{{\mathbf{x}}}_{t}} \in {{\Re }^{n}}$ – случайный процесс, являющийся решением СДУ Ито (1); второй интеграл в правой части (1) понимается как стохастический интеграл Итo; ${\mathbf{a}}:{{\Re }^{n}} \times [0,T] \to {{\Re }^{n}}$, $B:{{\Re }^{n}} \times [0,T] \to {{\Re }^{{n \times m}}}$ – измеримые при всех $({\mathbf{x}},t) \in {{\Re }^{n}} \times [0,T]$ функции, для которых существует правая часть (1) и которые удовлетворяют стандартным условиям существования и единственности сильного решения ${{{\mathbf{x}}}_{t}} \in {{\Re }^{n}}$ СДУ Ито (1) (см. [1]); ${{{\mathbf{x}}}_{0}}$ и ${{{\mathbf{f}}}_{t}} - {{{\mathbf{f}}}_{0}}$ ($t > 0$) предполагаются независимыми, причем ${{{\mathbf{x}}}_{0}} \in {{\Re }^{n}}$ есть ${{{\text{F}}}_{0}}$-измеримая случайная величина, для которой

; ${\text{M}}$ – оператор математического ожидания.

Важность проблемы численного интегрирования СДУ Ито обусловливается широким кругом их приложений, связанных как с построением адекватных математических моделей динамических систем различной физической природы, находящихся под воздействием случайных возмущений [2]–[9], так и с применением данных уравнений при решении ряда математических задач, среди которых отметим задачи фильтрации сигналов на фоне случайных помех, стохастического оптимального управления, стохастической устойчивости, оценивания параметров стохастических систем и др. [2], [3], [6].

Одним из перспективных подходов к численному интегрированию СДУ Ито является подход, основанный на стохастических аналогах формулы Тейлора (так называемых разложениях Тейлора–Ито и Тейлора–Стратоновича) для решений данных уравнений [2], [3], [7]–[12]. Указанный подход предполагает конечную дискретизацию временнй переменной и численное моделирование решений СДУ Ито в дискретные моменты времени с помощью упомянутых стохастических аналогов формулы Тейлора.

Следует отметить, что в разложения Тейлора–Ито и Тейлора–Стратоновича входят повторные стохастические интегралы (ПСИ) Ито и Стратоновича соответственно, численное моделирование которых на стадии реализации численных методов для СДУ Ито является одной из основных проблем.

В наиболее общей форме записи в настоящей работе указанные ПСИ Ито и Стратоновича имеют соответственно следующий вид:

(2)

$J{{[{{\psi }^{{(k)}}}]}_{{T,t}}} = \int\limits_t^T \,{{\psi }_{k}}({{t}_{k}}) \ldots \int\limits_t^{{{t}_{2}}} \,{{\psi }_{1}}({{t}_{1}})d{\mathbf{w}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{w}}_{{{{t}_{k}}}}^{{({{i}_{k}})}},$

(3)

$J{\text{*}}{{[{{\psi }^{{(k)}}}]}_{{T,t}}} = \int\limits_t^{ * T} \,{{\psi }_{k}}({{t}_{k}}) \ldots \int\limits_t^{ * {{t}_{2}}} \,{{\psi }_{1}}({{t}_{1}})d{\mathbf{w}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{w}}_{{{{t}_{k}}}}^{{({{i}_{k}})}},$

где через

$\int {\kern 1pt} \quad {\text{и }}\quad \int\limits_{}^* {\kern 1pt} $

обозначены интегралы Ито и Стратоновича соответственно; ${{\psi }_{l}}(\tau ),$ $l = 1,\; \ldots ,\;k$, – непрерывные на промежутке $[t,T]$ функции; ${{{\mathbf{w}}}_{\tau }}$ – случайный вектор с $m + 1$ компонентой вида ${\mathbf{w}}_{\tau }^{{(i)}} = {\mathbf{f}}_{\tau }^{{(i)}}$ при $i = 1,\; \ldots ,\;m$ и ${\mathbf{w}}_{\tau }^{{(0)}} = \tau ;$ величины ${{i}_{1}},\; \ldots ,\;{{i}_{k}}$ принимают значения $0,1,\; \ldots ,\;m$; ${\mathbf{f}}_{\tau }^{{(i)}},$ $i = 1,\; \ldots ,\;m$, – независимые стандартные винеровские процессы; $k$ – кратность ПСИ.

Отметим, что в разложения Тейлора–Ито и Тейлора–Стратоновича [2], [3], [7]–[13] входят ПСИ Ито и Стратоновича следующего более частного вида:

(4)

$J_{{({{\lambda }_{1}} \ldots {{\lambda }_{k}})T,t}}^{{({{i}_{1}} \ldots {{i}_{k}})}} = \int\limits_t^T \ldots \int\limits_t^{{{t}_{2}}} \,d{\mathbf{w}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{w}}_{{{{t}_{k}}}}^{{({{i}_{k}})}},$

(5)

$J_{{({{\lambda }_{1}} \ldots {{\lambda }_{k}})T,t}}^{{ * ({{i}_{1}} \ldots {{i}_{k}})}} = \int\limits_t^{ * T} \ldots \int\limits_t^{ * {{t}_{2}}} \,d{\mathbf{w}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{w}}_{{{{t}_{k}}}}^{{({{i}_{k}})}},$

где ${{\lambda }_{l}} = 0$ при ${{i}_{l}} = 0$ и ${{\lambda }_{l}} = 1$ при ${{i}_{l}} \ne 0,$ $l = 1,\; \ldots ,\;k$.

Среднеквадратическая аппроксимация ПСИ вида (2)–(5) с помощью так называемого кусочно-постоянного базиса (другими словами ПСИ аппроксимируется интегральными суммами) приводит к достаточно большим вычислительным затратам [14], поскольку подразумевает дробление промежутка интегрирования $[t,T]$ ПСИ ($T - t$ и без того является достаточно малой величиной, так как играет роль шага интегрирования в численных методах для СДУ Ито).

Более эффективные методы аппроксимации ПСИ используют ряды Фурье и не требуют дробления указанного промежутка $[t,T]$. Один из таких методов предложен в [10] и развит в [2], [3], [13]. Данный метод, нашедший широкое применение, основан на разложении Карунена-Лоэва процесса броуновского моста [10] по собственным функциям его ковариации, которые образуют полный ортонормированный тригонометрический базис в пространстве ${{L}_{2}}([t,T])$.

Отметим, что в [14] был предложен более общий метод (далее метод обобщенных кратных рядов Фурье) среднеквадратической аппроксимации ПСИ вида (2), который основан на обобщенных кратных рядах Фурье, сходящихся в среднем в пространстве ${{L}_{2}}({{[t,T]}^{k}})$, где ${{[t,T]}^{k}}$ – гиперкуб; $k$ – кратность ПСИ. Метод обобщенных кратных рядов Фурье был разработан в [15]–[19]. Одной из важных особенностей данного метода является возможность выбора различных полных ортонормированных базисов в пространстве ${{L}_{2}}([t,T])$ (метод [10] допускает использование только тригонометрического базиса).

В связи с этим можно поставить задачу о сравнении эффективности применения различных полных ортонормированных базисов в пространстве ${{L}_{2}}([t,T])$ к численному интегрированию СДУ Ито, решение которой и составляет предмет настоящей статьи. Некоторые исследования в данном направлении были проведены в [14]. В частности, в [14] на примере стохастических интегралов 2 кратности вида (4) было показано, что применение функций Хаара и Радемахера–Уолша является малоэффективным в силу сложности полученных разложений.

Настоящая статья организована следующим образом. В разд. 2 приводятся основные теоремы и формулы метода обобщенных кратных рядов Фурье. Разд. 3 и 4 посвящены сравнительному анализу эффективности применения полиномов Лежандра и тригонометрических функций к численной реализации сильного численного метода порядка точности 1.0 (метод Мильштейна [10]) для СДУ Ито и сильного численного метода порядка точности 1.5 для указанных уравнений соответственно (определение сильного численного метода будет дано в разд. 3). Разд. 5 содержит подобный анализ для одного ПСИ Стратоновича вида (5), который входит в сильный численный метод порядка точности 2.0 для СДУ Ито. В разд. 6 формулируются основные выводы, полученные на основе результатов настоящей статьи.

2. МЕТОД ОБОБЩЕННЫХ КРАТНЫХ РЯДОВ ФУРЬЕ

Сформулируем основные теоремы метода обобщенных кратных рядов Фурье.

Пусть ${{\psi }_{l}}(\tau ),$ $l = 1,\; \ldots ,\;k$, – непрерывные на промежутке $[t,T]$ неслучайные функции.

Определим следующую функцию на гиперкубе ${{[t,T]}^{k}}$:

(6)

$K({{t}_{1}},\; \ldots ,\;{{t}_{k}}) = \left\{ \begin{gathered} {{\psi }_{1}}({{t}_{1}}) \ldots {{\psi }_{k}}({{t}_{k}})\quad {\text{п р и }}\quad {{t}_{1}} < \ldots < {{t}_{k}};\quad {{t}_{1}},\; \ldots ,\;{{t}_{k}} \in [t,T];\quad k \geqslant 2, \hfill \\ 0\quad {\text{и н а ч е }} \hfill \\ \end{gathered} \right.$

и $K({{t}_{1}}) \equiv {{\psi }_{1}}({{t}_{1}})$; ${{t}_{1}} \in [t,T]$.

Пусть – полная ортонормированная система функций в пространстве ${{L}_{2}}([t,T])$.

Поскольку $K({{t}_{1}},\; \ldots ,\;{{t}_{k}}) \in {{L}_{2}}({{[t,T]}^{k}})$, то кратный ряд Фурье по системе функции $K({{t}_{1}},\; \ldots ,\;{{t}_{k}})$ сходится к этой функции в гиперкубе ${{[t,T]}^{k}}$ в смысле среднего квадратического [20]:

(7)

$\mathop {\lim }\limits_{{{p}_{1}}, \ldots ,{{p}_{k}} \to \infty } \left\| {K({{t}_{1}},\; \ldots ,\;{{t}_{k}}) - \sum\limits_{{{j}_{1}} = 0}^{{{p}_{1}}} \ldots \sum\limits_{{{j}_{k}} = 0}^{{{p}_{k}}} \,{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}{{\phi }_{{{{j}_{1}}}}}({{t}_{1}}) \ldots {{\phi }_{{{{j}_{k}}}}}({{t}_{k}})} \right\| = 0,$

где

(8)

$\begin{gathered} {{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}} = \int\limits_{{{{[t,T]}}^{k}}} K({{t}_{1}},\; \ldots ,\;{{t}_{k}}){{\phi }_{{{{j}_{1}}}}}({{t}_{1}}) \ldots {{\phi }_{{{{j}_{k}}}}}({{t}_{k}})d{{t}_{1}} \ldots d{{t}_{k}}, \\ \mathop {\left\| f \right\|}\nolimits^2 = \int\limits_{{{{[t,T]}}^{k}}} {{f}^{2}}({{t}_{1}},\; \ldots ,\;{{t}_{k}})d{{t}_{1}} \ldots d{{t}_{k}}. \\ \end{gathered} $

Рассмотрим разбиение отрезка $[t,T]$ такое, что

(9)

$t = {{\tau }_{0}} < \ldots < {{\tau }_{N}} = T,\quad {{\Delta }_{N}} = \mathop {\max }\limits_{0 \leqslant j \leqslant N - 1} \Delta {{\tau }_{j}} \to 0\quad {\text{п р и }}\quad N \to \infty ,\quad \Delta {{\tau }_{j}} = {{\tau }_{{j + 1}}} - {{\tau }_{j}}.$

Теорема 1 (см. [14]–[19]). Пусть ${{\psi }_{l}}(\tau ),$ $l = 1,\; \ldots ,\;k$, – непрерывные на промежутке $[t,T]$ функции, а 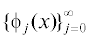– полная ортонормированная система непрерывных функций в пространстве ${{L}_{2}}([t,T])$. Тогда

(10)

$J{{[{{\psi }^{{\left( k \right)}}}]}_{{T,t}}} = \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{{{p}_{1}}, \ldots ,{{p}_{k}} \to \infty } \mathop \sum \limits_{{{j}_{1}} = 0}^{{{p}_{1}}} \ldots \mathop \sum \limits_{{{j}_{k}} = 0}^{{{p}_{k}}} \,{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}\left( {\zeta _{{{{j}_{1}}}}^{{\left( {{{i}_{1}}} \right)}} \ldots \zeta _{{{{j}_{k}}}}^{{\left( {{{i}_{k}}} \right)}} - \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{N \to \infty } \mathop \sum \limits_{\left( {{{l}_{1}}, \ldots ,{{l}_{k}}} \right) \in {{G}_{k}}} {{\phi }_{{{{j}_{1}}}}}({{t}_{1}}){\Delta }{\mathbf{w}}_{{{{\tau }_{{{{l}_{1}}}}}}}^{{\left( {{{i}_{1}}} \right)}} \ldots {{\phi }_{{{{j}_{k}}}}}({{t}_{k}}){\Delta }{\mathbf{w}}_{{{{\tau }_{{{{l}_{k}}}}}}}^{{\left( {{{i}_{k}}} \right)}}} \right),$

где $J{{[{{\psi }^{{(k)}}}]}_{{T,t}}}$ определен формулой (2);

${{{\text{L}}}_{k}} = \left\{ {({{l}_{1}},\; \ldots ,\;{{l}_{k}}):{{l}_{1}},\; \ldots ,\;{{l}_{k}} = 0,1,\; \ldots ,\;N - 1;\;{{l}_{g}} \ne {{l}_{r}}\;(g \ne r);\;g,r = 1,\; \ldots ,\;k} \right\};$

${\text{l}}.{\text{i}}.{\text{m}}.$ – предел в среднеквадратическом смысле; ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 0,1, \ldots ,\;m$;

(11)

$\zeta _{j}^{{(i)}} = \int\limits_t^T {{{\phi }_{j}}} (s)d{\mathbf{w}}_{s}^{{(i)}}$

суть стандартные гауссовские случайные величины при различных $i$ или $j$ (если $i \ne 0$); ${{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}$ – коэффициент Фурье вида (8); $\Delta {\mathbf{w}}_{{{{\tau }_{j}}}}^{{(i)}} = {\mathbf{w}}_{{{{\tau }_{{j + 1}}}}}^{{(i)}} - {\mathbf{w}}_{{{{\tau }_{j}}}}^{{(i)}},$ $i = 0,1,\; \ldots ,\;m$; $\mathop {\{ {{\tau }_{j}}\} }\nolimits_{j = 0}^N $ – разбиение промежутка $[t,T],$ которое удовлетворяет условию (9).

Преобразованные частные случаи формулы (10) при $k = 1,\; \ldots ,\;4$ имеют следующий вид [14]–[19]:

(12)

(13)

(14)

где ${{1}_{A}}$ – индикатор множества $A$.

В [15]–[19] теорема 1 адаптирована для ПСИ Стратоновича вида (3) кратностей 2–5.

Теорема 2 (см. [15]–[19]). Пусть – полная ортонормированная система полиномов Лежандра или система тригонометрических функций в пространстве ${{L}_{2}}([t,T]).$ При этом ${{\psi }_{2}}(s)$ – непрерывно дифференцируемая на промежутке $[t,T]$ функция, а ${{\psi }_{1}}(s)$, ${{\psi }_{3}}(s)$ – дважды непрерывно дифференцируемые на промежутке $[t,T]$ функции. Тогда

(15)

$J{\kern 1pt} {\text{*}}{{[{{\psi }^{{(k)}}}]}_{{T,t}}} = \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{p \to \infty } \sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^p {{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}} \zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}} \ldots \zeta _{{{{j}_{k}}}}^{{({{i}_{k}})}},$

где $k = 2,3,4,5$, причем ${{\psi }_{1}}(s),\; \ldots ,\;{{\psi }_{k}}(s) \equiv 1$ и ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 0,\;1,\; \ldots ,\;m$ в (15) при $k = 4,5$, а ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$ в (15) при $k = 2,3$; другие обозначения соответствуют обозначениям теоремы 1.

Интегралы $J{{[{{\psi }^{{(k)}}}]}_{{T,t}}}$ вида (2) допускают точное вычисление и эффективное оценивание среднеквадратической погрешности аппроксимации, что отражено в следующих двух теоремах.

Теорема 3 (см. [16]–[18]). Пусть выполнены условия теоремы 1 при ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$. Тогда

(16)

$\begin{gathered} {\text{M}}\left\{ {{{{(J{{{[{{\psi }^{{(k)}}}]}}_{{T,t}}} - J[{{\psi }^{{(k)}}}]_{{T,t}}^{q})}}^{2}}} \right\} = \int\limits_{{{{[t,T]}}^{k}}} {{K}^{2}}({{t}_{1}},\; \ldots ,\;{{t}_{k}})d{{t}_{1}} \ldots d{{t}_{k}} - \\ - \;\sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^q {{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}} {\text{M}}\left\{ {J{{{[{{\psi }^{{(k)}}}]}}_{{T,t}}}\sum\limits_{({{j}_{1}}, \ldots ,{{j}_{k}})} {\int\limits_t^T {{{\phi }_{{{{j}_{k}}}}}({{t}_{k}})} } \ldots \int\limits_t^{{{t}_{2}}} {{{\phi }_{{{{j}_{1}}}}}({{t}_{1}})} d{\mathbf{f}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{f}}_{{{{t}_{k}}}}^{{({{i}_{k}})}}} \right\}, \\ \end{gathered} $

где $J[{{\psi }^{{(k)}}}]_{{T,t}}^{q}$ – допредельное выражение в (10) при ${{p}_{1}} = \ldots = {{p}_{k}} = q$:

(17)

$J[{{\psi }^{{(k)}}}]_{{T,t}}^{q} = \sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^q {{{C}_{{{{j}_{{k \ldots }}}{{j}_{1}}}}}} \left( {\zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}} \ldots \zeta _{{{{j}_{k}}}}^{{({{i}_{k}})}} - \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{N \to \infty } \sum\limits_{({{l}_{1}}, \ldots ,{{l}_{k}}) \in {{G}_{k}}} {{{\phi }_{{{{j}_{1}}}}}} ({{t}_{1}})\Delta {\mathbf{w}}_{{{{\tau }_{{{{l}_{1}}}}}}}^{{({{i}_{1}})}} \ldots {{\phi }_{{{{j}_{k}}}}}({{t}_{k}})\Delta {\mathbf{w}}_{{{{\tau }_{{{{l}_{k}}}}}}}^{{({{i}_{k}})}}} \right),$

где

$\sum\limits_{({{j}_{1}}, \ldots ,{{j}_{k}})} $

есть сумма по всем возможным перестановкам $({{j}_{1}},\; \ldots ,\;{{j}_{k}})$, причем, если ${{j}_{r}}$ в перестановке $({{j}_{1}},\; \ldots ,\;{{j}_{k}})$ поменяется местами с ${{j}_{q}}$, то и ${{i}_{r}}$ поменяется местами с ${{i}_{q}}$ в перестановке $({{i}_{1}},\; \ldots ,\;{{i}_{k}})$; остальные обозначения такие же, как в теореме 1.

Теорема 4 (см. [16]–[18]). Пусть выполнены условия теоремы 1. Тогда справедлива оценка

${\text{M}}\left\{ {{{{(J{{{[{{\psi }^{{(k)}}}]}}_{{T,t}}} - J[{{\psi }^{{(k)}}}]_{{T,t}}^{q})}}^{2}}} \right\} \leqslant k!\left( {\int\limits_{{{{[t,T]}}^{k}}} {{{K}^{2}}} ({{t}_{1}},\; \ldots ,\;{{t}_{k}})d{{t}_{1}} \ldots d{{t}_{k}} - \sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^q {C_{{{{j}_{k}} \ldots {{j}_{1}}}}^{2}} } \right),$

где $T - t \in (0,1)$ при ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 0,1,\; \ldots ,\;m$ и $T - t \in (0, + \infty )$ при ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$; остальные обозначения такие же, как в теореме 1.

Отметим, что

${\text{M}}\left\{ {J{{{[{{\psi }^{{(k)}}}]}}_{{T,t}}}\int\limits_t^T {{{\phi }_{{{{j}_{k}}}}}} ({{t}_{k}}) \ldots \int\limits_t^{{{t}_{2}}} {{{\phi }_{{{{j}_{1}}}}}} ({{t}_{1}})d{\mathbf{f}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{f}}_{{{{t}_{k}}}}^{{({{i}_{k}})}}} \right\} = \int\limits_t^T {{{\psi }_{k}}} ({{t}_{k}}){{\phi }_{{{{j}_{k}}}}}({{t}_{k}}) \ldots \int\limits_t^{{{t}_{2}}} {{{\psi }_{1}}} ({{t}_{1}}){{\phi }_{{{{j}_{1}}}}}({{t}_{1}})d{{t}_{1}} \ldots d{{t}_{k}} = {{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}.$

Поэтому, в частности, в случае попарно различных чисел ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$ из теоремы 3 получим

(18)

${\text{M}}\left\{ {{{{(J{{{[{{\psi }^{{(k)}}}]}}_{{T,t}}} - J[{{\psi }^{{(k)}}}]_{{T,t}}^{q})}}^{2}}} \right\} = \int\limits_{{{{[t,T]}}^{k}}} {{{K}^{2}}} ({{t}_{1}},\; \ldots ,\;{{t}_{k}})d{{t}_{1}} \ldots d{{t}_{k}} - \sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^q {C_{{{{j}_{{k \ldots }}}{{j}_{1}}}}^{2}} .$

3. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ ПОЛИНОМОВ ЛЕЖАНДРА И ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ К АППРОКСИМАЦИИ ПСИ $J_{{(11)T,t}}^{{({{i}_{2}}{{i}_{1}})}}$

Применяя теорему 1 для случая тригонометрической системы функций, получаем (см. [14])

(19)

где ряд сходится в среднеквадратическом смысле; ${{i}_{1}},{{i}_{2}} = 1,\; \ldots ,\;m$;

$\zeta _{j}^{{(i)}} = \int\limits_t^T {{{\phi }_{j}}} (s)d{\mathbf{f}}_{s}^{{(i)}}$

суть независимые стандартные гауссовские случайные величины при различных $i$ или $j,$ причем

(20)

${{\phi }_{j}}({\mathbf{s}}) = \frac{1}{{\sqrt {T - t} }}\left\{ \begin{gathered} 1\quad {\text{п р и }}\quad j = 0, \hfill \\ \sqrt 2 \sin \tfrac{{2\pi r(s - t)}}{{T - t}}\quad {\text{п р и }}\quad j = 2r - 1, \hfill \\ \sqrt 2 \cos \tfrac{{2\pi r(s - t)}}{{T - t}}\quad {\text{п р и }}\quad j = 2r, \hfill \\ \end{gathered} \right.$

где $r = 1,2,\; \ldots \;.$

Кроме того

(21)

$J_{{(1)T,t}}^{{({{i}_{1}})}} = \sqrt {T - t} \zeta _{0}^{{({{i}_{1}})}},\quad {{i}_{1}} = 1,\; \ldots ,\;m.$

Отметим, что разложение (19) было впервые получено в [10] с помощью разложения процесса броуновского моста по собственным функциям его ковариации (см. разд. 1).

Рассмотрим разбиение отрезка $[0,T{\kern 1pt} {\text{*}}]$ такое, что $0 = {{s}_{0}} < \ldots < {{s}_{M}} = T{\kern 1pt} {\text{*}}$, ${{\Delta }_{M}} = \mathop {max}\limits_{0 \leqslant j \leqslant N - 1} ({{s}_{{j + 1}}} - {{s}_{j}})$.

Определение 1 (см. [2]). Будем говорить, что дискретная аппроксимация (численный метод) ${{{\mathbf{y}}}_{j}}$; $j = 0,1,\; \ldots ,\;M$, соответствующая максимальному шагу дискретизации ${{\Delta }_{M}}$, сходится сильно с порядком точности $\gamma > 0$ к случайному процессу ${{{\mathbf{x}}}_{t}}$, $t \in [0,T{\kern 1pt} {\text{*}}]$, если существуют постоянная $C > 0$, которая не зависит от ${{\Delta }_{M}}$ и $j$, $j = 0,1,\; \ldots ,\;M$, а также числа $\delta > 0$ такие, что

(22)

для всех ${{\Delta }_{M}} \in (0,\delta )$.

В ряде работ [9], [10] авторы рассматривают вместо сильной сходимости среднеквадратическую сходимость, что соответствует замене условия (22) на следующее условие:

(23)

$\mathop {({\text{M}}\{ {{{\left| {{{{\mathbf{x}}}_{j}} - {{{\mathbf{y}}}_{j}}} \right|}}^{2}}\} )}\nolimits^{1/2} \leqslant C{{({{\Delta }_{M}})}^{\gamma }},\quad j = 0,1,\; \ldots ,\;M.$

В (22) и (23) принято обозначение: ${{{\mathbf{x}}}_{{{{s}_{j}}}}}\;\mathop = \limits^{{\text{def}}} \;{{{\mathbf{x}}}_{j}}$, $j = 0,1, \ldots ,\;M$. Очевидно, что в силу неравенства Ляпунова из (23) следует (22).

Отметим, что для численной реализации явного сильного одношагового численного метода порядка точности 1.0 (метод Мильштейна [10]) для СДУ Ито (1), основанного на разложении Тейлора–Ито, достаточно взять следующие аппроксимации ПСИ:

(24)

$J_{{(1)T,t}}^{{({{i}_{1}})q}}\;\mathop = \limits^{{\text{def}}} \;J_{{(1)T,t}}^{{({{i}_{1}})}} = \sqrt {T - t} \zeta _{0}^{{({{i}_{1}})}},$

(25)

где ${{i}_{1}},{{i}_{2}} = 1,\; \ldots ,\;m$.

С помощью теоремы 3 получаем

(26)

${\text{M}}\left\{ {{{{(J_{{(11)T,t}}^{{({{i}_{2}}{{i}_{1}})}} - J_{{(11)T,t}}^{{({{i}_{2}}{{i}_{1}})q}})}}^{2}}} \right\} = \frac{{3{{{(T - t)}}^{2}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^q {\frac{1}{{{{r}^{2}}}}} } \right),\quad {{i}_{1}} \ne {{i}_{2}}.$

Нетрудно видеть, что метод из работы [10] или применение системы тригонометрических функций в теореме 1 имеют очевидный недостаток – разложения и среднеквадратические аппроксимации для ПСИ Ито, имеющих гауссовское распределение, получаются слишком сложными:

(27)

$J_{{(01)T,t}}^{{(0{{i}_{1}})}} = \frac{{\mathop {(T - t)}\nolimits^{3/2} }}{2}\left( {\zeta _{0}^{{({{i}_{1}})}} - \frac{{\sqrt 2 }}{\pi }\sum\limits_{r = 1}^\infty {\frac{1}{r}\zeta _{{2r - 1}}^{{({{i}_{1}})}}} } \right),$

$J_{{(001)T,t}}^{{(00{{i}_{1}})}} = \frac{{{{{(T - t)}}^{{5/2}}}}}{2}\left( {\frac{1}{3}\zeta _{0}^{{({{i}_{1}})}} + \frac{1}{{\sqrt 2 {{\pi }^{2}}}}\sum\limits_{r = 1}^\infty {\frac{1}{{{{r}^{2}}}}\zeta _{{2r}}^{{({{i}_{1}})}}} + \frac{1}{{\sqrt 2 \pi }}\sum\limits_{r = 1}^\infty {\frac{1}{r}\zeta _{{2r - 1}}^{{({{i}_{1}})}}} } \right),$

(28)

$J_{{(01)T,t}}^{{(0{{i}_{1}})q}} = \frac{{\mathop {(T - t)}\nolimits^{3/2} }}{2}\left( {\zeta _{0}^{{({{i}_{1}})}} - \frac{{\sqrt 2 }}{\pi }\sum\limits_{r = 1}^q {\frac{1}{r}\zeta _{{2r - 1}}^{{({{i}_{1}})}}} } \right),$

$J_{{(001)T,t}}^{{(00{{i}_{1}})q}} = \frac{{{{{(T - t)}}^{{5/2}}}}}{2}\left( {\frac{1}{3}\zeta _{0}^{{({{i}_{1}})}} + \frac{1}{{\sqrt 2 {{\pi }^{2}}}}\sum\limits_{r = 1}^q {\frac{1}{{{{r}^{2}}}}\zeta _{{2r}}^{{({{i}_{1}})}}} + \frac{1}{{\sqrt 2 \pi }}\sum\limits_{r = 1}^q {\frac{1}{r}\zeta _{{2r - 1}}^{{({{i}_{1}})}}} } \right),$

где сохранен смысл обозначений, входящих в (25).

Кроме того, в частности

(29)

${\text{M}}\left\{ {{{{(J_{{(01)T,t}}^{{(0{{i}_{1}})}} - J_{{(01)T,t}}^{{(0{{i}_{1}})q}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{3}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^q {\frac{1}{{{{r}^{2}}}}} } \right) \ne 0.$

С другой стороны, применение системы полиномов Лежандра в теореме 1 приводит к простым и широко известным формулам [2]:

(30)

$J_{{(01)T,t}}^{{(0{{i}_{1}})}} = \frac{{{{{(T - t)}}^{{3/2}}}}}{2}\left( {\zeta _{0}^{{({{i}_{1}})}} + \frac{1}{{\sqrt 3 }}\zeta _{1}^{{({{i}_{1}})}}} \right),$

(31)

$J_{{(001)T,t}}^{{(00{{i}_{1}})}} = \frac{{{{{(T - t)}}^{{5/2}}}}}{6}\left( {\zeta _{0}^{{({{i}_{1}})}} + \frac{{\sqrt 3 }}{2}\zeta _{1}^{{({{i}_{1}})}} + \frac{1}{{2\sqrt 5 }}\zeta _{2}^{{({{i}_{1}})}}} \right),$

где $\zeta _{0}^{{(i)}}$, $\zeta _{1}^{{(i)}}$, $\zeta _{2}^{{(i)}}$; $i = 1,\; \ldots ,\;m$ – независимые стандартные гауссовские величины.

В [10] было предложено скорректировать аппроксимации (25), (28) с целью уменьшения их среднеквадратических погрешностей следующим образом:

(32)

$J_{{(01)T,t}}^{{(0{{i}_{1}})q}} = \frac{{\mathop {(T - t)}\nolimits^{\tfrac{3}{2}} }}{2}\left( {\zeta _{0}^{{({{i}_{1}})}} - \frac{{\sqrt 2 }}{\pi }\left( {\sum\limits_{r = 1}^q {\frac{1}{r}\zeta _{{2r - 1}}^{{({{i}_{1}})}}} + \sqrt {{{\alpha }_{q}}} \xi _{q}^{{({{i}_{1}})}}} \right)} \right),$

(33)

где

(34)

$\xi _{q}^{{(i)}} = \frac{1}{{\sqrt {{{\alpha }_{q}}} }}\sum\limits_{r = q + 1}^\infty {\frac{1}{r}\zeta _{{2r - 1}}^{{(i)}}} ,\quad {{\alpha }_{q}} = \frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^q {\frac{1}{{{{r}^{2}}}}} ,$

а $\zeta _{0}^{{(i)}}$, $\zeta _{{2r}}^{{(i)}}$, $\zeta _{{2r - 1}}^{{(i)}}$, $\xi _{q}^{{(i)}}$; $r = 1,\; \ldots ,\;q$; $i = 1,\; \ldots ,\;m$, – независимые стандартные гауссовские случайные величины.

При этом для аппроксимаций (32) и (33) имеем (см. [10])

(35)

${\text{M}}\left\{ {{{{(J_{{(01)T,t}}^{{(0{{i}_{1}})}} - J_{{(01)T,t}}^{{(0{{i}_{1}})q}})}}^{2}}} \right\} = 0,$

(36)

${\text{M}}\left\{ {{{{(J_{{(11)T,t}}^{{({{i}_{2}}{{i}_{1}})}} - J_{{(11)T,t}}^{{({{i}_{2}}{{i}_{1}})q}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{2}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^q {\frac{1}{{{{r}^{2}}}}} } \right).$

Эта идея была развита в [2], [3], [13]. Например, аппроксимация $J_{{(001)T,t}}^{{(00{{i}_{1}})q}},$ соответствующая формулам (32), (33), имеет вид [2], [3], [13]

(37)

$J_{{(001)T,t}}^{{(00{{i}_{1}})q}} = \frac{{{{{(T - t)}}^{{5/2}}}}}{2}\left( {\frac{1}{3}\zeta _{0}^{{({{i}_{1}})}} + \frac{1}{{\sqrt 2 {{\pi }^{2}}}}\left( {\sum\limits_{r = 1}^q {\frac{1}{{{{r}^{2}}}}\zeta _{{2r}}^{{({{i}_{1}})}}} + \sqrt {{{\beta }_{q}}} \mu _{q}^{{({{i}_{1}})}}} \right) + \frac{1}{{\sqrt 2 \pi }}\left( {\sum\limits_{r = 1}^q {\frac{1}{r}\zeta _{{2r - 1}}^{{({{i}_{1}})}}} + \sqrt {{{\alpha }_{q}}} \xi _{q}^{{({{i}_{1}})}}} \right)} \right),$

${\text{M}}\left\{ {{{{(J_{{(001)T,t}}^{{(00{{i}_{1}})}} - J_{{(001)T,t}}^{{(00{{i}_{1}})q}})}}^{2}}} \right\} = 0,$

где $\xi _{q}^{{(i)}}$ и ${{\alpha }_{q}}$ определяются соотношениями (34),

(38)

$\mu _{q}^{{(i)}} = \frac{1}{{\sqrt {{{\beta }_{q}}} }}\sum\limits_{r = q + 1}^\infty {\frac{1}{{{{r}^{2}}}}\zeta _{{2r}}^{{(i)}}} ,\quad {{\beta }_{q}} = \frac{{{{\pi }^{4}}}}{{90}} - \sum\limits_{r = 1}^q {\frac{1}{{{{r}^{4}}}}} ,$

а $\zeta _{0}^{{(i)}}$, $\zeta _{{2r}}^{{(i)}}$, $\zeta _{{2r - 1}}^{{(i)}}$, $\xi _{q}^{{(i)}}$, $\mu _{q}^{{(i)}}$; $r = 1,\; \ldots ,\;q$; $i = 1,\; \ldots ,\;m$, – независимые стандартные гауссовские случайные величины.

Тем не менее разложения (32), (37) слишком сложны для аппроксимации двух гауссовских случайных величин $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(001)T,t}}^{{(00{{i}_{1}})}}$ (ср. с (30), (31)).

В разд. 4 мы увидим, что введение случайных величин $\xi _{q}^{{(i)}}$ и $\mu _{q}^{{(i)}}$ резко усложнит аппроксимацию ПСИ Ито $J_{{(111)T,t}}^{{({{i}_{3}}{{i}_{2}}{{i}_{1}})}}$, ${{i}_{1}},{{i}_{2}},{{i}_{3}} = 1,\; \ldots ,\;m$, которая необходима для численной реализации сильного численного метода порядка точности 1.5 для СДУ Ито (1), основанного на разложении Тейлора–Ито [2], [10]. Это связано с тем, что число $q$ в описанном подходе должно быть одним и тем же для всех ПСИ, входящих в рассматриваемый набор. Однако, очевидно, что из-за малости величины $T - t$ (она является шагом численного метода для СДУ Ито (1)), число $q$ для ПСИ Ито $J_{{(111)T,t}}^{{({{i}_{3}}{{i}_{2}}{{i}_{1}})}}$ могло бы быть выбрано существенно меньшим, чем в формуле (33). Эта особенность прослеживается также и для формул (32), (37).

Далее мы увидим, что применение полиномов Лежандра в теореме 1 позволяет выбирать различные числа $q$ для различных ПСИ Ито, причем некоторые из указанных чисел $q$ будут отличаться на порядки. Это обстоятельство позволяет резко снизить вычислительные затраты на аппроксимацию ПСИ Ито.

Отметим, что если отказаться от ввода случайных величин $\xi _{q}^{{(i)}}$ и $\mu _{q}^{{(i)}},$ то среднеквадратическая погрешность аппроксимации ПСИ Ито $J_{{(11)T,t}}^{{({{i}_{2}}{{i}_{1}})}}$ возрастет в 3 раза (см. (26)). Более того ПСИ Ито $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(001)T,t}}^{{(00{{i}_{1}})}}$ (имеющие гауссовское распределение) будут аппроксимироваться существенно хуже, чем при наличии случайных величин $\xi _{q}^{{(i)}}$ и $\mu _{q}^{{(i)}}.$

Используя теорему 1 и полную ортонормированную систему полиномов Лежандра в пространстве ${{L}_{2}}([t,T])$, получаем [14]–[19]

(39)

где ряд сходится в среднеквадратическом смысле; ${{i}_{1}},{{i}_{2}} = 1,\; \ldots ,\;m$;

$\zeta _{j}^{{(i)}} = \int\limits_t^T {{{\phi }_{j}}} (s)d{\mathbf{f}}_{s}^{{(i)}}$

суть стандартные гауссовские случайные величины при различных $i$ или $j$, где

(40)

${{\phi }_{j}}(x) = \sqrt {\frac{{2j + 1}}{{T - t}}} {{P}_{j}}\left( {\left( {x - \frac{{T + t}}{2}} \right)\frac{2}{{T - t}}} \right),\quad j = 0,1,2,\; \ldots ,$

а ${{P}_{j}}(x)$ – полином Лежандра.

С помощью теоремы 3 для случая ${{i}_{1}} \ne {{i}_{2}}$ нетрудно получить следующее равенство [14]–[19]:

(41)

${\text{M}}\left\{ {{{{(J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}} - J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})q}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{2}}}}{2}\left( {\frac{1}{2} - \sum\limits_{i = 1}^q {\frac{1}{{4{{i}^{2}} - 1}}} } \right),$

где

(42)

Сравним (42) с (33) и (41) с (36). Рассмотрим минимальные натуральные числа ${{q}_{{{\text{trig}}}}}$ и ${{q}_{{{\text{pol}}}}},$ которые удовлетворяют неравенствам

$\frac{{{{{(T - t)}}^{2}}}}{2}\left( {\frac{1}{2} - \sum\limits_{i = 1}^{{{q}_{{{\text{pol}}}}}} {\frac{1}{{4{{i}^{2}} - 1}}} } \right) \leqslant {{(T - t)}^{3}},$

$\frac{{{{{(T - t)}}^{2}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^{{{q}_{{{\text{trig}}}}}} {\frac{1}{{{{r}^{2}}}}} } \right) \leqslant {{(T - t)}^{3}}$

при различных значениях $T - t$ (см. табл. 1).

Таблица 1.

Числа ${{q}_{{{\text{trig}}}}}$, $q_{{{\text{trig}}}}^{ * }$, ${{q}_{{{\text{pol}}}}}$

$T - t$	${{2}^{{ - 5}}}$	${{2}^{{ - 6}}}$	${{2}^{{ - 7}}}$	${{2}^{{ - 8}}}$	${{2}^{{ - 9}}}$	${{2}^{{ - 10}}}$	${{2}^{{ - 11}}}$	${{2}^{{ - 12}}}$
${{q}_{{{\text{trig}}}}}$	3	4	7	14	27	53	105	209
$q_{{{\text{trig}}}}^{ * }$	6	11	20	40	79	157	312	624
${{q}_{{{\text{pol}}}}}$	5	9	17	33	65	129	257	513

На основании табл. 1 получаем следующее: ${{q}_{{{\text{pol}}}}}{\text{/}}{{q}_{{{\text{trig}}}}} \approx 1.67$, 2.22, 2.43, 2.36, 2.41, 2.43, 2.45, 2.45. С другой стороны, в (33) входят $4q + 4$ независимых стандартных гауссовских случайных величин, в то время как в (42) входят $2q + 2$ независимых стандартных гауссовских случайных величин. Кроме этого, (42) проще, чем (33). Таким образом, в данной ситуации мы можем говорить о примерно равных вычислительных затратах для формул (33) и (42).

Рассмотрим минимальные натуральные числа $q_{{{\text{trig}}}}^{ * }$, которые удовлетворяют неравенству

$\frac{{3{{{(T - t)}}^{2}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^{q_{{{\text{trig}}}}^{ * }} {\frac{1}{{{{r}^{2}}}}} } \right) \leqslant {{(T - t)}^{3}}$

при различных значениях $T - t$ (см. табл. 1).

В этой ситуации можно говорить о преимуществе полиномов Лежандра перед тригонометрическими функциями, поскольку $q_{{{\text{trig}}}}^{ * } > {{q}_{{{\text{pol}}}}}$ и (33) сложнее, чем (42).

4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ ПОЛИНОМОВ ЛЕЖАНДРА И ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ К АППРОКСИМАЦИИ ПСИ $J_{{(1)T,t}}^{{({{i}_{1}})}}$, $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$, $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(10)T,t}}^{{({{i}_{1}}0)}}$, $J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}}$

Хорошо известно (см. [2], [3], [7]–[10]), что для численной реализации сильных численных методов порядка точности 1.5 для СДУ Ито (1), основанных на разложении Тейлора–Ито, необходимо аппроксимировать следующий набор ПСИ Ито: $J_{{(1)T,t}}^{{({{i}_{1}})}}$, $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$, $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(10)T,t}}^{{({{i}_{1}}0)}}$, $J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}}$.

Предположим, что для построения аппроксимаций указанных ПСИ Ито используются теорема 1 и тригонометрическая система функций. В этом случае аппроксимации ПСИ Ито $J_{{(1)T,t}}^{{({{i}_{1}})}}$, $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$ определяются соответственно формулами (24), (32), (33). Аппроксимации ПСИ Ито $J_{{(10)T,t}}^{{({{i}_{1}}0)}}$, $J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}}$, соответствующие аппроксимациям (24), (32), (33), имеют соответственно следующий вид:

(43)

$J_{{(10)T,t}}^{{({{i}_{1}}0)q}} = \frac{{\mathop {(T - t)}\nolimits^{3/2} }}{2}\left( {\zeta _{0}^{{({{i}_{1}})}} + \frac{{\sqrt 2 }}{\pi }\left( {\sum\limits_{r = 1}^q {\frac{1}{r}\zeta _{{2r - 1}}^{{({{i}_{1}})}}} + \sqrt {{{\alpha }_{q}}} \xi _{q}^{{({{i}_{1}})}}} \right)} \right),$

$\begin{gathered} J_{{(111)T,t}}^{{({{i}_{3}}{{i}_{2}}{{i}_{1}})q}} = {{(T - t)}^{{3/2}}}\left( {\frac{1}{6}\zeta _{0}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}}} \right. + \frac{{\sqrt {{{\alpha }_{q}}} }}{{2\sqrt 2 \pi }}(\xi _{q}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}} - \xi _{q}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}}) + \\ + \;\frac{1}{{2\sqrt 2 {{\pi }^{2}}}}\sqrt {{{\beta }_{q}}} (\mu _{q}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}} - 2\mu _{q}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{3}})}} + \mu _{q}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}}) + \\ \end{gathered} $

(44)

$\begin{gathered} + \;\frac{1}{{2\sqrt 2 }}\sum\limits_{r = 1}^q {\left( {\frac{1}{{\pi r}}(\zeta _{{2r - 1}}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}} - \zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}}) + \frac{1}{{{{\pi }^{2}}{{r}^{2}}}}(\zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}} - 2\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{1}})}} + \zeta _{{2r}}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}})} \right)} + \\ + \;\sum\limits_{r = 1}^q {\left( {\frac{1}{{4\pi r}}} \right.(\zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}} - \zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}} - \zeta _{{2r - 1}}^{{({{i}_{2}})}}\zeta _{{2r}}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{1}})}} + \zeta _{{2r - 1}}^{{({{i}_{3}})}}\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}})} + \\ \end{gathered} $

$\begin{gathered} + \;\frac{1}{{8{{\pi }^{2}}{{r}^{2}}}}\left( {3\zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}} + \zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{3}})}} - 6\zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{2}})}} + } \right. \\ + \;\left. {\left. {3\zeta _{{2r - 1}}^{{({{i}_{2}})}}\zeta _{{2r - 1}}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{1}})}} - 2\zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{3}})}}\zeta _{0}^{{({{i}_{2}})}} + \zeta _{{2r}}^{{({{i}_{3}})}}\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}}} \right)} \right) + \left. {D_{{T,t}}^{{({{i}_{3}}{{i}_{2}}{{i}_{1}})q}}} \right), \\ \end{gathered} $

где

$ + \;\frac{1}{{4\sqrt 2 {{\pi }^{2}}}}\left( {\sum\limits_{r,m = 1}^q {\left( {\frac{2}{{rm}}} \right.} } \right.( - \zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2m - 1}}^{{({{i}_{2}})}}\zeta _{{2m}}^{{({{i}_{3}})}} + \zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{{2m - 1}}^{{({{i}_{3}})}} + \zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2m}}^{{({{i}_{2}})}}\zeta _{{2m - 1}}^{{({{i}_{3}})}} - \zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{2}})}}\zeta _{{2m - 1}}^{{({{i}_{3}})}}) + $

$ + \;\left. {\frac{1}{{m(r + m)}}( - \zeta _{{2(m + r)}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{{2m}}^{{({{i}_{3}})}} - \zeta _{{2(m + r) - 1}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{2}})}}\zeta _{{2m}}^{{({{i}_{3}})}} - \zeta _{{2(m + r) - 1}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{{2m - 1}}^{{({{i}_{3}})}} + \zeta _{{2(m + r)}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{2}})}}\zeta _{{2m - 1}}^{{({{i}_{3}})}})} \right) + $

$ + \;\sum\limits_{m = 1}^q {\sum\limits_{l = m + 1}^q {\left( {\frac{1}{{m(l - m)}}{\kern 1pt} } \right.} } (\zeta _{{2(l - m)}}^{{({{i}_{1}})}}\zeta _{{2l}}^{{({{i}_{2}})}}\zeta _{{2m}}^{{({{i}_{3}})}} + \zeta _{{2(l - m) - 1}}^{{({{i}_{1}})}}\zeta _{{2l - 1}}^{{({{i}_{2}})}}\zeta _{{2m}}^{{({{i}_{3}})}} - \zeta _{{2(l - m) - 1}}^{{({{i}_{1}})}}\zeta _{{2l}}^{{({{i}_{2}})}}\zeta _{{2m - 1}}^{{({{i}_{3}})}} + \zeta _{{2(l - m)}}^{{({{i}_{1}})}}\zeta _{{2l - 1}}^{{({{i}_{2}})}}\zeta _{{2m - 1}}^{{({{i}_{3}})}}) + $

$ + \;\left. {\left. {\frac{1}{{l(l - m)}}( - \zeta _{{2(l - m)}}^{{({{i}_{1}})}}\zeta _{{2m}}^{{({{i}_{2}})}}\zeta _{{2l}}^{{({{i}_{3}})}} + \zeta _{{2(l - m) - 1}}^{{({{i}_{1}})}}\zeta _{{2m - 1}}^{{({{i}_{2}})}}\zeta _{{2l}}^{{({{i}_{3}})}} - \zeta _{{2(l - m) - 1}}^{{({{i}_{1}})}}\zeta _{{2m}}^{{({{i}_{2}})}}\zeta _{{2l - 1}}^{{({{i}_{3}})}} - \zeta _{{2(l - m)}}^{{({{i}_{1}})}}\zeta _{{2m - 1}}^{{({{i}_{2}})}}\zeta _{{2l - 1}}^{{({{i}_{3}})}})} \right)} \right),$

где ${{i}_{1}} \ne {{i}_{2}}$, ${{i}_{1}} \ne {{i}_{3}}$, ${{i}_{2}} \ne {{i}_{3}}$; случайные величины $\xi _{q}^{{(i)}}$, $\mu _{q}^{{(i)}}$ и числа ${{\alpha }_{q}}$, ${{\beta }_{q}}$ определяются формулами (34), (38), причем $\zeta _{0}^{{(i)}}$, $\zeta _{{2r}}^{{(i)}}$, $\zeta _{{2r - 1}}^{{(i)}}$, $\xi _{q}^{{(i)}}$, $\mu _{q}^{{(i)}}$; $r = 1,\; \ldots ,\;q$; $i = 1,\; \ldots ,\;m$ – независимые стандартные гауссовские случайные величины.

Следует сказать несколько слов о формуле (44). Впервые аналог (44) был получен в [2], [3] с помощью разложения Карунена-Лоэва процесса броуновского моста по собственным функциям его ковариации, которое было предложено в [10]. Очевидно, что подстановка усеченных разложений компонент винеровского процесса, полученных с помощью указанного разложения процесса броуновского моста, в интеграл $J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}}$ с целью получения его разложения приводит к итеративной операции предельного перехода. Это означает, что авторы работ [2], [3] не вполне обоснованно выбирали в [2], [3] в аналоге формулы (44) верхний предел суммирования в двойной сумме равным $q$. С другой стороны, теорема 1 позволяет использовать только одну операцию предельного перехода при разложении ПСИ Ито вида (2). Это означает, что в теореме 1 можно положить, в частности, ${{p}_{1}} = \ldots = {{p}_{k}} = q$. В результате впервые обоснованно формула (44) была получена в [14]. Кроме этого, согласно теореме 2, левую часть (44) можно заменить на аппроксимацию ПСИ Стратоновича $J_{{(111)T,t}}^{{ * ({{i}_{3}}{{i}_{2}}{{i}_{1}})q}}$ и разложение (44) будет справедливо уже при всех возможных ${{i}_{1}},{{i}_{2}},{{i}_{3}} = 0,1,\; \ldots ,\;m$.

Среднеквадратические погрешности аппроксимаций (32), (33) ПСИ Ито $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$ определяются формулами (35), (36). Кроме того, для аппроксимаций (43), (44) имеем

(45)

${\text{M}}\left\{ {{{{(J_{{(10)T,t}}^{{({{i}_{1}}0)}} - J_{{(10)T,t}}^{{({{i}_{1}}0)q}})}}^{2}}} \right\} = 0,$

(46)

где ${{i}_{1}} \ne {{i}_{2}}$, ${{i}_{1}} \ne {{i}_{3}}$, ${{i}_{2}} \ne {{i}_{3}}$.

Отметим, что формула (46) была получена в [14] с помощью упрощенного варианта теоремы 3 в виде (18).

В табл. 2 приведено численное подтверждение правильности формулы (46) ($\varepsilon $ – правая часть (46)).

Таблица 2.

Численная проверка формулы (46)

$\varepsilon {\text{/}}{{(T - t)}^{3}}$	0.0459	0.0072	$7.5722 \times {{10}^{{ - 4}}}$	$7.5973 \times {{10}^{{ - 5}}}$	$7.5990 \times {{10}^{{ - 6}}}$
q	1	10	100	1000	10 000

Как уже отмечалось ранее, число $q$ должно быть одним и тем же в формулах (32), (33), (43), (44). Это является очевидным недостатком данного подхода, поскольку (как обсуждалось ранее) число $q$ в (44) могло бы быть выбрано существенно меньшим, чем в (33).

Рассмотрим теперь аппроксимации ПСИ Ито $J_{{(1)T,t}}^{{({{i}_{1}})}}$, $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$, $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(10)T,t}}^{{({{i}_{1}}0)}}$, $J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}},$ ${{i}_{1}},{{i}_{2}},{{i}_{3}} = 1,\; \ldots ,\;m$, с помощью теоремы 1 и системы полиномов Лежандра. В этом случае аппроксимации ПСИ Ито $J_{{(1)T,t}}^{{({{i}_{1}})}},$ $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$ $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$ определяются соответственно формулами (24), (30), (42). Аппроксимации ПСИ Ито $J_{{(10)T,t}}^{{({{i}_{1}}0)}}$, $J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}}$, соответствующие аппроксимациям (24), (30), (42), имеют соответственно следующий вид:

(47)

$J_{{(10)T,t}}^{{({{i}_{1}}0)}} = \frac{{{{{(T - t)}}^{{3/2}}}}}{2}\left( {\zeta _{0}^{{({{i}_{1}})}} - \frac{1}{{\sqrt 3 }}\zeta _{1}^{{({{i}_{1}})}}} \right),$

(48)

(49)

$\begin{gathered} J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{1}}{{i}_{1}})}} = \frac{1}{6}{{(T - t)}^{{3/2}}}({{(\zeta _{0}^{{({{i}_{1}})}})}^{3}} - 3\zeta _{0}^{{({{i}_{1}})}}), \\ {{C}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}} = \int\limits_t^T {{{\phi }_{{{{j}_{3}}}}}(z)} \int\limits_t^z {{{\phi }_{{{{j}_{2}}}}}(y)} \int\limits_t^y {{{\phi }_{{{{j}_{1}}}}}(x)} dxdydz = \frac{{\sqrt {(2{{j}_{1}} + 1)(2{{j}_{2}} + 1)(2{{j}_{3}} + 1)} }}{8}{{(T - t)}^{{3/2}}}{{{\bar {C}}}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}}, \\ \end{gathered} $

(50)

${{\bar {C}}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}} = \int\limits_{ - 1}^1 {{{P}_{{{{j}_{3}}}}}(z)} \int\limits_{ - 1}^z {{{P}_{{{{j}_{2}}}}}(y)} \int\limits_{ - 1}^y {{{P}_{{{{j}_{1}}}}}(x)} dxdydz,$

где ${{\phi }_{j}}(x)$ определяются формулой (40), а ${{P}_{i}}(x)$ – полиномы Лежандра, $i = 0,1,2,\; \ldots $ .

Среднеквадратическая погрешность аппроксимации (42) определяется формулой (41). С помощью теорем 3 и 4 получим

(51)

${\text{M}}\left\{ {{{{(J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}}){{q}_{1}}}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{3}}}}{6} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {C_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}^{2},} \quad {{i}_{1}} \ne {{i}_{2}},\;{{i}_{1}} \ne {{i}_{3}},\;{{i}_{2}} \ne {{i}_{3}},$

(52)

${\text{M}}\left\{ {{{{(J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}}){{q}_{1}}}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{3}}}}{6} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {C_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}^{2}} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {{{C}_{{{{j}_{2}}{{j}_{3}}{{j}_{1}}}}}} {{C}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}},\quad {{i}_{1}} \ne {{i}_{2}} = {{i}_{3}},$

(53)

${\text{M}}\left\{ {{{{(J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}}){{q}_{1}}}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{3}}}}{6} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {C_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}^{2}} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {{{C}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}}} {{C}_{{{{j}_{1}}{{j}_{2}}{{j}_{3}}}}},\quad {{i}_{1}} = {{i}_{3}} \ne {{i}_{2}},$

(54)

${\text{M}}\left\{ {{{{(J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}}){{q}_{1}}}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{3}}}}{6} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {C_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}^{2}} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {{{C}_{{{{j}_{3}}{{j}_{1}}{{j}_{2}}}}}} {{C}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}},\quad {{i}_{1}} = {{i}_{2}} \ne {{i}_{3}},$

(55)

${\text{M}}\left\{ {{{{(J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}}){{q}_{1}}}})}}^{2}}} \right\} \leqslant 6\left( {\frac{{{{{(T - t)}}^{3}}}}{6} - \sum\limits_{{{j}_{3}},{{j}_{2}},{{j}_{1}} = 0}^{{{q}_{1}}} {C_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}^{2}} } \right),$

где в (55) предполагается, что ${{i}_{1}},{{i}_{2}},{{i}_{3}} = 1,\; \ldots ,\;m$.

Сравним эффективность применения полиномов Лежандра и тригонометрических функций при аппроксимации ПСИ Ито $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$, $J_{{(111)T,t}}^{{({{i}_{1}}{{i}_{2}}{{i}_{3}})}}$.

Рассмотрим следующие условия:

(56)

$\frac{{{{{(T - t)}}^{2}}}}{2}\left( {\frac{1}{2} - \sum\limits_{i = 1}^q {\frac{1}{{4{{i}^{2}} - 1}}} } \right) \leqslant {{(T - t)}^{4}},$

(57)

${{(T - t)}^{3}}\left( {\frac{1}{6} - \sum\limits_{{{j}_{1}},{{j}_{2}},{{j}_{3}} = 0}^{{{q}_{1}}} {\frac{{{{{({{C}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}})}}^{2}}}}{{{{{(T - t)}}^{3}}}}} } \right) \leqslant {{(T - t)}^{4}},$

(58)

$\frac{{{{{(T - t)}}^{2}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^p {\frac{1}{{{{r}^{2}}}}} } \right) \leqslant {{(T - t)}^{4}},$

(59)

где ${{i}_{1}} \ne {{i}_{2}}$, ${{i}_{1}} \ne {{i}_{3}}$, ${{i}_{2}} \ne {{i}_{3}}$, а ${{C}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}}$ определяется формулой (49).

В табл. 3 и 4 приведены минимальные натуральные числа $q$, ${{q}_{1}}$, $p$, ${{p}_{1}}$, удовлетворяющие условиям (56)–(59) соответственно. Из табл. 3 следует, что ${{q}_{1}} \ll q$ (случай полиномов Лежандра). Как отмечалось ранее, мы не можем выбирать различные числа $p$, ${{p}_{1}}$ для случая тригонометрических функций, т.е. мы должны положить $q = p$ в (32), (33), (43), (44). Это ведет к большим вычислительным затратам (см. достаточно сложную формулу (44)). С другой стороны, мы можем выбрать различные числа $q$ в (32), (33), (43), (44), но при этом необходимо исключить случайные величины $\xi _{q}^{{(i)}},$ $\mu _{q}^{{(i)}}$ из (32), (33), (43), (44). Тогда по теореме 3 при ${{i}_{1}} \ne {{i}_{2}}$, ${{i}_{2}} \ne {{i}_{3}}$, ${{i}_{1}} \ne {{i}_{3}}$ получим

(60)

$\frac{{3{{{(T - t)}}^{2}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^{p*} {\frac{1}{{{{r}^{2}}}}} } \right) \leqslant {{(T - t)}^{4}},$

(61)

где левые части (60), (61) соответствуют (33), (44) без слагаемых, содержащих случайные величины $\xi _{q}^{{(i)}}$, $\mu _{q}^{{(i)}}$. В табл. 4 приведены минимальные натуральные числа $p{\text{*}}$, $p_{1}^{ * }$, которые удовлетворяют условиям (60), (61).

Таблица 3.

Числа q, q₁

$T - t$	0.08222	0.05020	0.02310	0.01956
q	19	51	235	328
q₁	1	2	5	6

Таблица 4.

Числа p, p₁, p, $p_{1}^{ }$

$T - t$	0.08222	0.05020	0.02310	0.01956
p	8	21	96	133
p₁	1	1	3	4
p*	23	61	286	398
$p_{1}^{ * }$	1	2	4	5

Следует отметить, что в данном случае среднеквадратическая ошибка аппроксимации ПСИ Ито $J_{{(11)T,t}}^{{({{i}_{1}}{{i}_{2}})}}$ становится в 3 раза больше (см. (60), (36)) и ПСИ Ито $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(10)T,t}}^{{({{i}_{1}}0)}}$ аппроксимируются хуже (см. (35), (45)):

(62)

${\text{M}}\left\{ {{{{(J_{{(01)T,t}}^{{(0{{i}_{1}})}} - J_{{(01)T,t}}^{{(0{{i}_{1}})q}})}}^{2}}} \right\} = {\text{M}}\left\{ {{{{(J_{{(10)T,t}}^{{({{i}_{1}}0)}} - J_{{(10)T,t}}^{{({{i}_{1}}0)q}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{3}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^q {\frac{1}{{{{r}^{2}}}}} } \right),$

где $J_{{(01)T,t}}^{{(0{{i}_{1}})q}}$, $J_{{(10)T,t}}^{{({{i}_{1}}0)q}}$ определяются равенством (28) и равенством (43) без учета случайной величины $\xi _{q}^{{(i)}}$.

Заметим, что числа ${{q}_{{{\text{trig}}}}}$ в табл. 1 соответствуют минимальным натуральным числам ${{q}_{{{\text{trig}}}}}$, которые удовлетворяют условию

(63)

$\frac{{{{{(T - t)}}^{3}}}}{{2{{\pi }^{2}}}}\left( {\frac{{{{\pi }^{2}}}}{6} - \sum\limits_{r = 1}^{{{q}_{{{\text{trig}}}}}} {\frac{1}{{{{r}^{2}}}}} } \right) \leqslant {{(T - t)}^{4}}.$

С другой стороны, правые части (30), (47) содержат только 2 независимые стандартные гауссовские случайные величины.

Таким образом, в рассмотренных ситуациях можно говорить о преимуществе полиномов Лежандра перед тригонометрическими функциями при аппроксимации ПСИ Ито.

В табл. 5 приведено численное подтверждение правильности формулы (61) ($\varepsilon $ – правая часть (61)).

Таблица 5.

Численная проверка формулы (61)

$\varepsilon {\text{/}}{{(T - t)}^{3}}$	0.0629	0.0097	0.0010	$1.0129 \times {{10}^{{ - 4}}}$	$1.0132 \times {{10}^{{ - 5}}}$
q	1	10	100	1000	10 000

5. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ ПОЛИНОМОВ ЛЕЖАНДРА И ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ К АППРОКСИМАЦИИ ПСИ СТРАТОНОВИЧА $J_{{(011)T,t}}^{{ * (0{{i}_{1}}{{i}_{2}})}}$

Сравним вычислительные затраты на аппроксимацию ПСИ Стратоновича $J_{{(011)T,t}}^{{ * (0{{i}_{1}}{{i}_{2}})}},$ ${{i}_{1}},{{i}_{2}} = 1,\; \ldots ,\;m$, при использовании полиномов Лежандра и тригонометрических функций в рамках метода обобщенных кратных рядов Фурье. Указанный ПСИ Стратоновича входит в разложение Тейлора–Стратоновича [2], [12], [13] и встречается при численной реализации сильного численного метода порядка точности 2.0 для СДУ Ито (1), основанного на разложении Тейлора–Стратоновича.

Используя теорему 2 для случая тригонометрических функций, получаем [15]–[18]:

$J_{{(011)T,t}}^{{ * (0{{i}_{2}}{{i}_{1}})q}} = {{(T - t)}^{2}}\left( {\frac{1}{6}\zeta _{0}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}}} \right. + \frac{1}{{2\sqrt 2 \pi }}\sqrt {{{\alpha }_{q}}} \xi _{q}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}} + \frac{1}{{2\sqrt 2 {{\pi }^{2}}}}\sqrt {{{\beta }_{q}}} (\mu _{q}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}} - 2\mu _{q}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}}) + $

(64)

$ + \;\frac{1}{{2\sqrt 2 }}\sum\limits_{r = 1}^q {\left( {\frac{1}{{\pi r}}\zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}} + \frac{1}{{{{\pi }^{2}}{{r}^{2}}}}(\zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{0}^{{({{i}_{2}})}} - 2\zeta _{{2r}}^{{({{i}_{2}})}}\zeta _{0}^{{({{i}_{1}})}})} \right)} + \frac{1}{{2{{\pi }^{2}}}}\mathop {\sum\limits_{r,l = 1}^q {\frac{1}{{{{r}^{2}} - {{l}^{2}}}}} }\limits_{r \ne l} \left( {\zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2l}}^{{({{i}_{2}})}} + \frac{r}{l}\zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2l - 1}}^{{({{i}_{2}})}}} \right) + $

$ + \;\sum\limits_{r = 1}^q {\left( {\frac{1}{{4\pi r}}(\zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{2}})}} - \zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{2}})}}) + \left. {\frac{1}{{8{{\pi }^{2}}{{r}^{2}}}}(3\zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2r - 1}}^{{({{i}_{2}})}} + \zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2r}}^{{({{i}_{2}})}})} \right)} \right)} .$

Для случая ${{i}_{1}} \ne {{i}_{2}}$ с помощью теоремы 3 находим [15]–[18]:

(65)

Аналоги формул (64), (65) для случая полиномов Лежандра имеют следующий вид [15]–[18]:

$\begin{gathered} J_{{(011)T,t}}^{{ * (0{{i}_{1}}{{i}_{2}})q}} = \frac{{{{{(T - t)}}^{2}}}}{4}\left( {\left( {\zeta _{0}^{{({{i}_{1}})}} + \frac{1}{{\sqrt 3 }}\zeta _{1}^{{({{i}_{1}})}}} \right)\zeta _{0}^{{({{i}_{2}})}} + \sum\limits_{i = 1}^q {\frac{1}{{\sqrt {4{{i}^{2}} - 1} }}(\zeta _{{i - 1}}^{{({{i}_{1}})}}\zeta _{i}^{{({{i}_{2}})}} - \zeta _{i}^{{({{i}_{1}})}}\zeta _{{i - 1}}^{{({{i}_{2}})}})} } \right. + \\ + \;\left. {\sum\limits_{i = 0}^q {\left( {\frac{{(i + 1)\zeta _{{i + 2}}^{{({{i}_{2}})}}\zeta _{i}^{{({{i}_{1}})}} - (i + 2)\zeta _{i}^{{({{i}_{2}})}}\zeta _{{i + 2}}^{{({{i}_{1}})}}}}{{\sqrt {(2i + 1)(2i + 5)} (2i + 3)}} + \frac{{\zeta _{i}^{{({{i}_{1}})}}\zeta _{i}^{{({{i}_{2}})}}}}{{(2i - 1)(2i + 3)}}} \right)} } \right), \\ \end{gathered} $

$\begin{gathered} {\text{M}}\left\{ {{{{(J_{{(011)T,t}}^{{ * (0{{i}_{1}}{{i}_{2}})}} - J_{{(011)T,t}}^{{ * (0{{i}_{1}}{{i}_{2}})q}})}}^{2}}} \right\} = \frac{{{{{(T - t)}}^{4}}}}{{16}}\left( {\frac{5}{9} - 2\sum\limits_{i = 2}^q {\frac{1}{{4{{i}^{2}} - 1}}} - } \right. \\ - \;\sum\limits_{i = 1}^q {\frac{1}{{{{{(2i - 1)}}^{2}}{{{(2i + 3)}}^{2}}}}} - \left. {\sum\limits_{i = 0}^q {\frac{{{{{(i + 2)}}^{2}} + {{{(i + 1)}}^{2}}}}{{(2i + 1)(2i + 5){{{(2i + 3)}}^{2}}}}} } \right), \\ \end{gathered} $

где в (67) полагается ${{i}_{1}} \ne {{i}_{2}}$.

В табл. 6 и 7 приведена численная проверка правильности формул (65) и (67) ($\varepsilon $ – правая часть (65), (67)).

Таблица 6.

Численная проверка формулы (65)

$4\varepsilon {\text{/}}{{(T - t)}^{4}}$	0.0540	0.0082	$8.4261 \times {{10}^{{ - 4}}}$	$8.4429 \times {{10}^{{ - 5}}}$	$8.4435 \times {{10}^{{ - 6}}}$
q	1	10	100	1000	10 000

Таблица 7.

Численная проверка формулы (67)

$16\varepsilon {\text{/}}{{(T - t)}^{4}}$	0.3797	0.0581	0.0062	$6.2450 \times {{10}^{{ - 4}}}$	$6.2495 \times {{10}^{{ - 5}}}$
q	1	10	100	1000	10 000

Сравним (64) и (66). Формула (64) существенно сложнее, чем (66) даже при одинаковых $q$, поскольку в (64) входит двойная сумма вида

$\frac{1}{{2{{\pi }^{2}}}}\mathop {\sum\limits_{r,l = 1}^q {\frac{1}{{{{r}^{2}} - {{l}^{2}}}}} }\limits_{r \ne l} \left( {\zeta _{{2r}}^{{({{i}_{1}})}}\zeta _{{2l}}^{{({{i}_{2}})}} + \frac{r}{l}\zeta _{{2r - 1}}^{{({{i}_{1}})}}\zeta _{{2l - 1}}^{{({{i}_{2}})}}} \right).$

Как отмечалось ранее, число $q$ в (64) должно быть равно числу $q$, входящему в формулу (33) (${{i}_{1}} \ne {{i}_{2}}$), т.е. должно быть существенно бльшим, чем число $q$ из формулы (66). В результате мы получаем очевидное преимущество формулы (66) по вычислительным затратам. Ранее также отмечалось, что можно отказаться от ввода случайных величин $\xi _{q}^{{(i)}}$ и $\mu _{q}^{{(i)}}$. При этом появляется возможность выбора различных чисел $q$ для различных ПСИ. В результате число $q$ в (64) может быть выбрано меньшим, но тогда среднеквадратическая погрешность аппроксимации ПСИ $J_{{(11)T,t}}^{{ * ({{i}_{2}}{{i}_{1}})}},$ ${{i}_{1}} \ne {{i}_{2}}$, будет в 3 раза больше (см. (26)). Более того, ПСИ $J_{{(01)T,t}}^{{ * (0{{i}_{1}})}}$, $J_{{(10)T,t}}^{{ * ({{i}_{1}}0)}}$, $J_{{(001)T,t}}^{{ * (00{{i}_{1}})}}$ (имеющие гауссовское распределение) будут аппроксимироваться с помощью суммы достаточно большого числа независимых стандартных гауссовских случайных величин (см. (62), (63) и минимальные числа ${{q}_{{{\text{trig}}}}}$ в табл. 1, которые соответствуют (63)). Для случая же полиномов Лежандра для аппроксимации ПСИ $J_{{(01)T,t}}^{{ * (0{{i}_{1}})}}$, $J_{{(10)T,t}}^{{ * ({{i}_{1}}0)}}$, $J_{{(001)T,t}}^{{ * (00{{i}_{1}})}}$ потребуется всего лишь 3 независимые стандартные гауссовские случайные величины (см. (30), (31), (47)). Таким образом, мы снова можем говорить о преимуществе полиномов Лежандра в рамках рассматриваемой проблемы.

6. ЗАКЛЮЧЕНИЕ

На основании результатов настоящей статьи можно сделать следующие основные выводы.

1. Можно говорить о примерно одинаковых вычислительных затратах для формул (33) и (42). Это означает, что вычислительные затраты на реализацию метода Мильштейна [10] (явный одношаговый сильный численный метод порядка точности 1.0 для СДУ Ито) для случая полиномов Лежандра и случая тригонометрических функций являются приблизительно одинаковыми. Такой же вывод будет верен для сильных неявных и не обязательно одношаговых численных методов (в том числе методов типа Рунге–Кутты) порядка точности 1.0 для СДУ Ито, основанных на разложениях Тейлора–Ито или Тейлора–Стратоновича, поскольку указанные методы, как правило, используют тот же набор ПСИ, что и метод Мильштейна.

2. Если мы не вводим случайные величины $\xi _{q}^{{(i)}}$ (см. (33)), то среднеквадратическая погрешность аппроксимации ПСИ $J_{{(11)T,t}}^{{({{i}_{2}}{{i}_{1}})}}$ будет в 3 раза больше (см. (26)). В этой ситуации будет наблюдаться преимущество по вычислительным затратам полиномов Лежандра по сравнению с тригонометрическими функциями при численной реализации метода Мильштейна. Более того, ПСИ $J_{{(01)T,t}}^{{(0{{i}_{1}})}}$, $J_{{(10)T,t}}^{{({{i}_{1}}0)}}$, $J_{{(001)T,t}}^{{(00{{i}_{1}})}}$ (с гауссовским распределением), необходимые для построения сильных численных методов более высоких порядков точности, чем 1.0 для СДУ Ито будут аппроксимироваться с помощью сумм достаточно большого числа независимых стандартных гауссовских случайных величин. Для случая полиномов Лежандра при аппроксимации указанных ПСИ потребуется всего лишь 3 независимые стандартные гауссовские случайные величины.

3. Если говорить о сильных численных методах порядка точности 1.5 для СДУ Ито, построенных на основе разложений Тейлора–Ито или Тейлора–Стратоновича, то числа $q$ и ${{q}_{1}}$ (см. (42), (48)) различны, причем ${{q}_{1}} \ll q$ (случай полиномов Лежандра). Число $q$ должно быть одинаковым в формулах (32), (33), (43), (44) (случай тригонометрических функций). Это ведет к существенным вычислительным затратам (см. достаточно сложную формулу (44)). С другой стороны, можно выбирать различные числа $q$ в (32), (33), (43), (44), но тогда придется исключить случайные величины $\xi _{q}^{{(i)}}$, $\mu _{q}^{{(i)}}$ из указанных формул. Это приведет к существенному увеличению вычислительных затрат по причинам, описанным в выводе 2. Очевидно, что отмеченные особенности сохранятся применительно к сильным численным методам порядка точности $\gamma $ ($\gamma = 2.0,\;2.5,\; \ldots $) для СДУ Ито. Таким образом, в данном случае наблюдается существенное преимущество системы полиномов Лежандра перед системой тригонометрических функций по вычислительным затратам на реализацию отмеченных численных методов для СДУ Ито.

Список литературы

Гихман И.И., Скороход А.В. Стохастические дифференциальные уравнения и их приложения. Киев: Наук. думка, 1982. 612 с.
Kloeden P.E., Platen E. Numerical solution of stochastic differential equations. Berlin: Springer, 1992. 632 p.
Kloeden P.E., Platen E., Schurz H. Numerical solution of SDE through computer experiments. Berlin: Springer, 1994. 292 p.
Arato M. Linear stochastic systems with constant coefficients. A statistical approach. Berlin, Heidelberg, N.Y.: Springer, 1982. 289 p.
Ширяев А.Н. Основы стохастической финансовой математики. Т. 2. М.: Фазис, 1998. 544 с.
Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов: Нелинейная фильтрация и смежные вопросы. М.: Наука, 1974. 696 с.
Platen E., Bruti-Liberati N. Numerical solution of stochastic differential equations with jumps in finance. Berlin, Heidelberg: Springer, 2010. 868 p.
Han X., Kloeden P.E. Random ordinary differential equations and their numerical solution. Singapore: Springer, 2017. 250 p.
Milstein G.N., Tretyakov M.V. Stochastic numerics for mathematical physics. Berlin: Springer, 2004. 616 p.
Мильштейн Г.Н. Численное интегрирование стохастических дифференциальных уравнений. Свердловск: Изд-во Уральск. ун-та, 1988. 224 с.
Platen E., Wagner W. On a Taylor formula for a class of Ito processes // Probab. Math. Statist. 1982. № 3. P. 37–51.
Kloeden P.E., Platen E. The Stratonovich and Ito-Taylor expansions // Math. Nachr. 1991. V. 151. P. 33–50.
Kloeden P.E., Platen E., Wright I.W. The approximation of multiple stochastic integrals // Stoch. Anal. Appl. 1992. V. 10. № 4. P. 431–441.
Кузнецов Д.Ф. Численное интегрирование стохастических дифференциальных уравнений. 2. СПб: Изд-во Политехн. ун-та, 2006. 764 с.
Kuznetsov D.F. Strong Approximation of Multiple Ito and Stratonovich Stochastic Integrals: Multiple Fourier Series Approach. St.-Petersburg: Polytechnical University Publishing House, 2011. 284 p.
Кузнецов Д.Ф. Стохастические дифференциальные уравнения: теория и практика численного решения. С программами в среде MATLAB, 6-е изд. Электр. Журн. Диффер. уравн. и процессы управл. 2018. № 4. 1073 с. Доступно по ссылке: http://diffjournal.spbu.ru/EN/numbers/2018.4/article.2.1.html
Кузнецов Д.Ф. К Численному моделированию многомерных динамических систем при случайных возмущениях с порядками сильной сходимости 1.5 и 2.0 // Автомат. и телемехан. 2018. № 7. С. 80–98.
Кузнецов Д.Ф. Разработка и применение метода Фурье к численному интегрированию стохастических дифференциальных уравнений Ито // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 7. С. 1109–1122.
Кузнецов Д.Ф. К численному моделированию многомерных динамических систем при случайных возмущениях с порядком сильной сходимости 2.5 // Автомат. и телемехан. 2019. № 5. С. 99–117.
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1976. 543 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал