Журнал вычислительной математики и математической физики, 2020, T. 60, № 10, стр. 1711-1720

ВВЕДЕНИЕ

В работе рассматривается задача Дирихле для полупространства ${\text{\{ }}(x,y) \in {{\mathbb{R}}^{d}} \times {{\mathbb{R}}_{ + }}{\text{\} }}$ и ставится вопрос о наилучшем восстановлении решения этой задачи на гиперплоскости, “параллельной” ${{\mathbb{R}}^{d}}$ по неточным измерениям данного решения на конечном числе других гиперплоскостей, параллельных исходной. Найдены явные выражения для оптимальных методов восстановления и вычислена соответствующая погрешность восстановления. Следует отметить, что оптимальные методы линейны и используют не всю доступную информацию об измерениях решения задачи Дирихле, а лишь информацию о его измерениях на не более, чем двух гиперплоскостях.

Задача, рассматриваемая в данной работе, относится к тематике, связанной с вопросами оптимального восстановления значений линейных функционалов и операторов на множествах элементов, заданных неточно. Эта проблематика возникла во второй половине прошлого века и была инициирована, в идейном плане, работами К. Шеннона и А.Н. Колмогорова. Первая постановка задачи оптимального восстановления линейного функционала на классе элементов, известных приближенно, принадлежит А.С. Смоляку [1]. В дальнейшем эта тематика активно развивалась. Начальный этап ее развития отражен в обзорах [2]–[4]. Впоследствии основное внимание уделялось задачам восстановления функций и их производных по неточно заданному спектру и задачам оптимального восстановления решений уравнений математической физики (см., например, [5]–[13]). Настоящая работа примыкает ко второму циклу задач.

ПОСТАНОВКА ЗАДАЧИ И ФОРМУЛИРОВКА ОСНОВНОГО РЕЗУЛЬТАТА

Рассмотрим задачу Дирихле:

где $\Delta $ – оператор Лапласа в ${{\mathbb{R}}^{{d + 1}}}$и $f( \cdot ) \in {{L}_{2}}({{\mathbb{R}}^{d}})$, заключающуюся в нахождении гармонической функции $u( \cdot , \cdot )$ в полупространстве $\{ (x,y) \in {{\mathbb{R}}^{{d + 1}}}:y > 0\} $ такой, что $u( \cdot ,y) \in {{L}_{2}}({{\mathbb{R}}^{d}})$ для любого $y > 0$, $su{{p}_{{y > 0}}}{{\left\| {u( \cdot ,y)} \right\|}_{{{{L}_{2}}({{\mathbb{R}}^{d}})}}} < \infty $ и $u( \cdot ,y) \to f( \cdot )$ при $y \to 0$ в метрике ${{L}_{2}}({{\mathbb{R}}^{d}})$.

В этом случае решение данной задачи единственно и задается интегралом Пуассона (см., например, [14])

где $\left| {\, \cdot \,} \right|$ обозначает евклидову норму в ${{\mathbb{R}}^{d}}$.

Мы ставим следующую задачу. Пусть заданы числа ${{\delta }_{i}} > 0$, $i = 1,\; \ldots ,\;n$, и пусть приближенно известны значения функции $u( \cdot , \cdot )$ на $n$ гиперплоскостях: $y = {{y}_{i}}$, $i = 1,\; \ldots ,\;n$, где $0 \leqslant {{y}_{1}} < {{y}_{2}}$ < ... < y_n. Точнее говоря, известны функции ${{z}_{i}}( \cdot ) \in {{L}_{2}}({{\mathbb{R}}^{d}})$ такие, что

По этой информации мы хотим восстановить (по возможности, наилучшим образом) решение задачи Дирихле на гиперплоскости $y = Y$, $Y > 0$, в метрике ${{L}_{2}}({{\mathbb{R}}^{d}})$.

Поступаем следующим образом. Любое отображение $\varphi $: ${{({{L}_{2}}({{\mathbb{R}}^{d}}))}^{n}}\, = \,{{L}_{2}}({{\mathbb{R}}^{d}})\, \times \, \ldots \, \times \,{{L}_{2}}({{\mathbb{R}}^{d}})\, \to \,{{L}_{2}}({{\mathbb{R}}^{d}})$ объявляется методом восстановления. Погрешностью метода $\varphi $ назовем величину

где $\bar {z}( \cdot ) = ({{z}_{1}}( \cdot ),\; \ldots ,\;{{z}_{n}}( \cdot ))$ (наборы $({{y}_{1}},\; \ldots ,\;{{y}_{n}})$ и $({{\delta }_{1}},\; \ldots ,\;{{\delta }_{n}})$ фиксированы и поэтому зависимость от них не отмечаем).

Нас интересует наименьшая возможная погрешность, т.е. величина

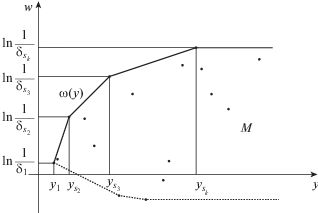
где нижняя грань берется по всем отображениям $\varphi $: ${{({{L}_{2}}({{\mathbb{R}}^{d}}))}^{n}} \to {{L}_{2}}({{\mathbb{R}}^{d}})$, которую назовем погрешностью оптимального восстановления, и те методы, на которых эта нижняя грань достигается, т.е. методы $\hat {\varphi }$, для которых Такие методы назовем оптимальными методами восстановления.

Перед формулировкой теоремы приведем некоторые определения. На двумерной плоскости $(y,t)$ рассмотрим множество

представляющее собой алгебраическую сумму выпуклой оболочки $n$ точек и полупрямой (см. фиг. 1).

Определим функцию $\omega ( \cdot )$ на $[0, + \infty )$ по правилу: $\omega (y) = max{\text{\{ }}t \in \mathbb{R}:(y,t) \in M{\text{\} }}$, причем $\omega (y) = - \infty $, если множество в фигурных скобках пусто. Ясно, что $\omega ( \cdot )$ – вогнутая ломаная на $[{{y}_{1}}, + \infty )$. Пусть ${{y}_{{{{s}_{1}}}}} < \; \ldots \; < {{y}_{{{{s}_{k}}}}}$ – ее точка излома (считаем, что ${{y}_{1}}$ – также точка излома, т.е. ${{y}_{1}} = {{y}_{{{{s}_{1}}}}}$).

Если $Y \in ({{y}_{{{{s}_{j}}}}},{{y}_{{{{s}_{{j + 1}}}}}})$, $1 \leqslant j \leqslant k - 1$, то положим

Легко видеть, что это положительные числа, причем ${{\hat {\lambda }}_{{{{s}_{j}}}}} < 1$.

Для данного $Y$ определим еще положительное число

Пусть $F$ – преобразование Фурье в ${{L}_{2}}({{\mathbb{R}}^{d}})$. Если $f( \cdot ) \in {{L}_{2}}({{\mathbb{R}}^{d}})$, то $F[f]( \cdot )$ обозначает образ функции $f( \cdot )$ при действии преобразования Фурье.

Для $r > 0$ положим $B(r) = {\text{\{ }}\xi \in {{\mathbb{R}}^{d}}:\left| \xi \right| \leqslant r{\text{\} }}$ (замкнутый шар в ${{\mathbb{R}}^{d}}$ с центром в нуле радиуса $r$).

Теорема. Для любого $Y \geqslant 0$ справедливо равенство

Если $Y \in ({{y}_{{{{s}_{j}}}}},{{y}_{{{{s}_{{j + 1}}}}}})$, $1 \leqslant j \leqslant k - 1$, то множество измеримых функций $a( \cdot )$ на ${{\mathbb{R}}^{d}}$ таких, чтодля п.в. $\xi \in B({{\gamma }_{j}})$ и $a(\xi ) = 0$, когда $\xi \notin B({{\gamma }_{j}})$, не пусто. Для каждой такой функции $a( \cdot )$ метод ${{\hat {\varphi }}_{a}}$, определенный формулойгде $F[{{K}_{{aj}}}](\xi ) = {{e}^{{ - (Y - {{y}_{{{{s}_{j}}}}})\left| \xi \right|}}} - a(\xi ){{e}^{{ - ({{y}_{{{{s}_{{j + 1}}}}}} - {{y}_{{{{s}_{j}}}}})\left| \xi \right|}}}$ и $F[{{K}_{a}}](\xi ) = a(\xi )$ для п.в. $\xi \in {{\mathbb{R}}^{d}}$, является оптимальным.

Если $Y = {{y}_{{{{s}_{j}}}}}$, $1 \leqslant j \leqslant k$, то метод $\hat {\varphi }$, определенный формулой $\hat {\varphi }({{z}_{1}}( \cdot ),\; \ldots ,\;{{z}_{n}}( \cdot ))( \cdot ) = {{z}_{{{{s}_{j}}}}}( \cdot )$, является оптимальным.

Если $Y > {{y}_{{{{s}_{k}}}}}$, то метод $\hat {\varphi }$, определенный формулой $\hat {\varphi }({{z}_{1}}( \cdot ),\; \ldots ,\;{{z}_{n}}( \cdot ))( \cdot ) = (K * {{z}_{{{{s}_{k}}}}})( \cdot )$, где F[K](ξ) = = ${{e}^{{ - (Y - {{y}_{{{{s}_{k}}}}})|\xi |}}}$ для п.в. $\xi \in {{\mathbb{R}}^{d}}$, является оптимальным.

Сделаем некоторые замечания по поводу сформулированной теоремы.

1. Если ${{y}_{1}} > 0$ и $0 \leqslant Y < {{y}_{1}}$, то $\omega (Y) = - \infty $ и тем самым $E(Y) = + \infty $, т.е. прошлое нельзя восстановить по неточному настоящему. В этом случае любой метод можно считать оптимальным.

2. Из неравенства (3) следует, что функции $a( \cdot )$ ограничены, а так как они равны нулю за пределами некоторого шара, то они принадлежат и ${{L}_{2}}({{\mathbb{R}}^{d}})$. Следовательно, формулы для оптимальных методов определены корректно.

3. Оптимальные методы линейны, “сглаживают” наблюдения и используют информацию о не более чем двух измерениях.

4. Если $Y = {{y}_{i}}$ и ${{y}_{i}}$ не является точкой излома функции $\omega ( \cdot )$, то оптимальный метод позволяет данное измерение уточнить.

5. Случай $Y > {{y}_{{{{s}_{k}}}}}$ означает, что оптимальный метод есть решение задачи Дирихле на гиперплоскости $y = Y - {{y}_{{{{s}_{k}}}}}$ с начальной функцией ${{z}_{{{{s}_{k}}}}}( \cdot )$.

ДОКАЗАТЕЛЬСТВО ОСНОВНОГО РЕЗУЛЬТАТА

Начнем с доказательства того, что

для любого $Y \geqslant 0$.

Пусть $Y \geqslant 0$. Покажем сначала, что $E(Y)$ не меньше значения следующей задачи

т.е. верхней грани максимизируемого функционала при данных ограничениях.

Действительно, пусть функция ${{f}_{0}}( \cdot )$ допустима в задаче (5) (т.е. удовлетворяет ограничениям этой задачи). Тогда функция $ - {{f}_{0}}( \cdot )$ также допустима, поскольку $u( \cdot ,y, - {{f}_{0}}) = - u( \cdot ,y,{{f}_{0}})$, и мы имеем для любого метода $\varphi $

Переходя слева к верхней грани по всем допустимым функциям в задаче (5), а затем справа к нижней грани по всем методам $\varphi $, получим, что Это и означает, что погрешность оптимального восстановления $E(Y)$ не меньше значения задачи (5). Найдем теперь это значение.

Хорошо известно (см., например, [14]), что

для любого $y > 0$ и для п.в. $\xi \in {{\mathbb{R}}^{d}}$. Тогда согласно теореме Планшереля Отсюда получаем, что квадрат значения задачи (5) равен значению такой задачи: Можно считать, что переменными здесь являются положительные меры $d{{\mu }_{f}}(\xi ) = {{(2\pi )}^{{ - d}}}{{\left| {F[f](\xi )} \right|}^{2}}d\xi $ на ${{\mathbb{R}}^{d}}$, порожденные функциями $f( \cdot ) \in {{L}_{2}}({{\mathbb{R}}^{d}})$. Для нахождения значения данной задачи удобно рассмотреть более общую постановку, а именно, задачу на множестве всех положительных борелевских мер на ${{\mathbb{R}}^{d}}$: Сопоставим этой задаче следующую функцию Лагранжа: где $\lambda = ({{\lambda }_{1}},{{\lambda }_{2}},\; \ldots ,\;{{\lambda }_{n}})$ – набор множителей Лагранжа.

Нетрудно проверить, что если существует допустимая в задаче (8) мера $d\hat {\mu }( \cdot )$ и набор множителей Лагранжа $\hat {\lambda } = ({{\hat {\lambda }}_{1}},{{\hat {\lambda }}_{2}},\; \ldots ,\;{{\hat {\lambda }}_{n}})$ такие, что выполняются условия

a) $\mathop {min}\limits_{d\mu ( \cdot ) \geqslant 0} L(d\mu ( \cdot ),\widehat \lambda ) = L(d\widehat \mu ( \cdot ),\widehat \lambda )$;

б) ${{\hat {\lambda }}_{i}} \geqslant 0,\quad 1 \leqslant i \leqslant n$;

в) ${{\hat {\lambda }}_{i}}\left( {\int_{{{\mathbb{R}}^{d}}}^{} {{{e}^{{ - 2{{y}_{i}}|\xi |}}}d\hat {\mu }(\xi )} - \delta _{i}^{2}} \right) = 0$, $i = 1,\; \ldots ,\;n$,

то $d\hat {\mu }( \cdot )$ – решение задачи (8).

Действительно, для любой допустимой в задаче (8) меры $d\mu ( \cdot )$ имеем, используя б), а затем а) и в):

т.е. $d\hat {\mu }( \cdot )$ – решение задачи (8).

Предъявим теперь допустимую в задаче (8) меру $d\hat {\mu }( \cdot )$ и набор множителей Лагранжа $\hat {\lambda } = ({{\hat {\lambda }}_{1}},{{\hat {\lambda }}_{2}},\; \ldots ,\;{{\hat {\lambda }}_{n}})$, для которых выполняются условия а)–в).

Рассмотрим отдельно несколько случаев.

$1)$ Пусть $Y \in [{{y}_{1}},{{y}_{{{{s}_{k}}}}})$. Тогда $Y \in [{{y}_{{{{s}_{j}}}}},{{y}_{{{{s}_{{j + 1}}}}}})$ для некоторого $1 \leqslant j \leqslant k - 1$. Пусть сначала $Y > {{y}_{{{{s}_{j}}}}}$.

Фиксируем вектор ${{\xi }_{0}} \in {{\mathbb{R}}^{d}}$ такой, что

Определение корректно, так как выражение справа положительно по построению ломаной $\omega ( \cdot )$.

Положим

и определим меру $d\hat {\mu }( \cdot )$ по формуле $d\hat {\mu }( \cdot ) = C\delta ( \cdot - {{\xi }_{0}})$, где $\delta ( \cdot - {{\xi }_{0}})$ – мера Дирака в точке ${{\xi }_{0}}$. Ясно, что это положительная борелевская мера на ${{\mathbb{R}}^{d}}$. Покажем, что она допустима в задаче (8).

Действительно, все точки $({{y}_{i}},ln(1{\text{/}}{{\delta }_{i}}))$, $i = 1,2,\; \ldots ,\;n$, лежат не выше графика ломаной $\omega ( \cdot )$, а так как эта ломаная вогнута, то ее график лежит не выше прямой

соединяющей точки и $({{y}_{{{{s}_{j}}}}},ln(1{\text{/}}{{\delta }_{{{{s}_{j}}}}}))$ и $({{y}_{{{{s}_{{j + 1}}}}}},ln(1{\text{/}}{{\delta }_{{{{s}_{{j + 1}}}}}}))$. Используя это обстоятельство и выражения для $C$ и $\left| {{{\xi }_{0}}} \right|$, будем иметь т.е. мера $d\hat {\mu }( \cdot )$ допустима в задаче (8).

Пусть набор множителей Лагранжа $\widehat \lambda = ({{\widehat \lambda }_{1}},{{\widehat \lambda }_{2}},\; \ldots ,\;{{\widehat \lambda }_{n}})$ таков, что ${{\hat {\lambda }}_{{{{s}_{j}}}}}$ и ${{\hat {\lambda }}_{{{{s}_{{j + 1}}}}}}$ – те, что определены перед формулировкой теоремы и ${{\hat {\lambda }}_{i}} = 0$, если $i \ne {{s}_{j}},{{s}_{{j + 1}}}$.

Проверим, что с мерой $d\hat {\mu }( \cdot )$ и набором $\hat {\lambda }$ выполняются выписанные выше условия а)–в).

Ясно, что ${{\hat {\lambda }}_{i}} \geqslant 0$, $i = 1,\; \ldots ,\;n$, и тем самым условие б) выполнено. Проверим выполнение условия а).

Запишем функцию Лагранжа с данным набором $\hat {\lambda }$ в виде

где Несложный подсчет показывает, что $h\left( {\left| {{{\xi }_{0}}} \right|} \right) = h{\text{'}}\left( {\left| {{{\xi }_{0}}} \right|} \right) = 0$, и поскольку функция $\alpha \mapsto h(\alpha )$, очевидно, выпукла, то $h(\alpha ) \geqslant 0$ для всех $\alpha \in \mathbb{R}$. Учитывая это, будем иметь для любого $d\mu ( \cdot ) \geqslant 0$т.е. выполнено условие а).

Далее, легко проверить, что

и, значит, выполнено условие $(c)$.

Итак, вследствие доказанного выше, мера $d\hat {\mu }( \cdot )$ является решением задачи (8).

Подставляя меру $d\hat {\mu }( \cdot )$ в максимизируемый функционал в задаче (8), найдем ее значение:

Случай, когда $Y = {{y}_{{{{s}_{j}}}}}$, рассматривается аналогично, но проще и поэтому на нем не останавливаемся.

$2)$ Пусть $Y \geqslant {{y}_{{{{s}_{k}}}}}$. Положим ${{\hat {\lambda }}_{{{{s}_{k}}}}} = 1$, ${{\hat {\lambda }}_{i}} = 0$, $i \ne {{s}_{k}}$ и $d\hat {\mu }( \cdot ) = \delta _{{{{s}_{k}}}}^{2}\delta ( \cdot )$, где $\delta ( \cdot )$ – функция Дирака в нуле. Функция $h \mapsto h(\alpha )$ в данном случае имеет вид

Следовательно, $h\left( {\left| \xi \right|} \right) \geqslant 0$ для всех $\xi \in {{\mathbb{R}}^{d}}$, и ясно, что $h(0) = 0$. Тогда те же рассуждения, что и выше, показывают, что справедливо условие а).

На полупрямой $[{{t}_{{{{s}_{k}}}}},\infty )$ функция $\omega ( \cdot )$ тождественно равна $ln(1{\text{/}}{{\delta }_{{{{s}_{k}}}}})$, и понятно, что $ln(1{\text{/}}{{\delta }_{i}}) \leqslant ln(1{\text{/}}{{\delta }_{{{{s}_{k}}}}})$, $1 \leqslant i \leqslant n$. Отсюда получаем, что

т.е. мера $d\hat {\mu }( \cdot )$ допустима в задаче (8) и, в частности, выполнено условие в).

Таким образом, мера $d\hat {\mu }( \cdot )$ – решение задач (8) и значение этой задачи таково

$3)$ Пусть ${{y}_{1}} > 0$ и $Y < {{y}_{1}}$. Покажем, что в этом случае значение задачи (8) равно $ + \infty $. Пусть ${{t}_{0}} < 0$. Существует, очевидно, прямая $t = ay + b$, $a > 0$, которая разделяет точку $(Y,{{t}_{0}})$ и множество $M$, т.е. ${{t}_{0}} - aY \geqslant b \geqslant t - ay$ для любой пары $(t,y) \in M$. В частности,

Обозначая $C = {{e}^{{ - 2b}}}$ и выбирая ${{\xi }_{0}} \in {{\mathbb{R}}^{d}}$ так, чтобы ${{\left| {{{\xi }_{0}}} \right|}^{2}} = a$, получаем из неравенств справа в (13), что $Cexp( - 2{{\left| {{{\xi }_{0}}} \right|}^{2}}{{y}_{i}}) \leqslant \delta _{i}^{2}$, $1 \leqslant i \leqslant n$, т.е. мера Дирака в точке ${{\xi }_{0}}$, умноженная на $C$, допустима в задаче (8). Из левого неравенства в (13) следует, что $Cexp( - 2{{\left| {{{\xi }_{0}}} \right|}^{2}}Y) \geqslant exp( - 2{{t}_{0}})$. Это означает (в силу произвольности ${{t}_{0}}$), что значение задачи (8) равно $ + \infty $. Отсюда, как и в предыдущих случаях, следует, что значение задачи (1) равно $ + \infty $.

Итак, доказано, что значение задачи (8) равно ${{e}^{{ - 2\omega (Y)}}}$ для всех $Y \geqslant 0$.

Очевидно, что значение задачи (8) не меньше значения задачи (7). Покажем, что на самом деле эти значения совпадают.

Пусть $Y \in [{{y}_{{{{s}_{j}}}}},{{y}_{{{{s}_{{j + 1}}}}}})$, $1 \leqslant j \leqslant k - 1$, и вектор ${{\xi }_{0}} = ({{\xi }_{{01}}},\; \ldots ,\;{{\xi }_{{0d}}})$ (см. (9)) такой, что ${{\xi }_{{0i}}} \geqslant 0$, $i = 1$, ..., d. Для каждого $k \in \mathbb{N}$ положим ${{\square }_{k}}\; = {\text{\{ }}\xi = ({{\xi }_{1}},\; \ldots ,\;{{\xi }_{d}}) \in {{\mathbb{R}}^{d}}:{{\xi }_{{0i}}} \leqslant {{\xi }_{i}} \leqslant {{\xi }_{{0i}}} + 1{\text{/}}k,\;i = 1,\; \ldots ,\;d{\text{\} }}$ и определим функцию ${{\psi }_{k}}( \cdot )$, $k \in \mathbb{N}$, по формуле

Ясно, что эти функции принадлежат ${{{\text{L}}}_{2}}({{\mathbb{R}}^{d}})$. Положим ${{\varphi }_{k}}( \cdot ) = {{F}^{{ - 1}}}[{{\psi }_{k}}]( \cdot )$ (${{F}^{{ - 1}}}$ – обратное преобразование Фурье в ${{L}_{2}}({{\mathbb{R}}^{d}})$) и покажем, что функции ${{\varphi }_{k}}( \cdot )$, $k \in \mathbb{N}$, допустимы в задаче (7).

Действительно, если $\xi \in \;{{\square }_{k}}$, то $\left| {{{\xi }_{0}}} \right| \leqslant \left| \xi \right| \leqslant \left| {{{\xi }_{0}}} \right| + \sqrt d {\text{/}}k$ и мы имеем

т.е. функции ${{\varphi }_{k}}( \cdot )$, $k \in \mathbb{N}$, допустимы в задаче (7).

Значение максимизируемого функционала в этой задаче на этих функциях таково

Если $k \to \infty $, то это выражение стремится к величине и значит, значение задачи (7) равно ${{e}^{{ - 2\omega (Y)}}}$.

В случаях, когда $Y \geqslant {{y}_{{{{s}_{k}}}}}$ или $0 \leqslant Y < {{y}_{1}}$, рассуждения аналогичны (и проще) и поэтому мы их опускаем.

Итак, для всех $Y \geqslant 0$ доказано, что значение задачи (7) равно ${{e}^{{ - 2\omega (Y)}}}$ и тем самым, в силу (6), справедлива оценка (4).

Перейдем теперь к построению оптимальных методов восстановления. Здесь также рассматриваем несколько случаев.

$1)$ Пусть $Y \in ({{y}_{{{{s}_{j}}}}},{{y}_{{{{s}_{{j + 1}}}}}})$, $1 \leqslant j \leqslant k - 1$. Поскольку в полученной выше оценке снизу для $E(Y)$ участвуют измерения только на гиперплоскостях $y = {{y}_{{{{s}_{j}}}}}$ и $y = {{y}_{{{{s}_{{j + 1}}}}}}$, то оптимальные методы будем искать среди тех методов, которые используют только эти измерения. Кроме того, мы восстанавливаем линейный оператор, который в образах Фурье есть умножение на некоторую функцию из ${{L}_{\infty }}({{\mathbb{R}}^{d}})$. В этой связи будем искать оптимальные методы среди методов вида

Здесь ${{\Lambda }_{k}}{{L}_{2}}({{\mathbb{R}}^{d}}) \to {{L}_{2}}({{\mathbb{R}}^{d}})$, $k = j,j + 1$, – операторы, которые в образах Фурье действуют для п.в. $\xi \in {{\mathbb{R}}^{d}}$ и любых $z( \cdot ) \in {{L}_{2}}({{\mathbb{R}}^{d}})$ по правилу где ${{a}_{k}}( \cdot ) \in {{L}_{\infty }}({{\mathbb{R}}^{d}})$, $k = j,j + 1$.

Ясно, что ${{\Lambda }_{j}}$ и ${{\Lambda }_{{j + 1}}}$ – линейные операторы и легко убедиться, используя теорему Планшереля, что они непрерывны.

Наша цель – найти такие функции ${{a}_{j}}( \cdot )$ и ${{a}_{{j + 1}}}( \cdot )$, что погрешность соответствующего метода указанного вида не будет превосходить ${{e}^{{ - \omega (Y)}}}$. Тогда в силу оценки (4) такой метод будет оптимальным.

Пусть ${{a}_{k}}( \cdot ) \in {{L}_{\infty }}({{\mathbb{R}}^{d}})$, $k = j,j + 1$. Погрешность метода, соответствующего этим функциям, по определению есть значение следующей задачи

Переходя к образам Фурье, получим, согласно теореме Планшереля, что квадрат значения задачи (14) равен значению такой задачи

Пусть $f( \cdot ) \in {{L}_{2}}({{\mathbb{R}}^{d}})$ и ${{z}_{{{{s}_{k}}}}}( \cdot ) = u( \cdot ,{{y}_{{{{s}_{k}}}}},f)$, $k = j,j + 1$. Тогда тройка $(f( \cdot ),{{z}_{{{{s}_{j}}}}}( \cdot ),{{z}_{{{{s}_{{j + 1}}}}}}( \cdot ))$ допустима в задаче (14) и подынтегральное выражение в максимизируемом функционале на этой тройке в задаче (15) запишется в виде

Если выражение в круглых скобках в правой части этого равенства отлично от нуля на множестве положительной меры, то легко подобрать такую функцию $f( \cdot ) \in {{L}_{2}}({{\mathbb{R}}^{d}})$, что все выражение справа будет положительно на некотором множестве положительной меры. Тогда умножая $f( \cdot )$ на достаточно большое по модулю число, получаем, что максимизируемый интеграл в задаче (15) может принимать сколь угодно большие значения, т.е. значение этой задачи (а значит, и задачи (14)) равно $ + \infty $. Поскольку нас интересуют методы, погрешность которых не превосходит ${{e}^{{ - \omega (Y)}}}$, то этот случай нам не интересен. Поэтому далее считаем, что функции ${{a}_{j}}( \cdot )$ и ${{a}_{{j + 1}}}( \cdot )$ связаны соотношением для п.в. $\xi \in {{\mathbb{R}}^{d}}$.

С учетом этого равенства выражение под знаком интеграла в максимизируемом функционале в задаче (15) можно записать следующим образом:

Оценим это выражение. Пусть ${{\hat {\lambda }}_{{{{s}_{j}}}}}$ и ${{\hat {\lambda }}_{{{{s}_{{j + 1}}}}}}$ – множители Лагранжа, определенные перед формулировкой теоремы. Тогда продолжая (17), будем иметь по неравенству Коши–Буняковского

Обозначим через $S( \cdot )$ функцию в больших скобках в правой части этого неравенства. Ясно, что $S( \cdot ) \in {{L}_{\infty }}({{\mathbb{R}}^{d}})$. Слева в этом неравенстве – выражение под знаком интеграла в максимизируемом функционале в задаче (15). Интегрируя неравенство (18) и учитывая ограничения в задаче (15), получаем, что ее значение не превосходит величины Покажем, что Действительно, используя то, что ${{e}^{{ - 2\omega (Y)}}}$ есть решение задачи (8), равенства (12) и то, что $h\left( {\left| {{{\xi }_{0}}} \right|} \right) = 0$, приходим к нужному равенству: Из (19) и (20) следует, что значение задачи (15) не превосходит величины ${{\left\| {S( \cdot )} \right\|}_{{{{L}_{\infty }}({{\mathbb{R}}^{d}})}}}{{e}^{{ - 2\omega (Y)}}}$. Сравнивая это с неравенством (4), видим, что если функции ${{a}_{j}}( \cdot )$ и ${{a}_{{j + 1}}}( \cdot )$, связанные соотношением (16), таковы, что ${{\left\| {S( \cdot )} \right\|}_{{{{L}_{\infty }}({{\mathbb{R}}^{d}})}}} \leqslant 1$, то соответствующий метод оптимален.

Обозначим $a( \cdot ) = {{a}_{{j + 1}}}( \cdot )$. Тогда ${{a}_{j}}(\xi ) = {{e}^{{ - (Y - {{y}_{{{{s}_{j}}}}})|\xi |}}} - a(\xi ){{e}^{{ - ({{y}_{{{{s}_{{j + 1}}}}}} - {{y}_{{{{s}_{j}}}}})|\xi |}}}$ для п.в. $\xi \in {{\mathbb{R}}^{d}}$ в силу (16). В этих обозначениях условие ${{\left\| {S( \cdot )} \right\|}_{{{{L}_{\infty }}({{\mathbb{R}}^{d}})}}} \leqslant 1$ равносильно тому, что

для п.в. $\xi \in {{\mathbb{R}}^{d}}$, и, следовательно, задача о нахождении оптимальных методов свелась к нахождению таких функций $a( \cdot ) \in {{L}_{\infty }}({{\mathbb{R}}^{d}})$, для которых справедливо соотношение (21).

Выделяя полный квадрат, нетрудно проверить, что (21) равносильно такому неравенству

где $g(\xi ) = {{\hat {\lambda }}_{{{{s}_{j}}}}}{{e}^{{ - 2{{y}_{{{{s}_{j}}}}}|\xi |}}} + {{\hat {\lambda }}_{{{{s}_{{j + 1}}}}}}{{e}^{{ - 2{{y}_{{{{s}_{{j + 1}}}}}}|\xi |}}} - {{e}^{{ - 2Y|\xi |}}}$. Поскольку $g(\xi ) = {{e}^{{ - 2Y|\xi |}}}h\left( {\left| \xi \right|} \right)$, где функция $\alpha \mapsto h(\alpha )$ на $\mathbb{R}$, определенная формулой (11), неотрицательна, то функция $g( \cdot )$ также неотрицательна.

Функции $a( \cdot )$, удовлетворяющие соотношению (22), очевидно, существуют. Тем самым каждая такая функция удовлетворяет неравенству (21) и при этом, в силу определения ${{\gamma }_{j}}$, данное неравенство сохранится, если $a(\xi ) = 0$, когда $\xi \notin B({{\gamma }_{j}})$. Таким образом, для случая, когда $Y \in ({{y}_{{{{s}_{j}}}}},{{y}_{{{{s}_{{j + 1}}}}}})$, $1 \leqslant j \leqslant k - 1$, оптимальные методы построены.

Случаи, когда $Y = {{y}_{{{{s}_{j}}}}}$, $1 \leqslant j \leqslant k$, и $Y > {{y}_{{{{s}_{k}}}}}$ рассматриваются аналогично, но значительно проще, и поэтому на этом останавливать не будем.