Журнал вычислительной математики и математической физики, 2020, T. 60, № 10, стр. 1676-1696

ВВЕДЕНИЕ

В работе продолжаются исследования влияния инвестиций на вероятность неразорения (ВНР) страховой компании (СК) в так называемой дуальной модели риска, начатые в [1]. Данная модель является дуальной по отношению к классической модели коллективного риска в страховании – модели Крамéра–Лундберга (КЛ) – и может рассматриваться как коллективная модель пенсионного страхования, или модель пожизненной ренты. Дуальная модель риска, называемая также моделью аннуитета в страховании жизни (life annuity insurance model, см. [2]), получается из модели КЛ заменой знаков на противоположные у составляющих случайного процесса, описывающего динамику рискового резерва (процесса риска). Получившиеся в результате такой инверсии составляющие указанного процесса приобретают новый смысл: детерминированная линейно убывающая функция соответствует суммарной выплате пенсий (пособия) по портфелю договоров, а составной пуассоновский процесс с положительными скачками определяет случайные приращения резерва (доходы СК) в случайные моменты перехода к СК собственности страхователей. (Подробнее о дуальной модели риска и некоторых задачах для нее см. [3]–[5].)

В [1] поставлена, исследована (и полностью решена в случае экспоненциального распределения случайных доходов СК) задача об определении влияния рисковых инвестиций на ВНР в дуальной модели риска, а именно, в предположении, что все свои страховые резервы СК инвестирует в два вида активов – рисковые, цена которых подчиняется процессу геометрического броуновского движения, и безрисковые (банковский счет с постоянной процентной ставкой). При этом предполагается, что в инвестиционном портфеле сохраняется постоянная пропорция активов двух указанных видов, причем доля рискового актива строго положительна. Такие стратегии инвестиций (как при постоянной положительной, так и при нулевой доле рискового актива) называем простыми стратегиями, причем при положительной доле рискового актива – простыми рисковыми стратегиями, или, для краткости, рисковыми инвестициями. В данной работе изучается проблема исследования ВНР в случае простой безрисковой стратегии, т.е. когда доля рисковых инвестиций в инвестиционном портфеле нулевая и резерв СК полностью инвестируется в безрисковый актив. С точки зрения постановки задачи этот случай может рассматриваться как вырожденный по отношению к исследованной в [1] более общей ситуации. При этом следует отметить, что утверждения о виде ВНР, доказанные для простой рисковой стратегии в [1], не дают возможности получить ответ в “вырожденной” модели, устремляя долю рискового актива к нулю, – такой переход оказывается сингулярным по параметру, и по этой причине задача требует отдельного рассмотрения.

Исследование в рамках данной модели при простых стратегиях инвестиций – как рисковых, так и безрисковых – основано на связи ВНР как функции начального капитала (НК) с решением корректно поставленных сингулярных задач для некоторых интегродиффeренциальных уравнений (ИДУ). Эти ИДУ порождаются инфинитезимальными операторами случайных процессов, описывающих динамику резерва СК при использовании соответствующей инвестиционной политики.

В случае рисковых инвестиций и экспоненциального распределения случайных доходов для поставленной сингулярной краевой задачи (КрЗ) в [1] доказаны существование и единственность ее решения, исследовано его асимптотическое поведение как при больших, так и при малых значениях НК, а также предложен алгоритм численного решения этой задачи (как отмечено в [1], асимптотическое поведение ВНР при больших значениях НК ранее исследовалось в [6] другими методами). На основании теоретических исследований и численных экспериментов сделаны выводы о влиянии на ВНР рисковых инвестиций в рассматриваемой модели. В частности, теоретически показано, что при положительной нагрузке безопасности в дуальной модели риска (т.е. при условии на параметры модели, когда ожидаемый доход СК в единицу времени от случайных поступлений больше выплачиваемых пенсий) и при больших значениях НК рисковые инвестиции не выгодны, так как дают уменьшение ВНР по сравнению с ВНР в случае отсутствия инвестиций. Точнее, при так называемых “надежных” рисковых инвестициях асимптотическое стремление ВНР к единице (при больших НК) характеризуется степенной функцией, в то время как при отсутствии инвестиций – экспонентой; “ненадежные” инвестиции вообще дают разорение с вероятностью единица. В то же время результаты численных расчетов в [1] позволили прийти к выводу о том, что даже в случае отрицательной нагрузки безопасности в исходной модели страхового риска применение достаточно надежного рискового инвестиционного портфеля (т.е. портфеля с не слишком большой волатильностью) позволяет повышать ВНР при малых значениях НК – когда разорение в отсутствие инвестиций наиболее вероятно (а при отрицательной нагрузке безопасности и вовсе неминуемо).

Для более полного (по сравнению с [1]) исследования роли рисковых инвестиций в повышении платежеспособности СК необходимо провести сравнение ВНР, получаемой в результате применения простых рисковых стратегий, с ВНР, соответствующей применению безрисковой стратегии. Так как сравнение рисковых и безрисковой простых стратегий является итоговой целью данной работы, здесь кратко описывается подход к изучению ВНР, используемый в [1], и приводятся основные результаты. Это дает возможность увидеть, с одной стороны, единство используемого метода, основанного на исследовании сингулярных задач для ИДУ, а с другой стороны, обнаружить, что “вырожденный” случай приводит к задаче качественно другого вида, что и является причиной его отдельного изучения в данной работе.

Работа организована следующим образом.

В разд. 1 даются описание модели и постановка задачи, которая рассматривается также в контексте более общей модели, предполагающей использование рисковых стратегий. Приводятся вспомогательные результаты, касающиеся ВНР, в частности, ее связи с решениями сингулярных задач для ИДУ.

В разд. 2 формулируются доказанные в [1] некоторые утверждения для модели с простыми рисковыми стратегиями инвестиций и экспоненциальным распределением случайных поступлений: основная теорема о виде ВНР как решения сингулярной КрЗ для ИДУ второго порядка, лемма об эквивалентности этой задачи для ИДУ и некоторой сингулярной КрЗ для обыкновенного дифференциального уравнения (ОДУ) третьего порядка, на которой основывается доказательство основной теоремы.

В разд. 3 приводятся сингулярные задачи для вырожденных (по отношению к общей модели) ИДУ первого порядка и ОДУ второго порядка, доказываются лемма об их эквивалентности и основная теорема о виде ВНР как решения сингулярной задачи для ИДУ. Указанные утверждения не являются следствием доказанных в [1] соответствующих утверждений для более общей модели, так как задачи для ИДУ сформулированы при различных условиях на решения, продиктованных свойствами ВНР – различными в “общем” и “вырожденном” случаях. Более того, исследование свойств решений показывает, что эти решения в двух описанных случаях действительно находятся, вообще говоря, в различных классах функций – таких, что ни один из них не включает в себя другой. В частности, показано, при каких параметрах модели в случае безрисковой стратегии ВНР является негладким вязкостным решением соответствующего ИДУ, определенного на ${{\mathbb{R}}_{ + }}$, в то время как при рисковых инвестициях решения являются дважды непрерывно дифференцируемыми функциями (о вязкостных решениях в некоторой более общей модели см. [7], о применении понятия вязкостного решения к исследованию ВНР в дуальной модели риска см. [8]).

В разд. 4 приводятся результаты численных исследований влияния на ВНР простых инвестиционных стратегий – как рисковых, так и безрисковых, – и сравнительный анализ этих результатов. В конце работы делаются заключительные выводы.

Данная работа (в совокупности с [1]) является итоговой по дуальной модели риска с простыми стратегиями инвестиций и экспоненциальным распределением случайных доходов (некоторые ее результаты коротко отражены в [9], [10]).

Далее используются обозначения: ${\mathbf{P}}(A)$ – вероятность события $A$; ${\mathbf{E}}X$ – математическое ожидание случайной величины $X$. Остальные обозначения и сокращения вводятся по мере необходимости.

1. ОПИСАНИЕ МОДЕЛИ ПЕНСИОННОГО СТРАХОВАНИЯ (ДУАЛЬНОЙ МОДЕЛИ РИСКА) С БЕЗРИСКОВЫМИ ИНВЕСТИЦИЯМИ

2. ФОРМУЛИРОВКА ОСНОВНЫХ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ СИНГУЛЯРНОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ ИДУ, СООТВЕТСТВУЮЩЕЙ ИНФИНИТЕЗИМАЛЬНОМУ ОПЕРАТОРУ ПРОЦЕССА РИСКА В СЛУЧАЕ РИСКОВЫХ ИНВЕСТИЦИЙ И ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ СКАЧКОВ

В этом разделе формулируются некоторые суммарные результаты [1] по задаче, указанной в названии (с добавлением некоторых замечаний), необходимые для дальнейшего сравнения рисковых и безрисковых стратегий.

Далее, если не оговорено особо, при $0 < \alpha \leqslant 1$ опускаем индекс $\alpha $ в обозначениях СДУ (1.9) и ИДУ (1.15) и полагаем $\mu > 0$, $\sigma > 0$. В этом случае (1.9) и (1.15) приобретают соответственно вид

При $\alpha = 0$ из (1.10) получаем $\mu = r$, $\sigma = 0$, и тогда имеем дело с СДУ (1.8) и ИДУ (1.18).

Для дальнейшего заметим, что невольтерров интегральный оператор в (1.13) может быть переписан в виде

3. БЕЗРИСКОВАЯ СТРАТЕГИЯ ИНВЕСТИЦИЙ: ВЫРОЖДЕННЫЕ СИНГУЛЯРНЫЕ ЗАДАЧИ ДЛЯ ИДУ И ОДУ И ИХ ИССЛЕДОВАНИЕ

Напомним, что безрисковой стратегией инвестиций называем простую стратегию, состоящую в инвестировании всего резерва СК в безрисковый актив – банковский счет с постоянной процентной ставкой, т.е. весь капитал фонда постоянно держится на банковском счете, эволюция которого описывается ОДУ (1.7), где ${{B}_{t}}$ – величина банковского счета в момент времени $t$ ($t \geqslant 0$) при постоянной процентной ставке $r > 0$. Тогда динамика капитала ${{X}_{t}}$ (результирующий процесс риска) в соответствующей модели описывается начальной задачей для СДУ (1.8), где ${{R}_{t}}$ определено в (1.1). Эта модель рассматривается в подразд. 1.2 как частный случай более общей модели с простыми стратегиями инвестиций, описываемой СДУ (1.9), и этот случай соответствует значению $\alpha = 0$.

Для ВНР $\varphi (u)$ процесса (1.8), в силу лемм 1 и 2, имеют место соотношения (1.11), (1.12). Целью данного раздела является изучение влияния безрисковых инвестиций на ВНР при НК $u$, находящемся в интервале $[0,\;c{\text{/}}r]$; кроме того, предполагается сравнить его с влиянием рисковых инвестиций, изученным в [1].

Обратимся к ИДУ

которое является частным случаем ИДУ (1.14) при $\alpha = 0$ (с учетом преобразования (2.3) интегрального оператора в (1.13) и замены обозначения $r$ на $\mu $). Таким образом, ИДУ (3.1) можно рассматривать как “вырожденное” по отношению к сингулярному ИДУ второго порядка (1.14) для той же исходной модели риска (1.1) в условиях вложения фиксированной доли $\alpha $ текущего капитала в рисковый актив. С другой стороны, ИДУ (1.14) вырождается в ИДУ (3.1) при ${{\sigma }^{2}} \to 0$ и $\alpha = 1$, т.е. при вложении всего капитала в акции при стремлении к нулю их волатильности. Напомним, что в случае $F(z)$, имеющей вид (1.4) (т.е. в случае экспоненциального распределения скачков процесса риска), ИДУ (1.14) при $\alpha = 1$ приобретает вид (2.5).

Как и в случае рисковых инвестиций, будем изучать далее случай экспоненциального распределения скачков процесса риска (размеров случайных доходов). Тогда, с учетом обозначения (2.4) для интегрального оператора, перепишем ИДУ (3.1) в виде

Нелокальное соотношение в нуле (1.23) для решения ИДУ (3.2) в классе $\mathcal{L}$, в предположении конечности производной этого решения в нуле, приобретает вид из которого следует неравенство $f{\kern 1pt} {\text{'}}( + 0) > 0$ (см. также утверждение 3) леммы 3).

Поставим (пока формально) сингулярную задачу для ИДУ (3.2):

Лемма 6. Пусть в ИДУ (3.3) все параметры $c$, $m$, $\lambda $, $r$ – фиксированные положительные числа. Тогда сингулярная задача (3.3)–(3.6) для ИДУ первого порядка эквивалентна сингулярной задаче для ОДУ второго порядка

с теми же условиями (3.4)–(3.6).

Доказательство. Докажем, что любое решение ИДУ (3.3) является также решением ОДУ (3.7). Нетрудно подсчитать, что для оператора, введенного в (2.4), имеет место соотношение

Дифференцируя исходное ИДУ (3.3) и учитывая соотношение (3.8), получаем Взяв очевидную линейную комбинацию ИДУ (3.3) и ИДУ (3.9), приводящую к исключению интегрального слагаемого $({{J}_{m}}f)(u)$, получаем ОДУ (3.7).

Обратно: пусть функция $\hat {f}(u)$ удовлетворяет ОДУ (3.7) и условиям (3.4), (3.6). Покажем, что она удовлетворяет также ИДУ (3.3). Обозначим левую часть ИДУ (3.3) с функцией $\hat {f}(u)$ через $h(u)$, т.е.

Дифференцируя (3.10) и учитывая ОДУ (3.7), получаем, что $h(u)$ удовлетворяет ОДУ решение которого имеет вид где $C$ – произвольная постоянная. Кроме того, в силу условий (3.5), (3.6) для $h(u)$ выполнено соотношение $li{{m}_{{u \uparrow c/r}}}h(u) = 0,$ откуда, учитывая общий вид решения (3.12), получаем $h(u) \equiv 0$. Лемма доказана.

Теорема 4. Пусть в ИДУ (3.3) все параметры $c$, $m$, $\lambda $, $r$ – фиксированные положительные числа, и пусть функция $f(u)$ является решением сингулярной задачи для ИДУ (3.3)–(3.6). Тогда

где $g(u)$ есть решение сингулярной задачи для ОДУ с условием нормировкиОбратно: если функция $g(u)$ есть решение сингулярной задачи для ОДУ (3.14)–(3.16), то функция $f(u)$, определенная в (3.13) при $0 \leqslant u < c{\text{/}}r$ и равная единице при $u \geqslant c{\text{/}}r$, есть решение сингулярной задачи для ИДУ (3.3)–(3.6).

Доказательство этой теоремы аналогично доказательству теоремы 2 из [1].

Заметим, что то же ОДУ (3.14) получается из ОДУ (2.17) при $\sigma = 0$, $\mu = r$ (см. также ОДУ (2.22) в замечании 1). Нетривиальные решения ОДУ (3.14) на интервале $[0,\;c{\text{/}}r]$ определяются явно с точностью до постоянного множителя, в котором в качестве неопределенной константы положим ${{D}_{1}} = li{{m}_{{u \to 0}}}g(u)$ (для удобства дальнейшего согласования с формулой (2.11)). Тогда из этого семейства

выделим нужное решение $g(u)$ условием нормировки (3.16), откуда получим В итоге для $u \in [0,c{\text{/}}r]$ имеем Тогда функция $f(u)$ на интервале $[0,c{\text{/}}r)$ определяется формулой (3.13).

В соответствии с приведенными выше утверждениями получаем, что определенная таким образом функция $f(u)$ удовлетворяет ИДУ (3.2) (за исключением, быть может, точки $c{\text{/}}r$) и принадлежит классу $\mathcal{L}$. Следовательно, для этой функции выполнены условия леммы 3. По теореме 1, для любого $u \in {{\mathbb{R}}_{ + }}$ значение $f(u)$ определяет ВНР для процесса (1.8) с начальным условием ${{X}_{0}} = u$, т.е. $f \equiv \varphi $. Кроме того, в силу утверждения 1) леммы 3, для функции ВНР с необходимостью выполнено условие (3.6) (то же следует из формулы (3.18)). Таким образом, получаем, что верна следующая основная

Теорема 5. Пусть $F(z) = 1 - exp( - z{\text{/}}m)$, все параметры $r$, $c$, $m$, $\lambda $ – фиксированные положительные числа. Тогда:

(I) ВНР $\varphi (u)$ процесса (1.8) с начальным условием ${{X}_{0}} = u$, $u \geqslant 0$, принадлежит классу $\mathcal{L}$ и является решением сингулярной задачи для ИДУ (3.3)–(3.6);

(II) это решение единственно в классе $\mathcal{L}$ и определяется соотношениями

где $g(u)$ определяется формулой (3.18).

Замечание 3. Из (3.18) следует, что при $u \to + 0$ решение $g(u)$ (производная ВНР) имеет положительный конечный предел (при этом удовлетворяется соотношение (1.24)). В то же время характер поведения $g(u)$ в окрестности точки $u = \tilde {u} = c{\text{/}}r$ зависит от соотношения параметров $\lambda $ и $r$:

(1) при $\lambda > r$ будет $li{{m}_{{u \uparrow c/r}}}g(u) = 0$;

(2) при $\lambda = r$ имеем положительный конечный предел,

а для функций $g(u)$, $\varphi (u)$ из (3.18), (3.19) окончательно имеем

(3) при $\lambda < r$ будет $li{{m}_{{u \uparrow c/r}}}g(u) = \infty $, где функция $g(u)$ интегрируема в точке $u = \tilde {u} = c{\text{/}}r$.

Таким образом, получаем, что ВНР в рассматриваемой модели является непрерывной, но, вообще говоря, негладкой функцией НК $u$: в случае выполнения (1.4) и при условии $\lambda \leqslant r$ она имеет точку разрыва производной $u = \tilde {u} = c{\text{/}}r > 0$ (при $\lambda > r$ ВНР является гладкой функцией на всей неотрицательной полуоси). Здесь можно отметить, что при $\lambda \leqslant r$ ВНР является вязкостным негладким решением ИДУ (3.2) (о понятии вязкостных решений в некоторой более общей модели см. [7]).

Замечание 4. Доказательство существования вязкостного решения ИДУ с заданными краевыми условиями может служить, наряду с теоремой достаточности, инструментом обоснования того факта, что полученное решение определяет ВНР в рассматриваемой модели. При этом принимаются во внимание доказанные в [7] утверждения: теорема о том, что ВНР является вязкостным решением соответствующего ИДУ, и теорема единственности вязкостного решения ИДУ с заданными краевыми условиями в нуле и на бесконечности (подробнее о применении этого подхода см. в [8]).

Для полноты описания поведения данной функции, в частности, ее выпуклости или вогнутости в окрестности нуля и возможного излома в точке $u = \tilde {u} = c{\text{/}}r$, а также наличия или отсутствия точки перегиба на $(0,c{\text{/}}r)$, вычислим производную от $g(u)$:

где ${{D}_{1}}$ определено в (3.17). В частности, получаем т.е. здесь имеет место такая же связь второй и первой производных функции $\varphi (u)$ в нуле, что и в случае ${{\sigma }^{2}} > 0$ (при замене $\mu $ на $r$; ср. c представлением (2.11) с учетом формулы (2.12)). Отсюда знак $\varphi {\text{''}}( + 0)$ определяется знаком выражения в квадратных скобках в соотношении (3.20). При этом функция $g{\text{'}}(u)$ в точке обращается в ноль, и нетрудно проверить, что это точка безусловного максимума $g(u)$.

Замечание 5. Опишем более подробно качественное поведение функции $\varphi (u)$, включая поведение ее первой и второй производных, на интервале $(0,\;c{\text{/}}r)$ в зависимости от параметров модели и с использованием понятия нагрузки безопасности (1.3).

(1) Пусть $\lambda > 2r$. Тогда $li{{m}_{{u \uparrow c/r}}}\varphi {\text{''}}(u) = 0$, и функция $\varphi (u)$ дважды непрерывно дифференцируема на $(0,\infty )$.

Если при этом $\rho \geqslant rm{\text{/}}c$, то $\hat {u} \leqslant 0$, где $\hat {u}$ определена в (3.21), $li{{m}_{{u \downarrow 0}}}\varphi {\text{''}}(u) \leqslant 0$, и $\varphi (u)$ – вогнутая функция на ${{\mathbb{R}}_{ + }}$.

Если $\rho < rm{\text{/}}c$, то $0 < \hat {u} < c{\text{/}}r$, так что на интервале $(0,c{\text{/}}r)$ имеется точка перегиба функции $\varphi (u)$, $li{{m}_{{u \downarrow 0}}}\varphi {\text{''}}(u) > 0$, и в окрестности нуля $\varphi (u)$ – выпуклая функция (ср. с п. (V) теоремы 2).

(2) Пусть $r < \lambda \leqslant 2r$. Тогда на интервале $(0,\;\infty )$ функция $\varphi (u)$ не является дважды непрерывно дифференцируемой функцией, так как $li{{m}_{{u \uparrow c/r}}}\varphi {\text{''}}(u) = - \infty $ при $\lambda < 2r$, а при $\lambda = 2r$ постоянная ${{D}_{1}}$ вычисляется явно,

и имеем точный ответ Выводы относительно поведения функции в нуле остаются такими же, как в п. (1) этого замечания.

(3) Пусть $\lambda \leqslant r$. Тогда функция $\varphi (u)$ не является гладкой, имея разрыв производной в точке $u = \tilde {u} = c{\text{/}}r$ (см. пп. (2) и (3) замечания 3). При этом $\hat {u} \geqslant c{\text{/}}r$, $li{{m}_{{u \downarrow 0}}}\varphi {\text{''}}(u) > 0$, и $\varphi (u)$ – выпуклая функция на отрезке $[0,c{\text{/}}r]$.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ИССЛЕДОВАНИЙ ВНР КАК ФУНКЦИИ НК: CЛУЧАИ РИСКОВЫХ И БЕЗРИСКОВЫХ ИНВЕСТИЦИЙ И ИХ СРАВНЕНИЕ

По аналогии с [13], приведем замечание о размерности параметров модели и способе их “обезразмеривания” для последующих вычислений.

Замечание 6. В ИДУ (2.5), (3.3) параметр $m$ – безразмерный (при безразмерных переменных $u$ и $\varphi $), а каждый из параметров ${{\sigma }^{2}}$, $\mu $, $r$, $c$ и $\lambda $ имеет размерность $1{\text{/}}[t]$, где $[t]$ – размерность времени. Чтобы перейти к безразмерным величинам, достаточно разделить ИДУ (2.5) (или (3.3)) на какую-либо характерную положительную постоянную той же размерности: такое деление приводит задачу (2.5)–(2.9) (или (3.3)–(3.6)) к задаче того же вида с новыми параметрами ${{\tilde {\sigma }}^{2}}$, $\tilde {\mu }$, $\tilde {c}$ и $\tilde {\lambda }$ ($\tilde {r}$, $\tilde {c}$ и $\tilde {\lambda }$ соответственно). В частности, удобно в (2.5)–(2.9) и (3.3)–(3.6) в качестве параметра “обезразмеривания” выбрать $\lambda $: если положить $\lambda = 1$, то остальные параметры будут измеряться в долях $\lambda $ и при необходимости их можно пересчитать в размерном виде простым умножением на величину $\lambda > 0$. В результате, оставляя $\lambda $ в формулах, как это принято в литературе, полагаем всюду в расчетах $\lambda = 1$.

Чтобы завершить начатое в [1] исследование роли рисковых активов в возможном увеличении ВНР в рассматриваемой дуальной модели риска, необходимо сравнить ее с влиянием, которое оказывает на ВНР в области малых значений НК вложение всего текущего капитала в безрисковый актив, а также провести сравнение различных простых инвестиционных стратегий, соответствующих различным долям рискового актива в портфеле. Для этой цели проводятся численные расчеты ВНР как решений соответствующих исследованных сингулярных задач для ИДУ.

Напомним, что при больших значениях НК вопрос о сравнении простых рисковых и безрисковой стратегий имеет простое теоретическое обоснование в виде леммы 2. Но несмотря на то, что безрисковый актив однозначно предпочтительнее в этом случае, так как дает неразорение с вероятностью единица при достаточно больших НК (точнее, при значениях, не меньших величины $c{\text{/}}r$), при малых его значениях ответ на вопрос может быть получен путем численных расчетов.

Кроме того, напомним, что асимптотическое представление ВНР (2.15) при простых рисковых стратегиях, переписанное с учетом опущенного в подразд. 2.1 индекса $\alpha $ (доли рискового актива в портфеле, $0 < \alpha \leqslant 1$), имеет вид

где параметры ${{\mu }_{\alpha }}$, $\sigma _{\alpha }^{2}$ определены в (1.10) и удовлетворяют условию (1.16), а $0 < K$ – постоянная, которая не может быть определена методами локального анализа и находится численно – решением соответствующей сингулярной КрЗ для ВНР. Тем самым данная постоянная зависит от параметров модели и характер этой зависимости, в том числе зависимости от $\alpha $, неизвестен. Несмотря на то что показатель степени в асимптотическом представлении (4.1), очевидно, является убывающей функцией $\alpha $, однозначно судить о возрастании ВНР при уменьшении $\alpha $ не представляется возможным в силу указанной причины. Таким образом, в каждой конкретной ситуации для сравнения различных простых рисковых портфелей также необходимы численные расчеты.

Если асимптотически экспоненциальное возрастание к единице ВНР делает трудно различимым эффект влияния на ВНР изменения доли рискового актива в портфеле, то в области малых значений НК численные расчеты покажут, что этот эффект уже хорошо заметен, и он может быть противоположными при различных параметрах модели. Кроме того, в некоторых случаях при малых НК влияние рисковых инвестиций по сравнению с безрисковыми оказывается полностью противоположным их влиянию при больших НК, а именно, рисковый портфель дает большие значения ВНР, чем безрисковые инвестиции.

Далее для моделей с рисковыми и безрисковыми инвестициями приводятся графики $\varphi (u)$ зависимостей ВНР от НК при разных наборах значений параметров задач. При $\mu > 0$, $\sigma \ne 0$ для всех примеров расчетов выполняется либо условие надежности акций (2.10), либо условие надежности для рассматриваемых портфелей (1.16); при положительной нагрузке безопасности $\rho $ дается также сравнение результатов расчетов с аналитическим решением ${{\varphi }_{0}}(u)$ в модели без инвестиций (см. (1.6)). Параметры задач $\mu $, ${{\sigma }^{2}}$, $c$, $\lambda $ указываются в безразмерном виде (см. замечание 6).

Графики этого раздела иллюстрируют утверждения теорем 2, 5 и замечаний 3, 5. Кроме того, на основе анализа численных примеров проводится сравнение влияния на ВНР рисковых и безрисковых инвестиций, а также различных простых стратегий при любых значениях НК.

Для всех примеров расчетов зафиксированы значения $\lambda = 1$, $m = 2$. Для графиков 1 на фиг. 1–6 зафиксировано значение ${{\sigma }^{2}} = 0.3$; для всех графиков 2 на фиг. 1–8 и графиков 5 на фиг. 9–11 зафиксировано значение ${{\sigma }^{2}} = 0$ (решения в модели с безрисковыми инвестициями). Аналитические формулы для решений при $\lambda = r$ и $\lambda = 2r$, приведенные в замечаниях 3 и 5, наряду с качественным анализом поведения решений в нуле и в особой точке $u = c{\text{/}}r$, могут служить дополнительным контролем правильности вычислений.

Данные к графикам на фиг. 1: $c = 4$ ($\rho = - 1{\text{/}}2$); для графиков 1 (решения в модели с рисковыми инвестициями): $\mu = 0.7$, $\varphi {\text{'}}(0) \approx 0.042$, $\varphi {\text{''}}(0) \approx 0.018$; для графиков 2 (решения в модели с безрисковыми инвестициями при $\lambda > 2r$): $r = 0.3$ ($c{\text{/}}r = 40{\text{/}}3 \approx 13.3333$), $\varphi {\text{'}}(0) \approx 0.02$, $\varphi {\text{''}}(0) \approx 0.00658$ на фиг. 1а; $r = 0.1$ ($c{\text{/}}r = 40$), $\varphi {\text{'}}(0) \approx 0.001461$, $\varphi {\text{''}}(0) \approx 0.0004$ на фиг. 1б.

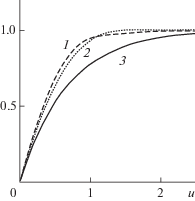
Данные к графикам на фиг. 2: $c = 0.5$ ($\rho = 3$); для графика 1 (решение в модели с рисковыми инвестициями): $\mu = 0.7$ ($\rho > \mu m{\text{/}}c = 2.8$, $\varphi {\text{'}}(0) \approx 1.737$, $\varphi {\text{''}}(0) \approx - 1.472$); для графика 2 (решение в модели с безрисковыми инвестициями при $\lambda > 2r$): $r = 0.3$ ($\rho > rm{\text{/}}c = 1.2$, $\varphi {\text{'}}(0) \approx 1.63$, $\varphi {\text{''}}(0) \approx - 1.467$; $c{\text{/}}r = 5{\text{/}}3 \approx 1.6666$); для графика 3 (решение в модели без инвестиций): $\varphi _{0}^{'}(0) = 1.5$, $\varphi _{0}^{{''}}(0) = - 2.25$.

Данные к графикам на фиг. 3: $c = 4$ ($\rho = - 1{\text{/}}2$); для графика 1 (решение в модели с рисковыми инвестициями): $\mu = 0.7$ ($\varphi {\text{'}}(0) \approx 0.042$, $\varphi {\text{''}}(0) \approx 0.018$); для графика 2 (решение в модели с безрисковыми инвестициями при $\lambda = 2r$): $r = 0.5$ ($\varphi {\text{'}}(0) \approx 0.04$, $\varphi {\text{''}}(0) \approx 0.015$; $c/r = 40{\text{/}}5 = 8$).

Данные к графикам на фиг. 4, 5: $c = 4$ ($\rho = - 1{\text{/}}2$); для графиков 1 (решения в модели с рисковыми инвестициями): $\mu = 1$ ($\varphi {\text{'}}(0) \approx 0.065$, $\varphi {\text{''}}(0) \approx 0.035$) на фиг. 4 и $\mu = 1.5$ ($\varphi {\text{'}}(0) \approx 0.093$, $\varphi {\text{''}}(0) \approx 0.078$) на фиг. 5; для графиков 2 (решение в модели с безрисковыми инвестициями): $r = 0.75$ ($\varphi {\text{'}}(0) \approx 0.061$, $\varphi {\text{''}}(0) \approx 0.027$; $c{\text{/}}r = 400{\text{/}}75 \approx 5.3333$) на фиг. 4 (случай $r < \lambda < 2r$); $r = 1$ ($\varphi {\text{'}}(0) \approx 0.066$, $\varphi {\text{''}}(0) \approx 0.039$; $c{\text{/}}r = 4$) на фиг. 5 (случай $\lambda = r$).

Данные к графикам на фиг. 6: $c = 4$ ($\rho = - 1{\text{/}}2$); для графика 1: $\mu = 1.75$ ($\varphi {\text{'}}(0) \approx 0.105$, $\varphi {\text{''}}(0)\, \approx \,0.085$); для графика 2: $r = 1.5$ ($\varphi {\text{'}}(0) \approx 0.104$, $\varphi {\text{''}}(0) \approx 0.065$; $c{\text{/}}r = 40{\text{/}}15 \approx 2.6666$) (случай $\lambda $ < r).

Данные к графикам на фиг. 7а (графики на фиг. 7б те же в другом масштабе): $c = 1.95$ ($\rho \approx 0.026$); для графика 1: $\mu = 0.2$ ($\rho < \mu m{\text{/}}c \approx 0.2$) и ${{\sigma }^{2}} = 0.275$, $\varphi {\text{'}}(0) \approx 0.065$, $\varphi {\text{''}}(0) \approx 0.005457$; для графика 2: ${{\sigma }^{2}} = 0$, $r = 0.01$ ($\rho > rm{\text{/}}c \approx 0.01$), $\varphi {\text{'}}(0) \approx 0.048$, $\varphi {\text{''}}(0) \approx - 0.000368$ (случай $\lambda > r$); для графика 3 – графика функции ${{\varphi }_{0}}(u)$ в модели без инвестиций: $\mu = {{\sigma }^{2}} = 0$, $\varphi _{0}^{'}(0) \approx 0.013$, $\varphi _{0}^{{''}}(0) \approx - 0.000164$.

Графики на фиг. 1–7 демонстрируют преимущества применения рисковых инвестиций по сравнению с безрисковыми в зоне малых значений НК, причем это преимущество может быть более или менее значительным в зависимости от параметров, в частности, от разницы между параметрами $\mu $ и $r$. Кроме того, фиг. 3–6 демонстрируют зависимость наличия или отсутствия гладкости ВНР, соответствующей безрисковой стратегии, от соотношения параметров $\lambda $ и $r$ (см. также замечания 3, 5).

Данные к графикам на фиг. 8: $c = 4$ ($\rho = - 1{\text{/}}2$); для графика 1: $\mu = 0.25$ ${{\sigma }^{2}} = 0.2$, $\varphi {\text{'}}(0) \approx 0.00734$, $\varphi {\text{''}}(0) \approx 0.002392$; для графика 2: ${{\sigma }^{2}} = 0$, $r = 0.2$, $\varphi {\text{'}}(0) \approx 0.009743$, $\varphi {\text{''}}(0) \approx 0.002923$ (случай $\lambda > r$).

Графики на фиг. 8 показывают, что при малой разнице параметров $\mu $ и $r$ безрисковый актив может полностью доминировать рисковый с рассматриваемыми параметрами при всех значениях НК.

Данные к графикам на фиг. 9а (графики на фиг. 9б те же в другом масштабе): $c = 4$ ($\rho = - 1{\text{/}}2$); параметры составляющих портфеля: $\mu = 0.25$, ${{\sigma }^{2}} = 0.855$; $r = 0.1$; для графика 1: $\alpha = 2{\text{/}}3$, φ'(0) ≈ ≈ $0.0003634$, $\varphi {\text{''}}(0) \approx 0.0001617$; для графика 2: $\alpha = 0.5$, $\varphi {\text{'}}(0) \approx 0.002272$, $\varphi {\text{''}}(0) \approx 0.0006904$; для графика 3: $\alpha = 1{\text{/}}3$, $\varphi {\text{'}}(0) \approx 0.003087$, $\varphi {\text{''}}(0) \approx 0.001055$; для графика $4$: $\alpha = 0.1$, $\varphi {\text{'}}(0) \approx 0.002273$, $\varphi {\text{''}}(0) \approx 0.0006872$; для графика 5: $\alpha = 0$, $\varphi {\text{'}}(0) \approx 0.001461$, $\varphi {\text{''}}(0) \approx 0.0004019$ (случай $\lambda > r$).

Данные к графикам на фиг. 10а (графики на фиг. 10б те же в другом масштабе): $c = 4$ ($\rho $ = –1/2); параметры составляющих портфеля: $\mu = 0.25$, ${{\sigma }^{2}} = 0.855$; $r = 0.24$; для графика 1: $\alpha = 2{\text{/}}3$, $\varphi {\text{'}}(0) \approx 0.002442$, $\varphi {\text{''}}(0) \approx 0.0008301$; для графика 2: $\alpha = 0.5$, $\varphi {\text{'}}(0) \approx 0.006558$, $\varphi {\text{''}}(0) \approx 0.001938$; для графика 3: $\alpha = 1{\text{/}}3$, $\varphi {\text{'}}(0) \approx 0.01$, $\varphi {\text{''}}(0) \approx 0.003708$; для графика 4: $\alpha = 0.1$, $\varphi {\text{'}}(0) \approx 0.014$, $\varphi {\text{''}}(0) \approx 0.004755$; для графика 5: $\alpha = 0$, $\varphi {\text{'}}(0) \approx 0.014$, $\varphi {\text{''}}(0) \approx 0.004306$ (случай $\lambda > r$).

Данные к графикам на фиг. 11а (графики на фиг. 11б те же в другом масштабе): $c = 4$ ($\rho $ = –1/2); параметры составляющих портфеля: $\mu = 0.25$, ${{\sigma }^{2}} = 0.3$; $r = 0.01$; для графика 1: $\alpha = 1$, φ'(0) ≈ 0.00681, $\varphi {\text{''}}(0) \approx 0.121$; для графика 2: $\alpha = 0.5$, $\varphi {\text{'}}(0) \approx 0.002296$, $\varphi {\text{''}}(0) \approx 0.0007372$; для графика 3: $\alpha = 1{\text{/}}3$, $\varphi {\text{'}}(0) \approx 0.0009082$, $\varphi {\text{''}}(0) \approx 0.0002571$; для графика 4: $\alpha = 0.1$, $\varphi {\text{'}}(0) \approx 0.0000042$, $\varphi {\text{''}}(0) \approx 0.0000016$; для графика 5: $\alpha = 0$, $\varphi {\text{'}}(0) \approx 0$, $\varphi {\text{''}}(0) \approx 0$ (случай $\lambda > r$).

Графики на фиг. 9–11 показывают, как может меняться ВНР при изменении доли рискового актива в портфеле. Наиболее явно это влияние можно проследить при малых значениях НК. На фигурах видно, что для выбранных значений доли рискового актива возможны различные ситуации при ее уменьшении вплоть до нулевого значения: на фиг. 9б ВНР сначала возрастает (графики 1–3), а потом убывает (графики 3–5); на фиг. 10б ВНР только возрастает; a на фиг. 11б – только убывает.

ЗАКЛЮЧИТЕЛЬНЫЕ ВЫВОДЫ

Завершено начатое в [1] исследование задачи о влиянии простых инвестиционных стратегий на ВНР в коллективной модели пенсионного страхования в случае экспоненциального распределения случайных доходов СК по договорам пожизненной ренты. Рассматривается ВНР на бесконечном интервале времени при постоянном сохранении фиксированной пропорции рискового и безрискового активов, причем доля рискового актива в инвестиционном портфеле может быть как строго положительной (рисковые инвестиции), так и нулевой (безрисковые инвестиции).

В данной работе кратко формулируются результаты исследования влияния рисковых инвестиций, подробно изложенные в [1], основное же внимание уделяется изучению ВНР при безрисковой стратегии и сравнению ее с рисковыми стратегиями с точки зрения возможности увеличения ВНР при различных значениях НК. Исследование в рамках данной модели, как и в [1], основано на связи ВНР как функции НК с решением корректно поставленной сингулярной задачи для ИДУ, порожденного инфинитезимальным оператором случайного процесса, описывающего динамику резерва СК при рассматриваемой инвестиционной стратегии. Показано, что ИДУ в данном случае является “вырожденным” по отношению к исследованному в [1], однако, сингулярная задача для ИДУ ставится в принципиально другом классе, свойства функций которого определяются “физическими” свойствами ВНР в модели с безрисковыми инвестициями. В частности, устанавливается, что при значениях НК, не меньших величины $c{\text{/}}r$, разорение никогда не произойдет, т.е. ВНР при таких значениях равна единице, что невозможно при рисковых инвестициях. С другой стороны, в то время как ВНР в модели с рисковыми инвестициями является, по крайней мере, дважды непрерывно дифференцируемой функцией, выясняется, что ВНР при безрисковой стратегии может (при некоторых соотношениях параметров модели) оказаться даже негладкой функцией, имея разрыв производной в точке $c{\text{/}}r$ и удовлетворяя ИДУ всюду, за исключением указанной точки (см. фиг. 5, 6).

В результате исследования ВНР в модели с безрисковой стратегией и экспоненциальным распределением случайных доходов доказаны существование и единственность решения соответствующей “вырожденной” сингулярной задачи для ИДУ и эквивалентность этой задачи некоторой сингулярной задаче для ОДУ, получено ее явное решение, исследованы свойства этого решения, позволяющие судить о качественном характере поведения ВНР при значениях НК, меньших величины $c{\text{/}}r$.

При заданных параметрах процесса страхового риска и финансовых активов судить о целесообразности включения в портфель рисковых активов в той или иной пропорции по отношению к безрисковой части с точки зрения возможности увеличения ВНР при малых значениях НК (точнее, при НК, не превосходящем величины $c{\text{/}}r$), позволяют теоретически обоснованные численные расчеты, примеры которых представлены на фиг. 1–11. (При значениях НК, не меньших этого уровня, как уже говорилось, неразорение с вероятностью единица обеспечивается вложением всего капитала в безрисковый актив, а вложение в рисковый всегда приводит к ненулевой вероятности разорения, и включать его в портфель в таком случае не является целесообразным.) Представленные графики показывают, что при малых значениях НК простые рисковые стратегии (напомним, что параметры $\mu $, $\sigma $ могут интерпретироваться как параметры инвестиционного портфеля) в некоторых случаях дают существенное увеличение ВНР по сравнению с безрисковой стратегией. С другой стороны, как показано в [1], применение рисковых портфелей с относительно большой волатильностью дает уменьшение ВНР по сравнению с ВНР в модели без инвестиций при любом значении НК, и в этом случае безрисковые инвестиции, очевидно, являются предпочтительными.

Как уже отмечалось в [1], для того, чтобы более полно ответить на вопрос о том, какую роль рисковые активы могут играть в увеличении ВНР, необходимо изучить задачу оптимального динамического управления портфелем активов, в предположении, что доля рискового актива может меняться со временем. Эта задача является предметом отдельного рассмотрения, связанного с исследованием нелинейных ИДУ, что выходит за рамки данной работы (о проблеме оптимального управления инвестициями в разных постановках для классической модели коллективного риска см. [14]–[17]).