Журнал вычислительной математики и математической физики, 2020, T. 60, № 10, стр. 1795-1804

1. ВВЕДЕНИЕ

Реальные социумы редко приходят к консенсусу, хотя его достижение предсказывается классом математических моделей, называемых моделями динамики мнений. Наиболее известная и ранняя работа данного направления, принадлежащая М. де Груту, так и называется: “Достижение консенсуса” [1]. В упрощенном виде, механика таких моделей имеет следующий вид. Позиция индивида по некоторой теме в конкретный момент времени представляется скалярной величиной. Он обсуждает данную тему с другими индивидами, и все они корректируют свои позиции, делая шаги навстречу друг другу. Таким образом, гипотеза о поведении индивида состоит в том, что свою позицию в момент времени $t + 1$ он определяет как взвешенное среднее позиций различных индивидов (в том числе своей) в момент времени $t$. Величины весов задаются так называемой матрицей влияния, элементы которой имеют смысл влиятельности мнения $j$-го индивида для $i$-го. При таком предположении в обществе неминуемо достигается консенсус, т.е. все индивиды с течением времени приходят к одному и тому же мнению (за исключением особого случая, когда матрица влияния распадается на отдельные блоки).

На сегодняшний день существует довольно много публикаций по моделям динамики мнений (см., например, литературу в [2]–[5]). Между тем, реальные общества (и большие группы) редко приходят к консенсусу; более того, часто динамика направлена в сторону поляризации мнений, а не достижения консенсуса. Иногда формируются взаимодействующие сообщества “левых” и “правых”, которые не сближаются друг с другом. Часто возникают группы идеологических меньшинств, называемые эхо-камерами (см. [6]–[8]), способные оставаться на своей позиции (или радикализироваться), несмотря на информационное доминирование “партии большинства”. Не достижение консенсуса, а наоборот, поляризация фиксируется постоянно растущей в объеме политологической литературой (см., например, [9]).

Поэтому для того, чтобы описать социальную реальность, требуется математическая модель, основанная на более сложных положениях о поведении индивидов.

В работе [7] мы предложили такую модель, основанную на нейрологической схеме Рашевского (см. [10]). Настоящая работа посвящена анализу ее математических свойств.

Данная модель лежит в русле моделирования информационного противоборства, в рамках которого можно выделить несколько подходов. Так, ряд работ посвящены моделям конкурирующих слухов (competing rumors) (см. [11], [12]). Они разрабатываются в рамках традиции моделей слухов (rumor models), исходящей из аналогии между передачей информации от индивида к индивиду и эпидемии заражением, и не учитывающей влияния масс-медиа. Данная традиция восходит к ранним работам [13], [14].

Альтернативный подход, предложенный в работе [15] (см. также [16]), учитывает не только межличностную коммуникацию, но и влияние масс-медиа. Эмпирическое основание для этого дает, в частности, работа [17], в которой изучались этнические чистки в Руанде, и было показано, что чистки были наиболее интенсивными в деревнях, принимающих радиостанцию RTLM (которая пропагандировала насилие), а также соседних, связанных с ними межличностной коммуникацией жителей.

Если говорить в целом об эмпирических работах соответствующей тематики, то большинство из них анализирует содержание публикаций в интернете либо поисковых запросов (см., например, [18]–[20]).

Настоящая работа развивает подход, в котором основное внимание уделяется принятию индивидом решения о том, какую из двух конкурирующих партий поддержать.

Рассматривается процесс пропагандистской битвы (propaganda battle) противоборства двух партий: Левой ($L$) и Правой ($R$). Каждая из них имеет аффилированные СМИ, распространяющие информационные сообщения в пользу своей партии. Эти сообщения распространяются далее сторонниками, причем в каждый момент времени каждый член населения является сторонником ровно одной из партий. С течением времени индивид может переходить на сторону другой партии неограниченное количество раз.

Математическая модель основана на нейрологической схеме Рашевского (см. [10]), на выходе которой формируется манифестируемая политическая позиция, т.е. поддержка конкретным индивидом той или иной партии (см. также похожее, но иное применение данного подхода в [21]). Эта манифестируемая позиция индивида $i$ отражает его латентную позицию ${{\lambda }_{i}}\left( t \right)$, которая является непрерывной скалярной функцией времени. Именно, манифестируемая позиция в момент времени $t$ равна $R$, если ${{\lambda }_{i}}\left( t \right) \geqslant 0$, и она равна $L$, если ${{\lambda }_{i}}\left( t \right) < 0$. Чем больше абсолютное значение ${{\lambda }_{i}}\left( t \right)$, тем более твердым является сторонник партии.

Далее, латентная позиция индивида имеет вид ${{\lambda }_{i}}\left( t \right) = {{\varphi }_{i}} + \psi \left( t \right)$, где ${{\varphi }_{i}}$ – это постоянная в течение битвы установка (attitude) данного индивида, описывающая его предрасположенность к поддержке той или иной партии, $\psi \left( t \right)$ – динамическая составляющая, которая одинакова для всех членов населения и меняется в ходе пропагандисткой битвы под влиянием информационных факторов, таких как пропагандистское медиавещание сторон и межличностное общение. Очевидно, что рост функции $\psi \left( t \right)$ описывает рост численности сторонников партии $R$ и наоборот.

2. БАЗОВАЯ МОДЕЛЬ

В этом разделе описывается базовая модель выбора позиций индивидами (см. [22]).

В соответствии со сказанным выше численность сторонников Правой партии равна

а Левой партии где $n\left( \varphi \right)$ – распределение установок среди индивидов в населении.

Функция $n\left( \varphi \right)$ является основной характеристикой социума. Например, нормальное распределение с центром в нуле соответствует консолидированному обществу, в котором большинство членов имеют центристскую политическую позицию. Двугорбая функция $n\left( \varphi \right)$ с одним горбом левее нуля, другим – правее, соответствует поляризованному обществу, в котором преобладают индивиды выраженных левых и правых взглядов, а политический центр является малочисленным (см., например, [9]).

Уравнение для функции $\psi \left( t \right)$ имеет вид

где ${{b}_{R}}$ (${{b}_{L}}$) – интенсивность пропаганды Правой (Левой) партии через СМИ, $C$ – положительная величина, описывающая активность в распространении информации через межличностную коммуникацию. Слагаемое $a\psi $ описывает релаксацию.

Из (2.1)–(2.3) получаем базовую модель (см. [22])

где ${{N}_{0}}$ – размер всего населения.

Начальное условие для уравнения (2.4) имеет вид

На основании данной базовой модели в [22] была разработана более сложная модель, учитывающая ассортативность и дифференцированное пользование средствами массовой информации, а в [23] – модель информационного противоборства, учитывающая положения теории информационной повестки дня (см. [24], [25]).

3. ИССЛЕДУЕМАЯ МОДЕЛЬ

Предположим теперь, что население состоит из двух групп, каждая из которых характеризуется собственным распределением ${{n}_{1}}\left( \varphi \right)$, ${{n}_{2}}\left( \varphi \right)$, и люди больше общаются внутри своих групп, чем с членами другой группы. Пусть ${{N}_{1}}$ – размер первой группы, а ${{N}_{2}}$ – размер второй группы. Далее, первая группа имеет распределение, смещенное влево (индивиды предрасположены к поддержке партии $L$), для определенности положим его нормальным:

и распределение второй группы смещено вправо (индивиды предрасположены к поддержке партии $R$): Здесь параметр $p > 0$ описывает поляризацию населения. Для симметрии положим этот параметр одинаковым для каждой из групп.

Характер межгруппового общения математически описывается параметром $\gamma $, который представляет ассортативность. По своему смыслу $\gamma $ – это доля контактов внутри группы в общем количестве контактов каждого индивида. Считается, что индивид внутри своей группы общается как минимум не менее интенсивно, чем с представителями других групп, поэтому $\gamma \geqslant 1{\text{/}}2$. При этом $\gamma = 1$ означает, что каждый человек общается только с членами своей группы, а $\gamma = 0.5$ относится к ситуации, в которой у людей нет предпочтений в общении. Таким образом, $\gamma \in \left[ {1{\text{/}}2;1} \right]$.

Окончательно модель из [22] имеет вид

Итак, описываемая моделью социальная ситуация следующая. Общество состоит из двух групп. Члены каждой из групп коммуницируют в большей мере в своем кругу, но отчасти также (при $\gamma < 1$) с членами другой группы. Все члены общества в равной мере подвержены влиянию медийной пропаганды обеих партий.

Замечание. Дизайн модели позволяет рассматривать ситуации с неполным охватом аудитории средствами массовой информации и с дифференцированным потреблением информации, когда одна группа больше получает пропаганду Левой партии, другая – Правой; в связи с этим см. Заключение.

Из уравнений (3.3) определяются функции ${{\psi }_{1}}\left( t \right)$, ${{\psi }_{2}}\left( t \right)$, что позволяет найти численности сторонников каждой из партий в каждой из групп по формулам, аналогичным (2.1), (2.2).

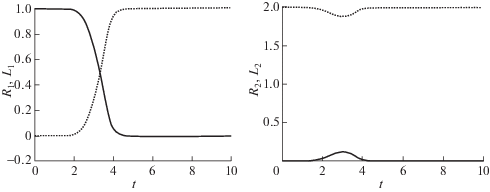
Вычислительные эксперименты показывают, что при определенных параметрах и начальных условиях динамика числа сторонников в одной из групп может быть немонотонна (фиг. 1).

4. КОЛИЧЕСТВО ПОЛОЖЕНИЙ РАВНОВЕСИЯ И ИХ УСТОЙЧИВОСТЬ

Настоящий раздел посвящен аналитическому исследованию системы (3.3). При этом мы не рассматриваем “крайние” случаи, т.е. считаем, что $\gamma \in \left( {1{\text{/}}2;1} \right)$. При различных значениях параметров система может иметь разное количество устойчивых стационарных решений. Некоторые из этих стационарных решений соответствуют победе (т.е. большему числу сторонников при $t \to \infty $) Правой партии, другие – Левой. Далее нас будет интересовать вопрос о количестве состояний равновесия, их устойчивости и исходе информационной борьбы в зависимости от параметров модели.

Уравнения (3.3) могут быть записаны в виде

Поделим каждое из уравнений на $a\left( {1 - \gamma } \right)$ (как указано выше, мы не рассматриваем вырожденный случай, когда $\gamma = 1$), получим

Введем обозначения

Тогда уравнения примут вид

Отсюда следует, что по разные стороны от кривой ${{\psi }_{2}} = f\left( {{{\psi }_{1}}} \right)$ разные знаки имеет величина $\gamma \tfrac{{d{{\psi }_{1}}}}{{dt}} - \left( {1 - \gamma } \right)\tfrac{{d{{\psi }_{2}}}}{{dt}} = \tfrac{d}{{dt}}\left[ {\gamma {{\psi }_{1}} - \left( {1 - \gamma } \right){{\psi }_{2}}} \right]$), а по разные стороны от кривой ${{\psi }_{1}} = g\left( {{{\psi }_{2}}} \right)$ разные знаки имеет величина $\left( {1 - \gamma } \right)\tfrac{{d{{\psi }_{1}}}}{{dt}} - \gamma \tfrac{{d{{\psi }_{2}}}}{{dt}}$.

Это соображение позволяет строить фазовые портреты при различных значениях параметров. При выполнении условий ${{\psi }_{1}} = g\left( {{{\psi }_{2}}} \right)$, ${{\psi }_{2}} = f\left( {{{\psi }_{1}}} \right)$, имеем

что означает при условии $\gamma > 1{\text{/}}2$т.е. точка пересечения ${{\psi }_{2}} = f\left( {{{\psi }_{1}}} \right)$ и ${{\psi }_{1}} = g\left( {{{\psi }_{2}}} \right)$ представляет положение равновесия системы (3.1).

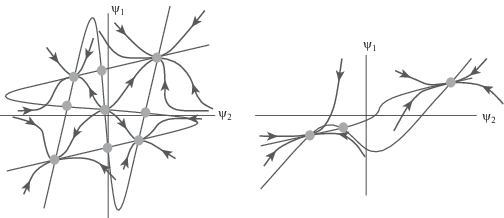
Ввиду нормальности распределений $n\left( \varphi \right)$ кривая ${{\psi }_{2}} = f\left( {{{\psi }_{1}}} \right)$ имеет N-образную форму, а кривая ${{\psi }_{1}} = g\left( {{{\psi }_{2}}} \right)$ – S-образную (см. фиг. 2). Следовательно, они могут иметь от 1 до 9 пересечений в зависимости от параметров.

При построении фазового портрета будем использовать следующий алгоритм.

1. Проводим прямые из семейств $\gamma {{\psi }_{1}} - \left( {1 - \gamma } \right){{\psi }_{2}} = C$ и $\left( {1 - \gamma } \right){{\psi }_{1}} - \gamma {{\psi }_{2}} = C$, где $C$ – некий параметр.

2. Фиксируем какую-либо точку фазовой плоскости. Она является точкой пересечения некоторых двух прямых из различных семейств. Если эта точка лежит выше (ниже) кривой ${{\psi }_{1}} = g\left( {{{\psi }_{2}}} \right)$, то при $t \to + \infty $ она перейдет в точку на прямой из семейства $\left( {1 - \gamma } \right){{\psi }_{1}} - \gamma {{\psi }_{2}} = C$, которая лежит ниже (выше) исходной прямой из этого семейства. Если точка лежит правее (левее) кривой ${{\psi }_{2}} = f\left( {{{\psi }_{1}}} \right)$, то при $t \to + \infty $ она перейдет в точку на прямой из семейства $\gamma {{\psi }_{1}} - \left( {1 - \gamma } \right){{\psi }_{2}} = C$, которая находится левее (правее) исходной прямой из того же семейства.

3. Повторяем первые два пункта для других точек фазовой плоскости.

Рассмотрим наиболее сложный случай с 9 положениями равновесия. Этот случай возможен, когда $\gamma $ близко к 1 (параметр $\gamma $ отвечает за “высоту” пиков), т.е. люди предпочитают общение внутри своей группы. Используя кривые (4.3), построим фазовый портрет (фиг. 2). Здесь 4 устойчивых узла, 1 неустойчивый узел и 4 седла.

Из геометрических соображений (см. описанный выше алгоритм) следует, что (здесь и далее значения функций берутся в точке равновесия):

• если $\left( {f\left( {{{\psi }_{2}}} \right)} \right){\kern 1pt} ' < \left( {{{g}^{{ - 1}}}\left( {{{\psi }_{1}}} \right)} \right){\kern 1pt} '$, положение равновесия – неустойчивый узел;

• если $\left( {f\left( {{{\psi }_{2}}} \right)} \right){\kern 1pt} ' > \left( {{{g}^{{ - 1}}}\left( {{{\psi }_{1}}} \right)} \right){\kern 1pt} '$ и $\left( {f\left( {{{\psi }_{2}}} \right)} \right){\kern 1pt} ' < 0$, положение равновесия – устойчивый узел;

• в любом другом случае положение равновесия – седло (мы не рассматриваем случаи, когда $f\left( {{{\psi }_{1}}} \right)$ и $g\left( {{{\psi }_{2}}} \right)$ касаются).

Дадим аналитическое обоснование этим соображениям.

Теорема. Если кривые $f\left( {{{\psi }_{1}}} \right)$ и $g\left( {{{\psi }_{2}}} \right)$ пересекаются (а не касаются), при этом в точке их пересечения

• $(f({{\psi }_{2}})){\kern 1pt} ' < ({{g}^{{ - 1}}}({{\psi }_{1}})){\kern 1pt} '$, то положение равновесия – неустойчивый узел;

• $(f({{\psi }_{2}})){\kern 1pt} ' > ({{g}^{{ - 1}}}({{\psi }_{1}})){\kern 1pt} '$ и $\left( {f\left( {{{\psi }_{2}}} \right)} \right){\kern 1pt} ' < 0$, то положение равновесия – устойчивый узел.

В любом другом случае положение равновесия – седло.

Доказательство. Запишем систему (3.3) в виде

Матрица Якоби имеет вид

Исследуем теперь собственные значения матрицы, для чего решим следующее характеристическое уравнение:

Чтобы положение равновесия было седлом, собственные значения должны иметь разные знаки. По теореме Виета, если решения квадратного уравнения принимают значения разных знаков, то свободный член отрицателен, т.е.

Так как $\left[ {\mathop {\left( {\tfrac{\gamma }{{1 - \gamma }}} \right)}\nolimits^2 - 1} \right] > 0$, то знак левой части (4.10) зависит от знака выражения $f{\kern 1pt} {\text{'}}g{\kern 1pt} {\text{'}} - 1$. Таким образом, положение равновесия – седло, если $f{\kern 1pt} {\text{'}}g{\kern 1pt} ' < 1$. Если производные принимают значения разных знаков, то это неравенство выполняется автоматически, если же они имеют один и тот же знак, то мы можем записать это неравенство в виде следующего условия: $\left| {f{\kern 1pt} {\text{'}}{\kern 1pt} } \right| < \tfrac{1}{{\left| {g{\kern 1pt} '{\kern 1pt} } \right|}} = {\text{|}}({{g}^{{ - 1}}}){\text{|}}$.

Итак, геометрически положение равновесия – седло, если угловые коэффициенты имеют различные знаки, или модуль наклона функции $f\left( {{{\psi }_{2}}} \right)$ меньше, чем модуль наклона ${{g}^{{ - 1}}}\left( {{{\psi }_{1}}} \right)$. В противном случае положение равновесия – узел (ввиду положительности детерминанта собственные значения вещественны). Все это также подтверждается графиком.

Если собственные значения имеют один и тот же знак и оба отрицательны, то положение равновесия является устойчивым узлом.

Для того чтобы оба собственных значения были отрицательны, необходимо, чтобы в положении равновесия выполнялось неравенство $ - 2 + \tfrac{\gamma }{{1 - \gamma }}g{\kern 1pt} {\text{'}} + \tfrac{\gamma }{{1 - \gamma }}f{\kern 1pt} ' > 0$, т.е. $f{\kern 1pt} {\text{'}} + g{\kern 1pt} {\text{'}} > \tfrac{{2\left( {1 - \gamma } \right)}}{\gamma }$. Покажем, что если производные положительные и графики пересекаются в соответствующем порядке ($\left| {f{\kern 1pt} '{\kern 1pt} } \right| > {\text{|}}({{g}^{{ - 1}}}){\kern 1pt} '{\kern 1pt} {\text{|}}$), то положение равновесия – устойчивый узел. Тогда теорема будет доказана. Данные аналитические закономерности соответствуют графикам на фиг. 2.

Лемма. Пусть $1{\text{/}}2 < \gamma < 1$. Пусть также в некоторой точке $\left( {{{\psi }_{1}},{{\psi }_{2}}} \right)$ имеют место соотношения

Тогда

Доказательство. Обозначим

Тогда неравенство (4.13) примет вид

Так как $\tfrac{\gamma }{{1 - \gamma }} > {{\delta }_{1}}$, $\tfrac{\gamma }{{1 - \gamma }} > {{\delta }_{2}}$, то

В то же время из (4.16) следует, что

Из (4.17), (4.18) имеем

т.е.

Из неравенства (4.16) следует неравенство

т.е.

Отсюда имеем

что и требовалось доказать.

Таким образом, приведенным перед теоремой геометрическим наблюдениям дано аналитическое обоснование.

Как указывалось выше, наличию девяти положений равновесия способствует большое значение параметра $\gamma $. Четыре из них на фиг. 2 являются асимптотически устойчивыми. Например, положение равновесия в первой четверти (${{\psi }_{1}} > 0$, ${{\psi }_{2}} > 0$) соответствует победе Правой партии в обеих группах и, следовательно, в обществе в целом. Положение равновесия во второй четверти (${{\psi }_{1}} < 0$, ${{\psi }_{2}} > 0$) соответствует победе Левой партии в первой группе, Правой партии – во второй и т.д.

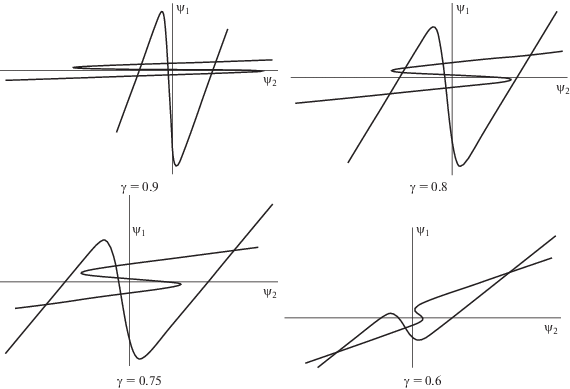
При уменьшении параметра $\gamma $ уменьшается количество положений равновесия, в том числе устойчивых положений равновесия. На фиг. 3 приведен один из возможных сценариев. В данном случае, при $\gamma = 0.8$, фазовый портрет имеет меньше (по сравнению с $\gamma = 0.9$) на одну асимптотически устойчивую точку равновесия и на одну неустойчивую. Другими словами, точка равновесия в четвертой четверти вырождается (т.е. из списка возможных исходов пропагандистской битвы исчезает исход, при котором Правая партия побеждает во второй группе, а Левая партия – в первой). При дальнейшем уменьшении параметра $\gamma $ вырождаются другие положения равновесия, и при $\gamma $, близком к $1{\text{/}}2$, в данном примере остаются только два устойчивых положения равновесия, одно из которых соответствует победе партии $R$ в обеих группах, а другое – победе партии $L$ в обеих группах.

5. ЗАКЛЮЧЕНИЕ

Вернемся к проблеме, поставленной в начале настоящей статьи. Почему реальные общества редко приходят к консенсусу, хотя в соответствии с моделями динамики мнений он является естественным исходом общественной дискуссии?

Одна из причин, имеющих место в большинстве реальных ситуаций, состоит в так называемой селективной экспозиции (selective exposure) (см. [26], [27]), игнорируемой моделями динамики мнений: сторонники одной социальной группы читают левые газеты, сторонники другой группы – правые газеты, что позволяет каждой из групп удержаться от “сползания” к политическому центру. В терминах модели настоящей работы это означало бы, что параметры ${{b}_{R}},{{b}_{L}}$ имеют различные значения в двух группах. Другими словами, первая группа не только имеет левые взгляды (в соответствии с (3.1)), но также склонна читать левую прессу, т.е. для этой группы ${{b}_{R}} - {{b}_{L}} < 0$. Аналогично для второй группы ${{b}_{R}} - {{b}_{L}} > 0$. Однако селективная экспозиция не является необходимым условием отсутствия консенсуса.

Модель выбора позиций индивидами показывает, что даже при недифференцированном получении информации из СМИ в обществе действуют механизмы, препятствующие формированию консенсуса.

Прежде всего данная модель учитывает, что у каждого индивида имеется установка, т.е. предрасположенность к поддержке той или иной партии, сформированная до рассматриваемого противоборства и отражающая его социальный статус, экономическое положение и т.д.

Другое важное отличие от моделей динамики мнений состоит в характере коммуникации между индивидами. Поясним это на следующем примере. Предположим, что индивид А имеет латентную позицию ${{\psi }_{A}} = 2$. Какое влияние на него оказывает индивид В, имеющий позицию ${{\psi }_{B}} = 1$? Логика моделей динамики мнений предполагает, что он убеждает индивида А сдвинуться налево, так как сам находится левее него. В противоположность этому, модель данной работы исходит из того, что оба они – сторонники Правой партии, поэтому индивид В укрепляет индивида А в его верности этой партии. При определенных параметрах это означает, что в результате коммуникации они оба могут сдвинуть свои позиции направо.

Таким образом, индивиды, например, правых взглядов, могут удерживать свою политическую позицию, коммуницируя между собой, даже если они находятся в меньшинстве, а их оппоненты доминируют в СМИ. Именно такая социальная структура называется эхо-камерой. Тем самым, в обществе поддерживается одновременное существование различных политических мнений.