Журнал вычислительной математики и математической физики, 2020, T. 60, № 11, стр. 1815-1822

ВВЕДЕНИЕ

Апостериорным оценкам погрешности для конечно-элементных решений бигармонического уравнения, уравнения изгиба тонких пластин, так же как для сингулярно возмущенных уравнений типа ${{\varepsilon }^{2}}{{\Delta }^{2}}u - \Delta u = \phi $, посвящен целый ряд работ. Такие оценки получены для конформных, неконформных, смешанных методов, разрывного метода Галеркина (DG) и других (см. [1]–[14]). Однако, насколько известно автору, отсутствуют работы, посвященные задаче об изгибе тонкой пластины на винклеровском основании с кусочно постоянным коэффициентом постели, имеющим значительные скачки. В то же время известны работы по апостериорным оценкам погрешности для уравнения реакции-диффузии 2-го порядка с разрывным кусочно постоянным коэффициентом реакции. В них, как правило, допускалось только достаточно “мягкое” изменение коэффициента реакции между соседними конечными элементами, один из вариантов которого можно найти, например, в [15], [16]. В данной работе показано, что это ограничение может быть снято, а область допустимых величин скачков существенно расширена при незначительном ухудшении коэффициентов перед типичными нормами в правых частях апостериорных оценок.

Мы рассматриваем модельную задачу

с $f \in {{L}^{2}}(\Omega )$ и первым краевым условием, в котором ${\mathbf{\nu }}$ – внутренняя нормаль к границе области. Основное отличие от предшествующих работ, включая работы автора [17]–[20], в том, что коэффициент $\sigma = {{\Bbbk }^{2}}$ предполагается поэлементно постоянным и удовлетворяет лишь одному ограничению $\sigma \leqslant c{{h}^{{ - 4}}}$, $c = {\text{const}}$. Очевидно, это относительно слабое ограничение, допускающее весьма большие значения коэффициента и его скачков между смежными конечными элементами. Несколько удивительным оказалось то, что отличия апостериорных оценок, доказываемых в настоящей работе, от полученных при $\sigma \equiv {\text{const}}$ для уравнений 2-го порядка в [17], [18] и для уравнений порядка $2n$, $n \geqslant 1$, в [19], [20] нельзя назвать существенными: в их правых частях содержатся такие же нормы, а коэффициенты перед ними отличаются не более, чем в два раза. К тому же с использованием аппроксимационных свойств ${{L}^{2}}$- и ${{H}^{2}}$-проекций функций на конечно-элементные пространства доказательства оценок простые.

Апостериорные оценки погрешности из работ [17], [18] названы согласованными, благодаря двум важным свойствам:

1) порядок их точности относительно размера сетки $h$ такой же, как априорных оценок точных по порядку,

2) доказательство свойства 1), как и вычисление оценок, может быть выполнено с помощью тестирующих потоков (напряжений/усилий), обладающих лишь достаточными аппроксимационными свойствами и не требующих уравновешивания.

Так называемые эффективные апостериорные оценки погрешности, т.е. такие, для которых есть обратные оценки, являются согласованными и обе точны по порядку. Однако согласованность существенно более просто проверяемое свойство, чем эффективность.

К числу широко применяемых на практике относятся два типа оценок – апостериорные оценки через невязку и оценки, основанные на применении уравновешенных потоков/напря-жений/моментов. К недостаткам оценок первого типа относится то, что их вывод существенно опирается на оценки аппроксимации, в результате чего коэффициенты в оценках существенно зависят от сетки и могут быть завышены. Такого рода эффективная оценка для задачи $\Delta \Delta u = f$ дана, например, в [13]. При применении оценок второго типа для каждого численного решения, например, уравнений второго порядка, находится лишь единственный тестирующий поток, вычисляемый посредством “равновесной” процедуры восстановления потока (equilibrated recovery procedure, см. [21]), зависящей не только от сетки, но и от решаемой задачи. Это понижает универсальность таких оценок. Кроме того, уравновешивание увеличивает диффузионную составляющую ошибки, и степень ее увеличения устанавливается только обратной оценкой, постоянные в которой чаще всего не оптимистичны. В итоге апостериорные оценки обоих типов, интенсивно развивавшиеся несколько последних десятилетий, имеют свои ограничения и их реальная точность, как правило, нуждается в проверке практикой.

Согласованные оценки более универсальны, поскольку для достижения неулучшаемой по порядку точности допускают применение любого тестирующего потока с аппроксимирующими свойствами такими же, как у численного потока, или лучшими. При этом известны многочисленные такие процедуры, преимущественно для восстановления потоков (см. [21]–[24]), глубоко изученные и созданные для оценщиков ошибки через невязку, широко используемых на практике. Главное преимущество согласованных оценок перед оценками со свободной вектор-функцией потока, известными ранее, в том, что они позволяют на порядок уточнить коэффициент перед ${{L}^{2}}$-нормой невязки в правой части (см. [17]–[20]). Техника вывода согласованных, гарантированных, робастных, вычисляемых апостериорных оценок погрешности переносится в настоящей работе на случай поэлементно постоянного коэффициента реакции со значительными скачками на межэлементных границах.

Обозначения ${{\left\| {\, \cdot \,} \right\|}_{k}}$ и ${{\left| {\, \cdot \,} \right|}_{k}}$ используются для норм и квазинорм в соболевских пространствах ${{H}^{k}}(\Omega ) = W_{2}^{k}(\Omega )$ при соглашении, что ${{\left| {\, \cdot \,} \right|}_{0}} = {{\left\| {\, \cdot \,} \right\|}_{0}} = \left\| {\, \cdot \,} \right\|$. Дополнительно нам понадобятся пространства $H_{0}^{2}(\Omega ): = {\text{\{ }}{v} \in {{H}^{2}}(\Omega ):u = \partial u{\text{/}}\partial {v} = 0\;{\text{on}}\;\partial \Omega {\text{\} }}$, $H_{0}^{2}(\Omega ,\Delta \Delta ) = {\text{\{ }}{v} \in H_{0}^{2}(\Omega ):\Delta \Delta {v} \in {{L}^{2}}(\Omega ){\text{\} }}$ и ${{{\mathbf{L}}}^{2}}(\Omega ) = {{({{L}^{2}}(\Omega ))}^{4}}$. В связи с задачей (1) полезно ввести пространство ${\mathbf{M}}(\Omega ) = {\text{\{ }}{\mathbf{m}} = {\text{\{ }}{{m}_{{k,l}}}{\text{\} }}_{{k,l = 1}}^{2} \in $ $ \in {{{\mathbf{L}}}^{2}}(\Omega ):{{m}_{{1,2}}} = {{m}_{{2,1}}}{\text{\} }}$ вектор-функций ${\mathbf{m}}$ и операторы $\mathcal{D}:{{H}^{2}}(\Omega ) \to {\mathbf{M}}(\Omega )$ и $\mathcal{D}{\kern 1pt} *:{\mathbf{M}}(\Omega ) \cap $ $ \cap \;{{{\mathbf{L}}}^{2}}(\Omega ,\mathcal{D}{\kern 1pt} *) \to {{L}^{2}}(\Omega )$, определяемые соотношениями

где ${{{\mathbf{L}}}^{2}}(\Omega ,\mathcal{D}{\kern 1pt} {\text{*}}) = {\text{\{ }}{\mathbf{m}} \in {\mathbf{M}}(\Omega ):\mathcal{D}{\kern 1pt} {\text{*}}{\mathbf{m}} \in {{L}^{2}}(\Omega ){\text{\} }}$. Если (1) есть задача об изгибе тонкой пластинки, вектор-функции ${\mathbf{m}} = \mathcal{D}u$ имеют смысл компонент изгибающих и крутящих моментов. Мы будем называть ${{m}_{{k,l}}}$ моментами, хотя в общем случае (коэффициент Пуассона и цилиндрическая жесткость не равны соответственно нулю и единице) они определяются более сложными выражениями. Там, где это не вызывает недоразумений, для норм ${{\left\| {\, \cdot \,} \right\|}_{{{{{\mathbf{L}}}^{2}}( \cdot )}}}$ в пространствах ${{{\mathbf{L}}}^{2}}({\kern 1pt} \cdot {\kern 1pt} )$ используется обозначение $\left\| {\, \cdot \,} \right\|$, например, $\left\| {\mathbf{m}} \right\|$ обозначает ${{\left\| {\mathbf{m}} \right\|}_{{{{{\mathbf{L}}}^{2}}(\Omega )}}}$.

Для простоты мы ограничиваемся случаем полигональной области $\Omega \subset {{\mathbb{R}}^{d}}$, $d = 2$, которая триангулирована совместными квазиоднородными треугольными конечными элементами ${{\tau }_{r}}$, $r = 1,\;2,\; \ldots ,\;\mathcal{R}$, размера $h$, понимаемого как наибольший из диаметров треугольников ${{\tau }_{r}}$ (см. [25], [26]). Предполагаем, что комплекс конечных элементов индуцирует пространство ${{\mathcal{V}}_{h}}(\Omega ) \subset {{H}^{2}}(\Omega )$ и подпространство ${{\mathcal{V}}_{{h,0}}}(\Omega ) = {\text{\{ }}{v} \in {{\mathcal{V}}_{h}}(\Omega ):{v} = \partial {v}{\text{/}}\partial {\mathbf{\nu }} = 0\;{\text{on}}\;\partial \Omega {\text{\} }}$. На самом деле, результаты обобщаются на произвольные достаточно гладкие области, поскольку приемы, предложенные в [27], [28], позволяют получать конечно-элементные комплексы, определенные на таких областях посредством использования вблизи гранцы специальных криволинейных конечных элементов. Они порождают пространства ${{\mathcal{V}}_{{h,0}}}(\Omega )$, которые обеспечивают те же порядки аппроксимации и сходимости, как в случае полигональных $\Omega $.

1. ОБЩАЯ АПОСТЕРИОРНАЯ ОЦЕНКА

Пусть $a(w,{v}) = (\mathcal{D}w,\mathcal{D}{v})$, $\mathbb{V}(\Omega )$ – гильбертово пространство функций со скалярным произведением $[w,{v}] = a(w,{v}) + (\sigma w,{v})$ и нормой ${{\left| {\left\| {v} \right\|} \right|}^{2}} = [{v},{v}]$, и ${{\mathbb{V}}_{0}}(\Omega ) = {\text{\{ }}{v} \in \mathbb{V}(\Omega ):{v} = \partial {v}{\text{/}}\partial {\mathbf{\nu }} = 0\;{\text{on}}\;\partial \Omega {\text{\} }}$. В слабой форме задачи (1) требуется найти функцию $u \in {{\mathbb{V}}_{0}}(\Omega )$, удовлетворяющую интегральному тождеству

где $\sigma = {{\sigma }_{r}} = {\text{const}}$ при $x \in {{\tau }_{r}}$, $r = 1,\;2\; \ldots ,\;\mathcal{R}$. Для широкого круга приближений решения $u$, в том числе полученных численными методами, слабая норма погрешности приближения меньше его сильной нормы. То есть, если ${v}$ – такое приближение, ${v} \in H_{0}^{2}(\Omega )$, и $e = {v} - u$ – его погрешность, то при некотором ${{\lambda }_{e}} > 1$ выполняется, например, неравенство, ср. [19, (5)], Ниже используются также обозначения ${{\sigma }_{{{\text{max}}}}} = {{\left\| \sigma \right\|}_{{{{L}^{\infty }}(\Omega )}}}$ и ${{\sigma }_{{{\text{min}}}}} = mi{{n}_{{x \in \Omega }}}\sigma $.

Лемма 1. Пусть $u \in H_{0}^{2}(\Omega ,\Delta \Delta )$, выполняется неравенство (3), $\sigma $ – произвольная неотрицательная поэлементно постоянная функция и $\sigma \leqslant {{\sigma }_{ * }}$ при некотором ${{\sigma }_{ * }} = {\text{const}} \leqslant {{\lambda }_{{\text{e}}}}$. Тогда для любой функции ${v} \in H_{0}^{2}(\Omega )$ и любой вектор-функции ${\mathbf{m}} \in {\mathbf{M}}(\Omega ) \subset {{{\mathbf{L}}}^{2}}(\Omega ,\mathcal{D}{\kern 1pt} *)$ справедлива оценка

в которой $\Theta = max({{\Theta }_{e}},\gamma )$ и

Доказательство. Доказательство лишь незначительно отличается от доказательства [19, теорема 1] для уравнений порядка $2n$ типа реакции-диффузии с постоянным $\sigma = {\text{const}}$, см. также [17, lemma 1], и поэтому представлено кратко. Интегрируя по частям и применяя неравенство Коши, получаем

Для второго сомножителя правой части, используя (3), при любом $\beta \in [1,{{\sigma }_{ * }}{\text{/}}{{\sigma }_{{{\text{max}}}}}]$ можно написать Теперь выберем такое $\beta = \beta ({{\lambda }_{e}},{{\sigma }_{ * }},{{\sigma }_{{{\text{min}}}}})$, чтобы правая часть (7) приняла форму $\beta {{\left| {\left\| e \right\|} \right|}^{2}}$. Для этого должно выполняться условие из которого получаем $\beta $, данное в (5).

Коэффициент $\beta $, найденный согласно (5), может быть больше ${{\sigma }_{ * }}{\text{/}}{{\sigma }_{{{\text{max}}}}}$. В этом случае $\beta = {{\sigma }_{ * }}{\text{/}}{{\sigma }_{{{\text{max}}}}}$ – максимальное допустимое значение и, переобозначив его через $\gamma $, подставляем в правую часть (7). Комбинируя рассмотренные два случая, приходим к выражению для $\Theta $, фигурирующему в (4).

Сделаем несколько замечаний относительно коэффициентов перед нормами в правой части (4). Прежде всего мы видим, что всегда $\Theta \leqslant 2$. При $\sigma = {\text{const}}$, что означает ${{\sigma }_{{{\text{min}}}}} = {{\sigma }_{{{\text{max}}}}} = \sigma $, имеем $\Theta = \beta = ({{\lambda }_{{\text{e}}}} + {{\sigma }_{ * }}){\text{/}}({{\lambda }_{{\text{e}}}} + \sigma )$, и, как известно (см., например, [19]), ${{\lambda }_{{\text{e}}}} = \mathcal{O}({{h}^{{ - 4}}})$ для решений методом конечных элементов в ${{H}^{4}}$-регулярных областях. Следовательно, в этом случае (4) совпадает с согласованными оценками из [19] (точными по порядку для приближенных решений методом конечных элементов при подстановке в них тестирующих моментов достаточной точности) и обладает указанными в этой работе достоинствами. Из (5) следует, что среди значений $\varkappa : = {{\sigma }_{ * }}{\text{/}}{{\sigma }_{{{\text{max}}}}}$, при которых можно использовать $\Theta = \beta $, наименьшая величина, обозначаемая $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varkappa } $, достигает максимума при ${{\sigma }_{ * }} = {{\lambda }_{{\text{e}}}}$ и ${{\sigma }_{{{\text{min}}}}} = 0$. При этом $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varkappa } = 2$ и уменьшается при ${{\sigma }_{ * }} < {{\lambda }_{{\text{e}}}}$.

Очевидно, что в общем случае простейшим выбором для использования в (4), (5) будет ${{\sigma }_{ * }} = {{\lambda }_{e}} = 1{\text{/}}{{c}_{F}}$, где ${{c}_{F}}$ – постоянная из неравенства типа неравенства Фридрихса

Если дополнительно ${{\sigma }_{{{\text{min}}}}} = 0$, то $\Theta = 2$, и оценка (4) принимает простейший вид аналогичный известной оценке для приближенных решений уравнения Пуассона (см., например, [29]). Однако необходимо иметь в виду два обстоятельства. 1) В соответствии с леммой 1 оценка (10) справедлива не только при постоянном $\sigma $, но и при кусочно-постоянном с произвольными ${{\sigma }_{r}}$ из отрезка $[0,{{c}_{F}}]$. Это относится и к оценке работы [29], полученной для случая постоянного $\sigma $. 2) Выбор ${{\sigma }_{ * }} = {{\lambda }_{e}} = 1{\text{/}}{{c}_{F}}$ делает коэффициент перед нормой невязки в $\mathcal{M}$ (см. (4)) значительно превосходящим его точное значение.

Если $u \in H_{0}^{2}(\Omega ,\Delta \Delta )$ и ${v}$ принадлежит тому же пространству, что может иметь место при применении метода Галеркина, то можно использовать ${\mathbf{m}} = \mathcal{D}{v}$. При этом апостериорная оценка в случае ${{\sigma }_{{{\text{min}}}}} = 0$ принимает вид

2. АПОСТЕРИОРНЫЕ ОЦЕНКИ ПОГРЕШНОСТИ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ

В этом разделе мы получим две оценки на основе двух предположений (А) и (В), сформулированных ниже. Пусть $H_{0}^{l}(\Omega ): = {{H}^{l}}(\Omega ) \cap H_{0}^{2}(\Omega )$, $l \geqslant 2$, и 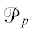– пространство полиномов степени не выше $p$ по совокупности переменных.

(A) Область триангулирована геометрически совместными треугольными конечными элементами, удовлетворяющими условиям квазиоднородности с параметром сетки $h$, понимаемым как максимальный из диаметров конечных элементов (см., например, [26], [30]). Конечно-элементный ансамбль индуцирует пространство ${{\mathcal{V}}_{{h,0}}}(\Omega ) = \{ {v} \in H_{0}^{2}(\Omega ):{{\left. {v} \right|}_{{{{\tau }_{r}}}}} \in {{\mathcal{P}}_{p}},\;r = 1,\;2,\; \ldots ,\;\mathcal{R}\} $, при этом существует такой линейный оператор ${{Q}_{h}}:H_{0}^{2}(\Omega ) \mapsto {{\mathcal{V}}_{{h,0}}}(\Omega )$, что для $\forall w \in H_{0}^{l}(\Omega )$ найдется аппроксимация $\tilde {w} = {{Q}_{h}}w$, для которой

для $k = 0,\;1,\;2$, $l = 2,\; \ldots ,\;p + 1$.

(B) Область $\Omega $ такова, что при $\sigma \equiv 0$, любой $f \in {{L}^{2}}(\Omega )$ и некоторой постоянной ${{c}_{ \circ }}$, решение $u$ задачи (1) удовлетворяет неравенству

Заметим, что если $\sigma = {\text{const}} \geqslant 1$, то постоянная ${{c}_{ \circ }}$ не больше удвоенной ${{c}_{ \circ }}$ для случая $\sigma \equiv 0$ (см. [19]).

В некоторых ситуациях неравенство (3) доказывается просто. Введем обозначения ${{e}_{{{\text{fem}}}}} = {{u}_{{{\text{fem}}}}} - u$ (${{u}_{{{\text{fem}}}}}$ – решение метода конечных элементов для задачи (1)), ${{u}_{\Delta }}$ – конечно-элементная функция, минимизирующая функционал ${{\left\| {\mathcal{D}({v} - u)} \right\|}^{2}}$ на ${v} \in {{\mathcal{V}}_{{h,0}}}(\Omega )$, ${{e}_{\Delta }} = {{u}_{\Delta }} - u$ – соответствующая погрешность, и, наконец, ${{\lambda }_{\Delta }}$ – число, удовлетворяющее неравенству

Через ${{\lambda }_{{{\text{fem}}}}}$ обозначим число ${{\lambda }_{{\text{e}}}}$ для погрешности $e = {{e}_{{{\text{fem}}}}}$.

Теорема 1. Пусть $u \in H_{0}^{2}(\Omega ,\Delta \Delta )$, выполняются предположения (A), (B), $\sigma $ – произвольная положительная поэлементно постоянная функция со значениями ${{\sigma }_{r}}$ на отрезке $[{{\sigma }_{{{\text{min}}}}},{{\sigma }_{{{\text{max}}}}}]$ и $\sigma \leqslant {{\sigma }_{ * }}$ при некотором ${{\sigma }_{ * }} = {\text{const}} \leqslant {{\lambda }_{{{\text{fem}}}}}$. Пусть также ${{\sigma }_{{{\text{max}}}}}{\text{/}}{{\sigma }_{{{\text{min}}}}} \geqslant {{c}_{\sigma }} > 0$. Тогда для $e = {{e}_{{{\text{fem}}}}}$ справедлива апостериорная оценка (4), (5) с $\lambda _{{\text{e}}}^{{ - 1}} = \lambda _{{{\text{fem}}}}^{{ - 1}} = {{c}_{\sigma }}{{({{c}_{ \circ }}{{c}_{{2,4}}}{{h}^{2}})}^{2}}$.

Доказательство. Помимо леммы 1, ключевым фактом доказательства является неравенство

которое является следствием оценки скорости сходимости в ${{H}^{2}}(\Omega )$, вытекающей из (12), (13), и трюка Обэна–Нитше (см. [31], [32]). Доказательство (15) для более общего случая можно найти в [19, lemma 1]. В рассматриваемом случае определения погрешностей ${{e}_{{{\text{fem}}}}}$ и $e$ приводят к неравенствам при этом первое из них получаем аналогично случаю $\sigma = {\text{const}}$ (см. [18]). Из (16) следует и, комбинируя (15), (17) и лемму 1, подтверждаем теорему 1.

Имеется другой путь вывода апостериорной оценки, робастной для всех $\sigma \leqslant \mathbb{C}{{h}^{{ - 4}}}$, $\mathbb{C} = {\text{const}}$, в отличие от оценки (4), (5), (17), теряющей точность с ростом ${{c}_{\sigma }}$ (см. ниже). Обозначение $\hat {f}$ используем для функции, имеющей на каждом конечном элементе вид ${{\left. {\hat {f}} \right|}_{{{{\tau }_{r}}}}} = {{f}_{r}} = Q_{h}^{r}f$, где $Q_{h}^{r}:{{L}^{2}}({{\tau }_{r}}) \mapsto {{\mathcal{P}}_{p}}$ – оператор ортогональной ${{L}^{2}}$-проекции на пространство ${{\mathcal{P}}_{p}}$ полиномов степени не выше $p$.

Теорема 2. Пусть $u \in H_{0}^{2}(\Omega ,\Delta \Delta )$, ${{u}_{{{\text{fem}}}}} \in {{\mathcal{V}}_{{h,0}}}(\Omega )$, где ${{u}_{{{\text{fem}}}}}$ – решение метода конечных элементов, и ${\mathbf{m}} \in {{{\mathbf{L}}}^{2}}(\Omega ,\mathcal{D}{\kern 1pt} *)$. Пусть также предположения (A), (B) выполняются и $0 \leqslant \sigma \leqslant {{\sigma }_{ * }} \leqslant {{\lambda }_{\Delta }}$. Тогда

причем $\Theta = 1 + {{\sigma }_{ * }}{\text{/}}\lambda $, и можно принять ${{\lambda }_{\Delta }} = \mathbb{C}{{h}^{{ - 4}}}$, $\mathbb{C} = 1{\text{/}}{{({{c}_{ \circ }}{{c}_{{2,4}}})}^{2}}$.

Доказательство. Так же, как в (6), для $e = {{e}_{{{\text{fem}}}}} = {{u}_{{{\text{fem}}}}} - u$ и $\forall w \in {{\mathcal{V}}_{{h,0}}}(\Omega )$, интегрируя по частям и применяя неравенство Коши, получаем

Пусть ${{Q}_{\Delta }}:H_{0}^{2}(\omega ) \mapsto {{\mathcal{V}}_{{h,0}}}$ – оператор ортогонального проектирования, сопоставляющий ${{u}_{\Delta }}$ каждой функции $u \in H_{0}^{2}(\omega )$. Положив $w = - {{Q}_{\Delta }}{{e}_{{{\text{fem}}}}}$, видим, что $e + w = (I - {{Q}_{\Delta }})e = e$ и далее Нормы $\left\| {\Delta {{e}_{\Delta }}} \right\|$ и $\left\| {{{e}_{\Delta }}} \right\|$ оценены в (16) и (14), (17) соответственно. Как следствие, получаем оценку которая вместе с (19) завершает доказательство.

Для повышения точности апостериорной оценки важен правильный выбор вектор-функции моментов ${\mathbf{m}}$, для вычисления которой применяется, как правило, процедура восстановления моментов. Эти процедуры являются аналогами процедур восстановления потоков для решений метода конечных элементов эллиптических уравнений второго порядка и по решению ${{u}_{{{\text{fem}}}}}$ вычисляют вектор-функцию ${\mathbf{m}}$ подходящего конечно-элементного пространства $\mathbb{M}(\Omega ) \subset {{{\mathbf{L}}}^{2}}(\Omega ,\mathcal{D}*)$. Наиболее популярную из них называют процедурой осреднения. В ней любой узловой параметр функции ${{m}_{{k,l}}}$ любого узла определяется осреднением с весами значений ${{\partial }^{2}}{{u}_{{{\text{fem}}}}}{\text{/}}\partial {{x}_{k}}\partial {{x}_{l}}$ или производных от ${{\partial }^{2}}{{u}_{{{\text{fem}}}}}{\text{/}}\partial {{x}_{k}}\partial {{x}_{l}}$, соответствующих узловому параметру, по элементам, содержащим узел. Весами служат отношения площадей конечных элементов к площади звезды конечных элементов, содержащих узел (см. [13], [21], [22]). В качестве $\mathbb{M}(\Omega )$ удобно использовать пространство $\mathbb{M}(\Omega ) = {{[{{\mathcal{V}}_{h}}(\Omega )]}^{4}}$. Однако для согласованности порядков точности левой и правой частей апостериорной оценки достаточно использовать более простые пространства, обеспечивающие на два порядка меньшие, чем пространство ${{[{{\mathcal{V}}_{h}}(\Omega )]}^{4}}$, порядки аппроксимации. Нередко прибегают к процедуре наименьших квадратов, определяя моменты ${{m}_{{k,l}}}$ как ${{L}^{2}}(\Omega )$ ортогональные проекции производных ${{\partial }^{2}}{{u}_{{{\text{fem}}}}}{\text{/}}\partial {{x}_{k}}\partial {{x}_{l}}$ на соответствующее подпространство ${{\mathbb{M}}_{{k,l}}}(\Omega )$ пространства $\mathbb{M}(\Omega )$. Примеры процедур восстановления моментов и потоков можно найти в [13], [21], [33] и других работах.

ЗАКЛЮЧЕНИЕ

Как отмечалось во введении, известные апостериорные оценки погрешности при поэлементно постоянном коэффициенте реакции были получены при условии его слабой локальной вариации. Последнее может подразумевать, например, что на каждой подобласти ${{\bar {\delta }}_{r}}: = \cup {{\bar {\tau }}_{{r'}}}$, являющейся объединением таких конечных элементов, для которых ${{\bar {\tau }}_{{r'}}} \cap {{\bar {\tau }}_{r}} \ne \emptyset $, имеем ${{\sigma }_{{r'}}} \leqslant \hat {c}{{\sigma }_{r}}$ для ${{\sigma }_{r}} > 0$ и ${{\sigma }_{{r'}}} \leqslant \hat {c}$ для ${{\sigma }_{r}} = 0$. Оценки данной работы имеют более широкий круг применения. Например, теорема 2 применима к задачам с хаотическим изменением $\sigma $ от элемента к элементу в достаточно широком диапазоне $[0,\mathbb{C}{{h}^{{ - 4}}}]$. В то же время коэффициенты перед типичными нормами в правой части апостериорных оценок только незначительно хуже коэффициентов в оценках для задач с постоянным $\sigma $. К положительным свойствам одной из полученных оценок относится так же то, что известные гарантированные, робастные, согласованные оценки для $\sigma = {\text{const}}$ являются ее частным случаем.