Журнал вычислительной математики и математической физики, 2020, T. 60, № 11, стр. 1998-2011

ВВЕДЕНИЕ

Проблема истечения газа из каналов в вакуум возникает во многих приложениях. Одним из важных примеров является вопрос о диффузии газа через микротрещины с последующим истечением газа в вакуум. Простейшей моделью микротрещины может служить микроканал между параллельными пластинами. Для теоретического исследования течений в микроканалах и истечения в вакуум необходимо привлекать кинетическую теорию газов, охватывающую все режимы течений, от сплошной среды до разреженного газа. Исследованиям течений разреженного газа в каналах и микроканалах посвящено множество работ, в том числе фундаментальная статья [1] и монография [2]. Подавляющее большинство этих работ основано на линеаризованном одномерном по физическому пространству кинетическом уравнении для длинных каналов и труб при малых перепадах (градиентах) давления и температуры. Возможность и условия локальной линеаризации задачи для длинных труб при конечных перепадах давления установлены в работе [3]. Там же предложен метод исследования течений в длинных каналах конечной длины при произвольных перепадах давления на концах трубы, но в условиях, когда концевыми эффектами можно пренебречь. Метод основан на гипотезе плоских поперечных сечений: в каждом сечении течение определяется путем решения линейного кинетического уравнения для трубы бесконечной длины при известном распределении давления вдоль трубы. После [3] метод систематически применялся в работах Шарипова и др. (см., например, [4], [5]). Недавно появились работы, в которых предлагаются поправки к решению за счет концевых эффектов [6], [7]. Анализ поправок основан на линейном кинетическом уравнении и потому не пригоден в случае больших отношений давления, в особенности при истечении в вакуум. В работе [8] представлено сравнение имеющихся в литературе численных результатов расчета расхода массы для чисел Кнудсена ${\text{Kn}} \geqslant {{10}^{{ - 2}}}$, полученных с использованием линейных и нелинейных кинетических моделей.

Необходимое условие линеаризации задачи состоит в том, что течение должно быть медленным, скорость потока по абсолютной величине должна быть мала по сравнению со скоростью звука. Необходимость этого условия подчеркнута в [3]. При использовании линейной теории и основанных на ней методов расчета необходимо контролировать выполнение этого условия. В работах по течениям газа в трубах и каналах большой конечной длины, в частности, в [4], [5], обычно приводятся результаты по расходу массы газа, но нигде не упоминается о том, что условие малости скорости потока действительно выполняется. В работе [3] уже в названии декларируется, что метод локальной линеаризации справедлив для длинных труб при любых значениях отношения давлений в камерах, где газ покоится. Однако из условия постоянства расхода газа через любое поперечное сечение канала при изотермическом течении плотность газа монотонно убывает по мере приближения к выходному сечению, а скорость течения возрастает и может достигать сколь угодно больших значений, если отношение давлений достаточно велико. Решение задачи в полной нелинейной постановке без упрощающих предположений для всей области, выполненное в [9] для длинных каналов, показывает, что область больших скоростей потока не ограничивается малой окрестностью выходного сечения канала (порядка ширины канала или радиуса трубы), а простирается на расстояния порядка длины канала. Такое поведение скорости (и плотности) нельзя назвать концевым эффектом. Поведение параметров течения для очень длинных каналов требует дополнительного исследования.

В связи с применением результатов работы [3] необходимо отметить еще одно обстоятельство, связанное с определением понятия “длинный” канал. В начале заметки [3] отмечено, что при малых числах Кнудсена ${\text{Kn}}$ локальная линеаризация задачи возможна при условии, что в сечении трубы справедливо неравенство, которое можно переписать в упрощенном виде ${\text{Kn}} \cdot L \gg 1$, где $L$ – относительная длина трубы или канала (отнесено к радиусу трубы или к ширине канала). Позднее в работах [10], [11] это же условие было получено независимо и интерпретировано как условие, при котором трубу можно считать длинной. Иными словами, при малых числах Кнудсена трубу (или канал) можно считать длинной, если выполняется условие ${\text{Kn}} \cdot L \gg 1$: геометрическое условие $L \gg 1$ не является достаточным. Однако ни в фундаментальных трудах [1], [2], ни в других работах, следующих за [3], выписанное выше условие даже не упоминается.

Подводя итоги сказанному выше, приходим к заключению, что описанная выше приближенная схема, основанная на приближении плоских сечений, работает для достаточно разреженных газов и при значениях отношения давлений порядка единицы. Вопрос о пределах применимости схемы при малых числах Кнудсена в камере высокого давления и при больших значениях отношения давления в камерах, а тем более при истечении в вакуум нуждается в дальнейшей проработке.

Целью данной работы является создание гибридного метода построения решения задачи об истечении разреженного газа через очень длинный канал в вакуум из резервуара высокого давления, в котором число Кнудсена мало. На основании асимптотических оценок при больших относительных длинах каналов область течения разбивается на три подобласти: 1) окрестность входа в канал; 2) основной участок течения в канале, занимающий почти всю длину канала; 3) окрестность выхода из канала. В подобласти (1) течение не рассматривается в силу малой скорости потока. На основном участке (2) течение медленное и происходит под действием малого градиента давления (область диффузии). В подобласти (3) поток ускоряется, газ расширяется в канале и вакуумной камере. На участке диффузии течение является сплошносредным, поэтому используются известные результаты линейной одномерной теории течений вязкого газа в длинных каналах (течение Пуайзеля). В подобласти ускоренного течения решается полное нелинейное кинетическое уравнение (S-модель). Условие асимптотического сращивания решений в двух подобластях заменяется граничным условием сопряжения решений в некотором сечении, положение которого выбирается из условия гладкости полного решения задачи. Кинетическое уравнение в области (3) решается методом установления по времени с помощью консервативной схемы конечных объемов со вторым порядком аппроксимации по всем переменным. Предлагаемый метод решения можно считать гибридным ввиду одновременного решения уравнений Навье–Стокса и кинетического уравнения.

1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ

Рассмотрим стационарное истечение одноатомного газа из резервуара I высокого давления и бесконечной емкости в резервуар II низкого давления также бесконечной емкости через очень длинный плоский канал между параллельными пластинами. Пусть $a$ – ширина канала, $l$ – его длина. Канал называем очень длинным, если относительная длина его $L = l{\text{/}}a > 1000$. В контейнерах I и II вдали от входного и выходного сечений канала газ покоится при давлении, числовой плотности и температуре ${{p}_{{\text{I}}}}$, ${{n}_{{\text{I}}}}$, ${{T}_{{\text{I}}}}$ в резервуаре I и ${{p}_{{{\text{II}}}}}$, ${{n}_{{{\text{II}}}}}$, ${{T}_{{{\text{II}}}}}$ в резервуаре II. Будем рассматривать случай, когда ${{T}_{{{\text{II}}}}} = {{T}_{{\text{I}}}}$, предполагаем, что температура поверхности канала и поверхности сосудов также постоянна и равна температуре покоящегося газа в сосудах, т.е. ${{T}_{w}} = {{T}_{{\text{I}}}}$.

Введем декартову систему координат $(x,y)$ с началом в центре входного сечения канала. Канал занимает пространство $(0 < x < l,\; - {\kern 1pt} a{\text{/}}2 < y < + a{\text{/}}2)$, левый резервуар расположен в полупространстве $x < 0$, правый – при $x > l$. При ${{p}_{{\text{I}}}} > {{p}_{{{\text{II}}}}}$ газ течет слева направо из резервуара I в резервуар II. Нас будет интересовать случай очень больших отношений давлений ${{p}_{{\text{I}}}}{\text{/}}{{p}_{{{\text{II}}}}} \gg 1$, включая случай истечения в вакуум, т.е. ${{p}_{{{\text{II}}}}} = 0$. Хотя в окрестности входа в канал газ ведет себя как сплошная среда, по мере приближения к выходному сечению течение все в большей степени приобретает черты разреженности и истекает в вакуум почти как в бесстолкновительном режиме. Таким образом, в рассматриваемом течении число Кнудсена покрывает весь диапазон возможных значений. В этих условиях анализ течения должен быть основан на кинетической теории газов.

Состояние разреженного газа в точке $(x,y)$ в момент времени $t$ определяется функцией распределения молекул по скоростям $f(t,x,y,{{\xi }_{x}},{{\xi }_{y}},{{\xi }_{z}})$, где $({{\xi }_{x}},{{\xi }_{y}},{{\xi }_{z}})$ – компоненты вектора молекулярной скорости по направлениям $(x,y,z)$ соответственно. Предполагаем, что функция распределения удовлетворяет уравнению Больцмана с оператором столкновений в форме S-модели [12]:

Здесь ${\text{Pr}}$ – число Прандтля (${\text{Pr}} = 1$ соответствует модели БГК [13]), $R$ – газовая постоянная, $\mu $ – коэффициент вязкости, $p$ – давление. Предполагается суммирование по греческим индексам. В дальнейшем будем рассматривать взаимодействие молекул по модели твердых сфер, так что $\mu (T) = {{\mu }_{I}}\sqrt {T{\text{/}}{{T}_{I}}} $.

Макроскопические параметры, такие как числовая $n$ и массовая $\rho $ плотности, вектор средней скорости ${\mathbf{u}} = ({{u}_{1}},{{u}_{2}},{{u}_{3}})$, давление $p$, температура $T$ и поток тепла $q = ({{q}_{1}},{{q}_{2}},{{q}_{3}})$ выражаются через функцию распределения в виде интегралов ($m$ – масса молекулы):

Граничные условия на верхней поверхности канала $y = \pm a$ и вертикальных стенках резервуаров задаются в виде локально-максвелловской функции, соответствующей граничному условию диффузного отражения:

Здесь ${{n}_{w}}(t,{\mathbf{x}})$ – плотность отраженных молекул (определяется условиями непротекания), ${{\xi }_{n}}$ – проекция вектора скорости молекулы ${\mathbf{\xi }}$ на внешную единичную нормаль к поверхности.

Состояние газа можно характеризовать с помощью числа Кнудсена:

либо, что более удобно в расчетах, параметром разреженности $\delta $ (см. [1], [2]): где $\lambda $ – средняя длина свободного пробега, $\beta = \sqrt {2RT} $ – наиболее вероятная скорость молекул. В рамках настоящей работы в контейнере высокого давления газ рассматривается как сплошная среда в то время как в канале и резервуаре II локальное число Кнудсена может принимать произвольные значения ${\text{K}}{{{\text{n}}}_{{\text{I}}}} < {\text{Kn}} < \infty $.

2. ПРИБЛИЖЕНИЕ ДЛИННОЙ ТРУБЫ

Проведем простой асимптотический анализ задачи при $L = l{\text{/}}a \gg 1$. Принято считать, что для длинных каналов возможна линеаризация задачи, если локальный относительный градиент давления (и температуры) достаточно мал, т.е.

Это условие неоспоримо, но в общем случае оно не входит в условия задачи. Только в случае малой разности давлений ${{p}_{{\text{I}}}} - {{p}_{{{\text{II}}}}}$ можно гарантировать, что и, следовательно, обеспечить выполнение условия (4). Оценку (5) обычно используют и в случае конечного перепада давлений, ссылаясь на то, что для длинных каналов всегда имеет место неравенство (см. [1], [2]) Однако из условия (6) не следует, что оценка (5) справедлива почти для всех сечений канала, за исключением малых окрестностей его концов. В наших условиях давление – функция монотонно убывающая. Положим на время, что давление на концах канала совпадает со значениями ${{p}_{{\text{I}}}}$, ${{p}_{{{\text{II}}}}}$ в резервуарах. Можно утверждать, что существует интервал $({{x}_{1}} < x < {{x}_{2}})$, в котором оценка (5) имеет место. Интервал $({{x}_{2}},L)$ в общем случае может иметь порядок $L$, тем более при больших значениях отношения давлений ${{p}_{{{\text{II}}}}}{\text{/}}{{p}_{{\text{I}}}}$, но всегда значительно больше ширины канала $a$.

Помимо критического анализа оценки (5), обратим внимание на следующее обстоятельство. В работах по течениям в длинных каналах предполагается, что давление, плотность и температура в канале не зависят от поперечной координаты. В обоснование этого допущения иногда приводятся соображения качественного характера. Математическое обоснование на уровне простых асимптотических оценок для линеаризованной задачи было дано в работе [14]. Ниже тот же прием используется для обоснования локальной линеаризации кинетического уравнения для длинных каналов при произвольных значениях отношения давлений в резервуарах. Специально рассмотрен случай малых чисел Кнудсена.

Обратимся к кинетическому уравнению (1), следуя работе [14]. Можно предположить, что на интервале $({{x}_{1}},{{x}_{2}})$ первое слагаемое в левой части имеет порядок $1{\text{/}}L$ по сравнению со вторым (в предположении, что компоненты молекулярной скорости ${{\xi }_{x}}$, ${{\xi }_{y}}$ имеют один порядок) и может быть опущено в нулевом приближении. В результате уравнение принимает вид

При любом конечном значении частоты столкновений $\nu $ это уравнение имеет простейшее решение, удовлетворяющее граничному условию и соответствующее локальному термодинамическому равновесию со стенкой Здесь аргумент $x$ играет роль параметра. Движение в канале возникает вследствие зависимости ${{n}_{w}}(x)$, которая определяется по первому приближению к решению задачи и имеет порядок $1{\text{/}}L$. Уравнение первого приближения получается подстановкой (8) в левую и правую части уравнения (1) и путем линеаризации правой части этого уравнения. В результате получаем линейное, одномерное по физическому пространству уравнение, подобное (7), но неоднородное, содержащее в правой части логарифмическую производную от плотности. В дальнейшем это уравнение нам не понадобится, и мы его не выписываем. Отметим только, что в качестве силы, вынуждающей движение, первоначально выступает производная от плотности, а не от давления, хотя в данном изотермическом случае обе производные равносильны.

Сказанное выше справедливо для любых, но конечных $\delta $. Предел $\delta = \infty $ рассмотрим отдельно и более подробно.

3. АСИМПТОТИЧЕСКОЕ ПРИБЛИЖЕНИЕ ПРИ $L \to \infty $, $\delta \to \infty $

Течение в сплошносредной части считаем изотермическим, так что $T(x) \equiv {{T}_{w}} = {{T}_{I}}$, $\mu (T) \equiv {{\mu }_{I}}$. Оценки членов уравнения (1) по параметру $1{\text{/}}L$ остаются справедливыми, однако при $\delta \to \infty $ вместо (7) имеет место асимптотическое решение

Локально-максвелловское приближение (9) является более общим по сравнению с (8), поскольку в нем присутствуют все пять макропараметров потока (скорость течения, плотность и температура), причем зависимость их от координат произвольна. Применяя обычные оценки при ${\text{Kn}} \to 0$ в рамках метода Чепмена–Энскога или (что проще) в рамках системы уравнений моментов, получаем обычные уравнения Навье–Стокса. Далее производим оценки членов в этих уравнениях, пользуясь приближением длинного канала, и приходим к выводу, что и что основное уравнение в системе уравнений Навье–Стокса имеет тот же вид, что и для течения Пуазейля в случае несжимаемой жидкости Профиль скорости имеет параболический вид Расход газа получается интегрированием по координате $y$ и выражается формулой

Оценим расход, полагая участок диффузии равным всему каналу ${{x}_{2}} - {{x}_{1}} = l$, давление на его границах равным давлению в резервуарах ${{p}_{1}} = {{p}_{{\text{I}}}}$, ${{p}_{2}} = {{p}_{{{\text{II}}}}}$. Интегрируя (10) по $x$ от ${{x}_{1}} = {{x}_{{\text{I}}}} = 0$ до ${{x}_{{{\text{II}}}}}$, получаем

Далее, интегрируя (10) от ${{x}_{{\text{I}}}} = 0$ до произвольного $x \geqslant {{x}_{2}}$, полагая $\dot {M} \approx {{\dot {M}}_{{NS}}}$, ${{p}_{1}} \approx {{p}_{{\text{I}}}}$ и подставляя явное выражение для константы ${{A}_{{\text{I}}}}$, получаем явные выражения для макропараметров: Здесь $\eta = {{p}_{{{\text{II}}}}}{\text{/}}{{p}_{{\text{I}}}}$ – отношение давлений газа в резервуарах. Истечение в вакуум соответствует $\eta = 0$.

4. ГИБРИДНЫЙ МЕТОД ПОСТРОЕНИЯ ПОЛЯ ТЕЧЕНИЯ

Как уже было отмечено, построение решения задачи для $L \geqslant {{10}^{3}}$ и высокой плотности газа в первом резервуаре ${{\delta }_{{\text{I}}}} \gg 1$ путем прямого численного решения кинетического уравнения (1) во всей области течения требует большого расхода вычислительных ресурсов, см., например, [9]. При таких параметрах задачи расход газа и поле течения в большей части канала могут быть с достаточной точностью оценены с помощью приближенных подходов, например, формул (11), (12). Однако течение в кинетической области вблизи выхода из канала $(l - x){\text{/}}l \ll 1$ и в резервуаре низкого давления, где локальное число Кнудсена велико и течение может становиться сверхзвуковым, с помощью приближенных подходов не определяется.

Предлагаемый здесь гибридный метод решения задачи позволяет построить картину течения в кинетической области ${{x}_{2}} \leqslant x < + \infty $ за существенно меньшее время счета по сравнению с прямым расчетом всей задачи по кинетическому уравнению. Основная идея метода состоит в следующем. Сначала при помощи формул (12) выбирается значение параметра ${{x}_{2}}$ таким образом, чтобы локальное значение параметра разреженности (или числа Кнудсена)

соответствовало сплошносредному режиму течения, а максимальное значение локального числа Маха одноатомного газа было мало. Другими словами, течение газа в сечении $x = {{x}_{2}}$ должно быть медленным течением сплошной среды. При этом функция распределения будет близка к навье-стоксовской, соответствующей изотермическому течению.

После этого левый резервуар и часть канала $x < {{x}_{2}}$ заменяются граничным условием для функции распределения для влетающих молекул ${{\xi }_{x}} > 0$ в сечении ${{x}_{2}}$. Так как главная часть навье-стоксовской функции распределения является локально-максвелловской функцией, то в качестве граничного условия полагаем

В оставшейся части канала $x \geqslant {{x}_{2}}$ и правом резервуаре сохраняются граничные условия диффузного отражения, описанные выше в формуле (3).

Для решения полученной задачи в области $x \geqslant {{x}_{2}}$ используется метод дискретных скоростей. Для проведения расчетов удобно использовать безразмерные переменные. В отличие от обычного способа перехода к таким переменным в качестве масштаба плотности удобно выбрать не плотность газа в первом резервуаре, а значение плотности ${{n}_{2}} = {{n}_{{NS}}}({{x}_{2}})$ на границе $x = {{x}_{2}}$. Таким образом, в качестве масштабов длины, скорости, времени, плотности, температуры, давления, потока тепла, функции распределения и вязкости примем величины

В качестве масштаба расхода массы $\dot {M}$ принимается величина ${{\rho }_{2}}{{\beta }_{{\text{I}}}}a$. Ниже все безразмерные величины обозначены теми же буквами, что и размерные.

Кинетическое уравнение (1) принимает вид

Функция $\phi (x)$ была определена в (12), при этом ${{\rho }_{{NS}}}({{x}_{2}}){\text{/}}{{\rho }_{{\text{I}}}} = {{p}_{{NS}}}({{x}_{2}}){\text{/}}{{p}_{{\text{I}}}} = \phi ({{x}_{2}}) = {{\phi }_{2}}$.

В безразмерном виде выражения (12) для сплошносредного решения ${{\rho }_{{NS}}}(x)$, ${{u}_{{NS}}}(x,y)$, ${{\dot {M}}_{{NS}}}$ принимают вид

Безразмерные выражения для макроскопических величин имеют обычный вид:

Граничные условия (3) на поверхности канала и вертикальных стенках резервуара записываются в виде

Во входном сечении расчетной области $x = {{x}_{2}}$ граничное условие (13) для функции распределения влетающих молекул ${{\xi }_{x}} > 0$ имеет вид

Здесь учтено, что в безразмерных переменных ${{p}_{{NS}}}({{x}_{2}}) \equiv 1$.

Поставленная двумерная задача допускает существенное упрощение путем введения редуцированных функций распределения, что было использовано в [15]. Так как в настоящей работе расчеты проводились с помощью параллельного трехмерного кода “Несветай”, разработанного ранее первым автором в [16]–[18] и использовавшегося для расчета течений в каналах произвольной формы сечения (см. [11], [19]–[21]), переход к редуцированным функциям не применялся. Вместо этого использовалась трехмерная пространственная сетка с учетом особенностей решаемой плоской задачи.

Стационарное решение задачи строится неявным методом установления по времени второго порядка аппроксимации по всем переменным. Начальные условия для функции распределения в области ${{x}_{2}} \leqslant x \leqslant {{x}_{{{\text{II}}}}}$ имеют вид локально-максвелловской функции с параметрами, взятыми из аналитического решения (15) либо с помощью построения решения уравнений Навье–Стокса вязкого газа с помощью стороннего кода, например [22], [23]. В резервуаре низкого давления в начальный момент времени функция распределения равняется максвелловской с плотностью $n = {{n}_{{{\text{II}}}}} = \eta {\text{/}}{{\phi }_{2}}$, скоростью $u = 0$ и температурой ${{T}_{{{\text{II}}}}} = 1$. Для ускорения вычислений  в коде “Несветай” реализован двухуровневый алгоритм организации параллельных вычислений на современных многопроцессорных суперЭВМ с возможностью использования десятков тысяч ядер [24]. В результате может достигаться значительное ускорение относительно расчета на одном ядре.

5. ПРИМЕР РАСЧЕТА ТЕЧЕНИЯ В КАНАЛЕ

Далее в работе рассматривается только наиболее интересный случай истечения газа в вакуум ${{p}_{{{\text{II}}}}}{\text{/}}{{p}_{{\text{I}}}} = 0$. Для иллюстрации эффективности нового метода решения были выбраны следующие значения относительной длины канала и параметра разреженности в резервуаре высокого давления: $L = {{10}^{6}}$, ${{\delta }_{{\text{I}}}} = {{10}^{4}}$.

Расчеты проводились для значений длины оставшейся в расчете части канала $L - {{x}_{2}} = 50$, $100$, $200$, что позволяет исследовать влияние положения границы ${{x}_{2}}$ на решение задачи. Остановимся коротко на параметрах расчетной сетки. Разбиение на ячейки в физическом пространстве проводилось следующим образом. Поперек канала использовалось неравномерное разбиение на 21 ячейку со сгущением к боковой поверхности; размер первой ячейки у поверхности ${{h}_{n}} = 0.02$. Вдоль канала расчетная сетка сгущалась к выходу $x = L$, так что у выходного сечения размер ячейки $hs = 0.05$. Вблизи сечения ${{x}_{2}}$ размер ячейки по направлению координаты $x$ выбирался автоматически программой построения сетки. В направлении $z$ расчетная область имела единичный размер и разбивалась на 3 ячейки.

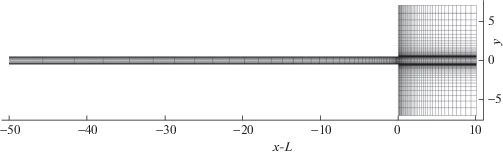
В табл. 1 приведены зависимости от выбора положения границы ${{x}_{2}}$ значения параметра разреженности ${{\delta }_{2}}$, числа Маха на оси ${{{\text{M}}}_{2}}$ и общего числа расчетных ячеек в физическом пространстве $3{{N}_{{xy}}}$, где ${{N}_{{xy}}}$ – число ячеек в плоскости $x - y$. Для ${{x}_{2}} = 10$, $25$ расчетная сетка не строилась. Видно, что для всех выбранных значений ${{x}_{2}}$ число Маха ${\text{M}}$ является приемлемым для метода, однако значение ${{\delta }_{2}}$ принимает подходящие значения только с $L - {{x}_{2}} \geqslant 50$. При этом достаточно ограничиться ${{x}_{2}} \leqslant 200$. На фиг. 1 приведен вид расчетной области и сетки в физическом пространстве для $L - {{x}_{2}} = 50$. Хорошо видно сгущение сетки к выходному сечению канала и его стенкам. В то же время шаг сетки по координате $x$ вблизи границы $x = {{x}_{2}}$ является довольно большим, так как изменения расчетных величин вдоль канала вблизи ${{x}_{2}}$ малы.

Для точности вычисления макропараметров газа во втором резервуаре существенное влияние оказывает выбор параметров расчетной сетки в скоростном пространстве. Для аккуратного нахождения расхода массы достаточно ограничиться равномерной сеткой с шагом $\Delta \xi = 0.4$, однако при вычислении макропараметров в области разреженного течения $x > L$ с большими локальными значениями числа Кнудсена проявляется так называемый эффект луча (ray effect), результатом которого является появление колебаний в функции распределения и полях макроскопических величин [25], [26]. Поэтому требуется использовать неравномерную скоростную сетку с сильным сгущением узлов. В настоящей работе такая сетка строилась в три этапа. Сначала в плоскости ${{\xi }_{x}} - {{\xi }_{y}}$ задавалась двухмерная сетка из $50 \times 50$ ячеек со сгущением до $\Delta \xi = 0.05$ вблизи точки ${{\xi }_{x}} = {{\xi }_{y}} = 0$. На втором этапе трехмерная расчетная сетка по скорости получается трансляцией двухмерной сетки вдоль координаты ${{\xi }_{z}}$ с шагом $\Delta {{\xi }_{z}} = 0.4$. В окончательной сетке остаются узлы, лежащие внутри сферы (см. [27], [28]) ${\text{|}}\xi {\text{|}} \leqslant 3.5\sqrt {\max T} \approx 4$. Полученная сетка приведена на фиг. 2. Полное число ячеек в скоростной сетке равнялось 29 816. Для $L - {{x}_{2}} = 200$ общее число ячеек 6-мерной расчетной сетки $ \approx {\kern 1pt} 548$ млн.

Перейдем к рассмотрению результатов. При этом при визуализации поля плотности для удобства будем использовать более привычную безразмерную величину $n{\text{/}}{{n}_{{\text{I}}}}$, а не расчетную $n{\text{/}}{{n}_{2}}$.

Одним из способов оценки правильности выбора положения границы ${{x}_{2}}$ является совпадение расхода массы, вычисленного по кинетическому решению, со сплошносредним значеним ${{\dot {M}}_{{NS}}}$, которое используется для постановки граничного условия в сечении ${{x}_{2}}$. Помимо этого, в расчетах контролируется условие постоянства расхода по длине канала при ${{x}_{2}} \leqslant x \leqslant L$. В табл. 2 приведены результаты расчета расхода массы и величина отклонения среднего по длине канала расхода от значения ${{\dot {M}}_{{NS}}}$ в зависимости от ${{x}_{2}}$. Для всех значений $L - {{x}_{2}}$ видна хорошая точность выполнения условия $\dot {M} = {\text{const}}$. При этом отклонение расхода от сплошносредного значения убывает практически линейно с ростом длины секции канала $L - {{x}_{2}}$. В целом для расчета расхода массы выбор ${{x}_{2}} = 200$ обеспечивает высокую для практических приложений точность (и оптимальный по соотношению точность/затраты машинного времени результат). Тем более, что для многих инженерных приложений достаточно обеспечить 10%-ю точность расчета расхода массы [8]. Как показали тестовые расчеты на грубых пространственных сетках, дальнейший перенос границы ${{x}_{2}}$ в глубь канала существенно увеличивает требуемое для построения стационарного решения число шагов по времени, но не позволяет принципиально уменьшить отклонение $\dot {M}$ от сплошносредной оценки ${{\dot {M}}_{{NS}}}$.

На фиг. 3 приведено распределение безразмерных плотности и температуры газа вдоль оси канала и резервуара II для $L - {{x}_{2}} = 50$, $200$ в сравнении с асимптотическим решением (12) во всей расчетной области. На фиг. 4, 5 представлены распределения безразмерных плотности, температуры, давления и числа Маха в окрестности выхода из канала и внутри резервуара II. Видно хорошее согласие профилей макроскопических величин, полученных для разных значений ${{x}_{2}}$. Условие постоянства температуры в канале выполняется с высокой точностью вплоть до окрестности выходного сечения. Отклонение температуры от константы хорошо согласуется с разгоном газа до около- и сверхзвуковых скоростей вблизи выходного сечения и в резервуаре II. Согласие с асимптотическим решением также является вполне приемлемым в области сплошносреднего течения, что подтверждает правильность работы нашего метода.

Из представленых кривых можно сделать следующий вывод: если основной целью расчетов является получение струи газа в области вакуума, требования по точности вычисления $\dot {M}$ могут быть ослаблены. Численное решение задачи при $L - {{x}_{2}} = 50$ требует примерно в 10 раз меньше времени, чем для $L - {{x}_{2}} = 200$, и может быть получено за разумное время на современном десктопном компьютере с 16 физическими ядрами.

На фиг. 6, 7, 8 представлены линии уровня температуры, плотности и числа Маха для случая $L - {{x}_{2}} = 200$. Снова отмечаем хорошее выполнение условия постоянства температуры в канале вплоть до окрестности выходного сечения. Для выбранного размера резервуара II в линиях уровня всех расчетных величин практически отсутствуют характерные для эффекта луча артефакты.

ЗАКЛЮЧЕНИЕ

В работе предложен гибридный метод построения поля течения разреженного газа, возникающего при истечении через очень длинный плоский канал из резервуара высокого давления в резервуар низкого давления, включая случай истечения в вакуум. В основе метода лежат следующие соображения. При достаточной большой длине канала расход массы газа определяется медленным течением в основном участке канала, и при малых числах Кнудсена представляет собой изотермическое течение Пуайзеля. Окрестность истечения газа в резервуар низкого давления охватывает малую часть длины канала, но значительно больше ширины канала. Структура истекающей струи описывается нелинейным кинетическим уравнением с известным значением расхода массы, задаваемым на входе в рассматриваемую окрестность, т.е. в сечении $x = {{x}_{2}}$, положение которого определяется условием удовлетворения равенства потоков массы. Данное уравнение решается неявным методом дискретных скоростей. Так как в предлагаемом подходе кинетическое уравнение решается в относительно небольшой от размера всего канала области течения, требуемое для построения решения время счета сокращается на порядки по сравнению с прямым кинетическим расчетом течения во всем канале. Приведенные примеры расчетов показывают работоспособность и высокую точность метода при расчете истечения газа в вакуум.

Расчеты проводились на вычислительных мощностях Межведомственного суперкомпьютерного центра РАН (http://www.jscc.ru/).