Журнал вычислительной математики и математической физики, 2020, T. 60, № 12, стр. 2177-2184

Построение z-переставленных матриц в QTT-формате

Л. Б. Маркеева^1, *, И. В. Цыбулин²

¹ Сколковский Институт Науки и Техники
143026 Москва, ул. Большой бульвар, 30, Россия

² Яндекс
119021 Москва, ул. Льва Толстого, 16, Россия

^* E-mail: l.markeeva@skoltech.ru

Поступила в редакцию 27.07.2020
После доработки 27.07.2020
Принята к публикации 04.08.2020

DOI: 10.31857/S0044466920120091

Полный текст (PDF)

Аннотация

В работе представлен метод построения матриц в QTT-формате, столбцы и строки которых переупорядочены специальным образом – z-перестановкой. Для получения матрицы в данной перестановке вводится новая операция в QTT-формате (Quantized Tensor Train) – z-kron. Такое переупорядочивание позволяет уменьшить QTT-ранги аппроксимации матрицы жесткости, что позволяет ускорить сходимость численного решения системы. Например, при решении задачи Дирихле для уравнения Пуассона методом конечных элементов (МКЭ), где для хранения матрицы коэффициентов используются QTT-формат, переупорядочение строк и столбцов в матрице коэффициентов размера $n \times n$, где $n = {{4}^{d}}$, позволяет предотвратить экспоненциальный по $d$ рост рангов. Библ. 9. Фиг. 3.

Ключевые слова: малоранговые тензорные аппроксимации, метод конечных элементов, z-перестановка, z-крон, tensor train, quantized tensor train.

ВВЕДЕНИЕ

В работах [1] и [2] было показано, что для класса эллиптических уравнений в полигональных ограниченных двумерных областях с аналитическими правыми частями существуют малопараметрические аппроксимации решения в формате квантизованного тензорного поезда (quantized tensor train, QTT). Точность приближения решения убывает экспоненциально с числом параметров в ТТ-разложении, что позволяет говорить об оптимальном алгоритме решения таких задач. Для реализации эффективного практического алгоритма необходимо решить несколько задач, одной из таких задач посвящена данная работа. Основная идея подхода состоит в том, что используются конечные элементы низкого порядка на очень мелкой “виртуальной” сетке, а аппроксимация строится на дискретном уровне. Оказывается, что нумерация конечных элементов играет важную роль в структуре возникающих тензоров. Для получения небольшого числа параметров, необходимо использовать так называемую z-перестановку (см. ниже фиг. 3). Сама матрица перестановки имеет полный тензорный ранг, поэтому необходимо уметь формировать переставленную матрицу напрямую. Основное предположение состоит в том, что дискретная матрица жесткости может быть представлена в виде суммы кронекеровских произведений матриц, соответствующих “одномерным” операторам. Для этого случая мы предлагаем и обосновываем метод построения QTT-представления для матриц жесткости в z-перестановке. Основой для этого служит модифицированная операция кронекеровского произведения (z-kron), которая позволяет напрямую собирать матрицы, в которых переставлены строки и столбцы в соответствии с z-перестановкой, из QTT-представлений матриц, соответствующих “одномерным” операторам.

В разд. 1 приводится основная информация о QTT-формате и важных для данной работы операциях. В разд. 2 вводится операция z-крон и доказывается, что она порождает QTT-матрицы с переставленными строками и столбцами в z-перестановке. Разд. 3 содержит эксперименты, которые показывают, что матрица коэффициентов метода конечных элементов имеет более маленькие ранги аппроксимации будучи z-переставленной по сравнению с каноническим порядком строк и столбцов.

1. QTT-ФОРМАТ

В данном разделе будут описаны основные идеи TT- и QTT-форматов. Более детальная информация о свойствах TT-формата представлена в [3].

Tensor Train формат (TT-формат) – это нелинейный метод малоранговой аппроксимации многомерных массивов (тензоров). Рассмотрим $d$-мерный тензор $T \in {{\mathbb{R}}^{{{{n}_{1}} \times \ldots \times {{n}_{d}}}}}$. Мы говорим, что тензор $T$ представлен в ТТ-формате, если его элемент представляется в виде

(1)

${{T}_{{{{i}_{1}} \cdots {{i}_{d}}}}} = \sum\limits_{{{\alpha }_{1}} = 1}^{{{r}_{1}}} \cdots \sum\limits_{{{\alpha }_{{d - 1}}}}^{{{r}_{{d - 1}}}} {{{G}_{1}}} ({{i}_{1}},{{\alpha }_{1}}){{G}_{2}}({{\alpha }_{1}},{{i}_{1}},{{\alpha }_{2}}) \ldots {{G}_{{d - 1}}}({{\alpha }_{{d - 2}}},{{i}_{{d - 1}}},{{\alpha }_{{d - 1}}}){{G}_{d}}({{\alpha }_{{d - 1}}},{{i}_{d}}),$

где $0 \leqslant {{i}_{k}} \leqslant {{n}_{k}} - 1$, $k \in \left[ {1 \ldots d} \right]$; ${{G}_{t}}$ называется ядром; $t \in \left[ {1 \ldots d} \right]$; ${{G}_{2}},\; \ldots ,\;{{G}_{{d - 1}}}$ – трехмерные тензоры с размерами ${{r}_{{j - 1}}} \times {{n}_{j}} \times {{r}_{j}}$; ${{G}_{1}}$, ${{G}_{d}}$ – матрицы размеров ${{n}_{1}} \times {{r}_{1}}$ и ${{r}_{{d - 1}}} \times {{n}_{d}}$ соответственно. Верхние пределы суммирования ${{r}_{1}} \ldots {{r}_{{d - 1}}}$ в (1) называются рангами аппроксимации или просто рангами.

Уравнение (1) можно представить как произведение матриц

(2)

${{T}_{{{{i}_{1}} \ldots {{i}_{d}}}}} = {{G}_{1}}({{i}_{1}}){{G}_{2}}({{i}_{2}}) \ldots {{G}_{{d - 1}}}({{i}_{{d - 1}}}){{G}_{d}}({{i}_{d}}),$

где ${{G}_{k}}({{i}_{k}})$ – матрица размера ${{r}_{{k - 1}}} \times {{r}_{k}}$, $k \in \left[ {1 \ldots d} \right]$.

Объем памяти, занимаемый тензором $T$, может быть оценен по следующей формуле:

(3)

$S = {{r}_{1}}{{n}_{1}} + \sum\limits_{i = 2}^{d - 1} {{{r}_{{i - 1}}}} {{n}_{i}}{{r}_{i}} + {{r}_{{d - 1}}}{{n}_{d}}.$

Дополнительно введем понятие эффективного ранга (e.rank) ${{r}_{e}}$, которое может быть вычислено путем решения следующего уравнения:

(4)

$S = {{r}_{1}}{{n}_{1}} + \sum\limits_{i = 2}^{d - 1} {{{r}_{{i - 1}}}} {{n}_{i}}{{r}_{i}} + {{r}_{{d - 1}}}{{n}_{d}} = {{r}_{e}}{{n}_{1}} + \sum\limits_{i = 2}^{d - 1} {r_{e}^{2}} {{n}_{i}} + {{r}_{e}}{{n}_{d}}.$

Перейдем к представлению многомерных матриц в TT-формате. Рассмотрим многомерную матрицу $M \in {{\mathbb{R}}^{{({{n}_{1}} \times \ldots \times {{n}_{d}}) \times ({{m}_{1}} \times \ldots \times {{m}_{d}})}}}$. Элемент с индексом ${{i}_{1}} \ldots {{i}_{d}}$; ${{j}_{1}} \ldots {{j}_{d}}$ представляется в TT-формате в виде

(5)

${{M}_{\begin{subarray}{l} {{i}_{1}} \ldots {{i}_{d}} \\ {{j}_{1}} \ldots {{j}_{d}} \end{subarray} }} = \sum\limits_{{{\alpha }_{1}} = 1}^{{{r}_{1}}} \cdots \sum\limits_{{{\alpha }_{{d - 1}}} = 1}^{{{r}_{{d - 1}}}} {{{V}_{1}}} ({{i}_{1}},{{j}_{1}},{{\alpha }_{1}}){{V}_{2}}({{\alpha }_{1}},{{i}_{2}},{{j}_{2}},{{\alpha }_{2}}) \ldots {{V}_{{d - 1}}}({{\alpha }_{{d - 2}}},{{i}_{{d - 1}}},{{j}_{{d - 1}}},{{\alpha }_{{d - 1}}}){{V}_{d}}({{\alpha }_{{d - 1}}},{{i}_{d}},{{j}_{d}}),$

где $0 \leqslant {{i}_{k}} \leqslant {{n}_{k}} - 1$, $0 \leqslant {{j}_{k}} \leqslant {{m}_{k}} - 1$, ${{V}_{j}}$ при $j \in [2 \ldots d - 1]$ – это четырехмерные тензоры с размерностями ${{r}_{{j - 1}}} \times {{n}_{j}} \times {{m}_{j}} \times {{r}_{j}}$; ${{V}_{1}}$ и ${{V}_{d}}$ – трехмерные тензоры с размерностями ${{n}_{1}} \times {{m}_{1}} \times {{r}_{1}}$ и ${{r}_{d}} \times {{n}_{d}} \times {{m}_{d}}$ соответственно.

В матричной форме (5) может быть представлено в виде

(6)

${{M}_{\begin{subarray}{l} {{i}_{1}} \ldots {{i}_{d}} \\ {{j}_{1}} \ldots {{j}_{d}} \end{subarray} }} = {{V}_{1}}({{i}_{1}},{{j}_{1}}){{V}_{2}}({{i}_{2}},{{j}_{2}}) \ldots {{V}_{{d - 1}}}({{i}_{{d - 1}}},{{j}_{{d - 1}}}){{V}_{d}}({{i}_{d}},{{j}_{d}}),$

где ${{V}_{k}}({{i}_{k}},{{j}_{k}})$ – матрица размера ${{r}_{{k - 1}}} \times {{r}_{k}}$, $k \in [1 \ldots d]$, а пара ${{i}_{k}},{{j}_{k}}$ представляет собой “длинный индекс”. Важно отметить, что ядра ${{V}_{k}}$ могут рассматриваться как блочные матрицы размера ${{r}_{{k - 1}}} \times {{r}_{k}}$, в которых каждый блок имеет размерность ${{n}_{k}} \times {{m}_{k}}$.

Из (5) следует, что если TT-ранг $M$ равен 1, то $M$ может быть представлена как кронекерово произведение матриц:

(7)

$M = {{M}_{1}} \otimes {{M}_{2}} \otimes \ldots \otimes {{M}_{{d - 1}}} \otimes {{M}_{d}},$

где ${{M}_{k}}$ – это матрицы размера ${{n}_{k}} \times {{m}_{k}}$, $k \in [1 \ldots d]$.

Сложность многих основных операций с тензорами в ТТ-формате может быть оценена сверху как $dn{{r}^{\alpha }}$, где $\alpha \in \left\{ {2,3} \right\}$, $n = max({{n}_{1}},\; \ldots \;{{n}_{d}})$, $r = max({{r}_{1}},\; \ldots \;{{r}_{{d - 1}}}).$

QTT-формат возникает при введении “виртуальных размерностей”, а именно, когда индексы исходного тензора (например, вектора) представляются $n$-арным кодом. Рассмотрим пример с бинарным кодированием индексов вектора ${v} \in {{R}^{{{{2}^{d}}}}}$. Данный вектор может быть представлен в виде тензора $V$ с размерностями $\underbrace {2 \times 2 \times \; \ldots \; \times 2}_{d\;{\text{раз}}}$. QTT-разложением или QTT-аппроксимацией назовем ТТ-разложение или ТТ-аппроксимацию тензора $V$. Превращение вектора ${v}$ в $d$-мерный тензор эквивалентно кодированию индекса этого вектора $0 \leqslant i \leqslant {{2}^{d}} - 1$ в бинарном формате:

(8)

$i = \overline {{{i}_{1}},{{i}_{2}},\; \ldots \;{{i}_{d}}} = \sum\limits_{k = 1}^d {{{2}^{{k - 1}}}} {{i}_{k}} \leftrightarrow ({{i}_{1}},{{i}_{2}},\; \ldots \;{{i}_{d}}),$

где ${{i}_{k}} \in {\text{\{ }}0,\;1{\text{\} }}$, $k \in [1 \ldots d]$. Аналогичная идея используется для представления матрицы ${\mathbf{M}} \in {{R}^{{{{2}^{d}} \times {{2}^{d}}}}}$ в QTT-формате.

Полезной вспомогательной операцией является сильное произведение Кронекера (см. [4]) $ \triangleright \triangleleft $, которая определяется как операция между двумя блочными матрицами. Использование такой операции для компактного представления ТТ-разложений различных тензоров было предложено в работе [5].

Каждое ядро в TT-представлении матрицы можно рассматривать как блочную матрицу. Тогда операция $ \triangleright \triangleleft $ похожа на матричное произведение, но элементы блочных матриц перемножаются друг с другом с использованием кронекеровского произведения вместо матричного произведения, тогда как умножение блочных матриц происходит по стандартному правилу.

(9)

$\begin{gathered} C = K \triangleright \triangleleft L = \left[ {\begin{array}{*{20}{c}} {{{K}_{{11}}}}& \ldots &{{{K}_{{1{{r}_{2}}}}}} \\ \vdots & \ddots & \vdots \\ {{{K}_{{{{r}_{1}}1}}}}& \ldots &{{{K}_{{{{r}_{1}}{{r}_{2}}}}}} \end{array}} \right] \triangleright \triangleleft \left[ {\begin{array}{*{20}{c}} {{{L}_{{11}}}}& \ldots &{{{L}_{{1{{r}_{3}}}}}} \\ \vdots & \ddots & \vdots \\ {{{L}_{{{{r}_{2}}1}}}}& \ldots &{{{L}_{{{{r}_{2}}{{r}_{3}}}}}} \end{array}} \right] = \\ = \left[ {\begin{array}{*{20}{c}} {{{K}_{{11}}} \otimes {{L}_{{11}}} + \ldots + {{K}_{{1{{r}_{2}}}}} \otimes {{L}_{{{{r}_{2}}1}}}}& \ldots &{{{K}_{{11}}} \otimes {{L}_{{1{{r}_{3}}}}} + \ldots + {{K}_{{1{{r}_{2}}}}} \otimes {{L}_{{{{r}_{2}}{{r}_{3}}}}}} \\ \vdots & \ddots & \vdots \\ {{{K}_{{{{r}_{1}}1}}} \otimes {{L}_{{11}}} + \ldots + {{K}_{{{{r}_{1}}{{r}_{2}}}}} \otimes {{L}_{{{{r}_{2}}1}}}}& \ldots &{{{K}_{{{{r}_{1}}1}}} \otimes {{L}_{{1{{r}_{3}}}}} + \ldots + {{K}_{{{{r}_{1}}{{r}_{2}}}}} \otimes {{L}_{{{{r}_{2}}{{r}_{3}}}}}} \end{array}} \right]. \\ \end{gathered} $

Например,

(10)

$C = \left[ {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} 1&2 \\ 3&4 \end{array}} \right)} \\ {\left( {\begin{array}{*{20}{c}} 1&2 \\ 3&4 \end{array}} \right)} \end{array}} \right] \triangleright \triangleleft \left[ {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)}&{\left( {\begin{array}{*{20}{c}} 1&2 \\ 2&1 \end{array}} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} 1&0&2&0 \\ 0&1&0&2 \\ 3&0&4&0 \\ 0&3&0&4 \end{array}} \right)}&{\left( {\begin{array}{*{20}{c}} 2&1&4&2 \\ 1&2&2&4 \\ 6&3&8&4 \\ 3&6&4&8 \end{array}} \right)} \\ {\left( {\begin{array}{*{20}{c}} 1&0&2&0 \\ 0&1&0&2 \\ 3&0&4&0 \\ 0&3&0&4 \end{array}} \right)}&{\left( {\begin{array}{*{20}{c}} 2&1&4&2 \\ 1&2&2&4 \\ 6&3&8&4 \\ 3&6&4&8 \end{array}} \right)} \end{array}} \right].$

Такая операция позволяет компактно записывать матрицы в ТТ-формате. В частности, для QTT-формата представление имеет вид (см. [6])

(11)

$M = {{J}_{1}} \triangleright \triangleleft \ldots \triangleright \triangleleft {{J}_{d}},$

где ${{J}_{i}}$ размера ${{r}_{{i - 1}}} \times {{r}_{i}}$, с размером блока ${{n}_{i}} \times {{m}_{i}}$, где $i \in [1,d]$.

В следующем разделе мы покажем, как строить матрицы в QTT-формате с переставленными в z-последовательности строками и столбцами при помощи операции z-kron.

2. ОПЕРАЦИЯ Z-ПРОИЗВЕДЕНИЯ

В данном разделе вводится понятие z-нумерации (z-перестановки, z-последовательности), и вводится операция z-крон, которая позволяет строить QTT-матрицы размера ${{4}^{d}} \times {{4}^{d}}$, в которых строки и столбцы переупорядочены в z-последовательности.

2.1. Порядок элементов в матрицах

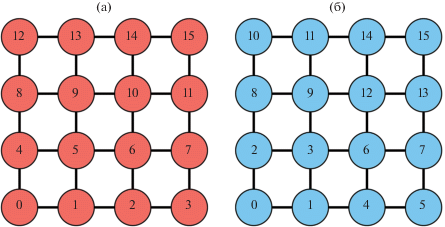
Рассмотрим квадрат, на котором введена равномерная сетка с числом узлов ${{2}^{d}} \times {{2}^{d}}$ (т.е. всего ${{4}^{d}}$ узлов). Координата каждого узла в сетке однозначно задается парой чисел ($i$, $j$), где $i,j \in [0,{{2}^{d}} - 1]$. Нам необходимо пронумеровать узлы этой сетки. Каноническое упорядочивание связано с последовательным обходом элементов сетки по столбцам или строкам, а z-упорядочивание имеет более сложную структуру. Эти нумерации представлены на фиг. 1.

Фиг. 1.

Примеры нумерации элементов сетки: (а) – каноническая нумерация, (б) – z-нумерация.

1. Каноническая нумерация. Позиция узла с номером ($i$, $j$) в канонической нумерации определяется по формуле:

(12)

$\mathcal{L}(i,j) = i + {{2}^{d}}j;$

2. z-нумерация. Представим $i$ и $j$ в бинарном формате:

(13)

$i = \sum\limits_{k = 1}^d {{{2}^{{k - 1}}}} {{i}_{k}} \leftrightarrow ({{i}_{1}},{{i}_{2}},\; \ldots {{i}_{d}}),\quad j = \sum\limits_{k = 1}^d {{{2}^{{k - 1}}}} {{j}_{k}} \leftrightarrow ({{j}_{1}},{{j}_{2}},\; \ldots \;{{j}_{d}}).$

Позиция узла с номером ($i$, $j$) в z-нумерации определяется по формуле:

(14)

$\mathcal{Z}(i,j) = {{i}_{1}} + 2{{j}_{1}} + 4{{i}_{2}} + 8{{j}_{2}} + \; \ldots \; + {{2}^{{2d - 2}}}{{i}_{d}} + {{2}^{{2d - 1}}}{{j}_{d}} = \sum\limits_{k = 1}^d {{{2}^{{2k - 2}}}} {{i}_{k}} + \sum\limits_{k = 1}^d {{{2}^{{2k - 1}}}} {{j}_{k}}.$

2.2. Z-крон

Предположим, что на нашей равномерной сетке с ${{4}^{d}}$ узлами задан линейный оператор, который определяется матрицей размера ${{4}^{d}} \times {{4}^{d}}$. Различная нумерация узлов сетки будет приводить к перестановке строк и столбцов матрицы. Мы будем рассматривать матрицы, которые являются кронекеровым произведением двух “одномерных” QTT-матриц:

(15)

${{K}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}} \\ {{j}_{1}}, \ldots ,{{j}_{d}} \end{subarray} }} = {{K}_{1}}({{i}_{1}},{{j}_{1}})\; \ldots \;{{K}_{d}}({{i}_{d}},{{j}_{d}}),\quad {{L}_{\begin{subarray}{l} i_{1}^{'}, \ldots ,i_{d}^{'} \\ j_{1}^{'}, \ldots ,j_{d}^{'} \end{subarray} }} = {{L}_{1}}(i_{1}^{'},j_{1}^{'})\; \ldots \;{{L}_{d}}(i_{d}^{'},j_{d}^{'}),\quad {\text{где}}\quad {{i}_{k}} \in {\text{\{ }}0,\;1{\text{\} }}.$

Хорошо известно [3], что кронекерово произведение двух $d$-мерных QTT-матриц представляет собой $2d$-мерную QTT-матрицу, где каждый элемент вычисляется по формуле:

(16)

${{M}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}},i_{1}^{'}, \ldots ,i_{d}^{'} \\ {{j}_{1}}, \ldots ,{{j}_{d}},j_{1}^{'}, \ldots ,j_{d}^{'} \end{subarray} }} = {{K}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}} \\ {{j}_{1}}, \ldots ,{{j}_{d}} \end{subarray} }}{{L}_{\begin{subarray}{l} i_{1}^{'}, \ldots ,i_{d}^{'} \\ j_{1}^{'}, \ldots ,j_{d}^{'} \end{subarray} }} = {{K}_{1}}({{i}_{1}},{{j}_{1}})\; \ldots \;{{K}_{d}}({{i}_{d}},{{j}_{d}}){{L}_{1}}(i_{1}^{'},j_{1}^{'})\; \ldots \;{{L}_{d}}(i_{d}^{'},j_{d}^{'}).$

Классическое кронекерово произведение соответствует канонической нумерации узлов квадратной сетки. Для получения линейного оператора, соответствующего z-перестановке, необходимо ввести новую операцию, которую мы называем z-kron и обозначаем через $ \oslash $. Данная операция применяется к двум $d$-мерным QTT-матрицам из (15). Результатом операции является TT-матрица $M \in {{\mathbb{R}}^{{{{4}^{d}} \times {{4}^{d}}}}}$, содержащая $d$ ядер. Каждый элемент матрицы определяется в виде

(17)

${{M}_{\begin{subarray}{l} {{z}_{1}}, \ldots ,{{z}_{d}} \\ z_{1}^{'}, \ldots ,z_{d}^{'} \end{subarray} }} = {{K}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}} \\ {{j}_{1}}, \ldots ,{{j}_{d}} \end{subarray} }}{{L}_{\begin{subarray}{l} i_{1}^{'}, \ldots ,i_{d}^{'} \\ j_{1}^{'}, \ldots ,j_{d}^{'} \end{subarray} }},\quad {\text{где}}\quad {{z}_{k}} = {{i}_{k}} + 2{{j}_{k}},\quad z_{k}^{'} = i_{k}^{'} + 2j_{k}^{'},\quad k \in [1\; \ldots \;d].$

Такая матрица в QTT-формате может быть записана как $M = {{K}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}} \\ {{j}_{1}}, \ldots ,{{j}_{d}} \end{subarray} }} \oslash {{L}_{\begin{subarray}{l} i_{1}^{'}, \ldots ,i_{d}^{'} \\ j_{1}^{'}, \ldots ,j_{d}^{'} \end{subarray} }}$ и представлена в виде

(18)

${{M}_{\begin{subarray}{l} {{z}_{1}}, \ldots ,{{z}_{d}} \\ z_{1}^{'}, \ldots ,z_{d}^{'} \end{subarray} }} = {{M}_{1}}({{z}_{1}},z_{1}^{'}){{M}_{2}}({{z}_{2}},z_{2}^{'})\; \ldots \;{{M}_{d}}({{z}_{d}},z_{d}^{'}),$

где ${{M}_{k}}$ получаются через кронекерово произведение ${{M}_{k}}({{z}_{k}},z_{k}^{'}) = L(i_{k}^{'},j_{k}^{'}) \otimes K({{i}_{k}},{{j}_{k}})$.

Покажем, что ${{M}_{k}}({{z}_{k}},z_{k}^{'}) = L(i_{k}^{'},j_{k}^{'}) \otimes K({{i}_{k}},{{j}_{k}})$ действительно приводит нас к (17):

(19)

$\begin{gathered} {{M}_{\begin{subarray}{l} {{z}_{1}}, \ldots ,{{z}_{d}} \\ z_{1}^{'}, \ldots ,z_{d}^{'} \end{subarray} }} = {{K}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}} \\ {{j}_{1}}, \ldots ,{{j}_{d}} \end{subarray} }} \oslash {{L}_{\begin{subarray}{l} i_{1}^{'}, \ldots ,i_{d}^{'} \\ j_{1}^{'}, \ldots ,j_{d}^{'} \end{subarray} }} = ({{L}_{1}}(i_{1}^{'},j_{1}^{'}) \otimes {{K}_{1}}({{i}_{1}},{{j}_{1}})) \cdots ({{L}_{d}}(i_{d}^{'},j_{d}^{'}) \otimes {{K}_{d}}({{i}_{d}},{{j}_{d}})) = \\ = \;({{L}_{1}}(i_{1}^{'},j_{1}^{'}) \ldots {{L}_{d}}(i_{d}^{'},j_{d}^{'})) \otimes ({{K}_{1}}({{i}_{1}},{{j}_{1}}) \ldots {{K}_{d}}({{i}_{d}},{{j}_{d}})). \\ \end{gathered} $

Учитывая тот факт, что кронекерово произведение двух чисел есть умножение, получаем

(20)

$({{L}_{1}}(i_{1}^{'},j_{1}^{'}) \ldots {{L}_{d}}(i_{d}^{'},j_{d}^{'})) \otimes ({{K}_{1}}({{i}_{1}},{{j}_{1}}) \ldots {{K}_{d}}({{i}_{d}},{{j}_{d}})) = {{L}_{1}}(i_{1}^{'},j_{1}^{'}) \ldots {{L}_{d}}(i_{d}^{'},j_{d}^{'}){{K}_{1}}({{i}_{1}},{{j}_{1}}) \ldots {{K}_{d}}({{i}_{d}},{{j}_{d}}) = {{M}_{\begin{subarray}{l} {{z}_{1}}, \ldots ,{{z}_{d}} \\ z_{1}^{'}, \ldots ,z_{d}^{'} \end{subarray} }}.$

2.3. Связь z-крона и z-нумерации

Снова рассмотрим две QTT-матрицы:

(21)

${{A}_{\begin{subarray}{l} {{k}_{1}}, \ldots ,{{k}_{d}} \\ {{l}_{1}}, \ldots ,{{l}_{d}} \end{subarray} }} = {{A}_{1}}({{k}_{1}},{{l}_{1}}) \ldots {{A}_{d}}({{k}_{d}},{{l}_{d}}),\quad {{B}_{\begin{subarray}{l} {{m}_{1}}, \ldots ,{{m}_{d}} \\ {{n}_{1}}, \ldots ,{{n}_{d}} \end{subarray} }} = {{B}_{1}}({{m}_{1}},{{n}_{1}}) \ldots {{B}_{d}}({{m}_{d}},{{n}_{d}}),\quad {{k}_{t}},{{l}_{t}},{{m}_{t}},{{n}_{t}} \in {\text{\{ }}0,\;1{\text{\} }}.$

Пусть

(22)

${{C}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}} \\ {{j}_{1}}, \ldots ,{{j}_{d}} \end{subarray} }} = {{A}_{\begin{subarray}{l} {{k}_{1}}, \ldots ,{{k}_{d}} \\ {{l}_{1}}, \ldots ,{{l}_{d}} \end{subarray} }} \oslash {{B}_{\begin{subarray}{l} {{m}_{1}}, \ldots ,{{m}_{d}} \\ {{n}_{1}}, \ldots ,{{n}_{d}} \end{subarray} }},\quad {{i}_{t}},{{j}_{t}} \in {\text{\{ }}0,\;1,\;2,\;3{\text{\} }}.$

Обозначим через ${\mathbf{A}}$, ${\mathbf{B}}$, ${\mathbf{C}}$ матрицы $A,\;B,\;C$ в обычном представлении. Матрицы, индексы которых были квантизованы и представлены TT-матрицами, будем обозначать как ${{A}_{\begin{subarray}{l} {{k}_{1}}, \ldots ,{{k}_{d}} \\ {{l}_{1}}, \ldots ,{{l}_{d}} \end{subarray} }}$, ${{B}_{\begin{subarray}{l} {{m}_{1}}, \ldots ,{{m}_{d}} \\ {{n}_{1}}, \ldots ,{{n}_{d}} \end{subarray} }}$, ${{C}_{\begin{subarray}{l} {{i}_{1}}, \ldots ,{{i}_{d}} \\ {{j}_{1}}, \ldots ,{{j}_{d}} \end{subarray} }}$ соответственно; $q$-е ядро $A,B,C$ по-прежнему обозначаем через ${{A}_{q}}$, ${{B}_{q}}$, ${{C}_{q}}$. Тогда верна следующая теорема.

Теорема 1. Для (22) верно, что

(23)

${{{\mathbf{C}}}_{{ij}}} = {{{\mathbf{A}}}_{{kl}}}{{{\mathbf{B}}}_{{mn}}},\quad i = \mathcal{Z}(k,m),\quad j = \mathcal{Z}(l,n).$

Доказательство. Выделим младший разряд в индексах:

(24)

$\begin{gathered} {{i}^{H}} = \left\lfloor {i{\text{/}}4} \right\rfloor ,\quad {{i}^{L}} = i\bmod 4,\quad {{j}^{H}} = \left\lfloor {j{\text{/}}4} \right\rfloor ,\quad {{j}^{L}} = jmod4, \\ {{k}^{H}} = \left\lfloor {k{\text{/}}2} \right\rfloor ,\quad {{k}^{L}} = kmod2,\quad {{m}^{H}} = \left\lfloor {m{\text{/}}2} \right\rfloor ,\quad {{m}^{L}} = mmod2, \\ {{l}^{H}} = \left\lfloor {l{\text{/}}2} \right\rfloor ,\quad {{l}^{L}} = lmod2,\quad {{n}^{H}} = \left\lfloor {n{\text{/}}2} \right\rfloor ,\quad {{n}^{L}} = nmod2. \\ \end{gathered} $

Сначала докажем, что

(25)

$i = \mathcal{Z}(k,m) \Leftrightarrow {{i}^{H}} = \mathcal{Z}({{k}^{H}},{{m}^{H}}),\quad {{i}^{L}} = \mathcal{Z}({{k}^{L}},{{m}^{L}}).$

Действительно, полагая ${{i}^{H}} = \mathcal{Z}({{k}^{H}},{{m}^{H}})$, ${{i}^{L}} = \mathcal{Z}({{k}^{L}},{{m}^{L}})$, по формуле (14) получаем

(26)

$\begin{gathered} \mathcal{Z}(k,m) = \mathcal{Z}(2{{k}^{H}} + {{k}^{L}},\;2{{m}^{H}} + {{m}^{L}}) = \sum\limits_{t = 2}^d {{{2}^{{2t - 2}}}} k_{{t - 1}}^{H} + {{k}^{L}} + \sum\limits_{t = 2}^d {{{2}^{{2t - 1}}}} m_{{t - 1}}^{H} + 2{{m}^{L}} = \\ = \;4\left( {\sum\limits_{t = 1}^{d - 1} {{{2}^{{2t - 2}}}} k_{t}^{H} + \sum\limits_{t = 1}^{d - 1} {{{2}^{{2t - 1}}}} m_{t}^{H}} \right) + {{k}^{L}} + 2{{m}^{L}} = 4Z({{k}^{H}},{{m}^{H}}) + Z({{k}^{L}},{{m}^{L}}) = 4{{i}^{H}} + {{i}^{L}} = i, \\ \end{gathered} $

где $k_{t}^{H}$, $m_{t}^{H}$ есть $t$-й разряд числа ${{k}^{H}}$, ${{m}^{H}}$ соответственно.

Далее применим метод математической индукции по $d$ для доказательства (23).

1. $d = 1$: этот результат следует из свойств кронекерового произведения:

(27)

${{{\mathbf{C}}}_{{ij}}} = {{A}_{\begin{subarray}{l} k \\ l \end{subarray} }} \oslash {{B}_{\begin{subarray}{l} m \\ n \end{subarray} }} = {{B}_{\begin{subarray}{l} m \\ n \end{subarray} }} \otimes {{A}_{\begin{subarray}{l} k \\ l \end{subarray} }} = {{{\mathbf{B}}}_{{mn}}}{{{\mathbf{A}}}_{{kl}}}.$

2. По свойству кронекерова произведения имеем

(28)

$i = k + 2m = \mathcal{Z}(k,m),\quad j = l + 2n = \mathcal{Z}(l,n).$

3. Пусть для $d = q$ утверждение теоремы (23) истинно. Тогда для любых ${{A}^{q}}$, ${{B}^{q}}$, ${{C}^{q}}$ имеем

(29)

${\mathbf{C}}_{{ij}}^{q} = {\mathbf{A}}_{{kl}}^{q}{\mathbf{B}}_{{mn}}^{q},\quad i = \mathcal{Z}(k,m),\quad j = \mathcal{Z}(l,n);$

здесь верхний индекс $q$ обозначает, что данное уравнение выписано для $d = q$.

Теперь рассмотрим $(i,j)$ элемент матрицы ${{{\mathbf{C}}}^{{q + 1}}}$ для $d = q + 1$. Напомним, что $i,j$-й элемент матрицы ${\mathbf{C}}$ имеет TT-индекс $\begin{gathered} {{i}_{1}} \ldots {{i}_{d}} \hfill \\ {{j}_{1}} \ldots {{j}_{d}} \hfill \\ \end{gathered} $, где $0 \leqslant {{i}_{t}}$, ${{j}_{t}} \leqslant 4$. Также используем обозначения (24).

Пусть $L(a) = amod2$, $H(a) = \left\lfloor {a{\text{/}}2} \right\rfloor $, тогда получим

(30)

$\begin{gathered} {\mathbf{A}}_{{kl}}^{{q + 1}}{\mathbf{B}}_{{mn}}^{{q + 1}} = {\mathbf{C}}_{{ij}}^{{q + 1}} = \Pi _{{t = 1}}^{{q + 1}}{{({{B}_{t}} \otimes {{A}_{t}})}_{{{{i}_{t}},{{j}_{t}}}}} = \Pi _{{t = 1}}^{{q + 1}}{{({{B}_{t}})}_{{H({{i}_{t}}),H({{j}_{t}})}}}{{({{A}_{t}})}_{{L({{i}_{t}}),L({{j}_{t}})}}} = \\ = \;[\Pi _{{t = 1}}^{q}{{({{B}_{t}})}_{{H({{i}_{t}}),H({{j}_{t}})}}}{{({{A}_{t}})}_{{L({{i}_{t}}),L({{j}_{t}})}}}]{{({{B}_{{q + 1}}})}_{{H({{i}^{L}}),H({{j}^{L}})}}}{{({{A}_{{q + 1}}})}_{{L({{i}^{L}}),L({{j}^{L}})}}} = \\ = \;{\mathbf{A}}_{{{{k}^{H}}{{l}^{H}}}}^{q}{\mathbf{B}}_{{{{m}^{H}}{{n}^{H}}}}^{q}{{({{B}_{{q + 1}}})}_{{H({{i}^{L}}),H({{j}^{L}})}}}{{({{A}_{{q + 1}}})}_{{L({{i}^{L}}),L({{j}^{L}})}}}. \\ \end{gathered} $

Из предположения индукции имеем

(31)

${{i}^{H}} = \mathcal{Z}({{k}^{H}},{{m}^{H}}),\quad {{j}^{H}} = \mathcal{Z}({{l}^{H}},{{n}^{H}}).$

Из (30) следует, что

(32)

${\mathbf{A}}_{{kl}}^{{q + 1}} = {\mathbf{A}}_{{{{k}^{H}}{{l}^{H}}}}^{q}{{({{A}_{{q + 1}}})}_{{L({{i}^{L}}),L({{j}^{L}})}}}.$

С другой стороны, верно

(33)

${\mathbf{A}}_{{kl}}^{{q + 1}} = \Pi _{{t = 1}}^{{q + 1}}{{({{A}_{t}})}_{{{{k}_{t}},{{l}_{t}}}}} = [\Pi _{{t = 1}}^{q}{{({{A}_{t}})}_{{k_{t}^{H},l_{t}^{H}}}}]{{({{A}_{{q + 1}}})}_{{{{k}^{L}},{{l}^{L}}}}} = {\mathbf{A}}_{{{{k}^{H}}{{l}^{H}}}}^{q}{{({{A}_{{q + 1}}})}_{{{{k}^{L}},{{l}^{L}}}}}.$

Отсюда следует, что

(34)

${{k}^{L}} = {{i}^{L}}mod2,\quad {{l}^{L}} = {{j}^{L}}mod2,$

а из (34), (31) и (25) следует (23) для $d = q + 1$.

3. ЧИСЛЕННАЯ ИЛЛЮСТРАЦИЯ

В качестве численной иллюстрации предложенного алгоритма сборки матриц жесткости в z-перестановке рассмотрим модельную задачу Дирихле для уравнения Пуассона с единичной правой частью и нулевыми граничными условиями Дирихле в ограниченной двумерной области $\Omega $ с кусочно-гладкой границей $\partial \Omega $:

(35)

$\begin{array}{*{20}{c}} { - \Delta u = 1\quad {\text{в}}\quad \Omega ,} \\ {{{{\left. u \right|}}_{{\partial \Omega }}} = 0.} \end{array}$

В качестве областей $\Omega \subseteq {{\mathbb{R}}^{2}}$ мы рассмотрим многоугольные ограниченные области, показанные на фиг. 2. Хорошо известно [7], что задача корректно поставлена в $H_{0}^{1}$. Наличие углов приводит к возникновению угловых сингулярностей, которые необходимо разрешать с использованием адаптивных методов; преимущество тензорного подхода состоит в том, что можно использовать очень мелкие “виртуальные” равномерные сетки, достаточные для разрешения угловых сингулярностей, и уменьшать число параметров за счет использования малопараметрических представлений для приближения дискретного решения. Эта идея получила свое развитие в работе [8], где удалось достигнуть очень мелких сеток, вплоть до ${{2}^{{60}}}$ “виртуальных” узлов. В нашем примере для построения матриц жесткости в тензорном формате область разбивается на четырехугольники, как показано на фиг. 2. Каждый четырехугольник отображается на квадрат, в соответствующем квадрате строится равномерная сетка, и используются билинейные конечные элементы. Схема дискретизации из [9] предназначена для дискретизации эллиптических уравнений на непрямоугольной области, таким образом, чтобы были эффективно применимы тензорные методы.

Фиг. 2.

Примеры областей и их разбиение на четырехугольные подобласти и визуализация решения задачи Дирихле для уравнения Пуассона с нулевым граничным условием и единичной правой частью. (а) – остроугольный треугольник, разбитый на 3 четырехугольника, (б) – пятиконечная звезда, разбитая на 5 четырехугольников.

Фиг. 3.

(а) – график зависимости эффективного ранга глобальной матрицы жесткости в методе конечных элементов от d для канонического порядка и z-переставленных строк и столбцов, (б) – график отношения эффективного ранга канонического порядка элементов и z-перестановки для той же матрицы.

Матрица жесткости строится в двух перестановках, которые обсуждались в данной работе. Цель эксперимента состоит в том, чтобы сравнить число параметров, требуемое для представления матриц.

Мы проверили различные области $\Omega $ с различным числом подобластей $q$ от 3 до 11 (все результаты доступны по ссылке: https://github.com/RerRayne/qtt-laplace).

Вне зависимости от выбираемой нами конфигурации поведение эффективных QTT-рангов глобальной матрицы жесткости совпадало с представленным на фиг. 3. В статье [2] показано, что QTT-ранги растут не более чем экспоненциально. В наших экспериментах для канонического порядка мы наблюдали полиномиальный рост QTT-рангов со степенью порядка $2.8$. В случае z-нумерации строк и столбцов эффективные ранги растут линейно по $d$.

ЗАКЛЮЧЕНИЕ

Данная работа развивает QTT-технологию решения задач математической физики, которая затронута в нескольких недавних работах. Основной результат состоит во введении новой операции между матрицами, которая позволяет строить представление двумерных операторов в z-перестановке из их одномерных представлений. Численные эксперименты показали, что в примерах, рассмотренных ранее в [9], такое представление позволяет получить логарифмическую зависимость объема памяти, необходимой для хранения дискретизованного оператора, от числа неизвестных, что позволяет использовать эффективные тензорные решатели. Стоит отметить, что практическое применение такой технологии и ее сравнение с другими известными подходами (адаптивные сетки, hp-метод, спектральные методы и др.) еще только предстоит сделать. Только недавно удалось преодолеть принципиальные сложности, связанные с обусловленностью дискретных операторов на очень мелких виртуальных сетках [8]. Мы рассчитываем в дальнейших работах получить практически применимые результаты для решения различных классов двумерных и трехмерных задач математической физики.

Список литературы

Morton G. A computer oriented geodetic data base and a new technique in file sequencing. Ottawa: International Business Machines Company, 1966.
Kazeev V., Schwab C. Quantized tensor-structured finite elements for second-order elliptic PDEs in two dimensions // Numerische Mathematik. 2018. V. 1. № 138. P. 133–190.
Oseledets I. Tensor-train decomposition // SIAM Journal on Scientific Comput. 2011. V. 5. № 33. P. 2295–2317.
De Launey W., Seberry J. The strong Kronecker product // J. of Combinatorial Theory. 1994. V. 2. № 66. P. 192–213.
Kazeev V., Khoromskij B. Low-rank explicit QTT representation of the Laplace operator and its inverse // SIAM Journal on Matrix Analys. and Applicat. 2012. V. 3. № 33. P. 742–758.
Kazeev V., Reichmann O., Schwab C. Low-rank tensor structure of linear diffusion operators in the TT and QTT formats // Linear Algebra and its Applicat. 2013. V. 11. № 438. P. 4204–4221.
Strang G., Fix G. An analysis of the finite element method. New Jersey: Prentice-hall Englewood Cliffs, 1973.
Bachmayr M., Kazeev V. Stability of Low-Rank Tensor Representations and Structured Multilevel Preconditioning for Elliptic PDEs // Foundations of Comput. Math. 2020. P. 1–62.
Markeeva L., Tsybulin I., Oseledets I. QTT-isogeometric solver in two dimensions: arXiv preprint arXiv:1802.02839. 2018.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал