Журнал вычислительной математики и математической физики, 2020, T. 60, № 12, стр. 2162-2176
Численное сравнение обобщенной модели Максвелла и модели Черчиньяни–Лэмпис
А. А. Фролова *
ВЦ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия
* E-mail: aafrolova@yandex.ru
Поступила в редакцию 27.02.2020
После доработки 15.06.2020
Принята к публикации 04.08.2020
Аннотация
Исследуется анизотропная модель взаимодействия газа с поверхностью для возможного использования ее в качестве граничного условия при решении кинетического уравнения. Проводится численное сравнение значений поверхностных аэродинамических коэффициентов и температуры, полученных с применением двухпараметрического варианта анизотропной модели отражения и граничного условия Черчиньяни–Лэмпис, для задач внешнего обтекания при различных значениях параметров разреженности и коэффициентов аккомодации. Показано влияние геометрии обтекаемого тела на степень отличия решений при использовании различных моделей граничных условий. Библ. 32. Фиг. 10. Табл. 3.
1. ВВЕДЕНИЕ
Выбор граничного условия отражения, аппроксимирующего взаимодействие частиц с поверхностью, является одним из определяющих факторов при исследовании течений разреженного газа. Созданию моделей, описывающих взаимодействие частиц с твердыми телами, посвящено много теоретических исследований. Мы упомянем только некоторые из них, а более полный обзор можно найти, например, в [1].
Проблема взаимодействия газа с поверхностью имеет различные уровни детализации, связанные между собой, и в зависимости от масштаба исследуемого процесса используется атомно-молекулярное, кинетическое или газодинамическое описание. На газодинамическом уровне задаются функциональные связи макропараметров, которые либо определяются феноменологически, либо могут быть получены по функции распределения отраженных частиц, например, методом Чепмена–Энскога [2].
При задании граничного условия (ядер рассеивания или соответствующих функций распределения) на кинетическом уровне применяются различные приближенные модели, например, см. [3]. Параметры моделей определяются из экспериментальных данных или из расчетов методом молекулярной динамики, позволяющих учесть атомную структуру поверхностного слоя. Молекулярное моделирование, широко применяемое в последнее время, представляет собой расчет большого количества траекторий движения с использованием системы уравнений Ньютона взаимодействующих частиц с начальными условиями для координат и скоростей. При этом могут быть учтены степень шероховатости поверхности, величина адсорбирующего слоя, потенциалы взаимодействия молекул газа как между собой, так и с атомами кристаллической решетки. Усреднение макропараметров движения по траекториям позволяет вычислить изменение импульса и энергии при взаимодействии газа с телом и получить соответствующие коэффициенты аккомодации, а также определить функцию распределения отраженных частиц для рассчитываемого случая [4]–[6].
Однако в силу большого количества факторов, влияющих на отражение, молекулярное моделирование не позволяет определить общую зависимость функции распределения для замыкания задачи на кинетическом уровне. Поэтому в последнее время стали использоваться гибридные алгоритмы, основанные на сращивании решений, получаемых методом молекулярной динамики в окрестности тела и прямого статистического моделирования (Direct Simulation Monte Carlo, DSMC) в остальной части течения [7]. Несмотря на возможность получения более точного решения, применение молекулярного моделирования даже в небольших областях приводит к длительным вычислительным расчетам, что существенно уменьшает эффективность такого подхода.
Идеи создания единого подхода на основе кинетических уравнений для определения закона взаимодействия газа с поверхностью были предложены в [8], [9], но сложность этих методов пока не позволяет использовать полученные результаты. Поскольку определение достаточно общей функциональной зависимости граничного условия для кинетического описания сталкивается со многими теоретическими трудностями, применяются модельные граничные условия, которые, как правило, учитывают лишь некоторые аспекты взаимодействия частиц с поверхностью.
Как известно, самой простой моделью отражения является условие Максвелла, представляющее линейную комбинацию диффузного и зеркального отражений. Функция распределения в этой модели содержит один свободный параметр и не может описать сложные процессы взаимодействия частиц с кристаллической решеткой. Несмотря на это, условие Максвелла часто используется при расчетах реальных задач, особенно при исследовании течений, ограниченных микрошероховатыми поверхностями.
Создание моделей взаимодействия частиц с поверхностями, более точно согласующихся с экспериментами, привело к разработке других аппроксимаций. Наиболее известными из них являются модели Эпштейна [10], Ночиллы [11], Черчиньяни–Лэмпис (C–L) [3], [12] и Лорда (C–L–L) [13].
Несмотря на более реалистичное описание отражения, модельные граничные условия в некоторых случаях дают функции распределения, существенно отличающиеся от получаемых в экспериментах и в расчетах методом молекулярной динамики [14], [15]. Этот факт приводит к необходимости коррекции существующих моделей. Так, синтез условий C–L и Эпштейна и учет зависимости коэффициентов аккомодации от скорости частиц предложены в [15], [2], а комбинация ядер рассеивания C–L и Максвелла в [4]. В [16] построено обобщенное условие Максвелла (анизотропная модель отражения Максвелла (AM)).
Так как широкого использования указанных граничных условий пока еще нет, то представляет интерес рассмотреть, какие решения дают эти модели в стандартных задачах газовой динамики.
В настоящей статье мы рассмотрим более подробно условие AM и сравним его двухпараметрическую версию с моделью граничных условий C–L для внешних задач обтекания. Выбор модели отражения C–L для сравнения объясняется тем, что несмотря на присущие данной модели ограничения, в настоящее время она считается наиболее физически корректной.
Отметим, что представленные в литературе решения с граничными условиями C–L и C–L–L получены либо методом DSMC, либо для линеаризованного уравнения Больцмана в [17]–[22]. Методом дискретных ординат в рамках полного уравнения Больцмана решение с этими условиями получено в [23] только для медленных течений, а расчетов в сверхзвуковых режимах в литературе не встречается. Это связано со значительным ростом времени расчета ядра C–L при увеличении числа узлов скоростной сетки. Условие AM более экономично, поэтому определение областей параметров, где эти условия дают близкие результаты, представляется важным. Кроме этого, существенно также определить, какое физическое решение дает граничное условие AM.
2. КИНЕТИЧЕСКИЕ УРАВНЕНИЯ И МОДЕЛИ ГРАНИЧНЫХ УСЛОВИЙ
Уравнение Больцмана без учета силового члена записывается в виде (см. [24])
Используя функцию распределения, макроскопические переменные, такие как плотность числа частиц n, средняя скорость u, температура T, вектор теплового потока q, давление $p$, определяются по формулам:
Для уменьшения численных затрат интеграл столкновений в кинетическом уравнении аппроксимируется модельным оператором в виде
В случае модели Шахова (S-модель) [25]Проблема описания взаимодействия частиц с поверхностью в строгой постановке была сформулирована в терминах теории ядер рассеяния K. Черчиньяни [3], [12], согласно которой функции распределения отраженных и падающих частиц $~{{f}_{r}}({\mathbf{\xi }}),\;{{f}_{i}}({\mathbf{\xi }}{\kern 1pt} {\text{'}})$ связаны ядром рассеяния $R({\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }})$ следующим образом:
неотрицательности,
нормировки
и взаимности
Используя данную терминологию, ядро рассеяния частиц для граничного условия Максвелла, представляющего линейную комбинацию диффузного и зеркального отражений, записывается в виде
Ядро рассеивания модели C–L представляется в виде произведения трех одномерных ядер
(1)
${{R}_{{CL}}}\left( {{\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }}~} \right) = {{R}_{{CLn}}}(\xi _{n}^{'} \to {{\xi }_{n}}){{R}_{{CLt}}}(\xi _{t}^{'} \to {{\xi }_{t}}){{R}_{{CLs}}}(\xi _{s}^{'} \to {{\xi }_{s}}),$(2)
$\begin{gathered} {{R}_{{CLn}}}(\xi _{n}^{'} \to {{\xi }_{n}}) = \frac{{2\beta _{w}^{2}{{\xi }_{n}}}}{{{{\alpha }_{n}}}}\exp \left[ { - \frac{{~~\beta _{w}^{2}(~\xi _{n}^{2} - (1 - {{\alpha }_{n}})\xi {{{_{n}^{'}}}^{2}})}}{{{{\alpha }_{n}}}}} \right]{{I}_{0}}\left( {\frac{{2\beta _{w}^{2}{{\xi }_{n}}\xi _{n}^{'}\sqrt {1 - {{\alpha }_{n}}} }}{{{{\alpha }_{n}}}}} \right), \\ {{R}_{{CLt,s}}}(\xi _{{t,s}}^{'} \to {{\xi }_{{t,s}}}) = \frac{{{{\beta }_{w}}}}{{\sqrt {\pi (2 - ~{{\alpha }_{{t,s}}}){{\alpha }_{{t,s}}}} }}\exp \left[ { - \frac{{~~\beta _{w}^{2}{{{(~{{\xi }_{{t,s}}} - (1 - {{\alpha }_{{t,s}}})\xi _{{t,s}}^{'})}}^{2}}}}{{(2 - {{\alpha }_{{t,s}}}){{\alpha }_{{t,s}}}}}} \right], \\ \end{gathered} $Коэффициенты ${{\alpha }_{n}}(0 \leqslant {{\alpha }_{n}} \leqslant 1)$ и ${{\alpha }_{{t,s}}}(0 \leqslant {{\alpha }_{{t,s}}} \leqslant 2)$ являются свободными параметрами модели.
Ядро (1) с тремя свободными параметрами было получено в [12], но так как анизотропия поверхности не рассматривалась, то полагалось, что ${{\alpha }_{t}} = {{\alpha }_{s}}$. Анизотропный вариант был рассмотрен в [28] при получении граничных условий для температуры и скорости на теле в газодинамическом режиме для анизотропной поверхности. Для изотропного случая [12] коэффициент ${{\alpha }_{t}}$ ($0 \leqslant {{\alpha }_{t}} \leqslant 2)$ определяет аккомодацию тангенциального импульса ${{P}_{{it}}}$, приносимого на поверхность падающими частицами, а коэффициенты ${{\alpha }_{n}}\left( {0 \leqslant {{\alpha }_{n}} \leqslant 1} \right)$ и ${{\alpha }_{{Et}}} = \left( {2 - {{\alpha }_{t}}} \right){{\alpha }_{t}}$ – аккомодацию кинетических энергий ${{E}_{{in}}},\;{{E}_{{it}}}$, приносимых падающими частицами $~~$по нормали к поверхности и в тангенциальной плоскости, согласно следующим формулам:
где ${{P}_{{rt}}},\;{{E}_{{rn}}},\;{{E}_{{rt}}}$ – импульс и энергии, уносимые отраженными частицами, а ${{E}_{{wn}}},\;{{E}_{{wt}}}$ – энергии при равновесии газа с поверхностью тела.Модель C–L для изотропной поверхности имеет предельные значения параметров: ${{\alpha }_{n}} = {{\alpha }_{t}} = 1$, ${{\alpha }_{n}} = {{\alpha }_{t}} = 0$, ${{\alpha }_{n}} = 1 \vee {{\alpha }_{t}} = 0$, ${{\alpha }_{n}} = 0 \vee {{\alpha }_{t}} = 1$ (значение ${{\alpha }_{t}} = 2~$не рассматривается). Данные предельные значения соответствуют полному диффузному отражению, полному зеркальному отражению и частично диффузному и частично зеркальному отражениям. Соответствующие ядра рассеяния имеют вид
(3)
${{R}_{{CL}}}({\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }}) = {{R}_{{{\text{diff}}}}}\quad {\text{при}}\quad {{\alpha }_{n}} = {{\alpha }_{t}} = 1,$(4)
${{R}_{{CL}}}({\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }}) = {{R}_{{{\text{spec}}}}}\quad {\text{при}}\quad {{\alpha }_{n}} = {{\alpha }_{t}} = 0,$(5)
${{R}_{{CL}}}({\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }}) = 2{{\xi }_{n}}\beta _{w}^{2}\exp [ - ~\beta _{w}^{2}\xi _{n}^{2}]{\kern 1pt} \delta ({\mathbf{\xi }}_{t}^{'} - {{{\mathbf{\xi }}}_{t}})\quad {\text{при}}\quad {{\alpha }_{n}} = 1 \vee {{\alpha }_{t}} = 0,$(6)
${{R}_{{CL}}}({\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }}) = \beta _{w}^{2}{\text{/}}\pi \exp [ - ~\beta _{w}^{2}(\xi _{t}^{2} + \xi _{s}^{2})]\delta ({{\xi }_{n}} + \xi _{n}^{'})\quad {\text{при}}\quad {{\alpha }_{n}} = 0 \vee {{\alpha }_{t}} = 1.$(7)
${{R}_{{GM}}}({\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }}) = {{R}_{{GMn}}}(\xi _{n}^{'} \to {{\xi }_{n}}){{R}_{{GMt}}}({\mathbf{\xi }}_{t}^{'} \to {{{\mathbf{\xi }}}_{t}}),$(8)
$\begin{gathered} {{R}_{{GMn}}}(\xi _{n}^{'} \to {{\xi }_{n}}) = {{\alpha }_{{GMn}}}{\kern 1pt} 2{{\xi }_{n}}{\kern 1pt} \beta _{w}^{2}\exp [ - \beta _{w}^{2}\xi _{n}^{2}] + (1 - {{\alpha }_{{GMn}}})\delta (~{{\xi }_{n}} + \xi _{n}^{'}), \\ {{R}_{{GMt}}}({\mathbf{\xi }}_{t}^{'} \to {{{\mathbf{\xi }}}_{t}}) = {{\alpha }_{{GMt}}}(\beta _{w}^{2}{\text{/}}\pi )\exp [ - \beta _{w}^{2}(\xi _{t}^{2} + \xi _{s}^{2})] + (1 - {{\alpha }_{{GMt}}})\delta (~{{\xi }_{t}} - \xi _{t}^{'})\delta (~{{\xi }_{s}} - \xi _{s}^{'}). \\ \end{gathered} $(9)
${{R}_{{AM}}}({\mathbf{\xi }}{\kern 1pt} ' \to {\mathbf{\xi }}) = {{R}_{{AMn}}}(\xi _{n}^{'} \to {{\xi }_{n}}){{R}_{{AMt}}}(\xi _{t}^{'} \to {{\xi }_{t}}){{R}_{{AMs}}}(\xi _{s}^{'} \to {{\xi }_{s}}),$Очевидно, что ядра рассеяния (7), (9) обладают свойствами положительности, нормировки, взаимности и имеют такую же структуру, как и ядро C–L (1). А именно, ядра рассеяния представляются в виде произведения ядер по ортогональным направлениям с независимыми параметрами. Отличие состоит в функции, связывающей диффузное и зеркальное отражение по каждому направлению, что является одним из основных факторов при моделировании взаимодействия газа с поверхностью. Отметим, что граничное условие Максвелла не является частным случаем условия АМ и GM ни при каких значениях коэффициентов аккомодации, и также условие GM не является частным случаем условия АМ.
Отличительной особенностью преобразования (9) является разбиение функции отражения (если ${{\alpha }_{{n,t,s}}} \ne 0,1$) на восемь пучков различной интенсивности. Если, например, функция распределения скоростей падающих частиц является функцией Максвелла ${{F}_{M}}(n,{\mathbf{u}},T)$, то экстремумы отраженной функции распределения будут локализованы на осях, в центре системы координат, на ортогональных плоскостях и в точке, соответствующей зеркальному отражению. Отметим, что локальная немонотонность отраженной функции распределения, обычно наблюдаемая в экспериментах или при молекулярном моделировании, не связана жестко с нормальным и тангенциальными направлениями, а зависит от углов падения, структуры шероховатости, температуры поверхности и т.д. Наличие же фиксированных направлений отражения независимо от параметров падающих молекул может приводить к сужению области применения анизотропной модели. То же самое относится и к модели (7), которая разбивает отраженную функцию на четыре пучка. Поэтому вопрос, что же дают эти модели при решении задач в стандартных постановках, представляется важным.
В настоящем исследовании мы рассмотрим двухпараметрическую модель (7) и сравним ее с широко используемой моделью C–L для изотропной поверхности, так как обе эти модели имеют два свободных параметра.
Нетрудно показать, что параметры ${{\alpha }_{{GMn}}},\;{{\alpha }_{{GMt}}}$ являются коэффициентами аккомодации импульса и энергии вдоль нормального и тангенциального направлений, соответственно,
3. СРАВНЕНИЕ МОДЕЛИ ЧЕРЧИНЬЯНИ–ЛЭМПИС И ОБОБЩЕННОЙ МОДЕЛИ МАКСВЕЛЛА ПРИ СВЕРХЗВУКОВОМ ОБТЕКАНИИ ТЕЛ
В настоящем исследовании рассматривается стационарная проблема сверхзвукового обтекания тел различной геометрии в двумерном случае. Для оценки различия решений проводится сравнение поведения температуры в поле течения и поверхностных коэффициентов давления, трения и теплового потока ${{C}_{p}}$, ${{C}_{f}}$, ${{C}_{h}}$, которые определяются из следующих формул:
Численный расчет проводится методом дискретных ординат с использованием кинетического модуля программного комплекса Unified Flow Solver (UFS) [31], использующего для решения расщепление кинетического уравнения на этапы свободномолекулярного течения и релаксацию. В дискретном скоростном пространстве выбирается равномерная кубическая сетка. В физическом пространстве используется иерархическая адаптивно измельчаемая сетка. В пространственных координатах применяется метод конечных объемов второго порядка на неструктурированной декартовой сетке. Поверхность тела аппроксимируется с помощью метода скошенных ячеек. Стационарное решение ищется с помощью явного по времени метода установления. Интеграл столкновений в кинетическом уравнении аппроксимируются согласно S-модели Шахова [25]. Для выполнения законов сохранения релаксационного оператора используется итерационная процедура Ньютона. Предполагается, что газ является одноатомным и закон вязкости соответствует взаимодействию по модели твердых сфер $\mu = {{\mu }_{\infty }}\sqrt {T{\text{/}}{{T}_{\infty }}} $.
При расчетах используются безразмерные величины введением характерных значений длины d, температуры ${{T}_{\infty }}$, плотности ${{\rho }_{\infty }}~$ и наиболее вероятной молекулярной скорости $~{{{v}}_{m}} = \sqrt {~2R{{T}_{\infty }}~} $. Тепловой поток, давление и вязкость обезразмериваются на ${{\rho }_{\infty }}{v}_{m}^{3}{\text{/}}2$, $~{{\rho }_{\infty }}{v}_{m}^{2}{\text{/}}2$ и ${{\mu }_{\infty }} = \mu ({{T}_{\infty }})$ соответственно. Введение характерных величин приводит к безразмерной форме кинетическое уравнение с частотой столкновения в виде
где ${\text{Kn}} = {{\lambda }_{\infty }}{\text{/}}d$– число Кнудсена, $~{{\lambda }_{\infty }}$ – длина свободного пробега, определяемая из закона вязкости для модели твердых сфер.Вычисления, представленные ниже, выполнены с размером ячейки в скоростном пространстве ${\Delta \xi } = 0.2 - 0.3$. Для контроля результатов использовались скоростные сетки с шагами ${\Delta \xi } = 0.1,\;0.15$. Адаптация сетки в физическом пространстве выполнялась по расстоянию от тела. Минимальный размер ячейки около поверхности выбирался от $h{\text{/}}d = 5 \times {{10}^{{ - 3}}}$ до $h{\text{/}}d = 2 \times {{10}^{{ - 2}}}$ в зависимости от числа Кнудсена.
При численном решении в двумерной геометрии кинетическое уравнение может быть сведено к системе уравнений для двух усредненных функций:
Для сравнения решений рассматриваются три варианта значений коэффициентов аккомодации (см. табл. 1).
Таблица 1.
Варианты коэффициентов аккомодации при сравнении моделей C–L и GM
| Модель отражения | Вариант 1 | Вариант 2 | Вариант 3 | |||
|---|---|---|---|---|---|---|
| C–L модель $({{\alpha }_{n}},\;{{\alpha }_{t}})$ | $0.5$ | $1$ | $0.5$ | $0.3$ | $0.1$ | $0.1056$ |
| GM модель $({{\alpha }_{{GMn}}},\;{{\alpha }_{{GMt~}}})$ | $0.5$ | $1$ | $0.5$ | $0.51$ | $0.1$ | $0.2$ |
При этом коэффициенты выбраны так, чтобы обмены тангенциальной и нормальной энергий для обоих моделей отражения совпадали в свободно молекулярном режиме, т.е. ${{\alpha }_{n}} = {{\alpha }_{{GMn}}}$, $~{{\alpha }_{{Et}}} = (2 - {{\alpha }_{t}}){{\alpha }_{t}} = {{\alpha }_{{GMt}}}$. Отметим, что коэффициенты аккомодации нормального импульса при таком выборе будут различными. Приведенные варианты соответствуют трем различным режимам отражения.
Вариант 1. Коэффициенты аккомодации тангенциальных импульса и энергии выбираются равными и ${{\alpha }_{t}} = {{\alpha }_{{GMt}}} = {{\alpha }_{{Et}}} = 1$. Такое значение аккомодации тангенциального импульса наблюдается при отражении тяжелых атомов (Xe, Kr) от металлических (обычных технических) поверхностей [32].
Вариант 2. Коэффициенты аккомодации тангенциального импульса $\left( {{{\alpha }_{{GMt}}} = 0.51,\;{{\alpha }_{t}} = 0.3} \right)~$ соответствуют взаимодействию частиц с более гладкими, обработанными поверхностями. Для этих вариантов коэффициенты аккомодации энергии по нормали ${{\alpha }_{n}} = {{\alpha }_{{GMn}}}$ = 0.5 заданы одинаково удаленными от предельных значений 0 и 1, при которых ${{R}_{{GMn}}}$ = ${{R}_{{CLn}}}$.
Вариант 3. Коэффициенты аккомодации соответствуют случаю обтекания тела с гладкой, чистой поверхностью, и близкие значения коэффициентов были получены при молекулярном моделировании отражения атомов Xe от поверхности полупроводника GaSe [14].
4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ
Пример 1. В данном случае рассматривается сверхзвуковое обтекание круглого цилиндра с постоянной заданной температурой на поверхности ${{T}_{w}}$ и скоростью набегающего потока c числом Маха М = 5. Характерный параметр длины d выбирается равным диаметру цилиндра. Безразмерные параметры набегающего потока (плотность числа частиц, скорость, температура) имеют следующие значения: $n = 1,$ ${{u}_{x}} = 4.65,$ ${{u}_{y}} = 0,$ $T = 1$, температура поверхности ${{T}_{w}} = 1$.
Для иллюстрации различия граничных функций распределения на фиг. 1 и 2 показаны изолинии функции распределения отраженных частиц ${{f}_{{r0}}}({\mathbf{\xi }})$ для потоков газа, направленных под углами 0° и 60° к нормали поверхности. Функция распределения падающих частиц соответствует ${{F}_{M}}(n,{\mathbf{u}},T)$ с параметрами $n = 1,$ $\left| {\mathbf{u}} \right| = 4.65,$ $T = 1$. Видно, что функция распределения отраженных частиц модели GM имеет максимумы, соответствующие ядрам (3)–(6) и функции $~{{F}_{M}}(n,{\mathbf{u}}{\kern 1pt} *,T)$, где $u_{x}^{*} = - {{u}_{x}},$ $u_{y}^{*} = {{u}_{y}}$. В то же время функция отражения в модели C–L остается близкой к отраженной зеркально.
Фиг. 1.
Изолинии функции распределения отраженных частиц для потока, падающего по нормали к поверхности, при коэффициентах аккомодации (а) вариант 1 и вариант 2, (б) вариант 3. Сплошные линии – модель GM, штриховые линии– модель C–L.

Фиг. 2.
Изолинии функции распределения отраженных частиц для потока, падающего под углом 60° к нормали поверхности, при коэффициентах аккомодации (а) вариант 1, (б) вариант 2, (в) вариант 3. Сплошные линии – модель GM, штриховые линии модель – C–L.

Максимальные относительные различия ${{\delta }_{с}} = \Delta {{C}_{h}}{\text{/}}{{C}_{h}}$, ${{\delta }_{f}} = \Delta {{C}_{f}}{\text{/}}{{C}_{f}}$, ${{\delta }_{p}} = \Delta {{C}_{p}}{\text{/}}{{C}_{p}}$ при использовании моделей GM и C–L для всех вариантов коэффициентов аккомодации и значений числа Кнудсена (Kn = ∞, 1, 0.1) представлены в табл. 2.
Таблица 2.
Относительные различия поверхностных коэффициентов для моделей C–L и GM при обтекании круглого цилиндра
| Kn | Вариант 1 (%) | Вариант 2 (%) | Вариант 3 (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ${{\delta }_{с}}$ | ${{\delta }_{f}}$ | ${{\delta }_{p}}$ | ${{\delta }_{с}}$ | ${{\delta }_{f}}$ | ${{\delta }_{p}}$ | ${{\delta }_{с}}$ | ${{\delta }_{f}}$ | ${{\delta }_{p}}$ | |
| $\infty $ | 0.02 | 0.01 | 7.0 | 0.1 | 41.2 | 7.0 | 0.1 | 47.2 | 1.58 |
| 1.0 | 0.2 | 2.0 | 0.9 | 1.7 | 39.0 | 3.9 | 0.2 | 47.0 | 1.55 |
| 0.1 | 1.1 | 1.0 | 0.02 | 4.7 | 30.0 | 0.7 | 0.7 | 44.1 | 0.45 |
Результаты расчетов для вариантов 2 и 3 представлены на фиг. 3–7. Профили поверхностных коэффициентов, как функции от угла ϕ, отсчитываемого от точки торможения, показаны на фиг. 3 и 4, а профили температуры вдоль линии торможения и изолинии температуры при Kn = 1 на фиг. 5–7.
Фиг. 3.
Обтекание круглого цилиндра, вариант 2. Профили поверхностных коэффициентов, (а) теплопередачи Ch, (б) трения Cf, (в) давления Cp. Кривые (1, 3, 5) – граничное условие модель GM, (2, 4, 6) – модель C–L. Профили (1, 2) соответствуют Kn = ∞, (3, 4) – Kn = 1, (5, 6) – Kn = 0.1.
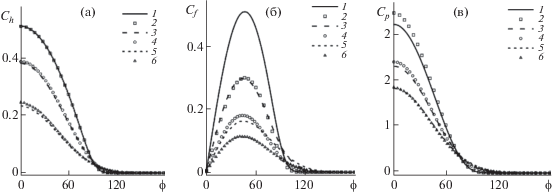
Фиг. 4.
Обтекание круглого цилиндра, вариант 3. Профили поверхностных коэффициентов, (а) теплопередачи Ch, (б) трения Cf, (в) давления Cp. Кривые (1, 3, 5) – граничное условие модель GM, (2, 4, 6) – модель C–L. Профили (1, 2) соответствуют Kn = ∞, (3, 4) – Kn = 1, (5, 6) –Kn = 0.1.

Фиг. 5.
Температура вдоль линии торможения, вариант 2 при (а) Kn = ∞, Kn = 1, (б) Kn = 0.1. Кривые (1, 3, 5) – модель GM, (2, 4, 6) – модель C–L. Профили (1, 2) соответствуют Kn = ∞, (3, 4) – Kn = 1, (5, 6) –Kn = 0.1.

Фиг. 6.
Температура для варианта 3 вдоль линии торможения при (а) Kn = ∞, Kn = 1, (б) Kn = 0.1. Кривые (1, 3, 5) – модель GM, (2, 4, 6) – модель C–L. Профили (1, 2) соответствуют Kn = ∞, (3, 4) – Kn = 1, (5, 6) –Kn = 0.1.

Фиг. 7.
Изолинии температуры при Kn = 1 для коэффициентов аккомодации (а) вариант 2, (б) вариант 3. Результаты для модели C–L – нижняя часть графика, для модели GM – верхняя.
Как видно из табл. 2 и фиг. 3, 4, с уменьшением числа Кнудсена относительная разница коэффициентов теплопередачи для всех вариантов увеличивается, а большое значение величины δp при Kn = ∞, вызванное отличием обменов нормального импульса, уменьшается. Максимальные значения δc и δp наблюдаются в варианте 2, что связано с наибольшим различием функций распределения для этого случая. Относительная разница коэффициентов поверхностного трения δf, которая в свободно молекулярном режиме определяется как ${{\delta }_{f}} = 1 - {{a}_{t}}{\text{/}}{{a}_{{GMt}}}~$, при уменьшении числа Кнудсена уменьшается. Близкие значения Cp и Ch получаются для вариантов 1 и 3, несмотря на различие функций отражения и коэффициентов аккомодации тангенциального импульса (для варианта 3).
Отличие профилей температуры в свободномолекулярном режиме (фиг. 5а и 6а) показывает влияние различных граничных функций распределения. С уменьшением числа Кнудсена относительная разность температур становится меньше и локализуется около поверхности. При Kn = 0.1 она составляет 1%, 7% и 4% для вариантов 1, 2 и 3 соответственно. Как видно на фиг. 7, изолинии температуры при Kn = 1 для вариантов 2 и 3 дают близкое поведение при использовании разных моделей отражения, хотя наблюдаются отличия в окрестности точки торможения и смещение изолиний в области течения. Изолинии температур для варианта 1 не приводятся, так как они практически совпадают.
Пример 2. В этом случае проводится сравнение решений для задачи обтекания цилиндра с сечением, имеющим угловой профиль спереди и скругление на задней кромке (фиг. 10). Полуугол заострения составляет 30 град., характерный параметр длины d равен максимальной ширине сечения. Скорость набегающего потока соответствует числу Маха M = 5, а температура поверхности ${{T}_{w}} = 1.5$.
Также как и в предыдущем примере, рассматриваются те же три варианта коэффициентов аккомодации и параметров разреженности. Отметим, что в отличие от обтекания круглого цилиндра, течение вблизи острого угла характеризуется сильной неравновесностью функции распределения и большей скоростью вдоль поверхности.
Относительные разницы поверхностных коэффициентов ${{\delta }_{с}} = \Delta {{C}_{h}}{\text{/}}{{C}_{h}}$, ${{\delta }_{f}} = \Delta {{C}_{f}}{\text{/}}{{C}_{f}}$, ${{\delta }_{p}} = \Delta {{C}_{p}}{\text{/}}{{C}_{p}}$ для трех вариантов коэффициентов аккомодации при различных параметрах разреженности представлены в табл. 3.
Из приведенных в табл. 3 результатов видно, что отличия поверхностных коэффициентов для варианта 1 имеют тот же порядок, что и полученные в случае обтекания круглого цилиндра. Однако для вариантов 2 и 3 наблюдается большее расхождение решений, которое видно также на фиг. 8 и 9, где показаны поверхностные коэффициенты вдоль контура как функции расстояния l/d, отсчитываемого от точки торможения. Для вариантов 2 и 3 наблюдаются значительные отличия значений Cp около угловой точки и коэффициента теплопередачи Ch в области разрежения (начало скругления).
Таблица 3.
Относительные разницы поверхностных коэффициентов для моделей C–L и GM при обтекании углового профиля
| Kn | Вариант 1 (%) | Вариант 2 (%) | Вариант 3 (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ${{\delta }_{с}}$ | ${{\delta }_{f}}$ | ${{\delta }_{p}}$ | ${{\delta }_{с}}$ | ${{\delta }_{f}}$ | ${{\delta }_{p}}$ | ${{\delta }_{с}}$ | ${{\delta }_{f}}$ | ${{\delta }_{p}}$ | |
| $\infty $ | 0.01 | 0.01 | 2.2 | 0.01 | 41.3 | 2.2 | 0.01 | 47.2 | 0.63 |
| 1.0 | 2.1 | 2.4 | 2.9 | 6.1 | 32.0 | 9.0 | 1.7 | 44.9 | 4.5 |
| 0.1 | 1.2 | 1.3 | 1.8 | 13.4 | 8.0 | 17.6 | 10.1 | 30.0 | 15.2 |
Фиг. 8.
Угловой профиль, вариант 2. Профили поверхностных коэффициентов, (а) теплопередачи Ch, (б) трения Cf, (в) давления Cp. Профили (1, 3) – модель GM, (2, 4) – модель C–L , кривые (1, 2) – Kn = 1, кривые (3, 4) – Kn = 0.1.

Фиг. 9.
Угловой профиль, вариант 3. Профили поверхностных коэффициентов, (а) теплопередачи Ch, (б) трения Cf, (в) давления Cp. Профили (1, 3) – модель GM, (2, 4) – модель C–L, кривые (1, 2) соответствуют Kn = 1, кривые (3, 4) – Kn = 0.1.

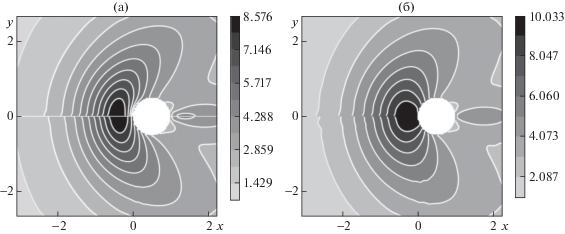
Фиг. 10.
Изолинии температуры при Kn = 1 для коэффициентов аккомодации (а) вариант 1, (б) вариант 2, (в) вариант 3. Результаты для модели C–L – нижняя часть графика, для модели GM – верхняя.

Температурные поля для вариантов 1–3 при Kn = 1 представлены на фиг. 10а, б, в соответственно. Как видно на фиг. 10а, изолинии температур для обеих моделей практически совпадают, поскольку ядра отражения скоростей по тангенциальному направлению равны при ${{\alpha }_{t}} = {{\alpha }_{{GMt}}} = 1$, а ядра (2) и (8) становятся близкими из-за уменьшения нормальной компоненты средней скорости падающих частиц вследствие релаксации.
Температурные поля для вариантов 2 и 3 имеют качественные отличия. Граничное условие модели GM содержит диффузию (существенную в варианте 2), которая оказывает влияние на отражение около угловой точки и дает прогрев газа вдоль оси симметрии (фиг. 10б). Кроме этого, из-за одинаковой ориентации нормали к поверхности на прямолинейном участке тела сильнее проявляются эффекты отражения, соответствующие ядрам (5), (6), что приводит к увеличению температуры газа по нормальному направлению к телу (фиг. 10б, в). В отличие от модели GM ядро рассеяния C–L преобразовывает функцию распределения падающих частиц в функцию распределения, близкую к зеркально отраженной с деформацией и сдвигом, зависящими от значений коэффициентов аккомодации (фиг. 2б, в). В случае варианта 3 полученное течение газа близко, как видно из фиг. 10 в, к течению с зеркальным отражением частиц и физически более реалистично при обтекании тела с гладкой, чистой поверхностью.
При обтекании цилиндра граничные условия GM и C–L дают значительно более близкие решения при Kn ≤ 1. Объясняется это как меньшими значениями средней скорости около поверхности затупленного тела, так и тем, что значительный вклад в решение дает область около точки торможения, где средняя скорость частиц, приходящих на тело, направлена под малым углом к нормали. В этом случае функции распределения отраженных частиц в свободномолекулярном режиме близки к приведенным на фиг. 1а, б. С уменьшением числа Kn (из-за релаксации к равновесию) нормальная компонента средней скорости падающих частиц уменьшается, что приводит к меньшему различию функций распределения отраженных частиц и более близкому решению.
5. ЗАКЛЮЧЕНИЕ
Проведенный сравнительный анализ моделей отражения C–L и GM обнаруживает разную степень отличия решений при обтекании круглого цилиндра и цилиндра, имеющего угловой профиль. Сопоставление решений при обтекании круглого цилиндра с умеренными числами Маха показывает, что граничные условия GM и C–L дают удовлетворительное согласование результатов при Kn ≤ 1.
При обтекании тела с угловым профилем решения с рассмотренными граничными условиями могут иметь качественное отличие как в поведении температуры в поле течения, так и в значениях поверхностных аэродинамических коэффициентов при уменьшении параметра разреженности.
Различное влияние на степень отличия решений при использовании разных моделей отражения оказывают также и значения коэффициентов аккомодации. Так, при полной аккомодации тангенциального импульса (${{\alpha }_{t}} = {{\alpha }_{{GMt}}} = 1$) течения оказываются близкими независимо от геометрии обтекаемого тела. При малых значениях коэффициентов аккомодации обнаруживается сильная чувствительность к геометрии профиля. Этот эффект объясняется наличием дополнительного диффузно-зеркального ядра отражения в модели GM, дающего прогрев газа по нормали к поверхности, что в свою очередь приводит к отличию от почти зеркального отражения, получаемого при использовании модели C–L.
Численные расчеты программным комплексом UFS проводились на вычислительных ресурсах Межведомственного суперкомпьютерного центра РАН.
Список литературы
Wu L., Struchtrup H. Assessment and development of the gas kinetic boundary condition for the Boltzmann equation // J. Fluid Mech. 2017. V. 823. P. 511–537.
Struchtrup H. Maxwell boundary condition and velocity dependent accommodation coefficient // Phys. Fluids. 2013. V. 25. P. 112001.
Cercignani C., Lampis M. Kinetic models for gas-surface interactions // Transport Theory Statist. Phys. 1971. V.1. № 2. P. 101–114.
Yamamoto K., Takeuchi H., Hyakutake T. Scattering properties and scattering kernel based on the molecular dynamics analysis of gas-wall interaction // Phys. Fluids. 2007. V. 19. P. 087102.
Finger G.W., Kapat J.S., Bhattacharya A. Molecular dynamics simulation of adsorbent layer effect on tangential momentum accommodation coefficient // J. Fluids Engng. 2007. V. 129. № 1. P. 31–39.
Ковалев В.Л., Якунчиков А.Н. Коэффициенты аккомодации для молекулярного водорода на поверхности графита // Изв. РАН. Механ. жидкости и газа. 2010. № 6. С. 158–165.
Liang T., Ye W. An efficient DSMC/MD algorithm for accurate modeling of micro gas flows // Commun. Comput. Phys. 2014. V. 15. № 1. P. 246–264.
Brull S., Charrier P., Mieussens L. Gas surface interaction and boundary condition for the Boltzmann equation // Kinet. Relat. Models. 2014. V. 7. №. 2. P. 219–251.
Aoki K., Giovangigli V. Kinetic model of adsorption on crystal surfaces // Physical Review E. 2019. V. 99. P. 052137.
Epstein M. A model of the wall boundary condition in kinetic theory // AIAA Journal. 1967. V. 5. № 10. P. 1797–1800.
Nocilla S. The surface re-emission law in free molecule flow, ed. J.A. Laurmann, Rarefied Gas Dynamics, New York: Academic Press, 1963.
Cercignani C., Theory and application of the Boltzmann equation. Edinburgh and London: Academic Press, 1975.
Lord R.G. Some extensions to the Cercignani–Lampis gas-surface scattering kernel // Phys. Fluids A. 1991. V. 3. P. 706–710.
Bruno D., Cacciatore M., Longo S., Rutigliano M. Gas-surface scattering models for particle fluid dynamics: a comparison between analytical approximate models and molecular dynamics calculations // Chem. Phys. Lett. 2000. V. 320. № 3. P. 245–254.
Ковалев В.Л., Якунчиков А.Н. Анализ моделей рассеяния на основе результатов траекторных расчетов // Изв. РАН. Механ. жидкости и газа. 2012. № 5. С. 80–87.
Dadzie S.K., Meolans J.G. Anisotropic scattering kernel: Generalized and modified Maxwell boundary conditions // J. Math. Phys. 2004. V. 45. № 5. P. 1804–1819.
Padilla J.F., Boyd I.D. Assessment of gas-surface interaction models for computation of rarefied hypersonic flow // J. Thermophys. Heat Transf. 2009. V. 23. P. 96–105.
Zay Yar Myo Myint, Gorelov S.L. Gas-surface interaction effect on aerodynamics of reentry vehicles // International Journal of Educational Research and Information Science. 2018. V. 5. № 1. P. 1–9.
Vargas M., Stefanov S., Valougeorgis D. On the effect of the boundary condition and the collision model on rarefied gas flows // 27th International Symposium on Rarefied Gas Dynamics. 2010 AIP conf. Proc. 2011. V. 1333. P. 354–359.
Sazhin O. Impact of the gas-surface scattering and gas molecule-molecule interaction on the mass flow rate of the rarefied gas through a short channel into a vacuum // J. Vac. Sci. Technol. A Vacuum Surface and Films. 2010. V. 28. № 6. P. 1393–1398.
Sharipov F. Application of the Cercignani–Lampis scattering kernel to calculations of rarefied gas flows. III. Poiseuille flow and thermal creep through a long tube // Eur. J. Mech. B/Fluids. 2003. V. 22. № 2. P. 145–154.
Pantazis S., Varoutis S., Hauer V., Day C., Valougeorgis D. Gas-surface scattering effect on vacuum gas flows through rectangular channels // Vacuum. 2011. V 85. № 12. P. 1161–1164.
Rovenskaya O., Croce G. The effect of boundary conditions for highly rarefied gas flow, Parallel Computational Fluid Dynamics Conference (ParCFD2013), Procedia Engng. 2013. V. 61. P. 284–291.
Коган М.Н. Динамика разреженного газа. М.: Наука, 1967.
Шахов Е.М. Обобщение релаксационного кинетического уравнения Крука // Изв. АН СССР. Механ. жидкости и газа. 1968. № 5. С. 142–145.
Titarev V.A. Application of model kinetic equations to hypersonic rarefied gas flows // Computers & Fluids, Special issue “Nonlinear flow and transport”. 2018. V. 169. P. 62–70.
Титарев В.А., Фролова А.А. Применение модельных кинетических уравнений для расчетов сверх- и гиперзвуковых течений молекулярного газа // Изв. РАН. Механ. жидкости и газа. 2018. № 4. С. 95–112.
To Q.D., Vu V.H., Lauriat G., Léonard C. Boundary conditions for gas flow problem from anisotropic scattering kernels // J. Math. Phys. 2015. V. 56. P. 103101.
Yamamoto K., Takeuchi H., Hyakutake T. Characteristics of reflected gas molecules at a solid surface // Phys. Fluids. 2006. V. 18. P. 046103.
Pham T.T., To Q.D., Lauriat G., Leonard C. Tensorial slip theory for gas flows and comparison with molecular dynamics simulations using an anisotropic gas-wall collision mechanism // Phys. Rev. E. 2013. V. 87. P. 053012.
Kolobov V., Arslanbekov R., Aristov V., Frolova A., Zabelok S. Unified solver for rarefied and continuum flows with adaptive mesh and algorithm refinement // J. Comput. Phys. 2007. V. 223. P. 589–608.
Porodnov B.T., Suetin P.E., Borisov S.F., Akinshin V.D. Experimental investigation of rarefied gas flow in different channels // J. Fluid Mech. 1974. V. 64. № 3. P. 417–437.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики


