Журнал вычислительной математики и математической физики, 2020, T. 60, № 9, стр. 1472-1495
Испытание нового консервативного метода решения задачи Коши для гамильтоновых систем на модельных задачах
П. А. Александров 1, *, Г. Г. Еленин 1, **
1 Московский государственный университет им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
* E-mail: petr_aleksandrov@mail.ru
** E-mail: elenin2@rambler.ru
Поступила в редакцию 17.04.2017
После доработки 19.12.2019
Принята к публикации 09.04.2020
Аннотация
Работа содержит результаты детальных испытаний нового вычислительного метода решения задачи Коши для гамильтоновых систем на двух модельных задачах: об одномерном движении материальной точки в поле кубического потенциала и задаче Кеплера. Исследуются глобальные свойства полученных приближенных решений, такие как симплектичность, обратимость во времени, сохранение полной энергии, а также точность численных решений задачи Кеплера. Указанный вычислительный метод сравнивается с известными трехстадийными симметрично-симплектическими методами Рунге–Кутты, методом дискретного градиента и неявными гнездовыми методами Рунге–Кутты. Библ. 31. Фиг. 9.
1. ВВЕДЕНИЕ
Гамильтоновы системы обыкновенных дифференциальных уравнений широко используются при математическом моделировании явлений молекулярной динамики, небесной механики и астрофизики [1]–[4]. Точные решения задачи Коши для этих уравнений обладают глобальными свойствами: симплектичностью, обратимостью во времени, сохранением фазового объема, а также сохранением полного импульса, полного момента импульса и полной энергии при отсутствии внешних сил [3, с. 98, 143, 184, 227], [4, с. 102, 312], [5]. Только в немногих случаях удается найти аналитическое решение задачи Коши для гамильтоновой системы. Поэтому для решения задачи применяются численные методы. Однако многие широко распространенные численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений дают приближенные решения, не обладающие глобальными свойствами точного решения. К настоящему времени известны численные методы решения задачи Коши для гамильтоновых систем, дающие приближенные решения, обладающие всеми указанными глобальными свойствами, кроме свойства сохранения полной энергии. К таким методам относятся симметрично-симплектические методы Рунге–Кутты [3, с. 191], [4, с. 315], [6]–[8].
Наличие максимального числа указанных выше глобальных свойств у численного решения важно при решении гамильтоновых систем на больших промежутках времени. Поэтому построение таких численных методов решения задачи Коши для гамильтоновых систем, которые дают приближенные решения с максимальным числом глобальных свойств, представляет собой актуальную задачу.
В работах [9]–[12] предложен подход к построению на основе семейств симметрично-симплектических методов Рунге–Кутты консервативных вычислительных методов решения задачи Коши для гамильтоновых систем. В настоящей работе предлагается вычислительный метод на основе двухпараметрического семейства трехстадийных симметрично-симплектических методов Рунге–Кутты, которые имеют по крайней мере четвертый порядок аппроксимации. Проводится апостериорный анализ глобальных свойств приближенных решений модельной задачи об одномерном движении материальной точки в поле кубического потенциала (симплектичности, обратимости во времени и сохранения полной энергии). Также проводится анализ численных решений модельной задачи о плоском движении двух тел единичной массы. Предлагаемый метод сравнивается с указанными трехстадийными симметрично-симплектическими методами Рунге–Кутты, методом дискретного градиента и неявными гнездовыми методами Рунге–Кутты. Показываются преимущества нового метода.
2. ПОСТАНОВКА МОДЕЛЬНЫХ ЗАДАЧ
Задача Коши для автономной гамильтоновой системы, описывающей механическую систему с числом степеней свободы $d$, имеет вид [3, с. 181]–[5]:
Отображение начального состояния в текущее состояние ${{\varphi }_{t}}{\kern 1pt} :\;({{{\mathbf{p}}}_{0}},{{{\mathbf{q}}}_{0}}) \to \left( {{\mathbf{p}}(t),{\mathbf{q}}(t)} \right)$ имеет следующие глобальные свойства.
2. Сохранение фазового объема [3], [4].
3. Обратимость во времени [3, с. 143]:
4. Сохранение полной энергии $H({\mathbf{p}},{\mathbf{q}})$ [3], [5]:
В случае гамильтоновой системы, описывающей движение $N$ попарно взаимодействующих частиц, с гамильтонианом
5. Сохранение полного импульса:
2.1. Модельная задача 1
В качестве первой модельной задачи выбрана задача об одномерном движении материальной точки единичной массы в поле кубического потенциала ${{U}_{C}}(q) = {{q}^{3}}{\text{/}}3 - {{q}^{2}}{\text{/}}2$ [9], [11]–[14]. В данном случае число степеней свободы равно 1, импульс материальной точки $p(t)$ и координата $q(t)$ являются скалярами. Гамильтониан $H(p,q) = {{p}^{2}}{\text{/}}2 + {{U}_{C}}(q)$.
В настоящей работе используются только периодические решения модельной задачи 1, которые существуют при $0 < {{q}_{0}} < 1.5$, ${\text{|}}{{p}_{0}}{\text{|}} < {{q}_{0}}{{(1 - 2{{q}_{0}}{\text{/}}3)}^{{0.5}}}$. Период решения зависит от начального значения гамильтониана ${{H}_{0}}$ и вычисляется по формуле
У периодического решения задачи для каждого $q \in [{{q}_{{{\text{min}}}}},{{q}_{{{\text{max}}}}}]$ значение импульса вычисляется по формуле $p = \pm {{\left( {2{{H}_{0}} - 2{{q}^{3}}{\text{/}}3 + {{q}^{2}}} \right)}^{{0.5}}}$.
2.2. Модельная задача 2
В качестве второй модельной задачи выбрана задача о плоском движении двух тел единичной массы (задача Кеплера) с гамильтонианом [3, с. 9]
Для рассматриваемой задачи известно аналитическое решение [15, с. 56], [3], [5, с. 49]. Возможны три случая: эллиптическая, параболическая и гиперболическая орбиты. Для эллиптической орбиты формулы аналитического решения имеют следующий вид:
где $a$ – большая полуось орбиты, $e \in [0,1)$ – эксцентриситет орбиты, $E$ – эксцентрическая аномалия. $E$ находится как решение уравнения Кеплера где ${{t}_{{\text{П}}}}$ – момент времени, в который второе тело проходит через перицентр.3. ПОСТРОЕНИЕ ВЫЧИСЛИТЕЛЬНОГО МЕТОДА
3.1. Двухпараметрическое семейство трехстадийных симметрично-симплектических методов Рунге–Кутты
Рассмотрим двухпараметрическое семейство трехстадийных симметрично-симплектических методов Рунге–Кутты с таблицей Бутчера следующего вида [11], [16], [17]:
| $0.5 + {{\tilde {c}}_{1}}({{b}_{1}})$ | $0.5{{b}_{1}}$ | $(1 - 2{{b}_{1}})(0.5 + {{s}_{{12}}})$ | $0.5{{b}_{1}} + {{\tilde {c}}_{1}}({{b}_{1}}) - (1 - 2{{b}_{1}}){{s}_{{12}}}$ |
| $0.5$ | ${{b}_{1}}(0.5 - {{s}_{{12}}})$ | $0.5 - {{b}_{1}}$ | ${{b}_{1}}(0.5 + {{s}_{{12}}})$ |
| $0.5 - {{\tilde {c}}_{1}}({{b}_{1}})$ | $0.5{{b}_{1}} - {{\tilde {c}}_{1}}({{b}_{1}}) + (1 - 2{{b}_{1}}){{s}_{{12}}}$ | $(1 - 2{{b}_{1}})(0.5 - {{s}_{{12}}})$ | $0.5{{b}_{1}}$ |
| ${{b}_{1}}$ | $1 - 2{{b}_{1}}$ | ${{b}_{1}}$ |
Здесь ${{b}_{1}}$ и ${{s}_{{12}}}$ – свободные параметры семейства, ${{b}_{1}} > 1{\text{/}}6$, ${{\tilde {c}}_{1}}({{b}_{1}}) = 0.5{{(6{{b}_{1}})}^{{ - 0.5}}}$. Методы являются неявными. Значениям ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = s_{{12}}^{*} = 0.75 \times {{0.6}^{{0.5}}} \approx 0.580948$ соответствует единственный метод шестого порядка аппроксимации – метод Кунцмана–Бутчера [4, с. 209]. Остальным значениям параметров соответствуют методы четвертого порядка. При ${{b}_{1}} = 0.5$ независимо от значения ${{s}_{{12}}}$ методы вырождаются в двухстадийный симметрично-симплектический метод Рунге–Кутты – метод Хаммера–Холлингсуорта четвертого порядка [4, с. 207], [17].
Применительно к модельным задачам формулы методов имеют вид
(3.1)
${{{\mathbf{p}}}_{{n + 1}}} = {{{\mathbf{p}}}_{n}} - \tau \left( {{{b}_{1}}\nabla U({{{\mathbf{q}}}_{n}} + {{{\mathbf{Z}}}_{{1n}}}) + (1 - 2{{b}_{1}})\nabla U({{{\mathbf{q}}}_{n}} + {{{\mathbf{Z}}}_{{2n}}}) + {{b}_{1}}\nabla U({{{\mathbf{q}}}_{n}} + {{{\mathbf{Z}}}_{{3n}}})} \right),$(3.2)
${{{\mathbf{q}}}_{{n + 1}}} = {{{\mathbf{q}}}_{n}} + \tau {{{\mathbf{p}}}_{n}} - {{\tau }^{2}}\sum\limits_{i = 1}^3 \,{{\overline b }_{i}}\nabla U({{{\mathbf{q}}}_{n}} + {{{\mathbf{Z}}}_{{in}}}),$(3.3)
${{{\mathbf{Z}}}_{{in}}} = \tau {{c}_{i}}{{{\mathbf{p}}}_{n}} - {{\tau }^{2}}\sum\limits_{j = 1}^3 \,{{\bar {a}}_{{ij}}}\nabla U({{{\mathbf{q}}}_{n}} + {{{\mathbf{Z}}}_{{jn}}}),\quad i = 1,2,3.$Для решения (3.3) далее в работе использована модификация метода простой итерации [18, с. 191], [19, с. 381] – метод покоординатных итераций [20, с. 321], [21, с. 285]. На $(k + 1)$-й итерации приближение ${\mathbf{Z}}_{{in}}^{{(k + 1)}}$ решения системы (3.3) вычисляется по следующим формулам:
Решение существует и единственно в некоторой окрестности $Q$ точки ${{{\mathbf{q}}}_{n}}$ при выполнении следующего условия [4, с. 206]:
(3.4)
$\tau < \mathop {\left( {\mathop {max}\limits_i \sum\limits_{k = 1}^3 \,\left| {{{{\bar {a}}}_{{ik}}}} \right| \cdot \mathop {sup}\limits_{{\mathbf{q}} \in Q} \mathop {max}\limits_i \sum\limits_j \left| {\frac{{{{\partial }^{2}}U}}{{\partial {{q}_{i}}\partial {{q}_{j}}}}({\mathbf{q}})} \right|} \right)}\nolimits^{ - 0.5} .$В качестве начальных приближений при расчетах, описанных далее в настоящей работе, использованы ${\mathbf{Z}}_{{in}}^{{(0)}} = \tau {{c}_{i}}{{{\mathbf{p}}}_{n}}$ [3]. Как показали исследования для модельной задачи 1, в подавляющем большинстве случаев эти начальные приближения обеспечили меньшее число итераций, чем приближения ${\mathbf{Z}}_{{in}}^{{(0)}} = 0$. Итерационный процесс останавливался [22], если
Кубический потенциал является простейшим потенциалом, при котором любой метод рассматриваемого семейства не сохраняет полную энергию при фиксированных значениях свободных параметров ${{b}_{1}}$ и ${{s}_{{12}}}$. В случаях линейного и квадратичного потенциалов методы рассматриваемого семейства сохраняют полную энергию, как и все симплектические методы Рунге–Кутты [3, с. 101]. Далее будем искать связь между этими параметрами, при которой полная энергия сохраняется.
3.2. Метод нулевого дисбаланса полной энергии
В работе [11] предложено семейство консервативных вычислительных методов решения задачи Коши для гамильтоновых систем. Методы основаны на двухпараметрическом семействе методов Рунге–Кутты (3.1)–(3.3). Система разрешающих уравнений (3.3) методов Рунге–Кутты дополняется уравнением нулевого дисбаланса полной энергии
гдеРасширенная система разрешающих уравнений (3.3), (3.5) в описанных ниже расчетах решалась с помощью двух вложенных друг в друга итерационных процессов. На внешних итерациях решалось уравнение (3.5), т.е. для фиксированного допустимого значения ${{b}_{1}} = 5{\text{/}}18$ находилось значение ${{s}_{{12}}}$, обеспечивающее сохранение полной энергии. Для определения ${{{\mathbf{Z}}}_{{in}}}$ и, следовательно, ${{{\mathbf{p}}}_{{n + 1}}}$ и ${{{\mathbf{q}}}_{{n + 1}}}$ по известным ${{b}_{1}}$ и ${{s}_{{12}}}$ использован внутренний итерационный процесс, описанный в предыдущем подразделе 3.1. Таким образом, на каждом временном шаге система (3.3) при фиксированных ${{b}_{1}}$, ${{s}_{{12}}}$ могла решаться несколько раз, каждый раз – для другого ${{s}_{{12}}}$. При втором и следующих на текущем временном шаге решениях (3.3) в качестве начальных приближений использовались решения (3.3), полученные при предыдущем решении этой системы (т.е. для другого значения ${{s}_{{12}}}$).
Для решения уравнения (3.5) могут быть использованы метод секущих или метод Мюллера [23]. Метод Мюллера аналогичен методу секущих, но использует приближение квадратичной функцией. В качестве следующего приближения решения уравнения выбирается нуль квадратичной функции, ближайший к текущему приближению. В настоящей работе в тех случаях, когда квадратичная функция не имеет нулей, в качестве следующего приближения выбирался минимум модуля этой функции. В настоящей работе итерационный процесс останавливался при выполнении условия
(3.6)
$\left| {\Delta H\left( {s_{{12}}^{{(j)}}} \right)} \right| \leqslant {{\varepsilon }_{{\Delta H}}}$3.3. Исследование эффективности методов решения уравнения нулевого дисбаланса полной энергии
Для ответа на вопрос, какой вычислительный метод решения уравнения (3.5) эффективнее (метод секущих или метод Мюллера), проведены две серии вычислительных экспериментов с модельной задачей 1. В первой серии использовались числа с плавающей запятой двойной точности (длина мантиссы 53 бит), во второй серии – числа с плавающей запятой повышенной точности (длина мантиссы 448 бита). Для работы с числами повышенной точности применялась программная библиотека GNU MPFR [25]. Расчеты проводились для множества начальных значений ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$, величин шага $\tau \in \Theta $ и отрезков интегрирования длиной $10T$. Период точного решения $T$ разный для разных начальных значений гамильтониана ${{H}_{0}}$. Здесь и далее
Найдены $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},\tau \in \Theta }}}{{N}_{{{\text{внешн}},{\text{ср}}}}}$ и $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},\tau \in \Theta }}}{{N}_{{{\text{внутр}},{\text{ср}}}}}$. Здесь ${{N}_{{{\text{внешн}},{\text{ср}}}}}$ – среднее на один временной шаг число внешних итераций, ${{N}_{{{\text{внутр}},{\text{ср}}}}} = \sum\nolimits_{n = 1}^N \,{{N}_{{{\text{внутр}},n}}}{\text{/}}(N)$ – среднее на один временной шаг число внутренних итераций, ${{N}_{{{\text{внутр}},n}}}$ – суммарное число внутренних итераций на $n$-м шаге по времени (учитывались все внешние итерации), N – число шагов по времени. Результаты расчетов представлены в табл. 1. Равенство нулю ${{\varepsilon }_{{\Delta H}}}$ означает, что условие остановки внешних итераций (3.6) не использовалось (за исключением случаев точного равенства $\Delta H\left( {s_{{12}}^{{(j)}}} \right) = 0$).
Таблица 1.
Число итераций различных методов решения уравнения (3.5)
| Метод | Точность | ${{\varepsilon }_{{{\text{abs}}}}}$ | ${{\varepsilon }_{{{\text{rel}}}}}$ | ${{\varepsilon }_{{\Delta H}}}$ | ${{\varepsilon }_{s}}$ | $\mathop {max}\limits_{{{p}_{0}} = 0,\,{{q}_{0}} \in {{Q}_{0}},\,\tau \in \Theta } $ | |
|---|---|---|---|---|---|---|---|
| ${{N}_{{{\text{внешн}},{\text{ср}}}}}$ | ${{N}_{{{\text{внутр}},{\text{ср}}}}}$ | ||||||
| Метод секущих | Двойная | $5 \times {{10}^{{ - 32}}}$ | $8 \times {{10}^{{ - 13}}}$ | $3 \times {{10}^{{ - 16}}}$ | $3 \times {{10}^{{ - 16}}}$ | 2.4 | 19.4 |
| Повышенная | ${{10}^{{ - 300}}}$ | ${{10}^{{ - 70}}}$ | 0 | ${{10}^{{ - 65}}}$ | 7.2 | 188.9 | |
| Метод Мюллера | Двойная | $5 \times {{10}^{{ - 32}}}$ | $8 \times {{10}^{{ - 13}}}$ | $3 \times {{10}^{{ - 16}}}$ | $3 \times {{10}^{{ - 16}}}$ | 1.1 | 21.2 |
| Повышенная | ${{10}^{{ - 300}}}$ | ${{10}^{{ - 70}}}$ | 0 | ${{10}^{{ - 65}}}$ | 5.4 | 174.4 | |
Согласно представленным результатам, величина $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},\tau \in \Theta }}}{{N}_{{{\text{внутр}},{\text{ср}}}}}$ немного меньше для метода секущих в случае двойной точности и меньше для метода Мюллера в случае повышенной точности. Поэтому для решения уравнения (3.5) при вычислениях, рассматриваемых в разд. 6, 7, применялся метод Мюллера с указанными выше начальными приближениями.
4. МЕТОД ДИСКРЕТНОГО ГРАДИЕНТА
К вычислительным методам решения задачи Коши для гамильтоновых систем, дающим приближенные решения, обладающие свойствами обратимости и сохранения полной энергии, относятся методы дискретного градиента [3, с. 171]. В настоящей работе проводится сравнение предлагаемого вычислительного метода нулевого дисбаланса полной энергии с одним из методов дискретного градиента, формулы которого для модельной задачи 1 имеют вид
Этот метод является неявным. Приведем систему (4.1), (4.2) к одному уравнению, для чего подставим в (4.1) вместо ${{p}_{{n + 1}}}$ правую часть (4.2). Для решения полученного уравнения в настоящей работе применен метод простой итерации с начальным приближением $q_{{n + 1}}^{{(0)}} = {{q}_{n}} + \tau {{p}_{n}}$. Если приближение решения на $j$-м шаге метода простой итерации $q_{{n + 1}}^{{(j)}} = {{q}_{n}}$, то выражение $\left( {{{U}_{C}}({{q}_{{n + 1}}}) - {{U}_{C}}({{q}_{n}})} \right){\text{/}}({{q}_{{n + 1}}} - {{q}_{n}})$ заменялось на $U_{C}^{'}({{q}_{n}})$. Итерации прекращались, если $\left| {q_{{n + 1}}^{{(j + 1)}} - q_{{n + 1}}^{{(j)}}} \right| \leqslant {{\varepsilon }_{{{\text{abs}}}}} + {{\varepsilon }_{{{\text{rel}}}}}\left| {q_{{n + 1}}^{{(j + 1)}}} \right|$, где ${{\varepsilon }_{{{\text{abs}}}}} \geqslant 0$, ${{\varepsilon }_{{{\text{rel}}}}} \geqslant 0$ – заданные параметры, определяющие точность нахождения ${{q}_{{n + 1}}}$.Для исследования трудоемкости вычислений методом дискретного градиента проведены вычислительные эксперименты для различных значений ${{\varepsilon }_{{abs}}}$, ${{\varepsilon }_{{rel}}}$ и длины мантиссы. Подсчитано среднее на один временной шаг число итераций ${{N}_{{{\text{итер}},{\text{ср}}}}} = \sum\nolimits_{n = 1}^N \,{{N}_{{{\text{итер}},n}}}{\text{/}}N$, где ${{N}_{{{\text{итер}},n}}}$ – число итераций на $n$-м шаге по времени, $N$ – число шагов по времени. Использовались отрезки интегрирования длиной $10T$. Полученные значения $ma{{x}_{{{{p}_{0}} = 0,\,{{q}_{0}} \in {{Q}_{0}},\,\tau \in \{ 0.0002{{T}_{{\text{Г}}}}\} \, \cup \,\Theta }}}{{N}_{{{\text{итер}},{\text{ср}}}}}$ представлены в табл. 2.
Таблица 2.
Среднее число итераций на один шаг метода дискретного градиента
| Длина мантиссы | ${{\varepsilon }_{{{\text{abs}}}}}$ | ${{\varepsilon }_{{{\text{rel}}}}}$ | $\mathop {max}\limits_{{{p}_{0}} = 0,\,{{q}_{0}} \in {{Q}_{0}},\,\tau \in \{ 0.0002{{T}_{{\text{Г}}}}\} \cup \Theta } {{N}_{{{\text{итер}},{\text{ср}}}}}$ |
|---|---|---|---|
| 53 бита | $5 \times {{10}^{{ - 32}}}$ | $4 \times {{10}^{{ - 11}}}$ | 6.6 |
| 448 бита | ${{10}^{{ - 300}}}$ | ${{10}^{{ - 70}}}$ | 43.3 |
5. НЕЯВНЫЕ ГНЕЗДОВЫЕ МЕТОДЫ РУНГЕ–КУТТЫ
Для решения задачи Коши для гамильтоновых систем ранее были предложены неявные гнездовые методы Рунге–Кутты (НГРК-методы): двухуровневый и трехуровневый типа Гаусса и двухуровневый типа Лобатто [26]–[28]. Двухуровневый метод типа Гаусса имеет четвертый порядок аппроксимации. Таблица Бутчера этого метода представлена ниже:
| $0$ | $0$ | $0$ | $0$ | $0$ |
| ${{c}_{2}}$ | $\left( {6({{c}_{2}} + \theta ) - 5} \right){\text{/}}12$ | $0.5(1 - \theta )$ | $0.5(1 - \theta )$ | $\left( {6({{c}_{2}} + \theta ) - 7} \right){\text{/}}12$ |
| ${{c}_{3}}$ | $\left( {7 - 6({{c}_{2}} + \theta )} \right){\text{/}}12$ | $0.5\theta $ | $0.5\theta $ | $\left( {5 - 6({{c}_{2}} + \theta )} \right){\text{/}}12$ |
| $0$ | $0$ | $0.5$ | $0.5$ | $0$ |
| $0$ | $0.5$ | $0.5$ | $0$ |
Здесь ${{c}_{2}} = \left( {3 - {{3}^{{0.5}}}} \right){\text{/}}6$, ${{c}_{3}} = \left( {3 + {{3}^{{0.5}}}} \right){\text{/}}6$ и $\theta = 0.5 + 2 \times {{3}^{{0.5}}}{\text{/}}9$.
Трехуровневый метод типа Гаусса шестого порядка аппроксимации имеет следующую таблицу Бутчера:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ${{c}_{2}}$ | $\tfrac{{{{c}_{3}}}}{6}$ | 0 | 0 | $\tfrac{{35 - 40{{c}_{3}}}}{{108}}$ | $\tfrac{{56 - 64{{c}_{3}}}}{{108}}$ | $\tfrac{{35 - 40{{c}_{3}}}}{{108}}$ | $\tfrac{{{{c}_{3}} - 1}}{6}$ |
| ${{c}_{3}}$ | $\tfrac{{{{c}_{2}}}}{6}$ | 0 | 0 | $\tfrac{{35 - 40{{c}_{2}}}}{{108}}$ | $\tfrac{{56 - 64{{c}_{2}}}}{{108}}$ | $\tfrac{{35 - 40{{c}_{2}}}}{{108}}$ | $\tfrac{{{{c}_{2}} - 1}}{6}$ |
| ${{c}_{4}}$ | $\tfrac{{20{{c}_{6}} - 3}}{{200}}$ | $\tfrac{{36{{c}_{6}} + 18{{c}_{3}} - 27}}{{200}}$ | $\tfrac{{36{{c}_{6}} - 18{{c}_{3}} - 9}}{{200}}$ | $\tfrac{{39{{c}_{4}} - 7}}{{90}}$ | $\tfrac{{780{{c}_{4}} - 140}}{{1125}}$ | $\tfrac{{39{{c}_{4}} - 7}}{{90}}$ | $\tfrac{{3 - 20{{c}_{4}}}}{{200}}$ |
| ${{c}_{5}}$ | $\tfrac{1}{{32}}$ | $\tfrac{{{{{27}}^{{0.5}}}}}{{32}}$ | $ - \tfrac{{{{{27}}^{{0.5}}}}}{{32}}$ | $\tfrac{5}{{36}}$ | $\tfrac{2}{9}$ | $\tfrac{5}{{36}}$ | $ - \tfrac{1}{{32}}$ |
| ${{c}_{6}}$ | $\tfrac{{20{{c}_{4}} - 3}}{{200}}$ | $\tfrac{{36{{c}_{4}} + 18{{c}_{3}} - 27}}{{200}}$ | $\tfrac{{36{{c}_{4}} - 18{{c}_{3}} - 9}}{{200}}$ | $\tfrac{{39{{c}_{6}} - 7}}{{90}}$ | $\tfrac{{780{{c}_{6}} - 140}}{{1125}}$ | $\tfrac{{39{{c}_{6}} - 7}}{{90}}$ | $\tfrac{{3 - 20{{c}_{6}}}}{{200}}$ |
| 1 | 0 | 0 | 0 | $\tfrac{5}{{18}}$ | $\tfrac{4}{9}$ | $\tfrac{5}{{18}}$ | 0 |
| 0 | 0 | 0 | $\tfrac{5}{{18}}$ | $\tfrac{4}{9}$ | $\tfrac{5}{{18}}$ | 0 |
Здесь ${{c}_{2}} = 0.5 - {{3}^{{0.5}}}{\text{/}}6$, ${{c}_{3}} = 0.5 + {{3}^{{0.5}}}{\text{/}}6$, ${{c}_{4}} = 0.5 - 0.1 \times {{15}^{{0.5}}}$, ${{c}_{5}} = 0.5$ и ${{c}_{6}} = 0.5 + 0.1 \times {{15}^{{0.5}}}$.
Таблица Бутчера двухуровневого метода типа Лобатто четвертого порядка аппроксимации имеет следующий вид:
Этот метод совпадает с методом Лобатто IIIA четвертого порядка. Далее в работе не будет делаться различий между двухуровневым НГРК-методом типа Лобатто и методом Лобатто IIIA четвертого порядка.
В описанных ниже расчетах использовалась редуцированная система разрешающих уравнений НГРК-методов, аналогичная (3.3). Для решения этой системы применялся метод покоординатных итераций с теми же начальными приближениями, что и в случае трехстадийных симметрично-симплектических методов Рунге–Кутты.
Указанные методы являются сопряженными с симплектическим методом, по меньшей мере до шестого порядка включительно [26]–[28], и симметричными.
Определение 1. Пусть ${{\Phi }_{\tau }}:({{{\mathbf{p}}}_{0}},{{{\mathbf{q}}}_{0}}) \to ({{{\mathbf{p}}}_{1}},{{{\mathbf{q}}}_{1}})$ – отображение, осуществляемое на одном шаге вычислительным методом решения задачи Коши для гамильтоновой системы, имеющим порядок $m$. Этот метод называется сопряженным с симплектическим методом до порядка $m + r$ включительно (где $r \geqslant 0$) [29], если существует замена координат $(\underline {\mathbf{p}} ,\underline {\mathbf{q}} ) = \chi ({\mathbf{p}},{\mathbf{q}})$, которая $O({{\tau }^{m}})$-близка к единичному преобразованию, такая, что ${{\Psi }_{\tau }} = \chi \circ {{\Phi }_{\tau }} \circ {{\chi }^{{ - 1}}}$ удовлетворяет
6. СРАВНЕНИЕ ВЫЧИСЛИТЕЛЬНЫХ МЕТОДОВ НА МОДЕЛЬНОЙ ЗАДАЧЕ 1
Представим результаты исследований симплектичности, обратимости и консервативности предлагаемого вычислительного метода нулевого дисбаланса полной энергии на модельной задаче 1. Сравним свойства этого метода со свойствами трехстадийных симметрично-симплектических методов Рунге–Кутты при ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = s_{{12}}^{*}$; ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = 0$; ${{b}_{1}} = 0.5$, ${{s}_{{12}}} = 0$; со свойствами метода дискретного градиента и неявных гнездовых методов Рунге–Кутты. Несмотря на то что при ${{b}_{1}} = 0.5$ трехстадийный симметрично-симплектический метод Рунге–Кутты вырождается в двухстадийный, далее в работе он рассматривается как трехстадийный. Вычисления для ${{b}_{1}} = 0.5$ проводились по тем же формулам, что и для ${{b}_{1}} = 5{\text{/}}18$.
При исследованиях использованы начальные значения ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ и величины шага $\tau \in \Theta $. Для метода дискретного градиента также использована величина шага $\tau = 0.0002{{T}_{{\text{Г}}}}$. Расчеты проводились с применением чисел с плавающей запятой двойной и повышенной точности. В случае чисел двойной точности использовались значения параметров ${{\varepsilon }_{{{\text{abs}}}}} = 5 \times {{10}^{{ - 32}}}$, ${{\varepsilon }_{{{\text{rel}}}}} = 8 \times {{10}^{{ - 13}}}$ для метода нулевого дисбаланса полной энергии (со значениями ${{\varepsilon }_{{\Delta H}}} = {{\varepsilon }_{s}} = 3 \times {{10}^{{ - 16}}}$) и методов Рунге–Кутты. Для метода дискретного градиента ${{\varepsilon }_{{{\text{abs}}}}} = 5 \times {{10}^{{ - 32}}}$, ${{\varepsilon }_{{{\text{rel}}}}} = 4 \times {{10}^{{ - 11}}}$. В случае чисел повышенной точности для всех методов применялись значения параметров ${{\varepsilon }_{{{\text{abs}}}}} = {{10}^{{ - 300}}}$, ${{\varepsilon }_{{{\text{rel}}}}} = {{10}^{{ - 70}}}$, также для метода нулевого дисбаланса: ${{\varepsilon }_{{\Delta H}}} = 0$, ${{\varepsilon }_{s}} = {{10}^{{ - 65}}}$.
Для модельной задачи 1 имеет место неравенство $\mathop {sup}\limits_{q \in ( - 0.5,2)} {\text{|}}U_{C}^{{''}}(q){\text{|}} < 3$. Поэтому для трехстадийных симметрично-симплектических методов Рунге–Кутты, соответствующих значениям параметров ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} \in [ - 0.5,1.5]$ и ${{b}_{1}} = 0.5$, ${{s}_{{12}}} = 0$, при $\tau \leqslant 0.05{{T}_{{{\text{Г}}\;}}}$ в случае решения задачи Коши с начальными значениями ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ условие (3.4) выполнено. Для всех трех НГРК-методов аналогичные условия в этом случае при $\tau \leqslant 0.05{{T}_{{{\text{Г}}\;}}}$ также выполнены.
6.1. Симплектичность
Для исследования симплектичности рассматриваемых методов введем матрицы глобального дефекта симплектичности
Для вычисления частных производных использовались правые разностные производные [18, с. 34].
Приведем результаты расчетов повышенной точности. Приращение аргумента в формуле правой разностной производной в этом случае равно ${{10}^{{ - 30}}}$. Исследования проводились на малых промежутках времени, сравнимых с периодом, и на больших промежутках времени длиной $1000T$.
Метод нулевого дисбаланса полной энергии. Рассмотрим сначала $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ для этого метода на малых промежутках времени. На фиг. 1 изображены графики зависимостей $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ от времени при различных $({{p}_{0}},{{q}_{0}})$ и $\tau = 0.05{{T}_{{\text{Г}}}}$. Согласно графикам, эти зависимости $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ являются почти периодическими.
Фиг. 1.
Зависимости компонент глобального (а) и локального (б) дефектов симплектичности от времени для метода нулевого дисбаланса полной энергии при $\tau = 0.05{{T}_{{\text{Г}}}}$. Сплошной линии соответствуют ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$ и $T \approx 6.30799$; штриховой – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.5$ и $T \approx 6.90164$; штрихпунктирной – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.05$ и $T \approx 11.00104$.

Теперь рассмотрим $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ на больших отрезках времени. В табл. 3 представлены максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ на отрезках $t \in [0,1000T]$ для разных начальных значений $({{p}_{0}},{{q}_{0}})$ и величин шага $\tau $. Согласно полученным результатам для ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ и $\tau \in \Theta $, максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ убывают при уменьшении $\tau $.
Таблица 3.
Максимальные абсолютные значения компонент глобального и локального дефектов симплектичности ($\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ и $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$)
| $({{p}_{0}},{{q}_{0}})$ | $\tau $ | Метод нулевого дисбаланса | Метод дискретного градиента | ||
|---|---|---|---|---|---|
| $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$ | ||
| $(0,0.99)$ | $0.0002{{T}_{{\text{Г}}}}$ | $5.24636 \times {{10}^{{ - 9}}}$ | $3.29629 \times {{10}^{{ - 12}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | $6.24839 \times {{10}^{{ - 12}}}$ | $5.19698 \times {{10}^{{ - 13}}}$ | $1.31029 \times {{10}^{{ - 5}}}$ | $4.11427 \times {{10}^{{ - 7}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $4.01255 \times {{10}^{{ - 10}}}$ | $6.65512 \times {{10}^{{ - 11}}}$ | $5.22559 \times {{10}^{{ - 5}}}$ | $3.27687 \times {{10}^{{ - 6}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $4.59704 \times {{10}^{{ - 9}}}$ | $1.13794 \times {{10}^{{ - 9}}}$ | $1.16997 \times {{10}^{{ - 4}}}$ | $1.09785 \times {{10}^{{ - 5}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $2.60650 \times {{10}^{{ - 8}}}$ | $8.53399 \times {{10}^{{ - 9}}}$ | $2.06571 \times {{10}^{{ - 4}}}$ | $2.57582 \times {{10}^{{ - 5}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $1.00494 \times {{10}^{{ - 7}}}$ | $4.07494 \times {{10}^{{ - 8}}}$ | $3.19951 \times {{10}^{{ - 4}}}$ | $4.96567 \times {{10}^{{ - 5}}}$ | |
| $(0,0.9)$ | $0.0002{{T}_{{\text{Г}}}}$ | $5.09865 \times {{10}^{{ - 8}}}$ | $3.19519 \times {{10}^{{ - 11}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | $4.99523 \times {{10}^{{ - 12}}}$ | $6.07080 \times {{10}^{{ - 13}}}$ | $1.27333 \times {{10}^{{ - 4}}}$ | $3.98809 \times {{10}^{{ - 6}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $3.21077 \times {{10}^{{ - 10}}}$ | $7.77102 \times {{10}^{{ - 11}}}$ | $5.07744 \times {{10}^{{ - 4}}}$ | $3.17641 \times {{10}^{{ - 5}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $3.68426 \times {{10}^{{ - 9}}}$ | $1.32787 \times {{10}^{{ - 9}}}$ | $1.13651 \times {{10}^{{ - 3}}}$ | $1.06423 \times {{10}^{{ - 4}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $2.09243 \times {{10}^{{ - 8}}}$ | $9.94924 \times {{10}^{{ - 9}}}$ | $2.00594 \times {{10}^{{ - 3}}}$ | $2.49711 \times {{10}^{{ - 4}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $8.09706 \times {{10}^{{ - 8}}}$ | $4.74513 \times {{10}^{{ - 8}}}$ | $3.10558 \times {{10}^{{ - 3}}}$ | $4.81452 \times {{10}^{{ - 4}}}$ | |
| $(0,0.5)$ | $0.0002{{T}_{{\text{Г}}}}$ | $2.27929 \times {{10}^{{ - 7}}}$ | $1.35021 \times {{10}^{{ - 10}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | $1.47980 \times {{10}^{{ - 11}}}$ | $1.36265 \times {{10}^{{ - 12}}}$ | $5.69173 \times {{10}^{{ - 4}}}$ | $1.68529 \times {{10}^{{ - 5}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $9.46381 \times {{10}^{{ - 10}}}$ | $1.74035 \times {{10}^{{ - 10}}}$ | $2.26895 \times {{10}^{{ - 3}}}$ | $1.34236 \times {{10}^{{ - 4}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.07668 \times {{10}^{{ - 8}}}$ | $2.96266 \times {{10}^{{ - 9}}}$ | $5.07642 \times {{10}^{{ - 3}}}$ | $4.49820 \times {{10}^{{ - 4}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $6.03912 \times {{10}^{{ - 8}}}$ | $2.20815 \times {{10}^{{ - 8}}}$ | $8.95436 \times {{10}^{{ - 3}}}$ | $1.05583 \times {{10}^{{ - 3}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $2.29850 \times {{10}^{{ - 7}}}$ | $1.04605 \times {{10}^{{ - 7}}}$ | $1.38527 \times {{10}^{{ - 2}}}$ | $2.03692 \times {{10}^{{ - 3}}}$ | |
| $(0,0.05)$ | $0.0002{{T}_{{\text{Г}}}}$ | $3.81200 \times {{10}^{{ - 7}}}$ | $1.90256 \times {{10}^{{ - 10}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | $2.47473 \times {{10}^{{ - 11}}}$ | $2.08687 \times {{10}^{{ - 12}}}$ | $9.52031 \times {{10}^{{ - 4}}}$ | $2.37471 \times {{10}^{{ - 5}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $1.58237 \times {{10}^{{ - 9}}}$ | $2.66286 \times {{10}^{{ - 10}}}$ | $3.79658 \times {{10}^{{ - 3}}}$ | $1.89157 \times {{10}^{{ - 4}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.79965 \times {{10}^{{ - 8}}}$ | $4.52615 \times {{10}^{{ - 9}}}$ | $8.49956 \times {{10}^{{ - 3}}}$ | $6.33925 \times {{10}^{{ - 4}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.00898 \times {{10}^{{ - 7}}}$ | $3.36624 \times {{10}^{{ - 8}}}$ | $1.50059 \times {{10}^{{ - 2}}}$ | $1.48833 \times {{10}^{{ - 3}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $3.83471 \times {{10}^{{ - 7}}}$ | $1.59026 \times {{10}^{{ - 7}}}$ | $2.32422 \times {{10}^{{ - 2}}}$ | $2.87261 \times {{10}^{{ - 3}}}$ | |
Трехстадийные симметрично-симплектические методы Рунге–Кутты. Для этих методов Рунге–Кутты (постоянные ${{b}_{1}}$, ${{s}_{{12}}}$) $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ в случае точного решения системы разрешающих уравнений (3.3), точного вычисления производных и точной арифметики равны нулю. Однако значения этих величин, вычисленные с помощью правых разностей, в общем случае не равны нулю из-за погрешности машинной арифметики и погрешностей решения системы разрешающих уравнений и вычисления производных. Расчеты показывают, что значения дефектов симплектичности удовлетворяют неравенствам ${\text{|}}\Delta {{S}_{{n,12}}}{\text{|}} < {{10}^{{ - 20}}}$, ${\text{|}}\delta {{S}_{{n,12}}}{\text{|}} < {{10}^{{ - 31}}}$ на промежутках времени $t \in [0,1000T].$
Метод дискретного градиента. На фиг. 2 показаны графики зависимостей $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ от времени на малом промежутке времени. В табл. 3 представлены максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ на отрезках $t \in [0,1000T]$ для разных начальных значений $({{p}_{0}},{{q}_{0}})$ и величин шага $\tau $. Как показали исследования для ${{p}_{0}} = 0$ и ${{q}_{0}} \in {{Q}_{0}}$, максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ убывают при уменьшении ${{H}_{0}}$ и $\tau $.
Фиг. 2.
Зависимости компонент глобального (а) и локального (б) дефектов симплектичности от времени для метода дискретного градиента при $\tau = 0.05{{T}_{{\text{Г}}}}$. Сплошной линии соответствуют ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$ и $T \approx 6.30799$; штриховой – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.5$ и $T \approx 6.90164$; штрихпунктирной – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.05$ и $T \approx 11.00104$.

Неявные гнездовые методы Рунге–Кутты. На фиг. 3–5 изображены графики зависимостей $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ от времени на малом промежутке времени для НГРК-методов. Согласно проведенным исследованиям для ${{p}_{0}} = 0$ и ${{q}_{0}} \in {{Q}_{0}}$, эти зависимости для всех трех рассматриваемых НГРК-методов являются почти периодическими. Форма графиков, соответствующих одинаковым ${{q}_{0}}$, на фиг. 3 и 5 совпадает. В табл. 4 представлены максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ на отрезках $t \in [0,1000T]$ для НРГК-методов типа Гаусса при разных начальных значениях $({{p}_{0}},{{q}_{0}})$ и величинах шага $\tau $. Максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ для метода Лобатто IIIA примерно в 1.7 раза меньше соответствующих значений для двухуровневого НГРК-метода типа Гаусса. При ${{p}_{0}} = 0$ и ${{q}_{0}} \in {{Q}_{0}}$ максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ для всех рассматриваемых НГРК-методов убывают при уменьшении $\tau $.
Фиг. 3.
Зависимости компонент глобального (а) и локального (б) дефектов симплектичности от времени для двухуровневого НГРК-метода типа Гаусса при $\tau = 0.05{{T}_{{\text{Г}}}}$. Сплошной линии соответствуют ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$ и $T \approx 6.30799$; штриховой – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.5$ и $T \approx 6.90164$; штрихпунктирной – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.05$ и $T \approx 11.00104$.

Фиг. 4.
Зависимости компонент глобального (а) и локального (б) дефектов симплектичности от времени для трехуровневого НГРК-метода типа Гаусса при $\tau = 0.05{{T}_{{\text{Г}}}}$. Сплошной линии соответствуют ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$ и $T \approx 6.30799$; штриховой – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.5$ и $T \approx 6.90164$; штрихпунктирной – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.05$ и $T \approx 11.00104$.

Фиг. 5.
Зависимости компонент глобального (а) и локального (б) дефектов симплектичности от времени для метода Лобатто IIIA при $\tau = 0.05{{T}_{{\text{Г}}}}$. Сплошной линии соответствуют ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$ и $T \approx 6.30799$; штриховой – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.5$ и $T \approx 6.90164$; штрихпунктирной – ${{p}_{0}} = 0$, ${{q}_{0}} = 0.05$ и $T \approx 11.00104$.

Таблица 4.
Максимальные абсолютные значения компонент глобального и локального дефектов симплектичности ($\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ и $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$) для НГРК-методов
| $({{p}_{0}},{{q}_{0}})$ | $\tau $ | Двухуровневый НГРК-метод типа Гаусса | Трехуровневый НГРК-метод типа Гаусса | ||
|---|---|---|---|---|---|
| $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$ | ||
| $(0,0.99)$ | $0.01{{T}_{{\text{Г}}}}$ | $7.18891 \times {{10}^{{ - 9}}}$ | $2.25863 \times {{10}^{{ - 10}}}$ | $6.01812 \times {{10}^{{ - 13}}}$ | $1.89359 \times {{10}^{{ - 14}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $1.14917 \times {{10}^{{ - 7}}}$ | $7.21737 \times {{10}^{{ - 9}}}$ | $3.85001 \times {{10}^{{ - 11}}}$ | $2.42159 \times {{10}^{{ - 12}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $5.80870 \times {{10}^{{ - 7}}}$ | $5.46775 \times {{10}^{{ - 8}}}$ | $4.38238 \times {{10}^{{ - 10}}}$ | $4.13124 \times {{10}^{{ - 11}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.83188 \times {{10}^{{ - 6}}}$ | ${\text{2}}{\text{.29647}} \times {{10}^{{ - 7}}}$ | $2.45993 \times {{10}^{{ - 9}}}$ | $3.08837 \times {{10}^{{ - 10}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $4.45992 \times {{10}^{{ - 6}}}$ | $6.97838 \times {{10}^{{ - 7}}}$ | $9.37226 \times {{10}^{{ - 9}}}$ | $1.46863 \times {{10}^{{ - 9}}}$ | |
| $(0,0.9)$ | $0.01{{T}_{{\text{Г}}}}$ | $6.94312 \times {{10}^{{ - 8}}}$ | $2.22757 \times {{10}^{{ - 9}}}$ | $5.84870 \times {{10}^{{ - 12}}}$ | $2.07472 \times {{10}^{{ - 13}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $1.10987 \times {{10}^{{ - 6}}}$ | $7.11756 \times {{10}^{{ - 8}}}$ | $3.74164 \times {{10}^{{ - 10}}}$ | $2.65278 \times {{10}^{{ - 11}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $5.60999 \times {{10}^{{ - 6}}}$ | $5.39143 \times {{10}^{{ - 7}}}$ | $4.25908 \times {{10}^{{ - 9}}}$ | $4.52440 \times {{10}^{{ - 10}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.76917 \times {{10}^{{ - 5}}}$ | $2.26401 \times {{10}^{{ - 6}}}$ | $2.39076 \times {{10}^{{ - 8}}}$ | $3.38097 \times {{10}^{{ - 9}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $4.30712 \times {{10}^{{ - 5}}}$ | $6.87812 \times {{10}^{{ - 6}}}$ | $9.10892 \times {{10}^{{ - 8}}}$ | $1.60697 \times {{10}^{{ - 8}}}$ | |
| $(0,0.5)$ | $0.01{{T}_{{\text{Г}}}}$ | $2.70485 \times {{10}^{{ - 7}}}$ | $1.11316 \times {{10}^{{ - 8}}}$ | $2.61469 \times {{10}^{{ - 11}}}$ | $1.65969 \times {{10}^{{ - 12}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $4.32314 \times {{10}^{{ - 6}}}$ | $3.55440 \times {{10}^{{ - 7}}}$ | $1.67293 \times {{10}^{{ - 9}}}$ | $2.12060 \times {{10}^{{ - 10}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $2.18468 \times {{10}^{{ - 5}}}$ | $2.68938 \times {{10}^{{ - 6}}}$ | $1.90468 \times {{10}^{{ - 8}}}$ | $3.61245 \times {{10}^{{ - 9}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $6.88722 \times {{10}^{{ - 5}}}$ | $1.12757 \times {{10}^{{ - 5}}}$ | $1.06948 \times {{10}^{{ - 7}}}$ | $2.69501 \times {{10}^{{ - 8}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $1.67593 \times {{10}^{{ - 4}}}$ | $3.41863 \times {{10}^{{ - 5}}}$ | $4.07639 \times {{10}^{{ - 7}}}$ | $1.27820 \times {{10}^{{ - 7}}}$ | |
| $(0,0.05)$ | $0.01{{T}_{{\text{Г}}}}$ | $2.86393 \times {{10}^{{ - 7}}}$ | $1.72683 \times {{10}^{{ - 8}}}$ | $4.37323 \times {{10}^{{ - 11}}}$ | $3.06177 \times {{10}^{{ - 12}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $4.57457 \times {{10}^{{ - 6}}}$ | $5.51183 \times {{10}^{{ - 7}}}$ | $2.79861 \times {{10}^{{ - 9}}}$ | $3.91080 \times {{10}^{{ - 10}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $2.30934 \times {{10}^{{ - 5}}}$ | $4.16782 \times {{10}^{{ - 6}}}$ | $3.18731 \times {{10}^{{ - 8}}}$ | $6.65850 \times {{10}^{{ - 9}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $7.26954 \times {{10}^{{ - 5}}}$ | $1.74588 \times {{10}^{{ - 5}}}$ | $1.79048 \times {{10}^{{ - 7}}}$ | $4.96376 \times {{10}^{{ - 8}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $1.76560 \times {{10}^{{ - 4}}}$ | $5.28722 \times {{10}^{{ - 5}}}$ | $6.82848 \times {{10}^{{ - 7}}}$ | $2.35199 \times {{10}^{{ - 7}}}$ | |
Из анализа графиков на фиг. 1–5, табл. 3, 4 и не приведенных в настоящей работе данных для остальных начальных значений ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ следует, что абсолютные значения компонент дефектов симплектичности всех рассматриваемых методов не имеют тенденции к возрастанию на больших промежутках времени.
Сравнение фиг. 1 и 2, данные табл. 3 и данные для остальных $({{p}_{0}},{{q}_{0}})$ указывают на то, что $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ и $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$ для нового консервативного метода нулевого дисбаланса полной энергии при одинаковых значениях шага по крайней мере на 3 порядка меньше, чем соответствующие значения для метода дискретного градиента. Компоненты дефектов симплектичности обоих методов имеют сравнимые величины, если шаг в методе дискретного градиента на 2 порядка меньше.
Максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ для двухуровневого НРГК-метода типа Гаусса и метода Лобатто IIIA на порядок или несколько порядков больше, чем соответствующие величины для метода нулевого дисбаланса (при фиксированных ${{q}_{0}}$, $\tau $).
Максимальные абсолютные значения $\Delta {{S}_{{n,12}}}$ и $\delta {{S}_{{n,12}}}$ для трехуровневого НГРК-метода типа Гаусса имеют сопоставимые величины (отличаются не более чем в 3 раза) с соответствующими значениями для метода нулевого дисбаланса, за исключением начальных значений ${{p}_{0}} = 0$, ${{q}_{0}} = 0.99$. В последнем случае трехуровневый НГРК-метод типа Гаусса дает меньшие $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ и $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$. При ${{p}_{0}} = 0$, ${{q}_{0}} \in \{ 0.7,0.8,0.9\} $ метод нулевого дисбаланса дает меньшие $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$, но большие $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$, чем трехуровневый НГРК-метод типа Гаусса. При ${{p}_{0}} = 0$, ${{q}_{0}} \in \{ 0.05,0.1,0.2,0.3,0.4,0.5,0.6\} $ метод нулевого дисбаланса дает меньшие $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$ и $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$.
Вычисления на двойной точности. При численном вычислении частных производных приращение аргумента должно быть не меньше величины, линейно зависящей от квадратного корня из величины погрешности вычисления функции [18, с. 186], [20], [21]. Из-за этого двойной точности может быть недостаточно для вычисления $\Delta {{S}_{{n,12}}}$, $\delta {{S}_{{n,12}}}$. Как показали расчеты, зависимости $\Delta {{S}_{{n,12}}}$, $\delta {{S}_{{n,12}}}$ в таком случае могут значительно отличаться от зависимостей, полученных в случае повышенной точности, например, не быть периодическими и нарастать со временем. Отметим, что в случае метода нулевого дисбаланса для установления почти периодической зависимости $\Delta {{S}_{{n,12}}}$ от времени при ${{p}_{0}} = 0$, ${{q}_{0}} = 0.05$, $\tau = 0.05{{T}_{{\text{Г}}}}$, $t \in [0,1000T]$ нужно использовать приращение аргумента в правой разностной производной менее ${{10}^{{ - 18}}}$, которое слишком мало для вычислений на двойной точности.
Выводы. Итак, строго говоря, метод нулевого дисбаланса полной энергии, метод дискретного градиента и НГРК-методы не являются симплектическими. Однако максимальные абсолютные значения компонент дефектов симплектичности $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$, $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$ для метода нулевого дисбаланса на порядки меньше соответствующих значений для метода дискретного градиента. Двухуровневые НГРК-методы (типа Гаусса и Лобатто) также дают бóльшие значения $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$, $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$, чем метод нулевого дисбаланса. Только трехуровневый НГРК-метод типа Гаусса при ${{p}_{0}} = 0$, ${{q}_{0}} \in \{ 0.7,0.8,0.9,0.99\} $ (из рассмотренных ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$) дает меньшие значения $\mathop {max}\limits_n {\text{|}}\delta {{S}_{{n,12}}}{\text{|}}$ и при ${{p}_{0}} = 0$, ${{q}_{0}} = 0.99$ – меньшие значения $\mathop {max}\limits_n {\text{|}}\Delta {{S}_{{n,12}}}{\text{|}}$, чем метод нулевого дисбаланса.
6.2. Обратимость
Для исследования обратимости численного решения задачи Коши введем векторы $\Delta {{\rho }_{n}}$, $\delta {{\rho }_{n}}$ – глобального и локального дефектов обратимости на $n$-м шаге. В случае модельной задачи 1 $\Delta {{\rho }_{n}} \in {{R}^{2}}$, $\delta {{\rho }_{n}} \in {{R}^{2}}$. Глобальный дефект обратимости $\Delta {{\rho }_{n}}$ вычисляется следующим образом. Пусть имеется значение численного решения $({{p}_{n}},{{q}_{n}})$, найденное исследуемым методом для начальных значений $({{p}_{0}},{{q}_{0}})$. Для начальных значений $( - {{p}_{n}},{{q}_{n}})$ тем же методом находится значение решения $(\mathop {\underline p }\nolimits_{2n} ,\mathop {\underline q }\nolimits_{2n} )$ с помощью $n$ шагов. Тогда имеем
Локальный дефект обратимости $\delta {{\rho }_{n}}$ вычисляется следующим способом. Возьмем приближенное значение решения $({{p}_{n}},{{q}_{n}})$, найденное исследуемым методом. Сделаем один шаг метода для начальных значений $( - {{p}_{n}},{{q}_{n}})$, получим $(\mathop {\underline p }\nolimits_{n + 1} ,\mathop {\underline q }\nolimits_{n + 1} )$. Значение $\delta {{\rho }_{n}}$ вычисляется по формуле
Максимальные по ${{q}_{0}}$, $\tau $ и $n$ значения компонент глобального и локального дефектов обратимости ($ma{{x}_{{{{p}_{0}} = 0,\,{{q}_{0}} \in {{Q}_{0}},\,\tau \in \Theta ,n}}}{{\left\| {\Delta {{\rho }_{n}}} \right\|}_{c}}$ и $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},\tau \in \Theta ,n}}}{{\left\| {\delta {{\rho }_{n}}} \right\|}_{c}}$) указаны в табл. 5. Глобальный дефект обратимости вычислялся на временны́х отрезках $t \in [0,200T]$ в случае двойной точности и $t \in [0,50T]$ в случае повышенной; локальный дефект обратимости – на отрезках $t \in [0,1000T]$. Вычисление $\Delta {{\rho }_{n}}$ на более коротких временны́х отрезках обусловлено длительностью расчетов.
Таблица 5.
Максимальные по ${{q}_{0}}$, $\tau $ и $n$ абсолютные значения компонент дефектов обратимости
| Метод | Точность | $max{{\left\| {\Delta {{\rho }_{n}}} \right\|}_{c}}$ | $max{{\left\| {\delta {{\rho }_{n}}} \right\|}_{c}}$ |
|---|---|---|---|
| Метод нулевого дисбаланса | Двойная | $3.69387 \times {{10}^{{ - 10}}}$ | $1.42833 \times {{10}^{{ - 10}}}$ |
| Повышенная | $2.63898 \times {{10}^{{ - 73}}}$ | $2.81931 \times {{10}^{{ - 72}}}$ | |
| Метод Кунцмана–Бутчера шестого порядка | Двойная | $1.45338 \times {{10}^{{ - 10}}}$ | $6.66134 \times {{10}^{{ - 16}}}$ |
| Повышенная | $1.52539 \times {{10}^{{ - 70}}}$ | $1.12618 \times {{10}^{{ - 74}}}$ | |
| Трехстадийный симметрично-симплектический метод Рунге–Кутты, ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = 0$ |
Двойная | $1.14293 \times {{10}^{{ - 10}}}$ | $8.88178 \times {{10}^{{ - 16}}}$ |
| Повышенная | $6.54781 \times {{10}^{{ - 70}}}$ | $7.32289 \times {{10}^{{ - 74}}}$ | |
| Трехстадийный симметрично-симплектический метод Рунге–Кутты, ${{b}_{1}} = 0.5$, ${{s}_{{12}}} = 0$ |
Двойная | $1.21094 \times {{10}^{{ - 10}}}$ | $4.44089 \times {{10}^{{ - 16}}}$ |
| Повышенная | $4.50252 \times {{10}^{{ - 70}}}$ | $2.99596 \times {{10}^{{ - 74}}}$ | |
| Метод дискретного градиента | Двойная | $3.09634 \times {{10}^{{ - 6}}}$ | $5.01936 \times {{10}^{{ - 10}}}$ |
| Повышенная | $1.81732 \times {{10}^{{ - 67}}}$ | $1.03077 \times {{10}^{{ - 71}}}$ | |
| Двухуровневый НГРК-метод типа Гаусса | Двойная | $1.47612 \times {{10}^{{ - 10}}}$ | $1.11022 \times {{10}^{{ - 15}}}$ |
| Повышенная | $4.14122 \times {{10}^{{ - 70}}}$ | $2.47093 \times {{10}^{{ - 73}}}$ | |
| Трехуровневый НГРК-метод типа Гаусса | Двойная | $1.35092 \times {{10}^{{ - 10}}}$ | $8.88178 \times {{10}^{{ - 16}}}$ |
| Повышенная | $5.22270 \times {{10}^{{ - 70}}}$ | $1.14498 \times {{10}^{{ - 73}}}$ | |
| Метод Лобатто IIIA | Двойная | $1.85595 \times {{10}^{{ - 10}}}$ | $1.05471 \times {{10}^{{ - 15}}}$ |
| Повышенная | $5.52514 \times {{10}^{{ - 70}}}$ | $1.39912 \times {{10}^{{ - 73}}}$ |
Для метода дискретного градиента при $\tau = 0.0002{{T}_{{\text{Г}}}}$ получены равенства: $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},n}}}{{\left\| {\Delta {{\rho }_{n}}} \right\|}_{c}} = $ $ = 4.87092 \times {{10}^{{ - 10}}}$, $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},n}}}{{\left\| {\delta {{\rho }_{n}}} \right\|}_{c}} = 9.86548 \times {{10}^{{ - 8}}}$ для двойной точности; $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},n}}}{{\left\| {\Delta {{\rho }_{n}}} \right\|}_{c}} = $ $ = 1.85364 \times {{10}^{{ - 72}}}$, $ma{{x}_{{{{p}_{0}} = 0,{{q}_{0}} \in {{Q}_{0}},n}}}{{\left\| {\delta {{\rho }_{n}}} \right\|}_{c}} = 1.12959 \times {{10}^{{ - 76}}}$ для повышенной точности. В этих случаях расчеты $\Delta {{\rho }_{n}}$ проводились для $t \in [0,10T]$.
Сравним глобальный и локальный дефекты обратимости используя максимальные по ${{q}_{0}}$, $\tau $ и $n$ абсолютные значения компонент. Глобальный и локальный дефекты обратимости значительно меньше в случае повышенной точности. Методы нулевого дисбаланса и трехстадийные симметрично-симплектические методы Рунге–Кутты имеют примерно одинаковые глобальные дефекты обратимости в случае двойной точности. В случае повышенной точности глобальный дефект обратимости для метода нулевого дисбаланса на три порядка меньше, чем глобальные дефекты обратимости для трехстадийных симметрично-симплектических методов Рунге–Кутты. Локальные дефекты обратимости трехстадийных симметрично-симплектических методов Рунге–Кутты меньше на шесть (в случае двойной точности) или два (в случае повышенной точности) порядка, чем соответствующие дефекты метода нулевого дисбаланса. Метод дискретного градиента дает глобальный дефект обратимости, который на несколько порядков больше соответствующего дефекта метода нулевого дисбаланса. Локальный дефект обратимости метода дискретного градиента имеет примерно такой же порядок, как и локальный дефект обратимости метода нулевого дисбаланса. Дефекты обратимости НГРК-методов отличаются от соответствующих дефектов обратимости трехстадийных симметрично-симплектических методов Рунге–Кутты не более чем на один порядок. Для всех восьми вычислительных методов компоненты глобального дефекта обратимости могут нарастать со временем, компоненты локального дефекта обратимости колеблются в окрестности 0.
Таким образом, все восемь вычислительных методов с большой точностью являются обратимыми.
6.3. Дисбаланс полной энергии
Рассмотрим значения дисбаланса полной энергии $\Delta {{H}_{n}} = H({{p}_{n}},{{q}_{n}}) - {{H}_{0}}$, полученные при использовании исследуемых методов решения задачи Коши. В табл. 6 приведены максимальные абсолютные значения дисбаланса полной энергии на отрезках $t \in [0,1000T]$ для различных $({{p}_{0}},{{q}_{0}})$ и $\tau $ при двойной и повышенной точности.
Таблица 6.
Максимальные абсолютные значения дисбаланса полной энергии $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$
| $({{p}_{0}},{{q}_{0}})$ | $\tau $ | Метод нулевого дисбаланса | Метод дискретного градиента | ||
|---|---|---|---|---|---|
| $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, двойная точность | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, повышенная точность | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, двойная точность | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, повышенная точность | ||
| $(0,0.99)$ | $0.0002{{T}_{{\text{Г}}}}$ | $6.73545 \times {{10}^{{ - 13}}}$ | $7.23895 \times {{10}^{{ - 75}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | ${\text{2}}{\text{.22045}} \times {{10}^{{ - 16}}}$ | $2.47992 \times {{10}^{{ - 133}}}$ | $9.40412 \times {{10}^{{ - 12}}}$ | $7.80964 \times {{10}^{{ - 72}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $3.88578 \times {{10}^{{ - 16}}}$ | $9.01163 \times {{10}^{{ - 134}}}$ | $4.74581 \times {{10}^{{ - 12}}}$ | $3.91315 \times {{10}^{{ - 72}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $8.68750 \times {{10}^{{ - 15}}}$ | $8.83965 \times {{10}^{{ - 134}}}$ | $5.88141 \times {{10}^{{ - 13}}}$ | $1.59800 \times {{10}^{{ - 72}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $5.44842 \times {{10}^{{ - 14}}}$ | $9.29367 \times {{10}^{{ - 133}}}$ | $3.86146 \times {{10}^{{ - 11}}}$ | $6.59723 \times {{10}^{{ - 71}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $9.82547 \times {{10}^{{ - 15}}}$ | $7.39955 \times {{10}^{{ - 128}}}$ | $9.03436 \times {{10}^{{ - 12}}}$ | $4.27725 \times {{10}^{{ - 71}}}$ | |
| $(0,0.9)$ | $0.0002{{T}_{{\text{Г}}}}$ | $9.08718 \times {{10}^{{ - 14}}}$ | $1.91177 \times {{10}^{{ - 72}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | $9.88098 \times {{10}^{{ - 15}}}$ | $1.69914 \times {{10}^{{ - 133}}}$ | $2.90737 \times {{10}^{{ - 12}}}$ | $3.69337 \times {{10}^{{ - 73}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $7.04992 \times {{10}^{{ - 15}}}$ | $1.31391 \times {{10}^{{ - 133}}}$ | $1.37931 \times {{10}^{{ - 10}}}$ | $1.84847 \times {{10}^{{ - 70}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.67644 \times {{10}^{{ - 14}}}$ | $1.00435 \times {{10}^{{ - 133}}}$ | $1.98686 \times {{10}^{{ - 10}}}$ | $5.82691 \times {{10}^{{ - 70}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.42109 \times {{10}^{{ - 14}}}$ | $1.70400 \times {{10}^{{ - 127}}}$ | $6.63671 \times {{10}^{{ - 11}}}$ | $1.70315 \times {{10}^{{ - 70}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $6.66134 \times {{10}^{{ - 15}}}$ | $9.51028 \times {{10}^{{ - 126}}}$ | $2.01017 \times {{10}^{{ - 10}}}$ | $4.68915 \times {{10}^{{ - 70}}}$ | |
| $(0,0.5)$ | $0.0002{{T}_{{\text{Г}}}}$ | $5.02515 \times {{10}^{{ - 14}}}$ | $7.98058 \times {{10}^{{ - 73}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | $2.02199 \times {{10}^{{ - 14}}}$ | $1.73009 \times {{10}^{{ - 133}}}$ | $6.08435 \times {{10}^{{ - 11}}}$ | $3.16801 \times {{10}^{{ - 70}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $2.42584 \times {{10}^{{ - 14}}}$ | $2.01214 \times {{10}^{{ - 133}}}$ | $1.53261 \times {{10}^{{ - 10}}}$ | $6.47078 \times {{10}^{{ - 70}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.47105 \times {{10}^{{ - 14}}}$ | $6.98747 \times {{10}^{{ - 129}}}$ | $2.13078 \times {{10}^{{ - 10}}}$ | $3.84879 \times {{10}^{{ - 70}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.62509 \times {{10}^{{ - 14}}}$ | $8.90627 \times {{10}^{{ - 125}}}$ | $9.54080 \times {{10}^{{ - 11}}}$ | $1.29484 \times {{10}^{{ - 70}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $1.18516 \times {{10}^{{ - 14}}}$ | $2.56209 \times {{10}^{{ - 124}}}$ | $2.23205 \times {{10}^{{ - 10}}}$ | $1.20628 \times {{10}^{{ - 69}}}$ | |
| $(0,0.05)$ | $0.0002{{T}_{{\text{Г}}}}$ | $1.14053 \times {{10}^{{ - 13}}}$ | $4.60658 \times {{10}^{{ - 73}}}$ | ||
| $0.01{{T}_{{\text{Г}}}}$ | $3.16721 \times {{10}^{{ - 14}}}$ | $2.01329 \times {{10}^{{ - 133}}}$ | $2.43110 \times {{10}^{{ - 10}}}$ | $2.84821 \times {{10}^{{ - 70}}}$ | |
| $0.02{{T}_{{\text{Г}}}}$ | $2.66148 \times {{10}^{{ - 14}}}$ | $2.87947 \times {{10}^{{ - 133}}}$ | $8.76701 \times {{10}^{{ - 10}}}$ | $1.11147 \times {{10}^{{ - 69}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $2.22806 \times {{10}^{{ - 14}}}$ | $1.99834 \times {{10}^{{ - 126}}}$ | $1.34940 \times {{10}^{{ - 9}}}$ | $1.26395 \times {{10}^{{ - 69}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.17282 \times {{10}^{{ - 14}}}$ | $3.93408 \times {{10}^{{ - 124}}}$ | $1.55177 \times {{10}^{{ - 9}}}$ | $8.95555 \times {{10}^{{ - 70}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $4.11392 \times {{10}^{{ - 14}}}$ | $1.02944 \times {{10}^{{ - 123}}}$ | $1.98462 \times {{10}^{{ - 9}}}$ | $1.74669 \times {{10}^{{ - 69}}}$ | |
Метод нулевого дисбаланса полной энергии. Как показали вычисления для ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ и $\tau \in \Theta $, абсолютные значения дисбаланса полной энергии на приближенном решении модельной задачи, полученном методом нулевого дисбаланса полной энергии при повышенной точности, не превышают величины порядка ${{10}^{{ - 123}}}$. Для двойной точности абсолютные значения дисбаланса полной энергии не превышают величины порядка ${{10}^{{ - 14}}}$ и практически не зависят от рассматриваемых величин шага.
Метод дискретного градиента. Абсолютные значения дисбаланса полной энергии для метода дискретного градиента не превышают величины порядка ${{10}^{{ - 69}}}$ в случае повышенной точности. Для двойной точности абсолютные значения дисбаланса полной энергии не превышают величины порядка ${{10}^{{ - 9}}}$.
Трехстадийные симметрично-симплектические методы Рунге–Кутты. Для трехстадийных симметрично-симплектических методов Рунге–Кутты при повышенной точности зависимости дисбаланса полной энергии $\Delta {{H}_{n}}$ от времени являются почти периодическими. В случае двойной точности при ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = 0$ и ${{b}_{1}} = 0.5$, ${{s}_{{12}}} = 0$ зависимости $\Delta {{H}_{n}}$ также являются почти периодическими. Однако для двойной точности зависимости $\Delta {{H}_{n}}$ при ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = s_{{12}}^{*}$ и некоторых комбинациях ${{p}_{0}}$, ${{q}_{0}}$ и $\tau $ (например, при ${{p}_{0}} = 0$, ${{q}_{0}} = 0.99$, $\tau = 0.01{{T}_{{\text{Г}}}}$) не являются периодическими.
Максимальные абсолютные значения дисбаланса полной энергии $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ для повышенной точности на отрезках $t \in [0,1000T]$ при различных начальных значениях $({{p}_{0}},{{q}_{0}})$, значениях параметров ${{b}_{1}}$, ${{s}_{{12}}}$ и величинах шага $\tau $ приведены в табл. 7. Для двойной точности величины $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ при указанных в табл. 7 значениях $({{p}_{0}},{{q}_{0}})$ имеют тот же порядок и отличаются не более чем на один знак после запятой, за исключением значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}} = 6.21725 \times {{10}^{{ - 15}}}$ для ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$, $\tau = 0.01{{T}_{{\text{Г}}}}$, ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = s_{{12}}^{*}$, а также значений $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}} < 3 \times {{10}^{{15}}}$ для ${{p}_{0}} = 0$, ${{q}_{0}} = 0.99$, $\tau \in \{ 0.01{{T}_{Г}},0.02{{T}_{Г}},0.03{{T}_{Г}}\} $, b1 = 5/18, ${{s}_{{12}}} = s_{{12}}^{*}$. Согласно данным расчетов для ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ и $\tau \in \Theta $, максимальные абсолютные значения дисбаланса полной энергии $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ убывают при уменьшении $\tau $.
Таблица 7.
Максимальные абсолютные значения дисбаланса полной энергии $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ для трехстадийных симметрично-симплектических методов Рунге–Кутты. Вычисления с повышенной точностью
| $({{p}_{0}},{{q}_{0}})$ | $\tau $ | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ при ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = s_{{12}}^{ * }$ | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ при ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = 0$ | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ при ${{b}_{1}} = 0.5$, ${{s}_{{12}}} = 0$ |
|---|---|---|---|---|
| $(0,0.99)$ | $0.01{{T}_{{\text{Г}}}}$ | $2.51092 \times {{10}^{{ - 18}}}$ | $2.36806 \times {{10}^{{ - 13}}}$ | $7.14329 \times {{10}^{{ - 14}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $1.60601 \times {{10}^{{ - 16}}}$ | $3.78898 \times {{10}^{{ - 12}}}$ | $1.14293 \times {{10}^{{ - 12}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.82749 \times {{10}^{{ - 15}}}$ | $1.91826 \times {{10}^{{ - 11}}}$ | $5.78617 \times {{10}^{{ - 12}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.02535 \times {{10}^{{ - 14}}}$ | $6.06316 \times {{10}^{{ - 11}}}$ | ${\text{1}}{\text{.82879}} \times {{10}^{{ - 11}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $3.90432 \times {{10}^{{ - 14}}}$ | $1.47362 \times {{10}^{{ - 10}}}$ | $4.46518 \times {{10}^{{ - 11}}}$ | |
| $(0,0.9)$ | $0.01{{T}_{{\text{Г}}}}$ | $2.47054 \times {{10}^{{ - 15}}}$ | $2.15749 \times {{10}^{{ - 10}}}$ | $6.49183 \times {{10}^{{ - 11}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $1.58115 \times {{10}^{{ - 13}}}$ | $3.45270 \times {{10}^{{ - 9}}}$ | $1.03870 \times {{10}^{{ - 9}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.80107 \times {{10}^{{ - 12}}}$ | $1.74856 \times {{10}^{{ - 8}}}$ | $5.25848 \times {{10}^{{ - 9}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $1.01203 \times {{10}^{{ - 11}}}$ | $5.52931 \times {{10}^{{ - 8}}}$ | $1.66201 \times {{10}^{{ - 8}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $3.86114 \times {{10}^{{ - 11}}}$ | $1.35095 \times {{10}^{{ - 7}}}$ | $4.05800 \times {{10}^{{ - 8}}}$ | |
| $(0,0.5)$ | $0.01{{T}_{{\text{Г}}}}$ | $2.39557 \times {{10}^{{ - 13}}}$ | $1.57808 \times {{10}^{{ - 8}}}$ | $4.68660 \times {{10}^{{ - 9}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $1.53504 \times {{10}^{{ - 11}}}$ | $2.52719 \times {{10}^{{ - 7}}}$ | $7.49860 \times {{10}^{{ - 8}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.75217 \times {{10}^{{ - 10}}}$ | $1.28135 \times {{10}^{{ - 6}}}$ | $3.79627 \times {{10}^{{ - 7}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $9.87470 \times {{10}^{{ - 10}}}$ | $4.05874 \times {{10}^{{ - 6}}}$ | $1.19989 \times {{10}^{{ - 6}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $3.78227 \times {{10}^{{ - 9}}}$ | $9.93904 \times {{10}^{{ - 6}}}$ | $2.92989 \times {{10}^{{ - 6}}}$ | |
| $(0,0.05)$ | $0.01{{T}_{{\text{Г}}}}$ | $7.62720 \times {{10}^{{ - 13}}}$ | $4.12329 \times {{10}^{{ - 8}}}$ | $1.20741 \times {{10}^{{ - 8}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $4.88835 \times {{10}^{{ - 11}}}$ | $6.60585 \times {{10}^{{ - 7}}}$ | $1.93187 \times {{10}^{{ - 7}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $5.58168 \times {{10}^{{ - 10}}}$ | $3.35167 \times {{10}^{{ - 6}}}$ | $9.78048 \times {{10}^{{ - 7}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $3.14727 \times {{10}^{{ - 9}}}$ | $1.06274 \times {{10}^{{ - 5}}}$ | $3.09144 \times {{10}^{{ - 6}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $1.20635 \times {{10}^{{ - 8}}}$ | $2.60599 \times {{10}^{{ - 5}}}$ | $7.54920 \times {{10}^{{ - 6}}}$ |
Итак, выбор значений ${{s}_{{12}}}$ в соответствии с уравнением нулевого дисбаланса (3.5), как правило, уменьшает абсолютное значение дисбаланса и делает его практически не зависимым от изменений величины шага в разумных пределах. Только в случае двойной точности при некоторых из рассмотренных комбинаций ${{p}_{0}}$, ${{q}_{0}}$, $\tau $ (при ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$, $\tau = 0.01{{T}_{{\text{Г}}}}$; ${{p}_{0}} = 0$, ${{q}_{0}} = 0.99$, $\tau \in \{ 0.03{{T}_{Г}},0.04{{T}_{Г}}\} $) значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ при постоянных ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = s_{{12}}^{*}$ меньше, чем для метода нулевого дисбаланса. Отметим, что при ${{p}_{0}} = 0$, ${{q}_{0}} = 0.99$, $\tau \in \{ 0.01{{T}_{Г}},0.02{{T}_{Г}}\} $ в случае двойной точности значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ для постоянных ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = s_{{12}}^{*}$ и для метода нулевого дисбаланса совпадают точно. Это вызвано тем, что условие остановки внешних итераций (3.6) метода нулевого дисбаланса удовлетворяется уже для начального приближения $s_{{12}}^{{(0)}} = s_{{12}}^{*}$ на всех шагах метода нулевого дисбаланса, т.е. внешние итерации при расчетах фактически не выполнялись. При ${{b}_{1}} = 5{\text{/}}18$, ${{s}_{{12}}} = 0$ и ${{b}_{1}} = 0.5$, ${{s}_{{12}}} = 0$ для двойной точности, а также при всех рассмотренных комбинациях постоянных ${{b}_{1}}$, ${{s}_{{12}}}$ для повышенной точности получаются бóльшие $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, чем при использовании метода нулевого дисбаланса (по данным расчетов для ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $).
На фиг. 6 изображены графики зависимостей значения ${{s}_{{12}}}$ от времени для метода нулевого дисбаланса. Зависимости являются почти периодическими в случае повышенной точности вычислений при ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ и $\tau \in \Theta $. Величины ${{s}_{{12}}}$ отличаются от $s_{{12}}^{*}$ не более чем в третьем знаке после запятой. Такие поправки позволяют уменьшить дисбаланс полной энергии, особенно в случае повышенной точности.
Фиг. 6.
Графики зависимостей ${{s}_{{12}}}$ от времени при $\tau = 0.05{{T}_{{\text{Г}}}}$ и следующих начальных значениях: ${{p}_{0}} = 0$, ${{q}_{0}} = 0.9$ (сплошная линия); ${{p}_{0}} = 0$, ${{q}_{0}} = 0.5$ (штриховая линия); ${{p}_{0}} = 0$, ${{q}_{0}} = 0.05$ (штрихпунктирная линия).

Метод дискретного градиента в случае повышенной точности также обеспечивает при ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ и $\tau \in \Theta $ гораздо меньшие значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, чем трехстадийные симметрично-симплектические методы Рунге–Кутты. Однако для двойной точности метод Кунцмана–Бутчера обеспечивает для большинства комбинаций ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $ меньшие $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$. При ${{b}_{1}} = 5{\text{/}}18,$ ${{b}_{1}} = 0.{\text{5}}$ и ${{s}_{{12}}} = 0$ трехстадийные симметрично-симплектические методы Рунге–Кутты дают бóльшие значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, чем метод дискретного градиента, для подавляющего большинства комбинаций ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $ в случае двойной точности.
Неявные гнездовые методы Рунге–Кутты. Характеристики зависимостей дисбаланса полной энергии $\Delta {{H}_{n}}$ от времени для НГРК-методов аналогичны характеристикам соответствующих зависимостей для трехстадийных симметрично-симплектических методов Рунге–Кутты. При повышенной точности зависимости $\Delta {{H}_{n}}$ от времени являются почти периодическими. Для двойной точности – зависимости почти периодические в случае двухуровневого метода типа Гаусса и метода Лобатто IIIA. Для трехуровневого метода типа Гаусса зависимости $\Delta {{H}_{n}}$ могут не являться периодическими при двойной точности.
Максимальные абсолютные величины дисбаланса полной энергии $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ в случае повышенной точности на отрезках $t \in [0,1000T]$ для НГРК-методов при различных начальных значениях $({{p}_{0}},{{q}_{0}})$ представлены в табл. 8. Для двойной точности величины $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ при указанных в этой таблице $({{p}_{0}},{{q}_{0}})$ имеют тот же порядок и отличаются не более чем на один знак после запятой, за исключением значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}} = 4.16334 \times {{10}^{{ - 16}}}$ для трехуровневого НГРК-метода типа Гаусса при ${{p}_{0}} = 0$, ${{q}_{0}} = 0.99$, $\tau = 0.01{{T}_{{\text{Г}}}}$. По крайней мере для ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$ и $\tau \in \Theta $ максимальные абсолютные значения дисбаланса полной энергии $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ убывают при уменьшении $\tau $.
Таблица 8.
Максимальные абсолютные значения дисбаланса полной энергии $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ для НГРК-методов. Вычисления с повышенной точностью
| $({{p}_{0}},{{q}_{0}})$ | $\tau $ | Двухуровневый НГРК-метод типа Гаусса | Трехуровневый НГРК-метод типа Гаусса | Метод Лобатто IIIA |
|---|---|---|---|---|
| $(0,0.99)$ | $0.01{{T}_{{\text{Г}}}}$ | $1.66635 \times {{10}^{{ - 13}}}$ | $1.56960 \times {{10}^{{ - 17}}}$ | $1.07149 \times {{10}^{{ - 13}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $2.66415 \times {{10}^{{ - 12}}}$ | $1.00397 \times {{10}^{{ - 15}}}$ | $1.71440 \times {{10}^{{ - 12}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.34704 \times {{10}^{{ - 11}}}$ | $1.14249 \times {{10}^{{ - 14}}}$ | $8.67925 \times {{10}^{{ - 12}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $4.24983 \times {{10}^{{ - 11}}}$ | $6.41063 \times {{10}^{{ - 14}}}$ | $2.74318 \times {{10}^{{ - 11}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $1.03521 \times {{10}^{{ - 10}}}$ | $2.44122 \times {{10}^{{ - 13}}}$ | $6.69775 \times {{10}^{{ - 11}}}$ | |
| $(0,0.9)$ | $0.01{{T}_{{\text{Г}}}}$ | $1.51438 \times {{10}^{{ - 10}}}$ | $1.43177 \times {{10}^{{ - 14}}}$ | $9.73775 \times {{10}^{{ - 11}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $2.42118 \times {{10}^{{ - 9}}}$ | $9.15804 \times {{10}^{{ - 13}}}$ | $1.55804 \times {{10}^{{ - 9}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $1.22418 \times {{10}^{{ - 8}}}$ | $1.04215 \times {{10}^{{ - 11}}}$ | $7.88771 \times {{10}^{{ - 9}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $3.86217 \times {{10}^{{ - 8}}}$ | $5.84756 \times {{10}^{{ - 11}}}$ | $2.49300 \times {{10}^{{ - 8}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $9.40766 \times {{10}^{{ - 8}}}$ | $2.22676 \times {{10}^{{ - 10}}}$ | $6.08690 \times {{10}^{{ - 8}}}$ | |
| $(0,0.5)$ | $0.01{{T}_{{\text{Г}}}}$ | $1.09324 \times {{10}^{{ - 8}}}$ | $1.11470 \times {{10}^{{ - 12}}}$ | $7.02990 \times {{10}^{{ - 9}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $1.74776 \times {{10}^{{ - 7}}}$ | $7.12939 \times {{10}^{{ - 11}}}$ | $1.12479 \times {{10}^{{ - 7}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $8.83597 \times {{10}^{{ - 7}}}$ | $8.11186 \times {{10}^{{ - 10}}}$ | $5.69435 \times {{10}^{{ - 7}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $2.78724 \times {{10}^{{ - 6}}}$ | $4.55066 \times {{10}^{{ - 9}}}$ | $1.79979 \times {{10}^{{ - 6}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $6.78789 \times {{10}^{{ - 6}}}$ | $1.73240 \times {{10}^{{ - 8}}}$ | $4.39450 \times {{10}^{{ - 6}}}$ | |
| $(0,0.05)$ | $0.01{{T}_{{\text{Г}}}}$ | $2.81641 \times {{10}^{{ - 8}}}$ | $3.30192 \times {{10}^{{ - 12}}}$ | $1.81111 \times {{10}^{{ - 8}}}$ |
| $0.02{{T}_{{\text{Г}}}}$ | $4.50202 \times {{10}^{{ - 7}}}$ | $2.11173 \times {{10}^{{ - 10}}}$ | $2.89780 \times {{10}^{{ - 7}}}$ | |
| $0.03{{T}_{{\text{Г}}}}$ | $2.27557 \times {{10}^{{ - 6}}}$ | $2.40252 \times {{10}^{{ - 9}}}$ | $1.46705 \times {{10}^{{ - 6}}}$ | |
| $0.04{{T}_{{\text{Г}}}}$ | $7.17600 \times {{10}^{{ - 6}}}$ | $1.34760 \times {{10}^{{ - 8}}}$ | $4.63697 \times {{10}^{{ - 6}}}$ | |
| $0.05{{T}_{{\text{Г}}}}$ | $1.74694 \times {{10}^{{ - 5}}}$ | $5.12919 \times {{10}^{{ - 8}}}$ | $1.13226 \times {{10}^{{ - 5}}}$ |
Как показали расчеты для ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $, в случае повышенной точности значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ для НГРК-методов значительно больше соответствующих значений для метода нулевого дисбаланса полной энергии и метода дискретного градиента. В случае двойной точности при ${{p}_{0}} = 0$, ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $ значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ для НГРК-методов больше соответствующих значений для метода нулевого дисбаланса. Двухуровневый НГРК-метод типа Гаусса дает бóльшие значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, чем метод дискретного градиента при всех ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $, кроме ${{q}_{0}} = 0.99$, $\tau \in \{ 0.01{{T}_{Г}},0.02{{T}_{Г}}\} $. Метод Лобатто IIIA также дает бóльшие значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, чем метод дискретного градиента при всех ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $, кроме ${{q}_{0}} = 0.99$, $\tau \in \{ 0.01{{T}_{Г}},0.02{{T}_{Г}},0.04{{T}_{Г}}\} $. Только трехуровневый НГРК-метод типа Гаусса дает для большиства комбинаций ${{q}_{0}} \in {{Q}_{0}}$, $\tau \in \Theta $ (для 28 комбинаций из 55) меньшие значения $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$, чем метод дискретного градиента.
7. СРАВНЕНИЕ ВЫЧИСЛИТЕЛЬНЫХ МЕТОДОВ НА МОДЕЛЬНОЙ ЗАДАЧЕ 2
Перейдем теперь к модельной задаче 2. Для сравнения метода нулевого дисбаланса полной энергии, трехстадийного симметрично-симплектического метода Рунге–Кутты – метода Кунцмана–Бутчера шестого порядка и НГРК-методов используем дисбаланс полной энергии $\Delta {{H}_{n}} = H({{{\mathbf{p}}}_{n}},{{{\mathbf{q}}}_{n}}) - {{H}_{0}}$ и дисбаланс углового момента $\Delta {{L}_{n}} = L({{{\mathbf{p}}}_{n}},{{{\mathbf{q}}}_{n}}) - {{L}_{0}}$, а также погрешность $\mathop {\left\| {{{{\mathbf{q}}}_{n}} - {\mathbf{q}}({{t}_{n}})} \right\|}\nolimits_2 $. Здесь ${{{\mathbf{p}}}_{n}}$, ${{{\mathbf{q}}}_{n}}$ – приближенные значения векторов импульсов и координат на $n$-м шаге вычислительного метода соответственно; ${\mathbf{q}}({{t}_{n}})$ – значение аналитического решения в момент времени ${{t}_{n}}$, соответствующий $n$-му шагу вычислительного метода. В качестве начальных условий взяты ${{q}_{1}}(0) = 1 - e$, ${{p}_{1}}(0) = 0$, ${{q}_{2}}(0) = 0,$ ${{p}_{2}}(0) = {{(1 + e)}^{{0.5}}}{\text{/}}{{(1 - e)}^{{0.5}}}$ [3, с. 12], [28]. В этом случае $a = 1$, ${{t}_{{\text{П}}}} = 0$. При $e = 0.2$, $\tau \leqslant 0.2$ и $e = 0.9$, $\tau \leqslant 0.007$ условие (3.4) и аналогичные условия для рассматриваемых НГРК-методов выполнены. Вычисления проведены с использованием чисел двойной точности. Отрезок интегрирования для $e = 0.2$: $t \in [0,{{10}^{6}}]$, для $e = 0.9$: $t \in [0,{{10}^{5}}]$. Для всех вычислительных методов использованы следующие значения параметров, задающих точность решения системы разрешающих уравнений: ${{\varepsilon }_{{abs}}} = 5 \times {{10}^{{ - 32}}}$, ${{\varepsilon }_{{rel}}} = 8 \times {{10}^{{ - 13}}}$. Также для метода нулевого дисбаланса полнoй энергии: ${{\varepsilon }_{{\Delta H}}} = 2 \times {{10}^{{ - 14}}}$, ${{\varepsilon }_{s}} = 3 \times {{10}^{{ - 16}}}$. Для решения уравнения Кеплера (2.1) применялся метод простой итерации ${{E}^{{(i + 1)}}} = t + esin{{E}^{{(i)}}}$ с начальным приближением ${{E}^{{(0)}}} = 0$ и условием остановки $\left| {{{E}^{{(i + 1)}}} - {{E}^{{(i)}}}} \right| \leqslant 5 \times {{10}^{{ - 32}}} + 2 \times {{10}^{{ - 15}}}{{E}^{{(i + 1)}}}$.
Решения, полученные с помощью метода нулевого дисбаланса полной энергии и трехуровневого НГРК-метода типа Гаусса, а также графики зависимостей дисбаланса полной энергии и дисбаланса углового момента от времени изображены на фиг. 7, 8. Максимумы погрешности и абсолютных значений дисбаланса полной энергии и дисбаланса углового момента на отрезке интегрирования для разных вычислительных методов и значений $e$ и $\tau $ приведены в табл. 9–12.
Фиг. 7.
Решения модельной задачи 2 для $e = 0.2$, полученные с помощью метода нулевого дисбаланса полной энергии (а) и трехуровневого НГРК-метода типа Гаусса (б) при $\tau = 0.2$.

Фиг. 8.
Решение модельной задачи 2 для $e = 0.9$, полученное с помощью метода нулевого дисбаланса при $\tau = 0.007$ (а); графики зависимостей соответствующих дисбаланса полной энергии $\Delta {{H}_{n}}$ (черная линия) и дисбаланса углового момента (серая линия) $\Delta {{L}_{n}}$ от времени (б).

Таблица 9.
Погрешность численного решения, дисбаланс полной энергии и дисбаланс углового момента для $e = 0.2$ и $\tau = 0.1$
| Метод | $\mathop {max}\limits_n \mathop {\left\| {{{{\mathbf{q}}}_{n}} - {\mathbf{q}}({{t}_{n}})} \right\|}\nolimits_2 $ | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\Delta {{L}_{n}}{\text{|}}$ |
|---|---|---|---|
| Метод нулевого дисбаланса | 0.000288123 | $8.88289 \times {{10}^{{ - 13}}}$ | $7.64533 \times {{10}^{{ - 12}}}$ |
| Метод Кунцмана–Бутчера шестого порядка | 0.00262813 | $2.65126 \times {{10}^{{ - 10}}}$ | $8.23142 \times {{10}^{{ - 12}}}$ |
| Двухуровневый НГРК-метод типа Гаусса | 2.32530 | $2.35733 \times {{10}^{{ - 6}}}$ | $2.14359 \times {{10}^{{ - 6}}}$ |
| Трехуровневый НГРК-метод типа Гаусса | 0.00412766 | $1.08454 \times {{10}^{{ - 9}}}$ | $1.10332 \times {{10}^{{ - 9}}}$ |
| Метод Лобатто IIIA четвертого порядка | 0.933706 | $9.81360 \times {{10}^{{ - 7}}}$ | $1.18249 \times {{10}^{{ - 6}}}$ |
Таблица 10.
Погрешность численного решения, дисбаланс полной энергии и дисбаланс углового момента для $e = 0.2$ и $\tau = 0.2$
| Метод | $\mathop {max}\limits_n \mathop {\left\| {{{{\mathbf{q}}}_{n}} - {\mathbf{q}}({{t}_{n}})} \right\|}\nolimits_2 $ | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\Delta {{L}_{n}}{\text{|}}$ |
|---|---|---|---|
| Метод нулевого дисбаланса | 0.0185422 | $4.74332 \times {{10}^{{ - 12}}}$ | $1.43392 \times {{10}^{{ - 11}}}$ |
| Метод Кунцмана–Бутчера шестого порядка | 0.166603 | $1.64597 \times {{10}^{{ - 8}}}$ | $1.21343 \times {{10}^{{ - 11}}}$ |
| Двухуровневый НГРК-метод типа Гаусса | 2.39903 | $3.77411 \times {{10}^{{ - 5}}}$ | $3.43200 \times {{10}^{{ - 5}}}$ |
| Трехуровневый НГРК-метод типа Гаусса | 0.260814 | $6.91188 \times {{10}^{{ - 8}}}$ | $7.03130 \times {{10}^{{ - 8}}}$ |
| Метод Лобатто IIIA четвертого порядка | 2.39926 | $1.55611 \times {{10}^{{ - 5}}}$ | $1.88551 \times {{10}^{{ - 5}}}$ |
Таблица 11.
Погрешность численного решения, дисбаланс полной энергии и дисбаланс углового момента для $e = 0.9$ и $\tau = 0.00372$
| Метод | $\mathop {max}\limits_n \mathop {\left\| {{{{\mathbf{q}}}_{n}} - {\mathbf{q}}({{t}_{n}})} \right\|}\nolimits_2 $ | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\Delta {{L}_{n}}{\text{|}}$ |
|---|---|---|---|
| Метод нулевого дисбаланса | 0.000199072 | $5.32552 \times {{10}^{{ - 12}}}$ | $1.71252 \times {{10}^{{ - 13}}}$ |
| Метод Кунцмана–Бутчера шестого порядка | 0.00879098 | $6.78523 \times {{10}^{{ - 9}}}$ | $2.23876 \times {{10}^{{ - 13}}}$ |
| Двухуровневый НГРК-метод типа Гаусса | 2.00018 | $2.48121 \times {{10}^{{ - 5}}}$ | $9.87110 \times {{10}^{{ - 7}}}$ |
| Трехуровневый НГРК-метод типа Гаусса | 0.0215199 | $1.79142 \times {{10}^{{ - 8}}}$ | $6.78932 \times {{10}^{{ - 10}}}$ |
| Метод Лобатто IIIA четвертого порядка | 0.618039 | $5.71425 \times {{10}^{{ - 6}}}$ | $2.89619 \times {{10}^{{ - 7}}}$ |
Таблица 12.
Погрешность численного решения, дисбаланс полной энергии и дисбаланс углового момента для $e = 0.9$ и $\tau = 0.007$
| Метод | $\mathop {max}\limits_n \mathop {\left\| {{{{\mathbf{q}}}_{n}} - {\mathbf{q}}({{t}_{n}})} \right\|}\nolimits_2 $ | $\mathop {max}\limits_n {\text{|}}\Delta {{H}_{n}}{\text{|}}$ | $\mathop {max}\limits_n {\text{|}}\Delta {{L}_{n}}{\text{|}}$ |
|---|---|---|---|
| Метод нулевого дисбаланса | 0.00874868 | $3.74079 \times {{10}^{{ - 12}}}$ | $1.28952 \times {{10}^{{ - 13}}}$ |
| Метод Кунцмана–Бутчера шестого порядка | 0.323379 | $3.13309 \times {{10}^{{ - 7}}}$ | $4.28046 \times {{10}^{{ - 13}}}$ |
| Двухуровневый НГРК-метод типа Гаусса | 2.34503 | 0.000313777 | $1.24708 \times {{10}^{{ - 5}}}$ |
| Трехуровневый НГРК-метод типа Гаусса | 0.571948 | $8.16647 \times {{10}^{{ - 7}}}$ | $3.05682 \times {{10}^{{ - 8}}}$ |
| Метод Лобатто IIIA четвертого порядка | 2.09520 | $7.53955 \times {{10}^{{ - 5}}}$ | $3.62464 \times {{10}^{{ - 6}}}$ |
Анализ приведенных рисунков и таблиц показывает, что предлагаемый метод нулевого дисбаланса полной энергии дает более точные численные решения, чем указанные другие вычислительные методы. Максимальные по времени значения ${\text{|}}\Delta {{H}_{n}}{\text{|}}$ и ${\text{|}}\Delta {{L}_{n}}{\text{|}}$ меньше в случае метода нулевого дисбаланса, за исключением случая $e = 0.2$, $\tau = 0.2$, когда метод Кунцмана–Бутчера обеспечивает немного меньшее максимальное значение ${\text{|}}\Delta {{L}_{n}}{\text{|}}$.
Погрешность численных решений заключается как в запаздывании (опережении) описываемого движения в плоскости $({{q}_{1}},{{q}_{2}})$ относительно истинного движения, так и в отклонении от истинной эллиптической траектории (фиг. 9).
Фиг. 9.
Точное и численное решения модельной задачи 2 для $e = 0.2$. Численное решение получено методом Лобатто IIIA при $\tau = 0.2$. Сплошной линии соответствует компонента точного решения ${{q}_{1}}$, штриховой – ${{q}_{2}}$. Треугольниками отмечены значения компоненты ${{q}_{1}}$ численного решения, квадратиками – значения компоненты ${{q}_{2}}$ численного решения.
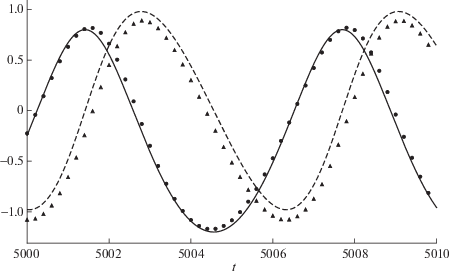
Проведем приближенное сравнение эффективности метода нулевого дисбаланса и метода Кунцмана–Бутчера. В случае метода нулевого дисбаланса наибольшие затраты приходятся на внутренние итерации, которые по трудоемкости равны итерациям при решении системы разрешающих уравнений метода Кунцмана–Бутчера. Поэтому для сравнения можно использовать суммарное число этих итераций на всем отрезке интегрирования. В табл. 13 представлено суммарное число итераций на всем отрезке интегрирования для метода нулевого дисбаланса полной энергии и метода Кунцмана–Бутчера шестого порядка. Согласно этой таблице суммарное число итераций для метода Кунцмана–Бутчера меньше суммарного числа внутренних итераций для метода нулевого дисбаланса. В случае $e = 0.2$ даже для меньшей величины шага $\tau = 0.1$ метод Кунцмана–Бутчера требует меньше итераций, чем метод нулевого дисбаланса для $\tau = 0.2$, обеспечивая при этом лучшую точность. Таким образом, в этом случае метод Кунцмана–Бутчера представляется более эффективным. Однако при $e = 0.9$ для достижения точности около $0.00874868$ требуется меньше внутренних итераций для метода нулевого дисбаланса, чем итераций для метода Кунцмана–Бутчера. Это объясняется тем, что в этом случае для достижения такой точности шаг в методе Кунцмана–Бутчера нужно брать меньше, чем в методе нулевого дисбаланса. Следовательно, в данной ситуации более эффективным представляется метод нулевого дисбаланса.
Таблица 13.
Суммарное число итераций на всем отрезке интегрирования для метода нулевого дисбаланса и метода Кунцмана–Бутчера шестого порядка
| $e = 0.2$, $T = {{10}^{6}}$ | $e = 0.9$, $T = {{10}^{5}}$ | |||
|---|---|---|---|---|
| $\tau = 0.1$ | $\tau = 0.2$ | $\tau = 0.00372$ | $\tau = 0.007$ | |
| Суммарное число внешних итераций для метода нулевого дисбаланса |
9 805 323 | 4 999 172 | 1 165 535 | 1 023 253 |
| Суммарное число внутренних итераций для метода нулевого дисбаланса |
167 663 876 | 96 983 568 | 93 864 364 | 54 702 900 |
| Суммарное число итераций для метода Кунцмана–Бутчера шестого порядка |
50 000 005 | 27 834 755 | 82 577 422 | 44 887 735 |
8. ВЫВОДЫ
Детальные исследования нового консервативного метода нулевого дисбаланса полной энергии и других рассмотренных методов на модельной задаче об одномерном движении материальной точки в поле кубического потенциала позволяют сделать следующие выводы.
1. Расширенная система разрешающих уравнений (3.3), (3.5) имеет решения в случае финитных движений материальной точки при разумных значениях величины шага $\tau \leqslant 0.05{{T}_{{\text{Г}}}}$.
2. Метод нулевого дисбаланса полной энергии, метод дискретного градиента и рассмотренные НГРК-методы, строго говоря, не являются симплектическими. Однако максимальные абсолютные значения ненулевых компонент глобального и локального дефектов симплектичности нового метода на несколько порядков меньше соответствующих величин для метода дискретного градиента. Компоненты дефектов симплектичности обоих методов имеют сравнимые величины, если шаг в методе дискретного градиента существенно меньше шага в методе нулевого дисбаланса. Максимальные абсолютные значения ненулевых компонент глобального и локального дефектов симплектичности НГРК-методов в подавляющем большинстве случаев имеют тот же или больший порядок, что и соответствующие величины для метода нулевого дисбаланса.
3. Метод нулевого дисбаланса полной энергии, рассмотренные трехстадийные симметрично-симплектические методы Рунге–Кутты, метод дискретного градиента и НГРК-методы с высокой точностью являются обратимыми во времени.
4. Метод нулевого дисбаланса полной энергии и метод дискретного градиента обеспечивают с высокой точностью нулевой дисбаланс полной энергии. Максимальные абсолютные значения дисбаланса полной энергии в случае трехстадийных симметрично-симплектических методов Рунге–Кутты и НГРК-методов при повышенной точности значительно больше. В подавляющем большинстве случаев при двойной точности это соотношение для метода нулевого дисбаланса и рассмотренных методов Рунге–Кутты также выполнено. Максимальные абсолютные значения дисбаланса полной энергии в случае метода нулевого дисбаланса практически не зависят от допустимых величин шага.
В случае задачи Кеплера метод нулевого дисбаланса полной энергии обеспечивает лучшую точность и меньшие максимальные абсолютные значения дисбалансa полной энергии и дисбаланса углового момента, чем трехстадийный симметрично-симплектический метод Рунге–Кутты – метод Кунцмана–Бутчера шестого порядка, и рассмотренные НГРК-методы. Исключение составляет только дисбаланс углового момента для $e = 0.2$, $\tau = 0.2$, когда метод Кунцмана–Бутчера шестого порядка дает немного меньшее максимальное абсолютное значение.
Результаты исследований показывают преимущества нового метода как в сравнении с трехстадийными симметрично-симплектическими методами Рунге–Кутты, так и с методом дискретного градиента и НГРК-методами. Основным преимуществом является возможность проведения расчетов с более крупным шагом.
Отметим, что подробное сравнение времени счета для различных методов не входит в цели настоящей работы. На время счета влияет не только вычислительный метод, но и особенности его программной реализации [30]. Представленные результаты позволяют сделать вывод о том, что в некоторых случаях метод нулевого дисбаланса может быть эффективнее метода Кунцмана–Бутчера шестого порядка, в то время как в других случаях метод Кунцмана–Бутчера шестого порядка является более эффективным, чем метод нулевого дисбаланса.
Для построения графиков, представленных в работе, использовалась библиотека Matplotlib [31].
Список литературы
Allen M.P., Tildesley D.J. Computer Simulation of Liquids. Oxford: Clarendon Press, 1991.
Deuflhard P., Hermans J., Leimkuhler B. et al. Computational Molecular Dynamics: Challenges, Methods, Ideas. Vol. 4 of Lecture Notes in Computational Science and Engeneering. Berlin: Springer, 1998.
Hairer E., Lubich C., Wanner G. Geometric Numerical Integration. Berlin: Springer, 2006.
Hairer E., Norsett S.P., Wanner G. Solving Ordinary Differential Equations I. Nonstiff Problems. Second Revised Edition. Berlin: Springer, 1993.
Ландау Л.Д., Лившиц Е.М. Теоретическая физика, том 1. Механика. Издание второе, исправленное. М.: Наука, Гл. ред. физ-мат. лит., 1965. 204 с.
Lasagni F.M. Canonical Runge–Kutta methods // Journal of Applied Mathematics and Physics (ZAMM). 1988. V. 39. Issue 6. P. 952–953.
Sanz-Serna J.M. Runge–Kutta schemes for hamiltonian systems // BIT. 1988. V. 28. № 4. P. 877–883.
Сурис Ю.Б. О сохранении симплектической структуры при численном решении гамильтоновых систем // Численное решение обыкновенных дифференциальных уравнений. М.: ИПМ. АН СССР. 1988. С. 148–160.
Еленин Г.Г., Шляхов П.И. О консервативности двухстадийных симметрично-симплектических методов Рунге–Кутты и метода Штермера-Верле // Дифференц. ур-ния. 2010. Т. 46. № 7. С. 983–989.
Brugnano L., Iavernaro F., Trigiante D. Energy and quadratic invariants – preserving integrators based upon Gauss collocation formulae // SIAM Journal on Numerical Analysis. 2012. V. 50. № 6. P. 2897–2916.
Еленин Г.Г., Александров П.А. О консервативности двухпараметрического семейства трехстадийных симметрично-симплектических методов Рунге–Кутты // Дифференц. ур-ния. 2012. Т. 48. № 7. С. 981–989.
Александров П.А., Еленин Г.Г. О возможности построения консервативного вычислительного метода решения задачи Коши для гамильтоновых систем на основе двухстадийных симметрично-симплектических методов Рунге–Кутты // Матем. моделирование. 2014. Т. 26. № 10. С. 47–63.
Еленин Г.Г., Александров П.А. Точные решения системы разрешающих уравнений семейства симметрично-симплектических методов Рунге–Кутты для задачи о движении материальной точки в поле кубического потенциала: Препринт. М.: МАКС Пресс, 2011. 60 с.
Александров П.А., Еленин Г.Г. О сохранении полной энергии на одном шаге метода средней точки: Препринт. М.: МАКС Пресс, 2012. 20 с.
Охоцимский Д.Е., Сихарулидзе Ю.Г. Основы механики космического полета: Учеб. пособие. М.: Наука. Гл. ред. физ.-мат. лит., 1990. 448 с.
Oewel W., Sofrouniou M. Symplectic Runge–Kutta schemes II: classification of symmetric methods. Preprint. University of Paderborn, 1997.
Еленин Г.Г., Шляхов П.И. Геометрическая структура пространства параметров трехстадийных симплектических методов Рунге–Кутты // Матем. моделирование. 2011. Т. 23. № 5. С. 16–34.
Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов. М.: Наука, Гл. ред. физ-мат. лит., 1989. 432 с.
Треногин В.А. Функциональный анализ: Учебник. 4-е изд., испр. М.: Физматлит, 2007. 488 с.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987. 598 с.
Вержбицкий В.М. Основы численных методов: Учебник для вузов. – 2-e издание, переработанное. М.: Высш. шк., 2005. 840 с.
Galassi M., Davies J., Theiler J. et al. GNU Scientific Library Reference Manual (3rd Ed.). 3rd Revised edition edition. Network Theory Ltd., 2009.
Muller D.E. A method for solving algebraic equations using an automatic computer // Mathematical Tables and Other Aids to Computation. 1956. V. 10. № 5. P. 208–215.
Дэннис Дж., Шнабель Р. Численные методы безусловной оптимизации и решения нелинейных уравнений: Пер. с англ. М.: Мир, 1988. 440 с.
Fousse L., Hanrot G., Lefèvre V., Pelissier P., Zimmermann P. MPFR: A multiple-precision binary floating-point library with correct rounding // ACM Transactions on Mathematical Software. June 2007. V. 33. Issue 2.
Kulikov G.Yu., Shindin S.K. Adaptive nested implicit Runge–Kutta formulas of Gauss type. // Applied Numerical Mathematics. March-April 2009. V. 59. Issues 3–4. P. 707–722.
Kulikov G.Yu. Automatic error control in the Gauss-type nested implicit Runge–Kutta formula of order 6 // Russian J. Numer. Anal. Math. Modelling. 2009. V. 24. № 2. P. 123–144.
Куликов Г.Ю. Вложенные симметричные неявные гнездовые методы Рунге–Кутты типов Гаусса и Лобатто для решения жестких обыкновенных дифференциальных уравнений и гамильтоновых систем // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 6. С. 986–1007.
Hairer E., Zbinden C.J. On conjugate-symplecticity of B-series integrators // IMA Journal of Numerical Analysis. 1 January 2013. V. 33. Issue 1. P. 57–79.
Гербер Р., Бик А., Смит К., Тиан К. Оптимизация ПО. Сборник рецептов. СПб.: Питер, 2010. 352 с.
Hunter J.D. Matplotlib: A 2D graphics environment // Computing in Science & Engng. 2007. V. 9. № 3. P. 90–95.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики




