1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 1, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 1, стр. 20-31

Ускоренный метаалгоритм для задач выпуклой оптимизации

А. В. Гасников 1, 2, Д. М. Двинских 2, 1, 3, П. Е. Двуреченский 3, 2, Д. И. Камзолов 1, *, В. В. Матюхин 1, Д. А. Пасечнюк 1, Н. К. Тупица 1, А. В. Чернов 1

1 Московский физико-технический институт (национальный исследовательский университет)
141701 М.о., Долгопрудный, Институтский пер., 9, Россия

2 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный пер., 19, стр. 1, Россия

3 Институт прикладного анализа и стохастики им. К. Вейерштрасса
Берлин, Германия

* E-mail: kamzolov.dmitry@phystech.edu

Поступила в редакцию 18.04.2020
После доработки 16.06.2020
Принята к публикации 18.09.2020

Полный текст (PDF)

Аннотация

Предлагается оболочка, названная “ускоренный метаалгоритм”, которая позволяет единообразно получать ускоренные методы решения задач выпуклой безусловной минимизации в различных постановках на базе неускоренных вариантов. В качестве приложений приводятся квазиоптимальные алгоритмы для минимизации гладких функций с липшицевыми производными произвольного порядка, а также для решения гладких минимаксных задач. Предложенная оболочка является более общей, чем существующие, а также позволяет получать лучшие оценки скорости сходимости и практическую эффективность для ряда постановок задач. Библ. 26. Фиг. 2.

Ключевые слова: выпуклая оптимизация, проксимальный ускоренный метод, тензорные методы, неточный оракул, слайдинг, каталист.

1. ВВЕДЕНИЕ

В последние 15 лет в численных методах гладкой выпуклой оптимизации преобладают так называемые ускоренные методы. Прообразом таких методов является метод тяжелого шарика Б.Т. Поляка и моментный метод Ю.Е. Нестерова (см. [1], [2]). Оказалось, что для многих задач гладкой выпуклой оптимизации оптимальные методы (с точки зрения числа вычислений градиента функции; в общем случае, старших производных) могут быть найдены среди ускоренных методов (см. [1]–[3]). Появилось огромное число работ, в которых предлагаются различные варианты ускоренных методов для разных классов задач (см., например, обзор литературы в [1], [3]). Каждый раз процедура ускорения принимала свою причудливую форму. Естественно, возникло желание как-то унифицировать все это. В 2015 г. это было сделано для широкого класса (рандомизированных) градиентных методов с помощью проксимальной ускоренной оболочки, названной Каталист (см. [4]). (Здесь и далее в качестве названий подходов/алгоритмов иногда будут использоваться англицизмы. Дело в том, что дословный перевод исходно английских выражений на русский язык может только запутывать дело. Отметим также, что под “проксимальной оболочкой” здесь и далее имеется в виду просто проксимальный алгоритм. Слово “оболочка” подразумевает, что в проксимальном алгоритме на каждой итерации имеется своя внутренняя (вспомогательная) задача оптимизации, которую, как правило, нельзя решить аналитически. Ее нужно решать численно. Поэтому внешний проксимальный метод можно понимать как “оболочку” для метода, использующегося для решения внутренней задачи.) С 2013 г. данные результаты стали активно переноситься на тензорные методы (использующие старшие производные) (см. [5]–[8]). В самое последнее время предпринимаются попытки унификации процедур ускорения для седловых задач и задач со структурой (композитных задач) (см. [9]–12]). Во всех этих направлениях по-прежнему использовалось значительное разнообразие ускоренных проксимальных оболочек (см. [1], [4]–[8], [10], [11], [13]– [16]). Метод из данной работы будет во многом базироваться на схеме из [14]. (Строго говоря, это даже не метод (алгоритм), а скорее оболочка (в смысле, определенном выше). В данной статье было выбрано название “ускоренный метаалгоритм”. Первое слово поясняет цель разрабатываемой оболочки – ускорение метода, использующегося в качестве базового (решающего внутреннюю задачу). Однако, в отличие от стандартной (ускоренной) оболочки, в предложенной в данной статье оболочке все же в ряде важных случаев вспомогательная задача решается аналитически и, стало быть, говорить об этой оболочке, как “оболочке”, а не как об обычном алгоритме, не совсем корректно. Поэтому было решено использовать более нейтральное в этом смысле слово – “метаалгоритм”.)

В данной работе показывается, что достаточно изучить всего одну ускоренную проксимальную оболочку, которая позволяет получать все известные нам ускоренные методы для задач гладкой выпуклой безусловной оптимизации. Причем в ряде случаев предложенный ускоренный метаалгоритм позволяет убирать логарифмические зазоры в оценках сложности (по сравнению с нижними оценками), имевшие место в предыдущих подходах.

2. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Рассмотрим следующую задачу (${{x}_{*}}$ – решение задачи):

(1)
$\mathop {min}\limits_{x \in {{\mathbb{R}}^{d}}} \{ F(x): = f(x) + g(x)\} ,$
где $f$ и $g$ – выпуклые функции.

Везде в дальнейшем под $\left\| {\, \cdot \,} \right\|$ будем понимать обычную евклидову норму в пространстве ${{\mathbb{R}}^{d}}$,

${{D}^{k}}f(x){{[h]}^{k}} = \sum\limits_{{{i}_{1}},...,{{i}_{d}} \geqslant 0:\,\sum\nolimits_{j = 1}^d \,{{i}_{j}} = k} \,\frac{{{{\partial }^{k}}f(x)}}{{\partial x_{1}^{{{{i}_{1}}}}...\partial x_{d}^{{{{i}_{d}}}}}}h_{1}^{{{{i}_{1}}}} \cdot ... \cdot h_{d}^{{{{i}_{d}}}},$
$\left\| {{{D}^{k}}f(x)} \right\| = \mathop {max}\limits_{\left\| h \right\| \leqslant 1} \left\| {{{D}^{k}}f(x){{{[h]}}^{k}}} \right\|.$
Будем считать, что $f$ имеет липшицевы производные порядка $p$ ($p \in \mathbb{N}$):
(2)
$\left\| {{{D}^{p}}f(x) - {{D}^{p}}f(y)} \right\| \leqslant {{L}_{{p,f}}}\left\| {x - y} \right\|.$
Здесь и далее (см., например, (7)) можно считать, что $x,y \in {{\mathbb{R}}^{d}}$ принадлежат евклидову шару с центром в точке ${{x}_{ * }}$ и радиусом $O\left( {\left\| {{{x}_{0}} - {{x}_{*}}} \right\|} \right)$, где ${{x}_{0}}$ – точка старта (см. [6]).

Введем аппроксимацию рядом Тейлора функции $f$:

${{\Omega }_{p}}(f,x;y) = f(x) + \sum\limits_{k = 1}^p \,\frac{1}{{k!}}{{D}^{k}}f(x)\mathop {[y - x]}\nolimits^k ,\quad y \in {{\mathbb{R}}^{d}}.$
Заметим, что из (2) следует (см. [17]), что

(3)
$\left| {f(y) - {{\Omega }_{p}}(f,x;y)} \right| \leqslant \frac{{{{L}_{{p,f}}}}}{{(p + 1){\kern 1pt} !}}{{\left\| {y - x} \right\|}^{{p + 1}}}.$

Доказательство следующей теоремы см. в Приложении 1 (литературный обзор см. в [11]).

Algorithm 1.  Ускоренный Метаалгоритм (УМ) (УМ(${{x}_{0}}$, $f$, $g$, $p$, $H$, $k$))

1: Input: $p \in \mathbb{N}$, $f{\kern 1pt} :\;{{\mathbb{R}}^{d}} \to \mathbb{R}$, $g{\kern 1pt} :\;{{\mathbb{R}}^{d}} \to \mathbb{R}$, $H > 0$.

2: ${{A}_{0}} = 0,{{y}_{0}} = {{x}_{0}}$.

3: for $k = 0$ to $k = K - 1$

4:  Определить пару ${{\lambda }_{{k + 1}}} > 0$ и ${{y}_{{k + 1}}} \in {{\mathbb{R}}^{d}}$ из условий

$\frac{1}{2} \leqslant {{\lambda }_{{k + 1}}}\frac{{H{{{\left\| {{{y}_{{k + 1}}} - {{{\tilde {x}}}_{k}}} \right\|}}^{{p - 1}}}}}{{p!}} \leqslant \frac{p}{{p + 1}},$
    где

${{y}_{{k + 1}}} = \mathop {\operatorname{argmin} }\limits_{y \in {{\mathbb{R}}^{d}}} \left\{ {{{{\widetilde \Omega }}^{k}}(y): = {{\Omega }_{p}}(f,{{{\tilde {x}}}_{k}};y) + g(y) + \frac{H}{{(p + 1)!}}{{{\left\| {y - {{{\tilde {x}}}_{k}}} \right\|}}^{{p + 1}}}} \right\},$
${{a}_{{k + 1}}} = \frac{{{{\lambda }_{{k + 1}}} + \sqrt {\lambda _{{k + 1}}^{2} + 4{{\lambda }_{{k + 1}}}{{A}_{k}}} }}{2},\quad {{A}_{{k + 1}}} = {{A}_{k}} + {{a}_{{k + 1}}},$
${{\tilde {x}}_{k}} = \frac{{{{A}_{k}}}}{{{{A}_{{k + 1}}}}}{{y}_{k}} + \frac{{{{a}_{{k + 1}}}}}{{{{A}_{{k + 1}}}}}{{x}_{k}}.$

5:  ${{x}_{{k + 1}}}: = {{x}_{k}} - {{a}_{{k + 1}}}\nabla f({{y}_{{k + 1}}}) - {{a}_{{k + 1}}}\nabla g({{y}_{{k + 1}}})$.

6: end for

7: return ${{y}_{K}}$

Теорема 1. Пусть ${{y}_{k}}$ – выход алгоритма 1 УМ(${{x}_{0}}$, $f$, $g$, $p$, $H$, $k$) после $k$ итераций при $p \geqslant 1$ и $H \geqslant (p + 1){{L}_{{p,f}}}$. Тогда

(5)
$F({{y}_{k}}) - F({{x}_{*}}) \leqslant \frac{{{{c}_{p}}H{{R}^{{p + 1}}}}}{{{{k}^{{\tfrac{{3p + 1}}{2}}}}}},$
где ${{c}_{p}} = {{2}^{{p - 1}}}{{(p + 1)}^{{\tfrac{{3p + 1}}{2}}}}{\text{/}}p!$, $R = \left\| {{{x}_{0}} - x{\kern 1pt} *} \right\|$.

Более того, при $p \geqslant 2$ для достижения точности $\varepsilon $: $F({{y}_{k}}) - F({{x}_{ * }}) \leqslant \varepsilon $ на каждой итерации УМ вспомогательную задачу (4) придется перерешивать для подбора пары $({{\lambda }_{{k + 1}}},{{y}_{{k + 1}}})$ не более чем $O(\ln ({{\varepsilon }^{{ - 1}}}))$ раз.

Заметим, что приведенная выше теорема будет справедлива и при условии $H \geqslant 2{{L}_{{p,f}}}$ (независимо от $p \in \mathbb{N}$). Это выводится из (3). Условие $H \geqslant (p + 1){{L}_{{p,f}}}$ было использовано, поскольку оно гарантирует выпуклость вспомогательной подзадачи (4) (см. [17]). При этом условии и $g \equiv 0$ для $p = 1,2,3$ существуют эффективные способы решения вспомогательной задачи (4) (см. [17]). Для $p = 1$ существует явная формула для решения (4), для $p = 2,3$ сложность (4) такая же (с точностью до логарифмического по $\varepsilon $ множителя), как у итерации метода Ньютона (см. [17]).

Отметим, что вспомогательную задачу (4) не обязательно решать точно: достаточно (см. [11], [18]) найти точку $\mathop {\tilde {y}}\nolimits_{k + 1} $, удовлетворяющую условию

(6)
$\left\| {\nabla {{{\widetilde \Omega }}^{k}}({{{\tilde {y}}}_{{k + 1}}})} \right\| \leqslant \frac{1}{{4p(p + 1)}}\left\| {\nabla F({{{\tilde {y}}}_{{k + 1}}})} \right\|.$
Такая модификация приведет лишь к появлению множителя $12{\text{/}}5$ в правой части (5).

Будем говорить, что функция $F$ является $r$-равномерно выпуклой ($p + 1 \geqslant r \geqslant 2$) с константой ${{\sigma }_{r}} > 0$, если

(7)
$F(y) \geqslant F(x) + \langle \nabla F(x),y - x\rangle + \frac{{{{\sigma }_{r}}}}{r}{{\left\| {y - x} \right\|}^{r}},\quad x,y \in {{\mathbb{R}}^{d}}.$

В этом случае, используя [19]:

$F({{\tilde {y}}_{{k + 1}}}) - F({{x}_{*}}) \leqslant \frac{{r - 1}}{r}\mathop {\left( {\frac{1}{{{{\sigma }_{r}}}}} \right)}\nolimits^{\tfrac{1}{{r - 1}}} {{\left\| {\nabla F({{{\tilde {y}}}_{{k + 1}}})} \right\|}^{{\tfrac{r}{{r - 1}}}}},$
можно завязать критерий (6) на желаемую точностью (по функции) решения исходной задачи $\varepsilon $ (см. [11]): $\left\| {\nabla {{{\widetilde \Omega }}^{k}}({{{\tilde {y}}}_{{k + 1}}})} \right\| = O({{({{\epsilon }^{{r - 1}}}{{\sigma }_{r}})}^{{1/r}}})$.

Более того, для $p = 1$ приведенные здесь выкладки можно уточнить, подчеркнув тем самым, что сложность решения вспомогательной задачи может даже не зависеть от $\varepsilon $. Оказывается (см. [16]), что условие

(8)
$\left\| {{{{\tilde {y}}}_{{k + 1}}} - y_{{k + 1}}^{*}} \right\| \leqslant \frac{H}{{3H + 2L_{1}^{g}}}\left\| {{{{\tilde {x}}}_{k}} - y_{{k + 1}}^{*}} \right\|,$
где $y_{{k + 1}}^{ * }$ – точное решение задачи (4), а $L_{1}^{g}$ – константа Липшица градиента $\nabla g$, в теоретическом плане гарантирует то же, что и условие (6) при $p = 1$. А именно, теорема 1 останется верной с добавлением в правую часть (5) множителя $12{\text{/}}5$.

Отметим, что оценка скорости сходимости (5) с точностью до числового множителя ${{c}_{p}}$ не может быть улучшена для класса выпуклых задач (1) с липшицевой $p$-й производной и для широкого класса тензорных методов порядка $p$, описанном в [17]. При дополнительном предположении равномерной выпуклости $F$ оптимальный метод можно построить на базе УМ с помощью процедуры рестартов (см. [11]) (см. алгоритм 2).

Algorithm 2.  Рестартованный УМ(${{x}_{0}}$, $f$, $g$, $p$, $r$, ${{\sigma }_{r}}$, $H$, $k$)

1: Input: $r$-равномерно выпуклая функция $F = f + g:{{\mathbb{R}}^{d}} \to \mathbb{R}$ с константой ${{\sigma }_{r}}$ и УМ(${{x}_{0}}$, $f$, $g$, $p$, $H$, $K$).

2: ${{z}_{0}} = {{x}_{0}}$.

3: for$k = 0$ to $K$

4:  ${{R}_{k}} = {{R}_{0}} \cdot {{2}^{{ - k}}}$,

(9)
${{N}_{k}} = max\left\{ {\left\lceil {\mathop {\left( {\frac{{r{{c}_{p}}H{{2}^{r}}}}{{{{\sigma }_{r}}}}R_{k}^{{p + 1 - r}}} \right)}\nolimits^{\tfrac{2}{{3p + 1}}} } \right\rceil ,1} \right\}.$

5:  ${{z}_{{k + 1}}}: = {{y}_{{{{N}_{k}}}}}$, где ${{y}_{{{{N}_{k}}}}}$ – выход УМ(${{z}_{k}}$, $f$, $g$, $p$, $H$, ${{N}_{k}}$).

6: end for

7: return ${{z}_{K}}$

Теорема 2. Пусть ${{y}_{k}}$ – выход алгоритма 2 после $k$ итераций. Тогда если $H \geqslant (p + 1){{L}_{{p,f}}}$, ${{\sigma }_{r}} > 0$, то общее число вычислений (4) для достижения $F({{y}_{k}}) - F({{x}_{*}}) \leqslant \varepsilon $ будет:

$N = \tilde {O}\left( {\mathop {\left( {\frac{{H{{R}^{{p + 1 - r}}}}}{{{{\sigma }_{r}}}}} \right)}\nolimits^{\tfrac{2}{{3p + 1}}} } \right),$
где $\tilde {O}(\,)$ – означает то же самое, что $O(\,)$ с точностью до множителя $ln({{\varepsilon }^{{ - 1}}})$.

Все, что было сказано после теоремы 1, можно отметить и в данном случае.

3. ПРИЛОЖЕНИЯ

3.1. Ускоренные методы композитной оптимизации

Если не думать о сложности решения подзадачи (4), например, считать, что $g$ – какая-то простая функция и (4) решается по явным формулам (как, например, для задачи LASSO), то УМ описывает класс ускоренных методов (1-, 2-, 3-го, … порядков) композитной оптимизации (см. [1], [2], [6]). При этом функция $g$ не обязана быть гладкой. В общем случае в строчке 5 алгоритма 1 под $\nabla g({{y}_{{k + 1}}})$ следует понимать такой субградиент функции $g$ в точке ${{y}_{{k + 1}}}$, с которым субградиент правой части (4) равен (близок) к нулю (немного переписав метод, от последнего ограничения можно отказаться). Отметим, что при $p = 1$ необходимость в поиске параметра ${{\lambda }_{{k + 1}}}$ исчезает, что делает метод заметно проще.

3.2. Ускоренные проксимальные методы. Каталист

Если считать $p = 1$, a $f \equiv 0$, $H > 0$, то получится ускоренный проксимальный метод. Отличительная особенность такого метода (см. также [16]) от других известных ускоренных проксимальных методов заключается в том, что не требуется очень точно решать вспомогательную задачу. Критерий (8) и сильная (2-равномерная) выпуклость вспомогательной подзадачи (4) указывают на то, что сложность решения (8) может не зависеть от желаемой точности решения исходной задачи $\varepsilon $. Таким образом, не теряется логарифмический множитель при использовании такой проксимальной оболочки для ускорения различных неускоренных процедур. Собственно, последнее направление получило название Каталист (см. [4]). До настоящего момента идея (Каталист) использования ускоренной проксимальной оболочки для ‘обертывания’ неускоренных методов, решающих вспомогательную задачу (4) на каждой итерации (при должном выборе параметра $H$), являлась наиболее общей идеей разработки ускоренных методов для разных задач. Мы получаем Каталист просто как частный случай УМ. Примеры использования Каталист будут приведены в п. 3.4.

3.3. Разделение оракульных сложностей

Если считать, что для $g$ имеем ${{L}_{{p,g}}} < \infty $ (см. (2)) и на вспомогательную задачу (4) смотреть как на равномерно выпуклую достаточно гладкую задачу (с $f: = g$, $g(x): = {{\Omega }_{p}}\left( {f,{{{\tilde {x}}}_{k}};x} \right) + $ $ + \;\tfrac{{(p + 1){{L}_{{p,f}}}}}{{\left( {p + 1} \right)!}}{{\left\| {x - {{{\tilde {x}}}_{k}}} \right\|}^{{p + 1}}}$), то для решения (4), в свою очередь, можно использовать Рестартованный УМ c $H \simeq (p + 1){{L}_{{p,g}}}$. В случае, когда ${{L}_{{p,f}}} \leqslant {{L}_{{p,g}}}$ удается получить такие оценки сложности (см. [11], [3]) (см. теорему 1):

${{N}_{f}} = \tilde {O}\left( {\mathop {\left( {\tfrac{{{{L}_{{p,f}}}{{R}^{{p + 1}}}}}{\varepsilon }} \right)}\nolimits^{\tfrac{2}{{3p + 1}}} } \right)~--{\text{ число вызовов оракула для функции}}\;f,$
${{N}_{g}} = \tilde {O}\left( {\mathop {\left( {\tfrac{{{{L}_{{p,g}}}{{R}^{{p + 1}}}}}{\varepsilon }} \right)}\nolimits^{\tfrac{2}{{3p + 1}}} } \right)~--{\text{ число вызовов оракула для функции}}\;g.$
Вызов оракула подразумевает вычисление (старших) производных до порядка $p$ включительно. Таким образом, число вызовов оракула для каждой из функции $f$, $g$ является квазиоптимальным, т.е. оптимальным с точностью до логарифмического (от желаемой точности по функции) множителя. Аналогичные оценки можно получить и в $r$-равномерно ($r \geqslant 2$) выпуклом случае (см. п. 3.4).

Заметим, что при $p = 1$ внутреннюю задачу (4) не обязательно решать Рестартованным УМ. Можно использовать (ускоренные) покомпонентные и безградиентные методы, методы редукции дисперсии (см. [1], [3], [20]). Причем ускорение можно получить из базовых неускоренных вариантов этих методов с помощью УМ (см. п. 3.2). По сравнению с оболочкой, использованной в [10], УМ дает оценку сложности на логарифмический множитель лучше. Это следует из теоретического анализа и было подтверждено в экспериментах (см. [21]).

3.4. Ускоренные методы для седловых задач

Следуя, например, [9], [12], рассмотрим выпукло-вогнутую седловую задачу

(10)
$\mathop {min}\limits_{x \in {{\mathbb{R}}^{{{{d}_{x}}}}}} \{ F(x): = f(x) + \underbrace {\mathop {max}\limits_{y \in {{\mathbb{R}}^{{{{d}_{y}}}}}} \{ G(x,y) - h(y)\} }_{g(x) = G(x,y{\kern 1pt} *(x)) - h(y{\kern 1pt} *(x))}\} ,$
где $y{\kern 1pt} *(x) = argma{{x}_{{y \in {{\mathbb{R}}^{{{{d}_{y}}}}}}}}\{ G(x,y) - h(y)\} $. Будем считать, что $\nabla f,\;\nabla G,\;\nabla h$ являются соответственно ${{L}_{f}},\;{{L}_{G}},\;{{L}_{h}}$-липшицевыми. Также будем считать, что $f(x) + G(x,y)$ является ${{\mu }_{x}}$-сильно (2-равномерно) выпуклой по $x$, а $G(x,y) - h(y)$ является ${{\mu }_{y}}$-сильно (2-равномерно) вогнутой по $y$. Тогда $F(x)$ будет ${{\mu }_{x}}$-сильно выпуклой, а $\nabla g$ будет ${{L}_{g}} = ({{L}_{G}} + 2L_{G}^{2}{\text{/}}{{\mu }_{y}})$-липшицевым (см. [9], [12]).

Если считать, что доступен $\nabla g$, то внешнюю задачу (10) можно решать ускоренным слайдингом (например, в варианте УМ с $p = 1$, см. п. 3.3) за $\tilde {O}(\sqrt {{{L}_{f}}{\text{/}}{{\mu }_{x}}} )$ вычислений $\nabla f$ и $\tilde {O}(\sqrt {{{L}_{g}}{\text{/}}{{\mu }_{x}}} )$ вычислений $\nabla g$.

Чтобы приближенно посчитать $\nabla g(x) = {{\nabla }_{x}}G(x,y{\kern 1pt} *{\kern 1pt} (x))$, надо решить (с достаточной точностью) вспомогательную задачу в (10), т.е. найти с нужной точностью $y{\kern 1pt} *{\kern 1pt} (x)$. Это, в свою очередь, также можно сделать с помощью слайдинга (УМ с $p = 1$) за $\tilde {O}(\sqrt {{{L}_{h}}{\text{/}}{{\mu }_{y}}} )$ вычислений $\nabla h$ и $\tilde {O}(\sqrt {{{L}_{G}}{\text{/}}{{\mu }_{y}}} )$ вычислений ${{\nabla }_{y}}G$.

Резюмируя написанное, получаем, что исходную задачу (10) можно решить за $\tilde {O}(\sqrt {{{L}_{f}}{\text{/}}{{\mu }_{x}}} )$ вычислений $\nabla f$, $\tilde {O}(\sqrt {{{L}_{g}}{\text{/}}{{\mu }_{x}}} ) \simeq \tilde {O}\left( {\sqrt {L_{G}^{2}{\text{/}}({{\mu }_{x}}{{\mu }_{y}})} } \right)$ вычислений ${{\nabla }_{x}}G$, $\tilde {O}\left( {\sqrt {L_{G}^{3}{\text{/}}({{\mu }_{x}}\mu _{y}^{2})} } \right)$ вычислений ${{\nabla }_{y}}G$, $\tilde {O}\left( {\sqrt {{{L}_{h}}L_{G}^{2}{\text{/}}({{\mu }_{x}}\mu _{y}^{2})} } \right)$ вычислений $\nabla h$. Поменяв порядок взятия $min$ и $max$ аналогичным образом, можно прийти к оценкам $\tilde {O}(\sqrt {{{L}_{h}}{\text{/}}{{\mu }_{y}}} )$ вычислений $\nabla h$, $\tilde {O}\left( {\sqrt {L_{G}^{2}{\text{/}}({{\mu }_{x}}{{\mu }_{y}})} } \right)$ вычислений ${{\nabla }_{y}}G$, $\tilde {O}\left( {\sqrt {L_{G}^{3}{\text{/}}(\mu _{x}^{2}{{\mu }_{y}})} } \right)$ вычислений ${{\nabla }_{x}}G$, $\tilde {O}\left( {\sqrt {{{L}_{f}}L_{G}^{2}{\text{/}}(\mu _{x}^{2}{{\mu }_{y}})} } \right)$ вычислений $\nabla f$.

Оценки, полученные на число вычислений ${{\nabla }_{x}}G$ и $\nabla f$, в последнем случае не являются оптимальными (см. [12]). Чтобы улучшить данные оценки (сделать их оптимальными с точностью до логарифмических множителей (см. [12])), воспользуемся Каталистом (см. п. 3.2) (УМ, с $p = 1$, $H \gg {{\mu }_{x}}$, $f \equiv 0$, $g = F$, где $F$ определяется (10)). Если параметр метода $H$, то число итераций метода будет $\tilde {O}(\sqrt {H{\text{/}}{{\mu }_{x}}} )$ (см. теорему 2). На каждой итерации необходимо будет решать с должной точностью задачу вида (10), в которой ${{L}_{f}}: = {{L}_{f}} + H$, ${{\mu }_{x}}: = {{\mu }_{x}} + H \simeq H$. Таким образом, для решения внутренней седловой задачи потребуется $\tilde {O}(\sqrt {{{L}_{h}}{\text{/}}{{\mu }_{y}}} )$ вычислений $\nabla h$, $\tilde {O}\left( {\sqrt {L_{G}^{2}{\text{/}}(H{{\mu }_{y}})} } \right)$ вычислений ${{\nabla }_{y}}G$, $\tilde {O}\left( {\sqrt {L_{G}^{3}{\text{/}}({{H}^{2}}{{\mu }_{y}})} } \right)$ вычислений ${{\nabla }_{x}}G$, $\tilde {O}\left( {\sqrt {({{L}_{f}} + H)L_{G}^{2}{\text{/}}({{H}^{2}}{{\mu }_{y}})} } \right)$ вычислений $\nabla f$. Считая для наглядности ${{L}_{f}} \geqslant {{L}_{G}}$, выберем $H = {{L}_{G}}$. Тогда итоговые оценки на число вычислений соответствующих градиентов будут такие: $\tilde {O}(\sqrt {{{L}_{h}}{{L}_{G}}{\text{/}}({{\mu }_{x}}{{\mu }_{y}})} )$ вычислений $\nabla h$, $\tilde {O}\left( {\sqrt {L_{G}^{2}{\text{/}}({{\mu }_{x}}{{\mu }_{y}})} } \right)$ вычислений ${{\nabla }_{y}}G$, $\tilde {O}\left( {\sqrt {L_{G}^{2}{\text{/}}({{\mu }_{x}}{{\mu }_{y}})} } \right)$ вычислений ${{\nabla }_{x}}G$, $\tilde {O}\left( {\sqrt {{{L}_{f}}{{L}_{G}}{\text{/}}({{\mu }_{x}}{{\mu }_{y}})} } \right)$ вычислений $\nabla f$.

За счет использования УМ приведенная выше схема улучшает похожую схему рассуждений из [12] на логарифмический (по желаемой точности решения задачи) множитель, и обобщает ее на случай отличных от тождественного нуля функций $f$ и $h$.

Приведенная здесь схема рассуждений наглядно демонстрирует, как из одной универсальной схемы ускорения удается получить (‘собрать как в конструкторе’) оптимальный метод с точностью до логарифмического (по желаемой точности множителя (при $f \equiv 0$ и $h \equiv 0$ – только при этих условиях известны нижние оценки (см. [12])).

3.5. Сравнение с алгоритмом Монтейро–Свайтера

Следуя [22], рассмотрим задачу оптимизации

$\mathop {min}\limits_{x \in {{\mathbb{R}}^{n}}} \{ F(x): = \underbrace {log\left( {\sum\limits_{k = 1}^p \,exp\left( {\langle {{A}_{k}},x\rangle } \right)} \right)}_{ = f(x)} + \underbrace {\frac{1}{2}\left\| {Gx} \right\|_{2}^{2}}_{ = g(x)}\} ,$
где $n = 500$, $p = 20\,000$, $A$ – разреженная $p \times n$ матрица с коэффициентом разреженности $0.001$ (под коэффициентом разреженности в данном случае понимается отношение числа ненулевых элементов матрицы к общему числу ее элементов), чьи ненулевые элементы есть независимые одинаково распределенные случайные величины из равномерного распределения $\mathcal{U}( - 1,1)$, а матрица ${{G}^{2}}$ получается из следующего выражения:
${{G}^{2}} = \sum\limits_{i = 1}^n \,{{\lambda }_{i}}\tilde {e}_{i}^{ \top }{{\tilde {e}}_{i}},$
где $\sum\nolimits_{i = 1}^n \,{{\lambda }_{i}} = 1$ и ${{[{{\tilde {e}}_{i}}]}_{j}} \sim \mathcal{U}(1,2)$ для каждой пары $i,j$.

Здесь $f$ имеет липшицев градиент с константой Липшица:

${{L}_{f}} = \mathop {max}\limits_{i = 1,...,n} \left\| {{{A}^{{\left\langle k \right\rangle }}}} \right\|_{2}^{2},$
где через ${{A}^{{\left\langle k \right\rangle }}}$ обозначен $k$-й столбец матрицы $A$.

На примере данной задачи сравним работу ускоренных методов, полученных с помощью алгоритма Монтейро–Свайтера (см. [7]) ($L = 20{{L}_{f}}$) и с помощью УМ ($H = {{L}_{f}}$) при использовании для решения вспомогательной задачи покомпонентного градиентного метода Нестерова (ПГМ) (см. [23]) ($\beta = 1{\text{/}}2$).

На фиг. 1 покомпонентный метод, ускоренный с помощью алгоритма Монтейро–Свайтера, сравнивается с методом, ускоренным оболочкой УМ с различным числом итераций метода для решений вспомогательной задачи (${{K}_{{{\text{внутр}}}}} = k$ соответствует $kn$ итерациям покомпонентного метода), и быстрым градиентным методом (БГМ). Представлен трехмерный график зависимости величины $(F({{x}_{k}}) - F(x{\kern 1pt} *)){\text{/}}(F({{x}_{0}}) - F(x{\kern 1pt} *))$ (в log масштабе, $F(x{\kern 1pt} *)$ выбирается равным значению $F$ в точке, полученной после $25\,000$ итераций БГМ) от числа вычислений компонент градиентов $\nabla {{f}_{i}}$ и $\nabla {{g}_{i}}$, а также его двухмерные проекции. Так как некоторые методы требуют вычисления полного значения градиента ($\nabla f$ или $\nabla g$), обращения к оракулам в таком случае учитываются с весом ${{t}_{1}}{\text{/}}{{t}_{2}} \approx 2.5$, где ${{t}_{1}}$ – среднее время вычисления полного градиента, ${{t}_{2}}$ – среднее время вычисления одной компоненты. Как можно видеть из графиков, число обращений к оракулу $\nabla {{f}_{i}}$ ускоренного с помощью оболочки УМ метода меньше, чем у быстрого градиентного метода. Кроме того, оболочка УМ позволяет значительно сократить число обращений к оракулу $\nabla {{g}_{i}}$ по сравнению с алгоритмом Монтейро–Свайтера.

Фиг. 1.

Зависимость величины $(F({{x}_{k}}) - F(x{\kern 1pt} *)){\text{/}}(F({{x}_{0}}) - F(x{\kern 1pt} *))$ (в log масштабе) от числа вычислений компонент градиентов $\nabla {{f}_{i}}$ и $\nabla {{g}_{i}}$. Двухмерные проекции.

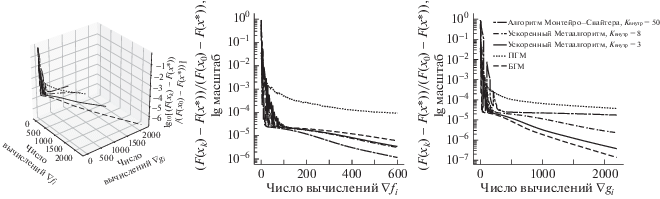
На фиг. 2 сравнивается работа методов в зависимости от времени работы и числа итераций внутреннего метода. Как видно на фиг. 2, ускоренный с помощью оболочки УМ метод сходится по времени работы с большей скоростью, чем метод, ускоренный с помощью алгоритма Монтейро–Свайтера, а также с большей скоростью, чем быстрый градиентный метод.

Фиг. 2.

Зависимость величины $(F({{x}_{k}}) - F(x{\kern 1pt} *)){\text{/}}(F({{x}_{0}}) - F(x{\kern 1pt} *))$ (в log масштабе) от времени работы и числа итераций внутреннего метода.

4. ВОЗМОЖНЫЕ ОБОБЩЕНИЯ

Приводимые выше конструкции существенным образом базируются на том, что рассматриваются задачи безусловной оптимизации и используется евклидова норма. На данный момент открытым остается вопрос о перенесении приведенных в статье результатов на задачи безусловной оптимизации с заменой евклидовой нормы на дивергенцию Брэгмана (см. [1], [5]). Тем более открытым остается вопрос об использовании других (более общих) моделей в построении мажоранты целевой функции (3) (см. [1]).

В [24] было подмечено (в том числе и в модельной общности), что для получения оптимальных версий ускоренных алгоритмов для задач стохастической оптимизации нужно уметь оценивать, как накапливается малый шум в градиенте в таких методах. Таким образом, строятся ускоренные стохастические градиентные методы на базе ускоренных не стохастических (детерминированных) и конструкции, названной минибатчингом (замена градиента в детерминированном методе его оценкой, построенной на базе стохастических градиентов). Насколько нам известно, для тензорных методов вопрос построения ускоренных методов для задач стохастической оптимизации остается открытым. В частности, не известен ответ на такой вопрос: верно ли, что для задач сильно выпуклой стохастической оптимизации требования к точности аппроксимации старших производных с помощью минибатчинга снижаются по мере роста порядка производных, как это имеет место в невыпуклом случае (см. [25])? Для ответа на этот вопрос для тензорных методов также как и для градиентных $p = 1$ может пригодиться анализ чувствительности исследуемых методов к неточности в вычислении производных. Некоторый задел в этом направлении уже имеется (см. [26]). В частности, при $p = 1$ УМ демонстрирует стандартное для ускоренных методов накопление неточностей в градиенте (см. [24]).

Из статьи может показаться, что для безусловных достаточно гладких задач выпуклой оптимизации предлагаемый в статье подход дает возможность всегда строить “оптимальные” методы. На самом деле это не совсем так. Во-первых, построение оптимальных методов даже на базе одного только УМ может быть совсем не простой задачей, как показывает пример из п. 3.4. Во-вторых, оговорка “с точностью до логарифмических множителей” весьма существенна. В частности, до сих пор остается открытым вопрос о том, устраним ли логарифмический мультипликативный зазор (по желаемой точности решения задачи по функции) между нижними оценками и тем, что дает УМ и другие ускоренные тензорные методы ($p \geqslant 2$) (см. теорему 1). В-третьих, упомянутые нижние оценки были получены для класса крыловских методов (для тензорных методов чуть иначе (см. [17])), однако, предлагаемая оболочка УМ в некоторых вариантах ее использования, в том числе в проксимальном варианте (Каталист) (см. п. 3.2), выводит из класса допустимых методов, для которого были полученые нижние оценки.

Список литературы

  1. Гасников А.В. Современные численные методы оптимизации. Метод универсального градиентного спуска. М.: МФТИ, 2018.

  2. Nesterov Yu. Lectures on convex optimization. V. 137. Berlin, Germany: Springer, 2018.

  3. Lan G. Lectures on optimization. Methods for Machine Learning // https://pwp.gatech.edu/guanghui-lan/publications/

  4. Lin H., Mairal J., Harchaoui Z. Catalyst acceleration for first-order convex optimization: from theory to practice // J. Machine Learning Res. 2017. V. 18. No. 1. P. 7854–7907.

  5. Doikov N., Nesterov Yu. Contracting proximal methods for smooth convex optimization // arXiv:1912.07972.

  6. Gasnikov A., Dvurechensky P., Gorbunov E., Vorontsova E., Selikhanovych D., Uribe C.A., Jiang B., Wang H., Zhang S., Bubeck S., Jiang Q. Near  Optimal  Methods for Minimizing Convex Functions with Lipschitz $p$-th Derivatives // Proceed. Thirty-Second Conf. Learning Theory. 2019. P. 1392–1393.

  7. Monteiro R.D.C., Svaiter B.F. An accelerated hybrid proximal extragradient method for convex optimization and its implications to second-order methods // SIAM J. Optimizat. 2013. V. 23. № 2. P. 1092–1125.

  8. Nesterov Yu. Inexact Accelerated High-Order Proximal-Point Methods // CORE Discussion paper 2020/8.

  9. Alkousa M., Dvinskikh D., Stonyakin F., Gasnikov A. Accelerated methods for composite non-bilinear saddle point problem // arXiv:1906.03620.

  10. Ivanova A., Gasnikov A., Dvurechensky P., Dvinskikh D., Tyurin A., Vorontsova E., Pasechnyuk D. Oracle Complexity Separation in Convex Optimization // arXiv:2002.02706

  11. Kamzolov D., Gasnikov A., Dvurechensky P. On the optimal combination of tensor optimization methods // arXiv:2002.01004

  12. Lin T., Jin C., Jordan M. Near-optimal algorithms for minimax optimization // arXiv:2002.02417.

  13. Gasnikov A., Dvurechensky P., Gorbunov E., Vorontsova E., Selikhanovych D., Uribe C.A. Optimal Tensor Methods in Smooth Convex and Uniformly ConvexOptimization // Proc. Thirty-Second Conf. Learning Theory. 2019. P. 1374–1391.

  14. Bubeck S., Jiang Q., Lee Y.T., Li Y., Sidford A. Near-optimal method for highly smooth convex optimization // Proc. Thirty-Second Conf. Learning Theory. 2019. P. 492–507.

  15. Jiang B., Wang H., Zhang S. An optimal high-order tensor method for convex optimization // Proc. Thirty-Second Conf. Learning Theory. 2019. P. 1799–1801.

  16. Ivanova A., Grishchenko D., Gasnikov A., Shulgin E. Adaptive Catalyst for smooth convex optimization // arXiv:1911.11271

  17. Nesterov Yu. Implementable tensor methods in unconstrained convex optimization // Math. Program. 2019. P. 1–27.

  18. Kamzolov D., Gasnikov A. Near-Optimal Hyperfast Second-Order Method for convex optimization and its Sliding // arXiv:2002.09050

  19. Grapiglia G.N., Nesterov Yu. On inexact solution of auxiliary problems in tensor methods for convex optimization // arXiv:1907.13023

  20. Dvurechensky P., Gasnikov A., Tiurin A. Randomized Similar Triangles Method: A unifying framework for accelerated randomized optimization methods (Coordinate Descent, Directional Search, Derivative-Free Method) // arXiv:1707.08486

  21. Ссылка: исходный код экспериментов на GitHub https://github.com/dmivilensky/composite-accelerated-method

  22. Spokoiny V., Panov M. Accuracy of Gaussian approximation in nonparametric Bernstein–von Mises Theorem // arXiv preprint arXiv:1910.06028. 2019.

  23. Nesterov Yu., Stich S.U. Efficiency of the accelerated coordinate descent method on structured optimization problems // SIAM Journal on Optimization. 2017. T. 27. №. 1. C. 110–123.

  24. Dvinskikh D., Tyurin A., Gasnikov A., Omelchenko S. Accelerated and nonaccelerated stochastic gradient descent with model conception // arXiv:2001.03443

  25. Lucchi A., Kohler J. A Stochastic Tensor Method for Non-convex Optimization // arXiv:1911.10367

  26. Baes M. Estimate sequence methods: extensions and approximations // Inst.r Operat. Res. ETH, Zürich, Switzerland, 2009.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал