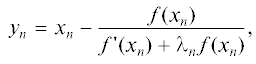1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 1, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 1, стр. 32-46

Об оптимальном выборе параметров в двухточечных итерационных методах решения нелинейных уравнений

Т. Жанлав 1, *, Х. Отгондорж 1, 2, **

1 Институт математики и информационных технологий, Монгольская Академия Наук
13330 Улан-батор, Монголия

2 Факультет Прикладных Наук, Монгольский Государственный Университет Науки и Технологии
14191 Улан-батор, Монголия

* E-mail: tzhanlav@yahoo.com
** E-mail: otgondorj@gmail.com

Поступила в редакцию 05.11.2019
После доработки 07.07.2020
Принята к публикации 18.09.2020

Полный текст (PDF)

Аннотация

Разрабатывается новый оптимальный двухпараметрический класс итерационных методов без производных с применением к итерациям типа Хансена–Патрика. Посредством самоускоряющихся параметров мы также получаем новые более высокого порядка методы с памятью. Впервые мы находим точные аналитические формулы для оптимального значения параметров. Увеличение порядка сходимости с $4$ до $7$ достигается без каких-либо дополнительных вычислений. Таким образом, предлагаемые методы с памятью обладают очень высокой вычислительной эффективностью. Численные примеры и сравнения с некоторыми существующими методами включены для подтверждения теоретических результатов и высокой вычислительной эффективности. Библ. 14. Табл. 6.

Ключевые слова: нелинейные уравнения, двухточечные итерации, методы с памятью, оптимальные методы.

1. ВВЕДЕНИЕ

В численном анализе и инженерных приложениях часто требуется решить нелинейное уравнение вида $f(x) = 0$, где $f:D \subset R \to R$ – скалярная функция, определенная на открытом интервале $D$. Основными методами решения такого уравнения являются метод Ньютона, заданный (см. [1] и так далее) ${{x}_{{n + 1}}} = {{x}_{n}} - \tfrac{{f({{x}_{n}})}}{{f{\kern 1pt} '({{x}_{n}})}}$, $n \geqslant 0$, и метод Стеффенсена [13], заданный

${{x}_{{n + 1}}} = {{x}_{n}} - \tfrac{{f{{{({{x}_{n}})}}^{2}}}}{{f({{x}_{n}} + f({{x}_{n}})) - f({{x}_{n}})}},\quad n \geqslant 0.$

В последние годы было предложено много итерационных методов более высокого порядка [1]–[6], в которых была введена концепция увеличения порядка сходимости. Достоинство таких методов заключается в том, что они быстро сходятся к требуемым решениям. Однако с увеличением порядка итеративного метода увеличивается количество функциональных вычислений на каждом шаге. Недавно исследователи предложили несколько двухпараметрических простых двухшаговых методов с памятью и без памяти [2], [8], [13], [14]. Авторы этих работ использовали символьные вычисления для получения порядка сходимости и уравнения ошибки. Такая процедура существенно облегчает громоздкие выкладки. Так, в полученном уравнении ошибки присутствуют параметры итерации. Удачные выборы этих параметров позволяют не только повышать порядок сходимости, но и построить новые итерационные методы с памятью. Основная цель данной работы – найти оптимальный выбор параметров ${{\tau }_{n}}$ и $\gamma $, $\lambda $ в двухточечных итерационных методах. Мы получили аналитические формулы для $\gamma $, $\lambda $ без использования метода символьных вычислений.

В разд. 2 мы получаем оптимальные двухточечные итерации Хансена–Патрика без производных. В разд. 3 мы предлагаем семейство двух параметрических оптимальных итераций и доказываем теорему о локальной сходимости. В разд. 4 мы предлагаем новые двухточечные итерации как с памятью, так и без памяти. В разд. 5 мы представляем результаты численных экспериментов, которые подтверждают теоретический вывод о порядке сходимости и сравнение с другими известными методами того же порядка сходимости.

2. ОПТИМАЛЬНЫЕ ДВУХТОЧЕЧНЫЕ ИТЕРАЦИИ

Рассмотрим двухточечные итерации вида

(2.1)
где ${{\tau }_{n}}$– параметр итерации. Известно, что оптимальный выбор параметра позволяет расширить область сходимости и увеличить скорость сходимости итераций (2.1). Достаточным условием сходимости четвертого порядка [3] является
(2.2)
${{\tau }_{n}} = 1 + {{\theta }_{n}} + 2\theta _{n}^{2} + O(f{{({{x}_{n}})}^{3}}),$
где
(2.3)
${{\theta }_{n}} = \frac{{f({{y}_{n}})}}{{f({{x}_{n}})}}.$
Условие (2.2) часто используется не только для проверки порядка сходимости итераций (2.1), но также для получения новых оптимальных методов. Для ясности мы напомним некоторые определения, нужные в дальнейшем. Многоточечные методы с порядком сходимости ${{2}^{{n - 1}}}$ называем оптимальным [10], где $n$ – количество вычислений функции на каждом шаге итерации. Еще одним из важных характеристик итерационных методов является их индекс эффективности $EI = {{\rho }^{{1/n}}}$, где $\rho $ – порядок сходимости. В качестве примера рассмотрим известное кубически сходящееся семейство итераций Лагерра (или итерации Хансена–Патрика) (2.1) с параметром ${{\tau }_{n}}$, заданным в виде
(2.4)
${{\tau }_{n}} = \frac{{\alpha + 1}}{{\alpha + {\text{sign}}(\alpha )\sqrt {1 - (\alpha + 1)\tfrac{{f{\kern 1pt} '{\kern 1pt} '({{x}_{n}})f({{x}_{n}})}}{{f{\kern 1pt} '{{{({{x}_{n}})}}^{2}}}}} }},\quad \alpha \ne - 1.$
Используя разложение Тейлора функции $f({{y}_{n}})$ в точке ${{x}_{n}}$, легко показать, что
(2.5)
${{\theta }_{n}} = \frac{{f{\kern 1pt} '{\kern 1pt} '({{x}_{n}})f({{x}_{n}})}}{{2f{\kern 1pt} '{{{({{x}_{n}})}}^{2}}}} + O(f{{({{x}_{n}})}^{2}}).$
Тогда (2.4) приводит к

(2.6)
${{\tau }_{n}} = \frac{{\alpha + 1}}{{\alpha \pm \sqrt {1 - 2(\alpha + 1){{\theta }_{n}} + O(f{{{({{x}_{n}})}}^{2}})} }},\quad \alpha \ne - 1.$

Пренебрегая малым членом $O(f{{({{x}_{n}})}^{2}})$ в (2.6), получаем

(2.7)
${{\tau }_{n}} = \frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{n}}} }},\quad \alpha \ne - 1.$
Кансел и др. в [2] рассматривали итерации (2.1) с параметром, определенным (2.7). Используя известное отношение
(2.8)
${{(1 - x)}^{\alpha }} = 1 - \alpha x + \frac{{\alpha (\alpha - 1)}}{2}{{x}^{2}} - \frac{{\alpha (\alpha - 1)(\alpha - 2)}}{6}{{x}^{3}} + \ldots ,\quad {\text{|}}x{\kern 1pt} {\text{|}} < 1,$
легко показать, что (2.7) имеет следующую асимптотику:
(2.9)
${{\tau }_{n}} = 1 + {{\theta }_{n}} + \frac{{\alpha + 3}}{2}\theta _{n}^{2} + O(\theta _{n}^{3}).$
Сравнение (2.9) с (2.2) показывает, что итерации (2.1) с параметром ${{\tau }_{n}}$, заданным (2.7), не являются оптимальными. Так как здесь требуются три вычисления функции $f({{x}_{n}}),$ $f({{y}_{n}})$ и $f{\kern 1pt} '({{x}_{n}})$ на каждом шаге итерации и порядок сходимости равен 3. Исключение составляет только $\alpha = 1$, т.е.
(2.10)
${{\tau }_{n}} = \frac{2}{{1 + \sqrt {1 - 4{{\theta }_{n}}} }},$
который удовлетворяет условию (2.2). Следует отметить, что с помощью ускоряющей процедуры для ${{\tau }_{n}}$ в [4] былa полученa итерация четвертого порядка (2.1) с ${{\tau }_{n}}$, заданным (2.10)). По этой причине значение, определенное (2.10), называется оптимальным. Отметим также, что в [6] была сделана попытка поиска оптимального параметра $\alpha $ семейства Лагерра с точки зрения сходимости. Как правило, итерация (2.1) с параметром ${{\tau }_{n}}$, заданным (2.7), имеет только третий порядок сходимости. Используя условие (2.2), можно найти оптимальную модификацию семейства Хансена–Патрика четвертого порядка. С этой целью мы ищем ${{\tau }_{n}}$ в виде
(2.11)
${{\tau }_{n}} = \frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{n}}} }}H({{\theta }_{n}}),\quad \alpha \ne - 1,$
где $H$– вещественная функция, удовлетворяющая условиям
(2.12)
$H(0) = 1,\quad H{\kern 1pt} '(0) = a,\quad H{\kern 1pt} '{\kern 1pt} '(0) = 2b.$
Находим $a$ и $b$ в (2.12) такими, что (2.11) удовлетворяет условию (2.2). Используя разложение Тейлора функций $H({{\theta }_{n}})$ и (2.9) в (2.11), получаем
(2.13)
${{\tau }_{n}} = 1 + (a + 1){{\theta }_{n}} + \left( {a + b + \frac{{\alpha + 3}}{2}} \right)\theta _{n}^{2} + \ldots \;.$
Сравнение (2.13) с (2.2) дает
$a = 0,\quad b = \frac{{1 - \alpha }}{2}.$
Таким образом, получаем оптимальный вариант семейства Хансена–Патрика (2.1) с параметром, определяемым в виде
(2.14)
${{\tau }_{n}} = \frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{n}}} }}\left( {1 + \frac{{1 - \alpha }}{2}\theta _{n}^{2}} \right),\quad \alpha \ne - 1.$
Когда $\alpha = 1$, (2.14) приводит к (2.10). Таким образом, показываем, что можно перейти от любых итераций третьего порядка (2.1) к оптимальным двухточечным итерациям, используя условие (2.2). Аналогично, легко показать, что итерации Хансена–Патрика имеют оптимальный четвертый порядок сходимости, если
(2.15)
${{\tau }_{n}} = \frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{n}}} }} + \frac{{1 - \alpha }}{2}\theta _{n}^{2}.$
Обратим внимание, что в [1] авторы предложили новую оптимальную модификацию четвертого порядка семейства Хансена–Патрика (2.1) с параметром, определяемым формулой
(2.16)
${{\tau }_{n}} = \frac{{\alpha + 1}}{{\alpha + \sqrt {\tfrac{{1 - (\alpha + 3){{\theta }_{n}} - ({{\alpha }^{2}} - 1)\theta _{n}^{2}}}{{1 + (\alpha - 1){{\theta }_{n}}}}} }},\quad \alpha \ne - 1.$
Несмотря на то что они оптимальны с индексом эффективности $EI = {{4}^{{1/3}}} \approx 1.587$, итерации (2.1) требуют вычисление производной первого порядка на каждом шаге итерации и поэтому не могут применяться к уравнениям с негладкими функциями. В [5] было дано правило для перехода итераций (2.1) в их оптимальный вариант без производных и наоборот. Согласно этому правилу легко получить вариант (2.1) без производной с помощью (2.16). Это имеет форму
(2.17)
$\begin{gathered} {{y}_{n}} = {{x}_{n}} - \frac{{f({{x}_{n}})}}{{{{\phi }_{n}}}}, \\ {{x}_{{n + 1}}} = {{x}_{n}} - {{\tau }_{n}}\frac{{f({{x}_{n}})}}{{{{\phi }_{n}}}}\quad {\text{или}}\quad \left( {{{x}_{{n + 1}}} = {{y}_{n}} - {{{\bar {\tau }}}_{n}}\frac{{f({{y}_{n}})}}{{{{\phi }_{n}}}}} \right), \\ \end{gathered} $
где
${{w}_{n}} = {{x}_{n}} + \gamma f({{x}_{n}}),\quad {{\phi }_{n}} = f[{{x}_{n}},{{w}_{n}}] = \frac{{f({{w}_{n}}) - f({{x}_{n}})}}{{{{w}_{n}} - {{x}_{n}}}},$
а также
(2.18)
${{\tau }_{n}} = 1 + {{\bar {\tau }}_{n}}{{\theta }_{n}},$
(2.19)
${{\bar {\tau }}_{n}} = \frac{1}{{{{\theta }_{n}}}}\left( {\frac{{\alpha + 1}}{{\alpha + \sqrt {\tfrac{{1 - (\alpha + 3){{\theta }_{n}} - ({{\alpha }^{2}} - 1)\theta _{n}^{2}}}{{1 + (\alpha - 1){{\theta }_{n}}}}} }} - 1} \right) + ({{\hat {d}}_{n}} - 2){{\theta }_{n}},$
(2.20)
${{\hat {d}}_{n}} = \frac{{2 + \gamma {{\phi }_{n}}}}{{1 + \gamma {{\phi }_{n}}}}.$
Аналогичным образом, используя достаточное условие сходимости четвертого порядка [7]
(2.21)
${{\bar {\tau }}_{n}} = 1 + {{\hat {d}}_{n}}{{\theta }_{n}} + O(f{{({{x}_{n}})}^{2}}),$
для (2.17) можно легко построить вариант итераций без производных (2.1), (2.14). Его можно записать как (2.17) с параметром
(2.22)
${{\bar {\tau }}_{n}} = \frac{1}{{{{\theta }_{n}}}}\left( {\frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{n}}} }}\left( {1 + \left( {{{{\hat {d}}}_{n}} - 2 - \frac{{\alpha - 1}}{2}} \right)\theta _{n}^{2}} \right) - 1} \right),\quad \alpha \ne - 1.$
Таким образом, имеем семейства итераций типа Хансена–Патрика без производных (2.17) с параметром, заданным двумя вариантами (2.19) и (2.22).

Замечание 1. В общем, мы можем рассмотреть следующую весовую функцию:

(2.23)
$W({{\theta }_{n}},\alpha ,m) = \frac{{\alpha + 1}}{{\alpha + \sqrt[m]{{1 - m(\alpha + 1){{\theta }_{n}}}}}} = 1 + {{\theta }_{n}} + \left( {1 - \frac{{1 - m}}{2}(\alpha + 1)} \right)\theta _{n}^{2} + \ldots $
в итерации (2.1). Мы называем $W({{\theta }_{n}},\alpha ,m)$ обобщенной весовой функцией Хансена–Патрика. Функция $W({{\theta }_{n}},\alpha ,2)$ приводит к (2.7). Легко показать, что итерационные методы (2.1) имеют оптимальный четвертый порядок сходимости, когда ${{\tau }_{n}}$ удовлетворяет одному из следующих условий:
(2.24)
${{\tau }_{n}} = W({{\theta }_{n}},\alpha ,m) + \left( {1 + \frac{{1 - m}}{2}(\alpha + 1)} \right)\theta _{n}^{2},\quad \alpha \ne - 1,$
и
(2.25)
${{\tau }_{n}} = W({{\theta }_{n}},\alpha ,m)H({{\theta }_{n}}),$
где $H$ – вещественная функция, удовлетворяющая следующим условиям:
(2.26)
$H(0) = 1,\quad H{\kern 1pt} '(0) = 0,\quad H{\kern 1pt} '{\kern 1pt} '(0) = 2\left( {1 + \frac{{1 - m}}{2}(\alpha + 1)} \right).$
Что касается $H$, можно выбрать, например, следующие функции:

$\begin{gathered} {{H}_{1}} = 1 + \left( {1 + \frac{{1 - m}}{2}(\alpha + 1)} \right)\theta _{n}^{2}, \\ {{H}_{2}} = \frac{1}{{1 - \left( {1 + \tfrac{{1 - m}}{2}(\alpha + 1)} \right)\theta _{n}^{2}}}, \\ {{H}_{3}} = \sqrt {1 + (2 + (1 - m)(\alpha + 1))\theta _{n}^{2}} . \\ \end{gathered} $

3. СЕМЕЙСТВО ДВУХПАРАМЕТРИЧЕСКИХ ОПТИМАЛЬНЫХ ИТЕРАЦИЙ, НЕ СОДЕРЖАЩИХ ПРОИЗВОДНЫЕ

Теперь рассмотрим двухпараметрическиe итерации без производных

(3.1)
$\begin{gathered} {{y}_{n}} = {{x}_{n}} - \frac{{f({{x}_{n}})}}{{{{\phi }_{n}} + \lambda f({{w}_{n}})}},\quad \lambda \in R, \\ {{x}_{{n + 1}}} = {{y}_{n}} - {{{\bar {\tau }}}_{n}}\frac{{f({{y}_{n}})}}{{{{\phi }_{n}} + \lambda f({{w}_{n}})}}, \\ \end{gathered} $
где ${{w}_{n}} = {{x}_{n}} + \gamma f({{x}_{n}}),$ $\gamma \in R,$ ${{\phi }_{n}} = f[{{x}_{n}},{{w}_{n}}] = \tfrac{{f({{w}_{n}}) - f({{x}_{n}})}}{{\gamma {{f}_{n}}}}$. Наша цель – найти ${{\bar {\tau }}_{n}}$ в (3.1) так, чтобы итерации (3.1) имели оптимальную сходимость четвертого порядка. Для этого сначала используем разложение Тейлора функции $f({{w}_{n}}) = f({{x}_{n}})(1 + \gamma {{\phi }_{n}})$ в точке ${{x}_{n}}$. Тогда мы получим
(3.2)
${{\phi }_{n}} = f{\kern 1pt} '({{x}_{n}})\left( {1 + \frac{{{{a}_{n}}}}{2}f{\kern 1pt} '({{x}_{n}})\gamma } \right) + O(f_{n}^{2}),\quad ({{f}_{n}}) = f({{x}_{n}}),$
где

(3.3)
${{a}_{n}} = \frac{{f{\kern 1pt} '{\kern 1pt} '({{x}_{n}})f({{x}_{n}})}}{{f{\kern 1pt} '{{{({{x}_{n}})}}^{2}}}}.$

Пусть ${{\eta }_{n}} = \tfrac{{f{\kern 1pt} '({{x}_{n}})}}{{{{\phi }_{n}}}}.$ Тогда, используя (3.2), получаем

(3.4)
${{\eta }_{n}} = \frac{1}{{1 + \tfrac{{{{a}_{n}}}}{2}f{\kern 1pt} '({{x}_{n}})\gamma + O(f_{n}^{2})}} = 1 - \frac{{{{a}_{n}}}}{2}f{\kern 1pt} '({{x}_{n}})\gamma + O(f_{n}^{2}).$
Разложение Тейлора $f({{y}_{n}})$ в точке ${{x}_{n}}$ дает
(3.5)
$f({{y}_{n}}) = f({{x}_{n}})\left( {1 - {{\eta }_{n}}\left( {1 - \frac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}} \right)} \right) + O(f_{n}^{2}) = f({{x}_{n}})\left( {1 - \left( {1 - \frac{{{{a}_{n}}}}{2}f{\kern 1pt} '({{x}_{n}})\gamma } \right)\left( {1 - \frac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}} \right)} \right) + O(f_{n}^{2}).$
Согласно (3.3), имеем $f({{y}_{n}}) = O(f{{({{x}_{n}})}^{2}})$. Аналогично, из второго шага в (3.1) получаем
(3.6)
$f({{x}_{{n + 1}}}) = \left( {1 - {{{\bar {\tau }}}_{n}}\frac{{f{\kern 1pt} '({{y}_{n}})}}{{{{\phi }_{n}} + \lambda f({{w}_{n}})}}} \right)f({{y}_{n}}) + O(f{{({{y}_{n}})}^{2}}).$
Из (3.5) и (3.6) ясно, что получим
(3.7)
$f({{x}_{{n + 1}}}) = O(f_{n}^{4}),$
если выбирать ${{\bar {\tau }}_{n}}$ так, чтобы
$1 - {{\bar {\tau }}_{n}}\frac{{f{\kern 1pt} '({{y}_{n}})}}{{{{\phi }_{n}} + \lambda f({{w}_{n}})}} = O(f_{n}^{2})$
или
(3.8)
${{\bar {\tau }}_{n}} = \frac{{{{\phi }_{n}} + \lambda f({{w}_{n}})}}{{f{\kern 1pt} '({{y}_{n}})}} + O(f_{n}^{2}).$
Разложение Тейлора $f{\kern 1pt} '({{y}_{n}})$ в точке ${{x}_{n}}$ дает
$f{\kern 1pt} '({{y}_{n}}) = f{\kern 1pt} '({{x}_{n}})\left( {1 - \frac{{f_{n}^{{''}}{{f}_{n}}}}{{f_{n}^{'}{{\phi }_{n}}\left( {1 + \tfrac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}} \right)}}} \right) + O(f_{n}^{2}),\quad f_{n}^{'} = f{\kern 1pt} '({{x}_{n}}).$
Используя (3.3) и (3.4) в последнем соотношении, мы получаем
(3.9)
$f{\kern 1pt} '({{y}_{n}}) = f_{n}^{'}(1 - {{a}_{n}}) + O(f_{n}^{2}).$
Подставляя (3.2) и (3.9) в (3.8), получаем
(3.10)
$\begin{gathered} {{{\bar {\tau }}}_{n}} = \frac{{1 + \tfrac{{{{a}_{n}}}}{2}f_{n}^{'}\gamma + \lambda \tfrac{{(1 + \gamma {{\phi }_{n}}){{f}_{n}}}}{{f_{n}^{'}}} + O(f_{n}^{2})}}{{1 - {{a}_{n}} + O(f_{n}^{2})}} = \left( {1 + \frac{{{{a}_{n}}}}{2}f_{n}^{'}\gamma + \frac{{\lambda (1 + \gamma {{\phi }_{n}}){{f}_{n}}}}{{f_{n}^{'}}}} \right)(1 + {{a}_{n}}) + O(f_{n}^{2}) = \\ \, = 1 + \left( {1 + \frac{{f_{n}^{'}\gamma }}{2}} \right){{a}_{n}} + \frac{{\lambda (1 + \gamma {{\phi }_{n}}){{f}_{n}}}}{{f_{n}^{'}}} + O(f_{n}^{2}). \\ \end{gathered} $
Согласно (3.3) и (3.4) имеем $f_{n}^{'} = {{\phi }_{n}} + O({{f}_{n}})$. Следовательно, можно заменить $f_{n}^{'}$ через ${{\varphi }_{n}}$ в (3.10) без потери точности. В результате имеем
(3.11)
${{\bar {\tau }}_{n}} = 1 + \frac{{2 + \gamma {{\phi }_{n}}}}{2}{{a}_{n}} + \frac{{\lambda (1 + \gamma {{\phi }_{n}}){{f}_{n}}}}{{{{\phi }_{n}}}} + O(f_{n}^{2}).$
Далее, используя разложение Тейлора $f({{y}_{n}})$ и (3.4), легко получить
(3.12)
$\begin{gathered} {{\theta }_{n}} = \frac{{{{a}_{n}}}}{2}(1 + \gamma f_{n}^{'}) + \frac{{\lambda (1 + \gamma {{\phi }_{n}})}}{{{{\phi }_{n}}}}f({{x}_{n}}) + O(f_{n}^{2}) = \frac{{{{a}_{n}}}}{2}(1 + \gamma {{\phi }_{n}}) + \frac{{\lambda (1 + \gamma {{\phi }_{n}})}}{{{{\phi }_{n}}}}f({{x}_{n}}) + O(f_{n}^{2}) = \\ \, = (1 + \gamma {{\varphi }_{n}})\left( {\frac{{{{a}_{n}}}}{2} + \lambda \frac{{f({{x}_{n}})}}{{{{\phi }_{n}}}}} \right) + O(f_{n}^{2}). \\ \end{gathered} $
Отсюда мы находим
(3.13)
$\frac{{{{a}_{n}}}}{2} = \frac{{{{\theta }_{n}}}}{{1 + \gamma {{\phi }_{n}}}} - \frac{{\lambda f({{x}_{n}})}}{{{{\phi }_{n}}}} + O(f_{n}^{2}).$
Подставляя (3.13) в (3.11), получаем
(3.14)
${{\bar {\tau }}_{n}} = 1 + {{\hat {d}}_{n}}{{\theta }_{n}} - \frac{{\lambda f({{x}_{n}})}}{{{{\phi }_{n}}}} + O(f_{n}^{2}).$
Таким образом, мы можем сформулировать полученные результаты.

Теорема 1. Предположим, что функция $f:D \subset R \to R$ достаточно дифференцируема и имеет простой ноль $x{\kern 1pt} * \in D$. Пусть начальное приближение ${{x}_{0}}$ достаточно близко к $x{\kern 1pt} *$, а параметр ${{\bar {\tau }}_{n}}$ удовлетворяет условию (3.14). Тогда итерационные методы (3.1) имеют оптимальную сходимость четвертого порядка.

Кансал и соавт. в [2] предложили новое трехпараметрическое оптимальное семейство итераций типа Хансена–Патрика без производных

(3.15)
$\begin{gathered} {{y}_{n}} = {{x}_{n}} - \frac{{f({{x}_{n}})}}{{{{\phi }_{n}} + \lambda f({{w}_{n}})}}, \\ {{x}_{{n + 1}}} = {{y}_{n}} - {{{\bar {\tau }}}_{n}}\frac{{f({{y}_{n}})}}{{f[y,{{w}_{n}}] + \lambda f({{w}_{n}})}}, \\ \end{gathered} $
где
(3.16)
${{\bar {\tau }}_{n}} = \frac{1}{{{{\theta }_{n}}}}\left( {\frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{n}}} }} - 1} \right)H({{\theta }_{n}}),\quad \alpha \ne - 1.$
Здесь $H$ – вещественная весовая функция, удовлетворяющая условию
(3.17)
$H(0) = 1,\quad H{\kern 1pt} '(0) = - \frac{{\alpha + 1}}{2},\quad \left| {H{\kern 1pt} '{\kern 1pt} '(0)} \right| < \infty .$
Обратим внимание, что итерации (3.15) имеют различие в знаменателе во втором этапе по сравнению с (3.1). Используя легко проверяемое соотношение
(3.18)
$f[y,{{w}_{n}}] + \lambda f({{w}_{n}}) = ({{\phi }_{n}} + \lambda f({{w}_{n}}))\left( {1 - \frac{{{{\phi }_{n}}{{\theta }_{n}} - \lambda f({{w}_{n}})}}{{(1 + \gamma {{\phi }_{n}})(\phi + \lambda f({{w}_{n}}))}}} \right) + O(f_{n}^{2}),$
второй шаг в (3.15) можно переписать в виде
${{x}_{{n + 1}}} = {{y}_{n}} - {{\bar {\tau }}_{n}}\frac{{f({{y}_{n}})}}{{{{\phi }_{n}} + \lambda f({{w}_{n}})}},$
где
(3.19)
${{\bar {\tau }}_{n}} = \left( {1 + \frac{{{{\phi }_{n}}{{\theta }_{n}} - \lambda f({{w}_{n}})}}{{(1 + \gamma {{\phi }_{n}})(\phi + \lambda f({{w}_{n}}))}}} \right)\frac{1}{{{{\theta }_{n}}}}\left( {\frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{n}}} }} - 1} \right)H({{\theta }_{n}}),\quad \alpha \ne - 1.$
Нетрудно показать, что ${{\bar {\tau }}_{n}}$, заданный по формуле (3.19), удовлетворяет условию (3.14). То есть, доказываем, что итерации (3.15)–(3.17) имеют сходимость четвертого порядка без использования символических вычислений, используемых в [2]. Двухпараметрическая итерация (3.1) с ${{\bar {\tau }}_{n}}$, заданным (3.19), представляет новый вариант семейства итераций типа Хансена–Патрика без производной. Аналогично, используя формулу (3.18), легко показать, что двухпараметрические методы четвертого порядка без производных, приведенные в [8], [10], [13], удовлетворяют условию (3.14).

Пусть $\gamma = 0$ в (3.1). Тогда (3.1) приводит к итерациям с одним параметром

(3.20)
$\begin{gathered} {{y}_{n}} = {{x}_{n}} - \frac{{f({{x}_{n}})}}{{f{\kern 1pt} '({{x}_{n}}) + \lambda f({{x}_{n}})}}, \\ {{x}_{{n + 1}}} = {{y}_{n}} - {{{\bar {\tau }}}_{n}}\frac{{f({{y}_{n}})}}{{f{\kern 1pt} '({{x}_{n}}) + \lambda f({{x}_{n}})}}. \\ \end{gathered} $
По теореме 1 итерации (3.20) имеют оптимальную сходимость четвертого порядка, когда ${{\bar {\tau }}_{n}}$ определяется в виде
(3.21)
${{\bar {\tau }}_{n}} = 1 + 2{{\theta }_{n}} - \frac{{\lambda f({{x}_{n}})}}{{f{\kern 1pt} '({{x}_{n}})}} + O(f_{n}^{2}).$
Итерации (3.20) требуют трех функциональных вычислений: $f({{x}_{n}})$, $f({{y}_{n}})$ и $f{\kern 1pt} '({{x}_{n}})$. Индекс эффективности итераций составляет $EI = \sqrt[3]{4} \approx 1.587.$ Теперь попробуем найти оптимальное значение свободного параметра $\lambda $. Для этого сначала используем разложение Тейлора $f({{y}_{n}})$ в точке ${{x}_{n}}$ и соотношение (2.8). В результате имеем
(3.22)
$f({{y}_{n}}) = f{{({{x}_{n}})}^{2}}\left( {\frac{\lambda }{{f_{n}^{'}}} + \frac{{f_{n}^{{''}}}}{{2f_{n}^{{'2}}}} - \frac{{{{\lambda }^{2}}{{f}_{n}}}}{{f_{n}^{{'2}}}} - \frac{{\lambda {{f}_{n}}f_{n}^{{''}}}}{{f_{n}^{{'3}}}} - \frac{{f_{n}^{{'''}}{{f}_{n}}}}{{6f_{n}^{{'3}}}}} \right) + O(f_{n}^{4}).$
Это означает, что $f({{y}_{n}}) = O(f_{n}^{2})$ для любого $\lambda $. Если выбираем
(3.23)
$\lambda = {{\lambda }_{n}} = - \frac{{f_{n}^{{''}}}}{{2f_{n}^{'}}}$
в (3.22), то получаем $f({{y}_{n}}) = O(f_{n}^{3})$. Назовем значение ${{\lambda }_{n}}$, заданное по формуле (3.23), оптимальным в том смысле, что оно увеличивает порядок сходимости последовательности ${{y}_{n}}$ с двух до трех. При выборе (3.23) выражение (3.22) можно записать в виде
(3.24)
$f({{y}_{n}}) = f({{x}_{n}})\left( {{{{\left( {\frac{{{{a}_{n}}}}{2}} \right)}}^{2}} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}}} \right) + O(f_{n}^{4}).$
Отсюда следует, что
${{\theta }_{n}} = {{\left( {\frac{{{{a}_{n}}}}{2}} \right)}^{2}} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}} + O(f_{n}^{3}),$
что подразумeвает
(3.25)
$\frac{{f_{n}^{{'''}}f_{n}^{2}}}{{f_{n}^{{'3}}}} = \frac{3}{2}a_{n}^{2} - 6{{\theta }_{n}} + O(f_{n}^{3}).$
Теперь рассмотрим разложение Тейлора $f({{x}_{{n + 1}}})$ в точке ${{y}_{n}}$:
(3.26)
$f({{x}_{{n + 1}}}) = f({{y}_{n}})\left( {1 - \frac{{f{\kern 1pt} '({{y}_{n}})}}{{f{\kern 1pt} '({{x}_{n}})}}{{{\bar {\tau }}}_{n}}\left( {1 - \frac{{\lambda {{f}_{n}}}}{{f_{n}^{'}}}} \right)} \right) + O(f{{({{y}_{n}})}^{2}}).$
Выше было показано, что $f({{y}_{n}}) = O(f_{n}^{3})$ при выборе (3.23). Следовательно, из (3.26) ясно, что
(3.27)
$f({{x}_{{n + 1}}}) = O(f{{({{x}_{n}})}^{6}}),$
если мы выберем ${{\bar {\tau }}_{n}}$ такой, что
$1 - \frac{{f{\kern 1pt} '({{y}_{n}})}}{{f{\kern 1pt} '({{x}_{n}})}}{{\bar {\tau }}_{n}}\left( {1 - \frac{{\lambda {{f}_{n}}}}{{f_{n}^{'}}}} \right) = O(f_{n}^{3})$
или
(3.28)
${{\bar {\tau }}_{n}} = \frac{1}{{1 - \tfrac{{\lambda {{f}_{n}}}}{{f_{n}^{'}}}}}\frac{{f{\kern 1pt} '({{x}_{n}})}}{{f{\kern 1pt} '({{y}_{n}})}} + O(f_{n}^{3}).$
Используя разложение Тейлора $f{\kern 1pt} '({{y}_{n}})$ в точке ${{x}_{n}}$, легко показать, что
$f{\kern 1pt} '({{y}_{n}}) = f{\kern 1pt} '({{x}_{n}})\left( {1 - {{a}_{n}} - \frac{{a_{n}^{2}}}{2} + \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{2f_{n}^{{'3}}}}} \right) + O(f_{n}^{3}).$
Учитывая (3.25), получаем
(3.29)
$\frac{{f{\kern 1pt} '({{x}_{n}})}}{{f{\kern 1pt} '({{y}_{n}})}} = \frac{1}{{1 - {{a}_{n}} + a_{n}^{2}{\text{/}}4 - 3{{\theta }_{n}} + O(f_{n}^{3})}} = 1 + {{a}_{n}} + \frac{{3a_{n}^{2}}}{4} + 3{{\theta }_{n}} + O(f_{n}^{3}).$
Подставив (3.23) и (3.29) в (3.28), получим
(3.30)
${{\bar {\tau }}_{n}} = 1 + \frac{{{{a}_{n}}}}{2} + \frac{{a_{n}^{2}}}{4} + 3{{\theta }_{n}} + O(f_{n}^{3}).$
Это означает, что соотношение (3.27) выполняется при выборах (3.30) и (3.23). Таким образом, верна

Теорема 2. Предположим, что функция $f:D \subset R \to R$ достаточно дифференцируема и имеет простой ноль $x{\kern 1pt} * \in D$. Пусть начальное приближение ${{x}_{0}}$ достаточно близко к $x{\kern 1pt} *$, а параметры ${{\lambda }_{n}}$ и ${{\bar {\tau }}_{n}}$ удовлетворяют условиям (3.23) и (3.30). Тогда итерационные методы (3.20) имеют сходимость шестого порядка.

На основе оптимального выбора параметров ${{\lambda }_{n}}$ и ${{\bar {\tau }}_{n}}$ можно построить новые сходящиеся итерации шестого порядка с памятью:

${{x}_{0}},\;{{\lambda }_{0}}\quad {\text{заданные}}.\quad {\text{Тогда}},$
${{\lambda }_{n}} = - \frac{{{{\Delta }_{n}}}}{{2f_{n}^{'}}},\quad n = 1,2, \ldots ,$
(3.31)
${{\bar {\tau }}_{n}} = 1 - \frac{{{{\lambda }_{n}}{{f}_{n}}}}{{f_{n}^{'}}} + {{\left( {\frac{{{{\lambda }_{n}}{{f}_{n}}}}{{f_{n}^{'}}}} \right)}^{2}} + 3{{\theta }_{n}},$
${{x}_{{n + 1}}} = {{y}_{n}} - {{\bar {\tau }}_{n}}\frac{{f({{y}_{n}})}}{{f{\kern 1pt} '({{x}_{n}}) + {{\lambda }_{n}}f({{x}_{n}})}},\quad n = 0,1, \ldots ,$
гдe

${{\Delta }_{n}} = \tfrac{{f({{x}_{n}} + \gamma f({{x}_{n}})) - 2f({{x}_{n}}) + f({{x}_{n}} - \gamma f({{x}_{n}}))}}{{{{{(\gamma f({{x}_{n}}))}}^{2}}}},\quad \gamma \in R{\backslash }\{ 0\} .$

Видно, что $f{\kern 1pt} '{\kern 1pt} '({{x}_{n}}) = {{\Delta }_{n}} + O(f_{n}^{2})$.

Замечание 2. Уравнение ошибки, полученное с помощью символьных вычислений, играет важную роль в создании новых методов (без производных) с памятью [1], [2], [8]–[13]. Например, с выбором

$\lambda = - {{c}_{2}} = - \frac{{f{\kern 1pt} '{\kern 1pt} '(x{\kern 1pt} *)}}{{2f{\kern 1pt} '(x{\kern 1pt} *)}},\quad \mathop {lim}\limits_{n \to \infty } {{\lambda }_{n}} = \lambda ,$
порядок сходимости методов увеличивается, в то время как на каждом шаге итерации мы имеем точную аналитическую формулу (3.23).

Аналогично, легко показать, что

(3.32)
$f({{x}_{{n + 1}}}) = O(f{{({{x}_{n}})}^{5}}),\quad {\text{если}}\quad {{\bar {\tau }}_{n}} = 1 + \frac{{{{a}_{n}}}}{2} + O(f_{n}^{2}).$
Следует отметить, что подобные с (3.20) методы были рассмотрены Вангом и соавт. в [8], где рассматривается
(3.33)
$\begin{gathered} {{y}_{n}} = {{x}_{n}} - \frac{{f({{x}_{n}})}}{{f{\kern 1pt} '({{x}_{n}}) + \lambda f({{x}_{n}})}}, \\ {{x}_{{n + 1}}} = {{y}_{n}} - \frac{{f({{y}_{n}})}}{{f{\kern 1pt} '({{x}_{n}}) + \gamma f({{x}_{n}})}}G({{\theta }_{n}}),\quad \lambda ,\gamma \in R, \\ \end{gathered} $
и показано, что (3.33) имеет сходимость четвертого порядка, когда
(3.34)
$\gamma = 2\lambda ,\quad G(0) = 1,\quad G{\kern 1pt} '(0) = 2,\quad \left| {G{\kern 1pt} '{\kern 1pt} '(0)} \right| < \infty .$
В [8] использовался самоускоряющийся параметр
(3.35)
${{\lambda }_{n}} = - \frac{{H_{m}^{{''}}({{x}_{n}})}}{{2H_{m}^{'}({{x}_{n}})}},\quad m = 2,3,4,$
в (3.33) и доказано, что порядок сходимости $R$ – итерационных методов (3.33) с параметром (3.35) с памятью составляет не менее $(5 + \sqrt {17} ){\text{/}}2 \approx 4.5616,$ $(5 + \sqrt {21} ){\text{/}}2 \approx 4.7913$ и $5$ соответственно. Здесь ${{H}_{m}}({{x}_{n}})$ – интерполяционный полином Эрмита со степенью $m = 2,3,4$, удовлетворяющий условию $H_{m}^{'}({{x}_{n}}) = f{\kern 1pt} '({{x}_{n}})$. Итерации (3.33) и (3.34) можно переписать как (3.20) с ${{\bar {\tau }}_{n}}$ вида
${{\bar {\tau }}_{n}} = \left( {1 - \frac{{\lambda {{f}_{n}}}}{{f_{n}^{'} + \lambda {{f}_{n}}}} + \cdots } \right)(1 + 2{{\theta }_{n}} + \cdots ) = 1 + \frac{{{{a}_{n}}}}{2} + O(f_{n}^{2}),$
т.е. ${{\bar {\tau }}_{n}}$ удовлетворяет условию (3.32). Если мы выберем ${{\lambda }_{n}}$ как в (3.31), тогда получим итерации с памятью:
${{x}_{0}},\;{{\lambda }_{0}}\quad {\text{заданные}}.\quad {\text{Тогда}},$
${{\lambda }_{n}} = - \frac{{{{\Delta }_{n}}}}{{2f_{n}^{'}}},\quad {{a}_{n}} = - \frac{{2{{\lambda }_{n}}{{f}_{n}}}}{{f_{n}^{'}}},\quad {{\bar {\tau }}_{n}} = 1 + \frac{{{{a}_{n}}}}{2},$
(3.36)
${{x}_{{n + 1}}} = {{y}_{n}} - {{\bar {\tau }}_{n}}\frac{{f({{y}_{n}})}}{{f{\kern 1pt} '({{x}_{n}}) + {{\lambda }_{n}}f({{x}_{n}})}},$
имеющие пятый порядок сходимости.

Замечание 3. Как уже упоминалось выше, при рассмотрении итераций типа Хансена–Патрика ${{\bar {\tau }}_{n}}$ определяется как (3.19).

4. НОВЫЕ ИТЕРАЦИОННЫЕ МЕТОДЫ С ПАМЯТЬЮ

Теперь мы приступим к созданию новых итерационных методов с памятью из (3.1), используя два самоускоряющихся параметра $\gamma $ и $\lambda $. Легко показать, что

(4.1)
${{w}_{n}} = {{x}_{n}} - \frac{{f({{x}_{n}})}}{{f{\kern 1pt} '({{x}_{n}})}},$
и
(4.2)
$f({{w}_{n}}) = \frac{{f_{n}^{{''}}f_{n}^{2}}}{{2f_{n}^{{'2}}}} + O(f_{n}^{3}),$
при выборе
(4.3)
$\gamma = {{\gamma }_{n}} = - \frac{1}{{f_{n}^{'}}}.$
Пусть $f({{x}_{n}}) \in {{C}^{4}}(I)$. Используя разложение Тейлора для $f({{w}_{n}})$ и (4.3), получаем
${{\phi }_{n}} = f_{n}^{'}\left( {1 - \frac{{{{a}_{n}}}}{2} + \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}}} \right) + O(f_{n}^{3}).$
Следовательно,
(4.4)
${{\eta }_{n}} = \frac{{f_{n}^{'}}}{{{{\phi }_{n}}}} = 1 + \frac{{{{a}_{n}}}}{2} + \frac{{a_{n}^{2}}}{4} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}} + O(f_{n}^{3}).$
Разложение Тейлора $f({{y}_{n}})$ в точке ${{x}_{n}}$ дает
(4.5)
$f({{y}_{n}}) = f({{x}_{n}})\left( {1 - \frac{{{{\eta }_{n}}}}{{1 + \tfrac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}}} + \frac{{{{a}_{n}}}}{2}{{{\left( {\frac{{{{\eta }_{n}}}}{{1 + \tfrac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}}}} \right)}}^{2}} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}}{{{\left( {\frac{{{{\eta }_{n}}}}{{1 + \tfrac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}}}} \right)}}^{3}}} \right) + O(f_{n}^{4}).$
В силу (4.2) и (4.4) имеем
(4.6)
$\begin{gathered} \frac{{{{\eta }_{n}}}}{{1 + \tfrac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}}} = \left( {1 + \frac{{{{a}_{n}}}}{2} + \frac{{a_{n}^{2}}}{4} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}} + \cdots } \right)\left( {1 - \frac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}} + \cdots } \right) = \\ \, = \left( {1 + \frac{{{{a}_{n}}}}{2} + \frac{{a_{n}^{2}}}{4} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}} - \frac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}} + O(f_{n}^{3})} \right). \\ \end{gathered} $
Используя (4.6) в (4.5), получаем
(4.7)
$\begin{gathered} f({{y}_{n}}) = f({{x}_{n}})\left( { - \frac{{{{a}_{n}}}}{2} - \frac{{a_{n}^{2}}}{4} + \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6\mathop {{{f}_{n}}}\nolimits^3 }} + \frac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}} + \frac{{{{a}_{n}}}}{2}(1 + {{a}_{n}}) - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}}} \right) + O(f_{n}^{4}) = \\ \, = f({{x}_{n}})\left( {\frac{{a_{n}^{2}}}{4} + \frac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}}} \right) + O(f_{n}^{4}). \\ \end{gathered} $
Из (4.7) ясно, что
(4.8)
$f({{y}_{n}}) = O(f_{n}^{4}),$
если
(4.9)
$\frac{{a_{n}^{2}}}{4} + \frac{{\lambda f({{w}_{n}})}}{{{{\phi }_{n}}}} = 0,$
или
(4.10)
${{\lambda }_{n}} = - \frac{{a_{n}^{2}{{\phi }_{n}}}}{{4f({{w}_{n}})}}.$
Используя (4.2) и (4.4) в (4.10), получаем
(4.11)
${{\lambda }_{n}} = - \frac{{f_{n}^{{''}}}}{{2f_{n}^{'}}},$
т.е. соотношение (4.8) выполняется при выборе (4.11). Далее из (3.6) и (4.8) ясно, что
(4.12)
$f({{x}_{{n + 1}}}) = O(f_{n}^{7}),$
если
(4.13)
${{\bar {\tau }}_{n}} = - \frac{{{{\phi }_{n}} + \lambda f({{w}_{n}})}}{{f{\kern 1pt} '({{y}_{n}})}} + O(f_{n}^{3})$
или
(4.14)
${{\bar {\tau }}_{n}} = \frac{{{{\phi }_{n}}}}{{f{\kern 1pt} '({{y}_{n}})}}\left( {1 - \frac{{a_{n}^{2}}}{4}} \right) + O(f_{n}^{3}).$
Разложение Тейлора $f{\kern 1pt} '({{y}_{n}})$ в точке ${{x}_{n}}$ дает
(4.15)
$f{\kern 1pt} '({{y}_{n}}) = f{\kern 1pt} '({{x}_{n}})\left( {1 - {{a}_{n}}\left( {\frac{{{{\eta }_{n}}}}{{1 - \tfrac{{a_{n}^{2}}}{4}}}} \right) + \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{2f_{n}^{{'3}}}}{{{\left( {\frac{{{{\eta }_{n}}}}{{1 - \tfrac{{a_{n}^{2}}}{4}}}} \right)}}^{2}}} \right) + O(f_{n}^{3}).$
Поскольку
(4.16)
$\frac{{{{\eta }_{n}}}}{{1 - \tfrac{{a_{n}^{2}}}{4}}} = \left( {1 + \frac{{{{a}_{n}}}}{2} + \frac{{a_{n}^{2}}}{4} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}} + \ldots } \right)\left( {1 + \frac{{a_{n}^{2}}}{4} + \ldots } \right) = 1 + \frac{{{{a}_{n}}}}{2} + \frac{{a_{n}^{2}}}{2} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}} + O(f_{n}^{3}),$
из (4.15) получаем
(4.17)
$f{\kern 1pt} '({{y}_{n}}) = f{\kern 1pt} '({{x}_{n}})\left( {1 - {{a}_{n}} - \frac{{a_{n}^{2}}}{2} + \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{2f_{n}^{{'3}}}}} \right) + O(f_{n}^{3}).$
Используя последнее выражение и (4.4) в (4.14), получаем
(4.18)
${{\bar {\tau }}_{n}} = 1 - \frac{{{{a}_{n}}}}{2} + \frac{3}{4}a_{n}^{2} + 2(1 + {{\gamma }_{n}}{{\phi }_{n}}) + O(f_{n}^{3}),$
где использована формула
(4.19)
$1 + {{\gamma }_{n}}{{\phi }_{n}} = \frac{{{{a}_{n}}}}{2} - \frac{{f_{n}^{{'''}}f_{n}^{2}}}{{6f_{n}^{{'3}}}} + O(f_{n}^{3}).$
Таким образом, можно сформулировать полученные результаты в виде теоремы.

Теорема 3. Предположим, что функция $f:D \subset R \to R$ достаточно дифференцируема и имеет простой ноль $x{\kern 1pt} * \in D$. Пусть начальное приближение ${{x}_{0}}$ достаточно близко к $x{\kern 1pt} *$, а параметры $\gamma $ и $\lambda $ в (3.1) выбираются как

$\gamma = {{\gamma }_{n}} = - \frac{1}{{f{\kern 1pt} '({{x}_{n}})}},\quad \lambda = {{\lambda }_{n}} = - \frac{{f{\kern 1pt} '{\kern 1pt} '({{x}_{n}})}}{{2f{\kern 1pt} '({{x}_{n}})}},$
и ${{\bar {\tau }}_{n}}$ определяется формулой (3.14) (либо (4.18)). Тогда итерационные методы (3.1) имеют порядок сходимости семь.

Таким образом, оптимальный выбор параметров позволяет увеличить порядок сходимости с $4$ до $7$. Однако значения $f{\kern 1pt} '({{x}_{n}})$ и $f{\kern 1pt} '{\kern 1pt} '({{x}_{n}})$ на практике недоступны, и такое ускорение сходимости не может быть реализовано. Но мы бы приблизили параметры ${{\gamma }_{n}}$ и ${{\lambda }_{n}}$. Они могут быть вычислены с использованием информации, доступной из текущей и предыдущей итераций. На основе вариантов (4.3) и (4.11) можно построить двухточечные итерации (без производных) с памятью и имеющие седьмой порядок сходимости:

${{x}_{0}},{{\lambda }_{0}},{{\gamma }_{0}}\quad {\text{заданные}}.\quad {\text{Тогда}}\quad {{w}_{0}} = {{x}_{0}} + {{\gamma }_{0}}f({{x}_{0}}),$
(4.20)
$\begin{gathered} {{\gamma }_{n}} = - \frac{1}{{N_{3}^{'}({{x}_{n}})}},\quad {{w}_{n}} = {{x}_{n}} + {{\gamma }_{n}}f({{x}_{n}}),\quad {{\lambda }_{n}} = - \frac{{N_{4}^{{''}}({{x}_{n}})}}{{2N_{4}^{'}({{x}_{n}})}},\quad n = 1,2, \ldots , \\ {{y}_{n}} = {{x}_{n}} - \frac{{f({{x}_{n}})}}{{{{\phi }_{n}} + {{\lambda }_{n}}f({{w}_{n}})}}, \\ \end{gathered} $
${{x}_{{n + 1}}} = {{y}_{n}} - {{\bar {\tau }}_{n}}\frac{{f({{y}_{n}})}}{{{{\phi }_{n}} + {{\lambda }_{n}}f({{w}_{n}})}},\quad n = 0,1, \ldots ,$
где ${{\bar {\tau }}_{n}}$ удовлетворяет условию (3.14). Здесь ${{N}_{3}}(t,{{x}_{n}},{{y}_{{n - 1}}},{{x}_{{n - 1}}},{{w}_{{n - 1}}})$ и ${{N}_{4}}(t,{{w}_{n}},{{x}_{n}},{{w}_{{n - 1}}},{{y}_{{n - 1}}},{{x}_{{n - 1}}})$– интерполяционные полиномы Ньютона третьей и четвертой степени, построенные через доступные узловые точки $({{x}_{n}},{{x}_{{n - 1}}},{{y}_{{n - 1}}},{{w}_{{n - 1}}})$ и $({{x}_{n}},{{w}_{n}},{{x}_{{n - 1}}},{{y}_{{n - 1}}},{{w}_{{n - 1}}})$ соответственно. Заметим, что в [13] получено вышеуказанное свойство при выборе

${{\lambda }_{n}} = - \frac{{N_{4}^{{''}}({{w}_{n}})}}{{2N_{4}^{'}({{w}_{n}})}}.$

5. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Чтобы продемонстрировать поведение сходимости и эффективность методов (3.1), (3.20), (3.36), (4.20), мы рассмотрим несколько числовых примеров и сделаем сравнения с существующими методами того же порядка. Расчеты были выполнены в Maple 18 с использованием арифметики с кратной точностью и с 1000 цифрами. Для численных расчетов мы использовали следующие функции [12], [13] и [14]:

$\begin{gathered} {{f}_{1}} = {{e}^{{{{x}^{3}} - x}}} - cos({{x}^{2}} - 1) + {{x}^{3}} + 1,\quad x{\kern 1pt} * = - 1, \\ {{f}_{2}} = {{e}^{{{{x}^{3}} - 3x}}}sinx + log({{x}^{2}} + 1),\quad x{\kern 1pt} * = 0, \\ {{f}_{3}} = ({{x}^{6}} + {{x}^{{ - 6}}} + 4)(x - 1)sin{{x}^{2}},\quad x{\kern 1pt} * = 1, \\ \end{gathered} $
и критерий остановки $\left| {{{x}_{n}} - x{\kern 1pt} *} \right| < {{10}^{{ - 60}}}$. Результаты расчетов приведены в табл. 1–6, где указаны числа итераций $(n)$, абсолютные погрешности $\left| {{{x}_{n}} - x{\kern 1pt} *} \right|$ и вычислительный порядок сходимости $(\rho )$, заданный по формуле

$\rho \approx \frac{{ln({\kern 1pt} \left| {{{x}_{n}} - x{\kern 1pt} *} \right|{\text{/}}\left| {{{x}_{{n - 1}}} - x{\kern 1pt} *} \right|{\kern 1pt} )}}{{ln({\kern 1pt} \left| {{{x}_{{n - 1}}} - x{\kern 1pt} *} \right|{\text{/}}\left| {{{x}_{{n - 2}}} - x{\kern 1pt} *} \right|{\kern 1pt} )}}.$
Таблица 1.  

${{f}_{1}} = {{e}^{{{{x}^{3}} - x}}} - cos({{x}^{2}} - 1) + {{x}^{3}} + 1$, ${{x}_{0}} = - 1.5,$ $x* = - 1$ [14]

Методы $n$ ${{\bar {\tau }}_{n}}$ $\left| {{{x}_{n}} - x{\kern 1pt} *} \right|$ $\rho $
(3.1) ($\lambda = - 0.1$, $\gamma = - 0.01$) 4 (3.14) 0.1014e–217 4.00
(3.1) ($\alpha = 1$, $\gamma = - 0.01$) 4 (3.19) 0.1544e–224 4.00
(3.20) ($\lambda = - 0.1$) 4 (3.21) 0.6919e–229 4.00
Dzunic [13] ($p = - 0.1$, $\gamma = - 0.01$, $g({{\theta }_{n}}) = 1 + {{\theta }_{n}}$) 4   0.4682e–222 4.00
Wang-Zhang [8] ($t = 8$, $\lambda = - 0.1$, $G({{\theta }_{n}}) = 1 + 2 * {{\theta }_{n}} + t * \theta _{n}^{2}$) 4   0.1974e–192 4.00
Kung-Traub [11] 4   0.9297e–173 4.00
Chebyshev-Halley [11] 4   0.5980e–175 4.00
Таблица 2.  

${{f}_{1}} = {{e}^{{{{x}^{3}} - x}}} - cos({{x}^{2}} - 1) + {{x}^{3}} + 1$, ${{x}_{0}} = - 1.5$, $x* = - 1$ [14]

Методы $n$ ${{\bar {\tau }}_{n}}$ $\left| {{{x}_{n}} - x{\kern 1pt} *} \right|$ $\rho $
(3.20) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$) 3 (3.21) 0.1735e–56 5.00
(3.20) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 3 (3.32) 0.7578e–99 5.00
(3.36) (${{\lambda }_{n}} = - {{\Delta }_{n}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 3   0.4079e–85 5.02
(3.33)–(3.35) [8] (${{\lambda }_{n}} = - H_{4}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 3   0.2404e–89 5.09
(3.20)  (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 3 (3.30) 0.6559e–176 6.00
(3.31) (${{\lambda }_{n}} = - {{\Delta }_{n}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 3   0.4538e–125 6.00
(3.1) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 3 (4.18) 0.3128e–93 7.00
(4.20) (${{\lambda }_{n}} = - N_{4}^{{''}}({{x}_{n}}){\text{/}}2N_{4}^{'}({{x}_{n}})$, ${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$) 3 (3.21) 0.4294e–162 7.06
Dzunic [13] (${{p}_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$), $g({{\theta }_{n}}) = 1 + {{\theta }_{n}}$ 3   0.1404e–157 7.06
Cordero [14] (${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$) 3   0.1114e–157 7.06
Kansal [2] (${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$), $\alpha = \beta = 1{\text{/}}2$ 3   0.1095e–100 7.08
Таблица 3.  

${{f}_{2}} = {{e}^{{{{x}^{3}} - 3x}}}sinx + log({{x}^{2}} + 1)$, ${{x}_{0}} = 1$, $x* = 0$ [12]

Методы $n$ ${{\bar {\tau }}_{n}}$ $\left| {{{x}_{n}} - x{\kern 1pt} *} \right|$ $\rho $
(3.1) ($\lambda = - 0.1$, $\gamma = - 0.01$) 4 (3.14) 0.1469e–82 4.00
(3.1) ($\alpha = 1$, $\gamma = - 0.01$) 4 (3.19) 0.6589e–68 3.99
(3.20) ($\lambda = - 0.1$) 4 (3.21) 0.3650e–83 4.00
Dzunic [13] ($p = - 0.1$, $\gamma = - 0.01$, $g({{\theta }_{n}}) = 1 + {{\theta }_{n}}$) 4   0.7008e–66 4.00
Wang-Zhang [8] ($t = 8$, $\lambda = - 0.1$, $G({{\theta }_{n}}) = 1 + 2 * {{\theta }_{n}} + t * \theta _{n}^{2}$) 5   0.7447e–204 4.00
Kung-Traub [11] 4   0.1469e–82 4.00
Chebyshev-Halley [11] 4   0.1975e–88 4.00
Таблица 4.  

${{f}_{2}} = {{e}^{{{{x}^{3}} - 3x}}}sinx + log({{x}^{2}} + 1)$, ${{x}_{0}} = 1$, $x* = 0$ [12]

Методы $n$ ${{\bar {\tau }}_{n}}$ $\left| {{{x}_{n}} - x{\kern 1pt} *} \right|$ $\rho $
(3.20) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$) 4 (3.21) 0.2170e–217 5.00
(3.20) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4 (3.32) 0.3916e–220 5.00
(3.36) (${{\lambda }_{n}} = - {{\Delta }_{n}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4   0.2326e–136 5.00
(3.33)–(3.35) [8] (${{\lambda }_{n}} = - H_{4}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4   0.2069e–122 5.00
(3.20)  (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4 (3.30) 0.3111e–233 6.00
(3.31) (${{\lambda }_{n}} = - {{\Delta }_{n}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4   0.2699e–291 6.00
(3.1) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4 (4.18) 0.1560e–119 7.00
(4.20) (${{\lambda }_{n}} = - N_{4}^{{''}}({{x}_{n}}){\text{/}}2N_{4}^{'}({{x}_{n}})$, ${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$) 4 (3.21) 0.3134e–416 7.00
Dzunic [13] (${{p}_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$), $g({{\theta }_{n}}) = 1 + {{\theta }_{n}}$ 4   0.3892e–330 6.99
Cordero [14] (${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$) 4   0.5524e–284 6.99
Kansal [2] (${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$), $\alpha = \beta = 1{\text{/}}2$ 4   0.8391e–293 6.98
Таблица 5.  

${{f}_{3}} = ({{x}^{6}} + {{x}^{{ - 6}}} + 4)(x - 1)sin{{x}^{2}}$, ${{x}_{0}} = 0.8$, $x* = 1$ [13]

Методы $n$ ${{\bar {\tau }}_{n}}$ $\left| {{{x}_{n}} - x{\kern 1pt} *} \right|$ $\rho $
(3.1) ($\lambda = - 0.1$, $\gamma = - 0.01$) 4 (3.14) 0.3589e–140 4.00
(3.1) ($\alpha = 1$, $\gamma = - 0.01$) 4 (3.19) 0.9036e–111 4.00
(3.20) ($\lambda = - 0.1$) 4 (3.21) 0.1007e–138 4.00
Dzunic [13] ($p = - 0.1$, $\gamma = - 0.01$, $g({{\theta }_{n}}) = 1 + {{\theta }_{n}}$) 4   0.4671e–130 4.00
Wang-Zhang [8] ($t = 8$, $\lambda = - 0.1$, $G({{\theta }_{n}}) = 1 + 2 * {{\theta }_{n}} + t * \theta _{n}^{2}$) 4   0.1552e–96 4.00
Kung-Traub [11] 4   0.2972e–132 4.00
Chebyshev-Halley [11] 4   0.2847e–118 4.00
Таблица 6.  

${{f}_{3}} = ({{x}^{6}} + {{x}^{{ - 6}}} + 4)(x - 1)sin{{x}^{2}}$, ${{x}_{0}} = 0.8$, $x* = 1$ [13]

Методы $n$ ${{\bar {\tau }}_{n}}$ $\left| {{{x}_{n}} - x{\kern 1pt} *} \right|$ $\rho $
(3.20) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$) 3 (3.21) 0.1344e–53 4.99
(3.20) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4 (3.32) 0.2239e–250 5.00
(3.36) (${{\lambda }_{n}} = - {{\Delta }_{n}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4   0.5113e–183 5.00
(3.33)–(3.35) [8] (${{\lambda }_{n}} = - H_{4}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4   0.1142e–213 5.00
(3.20)  (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4 (3.30) 0.2116e–259 6.00
(3.31) (${{\lambda }_{n}} = - {{\Delta }_{n}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 3   0.1080e–60 5.96
(3.1) (${{\lambda }_{n}} = - f_{n}^{{''}}{\text{/}}2f_{n}^{'}$, ${{\lambda }_{0}} = - 0.1$) 4 (4.18) 0.1802e–315 7.00
(4.20) (${{\lambda }_{n}} = - N_{4}^{{''}}({{x}_{n}}){\text{/}}2N_{4}^{'}({{x}_{n}})$, ${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$) 3 (3.21) 0.6532e–107 7.03
Dzunic [13] (${{p}_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$), $g({{\theta }_{n}}) = 1 + {{\theta }_{n}}$ 3   0.1364e–87 7.05
Cordero [14] (${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$) 3   0.8409e–80 7.04
Kansal [2] (${{\lambda }_{0}} = - 0.1$, ${{\gamma }_{0}} = - 0.01$), $\alpha = \beta = 1{\text{/}}2$ 3   0.9084e–72 7.02

Из табл. 1–6 видно, что результаты расчетов полностью подтверждают теоретический порядок сходимости, полученный в предыдущих разделах.

6. ВЫВОДЫ

Мы предлагаем новый класс оптимальных двухточечных итерационных методов, не содержащих производные, которые включают в себя два свободных параметра. Впервые мы нашли точные аналитические формулы для оптимальных значений этих параметров, что позволяет повышать порядок сходимости. На этой основе мы предлагаем новые итерационные методы с высоким порядком сходимости как с памятью, так и без памяти.

Список литературы

  1. Kansal M., Kanwar V., Bhatia S. New modifications of Hansen–Patrick’s family with optimal fourth and eighth orders of convergence // Appl. Math.Comput. 2015. V. 269. P. 507–519.

  2. Kansal M., Kanwar V., Bhatia S. Efficient derivative-free variants of Hansen-Patrick’s family with memory for solving nonlinear equations // Numer. Algor. 2016. V. 73. P. 1017–1036.

  3. Zhanlav T., Ulziibayar V., Chuluunbaatar O. Necessary and sufficient conditions for the convergence of two- and three-point Newton-type iterations // Comput. Math. Math. Phys. 2017. V. 57. P. 1090–1100.

  4. Zhanlav T., Chuluunbaatar O., Ulziibayar V. Accelerating the convergence of Newton-type iterations // J. Numer. Anal. Approx. Theory. 2017. V. 46. P. 162–180.

  5. Zhanlav T., Mijiddorj R., Otgondorj Kh. Constructive theory of designing optimal eighth-order derivative-free methods for solving nonlinear equations // AM. J. Comput. Math. 2020. V. 10. P. 100–117.

  6. Petković L.D., Petković M.S., Neta B. On optimal parameter of Laguerre’s family of zero-finding methods // Inter. Jourmal of Comput. Math. 2018. V. 95. 692–707.

  7. Zhanlav T., Chuluunbaatar O., Otgondorj Kh. A derivative-free families of optimal two-and three-point iterative methods for solving nonlinear equations // Comput. Math. Math. Phys. 2019. V. 59. P. 920–936.

  8. Wang X., Zhang T. A new family of Newton-type iterative methods with and without memory for solving nonlinear equations // Calcolo 2014. V. 51. P. 1–15.

  9. Wang X. A new accelerating technique applied to a variant of Cordero–Torregrosa method // J. Comput. Appl. Math. 2018. V. 330. P. 695–709.

  10. Petković M.S., Ilic S., Dzunić J. Derivative-free two-point methods with and without memory for solving nonlinear equations // Appl. Math. Comput. 2010. V. 217. P. 1887–1895.

  11. Argyros I.K., Kansal M., Kanwar V., Bajaj S. Higher-order derivative-free families of Chebyshev-Halley type methods with or without memory for solving nonlinear equations // Appl. Math. Comput. 2017. V. 315. P. 224–245.

  12. Lotfi T., Soleymani F., Ghorbanzadeh M., Assari P. On the construction of some tri-parametric iterative methods with memory // Numer. Algor. 2015. V. 70. P. 835–845.

  13. Dzunić J. On efficient two-parameter methods for solving nonlinear equations // Numer. Algor. 2013. V. 63. P. 549–569.

  14. Cordero A., Lotfi T., Bakhtiari P., Torregrosa J.R. An efficient two-parametric family with memory for nonlinear equations // Numer. Algor. 2015. V. 68. P. 323–335.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал