Журнал вычислительной математики и математической физики, 2021, T. 61, № 10, стр. 1715-1733
Отражение детонационной волны от плоскости симметрии внутри цилиндрической мишени для управляемого термоядерного синтеза
К. В. Хищенко 1, *, А. А. Чарахчьян 2, **
1 ОИВТ РАН
125412 Москва, ул. Ижорская 13, стр. 2, Россия
2 ВЦ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова 40, Россия
* E-mail: konst@ihed.ras.ru
** E-mail: chara@ccas.ru
Поступила в редакцию 02.02.2021
После доработки 14.03.2021
Принята к публикации 09.06.2021
Аннотация
Рассматривается осесимметричная задача о столкновении двух идущих навстречу одинаковых детонационных волн внутри предварительно сжатой мишени небольшого размера, состоящей из цилиндра с горючим в виде эквимолярной смеси дейтерия и трития, окруженного золотой оболочкой и зажигаемого с торцов пучком протонов. Изучается отражение возникающей нестационарной неплоской детонационной волны от плоскости симметрии. Обсуждаются зависимости от времени некоторых характеристик течения. Развита приближенная модель горения, позволяющая рассчитывать коэффициент выгорания горючего между отраженной детонационной волной и плоскостью симметрии после вынужденного прекращения двумерного расчета, в частности, из-за неустойчивости границы раздела горючего и оболочки. Изучена роль двух возможных механизмов развития неустойчивости границы раздела: ее импульсного ускорения детонационной волной (неустойчивость Рихтмайера–Мешкова) и высокоскоростного скольжения горючего вдоль границы раздела (неустойчивость Кельвина–Гельмгольца). Библ. 30. Фиг. 12. Табл. 2.
ВВЕДЕНИЕ
Современные исследования по управляемому инерциальному термоядерному синтезу ориентированы в основном на сферические мишени, так как на этом направлении есть надежда получить на создаваемых в настоящее время мощных лазерных установках выход термоядерной энергии, превышающий вложенную в мишень энергию. Привлекательной чертой цилиндрической мишени (цилиндр с термоядерным горючим, окруженный тяжелой оболочкой) является возможность получить незатухающую волну термоядерного горения, двигающуюся по холодному горючему вдоль оси мишени. Это позволяет, решив проблему зажигания небольшой мишени, имеющей небольшой коэффициент усиления энергии, увеличивать этот коэффициент, увеличивая размер мишени вдоль оси, что требует дополнительной энергии на сжатие мишени, но не на ее зажигание.
Остановимся на работах по цилиндрическим мишеням, в которых рассматривались волны термоядерного горения вдоль оси. В [1] рассматривается зажигание центральной части мишени, что моделируется заданием небольшой области с высокой температурой, примыкающей к плоскости симметрии задачи. Была продемонстрирована, в частности, возможность получения близкой к стационарной незатухающей детонационной волны.
В [2], [3] рассматривалась предварительно сжатая мишень (в соответствии с концепцией быстрого зажигания), которая зажигается с торца тем или иным драйвером. В [4]–[6] это был пучок тяжелых ионов. Получены близкие к стационарным детонационные волны и так называемые радиационные волны (см. [6]), основным механизмом распространения которых является нагрев холодного горючего высокочастотным излучением горячей плазмы.
В нашей работе [7] зажигающим драйвером является пучок протонов с глубиной прогрева горючего примерно в 10 раз меньше, чем для пучка тяжелых ионов. Было обнаружено, что возникающая после зажигания детонационная волна может со временем превратиться в близкую в стационарной безударную волну термоядерного горения, основным механизмом распространения которой является нелокальный нагрев $\alpha $-частицами, возникающими в реакции синтеза между ядрами дейтерия и трития (далее DT-реакции). Изучаются свойства такой волны, а также ее нестационарный предвестник, генерируемый высокочастотным излучением горячей плазмы. Близкие к стационарным радиационные волны в [7] нe обнаружены.
В настоящей работе рассматривается взаимодействие двух двигающихся навстречу детонационных волн, которые одновременно генерируются на противоположных торцах мишени одинаковыми зажигающими драйверами. Размер мишени выбирается сравнительно небольшим, для которого детонационная волна не успевает превратиться в безударную. Симметрия задачи позволяет рассматривать только половину мишени, которая ограничена плоскостью симметрии. В качестве зажигающего драйвера используется тот же пучок протонов, что и в [7].
Ранее нами рассматривалась аналогичная одномерная задача (см. [8]–[12]). Было показано, что при отражении детонационной волны от плоскости симметрии возникает волна, которая хорошо описывается точным решением уравнений гидродинамики из известного семейства (см. [13]). Это решение, которое можно легко получить непосредственно из уравнений гидродинамики, используется и в настоящей работе.
Математическая модель DT-горючего (эквимолярной смеси дейтерия и трития) является обычной моделью для плотной горячей плазмы. Она основана на уравнениях одножидкостной двухтемпературной гидродинамики с учетом электронной и ионной теплопроводности, излучения (в диффузионном по телесному углу и многогрупповом по частоте приближении) и нагрева плазмы горючего протонами зажигающего пучка и $\alpha $-частицами DT-реакции. Нагрев плазмы нейтронами DT-реакции не учитывается из-за большой длины свободного пробега.
Основное отличие нашей модели от моделей других авторов связано с переносом надтепловых $\alpha $-частиц. Обычно это диффузионное приближение нестационарного кинетического уравнения Фоккера–Планка в одногрупповом по скорости частицы (см. [4]) или многогрупповом (см. [5]) приближении. Как известно (см. [14]), почти вся траектория движения надтепловых тяжелых частиц является прямой линией. Поэтому естественно моделировать движение $\alpha $-частиц с помощью упрощенного уравнения Фоккера–Планка с отброшенным диффузионным слагаемым в пространстве скоростей (см. [15]), для которого траектория движения частицы является прямой линией. В настоящей работе мы используем стационарное уравнение Фоккера–Планка.
Как и в [4]–[7], рассматривается золотая оболочка. Для ее описания используются уравнения однотемпературной гидродинамики. Нагрев оболочки $\alpha $-частицами, излучением и тепловым потоком из горючего не учитывается. Отметим, что, как показано в [7], [16], учет охлаждения горючего за счет теплового потока в оболочку увеличивает энергию зажигания всего примерно на 10%.
Уравнение состояния горючего получено из полуэмпирического уравнения состояния водорода, основанного на модели из [17]. Для золота используется уравнение состояния из [18], обеспечивающее переход к уравнению состояния газа Ферми при сильном сжатии.
Горючее предполагается предварительно сжатым изэнтропически из нормального состояния (температура 4 K, давление одна атмосфера, плотность ${{\rho }_{a}} \approx 0.22$ г/см3) до плотности ${{\rho }_{0}} = 1000\;{{\rho }_{a}}$, что дает давление ${{p}_{0}} \approx 20$ ТПа. Оболочка предполагается предварительно сжатой изэнтропически до давления ${{p}_{0}}$, что дает плотность сжатой оболочки примерно 100 г/см3.
1. ПОСТАНОВКА ЗАДАЧИ И ЧИСЛЕННЫЙ МЕТОД
На фиг. 1 показана начальная конфигурация горючего и оболочки в цилиндрических координатах $z$, $r$. Горючее имеет форму цилиндра радиуса $R$ и высоты $H$. Перед цилиндром имеется дополнительная область, предназначенная для расчета горючего, вылетающего из мишени. Первоначально эта область заполнена парами DT-горючего с низкой плотностью и атмосферным давлением. Оболочка имеет форму цилиндрического слоя с размерами $\Delta R$ по координате $r$ и $H$ по $z$.
Фиг. 1.
Схема мишени и граничных условий: “Soft” – граница с мягкими условиями; “Free” – свободная граница; “Rigid” – плоскость симметрии.

На фиг. 1 указаны также типы условий на разных границах. На границах дополнительной области, кроме оси симметрии, ставятся условия равенства нулю пространственных производных термодинамических функций и скорости (мягкие условия). Мягкие условия ставятся также на прямолинейной границе AB, которая совпадает первоначально с торцевой границей мишени. Внешняя боковая граница оболочки является свободной границей с атмосферным давлением. На левых границах оболочки и горючего ставятся условия симметрии.
В дополнительной области не учитывается излучение, чтобы избежать не имеющих физического смысла решений уравнения диффузии излучения в оптически тонком случае. На линии BC для уравнения диффузии ставится условие отсутствия внешнего излучения. В дополнительной области мы также исключаем из рассмотрения нагрев разреженной DT-смеси протонным пучком.
В течение всего времени расчета границы AB и BC находятся на заданной прямой линии, но точки B и A могут двигаться вдоль этой линии в соответствии с движением границы раздела и внешней границы оболочки.
Мягкие граничные условия позволяют исключить из рассмотрения вылетающее за границу вещество. В то же время такие границы могут отражать идущие изнутри возмущения, искажая тем самым решение задачи. Во многих задачах можно избегать существенного искажения решения, выбирая подходящее положение границы или конструируя неотражающие граничные условия (см. [19]). Как показывают расчеты, рассмотренная выше тактика вычислений позволяет изучать зажигание мишени и отражение детонационной волны от плоскости симметрии. Существенное искажение решения происходит только после выхода из мишени отраженной волны.
В качестве зажигающего драйвера рассматривается моноэнергетический пучок протонов с энергией 1 МэВ. Интенсивность ${{J}_{{\text{b}}}}$ пучка не зависит от $r$ при $r \leqslant R$ и равна нулю при $r > R$. Функция ${{J}_{{\text{b}}}}(t)$ определяется двумя параметрами: максимальной интенсивностью ${{J}_{0}} = {{10}^{{19}}}$ Вт/см2 и временем действия пучка $\Delta {{t}_{{{\text{pr}}}}} = 80$ пс, которое, в свою очередь, определяет начальный интервал времени $\Delta {{t}_{{0{\text{pr}}}}} = 0.02\Delta {{t}_{{{\text{pr}}}}}$, в течение которого ${{J}_{{\text{b}}}}(t)$ увеличивается от 0 до ${{J}_{0}}$:
(1)
${{J}_{{\text{b}}}}(t) = \left\{ \begin{gathered} {{J}_{0}}t{\text{/}}\Delta {{t}_{{0{\text{pr}}}}},\quad t \leqslant \Delta {{t}_{{0{\text{pr}}}}}, \hfill \\ {{J}_{0}},\quad \Delta {{t}_{{0{\text{pr}}}}} < t \leqslant \Delta {{t}_{{{\text{pr}}}}}, \hfill \\ 0,\quad t > \Delta {{t}_{{{\text{pr}}}}}. \hfill \\ \end{gathered} \right.$Геометрические параметры мишени $R = 0.25$ мм (определяется условием близости энергии зажигания к пороговой энергии), $H = 0.6$ мм и $\Delta R = 0.2$ мм. Первые два параметра соответствуют значениям $R{{\rho }_{0}} \approx 0.55$ г/см2 и $H{{\rho }_{0}} \approx 1.3$ г/см2.
Применительно к DT-смеси уравнения гидродинамики имеют следующий вид:
(4)
$\rho \frac{{d{{\varepsilon }_{{\text{e}}}}}}{{dt}} = - {{p}_{{\text{e}}}}\nabla {\mathbf{u}} - \nabla {{{\mathbf{q}}}_{{\text{e}}}} + {{Q}_{{{\text{ei}}}}} + {{D}_{{\text{e}}}} + {{W}_{{\text{e}}}} + S,$(5)
$\rho \frac{{d{{\varepsilon }_{{\text{i}}}}}}{{dt}} = - {{p}_{{\text{i}}}}\nabla {\mathbf{u}} - \nabla {{{\mathbf{q}}}_{{\text{i}}}} - {{Q}_{{{\text{ei}}}}} + {{D}_{{\text{i}}}} + {{W}_{{\text{i}}}},$Уравнения (2)–(5) замыкаются уравнениями состояния для электронной ${{p}_{{\text{e}}}}(\rho ,{{T}_{{\text{e}}}})$, ${{\varepsilon }_{{\text{e}}}}(\rho ,{{T}_{{\text{e}}}})$ и ионной ${{p}_{{\text{i}}}}(\rho ,{{T}_{{\text{i}}}})$, ${{\varepsilon }_{{\text{i}}}}(\rho ,{{T}_{{\text{i}}}})$ компонент, где ${{T}_{{\text{e}}}}$ и ${{T}_{{\text{i}}}}$ – электронная и ионная температуры.
Учитывается только первичная реакция синтеза ядер дейтерия и трития, в результате которой возникают $\alpha $-частица с энергией 3.5 MэВ и нейтрон. Нейтроны полагаются вылетающими из горючего без взаимодействия с ним. Количество актов реакции синтеза в единице объема за единицу времени определяется известной формулой
(6)
$F = {{n}_{{\text{D}}}}{{n}_{{\text{T}}}}{{\left\langle {\sigma {v}} \right\rangle }_{{{\text{DT}}}}}({{T}_{{\text{i}}}}),$Выгорание ядер горючего описывается уравнениями
где индексы $j = {\text{D}}$ и T соответствуют дейтерию и тритию. Дополнительное слагаемое в уравнении неразрывности (2), вызванное изменением состава плазмы из-за DT-реакции, как и соответствующие изменения уравнений состояния, не учитываются.Перенос $\alpha $-частиц, которые являются существенно надтепловыми, описывается стационарным кинетическим уравнением в приближении Фоккера–Планка (см. [15]) относительно функции распределения $f({\mathbf{r}},{v},{\mathbf{\Omega }})$, которая определяет $f({\mathbf{r}},{v},{\mathbf{\Omega }})d{v}d\Omega $ как число частиц в единице объема вблизи точки ${\mathbf{r}}$, имеющих модуль скорости в интервале $d{v}$ вблизи ${v}$ и направление в интервале телесного угла $d\Omega $ вблизи единичного вектора ${\mathbf{\Omega }}$. Помимо функции $F$ задаются скорости торможения частицы (отрицательные по величине ускорения) на электронах ${{a}_{e}}({{T}_{e}},\rho ,{v})$ и ионах ${{a}_{i}}({{T}_{i}},{{T}_{e}},\rho ,{v})$, а также скорость частицы ${{{v}}_{{{\text{th}}}}}({{T}_{i}})$, при которой она термализуется (т.е. перестает рассматриваться как надтепловая частица). Для краткости записи заменим зависимость от термодинамических функций на зависимость от ${\mathbf{r}}$, полагая заданными функции ${{a}_{e}}({\mathbf{r}},{v})$, ${{a}_{i}}({\mathbf{r}},{v})$, $F({\mathbf{r}})$, ${{{v}}_{{{\text{th}}}}}({\mathbf{r}})$.
Пусть все рождающиеся частицы имеют одинаковый модуль скорости ${{{v}}_{0}}$ и однородное распределение по телесному углу. Тогда, в отсутствие диффузии функции распределения в скоростном пространстве, неоднородное кинетическое уравнение сводится к следующей задаче Коши для однородного уравнения (см. [15]):
(8)
$\begin{gathered} {v}({\mathbf{\Omega }}\nabla )f + \frac{{\partial af}}{{\partial {v}}} = 0,\quad f({\mathbf{r}},{{{v}}_{0}},{\mathbf{\Omega }}) = - \frac{{F({\mathbf{r}})}}{{4\pi a({\mathbf{r}},{{{v}}_{0}})}},\quad a = {{a}_{e}} + {{a}_{i}}, \\ {{{v}}_{m}}({\mathbf{r}},{\mathbf{\Omega }}) = max({{{v}}_{{{\text{th}}}}}({\mathbf{r}}),\;{{{v}}_{b}}({\mathbf{r}},{\mathbf{\Omega }})) \leqslant {v} \leqslant {{{v}}_{0}}, \\ \end{gathered} $Для расчета задачи (8) используется обратный трековый метод (см. [20]).
Нагрев DT-плазмы протонами описывается их торможением вдоль лучей $r = {\text{const}}$ в соответствии с уравнением
где ${{{v}}_{{\text{p}}}}$ – скорость протонов, уменьшающаяся от начального значения ${{{v}}_{{0{\text{p}}}}}$ до скорости термализации ${{{v}}_{{{\text{th}}}}}$.Интенсивность моноэнергетического пучка протонов внутри мишени определяется формулой $J = {{n}_{{\text{p}}}}{{{v}}_{{\text{p}}}}{{m}_{{\text{p}}}}{v}_{{\text{p}}}^{2}{\text{/}}2$, где ${{n}_{{\text{p}}}}$ – концентрация протонов, которая предполагается постоянной вплоть до их термализации, ${{m}_{{\text{p}}}}$ – масса протона. Значение ${{n}_{{\text{p}}}}$ определяется заданной начальной скоростью протонов ${{{v}}_{{0{\text{p}}}}}$ и интенсивностью пучка на входе в мишень (1). Слагаемые в правых частях уравнений (4) и (5) имеют вид
Излучение плазмы описывается диффузионным по телесному углу и многогрупповым по частоте $\nu $ приближением стационарного уравнения переноса. Многогрупповое приближение строится делением интервала $0 < \nu < \infty $ на $N$ групп ${{\nu }_{{l - 1}}} < \nu < {{\nu }_{l}}$, $l = 1,\;2,\; \ldots ,\;N$, ${{\nu }_{0}} = 0$, ${{\nu }_{N}} = \infty $. Уравнения диффузии в каждой группе имеют следующий вид:
гдеУравнения состояния для двухтемпературной гидродинамики и ссылки на работы, откуда брались формулы для коэффициентов приведенных выше уравнений, приведены в [7], [12].
Компьютерный код основан на развитом ранее коде для расчета осесимметричных течений плазмы и конденсированных сред на подвижных регулярных сетках, состоящих из гарантированно выпуклых четырехугольников (см. [21]–[26]).
Внешняя граница оболочки и ее граница с горючим выделяются явно в виде линий сетки. В основной расчетной области горючего сетка имеет ${{N}_{r}} = 40$ интервалов по оси $r$ вдоль плоскости симметрии и ${{N}_{z}} = 240$ интервалов вдоль оси симметрии. Проводились также контрольные расчеты с ${{N}_{z}} = 120$. Сетка в оболочке имеет 30 интервалов по оси $r$.
Возможность применения существенно более подробных сеток ограничена неустойчивостью границы раздела между горючим и оболочкой, которая проявляется в росте первоначально небольшого локального возмущения границы, возникающего при формировании детонационной волны. Для более подробных сеток возмущение растет быстрее, что приводит к остановке расчета из-за сильного искривления ячеек сетки вблизи границы раздела.
Число лучей для расчета задачи (8), выходящих из каждой ячейки сетки, ${{N}_{{{\text{tr}}}}} = 32$. Число групп для расчета излучения $N = 50$; $h{{\nu }_{1}}{\text{/}}{{k}_{{\text{B}}}} = 1.5$ кK, $h{{\nu }_{{N - 1}}}{\text{/}}{{k}_{{\text{B}}}} = 300$ МК. Здесь $h$ – постоянная Планка, ${{k}_{{\text{B}}}}$ – постоянная Больцмана.
2. ОТРАЖЕНИЕ ДЕТОНАЦИОННОЙ ВОЛНЫ
Детонационная волна возникает при $t \approx 0.15$ нс. Далее для краткости плоскость симметрии $z = 0$ будем называть стенкой. Заметим, что в отличие от детонации на основе химических реакций в газовых смесях, где детонационная волна сжигает все горючее, через которое она проходит, термоядерная реакция продолжается и после отражения.
На фиг. 2 показано поле давления в горючем (без дополнительной области) и в оболочке в четыре последовательных момента времени. Граница раздела между горючим и оболочкой, как и граница с дополнительной областью, показанa жирной линией. Стрелка указывает на локальное возмущение границы раздела, которое первоначально возникает при образовании детонационной волны, а затем растет из-за неустойчивости границы.
Фиг. 2.
Изобары (цифры вдоль кривых задают давление в ППа) в горючем (DT) и оболочке (Au) при $t = 0.2$ (а), 0.3 (б), 0.35 (в) и 0.5 нс (г); стрелка указывает на локальное возмущение границы; символ R на (в) и (г) указывает положение отраженной детонационной волны.

На фиг. 2а видна детонационная волна хорошо известного типа (см. [27]) с примыкающей к ее фронту волной разрежения. Момент времени $t = 0.2$ нс соответствует положению детонационной волны непосредственно перед ее взаимодействием со стенкой. Давление на фронте волны возрастает от оболочки к оси симметрии. Волна является неплоской: ее $z$-координата около оси симметрии заметно меньше, чем вблизи оболочки. Вблизи оси симметрии виден предвестник детонационной волны.
Начальная стадия отражения детонационной волны от стенки показана на фиг. 2б ($t = 0.3$ нс). Вблизи границы с оболочкой волна еще не дошла до стенки. Отражение остальной части волны дает область высокого давления около стенки. Дальнейшее формирование отраженной волны происходит в основном из-за движения этой области вдоль стенки, что будет обсуждаться ниже в связи с фиг. 3.
На фиг. 2в показана отраженная детонационная волна при $t = 0.35$ нс (сгущение изолиний отмечено символом R) почти сразу после образования. За фронтом волны давление вблизи оси симметрии слабо зависит от пространственных координат. Область высокого давления находится около границы с оболочкой, переместившись сюда из окрестности оси симметрии (см. фиг. 2б). Нормальная скорость границы раздела имеет максимум вблизи стенки.
В момент времени $t = 0.5$ нс (см. фиг. 2г) можно увидеть ударную волну в оболочке, которая отходит от границы раздела и усиливается вблизи стенки. Помимо локального возмущения границы раздела, показанного стрелкой, почти на всей границе возникает коротковолновое возмущение. В горючем отраженная волна уже частично вошла в дополнительную область.
Давление за отраженной волной слабо зависит от пространственных переменных не только вблизи оси симметрии, а почти везде, кроме небольшой окрестности границы раздела. Таким же свойством обладает и аналогичная одномерная задача из [12]. Течение между стенкой и отраженной волной хорошо описывается простым решением уравнений гидродинамики с линейным профилем скорости и не зависящими от пространственной координаты термодинамическими функциями. Возможность использования этого решения для приближенного описания рассматриваемой осесимметричной задачи будет обсуждаться ниже в разд. 4.
Вернемся к формированию отраженной детонационной волны. На фиг. 3 показаны профили давления и радиальной скорости $p(r)$ и ${{u}_{r}}(r)$ вдоль стенки в четыре промежуточных момента времени между моментом $t = 0.3$ нс, когда отраженная волна начинает формироваться (см. фиг. 2б) и моментом $t = 0.35$ нс, когда отраженная волна уже сформировалась (см. фиг. 2в).
Видно, что область высокого давления генерирует высокоскоростную струю горючего вдоль стенки и движется вместе со струей в направлении оболочки. Скорость горючего в струе возрастает со временем и достигает значения примерно 1000 км/с при $t = 0.33$ нс (см. сплошную линию 3 на фиг. 3). Удар струи по оболочке дает дополнительный рост давления горючего вблизи оболочки (см. штриховую линию 4 на фиг. 3) и ударную волну в ней, более сильную, чем ударная волна при движении детонационной волны вдоль границы раздела. Отметим также обратную волну в горючем, идущую от оболочки к оси симметрии, что можно увидеть на последнем профиле скорости с локальным минимумом (см. сплошную линию 4 на фиг. 3).
Фиг. 3.
Давление (штриховые линии) и радиальная скорость (сплошные линии) вдоль стенки (плоскости симметрии) как функции радиальной координаты при $t = 0.31$ (1), 0.32 (2), 0.33 (3) и 0.34 нс (4).

Расчет на сетке с ${{N}_{z}} = 240$ практически заканчивается при $t \approx 0.5$ нс вследствие падения шага по времени, определяемого условием устойчивости явной схемы для уравнений гидродинамики на сильно искривленных сетках, возникающих вблизи искривленных участков границы раздела.
Возможность выполнить расчет для $t > 0.5$ нс появляется при использовании более грубых сеток, на которых неустойчивость границы раздела не так сильно выражена. Однако точность такого расчета существенно снижается из-за взаимодействия отраженной волны с искусственной боковой границей дополнительной расчетной области. Несмотря на мягкие граничные условия, свободного вылета вещества за эту границу не происходит. По-видимому, для корректного расчета выхода отраженной волны из мишени требуется другая конфигурация дополнительной расчетной области.
Отсутствие бокового расширения вещества в дополнительной области показанo на фиг. 4 для расчета на сетке с ${{N}_{z}} = 120$ на временном интервале от 0.5 до 0.6 нс. Приведены две функции $\mathop {\bar {F}}\nolimits_{{\text{mn}}} (t)$ и $\mathop {\bar {F}}\nolimits_{{\text{ad}}} (t)$, полученные осреднением функции $F$ (см. (6)) по объемам основной и дополнительной расчетной области. Можно увидеть, что функция $\mathop {\bar {F}}\nolimits_{{\text{ad}}} (t)$ быстро растет со временем и при $t = 0.6$ нс почти совпадает с функцией $\mathop {\bar {F}}\nolimits_{{\text{mn}}} (t)$, что было бы невозможно при выбросе горючего через боковую границу дополнительной области.
3. ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ ХАРАКТЕРИСТИКИ ТЕЧЕНИЯ
На фиг. 5 показаны зависимости от времени максимальных по пространству значений термодинамических функций: давления и температур электронов, ионов и фотонов. Последняя температура определяется равенством
где ${{U}_{l}}$ – решение уравнения диффузии (9).Фиг. 5.
Максимальные по пространству давление ($p$) и температуры ионов (${{T}_{{\text{i}}}}$), электронов (${{T}_{{\text{e}}}}$) и фотонов (${{T}_{{\text{r}}}}$) как функции времени.

После образования детонационной волны и перед ее отражением от стенки точка с максимальным давлением находится на фронте волны вблизи оси симметрии. Как видно на фиг. 5, это давление растет со временем, что указывает на нестационарность детонационной волны.
До начала взаимодействия волны со стенкой электронная и ионная температуры достигают своих максимальных значений примерно 200 МK на некотором расстоянии от волны. Максимальная температура фотонов примерно в 20 раз меньше.
После отражения детонационной волны от стенки все характеристики, за исключением температуры фотонов, резко возрастают (максимальные электронная и ионная температуры примерно в 2–2.5 раза), а затем относительно медленно уменьшаются. Первый резкий рост максимального давления связан с ударом детонационной волны по стенке вблизи оси симметрии (см. фиг. 2б), а последующий пик является следствием удара высокоскоростной струи по оболочке около стенки (см. фиг. 3). Отраженная от оболочки волна сходится к оси симметрии и дает небольшой рост максимальных давления и ионной температуры при $t \approx 0.45$ нс. Прекращение падения максимальных давления и ионной температуры при $t \approx 0.5$ нс является следствием взаимодействия окружающего горючего с возмущениями границы раздела (см. фиг. 2г).
На фиг. 6 показаны коэффициент выгорания $B(t)$ (отношение количества актов DT-реакции к количеству ядер дейтерия в горючем при $t = 0$) и относительная потеря мощности $\alpha $-частиц
где ${{Y}_{\alpha }}$ – полная мощность нагрева плазмы $\alpha $-частицами: ${{P}_{\alpha }}$ – полная мощность возникающих $\alpha $-частиц: ${{W}_{{\text{e}}}}$ и ${{W}_{{\text{i}}}}$ – слагаемые в правых частях уравнений (4) и (5); $F$ – количество актов DT-реакции за единицу времени в единице объема, определяемое формулой (6); интегрирование выполняется по объему горючего.Фиг. 6.
Относительная потеря мощности $\alpha $-частиц (1) и коэффициент выгорания (2) для ${{N}_{z}} = 240$ (сплошная линия) и 120 (штриховая линия) как функции времени.

Величина ${{k}_{\alpha }}{{P}_{\alpha }}$ определяет энергию $\alpha $-частиц, термализующихся в горючем или вылетающих из него в единицу времени. Энергия термализованных за единицу времени $\alpha $-частиц заведомо мала в сравнении с ${{P}_{\alpha }}$. Даже если частица термализуется с максимальной для рассматриваемой задачи температурой примерно 500 МK (фиг. 5), энергия частицы составляет меньше 2% ее начальной энергии. Поэтому можно рассматривать функцию ${{k}_{\alpha }}(t)$ как долю энергии образующихся в единицу времени частиц, которая уносится вылетающими частицами из горючего. На фиг. 6 видно, что эта доля не мала.
Во время действия пучка протонов ($t \leqslant 0.08$ нс) ${{k}_{\alpha }} \approx 0.4$ за исключением небольшого начального интервала. Затем при $t \approx 0.25$ нс значение ${{k}_{\alpha }}$ уменьшается до примерно 0.25, и, начиная с $t \approx 0.31$ нс, функция ${{k}_{\alpha }}$ быстро увеличивается из-за увеличения средней длины свободного пробега $\alpha $-частиц, вызванного уменьшением плотности горючего.
При $t = 0.5$ нс коэффициент выгорания $B \approx 0.15$, что примерно в 2 раза меньше, чем в случае квазиодномерной модели из [12] с тем же значением начальной плотности и близкими значениями остальных параметров ($H = 0.5$ мм, радиус цилиндра, ограничивающего траектории $\alpha $-частиц, 0.1 мм). В следующем разделе будет представлена приближенная модель течения при $t > 0.5$ нс, которая позволяет оценить значение коэффициента выгорания после прекращения горения.
На фиг. 6 показана также функция $B{\text{'}}(t)$, полученная из двумерного расчета на более грубой сетке с ${{N}_{z}} = 120$. Видно, что $B{\text{'}}(t) < B(t)$. Это позволяет надеяться, что коэффициент выгорания, полученный на некоторой сетке, можно рассматривать в качестве нижней границы значения этого коэффициента в точном решении задачи. Это дает возможность исследовать мишени с большими значениями $H$, имеющими большой коэффициент выгорания (см. [12]), без увеличения числа узлов сетки вдоль оси симметрии пропорционально $H$.
4. НУЛЬМЕРНАЯ МОДЕЛЬ ГОРЕНИЯ МЕЖДУ СТЕНКОЙ И ОТРАЖЕННОЙ ВОЛНОЙ
Решение одномерных уравнений гидродинамики с линейным профилем скорости и постоянными по пространственной переменной термодинамическими функциями принадлежит известному семейству решений из [13], а также легко может быть получено из самих уравнений [12]. Скорость и плотность в этом решении имеют вид
(10)
${{u}_{z}} = \varphi (t)z,\quad \varphi (t) = \frac{1}{{C + t}},\quad \rho (t) = {{\rho }_{0}}\frac{{C + {{t}_{0}}}}{{C + t}},$На фиг. 7 показано поле функции ${{u}_{z}}{\text{/}}z$ в четыре момента времени после отражения детонационной волны. В табл. 1 приведены значения функции $\varphi (t)$ из уравнений (10), выбранные после анализа полей в качестве средних значений функции ${{u}_{z}}{\text{/}}z$ между стенкой и отраженной волной. Выбирая $\varphi = 13$ при $t = 0.35$ нс (см. фиг. 7a), мы рассматривали поле только около оси симметрии, так как вблизи оболочки располагается область высокого давления с большими градиентами термодинамических функций. В три последних момента времени функция ${{u}_{z}}{\text{/}}z$ слабо меняется почти во всей области между стенкой и отраженной волной.
Фиг. 7.
Изолинии функции ${{u}_{z}}{\text{/}}z$ (мкс–1) в горючем после отражения детонационной волны при $t = 0.35$ (а), 0.4 (б), 0.45 (в) и 0.5 нс (г).

Таблица 1.
Выбранные значения функции $\varphi (t)$ и рассчитанные значения постоянной $C$ и средней плотности $\rho $ в четыре момента времени после отражения детонационной волны
| $t$, нс | $\varphi $, мкс–1 | $C$, нс | $\rho $, г/см3 |
|---|---|---|---|
| 0.35 | 13 | $ - 0.27$ | 24 |
| 0.4 | 8 | $ - 0.275$ | 13 |
| 0.45 | 6 | $ - 0.28$ | 9 |
| 0.5 | 4.75 | $ - 0.29$ | 6.9 |
Значения постоянной $C$, вычисленные по соответствующим значениям $\varphi $ из уравнений (10) показаны в табл. 1. Слабая зависимость $C$ от времени указывает на возможность использования уравнений (10) для приближенного описания зависимости средней плотности в области между стенкой и отраженной волной от времени.
В последний момент $t = 0.5$ нс почти вся основная вычислительная область находится между стенкой отраженной волной. Следовательно, в качестве средней плотности между стенкой и отраженной волной можно взять плотность, осредненную по всему объему основной вычислительной области, и рассчитать среднюю плотность в три предыдущих момента из уравнений (10) с постоянными $C$, ${{\rho }_{0}}$ и ${{t}_{0}}$ для момента $t = 0.5$ нс. На фиг. 8 видно, что приведенное в табл. 1 значение плотности для момента $t = 0.35$ нс (24 г/см3) вполне удовлетворительно воспроизводит среднюю плотность между стенкой и отраженной волной около оси симметрии.
Построим модель, приближенно описывающую зависимость от времени осредненных по объему основной вычислительной области термодинамических функций, имея в виду возможность оценки коэффициента выгорания горючего после прекращения горения. Предположим, что скорость имеет только одну компоненту ${{u}_{z}}$ с линейным профилем пo z, наклон которого $\varphi (t)$, вместе с плотностью $\rho (t)$ описывается уравнениями (10) с ${{t}_{0}} = 0.5$ нс. Параметры $C$ и ${{\rho }_{0}}$ относятся к моменту ${{t}_{0}}$ и заданы в табл. 1. Плазма предполагается однотемпературной ${{T}_{e}} = {{T}_{i}} = T$. Подставляя уравнения (6) и (10) в уравнение (7) и полагая ${{n}_{{\text{D}}}} = {{n}_{{\text{T}}}} = n$, получаем следующее уравнение:
(11)
$n(t) = {{n}_{0}}\frac{{C + {{t}_{0}}}}{{C + t}}exp\left( { - \int\limits_{{{t}_{0}}}^t n {{{\left\langle {\sigma {v}} \right\rangle }}_{{{\text{DT}}}}}(T)dt} \right),$Полное число актов DT-реакции
(12)
${{N}_{{{\text{DT}}}}}(t) = {{N}_{{{\text{DT}}}}}({{t}_{0}}) + {{V}_{{{\text{mn}}}}}\int\limits_{{{t}_{0}}}^t F (n,T)dt,$Уравнения (10), (11) и (12) должны замыкаться уравнением для определения температуры $T$. Если охлаждение вследствие гидродинамического охлаждения было бы намного больше, чем для других механизмов ее охлаждения или нагрева, тогда связь между $\rho $ и $T$ определялась бы изэнтропой, проходящей через точку $({{\rho }_{0}},{{T}_{0}})$. В нашем случае это не так. Ниже для различных механизмов приведены значения полной мощности охлаждения или нагрева, которые являются интегралами по объему от суммы соответствующих слагаемых в правых частях уравнений (4) и (5), полученных из двумерного расчета при $t = {{t}_{0}}$ (в единицах ${{10}^{{16}}}$ Вт):
Необходимое уравнение для функции $T(t)$ берется в виде
где ${{(dT{\text{/}}dt)}_{{\text{g}}}}$ – производная вдоль изэнтропы, которая определяется производной $d\rho {\text{/}}dt$ из уравнения (10), $\chi = ({{Y}_{{\text{g}}}} + {{Y}_{\alpha }} + {{Y}_{{\text{r}}}} + {{Y}_{{\text{h}}}}){\text{/}}{{Y}_{{\text{g}}}} \approx 0.64$ – поправочный коэффициент, который приводит производные $dT{\text{/}}dt$ в соответствие с результатами двумерного расчета при $t = {{t}_{0}}$.Результат расчета коэффициента выгорания $B(t)$ для приближенной модели показан на фиг. 9. Коэффициент выгорания увеличивается со значения 0.15 при $t = 0.5$ нс до примерно 0.18.
5. НЕУСТОЙЧИВОСТЬ ГРАНИЦЫ РАЗДЕЛА МЕЖДУ ГОРЮЧИМ И ОБОЛОЧКОЙ
На фиг. 10 показана нормальная скорость границы раздела ${{U}_{{\text{n}}}}$ в зависимости от z в два момента времени, когда детонационная волна еще не достигла стенки около границы раздела. Колебание скорости при $z = {{z}_{{\text{d}}}} \approx 0.3$ мм возникает при формировании детонационной волны и вызывает локальное возмущение границы раздела на фиг. 2. Ускорение границы раздела справа от колебания (при $z > {{z}_{{\text{d}}}}$) связано с быстрым нагревом горючего пучком протонов. Граница раздела слева от колебания (при $z < {{z}_{{\text{d}}}}$) ускоряется детонационной волной. Увеличение ${{U}_{{\text{n}}}}$ с уменьшением $z$ связано с ростом давления на фронте волны по мере ее движения. Сравнение профилей ${{U}_{{\text{n}}}}(z)$ для двух моментов времени показывает, что после прохождения фронта нормальная скорость в фиксированной точке границы раздела уменьшается со временем из-за уменьшения давления за фронтом детонационной волны.
Фиг. 10.
Нормальная к границе раздела скорость как функция $z$ при $t = 0.25$ (штриховая линия) и 0.3 нс (сплошная линия); стрелка указывает на колебание скорости, которое вызывает локальное возмущение границы на фиг. 2.
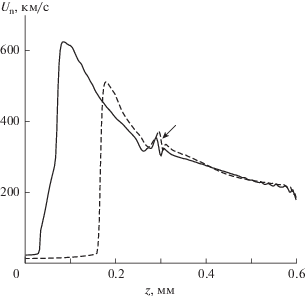
Отметим коротковолновые возмущения профиля ${{U}_{{\text{n}}}}(z)$ около крайней точки $z = 0.6$ мм, что, скорее всего, является чисто вычислительным эффектом. Для двух показанных моментов времени эти возмущения не приводят к заметным возмущениям границы. Однако появление коротковолновых возмущений границы раздела в более позднее время (см. фиг. 2г), скорее всего, вызвано коротковолновыми возмущениями профиля ${{U}_{{\text{n}}}}(z)$ на фиг. 10.
В рассматриваемой задаче могут иметь место два механизма развития неустойчивости границы раздела между горючим и оболочкой. Первый механизм – это неустойчивость Рихтмайера–Мешкова (РМ), связанная с импульсным (или близким к импульсному) ускорением границы, которое возникает при прохождении детонационной волны в горючем и генерирует ударную волну в оболочке. В случае плоской границы раздела, испытывающей одинаковое во всех точках границы импульсное ускорение, амплитуда $d$ малых синусоидальных возмущений с длиной волны $\lambda $ (амплитуда начального возмущения ${{d}_{0}} \ll \lambda $) растет линейно cо временем (см. [28]):
где $\Delta {{U}_{n}} > 0$ – изменение нормальной скорости границы раздела сред в результате импульсного ускорения, $A = \left| {{{\rho }_{1}} - {{\rho }_{2}}} \right|{\text{/}}({{\rho }_{1}} + {{\rho }_{2}})$ – число Атвуда, ${{\rho }_{1}}$ и ${{\rho }_{2}}$ – плотности сред по обе стороны границы, под параметрами ${{d}_{0}}$, ${{\rho }_{1}}$ и ${{\rho }_{2}}$ понимаются соответствующие значения после импульсного ускорения. Имеется простое обобщение формулы (13) на случай немалых начальных возмущений до стадии турбулентного перемешивания (см. [29]).Другим механизмом развития неустойчивости границы раздела в рассматриваемой задаче является неустойчивость Кельвина–Гельмгольца (КГ), возникающая при разрыве тангенциальной компоненты скорости. Амплитуда малого синусоидального возмущения плоской границы раздела сред, каждая из которых движется параллельно границе со своей постоянной скоростью, растет экспоненциально по времени (см. [30]):
где ${{A}_{{\text{K}}}} = {{({{\rho }_{1}}{{\rho }_{2}})}^{{1/2}}}{\text{/}}({{\rho }_{1}} + {{\rho }_{2}})$ – аналог числа Атвуда, ${{U}_{\tau }} > 0$ – относительная скорость движения сред. Ограничившись рассмотрением интервала времени, для которого $st \ll 1$, приходим к формулеСкорость роста амплитуды $\dot {d}$ для обоих типов неустойчивости имеет вид
где $\psi = \Delta {{U}_{n}}A$ для РМ-неустойчивости и $\psi = {{U}_{\tau }}{{A}_{{\text{K}}}}$ для КГ-неустойчивости.Вернемся к рассматриваемой двумерной задаче. Возьмем на границе раздела некоторую точку, которая определяется заданным отношением $\xi $ расстояния вдоль границы от точки до стенки к длине всей границы от стенки до точки B (см. фиг. 1). В расчете это означает выбор некоторого сеточного интервала на границе раздела (так как сеточные узлы вдоль границы раздела расставляются равномерно). Заметим, что координата $z$ точки с заданным $\xi $ меняется со временем незначительно.
Дальнейшее исследование основано на следующем предположении. Скорость роста малого возмущения границы вблизи этой точки с некоторой разумной точностью определяется формулой (14), где параметры ${{d}_{0}}$ и $\lambda $ полагаются одинаковыми для обоих типов неустойчивости, а параметр $\psi $ берется из решения двумерной задачи. Параметр $\Delta {{U}_{n}}$ полагается равным нормальной скорости выбранного интервала сразу после прохождения детонационной волны (выбиралось максимальное по времени значение ${{U}_{n}}$, см. фиг. 10). Параметры $A$ и ${{A}_{{\text{K}}}}$ вычисляются по значениям плотности, а параметр ${{U}_{\tau }}$ (касательная скорость) вычисляется по значениям компонент вектора скорости в примыкающих к интервалу ячейках сетки.
Далее фиксируется момент времени ${{t}_{ * }}$ прохождения детонационной волны через выбранную точку границы (в расчете выбирается момент достижения максимума ${{U}_{n}}$ на выбранном сеточном интервале), и для обоих видов неустойчивости вычисляется интеграл
(15)
$\eta (t) = \frac{{[d(t) - {{d}_{0}}]\lambda }}{{2\pi {{d}_{0}}}} = \int\limits_{{{t}_{ * }}}^t \psi (t{\text{'}})dt{\text{'}},$На фиг. 11 приведена функция $\eta (t - {{t}_{ * }})$ для обоих видов неустойчивости и функция ${{U}_{\tau }}(t - {{t}_{ * }})$ для точки на границе раздела с $\xi \approx 0.33$ (в момент прохождения фронта детонационной волны $z \approx 0.23$ мм). Единичный вектор вдоль границы раздела, на который проектируется вектор скорости при вычислении ${{U}_{\tau }}$, направлен по движению детонационной волны.
Фиг. 11.
Зависимости от времени функции $\eta $ (15), пропорциональной разности между текущей и начальной амплитудой малого возмущения границы раздела, для неустойчивости Рихтмайера–Мешкова (сплошная линия) и Кельвина–Гельмгольца (штриховая линия), а также касательной скорости вдоль границы раздела (штрихпунктирная линия) в точке границы с $z \approx 0.23$ мм.

Видно, что вначале КГ-неустойчивость дает более быстрый рост амплитуды. Затем скорость ${{U}_{\tau }}$ падает и даже меняет знак, что останавливает рост амплитуды. Отсюда можно сделать следующий вывод. Если формула (14) верна хотя бы качественно, т.е. скорость роста амплитуды малого возмущения для КГ-неустойчивости уменьшается вместе с разрывом касательной скорости на границе раздела, то заметное влияние КГ-неустойчивости на рост амплитуды возможно только на некотором расстоянии от фронта детонационной волны, скорее всего, после смены знака скорости ${{U}_{\tau }}$.
Рассмотрим теперь локальное возмущение границы раздела, возникающее при формировании детонационной волны, которое легко идентифицируется в каждый момент времени и позволяет получить хотя бы качественную информацию о скорости своего роста. Для расчета амплитуды локального возмущения в некоторый момент времени вначале визуально определяются крайние узлы, ограничивающие возмущение на линии разностной сетки, являющейся границей раздела. Затем через крайние узлы проводится прямая линия и вычисляются максимальное положительное ${{d}_{{{\text{per}} + }}}$ и минимальное отрицательное ${{d}_{{{\text{per}} - }}}$ расстояния от всех внутренних узлов до этой линии. Амплитуда возмущения определяется как ${{d}_{{{\text{per}}}}} = {{d}_{{{\text{per}} + }}} - {{d}_{{{\text{per}} - }}}$.
Рассчитанные значения функции ${{d}_{{{\text{per}}}}}$ в семь моментов времени показаны на фиг. 12. Значения скорости $ - {{u}_{z}}$ около локального возмущения границы раздела (которые являются неплохим приближением для значений рассмотренной выше скорости ${{U}_{\tau }}$) в те же моменты времени приведены в табл. 2. Уменьшение ${{u}_{z}}$ при $t = 0.5$ нс по сравнению с $t = 0.45$ нс объясняется тем, что при $t = 0.45$ нс отраженная детонационная волна еще не достигла локального возмущения границы раздела. Напомним, что момент $t = 0.35$ нс приблизительно соответствует появлению отраженной детонационной волны.
Таблица 2.
Скорость $ - {{u}_{z}}$ около локального возмущения границы в несколько моментов времени
| $t$, нс | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 |
|---|---|---|---|---|---|---|---|
| $ - {{u}_{z}}$, км/с | 400 | 200 | 0 | –300 | –600 | –1500 | –1000 |
В интервале времени между 0.25 и 0.35 нс скорость роста амплитуды $d{{d}_{{{\text{per}}}}}{\text{/}}dt$ почти не меняется, несмотря на изменение знака скорости $ - {{u}_{z}}$ при $t = 0.3$ нс. Из этого можно сделать вывод, что скорость роста амплитуды до отражения детонационной волны определяется РМ-неустойчивостью.
Можно также увидеть, что скорость роста амплитуды при $t > 0.35$ нс намного больше, чем при $t < 0.35$ нс. Увеличение скорости ${{u}_{z}}$ при $t > 0.35$ нс указывает на то, что указанное выше увеличение скорости роста амплитуды после отражения детонационной волны вызвано КГ-неустойчивостью.
ЗАКЛЮЧЕНИЕ
Рассматривается торцевое зажигание предварительно сжатой DT-мишени с золотой оболочкой двумя одинаковыми пучками протонов, параметры которых обеспечивают так называемое быстрое зажигание с минимальной энергией пучка. Рассматривается мишень небольшого размера вдоль оси (произведение начальной плотности на полуразмер примерно 1.3 г/см2).
Отражение возникающей нестационарной неплоской детонационной волны от плоскости симметрии начинается около оси, где возникает область высокого давления, генерирующая высокоскоростную струю DT-горючего вдоль стенки по направлению к границе с оболочкой. Образование отраженной волны заканчивается после удара этой струи по оболочке.
Перед отражением детонационной волны от плоскости симметрии температура электронов и ионов достигает своего максимума примерно 200 МK на некотором расстоянии от волны. Максимальная температура фотонов примерно в 20 раз меньше. При отражении детонационной волны максимальная ионная и электронная температуры быстро возрастают в 2–2.5 раза.
Значительная часть энергии $\alpha $-частиц выносится из мишени вылетающими частицами. Во время нагрева горючего пучком протонов доля энергетических потерь в единицу времени ${{k}_{\alpha }} \approx 0.4$. При движении детонационной волны коэффициент ${{k}_{\alpha }}$ постепенно уменьшается до примерно 0.25–0.3, а после отражения детонационной волны быстро возрастает из-за роста длины свободного пробега $\alpha $-частиц, вызванного уменьшением плотности горючего.
Коэффициент выгорания горючего после прекращения горения $B \approx 0.18$, что примерно в 2 раза меньше того значения, которое дает квазиодномерная модель для той же начальной плотности горючего и примерно того же размера мишени. Расчет на более грубой сетке дает несколько меньшее значение $B$. Это позволяет надеяться, что коэффициент выгорания, полученный на некоторой сетке, можно рассматривать в качестве нижней границы значения этого коэффициента в точном решении задачи.
В области между стенкой и отраженной волной термодинамические функции слабо зависят от пространственных координат, а компонента скорости вдоль оси ${{u}_{z}}$ как функция координаты $z$ имеет профиль, близкий к линейному. Это позволяет использовать известное решение одномерных уравнений гидродинамики для приближенного описания зависимости термодинамических функций от времени, определив произвольную постоянную в этом решении и вводя поправочный коэффициент, основанный на результатах двумерного расчета. Построенная таким образом модель горения позволяет рассчитывать коэффициент выгорания горючего после вынужденного прекращения двумерного расчета из-за сильного искривления ячеек разностной сетки вблизи искривленных участков границы раздела горючего и оболочки или падения точности расчета при выходе отраженной волны на границу расчетной области.
Изучена роль двух возможных механизмов развития неустойчивости границы раздела между горючим и оболочкой: импульсного ускорения границы раздела детонационной волной (неустойчивость Рихтмайера–Мешкова) и высокоскоростного скольжения горючего вдоль границы раздела (неустойчивость Кельвина–Гельмгольца). Рост малых синусоидальных возмущений границы раздела изучается на основе известных формул для плоской границы, коэффициенты которых берутся из расчета рассматриваемой задачи. Показано, что заметное влияние неустойчивости Кельвина–Гельмгольца на рост амплитуды возможно только на некотором расстоянии от фронта детонационной волны, скорее всего, после смены знака касательной составляющей скорости горючего из-за волны разрежения, примыкающей к фронту детонационной волны.
Проанализирована также эволюция небольшого локального возмущения границы раздела, возникающего в расчете при формировании детонационной волны. Сопоставление зависимостей от времени амплитуды возмущения и компоненты скорости горючего ${{u}_{z}}$ около возмущения, которую можно рассматривать в качестве скачка касательной скорости вдоль границы, позволяет сделать следующий вывод, близкий к сделанному выше при изучении роста малых синусоидальных возмущений. Скорость роста амплитуды возмущения до отражения детонационной волны определяется неустойчивостью Рихтмайера–Мешкова, а значительное увеличение скорости роста амплитуды после отражения вызвано неустойчивостью Кельвина–Гельмгольца.
Список литературы
Аврорин Е.Н., Бунатян А.А., Гаджиев А.Д. и др. Численные расчеты термоядерной детонации в плотной плазме // Физика плазмы. 1984. Т. 10. Вып. 3. С. 514–521.
Basov N.G., Gus’kov S.Yu., Feoktistov L.P. Thermonuclear gain of ICF targets with direct heating of ignitor // J. Sov. Laser Res. 1992. V. 13. № 5. P. 396–399. https://doi.org/10.1007/BF01124892
Tabak M., Hammer J., Glinsky M.E., et al. Ignition and high gain with ultrapowerful lasers // Phys. Plasm. 1994. V. 1. № 5. P. 1626–1634. https://doi.org/10.1063/1.870664
Basko M.M., Churazov M.D., Aksenov A.G. Prospects of heavy ion fusion in cylindrical geometry // Laser and Part. Beams. 2002. V. 20. P. 411–414. https://doi.org/10.1017/S0263034602203080
Vatulin V.V., Vinokurov O.A. Fast ignition of the DT fuel in the cylindrical channel by heavy ion beams // Laser and Part. Beams. 2002. V. 20. P. 415–418. https://doi.org/10.1017/S0263034602203092
Ramis R., Meyer-ter-Vehn J. On thermonuclear burn propagation in a pre-compressed cylindrical DT target ignited by a heavy ion beam pulse // Laser and Part. Beams. 2014. V. 32. P. 41–47. https://doi.org/10.1017/S0263034613000839
Фролова А.А., Хищенко К.В., Чарахчьян А.А. Быстрое зажигание пучком протонов и горение цилиндрической оболочечной DT-мишени // Физика плазмы. 2019. Т. 45. № 9. С. 804–824. https://doi.org/10.1134/S0367292119080043
Хищенко К.В., Чарахчьян А.А. Об одном свойстве двух симметрично сходящихся плоских волн термоядерного горения // ВАНТ. Сер. Матем. моделирование физ. процессов. 2013. Вып. 3. С. 30–40.
Charakhch’yan A.A., Khishchenko K.V. Symmetrically converging plane thermonuclear burn waves // Plasma Phys. Control. Fusion. 2013. V. 55. P. 105011. https://doi.org/10.1088/0741-3335/55/10/105011
Хищенко К.В., Чарахчьян А.А. Столкновение плоских волн термоядерной детонации в предварительно сжатой DT-смеси // Физика плазмы. 2015. Т. 41. № 3. С. 240–251. https://doi.org/10.7868/S0367292115020055
Хищенко К.В., Чарахчьян А.А. О некоторых свойствах плоских волн термоядерного горения // Прикл. механ. и техн. физ. 2015. Т. 56. № 1. С. 104–115. https://doi.org/10.15372/PMTF20150114
Charakhch’yan A.A., Khishchenko K.V. Plane thermonuclear detonation waves initiated by proton beams and quasi-one-dimensional model of fast ignition // Laser and Part. Beams. 2015. V. 33. P. 65–80. https://doi.org/10.1017/S0263034614000780
Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1972.
Дюдерштадт Дж., Мозес Г. Инерционный термоядерный синтез. М.: Энергоатомиздат, 1984.
Гуськов С.Ю., Розанов В.Б. Кинетика термоядерных частиц в лазерной плазме // Труды ФИАН. 1982. Т. 134. С. 115–122.
Charakhch’yan A.A., Frolova A.A., Khishchenko K.V. The role of heat loss at the fuel-shell interface during the fast ignition of cylindrical DT targets // J. Phys.: Conf. Ser. 2019. V. 1147. P. 012089. https://doi.org/10.1088/1742-6596/1147/1/012089
Khishchenko K.V. Equations of state for two alkali metals at high temperatures // J. Phys.: Conf. Ser. 2008. V. 98. P. 032023. https://doi.org/10.1088/1742-6596/98/3/032023
Holzapfel W.B. Equation of state for Cu, Ag, and Au and problems with shock wave reduced isotherms // High Pressure Res. 2010. V. 30. P. 372–394. https://doi.org/10.1080/08957959.2010.494845
Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001.
Фролова А.А., Хищенко К.В., Чарахчьян А.А. Трековый метод расчета нагрева плазмы заряженными продуктами термоядерных реакций для осесимметричных течений // Ж. вычисл. матем. и матем. физ. 2016. Т. 36. № 3. С. 443–454. https://doi.org/10.7868/S0044466916030054
Чарахчьян А.А. Расчет сжатия дейтерия в конической мишени в рамках уравнений Навье–Стокса для двухтемпературной магнитной гидродинамики // Ж. вычисл. матем. и матем. физ. 1993. Т. 33. № 5. С. 766–784.
Милявский В.В., Фортов В.Е., Фролова А.А., Хищенко К.В., Чарахчьян А.А., Шуршалов Л.В. Расчет ударного сжатия пористых сред в конических твердотельных мишенях с выходным отверстием // Ж. вычисл. матем. и матем. физ. 2006. Т. 46. № 5. С. 913–931. https://doi.org/10.1134/S0965542506050113
Иваненко С.А., Чарахчьян А.А. Алгоритм построения криволинейных сеток из выпуклых четырехугольников // Докл. АН СССР. 1987. Т. 295. № 2. С. 280–283.
Иваненко С.А., Чарахчьян А.А. Криволинейные сетки из выпуклых четырехугольников // Ж. вычисл. матем. и матем. физ. 1988. Т. 28. № 4. С. 503–514.
Charakhch’yan A.A., Ivanenko S.A. A variational form of the Winslow grid generator // J. Comput. Phys. 1997. V. 136. P. 385–398. https://doi.org/10.1006/jcph.1997.5750
Грынь В.И., Фролова А.А., Чарахчьян А.А. Сеточный генератор барьерного типа и его применение для расчета течений с подвижными границами // Ж. вычисл. матем. и матем. физ. 2003. Т. 43. № 6. С. 904–917.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Richtmyer R.D. Taylor instability in shock acceleration of compressible fluids // Commun. Pure Appl. Math. 1960. V. 13. P. 297–319. https://doi.org/10.1002/cpa.3160130207
Charakhch’yan A.A. Reshocking at the non-linear stage of Rictmyer–Meshkov instability // Plasma Phys. Controlled Fusion. 2001. V. 43. P. 1169–1179. https://doi.org/10.1088/0741-3335/43/9/301
Дразин Ф. Введение в теорию гидродинамической устойчивости. М.: Физматлит, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики






