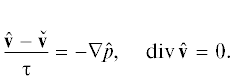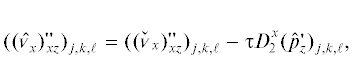Журнал вычислительной математики и математической физики, 2021, T. 61, № 11, стр. 1759-1778
О точности бикомпактных схем в задаче о распаде вихря Тейлора–Грина
М. Д. Брагин 1, *, Б. В. Рогов 1, **
1 ИПМ РАН
125047 Москва, Миусская пл., 4, Россия
* E-mail: michael@bragin.cc
** E-mail: rogov.boris@gmail.com
Поступила в редакцию 13.10.2020
После доработки 13.10.2020
Принята к публикации 07.07.2021
Аннотация
Впервые для нестационарных уравнений Навье–Стокса в случае несжимаемой жидкости строится высокоточная бикомпактная схема, имеющая четвертый порядок аппроксимации по пространству и второй – по времени. Для ее получения применяется метод расщепления по физическим процессам Марчука–Стрэнга. При дискретизации конвективной части уравнений дополнительно используется локально-одномерное расщепление по пространственным направлениям. На точном решении задачи о двумерном вихре Тейлора–Грина демонстрируется сеточная сходимость предлагаемой схемы с порядком выше теоретического. По разработанной бикомпактной схеме рассчитывается задача о распаде трехмерного вихря Тейлора–Грина (рассматриваются оба режима, и ламинарный, и турбулентный). Показывается, что эта схема хорошо разрешает вихревые структуры и с высокой точностью воспроизводит турбулентный спектр кинетической энергии. Библ. 29. Фиг. 8. Табл. 1.
ВВЕДЕНИЕ
Моделирование турбулентных течений вязкой жидкости является чрезвычайно востребованным при решении многих прикладных технических задач. Стандартный промышленный подход к расчету таких течений состоит в применении методики RANS (осредненных по Рейнольдсу уравнений Навье–Стокса) и численных схем второго порядка аппроксимации по пространству. Он позволяет достичь больших успехов в предсказании средних характеристик установившихся безотрывных течений, например, силы сопротивления, действующей на пассажирский самолет в крейсерском режиме полета. Однако этот подход оказывается недостаточно точным при исследовании более сложных явлений, таких как отрывные течения, генерация шумов свободными струями и обтекаемыми телами, смешение потоков жидкости при внутренних течениях и так далее [1]–[4]. Поскольку современное состояние вычислительной техники все еще не позволяет использовать DNS (прямое численное моделирование) при реальных числах Рейнольдса с разрешением всех пространственных масштабов течения на сетке, в настоящее время, по-видимому, единственной альтернативой оказывается методика LES (моделирование крупных вихрей), в которой крупные вихри непосредственно разрешаются и рассчитываются на сетке доступного размера, а более мелкие вихри и их влияние моделируются исходя из тех или иных априорных соображений. В свою очередь, LES-моделирование требует развития и использования численных схем, которые не только формально имеют пространственную аппроксимацию высокого порядка, но и обладают минимальными численными дисперсией и диссипацией [4], [5]. Подходящими видами схем для LES-моделирования представляются разрывные схемы Галеркина (подробные обзоры их применения могут быть найдены в работах [3], [5]), компактные схемы [6]–[8], схемы типа КАБАРЕ [9], [10].
В работах [11]–[22] предложен и развивается класс высокоточных бикомпактных схем. Аппроксимация пространственных производных в них является симметричной компактной (четвертого, шестого, восьмого и так далее порядков), при этом ее шаблон целиком помещается в одну ячейку сетки. В одномерном случае он включает в себя лишь два целых узла, что объясняет название этих схем. Отличительной чертой бикомпактных схем является сочетание нескольких положительных свойств: (а) спектральное разрешение, лучшее по сравнению с классическими компактными схемами равного порядка аппроксимации по пространству [18]–[20]; (б) равное число граничных условий в дифференциальной и дискретной постановках задачи; (в) неявность (слабые ограничения по устойчивости); (г) экономичность реализации, близкая к явным схемам. Первое из перечисленных свойств говорит о том, что бикомпактные схемы могут быть полезны для расчетов турбулентных течений по методике LES или ILES (неявный LES [23]). Однако, несмотря на всестороннюю изученность дисперсионных и диссипативных свойств бикомпактных схем в случае простейшего линейного уравнения переноса (в [18] рассмотрены полудискретные схемы четвертого порядка, в [19] – полудискретные схемы порядка не меньше шестого, в [20] – полностью дискретные схемы), еще ни разу эти свойства не были наглядно продемонстрированы на каком-нибудь практически значимом примере.
Таким образом, мы приходим к цели настоящей работы: (а) обобщить бикомпактные схемы на нестационарные трехмерные уравнения Навье–Стокса для несжимаемой жидкости; (б) посчитать задачу о распаде трехмерного вихря Тейлора–Грина в турбулентном режиме. Хотя эта задача предельно проста по своей постановке (к примеру, см. [24]), ее решение претерпевает весьма сложную эволюцию: начальный одночастотный вихрь дробится на вытянутые, нитеобразные вихревые структуры, которые затем истончаются и сильно спутываются между собой, постепенно превращаясь в однородную изотропную турбулентность. Эти процессы происходят и в более сложных, реальных постановках, поэтому задача о вихре Тейлора–Грина является широко употребимым тестом для численных схем, предназначенных для счета турбулентных течений.
Работа излагается следующим образом. В разд. 1 описывается бикомпактная схема с аппроксимацией четвертого порядка по пространству и второго порядка по времени для нестационарных трехмерных уравнений Навье–Стокса в случае несжимаемой жидкости. В разд. 2 проверяется сеточная сходимость этой схемы на точном решении задачи о двумерном вихре Тейлора–Грина. В разд. 3 приводятся и анализируются результаты расчетов по этой схеме задачи о распаде трехмерного вихря Тейлора–Грина (как в ламинарном, так и в турбулентном режимах).
1. СИСТЕМА УРАВНЕНИЙ И ЧИСЛЕННАЯ СХЕМА
1.1. Система уравнений
Рассмотрим безграничный объем ньютоновской несжимаемой жидкости. Ее изотермическое течение подчиняется уравнениям Навье–Стокса:
(1)
${{\partial }_{t}}{\mathbf{v}} + \operatorname{div} ({\mathbf{v}} \otimes {\mathbf{v}}) = - \nabla p + \frac{1}{{{\text{Re}}}}\Delta {\mathbf{v}},\quad \operatorname{div} {\mathbf{v}} = 0,\quad - {\kern 1pt} \infty < x,y,z < + \infty ,\quad t > 0,$1.2. Расщепление по физическим процессам
Построим для уравнений Навье–Стокса (1) бикомпактную схему четвертого порядка аппроксимации по пространству. Воспользуемся методом расщепления Марчука–Стрэнга [25[, [26] по физическим процессам. Систему (1) можно разбить на три части – конвективную:
вязкую: и часть с давлением и уравнением неразрывности: Дискретизацию каждой из этих частей обсудим по отдельности, а затем опишем общий алгоритм счета.Ясно, что любая машинная реализация упомянутого алгоритма потребует конечности расчетной области и постановки каких-то условий на ее границах. Поскольку в настоящей работе проводятся расчеты задачи о распаде вихря Тейлора–Грина, имеющей периодическое решение, ограничимся для определенности областью $D = {{(0,2\pi )}^{3}}$ и периодическими условиями на ее границе $\partial D$.
1.3. Сетка и представление решения на ней
Введем в замкнутой области $\bar {D}$ сетку
1) ${\mathbf{V}}_{{j,k,\ell }}^{n}$ – задана во всех узлах сетки $\Omega $ (индексы $j$, $k$, $\ell $ принимают как целые, так и полуцелые значения) и аппроксимирует в них скорость ${\mathbf{v}}$ в момент времени $t = {{t}^{n}}$, $n = 0,\;1, \ldots $;
2) ${\mathbf{v}}_{{j,k,\ell }}^{n}$, $({\mathbf{v}}_{x}^{'})_{{j,k,\ell }}^{n}$, $({\mathbf{v}}_{y}^{'})_{{j,k,\ell }}^{n}$, $({\mathbf{v}}_{z}^{'})_{{j,k,\ell }}^{n}$, $({\mathbf{v}}_{{xy}}^{{''}})_{{j,k,\ell }}^{n}$, $({\mathbf{v}}_{{yz}}^{{''}})_{{j,k,\ell }}^{n}$, $({\mathbf{v}}_{{xz}}^{{''}})_{{j,k,\ell }}^{n}$, $({\mathbf{v}}_{{xyz}}^{{'''}})_{{j,k,\ell }}^{n}$ – заданы только в целых узлах сетки $\Omega $ (индексы $j$, $k$, $\ell $ принимают только целые значения) и аппроксимируют в них при $t = {{t}^{n}}$ значения скорости ${\mathbf{v}}$ и семи ее производных по $x$, $y$, $z$, $xy$, $yz$, $xz$, $xyz$ соответственно. На совокупность этих сеточных функций можно смотреть как на одну сеточную функцию с большим числом компонент на один узел (24 компоненты – 3 компоненты скорости и по 7 производных для каждой из них). Отметим, что такая функция “хранит” примерно столько же чисел, сколько и функция ${\mathbf{V}}_{{j,k,\ell }}^{n}$, это количество порядка $24{{N}_{x}}{{N}_{y}}{{N}_{z}}$ при ${{N}_{x}},{{N}_{y}},{{N}_{z}} \gg 1$;
3) $p_{{j,k,\ell }}^{n}$, $(p_{x}^{'})_{{j,k,\ell }}^{n}$, $(p_{y}^{'})_{{j,k,\ell }}^{n}$, $(p_{z}^{'})_{{j,k,\ell }}^{n}$, $(p_{{xy}}^{{''}})_{{j,k,\ell }}^{n}$, $(p_{{yz}}^{{''}})_{{j,k,\ell }}^{n}$, $(p_{{xz}}^{{''}})_{{j,k,\ell }}^{n}$, $(p_{{xyz}}^{{'''}})_{{j,k,\ell }}^{n}$ – то же, что и в п. 2), только для давления $p$.
1.4. Аппроксимация конвективной части уравнений Навье–Стокса
Представим систему (2) в виде
(5)
${{\partial }_{t}}{\mathbf{v}} + {{\partial }_{x}}{{{\mathbf{F}}}^{x}}({\mathbf{v}}) + {{\partial }_{y}}{{{\mathbf{F}}}^{y}}({\mathbf{v}}) + {{\partial }_{z}}{{{\mathbf{F}}}^{z}}({\mathbf{v}}) = 0,$(6)
${{\partial }_{t}}{\mathbf{v}} + {{\partial }_{d}}{{{\mathbf{F}}}^{{d, \pm }}}({\mathbf{v}}) = 0,\quad d = x,y,z,$(7)
${{{\mathbf{F}}}^{{d, \pm }}}({\mathbf{v}}) = \frac{1}{2}{{{\mathbf{F}}}^{d}}({\mathbf{v}}) \pm C_{2}^{d}{\mathbf{v}},\quad d = x,y,z.$(8)
$C_{2}^{d} = (1 + 2\delta )\mathop {max}\limits_{j,k,\ell } \left| {({{{v}}_{d}})_{{j,k,\ell }}^{n}} \right|,\quad d = x,y,z,$Наконец, каждая из шести систем (6) решается при помощи одномерной бикомпактной схемы с аппроксимацией по времени методом трапеций (как в схеме Кранка–Николсона). В силу аналогичности этих систем друг другу мы остановимся подробно только на системе с потоком ${{{\mathbf{F}}}^{{x, + }}}({\mathbf{v}})$. Для нее указанная бикомпактная схема запишется следующим образом [12]:
 – это сеточные функции типа ${\mathbf{V}}_{{j,k,\ell }}^{n}$; первая означает искомое решение на неком промежуточном слое $t = \hat {t}$, а вторая – известное решение на промежуточном слое
– это сеточные функции типа ${\mathbf{V}}_{{j,k,\ell }}^{n}$; первая означает искомое решение на неком промежуточном слое $t = \hat {t}$, а вторая – известное решение на промежуточном слое 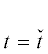 ; в данном случае
; в данном случае  . Далее, в описании общего алгоритма счета объясняется, что конкретно фигурирует в
схеме (9)
вместо ${\mathbf{\hat {V}}}$ и
. Далее, в описании общего алгоритма счета объясняется, что конкретно фигурирует в
схеме (9)
вместо ${\mathbf{\hat {V}}}$ и  . Символами $A_{0}^{x}$, $\Lambda _{1}^{x}$, $\Lambda _{2}^{x}$ обозначены следующие одномерные сеточные операторы:
. Символами $A_{0}^{x}$, $\Lambda _{1}^{x}$, $\Lambda _{2}^{x}$ обозначены следующие одномерные сеточные операторы:
 для всех $j$, $k$, $\ell $ (и целых, и полуцелых) определяются формулами:
Схема (9)
дополняется периодическим граничным условием:
для всех $j$, $k$, $\ell $ (и целых, и полуцелых) определяются формулами:
Схема (9)
дополняется периодическим граничным условием:
(10)
${{{\mathbf{\hat {V}}}}_{{0,k,\ell }}} = {{{\mathbf{\hat {V}}}}_{{{{N}_{x}},k,\ell }}}\quad \forall k,\ell .$ символически как действие оператора послойного перехода $S_{{{\text{conv}}}}^{{x, + }}(\tau )$:
Поток с противоположным знаком ${{{\mathbf{F}}}^{{x, - }}}({\mathbf{v}})$, а также направления $y$, $z$ (т.е. все остальные одномерные системы (6)) рассматриваются аналогично; операторы
перехода соответствующих им одномерных бикомпактных схем обозначим через $S_{{{\text{conv}}}}^{{x, - }}(\tau )$ и $S_{{{\text{conv}}}}^{{d, \pm }}(\tau )$, $d = y,z$.
символически как действие оператора послойного перехода $S_{{{\text{conv}}}}^{{x, + }}(\tau )$:
Поток с противоположным знаком ${{{\mathbf{F}}}^{{x, - }}}({\mathbf{v}})$, а также направления $y$, $z$ (т.е. все остальные одномерные системы (6)) рассматриваются аналогично; операторы
перехода соответствующих им одномерных бикомпактных схем обозначим через $S_{{{\text{conv}}}}^{{x, - }}(\tau )$ и $S_{{{\text{conv}}}}^{{d, \pm }}(\tau )$, $d = y,z$.
Итоговая симметризованная по $x$, $y$ локально-одномерная бикомпактная схема для конвективной части (2) определяется своим оператором перехода ${{S}_{{{\text{conv}}}}}(\tau )$:
Данная схема аппроксимирует периодическую краевую задачу для уравнений (2) с погрешностью $O({{\tau }^{2}},{{h}^{4}})$ при $\tau ,h \to 0$, где $h$ – максимальный пространственный шаг.Заметим, что для аппроксимации по времени совсем не обязательно использовать метод трапеций, вместо него, к примеру, можно выбрать любой другой $A$- или $L$-устойчивый диагонально-неявный метод Рунге–Кутты высокого порядка. Наше предпочтение методу трапеций обусловлено двумя факторами.
1. Порядок аппроксимации метода трапеций равен двум, что совпадает с порядком метода расщепления Марчука–Стрэнга.
2. Этот второй порядок экономично достигается лишь за одну неявную стадию.
1.5. Аппроксимация вязкой части уравнений Навье–Стокса
Сделаем небольшое отступление от нашего изложения, чтобы продемонстрировать, откуда получаются сеточные операторы, необходимые для написания бикомпактной схемы для системы (3).
Пусть $u(x)$ – произвольная достаточно гладкая функция. Введем тогда сеточные функции ${{u}_{j}} = u({{x}_{j}})$ и ${{(u_{x}^{'})}_{j}} = du({{x}_{j}}){\text{/}}dx$, где индекс $j$ пробегает только целые значения. Обратимся к ячейке $x \in [{{x}_{j}},{{x}_{{j + 1}}}]$: имея на ее границах четыре значения: ${{u}_{j}},\;{{u}_{{j + 1}}},\;{{(u_{x}^{'})}_{j}},\;{{(u_{x}^{'})}_{{j + 1}}}$, мы можем построить по ним кубический интерполяционный полином Эрмита ${{u}_{h}}(x)$, который будет приближать функцию $u(x)$ внутри ячейки с погрешностью $O(h_{{x,j + 1/2}}^{4})$ при ${{h}_{{x,j + 1/2}}} \to 0$. Нетрудно показать, что для полинома ${{u}_{h}}(x)$ имеют место такие формулы (ради компактности записи опускаем индекс $j + 1{\text{/}}2$ у шага ${{h}_{{x,j + 1/2}}}$):
(12)
$\begin{gathered} \frac{1}{{{{h}_{x}}}}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {{{u}_{h}}} (x)dx = \frac{{{{u}_{j}} + {{u}_{{j + 1}}}}}{2} + \frac{{{{h}_{x}}}}{{12}}[{{(u_{x}^{'})}_{j}} - {{(u_{x}^{'})}_{{j + 1}}}] \equiv \tilde {A}_{0}^{x}{{u}_{{j + 1/2}}}, \\ \frac{1}{{{{h}_{x}}}}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {\frac{{d{{u}_{h}}(x)}}{{dx}}} dx = \frac{{{{u}_{{j + 1}}} - {{u}_{j}}}}{{{{h}_{x}}}} \equiv \tilde {\Lambda }_{1}^{x}{{u}_{{j + 1/2}}}, \\ \frac{1}{{{{h}_{x}}}}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {\frac{{{{d}^{2}}{{u}_{h}}(x)}}{{d{{x}^{2}}}}} dx = \frac{{{{{(u_{x}^{'})}}_{{j + 1}}} - {{{(u_{x}^{'})}}_{j}}}}{{{{h}_{x}}}} \equiv \tilde {\Lambda }_{2}^{x}{{u}_{{j + 1/2}}}, \\ \frac{1}{{{{h}_{x}}}}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {\frac{{{{d}^{3}}{{u}_{h}}(x)}}{{d{{x}^{3}}}}} dx = \frac{6}{{h_{x}^{2}}}\left( {{{{(u_{x}^{'})}}_{j}} - 2\frac{{{{u}_{{j + 1}}} - {{u}_{j}}}}{{{{h}_{x}}}} + {{{(u_{x}^{'})}}_{{j + 1}}}} \right) \equiv \tilde {\Lambda }_{3}^{x}{{u}_{{j + 1/2}}} \\ \end{gathered} $Вернемся к системе (3). Возьмем ее саму и семь ее дифференциальных следствий – производных по $x$, $y$, $z$, $xy$, $yz$, $xz$, $xyz$, осредним эти восемь векторных уравнений по ячейке $[{{x}_{j}},{{x}_{{j + 1}}}] \times [{{y}_{k}},{{y}_{{k + 1}}}] \times [{{z}_{\ell }},{{z}_{{\ell + 1}}}]$ (т.е. проинтегрируем и поделим на объем ячейки), сведем кратные интегралы к повторным, одномерные интегралы приблизим по формулам (12), для аппроксимации по времени применим метод трапеций. В результате перечисленных действий получится следующая бикомпактная схема для системы (3):
 – это сеточные функции типа ${\mathbf{v}}_{{j,k,\ell }}^{n}$; первая означает некое промежуточное искомое решение, а вторая – некое известное
решение (сказанное распространяется также на отвечающие им всем их сеточные функции-производные).
Ради ясности перечислим все возможные варианты действия операторов ${{P}^{x}}$, ${{P}^{y}}$, ${{P}^{z}}$:
– это сеточные функции типа ${\mathbf{v}}_{{j,k,\ell }}^{n}$; первая означает некое промежуточное искомое решение, а вторая – некое известное
решение (сказанное распространяется также на отвечающие им всем их сеточные функции-производные).
Ради ясности перечислим все возможные варианты действия операторов ${{P}^{x}}$, ${{P}^{y}}$, ${{P}^{z}}$:
(14)
$\begin{gathered} {{{{\mathbf{\hat {v}}}}}_{{0,k,\ell }}} = {{{{\mathbf{\hat {v}}}}}_{{{{N}_{x}},k,\ell }}},\quad {{({\mathbf{\hat {v}}}_{x}^{'})}_{{0,k,\ell }}} = {{({\mathbf{\hat {v}}}_{x}^{'})}_{{{{N}_{x}},k,\ell }}} \\ {{{{\mathbf{\hat {v}}}}}_{{j,0,\ell }}} = {{{{\mathbf{\hat {v}}}}}_{{j,{{N}_{y}},\ell }}},\quad {{({\mathbf{\hat {v}}}_{y}^{'})}_{{j,0,\ell }}} = {{({\mathbf{\hat {v}}}_{y}^{'})}_{{j,{{N}_{y}},\ell }}}, \\ {{{{\mathbf{\hat {v}}}}}_{{j,k,0}}} = {{{{\mathbf{\hat {v}}}}}_{{j,k,{{N}_{z}}}}},\quad {{({\mathbf{\hat {v}}}_{z}^{'})}_{{j,k,0}}} = {{({\mathbf{\hat {v}}}_{z}^{'})}_{{j,k,{{N}_{z}}}}}, \\ j = 0,\;1,\;2,\; \ldots ,\;{{N}_{x}},\quad k = 0,\;1,\;2,\; \ldots ,\;{{N}_{y}},\quad \ell = 0,\;1,\;2,\; \ldots ,\;{{N}_{z}}. \\ \end{gathered} $Схема (13), (14) аппроксимирует периодическую краевую задачу для системы (3) с погрешностью $O({{\tau }^{2}},{{h}^{4}})$. Важно отметить, что описанный выше метод получения бикомпактной пространственной аппроксимации четвертого порядка для многомерного уравнения теплопроводности обобщает метод работы [11], в которой был рассмотрен только одномерный случай.
Обозначим оператор послойного перехода бикомпактной схемы (13), (14) как ${{S}_{{{\text{visc}}}}}(\tau )$:
Здесь и далее, записывая “${\mathbf{\hat {v}}}$” без индексов, мы будем иметь в виду всю восьмерку сеточных функций ${{{\mathbf{\hat {v}}}}_{{j,k,\ell }}}$, ${{({\mathbf{\hat {v}}}{{_{x}^{'}}_{x}})}_{{j,k,\ell }}}$, ${{({\mathbf{\hat {v}}}_{y}^{'})}_{{j,k,\ell }}}$, ${{({\mathbf{\hat {v}}}_{z}^{'})}_{{j,k,\ell }}}$, ${{({\mathbf{\hat {v}}}_{{xy}}^{{''}})}_{{j,k,\ell }}}$, ${{({\mathbf{\hat {v}}}_{{yz}}^{{''}})}_{{j,k,\ell }}}$, ${{({\mathbf{\hat {v}}}_{{xz}}^{{''}})}_{{j,k,\ell }}}$, ${{({\mathbf{\hat {v}}}_{{xyz}}^{{'''}})}_{{j,k,\ell }}}$ (аналогично для , ${{{\mathbf{v}}}^{n}}$).
, ${{{\mathbf{v}}}^{n}}$).
Поясним теперь, как именно из уравнений (13), (14) вычисляется искомое решение ${\mathbf{\hat {v}}}$. Предлагается использовать метод итерируемой приближенной факторизации (ИПФ). Пусть
${{{\mathbf{\hat {v}}}}^{{(s)}}}$ – приближение с номером $s$ к искомому решению ${\mathbf{\hat {v}}}$ ($s = 0,\;1,\; \ldots $), начальное приближение  ; обозначим через $\delta {{{\mathbf{\hat {v}}}}^{{(s + 1)}}} = {{{\mathbf{\hat {v}}}}^{{(s + 1)}}} - {{{\mathbf{\hat {v}}}}^{{(s)}}}$. Введем сеточные операторы:
; обозначим через $\delta {{{\mathbf{\hat {v}}}}^{{(s + 1)}}} = {{{\mathbf{\hat {v}}}}^{{(s + 1)}}} - {{{\mathbf{\hat {v}}}}^{{(s)}}}$. Введем сеточные операторы:
(16)
$B_{1}^{d}(\alpha ) = \tilde {A}_{0}^{d} - \alpha \tilde {\Lambda }_{2}^{d},\quad B_{2}^{d}(\alpha ) = \tilde {\Lambda }_{1}^{d} - \alpha \tilde {\Lambda }_{3}^{d},\quad d = x,y,z,$(17)
$\begin{gathered} B_{1}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{1C}}^{{(s)}},\quad B_{2}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{4C}}^{{(s)}}, \\ B_{1}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{2C}}^{{(s)}},\quad B_{2}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{7C}}^{{(s)}}, \\ B_{1}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{3C}}^{{(s)}},\quad B_{2}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{1}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{6C}}^{{(s)}}, \\ B_{1}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{5C}}^{{(s)}},\quad B_{2}^{z}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{y}(\tau {\kern 1pt} *{\kern 1pt} )B_{2}^{x}(\tau {\kern 1pt} *{\kern 1pt} )\delta {\mathbf{\hat {v}}}_{C}^{{(s + 1)}} = \varphi _{{8C}}^{{(s)}}, \\ \end{gathered} $1.6. Аппроксимация части уравнений Навье–Стокса, отвечающей за силы давления и несжимаемость жидкости
Здесь мы будем действовать иначе – сперва дискретизируем уравнения (4) по времени при помощи неявного методом Эйлера:
Затем, взяв дивергенцию от обеих частей первого уравнения и воспользовавшись вторым уравнением, получим два независимых уравнения: Таким образом, численное решение (4) разбивается на две отдельные подзадачи: решение уравнения Пуассона для давления (18) и пересчет скорости жидкости по формуле (19).Построение бикомпактной схемы для уравнения Пуассона (18) не составляет большого труда. Совершая в точности те же операции, что и при выводе схемы (13) для уравнения (3), получаем искомую схему:
(21)
$\begin{gathered} \mathop {\hat {p}}\nolimits_{0,k,\ell } = {{{\hat {p}}}_{{{{N}_{x}},k,\ell }}},\quad {{(\hat {p}_{x}^{'})}_{{0,k,\ell }}} = {{(\hat {p}_{x}^{'})}_{{{{N}_{x}},k,\ell }}} \\ \mathop {\hat {p}}\nolimits_{j,0,\ell } = {{{\hat {p}}}_{{j,{{N}_{y}},\ell }}},\quad {{(\hat {p}_{y}^{'})}_{{j,0,\ell }}} = {{(\hat {p}_{y}^{'})}_{{j,{{N}_{y}},\ell }}}, \\ {{{\hat {p}}}_{{j,k,0}}} = {{{\hat {p}}}_{{j,k,{{N}_{z}}}}},\quad {{(\hat {p}_{z}^{'})}_{{j,k,0}}} = {{(\hat {p}_{z}^{'})}_{{j,k,{{N}_{z}}}}}, \\ j = 0,\;1,\;2,\; \ldots ,\;{{N}_{x}},\quad k = 0,\;1,\;2,\; \ldots ,\;{{N}_{y}},\quad \ell = 0,\;1,\;2,\; \ldots ,\;{{N}_{z}}. \\ \end{gathered} $Бикомпактная схема (20), (21) аппроксимирует периодическую краевую задачу для уравнения Пуассона (18) с погрешностью $O({{h}^{4}})$. Заметим, что в погрешности нет члена $O({{h}^{4}}{\text{/}}\tau )$: хотя дивергенция скорости делится на $\tau $, она сама обязана иметь асимптотику $O(\tau )$, так как при сгущении сетки численное распределение давления сходится к точному и составляет конечную величину $O(1)$.
Для реализации схемы (20) применяется метод ИПФ. Уравнения этого метода для нее совершенно аналогичны тем, что были приведены выше для схемы (13) . Разница состоит лишь в том, что в качестве аргумента у операторов $B_{{1,2}}^{d}({\kern 1pt} \cdot {\kern 1pt} )$, $d = x,y,z$, выступает не модифицированный временной шаг $\tau {\kern 1pt} {\text{*}}$, а параметр $\theta > 0$ – настраиваемый параметр итерационного метода.
Обозначим нахождение давления $\hat {p}$ по схеме (20), (21)
символически как действие оператора ${{S}_{{{\text{ell}}}}}(\tau )$ на  :
:
Обратимся к пространственной дискретизации соотношения (19). Для компоненты скорости ${{{v}}_{x}}$ имеем
Проекция на сетку соотношения (23) и его дифференциальных следствий – производных по $y$, $z$, $yz$ дает следующие формулы:Что касается дискретизации соотношения (19) применительно к ${{{v}}_{y}}$ и ${{{v}}_{z}}$, то она выводится в полной аналогии с рассуждениями предыдущего абзаца, поэтому выписывать варианты формул (24), (26) для ${{{v}}_{y}}$ и ${{{v}}_{z}}$ мы не будем. Обозначим нахождение ${\mathbf{\hat {v}}}$ по формулам (24), (26) и их аналогам для ${{{v}}_{y}}$ и ${{{v}}_{z}}$ символически как действие оператора перехода ${{S}_{{{\text{pr}}}}}(\tau ,\hat {p})$:
1.7. Переходы между разными представлениями поля скоростей
Для составления полного алгоритма счета осталось рассмотреть и описать две операции: пересчет численного решения ${{{\mathbf{v}}}^{n}}$ в решение ${{{\mathbf{V}}}^{n}}$ и наоборот.
Переход от ${{{\mathbf{v}}}^{n}}$ к ${{{\mathbf{V}}}^{n}}$ осуществляется достаточно просто: решение ${{{\mathbf{v}}}^{n}}$ содержит всю информацию, необходимую для построения в каждой ячейке сетки трикубического (то есть трехмерного аналога бикубического) интерполяционного полинома Эрмита. Отметим, что совокупность этих полиномов представляет из себя трикубический сплайн гладкости 1. Этот сплайн позволяет посчитать скорость жидкости в любой точке $\bar {D}$ с четвертым порядком точности, в частности, в полуцелых узлах сетки $\Omega $. Следуя нашим обозначениям, обозначим пересчет ${{{\mathbf{v}}}^{n}}$ в ${{{\mathbf{V}}}^{n}}$ через действие оператора ${{S}_{{{\mathbf{v}} \to {\mathbf{V}}}}}$:
Переход от ${{{\mathbf{V}}}^{n}}$ к ${{{\mathbf{v}}}^{n}}$ выполняется при помощи пятиточечной конечно-разностной аппроксимации для первой производной с третьим порядком точности. На равномерной сетке формулы пересчета ${{{\mathbf{V}}}^{n}}$ в ${{{\mathbf{v}}}^{n}}$ имеют четвертый порядок точности и записываются в виде
(29)
$\begin{gathered} {\mathbf{v}}_{{j,k,\ell }}^{n} = {\mathbf{V}}_{{j,k,\ell }}^{n},\quad ({\mathbf{v}}_{x}^{'})_{{j,k,\ell }}^{n} = \frac{{8({\mathbf{V}}_{{j + 1/2,k,\ell }}^{n} - {\mathbf{V}}_{{j - 1/2,k,\ell }}^{n}) - ({\mathbf{V}}_{{j + 1,k,\ell }}^{n} - {\mathbf{V}}_{{j - 1,k,\ell }}^{n})}}{{6{{h}_{x}}}} \equiv D_{1}^{x}{\mathbf{V}}_{{j,k,\ell }}^{n}, \\ ({\mathbf{v}}_{y}^{'})_{{j,k,\ell }}^{n} = D_{1}^{y}{\mathbf{V}}_{{j,k,\ell }}^{n},\quad ({\mathbf{v}}_{z}^{'})_{{j,k,\ell }}^{n} = D_{1}^{z}{\mathbf{V}}_{{j,k,\ell }}^{n},\quad ({\mathbf{v}}_{{xy}}^{{''}})_{{j,k,\ell }}^{n} = D_{1}^{y}D_{1}^{x}{\mathbf{V}}_{{j,k,\ell }}^{n}, \\ ({\mathbf{v}}_{{yz}}^{{''}})_{{j,k,\ell }}^{n} = D_{1}^{z}D_{1}^{y}{\mathbf{V}}_{{j,k,\ell }}^{n},\quad ({\mathbf{v}}_{{xz}}^{{''}})_{{j,k,\ell }}^{n} = D_{1}^{z}D_{1}^{x}{\mathbf{V}}_{{j,k,\ell }}^{n},\quad ({\mathbf{v}}_{{xyz}}^{{'''}})_{{j,k,\ell }}^{n} = D_{1}^{z}D_{1}^{y}D_{1}^{x}{\mathbf{V}}_{{j,k,\ell }}^{n}, \\ j = 0,\;1,\;2,\; \ldots ,\;{{N}_{x}},\quad k = 0,\;1,\;2,\; \ldots ,\;{{N}_{y}},\quad \ell = 0,\;1,\;2,\; \ldots ,\;{{N}_{z}}. \\ \end{gathered} $1.8. Результирующая бикомпактная схема и общий алгоритм счета
Введенные выше операторы перехода (11), (15), (22), (27), (28) и (30) позволяют записать результирующую бикомпактную схему в максимально лаконичном виде:
(31)
$\begin{gathered} {\mathbf{\tilde {v}}} = {{S}_{{{\text{visc}}}}}\left( {\frac{\tau }{2}} \right){{S}_{{{\mathbf{V}} \to {\mathbf{v}}}}}{{S}_{{{\text{conv}}}}}(\tau ){{S}_{{{\mathbf{v}} \to {\mathbf{V}}}}}{{S}_{{{\text{visc}}}}}\left( {\frac{\tau }{2}} \right){{S}_{{{\text{pr}}}}}\left( {\frac{\tau }{2},{{p}^{n}}} \right){{{\mathbf{v}}}^{n}}, \\ {{p}^{{n + 1}}} = {{S}_{{{\text{ell}}}}}\left( {\frac{\tau }{2}} \right){\mathbf{\tilde {v}}},\quad {{{\mathbf{v}}}^{{n + 1}}} = {{S}_{{{\text{pr}}}}}\left( {\frac{\tau }{2},{{p}^{{n + 1}}}} \right){\mathbf{\tilde {v}}}. \\ \end{gathered} $Бикомпактная схема (31) аппроксимирует систему уравнений Навье–Стокса (1) с погрешностью $O({{\tau }^{2}},{{h}^{3}})$ на неравномерных пространственных сетках и с погрешностью $O({{\tau }^{2}},{{h}^{4}})$ на равномерных сетках. В любом случае, при $\tau = O(h)$ погрешность аппроксимации составляет $O({{\tau }^{2}})$. Отметим, что при такой связи между шагами $\tau $ и $h$ максимальное конвективное (гиперболическое) число Куранта остается постоянным при сгущении сетки, что вполне уместно и желательно при расчетах течений с доминированием процесса конвекции, т.е. при больших числах Рейнольдса.
Далее схему (31) мы будем сокращенно называть T2B4. Тем самым мы подчеркиваем, что для счета по времени применяется метод трапеций второго порядка, а для дискретизации пространственных производных в уравнениях (2), (3), (18) – бикомпактная аппроксимация четвертого порядка.
Дадим также словесное описание общего алгоритма счета по схеме T2B4. Переход со слоя ${{t}^{n}}$ на слой ${{t}^{{n + 1}}}$ делится на 9 этапов.
Шаг 1. Вычислить параметры потокового расщепления $C_{2}^{d}$, $d = x,y,z$, по формуле (8).
Шаг 2. Добавить к скорости ${{{\mathbf{v}}}^{n}}$ слагаемое $( - (\tau {\text{/}}2)\nabla {{p}^{n}})$ по формулам (24), (26) и их вариантам для ${{{v}}_{y}}$, ${{{v}}_{z}}$.
Шаг 3. Сделать полшага ($\tau {\text{/}}2$) по бикомпактной схеме (13), (14)
для вязкой части уравнений Навье–Стокса, взяв в качестве  скорость, найденную на шаге 2.
скорость, найденную на шаге 2.
Шаг 4. Построить в каждой ячейке сетки трикубический интерполяционный полином Эрмита для скорости, найденной на шаге 3. При помощи этого полинома посчитать значения скорости в полуцелых узлах сетки $\Omega $, отбросив после этого значения производных скорости в целых узлах.
Шаг 5. Сделать полный шаг ($\tau $) по локально-одномерной бикомпактной схеме (11)
для конвективной части уравнений Навье–Стокса, взяв вместо  скорость, полученную на шаге 4.
скорость, полученную на шаге 4.
Шаг 6. Посчитать по формулам (29) значения производных скорости, найденной на шаге 5, в целых узлах сетки $\Omega $, отбросив после этого значения скорости в полуцелых узлах.
Шаг 7. Сделать полшага ($\tau {\text{/}}2$) по бикомпактной схеме (13), (14)
для вязкой части уравнений Навье–Стокса, взяв в качестве  скорость, найденную на шаге 6.
скорость, найденную на шаге 6.
Шаг 8. Найти по бикомпактной схеме (20), (21)
искомое давление на верхнем слое ${{p}^{{n + 1}}}$, заменив при этом шаг $\tau $ на $\tau {\text{/}}2$, а скорость  на скорость, найденную на шаге 7.
на скорость, найденную на шаге 7.
Шаг 9. Получить искомую скорость на верхнем слое ${{{\mathbf{v}}}^{{n + 1}}}$, добавив к скорости, найденной на шаге 7, слагаемое $( - (\tau {\text{/}}2)\nabla {{p}^{{n + 1}}})$ по формулам (24), (26) и их вариантам для ${{{v}}_{y}}$, ${{{v}}_{z}}$.
2. ДВУМЕРНЫЙ ВИХРЬ ТЕЙЛОРА–ГРИНА: ПРОВЕРКА СХЕМЫ НА СЕТОЧНУЮ СХОДИМОСТЬ
Продемонстрируем сеточную сходимость бикомпактной схемы T2B4 (31) на точном решении задачи о двумерном вихре Тейлора–Грина:
(32)
$\begin{gathered} {{{v}}_{x}} = {{e}^{{ - t/{\text{Re}}}}}cosxsiny,\quad {{{v}}_{y}} = - {{e}^{{ - t/{\text{Re}}}}}sinxcosy,\quad {{{v}}_{z}} = 0, \\ p = - \frac{1}{4}{{e}^{{ - 2t/{\text{Re}}}}}(cos2x + cos2y). \\ \end{gathered} $Хотя задачу о двумерном вихре Тейлора–Грина можно и разумно решать в плоскости $Oxy$ на двумерной сетке, мы проведем вычисления во всех трех измерениях на трехмерной сетке, чтобы проверить именно трехмерную схему T2B4 и алгоритм счета для нее, описанные в разд. 1.
Расчеты выполним при ${\text{Re}} = 10$ до момента времени ${{t}_{{max}}} = 0.5$. Пространственные сетки равномерные, имеют размеры $N \times N \times 2$, где $N$ пробегает значения 25, 50, 100, 200, 400; шаг $\tau = {\text{const}}$, количество шагов по времени берется равным 10, 20, 40, 80, 160 соответственно (конвективное число Куранта в начальный момент времени $t = 0$ равно 0.4, вязкое – примерно 0.08 для сетки с $N = 25$). Параметр потокового расщепления $\delta = 0.2$, параметр метода ИПФ при решении уравнения Пуассона $\theta = 0.2$, относительная точность для всех итерационных методов ${\text{rtol}} = {{10}^{{ - 10}}}$.
В табл. 1 приведены абсолютные погрешности ${{E}_{\infty }}$ и локальные порядки сходимости ${{k}_{\infty }}$ бикомпактной схемы T2B4 в норме ${{L}_{\infty }}$ в момент времени $t = {{t}_{{max}}}$. Любопытно, что в данной конкретной задаче апостериорные порядки сходимости превосходят ожидаемый теоретический (второй): порядки сходимости для компонент скорости ${{{v}}_{x}}$ и ${{{v}}_{y}}$ меняются от 3 до 2.4; для давления $p$ – от примерно 2.25 до 2.4; погрешность в компоненте ${{{v}}_{z}}$ как минимум в ${{10}^{3}}$ раз меньше погрешностей в компонентах ${{{v}}_{x}}$ и ${{{v}}_{y}}$ на каждой сетке и быстро (с 4–5 порядком) стремится к величине, почти десятикратно меньшей ${\text{rtol}}$. Подводя итог, можно констатировать, что в данной постановке задачи о двумерном вихре Тейлора–Грина бикомпактная схема T2B4 сходится с порядком больше 2.
Таблица 1.
Абсолютные погрешности ${{E}_{\infty }}$ и локальные порядки сходимости ${{k}_{\infty }}$ бикомпактной схемы T2B4 в норме ${{L}_{\infty }}$ в задаче о двумерном вихре Тейлора–Грина
| $N$ | ${{E}_{\infty }}$, ${{k}_{\infty }}$ для ${{{v}}_{x}}$ | ${{E}_{\infty }}$, ${{k}_{\infty }}$ для ${{{v}}_{y}}$ | ${{E}_{\infty }}$, ${{k}_{\infty }}$ для ${{{v}}_{z}}$ | ${{E}_{\infty }}$, ${{k}_{\infty }}$ для $p$ | ||||
|---|---|---|---|---|---|---|---|---|
| 25 | 9.93E–04 | 9.84E–04 | 1.34E–07 | 8.13E–04 | ||||
| 50 | 1.25E–04 | 2.99 | 1.21E–04 | 3.02 | 3.96E–09 | 5.08 | 1.70E–04 | 2.26 |
| 100 | 1.68E–05 | 2.90 | 1.50E–05 | 3.01 | 3.11E–10 | 3.67 | 3.22E–05 | 2.40 |
| 200 | 2.79E–06 | 2.60 | 2.64E–06 | 2.50 | 7.63E–12 | 5.35 | 5.74E–06 | 2.49 |
| 400 | 5.25E–07 | 2.41 | 4.88E–07 | 2.44 | 7.28E–12 | 0.07 | 1.10E–06 | 2.39 |
Добавим, что метод ИПФ для схем (13) и (20) при $N = 100$ сходится до относительной погрешности ${\text{rtol}} = {{10}^{{ - 10}}}$ за 25 и 40 итераций соответственно; при менее жестком ограничении на точность итераций в ${\text{rtol}} = {{10}^{{ - 7}}}$ ИПФ сходится за 2 и 15 итераций соответственно.
3. ТРЕХМЕРНЫЙ ВИХРЬ ТЕЙЛОРА–ГРИНА
3.1. Начальное условие задачи
Начальное условие задачи о трехмерном вихре Тейлора–Грина имеет вид:
(33)
$\begin{gathered} {{\left. {{{{v}}_{x}}} \right|}_{{t = 0}}} = sinxcosycosz,\quad {{\left. {{{{v}}_{y}}} \right|}_{{t = 0}}} = - cosxsinycosz,\quad {{\left. {{{{v}}_{z}}} \right|}_{{t = 0}}} = 0, \\ {{\left. p \right|}_{{t = 0}}} = \frac{1}{{16}}(cos2x + cos2y)(2 + cos2z). \\ \end{gathered} $Посчитаем эту задачу по бикомпактной схеме T2B4 (31) при ${\text{Re}} = 400$, 800, 1600, рассмотрев тем самым оба режима распада. Счет будем вести до времени ${{t}_{{max}}} = 20$. Перечислим параметры схемы T2B4, общие для всех расчетов: $\delta = 0.2$, $\theta = 0.2$, ${\text{rtol}} = {{10}^{{ - 7}}}$. Сетки для всех вариантов задачи равномерные и по пространству, и по времени.
Необходимо также сделать два пояснения. Во-первых, (средняя удельная) кинетическая энергия жидкости ${{E}_{K}}$ определяется как
3.2. Результаты для Re = 400
Возьмем сетку по пространству ${{64}^{3}}$ ячеек, положим временной шаг $\tau = 0.02$ (конвективное число Куранта равно 0.5). Посчитанное поле модуля завихренности $\omega = \left| {\mathbf{\omega }} \right|$ изображено в моменты времени $t = 0$, 5, 10, 15, 17.5, 20 на фиг. 1. Видно, что распад начального вихря действительно происходит в ламинарном режиме: активного перемешивания слоев жидкости не наблюдается, завихренность по своей структуре остается упорядоченно ячеистой, с течением времени (при $t > 10$) вытягиваясь в длинные филаменты (волокна) и затухая. На фиг. 2 показаны две кривые скорости диссипации кинетической энергии $\varepsilon = - d{{E}_{K}}{\text{/}}dt$: одна получена по схеме T2B4, другая взята из работы [24] и полагается эталонной. Хотя в окрестности $t = 8$ схема T2B4 несколько занижает диссипацию ${{E}_{K}}$, в целом можно сказать, что на достаточно грубой сетке ${{64}^{3}}$ ячеек схема T2B4 воспроизводит эту зависимость близко к эталону.
Фиг. 1.
Поле завихренности $\omega = \left| {\operatorname{rot} {\mathbf{v}}} \right|$ в сечениях $x = \pi {\text{/}}2$, $y = \pi {\text{/}}2$, $z = 0$ в моменты времени $t = 0$, 5, 10, 15, 17.5, 20 при ${\text{Re}} = 400$ (ламинарный режим). Результаты получены по бикомпактной схеме T2B4 на сетке ${{64}^{3}}$ ячеек.

Фиг. 2.
Скорость диссипации кинетической энергии жидкости при ${\text{Re}} = 400$. Маркеры – расчет по бикомпактной схеме T2B4 на сетке ${{64}^{3}}$ ячеек, сплошная линия – эталонная зависимость из работы [24].

3.3. Результаты для Re = 800
Возьмем более подробную сетку по пространству ${{128}^{3}}$ ячеек, временной шаг пропорционально уменьшим до $\tau = 0.01$. Визуализация найденного поля $\omega $ в разные моменты времени приведена на фиг. 3. Из этой визуализации следует, что течение сохраняет более-менее упорядоченную ячеистую структуру вплоть до момента времени $t = 17.5$; однако, ко времени $t = 20$ движение жидкости становится полностью турбулентным, как и ожидалось. Из данных с фиг. 4 можно заключить, что при ${\text{Re}} = 800$ схема T2B4, как и в предыдущем варианте задачи при ${\text{Re}} = 400$, дает верную скорость диссипации кинетической энергии.
Фиг. 3.
Поле завихренности $\omega = \left| {\operatorname{rot} {\mathbf{v}}} \right|$ в сечениях $x = \pi {\text{/}}2$, $y = \pi {\text{/}}2$, $z = 0$ в моменты времени $t = 0$, 5, 10, 15, 17.5, 20 при ${\text{Re}} = 800$ (турбулентный режим). Результаты получены по бикомпактной схеме T2B4 на сетке ${{128}^{3}}$ ячеек.

Фиг. 4.
Скорость диссипации кинетической энергии жидкости при ${\text{Re}} = 800$. Маркеры – расчет по бикомпактной схеме T2B4 на сетке ${{128}^{3}}$ ячеек, сплошная линия – эталонная зависимость из работы [24].

3.4. Результаты для Re = 1600
Параметры сетки выберем такими же, как в предыдущем варианте: по пространству ${{128}^{3}}$ ячеек, по времени шаг $\tau = 0.01$. Отметим, что в данном варианте задачи на данной сетке “чистая” (без монотонизации) бездиссипативная бикомпактная схема T2B4 “разваливается” в момент времени $t \approx 7.4$, сразу после начала интенсивного вихреобразования. Эта проблема устраняется, если оператор перехода ${{S}_{{{\text{conv}}}}}(\tau )$ (11) лимитирован при помощи метода консервативной монотонизации [21]. Положим параметр этого метода ${{C}_{1}} = 0.5$, что на порядок меньше тех значений, которые обычно употребляются при расчетах задач с сильными разрывами (см. [21]).
На фиг. 5 приведена визуализация поля $\omega $ в разные моменты времени. Что разумно, течение при ${\text{Re}} = 1600$ по сравнению с течением при ${\text{Re}} = 800$ характеризуется более сильным производством завихренности; уже к моменту времени времени $t = 15$ всякая связь с начальной структурой движения потеряна, а при $t = 20$ вычислительная область целиком заполнена практически однородной изотропной турбулентностью.
Фиг. 5.
Поле завихренности $\omega = \left| {\operatorname{rot} {\mathbf{v}}} \right|$ в сечениях $x = \pi {\text{/}}2$, $y = \pi {\text{/}}2$, $z = 0$ в моменты времени $t = 0$, 5, 10, 15, 17.5, 20 при ${\text{Re}} = 1600$ (турбулентный режим). Результаты получены по монотонизированной бикомпактной схеме T2B4 на сетке ${{128}^{3}}$ ячеек.

Перейдем к анализу кривых диссипации кинетической энергии с фиг. 6. Из этой фигуры ясно, что при ${\text{Re}} = 1600$ монотонизированная схема T2B4 воспроизводит зависимость $\varepsilon (t)$ хуже, чем ее чистая версия при ${\text{Re}} = 400$, 800. Тем не менее нельзя не заметить две особенности. Во-первых, монотонизированная схема T2B4 дает кривую диссипации, примерно правильную по форме, но смещенную влево на $\Delta t \approx 0.3$. Другими словами, процесс превращения кинетической энергии в тепло идет по траектории верной формы, но с небольшим опережением. Во-вторых, если судить по данным для “чистой” схемы T2B4 (очевидно, доступным только до момента ее развала), то метод консервативной монотонизации не дает существенной численной прибавки к реальной диссипации. Из второго замечания следует, что опережение в диссипации кинетической энергии связано с подробностью сетки и погрешностями чистой бикомпактной аппроксимации, а не с методом консервативной монотонизации.
Фиг. 6.
Скорость диссипации кинетической энергии жидкости при ${\text{Re}} = 1600$. Круглые маркеры со сплошной линией – расчет по монотонизированной бикомпактной схеме T2B4 на сетке ${{128}^{3}}$ ячеек, треугольные маркеры – расчет по той же схеме без монотонизации, сплошная линия без маркеров – эталонная зависимость из работы [24].

Важнейшим требованием к любой численной схеме для счета турбулентных течений является то, что она должна как можно точнее воспроизводить спектр кинетической энергии ${{\sigma }_{K}}(k,t)$, где $k$ – волновое число, пробегающее значения $0,\;1,\; \ldots ,\;{{N}_{{min}}}{\text{/}}2$, ${{N}_{{min}}} = min({{N}_{x}},{{N}_{y}},{{N}_{z}})$. Уточним, что ${{\sigma }_{K}}(k,t)$ вычисляется по формуле (например, см. [24]):
Фигура 7 позволяет выяснить, насколько хорошо этому требованию удовлетворяет монотонизированная бикомпактная схема T2B4. Сравнение с эталонным спектром, полученным в работе [29] по псевдоспектральной схеме с очень высоким разрешением в ${{512}^{3}}$ степеней свободы (фактически это спектр сошедшегося решения), показывает, что схема T2B4 безукоризненно разрешает инерционный интервал, но несколько преувеличивает затухание мелких вихрей в диссипативном интервале. Впрочем, у схемы T2B4 диссипативный участок спектра не сваливается резко вниз, а идет почти параллельно эталону, что свидетельствует об умеренности численной диссипации, вносимой методом консервативной монотонизации [21].
Фиг. 7.
Спектр кинетической энергии жидкости при ${\text{Re}} = 1600$ в момент времени $t = 8.5$. Маркеры – расчет по монотонизированной бикомпактной схеме T2B4 на сетке ${{128}^{3}}$ ячеек, сплошная линия – эталонный расчет [29] по псевдоспектральной схеме с ${{512}^{3}}$ степенями свободы, штрихпунктир – кривая ${{\sigma }_{K}} = 0.1{{k}^{{ - 5/3}}}.$

Интересно сделать более серьезную проверку бикомпактной схемы T2B4 на разрешение спектра: выполним расчеты на менее подробной сетке из ${{64}^{3}}$ ячеек и на совсем редкой сетке из ${{32}^{3}}$ ячеек ($\tau = 0.02$ и 0.04 соответственно). Консервативную монотонизацию при этом выключим (${{C}_{1}} = 0$), так как схема T2B4 на этих сетках досчитывает задачу до конца без монотонизации. На фиг. 8 изображены полученные спектры. Очевидно, схема T2B4 корректно, без “загибов вниз”, воспроизводит инерционный участок спектра даже на сетке из ${{32}^{3}}$ ячеек, не разрешающей все мелкие вихри и часть вихрей среднего масштаба. Из этого можно сделать вывод, что бикомпактная схема T2B4 позволяет правильно рассчитывать динамику крупных вихрей, что очень важно при LES-моделировании.
Фиг. 8.
Спектр кинетической энергии жидкости при ${\text{Re}} = 1600$ в момент времени $t = 8.5$. Круглые маркеры – расчет по бикомпактной схеме T2B4 на сетке ${{64}^{3}}$ ячеек, треугольные маркеры – расчет по той же схеме на сетке ${{32}^{3}}$ ячеек, сплошная линия – эталонный расчет [29] по псевдоспектральной схеме с ${{512}^{3}}$ степенями свободы, штрихпунктир – кривая ${{\sigma }_{K}} = 0.1{{k}^{{ - 5/3}}}.$

ЗАКЛЮЧЕНИЕ
Для нестационарных уравнений Навье–Стокса в случае несжимаемой жидкости впервые разработана высокоточная бикомпактная схема. Она получена методом расщепления по физическим процессам Марчука–Стрэнга. Для счета конвективной части исходной системы уравнений применена уже известная локально-одномерная бикомпактная схема. Для счета вязкой части и части, отвечающей за силы давления и несжимаемость жидкости, выведены новые бикомпактные схемы. Методика построения последних обобщает уже имеющийся подход, ранее изложенный применительно к одномерному уравнению теплопроводности. При дискретизации каждой части расщепленной системы уравнений пространственные производные аппроксимированы с четвертым порядком, а временные (если они есть) – методом трапеций со вторым порядком. Реализация бикомпактных схем для вязкой части и для уравнения Пуассона на давление использует метод итерируемой приближенной факторизации (ИПФ). В свою очередь, счет по этому методу и по схеме для конвективной части сведены к совокупности независимых одномерных двухточечных прогонок, из чего следует экономичность результирующей бикомпактной схемы для суммарной системы уравнений.
Предлагаемая бикомпактная схема, обозначаемая как T2B4, испытана на сеточную сходимость в задаче о двумерном вихре Тейлора–Грина с известным точным решением. Конкретно в этой задаче схема T2B4 показала порядок сходимости выше теоретического, равного 2. При умеренных требованиях на относительную точность итераций (${{10}^{{ - 7}}}$ для сетки $100 \times 100$) метод ИПФ сходится достаточно быстро, за 2 итерации в вязкой части и за 15 итераций в уравнении Пуассона на давление.
По схеме T2B4 при числах Рейнольдса ${\text{Re}} = 400$, 800, 1600 посчитана задача о распаде трехмерного вихря Тейлора–Грина. Выяснено, что конвективный оператор перехода схемы T2B4 при ${\text{Re}} = 1600$ на сетках подробнее ${{64}^{3}}$ ячеек требует лимитирования наклонов (чтобы обеспечить устойчивость счета), для чего выбран метод консервативной монотонизации [21]. При всех рассмотренных ${\text{Re}}$ установлено хорошее согласие с эталонными данными для скорости диссипации кинетической энергии. Показано, что схема T2B4 при ${\text{Re}} = 1600$ с высоким качеством воспроизводит спектр кинетической энергии, в том числе и на очень грубой сетке ${{32}^{3}}$ ячеек, не разрешающей даже часть вихрей среднего масштаба в инерционном интервале спектра. Расчет на более подробной сетке ${{128}^{3}}$ ячеек, разрешающей часть диссипативного интервала спектра, выявил умеренность численной диссипации, вносимой методом консервативной монотонизации. Полученные результаты говорят о том, что бикомпактные схемы перспективны в приложении к расчетам ламинарно-турбулентных переходов и для моделирования турбулентных течений в рамках подходов LES/ILES.
Список литературы
Simulation of transition and turbulence decay in the Taylor–Green vortex / D. Drikakis, C. Fureby, F. Grinstein, D. Youngs // J. Turbul. 2007. V. 8. № 20. P. 1–12.
Kawai S., Lele S.K. Large-eddy simulation of jet mixing in supersonic crossflows // AIAA J. 2010. V. 48. № 9. P. 2063–2083.
Bull J.R., Jameson A. Simulation of the Taylor–Green vortex using high-order flux reconstruction schemes // AIAA J. 2015. V. 53. № 9. P. 2750–2761.
El Rafei M., Könözsy L., Rana Z. Investigation of numerical dissipation in classical and implicit large eddy simulations // Aerospace. 2017. V. 4. № 59. P. 1–20.
De la Llave Plata M., Couaillier V., Pape M.-C. On the use of a high-order discontinuous Galerkin method for DNS and LES of wall-bounded turbulence // Comput. Fluids. 2018. V. 176. P. 320–337.
Толстых А.И. Компактные разностные схемы и их применение в задачах аэрогидродинамики. М.: Наука, 1990.
Толстых А.И. Компактные и мультиоператорные аппроксимации высокой точности для уравнений в частных производных. М.: Наука, 2015. 350 с.
Grimich K., Cinnella P., Lerat A. Spectral properties of high-order residual-based compact schemes for unsteady compressible flows // J. Comput. Phys. 2013. V. 252. P. 142–162.
Новые алгоритмы вычислительной гидродинамики для многопроцессорных вычислительных комплексов / В.М. Головизнин, М.А. Зайцев, С.А. Карабасов, И.А. Короткин. М.: Изд-во Московского университета, 2013. 472 с.
Асфандияров Д.Г., Головизнин В.М., Финогенов С.А. Беспараметрический метод расчета турбулентного течения в плоском канале в широком диапазоне числе Рейнольдса // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 9. С. 1545–1558.
Рогов Б.В., Михайловская М.Н. О сходимости компактных разностных схем // Матем. моделирование. 2008. Т. 20. № 1. С. 99–116.
Михайловская М.Н., Рогов Б.В. Монотонные компактные схемы бегущего счета для систем уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 4. С. 672–695.
Рогов Б.В. Высокоточная монотонная компактная схема бегущего счета для многомерных уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 2. С. 264–274.
Chikitkin A.V., Rogov B.V., Utyuzhnikov S.V. High-order accurate monotone compact running scheme for multidimensional hyperbolic equations // Appl. Numer. Math. 2015. V. 93. P. 150–163.
Брагин М.Д., Рогов Б.В. Гибридные бикомпактные схемы с минимальной диссипацией для уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 958–972.
Брагин М.Д., Рогов Б.В. О точном пространственном расщеплении многомерного скалярного квазилинейного гиперболического закона сохранения // Докл. АН. 2016. Т. 469. № 2. С. 143–147.
Брагин М.Д., Рогов Б.В. Метод итерируемой приближенной факторизации операторов высокоточной бикомпактной схемы для систем многомерных неоднородных квазилинейных уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 3. С. 313–325.
Рогов Б.В., Брагин М.Д. О свойствах спектрального разрешения симметричных бикомпактных схем четвертого порядка аппроксимации // Докл. АН. 2017. Т. 475. № 2. С. 140–144.
Chikitkin A.V., Rogov B.V. Family of central bicompact schemes with spectral resolution property for hyperbolic equations // Appl. Numer. Math. 2019. V. 142. P. 151–170.
Rogov B.V. Dispersive and dissipative properties of the fully discrete bicompact schemes of the fourth order of spatial approximation for hyperbolic equations // Appl. Numer. Math. 2019. V. 139. P. 136–155.
Bragin M.D., Rogov B.V. Conservative limiting method for high-order bicompact schemes as applied to systems of hyperbolic equations // Appl. Numer. Math. 2020. V. 151. P. 229–245.
Брагин М.Д., Рогов Б.В. Высокоточные бикомпактные схемы для численного моделирования течений многокомпонентных газов с несколькими химическими реакциями // Матем. моделирование. 2020. Т. 32. № 6. С. 21–36.
Boris J.P. On large eddy simulation using subgrid turbulence models // Whither Turbulence? Turbulence at the Crossroads. Lecture Notes in Physics. 1990. P. 344–353.
Small-scale structure of the Taylor–Green vortex / M.E. Brachet, D.I. Meiron, S.A. Orszag et al. // J. Fluid Mech. 1983. V. 130. P. 411–452.
Марчук Г.И. Методы расщепления. М.: Наука, 1988. 263 с.
Strang G. On the construction and comparison of difference schemes // SIAM J. Numer. Anal. 1968. V. 5. № 2. P. 506–517.
Самарский А.А. Теория разностных схем. М.: Наука, 1989. 616 с.
Яненко Н.Н. Метод дробных шагов решений многомерных задач математической физики. Новосибирск: Наука, 1967. 197 с.
A comparison of vortex and pseudo-spectral methods for the simulation of periodic vertical flows at high Reynolds numbers / W.M. Van Rees, A. Leonard, D.I. Pullin, P. Koumoutsakos // J. Comput. Phys. 2011. V. 230. P. 2794–2805.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики