Журнал вычислительной математики и математической физики, 2021, T. 61, № 11, стр. 1873-1893

1. ВВЕДЕНИЕ. ДВУСПИРАЛЬНАЯ¹²² СХЕМА ТУЛИНА

1.1. Получено аналитическое решение плоской задачи теории струй идеальной жидкости (см. [1]–[4]) о симметричном кавитационном обтекании клина для ряда классических схем замыкания каверны³³. В первой части работы (см. [5]) решение для схем Гельмгольца–Кирхгофа, Жуковского–Рошко и Рябушинского было выписано через гипергеометрические функции Гаусса и Аппéля. В настоящей, второй части работы решение для двуспиральной схемы Тулина (см. [6]) дано в терминах гипергеометрической функции Лауричеллы⁴⁴. В дальнейшем планируется публикация аналитических решений для односпиральной (первой) схемы Тулина (см. [13]) и схемы Эфроса (см. [14]).

1.2. Как и принято в плоской теории струй идеальной жидкости (см. [1], [2], [15]), картина течения располагается на комплексной плоскости $z = x + iy$ и описывается в терминах комплексного потенциала $w = f(z) = \varphi (x,y) + i\psi (x,y)$, представляющего собой аналитическую функцию переменного $z$, где $\varphi (x,y)$ – потенциал скорости, а $\psi (x,y)$ – функция тока, так что уравнение линии тока есть $\psi (x,y) = \varepsilon $, где $\varepsilon = {\text{const}}$. Скорость жидкости ${\mathbf{V}}(z) = \operatorname{grad} \varphi (x,y)$ выражается через комплексный потенциал в виде его сопряженной производной

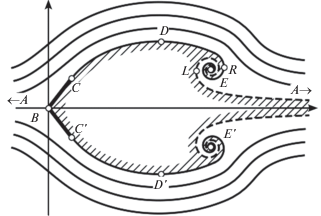
где $V(z) = \left| {{\mathbf{V}}(z)} \right|$ и $\theta (z) = \arg {\mathbf{V}}(z)$ – соответственно модуль и угол наклона скорости к оси $x$. Давление $p(z)$ в потоке связано со скоростью законом Бернулли где $\rho $ – плотность жидкости. Через комплексный потенциал выражаются и все остальные характеристики течения, в том числе коэффициент сопротивления ${{{\mathbf{C}}}_{x}}$, а также относительные длина $\mathfrak{L}$ и ширина $\mathfrak{W}$ каверны (см. разд. 3–6).

1.3. Рассмотрим симметричное относительно продольной оси $x$ кавитационное обтекание клина неограниченным по ширине потоком идеальной жидкости при замыкании каверны по двуспиральной схеме Тулина. Картина такого течения представлена на фиг. 1 в виде распределения линий тока. Через $A$ обозначена бесконечно удаленная точка на плоскости $z$; скорость жидкости на бесконечности равна ${{V}_{\infty }}$ и направлена вдоль оси $x$. Стенки клина, изображенные жирными линиями, имеют длину $l$ и наклонены к оси $x$ под углами $ \pm \pi \alpha $.

Подходя к острию $B$ клина, поток на фиг. 1 разделяется на два: верхний и нижний. Вместе с ним на этом острие разветвляется и линия тока, изначально идущая по отрицательной вещественной полуоси $(AB)$ и считающаяся “нулевой”, т.е. отвечающая уравнению $\psi (x,y) = 0$. Каждая из ее ветвей вместе с соответствующим потоком идет по своей, верхней $(BC)$ или нижней $(C{\kern 1pt} '{\kern 1pt} B)$ стенке клина⁵⁵, в конце которой она отрывается от его кромки (обозначенной соответственно через $C$ или $C{\kern 1pt} '$); таким образом, выполняются условия

Предполагается, что эти потоки при их дальнейшем движении “возвращаются” в бесконечно удаленную точку $A$ (двигаясь вправо на фиг. 1), а между ограничивающими эти потоки ветвями нулевой линии возникает пространство, которое моделирует каверну – область, заполненную парами или газом, а также след, т.е. присоединенную к каверне вниз по потоку область, представляющую собой вспененное (пронизанное мелкими пузырьками) турбулентное течение⁶⁶.

Оторвавшиеся от кромок С и $C{\kern 1pt} '$ участки $(CDE)$ и $(E{\kern 1pt} '{\kern 1pt} D{\kern 1pt} '{\kern 1pt} C{\kern 1pt} ')$ нулевой линии тока изображены на фиг. 1 сплошными линиями (обычной толщины). Они представляют собой свободные линии тока, т.е. дуги, вид которых заранее не известен и находится из условия, что со стороны газов, заполняющих каверну, на эти дуги действует заданное постоянное давление ${{p}_{Q}}$ (меньшее, чем давление ${{p}_{\infty }}$ на бесконечности). Тогда, согласно (2), на них должен быть постоянен и модуль скорости жидкости, обозначаемый через ${{V}_{Q}}$ $( > {\kern 1pt} {{V}_{\infty }})$, т.е. должно выполняться условие

Это условие, как показано далее, приводит к тому, что дуги $(CDE)$ и $(E{\kern 1pt} '{\kern 1pt} D{\kern 1pt} '{\kern 1pt} C{\kern 1pt} ')$ соответственно вблизи точек $E$ и $E{\kern 1pt} '$ являются закручивающимися спиралевидными линиями и образуют вихри с центрами в этих точках (фиг. 1). Если следовать движению жидкости, например, по линии $(DE)$, то она будет стремиться к точке $E$, закручиваясь по часовой стрелке.

Далее, в данной схеме Тулина принимается, что исходящие из точек $E$ и $E{\kern 1pt} '$ продолжения $(EA)$ и $(AE{\kern 1pt} ')$ нулевой линии (изображенные на фиг. 1 штриховыми линиями) представляют собой, как и предшествующие участки, свободные линии тока, но с другим заданным на них давлением, совпадающим с давлением на бесконечности ${{p}_{\infty }} > {{p}_{Q}}$; тогда с учетом (2) получаем

Из этого условия (как показано ниже) следует, что дуги $(EA)$ и ${{\varphi }_{C}}$ соответственно вблизи точек $E$ и $E{\kern 1pt} '$ являются раскручивающимися спиралевидными линиями (фиг. 1). В частности, если следовать движению жидкости по линии $(EA)$, то она, выйдя из точки $E$, будет удаляться от него, раскручиваясь против часовой стрелки.

Таким образом, условия (4), (5) приводят к тому, что линии $(DE)$ и $(EA)$ вблизи точки $E$ (а линии $(E{\kern 1pt} 'D{\kern 1pt} ')$, $(AE{\kern 1pt} ')$ – вблизи точки $E{\kern 1pt} '$) образуют вихрь, который (как показано ниже) асимптотически представляет собой пару подобных⁷⁷ логарифмических спиралей. С этим обстоятельством и связано название рассматриваемой схемы Тулина.

Согласно Тулину (см. [6]), центры $E$ и $E{\kern 1pt} '$ вихрей обозначают место замыкания каверны (фиг. 1), за которым ниже по потоку расположен след, так что исходящие из этих центров участки $(EA)$ и $(AE{\kern 1pt} ')$ нулевой линии тока принимаются в качестве граничных линий следа, который, распространяясь вниз по потоку, простирается до бесконечности – точки $A$.

Через $D$ обозначена точка на верхней ветви, а через и $D{\kern 1pt} '$ – на нижней ветви нулевой линии (фиг. 1), в которых скорость направлена, как и в бесконечности, параллельно оси $x$. Поскольку линии тока, ограничивающие каверну, как известно из [1], [2], должны быть обращены выпуклостью в сторону жидкости, то $D$ является наивысшей, а $D{\kern 1pt} '$ – наинизшей точками каверны. Расстояние между этими точками, отнесенное к размеру основания $2lsin(\pi \alpha )$ клина, принимается в качестве относительной ширины $\mathfrak{W}$ каверны, т.е.

где ${{y}_{D}}$ – ордината⁸⁸ точки $D$ на плоскости $z$. В качестве относительной длины $\mathfrak{L}$ каверны принимаем отношение абсциссы точки $E$ к размеру основания клина:

Определим еще крайнюю левую точку $L$ линии $(EA)$ и крайнюю правую точку $R$ линии $(DE)$ как точки, в которых угол наклона скорости равен $\theta = - \pi {\text{/}}2$ (фиг. 1 и 2а). Тогда можно говорить, что вихрь в верхней половине течения образован линией тока $(REL)$; аналогично можно определить вихрь и ограничивающие его точки и в нижней половине течения. Разность абсцисс точек $R$ и $L$ принимаем в качестве размера $\mathfrak{D}$ вихря, т.е.

Важной характеристикой описанной картины обтекания, как и других кавитационных течений, является число кавитации – известный параметр (см. [1], [2]), определяемый по формуле

или с учетом (2) с помощью эквивалентного равенства Отметим, что скорость жидкости ${{V}_{Q}}$ на поверхности каверны выражается через ${{V}_{\infty }}$ и $Q$ по формуле

1.4. Аналитическое решение рассматриваемой задачи для двуспиральной схемы Тулина построено в разд. 3 и 4. Осуществлена его численная реализация (разд. 5), в том числе вычислены значения коэффициента сопротивления ${{{\mathbf{C}}}_{x}}$, найдены относительная длина $\mathfrak{L}$ и относительная ширина $\mathfrak{W}$ каверны.

На основе этой численной реализации в разд. 5 построены также картины обтекания для различных значений входящих параметров. Следует отметить, что при сравнении этих картин с фиг. 1 может возникнуть недоразумение, связанное с тем, что на картинах, полученных путем вычислений, не видны вихри, центрами которых, согласно сказанному в п. 1.3, должны быть точки $E$ и $E{\kern 1pt} '$. Чтобы устранить это недоразумение, заметим, что представленная на фиг. 1 картина течения является условной с увеличенным для большей наглядности изображением вихревых спиралей⁹⁹. На самом же деле, согласно проведенному расчету, размер вихря $\mathfrak{D}$ имеет порядок ${{10}^{{ - 7}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 8}}}$ при остальных параметрах, лежащих в обычном диапазоне.

Данное значение согласуется с асимптотикой для этой величины $\mathfrak{D} \sim {{Q}^{{ - 2}}}exp( - {{\pi }^{2}}{\text{/}}Q)$, $Q \to 0$, полученной с помощью проведенного в разд. 6 асимптотического анализа решения. Ясно, что такой вихрь не различим на общей картине течения и может быть изображен лишь при локальном сильном увеличении (вид которого приведен ниже на фигуре в разд. 5). Выполненный анализ позволил также установить, что вблизи центра вихря $E$ линии $(RE)$ и $(EL)$ асимптотически представляют собой подобные логарифмические спирали. Уравнение для закручивающейся линии $(RE)$ в локальных полярных координатах $(r,\phi )$ с центром в полюсе $E$ дается формулой r(ϕ) = = 𝒜exp(2πϕ/Q), $\phi \to - \infty $; для раскручивающейся линии аналогичное уравнение отличается лишь на множитель $\sqrt {1 + Q} $.

Получена также асимптотика для числа $N$ оборотов вокруг точки $E$, совершаемых при движении жидкости вдоль линии тока $\{ z:\psi (z) = \varepsilon \} $, соответствующей малому положительному $\varepsilon $ (при остальных параметрах, как обычно, равных $l = 1$, ${{V}_{\infty }} = 1$); заметим, что если $\varepsilon = 0$, то число оборотов, очевидно, бесконечно. Эта асимптотика имеет вид $N \sim - Qln({{Q}^{2}}\varepsilon )$, $\varepsilon \to 0$.

Установлено еще, что относительная ширина следа $\mathfrak{S}(x)$, рассматриваемая как функция продольной координаты $x$, имеет при удалении от каверны и малых $Q$ следующий характер убывания: $\mathfrak{S}(x) \sim {{Q}^{{ - 2}}}{{(x{\text{/}}l)}^{{ - 1/2}}}$, $x \to + \infty $.

Кроме того, найден (согласующийся с [1], [2], [4]) вид асимптотик для величин ${{{\mathbf{C}}}_{x}}(Q)$, $\mathfrak{L}(Q)$, $\mathfrak{W}(Q)$ при стремлении числа кавитации $Q$ к нулю. Первые коэффициенты этих асимптотик выписаны в виде явных формул, а их численные значения приведены в таблицах, где эти значения даны не только для рассмотренной здесь двуспиральной схемы Тулина, но и для изучавшихся в первой части работы (см. [5]) схем Жуковского–Рошко и Рябушинского¹⁰¹⁰.

2. ОБЛАСТЬ ГОДОГРАФА И ОБЛАСТЬ ПОТЕНЦИАЛА

2.1. Поскольку для изучаемой задачи течение симметрично относительно оси $x$ (фиг. 1), то теоретические рассмотрения достаточно проводить только для его верхней половины – области ${{\mathcal{B}}_{z}}$, изображенной на фиг. 2а. Вместе с тем численно получаемую картину обтекания будем давать для всей области течения, как на фиг. 1.

Аналитическую функцию $\zeta = \omega (z)$, определяемую по формуле

или с учетом (1) по эквивалентной формуле называют функцией годографа скорости в форме Жуковского (см. [18]), а область ${{\mathcal{B}}_{\zeta }}: = \omega ({{\mathcal{B}}_{z}})$ – образ области ${{\mathcal{B}}_{z}}$ при отображении ζ = ω(z) – называют областью годографа.

Символ, обозначающий образ области или дуги при конформном отображении, снабжаем нижним индексом, указывающим плоскость, где расположен соответствующий образ. Вместе с тем точки на разных плоскостях, соответствующие друг другу при конформном отображении, обозначаем одинаковыми буквами.

2.2. Используя определение (10), построим область годографа для рассматриваемой задачи. Для этого пройдем границу $\partial {{\mathcal{B}}_{z}}$ в правильном направлении, т.е. так, что область ${{\mathcal{B}}_{z}}$ остается слева.

При движении по участку $(AB)$ скорость монотонно убывает от ${{V}_{\infty }}$ (в бесконечно удаленной точке $A$) до $0$ (в точке остановки $B$). Кроме того, согласно (3), здесь выполняется $\theta = 0$. Отсюда с помощью (9) и (10) находим, что образом этого участка на плоскости годографа $\zeta $ является отрезок вещественной оси

При движении по стенке клина $(BC)$ модуль скорости $V$ монотонно возрастает от $0$ до ${{V}_{Q}}$ и, кроме того, согласно (3), здесь $\theta = \pi \alpha $. Отсюда находим, что образом этого участка на плоскости годографа является прямолинейный отрезок Следующий участок $(CDE)$ есть свободная линия тока с заданным на ней по условию (4) модулем скорости, равным ${{V}_{Q}}$. Тогда его образ ${{(CDE)}_{\zeta }}$, согласно (10), должен лежать на мнимой оси $\{ \operatorname{Re} \zeta = 0\} $. В соответствии с фиг. 2а дуга $(CDE)$ представляет собой вблизи точки $E$ вихревую линию, закрученную по часовой стрелке, поэтому при движении по этой дуге угол наклона скорости монотонно падает от $\theta = \pi \alpha $ до $\theta = - \infty $. Отсюда получаем, что образом этого участка на плоскости годографа является прямолинейный отрезок Участок $(EA)$ также есть свободная линия тока с заданным, согласно (5), модулем скорости ${{V}_{\infty }}$. В соответствии с фиг. 2а эта дуга вблизи точки $E$ представляет собой вихревую линию, закрученную против часовой стрелки, а при приближении к бесконечности $A$ угол наклона скорости $\theta $ на этой дуге приближается к нулю. Таким образом, при движении по этой дуге угол $\theta $ монотонно возрастает от $ - \infty $ до нуля. Тогда из (9) и (10) следует, что образом этого участка служит отрезок

Граница области годографа построена, а вид этой области $\partial {{\mathcal{B}}_{\zeta }}$ дан на фиг. 2в. Отметим, что область годографа для двуспиральной схемы Тулина была приведена в [19] и [16] (при другом определении функции годографа).

2.3. Установим вид области потенциала ${{\mathcal{B}}_{w}}: = f({{\mathcal{B}}_{z}})$, используя стандартные рассуждения, приведенные, например, в [2, стр. 24].

Так как граница $\partial{ \mathcal{B}}$ является нулевой линией тока, то ее образ на плоскости потенциала соответствует значению $\psi = 0$. Вдоль этой линии тока имеем $d\varphi = Vd{{s}_{\varphi }}$, где $d{{s}_{\varphi }}$ – дифференциал длины дуги. Поскольку при стремлении к бесконечно удаленной точке $A$ величина $V$ стремится к значению ${{V}_{\infty }} > 0$, то величина $\varphi $ изменяется от $ - \infty $ до $ + \infty $ вдоль границы $\partial{ \mathcal{B}}$. Если же двигаться вдоль эквипотенциальной линии от нулевой линии тока – грацицы $\partial{ \mathcal{B}}$ до бесконечности (вверх на фиг. 2а), то величина $\psi $, представляющая собой расход жидкости, будет монотонно возрастать от нуля до $ + \infty $. Следовательно, образом ${{\mathcal{B}}_{w}}$ области ${{\mathcal{B}}_{z}}$ на плоскости годографа является верхняя полуплоскость

изображенная на фиг. 2б.

3. ОБЩИЙ ВИД РЕШЕНИЯ ЗАДАЧИ

3.1. Для решения задачи обтекания достаточно найти комплексный потенциал $w = f(z)$, через который выражаются все характеристики течения. Однако, поскольку обратную функцию $z = {{f}^{{ - 1}}}(w)$ находить и использовать проще, чем прямую, то именно ее мы и будем строить (как это обычно и делается).

Рассматриваемая задача о кавитационном обтекании клина заключается, таким образом, в построении функции $z = {{f}^{{ - 1}}}(w)$, исходя из заданных параметров: скорости ${{V}_{\infty }}$ потока на бесконечности, скорости ${{V}_{Q}}$ на поверхности каверны, геометрических параметров клина $l$ и $\alpha $, а также из заданного вида области годографа ${{\mathcal{B}}_{\zeta }}$ и области потенциала ${{\mathcal{B}}_{w}}$ с учетом соответствия между одноименными точками $A$, $B$, $C$ на плоскостях $z$ и $w$, указанными на фиг. 2. Координаты всех этих точек известны, кроме координаты ${{\varphi }_{C}}$ конца стенки клина на плоскости потенциала $w$; для этой величины ниже формируется уравнение.

Потенцируя равенство (11), получаем

используя здесь тождество и вводя функцию $F(w)$ по формуле находим равенство интегрируя которое, устанавливаем представление для искомой функции: С помощью формулы (14) легко выписываются представления для линий тока, а также для относительной длины $\mathfrak{L}$ и относительной ширины $\mathfrak{W}$ каверны (см. ниже. п. 4.7). Уравнение же для неизвестной координаты ${{\varphi }_{C}}$ получаем, интегрируя в представлении (14) по образу ${{(BC)}_{w}}$ этой стенки:

3.2. Коэффициент сопротивления ${{{\mathbf{C}}}_{x}}$ определяется, как известно, в виде отношения $x$-компоненты интеграла сил, действующих на клин, к произведению скоростного напора $\tfrac{1}{2}\rho V_{\infty }^{2}$ на   длину основания клина $2lsin(\pi \alpha )$. Используя закон Бернулли (2) и соотношение $\operatorname{Im} dz = \left| {dz} \right|\sin (\pi \alpha )$, выполняющееся на стенке $(BC)$ клина, по которой производится интегрирование, приходим к следующему выражению для этой величины:

Получаются два вспомогательных выражения: одно – из равенства (10) путем его потенцирования, умножения на сопряженное и вычитания результата из единицы, а второе – непосредственно из (13): Вынесем теперь $V_{Q}^{2}$ из-под знака интеграла (16), учтем вытекающую из (9) формулу $V_{Q}^{2}{\text{/}}V_{\infty }^{2} = 1 + Q$ и подставим в него первое равенство (17). Переходя в получающемся интеграле к переменной $w$ с помощью (12), учитывая соотношение $dz = {{f}^{{ - 1}}}{\kern 1pt} '(w)dw$ и второе равенство (17), а также тождество $\operatorname{Im} ({{e}^{\xi }} - {{e}^{{ - \overline \xi }}}) = 2\operatorname{Im} \operatorname{ch} \xi $, получаем где ${{(BC)}_{w}}$ есть образ при отображении $f$ дуги $(BC)$ на плоскости потенциала.

3.3. Для того чтобы выразить решение задачи и характеристики течения в аналитическом виде, введем вспомогательную полуплоскость ${{\mathcal{B}}_{t}}: = \{ \operatorname{Im} t > 0\} $ и на ней две функции: $w = \chi (t)$ и $\zeta = T(t)$, осуществляющие отображения

с соответствием между одноименными точками $A$, $B$, $C$ на плоскостях $t$, $w$, $\zeta $, легко усматриваемым из фиг. 2б, 2в, 2г. Тогда очевидно, что

Введем еще полукруг ${{\mathcal{B}}_{h}}: = \{ \left| h \right| < 1,\;\operatorname{Im} h > 0\} $, а на нем определим функцию $t = \Theta (h)$ по формуле

осуществляющую отображение $\Theta :{{\mathcal{B}}_{h}}\;\xrightarrow{{{\text{conf}}}}\;{{\mathcal{B}}_{t}}$ с указанным на фиг. 2г, 2д соответствием между одноименными точками $A$, $B$, $C$ на плоскостях $t$ и $h$.

На плоскости $h$ определим еще функцию $\zeta = \Omega (h)$ с помощью двойного тождества

она конформно преобразует полукруг ${{\mathcal{B}}_{h}}$ на область годографа ${{\mathcal{B}}_{\zeta }}$ c соответствием (вполне определенных на фиг. 2в, 2д) одноименных точек $A$, $B$, $C$ на плоскостях $h$ и $\zeta $. Отмеченные на границе $\partial {{\mathcal{B}}_{h}}$ полукруга точки $E$ и $D$ (фиг. 2д) определяются как образы одноименных точек на плоскости годографа; их координатам даны специальные обозначения:

3.4. Выполнив в интеграле (14) замену переменной

включая равенство (21), получим представление для искомой функции ${{f}^{{ - 1}}}(w)$: где верхний предел

Делая ту же замену в интеграле (15) с учетом соотношения

вытекающего из наблюдения, что образ ${{(BC)}_{\zeta }}$ стенки клина лежит (как видно на фиг. 2в) на прямой $\{ \operatorname{Im} \zeta = \pi \alpha \} $, переписываем уравнение (15) для ${{\varphi }_{C}}$ в виде а проведя эту же замену в интеграле (18) с учетом соотношения (25) и формулы получаем выражение для коэффициента сопротивления в виде

3.5. Найдем относительные длину $\mathfrak{L}$ и ширину $\mathfrak{W}$ каверны. Для этого, вычислив с помощью представления (24) абсциссу точки $E$ и ординату точки $D$ на плоскости $z$, подставим их соответственно в формулы (7) и (6); тогда получим

Координаты точек линии тока, соответствующей значению $\psi = \varepsilon $ функции тока, естественно параметризуются в виде ${{z}_{\varepsilon }}(\varphi ) = {{f}^{{ - 1}}}(\varphi + i\varepsilon )$, где параметр $\varphi \in ( - \infty , + \infty )$. Выражение для параметризованных таким образом координат легко следует из формулы (24):

где верхний предел равен $h(\varphi + i\varepsilon ) = {{\Theta }^{{ - 1}}} \circ {{\chi }^{{ - 1}}}(\varphi + i\varepsilon )$.

4. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ

4.1. Построим отображения (19), определенные на плоскости $t$. Первое из них, осуществляемое функцией $\zeta = T(t)$, конформно преобразует полуплоскость ${{\mathcal{B}}_{t}}: = \{ \operatorname{Im} t > 0\} $ на область годографа ${{\mathcal{B}}_{\zeta }}$, представляющую собой четырехугольник и изображенную на фиг. 2в. Оно выражается в виде интеграла Кристоффеля–Шварца (см. [15]) следующим образом:

где параметры ${{t}_{E}}$ (прообраз бесконечно удаленной точки $E$ на плоскости $\zeta $) и $\mathcal{K}$ подлежат нахождению. Нетрудно увидеть, что при обходе малой полуокружности, расположенной в $\{ \operatorname{Im} t > 0\} $, с центром в точке $t = 1$ приращение интеграла (31) равно изменению $\zeta $ при переходе вблизи точки $B$ от верхней к нижней стороне полосы¹¹¹¹ (по нормали к ним), т.е. равно $ - i\pi \alpha $ (фиг. 2в). Отсюда получаем соотношение Аналогично, при обходе расположенной в $\{ \operatorname{Im} t > 0\} $ малой полуокружности с центром в точке $t = {{t}_{E}}$ приращение этого интеграла равно изменению $\zeta $ при переходе от правой к левой стороне полосы вблизи точки $E$, т.е. равно $ - ln\sqrt {1 + Q} $. Отсюда получаем равенство

Из (32), (33) находим

Используя эти формулы и вычисляя интеграл (31) с помощью разложения подынтегрального выражения на простые дроби и применения подстановки $\sqrt t = \xi $, получаем где введено обозначение Отметим еще следующие вытекающие из (34) асимптотики для $\mathcal{K}$ и ${{t}_{E}}$:

Найдем координату ${{t}_{D}}$ прообраза точки $D$, расположенной на плоскости годографа в начале координат, т.е. величину ${{t}_{D}}$, удовлетворяющую условию

она понадобится при вычислении ширины каверны. Введем величину $\gamma = \sqrt {{{t}_{E}}{\text{/}}{{t}_{D}}} $, тогда Подставляя в условие (38) выражения (35) и легко устанавливаемое соотношение получаем после элементарных преобразований уравнение для $\gamma $: Используя здесь связь (36) величин $\beta $ и ${{t}_{E}}$, а также асимптотику ${{t}_{E}}$ из (37), находим, что $\gamma $ имеет следующую асимптотику при $Q \to 0$: $\gamma = {{\gamma }_{0}} + \mathcal{O}({{Q}^{2}})$, где ${{\gamma }_{0}}$ – решение уравнения (40) с правой частью, равной $( - 2)$; решение такого уравнения (с точностью до ${{10}^{{ - 10}}}$) есть ${{\gamma }_{0}} = 0.8335565596$. Для решения уравнения (40) применяем, например, метод Ньютона (см. [21]). Вычислив таким образом $\gamma $, получаем искомую координату Отметим еще легко следующую из (41) асимптотику этой координаты

4.2. Обратимся теперь к отображениям $\chi :{{\mathcal{B}}_{t}}\;\xrightarrow{{{\text{conf}}}}\;{{\mathcal{B}}_{w}}$ и $\Theta :{{\mathcal{B}}_{h}}\;\xrightarrow{{{\text{conf}}}}\;{{\mathcal{B}}_{t}}$. Функция $w = \chi (t)$ есть дробно-линейное отображение (19) полуплоскостей с соответствием одноименных точек $A$, $B$, $C$ (фиг. 2б и 2г). Оно выражается формулой

где ${{\varphi }_{C}}$ находится, как было отмечено выше (см. п. 3.1 и 3.5), из уравнения (26). Из (42) получаем Тогда (вещественные) координаты ${{\varphi }_{E}}$, ${{\varphi }_{D}}$ точек $E$, $D$ на плоскости $w$ записываются через найденные координаты одноименных точек на плоскости $t$ по формулам

Что же касается отображения $t = \Theta (h)$ полукруга ${{\mathcal{B}}_{h}}$ на полуплоскость ${{\mathcal{B}}_{t}}$, то оно дается формулой (20), а его производная и обратное к нему определяются равенствами

Координаты точек $E$ и $D$ на полуокружности $\{ h:\left| h \right| = 1,\;\operatorname{Im} h > 0\} $ (фиг. 2д), обозначенные, согласно (22), через $\mu $ и $\eta $, получаются подстановкой в первую формулу (45) найденных в (36) и (39) величин $\sqrt { - {{t}_{E}}} $ и $\sqrt { - {{t}_{D}}} $: где (напомним) $\beta $ дается равенством (36), а $\gamma $ есть решение уравнения (40).

4.3. Перейдем к получению явных аналитических выражений для искомых величин. Найдем прежде всего вид якобиана преобразования (23), подставив во второе равенство (43) выражение (20) и умножив результат на $\Theta {\kern 1pt} '(h)$ из (45):

Заметим, что для получения явных представлений мы будем в дальнейшем широко использовать гипергеометрическую функцию Лауричеллы для случая трех (комплексных) переменных ${{z}_{1}}$, ${{z}_{2}}$, ${{z}_{3}}$, определяемую¹²¹² с помощью интегрального представления типа Эйлера (см. [10]–[12])

где предполагается $\operatorname{Re} (b) > 0$, $\operatorname{Re} (c - b) > 0$; здесь $\Gamma (x)$ есть гамма-функция (см. [22]). Функция Лауричеллы записывается в виде следующего ряда: сходящегося в области $\{ \left| {{{z}_{j}}} \right| < 1,j = \overline {1,3} \} $; для ее представления вне указанной области можно воспользоваться формулами ее аналитического продолжения, полученными в [12]. В представлении (49) через ${{(x)}_{n}}$ обозначен символ Похгаммера (см. [22]), определяемый с помошью гамма-функции по формуле ${{(x)}_{n}} = \Gamma (x + n){\text{/}}\Gamma (x)$, иначе говоря,

4.4. Вычислим теперь выражение $\Omega (h)$, фигурирующее в формулах (24), (27)–(30) для искомых величин ${{f}^{{ - 1}}}$, ${{{\mathbf{C}}}_{x}}$, $\mathfrak{L}$, $\mathfrak{W}$, ${{z}_{{{{\psi }_{0}}}}}(\varphi )$ и в уравнении (26) для ${{\varphi }_{C}}$.

Для этого в соответствии с (21) подставим равенство (20) в выражение (35) для $T(t)$, обратив внимание, что в этом выражении первое слагаемое в скобках, согласно (45), равно $lnh$; в итоге получим

где в соответствии с (36) имеем Первый множитель в квадратных скобках (50) является вещественным числом; обозначим его через Нетрудно также убедиться, что если $h \in (0,1)$, то произведение двух последних сомножителей в квадратных скобках в (50) принимает вещественные значения, поэтому величина ${\text{Re}}\Omega (h)$, фигурирующая в (26), (27), равна в этом случае второму члену правой части (50):

Найдем теперь величину ${{\varphi }_{C}}$. Для этого подставим последнее выражение в (26) и обозначим возникающий при этом интеграл через ${{I}_{0}}$. Записывая его с помощью представления (48) через функцию Лауричеллы:

находим искомую формулу для ${{\varphi }_{C}}$ – образа $f(C)$ концевой точки $C$ стенки клина: Напомним, что вещественная величина $\tau $ дается формулой (52), число $\mu $ – формулой (46), и заметим, что интеграл ${{I}_{0}}$ является вещественнозначной функцией параметров $\alpha $ и $Q$.

Вычислим коэффициент сопротивления ${{{\mathbf{C}}}_{x}}$. Для этого подставим выражение (53) в формулу (27). Один из возникающих при этом интегралов – это ${{I}_{0}}$ из (54), а другой, обозначаемый через ${{I}_{1}}$, может быть выражен с помощью (48) через функцию Лауричеллы следующим образом:

Тогда для величины ${{{\mathbf{C}}}_{x}}$ получаем формулу

Найдем явное выражение для функции $z = {{f}^{{ - 1}}}(w)$. Используя формулы (50), (52), подставим в выражение (24) функцию $exp[\Omega (h)]$ и якобиан (47), а также учтем формулу (55); тогда получим

где Для того чтобы выразить интеграл в (58) через функцию Лауричеллы, разобьем его на два и  сделаем подстановку $\lambda = h\xi $, $\xi \in [0,1]$, $d\lambda = hd\xi $. Тогда этот интеграл запишется как ${{h}^{{1 - \alpha }}}{{I}_{2}}(h) - {{h}^{{2 - \alpha }}}{{I}_{3}}(h)$, где Таким образом, где $h = h(w)$ дается формулой (59).

Теперь, используя формулу (62), и в соответствии с равенствами (6), (7) находим относительную длину $\mathfrak{L}$ и относительную ширину $\mathfrak{W}$ каверны:

Наконец, в соответствии с (30) получаем, что параметрическое по $\varphi \in ( - \infty , + \infty )$ представление для координат ${{z}_{\varepsilon }}(\varphi )$ линии тока, соответствующей значению $\varepsilon $ функции $\psi $, дается формулой (62) с подстановкой $h = h(\varphi + i\varepsilon )$, где функция $h(w)$ определяется равенством (59). Описанный алгоритм вычисления координат ${{z}_{\varepsilon }}(\varphi )$ позволяет построить картину обтекания клина, соответствующую рассмотренной схеме.

5. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ

5.1. Осуществлена численная реализация полученного в разд. 4 решения задачи обтекания клина по двуспиральной схеме Тулина. Для различных значений угла $\pi \alpha $ наклона клина и числа кавитации $Q$ получены численные значения коэффициента сопротивления ${{{\mathbf{C}}}_{x}}$, помещенные в табл. 1.

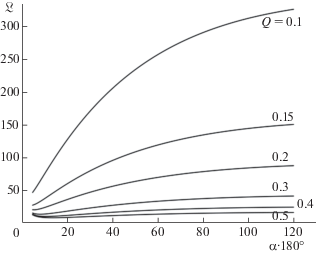
Вычислены также значения относительной длины $\mathfrak{L}$ и относительной ширины $\mathfrak{W}$ каверны, приведенные (соответственно на фиг. 3 и 4) в виде графиков зависимости этих величин от угла $\pi \alpha $ при различных $Q$.

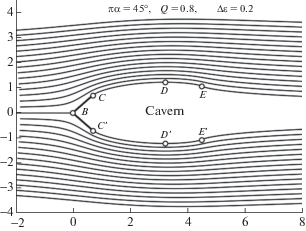
5.2. На основе численной реализации полученного решения построена также картина обтекания, т.е. изображено распределение линий тока $\{ \psi (x,y) = \varepsilon \} $ с шагом значений функции тока между соседними линиями тока, составляющим $\Delta \varepsilon = 0.2$. В работе даны три картины обтекания для $l = 1$, ${{V}_{\infty }} = 1$ и следующих значений остальных параметров:

– фиг. 5: $\alpha = 1{\text{/}}4$, т.е. $\pi \alpha = {{45}^{{^{ \circ }}}}$, $Q = 0.8$;

– фиг. 6: $\alpha = 1{\text{/}}2$, т.е. $\pi \alpha = {{90}^{{^{ \circ }}}}$, $Q = 0.7$;

– фиг. 7: $\alpha = 3{\text{/}}4$, т.е. $\pi \alpha = {{135}^{{^{ \circ }}}}$, $Q = 0.6$.

При рассмотрении этих картин и их сравнении с картиной обтекания, изображенной на фиг. 1, следует иметь в виду, что последняя носит условно-иллюстративный характер, а вихревые спирали на ней сильно увеличены (о чем было сказано в п. 1.4). По контрасту с фиг. 1, размер $\mathfrak{D}$ вихрей, получаемый в результате расчета, составил очень малую величину; напомним, что он определяется по формуле (8). Так, для случаев, изображенных на фиг. 5–7, он принимал следующие значения:

– фиг. 5: $\mathfrak{D} = 2.3 \times {{10}^{{ - 7}}}$;

– фиг. 6: $\mathfrak{D} = 1.1 \times {{10}^{{ - 7}}}$;

– фиг. 7: $\mathfrak{D} = 1.3 \times {{10}^{{ - 8}}}$.

Эти результаты согласуются с полученной в разд. 6 асимптотикой для $\mathfrak{D}$ при малых $Q$.

Ясно, что такой вихрь не может быть изображен на фоне общей картины течения, и для своего представления требует очень малого масштаба. Именно в таком масштабе $( \sim {{10}^{{ - 11}}})$ на фиг. 8 дана часть вихря $(REL)$ вблизи его центра $E$, где этот вихрь уже превратился в двойную спираль. Часть линии $(RE)$, т.е. часть закручивающейся спирали, изображена сплошной линией, а часть линии $(EL)$, т.е. раскручивающейся спирали, – штриховой линией. Там же даны три фрагмента линий тока, соответствующих $\psi = {{10}^{{ - 4}}}$, $\psi = {{10}^{{ - 6}}}$ и $\psi = {{10}^{{ - 9}}}$ вблизи того места внутри вихря $(REL)$, где эти линии максимально “углубляются” внутрь двойной спирали до точек своего разворота. Представляется, что эта картина, изображенная на фиг. 8, является весьма полезной для уяснения спиральной структуры вихрей в данной схеме.

Обратим еще внимание, что на картинах обтекания, помещенных на фиг. 5–7, линии $(EA)$ и $(AE{\kern 1pt} ')$ являются, согласно трактовке автора схемы Тулина, границей следа. Как видно на этих картинах, ширина следа $\mathfrak{S}(x)$ убывает при удалении от каверны. Асимптотика этой величины так же, как и ряда других важных характеристик течения, изучена в следующем разд. 6.

6. АСИМПТОТИКИ ХАРАКТЕРИСТИК РЕШЕНИЯ

6.1. Для того чтобы провести асимптотический анализ решения рассматриваемой задачи и его характеристик, получим вначале развернутое представление функции $z = {{f}^{{ - 1}}}(w)$, обратной к комплексному потенциалу, и выведем ее разложение вблизи точки $E$ – образа центра вихря на плоскости потенциала $w$.

Для этого, заменив с помощью формулы (43) переменную $t$ на ${{\chi }^{{ - 1}}}(w)$ в выражении (35) для отображения $\zeta = T(t)$, найдем, согласно (12), вид функции $\zeta = F(w)$, а подставив его в представление (14) для исследуемой функции $z = {{f}^{{ - 1}}}(w)$, получим

где ${{\varphi }_{E}}$ и ${{\varphi }_{C}}$ – координаты точек $E$ и $C$ на плоскости $w$, определяемых соответственно по формулам (44) и (55). Введя локальную переменную $u = w - {{\varphi }_{E}}$ с началом в точке $E$ на плоскости $w$, разложим подынтегральное выражение (65) в ряд по степеням переменного $u$. Интегрируя получаемое равенство, устанавливаем следующее разложение исследуемой функции ${{f}^{{ - 1}}}(w)$: где ${{z}_{E}}$ – координата точки $E$ на плоскости $z$, а коэффициенты ${{\mathcal{A}}_{1}}$, ${{\mathcal{A}}_{2}}$ даются формулами а ряд (66) сходится и представляет функцию ${{f}^{{ - 1}}}$ в полукруге $\{ w:\left| w \right| < \left| {{{\varphi }_{E}} - {{\varphi }_{C}}} \right|,\;\operatorname{Im} w > 0\} $.

6.2. Получим уравнения линий закручивающейся $(RE)$ и раскручивающейся $(EL)$, образующих вихрь с центром в точке $E$. Используя определенную в п. 6.2 локальную переменную $u$ с началом в точке $E$ на плоскости $w$, видим, что, согласно принцину соответствия границ, дуге $(RE)$ при отображении ${{f}^{{ - 1}}}$ отвечают отрицательные значения, а дуге $(EL)$ – положительные значения переменной $u$. Тогда, вводя на $f(RE)$ параметризацию по $\xi $,

где параметр $\xi \in (0,{{\xi }_{0}}),$ ${{\xi }_{0}} \in (0,1);$ подставим эти равенства в разложение (66). Учитывая еще, что, согласно (36), выполняется равенство $exp( - \pi \alpha \beta ) = 1{\text{/}}\sqrt {1 + Q} ,$ получаем параметрическое по $\xi $ представление для координат кривой $(RE)$: где величина $\alpha \beta $, напомним, определяется равенством (51). Вводя на плоскости $z$ локальные полярные координаты $(r,\phi )$ с началом в центре $E$ вихря и сравнивая полученное выражение (67) со стандартным представлением для спиралевидной кривой находим связь $\xi = exp(\phi {\text{/}}\alpha \beta )$ между параметрической переменной $\xi $ и полярным углом. Тогда уравнение в полярных координатах $r(\phi )$ линии $(RE)$ с относительной точностью до $exp(\phi {\text{/}}\alpha \beta )$ принимает вид Таким образом, кривая $(RE)$ вблизи центра вихря представляет собой закручивающуюся логарифмическую спираль. Принимая теперь во внимание соотношение (51), получаем первый (по малости $Q$) член асимптотики (68): где $\mathcal{A}$ – главный член разложения множителя при экспоненте в упомянутой асимптотике.

Для раскручивающейся дуги $(EL)$ переменная $u$ положительна, поэтому ${{u}^{{i\alpha \beta }}} = exp(i\alpha \beta lnu)$. Проводя рассуждения, аналогичные изложенным выше, устанавливаем уравнение в полярных координатах $r(\phi )$ линии $(EL)$:

Таким образом, кривые $(RE)$ и $(EL)$ вблизи центра вихря представляют собой две подобные логарифмические спирали с коэффициентом подобия $\sqrt {1 + Q} $.

6.3. Найдем число $N$ оборотов, совершаемых при движении жидкости вдоль линии тока $\{ z:\psi (z) = \varepsilon \} $, соответствующей малому положительному $\varepsilon $ (заметим, что число оборотов нулевой линии тока, очевидно, бесконечно).

Для этого найдем образ точки $w = {{\varphi }_{E}} + i\varepsilon $ на плоскости годографа при отображении $\zeta = F(w)$, значение которого находится, согласно (12), путем подстановки функции $t = {{\chi }^{{ - 1}}}(w)$ из (43) в выражение (35) для отображения $\zeta = T(t)$ с домножением в последней дроби числителя и знаменателя на ее знаменатель:

Подставляя сюда $w = {{\varphi }_{E}} + i\varepsilon $ и разлагая результат по степеням $\varepsilon $, получаем Отсюда, в частности, следует соотношение которое геометрически означает, что образ точки $w = {{\varphi }_{E}} + i\varepsilon $ асимптотически располагается посередине ширины вертикальной полосы на плоскости годографа.

Взяв теперь мнимую часть выражения (70) и разделив ее на $ - 2\pi $, мы и получим искомое количество оборотов:

полагая, что оно может принимать и дробные значения.

Из последнего соотношения вытекает асимптотика для числа $N$ при малых $Q$:

где $F(a,b;c;z)$ – гипергеометрическая функция Гаусса (см. [22]).

6.4. Найдем асимптотику размера $\mathfrak{D}$ вихрей, образуемых нулевой линией тока в зоне замыкания каверны. Для этого прежде всего найдем, опираясь на теорию конформного отображения сингулярно деформируемых областей (см. [23]) и исходя из представления (69), асимптотику отображения $\zeta = F(w)$ вблизи точки $E$ и обратим ее; в результате получим

Подставля сюда координату $\zeta = - i\pi {\text{/}}2$ точки $R$ на плоскости $\zeta $, находим ее образ на плоскости $w$: а подставив в то же представление координату $\zeta = - i\pi {\text{/}}2 + ln\sqrt {1 + Q} $ точки $L$ на плоскости $\zeta $, находим образ последней на $w$:

Теперь, чтобы вычислить искомый размер $\mathfrak{D}$, разложим подынтегральное выражение (65) в окрестности точки $w = {{\varphi }_{E}}$, проинтегрируем полученный результат от ${{\varphi }_{L}}$ до ${{\varphi }_{R}}$ и подставим полученные соотношения (71) и (72). В итоге получим

6.5. Установим асимптотику убывания относительной (т.е. отнесенной к длине стенки клина $l$) ширины следа $\mathfrak{S}(x)$ при $x \to + \infty $. Для этого найдем разложение подынтегрального выражения (65) вблизи бесконечности по дробным степеням $w$, имеющее вид

Тогда, проинтегрировав его, получаем разложение функции ${{f}^{{ - 1}}}(w)$ вблизи точки $w = \infty $Чтобы получить поведение относительной ширины следа $\mathfrak{S}(x)$ при $x \to + \infty $, положим в найденном разложении $w \to + \infty $ и выделим в нем вещественную $x(w)$ и мнимую $y(w)$ части: Выражая из первого равенства зависимость $w(x)$ и подставляя ее во второе, получаем уравнение $y(x)$ для границы следа, умножив которое на два и разделив на $l$, находим асимптотику относительной ширины следа Отсюда, тем же путем, что и выше, находим первый (по малости $Q$) член разложения этой асимптотики в виде

6.6. Выведем асимптотику коэффициента сопротивления¹³¹³ ${\mathbf{C}}_{x}^{T}(Q)$ при малых числах кавитации $Q$. Будем исходить из выражения (57) для этой величины. Используя разложение параметра $\beta $ из формулы (36) по степеням $Q$, последовательно получаем аналогичные разложения для величины $\tau $ из (52) и интегралов ${{I}_{0}}$, ${{I}_{1}}$ из (54), (56). Подставляя эти разложения в (57), устанавливаем искомую асимптотику в виде

где

Отметим, что в асимптотике (74) первый коэффициент ${\mathbf{C}}_{x}^{H}$, определяемый формулой (75), является общим для всех исследованных в [5] и настоящей работе схем, начиная со схемы Гельмгольца–Кирхгофа, поэтому он отмечен верхним индексом $H$. Вид асимптотики для этих схем отличается только коэффициентом при ${{Q}^{2}}$.

В табл. 2 для различных значений угла $\pi \alpha $, измеряемого в градусах, приведены величины коэффициентов ${\mathbf{C}}_{x}^{H}$, $E_{2}^{Z}$, $E_{2}^{R}$, $E_{2}^{T}$, где верхние индексы $Z$, $R$ и $T$ соответствуют схемам Жуковского–Рошко, Рябушинского и Тулина.

6.7. Построим теперь асимптотики для относительной длины $\mathfrak{L}$ и относительной ширины $\mathfrak{W}$ каверны. Будем исходить из выражений (63) и (64) для этих величин. Используя разложение параметра $\beta $ из формулы (36) по степеням $Q$ и аналогичное разложение для $\gamma $, найдем разложения для $\mu $ и $\eta $, определяемых из (46). Подставляя эти результаты в представления (60), (61) для интегралов ${{I}_{2}}$, ${{I}_{3}}$, выраженных через функцию Лауричеллы, и используя формулы (см. [12], [24]) аналитического продолжения в окрестность особой точки ${{z}_{k}} = 1$ для всех трех аргументов этой функции, а результат – в (63) и (64), устанавливаем искомые асимптотики:

Таким образом, при убывании числа кавитации $Q$ относительная длина $\mathfrak{L}$ каверны растет значительно быстрее, чем ее относительная ширина $\mathfrak{W}$.