1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 12, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 12, стр. 2109-2124

Новые граничные условия для одномерных сетевых моделей гемодинамики

С. С. Симаков 1, 2, 3, *

1 МФТИ
141707 М.о., Долгопрудный, Институтский пер., 9, Россия

2 Сеченовский университет
119991 Москва, ул. Трубецкая, 8, стр. 2, Россия

3 ИВМ РАН
119333 Москва, ул. Губкина, 8, Россия

* E-mail: simakov.ss@phystech.edu

Поступила в редакцию 23.03.2021
После доработки 21.06.2021
Принята к публикации 04.08.2021

Полный текст (PDF)

Аннотация

Для одномерной сетевой модели гемодинамики предложены новые граничные условия в областях соединения нескольких сосудов. Показано, что новые условия обеспечивают непрерывность решения и его производных в точках соединения сосудов. При асимптотическом переходе они позволяют получать решения, совпадающие с решением в одном сплошном сосуде. Предложены неотражающие граничные условия на концах терминальных сосудов. Представлены результаты численных экспериментов, подтверждающие выводы теоретического анализа. Библ. 51. Фиг. 11.

Ключевые слова: математическое моделирование, гемодинамика, граничные условия, осреднение.

1. ВВЕДЕНИЕ

Сердечно-сосудистые заболевания по прежнему являются лидирующим фактором смертности и инвалидизации во всем мире. Поэтому изучение процессов, связанных с течением крови в сердечно-сосудистой системе, остается актуальной темой многих современных научных исследований, в том числе математических.

Детальное моделирование гемодинамики в крупных сосудах осуществляется с помощью уравнений Навье–Стокса. Такой подход подразумевает решение уравнений в частных производных в областях сложной формы с подвижными границами. Использование моделей данного класса является весьма трудоемким и ресурсоемким. Они используются для локального анализа кровотока в аорте и ее ветвях, в магистральных церебральных сосудах, в аневризмах [1].

Один из широко распространенных и хорошо себя зарекомендовавших подходов к моделированию течения крови в артериальной части кровеносной системы человека состоит в использовании сетевых одномерных динамических моделей [2], [3]. Кровоток в сосудах считается аналогичным пульсирующему течению вязкой несжимаемой жидкости по сети эластичных трубок [4]. Модель движения жидкости в отдельной трубке строится путем осреднения по поперечному сечению уравнений Навье-Стокса [5]. Основные предположения данного подхода и их значимость обсуждаются, например, в [6], [7]. В случае крупных и средних артерий модель асимптотически представима в виде системы нелинейных гиперболических уравнений [7], что существенно расширяет спектр эффективных методов ее численного решения [8].

Обобщение на течение по сети эластичных трубок производится путем постановки начальных и граничных условий на входе в сеть, в точках соединения трубок и в концевых точках терминальных трубок. Граничные условия на входе в сеть, как правило, связаны с моделью функции сердца или сердечного выброса. Сердечный выброс может быть задан в виде функции от времени, получаемой на основе клинических или физиологических данных. Он может быть рассчитан с помощью модели выброса из желудочков в зависимости от давления наполнения предсердий [2], [9], [10]. Используется также пространственно осредненная динамическая модель сердца [3], в том числе, с учетом динамики его клапанов [11].

Граничные условия в концевых точках терминальных трубок связываются с давлением в микроциркуляторном русле и в венах с помощью закона Пуазейля [4] или с помощью моделей самоподобных древовидных структур, имитирующих области мелких сосудов и микроциркуляции [12]. Широко распространены пространственно осредненные модели виндкесселя, учитывающие импеданс микрососудистого русла, его эластичность и гидродинамическое сопротивление, нелинейно зависящее от давления [13]. Сравнительный анализ использования самоподобных древовидных структур и модели виндекесселя в качестве терминальных граничных условий представлен в [14].

На основе описанного инструментария разработаны методики персонализированного моделирования кровотока на локальных участках артериальной сети (коронарные сосуды, сосуды церебрального отдела, сосуды нижних конечностей и др.) на основе индивидуальных данных конкретного пациента. При этом структурная схема рассматриваемого участка может быть задана с различной точностью на основе данных анатомических атласов, физиологических данных [15], [16], агрегированных данных клинических и лабораторных исследований [17], [18], трехмерных анатомических моделей с высокой степенью детализации [19]. Максимальное правдоподобие структуры сосудистой сети достигается с использованием алгоритмов сегментации медицинских изображений (МРТ/КТ), производящих в начале трехмерную геометрию сосудистого русла, затем выделяющих центральные линии и, в итоге, выполняющих их спрямление с сохранением информации о длинах и диаметрах сосудистых участков [20], [21].

Несмотря на многочисленные допущения при выводе уравнений одномерной модели, неточности и высокую вариабельность входных данных, сопоставление результатов расчетов с данными из других источников позволило обосновать применимость данного подхода. Сравнение результатов одномерного и трехмерного моделирования представлено, например, в [22], [23]. Сопоставление расчетов, выполненных с помощью одномерной модели, и результатов лабораторных экспериментов с упругими трубками и вязкой жидкостью может быть найдено в [24], [25], [26]. Систематическое сравнение результатов персонализированного моделирования гемодинамики в одномерном приближении с клиническими данными представлено в работах [27], [28], [29].

Аналогичный подход используется для описания динамики дыхательного газа в дыхательной системе [3], [30], течения лимфы в лимфатической системе [31], [32], [33], движения транспорта по дорожной сети мегаполиса, передачи информации в компьютерных сетях, распространения газовых примесей в вентиляционных сооружениях [34] и др.

Несмотря на широкое распространение одномерных моделей, некоторые аспекты их математических формулировок до сих пор обсуждаются. Например, в [35] показано, что произвол в выборе начальных условий может при определенных условиях нарушить единственность решения. Большинство современных математических формулировок граничных условий в точках соединения однотипных сосудов не обеспечивают гладкости решения и его сходимости к решению в одном сосуде при предельном переходе, состоящем в стремлении к нулю диаметра одного из сосудов в бифуркации при условии равенства между собой диаметров и упругих свойств двух других сосудистых сегментов. В данной работе предлагается формулировка граничных условий в области стыковок сосудов, свободная от этого недостатка.

Тестирование сетевых моделей производится на упрощенных конфигурациях трубок с параметрами, характерными для сосудов. При этом известные на сегоднящний день граничные условия на выходах из сети оказывают существенное влияние на исследуемое внутри сети решение в силу наличия отраженных волн. Эта проблема устраняется в данной работе путем формулировки новых неотражающих граничных условий в концевых точках терминальных трубок (сосудов).

Оставшаяся часть статьи имеет следующую структуру. Разд. 2 посвящен описанию и анализу используемых математических моделей. В п. 2.1 кратко представлена одномерная и полностью осредненная по пространству (нульмерная) модель течения вязкой несжимаемой жидкости в упругой трубке. В п. 2 кратко рассматриваются три варианта широко распространенных граничных условий в области соединения сосудов. Граничные условия в концевых точках представлены в п. 3. В данном разделе впервые предложены неотражающие граничные условия на концах терминальных сосудов. Анализ существующих и постановка новых граничных условий представлены в п. 4. Показано, что новые условия обеспечивают непрерывность решения и его производных в точках соединения сосудов. При соответствующем асимптотическом переходе они позволяют получать решения, совпадающие с решением в одном сплошном сосуде. Результаты численных экспериментов, подтверждающих теоретический анализ, представлены в разд. 3. Итоги подводятся в разд. 4.

2. ОДНОМЕРНАЯ СЕТЕВАЯ МОДЕЛЬ ГЕМОДИНАМИКИ

2.1. Осредненные по пространству модели течения вязкой несжимаемой жидкости в упругой трубке/сосуде

Рассмотрим течение вязкой несжимаемой ньютоновской жидкости в упругой трубке, диаметр которой намного меньше ее длины. Oсреднение уравнений Навье-Стокса по поперечному сечению такой трубки в предположении, что скорость направлена вдоль оси трубки, а смещения стенки происходят в плоскости, перпендикулярной этой линии, дает (Более подробно о всех предположениях и выводе уравнений см., например, [5], [6], [7].)

(2.1)
$\frac{{\partial S}}{{\partial t}} + \frac{{\partial \left( {Su} \right)}}{{\partial x}} = 0,$
(2.2)
$\frac{{\partial u}}{{\partial t}} + \left( {\alpha - \frac{1}{2}} \right)\frac{{\partial {{u}^{2}}}}{{\partial x}} + \left( {\alpha - 1} \right)\frac{{{{u}^{2}}}}{S}\frac{{\partial S}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} = {{K}_{r}}\frac{u}{S},$
где $t$ – время, $x$ – координата, отсчитываемая вдоль оси трубки, $S\left( {t,x} \right)$ – площадь поперечного сечения трубки с координатой x, $u\left( {t,x} \right)$ – осредненная по поперечному сечению скорость, ρ = = 1.04 г/см3 – плотность крови, $\nu = 4 \times {{10}^{{ - 2}}}$ см2/с – вязкость крови,
(2.3)
${{K}_{r}} = - 2\pi \left( {\gamma + 2} \right)\nu ,\quad \alpha = \frac{{\gamma + 2}}{{\gamma + 1}},$
$\gamma $ – параметр, определяющий форму профиля скорости (для параболического профиля $\gamma = 2$, для плоскопараллельного профиля $\gamma = 11$).

В [7] показано, что если упругие свойства стенки сосуда описываются соотношением

(2.4)
$P\left( S \right) = {{p}_{{ext}}} + {{\rho }_{w}}c_{0}^{2}({{e}^{{S/{{S}_{0}} - 1}}} - 1),$
где ${{S}_{0}}$ – поперечное сечение трубки с жидкостью в недеформированном состоянии, c0 – скорость распространения малых возмущений в материале стенки сосуда, то одномерная модель (2.1), (2.2), (2.4) для артерий представляет собой систему нелинейных гиперболических уравнений в дивергентном виде
(2.5)
$\partial {\mathbf{V}}{\text{/}}\partial t + \partial {\mathbf{F}}\left( {\mathbf{V}} \right){\text{/}}\partial x = {\mathbf{G}}\left( {\mathbf{V}} \right),$
где

${\mathbf{V}} = \left( {\begin{array}{*{20}{c}} S \\ u \end{array}} \right),\quad {\mathbf{F}} = \left( {\begin{array}{*{20}{c}} {Su} \\ {\frac{{{{u}^{2}}}}{2} + \frac{{P(S)}}{\rho }} \end{array}} \right),\quad {\mathbf{G}} = \left( {\begin{array}{*{20}{c}} 0 \\ { - {{K}_{r}}\frac{u}{S}} \end{array}} \right).$

Для сегмента упругой цилиндрической трубки с длиной по порядку величины, равной пространственному шагу сетки при дискретизации уравнений (2.5) во внутренних точках $\left( {L \approx \Delta x} \right)$, (2.2) может быть сведено к виду [7]

(2.6)
$I\frac{{{{d}^{2}}V}}{{d{{t}^{2}}}} + {{R}_{h}}\frac{{dV}}{{dt}} + \Delta P = 0,$
где $V = LS$ – объем рассматриваемой области, $Q = \frac{{dV}}{{dt}}$ – объемный поток, $I = \rho {{L}^{2}}{{V}^{{ - 1}}}$, Rh = = $2\pi \nu (\gamma + 2)\rho {{L}^{3}}{{V}^{{ - 2}}}$, $\Delta P$ – перепад давления между входным и выходным сечениями. Данное соотношение далее будет использовано для формулировки новых граничных условий в области соединения упругих трубок/сосудов (см. п. 2.4).

2.2. Граничные условия в областях соединения сосудов

Обобщение одномерной модели течения вязкой несжимаемой жидкости в эластичной трубке (2.5) для описания потока в сети, образованной такими трубками, производится путем постановки граничных условий на входах и выходах из нее (соединения с камерами сердца и концевые точки терминальных сосудов), а также во внутренних точках сети, представляющих собой соединения сосудистых сегментов (бифуркации артерий, анастамозы, артериовенозные соединения и др.). В данном разделе кратко рассматриваются три варианта широко распространенных граничных условий в области соединения сосудов. Их анализ и постановка новых граничных условий представлены в п. 2.4.

Во внутренних точках каждого сосудистого сегмента рассматривается система двух нелинейных уравнений (2.5), имеющая гиперболический тип. Поэтому количество граничных условий на каждом конце сосудистого сегмента должно быть равно двум. При этом граничные условия должны включать условия совместности вдоль характеристик, покидающих область.

В [6], [9], [34], [45], [47], [48] и др. показано, что в концевых точках одномерных областей интегрирования (2.5) существуют две характеристики. Многократно отмечается [3], [5], [9], [45] и др., что в большинстве физиологических режимов течение крови является дозвуковым. Т.е. одна из характеристик всегда направлена внутрь области интегрирования, а вторая – вне ее. Таким образом, на каждом конце сосуда требуется учет одного условия совместности

(2.7)
${{\omega }_{{ki}}} \cdot \left( {\frac{{\partial {{{\mathbf{V}}}_{k}}}}{{\partial t}} + {{\lambda }_{{ki}}}\frac{{\partial {{{\mathbf{V}}}_{k}}}}{{\partial x}}} \right) = {{{\mathbf{G}}}_{k}},\quad k = {{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{{{{M}_{l}}}}},\quad i = 1,2,$
и одного дополнительного граничного условия. Здесь l – индекс точки соединения сосудов, ${\text{\{ }}{{k}_{1}}, \ldots ,{{k}_{{{{M}_{l}}}}}{\text{\} }}$ – индексы сосудов в точке соединения, ${{M}_{l}}$ – количество сосудов в точке соединения, ${{\lambda }_{{ki}}},{{\omega }_{{ki}}}$ – собственное значение и соответствующий левый собственный вектор матрицы $\partial {\mathbf{F}}{\text{/}}\partial {\mathbf{V}}$. Конкретное значение i устанавливается в соответствии с наклоном характеристики и типом концевой точки сосуда (начало или конец). В начале сосуда ${{\lambda }_{{ki}}} < 0$, в конце сосуда ${{\lambda }_{{ki}}} > 0$. Конкретный вид ${{\lambda }_{{ki}}}$ и ${{\omega }_{{ki}}}$ найден, например, в [6], [9], [34] и др.

В каждой точке соединения сосудов закон сохранения массы принято записывать в виде

(2.8)
$\sum\limits_{k = {{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{{{{M}_{l}}}}}} {{\varepsilon }_{k}}{{S}_{k}}\left( {t,{{{\tilde {x}}}_{k}}} \right){{u}_{k}}\left( {t,{{{\tilde {x}}}_{k}}} \right) = 0,$
где ${{\varepsilon }_{k}} = 1,{{\tilde {x}}_{k}} = 0$ для сосуда, исходящего из точки соединения, ${{\varepsilon }_{k}} = - 1,{{\tilde {x}}_{k}} = {{L}_{k}}$ для сосуда, входящего в точку соединения.

При соединении ${{M}_{l}}$ сосудов условия (2.7), (2.8) дают ${{M}_{l}} + 1$ уравнение. В то время как количество неизвестных ${{S}_{{{{k}_{l}}}}}$, ${{u}_{{{{k}_{l}}}}}$ равно $2{{M}_{l}}$. Оставшиеся граничные условия могут быть получены в предположении о сохранении полного давления [2], [12], [18], [19], [47], [48]

(2.9)
$\frac{{u_{k}^{2}\left( {t,{{{\tilde {x}}}_{k}}} \right)}}{2} + \frac{{{{P}_{k}}\left( {{{S}_{k}}\left( {t,{{{\tilde {x}}}_{k}}} \right)} \right)}}{\rho } = {{I}^{l}},\quad k = {{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{{{{M}_{l}}}}},$
статического давления
(2.10)
${{P}_{k}}\left( {{{S}_{k}}\left( {t,{{{\tilde {x}}}_{k}}} \right)} \right) = \rho {{I}^{l}},\quad k = {{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{{{{M}_{l}}}}},$
или выполнения закона Пуазейля [3]
(2.11)
${{P}_{k}}\left( {{{S}_{k}}\left( {t,{{{\tilde {x}}}_{k}}} \right)} \right) - {{p}^{l}}\left( t \right) = {{\varepsilon }_{k}}R_{k}^{l}{{S}_{k}}\left( {t,{{{\tilde {x}}}_{k}}} \right){{u}_{k}}\left( {t,{{{\tilde {x}}}_{k}}} \right),\quad k = {{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{{{{M}_{l}}}}},$
где ${{I}^{l}}$ и ${{p}^{l}}$ – соответственно полное и статическое давление в узле $l$, $R_{k}^{l}$ – гидродинамическое сопротивление концевой точки сосуда в узле $l$.

Уравнения (2.7), (2.8), объединенные с одним из уравнений (2.9), (2.10) или (2.11) образуют систему, содержащую $2{{M}_{l}} + 1$ алгебраических и дифференциальных уравнений, которая на текущем шаге по времени может быть решена, например, методом Ньютона с использованием в качестве начального приближения значений на предыдущем шаге по времени.

2.3. Граничные условия в концевых точках сети

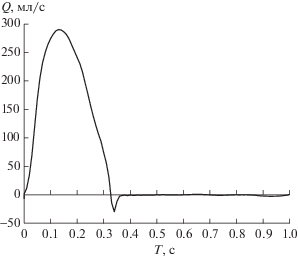
Параметры модельных сосудистых сегментов, на которых проводились численные расчеты в данной работе, близки к характерным параметрам аорты человека (см. п. 3). На входе в сосудистую сеть в качестве граничного условия задавалась характерная зависимость сердечного выброса Qh от времени [16] (см. фиг. 1)

(2.12)
${{S}_{{in}}}\left( {t,0} \right){{u}_{{in}}}\left( {t,0} \right) = {{Q}_{h}}\left( t \right).$
Фиг. 1.

Граничное условие на входе в сосудистую сеть $\left( {{{Q}_{h}}(t)} \right)$.

При проведении численных расчетов (см. п. 3) в концевых точках концевых (терминальных) сосудов ставились неотражающие граничные условия в виде

(2.13)
${{\omega }_{{q1}}} \cdot \left( {\frac{{\partial {{{\mathbf{V}}}_{q}}}}{{\partial t}} + {{\lambda }_{{q1}}}\frac{{\partial {{{\mathbf{V}}}_{q}}}}{{\partial x}}} \right) = {{\omega }_{{q2}}} \cdot \left( {\frac{{\partial {{{\mathbf{V}}}_{q}}}}{{\partial t}} + {{\lambda }_{{q2}}}\frac{{\partial f{{V}_{q}}}}{{\partial x}}} \right),$
где q – индекс концевого сосуда, ${{\lambda }_{{q1}}}$, ${{\omega }_{{qi}}}$ – собственные значения и левые собственные векторы матрицы $\mathop {\left( {\partial {\mathbf{F}}{\text{/}}\partial {\mathbf{V}}} \right)}\nolimits_q $ при $x = {{L}_{q}}$

$\mathop {\left( {\frac{{\partial {\mathbf{F}}}}{{\partial {\mathbf{V}}}}} \right)}\nolimits_q = \left( {\begin{array}{*{20}{c}} {{{u}_{q}}}&{{{S}_{q}}} \\ {\frac{1}{\rho }\frac{{\partial {{P}_{q}}}}{{\partial {{S}_{q}}}}}&{{{u}_{q}}} \end{array}} \right),$
${{\lambda }_{{qi}}} = {{u}_{q}} + {{( - 1)}^{i}}\sqrt {\frac{{{{S}_{q}}}}{\rho }\frac{{\partial {{P}_{q}}}}{{\partial {{S}_{q}}}}} ,\quad {{\omega }_{{qi}}} = \left\{ {\sqrt {\frac{1}{{\rho {{S}_{q}}}}\frac{{\partial {{P}_{q}}}}{{\partial {{S}_{q}}}}} ,{{{( - 1)}}^{i}}} \right\},\quad i = 1,2.$

Для конца терминального сосуда значение i = 1 соответствует характеристике, покидающей область интегрирования (${{\lambda }_{{q1}}} > 0$), а значение i = 2 соответствует характеристике, идущей внутрь области (${{\lambda }_{{q2}}} < 0$). Поэтому неотражающие условия на конце терминального сосуда представляют собой (13) совместно с (7) при i = 1. Неявная дискретизация (7) c первым порядком дает

(2.14)
${{\omega }_{i}} \cdot \left( {\frac{{{\mathbf{V}}\left( {{{t}_{{n + 1}}},{{x}_{L}}} \right) - {\mathbf{V}}\left( {{{t}_{n}},{{x}_{L}}} \right)}}{\tau } + {{\lambda }_{i}}\frac{{{\mathbf{V}}\left( {{{t}_{{n + 1}}},{{x}_{L}}} \right) - {\mathbf{V}}\left( {{{t}_{{n + 1}}},{{x}_{{L - 1}}}} \right)}}{h}} \right) = {\mathbf{G}}\left( {{{t}_{{n + 1}}},{{x}_{{L - 1}}}} \right),$
индекс q, показывающий номер терминального сосуда, опущен для краткости, ${{x}_{L}} = {{L}_{q}}$, xL – 1 = = ${{L}_{q}} - {{h}_{q}}$, ${{h}_{q}}$, $\tau $ — шаги дискретизации по пространству и времени. Условия (2.7) могут быть дискретизированы и с более высоким порядком [49].

Поскольку расчеты во внутренних и граничных точках производятся поочередно (см. п. 3), то в (2.14) неизвестными величинами являются $S\left( {{{t}_{{n + 1}}},{{x}_{L}}} \right)$, $u\left( {{{t}_{{n + 1}}},{{x}_{L}}} \right)$. Тогда представим (2.15) в виде

(2.15)
$S\left( {{{t}_{{n + 1}}},{{x}_{L}}} \right) = {{\alpha }_{i}}u\left( {{{t}_{{n + 1}}},{{x}_{L}}} \right) + {{\beta }_{i}},\quad i = 1,2,$
где ${{\alpha }_{i}},{{\beta }_{i}}$ зависят от известных в данный момент времени ${{t}_{{n + 1}}}$ величин, определенных на предыдущем шаге по времени ${{t}_{n}}$ и на текущем шаге по времени во внутренних точках.

В итоге разностная дискретизация неотражающих граничных условий на конце терминального сосуда (2.13) совместно с (2.7) при $i = 1$ имеет вид

(2.16)
${{S}_{q}}\left( {t,{{L}_{q}}} \right) = - \frac{{{{\beta }_{2}} - {{\beta }_{1}}}}{{{{\alpha }_{2}} - {{\alpha }_{1}}}},\quad {{u}_{q}}\left( {t,{{L}_{q}}} \right) = \frac{{{{\beta }_{1}}{{\alpha }_{2}} - {{\beta }_{2}}{{\alpha }_{1}}}}{{{{\alpha }_{2}} - {{\alpha }_{1}}}}.$

2.4. Граничные условия в области соединения сосудов и непрерывность решения

Условия (2.8), объединенные с (2.9), (2.10) или (2.11), широко используются в одномерных сетевых моделях гемодинамики. Условие (2.8) является следствием (2.1) при $S_{t}^{'} \approx 0$. Условие (2.9) следует из второго уравнения в (2.5) при $u_{t}^{'} \approx 0$ и пренебрежении вязким трением в области соединения. Условие (2.10) может быть получено из (2.2) при и . Ни один из вариантов граничных условий (2.7), (2.8), объединенных с (2.9), (2.10) или (2.11), не обеспечивает непрерывность производных решения по времени в области соединения сосудов в следующих двух предельных случаях: соединение двух одинаковых сосудов и соединение двух одинаковых сосудов с третьим сосудом, имеющим бесконечно малый диаметр. В этих случаях решение в области соединения должно совпадать с решением для одного более длинного сосуда без выделения области соединения внутри него (сплошной сосуд). Следует также отметить, что для граничных условий (2.7), (2.8), (2.9) и использования схем второго порядка аппроксимации для дискретизации как уравнений внутри одномерных областей (2.5), так и для условий совместности (2.7), эффективный порядок сходимости не превышал 1.7 [49], что говорит о существенном вкладе погрешности математической модели в области соединения.

Для решения этой проблемы используем подход, аналогичный [42], в котором для постановки граничных условий между одномерной и трехмерной областью использовалась пространственно осредненная динамическая модель упругого резервуара. Пусть область соединения N образована M сосудами (см. фиг. 2).

Фиг. 2.

Схема области соединения сосудов.

Граничные условия в области соединения включают закон сохранения массы и импульса, которые, используя (2.6), запишем в виде

(2.17)
$\frac{{d{{V}_{N}}}}{{dt}} = \sum\limits_{j = 1}^M {{\varepsilon }_{j}}{{S}_{j}}{{u}_{j}},\quad j = 1, \ldots M,$
(2.18)
${{I}_{N}}\frac{{{{d}^{2}}{{V}_{N}}}}{{d{{t}^{2}}}} + {{R}_{N}}\frac{{d{{V}_{N}}}}{{dt}} + {{P}_{{{\text{int}}}}} - {{P}_{{{\text{ext}}}}} = 0,$
где ${{P}_{{{\text{ext}}}}}$ – среднее давление на границе области соединения сосудов, ${{P}_{{{\text{int}}}}}$ – давление в области соединения, которое определяется упругостью стенок области. Здесь и далее в этом разделе для компактности записи считаем ${{S}_{j}} = {{S}_{j}}\left( {t,\mathop {\tilde {x}}\nolimits_j } \right)$, ${{u}_{j}} = {{u}_{j}}\left( {t,\mathop {\tilde {x}}\nolimits_j } \right)$.

Для окончательной постановки задачи в области соединения сосудов необходимо задание начальных условий для (2.18) и определения такой методики вычисления ${{P}_{{{\text{ext}}}}}$, ${{P}_{{{\text{int}}}}}$ с учетом свойств всех соединяющихся сосудов, которая бы обеспечивала корректную асимптотику при предельном переходе к сплошному сосуду, включая непрерывность упругих свойств материала стенки.

Материал стенки артерий имеет трехслойную структуру. Два из них (медиа и адвентиция) могут быть представлены как композитный материал, состоящий из однородного изотропного матрикса, усиленного двумя семействами спиральных волокон [36], [44]. В здоровых сосудах эти слои полностью определяют упругий отклик при нагрузке внутренним давлением. Материал области соединения имеет ту же структуру и упругие свойства. Однако следует учесть, что область соединения сформирована из тканей, упругие свойства которых должны быть близки всем формирующим ее сосудам (как входящим, так и исходящим). Свойства этих сосудов могут отличаться между собой. Примем во внимание еще тот факт, что при отхождении мелкого сосуда от крупного магистрального материал области соединения фактически имеет те же свойства, что и магистральный сосуд. Основываясь на приведенных рассуждениях, запишем определяющее соотношение для области соединения сосудов в виде

(2.19)
${{P}_{{{\text{int}}}}}\left( {{{V}_{N}}} \right) = \frac{{\sum\limits_{j = 1}^M {{P}_{j}}\left( {\frac{{{{V}_{N}}}}{{{{L}_{N}}}}} \right)\mathop {\left( {{{S}_{0}}} \right)}\nolimits_j^l }}{{M\sum\limits_{j = 1}^M \mathop {\left( {{{S}_{0}}} \right)}\nolimits_j^l }}.$

Здесь ${{P}_{j}}$ – определяющее соотношение (2.4) для сосуда $j$. Наилучший результат достигается при $l = 5$. При этом значении $l$ в случае ответвления с малым относительно магистрального сосуда диаметром давление в магистрали наиболее близко к давлению в сплошном сосуде (см. п. 3.2). При дальнейшем увеличении $l > 5$ существенного изменения в решении не происходит. Величина ${{V}_{N}}L_{N}^{{ - 1}}$ имеет смысл характерного поперечного сечения области соединения. Вклад давлений на концах сосудов в среднее давление на границе области можно оценить с помощью закона Пуазейля

${{P}_{j}}\left( {{{S}_{j}}} \right) - {{P}_{{{\text{int}}}}} = {{R}_{j}}{{S}_{j}}{{u}_{j}} \sim S_{j}^{4},$
поскольку гидродинамическое сопротивление ${{R}_{j}} \sim S_{j}^{2}$, а с учетом (2.15) ${{u}_{j}} \sim {{S}_{j}}$

(2.20)
${{P}_{{{\text{ext}}}}}\left( {{{S}_{1}},{{S}_{2}},...,{{S}_{M}}} \right) = \frac{{\sum\limits_{j = 1}^M \,{{P}_{j}}\left( {{{S}_{j}}} \right)S_{j}^{4}}}{{\sum\limits_{j = 1}^M \,S_{j}^{4}}}.$

При соединении двух одинаковых сосудов (2.19), (2.20) дают

${{P}_{{{\text{int}}}}}\left( {{{V}_{N}}} \right) = {{P}_{1}}\left( {\frac{{{{V}_{N}}}}{{{{L}_{N}}}}} \right) = {{P}_{2}}\left( {\frac{{{{V}_{N}}}}{{{{L}_{N}}}}} \right),$
${{P}_{{{\text{ext}}}}}\left( {{{S}_{1}},{{S}_{2}}} \right) \approx \frac{1}{2}\left( {{{P}_{1}}\left( {{{S}_{1}}} \right) + {{P}_{2}}\left( {{{S}_{2}}} \right)} \right),$
поскольку ${{S}_{1}} \approx {{S}_{2}}$. То есть область соединения имеет те же упругие свойства, что и образующие ее сосуды, а среднее давление на границе определяется средним давлением на концах сосудов.

В случае отхождения мелкого сосуда от крупного магистрального сосуда ${{S}_{1}} \approx {{S}_{2}} \approx S \gg {{S}_{3}}$, ${{P}_{1}} = {{P}_{2}} = P$

${{P}_{{{\text{int}}}}}\left( {\frac{{{{V}_{N}}}}{{{{L}_{N}}}}} \right) = P\left( {\frac{{{{V}_{N}}}}{{{{L}_{N}}}}} \right) + \frac{1}{2}\mathop {\left( {\frac{{{{S}_{3}}}}{S}} \right)}\nolimits^5 \cdot {{P}_{3}}\left( {\frac{{{{V}_{N}}}}{{{{L}_{N}}}}} \right) \approx P\left( {\frac{{{{V}_{N}}}}{{{{L}_{N}}}}} \right),$
${{P}_{{{\text{ext}}}}}\left( {{{S}_{1}},{{S}_{2}},{{S}_{3}}} \right) \approx \frac{1}{2}\left( {{{P}_{1}}\left( {{{S}_{1}}} \right) + {{P}_{2}}\left( {{{S}_{2}}} \right)} \right) + \frac{1}{2}\mathop {\left( {\frac{{{{S}_{3}}}}{S}} \right)}\nolimits^5 \cdot {{P}_{3}}\left( {{{S}_{3}}} \right) \approx \frac{1}{2}\left( {{{P}_{1}}\left( {{{S}_{1}}} \right) + {{P}_{2}}\left( {{{S}_{2}}} \right)} \right),$
т.е. упругость области соединения практически полностью определяется упругостью магистральных сосудов, а среднее давление на границе определяется средним давлением на концах магистральных сосудов, поскольку даже большое давление в мелком сосуде не оказывает существенного влияния в силу большего гидродинамического сопротивления этого сосуда.

Будем считать, что характерный линейный размер области соединения определяется усреднением характерных линейных размеров концевых участков сосудов, полученных при дискретизации внутренней области сосудов по пространству с шагом ${{h}_{j}}$ с учетом пропорциональности диаметрам сосудов dj

(2.21)
${{L}_{N}} = \frac{{\sum\limits_{j = 1}^M \,{{h}_{j}}{{d}_{j}}}}{{\sum\limits_{j = 1}^M \,{{d}_{j}}}}.$

По предположению одномерной модели ${{d}_{j}} \ll {{L}_{j}}$ и можно выбрать ${{h}_{j}} \approx {{d}_{j}}$.

Как при соединении двух одинаковых сосудов, так и при отхождении мелкого сосуда от крупного магистрального сосуда $(\mathop {{{S}_{0}}}\nolimits_1 = \mathop {{{S}_{0}}}\nolimits_2 \gg \mathop {{{S}_{0}}}\nolimits_3 )$, (2.21) дает

${{L}_{N}} \approx {{h}_{1}} \approx {{h}_{2}}.$

Характерный начальный объем ${{V}_{N}}\left( 0 \right)$ области соединения определяется усреднением объемов концевых участков сосудов $\mathop {{{V}_{0}}}\nolimits_j = \mathop {{{S}_{0}}}\nolimits_j {{h}_{j}}$, полученных при дискретизации сосудов с шагом ${{h}_{j}}$ с учетом пропорциональности $\mathop {({{S}_{{0j}}})}\nolimits^l $

(2.22)
${{V}_{N}}(0) = \frac{{\sum\limits_{j = 1}^M \mathop {{{V}_{0}}}\nolimits_j \mathop {\left( {{{S}_{{0j}}}} \right)}\nolimits^l }}{{\sum\limits_{j = 1}^M \mathop {\left( {{{S}_{{0j}}}} \right)}\nolimits^l }}.$

Выбор конкретного значения $l$ в (2.22) не оказывает существенного влияния, поскольку перед началом основных расчетов проводятся предварительные расчеты до достижения всеми переменными, заданными в расчетных узлах сосудистой сети, периодического режима. Следует, однако, отметить, что при l = 0 для областей соединения сосудов с существенно разными $\mathop {{{S}_{0}}}\nolimits_j $ значение ${{V}_{N}}(0)$, вычисленное по (2.22), может оказаться далеким от значений при периодическом режиме течения и для достижения этого режима может потребоваться большее время для предварительных расчетов. Например, при отхождении мелкого сосуда от крупного магистрального сосуда (S01 = = $\mathop {{{S}_{0}}}\nolimits_2 \gg \mathop {{{S}_{0}}}\nolimits_3 )$ получаем ${{V}_{N}}\left( 0 \right) \approx \frac{2}{3}\mathop {{{V}_{0}}}\nolimits_{1,2} $, хотя, очевидно, в этом случае хорошим начальным условием, близким к периодическому режиму, является ${{V}_{N}}\left( 0 \right) \approx \frac{2}{3}\mathop {{{V}_{0}}}\nolimits_{1,2} $. Поэтому в (2.22) следует выбирать по крайней мере l ≥ 1.

Область соединения сосудов имеет сложную трехмерную геометрию и структуру материала стенки. Течения в таких областях существенно трехмерные и должны изучаться с помощью совместных упруго-гидродинамических (FSI) моделей (см., например, [6]). Предложенный в данном разделе подход позволяет оценить параметры кровотока при протекании через область соединения сосудов с точностью приемлемой для моделирования с использованием одномерной модели (2.5). Адекватность подхода подтверждается вычислительными экспериментами (см. п. 3).

Условия (2.17), (2.18), как и ранее, дополняются соответствующими условиями совместности (2.7) вдоль характеристики, покидающей область интегрирования.

В результате алгоритм вычисления граничных условий на концах сосудов, формирующих область соединения N при переходе между слоями по времени ${{t}_{n}}$ и ${{t}_{{n + 1}}}$, состоит в решении задачи Коши для уравнения (2.18) с начальными условиями ${{V}_{N}}({{t}_{n}})$ (известно с предыдущего шага) и $\frac{{d{{V}_{N}}\left( {{{t}_{n}}} \right)}}{{dt}}$ (определяется из (2.17) при $t = {{t}_{n}}$). При использовании явного метода (2.20) содержит значения Sj при $t = {{t}_{n}}$ и интегрирование (2.18) не представляет труда. После этого Sj при $t = {{t}_{{n + 1}}}$ находятся как корни уравнений ${{P}_{j}}({{S}_{j}}) = {{P}_{{{\text{int}}}}}\left( {{{V}_{N}}\left( {{{t}_{{n + 1}}}} \right)} \right)$, и, далее, ${{u}_{j}}$ из дискретизации условий совместности (2.15) вдоль характеристики, покидающей область интегрирования. При использовании неявного метода для (2.18) уравнение (2.20) содержит значения Sj при $t = {{t}_{{n + 1}}}$. Это приводит к возникновению вложенного итерационного процесса, поскольку неизвестными теперь являются не только ${{V}_{N}}$ и $\frac{{d{{V}_{n}}}}{{dt}}$, но и Sj.

В заключениe данного раздела отметим следующее. Пусть один из входящих в область соединения сосудов ${{j}_{1}}$ и один из исходящих из области соединения сосудов ${{j}_{2}}$ имеют одинаковые свойства ($\mathop {({{c}_{0}})}\nolimits_{{{j}_{1}}} = {{({{c}_{0}})}_{{{{j}_{2}}}}}$, $\mathop {({{S}_{0}})}\nolimits_{{{j}_{1}}} = (\mathop {{{S}_{0}})}\nolimits_{{{j}_{2}}} )$). Пусть диаметры остальных сосудов стремятся к нулю. При ${{h}_{{{{j}_{1}}}}} = {{h}_{{{{j}_{2}}}}} = h$ и в силу сделанных предположений имеем решение, которое асимптотически совпадает с решением (2.5) для одного сосуда длины 2L с точностью $O(h)$.

3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Рассмотрим две группы численных экспериментов. В первой группе численных экспериментов (см. п. 3.1) рассмотрим случай соединения двух одинаковых сосудов и одного сосуда с теми же параметрами, но вдвое большей длины (модель сплошного сосуда). Будем сравнивать численное решение в соединенных сосудах с численным решением в сплошном сосуде в зависимости от модели граничных условий в узле. Численное решение в сплошном сосуде будем считать эталонным, поскольку получение аналитического решения данной задачи не представляется возможным.

Во второй группе численных экспериментов (см. п. 3.2) рассмотрим модификацию случая, рассматриваемого в первой группе, состоящую в добавлении бокового ответвления. Будем сравнивать численное решение в двух магистральных сосудах с численным решением в сплошном сосуде в зависимости от радиуса (поперечного сечения) ответвления.

Для всех случаев скорость распространения малых возмущений в стенке сосуда ${{c}_{0}} = 900$ см/с, шаг по пространству h = 1 см, шаг по времени $\tau = 5 \times {{10}^{{ - 5}}}$ c. Для всех случаев, за исключением модели сплошного сосуда $L = 10$ см. Для сплошного сосуда L = 21 см. В первой группе численных экспериментов для всех случаев d = 2 см. Во второй группе ${{d}_{1}} = {{d}_{2}} = {{d}_{{{\text{single}}}}} = 2$ см, 0.4 см ≤ d3 ≤ 2 см $\left( {\mathop {({{S}_{0}})}\nolimits_j = \frac{{\pi d_{j}^{2}}}{4}} \right)$.

Расчеты во внутренних точках сосудов проводились с помощью монотонной сеточно-характеристической схемы первого порядка [51]. Расчеты области соединения сосудов проводились с помощью явного метода Эйлера первого порядка. Расчет внутренних и граничных точек производился поочередно, что в целом представляет собой вариант схемы с расщеплением. Используемый шаг по времени обеспечивает устойчивость обоих методов.

3.1. Сравнение модели сплошного сосуда с моделями сосуда, разделенного точкой соединения

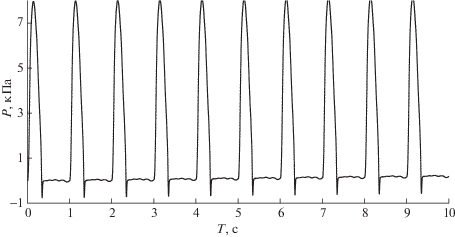
Рассмотрим модель, состоящую из двух последовательно соединенных сосудов, параметры которых близки к типичным параметрам аорты человека. Рассмотрим влияние модели граничных условий в области соединения на численное решение. Будем рассматривать три типа граничных условий в области соединения, которые включают в себя (2.9), (2.10) или (2.18) и один сплошной сосуд вдвое большей длины. На фиг. 5 и фиг. 6 представлены результаты расчетов давления $P$ и скорости $u$ с граничными условиями, включающими (2.18) в течениe 10 сердечных циклов (10 с) на расстоянии 11 см от входа в первый сосуд. Это соответствует началу второго сосуда, находящегося вблизи точки соединения сосудов. Временной период, равный десяти сердечным циклам, выбран исходя из необходимости контроля за установлением периодического режима, поскольку начальные условия этому режиму не соответствуют. Как видно из фиг. 5, 6, установление периодического режима происходит за один сердечный цикл. Однако в модели сосудистой сети, содержащей десятки или сотни элементов, для этого требуется более длительное время. Отсчет давления производится от минимального (диастолического) давления в аорте. Результаты расчетов находятся в физиологическом диапазоне [15], [16].

Будем сравнивать численное решение в соединенных сосудах с численным решением в сплошном сосуде в зависимости от модели граничных условий в узле. Будем трактовать эту разность как погрешность. На фиг. 3, 4 представлены абсолютные отклонения давления dP и скорости du в центре сплошного сосуда (на расстоянии 11 см от входа) между численным решением в сплошном сосуде и численными решениями в моделях с использованием (2.9) и (2.18). Максимальные абсолютные отклонения для обеих моделей наблюдаются в начале и в конце систолы. Модель с использованием (2.9) демонстрирует существенно более высокую погрешность в начале систолы.

Фиг. 3.

Динамика абсолютной погрешности давления на расстоянии 11 см от входа для модели с использованием (2.18) (круглые маркеры) и модели с использованием (2.9) (без маркеров).

Фиг. 4.

Динамика абсолютной погрешности скорости на расстоянии 11 см от входа для модели с использованием (2.18) (круглые маркеры) и модели с использованием (2.9) (без маркеров).

Фиг. 5.

Давление на расстоянии 11 см от входа по модели с использованием (2.18).

Фиг. 6.

Скорость на расстоянии 11 см от входа по модели с использованием (2.18).

Более высокая погрешность для модели с использованием (2.9) объясняется тем, что на каждом шаге по времени в области соединения сосудов решается система нелинейных уравнений методом Ньютона. Начальное приближение задается на основе значений с предыдущего шага по времени. Однако в начале и в конце систолы наблюдается резкое изменение решения, что приводит к ухудшению точности начального приближения. Увеличение шага по времени приводит к дополнительному ухудшению точности и, в итоге, к нарушению критериев на выбор начального приближения и неустойчивости решения системы нелинейных уравнений в области соединения сосудов. Это ограничение может оказаться более жестким, чем ограничение на шаг, налагаемое условием устойчивости разностной схемы во внутренних точках сосуда.

Увеличение погрешности в начале и конце систолы для модели с использованием (2.18) также связано с выбором начальных условий для задачи Коши с использованием значений на предыдущем шаге по времени. В данном случае проблема может быть решена повышением порядка аппроксимации численного метода для решения задачи Коши и использования неявных схем.

На фиг. 7, 8 представлены распределения максимальных по времени абсолютных отклонений давления dP и скорости du между численным решением в сплошном сосуде и численными решениями в моделях с использованием (2.9) и (2.18) по длине сосуда. Как видно из фиг. 3, 4, максимумы для модели с использованием (2.9) достигаются периодически в начале каждой систолы, а максимумы для модели с использованием (2.18) достигаются периодически в конце каждой систолы.

Фиг. 7.

Максимум абсолютной погрешности давления по длине сосуда для модели с использованием (2.18) (круглые маркеры) и модели с использованием (2.9) (без маркеров).

Фиг. 8.

Максимум абсолютной погрешности скорости по длине сосуда для модели с использованием (2.18) (круглые маркеры) и модели с использованием (2.9) (без маркеров).

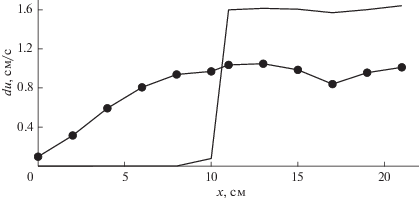
Следует отметить, что на фиг. 7, 8 для модели с использованием (2.9) в области соединения сосудов наблюдается скачок абсолютного отклонения численного решения как давления, так и скорости. Для модели с использованием (2.18) происходит незначительное падение абсолютного отклонения давления. При этом абсолютная погрешность скорости непрерывна. Таким образом, наличие точки соединения сосудов с использованием (2.9) приводит к значительному повышению абсолютной погрешности.

Максимальная относительная разница численных решений между моделью с использованием (2.9) и моделью с использованием (2.10) составила не более 0.5% для давления и 0.1% для скорости. Поэтому для сохранения наглядности результаты расчетов по модели с использованием (2.10) на фиг. 5–8 не представлены. Все сказанное относительно модели с использованием (2.9) остается справедливым и для модели с использованием (2.10).

3.2. Сравнение модели сплошного сосуда с моделью бифуркации

Рассмотрим модель, состоящую из двух последовательно соединенных магистральных сосудов, к которым присоединен еще один сосуд (ответвление). Магистральные сосуды имеют те же параметры, что и в п. 3.1, а диаметр ответвления изменяется от 2 до 0.4 см. Соответственно, параметр S0 в ответвлении изменяется от 100 до 4% от соответствующего значения в магистральных сосудах.

На фиг. 9, 10 представлены пиковые (систолические) значения давления и скорости по длине двухсегментного магистрального сосуда в зависимости от диаметра ответвления, поскольку именно эти величины наиболее сильно отличаются по отношению к соответствующим величинам в одном сплошном сосуде (представлены на фиг. 9, 10 сплошной линией). Из фиг. 9 видно, что уменьшение диаметра приводит к повышению систолического давления в магистральном сосуде до величины, которая наблюдается в сплошном сосуде. Аналогично ведет себя и скорость на фиг. 10.

Фиг. 9.

Пиковое (систолическое) давление по длине магистрального сосуда в зависимости от диаметра ответвления.

Фиг. 10.

Пиковая (систолическая) скорость по длине магистрального сосуда в зависимости от диаметра ответвления.

Представление о количественной оценке сходимости к решению в сплошном сосуде дает фиг. 11. На нем представлена зависимость максимальной относительной разницы давления и скорости в зависимости от отношения параметра $\mathop {\left( {{{S}_{0}}} \right)}\nolimits_3 $ в ответвлении к $\mathop {\left( {{{S}_{0}}} \right)}\nolimits_{1,2} $ магистрального сосуда. При снижении $\mathop {({{S}_{0}})}\nolimits_3 {\text{/}}\mathop {({{S}_{0}})}\nolimits_{1,2} $ от 100 до 4% относительное отклонение как давления, так и скорости падает от 50 до 3%, что соответствует теоретическим ожиданиям в предельном случае при стремлении диаметра ответвления ${{d}_{3}}$ к нулю.

Фиг. 11.

Максимальное относительное отклонение скорости и давления от значений в сплошном сосуде в зависимости от площади ответвления.

4. ЗАКЛЮЧЕНИЕ

В данной работе впервые предложены и проанализированы новые граничные условия для области соединения сосудов, кровоток в которых описывается одномерной моделью гемодинамики. По построению новые граничные условия асимптотически обеспечивают непрерывность решения и производных решения по времени с первым порядком по пространству в двух случаях: при сравнении решения в сплошном сосуде и сосуде, разделенном точкой соединения; при сравнении решения в сплошном сосуде и магистральном сосуде с ответвлением при стремлении диаметра ответвления к нулю.

Проведены две серии численных экспериментов. Результаты первой серии позволяют провести сравнительный анализ поведения численного решения при использовании различных вариантов граничных условий в области соединения сосудов (непрерывность интеграла Бернулли, непрерывность давления, новые условия). Показано, что новые граничные условия дают меньшую абсолютную погрешность и обеспечивают гладкость решения. Результаты второй серии численно подтверждают сходимость решения в магистральном сосуде с ответвлением при стремлении диаметра ответвления к нулю к решению в сплошном сосуде.

Существует потенциал развития численной реализации новых граничных условий за счет повышения порядка аппроксимации и использования неявных схем. При этом, однако, придется преодолеть трудности, связанные с определением неизвестных на промежуточных и верхнем временном слое, что приведет к необходимости использования вложенных итерационных процедур, появлению ограничений, связанных с их сходимостью, соответствующему повышению вычислительных ресурсов.

Сравнение с моделью, использующей граничные условия, включающие в себя закон Пуазейля (2.11), методологически затруднено, поскольку (2.11) содержит дополнительный эмпирический параметр (гидродинамическое сопротивление $R$), определение которого связано с анализом данных конкретного пациента, а в общем виде неоднозначно. Тем не менее значения $R$, позволяющие достичь хорошего совпадения с моделью сплошного сосуда, существуют. В целом эта модель имеет те же недостатки, что и модели с использованием (2.9) или (2.10).

Использование в данной работе неотражающих граничных условий в концевых точках сосудов оправдывается тем, что рассматриваются модели локального участка сосудистого русла. Учет влияния граничных условий на уровне перехода артериальной сети в микроциркуляторную привело бы к ненужному усложнению модели. С другой стороны, использование широко распространенных видов граничных условий на выходе из сети такого малого масштаба (свободный сток, давление, модель виндкесселя и др.) приводит к появлению в решении отраженных волн, имеющих нефизиологическое происхождение, что затруднило бы сравнительный анализ. Следует отметить, что граничные условия вида (2.13) для одномерных моделей гемодинамики в данной работе используются впервые.

В данной работе расчеты проводились на локальных сосудистых структурах с параметрами, характерными для аорты человека. Применимость предлагаемого подхода для других условий, характерных для кровотока в других сосудах, не вызывает сомнений, поскольку параметры кровотока в аорте в определенном смысле являются лимитирующими: самая высокая жесткость стенки, самое высокое число Рейнольдса. В дальнейшем планируется провести апробацию предложенных граничных условий в точках соединения сосудов на сетях коронарных и церебральных сосудов, имеющих параметры реальных пациентов, а также на сети сосудов системного круга.

Список литературы

  1. Mamatyukov M.Y., Khe A.K., Parshin D.V., Plotnikov P.I., Chupakhin A.P. On the energy of a hydroelastic system: blood flow in an artery with a cerebral aneurysm // J. of applied mechanics and technical physics. 2019. V. 60. № 6. P. 977–988.

  2. Абакумов М.В., Гаврилюк К.В., Есикова Н.Б., Кошелев В.Б., Лукшин А.В., Мухин С.И., Соснин Н.В., Тишкин В.Ф., Фаворский А.П. Математическая модель гемодинамики сердечно-сосудистой системы // Дифференц. ур-ния. 1997. Т. 33. № 7. С. 892–898.

  3. Холодов А.С. Некоторые динамические модели внешнего дыхания и кровообращения с учетом их связности и переноса веществ // Компьютерные модели и прогресс медицины. М.: Наука, 2001. С. 127–163.

  4. Борзов А.Г., Мухин С.И., Соснин Н.В. Консервативные схемы переноса вещества по системе сосудов, замкнутых через сердце // Дифференц. ур-ния. 2012. Т. 48. № 7. С. 919–928.

  5. Formaggia L., Quarteroni A., Veneziani A. Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System. V. 1. Heidelberg: Springer, DE, 2009.

  6. Vassilevski Yu., Olshanskii M., Simakov S., Kolobov A., Danilov A. Personalized computational hemodynamics: models, methods, and applications for vascular surgery and antitumor therapy. London, San Diego, Cambridge, Oxford: Academic Press, 2020.

  7. Simakov S.S. Spatially averaged haemodynamic models for different parts of cardiovascular system // Russian j. of numerical analysis and mathematical modelling. 2020. V. 35. № 5. P. 285–294.

  8. Bessonov N., Sequeira A., Simakov S., Vassilevski Yu., Volpert V. Methods of blood flow modelling // Mathematical modelling of natural phenomena. 2016. V. 11. № 1. P. 1–25.

  9. Абакумов М.В., Ашметков И.В., Есикова Н.Б., Кошелев В.Б., Мухин С.И., Соснин Н.В., Тишкин В.Ф., Фаворский А.П., Хруленко А.Б. Методика математического моделирования сердечно-сосудистой системы // Матем. моделирование. 2000. Т. 12. № 2. С. 106–117.

  10. Буничева А.Я., Мухин С.И., Соснин Н.В., Хруленко Н.Б. Математическое моделирование квазиодномерной гемодинамики // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 8. С. 1381–1392.

  11. Simakov S.S. Lumped parameter heart model with valve dynamics // Russian j. of numerical analysis and mathematical modelling. 2019. V. 34. № 5. P. 289–300.

  12. Olufsen M.S., Peskin C.S., Kim W.Y., Pedersen E.M., Nadim A., Larsen J. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions // Annals of biomedical engineering. 2000. V. 28. P. 1281–1299.

  13. Mynard J.P., Smolich J.J. One-dimensional haemodynamic modeling and wave dynamics in the entire adult circulation // Annals of biomedical engineering. 2015. V. 43. № 6. P. 1443–1460.

  14. Guan D., Liang F., Gremaud P.A. Comparison of the Windkessel model and structured-tree model applied to prescribe outflow boundary conditions for a one-dimensional arterial tree model // J. of biomechanics. 2016. V. 49. № 9. P. 1583–1592.

  15. Schmidt R.F., Thews G. Human Physiology. Berlin: Springer-Verlag, Germany, 1989.

  16. Ganong W.F. Review of Medical Physiology. Stamford, CT: Appleton and Lange, 1999.

  17. Avolio A.P. Multi-branched model of the human arterial system // Medical & biological engineering & computing. 1980. V. 18. P. 709–718.

  18. Alastruey J., Parker K.H., Peiró J., Sherwin S.J. Analysing the pattern of pulse waves in arterial networks: a time-domain study // J. of engineering mathematics. 2009. V. 64. № 4. P. 331–351.

  19. Blanco P.J., Watanabe S.M., Passos M.A.R.F., Lemos P.A., Feijóo R.A. An anatomically detailed arterial network model for one-dimensional computational hemodynamics // IEEE Transaction on biomedical engineering. 2015. V. 62. № 11. P. 736–753.

  20. Vassilevski Y.V., Danilov A.A., Simakov S.S., Gamilov T.M., Ivanov Y.A., Pryamonosov R.A. Patient-specific anatomical models in human physiology // Russian j. of numerical analysis and mathematical modelling. 2015. V. 30. № 3. P. 185–201.

  21. Danilov A., Ivanov Yu., Pryamonosov R., Vassilevski Yu. Methods of graph network reconstruction in personalized medicine // International j. for numerical methods in biomedical engineering. 2016. V. 32. № 8. e02754.

  22. Xiao N., Alastruey-Arimon J., Figueroa C.A. A systematic comparison between 1D and 3D hemodynamics in compliant arterial models // International j. for numerical methods in biomedical engineering. 2014. V. 30. № 2. C. 204–231.

  23. Гогниева Д.Г., Першина Е.С., Митина Ю.О., Гамилов Т.М., Прямоносов Р.А., Гогиберидзе Н.А., Рожков А.Н., Василевский Ю.В., Симаков С.С., Лианг Ф., Синицын В.Е., Бетелин В.Б., Щекочихин Д.Ю., Сыркин А.Л., Копылов Ф.Ю. Сравнение диагностической эффективности методик неинвазивного расчета фракционного резерва кровотока, основанных на построении одномерной и трехмерной математических моделей // Кардиоваскулярная терапия и профилактика. 2020. Т. 19. № 2. 2303.

  24. Alastruey J., Khir A.W., Matthys K.S., Segers P., Sherwin S.J., Verdonck P.R., Parker K.H., Peiró J. Pulse wave propagation in a model human arterial network: assessment of 1-D visco-elastic simulations against in vitro measurements // J. of biomechanics. 2011. V. 44. № 12. P. 2250–2258.

  25. Boileau E., Nithiarasu P., Blanco P.J., Müller L.O., Fossan F.E., Hellevik L.R., Donders W.P., Huberts W., Willemet M., Alastruey J. A benchmark study of numerical schemes for one-dimensional arterial blood flow modelling // International j. for numerical methods in biomedical engineering. 2015. V. 31. № 10. e02732.

  26. Dobroserdova T., Simakov S., Gamilov T., Pryamonosov R., Sakharova E. Patient-specific blood flow modelling for medical applications // MATEC Web of Conferences. 2016. V. 76. 05001.

  27. Sughimoto K., Liang F., Takahara Y., Mogi K., Yamazaki K., Takagi S., Liu H. Assessment of cardiovascular function by combining clinical data with a computational model of the cardiovascular system // The j. of thoracic and cardiovascular surgery. 2013. V. 145. № 5. P. 1367–1372.

  28. Carson J.M., Pant S., Roobottom C., Alcock R., Javier Blanco P., Alberto Bulant C., Vassilevski Y., Simakov S., Gamilov T., Pryamonosov R., Liang F., Ge X., Liu Y., Nithiarasu P. Non-invasive coronary CT angiography-derived fractional flow reserve: A benchmark study comparing the diagnostic performance of four different computational methodologies // International j. for numerical methods in biomedical engineering. 2019. V. 35. № 10. e03235.

  29. Gognieva D., Mitina Y., Gamilov T., Pryamonosov R., Vasilevskii Y., Simakov S., Liang F., Ternovoy S., Serova N., Tebenkova E., Sinitsyn V., Pershina E., Abugov S., Mardanian G., Zakarian N., Kirakosian V., Betelin V., Shche-kochikhin D., Syrkin A., Kopylov P. Noninvasive assessment of the fractional flow reserve with the CT FFRc 1D method: final results of a pilot study // Global heart. 2021. V. 16. № 1. 1.

  30. Golov A., Simakov S., Soe Y.N., Pryamonosov R., Mynbaev O., Kholodov A. Multiscale CT-based computational modeling of alveolar gas exchange during artificial lung ventilation, cluster (Biot) and periodic (Cheyne-Stokes) breathings and bronchial asthma attack // Computation. 2017. V. 5. № 1. 11.

  31. Мозохина А.С., Мухин С.И. О квазиодномерном течении жидкости с анизотропной вязкостью в сокращающемся сосуде // Дифференц. ур-ния. 2018. Т. 54. № 7. С. 956–962.

  32. Savinkov R., Grebennikov D., Puchkova D., Chereshnev V., Sazonov I., Bocharov G. Graph theory for modeling and analysis of the human lymphatic system // Mathematics. 2020. V. 8. № 12. 2236.

  33. Mozokhina A., Savinkov R. Mathematical modelling of the structure and function of the lymphatic system // Mathematics. 2020. V. 8. № 9. 1467.

  34. Холодов Я.А. Разработка сетевых вычислительных моделей для исследования нелинейных волновых процессов на графах // Компьютерные исследования и моделирование. 2019. Т. 11. № 5. С. 777–814.

  35. Poroshina A.B., Vedeneev V.V. Existence and uniqueness of steady state of elastic tubes conveying power law fluid // Russian j. of biomechanics. 2018. V. 22. № 2. P. 169–193.

  36. Holzapfel G.A. A new constitutive framework for arterial wall mechanics and a comparative study of material models // J. of elasticity. 2001. V. 61. P. 1–48.

  37. Sackinger P.A., Schunk P.R., Rao R.R. A Newton-Raphson pseudo-solid domain mapping technique for free and moving boundary problems: a finite element implementation // J. of computational physics. 1996. V. 125. № 1. P. 83–103.

  38. Rosar M.E., Peskin C.S. Fluid flow in collapsible elastic tubes: A three-dimensional numerical model // New York j. of mathematics. 2001. V. 7. P. 281–302.

  39. Quarteroni A., Tuveri M., Veneziani A. Computational vascular fluid dynamics: problems, models and methods // Computing and visualization in science. 2000. V. 2. P. 163–197.

  40. Danilov A., Lozovskiy A., Olshanskii M., Vassilevski Y. A finite element method for the Navier-Stokes equations in moving domain with application to hemodynamics of the left ventricle // Russian j. of numerical analysis and mathematical modelling. 2017. V. 32. № 4. P. 225–236.

  41. Vassilevski Y., Danilov A., Lozovskiy A., Olshanskii M., Salamatova V., Chang S.M., Han Y., Lin C.H. A stable method for 4D CT-based CFD simulation in the right ventricle of a TGA patient // Russian j. of numerical analysis and mathematical modelling. 2020. V. 35. № 5. P. 315–324.

  42. Dobroserdova T., Olshanskii M., Simakov S. Multiscale coupling of compliant and rigid walls blood flow models // International j. for numerical methods in fluids. 2006. V. 82. № 12. P. 799–817.

  43. Čanić S., Kim E.H. Mathematical analysis of the quasilinear effects in a hyperbolic model blood flow through compliant axi-symmetric vessels // Mathematical methods in the applied sciences. 2003. V. 26. P. 1161–1186.

  44. Vassilevski Y.V., Salamatova V.Y., Simakov S.S. On the elasticity of blood vessels in one-dimensional problems of hemodynamics // Computational mathematics and mathematical physics. 2015. T. 55. № 9. P. 1567–1578.

  45. Van de Vosse F.N., Stergiopulos N. Pulse wave propagation in the arterial tree // Annual review of fluid mechanics. 2011. V. 436. P. 467–499.

  46. Симаков С.С. Современные методы математического моделирования кровотока с помощью осредненных моделей // Компьютерные исследования и моделирование. 2018. Т. 10. № 5. С. 581–604.

  47. Müller L.O., Toro E. A global multiscale mathematical model for the human circulation with emphasis on the venous system // International j. of numerical methods in biomedical engineering. 2014. V. 30. № 7. P. 681–725.

  48. Sherwin S., Franke V., Peiró J., Parker K. One-dimensional modelling of a vascular network in space-time variables // J. of engineering mathematics. 2003. V. 47. P. 217–250.

  49. Simakov S., Gamilov T. Computational study of the cerebral circulation accounting for the patient-specific anatomical features // Smart innovation, systems and technologies: International conference on 50 years of the development of grid-characteristic method, GCM50 2018. 2019. V. 133. P. 309–330.

  50. Milisic V., Quarteroni A. Analysis of lumped parameter models for blood flow simulations and their relation with 1D models // ESAIM: Mathematical modelling and numerical analysis. 2004. V. 38. № 4 P. 613–632.

  51. Магомедов К.М., Холодов А.С. Сеточно-характеристические численные методы. М.: Юрайт, 2018.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал