Журнал вычислительной математики и математической физики, 2021, T. 61, № 2, стр. 268-280

2.1. Краткое описание численного метода

В настоящей работе использован пакет программ HSFlow++ [3], с помощью которого проводится прямое численное моделирование течений в рамках уравнений Навье–Стокса. Дифференциальные уравнения решаются в криволинейной системе координат $(\xi ,\eta ,\zeta )$ в безразмерном дивергентном виде:

Для численного решения используются безразмерные значения. Декартовы координаты $x* = xL$, $y* = yL$, $z* = zL$ отнесены к характерному масштабу длины $L$, время $t* = tL{\text{/}}{{V}_{\infty }}$ – к характерному масштабу времени $L{\text{/}}{{V}_{\infty }}$, компоненты вектора скорости $u* = u{{V}_{\infty }}$, ${v}* = {v}{{V}_{\infty }}$, $w* = w{{V}_{\infty }}$ – к модулю вектора скорости набегающего потока ${{V}_{\infty }}$, давление $p* = p({{\rho }_{\infty }}V_{\infty }^{2})$ – к удвоенному скоростному напору набегающего потока, остальные газодинамические переменные – к их значениям в набегающем потоке. Звездочка в верхнем индексе обозначает размерную величину; если звездочка отсутствует, переменная предполагается безразмерной. Символ “$\infty $” обозначает значение переменной в набегающем потоке.

Для аппроксимации дифференциальных уравнений используются полностью неявный метод конечного объема и схема второго порядка аппроксимации по времени:

При определении конвективных потоковых величин на гранях ячейки сетки, например, ${\mathbf{E}}_{{i + 1/2,j,k}}^{{n + 1}}$, потоки расщепляются по направлениям. Для каждого направления определяется матрица Якоби ($A = \partial {\mathbf{E}}{\text{/}}\partial {\mathbf{Q}}$ для направления $\xi $), которая диагонализируется в виде $A = B{\Lambda }{{B}^{{ - 1}}}$, где B – матрица, составленная из правых собственных векторов, а Λ – диагональная матрица собственных значений матрицы A. Конвективная составляющая потоковых величин $E$, $G$, $F$ на грани ячейки аппроксимируется с использованием монотонной схемы типа Годунова:

где нижними индексами L и R отмечены величины, рассчитанные справа и слева на рассматриваемой грани с использованием восстановленных с помощью процедуры реконструкции значений газодинамических переменных. Например, для грани i + 1/2 индекс L соответствует ячейке i, а индекс R – ячейке i + 1. Нижним индексом LR отмечены величины, вычисляемые с помощью приближенного метода Роу решения задачи Римана о распаде произвольного разрыва. Модификация собственных значений $\varphi (\lambda )$ обеспечивает физически корректное изменение энтропии на разрывах. В работе использована процедура реконструкции по методу WENO-3.

Для аппроксимации диффузионной составляющей векторов $E$, $G$, $F$ на грани элементарной ячейки применена разностная схема типа центральных разностей второго порядка точности:

где $q$ – любая из неконсервативных (“примитивных”) зависимых переменных задачи, газодинамическая функция $u$, ${v}$, $w$, $p$ или $T$.

После аппроксимаций уравнений Навье–Стокса и граничных условий интегрирование исходных уравнений в частных производных сводится к решению системы нелинейных алгебраических уравнений R(U) = 0, где R – оператор дискретизации, вычисляющий вектор невязки согласно аппроксимации уравнений, $U$ – вектор искомых неконсервативных переменных (u, ${v}$, w, p, T) (компоненты скорости, давление, температура) во всех узлах расчетной сетки. Длина вектора $U$ составляет ${{n}_{q}}N$, где N – полное число узлов расчетной сетки, включая граничные, ${{n}_{q}}$ – число неизвестных в каждом узле (${{n}_{q}} = 5(u,{v},w,p,T)$ в трехмерной постановке и ${{n}_{q}} = 4(u,{v},p,T)$ в двухмерной). Система сеточных уравнений R(U) = 0 решается с помощью модифицированного метода Ньютона–Рафсона

где $k$, ${{k}_{0}}$ – номера итераций по нелинейности, ${{k}_{0}} \leqslant k$, ${{J}^{{[{{k}_{0}}]}}} = {{\left( {\partial R{\text{/}}\partial U} \right)}^{{[{{k}_{0}}]}}}$ – матрица Якоби системы нелинейных уравнений, $R({{U}^{{[k]}}})$ – вектор невязки, $\tau $ – параметр регуляризации. Здесь выражение ${{({{J}^{{[{{k}_{0}}]}}})}^{{ - 1}}}R({{U}^{{[k]}}}) \equiv {{Y}^{{[k]}}}$ является решением линейной системы уравнений Параметр регуляризации метода Ньютона относительно начального приближения ${{\tau }^{{[k]}}}$ определяется по формуле По мере сходимости итерационного процесса ${{\tau }^{{[k]}}} \to 1$, а скорость сходимости теоретически стремится к квадратичной.

Получение аналитического вида матрицы Якоби $J$ для рассматриваемой численной схемы, включающей решение задачи Римана о распаде разрыва, представляется весьма трудоемким. В   настоящей программе применяется универсальный метод формирования матрицы ${{J}^{{[{{k}_{0}}]}}} = {{(\partial R{\text{/}}\partial U)}^{{[{{k}_{0}}]}}}$ на итерации по нелинейности ${{k}_{0}}$ с помощью процедуры конечных приращений вектора невязки $R$ по вектору искомых переменных $U$. При этом m-й столбец матрицы ${{J}^{{[{{k}_{0}}]}}}$ вычисляется как в виде

где ${{e}_{m}}$ – единичный вектор длины ${{n}_{q}}N$, полностью состоящий из 0, кроме единственной 1 на позиции m. Такая методика вычисления Якобиана применима к произвольной системе сеточных уравнений.

2.2. Параметры потока и постановка расчетной задачи

Рассматривается номинально двухмерное течение над заостренной плоской пластиной при числе Маха набегающего потока ${{M}_{\infty }} = 3$, температуре набегающего потока ${{T}_{\infty }} = 103.6$ K. Расчет эволюции возмущений проводится в подобласти; процедура расчета аналогична процедуре, описанной в [4]. Число Рейнольдса составляет ${{\operatorname{Re} }_{{1,\infty }}} = 2.181 \times {{10}^{6}}$ м^–1. Число Прандтля принимается постоянным: $\Pr = \mu {{c}_{p}}{\text{/}}\lambda = 0.71$. Уравнения Навье–Стокса замыкаются уравнением состояния $\gamma M_{\infty }^{2}p = \rho T$, где γ = 1.4 – показатель адиабаты. Динамический коэффициент молекулярной вязкости рассчитывается по формуле Сазерленда: $\mu = (1 + {{T}_{\mu }}){\text{/}}(T + {{T}_{\mu }}){{T}^{{3/2}}}$, где ${{T}_{\mu }} = T_{\mu }^{*}{\text{/}}T_{\infty }^{*} = 110.4\;{\text{K/}}103.6\;{\text{K}} \approx 1.07$.

Численное интегрирование проводится в прямоугольной области, показанной на фиг. 1. На входной и верхней границах фиксируются безразмерные параметры набегающего потока: $(u,{v},w,p,T) = (1,0,0,1{\text{/}}\gamma M_{\infty }^{2},1)$. Для стационарных расчетов стенка принимается теплоизолированной с условиями прилипания на ней. Выходной границе предшествует буферная зона с укрупненными ячейками по x и y для демпфирования выходящих через границу возмущений. На выходной границе накладываются мягкие условия как линейная экстраполяция примитивных переменных из расчетной области. На боковых границах z_min и z_max ставятся условия симметрии.

Расчет проводится следующим образом. Во-первых, двухмерное стационарное невозмущенное течение над плоской пластиной рассчитывается до достижения невязкой величины 10^–8. Во-вторых, из полученного решения вырезается подобласть, в которой далее будет моделироваться развитие возмущений; на новых входных границах подобласти фиксируются газодинамические величины из расчета на первом шаге; стационарное поле устанавливается дополнительно до полной сходимости (величина невязки не превосходит 10^–8). В-третьих, полученное в подобласти стационарное поле дублируется в третьем поперечном направлении $z$; распределение температуры по поверхности фиксируется; в пограничный слой вводятся возмущения типа “вдув–отсос” по процедуре, описанной ниже. Нестационарный расчет проводится до установления квазистационарного режима течения. При таком подходе поверхность пластины является адиабатической, но пульсации температуры на поверхности отсутствуют.

2.3. Генератор возмущений

Генератор возмущений моделируется при $x{\kern 1pt} * \in [x_{1}^{*},x_{2}^{*}] = [0.394,0.452]$ м в соответствии с работой [1]. В этом диапазоне нормальная составляющая вектора скорости имеет вид

где где $T = 2\pi {\text{/}}\omega $, $A(t)$ – амплитуда, $\varepsilon = 0.00573$. Остальные параметры потока в области генератора вычисляются как для случая стенки без генератора. Возмущение с частотой $\omega _{0}^{*}{\text{/}}2\pi = f_{0}^{*} = 6.36$ кГц и волновым числом $\beta _{0}^{*} = 211.52$ м^–1 будем называть фундаментальным.

Как будет показано далее, результаты настоящих расчетов хорошо согласуются с результатами работы [1] как качественно, так и количественно. Однако амплитуда возмущений $\varepsilon $ в настоящей работе отличается от амплитуды из работы [1] практически вдвое (в работе [1] $\varepsilon = 0.003$) и подобрана для совпадения положения начала ЛТП. Как показано ниже, численная диссипация не влияет на положение ЛТП в настоящей работе. Поэтому, вероятно, в работе [1] амплитуда возмущений указана ошибочно.

2.4. Расчетная сетка

Характерный масштаб длины выбран как $L = {\text{0}}{\text{.7239}}$ м. Продольный размер буферной зоны, которая ограничена пунктирным прямоугольником на фиг. 1, составляет полторы длины волны фундаментального возмущения, или 1.5λ_x, где ${{\lambda }_{х}} = х_{2}^{*} - х_{1}^{*}$.

На фиг. 1 показаны расчетная область и расчетная сетка (вид сбоку). Подобласть для проведения основных нестационарных расчетов ограничена сплошным прямоугольником и начинается на расстоянии $x_{0}^{*} = 0.258$ м от передней кромки пластины. Длина подобласти в 14.3 раза больше продольной длины волны фундаментального возмущения. Высота подобласти выбрана $y_{H}^{*} = 0.03$ м, что составляет не менее пяти местных толщин пограничного слоя на выходной границе. Размер подобласти в боковом направлении составляет одну длину волны ${{\lambda }_{z}}$ в поперечном направлении, где ${{\lambda }_{z}} = 2\pi {\text{/}}\beta _{0}^{*} \approx 0.0297$ м.

Расчетная сетка представлена на фиг. 1а, соответствующие сеточные сгущения – на фиг. 1б и 1в. Основные расчеты настоящей работы проведены на сетке 80 миллионов узлов (подробная сетка). Эта сетка соответствует сетке из работы [1] в плоскости x0y. Сеточные линии распределены равномерно в поперечном направлении. На подробной сетке количество точек вдоль оси z составляет 201. Грубая сетка имеет вдвое меньше узлов по x и по z, чем подробная сетка. В вертикальном направлении количество точек для обеих сеток одинаково; поперек пограничного слоя приходится не менее 100 точек. На подробной сетке возмущение разрешено в боковом направлении (по z) 201 точкой на длину волны по z, а в продольном направлении (по x) – 320 точками. Стоит отметить, что для распространения монохроматической акустической волны в равномерном потоке требуется около 40 точек на длину волны, чтобы добиться близкого к естественному уровня вязкого затухания волны для используемого численного метода. Поэтому на построенных сетках численная диссипация фундаментального возмущения незначительна.

2.5. Анализируемые величины

Данные для обработки и сравнения собираются начиная с момента безразмерного времени $t = 2.261$ после ввода возмущений в пограничный слой, когда установился квазипериодический режим течения. В следующем разделе анализируются свойства переходного течения.

Анализ проводится для спектрального состава возмущений, где сопоставляются амплитуды отдельных гармоник Фурье или максимумы этих амплитуд по нормали к поверхности в рассматриваемом сечении x = const. Фурье-анализ и обработка нестационарных результатов выполнены с помощью возможностей языка программирования Python (библиотека numpy). Результат работы процедур быстрого преобразования Фурье по времени и координате z нормирован на ${{N}_{t}} \times {{N}_{z}}{\text{/}}4$, где N_t и N_z – количество точек анализируемого сигнала по времени и по координате z соответственно. В настоящей работе исследованы амплитуды гармоник пульсаций продольной компоненты скорости, давления, температуры, а также максимумы этих величин по нормали к поверхности.

Вихревая структура полей течения визуализируется с помощью Q-критерия: $Q = 0.5({{{\Omega }}_{{ij}}}{{{\Omega }}_{{ij}}} - {{S}_{{ij}}}{{S}_{{ij}}})$, ${{S}_{{ij}}} = 0.5({{\partial }_{j}}{{u}_{i}} + {{\partial }_{i}}{{u}_{j}})$, ${{{\Omega }}_{{ij}}} = 0.5({{\partial }_{j}}{{u}_{i}} - {{\partial }_{i}}{{u}_{j}})$, u_i – компоненты вектора скорости (для записи использованы тензорные обозначения; предполагается соглашение о суммировании по повторяющемуся в произведении индексу).

Также сопоставляются поля мгновенных значений продольной и поперечной компонент вектора завихренности и средние параметры течения (коэффициент трения, профили продольной компоненты скорости, осредненные по Фавру и по Рейнольдсу).

3.1. Структуры течения и спектральный состав возмущений

Мгновенная структура возмущенного течения представлена на фиг. 2 с помощью Q-критерия. Сразу за источником возмущений расположена область линейного развития возмущений, где они формируют X-образные структуры, усиливающиеся вниз по потоку. Вблизи $х* \approx 0.6$ мм появляются первые признаки нелинейного взаимодействия – возмущения начинают искажаться. При $х* \in (0.75,0.85)$ м наблюдается интенсивный нелинейный распад возмущений. За этой областью формируется зона молодой турбулентности с ростом мелкомасштабных вихрей. Эта зона развивается вниз по потоку.

Так как возбуждающие возмущения носят периодический характер с выделенной частотой, а нелинейные взаимодействия приводят к порождению кратных гармоник, то отклик пограничного слоя на такие возмущения также должен быть периодическим (квазистационарный режим течения). Для изучения спектральных свойств процесса ЛТП нестационарное течение сначала устанавливается до квазистационарного режима, а затем набирается статистика в течение пяти периодов квазигармонического режима. Пример квазистационарного сигнала в некоторой точке внутри пограничного слоя показан на фиг. 3а.

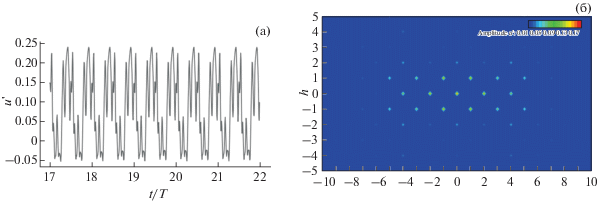
В каждом поперечном сечении x* = const возмущение можно представить через сумму гармонических колебаний путем преобразования Фурье. Для рассматриваемого течения вдоль плоской пластины разумно делать двухмерное преобразование Фурье по времени и поперечной координате для каждой линии x* = const, y* = const. Результат такого двухмерного преобразования можно представить в виде амплитуды гармоники $(f{\kern 1pt} {\text{*}},\beta {\kern 1pt} {\text{*}}) = (hf_{0}^{*},k\beta _{0}^{*})$. Таким образом, результат двухмерного преобразования Фурье можно представить в виде амплитуд двухмерных гармоник ${{\hat {u}}_{{hk}}}$. Пример представлен на фиг. 3б для начала области молодой турбулентности.

В описанной постановке фурье-спектр является симметричным, поэтому интерес представляет только часть спектра при h ≥ 0, k ≥ 0. Следует отметить, что пики спектра расположены в шахматном порядке, что объясняется квадратичным (нелинейным) взаимодействием возмущений друг с другом. Например, для стационарного возмущения и других четных частот h = 0, 2, 4, … наблюдаются только максимумы на четных волновых числах k = 2, 4, 6, …, а для нечетных частот h = 1, 3, 5, … – на нечетных волновых числах k = 1, 3, 5, … . Такая картина свойственна механизму наклонного распада, когда нелинейно (квадратично) взаимодействуют две гармоники с одинаковыми частотами, но противоположными по знаку волновыми числами. При этом частота удваивается, а волновое число обнуляется: [1, 1 ] + [1, –1] → [2, 0]. Чем ближе гармоника к фундаментальной гармонике, тем выше ее амплитуда. Это связано как с тем, что нелинейный распад продвигается в область высоких частот постепенно, так и с тем, что имеется численная пространственно-временная диссипация используемого численного метода. Расчеты настоящей работы выполнены на двух разных сетках, одна из которых вдвое мельче в продольном и боковом направлении. Как показано ниже, для обеих сеток результаты оказываются близкими.

Ниже полученные результаты сопоставляются с результатами работы [1].

3.2. Линейный режим

Рассмотрим линейный режим развития возмущений, который наблюдается примерно от x* = = 0.4 м до x* = 0.6 м. На фиг. 4 амплитуды фундаментальной моды $[1,\,1]$ пульсаций продольной компоненты вектора скорости u' в сечении x* = 0.5 м, полученные в настоящей работе, сопоставляются с результатами работы [1]. Для данного случая и для других линий x* = const, y* = const наблюдается хорошее согласование (фиг. 4а–4в).

Среди всех возможных линий y* = const для данного сечения x* = const можно выделить линию $y_{0}^{*}$, на которой амплитуда рассматриваемой гармоники максимальна. Для пульсаций u' или T  ' эта линия будет находиться в критическом слое пограничного слоя, ${{y}_{0}}{\text{/}}\delta \approx 0.65$. Эволюция такого максимума вниз по потоку хорошо согласуется с результатами [1] (фиг. 4г) даже на грубой сетке.

Инкремент роста возмущений является чувствительной к структуре стационарного решения характеристикой неустойчивого пограничного слоя. Рассмотрим эволюцию продольного инкремента роста возмущения продольной компоненты вектора скорости, ${{\alpha }_{i}} = - \frac{d}{{dx}}[\ln (u_{{\max }}^{'}(x))]$. Здесь нижний индекс max обозначает, что рассматриваются максимальная по y фурье-амплитуда гармоники. Фиг. 5а демонстрирует хорошее согласование уровня инкрементов в сечениях x = const. Начиная с $x{\kern 1pt} * \approx 0.65$ м, величина инкремента сильно растет. Этот момент соответствует началу нелинейной стадии развития возмущений.

Также следует отметить хорошее согласование в структуре возмущений внутри пограничного слоя для различных сечений y* = const, продемонстрированное на фиг. 5б, 5в.

3.3. Нелинейный режим

Рассмотрим нелинейную стадию развития возмущений. Момент проявления нелинейного взаимодействия можно отметить по картинам Q-критерия, на которых заметно усиление “канатообразных” структур (фиг. 6). Для малых значений Q (15 и 100) настоящие результаты и результаты [1] хорошо согласуются. Однако в области молодой турбулентности, где появляются мелкомасштабные структуры и максимальная величина Q растет (10 000 и 40 000), диссипативная схема не позволяет идеально воспроизвести результаты низкодиссипативной схемы [1]. Наиболее вероятными причинами этого расхождения являются применение в [1] спектрального метода в боковом направлении и использование высокочастотных гармоник, которые располагаются вблизи частоты (волнового числа) Найквиста для используемой подробной расчетной сетки и поэтому плохо разрешаются.

Рассмотрим далее процесс нелинейного распада с помощью эволюции максимальных по $y$ aмплитуд гармоник возмущений. Механизм наклонного резонанса последовательный. Изначально растет наиболее неустойчивая фундаментальная наклонная волна [1, ±1], что обусловлено чисто неустойчивостью пограничного слоя. При достижении некоторой критической амплитуды она начинает нелинейно взаимодействовать с собой, порождая кратные гармоники: h = 0 и h = 2, k = 0, k = 2, которые начинают расти благодаря нелинейному взаимодействию фундаментальных гармоник. Когда кратные гармоники достигают достаточных амплитуд, они начинают нелинейно взаимодействовать друг с другом и с фундаментальными гармониками, порождая все больше кратных гармоник. Такой процесс и его временная последовательность прослеживаются на фиг. 7 и фиг. 8, на которых изображена эволюция амплитуд гармоник вниз по потоку. Описанный механизм объясняет шахматную структуру спектра, приведенного на фиг. 3б.

Следует отметить хорошее совпадение в эволюции гармоник с работой [1] в областях линейного и слабонелинейного развития возмущений. Однако в области молодой турбулентности результаты, полученные на грубой сетке, начинают отличаться от результатов на подробной сетке. Последние продолжают хорошо согласовываться с результатами работы [1] для основных энергосодержащих частот h = 0, 1; k = 1, 2, и с ростом h и k начинает появляться небольшое рассогласование. При этом во всех случаях Фурье-амплитуды остаются на одном уровне и лишь разбегаются по фазе. Это может быть следствием накапливающейся ошибки более диссипативного метода. Однако в целом описанное сравнение результатов подтверждает надежность и применимость диссипативных схем для моделирования процесса ламинарно-турбулентного перехода.

На фиг. 9 приведены мгновенные структуры поперечного вектора завихренности в различных сечениях z* = const и сравнение полученных результатов (верхняя часть картины) с результатами работы [1] (нижняя часть картины после зеркального отражения). Видно, что вблизи $х* = 0.865$ м появляются мелкомасштабные структуры, свойственные развитой турбулентности. Детальное сравнение показывает, что вихри, полученные в настоящей работе, менее интенсивны по сравнению с вихрями из работы [1], и содержат меньше мелкомасштабных вихревых структур, что обсуждалось выше. Основные крупномасштабные структуры хорошо совпадают с [1].

Рассмотрим временную визуализацию процесса развития мелкомасштабных структур в конкретном сечении z = const. На фиг. 10 приведены мгновенные структуры поперечного вектора завихренности в различные моменты времени. На фиг. 10 дано сопоставление с результатами работы [5], в которой параметры задачи совпадают с параметрами работы [1], но расчеты проводились на измельченной сетке 211 млн. узлов. По результатам фиг. 10 можно сделать вывод о том, что скорость распространения вихрей внутри пограничного слоя составляет ≈0.7.

Фиг. 10 также демонстрирует развитие мелкомасштабных структур. Вихрь в точке $х* = 0.84$ м (фиг. 10а) передвигается через точку $х* = 0.87$ м (фиг. 10б) и доходит до точки $х* = 0.9$ м (фиг. 10в), где активно делится на мелкие вихри, которые далее сносятся потоком до $х* = 0.92$ м (фиг. 10г). К этому моменту времени в сечение $х* = 0.84$ м подходит новый вихрь, и процесс повторяется (квазистационарный режим).

Снова можно отметить, что диссипативная схема HSFlow++ хорошо воспроизводит крупномасштабные структуры, сохраняя их в качественном и количественном отношении. Однако мелкомасштабные структуры воспроизводятся недостаточно, чтобы полностью соответствовать результатам работы [5].

На фиг. 11 показаны мгновенные сечения продольной компоненты вектора завихренности, которые сопоставлены с результатами работы [1]. Структура течения симметрична относительно плоскости z* = 0; поэтому приводится только половина области по z*. В сечении $х* = 0.862$ м (фиг. 11а) расположен большой вихрь. С ростом $x$ растет и начинает распадаться при $х* = 0.866$ м (фиг. 11б), потом в точке $х* = 0.870$ м (фиг. 11в) образуется много мелких вихрей. Результаты, полученные на диссипативной численной схеме (настоящая работа), хорошо согласуются с результатами работы [1].

Рассмотрим зависимость осредненной величины коэффициента трения ${{с}_{f}}$ от продольной координаты x. Локальный коэффициент трения вычисляется по формуле

В настоящей работе рассматривается усреднение по времени в течение пяти периодов фундаментальной гармоники ${\Delta }t = 10\pi {\text{/}}{{\omega }_{0}}$ и по размаху z всей расчетной области:

Начиная с $х* = 0.72$ м величина c_f начинает резко усиливаться в окрестности точки $х* = 0.86$ м. В этом диапазоне результаты диссипативной схемы совпадают с результатами работы [1] даже на грубой сетке. Ниже по потоку результаты на грубой сетке оказываются ниже по сравнению с результатами на подробной сетке. Последние удовлетворительно согласуются с результатами работы [1] в области молодой турбулентности при x* ≥ 0.9 м.

На фиг. 13 показаны средние профили газодинамических переменных. Чем сильнее эффект нелинейных взаимодействий в рассматриваемом сечении, тем более наполнены средние профили. Сечение $х* = 0.996$ м вновь демонстрирует хорошее согласование результатов, полученных на диссипативной схеме, с результатами работы [1]. Фиг. 13 подтверждает, что несмотря на недостаточно детальную картину мелкомасштабных вихрей, полученную с помощью диссипативного метода, интегральные характеристики течения (средние профили газодинамических переменных, средний коэффициент трения) оказываются достаточно близки к результатам, полученным на низкодиссипативных схемах [1]. Этот вывод важен для прикладных задач, где нет необходимости подробно разрешать все структуры развитого турбулентного движения, но требуется получить надежные интегральные характеристики течения.