1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 2, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 2, стр. 281-302

Численное моделирование нестационарных дозвуковых течений вязкого газа на основе составных компактных схем высокого порядка

А. Д. Савельев *

Вычислительный центр им. А.А. Дородницына РАН Федерального исследовательского центра “Информатика и управление” РАН
119991 Москва, ул. Вавилова, 40, Россия

* E-mail: savel-cc09@yandex.ru

Поступила в редакцию 20.05.2020
После доработки 28.08.2020
Принята к публикации 16.09.2020

Полный текст (PDF)

Аннотация

Рассматривается семейство мультиоператорных компактных схем высокого порядка для расчетов течений вязкого газа на криволинейных сетках. В зависимости от количества используемых операторов порядок схемы для аппроксимации конвективных членов уравнений может составлять от 6-го до 22-го. С таким же порядком аппроксимируются вязкие члены исходных уравнений и метрические коэффициенты обобщенной криволинейной системы координат. На примере трех схем, в том числе самой трудоемкой из описываемых пятиоператорной, рассматривается их структура. Исследуется изменение аппроксимационных и диссипативных свойств схем, сопутствующее повышению их порядка. Выполняются сравнительные расчеты данными схемами дозвуковых течений газа на основе уравнений Эйлера и Навье–Стокса. Приводятся результаты расчетов вязкого дозвукового обтекания аэродинамического профиля в широком диапазоне изменения угла атаки и непроницаемого парашютного купола с использованием схемы 22-го порядка. Библ. 34. Табл. 9. Фиг. 13.

Ключевые слова: компактные разностные схемы, 22-й порядок аппроксимации, дозвуковые течения вязкого газа, отрыв пограничного слоя, аэродинамический профиль, купол парашюта.

1. ВВЕДЕНИЕ

В настоящее время все чаще для решения прикладных задач широко используются методы численного моделирования. При этом область расчета покрывается сеточными узлами с необходимой плотностью их распределения и решаются разностные аналоги уравнений сплошной среды в виде системы уравнений в частных производных на основе тех или иных дифференциальных операторов. При этом на конечный результат влияет как полнота описания выбранной модели течения за счет уточнения ее свойств, так и используемые разностные схемы. Дело в том, что конечно-разностное представление производных отличается от их исходных дифференциальных аналогов. Так, разложение в ряд Тейлора разностного аналога первой производной от некой гладкой функции $f$ по координате $x$ на сетке ${{\omega }_{h}} = \{ {{x}_{j}} = jh,\;h = {\text{const}}\} $ имеет вид

(1)
${{h}^{{ - 1}}}\Delta _{1}^{{(n)}}f = \frac{{\partial f}}{{\partial x}} + \sum\limits_{k = n}^\infty {{{\alpha }_{k}}\frac{{{{\partial }^{{k + 1}}}f}}{{\partial {{x}^{{k + 1}}}}}} {{h}^{k}},$
где $\Delta _{1}^{{\left( n \right)}}$ – сеточная функция, $n$ – порядок аппроксимации производной, а коэффициенты $\left| {{{\alpha }_{k}}} \right| \to 0$ при $k \to \infty $. У схем $n$-го порядка аппроксимации члены под знаком суммы со значениями $k < n$ отсутствуют. Поскольку суммарное влияние членов, остающихся под знаком суммы, снижается, это приводит к тому, что разностное решение на их основе в сравнении со схемами более низкого порядка становится ближе к решению исходных дифференциальных уравнений.

Примеры разностных схем с порядком аппроксимации выше второго для расчетов задач газовой динамики известны с конца 60-х годов. Примером может служить известная схема Русанова (см. [1]). Чуть позже были предложены несимметричные компактные схемы третьего порядка, учитывающие направление потока (см. [2]). В дальнейшем данный подход получил развитие и для схем более высокого порядка аппроксимации (см., например, [3]). В то же время за рубежом большее признание получили симметричные компактные аппроксимации, использующие пятиточечный шаблон (см. [4], [5]). Они, как правило, применяются для моделирования нестационарных течений, акустического излучения аэродинамических поверхности и струй (см. [6], [8]). Помимо компактных разностей высокого порядка, большое распространение получили схемы ENO и WENO, использующие некомпактную запись разностных операторов (см. [9], [10]), в том числе и на неструктурированных сетках (см. [11], [13]). В основном, они применяются при моделировании нестационарных невязких течений с контактными разрывами и скачками уплотнения. В целом можно отметить общее стремление к использованию при решении задач газовой динамики схем с порядком аппроксимации выше двух.

Составные компактные схемы (см. [14]) были построены на основе опыта, полученного при использовании разностных аппроксимаций типа (см. [2], [3]), при намерении получить более простое и эффективное управление их свойствами. Они представляют собой комбинацию симметричных компактных разностей высокого, изначально 6-го и 8-го порядков, и некомпактных четных разностей диффузного типа, ориентированных в соответствии с направлением характеристик. Позднее, когда были разработаны нецентрированные мультиоператорные схемы для уравнений газовой динамики (см. [15], [16]), мультиоператорный подход был использован и применительно к составным компактным схемам для описания конвективных и диффузных членов исходных уравнений. В [17] представлены схемы 6 -го, 10-го и 14-го порядков, в [18] – 18-го и 22-го.

При высокой аппроксимации составных компактных схем непосредственное их применение в задачах ударного взаимодействия затруднительно. Это связано с диссипативными свойствами используемых диффузных операторов, которые с ростом их порядка сильно снижаются. Между тем, существует малоисследованная область дозвуковых течений, моделирование которых представляет большой интерес. Численное исследование вихреобразования, отрыва ламинарного и турбулентного течений на гладкой изогнутой поверхности, генерация и распространение звуковых волн требуют использования разностных схем с высокой разрешающей способностью. При этом сравнительный анализ результатов, полученных на основе схем разного порядка аппроксимации, должен способствовать получению верных выводов о рассматриваемом течении.

2. ИСХОДНЫЕ УРАВНЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Будем рассматривать течения вязкого теплопроводного газа с постоянным отношением удельных теплоемкостей. В общем пространственном случае они описываются трехмерными уравнениями. Однако подобный подход требует несоизмеримо большего времени расчетов, чем решение двумерных уравнений. Если учитывать тот объем полезной информации, которую можно получить по двумерной технологии за время одного трехмерного расчета, напрашивается вывод о необходимости ее использования, по крайней мере, на начальном этапе решения задачи. На данном этапе будем использовать двумерные нестационарные осредненные уравнения Навье–Стокса, дополненные уравнениями SST-модели турбулентности (см. [19]). Обезразмеренные по параметрам набегающего потока и характерному линейному размеру, они имеют следующий вид в системе координат $\left( {x,y} \right)$:

$\frac{{\partial {\mathbf{U}}}}{{\partial t}} + \frac{{\partial {\mathbf{F}}}}{{\partial x}} + \frac{{\partial {\mathbf{G}}}}{{\partial y}} = {\text{R}}{{{\text{e}}}^{{ - {\text{1}}}}}\left( {\frac{{\partial {{{\mathbf{F}}}_{\mu }}}}{{\partial x}} + \frac{{\partial {{{\mathbf{G}}}_{\mu }}}}{{\partial y}}} \right) + {{C}_{{lt}}}{\mathbf{H}},$
${\mathbf{U}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u} \\ {\rho {v}} \\ e \\ {\rho k} \\ {\rho \omega } \end{array}} \right],\quad {\mathbf{F}} = \left[ {\begin{array}{*{20}{c}} {\rho u} \\ {\rho {{u}^{2}} + p + {{p}_{t}}} \\ {\rho u{v}} \\ {(e + p + {{p}_{t}})u} \\ {\rho uk} \\ {\rho u\omega } \end{array}} \right],\quad {\mathbf{G}} = \left[ {\begin{array}{*{20}{c}} {\rho {v}} \\ {\rho u{v}} \\ {\rho {{{v}}^{2}} + p + {{p}_{t}}} \\ {(e + p + {{p}_{t}}){v}} \\ {\rho {v}k} \\ {\rho {v}\omega } \end{array}} \right],\quad {\mathbf{H}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \\ {{{H}_{k}}} \\ {{{H}_{\omega }}} \end{array}} \right],\quad {\mathbf{\varphi }} = \left[ {\begin{array}{*{20}{c}} \rho \\ u \\ {v} \\ h \\ k \\ \omega \end{array}} \right],$
${{{\mathbf{F}}}_{\mu }} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\mu \left( {2{{u}_{x}} - \frac{2}{3}\nabla U} \right)} \\ {\mu ({{u}_{y}} + {{{v}}_{x}})} \\ {u{{\sigma }_{{xx}}} + {v}{{\tau }_{{xy}}} + \mu {{{\Pr }}^{{ - 1}}}{{h}_{x}}} \\ {{{\mu }_{k}}\Pr _{k}^{{ - {\text{1}}}}{{k}_{x}}} \\ {{{\mu }_{\omega }}\Pr _{\omega }^{{ - {\text{1}}}}{{\omega }_{x}}} \end{array}} \right],\quad {{{\mathbf{G}}}_{\mu }} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\mu ({{u}_{y}} + {{{v}}_{x}})} \\ {\mu \left( {2{{{v}}_{y}} - \frac{2}{3}\nabla U} \right)} \\ {u{{\tau }_{{yx}}} + {v}{{\sigma }_{{yy}}} + \mu {{{\Pr }}^{{ - 1}}}{{h}_{y}}} \\ {{{\mu }_{k}}\Pr _{k}^{{ - {\text{1}}}}{{k}_{y}}} \\ {{{\mu }_{\omega }}\Pr _{\omega }^{{ - {\text{1}}}}{{\omega }_{y}}} \end{array}} \right],$
$\begin{gathered} {{\sigma }_{{xx}}} = \mu \left( {2{{u}_{x}} - \frac{2}{3}\nabla U} \right),\quad \nabla U = {{u}_{x}} + {{{v}}_{y}}, \\ {{\tau }_{{xy}}} = {{\tau }_{{yx}}} = \mu ({{u}_{y}} + {{{v}}_{x}}),\quad p = (\gamma - 1){{\gamma }^{{ - 1}}}\rho h, \\ {{\sigma }_{{yy}}} = \mu \left( {2{{{v}}_{y}} - \frac{2}{3}\nabla U} \right),\quad e = \rho [{{\gamma }^{{ - 1}}}h + 0.5({{u}^{2}} + {{{v}}^{2}}) + k], \\ \end{gathered} $
$\begin{gathered} {{p}_{t}} = \frac{2}{3}\rho k,\quad \mu {\text{P}}{{{\text{r}}}^{{ - 1}}} = {{\mu }_{l}}{\text{Pr}}_{l}^{{ - 1}} + {{\mu }_{t}}{\text{Pr}}_{t}^{{ - 1}}, \\ \mu = {{\mu }_{l}} + {{\mu }_{t}},\quad {{\mu }_{k}}\Pr _{k}^{{ - 1}} = {{\mu }_{l}} + \Pr _{k}^{{ - 1}}{{\mu }_{t}}, \\ {\text{Re}} = {{\rho }_{\infty }}{{u}_{\infty }}c\mu _{{l\infty }}^{{ - 1}},\quad {{\mu }_{\omega }}\Pr _{\omega }^{{ - 1}} = {{\mu }_{l}} + \Pr _{\omega }^{{ - 1}}{{\mu }_{t}}, \\ \end{gathered} $
$\begin{array}{*{20}{c}} {{{H}_{k}} = \rho k\left( {\frac{\Omega }{{{{F}_{\mu }}}} - \beta {\text{*}}\omega } \right),} \\ {{{H}_{\omega }} = \rho \omega \left( {\chi \frac{\Omega }{{{{F}_{\mu }}}} - \beta \omega } \right) + 2\left( {1 - {{F}_{1}}} \right)\frac{{{{\sigma }_{{\omega 2}}}\rho }}{\omega }\left( {\frac{{\partial k}}{{\partial x}}\frac{{\partial \omega }}{{\partial x}} + \frac{{\partial k}}{{\partial y}}\frac{{\partial \omega }}{{\partial y}}} \right).} \end{array}$
Здесь $t$ и $x$, $y$ – время и декартовы координаты, $\rho $, $u$ и ${v}$ – плотность и компоненты вектора скорости соответственно, $h$ – энтальпия, $\gamma = 1.4$ – отношение удельных теплоемкостей, ${\mathbf{\varphi }}$ – вектор элементарных переменных, $\mu $ и ${{\mu }_{t}}$ – коэффициенты молекулярной и турбулентной вязкостей, $\Pr = 0.72$ и ${{\Pr }_{t}} = 0.9$ – молекулярное и турбулентное числа Прандтля, ${{C}_{{lt}}}$ – коэффициент подключения источниковых членов модели турбулентности. Для определения величины молекулярной вязкости ${{\mu }_{l}}$ используется формула Саттерлэнда (см. [20]). Коэффициент турбулентной вязкости определяется по формуле

${{\mu }_{t}} = \operatorname{Re} \frac{{\rho k}}{{{{F}_{\mu }}\omega }}.$

Необходимые константы и функции модели турбулентности (см. [19])

${{F}_{\mu }} = \max \left( {1;\;\Omega \frac{{{{F}_{2}}}}{{{{a}_{1}}\omega }}} \right),\quad {{F}_{2}} = \tanh \left\{ {{{{\left[ {\max \left( {\frac{{2{{k}^{{1/2}}}}}{{{{C}_{\mu }}\omega d}};\;\frac{{500{{\mu }_{l}}}}{{\operatorname{Re} \rho \omega {{d}^{2}}}}} \right)} \right]}}^{2}}} \right\},$
${{\Omega }^{2}} = 2{{\Omega }_{{xy}}}{{\Omega }_{{xy}}},\quad {{\Omega }_{{xy}}} = 0.5\left( {\frac{{\partial u}}{{\partial y}} - \frac{{\partial {v}}}{{\partial x}}} \right),\quad \beta * = {{C}_{\mu }} = 0.09,\quad {{a}_{1}} = 0.31,$
$d$ – расстояние до твердой поверхности. Поскольку модель представляет собой суперпозицию известных $k - \varepsilon $ и $k - \omega $ моделей, в ней используются две серии констант. Переход от констант внутреннего слоя к константам внешнего осуществляется с помощью функции перемешивания ${{F}_{1}}$:
$\phi = {{F}_{1}}{{\phi }_{1}} + (1 - {{F}_{1}}){{\phi }_{2}},\quad \phi = ({{\Pr }_{k}},{{\Pr }_{\omega }},\beta ,\chi ),$
где

${{F}_{1}} = \tanh \left( {{{{\left\{ {\min \left[ {\max \left( {\frac{{{{k}^{{1/2}}}}}{{{{C}_{\mu }}\omega d}};\;\frac{{500{{\mu }_{l}}}}{{\operatorname{Re} \rho \omega {{d}^{2}}}}} \right);\;\frac{{4{{\sigma }_{{\omega 2}}}\rho k}}{{C{{D}_{{k\omega }}}{{d}^{2}}}}} \right]} \right\}}}^{4}}} \right),$
$C{{D}_{{k\omega }}} = \max \left( {\frac{{2{{\sigma }_{{\omega 2}}}\rho }}{\omega }\left( {\frac{{\partial k}}{{\partial x}}\frac{{\partial \omega }}{{\partial x}} + \frac{{\partial k}}{{\partial y}}\frac{{\partial \omega }}{{\partial y}}} \right);\;{{{10}}^{{ - 20}}}} \right).$

Наборы констант для внутреннего и внешнего решений (1 и 2 соответственно) имеют значения

${{\Pr }_{{k1}}} = 0.85,\quad {{\Pr }_{{\omega 1}}} = 0.5,\quad {{\beta }_{1}} = 0.075,\quad {{\chi }_{1}} = 0.533,$
${{\Pr }_{{k2}}} = 1.0,\quad {{\Pr }_{{\omega 2}}} = 0.856,\quad {{\beta }_{2}} = 0.0828,\quad {{\chi }_{2}} = 0.44.$

На поверхности тела задаются условия прилипания для скорости, температура поверхности или условие равенства нулю нормального градиента температуры. Плотность газа на поверхности определяется путем решения уравнения неразрывности или из условия нулевого нормального градиента давления. Так же на твердой поверхности задаются нулевые значения кинетической энергии ${{k}_{w}}$ и турбулентной вязкости ${{\mu }_{{tw}}}$, а частота турбулентности в соответствии с рекомендациями из [19] определяется как

${{\omega }_{w}} = 10\frac{{6{{\mu }_{w}}}}{{\operatorname{Re} {{\rho }_{w}}{{\beta }_{1}}d_{w}^{2}}},$
где ${{d}_{w}}$ – расстояние до ближайшего узла разностной сетки.

На входной границе фиксируются параметры набегающего потока на бесконечности, а на выходной – условия свободного вытекания. При этом необходимо учитывать то, что возмущения, генерируемые обтекаемым телом, распространяются вверх против потока тем дальше, чем ниже число Маха набегающего потока. При достаточно близких внешних границах области расчета целесообразно использовать граничные условия на основе характеристик. В набегающем потоке задаются полные давление и температура, угол между горизонтальной и вертикальной компонентами скорости и решается уравнение на основе выходной характеристики. Напротив, на выходной границе задается давление, другие параметры экстраполируются. Кинетическая энергия турбулентности на бесконечности задается равной ${{k}_{\infty }} = {{10}^{{ - 6}}}$. При этом полагается, что турбулентная вязкость лежит в диапазоне $0.1 \leqslant {{\mu }_{{t\infty }}} \leqslant 1$, откуда и следует значение частоты турбулентности в набегающем потоке.

В представленном виде уравнения представляют собой законы сохранения осредненных по массе параметров потока. Если же полагать равенству нулю кинетической энергии турбулентности, вихревой вязкости и источниковых членов в уравнениях для $k$ и $\omega $, то полученные таким образом уравнения позволяют получать характеристики ламинарного течения вязкого газа. Вопреки названию и устоявшимся представлениям, такие течения далеко не всегда являются стационарными. Возникающие при высоких числах Рейнольдса отрывные и пульсационные эффекты провоцируют переход от ламинарного режима течения газа к турбулентному.

Далее производится переход к обобщенной криволинейной системе координат для возможности расчета обтекания тел с искривленными и изломанными границами. Данная процедура подробно описана в [21]. Согласно ей, область течения в физической плоскости $(x,y)$ отображается на единичный квадрат расчетной плоскости $(\xi ,\eta )$ с помощью преобразования общего вида $\xi = \xi (x,y)$, $\eta = \eta (x,y)$, $0 \leqslant \xi \leqslant 1$, $0 \leqslant \eta \leqslant 1$, а производные по декартовым координатам некой функции $f$ уравнениях приобретают вид

$\frac{{\partial f}}{{\partial x}} = \frac{1}{{{{J}^{{ - 1}}}}}\left( {\frac{{\partial f{{y}_{\eta }}}}{{\partial \xi }} - \frac{{\partial f{{y}_{\xi }}}}{{\partial \eta }}} \right),\quad \frac{{\partial f}}{{\partial y}} = \frac{1}{{{{J}^{{ - 1}}}}}\left( {\frac{{\partial f{{x}_{\xi }}}}{{\partial \eta }} - \frac{{\partial f{{x}_{\eta }}}}{{\partial \xi }}} \right),$
где ${{J}^{{ - 1}}} = {{x}_{\xi }}{{y}_{\eta }} - {{x}_{\eta }}{{y}_{\xi }}$ – якобиан, а ${{x}_{\xi }}$, ${{y}_{\xi }}$, ${{x}_{\eta }}$ и ${{y}_{\eta }}$ – метрические коэффициенты преобразования. Уравнения, использующиеся для проведения расчетов, приобретают следующий вид:
$\frac{{\partial {\mathbf{\hat {U}}}}}{{\partial t}} + \frac{{\partial {\mathbf{\hat {F}}}}}{{\partial \xi }} + \frac{{\partial {\mathbf{\hat {G}}}}}{{\partial \eta }} = {\text{R}}{{{\text{e}}}^{{ - {\text{1}}}}}\left( {\frac{{\partial {{{{\mathbf{\hat {F}}}}}_{\mu }}}}{{\partial \xi }} + \frac{{\partial {{{{\mathbf{\hat {G}}}}}_{\mu }}}}{{\partial \eta }}} \right) + {{C}_{{lt}}}{\mathbf{\hat {H}}},$
${\mathbf{\hat {U}}} = {{J}^{{ - 1}}}{\mathbf{U}},\quad {\mathbf{\hat {H}}} = {{J}^{{ - 1}}}{\mathbf{H}},{\mathbf{\hat {F}}} = {\mathbf{F}}{{y}_{\eta }} - {\mathbf{G}}{{y}_{\xi }},\quad {\mathbf{\hat {G}}} = {\mathbf{G}}{{x}_{\xi }} - {\mathbf{F}}{{x}_{\eta }},$
${{{\mathbf{\hat {F}}}}_{\mu }} = {{{\mathbf{F}}}_{\mu }}{{y}_{\eta }} - {{{\mathbf{G}}}_{\mu }}{{y}_{\xi }},\quad {{{\mathbf{\hat {G}}}}_{\mu }} = {{{\mathbf{G}}}_{\mu }}{{x}_{\xi }} - {{{\mathbf{F}}}_{\mu }}{{x}_{\eta }},$
а векторы ${{{\mathbf{\hat {F}}}}_{\mu }}$ и ${{{\mathbf{\hat {G}}}}_{\mu }}$ также содержат производные переменных и метрические коэффициенты. Таким образом, расчеты осуществляются на равномерной сетке, позволяющей применять компактные схемы высокого порядка.

3. РАЗНОСТНЫЕ ОПЕРАТОРЫ И ИХ СВОЙСТВА

Составные компактные разности были предложены в [14] на основе опыта практического применения несимметричных компактных аппроксимаций (см. [3]). Они основаны на идее разделения единого разностного оператора на части, каждая из которых отвечает за одно из его характерных свойств. Разностный аналог производной ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial x}}} \right. \kern-0em} {\partial x}}$, предназначенный для описания конвективных членов уравнений, на сетке ${{\omega }_{h}} = \{ {{x}_{j}} = jh,\;h = {\text{const}}\} $ имеет вид

(1)
$f_{j}^{'} = \left[ {\Delta _{1}^{{\left( {2l} \right)}} + {{{( - 1)}}^{m}}s\frac{{\Delta _{2}^{m}}}{{{{c}_{{2m}}}}}} \right]\frac{{{{f}_{j}}}}{{2h}},$
где $l,m = 1,\;2\; \ldots $ – коэффициенты при обозначении порядка центральной и повторной разностей, $s = \pm 1$ – параметр, учитывающий направление потока, а ${{c}_{{2m}}}$ – нормирующая константа, своя для каждого значения $m$. При этом операторами $\Delta _{1}^{{(2l)}}$ и $\Delta _{2}^{m}$ обозначены первая и $2m$-я разности, описываемые соответственно с помощью симметричного компактного и обычного оператора диффузного типа. Первый отвечает за аппроксимацию производной, второй способствует получению устойчивого решения задачи. Для их представления используются операторы на основе простейших разностей ${{\Delta }_{1}} = {{T}_{1}} - {{T}_{{ - 1}}}$, ${{\Delta }_{2}} = {{T}_{1}} - 2{{T}_{0}} + {{T}_{{ - 1}}}$, где $T$ – оператор сдвига ${{T}_{n}}{{f}_{j}} = f({{x}_{j}} + nh)$. Основу составных компактных схем представляет аппроксимирующий оператор, имеющий вид симметричной пятиточечной компактной разности
(2)
$f_{j}^{'} = \Delta _{1}^{{(2l)}}\frac{{{{f}_{j}}}}{{2h}} = {{(1 + a{{\Delta }_{2}})}^{{ - 1}}}(1 + b{{\Delta }_{2}}){{\Delta }_{1}}\frac{{{{f}_{j}}}}{{2h}}.$
Данная разность при произвольных значениях $a$ и $b$ формально имеет второй порядок аппроксимации и реализуется трехточечными прогонками. В случае $a$ = 1/5 и $b$ = 1/30 она представляет собой классическую Паде-разность 6-го порядка (см. [4]).

Повышение порядка аппроксимации обычно сопровождается укрупнением сеточного шаблона. Альтернативным направлением получения разностных схем с высокой разрешающей способностью является мультиоператорный подход, описанный в [15], [16]. Однако для составных компактных схем высокий порядок достигается не путем подбора весов компонентов мульти-оператора, как в [15], [16], а подбором значений коэффициентов $a$ и $b$ этих разностей при заданных весах. Веса всех разностных операторов равны и обратно пропорциональны их количеству. Мультиоператорное представление разности $\Delta _{1}^{{(2l)}}$ имеет вид

(3)
$\Delta _{1}^{{\left( k \right)}} = \frac{1}{n}{{\sum\limits_{p = 1}^n {(1 + {{a}_{p}}{{\Delta }_{2}})} }^{{ - 1}}}(1 + {{b}_{p}}{{\Delta }_{2}}){{\Delta }_{1}},$
где $n$ – количество используемых операторов, ${{a}_{p}}$ и ${{b}_{p}}$ – коэффициенты, свои для каждого оператора, а $k$ – общий порядок разностной аппроксимации. В зависимости от количества операторов порядок разностной схемы может меняться от 6 до 22 (см. [17], [18]). В данной работе используются разности 6-го, 14-го и 22-го порядков. Их коэффициенты представлены в табл. 1.

Таблица 1
n k p ${{a}_{p}}$ ${{b}_{p}}$
1 6 1 0.2 0.0333333333333
3 14 1 0.239048459346 –0.0567444588747
2 0.1624727238229 –0.0379667519389
3 0.0600172783691 0.0220795956071
5 22 1 0.245338324132 –0.0875922106964
2 0.149866943731 –0.0093729917038
3 0.026791341338 0.01450958533096
4 0.210093756803 –0.0538634205423
5 0.0821953482816 0.0172714185639

Поскольку разностные операторы (3) реализуются трехточечными прогонками, они требуют постановки соответствующих граничных условий для каждого внутреннего оператора. На каждой границе задаются по два граничных условия. Их вид представлен формулой (4), а необходимые коэффициенты сведены в табл. 2 и 3:

(4)
$\Delta _{{1,b}}^{{\left( k \right)}} = \frac{1}{n}\sum\limits_{p = 1}^n {{{{(a_{p}^{0}{{T}_{0}} + a_{p}^{1}{{T}_{{ + 1}}} + a_{p}^{2}{{T}_{{ + 2}}})}}^{{ - 1}}}} (b_{p}^{0}{{T}_{0}} + b_{p}^{1}{{T}_{{ + 1}}} + b_{p}^{2}{{T}_{{ + 2}}} + b_{p}^{3}{{T}_{{ + 3}}} + b_{p}^{4}{{T}_{{ + 4}}}).$
Таблица 2
N k p $a_{p}^{0}$ $b_{p}^{0}$ $b_{p}^{1}$
1 5 1 0.2 –0.61666666667 0.1333333333333
3 5 1 1.3707470112474 –2.392347386564 4.4383149363567
2 0.223948025612 –0.661256249069 0.2514243312644
3 0.0376713398493 –0.517006992215 0.0117873019992
5 5 1 140.32598921687 –233.9337759912 583.253061457344
2 0.2135067189865 –0.6541547386747 0.24209209266732
3 0.0120683273273 –0.5055658003922 0.00437413925759
4 0.7353423046579 –1.3806499641782 1.94820127241312
5 0.0673734960562 –0.53298694541299 0.028437971229197
Таблица 3
n k p $a_{p}^{0}$ $a_{p}^{1}$ $b_{p}^{0}$ $b_{p}^{1}$
1 6 1 0.06666666666 0.53333333333 –0.23888888889 –0.44444444444
3 6 1 –0.0308111106 0.49717689768 0.10516977549 –1.24740708804
2 0.18684519996 0.70131442416 –0.55589510643 0.090497388666
3 0.02370623266 0.65008260032 –0.3388766994 –0.17650437274
5 6 1 –0.00901353453 0.49965746749 0.09951983608 –1.27858087272
2 0.21224996404 0.78362809119 –0.65043676019 0.236544983249
3 0.00734736459 0.62242727035 –0.31561619167 –0.18828384108
4 –0.13495595651 0.44873160152 0.292203419413 –1.53813007655
5 0.0458509465 0.6872125923 –0.37520150835 –0.14849271155

Табл. 2 соответствует разности, содержащей две точки в левой части оператора. Остальные коэффициенты этого граничного оператора определяются из соотношений $a_{p}^{1}$ = 1 – $a_{p}^{0}$, $a_{p}^{2}$ = 0, $b_{p}^{2}$ = –2.5 – $a_{p}^{0}$ – 6$b_{p}^{0}$ – 3$b_{p}^{1}$, $b_{p}^{3}$ = 4 + 2$a_{p}^{0}$ + 8$b_{p}^{0}$ + 3$b_{p}^{1}$, $b_{p}^{4}$ = –1.5 – $a_{p}^{0}$ – 3$b_{p}^{0}$ – $b_{p}^{1}$, где $p$ меняется от 1 до $n$, $n$ – количество операторов в схеме, а $k$ – порядок аппроксимации.

Другое граничное условие содержит три узла сетки в левой части оператора. Коэффициенты $a_{p}^{0}$, $a_{p}^{1}$, $b_{p}^{0}$ и $b_{p}^{1}$ для него содержатся в табл. 3.

Остальные коэффициенты разностной формулы определяются соотношениями $a_{p}^{2}$ = 1 – $a_{p}^{0}$ – $a_{p}^{1}$, $b_{p}^{2}$ = –1.5 – 2$a_{p}^{0}$ – $a_{p}^{1}$ – 6$b_{p}^{0}$ – 3$b_{p}^{1}$, $b_{p}^{3}$ = 2 + 4$a_{p}^{0}$ + 2$a_{p}^{1}$ – 3$b_{p}^{0}$ – $b_{p}^{1}$, $b_{p}^{4}$ = –0.5 – 2$a_{p}^{0}$ – $a_{p}^{1}$ – 3$b_{p}^{0}$ – $b_{p}^{1}$.

Граничные условия, необходимые для получения решения с помощью прогонок, имеют порядки 5 и 6 не зависимо от количества операторов. Дело в том, что высокий порядок мультиоператорной схемы получается после суммирования отдельных операторов, каждый из которых имеет лишь второй порядок. При проведении прогонок граничные условия для каждого оператора формируются таким образом, чтобы остаточные члены их разложений приближались бы к остаточным членам соответствующих операторов. Использование традиционных односторонних разностей у границы снижает их порядок, хотя всего лишь в двух узлах.

Мультиоператорная формула (3) является бездиссипативной составляющей разности (1) и отвечает за аппроксимацию конвективных членов исходных уравнений. На ее основе также проводится вычисление смешанных производных вязких членов, компонент источникового вектора ${\mathbf{\hat {H}}}$ и метрических коэффициентов преобразования координат. Последнее особенно важно, так как обеспечивает выполнение условий

$\frac{{\partial {{y}_{\eta }}}}{{\partial \xi }} = \frac{{\partial {{y}_{\xi }}}}{{\partial \eta }},\quad \frac{{\partial {{x}_{\xi }}}}{{\partial \eta }} = \frac{{\partial {{x}_{\eta }}}}{{\partial \xi }},$
необходимых для отсутствия наведенных искажений решения при расчетах на криволинейных сетках. Мультиоператорные схемы годятся и для трехмерных расчетов. В этом случае требуется несколько иное определение метрических коэффициентов преобразования координат. Примеры проведения трехмерных расчетов с помощью компактных разностей на криволинейных сетках можно найти, например, в [5].

Аппроксимирующей составляющей разности (2) может оказаться вполне достаточно для расчетов участков течения с существенным влиянием вязких сил, например, в зонах отрыва пограничного слоя у препятствий на твердой поверхности. В общем же случае потоки необходимо корректировать. Для этого используются стабилизирующие добавки в виде четных разностей высокого порядка, которые на сетке ${{\omega }_{h}} = \{ {{x}_{j}} = jh,\;h = {\text{const}}\} $ выглядят следующим образом:

(5)
$\sum\limits_{n = 1}^3 {{{{( - 1)}}^{m}}c_{{2m}}^{{ - 1}}{{s}_{n}}\Delta _{2}^{{2m - 2}}({{\Delta }_{ - }}{{T}_{{1/2}}}{{{\mathbf{M}}}_{n}}{{\Delta }_{ + }}{\mathbf{\varphi }})} ,$
где ${{\Delta }_{ - }} = {{T}_{0}} - {{T}_{{ - 1}}}$, ${{\Delta }_{ + }} = {{T}_{1}} - {{T}_{0}}$, ${\mathbf{M}}$ – якобиевы матрицы расщепления векторов конвективных членов уравнений, полученные в соответствии с количеством собственных значений $\lambda _{n}^{\xi }$ и $\lambda _{n}^{\eta }$, n = 1–3,
${\mathbf{M}}_{n}^{\xi } = \frac{{\partial {{{{\mathbf{\hat {f}}}}}_{n}}}}{{\partial {\mathbf{\varphi }}}},\quad {\mathbf{M}}_{n}^{\eta } = \frac{{\partial {{{{\mathbf{\hat {g}}}}}_{n}}}}{{\partial {\mathbf{\varphi }}}},$
${{s}_{n}}$ – знаки собственных значений, ${{c}_{{2m}}}$ – коэффициенты. Процедура расщепления потоковых векторов ${\mathbf{\hat {F}}}$ и ${\mathbf{\hat {G}}}$ подробно описана в [22]. В данном случае они имеют вид
${\mathbf{\hat {F}}} = \sum\limits_{n = 1}^3 {{{{{\mathbf{\hat {f}}}}}_{n}}} ,\quad {\mathbf{\hat {G}}} = \sum\limits_{n = 1}^3 {{{{{\mathbf{\hat {g}}}}}_{n}}} ,$
где

${{{\mathbf{\hat {f}}}}_{1}} = \frac{{\rho \lambda _{1}^{\xi }(\gamma - 1)}}{\gamma }\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ u \\ {v} \end{array}} \\ {({{u}^{2}} + {{{v}}^{2}}){\text{/}}2 + k} \\ {\gamma k(\gamma - 1)} \\ {\gamma \omega (\gamma - 1)} \end{array}} \right],\quad {{{\mathbf{\hat {f}}}}_{2}} = \frac{{\rho \lambda _{2}^{\xi }}}{{2\gamma }}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ {u - {{{\hat {a}}}_{\xi }}{{y}_{\eta }}} \\ {{v} + {{{\hat {a}}}_{\xi }}{{x}_{\eta }}} \end{array}} \\ {h + ({{u}^{2}} + {{{v}}^{2}}){\text{/}}2 + k - {{w}_{\xi }}{{{\hat {a}}}_{\xi }}} \\ 0 \\ 0 \end{array}} \right],$
${{{\mathbf{\hat {f}}}}_{3}} = \frac{{\rho \lambda _{3}^{\xi }}}{{2\gamma }}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ {u + {{{\hat {a}}}_{\xi }}{{y}_{\eta }}} \\ {{v} - {{{\hat {a}}}_{\xi }}{{x}_{\eta }}} \end{array}} \\ {h + ({{u}^{2}} + {{{v}}^{2}}){\text{/}}2 + k + {{w}_{\xi }}{{{\hat {a}}}_{\xi }}} \\ 0 \\ 0 \end{array}} \right],\quad {{{\mathbf{\hat {g}}}}_{1}} = \frac{{\rho \lambda _{1}^{\eta }(\gamma - 1)}}{\gamma }\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ u \\ {v} \end{array}} \\ {({{u}^{2}} + {{{v}}^{2}}){\text{/}}2 + k} \\ {\gamma k(\gamma - 1)} \\ {\gamma \omega (\gamma - 1)} \end{array}} \right],$
${{{\mathbf{\hat {g}}}}_{2}} = \frac{{\rho \lambda _{2}^{\eta }}}{{2\gamma }}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ {u + {{{\hat {a}}}_{\eta }}{{y}_{\xi }}} \\ {{v} - {{{\hat {a}}}_{\eta }}{{x}_{\xi }}} \end{array}} \\ {h + ({{u}^{2}} + {{{v}}^{2}}){\text{/}}2 + k - {{w}_{\eta }}{{{\hat {a}}}_{\eta }}} \\ 0 \\ 0 \end{array}} \right],\quad {{{\mathbf{\hat {g}}}}_{3}} = \frac{{\rho \lambda _{3}^{\eta }}}{{2\gamma }}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ {u - {{{\hat {a}}}_{\eta }}{{y}_{\xi }}} \\ {{v} + {{{\hat {a}}}_{\eta }}{{x}_{\xi }}} \end{array}} \\ {h + ({{u}^{2}} + {{{v}}^{2}}){\text{/}}2 + k + {{w}_{\eta }}{{{\hat {a}}}_{\eta }}} \\ 0 \\ 0 \end{array}} \right],$
${{w}_{\xi }} = u{{y}_{\eta }} - {v}{{x}_{\eta }},\quad {{a}_{\xi }} = a{{(x_{\eta }^{2} + y_{\eta }^{2})}^{{1/2}}},\quad {{\hat {a}}_{\xi }} = {{a}_{\xi }}{{(x_{\eta }^{2} + y_{\eta }^{2})}^{{ - 1}}},$
$\lambda _{1}^{\xi } = {{w}_{\xi }},\quad \lambda _{2}^{\xi } = {{w}_{\xi }} - {{a}_{\xi }},\quad \lambda _{3}^{\xi } = {{w}_{\xi }} + {{a}_{\xi }},\quad s_{n}^{\xi } = \operatorname{sign} (\lambda _{n}^{\xi }),$
${{w}_{\eta }} = - u{{y}_{\xi }} + {v}{{x}_{\xi }},\quad {{a}_{\eta }} = a{{(x_{\xi }^{2} + y_{\xi }^{2})}^{{1/2}}},\quad {{\hat {a}}_{\eta }} = {{a}_{\eta }}{{(x_{\xi }^{2} + y_{\xi }^{2})}^{{ - 1}}},$
$\lambda _{1}^{\eta } = {{w}_{\eta }},\quad \lambda _{2}^{\eta } = {{w}_{\eta }} - {{a}_{\eta }},\quad \lambda _{3}^{\eta } = {{w}_{\eta }} + {{a}_{\eta }},\quad s_{n}^{\eta } = \operatorname{sign} (\lambda _{n}^{\eta }),$
$a = {{[\gamma (p + {{p}_{t}}){{\rho }^{{ - 1}}}]}^{{1/2}}}.$

Помимо конвективных членов, разностное представление которых можно осуществлять рассмотренным способом, в уравнениях динамики вязкого газа присутствуют диссипативные члены вида $\partial (\mu \partial f{\text{/}}\partial x){\text{/}}\partial x$. Обычно они описываются стандартным образом операторами второго порядка ${{\Delta }_{ - }}{{T}_{{1/2}}}\mu {{\Delta }_{ + }}{{f}_{j}}$. В данном случае будем применять разностные аппроксимации вида

(6)
${{\delta }^{{(k)}}}{{T}_{{1/2}}}({{I}^{{(k)}}}\mu ){{\delta }^{{(k)}}}{{f}_{j}},$
где ${{\delta }^{{(k)}}}$ и ${{I}^{{(k)}}}$ – формулы компактных разности и интерполяции. Их мультиоператорное представление выглядит следующим образом:
(7)
${{\delta }^{{\left( k \right)}}} = \frac{1}{n}\sum\limits_{p = 1}^n {{{{(1 + a_{p}^{\delta }{{\Delta }_{2}})}}^{{ - 1}}}{\kern 1pt} [(1 - 3b_{p}^{\delta })({{T}_{{1/2}}} - {{T}_{{ - 1/2}}}) + b_{p}^{\delta }({{T}_{{3/2}}} - {{T}_{{ - 3/2}}})]} ,$
(8)
${{I}^{{\left( k \right)}}} = \frac{1}{n}\sum\limits_{p = 1}^n {{{{(1 + a_{p}^{I}{{\Delta }_{2}})}}^{{ - 1}}}{\kern 1pt} [(1 - b_{p}^{I})({{T}_{{1/2}}} + {{T}_{{ - 1/2}}}) + b_{p}^{I}({{T}_{{3/2}}} + {{T}_{{ - 3/2}}})]} .$
Здесь $a_{p}^{\delta }$, $b_{p}^{\delta }$, $a_{p}^{I}$ и $b_{p}^{I}$ – коэффициенты свои для каждого оператора, их значения представлены в табл. 4 и 5. Видно, что с увеличением количества операторов растет и порядок аппроксимации.

Таблица 4
N k p $a_{p}^{\delta }$ $b_{p}^{\delta }$
1 6 1 0.1125 0.070833333333333
3 14 1 0.2109472736338 0.183939274770512
2 0.1186395423325546 0.057924127866374
3 0.031172041017277 –0.006104545653217
5 22 1 0.0141849346249354 –0.009836597930706
2 0.2324819204002052 0.218256088277739
3 0.0580630497952101 –0.000139903346171
4 0.120744725801449 0.0540743151222133
5 0.1849034349504165 0.1396908301158074
Таблица 5
n k p $a_{p}^{I}$ $b_{p}^{I}$
1 6 1 0.1875 0.03125
3 14 1 0.2376211084878 0.033945872641115
2 0.152815116744539 0.0218307309635056
3 0.047063774767658 0.0067233963953797
5 22 1 0.0730731233747809 0.0066430112158892
2 0.2449366217017918 0.0222669656092538
3 0.2068575917431287 0.0188052356130117
4 0.0198433083961389 0.0018039371269217
5 0.1427893547841596 0.0129808504349236

Расчет диссипативных членов уравнений проводится в два этапа. Сначала определяются производные параметров и интерполированные коэффициенты вязких членов в полуцелых узлах разностной сетки. При прогонках используются граничные условия следующего вида:

$\delta _{{1,b}}^{{(k)}} = \frac{1}{n}\sum\limits_{p = 1}^n {[b_{{1,p}}^{{\delta , - 1/2}}{{T}_{{ - 1/2}}} + b_{{1,p}}^{{\delta ,1/2}}{{T}_{{1/2}}} + b_{{1,p}}^{{\delta ,3/2}}{{T}_{{3/2}}} + b_{{1,p}}^{{\delta ,5/2}}{{T}_{{5/2}}}]} ,$
$I_{b}^{{(k)}} = \frac{1}{n}\sum\limits_{p = 1}^n {{{{(a_{p}^{{I,0}}{{T}_{0}} + a_{p}^{{I,1}}{{T}_{{ + 1}}} + a_{p}^{{I,2}}{{T}_{{ + 2}}})}}^{{ - 1}}}(b_{p}^{{I, - 1/2}}{{T}_{{ - 1/2}}} + b_{p}^{{I,1/2}}{{T}_{{1/2}}} + b_{p}^{{I,3/2}}{{T}_{{3/2}}} + b_{p}^{{I,3/2}}{{T}_{{5/2}}})} .$

Основные коэффициенты данных операторов и содержатся в табл. 6 и 7.

Таблица 6
n k p $b_{{1,p}}^{{\delta , - 1/2}}$
1 2 1 –1
3 3 1 –0.97299200113667
2 –0.93928458553382
3 –0.96272341332951
5 3 1 –0.97597846744436
2 –0.98577416787753
3 –0.94179704685862
4 –0.93332958932076
5 –0.95478739516539
Таблица 7
n k p $a_{p}^{{I,0}}$ $b_{p}^{{I, - 1/2}}$ $b_{p}^{{I,1/2}}$
1 5 1 0.375 0.078125 0.703125
3 6 1 0.4752422169756 0.03898841993765 0.89222282980377
2 0.30563023348908 0.047290135444342 0.68559055811956
3 0.09412754953532 0.023096444618009 0.53156161207667
5 6 1 0.146146246749562 0.030149555732161 0.562340590768969
2 0.489873243403584 0.0245218870179106 0.938574547959106
3 0.413715183486257 0.0350312986566758 0.827426523129242
4 0.039686616792278 0.0101077011467953 0.511167450478814
5 0.285578709568319 0.040814557446493 0.676115887663763

Остальные коэффициенты граничного условия для разности $\delta _{{1,b}}^{{(k)}}$ определяются из значений коэффициентов $b_{{1,p}}^{{\delta , - 1/2}}$ табл. 4 с помощью следующих соотношений: $b_{{1,p}}^{{\delta ,1/2}}$ = –2 – 3$b_{{1,p}}^{{\delta , - 1/2}}$, $b_{{1,p}}^{{3/2}}$ = = 3 + 3$b_{{1,p}}^{{\delta ,1/2}}$, $b_{{1,p}}^{{\delta ,5/2}}$ = –1 – $b_{{1,p}}^{{\delta ,1/2}}$.

Коэффициенты граничного условия для компактной интерполяции $I_{b}^{{(k)}}$ рассчитываются на основе данных табл. 7:

$\begin{gathered} a_{p}^{{I,1}} = 1--a_{p}^{{I,0}},\quad a_{p}^{{I,2}} = 0,\quad b_{p}^{{I,3/2}} = 1.5 + a_{p}^{{I,0}}--3b_{p}^{{I, - 1/2}}--2b_{p}^{{I,1/2}}, \\ b_{p}^{{I,5/2}} = --0.5--a_{p}^{{I,0}} + 2b_{p}^{{I, - 1/2}} + b_{p}^{{I,1/2}}. \\ \end{gathered} $

Далее следует расчет собственно вязких членов уравнений по формуле (7) с использованием граничных условий

$\delta _{{2,b}}^{{(k)}} = \frac{1}{n}\sum\limits_{p = 1}^n {{{{(a_{{2,p}}^{{\delta ,0}}{{T}_{0}} + a_{{2,p}}^{{\delta ,1}}{{T}_{1}})}}^{{ - 1}}}(b_{{2,p}}^{{\delta ,1/2}}{{T}_{{1/2}}} + b_{{2,p}}^{{\delta ,3/2}}{{T}_{{3/2}}} + b_{{2,p}}^{{\delta ,5/2}}{{T}_{{5/2}}} + b_{{2,p}}^{{\delta ,7/2}}{{T}_{{7/2}}})} $
и
$\delta _{{3,b}}^{{(k)}} = \frac{1}{n}\sum\limits_{p = 1}^n {{{{(a_{{3,p}}^{{\delta ,0}}{{T}_{0}} + a_{{3,p}}^{{\delta ,1}}{{T}_{1}} + a_{{3,p}}^{{\delta ,2}}{{T}_{2}})}}^{{ - 1}}}(b_{{3,p}}^{{\delta ,1/2}}{{T}_{{1/2}}} + b_{{3,p}}^{{\delta ,3/2}}{{T}_{{3/2}}} + b_{{3,p}}^{{\delta ,5/2}}{{T}_{{5/2}}} + b_{{4,p}}^{{\delta ,7/2}}{{T}_{{7/2}}})} ,$
базовые коэффициенты которых содержатся в табл. 8 и 9.

Таблица 8
n k p $a_{{2,p}}^{{\delta ,0}}$ $b_{{2,p}}^{{\delta ,1/2}}$
1 4 1 0.043478260869565 –1.0452898550724637
3 4 1 0.02775767820473 –1.028507357546134
2 0.064640062661807 –1.068564710857438
3 0.0387199336324187 –1.040163280594343
5 4 1 0.02461276898715095 –1.02520400541866
2 0.01443112691124347 –1.0146364217
3 0.0617998891964227 –1.06539682525146
4 0.071432869419425 –1.0761953281596
5 0.04735358370203 –1.04949456256945
Таблица 9
n k p $a_{{3,p}}^{{\delta ,0}}$ $a_{{3,p}}^{{\delta ,1}}$ $b_{{3,p}}^{{\delta ,1/2}}$
1 5 1 0.1125 2.475 –2.7708333333333
3 5 1 0.2109472736338 7.388653531518 –7.9944873535566
2 0.1186395423326 1.716747637802 –2.0119508503331
3 0.0311720410173 0.773892381696 –0.8301319180773
5 5 1 0.0141849346249 0.562139274664 –0.5806725459833
2 0.2324819204002 15.87727318258 –16.560493111661
3 0.0580630497952 0.881470184814 –0.9974563810583
4 0.1207447258015 1.569579725432 –1.8651434921575
5 0.1849034349504 3.719836618387 –4.2293343184042

Остальные коэффициенты оператора $\delta _{{2,b}}^{{(k)}}$ определяются зависимостями $a_{{2,p}}^{{\delta ,1}}$ = 1 – $a_{{2,p}}^{{\delta ,0}}$, $a_{{2,p}}^{{\delta ,2}}$ = 0, $b_{{2,p}}^{{\delta ,3/2}}$ = –2 – $a_{{2,p}}^{{\delta ,0}}$ – 3$b_{{2,p}}^{{\delta ,1/2}}$, $b_{{2,p}}^{{\delta ,5/2}}$ = 3 + 2$a_{{2,p}}^{{\delta ,0}}$ + 3$b_{{2,p}}^{{\delta ,1/2}}$, $b_{{2,p}}^{{\delta ,7/2}}$ = –1 – $a_{{2,p}}^{{\delta ,0}}$ – $b_{{2,p}}^{{\delta ,1/2}}$ с использованием данных табл. 8.

С помощью приведенных в табл. 9 коэффициентов все остальные коэффициенты разности $\delta _{{3,b}}^{{(k)}}$ находятся из соотношений $a_{{3,p}}^{{\delta ,2}}$ = 1 – $a_{{3,p}}^{{\delta ,0}}$ – $a_{{3,p}}^{{\delta ,1}}$, $b_{{3,p}}^{{\delta ,3/2}}$ = –1 – 2$a_{{3,p}}^{{\delta ,0}}$ –$a_{{3,p}}^{{\delta ,1}}$ – 3$b_{{3,p}}^{{\delta ,1/2}}$, $b_{{3,p}}^{{\delta ,5/2}}$ = 1 + 4$a_{{3,p}}^{{\delta ,0}}$ + + 2$a_{{3,p}}^{{\delta ,1}}$ + 3$b_{{3,p}}^{{\delta ,1/2}}$, $b_{{3,p}}^{{\delta ,7/2}}$ = –2$a_{{3,p}}^{{\delta ,0}}$ – $a_{{3,p}}^{{\delta ,1}}$ – $b_{{3,p}}^{{\delta ,1/2}}$.

Интегрирование разностных уравнений по времени может осуществляться двумя разными способами. Если размеры узлов сетки достаточно крупные и не слишком отличаются между собой, то целесообразно применять явный метод Рунге–Кутты 4-го порядка по времени. Соотношение временного и пространственного шагов при этом составляет 0.1–0.2. При наличии же тонких сдвиговых и пограничных слоев, требующих большого количества узлов для их подробного описания и значительных размерах области расчета, данный подход становится слишком затратным. В этом случае используется неявный метод Гаусса релаксации в линиях 2-го порядка. Отношение временного и пространственного шагов здесь близко к единице, а затраты на один шаг по времени меньше, чем для метода Рунге–Кутты.

Анализ свойств мультиоператорных разностей (3) проведем применительно к линейному скалярному уравнению ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial t + {{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial x = 0}}} \right. \kern-0em} {\partial x = 0}}}}} \right. \kern-0em} {\partial t + {{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial x = 0}}} \right. \kern-0em} {\partial x = 0}}}}$. Рассмотрим поведение таких характеристик, как дисперсия и диссипация, взяв за пример работы [3], [4]. Полагая, что решение уравнения в каждой точке $j$ на сетке ${{\omega }_{h}} = \{ {{x}_{j}} = jh,\;h = {\text{const}}\} $ имеет вид $U(t)\exp (ikhj)$, где $i$ – мнимая единица, а $k$ – волновое число, получаем обыкновенное дифференциальное уравнение $U_{t}^{'} + \omega (kh)U = 0$. Дискретизация временной производной не рассматривается. Для каждой разностной схемы посредством применения преобразования Фурье к исходным операторам ${{T}_{n}}$, ${{\Delta }_{1}}$ и ${{\Delta }_{2}}$, имеет место соответствующая комплексная функция $\omega (kh)$ и свои выражения для фазовой скорости (дисперсии) ${{D}_{\alpha }} = \operatorname{Re} \left[ {{{\omega (kh)} \mathord{\left/ {\vphantom {{\omega (kh)} {ikh}}} \right. \kern-0em} {ikh}}} \right]$ и диссипации ${{D}_{s}} = \operatorname{Re} \left[ {\omega (kh)} \right]$. Дисперсия ${{D}_{\alpha }}$, а точнее, выражение 1 – ${{D}_{\alpha }}$, характеризует собой фазовую ошибку, вносимую заменой дифференциального оператора разностным. Диссипация ${{D}_{s}}$ отражает способность разностной схемы противостоять возникающим паразитным осцилляциям решения. Поскольку для составных компактных схем разрешающая способность и стабилизирующие свойства не зависят одно от другого, целесообразно проследить за их изменением с ростом порядка аппроксимации используемых конечных разностей.

На фиг. 1 представлены зависимости схемного волнового числа $\alpha {\text{*}}$ и диссипации ${{D}_{s}}$ от волнового числа $\alpha = kh$ для центральных разностей 2-го, 6-го (кривые 1, 2) и мультиоператорных 14-го и 22-го порядков (кривые 3 и 4). Параметр $\alpha {\text{*}}$ представляет собой произведение фазовой скорости (дисперсии) схемы и физического волнового числа $\alpha $. Повышение порядка аппроксимации разностных схем ведет к монотонному улучшению их разрешающей способности. Свойства конечных разностей при этом асимптотически приближаются к свойствам разностей дифференциальных. Вместе с тем отметим, что приращение чувствительности схем с повышением их порядка аппроксимации постоянно уменьшается, и говорить о разностных операторах, свойства которых полностью совпадали бы со свойствами дифференциальных, не приходится. В данном случае схема 22 -го порядка демонстрирует отличие от идеальной теоретической кривой $\alpha * = \alpha $, отмеченной цифрой 5, лишь в области самых коротких волн, что характеризует ее значительно лучшую чувствительность по сравнению со схемами 2 -го и 6-го порядков.

Фиг. 1.

Дисперсионные и диссипативные свойства разностных операторов.

Операторы центральных разностей сами по себе не обладают какими-либо диссипативными свойствами, необходимыми для проведения устойчивых расчетов при численном моделировании различных задач вычислительной физики. Преодолевается этот недостаток за счет введения в дифференциальные схемы стабилизирующего механизма в виде отнормированных и ориентированных против потока операторов вида $\Delta _{2}^{m}$, представляющих собой операторы четных разностей. При этом общий порядок схемы может понижаться до $(2m - 1)$-го. В отличие от аппроксимирующих компонентов составных схем, для диссипативных операторов не используется мультиоператорный подход. В силу естественного устройства разностей диффузного типа повышение их порядка связано с укрупнением используемого сеточного шаблона.

Зависимости диссипации ${{D}_{s}}$ от волнового числа $\alpha $ для схем, использующих для стабилизации различные четные разности, представлены на фиг. 1б: кривая 1 соответствует 2-й разности, 2 – 8-й, 3 – 16-й, 4 – 24-й. С ростом значения $m$ наблюдается сильное снижение диссипативных свойств разностных схем в областях длинных и средних волн. С одной стороны, это обстоятельство накладывает существенные ограничения на их применение для задач, характеризующихся наличием сильных градиентов параметров потока в поле течения. С другой стороны, низкий уровень схемной вязкости не только допустим, но и желателен на участках течения с достаточно гладкими распределениями рассчитываемых величин. Повысить диссипативные свойства составных схем возможно путем использования линейных комбинаций четных разностей заданного и более высокого порядков на основе подхода, описанного в [23]. На фиг. 1б – это кривая 5, полученная для комбинации 22-й и 24-й разностей. Ее диссипативные свойства практически не отличаются от таковых 14-й разности.

4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

4.1. Турбулентный пограничный слой на плоской пластине

Рассмотрим формирование турбулентного пограничного слоя на плоской пластине потоком вязкого газа с числом Маха 0.003 и числом Рейнольдса, посчитанном по расстоянию от передней кромки пластины до расчетного сечения: 5 × 106. При температуре воздуха 300 K скорость течения соответствует физическому значению, примерно, 1 м/с, что больше напоминает течение жидкости, чем газа. Кинетическая энергия турбулентности в набегающем потоке ${{k}_{\infty }} = {{10}^{{ - 6}}}$, а вихревая вязкость ${{\mu }_{{t,\infty }}} = 0.5{{\mu }_{{l,\infty }}}$. В данном случае использование уравнения состояния дает вычислительную величину давления в среде, почти на пять порядков превышающую квадрат скорости. Расчет проводится на сетке с 300 узлами вдоль пластины и 200 узлами поперек. За характерный линейный размер принимается расстояние от передней кромки пластины до расчетного сечения $x{\text{'}} = x{\text{/}}L = 1$. Входная граница области расчета отстоит от передней кромки пластины на расстояние, равное 50 характерным размерам, а верхняя и выходная – на 10. Расстояние от поверхности пластины до ближайшего к ней узла внутренней области расчета составляет 10–5 от характерного размера.

Для расчета параметров потока в переходной области течения используется коэффициент ${{C}_{{lt}}}$, при этом его значения не вычисляются, а задаются в зависимости от значения числа Re и расстояния от передней кромки пластины $x{\text{'}}$. В том случае, когда течение считается ламинарным, коэффициент ${{C}_{{lt}}}$, стоящий перед источниковыми членами уравнения турбулентной вязкости, равен нулю. Переход задается за счет постепенного подключения в расчете вектора источниковых членов. При изменении величины $\operatorname{Re} \,x{\text{'}}$ от $5 \times {{10}^{5}}$ до ${{10}^{6}}$ значение коэффициента ${{C}_{{lt}}}$ меняется линейно от 0 до 1. Далее по потоку течение турбулентное, ${{C}_{{lt}}} = 1$.

На фиг. 2 представлено распределение местного коэффициента трения ${{C}_{f}} = 2\mu \frac{{\partial u}}{{\partial y}}{{({{\rho }_{\infty }}u_{\infty }^{2})}^{{ - 1}}}$. Цифрами 1 и 2 отмечены кривые ламинарного и турбулентного распределения коэффициента трения из [20]. Полученное в расчете распределение поверхностного трения с учетом обозначено цифрой 3. Оно согласуется с ламинарным распределением на начальном участке пластины и турбулентным на ее основном участке. Используемая модель турбулентной вязкости позволяет воспроизводить поверхностное трение на участке переходного течения. На фиг. 2 также представлены графики толщины вытеснения пограничного слоя $\delta {\text{*}}$– теоретическая кривая 4 и расчетная 5.

Фиг. 2.

Распределения коэффициента трения и толщины вытеснения пограничного слоя.

Полученные в расчетах профили коэффициента турбулентной вязкости ${{\mu }_{t}}$ и горизонтальной компоненты вектора скорости ${{u}^{ + }} = u{\text{/}}{{u}_{\tau }}$ представлены на фиг. 3. По оси абсцисс отложен параметр $\log ({{y}^{ + }})$, где ${{y}^{ + }} = y{{u}_{\tau }}{{\rho }_{w}}{{(\operatorname{Re} {{\mu }_{w}})}^{{ - 1}}}$ – универсальное расстояние, а по оси ординат ${{u}_{\tau }} = {{[{{\mu }_{w}}{{(\operatorname{Re} {{\rho }_{w}})}^{{ - 1}}}\partial u{\text{/}}\partial y]}^{{1/2}}}$ – динамическая скорость. Цифрой 1 отмечены теоретические кривые ламинарного подслоя и логарифмического участка пограничного слоя из [20]. Полученный в расчете профиль (цифра 2) достаточно хорошо с ними согласуется.

Фиг. 3.

Профиль скорости в пограничном слое.

4.2. Естественная деформация плоского изолированного вихря

Звуковое излучение вихрей эллиптической формы на основе решения уравнений Эйлера исследовалось в [24], [25]. Расчеты М.В. Липавского и А.И. Толстых с использованием мультиоператорных схем (см. [16]) впервые продемонстрировали превращение круглого вихря в эллиптический на относительно длительных временах расчета без какого-либо внешнего воздействия. В данном случае рассматривается одиночный круглый вихрь на искривленной сетке, азимутальная скорость ${{{v}}_{c}}$ которого на расстоянии от центра ${{r}_{c}}$ (характерные скорость и длина) соответствует числу Маха 0.2. Радиальная составляющая скорости вихря, вращающегося по часовой стрелке, в начальный момент времени полагается равной нулю, азимутальная при $r{\text{'}} = r{\text{/}}r{}_{c} \leqslant 1$ пропорциональна радиусу ${v} = {v}{}_{c}r{\text{'}}$, а при $r{\text{'}} > 1$ задается формулой ${v} = {{{v}}_{c}}\exp [0.5(1 - r{\kern 1pt} {{'}^{2}})]$ из [26]. Остальные параметры рассчитываются из адиабатических соотношений в предположении наличия на бесконечности условий торможения потока, что дает в качестве начального приближения решение, близкое к точному. Для стабилизации используется 24-я разность со значением нормирующей константы перед ней 0.2 вместо обычно используемой единицы. Интегрирование по времени проводится на основе метода Рунге–Кутты четвертого порядка. Соотношение шага по времени к минимальному расстоянию между узлами разностной сетки равняется 0.025.

Расчеты выполняются на сетке с 200 узлами по каждому пространственному направлению. Фрагмент ее центральной части приведен на фиг. 4. В отличие от предыдущих расчетов подобной задачи, здесь используется криволинейная сетка. Присутствие в уравнениях ненулевых метрических коэффициентов служит дополнительной проверкой работоспособности мультиоператорных схем.

Фиг. 4.

Фрагмент разностной сетки.

Полученное на момент времени $t{\text{'}} = t{{r}_{c}}{\text{/}}{{{v}}_{c}} = 2000$ поле относительного давления $\Delta p{\text{'}} = (p - {{p}_{i}}){\text{/}}{{p}_{0}}$, где ${{p}_{i}}$ – давление на начальный момент времени, а ${{p}_{0}}$– давление торможения, представлено на фиг. 5. Поле содержит 35 уровней в диапазоне изменения относительного давления от –0.0005 до 0.0005. Результаты получены на основе схемы 22 -го порядка. При вращении вихря эллиптической формы перед его большей полуосью возникает зона повышенного давления, а за ней – пониженного. Данные области давления распространяются в окружающем пространстве. Сам вихрь при этом продолжает вращение вокруг своей оси. В результате имеет место картина распространения звукового давления, напоминающая четырехлопастной вентилятор.

Фиг. 5.

Нестационарное относительное давление.

Изменение по времени $t{\kern 1pt} '$ вертикальной компоненты вектора скорости ${v}$ в точке $x{\text{'}} = 0$, $y{\text{'}} = 2$ представлено на фиг. 6: (а) – центрально-разностная схема 2 -го порядка, (б) – компактная схема 6 -го и (в) – мультиоператорная схема 22 -го порядков. Фрагменты (б) и (в) выполнены в одном временном масштабе, фрагмент (а) – в большем. Это вызвано тем, что уже при $t{\text{'}} = 40$ происходит развал решения, выполняемого по схеме 2 -го порядка. Схема 6 -го порядка разваливается при $t{\text{'}}$ немногим более 1000, а использование разности 22-го порядка позволяет проводить устойчивый расчет задачи по крайней мере вдвое дольше. Можно сделать вывод, что используемый стабилизатор в виде 24-й разности не справляется с ошибками аппроксимации, имеющими место для схем 2 -го и 6-го порядков. В то же время схема 22 -го за счет своей точности в более сильной коррекции не нуждается.

Фиг. 6.

Изменение по времени вертикальной компоненты вектора скорости.

Причину данной деформации круглого вихря следует искать во внутренних волновых процессах и сжимаемости газа. В процессе вращения вихря постепенно нащупывается резонансная частота, примерно на порядок меньшая частоты кругового вращения, под действием которой круглый вихрь превращается в эллиптический. Следует отметить, что начало трансформации вихря при расчетах схемами 6 -го и 22-го порядков наблюдается примерно в одно время. На волновую природу явления указывают также результаты других расчетов, согласно которым снижение числа Маха на границе ядра ${{{\text{M}}}_{c}}$ приводит к увеличению времени начала трансформации, а его рост – к снижению.

4.3. Обтекание поперечного ребра жесткости на пластине

Дозвуковые течения являются нестационарными по своей природе. Важную роль в них играют силы вязкости, ответственные за вихреобразование и отрыв пограничного слоя. За счет того, что каждая точка поля чувствует изменение давления в любой другой точке пространства, течение отличается высокой вариативностью, т.е. отсутствует полная повторяемость в периодических процессах, по крайней мере, при достаточно высоких числах $\operatorname{Re} $. Возникает вопрос, как могут отличаться результаты расчетов с использованием схем разного порядка аппроксимации и одинаковыми стабилизирующими операторами. При этом влияние самих стабилизирующих добавок должно быть минимальным за счет применения в них четных разностей высокого порядка.

Рассмотрим дозвуковое обтекание вязким газом невысокого ребра жесткости, расположенного на плоской пластине поперек набегающего потока. Число Маха набегающего потока ${{{\text{M}}}_{\infty }} = 0.1$. Число Рейнольдса, посчитанное по длине L – расстоянию от передней кромки пластины до ребра жесткости, 104. В данном двумерном случае ребро жесткости представляет собой прямоугольник высотой $h = 0.05L$ и толщиной 0.01L. Толщина пограничного слоя перед выступом примерно равняется его высоте $h$, а число Рейнольдса ${{\operatorname{Re} }_{h}} \approx 500$. На первом этапе расчета на основе схемы 6 -го порядка формируется поле течения. Далее используются схемы 6 -го, 14-го и 22-го порядков и расчеты ведутся до времени $t{\text{'}} = tL{\text{/}}{{U}_{\infty }}$ = 20, после чего полученные результаты сравниваются. Во всех трех случаях в качестве стабилизатора используется комбинация 22-й и 24-й разностей.

Мгновенное поле относительного давления $p{\text{'}} = p{\text{/}}{{p}_{\infty }}$, полученное с применением схемы 22 -го порядка, представлено на фиг. 7. Уровни нанесены в диапазоне от 0.996 до 1.002 с шагом 0.003. Там же приведены линии тока в виде линий постоянного значения функции тока $\psi = \int {\rho u\partial y - \int {\rho {v}\partial x} } $. Всего нанесено пять линий в диапазоне от –0.015 до 0.005 с шагом между ними 0.005. Повышенные уровни давления наблюдаются у передней кромки пластины, перед ребром жесткости и в зоне присоединения потока за ним, а области пониженного давления – в вихревых зонах ниже препятствия. Пограничный слой отрывается перед ребром жесткости и присоединяется к его передней поверхности ниже верхней кромки. Далее он снова отрывается с верхней поверхности ребра и образует нестационарную отрывную зону, протяженность которой более чем в 30 раз больше высоты обтекаемого препятствия. Удаленная от препятствия область отрыва совершает колебания, отделившиеся вихревые структуры сносятся вниз по потоку.

Фиг. 7.

Поле давления и линии тока отрывного течения.

На фиг. 8 представлены распределения вдоль координаты $x{\text{'}} = x{\text{/}}L$ коэффициента давления ${{C}_{p}} = 2(p - {{p}_{\infty }}){\text{/}}{{\rho }_{\infty }}U_{\infty }^{2}$. Кривая 1 получена с использованием схемы 6 -го порядка, 2 – 14-го и 3 – 22-го. В областях перед препятствием, где течение стационарно, результаты расчетов разными схемами хорошо совпадают между собой. Там же, где имеют место пульсации потока в следе за ребром жесткости, наблюдаются отличия. Это видно и на фиг. 9, где представлены зависимости по времени коэффициента давления на поверхности пластины в точке $x{\kern 1pt} ' = 2.25$. Минимальные амплитуды колебания коэффициента давления имеют место в расчете схемой 6 -го порядка, максимальные – в расчете схемой 22 -го порядка. При примерно одинаковом числе Струхаля колебания в данной точке $St = fh{\text{/}}{{U}_{\infty }}$ = 0.0168 ($f$ – частота колебания) амплитуда звукового давления при использовании схемы 6 -го порядка составляет 123 dB, 14-го и 22-го соответственно 131 и 134.6 dB.

Фиг. 8.

Распределение коэффициента давления.

Фиг. 9.

Изменение по времени коэффициента давления.

4.4. Обтекание аэродинамического профиля

На аэродинамической поверхности, движущейся под углом к встречному потоку воздуха, может возникать отрыв пограничного слоя, способный сильно влиять на ее подъемную силу. При этом общая картина течения существенно зависит от уровня вязкости в потоке. Шум аэродинамического профиля, возникающий при его ламинарном обтекании, исследуется в [5], [7] и многих других работах, механизм его возникновения рассматривается, в частности, в [27], [28]. Источником нестационарных эффектов является отрыв пограничного слоя, возникающий на его поверхности под влиянием положительного градиента давления. Эмпирические критерии отрыва ламинарного и турбулентного пограничных слоев сформулированы в [29]. В отличие от турбулентного режима течения, отрыв ламинарного пограничного слоя требует меньшего перепада давления, к тому же снижающегося с увеличением числа Рейнольдса. Подобные условия реализуются, например, в области применения малоразмерных беспилотных летательных аппаратов.

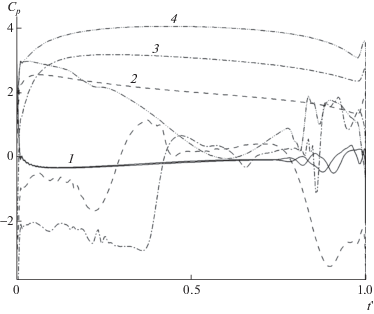
Рассмотрим течение, формирующееся около симметричного профиля NACA0012, при числе Маха набегающего потока 0.05 и числе Рейнольдса, посчитанном по хорде $c$, 105. В расчетах используется сетка типа $O$ с 500 узлами в каждом пространственном направлении. Расстояние до внешней границы составляет 20$c$, а от поверхности тела до ближайшего узла – 2.5 × 10–5$c$. На фиг. 10 представлены полученные графики распределения коэффициента давления по координате $x{\text{'}} = x{\text{/}}c$ для следующих значений угла атаки набегающего потока: 1 – 0°, 2 – 30°, 3 – 60° и 4 – 90°. Значение $x{\text{'}} = 0$ соответствует передней кромке профиля, $x{\text{'}} = 1$ – задней. Отрыв пограничного слоя возникает уже при нулевом значении угла атаки на сужающихся частях как верхней, так и нижней сторонах профиля. Значение сформулированного в [29] критерия отрыва ламинарного пограничного слоя

${{C}_{{lam}}} = \frac{{\operatorname{Re} \delta {\kern 1pt} {{*}^{2}}}}{2}\frac{{d{{C}_{p}}}}{{dx}}$
составляет 1.1. В данном расчете получено значение 1.3. Возникающие отрывы пограничного слоя формируют колеблющийся ближний след за профилем и волновые структуры, распространяющиеся вверх по потоку. Давление повышается и понижается попеременно на верхней и нижней поверхностях.

Фиг. 10.

Распределения коэффициента давления на поверхности.

При ненулевых углах атаки на наветренной стороне профиля давление повышенное и имеет форму плато. В то же время на подветренной стороне распределение давления неравномерно, что вызвано формирующимися здесь нестационарными отрывными течениями. Возникающий характер обтекания профиля неблагоприятно сказывается на его устойчивости.

Поля числа Маха представлены на фиг. 11: (а) – отмечен случай $\alpha $ = 0°, (б) – 10°, (в) – 30°, (г) – 60° и (д) – 90°. Диапазон изменения изолиний от 0.01 до 0.12 с шагом 0.01. Об интенсивности течения в следе за профилем можно судить по насыщенности его крупными и мелкими вихревыми структурами. Если при нулевом угле атаки значения чисел Маха не превышают 0.07–0.08, то при 60° они достигают максимальных зафиксированных значений 0.135. При угле атаки 10° отрыв потока происходит у передней кромки, далее вихревые зоны смещаются вниз вдоль верхней поверхности профиля, по границе пограничного слоя наблюдаются локальные ускорения потока. С увеличением угла атаки растут и размеры вихревых структур. Отрывы пограничного слоя происходят на передней и задней кромках профиля, взаимодействуют между собой и сносятся вниз по потоку, формируя вихревой след. Поток у наветренной поверхности тормозится, а за профилем образуется течение, напоминающее дорожку Кармана. На фиг. 11д, по времени относящейся к началу формирования подобного следа при его поперечном обтекании профиля, видны мелкие вихри, цепочкой выстраивающиеся вокруг зоны отрыва в нижней его части. Остатки таких же структур просматриваются и вокруг отрывной зоны, расположенной выше и правее предыдущей.

Фиг. 11.

Поля равных уровней числа Маха (а)–(д), давления и линии тока (е).

На фиг. 11е представлено поле относительного давления $p{\text{'}} = p{\text{/}}{{p}_{\infty }}$ и линии тока в виде изолиний функции тока $\psi $, полученные при угле атаки 90°. Диапазон изменения относительного давления от 0.976 до 1 с шагом 0.002. Предельные значения изолиний функции тока –1.1 и 1.4. Минимальный шаг изолиний вблизи нулевого значения 0.01, далее он увеличивается. Области пониженного давления совпадают с центрами вихрей. Искривлениe изолиний у подветренной поверхности профиля подтверждает сложность течения и насыщенность донной области взаимодействующими вихрями.

4.5. Обтекание парашютного купола

Парашютные системы широко применяются на практике и имеют богатую историю разработок. Их проектирование сегодня не обходится без этапа математического моделирования, которое включает в себя совместное решение ряда нелинейных задач, одной из которых является нестационарное обтекание парашютного купола встречным потоком воздуха. В свою очередь, течение около парашютного купола моделируется на основе метода дискретных вихрей (см. [30]) или решения уравнений Эйлера невязкого газа методами конечных разностей (см. [31], [32]). Есть также примеры расчетов с использованием уравнений Навье–Стокса вязкой несжимаемой жидкости (см. [33], [34]).

Рассматривается осесимметричное обтекание жесткого непроницаемого парашютного купола потоком вязкого газа. Число Маха набегающего потока 0.02, что соответствует скорости 6–7 м/с. Поверхность купола представляет собой дугообразный участок границы расчетной области с нулевой толщиной, поскольку везде, за исключением ближайшей окрестности кромки, координаты точек наветренной и подветренной поверхностей купола попарно совпадают друг с другом. За характерный линейный размер принимается длина половины дуги купола R. В расчете используется сетка с 400 узлами вдоль поверхности и 460 – в радиальном направлении. Минимальный размер между узлами составляет 10–3R, а внешняя граница отодвигается от поверхности на расстояние 102R.

Полученные поля числа Маха при ламинарном (число Рейнольдса 106) и турбулентном (${{\operatorname{Re} }_{{R,\infty }}} = 3 \times {{10}^{6}}$, ${{k}_{\infty }} = {{10}^{{ - 6}}}$, ${{\mu }_{{t,\infty }}}{\text{/}}{{\mu }_{{l,\infty }}} = 0.3$) обтекании представлены на фиг. 12 в цилиндрических координатах $z{\text{'}} = z{{R}^{{ - 1}}}$, $r{\text{'}} = r{{R}^{{ - 1}}}$. Диапазон изменения равных значений числа Маха 0.004 до 0.04 с шагом 0.004. Там же приведены изолинии функции тока $\psi $ в диапазоне от –3 до 0.5 с постоянным шагом 0.5. В обоих случаях за непроницаемым куполом формируются зоны возвратно-циркуляционного течения. Протяженность отрывной области значительно превышают размеры самого купола. В ламинарном случае, представленном на фиг. 12а, зона рециркуляции больше, чем в турбулентном (фиг. 12б). Это находит объяснение в более высоких значениях эффективной вязкости при использовании модели турбулентности. В зоне торможения перед куполом течение стационарно, у кромки наблюдаются колебания. В момент времени, зафиксированный на фиг. 12б, происходит отрыв вихря малого размера от основной возвратно-циркуляционной зоны.

Фиг. 12.

Поля равных уровней числа Маха и линии тока.

Распределение коэффициента давления ${{C}_{f}}$ вдоль поверхности купола представлено на фиг. 13. Нулевое значение координаты $s{\kern 1pt} ' = s{{R}^{{ - 1}}}$ соответствует кромке купола, отрицательные относятся к наветренной поверхности, положительные – подветренной. Результаты расчета ламинарного течения отмечены цифрой 1, турбулентного – цифрой 2. Различия между ними наблюдаются в районе парашютной кромки и на подветренной поверхности. Уровень донного давления для случая турбулентного течения ниже, чем ламинарного. Это означает, что в турбулентном течении коэффициент сопротивления выше. Используемые схемы высокого порядка и метод построения расчетной области могут служить основой для более совершенных расчетов на подвижных сетках с учетом проницаемости купола и напряжений в его оболочке.

Фиг. 13.

Распределения коэффициента давления.

ЗАКЛЮЧЕНИЕ

Рассмотренные мультиоператорные разностные схемы обладают высокими разрешающими способностями, что является их преимуществом при решении задач динамики вязкого сжимаемого газа. Максимальный достигнутый порядок аппроксимации схем составляет 22 при пяти используемых операторах. Диссипативные добавки на основе 22-й и 24-й разностей не имеют сильных стабилизирующих свойств. Они не дают возможности расчета задач с сильными градиентами параметров потока в поле течения, но позволяют моделировать дозвуковые течения вязкого сжимаемого газа при достаточно низких числах Маха. Данный класс задач имеет свою специфику и представляет интерес для практики. В качестве примера рассмотрены задачи обтекания вязким газом аэродинамического профиля в широком диапазоне изменения угла атаки и отрывного течения около непроницаемого парашютного купола.

Список литературы

  1. Русанов В.В. Разностные схемы третьего порядка точности для сквозного счета разрывных решений // Докл. АН СССР. 1968. Т. 180. № 6. С. 1303–1305.

  2. Толстых А.И. О методе численного решения уравнений Навье–Стокса сжимаемого газа в широком диапазоне чисел Рейнольдса // Докл. АН СССР. 1973. Т. 210. № 1. С. 48–51.

  3. Tolstykh A.I. High accuracy non-centered compact schemes for fluid dynamics applications. Singapore: World Scient., 1994.

  4. Lele S.K. Compact finite difference schemes with spectral-like resolution // J. Comput. Phys. 1992.V. 102. P. 16–42.

  5. Visbal M.R., Gaitonde D.V. On the use of high-order finite-difference schemes on curvilinear and deforming meshes // J. Comput. Phys. 2002. V. 181. P. 155–185.

  6. Mardsen O., Bogey C., Bailly C. High-order curvilinear simulations of flows around non-cartesian bodies // J. Comput. Acoustics. 2005. V. 13. № 4. P. 731–748.

  7. Tam C.K.W., Ju H. Numerical simulation of the generation of airfoil tones at a moderate Reynolds number // AIAA Paper № 2006–2502. 2006. 23 p.

  8. Sandberg R.D., Jones L.E., Sandham N.D., Joseph P.F. Direct numerical simulations of noise generated by airfoil trailing edges // AIAA Paper № 2007–3469. 2007. 15 p.

  9. Harten A. ENO schemes with subcell resolution // J. Comput. Phys. 1989. V. 83. P. 148–184.

  10. Harten A., Engquist B., Osher S., Chakravarthy S.R. Uniformly high order essentially non-oscillatory schemes III // J. Comput. Phys. 1987. V. 71. P. 231–303.

  11. Hu C., Shu C.W. Weighted essentially non-oscillatory schemes on triangular meshes // J. Comput. Phys. 1999. V. 150. P. 97–127.

  12. Dumbser M., Kaser M., Titarev V.A., Toro E.F. Quadrature-free non-oscillatory finite volume schemes on unstructured meshes for nonlinear hyperbolic systems // J. Comput. Phys. 2007. V. 226. P. 204–243.

  13. Abalakin A., Bachwalow P., Kozubskaya T. Edge-based reconstruction schemes for prediction of near field flow region in complex aeroacoustic problems // Int. J. Aeroacoustics. 2014. V. 13. № 3–4. P. 207–234.

  14. Савельев А.Д. Составные компактные схемы высокого порядка для моделирования течений вязкого газа // Ж. вычисл. матем. и матем. физ. 2007. Т. 47. № 8. С. 1389–1403.

  15. Толстых А.И. Мультиоператорные схемы произвольного порядка, использующие нецентрированные компактные аппроксимации // Докл. АН. 1999. Т. 366. № 3. С. 319–322.

  16. Толстых А.И. О мультиоператорном методе построения аппроксимаций и схем произвольно высокого порядка // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 1. С. 56–73.

  17. Савельев А.Д. О мультиоператорном представлении составных компактных схем // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 10. С. 1580–1593.

  18. Савельев А.Д. О разностных схемах 18-го и 22-го порядков для уравнений с конвективными и диффузными членами // Матем. моделирование. 2017. Т. 29. № 6. С. 35–47.

  19. Menter F.R. Zonal two equation $k - \omega $ turbulence models for aerodynamic flows // AIAA Paper 93–2906. 1993. 21 p.

  20. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1987. 840 с.

  21. Steger J.L. Implicit finite-difference simulation of flow about arbitrary two-dimensional geometries // AIAA J. 1978. V. 16. P. 678–685.

  22. Steger J.L., Warming R.F. Flux vector splitting of the inviscid gasdynamic equations with applications to finite-difference methods // J. Comput. Phys. 1981. V. 40. P. 263–293.

  23. Савельев А.Д. О структуре внутренней диссипации составных компактных схем для решения задач вычислительной газовой динамики // Ж. вычисл. матем. и матем. физ. 2009. Т. 49. № 12. С. 2232–2246.

  24. Chan W.M., Sheriff K., Pulliam T.H. Instabilities of two-dimensional inviscid compressible vortices // J. fluid mech. 1993. V. 253. P. 173–209.

  25. Яковлев П.Г. Излучение звука плоским локализованным вихрем // Акустический журнал. 2012. Т. 58. № 4. С. 563–568.

  26. Yee H.C., Sandham N.D., Djomehri M.J. Low dissipation high order shock-capturing methods using characteristic-based filters // J. Comput. Phys. 1999. V. 150. P. 199–238.

  27. Desquenes G., Terracol M., Sagaut P. Numerical investigation of the tone noise mechanism over laminar airfoils // J. Fluid Mech. 2007. V. 591. P. 155–182.

  28. Савельев А.Д. Мультиоператорные компактные схемы высокого порядка в численном моделировании нестационарного дозвукового обтекания аэродинамического профиля // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 2. С. 291–303.

  29. Бам-Зеликович Г.М. Расчет отрыва пограничного слоя // Изв. АН СССР. ОТН. 1954. № 12. С. 68–85.

  30. Белоцерковский С.М., Ништ М.И., Пономарев А.Т., Рысев О.В. Исследование парашютов и дельтапланов на ЭВМ. М.: Машиностр., 1987. 240 с.

  31. Днепров И.В., Пономарев А.Т., Рысев О.В., Семушин С.А. Исследование процессов нагружения и деформирования парашютов // Матем. моделирование. 1993. Т. 5. № 3. С. 97–109.

  32. Морозов В.И., Пономарев А.Т. Моделирование нагружения парашютов с учетом изменения формы и проницаемости купола // Вестн. Харьковского нац. университета. 2008. Сер. Матем. моделирование. № 809. С. 148–161.

  33. Tutt B., Charles R., Roland S., Noetscher G. Development of parachute simulation techniques in LS-DYNA // 11th Internat. LS-DYNA Users Conf. 2010. Detroit. P. 19–25.

  34. Yunpeng M., Jinge Z. The simulation of canopy fabric air permeability’s influence on the round parachute during the landing process // Int. Industrial Informat. Computer Engineer. Conf. 2015. Xi’an. Shaanxi. China. January 10–11. P. 2156–2159.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал