Журнал вычислительной математики и математической физики, 2021, T. 61, № 5, стр. 885-894
Расчет индуктивностей и пространственных распределений токов в модели сверхпроводникового нейрона
С. В. Бакурский 1, 2, 3, Н. В. Кленов 4, 5, М. Ю. Куприянов 1, И. И. Соловьев 1, 3, 6, М. М. Хапаев 1, 7, *
1 МГУ им. М.В. Ломоносова, НИИЯФ им. Д.В. Скобельцына
119991 Москва, Ленинские горы, 1, стр. 2, Россия
2 МФТИ
141701 М.о., Долгопрудный, Институтский пер., 9, Россия
3 ВНИИА им. Н.Л. Духова
127055 Москва, ул. Сущевская, 22, Россия
4 МГУ им. М.В. Ломоносова, Физический факультет
119991 Москва, Ленинские горы, 1, стр. 2, Россия
5 МТУСИ
111024 Москва, ул. Авиамоторная, 8а, Россия
6 ННГУ им. Н.И. Лобачевского
603950 Нижний Новгород, пр-т Гагарина, 23, Россия
7 МГУ им. М.В. Ломоносова,
факультет ВМК, каф. выч. методов
119991 Москва, Ленинские горы, 1, стр. 52, Россия
* E-mail: vmhap@cs.msu.su
Поступила в редакцию 24.12.2020
После доработки 24.12.2020
Принята к публикации 14.01.2021
Аннотация
Предложены математическая модель и вычислительный метод расчета индуктивностей и пространственных распределений сверхпроводящих токов в адиабатическом искусственном нейроне, представляющем собой многослойную структуру, содержащую джозефсоновские переходы. Вычислительный метод основан на совместном решении уравнений Лондонов для токов в слоях сверхпроводника и уравнений Максвелла, задающих пространственное распределение магнитного поля, а также модели листового тока, учитывающей конечную толщину проводящих слоев и токовых контактов. Этот подход эффективно учитывает межслойные контакты и джозефсоновские переходы в виде распределенных источников тока. Полученные уравнения решаются с использованием метода конечных элементов с плотными матрицами большой размерности. Представлены результаты расчетов для модели проектируемого нейрона с сигмоидальной передаточной функцией. С целью оптимизации конструкции устройства вычисляются как рабочие (запланированные на первом этапе проектирования), так и паразитные индуктивности, а также распределение токов. Предлагаемая методология и программное обеспечение могут быть использованы для моделирования широкого спектра сверхпроводящих устройств на основе сверхпроводниковых квантовых интерферометров. Библ. 19. Фиг. 4.
1. ВВЕДЕНИЕ
Одним из центральных вопросов, возникающих при разработке аналоговых и цифровых сверхпроводниковых микросхем, является создание численных алгоритмов, решающих задачу вычисления распределения сверхпроводящих токов в таких структурах, а также значений собственных и взаимных индуктивностей их отдельных частей. Это связано с тем, что работоспособность и производительность устройств на основе сверхпроводниковых квантовых интерферометров (СКВИДов) находятся в критической зависимости от индуктивностей отдельных компонентов таких устройств.
Расчет реальных индуктивностей особенно важен для устройств, преобразующих магнитный поток в ток или напряжение. Примером таких технических решений являются сверхпроводниковые антенны на основе би-СКВИДов и Д-СКВИДов. В этом случае преобразование потока в напряжение должно оставаться линейным с высокой точностью без использования цепей обратной связи [1]–[3].
В настоящее время особый интерес представляют нелинейные элементы сверхпроводниковых искусственных нейронных сетей с магнитным представлением информации. В этом случае преобразование магнитного потока в ток (функция активации) для нейрона должна с хорошей точностью совпадать с сигмоидальной функцией, либо с гиперболическим тангенсом [4].
Целью данной работы является разработка усовершенствованного вычислительного алгоритма и программы экстракции (расчета) рабочих и паразитных индуктивных коэффициентов сверхпроводниковых микросхем, в частности методики расчета индуктивностей для СКВИДов и устройств на основе СКВИДов. Эффективность разработанного подхода показана на примере одного из таких устройств, искусственного нейрона с сигмовидной активационной функцией [5]–[7]. В отличие от полупроводниковых аналогов сверхпроводниковые нейроны оказываются существенно менее сложными, и могут быть относительно просто изготовлены с использованием существующей микроэлектронной технологии. Однако их работоспособность требует высокой точности реализации нужного соотношения между значениями индуктивностей элементов схемы. В данной работе мы демонстрируем возможности и пределы применимости нашего вычислительного алгоритма и программы для вычисления индуктивностей [8] и [9] на примере решения актуальной проблемы — проектирования упомянутого сверхпроводникового нейрона.
Математическая модель, лежащая в основе расчетов пространственного распределения токов в сверхпроводниковых микроэлектронных структурах, основана на совместном решении уравнений Лондонов и Максвелла [10]. В стационарном случае такой подход приводит к интегральному уравнению относительно векторного потенциала [11], содержащему трехмерные интегралы.
Наш подход содержит ряд модификаций этого интегрального уравнения. Во-первых, используя то обстоятельство, что в рассматриваемых структурах толщина слоев невелика по сравнению с лондоновской глубиной проникновения магнитного поля в сверхпроводник, мы преобразуем объемные токи в листовые токи. Во-вторых, мы учитываем конечную толщину слоев в функции Грина, которая является ядром интегрального уравнения. В-третьих, для точного и простого учета межслойных соединений и джозефсоновских переходов мы разделяем ток на потенциальную и вихревую составляющие и представляем вихревую часть тока через функцию тока. Это сводит проблему к решению гиперсингулярного интегрального уравнения с хорошими математическими свойствами, что значительно упрощает численное решение. При таком подходе точно учитываются как магнитная, так и кинетическая части индуктивности фрагментов микросхем.
Для численного приближения и решения полученных уравнений мы используем метод конечных элементов с треугольными сетками и линейными конечными элементами. Такой подход приводит к двум плотным матрицам большой размерности. Первая матрица симметрична и имеет размерность, равную количеству ячеек в сетке. Она предназначена для хранения промежуточных результатов расчетов и для расчета полной энергии. Элементы этой матрицы Галеркина являются четырехкратными интегралами от функции Грина по ячейкам сетки. Вторая матрица является симметричной и положительно определенной. Это матрица системы линейных уравнений метода конечных элементов. Для решения этой системы линейных уравнений мы используем разложение Холецкого для плотно заполненных матриц.
Вычислительный алгоритм реализован в нашей программе 3D-MLSI [9].
В последнем разделе статьи возможности, преимущества и ограничения разработанного подхода иллюстрируются расчетом пространственного распределения сверхпроводящего тока для модели искусственного нейрона. Вычислительный алгоритм, разработанный в настоящей работе, может служить в качестве основы для применения алгоритмов скелетонной малоранговой аппроксимации плотных матриц в последующих исследованиях.
2. МОДЕЛЬ НЕЙРОНА
Искусственные свехпроводниковые нейроны [5]–[7] могут быть спроектированы на базе структур с двумя сверхпроводящими слоями над сверхпроводящим же экраном. Результат проектирования сверхпроводящего нейрона в виде упрощенной схемы показан на фиг. 1. Он включает в себя три разделенных диэлектриками металлических слоя: плоскость заземления M0, слой разводки M1 и слой с верхним покрытием M2. Верхний слой М2 в разных точках характеризуется разными расстояниями до подложки (разными высотами) и частично замыкается на М1, если М1 и М2 перекрываются. В наших расчетах мы используем упрощенную модель, показанную на фиг. 2. В этой модели слой M2 имеет постоянную высоту. Замыкания слоев M1–M2 представлены в виде пары токовых контактов прямоугольной формы.
Фиг. 1.
Модель нейрона, вид сверху (а) и боковые проекции (б)–(г). Показаны три сверхпроводящих слоя: слой заземления M0, средний слой M1 и верхний M2. Требуется вычислить индуктивности для двух токовых петель, показанных прерывистыми линиями и замыкающимися через слой M0. Джозефсоновские контакты между слоями М1 и М2 обозначены буквами JJ.

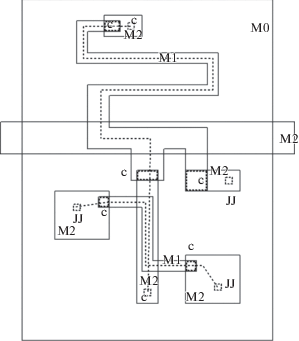
Фиг. 2.
Упрощенная модель нейрона. На фигуре показаны три слоя, M0 (нижний проводник, слой заземления), M1 (средний слой) и M2 (верхний слой), джозефсоновские переходы (JJ) и искусственные контакты между слоями (C). Первая токовая петля показана вертикальной пунктирной линией с возвратным током через слой M0. Вторая токовая петля, представляющая измерительный СКВИД, также показана пунктирной линией. Центральная горизонтальная полосковая линия является управляющим элементом. Размер шага сетки на фигуре 10 мкм.
При последующих расчетах мы будем считать, что лондоновская глубина проникновения $\lambda $ [10] для всех слоев одинакова и составляет $0.075$ мкм. Нижний слой M0 является базовой заземляющей плоскостью. Он собирает все возвратные токи из более высоких слоев. Толщину этого слоя будем считать равной $0.3$ мкм ($4\lambda $). Следующий слой – M1. Он не является сплошным и содержит несколько участков, по которым протекает ток. Полагаем, что его высота относительно верхней части нижнего слоя составляет $0.3$ мкм, а толщина – $0.11$ мкм (менее $2\lambda $). Верхний слой M2 находится на высоте $0.61$ мкм и имеет толщину $0.45$ мкм. Между верхним и нижним слоями имеется три джозефсоновских контакта и множество межслойных контактов. Оставшиеся после изготовления нейрона участки слоев представлены на фиг. 2. Средний и верхний слои отдельно представлены на фиг. 3. Там же приведена и конечно-элементная сетка. Ширина полос в М2 составляет $10$ мкм. Верхний и нижний слои довольно толстые по сравнению с $\lambda $. Это ограничивает точность расчетов в нашей математической модели на уровне 5% [8].
Фиг. 3.
Проводники в слоях M1 и M2 над замыкающей плоскостью M0 и конечно-элементная треугольная сетка.

Физическая постановка задачи наряду с описанием проводящей структуры должна содержать определение токов, для которых будут вычислены индуктивности. Эти токи, как правило, образуют токовые петли, замыкающиеся через заземляющий слой и проходящие через определенные контакты, в том числе через джозефсоновские переходы. Последовательность таких контактов определяет ток, для которого должны быть вычислены индуктивные коэффициенты. Два таких токовых контура представлены на фиг. 2. В свою очередь заданные процессы в контактах позволяют формулировать краевые и иные условия для постановки математической задачи. В результате каждый токовый контур дает одну строку (столбец) в матрице индуктивности. Диагональные элементы этой матрицы являются собственными индуктивностями, а внедиагональные элементы являются взаимными индуктивностями.
Для широких проводников, расположенных над плоскостью заземления, можно оценить собственные индуктивности, которые присутствуют в принципиальной схеме устройства. Однако невозможно достаточно точно оценить взаимные индуктивности, среди которых имеются паразитные связи, каковые невозможно заранее учесть при проектировании устройства. Единственным средством достаточно точного вычисления схемных и паразитных индуктивностей являются вычислительные методы.
3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ТОКОВ И ИНДУКТИВНОСТЕЙ
Вычислительный алгоритм этой работы является улучшенной и усовершенствованной версией алгоритмов, предложенных в [8] и [9].
Введем некоторые обозначения.
Пусть ${{N}_{c}}$ – число односвязных проводников. Проводник расположен в некотором слое металлизации. Каждый проводник занимает трехмерную область:
Пусть $\partial {{S}_{{ext,m}}}$ – граница проводника $m$, исключая границы возможно существующих отверстий. Толщина проводника $m$ составляет ${{t}_{m}} = h_{m}^{1} - h_{m}^{0}$. Пусть ${{N}_{h}}$ – общее количество всех отверстий во всех проводниках. Будем называть $\partial {{S}_{{h,k}}}$ границей отверстия $k$.
Всего имеется ${{N}_{T}}$ токовых контактов (терминалов) во всех проводниках, не менее двух терминалов для каждого проводника. Джозефсоновские переходы образуют пару терминалов на разных проводниках. Терминалы на $\partial {{S}_{{ext,m}}}$ являются внешними терминалами. Терминалы внутри ${{S}_{m}}$, например, в форме прямоугольников, являются внутренними терминалами. Джозефсоновский переход образует два внутренних терминала.
Обозначим через ${{N}_{t}}$ число замкнутых или открытых путей для интересующих нас полных токов. Каждый путь содержит некоторую цепочку терминалов. Ток может переходить от проводника к проводнику, а также между слоями через терминалы. Всего имеем $N = {{N}_{t}} + {{N}_{h}}$ независимых полных токов, так как существуют замкнутые токи вокруг отверстий.
В качестве результата нас интересует вычисление $N \times N$ матрицы индуктивности $L$ [8].
Математическая модель основана на стационарных уравнениях Лондонов и формулы Био–Савара для магнитного поля ${\mathbf{H}}$, а также выражения для полной энергии $E$:
(1)
$\begin{gathered} {{\lambda }^{2}}\nabla \times {\mathbf{j}} + {\mathbf{H}} = 0,\quad \nabla \times {\mathbf{H}} = {\mathbf{j}}, \\ E = \frac{{{{\mu }_{0}}}}{2}\iiint\limits_V {({{\lambda }^{2}}{{j}^{2}} + {\mathbf{j}} \cdot {\mathbf{A}})d{v}},\quad {\mathbf{A}}(r) = \frac{1}{{4\pi }}\iiint\limits_V {\frac{{{\mathbf{j}}(r{\kern 1pt} {\text{'}})}}{{\left| {r - r{\text{'}}{\kern 1pt} } \right|}}d{v}}, \\ \end{gathered} $(2)
${{\lambda }^{2}}{{{\mathbf{j}}}_{n}}(r) + \frac{1}{{4\pi }}\sum\limits_{m = 1}^{{{N}_{c}}} {\iiint\limits_{{{V}_{m}}} {\frac{{{{{\mathbf{j}}}_{m}}(r{\text{'}}{\kern 1pt} )}}{{\left| {r - r{\text{'}}{\kern 1pt} } \right|}}d{v}{\kern 1pt} {\text{'}}}} = \nabla {{\varphi }_{n}}(r),\quad n = 1,\; \ldots ,\;{{N}_{c}}.$Существует ряд специфических трудностей в моделировании сверхпроводящих токов. Первой трудностью является сложная топология распределения тока в объемной структуре. Известно [10], [11], что уравнение Лондонов приводит к концентрации тока вблизи поверхности сверхпроводников. Точный учет этого эффекта довольно сложен алгоритмически и приводит к продолжительным вычислениям, однако при некоторых условиях (тонкий проводник) его общее влияние на значения индуктивности является умеренным.
Другой трудностью является достаточно точное моделирование контактов и джозефсоновских переходов между слоями, так как контакт или переход занимают некоторую конечную область. Поэтому возникает необходимость использования физически релевантных моделей для растекания тока на терминалах.
Наконец, токи вокруг отверстий не имеют терминалов, так что их невозможно задать с помощью краевых условий для тока и фазы.
В нашем подходе мы используем возможность упростить задачу для случая сверхпроводящих слоев относительно небольшой, но конечной толщины. Обычно толщина сверхпроводящих слоев составляет порядка 1–3 лондоновской глубины проникновения. В этом случае для проводника $m$ мы можем использовать модель листового тока ${{{\mathbf{J}}}_{m}}(x,y) = ({{J}_{{m,x}}}(x,y),{{J}_{{m,y}}}(x,y))$. Полагая ${{j}_{z}} \approx 0$, получаем
(3)
${{{\mathbf{J}}}_{{m,x}}}(x,y) = \int\limits_{h_{m}^{0}}^{h_{m}^{1}} {{{{\mathbf{j}}}_{{m,x}}}} (x,y,z)dz,\quad {{{\mathbf{J}}}_{{m,y}}}(x,y) = \int\limits_{h_{m}^{0}}^{h_{m}^{1}} {{{{\mathbf{j}}}_{{m,y}}}} (x,y,z)dz.$Конечная толщина проводящих слоев эффективно учитывается путем усреднения уравнения (2) по толщине слоя и введения некоторой простой функции Грина вместо потенциала простого слоя с ядром ${1 \mathord{\left/ {\vphantom {1 {\left| {r - r{\text{'}}{\kern 1pt} } \right|}}} \right. \kern-0em} {\left| {r - r{\text{'}}{\kern 1pt} } \right|}}$, $r = (x,y)$:
(4)
$\lambda _{s}^{n}{{{\mathbf{J}}}_{n}}(r) + \frac{1}{{4\pi }}\sum\limits_{m = 1}^{{{N}_{c}}} {\iint\limits_{{{s}_{m}}} {{{{\mathbf{J}}}_{m}}}} (r{\text{'}}){{G}_{{mn}}}(r,r{\text{'}})ds{\text{'}} = \nabla {{\varphi }_{n}}(r),$(5)
${{G}_{{mn}}}(r,r{\text{'}}{\kern 1pt} ) = \frac{1}{4}\sum\limits_{k = 0}^1 {\sum\limits_{l = 0}^1 {{{{\left( {{{{\left| {r - r{\text{'}}{\kern 1pt} } \right|}}^{2}} + {{{(h_{m}^{k} - h_{n}^{l})}}^{2}}} \right)}}^{{ - 1/2}}}} } .$Затем с помощью оператора ротора ${{\nabla }_{ \bot }} = ({{\partial }_{y}}, - {{\partial }_{x}})$ интегральное уравнение для листовых токов преобразуется в гиперсингулярное интегральное уравнение. Гиперсингулярная форма уравнения предпочтительнее для численного решения, так как его интегральный оператор является симметричным и положительно-определенным.
Более того, в (2) мы исключаем член $\nabla {{\varphi }_{n}}(r)$. Для этого плотность тока сверхпроводимости представляется в виде суммы двух компонент:
(6)
${\mathbf{J}}_{m}^{{{\text{pot}}}}(r) = {{(\lambda _{m}^{s})}^{{ - 1}}}\nabla {{\varphi }_{m}}(r),\quad {\mathbf{J}}_{m}^{{{\text{rot}}}}(r) = {{\nabla }_{ \bot }}{{\psi }_{m}}(r).$Окончательно приходим к следующему интегральному уравнению для функции тока ${{\psi }_{n}}(r)$, $n = 1,\; \ldots ,\;{{N}_{c}}$:
(7)
$ - \lambda _{s}^{n}\Delta {{\psi }_{n}}(r) + \frac{1}{{4\pi }}\sum\limits_{m = 1}^{{{N}_{c}}} {\iint\limits_{{{s}_{m}}} {(\nabla {{\psi }_{m}}(r{\text{'}}{\kern 1pt} ),\nabla {\text{'}}{{G}_{{mn}}}(r,r{\text{'}}{\kern 1pt} )){\kern 1pt} ds{\text{'}}}} + {{F}_{n}}(r) = 0,$(8)
${{F}_{n}}(r) = \frac{1}{{4\pi }}\sum\limits_{m = 1}^{{{N}_{c}}} {\iint\limits_{{{s}_{m}}} {\frac{1}{{\lambda _{s}^{m}}}}} {\kern 1pt} (\nabla {{\varphi }_{m}}(r{\text{'}}{\kern 1pt} ),{{\nabla }_{ \bot }}{{G}_{{mn}}}(r,r{\text{'}}{\kern 1pt} )){\kern 1pt} ds{\text{'}}.$(9)
${{\psi }_{m}}(r) = {{I}_{{h,k}}},\quad r \in {{C}_{{h,k}}},\quad {{\psi }_{m}}(r) = 0,\quad r \in {{C}_{{ext,m}}}.$Для потенциала ${{\varphi }_{n}}(r)$ в (8) ставится вторая краевая задача
(11)
$\frac{1}{{\lambda _{s}^{n}}}\frac{{\partial {{\varphi }_{n}}(r)}}{{\partial {\mathbf{n}}}} = 0,\quad r \in \partial {{S}_{{ext,n}}} \cup \partial {{S}_{{h,k}}},\quad n = 1,\; \ldots ,\;{{N}_{c}},$(12)
${{f}_{m}}(r) = \frac{{{{I}_{k}}}}{{\left| {{{T}_{k}}} \right|}},\quad r \in {{T}_{k}},\quad {{f}_{m}}(r) = 0,\quad r \notin {{T}_{k}}.$Таким образом, для достижения общей цели необходимо последовательно решить ряд задач. Сначала решаются ${{N}_{c}}$ задач (10), (11) с заданным ${{I}_{k}}$ для ${\mathbf{J}}_{m}^{{{\text{pot}}}}(r)$. После этого решаются задачи (7)–(9). Наконец, полная энергия рассчитывается с использованием выражения:
(13)
$E = \frac{{{{\mu }_{0}}}}{2}\sum\limits_{n = 1}^{{{N}_{c}}} {\iint\limits_{{{S}_{n}}} {\left( {\lambda _{s}^{n}J_{n}^{2}(r) + \frac{1}{{4\pi }}\sum\limits_{m = 1}^{{{N}_{c}}} {\iint\limits_{{{S}_{m}}} {{{{\mathbf{J}}}_{n}}(r)}} \cdot {{{\mathbf{J}}}_{m}}(r{\text{'}}{\kern 1pt} {\kern 1pt} ){{G}_{{mn}}}(r,r{\text{'}}{\kern 1pt} {\kern 1pt} )ds{\text{'}}} \right)ds}} .$Для однослойной структуры ядра ${1 \mathord{\left/ {\vphantom {1 {\left| {r - r{\text{'}}{\kern 1pt} } \right|}}} \right. \kern-0em} {\left| {r - r{\text{'}}{\kern 1pt} } \right|}}$ и одного проводника уравнение для функции тока имеет вид
(14)
$ - {{\lambda }_{s}}\Delta \psi (r) + \frac{1}{{4\pi }}\iint\limits_S {\left( {\nabla \psi (r{\text{'}}{\kern 1pt} ),\nabla {\text{'}}\frac{1}{{\left| {r - r{\text{'}}{\kern 1pt} } \right|}}} \right)}ds{\text{'}} + F(r) = 0.$(15)
$L\psi (r) = \frac{1}{{4\pi }}\iint\limits_S {\left( {\nabla \psi (r{\text{'}}{\kern 1pt} ),\nabla {\text{'}}\frac{1}{{\left| {r - r{\text{'}}{\kern 1pt} } \right|}}} \right)}ds{\text{'}} = - \frac{1}{{4\pi }}\iint\limits_S {\frac{{\psi (r{\text{'}}{\kern 1pt} )}}{{{{{\left| {r - r{\text{'}}} \right|}}^{3}}}}}ds{\text{'}}.$Формула (15) важна для доказательства свойств интегрального оператора и корректности метода конечных элементов. Кроме того, представление интегрального оператора в гиперсингулярной форме может быть использовано для быстрой оценки и вычисления матричных элементов в методе конечных элементов для удаленных друг от друга точек сетки (см. [17]).
Если геометрические параметры задачи и лондоновская глубина проникновения представлены в микронах, то можно считать, что все уравнения приведены к безразмерной форме, а размерность индуктивностей составляет пикогенри.
4. ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ И ПРОГРАММА
Для решения обеих краевых задач (10), (11) и (7), (8) используется метод конечных элементов. Мы используем треугольные сетки и линейные лагранжевы конечные элементы [18]. Такой выбор приводит к простому и быстрому алгоритму сборки общей матрицы метода конечных элементов.
Для уравнения Пуассона (10), (11) используется аналогичный метод конечных элементов. Этот алгоритм описан в литературе.
Для краткости рассмотрим задачу с одним проводником. Тогда билинейная форма задачи для функции тока имеет вид
(16)
$a(u,{v}) = - {{\lambda }_{s}}\iint\limits_S {(\nabla u,\nabla {v})}{\kern 1pt} ds + \frac{1}{{4\pi }}\iint\limits_S {ds}\iint\limits_S {(\nabla u(r),\nabla {v}(r{\kern 1pt} {\text{'}}{\kern 1pt} )){\kern 1pt} }G(r,r{\kern 1pt} {\text{'}}{\kern 1pt} )ds{\text{'}}.$Сеточная аппроксимация функции тока с главными краевыми условиями имеет вид
где суммирование проводится по всем точкам сетки $J$, включая граничные точки, $\psi _{j}^{h}$ – приближенные значения функции тока в точках сетки, $u_{j}^{h}(r)$ – базисные функции интерполяции метода конечных элементов.В нашем вычислительном алгоритме используются линейные лагранжевы конечные элементы (P1). Эти элементы обладают достаточной гладкостью и удобны для аппроксимации гиперсингулярного оператора (15).
Такой метод конечных элементов приводит к системе линейных уравнений для $\psi _{i}^{h}$, $i \in I$, $I$ – внутренние точки сетки:
Матрица в (18) плотная, симметричная и при достаточно малом шаге сетки положительно-определенная. Размерность этой матрицы равна числу внутренних точек сетки ${{N}_{I}}$. Граничные значения $\psi (r)$ формируют правую часть как главное краевое условие.Таким образом, матричные элементы конечно-элементной матрицы $K$ имеют вид
Обоснование описанного метода конечных элементов для гиперсингулярного уравнения с ядром ${1 \mathord{\left/ {\vphantom {1 {{{{\left| {r - r{\text{'}}{\kern 1pt} } \right|}}^{3}}}}} \right. \kern-0em} {{{{\left| {r - r{\text{'}}{\kern 1pt} } \right|}}^{3}}}}$ было дано в [16].
Для решения линейных уравнений описанного метода конечных элементов мы используем разложение Холецкого для плотных матриц. Метод конечных элементов для (10), (11) основан на применении разреженных матриц.
Для построения треугольных сеток наша программа содержит собственный генератор. Также можно использовать известный генератор треугольных сеток Triangle [19].
В алгоритме есть несколько вычислительных процедур, занимающих много времени процессора. Первой процедурой является вычисление матрицы $K$ (19) и правой части $F(r)$ в (8). Второй процедурой является расчет полной энергии, определяемой выражением (13). Чтобы ускорить эти вычисления, мы вводим матрицу Галеркина $T$ взаимодействий между треугольниками на сетке метода конечных элементов, которая является общей частью обоих вычислений. Пусть ${{\Delta }_{i}}$ и ${{\Delta }_{j}}$ – треугольные ячейки, тогда элементы матрицы взаимодействия $T$ являются четырехкратными интегралами:
(20)
${{T}_{{ij}}} = \frac{1}{{4\pi }}\iint\limits_{{{\Delta }_{i}}} {ds{\text{'}}}\iint\limits_{{{\Delta }_{j}}} G(r,r{\text{'}}{\kern 1pt} ){\kern 1pt} ds.$Программная реализация численного алгоритма содержит вычислительные модули, написанные на C++ и работающие в Linux или Windows. Также нами разработан графический Windows интерфейс для визуализации входных данных и распределения тока [9].
5. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Рассмотрим модель нейрона для многослойного персептрона, см. фиг. 2. Исходные данные для расчетов первоначально были подготовлены в САПР в формате DXC (DXF), а затем в полуавтоматическом режиме преобразованы во входные данные для программы 3D-MLSI.
Схема содержит множество возможных токовых структур, которые можно использовать для прямого или косвенного вычисления схемных и паразитных индуктивностей. Для краткости рассмотрим пример с двумя замкнутыми токами. Во-первых, это горизонтальная замкнутая токовая петля с собственной индуктивностью ${{L}_{{11}}}$. Эта петля моделирует измерительный СКВИД с двумя джозефсоновскими контактами и возвратным током через заземленную поверхность. Второй контур с собственной индуктивностью ${{L}_{{22}}}$ – это вертикальная (на фигуре) петля с одним джозефсоновским переходом и обратным током через плоскость заземления. Обе петли показаны на фиг. 3.
Для расчета описанных индуктивностей с точностью 5–6% решалась задача с размерностями матриц ${{N}_{t}} = 12\,722$ и ${{N}_{I}} = 5770$. Всего система уравнений с матрицей $K$ решалась 3 раза. Были получены значения ${{L}_{{11}}} = 9.05$, ${{L}_{{12}}} = 1.8$ и ${{L}_{{22}}} = 26.3$ пикогенри. Линии тока для расчета ${{L}_{{11}}}$ представлены на фиг. 4. Ток через первый контур создает близкие к прямым линии тока. Токи экранирования на других частях конструкции образуют вихревые структуры. Полученные результаты были далее использованы при моделировании процессов в таком нейроне, а также для дальнейшей оптимизации его структуры.
Описанные вычисления оказались достаточно быстрыми и заняли несколько минут на процессоре Intel i7 в одноядерном режиме. Те же вычисления с более плотной сеткой и ${{N}_{I}} = 18\,694$ и ${{N}_{t}} = 42\,842$ заняли всю 16-гигабайтную память и потребовали несколько часов счета.
5. ВЫВОДЫ
Математическая модель настоящей работы является достаточно точной и эффективной для сверхпроводниковых схем с одним или несколькими слоями металлизации и толщиной слоев, сопоставимой с лондоновской глубиной проникновения. Алгоритм и программа применимы как к задачам с элементами схемы, несущими весь возвратный ток, так и к задачам без таких элементов, например, однослойным.
Вычислительный метод настоящей работы, программа и методология расчетов могут быть довольно просто использованы для вычисления индуктивностей схем небольших и умеренных размеров. Для моделирования больших схем требуется дополнить программу средствами автоматической подготовки входных данных, использующими данные систем автоматизированного проектирования и разработки (САПР) микросхем.
Другим необходимым и важным шагом является использование современных методов работы с плотно заполненными матрицами большой размерности с целью уменьшения требований к необходимой памяти и ускорения вычислений.
Авторы благодарят В. Больгинова за плодотворные обсуждения возможных реализаций моделей сверхпроводниковых нейронов.
Список литературы
Soloviev I.I., Klenov N.V., Schegolev A.E., Bakurskiy S.V., Kupriyanov M.Yu. Analytical derivation of DC SQUID response // Superconductor Sci. and Technology. 2016. V. 29. № 9. P. 094005.
Kornev V.K., Kolotinskiy N.V., Bazulin D.E., Mukhanov O.A. High linearity bi-SQUID: Design map // IEEE Transactions on Appl. Superconductivity. 2018. V. 28. № 7. P. 1–5.
Soloviev I.I., Ruzhickiy V.I., Klenov N.V., Bakurskiy S.V., Kupriyanov M.Yu. A linear magnetic flux-to-voltage transfer function of a differential DC SQUID // Superconductor Sci. and Technology. 2019. V. 32. № 7. P. 074005.
Katayama H., Fujii T., Hatakenaka N. Theoretical basis of SQUID-based artificial neurons // J. of Applied Physics. 2018. V. 124. № 15. P. 152106.
Soloviev I.I., Schegolev A.E., Klenov N.V., Bakurskiy S.V., Kupriyanov M.Y., Tereshonok M.V., Shadrin A.V., Stolyarov V.S., Golubov A.A. Adiabatic superconducting artificial neural network: Basic cells // J. of Applied Physics. 2018. V. 124. № 15. P. 152113.
Klenov N.V., Schegolev A.E., Soloviev I.I., Bakurskiy S.V., Tereshonok M.V. Energy efficient superconducting neural networks for high-speed intellectual data processing systems // IEEE Transactions on Appl. Superconductivity. 2018. V. 28. № 7. P. 1–6.
Schegolev A.E., Klenov N.V., Soloviev I.I., Tereshonok M.V. Adiabatic superconducting cells for ultra-low-power artificial neural networks // Beilstein J. Nanotechnol. 2016. V. 7. P. 1397–1403.
Khapaev M.M. Inductance extraction of multilayer finite-thickness superconductor circuits // IEEE Transactions on Microwave Theory and Techniques. 2001. V. 49. P. 217–220.
Khapaev M.M., Kupriyanov M.Y. Inductance extraction of superconductor structures with internal current sources // Superconductor Sci. and Technology. 2015. V. 28. № 5. P. 055013.
Schmidt V.V. The Physics of Superconductors: Introduction to Fundamentals and Applications. Berlin: Springer, 2010.
Orlando T.P., Delin K.A. Foundations of Applied Superconductivity. Addison–Wesley, 1991.
Kamon M., Tsuk M.J., White J.K. FASTHENRY: a multipole-accelerated 3D inductance extraction program // IEEE Transactions on Microwave Theory and Techniques. 1994. V. 42. № 9. P. 1750–1758.
Yucel A.C., Georgakis I.P., Polimeridis A.G., Bagci H., White J.K. VoxHenry: FFT-Accelerated Inductance Extraction for Voxelized Geometries // IEEE Transactions on Microwave Theory and Techniques. 2018. V. 66. № 4. P. 1723–1735.
Whiteley S.R. Fasthenry 3.0wr. http://www.wrcad.com
Fourie C.J., Jackman K. Software tools for flux trapping and magnetic field analysis in superconducting circuits // IEEE Transactions on Appl. Superconductivity. 2019. V. 29. 1301004.
Ervin V.J., Stephan E.P. A boundary element Galerkin method for a hypersingular integral equation on open surfaces // Mathematical Methods in the Applied Sciences. 1990. V. 13. P. 281–289.
Khapaev M.M., Kupriyanov M.Y. Sparse approximation of FEM matrix for sheet current integro-differential equation // Matrix Methods: Theory, Algorithms and Applications. Dedicated to the Memory of Gene Golub. 2010. P. 510–522.
Jin J.M. The Finite Element Method in Electromagnetics. John Wiley, 2015.
Shewchuk J.R. Delaunay refinement algorithms for triangular mesh generation // Computational Geometry: Theory and Applications. 2002. V. 22. I. 1–3. P. 21–74.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики



