Журнал вычислительной математики и математической физики, 2021, T. 61, № 5, стр. 744-758
Индуктивное восстановление матриц с отбором признаков
М. Буркина 3, И. Назаров 1, *, М. Панов 1, **, Г. Федонин 2, 3, 4, Б. Широких 1, 2, 3
1 Сколтех
121205 Москва, Большой бульвар, 30, стр. 1, Россия
2 ИППИ РАН
127051 Москва, Б. Каретный пер., 19, стр. 1, Россия
3 МФТИ
141700 М.о., Долгопрудный, Институтский пер., 9, Россия
4 Центральный НИИ эпидемиологии
111123 Москва, Новогиреевская ул., 3а, Россия
* E-mail: ivan.nazarov@skolkovotech.ru
** E-mail: m.panov@skoltech.ru
Поступила в редакцию 19.03.2020
После доработки 29.12.2020
Принята к публикации 14.01.2021
Аннотация
Рассматривается задача индуктивного восстановления матриц – восстановления матрицы с использованием побочных признаков для строк и столбцов. Однако во многих прикладных задачах подобная вспомогательная информация содержит избыточные или малоинформативные признаки, что делает необходимым шаг их отбора. В работе предлагается подход, основанный на факторизации матрицы с групповой LASSO регуляризацией на коэффициенты побочных признаков, который совмещает отбор признаков с восстановлением матрицы. При этом теоретически доказывается, что асимптотика ошибки восстановления предложенного подхода ниже, чем в методах, не производящих прореживание. Предлагается вычислительно эффективная итеративная процедура для одновременного восстановления матрицы и отбора признаков. Эксперименты на искусственных данных и данных из прикладных задач демонстрируют, что предложенный подход улучшает показатели качества благодаря отбору признаков. Библ. 38. Фиг. 2. Табл. 3.
1. ВВЕДЕНИЕ
Методы пополнения или восстановления матриц, matrix completion, находят широкое примение в рекомендательных системах [1], [2], задачах кластеризации [3], классификации с многими метками [4], [5], обработки сигналов [6], компьютерного зрения [7] и подобных. В традиционной постановке частично наблюдаемая низкоранговая матрица восстанавливается напрямую через скалярное произведение выученных строчных и колоночных факторов, или неявно с использованием ядерных методов (kernel trick). При этом каждый фактор является численным отражением признаков некоей сущности, связанной с той или иной строкой или столбцом. Теоретические основания, определяющие возможность восстановления низкоранговых матриц, рассмотрены в работах [8] и [9]. Например, в условиях независимого случайного наблюдения достаточно иметь доступ к $O(Nlo{{g}^{2}}N)$ элементам матрицы низкого ранга ${{n}_{1}} \times {{n}_{2}}$ для полного точного ее восстановления ($N = max{\text{\{ }}{{n}_{1}},{{n}_{2}}{\text{\} }}$). Оценка, не зависящая от распределения, приведенная в [10], позволяет достичь полного восстановления матриц, имея $O({{N}^{{3/2}}})$ наблюдения.
Зачастую в дополнение к элементам самой частично наблюдаемой матрицы доступны вспомогательные экзогенные характеристики сущностей, стоящих за ее строками и столбцами. Например, в [11] показано, что побочные признаки строк и столбцов в виде профилей пользователей или описания жанров кино, side-channel information, полезны в задаче рекомендательной системы. Подобная вспомогательная информация играет особо важную роль при решении проблемы “холодного старта” рекомендательной системы, так как в ситуации, когда необходимо предсказать “взаимодействие” наблюдавшихся ранее сущностей с новой доселе ненаблюдавшейся сущностью, единственной возможностью остается только делать выводы на основе побочных характеристик.
Подходы, тем или иными способом учитывающие побочные признаки при пополнении матрицы, носят название индуктивного восстановления матриц, inductive matrix completion (IMC), см. в том числе [12]–[18]. Ключевой теоретический результат, полученный на момент написания настоящей работы, заключается в том, что достаточный объем наблюдений для восстановления снижается до $O(logN)$ при условии, что побочные признаки имеют “хорошую” предсказательную силу. При этом вполне естественна ситуация, когда не все признаки релевантны или имеют хорошую предсказательную силу. Таким образом, становится очевидной необходимость разработки алгоритмов IMC, работающих в условиях избыточности побочных признаков и при этом сохраняющих гарантии по асимптотике достаточного объема наблюдений для восстановления. Немногие исследования обращаются к теме развития методов индуктивного восстановления матриц с отбором побочных признаков (прореживания), [16], [19] при том, что потенциал модификаций и улучшений существующих алгоритмов восстановления матриц в этом направлений велик.
Систематическое исследование проблемы индуктивного восстановления матриц началось с работы [12], в которой показано, что для полного восстановления достаточно наблюдать $O(logN)$ случайных элементов при условии использования нормы ${{\left\| M \right\|}_{ * }} = \sum\nolimits_i {{{\sigma }_{i}}} (M)$ сингулярных чисел ${{\sigma }_{i}}(M)$ матрицы $M$ в качестве регуляризатора, также известной как ядерная норма. В [20] рассмотрено представление матрицы в виде низкорангового произведения факторов и побочных признаков и изучена итеративная покоординатная процедура, возникающая в данной параметризации задачи. Предложенная параметризация нивелирует необходимость сингулярного разложения матрицы на каждой итерации, заменяя ее попеременным решением квадратичной задачи для каждого фактора. В [18] рассмотрены невыпуклый регуляризатор на факторы и 3-х фазная итеративная процедура восстановления, завершающаяся фазой проективного градиентного спуска, которая гарантирует, что вычисленные факторы находятся в окрестности оптимального решения задачи с высокой вероятностью по наблюдаемым выборкам.
В [14] рассматривается ситуация с несовершенными побочными признаками, которые не имеют достаточной предсказательной силы для полного восстановления матрицы, и, совместив индуктивный и классический подходы к восстановлению матриц, добиваются состоятельного восстановления матриц также и в случае “совершенных” побочных признаков. В [16] рассматривается аналогичная ситуация, где используется разреживающий регуляризатор на основе нормы сингулярных чисел целевой матрицы, приводя также оценки достаточного числа наблюдаемых элементов для восстановления. Однако в работе не исследуется эффект отбора признаков на получаемое решение, и предложенная процедура имеет высокую сложность по памяти и арифметическую сложность. В [19] рассматривается комбинаторная постановка задачи индуктивного восстановления матриц с отбором признаков, и приводится оценка ускоренной асимптотики достаточного объема наблюдений при наличии шума. В аналогичной постановке индуктивного восстановления ребер в графах в [21] получены минимакс оптимальные оценки достаточного объема наблюдений в режимах низкоранговой матрицы связности и избыточности побочных признаков, а также исследован баланс между вероятностью точного восстановления и вычислительной сложностью.
В настоящей работе мы предлагаем новый алгоритм индуктивного пополнения матриц, эффективно борющийся с избыточностью побочных признаков. Алгоритм отбирает релевантные характеристики при помощи включения регуляризатора в оптимизационную задачу факторизации матрицы, наводящего групповое прореживание на оцениваемые строчные и колоночные факторы. Мы приводим теоретические гарантии на оптимальность решения предложенной задачи IMC, которое, в свою очередь, ведет к улучшенной асимптотике достаточного объема наблюдений для индуктивного восстановления матрицы в ситуации, когда большая доля побочных признаков не имеют предсказательной силы. В частности, достаточный объем наблюдений асимптотически ниже, чем в случае, когда отбор признаков не производится.
Мы также предлагаем итеративную процедуру для численного решения предложенной невыпуклой оптимизационной задачи разреженного IMC, основанную на алгоритме ADMM [22], [23]. Приводимые нами экспериментальные свидетельства, демонстрируют, что предложенная процедура восстанавливает матрицу одновременно с отбором малоинформативных побочных признаков как на синтетических примерах, так и в наборах данных из практических приложений, при этом достигая показателей качества, сравнимых с алгоритмическими аналогами без прореживания. Реализация процедуры (https://github.com/premolab/SGIMC) позволяет индуктивно восстанавливать частично наблюдаемые матрицы больших размеров.
Изложение результатов начинается с постановки оптимизационной задачи для восстановления матриц с прореживающим регуляризатором в разд. 2. В разд. 3 приводятся оценки обобщающей способности предложенного метода и достаточного объема наблюдений для восстановления, а в разд. 4 приведена предложенная нами итеративная процедура. Затем в разд. 5 приводятся и обсуждаются полученные экспериментальные свидетельства. Изложение завершается разд. 6.
2. ПОСТАНОВКА ЗАДАЧИ ВОССТАНОВЛЕНИЯ МАТРИЦ С ПРОРЕЖИВАНИЕМ
Рассмотрим целевую матрицу $M \in {{\mathbb{R}}^{{{{n}_{1}} \times {{n}_{2}}}}}$, в которой наблюдаемы только значения ${{M}_{{ij}}}$ и некоторого множества $(i,j) \in \Omega \subset {\text{\{ }}1,\; \ldots ,\;{{n}_{1}}{\text{\} }} \times {\text{\{ }}1,\; \ldots ,\;{{n}_{2}}{\text{\} }}$. Предположим, что побочные признаки полностью наблюдаемы и представлены в виде матриц $X \in {{\mathbb{R}}^{{{{n}_{1}} \times {{d}_{1}}}}}$ и $Y \in {{\mathbb{R}}^{{{{n}_{2}} \times {{d}_{2}}}}}$ для строк и столбцов $M$ соответственно. Также допустим, что побочная информация имеет предсказательную силу применительно к значениям в $M$ через билинейную модель
для некоторой матрицы весов $W \in {{\mathbb{R}}^{{{{d}_{1}} \times {{d}_{2}}}}}$. Целью задачи индуктивного восстановления матрицы является оценка ненаблюдаемых элементов $M$ на основе наблюдаемых ${{M}_{\Omega }}$ и побочной строчных $X$ и столбцовых $Y$ характеристик.Главенствующим допущением в подходах к решению задачи IMC является предположение о том, что матрица $W$ имеет низкий ранг $k < min({{d}_{1}},{{d}_{2}})$, см. [12], [14]. При этом существуют два подхода к учету данного ограничения в итоговой оптимизационной задаче.
Подход 1. Использование ${{\ell }_{1}}$ нормы сингулярных чисел матрицы $W$, ядерная норма ${{\left\| W \right\|}_{ * }}$, в качестве разреживающего регуляризатора, приводящего к низкоранговым решениям ${{\left\| W \right\|}_{ * }}$, см. [12], [14], [16].
Подход 2. Явная параметризация $W$ в виде низкорангового произведения $U{{V}^{{\text{т}}}}$, где $U \in {{\mathbb{R}}^{{{{d}_{1}} \times k}}}$ и $V \in {{\mathbb{R}}^{{{{d}_{2}} \times k}}}$, см. [18], [20].
Мы сосредотачиваемся на втором подходе, поскольку он позволяет работать с матрицей весов $W$ неявно через ее факторы, что упрощает отбор признаков в задачах с большими объемами данных (${{d}_{1}},{{d}_{2}} \gg 1$).
Предположим, что $\mathcal{L}:\mathbb{R} \times \mathbb{R} \to \mathbb{R}$ является гладкой выпуклой функцией потерь в задаче машинного обучения, и рассмотрим следующую регуляризованную задачу минимизации:
(1)
$\mathop {min}\limits_{U,V} \sum\limits_{(i,j) \in \Omega } \mathcal{L} ({{M}_{{ij}}},{{(XU{{V}^{{\text{т}}}}{{Y}^{{\text{т}}}})}_{{ij}}}) + {{\lambda }_{U}}R(U) + {{\lambda }_{V}}R(V),$(2)
$\mathop {min}\limits_{U,V} \sum\limits_{(i,j) \in \Omega } \mathcal{L} ({{M}_{{ij}}},{{(XU{{V}^{{\text{т}}}}{{Y}^{{\text{т}}}})}_{{ij}}}) + {{\lambda }_{U}}{{\left\| U \right\|}_{{2,1}}} + {{\lambda }_{V}}{{\left\| V \right\|}_{{2,1}}}.$3. АНАЛИЗ АСИМПТОТИКИ ОШИБКИ ВОССТАНОВЛЕНИЯ
В данном разделе приводится анализ влияния отбора признаков на точность восстановления матриц.
Задачу индуктивного восстановления матрицы можно рассмотреть через призму машинного обучения с учителем. Действительно, наблюдаемые значения в разреженной матрице ${{M}_{\Omega }}$ можно рассматривать как случайную выборку значений неизвестной ненаблюдаемой матрицы $W{\text{*}}$, полученной с использованием линейных измерений, построенных на побочных признаках $X$ и $Y$. Таким образом, набор данных $(X,Y,{{M}_{\Omega }})$ представляется в виде выборки $S = ({{x}_{t}},{{y}_{t}},{{b}_{t}})_{{t = 1}}^{m}$ размера $m = \left| \Omega \right|$ при фиксированном обходе индексов из $\Omega $. Каждое значение ${{b}_{t}}$ в $S$ является результатом применения измерительного оператора ${{A}_{t}}$ к $W{\text{*}}$, который задан одноранговой матрицей ${{A}_{t}} = {{x}_{t}}y_{t}^{{\text{т}}}$ размера ${{d}_{1}} \times {{d}_{2}}$: ${{b}_{t}} = \left\langle {{{A}_{t}},W{\text{*}}} \right\rangle = x_{t}^{{\text{т}}}W{\text{*}}{{y}_{t}}$. С этого ракурса задача (2) эквивалентна оценке истинной $W{\text{*}}$ матрицей ранга $k$, заданной произведением $U$ и $V$, поскольку
Для понимания того, возможно ли в постановке (2) оценить истинную матрицу $W{\text{*}}$ и тем самым восстановить целевую матрицу $M$, рассмотрим задачу (2) с дополнительными ограничениями:
(3)
$\begin{gathered} \mathop {min}\limits_{U,V} \frac{1}{\Omega }\sum\limits_{(i,j) \in \Omega } \mathcal{L} ({{M}_{{ij}}},x_{i}^{{\text{т}}}W{{y}_{j}}) = \frac{1}{m}\sum\limits_{t = 1}^m \mathcal{L} ({{b}_{t}},\left\langle {{{A}_{t}},W} \right\rangle ), \\ {\text{при}}\;{\text{условии}}\;\;W = U{{V}^{{\text{т}}}},\quad {{\left\| U \right\|}_{{2,1}}} \leqslant {{C}_{U}},\quad {{\left\| V \right\|}_{{2,1}}} \leqslant {{C}_{V}}, \\ \end{gathered} $(4)
$\mathcal{F} = \left\{ {f:{{\mathbb{R}}^{{{{d}_{1}} \times {{d}_{2}}}}} \to \mathbb{R}:A \mapsto \left\langle {A,U{{V}^{{\text{т}}}}} \right\rangle ,\;(U,V) \in \Theta } \right\},$Для того, чтобы определить, может ли класс $\mathcal{F}$ обобщить конечный набор наблюдаемых значений $M$ на всю матрицу, необходимо оценить асимптотику ошибки восстановления этим классом. Для этого рассмотрим распределение $\mathcal{D}$ на $\mathcal{Z} \times \mathcal{T}$, где $\mathcal{Z} \subset {{\mathbb{R}}^{{{{d}_{1}} \times {{d}_{2}}}}}$ – множество матриц ${{d}_{1}} \times {{d}_{2}}$, а $\mathcal{T}$ является множеством допустимых значений в матрице $M$. Поскольку в задаче индуктивного восстановления множество $\mathcal{Z}$ задано набором ограниченных по норме матриц ранга $1$ вида $A = x{{y}^{{\text{т}}}}$, рассмотрим такие распределения $\mathcal{D}$ над $\mathcal{X} \times \mathcal{Y} \times \mathcal{T}$, для которых справедливо, что пространства побочных признаков $\mathcal{X} \subset {{\mathbb{R}}^{{{{d}_{1}}}}}$ и $\mathcal{Y} \subset {{\mathbb{R}}^{{{{d}_{2}}}}}$ являются ограниченными множествами. Отображение $\mathcal{X} \times \mathcal{Y}$ в $\mathcal{Z}$ имеет вид $(x,y) \mapsto x{{y}^{{\text{т}}}}$.
Оценка асимптотики ошибки восстановления также требует ограниченности функции потерь $\ell :\mathbb{R} \times \mathcal{T} \to \mathbb{R}$, относительно которой определяются понятия теоретического (ожидаемого) и эмпирического риска. В задаче восстановления бинарной матрицы $M$ множество $\mathcal{T}$ равно ${\text{\{ }}{\kern 1pt} - {\kern 1pt} 1,\; + {\kern 1pt} 1{\text{\} }}$ и используется бинарная функция потерь ($0{\kern 1pt} - {\kern 1pt} 1$ loss): $\ell (p,b) = {{1}_{{p \ne b}}}$. Однако для анализа асимптотики ошибки в задаче восстановления вещественной матрицы $\mathcal{T} = [ - B, + B]$ для некоторого $B > 0$ и функция потерь $\ell (p,b)$ равна ${{\left| {p - b} \right|}^{d}}$ при $d \geqslant 1$.
Определение 1 (Риск). Рассмотрим гипотезу, решающее правило или регрессионную функцию $f:\mathcal{Z} \to \mathbb{R}$. При заданном распределении $\mathcal{D}$, теоретический риск $f$ задан выражением
Для заданной выборки $S = ({{z}_{i}},{{b}_{i}})_{{i = 1}}^{m} \sim \mathcal{D}$, эмпирический риск $f$ вычисляется в виде
Для того чтобы получить оценку асимптотики верхней границы теоретического риска $R(\hat {f})$ минимизирующей гипотезы $\hat {f} = arg\;mi{{n}_{{f \in \mathcal{F}}}}\hat {R}(f)$, также известной как оценка обобщающей способности класса $\mathcal{F}$, в задаче (3), которая является эквивалентным представлением задачи SGIMC, рассмотрим более простой класс линейных гипотез на некотором $\mathcal{K} \subset {{\mathbb{R}}^{q}}$:
(5)
$\mathcal{H} = \left\{ {h:\mathcal{K} \to \mathbb{R}:{v} \mapsto \left\langle {v,\beta } \right\rangle ,\;\beta \in {{\mathbb{R}}^{q}},\;{{{\left\| \beta \right\|}}_{1}} \leqslant C} \right\},$Заметим, что в силу того, что пространства ${{\mathbb{R}}^{{{{d}_{1}} \times {{d}_{2}}}}}$ и ${{\mathbb{R}}^{q}}$ изоморфны для $q = {{d}_{1}}{{d}_{2}}$, класс гипотез $\mathcal{H}$ тождественен классу ${{\mathcal{F}}_{1}}$, более удобному для анализа в задаче оценки значений матриц:
Основной результат работы [24] дает равномерную оценку верхней границы теоретического риска с использованием понятия радемахеровской сложности (Rademacher complexity) класса гипотез [25]. Радемахеровская сложность класса $\mathcal{H} \subset {{\mathbb{R}}^{\mathcal{K}}}$ в условиях распределения ${{\mathcal{D}}_{\mathcal{K}}}$ на множестве $\mathcal{K}$ задается в виде
где математическое ожидание берется по всем выборкам $S$ размера $m$ независимых одинаково распределенных случайных величин из ${{\mathcal{D}}_{\mathcal{K}}}$. При этом эмпирическая радемахеровская сложность класса $\mathcal{H}$ при условии заданной выборки $S = ({{z}_{i}})_{{i = 1}}^{m} \subset \mathcal{K}$ определяется в виде где математическое ожидание обусловлено по выборке $S$ и берется по случайным векторам $\varepsilon = ({{\varepsilon }_{i}})_{{i = 1}}^{m}$ независимых равномерных случайных величин из ${\text{\{ }} - {\kern 1pt} 1,\; + 1{\text{\} }}$. В настоящем анализе мы рассматриваем классы измеримых функций, для которых супремум в (7) измерим, что выполняется для линейных гипотез над конечномерными пространствами ${{\mathbb{R}}^{m}}$. Заметим, что используемое в настоящей работе определение радемахеровской сложности совпадает с определением в [26], которое отличается от определения из [24] и [25] отсутствием множителя $2$.Основная теорема об оценке обобщающей способности класса функций через радемахеровскую сложность из работ [25] и [26, теорема 3.1, стр. 35] предлагает оценку верхней границы теоретического риска, равномерную по гипотезам из $\mathcal{H}$.
Теорема 1 (переформулировка). Рассмотрим $\rho $-липшицеву функцию потерь $\ell :\mathbb{R} \times \mathcal{T} \to [0,1]$, или бинарную функцию потерь $\ell $ с $\rho = 1{\text{/}}2$. Пусть $\mathcal{H}$ является классом функций из $\mathcal{K}$ в $\mathbb{R}$ и пусть $S = ({{z}_{i}},{{b}_{i}})_{{i = 1}}^{m}$ задает выборку независимых одинаково распределенных случайных величин из $\mathcal{D}$ в пространстве $\mathcal{K} \times \mathcal{T}$. Тогда для любой $\delta \in (0,1)$ с вероятностью не ниже $1 - \delta $ по выборкам $S \sim {{\mathcal{D}}^{m}}$ следующие неравенства выполняются одновременно (равномерно) для всех $h \in \mathcal{H}$
Таким образом, для того чтобы ограничить сверху теоретический риск, достаточно найти верхнюю границу эмпирической радемахеровской сложности ${{\hat {\mathcal{R}}}_{S}}(\mathcal{H})$. Для этого мы воспользуемся теоремой 2 из [24], которая приводит оценку сложности для класса линейных гипотез H, ограниченных шаром ${{L}_{1}}$-нормы (LASSO hypothesis).
Теорема 2 (LASSO). Пусть задана фиксированная выборка $S = ({{z}_{i}})_{{i = 1}}^{m}$ из $\mathcal{K} \subset {{\mathbb{R}}^{q}}$ размера $m$. Тогда справедлива следующая оценка сверху для ${{\hat {\mathcal{R}}}_{S}}(\mathcal{H})$ из (7):
(8)
${{\hat {\mathcal{R}}}_{S}}(\mathcal{H}) \leqslant \frac{C}{m}\left( {2 + \sqrt {logq} } \right)\sqrt {2\sum\limits_{i = 1}^m {\left\| {{{z}_{i}}} \right\|_{\infty }^{2}} } .$Таким образом, для любой выборки $S = ({{x}_{t}},{{y}_{t}},{{b}_{t}})_{{t = 1}}^{m}$ размера $m = \left| \Omega \right|$ независимых одинаково распределенных элементов $\mathcal{X} \times \mathcal{Y} \times \mathcal{T}$ согласно распределению $\mathcal{D}$ с ограниченным носителем, из анализа выше и оценки (8) следует, что эмпирическая радемахеровская сложность класса гипотез $\mathcal{F}$ задачи SGIMC ограничена сверху выражением
(9)
${{\hat {\mathcal{R}}}_{{{{S}_{\mathcal{Z}}}}}}(\mathcal{F}) \leqslant \tfrac{{{{C}_{U}}{{C}_{V}}}}{m}\left( {2 + \sqrt {log{{d}_{1}}{{d}_{2}}} } \right)\sqrt {2\sum\limits_{t = 1}^m {\left\| {{{A}_{t}}} \right\|_{{max}}^{2}} } ,$Для оценки асимптотики ошибки восстановления в задаче SGIMC воспользуемся оценкой (9) и теоремой 1 и, сделав некотoрое допущение относительно гипотезы $f{\text{*}}$, минимизирующей теоретический риск $R(f)$ по всем $f:A \mapsto \left\langle {A,W} \right\rangle $ и для всевозможных матриц $W \in {{\mathbb{R}}^{{{{d}_{1}} \times {{d}_{2}}}}}$ ранга $k$. Допущение заключается в следующем: рассмотрим задачу минимизации теоретического риска с требованием низкорангового решения для распределения $\mathcal{D}$ с ограничением на носитель ${{\left\| x \right\|}_{\infty }} \leqslant 1$ и ${{\left\| y \right\|}_{\infty }} \leqslant 1$, но без ограничений на нормы факторов $U$ и $V$:
с $U \in {{\mathbb{R}}^{{{{d}_{1}} \times k}}}$, $V \in {{\mathbb{R}}^{{{{d}_{2}} \times k}}}$, где $k$ равен рангу матрицы $M$, – и обозначим парой ${{U}_{ * }}$, ${{V}_{ * }}$ решение задачи (10). Если задача восстановления матрицы реализуема, т.е. минимизирующая пара $({{U}_{ * }},{{V}_{ * }})$ задачи (10) достигает нулевого теоретического риска (с бинарной функцией потерь, или ${{L}_{d}}$), тогда для любой выборки независимых одинаково распределенных случайных величин из $\mathcal{D}$ пара $(\hat {U},\hat {V})$, минимизирующая эмпирический риск, также его обнуляет. Действительно, если пара $(\hat {U},\hat {V})$, зависящая от $S$, является решением задачи (3) с эмпирическим риском вместо теоретического, тогда имеемЕсли рассматривается бинарная функция потерь $\ell $, или липшицева функция потерь с показателем $\rho $, тогда в реализуемом случае задачи индуктивного восстановления матриц с отбором признаков через групповую регуляризацию оценка верхней границы теоретического риска
является результатом следующей теоремы, являющейся основным результатом данного раздела.Теорема 3 (Основной результат). Рассмотрим задачу (3), в которой коэффициенты ${{C}_{U}} = {{\left\| {{{U}_{ * }}} \right\|}_{{2,1}}}$ и ${{C}_{V}} = {{\left\| {{{V}_{ * }}} \right\|}_{{2,1}}}$ определяются решением $({{U}_{ * }},{{V}_{ * }}) \in {{\mathbb{R}}^{{{{d}_{2}} \times k}}} \times {{\mathbb{R}}^{{{{d}_{2}} \times k}}}$ задачи (10). Тогда для любого $\delta > 0$ с вероятностью не ниже $1 - \delta $ справедлива следующая оценка верхней границы теоретического риска для пары $(\hat {U},\hat {V})$, минимизирующей эмпирический риск:
Если предположить, что теоретический риск минимизируется разреженным решением, т.е. некоторые строки матриц ${{U}_{ * }}$ и ${{V}_{ * }}$ полностью нулевые строки, тогда их ${{L}_{{2,1}}}$ нормы можно ограничить
Следствие 1. Если в дополнение к предпосылкам теоремы 3 предположить, что теоретический риск минимизируется разреженным решением (${{U}_{ * }}$ и ${{V}_{ * }}$ имеют не более чем ${{s}_{1}}$ и ${{s}_{2}}$ ненулевых строки), тогда с вероятностью не ниже $1 - \delta $ справедлива следующая оценка верхней границы:
Из асимптотики верхних оценок ошибок восстановления, выведенных выше, можно получить процедуру для решения задачи SGIMC с ограничениями (3), если сформулировать ее как задачу регуляризованной минимизации эмпирического риска для некоторых заданных радиусов ${{C}_{U}}$ и ${{C}_{V}}$. Действительно, если предположить, что пара $(\hat {U},\hat {V})$ решает
Заметим, что в случае разреженных матриц истинных факторов $U$ и $V$ регуляризация с помощью нормы Фробениуса приводит к асимптотике ошибки восстановления вида
4. ПРОЦЕДУРА ВОССТАНОВЛЕНИЯ С ПРОРЕЖИВАНИЕМ
В данном разделе приводится описание итеративной вычислительной процедуры, решающей предложенную задачу индуктивного восстановления матриц с отбором побочных признаков (SGIMC).
Задача индуктивного восстановления матриц с отбором признаков через групповую регуляризацию (SGIMC) для набора данных $({{M}_{\Omega }},X,Y)$ может быть сформулирована в виде следующей оптимизационной задачи: для заданного ранга $k \geqslant 1$ найти такие $U \in {{\mathbb{R}}^{{{{d}_{1}} \times k}}}$ и $V \in {{\mathbb{R}}^{{{{d}_{2}} \times k}}}$, которые доставляют минимум
(11)
$J(U,V) = \sum\limits_{(i,j) \in \Omega } \mathcal{L} ({{M}_{{ij}}},e_{i}^{{\text{т}}}XU{{V}^{{\text{т}}}}{{Y}^{{\text{т}}}}{{e}_{j}}) + {{\lambda }_{U}}{{\left\| U \right\|}_{{2,1}}} + {{\lambda }_{V}}{{\left\| V \right\|}_{{2,1}}},$Норма ${{\left\| U \right\|}_{{2,1}}}$ является групповым регуляризатором матрицы $U$, “мягко” отсекая строки $U$ с низкой ${{L}_{2}}$, тем самым производя отбор побочных признаков, поскольку восстановлениe матрицы $M$ происходит при помощи $XU = \sum\nolimits_{p = 1}^{{{d}_{1}}} {(X{{e}_{p}})} {\kern 1pt} {{({{U}^{{\text{т}}}}{{e}_{p}})}^{{\text{т}}}}$ в (11). Заметим, что приводимая ниже итеративная процедура также позволяет регуляризовать матрицы факторов с помощью нормы Фробениуса и поэлементной ${{L}_{1}}$ нормы для поэлементного разрежения.
Задача (11) является би-выпуклой задачей, т.е. функция $J(U,V)$ выпукла по каждому аргументу в отдельности, но не в совокупности. Естественным методом в данном случае является покоординатный спуск [20] – попеременная циклическая минимизация сначала по $U$ при фиксированной $V$, затем наоборот:
(12)
$\begin{gathered} {{U}_{{t + 1}}} = arg\mathop {min}\limits_{U \in {{\mathbb{R}}^{{{{d}_{1}} \times k}}}} J(U,{{V}_{t}}), \\ {{V}_{{t + 1}}} = arg\mathop {min}\limits_{V \in {{\mathbb{R}}^{{{{d}_{2}} \times k}}}} J({{U}_{{t + 1}}},V), \\ \end{gathered} $Структура функции потерь и регуляризации (11) означаeт, что целевая функция $J$ для набора данных $({{M}_{\Omega }},X,Y)$ совпадает с целевой функцией ${{J}^{{\text{т}}}}$ для $(M_{\Omega }^{{\text{т}}},Y,X)$, в которой роли аргументов $U$ и $V$ поменяны местами (транспонированная задача). Таким образом, частная целевая функция $V \mapsto J(U,V)$ при фиксированном $U$ тождественна $U \mapsto {{J}^{{\text{т}}}}(V,U)$ для транспонированной задачи, что приводит к тому, что достаточно разработать итеративную процедуру для решения $mi{{n}_{U}}J(U,V)$ для данных $({{M}_{\Omega }},X,Y)$ и фиксированного $V$, чтобы получить полную процедуру для покоординатного спуска (12).
Частная задача (11) по $U$ при фиксированном $V$ имеет вид
(13)
$\mathop {min}\limits_{U \in {{\mathbb{R}}^{{{{d}_{1}} \times k}}}} \sum\limits_{(i,j) \in \Omega } \mathcal{L} ({{M}_{{ij}}},{{p}_{{ij}}}) + {{\lambda }_{U}}R(U),$(14)
${{U}_{{t + 1}}} = arg\mathop {min}\limits_U \sum\limits_{\omega \in \Omega } \mathcal{L} ({{M}_{\omega }},{{p}_{\omega }}) + \frac{{{{\lambda }_{R}}}}{2}\left\| U \right\|_{F}^{2} + \frac{1}{{2\eta }}\left\| {U - ({{Z}_{t}} - {{\Phi }_{t}})} \right\|_{F}^{2},$(15)
${{Z}_{{t + 1}}} = arg\mathop {min}\limits_Z {{\lambda }_{U}}{{\left\| Z \right\|}_{{2,1}}} + \frac{1}{{2\eta }}\left\| {Z - ({{U}_{{t + 1}}} + {{\Phi }_{t}})} \right\|_{F}^{2},$4.1. Вычисление шага для $U$
Шаг для $U$, (14), является задачей минимизации гладкой выпуклой функции с квадратичным регуляризатором. Для ${{L}_{2}}$ функции потерь решение этой подзадачи имеет явный вид, выводимый из решения метода наименьших квадратов, а для гладких выпуклых функций потерь более общего вида $\mathcal{L}$, или в условиях нецелесообразности обращения матриц, $U$-шаг решается численно. Аналогичная проблема без специфичного для ADMM квадратичного регуляризатора решается в работе [31] методом сопряженных градиентов с доверительной областью (TRON), предложенного в [32] для решения линейных моделей высокой размерности. Градиент и произведение гессиан-вектор для шага (14) из некоторой точки $U$, которые необходимы для методa сопряженных градиентов, приводятся соответственно в (16) и (17) (см. также [31]):
(16)
${\text{gra}}{{{\text{d}}}_{U}} = {{X}^{{\text{т}}}}GQ + \left( {{{\lambda }_{R}} + \frac{1}{\eta }} \right)U - \frac{1}{\eta }({{Z}_{t}} - {{\Phi }_{t}}),$(17)
$\operatorname{Hess} {{V}_{U}}(D) = {{X}^{{\text{т}}}}(H \odot (XD{{Q}^{{\text{т}}}}))Q + \left( {{{\lambda }_{R}} + \frac{1}{\eta }} \right)D.$В работе [31] предложены ускоренные процедуры для ключевых матричных операций, необходимых для вычисления (16) и (17). Операция $S \mapsto {{X}^{{\text{т}}}}SQ$, происходящая в обоих выражениях, отображает ${{n}_{1}} \times {{n}_{2}}$ разреженную матрицу $S$ с индексами $\Omega $ в плотную матрицу ${{d}_{1}} \times k$, в то время как операция $D \mapsto XD{{Q}^{{\text{т}}}}$ переводит плотную ${{d}_{1}} \times k$ матрицу $D$ в разреженную матрицу размера ${{n}_{1}} \times {{n}_{2}}$ с индексами $\Omega $, т.е. имеющую разреженность, идентичную целевой матрице $M$. Для плотной матрицы $Q$ обе опреации имеют арифметическую сложность порядка $O(k\left| \Omega \right| + k \cdot \operatorname{nnz} (X))$, где $\operatorname{nnz} (X)$ равно ${{n}_{1}}{{d}_{1}}$ при условии плотной матрицы $X$, и количеству ненулевых значений, если $X$ разрежена.
4.2. Решение шага для $Z$
Целевая функция на шаге $Z$ (15) раскладывается на ${{d}_{1}}$ независимых подзадач, по одной на каждую строку матрицы $Z$:
5. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
В данном разделе приводится экспериментальное сравнение предложенного метода индуктивного восстановления матриц с групповым регуляризатором (SGIMC) с методом IMC, предложенным в [31], а также со стандартным методом восстановления матриц (MF), основанного на факторном разложения матриц, при помощи стохастического градиентного спуска. Раздел начинается с численного эксперимента на искусственных данных, нацеленного на изучение эффектов гиперпараметров задачи и ее размерности на качество восстановления матриц. Затем алгоритмы индуктивного восстановления матриц сравниваются в задаче кластеризации и восстановления матриц на реальных наборах данных. Мы не сравниваемся с процедурой IMC из работы [16], по причине того, что существующая реализация этого алгоритма не была работоспособной даже на задачах самой низкой размерности из рассматриваемых.
5.1. Искусственные данные
В экспериментах с искусственными данными мы рассматриваем задачу индуктивного восстановления разреженной ${{n}_{1}} \times {{n}_{2}}$ матрицу $M$, наблюдаемые значения которой находятся по индексам $\Omega $. Качество восстановления метода определяется по наименьшему значению целевой метрики, рассчитанному по значениям элементов матрицы $M$, отсутствующих в ${{M}_{\Omega }}$. Сама целевая метрика равна наименьшей относительной ошибке восстановления ${{{{{\left\| {\hat {M} - M} \right\|}}_{F}}} \mathord{\left/ {\vphantom {{{{{\left\| {\hat {M} - M} \right\|}}_{F}}} {{{{\left\| M \right\|}}_{F}}}}} \right. \kern-0em} {{{{\left\| M \right\|}}_{F}}}}$ с $\hat {M} = X\hat {U}{{\hat {V}}^{{\text{т}}}}{{Y}^{{\text{т}}}}$ по всем значениям коэффициентов регуляризации $\lambda = {{\lambda }_{U}} = {{\lambda }_{V}}$ в задаче (1) из некоторого множества. Задачей данного эксперимента является получение ответа на вопрос, помогает ли встроенный в SGIMC отбор побочных признаков при восстановлении матрицы, а также на вопрос, сравнима ли предложенная процедура с аналогами по качеству в ситуации отсутствия избыточности в побочных признаках. Детали проведенных экспериментов заключаются в следующем: побочные признаки $X$ и $Y$ задаются независимыми случайными гауссовскими матрицами размерности ${{n}_{1}} \times d$ и ${{n}_{2}} \times d$ с распределением $\mathcal{N}(0,\;0.05)$, и значениями ${{n}_{1}} = 800$, ${{n}_{2}} = 1600$ при разных $d$. Истинные значения факторов $U{\text{*}}$ и $V{\text{*}}$ задаются первыми $k = 25$ колонками единичной матрицы размера $d \times d$, создавая тем самым ситуацию, когда истинное число информативных побочных признаков $d{\text{*}}$ совпадает с $k$. Сама целевая матрица равна $M = XU{\text{*}}{{(YV*)}^{{\text{т}}}} + \varepsilon $, где $\varepsilon \sim \mathcal{N}(0,\;0.005)$.
Коэффициенты регуляризации ${{\lambda }_{U}}$ и ${{\lambda }_{V}}$ приравниваются и выбираются из множества ${\text{\{ }}{{10}^{{ - 5}}},{{10}^{{ - 4}}},{{10}^{{ - 3}}},{{10}^{{ - 2}}}{\text{\} }}$. При этом в каждом эксперименте варьируются также следующие параметры:
• предполагаемый ранг $\hat {k}$ матрицы $M$ либо недооценивает (20) истинный ранг $k = 25$, либо переоценивает его (30);
• число избыточных неинформативных побочных признаков равно $d - d* \geqslant 0$;
• показатель разреженности матрицы ${{M}_{\Omega }}$, т.е. доля наблюдаемых значений в ней, выбираются из $\rho = \tfrac{{\left| \Omega \right|}}{{{{n}_{1}}{{n}_{2}}}}$.
5.1.1. Показатель разреженности $\rho $. В данном эксперименте число признаков фиксировано $d = 100$ и предполагаемый ранг матрицы совпадает с истинным рангом $\hat {k} = k$. Показатель разреженности матрицы $\rho $ пробегает значения от $0.0005$ до $0.02$ с шагом $0.0015$. В данной постановке методы IMC и SGMIC достигают почти точного восстановления, когда матрица $M$ достаточно плотная (показатель $\rho > 0.1$). Приведенные на фиг. 1а результаты работы методов в режиме $\rho < 0.01$ показывают, что SGIMC требует меньшего объема наблюдаемых значений в матрице $M$ по сравнению с IMC для достижения сопоставимых ошибок восстановления. В то же самое время переоценка ранга также позволяет получить почти точное восстановление $M$.
Фиг. 1.
Относительная ошибка восстановления в эксперименте с искусственными данными: а – изменение $\rho $ разреженности матрицы ${{M}_{\Omega }}$, б – добавление малоинформативных признаков $d > d{\text{*}}$.
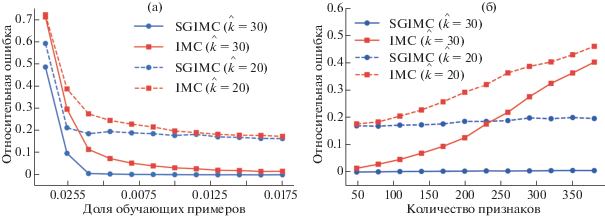
5.1.2. Избыточные признаки. В этом эксперименте показатель $\rho $ зафиксирован на уровне $0.2$ и число побочных признаков $d$ варьируется от $50$ до $400$ с шагом $50$. Добавленные избыточные признаки сверх первых $d{\text{*}}$ являются случайным шумом, значения целевой матрицы от которого не зависят. Это позволяет проверить качество отбора признаков в присутствии полностью неинформативных побочных признаков. Фиг. 1б демонстрирует, что процедура SGIMC отличает информативные признаки от малоинформативных, и показывает систематически хороший результат как в режиме переоценки, так и недооценки ранга.
5.2. Данные из прикладных задач
В этом разделе мы применяем процедуры IMC, SGIMC и MF на реальных наборах данных для того, чтобы сравнить их качества восстановления.
5.2.1. Кластеризация с примерами. Рассмотрим задачу кластеризации через обучение на примерах, или, иными словами, задачу выявления классов эквивалентности между объектами. Имеется матрица $X$ признаков размера $n \times d$ для $n$ сущностей и задача состоит в том, чтобы построить бинарный классификатор, определяющий, принадлежат ли сущности $i$ и $j$ одному и тому же классу или разным классам. Таким образом, исходный набор данных состоит из матрицы $M$ с ${{M}_{{ij}}} = 1$, если $i$ и $j$ принадлежат одному и тому классу, и $ - 1$ в противном случае.
Были выбраны три набора данных из [34] для кластеризации с примерами с помощью индуктивного восстановления матрицы: “Mushrooms”, “Segment” и “Covtype” в табл. 1. Заметим, что по причине сильной несбалансированности набор “Covtype” был предобработан для балансировки классов с помошью случайного сэмплирования из доминирующего класса и полного сохранения класса, находящегося в меньшинстве.
Таблица 1.
Общие характеристики наборов данных для кластеризации с примерами
| Количество | “Mushrooms” | “Segment” | “Covtype” |
|---|---|---|---|
| наблюдений $n$ | 8124 | 2319 | 7370 |
| признаков $d$ | 112 | 18 | 54 |
| классов $K$ | 2 | 7 | 7 |
Ввиду того, что матрица попарной принадлежности $M$ доступна полностью, каждый набор данных случайно разбивается на обучающую и тестовую выборки, причем доля обучающих примеров варьируется от $0.0005$ до $0.02$ из общего числа наблюдений. Качество восстановления матрицы измеряется точностью классификации на тестовой подвыборке.
Эксперименты показывают, что матрицы попарной принадлежности каждого набора данных имеют низкий ранг, и что качество кластеризации существенно зависит от $\hat {k} = 2,\; \ldots ,\;20$. Стратегия выбора оптимального значения коэффициентов регуляризации и усреднения по независимым повторениям эксперимента аналогична п. 13.
Предварительный анализ показывает, что для набора данных “Covtype” исходных побочных признаков недостаточно, чтобы IMC или SGIMC достигли точности выше $0.9$, даже если ранг матрицы переоценен (фиг. 2в). Для того чтобы результаты IMC и SGIMC были сравнимы с результатами MF, к побочным признакам $X$ были добавлены колонки диагональной единичной матрицы, что эквивалентно введению в модель фиктивных переменных (dummy variable), отражающих каждый отдельный объект. Это обогащение побочных признаков переводит методы индуктивного восстановления матриц в область методов трансдуктивного восстановления [14]. На фиг. 2б и 2в результаты обогащения побочных признаков обозначены через SGIMC-comb и IMC-comb.
Фиг. 2.
Точность восстановления в задаче кластеризации с примерами на разных наборах данных: а – “Mushrooms”, б – “Segment”, в – “Covtype”.

В табл. 2 приведены результаты эксперимента на полуискусственных данных, полученных добавлением умышленно малоинформативных данных к побочным признакам набора “Segment”. Точность на тестовой подвыборке явно показывает необходимость отбора и исключения шумных и неинформативных признаков: точность восстановления процедуры IMC [31], которая не производит отбор признаков, ниже чем восстановление с групповым регуляризатором SGIMC.
Таблица 2.
Точность классификации для набора “Segment”
| Дополнительные признаки | SGIMC | IMC |
|---|---|---|
| 0 | $0.901 \pm 0.003$ | $0.895 \pm 0.007$ |
| 50 | $0.885 \pm 0.003$ | $0.839 \pm 0.011$ |
| 100 | $0.880 \pm 0.006$ | $0.822 \pm 0.006$ |
| 200 | $0.869 \pm 0.007$ | $0.795 \pm 0.005$ |
| 300 | $0.871 \pm 0.019$ | $0.769 \pm 0.006$ |
| 400 | $0.851 \pm 0.014$ | $0.754 \pm 0.007$ |
5.2.2. Резистентность и восприимчивость бактерии M. tuberculosis. Данный набор является объединением наборов из работ [35]–[38]. Он состоит из реакций $4734$ штаммов возбудителей туберкулеза Mycobacterium tuberculosis на $13$ существующих антитуберкулезных препаратов. Задача состоит в том, чтобы предсказать реакцию штамма на каждый препарат (резистентность против восприимчивости). Для каждого штамма имеется сопутствующий ему вектор бинарных признаков длины $355\,709$, отвечающих за наличие или отсутствие определенной мутации в геноме бактерии. При этом к каждому препарату также прилагается набор из $28$ бинарных признаков, определяющих наличие специфических химических свойств у препарата. Для задач данного рода крайне важно, чтобы модель была интерпретируемой, что означает необходимость отбора нерелевантных свойств.
Поскольку число восприимчивых штаммов значительно превышает число штаммов, имеющих резистентность, качество восстановления измеряется с помошью метрики ${{F}_{1}}$, рассчитываемой на тестовой части набора. Значения метрики для каждого антибиотика по отдельности и всех в совокупности, представленные в табл. 3, были получены усреднением по десяти случайным разбиениям данных на обучающую и тестовую подвыборки в соотношении 1 : 1.
Таблица 3.
Метрика ${{F}_{1}}$ на наборе данных M. tuberculosis
| Препарат | SGIMC | IMC | Препарат | SGIMC | IMC |
|---|---|---|---|---|---|
| Все препараты | 0.59 | 0.57 | Capreomycin | 0.34 | 0.28 |
| Isoniazid | 0.89 | 0.86 | Amikacin | 0.47 | 0.42 |
| Ethambutol | 0.62 | 0.61 | Moxifloxacin | 0.45 | 0.38 |
| Rifampicin | 0.89 | 0.88 | Kanamycin | 0.40 | 0.40 |
| Pyrazinamide | 0.53 | 0.53 | Prothionamide | 0.52 | 0.52 |
| Streptomycin | 0.84 | 0.85 | Ciprofloxacin | 0.52 | 0.67 |
| Ofloxacin | 0.48 | 0.42 | Ethionamide | 0.50 | 0.47 |
Результаты проведенного эксперимента позволяют заключить, что SGIMC может классифицировать реакцию штаммов на большинство препаратов лучше по ${{F}_{1}}$, чем IMC. При этом IMC использует каждый из $355\,709$ побочных признаков штаммов, что не позволяет получить осмысленную интерпретацию резистентности M. tuberculosis к препаратам, в то время как SGIMC отбирает всего $ \approx {\kern 1pt} 6000$ из них и достигает сопоставимых показателей качества.
6. ЗАКЛЮЧЕНИЕ
В данной работе предлагается новый подход к индуктивному восстановлению матриц, который использует прореживающие регуляризаторы для отбора побочных признаков SGIMC. Эксперименты демонстрируют, что с помощью нового метода можно достичь высокого качествa восстановления матриц как на искусственных наборах данных, так и на данных из прикладных задач. Более того, в условиях наличия большого числа малоинформативных побочных признаков метод и предложенная вычислительная процедура работают лучше, чем аналоги. Теоретический анализ показывает, что регуляризатор ${{L}_{{1,2}}}$, наводящий групповое прореживание, позволяет улучшить асимптотическую верхнюю оценку ошибки восстановления матрицы.
Дальнейшее развитие метода индуктивного восстановления матриц с отбором признаков через групповую регуляризацию SGIMC предлагается совершать в направлении поиска иных паттернов разреженности, нежели чем построчно или по столбцам, которые естественно ожидать, например, в задачах классификации с многими метками. Дальнейшее теоретическое развитие метода может продолжаться в двух потенциальных направлениях. Первое касается разработки процедуры, имеющей глобальные гарантии сходимости, подобные [18], но работающие в условиях функции потерь более общего вида, нежели чем квадратичная, и с негладкими выпуклыми регуляризаторами, которые наводят разреженность и отбирают признаки. Второе направление затрагивает вопрос обобщения результата работы [21] в сторону постановки задачи индуктивного восстановления матриц общего плана для того, чтобы получить общую минимакс оценку границ ошибки восстановления.
Список литературы
Rennie J.D.M., Srebro N. Fast maximum margin matrix factorization for collaborative prediction // Proc. of the 22nd Internat. Conference on Machine Learning. 2005. P. 713–719.
Koren Y., Bell R., Volinsky C. Matrix factorization techniques for recommender systems // Computer. 2009. V. 42. № 8. P. 30–37.
Yi J., Yang T., Jin R., Jain A.K., Mahdavi M. Robust ensemble clustering by matrix completion // 2012 IEEE 12th Internat. Conference on Data Mining (ICDM). 2012. P. 1176–1181.
Argyriou A., Evgeniou T., Pontil M. Convex multi-task feature learning // Machine Learning. 2008. V. 73. № 3. P. 243–272.
Cabral R.S., Torre F., Costeira J.P., Bernardino A. Matrix completion for multi-label image classification // Advances in Neural Information Proc. Systems. 2011. P. 190–198.
Weng Z., Wang X. Low-rank matrix completion for array signal processing // 2012 IEEE Intern. Conference on Acoustics, Speech and Signal Proc. (ICASSP). 2012. P. 2697–2700.
Chen P., Suter D. Recovering the missing components in a large noisy low-rank matrix: Application to SFM // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004. V. 26. № 8. P. 1051–1063.
Candès E.J., Recht B. Exact matrix completion via convex optimization // Foundations of Comput. Math. 2009. V. 9. № 6. P. 717–772.
Candès E.J., Tao T. The power of convex relaxation: Near–optimal matrix completion // IEEE Transactions on Information Theory. 2010. V. 56. № 5. P. 2053–2080.
Shamir O., Shalev-Shwartz S. Matrix completion with the trace norm: learning, bounding, and transducing // J. of Machine Learning Research. 2014. V. 15. № 1. P. 3401–3423.
Hannon J., Bennett M., Smyth B. Recommending twitter users to follow using content and collaborative filtering approaches // Proc. of the Fourth ACM Conference on Recommender Systems. 2010. P. 199–206.
Xu M., Jin R., Zhou Z.-H. Speedup matrix completion with side information: Application to multi-label learning // Advances in Neural Information Proc. Systems. 2013. P. 2301–2309.
Natarajan N., Dhillon I.S. Inductive matrix completion for predicting gene-disease associations // Bioinformatics. 2014. V. 30. № 12. P. i60–i68.
Chiang K.-Y., Hsieh C.-J., Dhillon I.S. Matrix completion with Noisy side information // Proc. of the 28th Internat. Conference on Neural Information Proc. Systems – Vol. 2. 2015. P. 3447–3455.
Si S., Chiang K.-Y., Hsieh C.-J., Rao N., Dhillon I.S. Goal-directed inductive matrix completion // Proc. of the 22nd ACM SIGKDD Intern. Conference on Knowledge Discovery and Data Mining. 2016. P. 1165–1174.
Lu J., Liang G., Sun J., Bi J. A sparse interactive model for matrix completion with side information // Advances in Neural Information Proc. Systems. 2016. P. 4071–4079.
Guo Y. Convex Co-Embedding for Matrix Completion with Predictive Side Information // AAAI. 2017. P. 1955–1961.
Zhang X., Du S., Gu Q. Fast and sample efficient inductive matrix completion via multi-phase procrustes flow // Proc. of the 35th International Conference on Machine Learning. 2018. P. 5756–5765.
Soni A., Chevalier T., Jain S. Noisy inductive matrix completion under sparse factor models // 2017 IEEE Intern. Symposium on Information Theory (ISIT). 2017. P. 2990–2994.
Jain P., Netrapalli P., Sanghavi S. Low-rank matrix completion using alternating minimization // Proc. of the Forty-fifth Annual ACM Symposium on Theory of Computing. 2013. P. 665–674.
Berthet Q., Baldin N. Statistical and computational rates in graph logistic regression // Intern. Conference on Artificial Intelligence and Statistics. 2020. P. 2719–2730.
Bertsekas D.P., Tsitsiklis J.N. Parallel and distributed computation: numerical methods. US: Prentice hall Englewood Cliffs, 1989.
Boyd S., Parikh N., Chu E., Peleato B., Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers // Foundations and Trends in Machine Learning. 2011. V. 3. № 1. P. 1–122.
Maurer A., Pontil M. Structured sparsity and generalization // J. of Machine Learning Research. 2012. V. 13. P. 671–690.
Bartlett P.L., Mendelson S. Rademacher and Gaussian complexities: Risk bounds and structural results // J. of Machine Learning Research. 2002. V. 3. P. 463–482.
Mohri M., Rostamizadeh A., Talwalkar A. Foundations of Machine Learning. US: The MIT Press, 2012.
Glowinski R., Marroco A. Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation–dualité d’une classe de problémes de Dirichlet non linкires // ESAIM: Math. Model. and Numerical Analysis. 1975. V. 9. P. 41–76.
Gabay D., Mercier B. A dual algorithm for the solution of nonlinear variational problems via finite element approximation // Computers & Math. with Applications. 1976. V. 2. № 1. P. 17–40.
Gabay D. Chapter IX Applications of the Method of Multipliers to Variational Inequalities // Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary–Value Problems. 1983. P. 299–331.
Eckstein J., Bertsekas D.P. On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators // Math. Progr. 1992. V. 55. № 1. P. 293–318.
Yu H.-F., Jain P., Kar P., Dhillon I.S. Large-scale multi-label learning with missing labels // Proc. of the 31st Intern. Conference on Machine Learning. 2014. P. 593–601.
Lin C.-J., Weng R.C., Keerthi S.S. Trust region newton method for logistic regression // J. Mach. Learn. Res. 2008. V. 9. P. 627–650.
Simon N., Friedman J., Hastie T., Tibshirani R. A sparse-group Lasso // J. of Computational and Graphical Statistics. 2013. V. 22. № 2. P. 231–245.
Chang C.-C., Lin C.-J. LIBSVM: a library for support vector machines // ACM Transactions on Intelligent Systems and Technology (TIST). 2011. V. 2. № 3. P. 1–27.
Farhat M.R., Shapiro B.J., Kieser K.J., et al. Genomic analysis identifies targets of convergent positive selection in drug-resistant Mycobacterium tuberculosis // Nature Genetics. 2013. V. 45. P. 1183–1189.
Walker T.M., Kohl T.A., Omar S.V., et al. Whole-genome sequencing for prediction of Mycobacterium tuberculosis drug susceptibility and resistance: a retrospective cohort study // The Lancet Infectious Diseases. Appl. 2015. V. 15. № 10. P. 1193–1202.
Pankhurst L.J., Elias C. del O., Votintseva A.A., et al. Rapid, comprehensive, and affordable mycobacterial diagnosis with whole–genome sequencing: a prospective study // The Lancet Respiratory Medicine. 2016. V. 4. № 1. P. 49–58.
Coll F., Phelan J., Hill-Cawthorne G.A., et al. Genome-wide analysis of multi- and extensively drug-resistant Mycobacterium tuberculosis // Nature Genetics. 2018. V. 50. № 2. P. 307–316.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики








