1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 5, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 5, стр. 759-775

Вычисление собственных векторов несимметричных трехдиагональных матриц

П. Ван Дорен 1, *, Т. Лаудадио 2, **, Н. Мастронарди 2, ***

1 Department of Mathematical Engineering, Catholic University of Louvain
Louvain-la-Neuve, Belgium

2 Istituto per le Applicazioni del Calcolo
Bari, Italy

* E-mail: paul.vandooren@uclouvain.be
** E-mail: t.laudadio@cnr.it
*** E-mail: n.mastronardi@cnr.it

Поступила в редакцию 24.11.2020
После доработки 24.11.2020
Принята к публикации 14.01.2021

Полный текст (PDF)

Аннотация

Вычисление собственного разложения матриц является одной из наиболее изученных задач в вычислительной линейной алгебре. В частности, задачи нахождения собственных значений вещественных несимметричных трехдиагональных матриц возникают в самых разных приложениях. В этой статье рассматривается задача вычисления собственного вектора, соответствующего известному собственному значению вещественной несимметричной трехдиагональной матрицы, для чего разрабатывается алгоритм, комбинирующий итерации $QR$- и $QL$-алгоритмов со сдвигами, равными известному собственному значению. Численные эксперименты показывают надежность предложенного метода. Библ. 19. Фиг. 8. Табл. 2.

Ключевые слова: несимметричные трехдиагональные матрицы, собственные вектора, матрицы Бесселя.

1. ВВЕДЕНИЕ

Задачи нахождения собственных значений вещественных несимметричных трехдиагональных матриц возникают в самых разных приложениях. Например, несимметричная задача на собственные значения может быть сведена к несимметричной трехдиагональной форме за конечное число шагов [1]–[3]. В разреженном случае несимметричный алгоритм Ланцоша производит несимметричную трехдиагональную матрицу с помощью процесса биортогонализации Ланцоша [4]. Нули обобщенных полиномов Бесселя могут быть вычислены как собственные значения соответствующих матриц Бесселя, которые являются несимметричными трехдиагональными [5], [6]. Другие задачи на собственные значения, включая несимметричные трехдиагональные матрицы, могут быть найдены в [7].

Некоторые  методы  вычисления  собственных  значений несимметричных трехдиагональных матриц известны в литературе. Метод, описанный в [7], требует вычисления $p(\lambda ){\text{/}}p{\text{'}}{\kern 1pt} (\lambda ) = - 1{\text{/}}\operatorname{tr} ({{(T - \lambda I)}^{{ - 1}}})$, где $p(\lambda )$ является характеристическим полиномом матрицы $T$, что и делается с использованием $QR$-разложения $T - \lambda I$ и семисепарабельной структуры ${{(T - \lambda I)}^{{ - 1}}}$. Алгоритм, описанный в [8], основывается на $LR$-методе [9]. Неявный $QR$-метод [10], [11] также может быть использован для вычисления собственной структуры трехдиагональной матрицы. Но, к сожалению, он не использует трехдиагональную структуру задачи, и, таким образом, сложность кубически зависит от размера матрицы. Эта работа фокусируется на вычислении собственных векторов трехдиагональных матриц в случае, когда соответствующие собственные значения известны.

Хорошо известно, что в точной арифметике после одной итерации $QR$ $(QL)$-метода со сдвигом, равным собственному значению, это собственное значение возникает в нижнем правом (верхнем левом) углу матрицы и может быть отброшено [12]. К сожалению, оба метода могут страдать от прямой неустойчивости при работе в арифметике конечной точности [13], [14]. Для того, чтобы избежать явления неустойчивости, мы комбинируем итерации $QR$- и $QL$-методов со сдвигами, равными собственному значению $\lambda $.

В этой работе мы фокусируемся на вычислении левого собственного вектора, ассоциированного с известным собственным значением несимметричной трехдиагональной матрицы. Для краткости мы опускаем описание алгоритма вычисления правого собственного вектора, поскольку эта задача полностью аналогична. Численные примеры показывают надежность предложенного подхода.

Текст организован следующим образом. В разд. 2 приведены обозначения и базовые определения. В разд. 3 выделены основные особенности $QR$-метода. Предложенный алгоритм описан в разд. 4. В разд. 5 показано, как избежать комплексной арифметики в случае комплексно-сопряженных собственных значений. В разд. 6 мы приводим ряд численных примеров и завершаем статью разделом с заключительными замечаниями.

2. ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ

Матрицы обозначены с помощью заглавных букв, а их элементы с помощью строчных, т.е. элемент $(i,j)$ матрицы $T$ обозначен как ${{t}_{{i,j}}}$.

Подматрица матрицы $B$, взятая на строках $i,\;i + 1,\;i + 2,\; \ldots ,\;i + k$, где $1 \leqslant i \leqslant i + k \leqslant n$, и столбцах $j,\;j + 1,\;j + 2,\; \ldots ,\;j + \ell $, где $1 \leqslant j \leqslant j + \ell \leqslant n$, обозначена через ${{B}_{{i:i + k,j:j + \ell }}}$.

Единичная матрица порядка $n$ обозначена через ${{I}_{n}}$ или $I$, если это не вызывает неоднозначности. Матрица $T - \varkappa I$, где $\varkappa \in \mathbb{R}$, обозначена через $T(\varkappa )$.

Главная диагональ матрицы $B \in {{\mathbb{R}}^{{m \times n}}}$ обозначена через $\operatorname{diag} (B)$, а $i$-й вектор канонического базиса ${{\mathbb{R}}^{n}}$ обозначен через ${\mathbf{e}}_{i}^{{(n)}}$ или просто ${{{\mathbf{e}}}_{i}}$, если это не вызывает неоднозначности. Машинная точность обозначена через ${{\varepsilon }_{M}}$.

Определение 1. Столбцы $B \in {{\mathbb{R}}^{{m \times n}}}$, $m \geqslant n$, называются $\varepsilon $-линейно зависимыми, если ${{\sigma }_{n}}(B) \leqslant \varepsilon {{\left\| B \right\|}_{2}}$, где ${{\sigma }_{n}}(B)$ есть $n$-е сингулярное число $B,$ а $\varepsilon $ – произвольная точность.

3. ВЫЧИСЛЕНИЕ СОБСТВЕННОГО ВЕКТОРА С ПОМОЩЬЮ $QR$ И $QL$-МЕТОДОВ

Пусть $T \in {{\mathbb{R}}^{{n \times n}}}$ – неприводимая несимметричная трехдиагональная матрица

$T = \left[ {\begin{array}{*{20}{c}} {{{\alpha }_{1}}}&{{{\gamma }_{1}}}&{}&{} \\ {{{\beta }_{1}}}&{{{\alpha }_{2}}}& \ddots &{} \\ {}& \ddots & \ddots &{{{\gamma }_{{n - 1}}}} \\ {}&{}&{{{\beta }_{{n - 1}}}}&{{{\alpha }_{n}}} \end{array}} \right],$
т.е. ${{\beta }_{i}} \ne 0$, ${{\gamma }_{i}} \ne 0$, $i = 1,\; \ldots ,\;n - 1$, и пусть ${{\lambda }_{i}}$ ($i = 1,\; \ldots ,\;n$) – ее собственные значения. Поскольку $T$ – неприводимая, геометрическая кратность ее собственных значений равна $1$.

Сначала мы опишем, как левый собственный вектор ${\mathbf{y}}$, соответствующий собственному значению $\lambda $ матрицы $T$, может быть получен применением одной итерации $QR$- или $QL$-методов со сдвигом $\lambda $. К сожалению, оба метода могут страдать от прямой неустойчивости при работе в арифметике конечной точности. Далее мы анализируем причины такого поведения, а затем предлагаем алгоритм, основанный на подходящей комбинации вышеупомянутых методов, для преодоления явления неустойчивости.

3.1. $QR$-метод

Пусть $\varkappa \in \mathbb{C}$. Пусть $\hat {Q}\hat {R}$ является $QR$-разложением $T(\varkappa )$, где

$\hat {R} = \left[ {\begin{array}{*{20}{c}} {\mathop {\hat {\rho }}\nolimits_1 }&{\mathop {\hat {\gamma }}\nolimits_1 }&{\mathop {\hat {\beta }}\nolimits_1 }&{}&{} \\ {}&{\mathop {\hat {\rho }}\nolimits_2 }&{\mathop {\hat {\gamma }}\nolimits_2 }& \ddots &{} \\ {}&{}& \ddots & \ddots &{\mathop {\hat {\beta }}\nolimits_{n - 2} } \\ {}&{}&{}&{\mathop {\hat {\rho }}\nolimits_{n - 1} }&{\mathop {\hat {\gamma }}\nolimits_{n - 1} } \\ {}&{}&{}&{}&{\mathop {\hat {\rho }}\nolimits_n } \end{array}} \right],$
и $\hat {Q} = \hat {G}_{{n - 1}}^{H}\hat {G}_{{n - 2}}^{H}\; \cdots \;\hat {G}_{1}^{H}$, где ${{\hat {G}}_{i}}$ – вращения Гивенса:
${{\hat {G}}_{i}} = \left[ {\begin{array}{*{20}{c}} {{{I}_{{i - 1}}}}&{}&{}&{} \\ {}&{{{c}_{i}}}&{{{s}_{i}}}&{} \\ {}&{ - \mathop {\bar {s}}\nolimits_i }&{{{c}_{i}}}&{} \\ {}&{}&{}&{{{I}_{{n - i - 1}}}} \end{array}} \right],\quad c_{i}^{2} + {{\left| {{{s}_{i}}} \right|}^{2}} = 1,\quad i = 1,\; \ldots ,\;n - 1.$
Коэффициенты ${{c}_{i}}$, $i = 1,\; \ldots ,\;n - 1$, вращений Гивенса вещественны [12, с. 243]. Следовательно, $\hat {Q}$ является унитарной верхней хессенберговой матрицей:
$\hat {Q} = \left[ {\begin{array}{*{20}{c}} {{{c}_{1}}}&{ - {{s}_{1}}{{c}_{2}}}&{{{s}_{1}}{{s}_{2}}{{c}_{3}}}& \ddots &{{{{( - 1)}}^{{n - 2}}}{{c}_{{n - 1}}}\prod\limits_{i = 1}^{n - 2} {{{s}_{i}}} }&{{{{( - 1)}}^{{n - 1}}}\prod\limits_{i = 1}^{n - 1} {{{s}_{i}}} } \\ {\mathop {\bar {s}}\nolimits_1 }&{{{c}_{1}}{{c}_{2}}}&{ - {{c}_{1}}{{s}_{2}}{{c}_{3}}}& \ddots &{{{{( - 1)}}^{{n - 3}}}{{c}_{1}}{{c}_{{n - 1}}}\prod\limits_{i = 2}^{n - 2} {{{s}_{i}}} }&{{{{( - 1)}}^{{n - 2}}}{{c}_{1}}\prod\limits_{i = 2}^{n - 1} {{{s}_{i}}} } \\ {}&{\mathop {\bar {s}}\nolimits_2 }&{{{c}_{2}}{{c}_{3}}}& \ddots & \vdots & \vdots \\ {}&{}& \ddots & \ddots &{ - {{c}_{{n - 3}}}{{s}_{{n - 2}}}{{c}_{{n - 1}}}}&{{{c}_{{n - 3}}}{{s}_{{n - 2}}}{{s}_{{n - 1}}}} \\ {}&{}&{}&{{{{\bar {s}}}_{{n - 2}}}}&{{{c}_{{n - 2}}}{{c}_{{n - 1}}}}&{ - {{c}_{{n - 2}}}{{s}_{{n - 1}}}} \\ {}&{}&{}&{}&{{{{\bar {s}}}_{{n - 1}}}}&{{{c}_{{n - 1}}}} \end{array}} \right].$
В точной арифметике, если $\varkappa \equiv {{\lambda }_{i}}$, $i \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$, то оказывается, что ${{\hat {\rho }}_{n}} = 0$ и
(1)
${{{\mathbf{y}}}_{i}} \equiv \hat {Q}(:,n)$
является левым собственным вектором, соответствующим $\varkappa $.

Как было отмечено выше, в арифметике конечной точности может возникнуть прямая неустойчивость при $QR$-разложении $T({{\lambda }_{i}})$, и последний столбец $\hat {Q}$ может оказаться далек от искомого собственного вектора [13], [15].

В частности, если определить ${{\hat {R}}^{{(0)}}}({{\lambda }_{i}}) = T - {{\lambda }_{i}}{{I}_{n}}$, ${{\hat {R}}^{{(i)}}}({{\lambda }_{i}}) = {{\hat {G}}_{i}}{{\hat {R}}^{{(i - 1)}}}(\varkappa )$, $i = 1,\; \ldots ,\;n - 1$, прямая неустойчивость возникнет на $j$-м шаге $QR$-факторизации тогда и только тогда, когда $\hat {R}_{{1:j + 1,1:j + 1}}^{{(j)}}(\varkappa )$ близка к вырожденной и ${{c}_{j}}$ пренебрежимо мало. Это явление уже было описано в [13] для симметричного случая.

3.2. $QL$-метод

Пусть $\tilde {Q}\tilde {L} = T - \varkappa {{I}_{n}}$ является $QL$-разложением $T(\varkappa )$, полученным применением последовательности вращений Гивенса:

${{\tilde {G}}_{i}} = \left[ {\begin{array}{*{20}{c}} {{{I}_{{n - i - 1}}}}&{}&{}&{} \\ {}&{{{g}_{i}}}&{{{h}_{i}}}&{} \\ {}&{ - {{{\bar {h}}}_{i}}}&{{{g}_{i}}}&{} \\ {}&{}&{}&{{{I}_{{i - 1}}}} \end{array}} \right],\quad g_{i}^{2} + {{\left| {{{h}_{i}}} \right|}^{2}} = 1,\quad i = 1,\; \ldots ,n - 1.$
Оказывается, что
$\tilde {L} = \left[ {\begin{array}{*{20}{c}} {\mathop {\tilde {\rho }}\nolimits_1 }&{}&{}&{}&{} \\ {\mathop {\tilde {\gamma }}\nolimits_1 }&{\mathop {\tilde {\rho }}\nolimits_2 }&{}&{}&{} \\ {\mathop {\tilde {\beta }}\nolimits_1 }&{\mathop {\tilde {\gamma }}\nolimits_2 }& \ddots &{}&{} \\ {}& \ddots & \ddots &{\mathop {\tilde {\rho }}\nolimits_{n - 1} }&{} \\ {}&{}&{\mathop {\tilde {\beta }}\nolimits_{n - 2} }&{\mathop {\tilde {\gamma }}\nolimits_{n - 1} }&{\mathop {\tilde {\rho }}\nolimits_n } \end{array}} \right]$
и $\tilde {Q} = \tilde {G}_{{n - 1}}^{H}\tilde {G}H_{{n - 2}}^{{}}\; \cdots \;\tilde {G}_{1}^{H}$ является нижней хессенберговой матрицей:
$\tilde {Q} = \left[ {\begin{array}{*{20}{c}} {{{g}_{{n - 1}}}}&{{{{\bar {h}}}_{{}}}n - 1}&{}&{}&{}&{} \\ { - {{g}_{{n - 2}}}{{h}_{{n - 1}}}}&{{{g}_{{n - 2}}}{{g}_{{n - 1}}}}&{\mathop {\bar {h}}\nolimits_{n - 2} }&{}&{}&{} \\ {{{g}_{{n - 3}}}{{h}_{{n - 2}}}{{h}_{{n - 1}}}}&{ - {{g}_{{n - 3}}}{{h}_{{n - 2}}}{{g}_{{n - 1}}}}& \ddots & \ddots &{}&{} \\ \vdots & \vdots & \ddots &{{{g}_{3}}{{g}_{2}}}&{\mathop {\bar {h}}\nolimits_2 }&{} \\ {{{{( - 1)}}^{{n - 2}}}{{g}_{1}}\prod\limits_{i = 2}^{n - 1} {{{h}_{i}}} }&{{{{( - 1)}}^{{n - 3}}}{{g}_{1}}{{g}_{{n - 1}}}\prod\limits_{i = 2}^{n - 2} {{{h}_{i}}} }& \ddots &{ - {{g}_{3}}{{h}_{2}}{{g}_{1}}}&{{{g}_{2}}{{g}_{1}}}&{\mathop {\bar {h}}\nolimits_1 } \\ {{{{( - 1)}}^{{n - 1}}}\prod\limits_{i = 1}^{n - 1} {{{h}_{i}}} }&{{{{( - 1)}}^{{n - 2}}}{{g}_{{n - 1}}}\prod\limits_{i = 1}^{n - 2} {{{h}_{i}}} }& \ddots &{{{g}_{3}}{{h}_{2}}{{h}_{1}}}&{ - {{g}_{2}}{{h}_{1}}}&{{{g}_{1}}} \end{array}} \right].$
В точной арифметике, если $\varkappa \equiv {{\lambda }_{i}}$, $i \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$, то $\mathop {\tilde {\rho }}\nolimits_1 = 0$ и
(2)
${{{\mathbf{y}}}_{i}} \equiv \tilde {Q}(:,1)$
является левым собственным вектором, соответствующим ${{\lambda }_{i}}$.

В этом случае также может возникнуть прямая неустойчивость, и первый столбец $\tilde {Q}$ может быть отличным от искомого собственного вектора.

В частности, если определить ${{\tilde {L}}^{{(0)}}}({{\lambda }_{i}}) = T({{\lambda }_{i}})$, ${{\tilde {L}}^{{(i)}}}({{\lambda }_{i}}) = {{\tilde {G}}_{i}}{{\tilde {L}}^{{(i - 1)}}}({{\lambda }_{i}})$, $i = 1,\; \ldots ,\;n - 1$, прямая неустойчивость возникнет на $j$-м шаге при $QL$-разложении тогда и только тогда, когда $\tilde {L}_{{n - j:n,n - j:n}}^{{(j)}}(\varkappa )$ очень близка к вырожденной, и первый элемент собственного вектора, соответствующего наименьшему собственному значению, мал [13]. Из уравнения (2) этот элемент задается ${{g}_{j}}$. Таким образом, прямая неустойчивость возникает, если $\tilde {L}(j)_{{n - j:n,n - j:n}}^{{}}({{\lambda }_{i}})$ близка к вырожденной и ${{g}_{j}}$ пренебрежимо мал.

Чтобы выяснить, на каком шаге $QR$- и $QL$-методов возникает прямая неустойчивость, рассмотрим.

Следствие 1 (см. [16, с. 149]). Пусть $A \in {{\mathbb{C}}^{{m \times n}}}$ и пусть $B$ является ее подматрицей, полученной удалением $r$ столбцов из $A$. Тогда

(3)
${{\sigma }_{k}}(A) \geqslant {{\sigma }_{k}}(B) \geqslant {{\sigma }_{{k + r}}}(A),\quad k = 1,\; \ldots ,\;min{\text{\{ }}m,n{\text{\} }},$
где ${{\sigma }_{\ell }}(A) \equiv 0$ при $\ell > min{\text{\{ }}m,n{\text{\} }}$.

Пусть $\lambda $ – собственное значение $T$. Обозначим сингулярные числа $\hat {R}_{{1:i + 1,:}}^{{(i)}}(\lambda )$ как ${{\sigma }_{j}}(\hat {R}_{{1:i + 1,:}}^{{(i)}}(\lambda ))$, $j = 1,\; \ldots ,\;i + 1$, а сингулярные числа $\tilde {L}_{{n - i:n,:}}^{{(i)}}(\lambda )$ как ${{\sigma }_{j}}(\tilde {L}_{{n - i:n,:}}^{{(i)}}(\lambda ))$, $j = 1,\; \ldots ,\;i + 1$, при $i = 1,\; \ldots ,\;n - 1$ соответственно. Из следствия 1 имеем

$\begin{gathered} {{\sigma }_{{i + 1}}}(\hat {R}_{{1:i + 1,:}}^{{(i)}}(\lambda )) \geqslant {{\sigma }_{{i + 2}}}(\hat {R}_{{1:i + 2,:}}^{{(i + 1)}}(\lambda )), \\ {{\sigma }_{{i + 1}}}(\tilde {L}_{{n - i:n,:}}^{{(i)}}(\lambda )) \geqslant {{\sigma }_{{i + 2}}}(\tilde {L}_{{n - i - 1:n,:}}^{{(i + 1)}}(\lambda )),\quad i = 1,\; \ldots ,\;n - 2. \\ \end{gathered} $

Предположим, что ${{\sigma }_{{n - 1}}}(T(\lambda )) \gg \varepsilon > {{\sigma }_{n}}(T(\lambda )) = 0$.

Следующая лемма показывает, что матрицы $\hat {R}_{{1:j + 1,:}}^{{(j)}}(\lambda )$ и $\tilde {L}_{{j + 2:n,:}}^{{(n - j - 2)}}(\lambda )$ не могут одновременно иметь сингулярные числа меньше $\varepsilon $.

Лемма 1. Пусть ${{k}_{1}},{{k}_{2}} \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$, ${{k}_{1}} \ne {{k}_{2}}$, и

$\Delta = T(\lambda )[\begin{array}{*{20}{c}} {{{{\mathbf{e}}}_{{{{k}_{1}}}}}}&{{{{\mathbf{e}}}_{{{{k}_{2}}}}}} \end{array}].$
Тогда
(4)
${{\left\| \Delta \right\|}_{F}} \geqslant {{\left\| \Delta \right\|}_{2}} \geqslant {{\sigma }_{{n - 1}}}(T(\lambda )),$
где ${{\sigma }_{{n - 1}}}(T(\lambda ))$ является $(n - 1)$-м сингулярным числом $T(\lambda )$.

Доказательство. Из (3) мы имеем, что

${{\sigma }_{1}}(\Delta ) = {{\left\| \Delta \right\|}_{2}} \geqslant {{\sigma }_{{n - 1}}}(T(\lambda )),$
где ${{\sigma }_{1}}(\Delta )$ – максимальное сингулярное число $\Delta $, откуда следует (4).

Рассмотрим для каждого $j$ факторизацию $T(\lambda )$:

$T(\lambda ) = \left[ {\begin{array}{*{20}{c}} {{{{\hat {Q}}}^{{(j)}}}}&\vline & {} \\ \hline {}&\vline & {{{{\tilde {Q}}}^{{(n - j - 2)}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\hat {R}_{{1:j + 1,:}}^{{(j)}}(\lambda )} \\ \hline {\tilde {L}_{{j + 2:n,:}}^{{(n - j - 2)}}(\lambda )} \end{array}} \right],$
где ${{\hat {Q}}^{{(j)}}} = \hat {G}j_{{}}^{H}\hat {G}_{{j - 1}}^{H}\; \cdots \;\hat {G}_{1}^{H}$ и ${{\tilde {Q}}^{{(n - j - 2)}}} = \tilde {G}_{{n - j - 2}}^{H}\tilde {G}_{{n - j - 3}}^{H}\; \cdots \;\tilde {G}_{2}^{H}\tilde {G}_{1}^{H}$. Из леммы 1 следует, что только одна из $2$ подматриц может быть $\varepsilon $-зависима при $\varepsilon \leqslant {{\sigma }_{{n - 1}}}(T(\lambda ))$.

Обозначим ${{\hat {\sigma }}_{i}} = {{\sigma }_{i}}(\hat {R}_{{1:i,:}}^{{(i - 1)}}(\lambda ))$ и ${{\tilde {\sigma }}_{i}} = {{\sigma }_{{n - i + 1}}}(L_{{i:n,:}}^{{(n - i)}}(\lambda ))$, $i = 1,\; \ldots ,\;n$.

Лемма 2. Последовательность

${\text{\{ }}max({{\hat {\sigma }}_{i}},{{\tilde {\sigma }}_{i}}){\text{\} }}_{{i = 1}}^{n} = {\text{\{ }}{{\hat {\sigma }}_{1}},\; \ldots ,\;\mathop {\hat {\sigma }}\nolimits_{j - 1} ,max({{\hat {\sigma }}_{j}},{{\tilde {\sigma }}_{j}}),{{\tilde {\sigma }}_{{j + 1}}},\; \ldots ,\;{{\tilde {\sigma }}_{n}}{\text{\} }}$
унимодальна и имеет минимальное значение, равное $max({{\hat {\sigma }}_{j}},{{\tilde {\sigma }}_{j}})$ при некотором $j \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$. Более того, только один элемент последовательности может быть меньше ${{\sigma }_{{n - 1}}}(T(\lambda ))$.

Тогда из анализа возмущений при $QR$-разложении следует [17], что прямая неустойчивость при вычислении $\hat {Q}$ и, следовательно, косинусов ${{c}_{i}}$ не возникает на первых $j - 1$ шагах $QR$-разложения, а прямая неустойчивость при вычислении $\tilde {Q}$ не возникает на первых $n - j - 1$ шагах $QL$-факторизации, и, следовательно, для косинусов ${{g}_{i}}$. Для того, чтобы выбрать подходящий индекс $j$, можно воспользоваться последовательностями ${\text{\{ }}{{c}_{j}}{\text{\} }}_{{j = 1}}^{{n - 1}}$ и ${\text{\{ }}{{g}_{j}}{\text{\} }}_{{j = 1}}^{{n - 1}}$, как показано в следующих примерах.

Пример 1. Пусть $T \in {{\mathbb{R}}^{{n \times n}}}$, $n = 100$, является несимметричной неприводимой трехдиагональной матрицей, чьи элементы порождены функцией $randn$ из $MATLAB$, и пусть $\lambda $ является собственным значением $T$. Пусть $(\lambda ,{\mathbf{y}})$ является левой собственной парой $T$, полученной применением нескольких шагов метода обратных итераций к соответствующей паре, полученной функцией $eig$ из $MATLAB$. Заметим, что для таких матриц поведение, которое мы собираемся описать, наблюдается для всех собственных значений.

Последовательность косинусов $\left\{ {{{c}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$, порожденная $QR$-методом со сдвигом, равным $\lambda $ (обозначено “$ * $”), последовательность ${\text{\{ }}{{\hat {\sigma }}_{i}}{\text{\} }}_{{i = 1}}^{n}$ (обозначено “$\triangledown $”), модули элементов левого собственного вектора ${\mathbf{y}}$, соответствующего $\lambda $ (обозначено “$\diamond$”), и модули элементов последнего столбца $\hat {Q}$ (обозначено “$ + $”) изображены на фиг. 1 в логарифмическом масштабе.

Фиг. 1.

Пример 1: график $\left\{ {{{c}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$ (“$ * $”), $\left\{ {{{{\hat {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ (“$\triangledown $”), модули элементов левого собственного вектора ${\mathbf{y}}$, соответствующего $\lambda $ (“$\diamond$”), и модули элементов последнего столбца $\hat {Q}$ (“$ + $”), вычисленные на одной итерации $QR$-метода, примененного к $T(\lambda )$.

Последовательность косинусов ${\text{\{ }}{{g}_{i}}{\text{\} }}_{{i = 1}}^{{n - 1}}$, порожденная $QL$-методом со сдвигом, равным $\lambda $ (обозначено “$ * $”), последовательность $\left\{ {{{{\tilde {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ (обозначено “$\triangledown $”), модули элементов левого собственного вектора ${\mathbf{y}}$, соответствующего $\lambda $ (обозначено “$\diamond$”), и модули элементов первого столбца $\tilde {Q}$ (обозначено “$ + $”) изображены на фиг. 2 в логарифмическом масштабе.

Фиг. 2.

Пример 1: график $\left\{ {{{g}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$ (“$ * $”), ${\text{\{ }}{{\tilde {\sigma }}_{i}}{\text{\} }}_{{i = 1}}^{n}$ (“$\triangledown $”), модули элементов левого собственного вектора ${\mathbf{y}}$, соответствующего $\lambda $ (“$\diamond$”), и модули элементов первого столбца $\tilde {Q}$ (“$ + $”), вычисленные на одной итерации $QL$-метода, примененного к $T(\lambda )$.

На фиг. 1 можно видеть, что элементы последовательности ${\text{\{ }}{{c}_{i}}{\text{\} }}_{{i = 1}}^{{n - 1}}$ имеют поведение, похожее на элементы последовательности ${\text{\{ }}{{\hat {\sigma }}_{i}}{\text{\} }}_{{i = 1}}^{n}$ до тех пор, пока значение больше $\sqrt {{{\varepsilon }_{M}}} $. Затем возникает прямая неустойчивость, и оставшаяся часть элементов первой последовательности расходится с элементами второй. Аналогично, модули элементов последнего столбца $\hat {Q}$ соответствуют элементам ${\mathbf{y}}$ до тех пор, пока не возникает прямая неустойчивость.

С другой стороны, фиг. 2 показывает, что последние элементы последовательностей $\left\{ {{{g}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$ и $\left\{ {{{{\tilde {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ имеют похожее поведение до тех пор, пока элементы первой последовательности больше $\sqrt {{{\varepsilon }_{M}}} $. Это явление также описано в [13] для симметричных трехдиагональных матриц. Элементы ${\mathbf{y}}$ и первый столбец $\tilde {Q}$ также имеют похожее поведение.

Покомпонентные ошибки $\left| {{\mathbf{y}} - \hat {Q}(:,n)} \right|$ (обозначено “$ \times $”) и $\left| {{\mathbf{y}} - \tilde {Q}(:,1)} \right|$ (обозначено “$ + $”), последовательности ${\text{\{ }}{{\hat {\sigma }}_{i}}{\text{\} }}_{{i = 1}}^{n}$ (обозначено “$\diamond$”), $\left\{ {{{{\tilde {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ (обозначено “$\bigcirc $”), $\left\{ {{{c}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$ (обозначено “$\bigcirc $”) и $\left\{ {{{g}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$ (“$ * $”), и машинная точность ${{\varepsilon }_{M}}$ (обозначено синей линией) изображены в логарифмическом масштабе на фиг. 3.

Фиг. 3.

Пример 1: график $\left| {{\mathbf{y}} - \hat {Q}(:,n)} \right|$ (“$ \times $”), $\left| {{\mathbf{y}} - \tilde {Q}(:,1)} \right|$ (“$ + $”), ${\text{\{ }}{{\hat {\sigma }}_{i}}{\text{\} }}_{{i = 1}}^{n}$ (“$\diamond$”), ${\text{\{ }}{{\tilde {\sigma }}_{i}}{\text{\} }}_{{i = 1}}^{n}$ (“$\triangledown $”), ${\text{\{ }}{{c}_{i}}{\text{\} }}_{{i = 1}}^{{n - 1}}$ (“$\bigcirc $”) и ${\text{\{ }}{{g}_{i}}{\text{\} }}_{{i = 1}}^{{n - 1}}$ (“$ * $”), машинной точности ${{\varepsilon }_{M}}$ (синия линия) в логарифмическом масштабе.

Можно видеть, что покомпонентные ошибки $\left| {{\mathbf{y}} - \hat {Q}(:,1)} \right|$ всегда меньше ${{\varepsilon }_{M}}$ до $30$ позиции, в то время как $\left| {{\mathbf{y}} - \tilde {Q}(:,1)} \right|$ всегда меньше ${{\varepsilon }_{M}}$ после $30$ позиции, как и предсказано леммой 1.

Следовательно, для всех ${{\lambda }_{i}}$ существует индекс $j$ такой, что

$\begin{gathered} \left| {{{{\mathbf{y}}}_{k}} - \hat {Q}(k,1)} \right| \leqslant {v} \cdot {{\varepsilon }_{M}},\quad 1 \leqslant k \leqslant j, \\ \left| {{{{\mathbf{y}}}_{k}} - \tilde {Q}(k,1)} \right| \leqslant {v} \cdot {{\varepsilon }_{M}},\quad j + 1 \leqslant k \leqslant n, \\ \end{gathered} $
где ${v} \sim O(n)$.

Подводя итог, элементы последнего столбца $\hat {Q}$ вычисляются точно в верхней части до тех пор, пока не возникает прямая неустойчивость на $QR$-итерации, т.е. до тех пор, пока не появится индекс $j \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$ такой, что ${{T}_{{1:j,:}}}$ имеет почти линейно зависимые столбцы. С другой стороны, прямая неустойчивость во время $QL$-итерации может возникнуть только после $n - j - 1$ шагов, и элементы первого столбца $\tilde {Q}$ вычисляются точно в нижней части. Таким образом, важно правильно определить индекс $j$.

Замечание 1. Заметим, что в то время как последовательности $\left\{ {{{{\hat {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ и $\left\{ {{{{\tilde {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ монотонны, последовательности $\left\{ {{{c}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$ и $\left\{ {{{g}_{i}}} \right\}_{{i = 1}}^{{n - 1}}$ монотонными не являются. Однако в следующем разделе мы покажем, как найти подходящий индекс $j$ по элементам этих последовательностей.

4. КОМБИНИРОВАНИЕ $QR$ И $QL$-МЕТОДОВ ДЛЯ ВЫЧИСЛЕНИЯ СОБСТВЕННОГО ВЕКТОРА

В этом разделе описан метод нахождения индекса $j$, используемого для построения искомого собственного вектора при помощи вычисления первых $j$ элементов последнего столбца $\hat {Q}$ и последних $n - j$ элементов первой строки $\tilde {Q}.$

Пусть $\left\{ {{{{\hat {c}}}_{i}}} \right\}_{{i = 1}}^{n}$ и $\left\{ {{{{\tilde {g}}}_{i}}} \right\}_{{i = 1}}^{n}$ являются, соответственно, последовательностями коэффициентов вращений Гивенса, необходимых для вычисления $QR$ и $QL$-разложений матрицы $T(\lambda )$ в точной арифметике.

Если ${{\sigma }_{{n - 1}}}(T(\lambda )) \gg {{\sigma }_{n}}(T(\lambda ))$ и прямая неустойчивость возникла на $j$-м шаге $QR$-метода со сдвигом $\lambda $, то последовательность $\left\{ {{{c}_{i}}} \right\}_{{i = 1}}^{n}$ начинает расходиться с последовательностью $\left\{ {{{{\hat {c}}}_{i}}} \right\}_{{i = 1}}^{n}$ в окрестности индекса $j$. Как следствие, последний столбец $\hat {Q}$ соответствует ${\mathbf{y}}$ в первых $j$ элементах.

Аналогично, последовательность $\left\{ {{{g}_{i}}} \right\}_{{i = 1}}^{n}$ начинает расходиться с последовательностью $\left\{ {{{{\tilde {g}}}_{i}}} \right\}_{{i = 1}}^{n}$ в окрестности индекса $n - j$, и последние $n - j$ элементов первого столбца $\tilde {Q}$ совпадают с соответствующими элементами ${\mathbf{y}}$.

Следовательно, искомый индекс $j$ может быть вычислен следующим образом.

Положим ${{i}_{1}} = 1$, ${{i}_{2}} = n$, $R = T(\lambda )$, $L = T(\lambda )$ и вычислим вращения Гивенса

${{\hat {G}}_{{{{i}_{1}}}}} = \left[ {\begin{array}{*{20}{c}} {{{I}_{{{{i}_{1}} - 1}}}}&{}&{}&{} \\ {}&{{{c}_{{{{i}_{1}}}}}}&{{{s}_{{{{i}_{1}}}}}}&{} \\ {}&{ - {{s}_{{{{i}_{1}}}}}}&{{{c}_{{{{i}_{1}}}}}}&{} \\ {}&{}&{}&{{{I}_{{n - {{i}_{1}} - 1}}}} \end{array}} \right]\quad {\text{и}}\quad {{\tilde {G}}_{{{{i}_{2}} - 1}}} = \left[ {\begin{array}{*{20}{c}} {{{I}_{{{{i}_{2}} - 2}}}}&{}&{}&{} \\ {}&{{{g}_{{{{i}_{2}}}}}}&{{{h}_{{{{i}_{2}}}}}}&{} \\ {}&{ - {{h}_{{{{i}_{2}}}}}}&{{{g}_{{{{i}_{2}}}}}}&{} \\ {}&{}&{}&{{{I}_{{n - {{i}_{2}}}}}} \end{array}} \right],$
участвующие в соответствующих шагах $QR$ и $QL$-методов со сдвигом $\lambda $.

Если ${{c}_{{{{i}_{1}}}}} \geqslant {{g}_{{{{i}_{2}} - 1}}}$, то ${{\hat {G}}_{{{{i}_{1}}}}}$ применяется к $R:R \leftarrow {{\hat {G}}_{{{{i}_{1}}}}}R$ и положим ${{i}_{1}} = {{i}_{1}} + 1$, в противном случае ${{\tilde {G}}_{{{{i}_{2}}}}}$ применяется к $L:L \leftarrow {{\tilde {G}}_{{{{i}_{2}}}}}L$ и положим ${{i}_{2}} = {{i}_{2}} - 1$. Затем повторяем процедуру до тех пор, пока ${{i}_{1}} > {{i}_{2}}$.

Заметим, что последний столбец $\hat {Q}$ в (1) зависит от всех коэффициентов Гивенса ${{c}_{i}}$ и ${{s}_{i}}$, $i = 1,\; \ldots ,\;n - 1$, а первый столбец $\tilde {Q}$ в (2) зависит от всех коэффициентов Гивенса ${{g}_{i}}$ и ${{h}_{i}}$, $i = 1,\; \ldots ,\;n - 1$.

На первый взгляд можно подумать, что даже если “разделяющий” индекс $j$ уже найден, все равно необходимо вычислить и последний столбец $\hat {Q}$, и первый столбец $\tilde {Q}$ для того, чтобы построить искомый собственный вектор.

Далее мы покажем, что искомая аппроксимация собственного вектора может быть вычислена, зная только ${{c}_{i}}$ и ${{s}_{i}}$, $i = 1,\; \ldots ,\;j - 1$, и ${{g}_{i}}$ и ${{h}_{i}}$, $i = 1,\; \ldots ,\;n - j + 1$. На самом деле, если индекс $j$ определен, можно заметить, что “хорошая” часть вектора (1) может быть записана в виде

$\mathop {{\mathbf{\hat {y}}}}\nolimits_{1:j} = \left[ {\begin{array}{*{20}{c}} {{{{( - 1)}}^{{n - 1}}}\prod\limits_{i = 1}^{n - 1} {{{s}_{i}}} } \\ {{{{( - 1)}}^{{n - 2}}}{{c}_{1}}\prod\limits_{i = 2}^{n - 1} {{{s}_{i}}} } \\ {{{{( - 1)}}^{{n - 3}}}{{c}_{2}}\prod\limits_{i = 3}^{n - 1} {{{s}_{i}}} } \\ \vdots \\ {{{{( - 1)}}^{{n - j + 2}}}{{c}_{{j - 3}}}\prod\limits_{i = j - 2}^{n - 1} {{{s}_{i}}} } \\ {{{{( - 1)}}^{{n - j + 1}}}{{c}_{{j - 2}}}\prod\limits_{i = j - 1}^{n - 1} {{{s}_{i}}} } \\ {{{{( - 1)}}^{{n - j}}}{{c}_{{j - 1}}}\prod\limits_{i = j}^{n - 1} {{{s}_{i}}} } \end{array}} \right] = {{\gamma }^{{(u)}}}{{{\mathbf{\hat {y}}}}^{{(u)}}},$
в то время как “хорошая” часть вектора (2) может быть записана в виде
$\mathop {{\mathbf{\tilde {y}}}}\nolimits_{j:n} = \left[ {\begin{array}{*{20}{c}} {{{{( - 1)}}^{{j - 1}}}{{g}_{{n - j}}}\prod\limits_{i = n - j + 1}^{n - 1} {{{h}_{i}}} } \\ {{{{( - 1)}}^{j}}{{g}_{{n - j - 1}}}\prod\limits_{i = n - j}^{n - 1} {{{h}_{i}}} } \\ {{{{( - 1)}}^{{j + 1}}}{{g}_{{n - j - 2}}}\prod\limits_{i = n - j - 1}^{n - 1} {{{h}_{i}}} } \\ \vdots \\ {{{{( - 1)}}^{{n - 3}}}{{g}_{2}}\prod\limits_{i = 3}^{n - 1} {{{h}_{i}}} } \\ {{{{( - 1)}}^{{n - 2}}}{{g}_{1}}\prod\limits_{i = 2}^{n - 1} {} {{h}_{i}}} \\ {{{{( - 1)}}^{{n - 1}}}\prod\limits_{i = 1}^{n - 1} {{{h}_{i}}} } \end{array}} \right] = {{\gamma }^{{(b)}}}{{{\mathbf{\tilde {y}}}}^{{(b)}}},$
где ${{\gamma }^{{(u)}}} = {{( - 1)}^{{n - j}}}\prod\nolimits_{i = j}^{n - 1} {{{s}_{i}}} $, ${{\gamma }^{{(b)}}} = {{( - 1)}^{{j - 1}}}\prod\nolimits_{i = n - j + 1}^{n - 1} {{{h}_{i}}} $,
${{{\mathbf{\hat {y}}}}^{{(u)}}} = \left[ {\begin{array}{*{20}{c}} {{{{( - 1)}}^{{j - 1}}}\prod\limits_{i = 1}^{j - 1} {{{s}_{i}}} } \\ {{{{( - 1)}}^{{j - 2}}}{{c}_{1}}\prod\limits_{i = 2}^{j - 1} {{{s}_{i}}} } \\ {{{{( - 1)}}^{{j - 3}}}{{c}_{2}}\prod\limits_{i = 3}^{j - 1} {{{s}_{i}}} } \\ \vdots \\ {{{{( - 1)}}^{2}}{{c}_{{j - 3}}}\prod\limits_{i = j - 2}^{j - 1} {{{s}_{i}}} } \\ { - {{c}_{{j - 2}}}{{s}_{j}}} \\ {{{c}_{{j - 1}}}} \end{array}} \right],\quad {{{\mathbf{\tilde {y}}}}^{{(b)}}} = \left[ {\begin{array}{*{20}{c}} {{{g}_{{n - j}}}} \\ { - {{g}_{{n - j - 1}}}{{h}_{{n - j}}}} \\ {{{{( - 1)}}^{2}}{{g}_{{n - j - 2}}}\prod\limits_{i = n - j - 1}^{n - j} {{{h}_{i}}} } \\ \vdots \\ {{{{( - 1)}}^{{n - j - 2}}}{{g}_{2}}\prod\limits_{i = 3}^{n - j} {{{h}_{i}}} } \\ {{{{( - 1)}}^{{n - j - 1}}}{{g}_{1}}\prod\limits_{i = 2}^{n - j} {{{h}_{i}}} } \\ {{{{( - 1)}}^{{n - j}}}\prod\limits_{i = 1}^{n - j} {{{h}_{i}}} } \end{array}} \right].$
Тогда для начала мы нормализуем оба вектора следующим образом:
$\mathop {\mathbf{y}}\nolimits_{1:j} = \frac{{\mathop {{\mathbf{\hat {y}}}}\nolimits_{1:j}^{(u)} }}{{\mathop {{\mathbf{\hat {y}}}}\nolimits_j^{(u)} }},\quad \mathop {\mathbf{y}}\nolimits_{j + 1:n} = \frac{{\mathop {}\nolimits_{2:n - j + 1}^{(b)} }}{{\mathop {{\mathbf{\tilde {y}}}}\nolimits_1^{(b)} }},$
т.е. мы разделим первый вектор на его последнюю компоненту, а второй вектор на его первую компоненту для того, чтобы иметь $1$ на $j$-й позиции первого вектора и на первой позиции второго. А затем, наконец, нормализуем ${\mathbf{y}}$, т.е. $k{\mathbf{y}} = {{\mathbf{y}} \mathord{\left/ {\vphantom {{\mathbf{y}} {{{{\left\| {\mathbf{y}} \right\|}}_{2}}}}} \right. \kern-0em} {{{{\left\| {\mathbf{y}} \right\|}}_{2}}}}$.

Соответствующий псевдокод на $MATLAB$ приведен в табл. 1.

Таблица 1.  

Псевдокод на $MATLAB$ для вычисления собственного вектора несимметричной трехдиагональной матрицы при известном собственном значении $\lambda $

$function{\kern 1pt} {\kern 1pt} [y] = left\_eigv{\kern 1pt} {\kern 1pt} (T,\lambda ,n)$
$R = T - \lambda {{I}_{n}}$; $L = R$;
${{i}_{1}} = 1$; ${{i}_{2}} = n$;
${{G}_{1}} = givens{\kern 1pt} {\kern 1pt} (R({{i}_{1}},{{i}_{1}}),R({{i}_{1}} + 1,{{i}_{1}}))$; ${{G}_{2}} = givens{\kern 1pt} {\kern 1pt} (L({{i}_{2}},{{i}_{2}}),L({{i}_{2}} - 1,{{i}_{2}}))$;
${{c}_{1}}(1) = {{G}_{1}}({{i}_{1}},1)$; ${{s}_{1}}(1) = {{G}_{1}}({{i}_{1}},2)$; ${{c}_{2}}(n - 1) = {{G}_{2}}({{i}_{1}},1)$; ${{s}_{2}}({{i}_{2}} - 1) = {{G}_{2}}(1,2)$;
$while\;{{i}_{1}} < = {{i}_{2}}$,
$if\;{{c}_{1}}({{i}_{1}}) > {{c}_{2}}({{i}_{2}})$,
$R({{i}_{1}}:{{i}_{1}} + 1,:) = {{G}_{1}} * R({{i}_{1}}:{{i}_{1}} + 1,:)$;
${{i}_{1}} = {{i}_{1}} + 1$;
$if\;{\text{ }}{{i}_{1}} < n$,
${{G}_{1}} = givens{\kern 1pt} {\kern 1pt} (R({{i}_{1}},{{i}_{1}}),R({{i}_{1}} + 1,{{i}_{1}}))$;
${{c}_{1}}({{i}_{1}}) = {{G}_{1}}(1,1)$; ${{s}_{1}}({{i}_{1}}) = {{G}_{1}}(1,2)$;
$end$
$else$
${{G}_{2}} = {{G}_{2}}.{\text{'}}$;
$L({{i}_{2}} - 1:{{i}_{2}},:) = {{G}_{2}} * L({{i}_{2}} - 1:{{i}_{2}},:)$;
${{i}_{2}} = {{i}_{2}} - 1$;
$if\;{{i}_{2}} > 1$,
${{G}_{2}} = givens{\kern 1pt} {\kern 1pt} (L({{i}_{2}},{{i}_{2}}),L({{i}_{2}} - 1,{{i}_{2}}))$;
${{c}_{2}}({{i}_{2}} - 1) = {{G}_{2}}(1,1)$; ${{c}_{2}}({{i}_{2}} - 1) = {{G}_{2}}(1,1)$;
$end$
$end$
$end$
${\text{\% }}\;{\text{computation}}\;{\text{of}}\;{\text{the}}\;{\text{eigenvector}}$
$j = min({{i}_{1}},{{i}_{2}})$;
${{y}_{1}} = zeros{\kern 1pt} {\kern 1pt} (n,1)$; ${{y}_{2}} = zeros{\kern 1pt} {\kern 1pt} (n,1)$;
${{y}_{1}}(j) = 1$; ${{y}_{2}}(j) = 1$;
$for\;i = j - 1: - 1:1$,
$G = \left[ {\begin{array}{*{20}{c}} {{{c}_{1}}(i)}&{{{s}_{1}}(i)} \\ { - {{s}_{1}}(i)}&{{{c}_{1}}(i)} \end{array}} \right]$;
${{y}_{1}}(i:i + 1) = G{{.}^{{\text{T}}}}T * {{y}_{1}}(i:i + 1)$;
$end$
$for\;i = j:n - 1$,
$G = \left[ {\begin{array}{*{20}{c}} {{{c}_{2}}(i)}&{{{s}_{2}}(i)} \\ { - {{s}_{2}}(i)}&{{{c}_{2}}(i)} \end{array}} \right]$;
${{y}_{2}}(i:i + 1) = G * {{y}_{2}}(i:i + 1)$;
$end$
${{y}_{1}} = {{y}_{1}}{\text{/}}{{y}_{1}}(j)$; ${{y}_{2}} = {{y}_{2}}{\text{/}}{{y}_{2}}(j)$; $y = [{{y}_{1}}(1:j);{{y}_{2}}(j + 1:n)]$;
$y = y{\text{/}}{{\left\| y \right\|}_{2}}$;

Вместо того, чтобы останавливать алгоритм, когда ${{i}_{1}} > {{i}_{2}}$, выполним еще ${{j}_{f}}$ шагов $QR$-метода и ${{j}_{b}}$ шагов $QL$-метода, где ${{j}_{f}} = min{\text{\{ }}j + k,n{\text{\} }}$ и ${{j}_{b}} = max{\text{\{ }}1,j - k{\text{\} }}$ при $k \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$. В наших экспериментах было использовано $k = \left\lfloor {\sqrt n } \right\rfloor $. Затем вычислим новый вектор , где , $i = 1,\; \ldots ,\;n$, и выберем $j \in [{{j}_{b}},{{j}_{f}}]$ таким, что , $\ell \in [{{j}_{b}},{{j}_{f}}]$, $j \ne \ell $.

Соответствующий код на $MATLAB$ может быть получен от авторов.

5. КАК ИЗБЕЖАТЬ КОМПЛЕКСНОЙ АРИФМЕТИКИ

Если $T$ является несимметричной трехдиагональной матрицей, ее собственные значения могут быть комплексно-сопряженными.

Множители $QR$- и $QL$-разложения $T(\lambda )$ с комплексно-сопряженным сдвигом $\lambda $ также являются комплексными. Для того, чтобы избежать комплексной арифметики, могут быть применены неявные $QR$/$QL$ ($IQR$/$IQL$) методы с двойным сдвигом [10], [11]. В точной арифметике после одной итерации $IQR$-метода, примененного к $T$, с двойным сдвигом $\lambda $ и $\bar {\lambda },$ где $\bar {\lambda }$ обозначает комплексное сопряжение к $\lambda $, мы имеем блочно-хессенбергову структуру

$\left[ {\begin{array}{*{20}{c}} {H_{1}^{{(r)}}}&B \\ {}&{H_{2}^{{(r)}}} \end{array}} \right],$
где $H_{1}^{{(r)}} \in {{\mathbb{R}}^{{(n - 2) \times (n - 2)}}}$ и $H_{2}^{{(r)}} \in {{\mathbb{R}}^{{2 \times 2}}}$ являются хессенберговыми, а $\lambda $ и $\bar {\lambda }$ – собственные значения $H_{2}^{{(r)}}.$ Более того, последние два столбца множителя $Q$ являются вещественной и мнимой частями соответствующего собственного вектора.

К сожалению, одна итерация $IQR$-метода ($IQL$-метода) преобразовывает трехдиагональную матрицу $T$ в верхнюю (нижнюю) хессенбергову матрицу $H$, требуя $O({{n}^{2}})$ операций в арифметике конечной точности.

Поскольку построение собственного вектора с помощью предложенного метода опирается только на коэффициенты, участвующие во вращениях Гивенса, мы покажем, что нет необходимости обновлять всю хессенбергову матрицу $H$. Для того, чтобы вычислить коэффициенты Гивенса, достаточно только элементов, близких к трехдиагональной матрице. Продемонстрируем это с помощью первых двух шагов одной $IQR$-итерации со сдвигом $\lambda $, примененным к $T$. Эти шаги графически изображены на фиг. 4, где серая область обозначает часть матрицы, измененной при умножении на вращения Гивенса.

Фиг. 4.

Графическое изображение первых двух шагов одной $IQR$-итерации со сдвигом $\lambda $.

Пусть ${{T}_{0}} = T$. Пусть ${\mathbf{v}} \in {{\mathbb{R}}^{n}}$ является первым столбцом $(T - \lambda {{I}_{n}})(T - \bar {\lambda }{{I}_{n}})$. Тогда только первые три элемента ${\mathbf{v}}$ отличны от нуля.

На первом шаге $IQR$-итерации строятся два вращения Гивенса и такие, что

где ${{{\mathbf{e}}}_{1}} \in {{\mathbb{R}}^{n}}$ является первым вектором канонического базиса в ${{\mathbb{R}}^{n}}$. Затем первый шаг заканчивается применением следующего преобразования подобия к $T$:
(5)
Умножение (фиг. 4а $ \to $ б) приводит к “выпуклости” в позиции $(3,1)$, в то время как (фиг. 4б $ \to $ в) приводит к “выпуклости” в позиции $(4,2)$. Кроме того, и 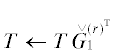(фиг. 4в $ \to $ г и фиг. 4г $ \to $ д соответственно) приводят к “выпуклости” в позиции $(4,1)$. Заметим, что в последующих операциях элементы первой строки $T$ (изображены синим на фиг. 4г) не играют роли при вычислении следующих коэффициентов Гивенса и могут быть отброшены.

На втором шаге вращения Гивенса и применены к $T$ для того, чтобы восстановить хессенбергову структуру, зануляя элементы $(4,1)$ и $(3,1)$ (обозначено “$ \otimes $” на фиг. 4д и ж). Поскольку и действуют на $4$-ю и $3$-ю строки и на $3$-ю и $2$-ю строки соответственно, появляются “выпуклости” в позициях $(4,2)$, $(5,2)$ и $(5,3)$ (фиг. 4и). Заметим, что после умножения вторая строка $T$ (изображено синим на фиг. 4г) не играет роли при вычислении других коэффициентов Гивенса, и может быть отброшена.

Подводя итог, в точной арифметике на каждом шаге $IQR$-метода нужно обновить только несколько элементов матрицы $T$ для того, чтобы вычислить последовательности вращений Гивенса и , причем число операций линейно зависит от $n$ – порядка матрицы $T$. Похожим образом на каждом шаге $IQL$-метода с двойным сдвигом $\lambda $ и $\bar {\lambda }$ нужно обновить только несколько элементов матрицы $T$ для того, чтобы вычислить две последовательности вращений Гивенса и , которые преобразовывают матрицу в подобную нижнюю блочно-хессенбергову матрицу

$\left[ {\begin{array}{*{20}{c}} {H_{1}^{{(l)}}}&{} \\ F&{H_{2}^{{(l)}}} \end{array}} \right],$
где $H_{1}^{{(l)}} \in {{\mathbb{R}}^{{2 \times 2}}}$ и $H_{2}^{{(l)}} \in {{\mathbb{R}}^{{(n - 2) \times (n - 2)}}}$ являются хессенберговыми, а $\lambda $ и $\bar {\lambda }$ – собственные значения $H_{1}^{{(l)}}$. Левый собственный вектор ${\mathbf{y}}$, соответствующий $\lambda $, может быть получен либо из последних двух столбцов ${{Q}^{{(r)}}}$, либо из первых двух столбцов ${{Q}^{{(l)}}}$:
${\mathbf{y}} \equiv {{{\mathbf{y}}}^{{(r)}}} \equiv {{{\mathbf{y}}}^{{(l)}}},$
где
(6)
${{{\mathbf{y}}}^{{(r)}}} = {{Q}^{{(r)}}}(:,n - 1) + i \cdot {{Q}^{{(r)}}}(:,n),\quad {{{\mathbf{y}}}^{{(l)}}} = {{Q}^{{(l)}}}(:,1) + i \cdot {{Q}^{{(l)}}}(:,2),$
и

В арифметике конечной точности аналогично случаю, анализируемому в разд. 3, при вычислении вышеупомянутых последовательностей может возникнуть прямая неустойчивость. Индекс $j$ может быть найден из последовательностей , $i = 1,\; \ldots ,\;n - 1$, и , $i = 1,\; \ldots ,\;n - 1$, порожденных итерацией $IQR$ и $IQL$-методов с двойным сдвигом $\lambda $ и $\bar {\lambda }$. Для краткости мы опускаем детали.

Применим $IQR$- и $IQL$-методы с двойным сдвигом к данным из примера 1. В частности, собственные векторы, обозначенные соответственно $\mathop {{\mathbf{\tilde {y}}}}\nolimits^{(r)} $ и $\mathop {{\mathbf{\tilde {y}}}}\nolimits^{(l)} $ в (6), были вычислены в арифметике конечной точности. На фиг. 5 в логарифмическом масштабе изображены покомпонентные ошибки $\left| {{\mathbf{y}} - \mathop {{\mathbf{\tilde {y}}}}\nolimits^{(r)} } \right|$ (обозначено “$ \times $”) и $\left| {{\mathbf{y}} - \mathop {{\mathbf{\tilde {y}}}}\nolimits^{(l)} } \right|$ (обозначено “$ + $”), последовательности $\left\{ {{{{\hat {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ (обозначено “$\diamond$”), $\left\{ {{{{\tilde {\sigma }}}_{i}}} \right\}_{{i = 1}}^{n}$ (обозначено “$\bigcirc $”), (обозначено “$\bigcirc $”) и (“$ * $”), машинная точность ${{\varepsilon }_{M}}$ (обозначено синей линией). Поведение векторов и последовательностей, изображенное на фиг. 5, то же самое, как описано в примере 4.

Фиг. 5.

Пример 1: график $\left| {{\mathbf{y}} - \mathop {{\mathbf{\tilde {y}}}}\nolimits^{(r)} } \right|$ (“$ \times $”), $\left| {{\mathbf{y}} - \mathop {{\mathbf{\tilde {y}}}}\nolimits^{(l)} } \right|$ (“$ + $”), ${\text{\{ }}\mathop {\hat {\sigma }}\nolimits_i {\text{\} }}_{{i = 1}}^{n}$ (“$\diamond$”), ${\text{\{ }}\mathop {\tilde {\sigma }}\nolimits_i {\text{\} }}_{{i = 1}}^{n}$ (“$\triangledown $”), (“$\bigcirc $”) и (“$ * $”), машинная точность ${{\varepsilon }_{M}}$ (синяя линия) в логарифмическом масштабе.

6. ЧИСЛЕННЫЕ ПРИМЕРЫ

Все численные эксперименты этого раздела были выполнены в $MATLAB$ $Ver. 2014b$ с машинной точностью ${{\varepsilon }_{M}} \sim 2.22 \times {{10}^{{ - 16}}}$.

Пример 2. В этом примере рассматривается несимметричная трехдиагональная матрица ${{T}_{n}} \in {{\mathbb{R}}^{{n \times n}}}$, $n = 200$, элементы которой порождены функцией $randn$ в $MATLAB$.

С помощью описанного метода были вычислены собственные векторы $\mathop {{\mathbf{\hat {y}}}}\nolimits_i $, $i = 1,\; \ldots ,\;n$, а затем собственные значения были пересчитаны с помощью отношения Рэлея:

${{\hat {\lambda }}_{i}} = \frac{{\mathop {{\mathbf{\hat {y}}}}\nolimits_i^{\text{H}} T\mathop {{\mathbf{\hat {y}}}}\nolimits_i }}{{\mathop {{\mathbf{\hat {y}}}}\nolimits_i^{\text{H}} \mathop {{\mathbf{\hat {y}}}}\nolimits_i }},\quad i = 1,\; \ldots ,\;n.$

На фиг. 6 изображены модули разности $\left| {\mathop {\hat {\lambda }}\nolimits_i - {{\lambda }_{i}}} \right|$, $i = 1,\; \ldots ,\;n$, где ${{\lambda }_{i}}$ – собственные значения, вычисленные функцией $eig$ в $MATLAB$. Можно видеть, что разность имеет порядок ${{\varepsilon }_{M}}$.

Фиг. 6.

Пример 2: ошибка $\left| {{{{\hat {\lambda }}}_{i}} - {{\lambda }_{i}}} \right|$, $i = 1,\; \ldots ,\;n$, в логарифмическом масштабе.

Для каждого собственного вектора $\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(1)} $, $i = 1,\; \ldots ,\;n$, вычисленного с помощью предложенного метода, обозначим

${{\nu }_{i}} = {{\left\| {\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} T - (\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} T\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(1)} )\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} } \right\|}_{2}}$
норму $i$-й невязки. Тогда оказывается, что

$1.16 \times {{10}^{{ - 13}}} = \mathop {max}\limits_k {{\nu }_{k}} \leqslant {{\nu }_{i}} \leqslant \mathop {min}\limits_k {{\nu }_{k}} = 2.18 \times {{10}^{{ - 16}}}.$

Можно сделать вывод, что собственные векторы, полученные с помощью предложенной процедуры, вычислены достаточно точно.

Пример 3. В этом примере мы рассмотрим матрицу Бесселя

$B_{n}^{{(a,b)}} = \left[ {\begin{array}{*{20}{c}} {{{\alpha }_{1}}}&{{{\gamma }_{1}}}&{}&{}&{} \\ {{{\beta }_{1}}}&{{{\alpha }_{2}}}&{{{\gamma }_{2}}}&{}&{} \\ {}&{{{\beta }_{2}}}& \ddots & \ddots &{} \\ {}&{}& \ddots &{{{\alpha }_{{n - 1}}}}&{{{\gamma }_{{n - 1}}}} \\ {}&{}&{}&{{{\beta }_{{n - 1}}}}&{{{\alpha }_{n}}} \end{array}} \right],$
где $n = 50$ и
${{\alpha }_{1}} = - \frac{b}{a},\quad {{\alpha }_{j}} = - b\frac{{a - 2}}{{(2j + a - 2)(2j + a - 4)}},\quad j = 2,\; \ldots ,\;n,$
${{\beta }_{1}} = - \frac{{{{\alpha }_{1}}}}{{a + 1}},\quad {{\alpha }_{j}} = - b\frac{j}{{(2j + a - 1)(2j + a - 2)}},\quad j = 2,\; \ldots ,\;n - 1,$
${{\gamma }_{1}} = - {{\alpha }_{1}},\quad {{\gamma }_{j}} = b\frac{{j + a - 2}}{{(2j + a - 2)(2j + a - 3)}},\quad j = 2,\; \ldots ,\;n - 1.$
Собственные значения матриц $B_{n}^{{(a,b)}}$ с ростом $n$ страдают от плохой обусловленности [5]. Положим $a = - 4.5$ и $b = 2$, как это сделано в [5], и будем обозначать $B_{{50}}^{{( - 4.5,2)}}$ просто как $B$. Эти матрицы имеют хорошо отделимые комплексные собственные значения.

Матрица $B$ и ее собственные значения ${{\lambda }_{i}}$, $i = 1,\; \ldots ,\;50$, были вычислены в $MATLAB$ с использованием арифметики переменной точности с $128$ значащими цифрами, а затем округлены до двойной точности. Таким образом, были получены $\tilde {B}$ и ${{\tilde {\lambda }}_{i}}$, $i = 1,\; \ldots ,\;50$.

Пусть ${{\hat {\lambda }}_{i}}$, $i = 1,\; \ldots ,\;50$, являются собственными значениями $\tilde {B}$, полученными с помощью $eig$ в $MATLAB$. На фиг. 7 $\{ {{\tilde {\lambda }}_{i}}\} _{{i = 1}}^{{50}}$ и $\} {{\hat {\lambda }}_{i}}\{ _{{i = 1}}^{{50}}$ обозначены “$\bigcirc $” и “$ \times $” соответственно. Заметим, что ${{\tilde {\lambda }}_{i}}$ и ${{\hat {\lambda }}_{i}}$ сильно отличаются, поскольку, как было отмечено выше, собственные значения $B$ страдают от плохой обусловленности с ростом $n$ [5].

Фиг. 7.

Пример 3: собственные значения матрицы $B$ обозначены “$ \circ $”, а величины, вычисленные с помощью $eig$ в $MATLAB$, обозначены “$ \times $”.

Левые собственные векторы, соответствующие собственным значениям ${{\tilde {\lambda }}_{i}}$ матрицы $\tilde {B}$, были вычислены с помощью предложенного метода и обозначены $\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(1)} $. Последний столбец матрицы $Q$ из $QR$-разложения матрицы $\tilde {B} - {{\tilde {\lambda }}_{i}}I$ обозначен через $\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(2)} $. Таким образом, новые аппроксимации собственных значений $\tilde {B}$ были вычислены как отношения Рэлея:

$\tilde {\lambda }_{i}^{{(1)}} = \mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{т}}}}} \tilde {B}{\mathbf{\tilde {y}}}_{i}^{{(1)}},\quad \tilde {\lambda }_{i}^{{(2)}} = \mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(2){\text{т}}} \tilde {B}{\mathbf{\tilde {y}}}_{i}^{{(2)}},\quad i = 1,\; \ldots ,\;50.$

Собственные значения ${{\tilde {\lambda }}_{i}}$ и вычисленные аппроксимации ($\tilde {\lambda }_{i}^{{(1)}}$ и $\tilde {\lambda }_{i}^{{(2)}}$, $i = 1,\; \ldots ,\;50$) собственных значений $\tilde {B}$ изображены на фиг. 8 и обозначены, соответственно, символами “$\bigcirc $”, “$\triangledown $” и “$ + $”.

Фиг. 8.

Пример 3. Графики ${{\tilde {\lambda }}_{i}}$, $\tilde {\lambda }_{i}^{{(1)}}$ и $\tilde {\lambda }_{i}^{{(2)}}$, $i = 1,\; \ldots ,\;50$, обозначены, соответственно, как “$\bigcirc $”, “$\triangledown $” и “$ + $”.

Заметим, что ${{\tilde {\lambda }}_{i}}$ и $\tilde {\lambda }_{i}^{{(1)}}$ хорошо совпадают, в то время как $\tilde {\lambda }_{i}^{{(2)}}$ отклоняется от ${{\tilde {\lambda }}_{i}}$ с ростом отрицательной мнимой части.

В табл. 2 приведены $ma{{x}_{i}}\left| {{{{\tilde {\lambda }}}_{i}} - \tilde {\lambda }_{i}^{{(1)}}} \right|$ и $ma{{x}_{i}}\left| {{{{\tilde {\lambda }}}_{i}} - \tilde {\lambda }_{i}^{{(2)}}} \right|$.

Таблица 2.  

$ma{{x}_{i}}\left| {{{{\tilde {\lambda }}}_{i}} - \tilde {\lambda }_{i}^{{(1)}}} \right|$ и $ma{{x}_{i}}\left| {{{{\tilde {\lambda }}}_{i}} - \tilde {\lambda }_{i}^{{(2)}}} \right|$

$ma{{x}_{i}}\left| {{{{\tilde {\lambda }}}_{i}} - \tilde {\lambda }_{i}^{{(1)}}} \right|$ $ma{{x}_{i}}\left| {{{{\tilde {\lambda }}}_{i}} - \tilde {\lambda }_{i}^{{(2)}}} \right|$
$3.06 \times {{10}^{{ - 15}}}$ $3.01 \times {{10}^{2}}$

Заметим, что если вычислить аппроксимацию собственного вектора ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} }}$ для одного из собственных значений ${{\tilde {\lambda }}_{i}}$ матрицы $\tilde {B}$ с помощью метода обратных итерацией, то вектор ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} }}$ оказывается далек от ${\mathbf{\tilde {y}}}_{i}^{{(1)}}$. Это поведение описано в [18]. Более того, соответствующее отношение Рэлея $\mathop {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} }}}\nolimits^{\text{H}} \tilde {B}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} }}{\text{/}}(\mathop {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} }}}\nolimits^{\text{H}} {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} }})$ далеко от собственного значения ${{\tilde {\lambda }}_{i}}$.

Для каждого собственного вектора $\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(1)} $, $i = 1,\; \ldots ,\;50$, вычисленного с помощью предложенного метода, обозначая через

${{\nu }_{i}} = {{\left\| {\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} \tilde {B} - (\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} \tilde {B}\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(1)} )\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} } \right\|}_{2}}$
норму $i$-й невязки, получаем, что

$3.06 \times {{10}^{{ - 15}}} = \mathop {max}\limits_k {{\nu }_{k}} \leqslant {{\nu }_{i}} \leqslant \mathop {min}\limits_k {{\nu }_{k}} = 2.61 \times {{10}^{{ - 16}}}.$

Пример 4. Рассмотрим в этом примере матрицы Клемента порядка $n = 200$ [7], также называемые матрицами Сильвестра–Каца [19]:

${{C}_{n}} = \left[ {\begin{array}{*{20}{c}} {}&{{{\gamma }_{1}}}&{}&{}&{} \\ {{{\beta }_{1}}}&{}&{{{\gamma }_{2}}}&{}&{} \\ {}&{{{\beta }_{2}}}&{}& \ddots &{} \\ {}&{}& \ddots &{}&{{{\gamma }_{{n - 1}}}} \\ {}&{}&{}&{{{\beta }_{{n - 1}}}}&{} \end{array}} \right],$
где ${{\gamma }_{i}} = i$ и ${{\beta }_{i}} = n - i$, $i = 1,\; \ldots ,\;n - 1$.

Собственные значения таких матриц равны [19] ${{\lambda }_{k}} = n - 2(k - 1)$ при $k = 1,\; \ldots ,\;n$, а соответствующая левая матрица собственных векторов [19] равна:

${{u}_{{k,j}}} = \sum\limits_{i = 0}^{min(k - 1,j - 1)} {{{{( - 1)}}^{i}}} \left( {\begin{array}{*{20}{c}} {j - 1} \\ i \end{array}} \right)\left( {\begin{array}{*{20}{c}} {n - j - 1} \\ {k - i - 1} \end{array}} \right).$

Также, в этом примере для каждого собственного вектора $\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(1)} $, $i = 1,\; \ldots ,\;n$, вычисленного с помощью предложенного метода, обозначая через

${{\nu }_{i}} = {{\left\| {\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} {{C}_{n}} - (\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} {{C}_{n}}\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{(1)} )\mathop {{\mathbf{\tilde {y}}}}\nolimits_i^{{{{(1)}}^{{\text{H}}}}} } \right\|}_{2}}$
норму $i$-й невязки, получаем, что

$5.67 \times {{10}^{{ - 13}}} = \mathop {max}\limits_k {{\nu }_{k}} \leqslant {{\nu }_{i}} \leqslant \mathop {min}\limits_k {{\nu }_{k}} = 4.49 \times {{10}^{{ - 16}}}.$

7. ЗАКЛЮЧЕНИЕ

В этой статье рассмотрена задача вычисления собственного вектора, соответствующего вычисленному собственному значению $\lambda $ несимметричной трехдиагональной матрицы $T$. Сначала описано, как левый собственный вектор ${\mathbf{y}}$, соответствующий собственному значению $\lambda $ матрицы $T$, может быть получен применением одной итерации $QR$- или $QL$-метода со сдвигом $\lambda $. К сожалению, оба метода страдают от прямой неустойчивости при работе в арифметике конечной точности.

Был предложен метод вычисления индекса $j$, который комбинирует собственные векторы, полученные итерацией $QR$- и итерацией $QL$-методов со сдвигом $\lambda $, избегая неустойчивости. Индекс $j$ вычисляется рассмотрением двух последовательностей косинусов, порожденных итерацией $QR$- и $QL$-методов со сдвигом $\lambda $. Искомый собственный вектор получается из первых $j$ коэффициентов Гивенса, порожденных $QR$-методом и первых $n - j$ коэффициентов Гивенса, порожденных $QL$-методом.

Итоговая сложность вычисления собственного вектора линейно зависит от размера матрицы.

Результаты численных экспериментов выглядят очень многообещающими, показывая, что собственные векторы вычисляются с высокой точностью.

Список литературы

  1. Sidje R.B., Burrage K. $QRT$: A $QR$- based tridiagonalization algorithm for nonsymmetric matrices // SIAM J. Matrix Anal. Appl. 2005. V. 26. № 3. P. 878–900.

  2. Dongarra J.J., Geist G.A., Romine C.H. Algorithm 710: FORTRAN subroutines for computing the eigenvalues and eigenvectors of a general matrix by reduction to general tridiagonal form // ACM Trans. Math. Softw. 1992. V. 18. № 4. P. 392–400.

  3. Wang H.H., Gregory R.T. On the reduction of an arbitrary real square matrix to tridiagonal form // Math. Comput. 1964. V. 18. P. 501–505.

  4. Freund R.W., Gutknecht M.H., Nachtigal N.M. An implementation of the lookahead Lanczos algorithm for non-Hermitian matrices // SIAM J. Sci. Comput. 1993. V. 14. P. 137–158.

  5. Ferreira C., Parlett B., Dopico F.M. Sensitivity of eigenvalues of an unsymmetric tridiagonal matrix // Numerische Mathematik. 2012. V. 122. № 3. P. 527–555.

  6. Pasquini L. Accurate computation of the zeros of the generalized Bessel polynomials // Numerische Mathematik. 2000. V. 86. № 3. P. 507–538.

  7. Bini D.A., Gemignani L., Tisseur F. The Ehrlich–Aberth method for the nonsymmetric tridiagonal eigenvalue problem // SIAM J. Matrix Anal. Appl. 2005. V. 27. № 1. P. 153–175.

  8. Dax A., Kaniel S. The $ELR$ method for computing the eigenvalues of a general matrix // SIAM Journal on Numerical Analysis. 1981. V. 18. № 4. P. 597–605.

  9. Rutishauser H. Solution of eigenvalue problems with the $LR$-transformation // Nat. Bur. Standards. 1958. V. 49. P. 47–81.

  10. Francis J. The $QR$ transformation a unitary analogue to the $LR$ transformation. I // Comput. J. 1961. V. 4. P. 265–271.

  11. Francis J. The $QR$ transformation a unitary analogue to the $LR$ transformation. II // Comput. J. 1961. V. 4. P. 332–345.

  12. Golub G.H., Van Loan C.F. Matrix Computations, 4th ed. Baltimore: Johns Hopkins University Press, 2013.

  13. Parlett B.N., Le J. Forward instability of tridiagonal $QR$ // SIAM J. Matrix Anal. Appl. 1993. V. 14. № 1. P. 279–316.

  14. Watkins D.S. The transmission of shifts and shift blurring in the $QR$ algorithm // Linear Algebra and its Applications. 1996. V. 241–243. P. 877–896.

  15. Mastronardi N., Taeter H., Dooren P.V. On computing eigenvectors of symmetric tridiagonal matrices // Structured Matrices in Numerical Linear Algebra: Analysis, Algorithms and Applications. 2019. V. 30. P. 181–195.

  16. Horn R.A., Johnson C.R. Topics in Matrix Analysis. New York: Cambridge University Press, 1991.

  17. Chang X.-W., Paige C.C., Stewart G.W. Perturbation analyses for the $QR$ factorization // SIAM J. Matrix Anal. Appl. 1997. V. 18. № 3. P. 775–791.

  18. Ipsen I.C.F. Computing an eigenvector with inverse iteration // SIAM Review. 1997. V. 39. № 2. P. 254–291.

  19. Chu W., Wang X. Eigenvectors of tridiagonal matrices of Sylvester type // Calcolo. 2008. V. 45. № 4. P. 217–233.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал