1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 5, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 5, стр. 813-826

О точности крестовых и столбцовых малоранговых maxvol-приближений в среднем

Н. Л. Замарашкин 1, *, А. И. Осинский 1, 2, **

1 ИВМ РАН
119333 Москва, ул. Губкина, 8, Россия

2 Сколтех
121205 Москва, Большой бульвар, 30, стр. 1, Россия

* E-mail: nikolai.zamarashkin@gmail.com
** E-mail: a.osinskiy@skoltech.ru

Поступила в редакцию 24.11.2020
После доработки 24.11.2020
Принята к публикации 14.01.2021

Полный текст (PDF)

Аннотация

В данной статье рассматривается проблема малорангового столбцового и крестового ($CGR$, $CUR$) приближения матриц по норме Фробениуса с точностью до фиксированного множителя $1 + \varepsilon $. Доказывается, что для случайных матриц в среднем справедлива оценка вида $1 + \varepsilon \leqslant \tfrac{{m + 1}}{{m - r + 1}}\tfrac{{n + 1}}{{n - r + 1}}$, где $m$ и $n$ – число строк и столбцов крестового приближения. Таким образом, оказывается, что матрицы, для которых принцип максимального объема не позволяет гарантировать высокой точности, довольно редки. Также рассматривается связь полученных оценок с методами поиска подматрицы максимального объема и максимального проективного объема. Численные эксперименты показывают близость теоретических оценок и достижимых на практике результатов быстрой крестовой аппроксимации. Библ. 16. Фиг. 1.

Ключевые слова: малоранговое приближение матриц, крестовое/скелетное разложение, максимальный объем.

1. ВВЕДЕНИЕ

Пусть матрица $A \in {{\mathbb{C}}^{{M \times N}}},$ а ${{A}_{r}}$ – ее наилучшее приближение ранга $r$ по норме Фробениуса

(1)
${{\left\| {A - {{A}_{r}}} \right\|}_{F}} = \mathop {min}\limits_{{\text{rank}}(B) \leqslant r} {{\left\| {A - B} \right\|}_{F}}.$
Построение приближения ${{A}_{r}}$ предполагает получение сингулярного разложения для $A,$ что слишком дорого для большого числа современных приложений, использующих малоранговые приближения. С другой стороны, как правило, не требуется искать именно ${{A}_{r}},$ а лишь такое приближение $\Psi ,$ $\operatorname{rank} (\Psi ) \leqslant r,$ что
(2)
${{\left\| {A - \Psi } \right\|}_{F}} = \left( {1 + \varepsilon } \right){{\left\| {A - {{A}_{r}}} \right\|}_{F}},$
для некоторого заданного $\varepsilon .$ Создание алгоритмов малой сложности для приближений матрицами малого ранга, удовлетворяющих (2), является интенсивной областью современных исследований [1]–[3].

В настоящей работе изучается точность так называемых $CGR$ (иногда говорят $CUR$) малоранговых приближений, основанных на столбцах $C \in {{\mathbb{C}}^{{M \times n}}}$ и строках $R \in {{\mathbb{C}}^{{m \times N}}}$ приближаемой матрицы $A.$ Поскольку выбранные строки и столбцы образуют в матрице $A$ крест, то такие приближения принято называть крестовыми.

Известные $CGR$ алгоритмы можно условно подразделить на $2$ группы: детерминистические и рандомизированные. На данный момент теория рандомизированных алгоритмов развита намного полнее, чем теория детерминистических. Однако, на наш взгляд, на практике детерминистические алгоритмы имеют ряд преимуществ. Во-первых, такие алгоритмы имеют меньшую сложность при получении приближений заданной точности. Во-вторых, что, возможно, даже более важно, наиболее востребованные алгоритмы используют для построения приближения лишь малую часть элементов приближаемой матрицы. Последнее делает детерминистические крестовые алгоритмы незаменимым инструментом при построении тензорных TT-приближений.

Настоящая работа является попыткой построения теории для детерминистических крестовых $CGR$ приближений с выбором столбцов $C$ и строк $R$ на основе обобщенного принципа максимального объема.

Объемом прямоугольной матрицы $B \in {{\mathbb{C}}^{{m \times n}}}$ называется произведение всех ее сингулярных чисел

$\operatorname{vol} (B) = \prod\limits_{i = 1}^{min(m,n)} \,{{\sigma }_{i}}(B).$
В соответствии с принципом максимального объема, малоранговое $CGR$ приближение высокой точности получается, если на пересечении строк $R$ и столбцов $C$ оказывается подматрица $\hat {A}$, обладающая максимальным объемом среди всех подматриц данного размера. Теоретическое обоснование высокой поэлементной точности (в норме Чебышёва ${{\left\| A \right\|}_{C}} = ma{{x}_{{i,j}}}{\text{|}}{{a}_{{i.j}}}{\text{|}}$) maxvol-приближений дано в [4] и обобщено в [5]. Этих оценок, тем не менее, недостаточно для доказательства существования приближений вида (2).

С другой стороны, рандомизированные алгоритмы крестовых приближений позволяют достичь высокой точности приближения в норме Фробениуса. Например, в [3] предложен алгоритм, гарантирующий точность

(3)
${{\left\| {A - CUR} \right\|}_{F}} \leqslant (1 + \varepsilon ){{\left\| {A - {{A}_{r}}} \right\|}_{F}},\quad \varepsilon = {\text{const}} \cdot \frac{r}{{n - 4r}},$
с числом $n$ строк $R$ и столбцов $C$ таким, что $n > 4r.$ Как следует из (3), увеличивая $n,$ можно делать точность приближения сколь угодно близкой к наилучшей. Оценка (3) является наилучшей известной оценкой крестовых аппроксимаций с точки зрения асимптотики по числу требуемых строк и столбцов $n$. Кроме того, нижние оценки в [6], [7] показывают, что асимптотическая оценка $\varepsilon = O(r{\text{/}}n)$ не может быть улучшена.

Несмотря на свойство асимптотической оптимальности, алгоритм из [3] обладает общими для рандомизированных алгоритмов недостатками. Во-первых, при построении приближения используются все элементы исходной матрицы. Кроме того, для достижения точности с $\varepsilon = 1$ реальный размер $n$ превышает заданный ранг в десятки раз при использовании медленного метода, на основе процедуры дерандомизации, и даже тысячи раз при использовании более быстрого полностью рандомизированного алгоритма. Эти недостатки, как будет видно, отсутствуют у алгоритмов, основанных на принципе обобщенного максимального объема.

Определенные основания для предположения, что крестовые приближения на принципе максимального объема обладают высокой точностью в фробениусовой норме, было получено в [8]. Было доказано, что при выборе подматрицы $\hat {A} \in {{\mathbb{C}}^{{r \times r}}}$ с вероятностью, пропорциональной квадрату ее объема, матожидание ошибки во фробениусовой норме, отличается от ошибки наилучшего приближения не более чем в $r + 1$ раз.

В настоящей работе мы определяем две вероятностные модели и рассматриваем подчиняющиеся им семейства случайных матриц. Мы доказываем, что средняя в норме Фробениуса ошибка $CGR$ приближения на основе принципа максимального объема отличается от ошибки наилучшего приближения не более чем в $r + 1$ раз. Более того, при использовании большего числа строк и столбцов можно получить среднюю погрешность, сколь угодно близкую к оптимальной, с числом строк и столбцов, существенно меньшим, чем в [3].

В работе также рассматривается средняя погрешность, даваемая так называемыми столбцовыми приближениями вида $CW,$ где $C$ – столбцы матрицы $A,$ содержащие подматрицу максимального объема. Эти результаты аналогичны результатам из [7], [9]. Численные эксперименты показывают высокое совпадение наблюдаемых погрешностей с их теоретическим предсказанием.

2. ПОЧЕМУ НЕОБХОДИМ ВЕРОЯТНОСТНЫЙ ПОДХОД?

Напомним наилучшие известные результаты для точности $CGR$ приближений. Все они относятся к поэлементной аппроксимации или, другими словами, к аппроксимации в $C$-норме.

Теорема 1 (см. [5]). Пусть $\hat {A} \in {{\mathbb{C}}^{{n \times r}}},$ $n \geqslant r,$ является подматрицей максимального объема матрицы $A$ ранга не ниже $r$. Пусть $C$ и $R$ – столбцы и строки матрицы $A$, содержащие $\hat {A}$. Тогда

(4)
${{\left\| {A - C{{{\hat {A}}}^{\dag }}R} \right\|}_{C}} \leqslant \sqrt {r + 1} \sqrt {\frac{{n + 1}}{{n - r + 1}}} {{\sigma }_{{r + 1}}}(A).$

Прямое применение неравенства (4) не позволяет получить оценку высокой точности для погрешности в норме Фробениуса. Действительно, суммируя квадрат ошибки для всех ненулевых элементов $A - C{{\hat {A}}^{{ - 1}}}R$, мы получим

${{\left\| {A - C{{{\hat {A}}}^{\dag }}R} \right\|}_{F}} \leqslant \sqrt {(M - r)(N - r)} {{\left\| {A - C{{{\hat {A}}}^{{ - 1}}}R} \right\|}_{C}},$
что в итоге приводит к
${{\left\| {A - C{{{\hat {A}}}^{\dag }}R} \right\|}_{F}} \leqslant \sqrt {(M - r)(N - r)} \sqrt {r + 1} \sqrt {\frac{{n + 1}}{{n - r + 1}}} {{\left\| {A - {{A}_{r}}} \right\|}_{F}}.$
От ошибки наилучшего приближения последняя оценка отличается на множитель, пропорциональный $\sqrt {(M - r)(N - r)} .$ Последний зависит от размера приближаемой матрицы и делает оценку бесполезной для матриц больших размеров.

Более того, избежать такого множителя в наихудшем случае невозможно. Рассмотрим матрицы $A \in {{\mathbb{R}}^{{(r + 1) \times N}}}$ вида

(5)
$A = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0& \ldots &0 \\ 0& \ddots &0&0&0& \ldots &0 \\ 0&0&1&0&0& \ldots &0 \\ 0&0&0&{\frac{1}{{\sqrt {N - r + 1} }}}&{\frac{1}{{\sqrt {N - r + 1} }}}& \ldots &{\frac{1}{{\sqrt {N - r + 1} }}} \\ 0&0&0&{ - \frac{{\varepsilon \sqrt {N - r} }}{{\sqrt {N - r + 1} }}}&{\frac{\varepsilon }{{\sqrt {N - r} \sqrt {N - r + 1} }}}& \ldots &{\frac{\varepsilon }{{\sqrt {N - r} \sqrt {N - r + 1} }}} \end{array}} \right].$
Каким бы ни было значение $\varepsilon $, матрица максимального объема находится в первых $r$ столбцах. Обозначим эти столбцы через $C,$
$C = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0& \ddots &0&0 \\ 0&0&1&0 \\ 0&0&0&{\frac{1}{{\sqrt {N - r + 1} }}} \\ 0&0&0&{ - \frac{{\varepsilon \sqrt {N - r} }}{{\sqrt {N - r + 1} }}} \end{array}} \right] \in {{\mathbb{R}}^{{(r + 1) \times r}}}.$
Оценим ошибку наилучшего столбцового приближения $CW$ для $A$. Заметим, что такое приближение достигается для матрицы $W = {{C}^{\dag }}A$. Действительно, обозначив через $b$ произвольный столбец в $A$, а через $w$ соответствующий ему столбец $W$, найдем
$\arg \mathop {min}\limits_w \mathop {\left\| {b - Cw} \right\|}\nolimits_2 = {{C}^{\dag }}b.$
Объединив все столбцы в матрицу $W$, получим $W = {{C}^{\dag }}A$. Поскольку ранг проектора $I - C{{C}^{\dag }}$ равен $1$, то матрица ошибки приближения $A - C{{C}^{\dag }}A$ будет ранга $1,$ и
${{\left\| {A - C{{C}^{\dag }}A} \right\|}_{2}} = {{\left\| {A - C{{C}^{\dag }}} \right\|}_{F}}.$
Прямыми вычислениями получаем
$\mathop {\left\| {A - C{{C}^{\dag }}A} \right\|}\nolimits_2 = \mathop {\left\| {A - \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0 \\ 0& \ddots &0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&{\frac{1}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}}&{\frac{{\varepsilon \sqrt {N - r} }}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}} \\ 0&0&0&{\frac{{\varepsilon \sqrt {N - r} }}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}}&{\frac{{{{\varepsilon }^{2}}\left( {N - r} \right)}}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}} \end{array}} \right]A} \right\|}\nolimits_2 .$
Учитывая то, что ошибка приближения в каждом из столбцов с номерами больше $r$ одна и та же, и то, что для одного столбца верно равенство
$\frac{{\mathop {\left\| {A - C{{C}^{\dag }}A} \right\|}\nolimits_2 }}{{\sqrt {N - r} }} = \mathop {\left\| {\left[ {\begin{array}{*{20}{c}} {1 - \frac{1}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}}&{\frac{{\varepsilon \sqrt {N - r} }}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}} \\ {\frac{{\varepsilon \sqrt {N - r} }}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}}&{1 - \frac{{{{\varepsilon }^{2}}\left( {N - r} \right)}}{{1 + {{\varepsilon }^{2}}\left( {N - r} \right)}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt {N - r + 1} }}} \\ {\frac{\varepsilon }{{\sqrt {N - r} \sqrt {N - r + 1} }}} \end{array}} \right]} \right\|}\nolimits_2 ,$
приходим к оценке
$\mathop {\left\| {A - C{{C}^{\dag }}A} \right\|}\nolimits_2 \geqslant \sqrt {N - r} \mathop {\left\| {\left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{{\varepsilon \left( {\sqrt {N - r} - 1{\text{/}}\sqrt {N - r} } \right)}}{{\left( {1 + {{\varepsilon }^{2}}\left( {N - r} \right)} \right)\sqrt {N - r + 1} }}} \end{array}} \right]} \right\|}\nolimits_2 = \varepsilon \Omega (\sqrt {N - r} ).$
Осталось заметить, что крестовое приближение, являясь частным случаем столбцового ($CUR$ = $CW$ для $W = UR$), не может давать оценку лучше.

Таким образом, при больших $N$ для крестовых алгоритмов, основанных на принципе максимального объема, нельзя гарантировать высокую точность получаемых приближений. Тем не менее наблюдаемая на практике высокая эффективность таких алгоритмов говорит в пользу того, что примеры, подобные рассмотренному выше, встречаются редко. Обоснование данного наблюдения является целью настоящей работы.

3. ВЕРОЯТНОСТНАЯ МЕРА

Формализуем понятие редкости, определив RANDSVD ансамбль на матрицах с фиксированными сингулярными числами.

Определение 1. Будем говорить, что $A$ является случайной и писать

$A \sim RANDSVD(\Sigma ),$
если она выбирается из множества матриц вида
$A = {{W}_{L}}\Sigma {{W}_{R}},$
где $\Sigma \in {{\mathbb{C}}^{{M \times N}}}$ – фиксированная матрица с неотрицательными элементами ${{\sigma }_{i}}$ на диагонали, а ${{W}_{L}} \in {{\mathbb{C}}^{{M \times M}}}$ и ${{W}_{R}} \in {{\mathbb{C}}^{{N \times N}}}$ – независимые случайные унитарные матрицы с определенной для них инвариантной мерой Хаара. Без ограничения общности считаем, что диагональные элементы ${{\sigma }_{i}}$ матрицы $\Sigma $ упорядочены в порядке невозрастания ${{\sigma }_{i}} \geqslant {{\sigma }_{{i + 1}}}.$

В соответствии с определением ансамбль RANDSVD($\Sigma $) получает структуру вероятностного пространства и содержит все матрицы, имеющие одну и ту же матрицу сингулярных чисел $\Sigma $. Редкие события будут определяться множествами матриц, имеющих малую вероятностную меру.

Замечание 1. RANDSVD ансамбль является довольно известной конструкцией в вычислительной математике. Случайную RANDSVD матрицу для некоторых распределений сингулярных чисел можно получить в Matlab с помощью вызова функции $gallery\left( {`randsvd', ...} \right)$. Кроме того, RANDSVD ансамбли используются при тестировании программного пакета LAPACK. LAPACK функция $zlange$ позволяет получить матрицу из данного ансамбля.

4. СТОЛБЦОВЫЕ АППРОКСИМАЦИИ

Вероятностную меру на множестве матриц можно использовать для получения разнообразных оценок в среднем. Нас будут интересовать средние погрешности некоторых малоранговых приближений. Мы начнем исследование со случая так называемых столбцовых приближений.

Столбцовым приближением ранга $r$ матрицы $A$ называется выражение вида $CW,$ где $C \in {{\mathbb{C}}^{{M \times n}}}$ – некоторые столбцы $A,$ а $W \in {{\mathbb{C}}^{{n \times M}}}$ – произвольная матрица ранга не выше $r,$ строки которой не обязаны принадлежать линейной оболочке строк $A.$

4.1. Модель RANDSVD шум

Пусть матрица $A$ представляется в виде

$A = Z + F = Z + {{W}_{L}}{{F}_{0}}{{W}_{R}},$
с фиксированной матрицей $Z,$ $\operatorname{rank} Z = r,$ и случайной RANDSVD(${{F}_{0}}$) матрицей $F.$ Таким образом, $A$ является суммой постоянной матрицы малого ранга $Z$ и случайной матрицы шума $F.$

Для матрицы $Z$ запишем ее сингулярное разложение в виде

$Z = U\Sigma V,\quad U \in {{\mathbb{C}}^{{M \times r}}},\quad V \in {{\mathbb{C}}^{{r \times N}}}.$
Сделаем важное наблюдение о том, что подматрица $\hat {Z} \in {{\mathbb{C}}^{{r \times n}}}$ максимального объема в $Z$ располагается в столбцах с теми же номерами, что и подматрица $\hat {V} \in {{\mathbb{C}}^{{r \times n}}}$ максимального объема в матрице $V.$

В дальнейшем мы будем часто использовать свойство ограниченности фробениусовой нормы, псевдообратной для подматрицы максимального объема $\hat {V}$ в ортонормированных строках $V.$

Утверждение 1 (см. [5]). Пусть 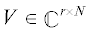– матрица с ортонормированными строками: $VV{\kern 1pt} * = {{I}_{r}},$ а – подматрица матрицы $V$, обладающая наибольшим объемом среди всех подматриц такого размера. Тогда

${{\left\| {{{{\hat {V}}}^{\dag }}} \right\|}_{F}} \leqslant \sqrt {r + \frac{{r(N - n)}}{{n - r + 1}}} .$

Кроме того, нам понадобится следующая простая

Лемма 1. Для произвольных фиксированных матриц $A$ и $B$ выполняется следующее соотношение:

${{\mathbb{E}}_{W}}\left\| {AWB} \right\|_{F}^{2} = \frac{{\left\| A \right\|_{F}^{2}\left\| B \right\|_{F}^{2}}}{N},$
где математическое ожидание берется по множеству случайных унитарных матриц $W \in {{\mathbb{C}}^{{N \times N}}}$ с заданной на них инвариантной мерой Хаара.

Доказательство. Пусть $A = {{U}_{A}}{{\Sigma }_{A}}{{V}_{A}}$ и $B = {{U}_{B}}{{\Sigma }_{B}}{{V}_{B}}$ – сингулярные разложения матриц $A$ и $B$. Тогда

$\left\| {AWB} \right\|_{F}^{2} = \left\| {{{U}_{A}}{{\Sigma }_{A}}{{V}_{A}}W{{U}_{B}}{{\Sigma }_{B}}{{W}_{B}}} \right\|_{F}^{2} = \left\| {{{\Sigma }_{A}}{{V}_{A}}W{{U}_{B}}{{\Sigma }_{B}}} \right\|_{F}^{2}.$
В силу унитарной инвариантности меры Хаара матрица $W{\kern 1pt} ' = {{V}_{A}}W{{U}_{B}}$ сама является случайной унитарной матрицей.

Представив квадрат нормы Фробениуса в виде суммы квадратов всех элементов ${{\Sigma }_{A}}W{\kern 1pt} '{{\Sigma }_{B}},$ и воспользовавшись тем, что для каждого элемента случайной унитарной матрицы $W{\kern 1pt} '$ справедливо соотношение $\mathbb{E}[{\kern 1pt} {\text{|}}{{w}_{{ij}}}{\kern 1pt} {{{\text{|}}}^{2}}] = 1{\text{/}}N$, запишем:

${{\mathbb{E}}_{W}}\left\| {AWB} \right\|_{F}^{2} = \sum\limits_{ij} \,{\text{|}}v_{{ij}}^{'}{\kern 1pt} {{{\text{|}}}^{2}}\sigma _{i}^{2}(A)\sigma _{j}^{2}(B) = \sum\limits_{ij} \,\frac{1}{N}\sigma _{i}^{2}(A)\sigma _{j}^{2}(B) = \frac{{\left\| A \right\|_{F}^{2}\left\| B \right\|_{F}^{2}}}{N}.$
Последнее равенство доказывает утверждение леммы.

Теперь мы готовы сформулировать теорему о средней точности столбцовых приближений.

Теорема 2. Пусть $A = Z + F$, $F \in $ RANDSVD $({{F}_{0}})$, $\operatorname{rank} Z = r,$ и

$Z = U\Sigma V,\quad U \in {{\mathbb{C}}^{{M \times r}}},\quad V \in {{\mathbb{C}}^{{r \times N}}},$
есть сингулярное разложение $Z.$ Если столбцы $C \in {{\mathbb{C}}^{{M \times n}}}$ матрицы $A$ выбираются как столбцы, соответствующие подматрице $\hat {V} \in {{\mathbb{C}}^{{r \times n}}},$ являющейся подматрицей максимального объема среди всех $r \times n$ подматриц матрицы $V,$ то

${{\mathbb{E}}_{{{{W}_{L}},{{W}_{R}}}}}\left[ {\left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2}} \right] \leqslant \frac{{n + 1}}{{n - r + 1}}\left\| F \right\|_{F}^{2}.$

Доказательство. Для доказательства теоремы прежде всего получим общее выражение погрешности.

Поскольку для столбцов $C$ матрицы $A$ выполняется соотношение

$C = U\Sigma \hat {V} + {{F}_{C}},$
с матрицей ${{F}_{C}},$ составленной из столбцов матрицы $F,$ соответствующих столбцам $C,$ то для ошибки столбцового приближения с матрицей $W = {{\hat {V}}^{\dag }}V$ справедливо представление
(6)
$A - C{{\hat {V}}^{\dag }}V = Z + F - (U\Sigma \hat {V} + {{F}_{C}}){{\hat {V}}^{\dag }}V = F - {{F}_{C}}{{\hat {V}}^{\dag }}V = F - F{{P}_{C}}{{\hat {V}}^{\dag }}V.$
Матрица ${{P}_{C}}$ составлена из столбцов единичной матрицы, для которых $A{{P}_{C}} = C,$ ${{F}_{C}} = F{{P}_{C}}$ и, соответственно, $\hat {V} = V{{P}_{C}}$. Используя тождество $I = (I - V{\kern 1pt} *{\kern 1pt} V) + V{\kern 1pt} *{\kern 1pt} V$ и применяя равенства $\hat {V} = V{{P}_{C}}$ и ${{\hat {V}}^{\dag }}\hat {V} = {{I}_{r}},$ преобразуем (6) к виду
(7)
$\begin{gathered} A - C{{{\hat {V}}}^{\dag }}V = F - F(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{{\hat {V}}}^{\dag }}V - FV{\kern 1pt} *{\kern 1pt} V{{P}_{C}}{{{\hat {V}}}^{\dag }}V = \\ \, = F - F(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{{\hat {V}}}^{\dag }}V - FV{\kern 1pt} *{\kern 1pt} V. \\ \end{gathered} $
Объединяя первое и третье слагаемые в (7), представим ошибку как сумму двух ортогональных слагаемых
(8)
$A - C{{\hat {V}}^{\dag }}V = F(I - V{\kern 1pt} *{\kern 1pt} V) - F(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{\hat {V}}^{\dag }}V.$
В силу столбцовой ортогональности матриц в правой части (8) справедливо равенство
(9)
$\begin{gathered} \left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2} = \left\| {F(I - V{\kern 1pt} *{\kern 1pt} V)} \right\|_{F}^{2} + \left\| {F(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2} = \\ \, = \left\| {{{F}_{0}}{{W}_{R}}(I - V{\kern 1pt} *{\kern 1pt} V)} \right\|_{F}^{2} + \left\| {{{F}_{0}}{{W}_{R}}(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{{\hat {V}}}^{\dag }}} \right\|_{F}^{2}, \\ \end{gathered} $
где мы учли, что фробениусова норма не меняется при умножении на ортонормированные строки $V$.

Применение леммы 1 к первому слагаемому в (9) приведет к оценке

(10)
${{\mathbb{E}}_{{{{W}_{R}}}}}\left[ {\left\| {{{F}_{0}}{{W}_{R}}(I - V{\kern 1pt} *{\kern 1pt} V)} \right\|_{F}^{2}} \right] = \frac{{\left\| F \right\|_{F}^{2}\left\| {I - V{\kern 1pt} *{\kern 1pt} V} \right\|_{F}^{2}}}{N} = \left\| F \right\|_{F}^{2}\frac{{N - r}}{N} = \left\| F \right\|_{F}^{2} - \frac{r}{N}\left\| F \right\|_{F}^{2}.$
Аналогично для второго слагаемого с $B = (I - {{V}^{ * }}V){{P}_{C}}\mathop {\hat {V}}\nolimits^\dag $ справедливо неравенство
${{\mathbb{E}}_{{{{W}_{R}}}}}\left[ {\left\| {{{F}_{0}}{{W}_{R}}(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}\mathop {\hat {V}}\nolimits^\dag } \right\|_{F}^{2}} \right] = \frac{{\left\| F \right\|_{F}^{2}\left\| {(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}\mathop {\hat {V}}\nolimits^\dag } \right\|_{F}^{2}}}{N} \leqslant \left\| F \right\|_{F}^{2}\frac{{\left\| {\mathop {\hat {V}}\nolimits^\dag } \right\|_{F}^{2}}}{N}.$
Так как $\hat {V}$ – подматрица максимального объема, то согласно утверждению 1 имеем
$\left\| {{{{\hat {V}}}^{\dag }}} \right\|_{F}^{2} \leqslant r + \frac{{r(N - n)}}{{n - r + 1}}$
и
${{\mathbb{E}}_{{{{W}_{R}}}}}\left[ {\left\| {{{F}_{0}}{{W}_{R}}(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{{\hat {V}}}^{\dag }}} \right\|_{F}^{2}} \right] \leqslant \left\| F \right\|_{F}^{2}\left( {\frac{r}{{n - r + 1}} + \frac{r}{N}} \right).$
Суммируя последнее выражение с (10), получаем

${{\mathbb{E}}_{{{{W}_{R}}}}}\left[ {\left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2}} \right] \leqslant \left\| F \right\|_{F}^{2} - \frac{r}{N}\left\| F \right\|_{F}^{2} + \frac{r}{{n - r + 1}}\left\| F \right\|_{F}^{2} + \frac{r}{N}\left\| F \right\|_{F}^{2} = \frac{{n + 1}}{{n - r + 1}}\left\| F \right\|_{F}^{2}.$

Замечание 2. Оценка из теоремы 2 близка по виду к результату [7]

$\mathbb{E}\left[ {\left\| {A - C{{C}^{\dag }}A} \right\|_{F}^{2}} \right] \leqslant \frac{{n + 1}}{{n - r + 1}}\left\| {A - {{A}_{r}}} \right\|_{F}^{2}.$
Однако смысл усреднений различен. В случае [7] матрица $A$ фиксирована, и усреднение берется по группам столбцов. В случае теоремы 2 усреднение берется по ансамблю матриц $A = Z + F.$

Замечание 3. Часть приведенных выше рассуждений можно применить для доказательства небольшой величины ошибки столбцовой аппроксимации даже в том случае, когда матрица $F$ не является случайной, но ее 2-норма сильно меньше нормы Фробениуса.

Действительно, из формулы (9) следует

$\begin{gathered} \mathop {\left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|}\nolimits_F^2 = \mathop {\left\| {F\left( {I - V{\kern 1pt} *{\kern 1pt} V} \right)} \right\|}\nolimits_F^2 + \mathop {\left\| {F\left( {I - V{\kern 1pt} *{\kern 1pt} V} \right){{P}_{C}}{{{\hat {V}}}^{\dag }}} \right\|}\nolimits_F^2 \leqslant \mathop {\left\| F \right\|}\nolimits_F^2 + \mathop {\left\| F \right\|}\nolimits_2^2 \mathop {\left\| {\left( {I - V{\kern 1pt} *{\kern 1pt} V} \right){{P}_{C}}{{{\hat {V}}}^{\dag }}} \right\|}\nolimits_F^2 = \\ \, = \mathop {\left\| F \right\|}\nolimits_F^2 + \mathop {\left\| F \right\|}\nolimits_2^2 \left( {\mathop {\left\| {{{{\hat {V}}}^{\dag }}} \right\|}\nolimits_F^2 - \mathop {\left\| {V{\kern 1pt} *{\kern 1pt} \hat {V}{{{\hat {V}}}^{\dag }}} \right\|}\nolimits_F^2 } \right) = \mathop {\left\| F \right\|}\nolimits_F^2 + \mathop {\left\| F \right\|}\nolimits_2^2 \left( {\mathop {\left\| {{{{\hat {V}}}^{\dag }}} \right\|}\nolimits_F^2 - r} \right) \leqslant \mathop {\left\| F \right\|}\nolimits_F^2 + \frac{{r(N - n)}}{{n - r + 1}}\mathop {\left\| F \right\|}\nolimits_2^2 . \\ \end{gathered} $
Данная оценка гарантирует эффективность выбора приближения на основе подматрицы максимального объема, когда сингулярные числа погрешности одинаковы или почти одинаковы.

4.2. Модель RANDSVD матрица

Рассмотрим другую вероятностную модель. А именно, предположим, что сами матрицы $A$ берутся из RANDSVD ансамбля. Анализ этого случая сложнее. Если в доказательстве теоремы 2 положение “хороших” столбцов $C$ в матрице $A$ не менялось от выбора случайной матрицы, то теперь это не так. Все столбцы в RANDSVD ансамбле равноправны, а положение столбцов, содержащих подматрицу большого объема, имеет случайный характер. Чтобы учесть это обстоятельство при вычислении средних погрешностей, нам понадобится обобщение леммы 1.

Лемма 2. Для случайной унитарной матрицы $W \in {{\mathbb{C}}^{{N \times N}}}$ будем рассматривать ее блочное представление вида

$W = \left[ {\begin{array}{*{20}{c}} {{{W}_{1}}} \\ {{{W}_{2}}} \end{array}} \right],$
где ${{W}_{1}} \in {{\mathbb{C}}^{{r \times N}}}$ – ее первые $r$ строк, а ${{W}_{2}} \in {{\mathbb{C}}^{{(N - r) \times N}}}$ – оставшиеся $N - r$ строк. Определим случайную матрицу $F$ соотношением вида
$F = {{F}_{2}}{{W}_{2}}$
с фиксированной матрицей ${{F}_{2}} \in {{\mathbb{C}}^{{M \times (N - r)}}}$.

Пусть ${{P}_{C}} \in {{\mathbb{C}}^{{M \times k}}}$ составлена из некоторых столбцов единичной матрицы, а ${{F}_{C}},$ как и ранее, определяется выражением ${{F}_{C}} = F{{P}_{C}}.$ Пусть, наконец, $G \in {{\mathbb{C}}^{{k \times K}}}$ – произвольная матрица.

Тогда для условного матожидания по $W$ при фиксированных строках ${{W}_{1}}$ справедливо неравенство

(11)
${{\mathbb{E}}_{W}}\left[ {\left\| {{{F}_{C}}G} \right\|_{F}^{2}\,{\text{|}}\,{{W}_{1}}} \right] \leqslant \frac{{\left\| {{{F}_{2}}} \right\|_{F}^{2}\left\| G \right\|_{F}^{2}}}{{N - r}}\left( {1 - \frac{{\left\| {{{W}_{1}}{{P}_{C}}G} \right\|_{F}^{2}}}{{\left\| G \right\|_{F}^{2}}}} \right).$

Доказательство. Пусть ${{F}_{2}} = {{U}_{F}}{{\Sigma }_{F}}{{V}_{F}}$ – сингулярное разложение матрицы ${{F}_{2}}$. Определим матрицу $\Psi $ в виде

$\Psi = \left[ {\begin{array}{*{20}{c}} {{{\Psi }_{1}}} \\ {{{\Psi }_{2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{I}_{{r \times r}}}}&0 \\ 0&{{{V}_{F}}} \end{array}} \right]W = \left[ {\begin{array}{*{20}{c}} {{{W}_{1}}} \\ {{{V}_{F}}{{W}_{2}}} \end{array}} \right].$
В силу унитарной инвариантности меры Хаара матрицы $\Psi $ имеют то же распределение, что и матрицы $W.$ Теперь ${{F}_{C}}$ можно представить в виде
(12)
${{F}_{C}} = {{U}_{F}}{{\Sigma }_{F}}{{\Psi }_{2}}{{P}_{C}}.$
Подставим (12) в $\left\| {{{F}_{C}}G} \right\|_{F}^{2}$ и воспользуемся унитарной инвариантностью фробениусовой нормы. Тогда
$\left\| {{{F}_{C}}G} \right\|_{F}^{2} = \left\| {{{U}_{F}}{{\Sigma }_{F}}{{\Psi }_{2}}{{P}_{C}}G} \right\|_{F}^{2} = \left\| {{{\Sigma }_{F}}{{\Psi }_{2}}{{P}_{C}}G} \right\|_{F}^{2}.$
Представим $\left\| {{{\Sigma }_{F}}{{\Psi }_{2}}{{P}_{C}}G} \right\|_{F}^{2}$ как сумму квадратов $2$-норм строк
(13)
$\left\| {{{F}_{C}}G} \right\|_{F}^{2} = \left\| {{{\Sigma }_{F}}{{\Psi }_{2}}{{P}_{C}}G} \right\|_{F}^{2} = \sum\limits_{k = 1}^{N - r} \,\sigma _{k}^{2}({{F}_{2}})\left\| {{{{({{\Psi }_{2}}{{P}_{C}})}}_{k}}G} \right\|_{2}^{2},$
где обозначение ${{({{\Psi }_{2}}{{P}_{C}})}_{k}}$ используется для строки матрицы ${{\Psi }_{2}}{{P}_{C}}$ с номером $k.$ Заметим, что строки ${{({{\Psi }_{2}}{{P}_{C}})}_{k}}$ распределены одинаково (это очевидным образом следует из того, что строки матрицы ${{W}_{2}}$ распределены одинаково). Более того, одинаково распределенными являются и строки ${{({{\Psi }_{2}}{{P}_{C}})}_{k}}G.$ Следовательно, учитывая ${{\Psi }_{1}} = {{W}_{1}},$ для произвольного $k$ получаем
(14)
$\begin{gathered} {{\mathbb{E}}_{\Psi }}\left[ {\left\| {{{{({{\Psi }_{2}}{{P}_{C}})}}_{k}}G} \right\|_{2}^{2}{{\Psi }_{1}}} \right] = \frac{1}{{N - r}}{{\mathbb{E}}_{\Psi }}\left[ {\sum\limits_{k = 1}^{N - r} \,\left\| {{{{({{\Psi }_{2}}{{P}_{C}})}}_{k}}G} \right\|_{2}^{2}{{\Psi }_{1}}} \right] = \\ = \frac{1}{{N - r}}{{\mathbb{E}}_{\Psi }}\left[ {\left\| {{{\Psi }_{2}}{{P}_{C}}G} \right\|_{F}^{2}{{\Psi }_{1}}} \right] = \frac{1}{{N - r}}{{\mathbb{E}}_{\Psi }}\left[ {\left( {\left\| {\Psi {{P}_{C}}G} \right\|_{F}^{2} - \left\| {{{\Psi }_{1}}{{P}_{C}}G} \right\|_{F}^{2}} \right){{\Psi }_{1}}} \right]. \\ \end{gathered} $
Поскольку второе слагаемое в (14) не меняется при усреднении, то имеем
(15)
${{\mathbb{E}}_{\Psi }}\left[ {\left\| {{{{({{\Psi }_{2}}{{P}_{C}})}}_{k}}G} \right\|_{2}^{2}\,{\text{|}}\,{{\Psi }_{1}}} \right] \leqslant \frac{1}{{N - r}}{{\mathbb{E}}_{\Psi }}\left[ {\left\| {\Psi {{P}_{C}}} \right\|_{2}^{2}\left\| G \right\|_{F}^{2}\,{\text{|}}\,{{\Psi }_{1}}} \right] - \frac{{\left\| {{{\Psi }_{1}}{{P}_{C}}G} \right\|_{F}^{2}}}{{N - r}} = \frac{{\left\| G \right\|_{F}^{2}}}{{N - r}}\left( {1 - \frac{{\left\| {{{W}_{1}}{{P}_{C}}G} \right\|_{F}^{2}}}{{\left\| G \right\|_{F}^{2}}}} \right).$
Усредняя (13) и подставляя в него (15), для ${{\mathbb{E}}_{W}}\left[ {\left\| {{{F}_{C}}G} \right\|_{F}^{2}{{W}_{1}}} \right]$ получаем

$\begin{gathered} {{\mathbb{E}}_{W}}\left[ {\left\| {{{F}_{C}}G} \right\|_{F}^{2}{{W}_{1}}} \right] = {{\mathbb{E}}_{\Psi }}\left[ {\sum\limits_{k = 1}^{N - r} \,\sigma _{k}^{2}({{F}_{2}})\left\| {{{{({{\Psi }_{2}}{{P}_{C}})}}_{k}}G} \right\|_{2}^{2}{{W}_{1}}} \right] = \\ = \sum\limits_{k = 1}^{N - r} \,\sigma _{k}^{2}({{F}_{2}}){{\mathbb{E}}_{\Psi }}\left[ {\left\| {{{{({{\Psi }_{2}}{{P}_{C}})}}_{k}}G} \right\|_{2}^{2}{{W}_{1}}} \right] \leqslant \frac{{\left\| {{{F}_{2}}} \right\|_{F}^{2}\left\| G \right\|_{F}^{2}}}{{N - r}} - \frac{{\left\| {{{F}_{2}}} \right\|_{F}^{2}\left\| {{{W}_{1}}{{P}_{C}}G} \right\|_{F}^{2}}}{{N - r}}. \\ \end{gathered} $

Следствие 1. При $r = 0$ мы получаем ${{W}_{2}} = W$, неравенства преобразуются в равенства, и оценка принимает вид

${{\mathbb{E}}_{W}}\left[ {\left\| {{{F}_{C}}G} \right\|_{F}^{2}} \right] = \frac{{\left\| {{{F}_{2}}} \right\|_{F}^{2}\left\| G \right\|_{F}^{2}}}{N},$
соответствующий утверждению леммы 1.

Замечание 4. Заметим, что оценка (11) леммы 2 не зависит от числа $k$ столбцов, которые были выбраны у случайной матрицы $F$ вида $F = {{F}_{2}}{{W}_{2}}$ с помощью проектора ${{P}_{C}}$.

Теперь мы готовы доказать аналог теоремы 2 для случая, когда сама матрица $A$ выбирается случайным образом из ансамбля RANDSVD

$A = {{W}_{L}}({{Z}_{0}} + {{F}_{0}}){{W}_{R}} = Z + F,$
причем ${{W}_{L}}$ и ${{W}_{R}}$ – случайные унитарные матрицы, а ${{Z}_{0}},$ ${\text{rank}}{{Z}_{0}} = r,$ и ${{F}_{0}}$ – фиксированные матрицы.

Теорема 3. Пусть

$A = Z + F = {{W}_{L}}{{Z}_{0}}{{W}_{R}} + {{W}_{L}}{{F}_{0}}{{W}_{R}},$
$A \in $ RANDSVD $({{Z}_{0}} + {{F}_{0}})$, ${\text{rank}}Z = r,$ и
$Z = U\Sigma V,\quad U \in {{\mathbb{C}}^{{M \times r}}},\quad V \in {{\mathbb{C}}^{{r \times N}}},$
есть сингулярное разложение $Z.$ Если столбцы $C \in {{\mathbb{C}}^{{M \times n}}}$ матрицы $A$ выбираются как столбцы, соответствующие подматрице $\hat {V} \in {{\mathbb{C}}^{{r \times n}}},$ являющейся подматрицей максимального объема среди всех $r \times n$ подматриц матрицы $V,$ то верно следующее:

${{\mathbb{E}}_{{{{W}_{L}},{{W}_{R}}}}}\left[ {\left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2}} \right] \leqslant \frac{{n + 1}}{{n - r + 1}}\left\| F \right\|_{F}^{2}.$

Доказательство. Зафиксируем матрицу ${{W}_{L}}.$ Как и ранее, справедливо равенство

(16)
$A - C{{\hat {V}}^{\dag }}V = F - {{F}_{C}}{{\hat {V}}^{\dag }}V.$
Повторяя преобразования из теоремы 2, будем иметь
(17)
$\left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2} = \left\| {F(I - V{\kern 1pt} *{\kern 1pt} V)} \right\|_{F}^{2} + \left\| {F(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{{\hat {V}}}^{\dag }}} \right\|_{F}^{2} \leqslant \left\| F \right\|_{F}^{2} + \left\| {{{F}_{0}}{{W}_{R}}(I - V{\kern 1pt} *{\kern 1pt} V){{P}_{C}}{{{\hat {V}}}^{\dag }}} \right\|_{F}^{2}.$
Займемся оценкой второго слагаемого в (17). Заметим, во-первых, что строки матрицы $V$ являются одинаково распределенными. Действительно, если обозначить через ${{V}_{0}} \in {{\mathbb{C}}^{{r \times N}}}$ правые сингулярные векторы ${{Z}_{0}}$, то $V = {{V}_{0}}{{W}_{R}}$. Кроме того,
$\hat {V} = {{V}_{0}}{{W}_{R}}{{P}_{C}}$
для некоторой матрицы ${{P}_{C}} \in {{\mathbb{C}}^{{N \times n}}},$ составленной из подмножества столбцов единичной матрицы. Подчеркнем, что ${{P}_{C}}$ не является фиксированной матрицей, поскольку выбор позиций столбцов, в которых находится подматрица $\hat {V}$ максимального 2-объема в $V$, вообще говоря, зависит от случайной матрицы ${{W}_{R}}$. В дальнейшем для ${{P}_{C}}$ будем указывать ее явную зависимость от ${{W}_{R}}$ (или других матриц) и писать ${{P}_{C}} = {{P}_{C}}({{W}_{R}}).$

Обозначим матрицу во втором слагаемом в (17) через $\Delta $ и подставим туда полученные выражения для $V$ и $\hat {V}$. Тогда имеем

(18)
$\begin{gathered} \Delta = {{F}_{0}}{{W}_{R}}\left( {I - V{\kern 1pt} *{\kern 1pt} V} \right){{P}_{C}}({{W}_{R}}){{{\hat {V}}}^{\dag }} = {{F}_{0}}{{W}_{R}}\left( {I - ({{V}_{0}}{{W}_{R}}){\kern 1pt} *{\kern 1pt} ({{V}_{0}}{{W}_{R}})} \right){{P}_{C}}({{W}_{R}})\mathop {\left( {{{V}_{0}}{{W}_{R}}{{P}_{C}}({{W}_{R}})} \right)}\nolimits^\dag = \\ \, = {{F}_{0}}(I - V_{0}^{*}{{V}_{0}}){{W}_{R}}{{P}_{C}}({{W}_{R}})\mathop {\left( {{{V}_{0}}{{W}_{R}}{{P}_{C}}({{W}_{R}})} \right)}\nolimits^\dag . \\ \end{gathered} $
Рассмотрим матрицу $F{\kern 1pt} ' = {{F}_{0}}(I - V_{0}^{*}{{V}_{0}})$ с сингулярным разложением $F{\kern 1pt} ' = {{U}_{{F{\kern 1pt} '}}}{{\Sigma }_{{F{\kern 1pt} '}}}{{V}_{{F{\kern 1pt} '}}}.$ Ранг $F{\kern 1pt} '$ не больше $N - r$, ее норма Фробениуса не превосходит ${{\left\| {{{F}_{0}}} \right\|}_{F}}$, а матрица правых сингулярных векторов ${{V}_{{F{\kern 1pt} '}}}$ ортогональна ${{V}_{0}}.$ Подставим ее в (18) и вычислим норму Фробениуса матрицы $\Delta $:
(19)
$\left\| \Delta \right\|_{F}^{2} = \left\| {\Sigma _{F}^{'}V_{F}^{'}{{W}_{R}}{{P}_{C}}({{W}_{R}})\mathop {\left( {{{V}_{0}}{{W}_{R}}{{P}_{C}}({{W}_{R}})} \right)}\nolimits^\dag } \right\|_{F}^{2}.$
Так как ${{V}_{0}}$ и $V_{F}^{'}$ ортогональны и образуют базис в ${{\mathbb{C}}^{N}}$, то соотношение
$\Psi = \left[ {\begin{array}{*{20}{c}} {{{\Psi }_{1}}} \\ {{{\Psi }_{2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{V}_{0}}} \\ {V_{F}^{'}} \end{array}} \right]{{W}_{R}}$
определяет случайную унитарную матрицу $\Psi .$ Более того, введенная ранее матрица ${{P}_{C}}$ определяется только элементами ${{\Psi }_{1}}.$ Действительно,
${{P}_{C}} = arg\mathop {max}\limits_{{{P}_{C}}} \,\operatorname{vol} ({{V}_{0}}{{W}_{R}}{{P}_{C}}) = arg\mathop {max}\limits_{{{P}_{C}}} \,\operatorname{vol} ({{V}_{0}}[\begin{array}{*{20}{c}} {V_{0}^{*}}&{V_{F}^{{*'}}} \end{array}]\Psi {{P}_{C}}) = arg\mathop {max}\limits_{{{P}_{C}}} \,\operatorname{vol} ({{\Psi }_{1}}{{P}_{C}}),$
а потому далее будем писать ${{P}_{C}} = {{P}_{C}}({{\Psi }_{1}})$. После соответствующих замен в (19) получим
(20)
$\left\| \Delta \right\|_{F}^{2} \leqslant \left\| {{{\Sigma }_{F}}{{\Psi }_{2}}{{P}_{C}}({{\Psi }_{1}})\mathop {\left( {{{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})} \right)}\nolimits^\dag } \right\|_{F}^{2}.$
Наконец, применим лемму 2 для оценки математического ожидания $\left\| \Delta \right\|_{F}^{2}$ по $\Psi $ при условии фиксированной ${{\Psi }_{1}}$
(21)
$\begin{gathered} {{\mathbb{E}}_{\Psi }}\left[ {\left\| \Delta \right\|_{F}^{2}{{\Psi }_{1}}} \right] \leqslant \frac{{{\text{|}}{\kern 1pt} {\text{|}}\Sigma _{F}^{'}{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}}_{F}^{2}}}{{N - r}}\mathop {\left\| {\mathop {\left( {{{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})} \right)}\nolimits^\dag } \right\|}\nolimits_F^2 - \frac{{{\text{|}}{\kern 1pt} {\text{|}}\Sigma _{F}^{'}{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}}_{F}^{2}}}{{N - r}}\mathop {\left\| {{{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})\mathop {\left( {{{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})} \right)}\nolimits^\dag } \right\|}\nolimits_F^2 = \\ \, = \frac{{{\text{|}}{\kern 1pt} {\text{|}}\Sigma _{F}^{'}{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}}_{F}^{2}}}{{N - r}}\left( {\mathop {\left\| {\mathop {\left( {{{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})} \right)}\nolimits^\dag } \right\|}\nolimits_F^2 - r} \right) \leqslant \frac{{\left\| F \right\|_{F}^{2}}}{{N - r}}\left( {\mathop {\left\| {\mathop {\left( {{{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})} \right)}\nolimits^\dag } \right\|}\nolimits_F^2 - r} \right). \\ \end{gathered} $
Так как $\hat {V} = {{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})$ подматрица максимального объема в строках ${{\Psi }_{1}}$, то в силу утверждения 1 справедливо неравенство
(22)
$\left\| {\mathop {\left( {{{\Psi }_{1}}{{P}_{C}}({{\Psi }_{1}})} \right)}\nolimits^\dag } \right\|_{F}^{2} \leqslant r + \frac{{r(N - n)}}{{n - r + 1}}.$
Откуда, после подстановки (22) в (21) и сокращений получаем
(23)
${{\mathbb{E}}_{\Psi }}\left[ {\left\| \Delta \right\|_{F}^{2}{{\Psi }_{1}}} \right] \leqslant \frac{r}{{n - r + 1}}\left\| F \right\|_{F}^{2}.$
Правая часть (23) не зависит от ${{\Psi }_{1}}$, поэтому эта же оценка верна и для безусловного среднего ${{\mathbb{E}}_{\Psi }}\left( {\left\| \Delta \right\|_{F}^{2}} \right).$ Окончательно имеем
${{\mathbb{E}}_{{{{W}_{R}}}}}\left[ {\left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2}} \right] = {{\mathbb{E}}_{\Psi }}\left[ {\left\| {A - C{{{\hat {V}}}^{\dag }}V} \right\|_{F}^{2}} \right] \leqslant \left\| F \right\|_{F}^{2} + \frac{r}{{n - r + 1}}\left\| F \right\|_{F}^{2} = \left( {\frac{{n + 1}}{{n - r + 1}}} \right)\left\| F \right\|_{F}^{2}.$
Поскольку оценка справедлива для любой фиксированной ${{W}_{L}},$ то усреднение по ней ничего не изменит, и утверждение теоремы доказано.

Замечание 5. Так как ${{W}_{L}}$ с самого начала фиксировалась, теорема верна и для семейства матриц, где умножение на ${{W}_{L}}$ не производится.

5. ОСНОВНОЙ РЕЗУЛЬТАТ ДЛЯ КРЕСТОВОЙ АППРОКСИМАЦИИ

Наконец, мы готовы перейти к доказательству основного результата о средней точности крестовых аппроксимаций, построенных на основе обобщенного принципа максимального проективного объема для матриц $A$ из RANDSVD ансамбля

$A = Z + F = {{W}_{L}}({{Z}_{0}} + {{F}_{0}}){{W}_{R}}.$

Напомним определение $r$-проективного объема.

Определение 2 (см. [5]). $r$-Проективным объемом матрицы $X$ называется произведение ее первых (наибольших) $r$ сингулярных чисел

${\text{vo}}{{{\text{l}}}_{r}}(X) = \prod\limits_{i = 1}^r \,{{\sigma }_{i}}(X).$

Почему мы говорим об обобщенном принципе максимального объема? На это есть несколько причин, но основной является следующая.

С точки зрения теории крестовых приближений идеальный принцип максимального проективного объема звучит так: если для матрицы $A$ требуется построить $CGR$ приближение ранга не выше $r,$ то в $A$ выбираются подматрица $\hat {A}$ максимального проективного объема, столбцы $C$ и строки $R,$ на пересечении которых стоит $\hat {A},$ а приближение имеет вид

$A \approx C\hat {A}_{r}^{\dag }R,\quad G = \hat {A}_{r}^{\dag },$
где $B_{r}^{\dag }$ обозначает обобщенную обратную для первых $r$ сингулярных чисел $B.$

Наиболее сложная часть данной конструкции состоит в анализе подматрицы максимального проективного объема и ее положения в исходной матрице. В работе мы предлагаем упрощенный подход, который и называем обобщенным принципом максимального проективного объема.

Пусть как и везде ранее

$Z = U\Sigma V,\quad U \in {{\mathbb{C}}^{{M \times r}}},\quad V \in {{\mathbb{C}}^{{r \times N}}}$
есть сингулярное разложение для $Z.$ Будем выбирать столбцы $C,$ строки $R$ и генератор $G$ с помощью следующего алгоритма обобщенного принципа максимального проективного объема:

1) столбцы $C = A{{P}_{C}}$ соответствуют столбцам ${{Z}_{C}} = Z{{P}_{C}},$ содержащим подматрицу максимального проективного объема в $Z;$

2) строки $R$ соответствуют подматрице максимального проективного объема в матрице $CZ_{C}^{\dag }Z;$

3) если $\hat {A}$ обозначает подматрицу матрицы $A,$ стоящую на пересечении столбцов $C$ и строк $R,$ то $G = \mathop {\left( {\hat {A}Z_{C}^{\dag }{{Z}_{C}}} \right)}\nolimits^\dag = \mathop {\left( {A\mathcal{P}} \right)}\nolimits^\dag ,$ где $\mathcal{P} = Z_{C}^{\dag }{{Z}_{C}}$ – ортопроектор на пространство размерности $r.$

Справедлива следующая

Теорема 4. Пусть $A \in $ RANDSVD $({{Z}_{0}} + {{F}_{0}})$

$A = Z + F = {{W}_{L}}{{Z}_{0}}{{W}_{R}} + {{W}_{L}}{{F}_{0}}{{W}_{R}},$
$\operatorname{rank} Z = r,$ и
$Z = U\Sigma V,\quad U \in {{\mathbb{C}}^{{M \times r}}},\quad V \in {{\mathbb{C}}^{{r \times N}}},$
есть сингулярное разложение $Z.$ Пусть столбцы $C \in {{\mathbb{C}}^{{M \times n}}},$ строки $R \in {{\mathbb{C}}^{{m \times N}}}$ и генератор $G \in {{\mathbb{C}}^{{n \times m}}}$ выбираются в соответствии с обобщенным принципом максимального проективного объема. Тогда имеем

${{\mathbb{E}}_{{{{W}_{L}},{{W}_{R}}}}}\left[ {\left\| {A - CGR} \right\|_{F}^{2}} \right] \leqslant \frac{{m + 1}}{{m - r + 1}}\frac{{n + 1}}{{n - r + 1}}\left\| F \right\|_{F}^{2}.$

Доказательство. Начнем доказательство с важного наблюдения. Рассмотрим произвольную матрицу $X \in {{\mathbb{C}}^{{M \times N}}}$ ранга $r.$ Пусть $X = {{U}_{X}}{{\Sigma }_{X}}{{V}_{X}}$ – сингулярное разложение $X$ с матрицами ${{U}_{X}} \in {{\mathbb{C}}^{{M \times r}}}$ и ${{V}_{X}} \in {{\mathbb{C}}^{{r \times N}}}.$ Тогда подматрица $\hat {X} \in {{\mathbb{C}}^{{m \times n}}}$ максимального проективного объема в $X$ удовлетворяет соотношению

$\hat {X} = {{\hat {U}}_{X}}{{\Sigma }_{X}}{{\hat {V}}_{X}},\quad {{\hat {U}}_{X}} \in {{\mathbb{C}}^{{m \times r}}},\quad {{\hat {V}}_{X}} \in {{\mathbb{C}}^{{r \times n}}},$
с подматрицами ${{\hat {U}}_{X}}$ и ${{\hat {V}}_{X}}$, имеющими максимальный объем в ${{U}_{X}}$ и ${{V}_{X}}$ соответственно.

Принимая во внимание выбор столбцов $C$ в матрице $A,$ можем записать

(24)
$CZ_{C}^{\dag }Z = C{{(U\Sigma \hat {V})}^{\dag }}U\Sigma V = C{{(\Sigma \hat {V})}^{\dag }}{{U}^{ * }}U\Sigma V = C{{(\Sigma \hat {V})}^{\dag }}\Sigma V = C{{(\hat {V})}^{\dag }}{{\Sigma }^{{ - 1}}}\Sigma V = C{{(\hat {V})}^{\dag }}V.$
По замечанию к теореме 3, приближение ранга $r$ вида $CZ_{C}^{\dag }Z$ в среднем обладает хорошими аппроксимационными свойствами. А именно,
(25)
${{\mathbb{E}}_{{{{W}_{R}}}}}\left[ {\left\| {A - CZ_{C}^{\dag }Z} \right\|_{F}^{2}} \right] = {{\mathbb{E}}_{{{{W}_{R}}}}}\left[ {\left\| {A - C{{{(\hat {V})}}^{\dag }}V} \right\|_{F}^{2}} \right] \leqslant \frac{{n + 1}}{{n - r + 1}}\left\| F \right\|_{F}^{2}.$
Обозначим через $\Phi $ матрицу $\Phi = CZ_{C}^{\dag }Z.$ Очевидным образом ранг $\Phi $ не превосходит $r.$ Применяя замечание к теореме 3 к $\Phi $ (только теперь рассматривается строчное приближение), запишем
(26)
$\begin{gathered} {{\mathbb{E}}_{{{{W}_{L}}}}}\left\| {A - \Phi \Phi _{R}^{\dag }R} \right\|_{F}^{2} = {{\mathbb{E}}_{{{{W}_{L}}}}}\left\| {A - C{{{(P_{R}^{T}CZ_{C}^{\dag }{{Z}_{C}})}}^{\dag }}R} \right\|_{F}^{2} = \\ \, = {{\mathbb{E}}_{{{{W}_{L}}}}}\left\| {A - C{{{(\hat {A}Z_{C}^{\dag }{{Z}_{C}})}}^{\dag }}R} \right\|_{F}^{2} \leqslant \frac{{m + 1}}{{m - r + 1}}\left\| {A - \Phi } \right\|_{F}^{2}, \\ \end{gathered} $
где по аналогии с ${{P}_{C}}$ матрица ${{P}_{R}}$ составлена из соответствующих столбцов единичной матрицы, а $\hat {A} = P_{R}^{T}A{{P}_{C}}$ – подматрица с большим проективным объемом. Комбинируя (25) и (26), заканчиваем доказательство теоремы

$\begin{gathered} {{\mathbb{E}}_{{{{W}_{L}},{{W}_{R}}}}}\left\| {A - CGR} \right\|_{F}^{2} = {{\mathbb{E}}_{{{{W}_{R}}}}}\left( {{{\mathbb{E}}_{{{{W}_{L}}}}}\left\| {A - C{{{(\hat {A}Z_{C}^{\dag }{{Z}_{C}})}}^{\dag }}R} \right\|_{F}^{2}} \right) \leqslant \frac{{m + 1}}{{m - r + 1}}{{\mathbb{E}}_{{{{W}_{R}}}}}\left\| {A - CZ_{C}^{\dag }Z} \right\|_{F}^{2} \leqslant \\ \, \leqslant \frac{{m + 1}}{{m - r + 1}}\frac{{n + 1}}{{n - r + 1}}\left\| {A - CZ_{C}^{\dag }Z} \right\|_{F}^{2} = \frac{{m + 1}}{{m - r + 1}}\frac{{n + 1}}{{n - r + 1}}\left\| F \right\|_{F}^{2}. \\ \end{gathered} $

Замечание 6. При $r = m = n$ коэффициент будет равен ${{(r + 1)}^{2}}$. Интересно, что тот же коэффициент наблюдается в аппроксимации по норме Чебышёва [10], и при усреднении по подматрицам с вероятностью, пропорциональной квадрату их объема [8]. В этом случае можно в условиях теоремы использовать понятие объема вместо проективного объема.

Тот факт, что коэффициент при ошибке крестовой аппроксимации является произведением коэффициентов для столбцовой и строковой аппроксимации, встречается в различных работах. Например, при переходе от $r + 1$ в столбцовой аппроксимации [9] к ${{(r + 1)}^{2}}$ в крестовой [8]. Та же ситуация наблюдается и в случае известных оценок точности малоранговых приближений в спектральной норме [5], [11], [12]. Наконец, аналогичное произведение появляется при оценке ошибки неполного LU разложения [13], которое основано на алгоритме неполного QR разложения [14].

Замечание 7. Тот факт, что подматрица $\hat {A},$ определяемая алгоритмом для обобщенного принципа максимального проективного объема, действительно обладает большим проективным объемом, едва ли вызывает сомнения. Однако конструкция обобщенного принципа имеет еще одно существенное отличие от конструкции “идеального”. А именно, в идеальной конструкции $G = \hat {A}_{r}^{\dag }$. В то же время для обобщенной конструкции $G = {{(\hat {A}\mathcal{P})}^{r}} = (\hat {A}\mathcal{P})_{r}^{\dag }$, с проектором $\mathcal{P} = Z_{C}^{\dag }{{Z}_{C}} = {{\hat {V}}^{\dag }}\hat {V}$. Подробный теоретический анализ этого различия выходит за рамки данной статьи. Практика показывает, что отличие несущественное.

6. СВЯЗЬ С ЧИСЛЕННЫМИ АЛГОРИТМАМИ

Прежде всего следует указать на то, что все доказанные результаты остаются в силе в случае замены подматриц максимального объема на подматрицы локально максимального объема.

Определение 3. Говорят, что подматрица $\hat {A}$ матрицы $A$ обладает локально максимальным объемом в матрице $A$, если объем любой другой подматрицы $\tilde {A}$ того же размера, и отличающейся от $\hat {A}$ не более чем в одной строке и в одном столбце

${\text{vol}}\left( {\tilde {A}} \right) \leqslant {\text{vol}}\left( {\hat {A}} \right).$

Алгоритмы maxvol [15] и Dominant-C [16] позволяют находить подматрицы локально максимального объема в предписанных строках и/или столбцах, а потому формально позволяют достичь доказанных ранее результатов, если только матрица $Z$ известна.

На практике наилучшее приближение $Z = {{A}_{r}}$ является неизвестным. Задача состоит именно в поиске приближения, близкого к наилучшему. Для этого поиск ведется в самой матрице $A$, а вместо проектора $P$ используется сокращенное сингулярное разложение подматрицы $\hat {A}$, что приводит к аппроксимации вида $C\hat {A}_{r}^{\dag }R$. В связи с тем, что доказанные выше результаты уже не гарантируют оценки ошибки ${{\left\| {A - C\hat {A}_{r}^{\dag }R} \right\|}_{F}}$, представляет интерес то, насколько ошибка на практике близка к той, что указана в теоремах. А именно, выполняется ли неравенство

(27)
$\mathbb{E}\left\| {A - C\hat {A}_{r}^{\dag }R} \right\|_{F}^{2} \leqslant \frac{{m + 1}}{{m - r + 1}}\frac{{n + 1}}{{n - r + 1}}\left\| {A - {{A}_{r}}} \right\|_{F}^{2}.$
Для более точного сравнения уточним смысл доказанных результатов. А именно, вместо того, чтобы явно оценивать ${\text{||}}\hat {V}{\text{||}}_{F}^{2}$ сверху, заменим оценку на ${{\mathbb{E}}_{V}}\left\| {\hat {V}} \right\|_{F}^{2}$, где $\hat {V}$ ищется как подматрица с локально максимальным объемом. В этом случае коэффициенты в (27) изменятся следующим образом:
(28)
Выражение (28) является наиболее близкой гипотезой. Матожидания вида ${{\mathbb{E}}_{V}}\left\| {\hat {V}} \right\|_{F}^{2}$ можно получить путем отдельной (независимой от $A$) генерации матриц $U$ и $V$, поиска в них подматриц локально максимального объема и последующего усреднения.

На фиг. 1 показаны численные значения величины $\left\| {A - C\hat {A}_{r}^{\dag }R} \right\|_{F}^{2}$ на основе алгоритмов, не использующих знания матрицы $Z$, в сравнении с правой частью (28).

Фиг. 1.

Кружки обозначают значения ${{\left\| {A - C\hat {A}_{r}^{\dag }R} \right\|}_{F}}{\text{/}}{{\left\| {A - {{A}_{r}}} \right\|}_{F}}$ для случайных $A \in {{\mathbb{R}}^{{N \times N}}}$, $N = 1000$, с сингулярными числами ${{\sigma }_{1}} = ... = {{\sigma }_{r}} = 100{{\sigma }_{{r + 1}}} = ... = 100{{\sigma }_{N}}$. Значения ошибки получены с помощью алгоритма maxvol-proj [16]. Линии показывают ожидаемое значение коэффициента аппроксимации для каждого ранга и размера. Данный коэффициент равен 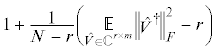. Различные цвета показывают результаты для различных размеров подматрицы $\hat {A} \in {{\mathbb{C}}^{{m \times n}}}$: $m = n = r$, $m = n = 2r$ и $m = n = 4r$.

Как видим, численные значения ошибки близки к предсказанным теоретически и обладают малой дисперсией, особенно при числе строк и столбцов, большем $r$. Более подробные эксперименты из [16] также подтверждают гипотезу (28).

Использованные для тестирования процедуры поиска подматриц локально максимального объема и большого проективного объема доступны в GitHub:

https://github.com/RodniO/Projective-volume-low-rank

7. ЗАКЛЮЧЕНИЕ

Полученные результаты показывают, что в определенном смысле для большинства матриц принцип максимального объема позволяет строить столбцовые и крестовые аппроксимации высокой точности с небольшим числом дополнительных строк и столбцов. Полученные оценки имеют тот же коэффициент вида $\tfrac{{n + 1}}{{n - r + 1}}$, что и наилучшие известные оценки крестовой и столбцовой аппроксимации и имеют ту же асимптотическую зависимость от числа строк и столбцов, что и наилучшие оценки снизу.

Список литературы

  1. Halko N., Martinsson P., Tropp J. Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions // SIAM Rev. 2011. V. 53. P. 217–288.

  2. Civril A., Magdon-Ismail M. Column subset selection via sparse approximation of SVD // Theor. Comput. Sci. 2012. V. 412. P. 1–14.

  3. Boutsidis C., Woodruff D.P. Optimal cur matrix decompositions // SIAM J. Comput. 2017. V. 46. P. 543–589.

  4. Goreinov S.A., Tyrtyshnikov E.E. The maximal-volume concept in approximation by low-rank matrices // Contemp. Math. 2001. V. 268. P. 47–51.

  5. Osinsky A.I., Zamarashkin N.L. Pseudo-skeleton approximations with better accuracy estimates // Linear Algebra Appl. 2018. V. 537. P. 221–249.

  6. Deshpande A., Vempala S. Adaptive sampling and fast low-rank matrix approximation // Lect. Not. Comp. Sci. 2006. V. 1. P. 292–303.

  7. Guruswami V., Sinop A.K. Optimal column-based low-rank matrix reconstruction // ArXiv e-prints. 2012. arXiv:1104.1732.

  8. Замарашкин Н.Л., Осинский А.И. О существовании близкой к оптимальной скелетной аппроксимации матрицы во фробениусовой норме // Докл. АН. 2018. Т. 479. № 5. С. 489–492.

  9. Deshpande A., Rademacher L. Efficient volume sampling for row/column subset selection // IEEE 51st Annual Symposium on Foundations of Computer Science. 2010. P. 329–338.

  10. Горейнов С.А., Тыртышников Е.Е. Квазиоптимальность скелетного приближения матрицы в чебышёвской норме // Докл. АН. 2011. Т. 438. № 5. С. 593–594.

  11. Goreinov S.A., Tyrtyshnikov E.E., Zamarashkin N.L. A theory of pseudo-skeleton approximations // Linear Algebra Appl. 1997. V. 261. P. 1–21.

  12. Michalev A.Y., Oseledets I.V. Rectangular maximum-volume submatrices and their applications // Linear Algebra Appl. 2018. V. 538. P. 187–211.

  13. Pan C.T. On the existence and computation of rank revealing LU factorizations // Linear Algebra Appl. 2000. V. 316. P. 199–222.

  14. Gu M., Eisenstat S.C. Efficient algorithms for computing a strong rank-revealing qr factorization // SIAM J. Sci. Comput. 1996. V. 17. No. 4. P. 848–869.

  15. Goreinov S.A., Oseledets I.V., Savostyanov D.V., Tyrtyshnikov E.E., Zamarashkin N.L. How to find a good submatrix // Matrix Methods: Theory, Algorithms, Applications / Ed. by V. Olshevsky, E. Tyrtyshnikov. World Scientific Publishing, 2010. P. 247–256.

  16. Osinsky A.I. Rectangular maximum volume and projective volume search algorithms // ArXiv e-prints. 2018. arXiv:1809.02334.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал