1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 6, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 6, стр. 1019-1033

Конечно-объемная схема для многокомпонентных сжимаемых течений на неструктурированной сетке в трехмерной программе фокус

И. В. Глазырин 1, *, Н. А. Михайлов 1, **

1 ФГУП “РФЯЦ–ВНИИТФ им. Aкад. Е.И. Забабахина”
456770 Челябинская обл., Снежинск, ул. Васильева, 13, Россия

* E-mail: i.v.glazyrin@vniitf.ru
** E-mail: n.a.mikhaylov@vniitf.ru

Поступила в редакцию 25.07.2019
После доработки 02.12.2020
Принята к публикации 11.02.2021

Полный текст (PDF)

Аннотация

В работе изложена конечно-объемная схема годуновского типа для системы уравнений идеальной многокомпонентной газовой динамики на неподвижной трехмерной неструктурированной сетке. Схема реализована в программе Фокус, предназначенной для расчетов сжимаемых неустойчивых и турбулентных течений. Потоки консервативных величин через грани ячеек вычисляются с использованием обобщенных на случай произвольной ориентации грани решателей Римана HLL и HLLC, не требующих перехода в локальную систему координат каждой грани. Для реконструкции компонент вектора скорости применяется подход, учитывающий направление течения, что улучшает описание сферически-симметричных течений. Библ. 29. Фиг. 10.

Ключевые слова: многокомпонентная газовая динамика, конечно-объемная схема годуновского типа, решатель Римана, реконструкция решения, трехмерная неструктурированная сетка, неустойчивость Рихтмайера–Мешкова, неустойчивость Рэлея–Тейлора.

1. ВВЕДЕНИЕ

Трехмерная программа Фокус, разрабатываемая в РФЯЦ–ВНИИТФ, предназначена для расчетов сжимаемых неустойчивых и турбулентных течений, характерных для физики высоких плотностей энергии. Численное моделирование таких течений, возникающих, например, при сжатии мишеней лазерного термоядерного синтеза, является существенным инструментом их исследования [1]–[4].

Система уравнений многокомпонентной газовой динамики в Фокус рассчитывается в рамках эйлерового подхода на неструктурированной сетке. Используются схемы годуновского типа [5]–[7]. В данной работе описывается базовая схема без выделения контактных границ в смешанных ячейках. Использование геометрического метода VOF [8] для минимизации численной диффузии будет описано в отдельной статье. Здесь основное внимание уделено двум методическим особенностям: формулировкам решателей Римана HLL и HLLC для произвольной ориентации оси без использования перехода в локальную систему координат граней ячеек и специальной реконструкции скорости, учитывающей направление течения. Ограничений на вид уравнений состояния (УРС) компонент смеси в схеме не накладывается – каждая компонента может иметь свое произвольное двухпараметрическое УРС, удовлетворяющее условию Бете–Вейля [9]. Распараллеливание рассматриваемой схемы в Фокус выполнено на распределенной памяти с помощью технологии MPI.

Среди других программ, разрабатываемых для расчетов указанного класса течений, можно отметить российские коды NUT3D [10], ЭГАК [11] и зарубежные HYDRA [12], Miranda [13], Flamenco [14].

В NUT3D используется схожая эйлерова схема для газовой динамики на кубической сетке. ЭГАК также является эйлеровой программой на кубической сетке, в которой расчетный шаг делится на два этапа: лагранжев шаг и пересчет величин на эйлерову сетку. Неструктурированная сетка в Фокус позволяет использовать адаптацию сетки под особенности течения и напрямую описывать сложные границы расчетных областей. При этом не требуются дополнительные алгоритмы, как, например, на границах уровней в методе локальной адаптации кубических сеток [15] или в методе погруженной границы [16].

Для тестирования программы выбраны представительные для физики высоких плотностей энергии задачи – задачи Римана на неструктурированной и сферической сетках, турбулентная стадия неустойчивости Рихтамайера–Мешкова, развитие неустойчивости Рэлея–Тейлора в волне разрежения.

2. СИСТЕМА УРАВНЕНИЙ МНОГОКОМПОНЕНТНОЙ ГАЗОВОЙ ДИНАМИКИ

Рассматривается следующая трехмерная система уравнений односкоростной многокомпонентной газовой динамики в эйлеровых переменных в декартовой системе координат $(x,y,z)$ с изобарическим замыканием [17]:

$\begin{gathered} \frac{\partial }{{\partial t}}{{\alpha }_{k}} + \nabla \cdot ({\mathbf{v}}{{\alpha }_{k}}) = {{\alpha }_{k}}\nabla \cdot {\mathbf{v}},\quad k = 1, \ldots ,N - 1, \\ \frac{\partial }{{\partial t}}({{\alpha }_{k}}{{\varrho }_{k}}) + \nabla \cdot ({\mathbf{v}}{{\alpha }_{k}}{{\varrho }_{k}}) = 0,\quad k = 1, \ldots ,N, \\ \end{gathered} $
(1)
$\begin{gathered} \frac{\partial }{{\partial t}}(\varrho {\mathbf{v}}) + \nabla \cdot ({\mathbf{v}}\varrho {\mathbf{v}}) + \nabla p = 0, \\ \frac{\partial }{{\partial t}}(\varrho E) + \nabla \cdot ({\mathbf{v}}(\varrho E + p)) = 0, \\ \end{gathered} $
$\begin{gathered} \varrho = \sum\limits_{k = 1}^N \,{{\alpha }_{k}}{{\varrho }_{k}}, \\ \sum\limits_{k = 1}^N \,{{\alpha }_{k}} = 1, \\ \end{gathered} $
где $\nabla = \left( {\partial {\text{/}}\partial x,\partial {\text{/}}\partial y,\partial {\text{/}}\partial z} \right)$, ${{\alpha }_{k}} = {{V}_{k}}{\text{/}}V$, ${{\varrho }_{k}} = {{m}_{k}}{\text{/}}{{V}_{k}}$, ${{m}_{k}}$ и ${{V}_{k}}$ – объемная доля, плотность, масса и объем $k$-й компоненты, ${\mathbf{v}} = ({{{v}}_{x}},{{{v}}_{y}},{{{v}}_{z}})$ – скорость, $E = {\text{|}}{\mathbf{v}}{\kern 1pt} {{{\text{|}}}^{2}}{\text{/}}2 + e$ – удельная полная энергия на единицу массы, $e = \left( {\sum\nolimits_{k = 1}^N {{{\alpha }_{k}}{{\varrho }_{k}}{{e}_{k}}} } \right){\text{/}}\varrho $ – удельная внутренняя энергия на единицу массы, ${{e}_{k}}({{\varrho }_{k}},p)$ – удельная внутренняя энергия $k$-й компоненты на единицу массы, $p = {{p}_{k}}({{\varrho }_{k}},{{e}_{k}})$ – давление.

Дифференциальную часть системы (1) можно записать в квазидивергентном виде:

(2)
$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \nabla \cdot {\mathbf{F}}({\mathbf{u}}) = {\mathbf{b}}({\mathbf{u}}),$
где

${\mathbf{u}} = ({{\alpha }_{1}}, \ldots ,{{\alpha }_{{N - 1}}},{{\varrho }_{1}}{{\alpha }_{1}}, \ldots ,{{\varrho }_{N}}{{\alpha }_{N}},\varrho {{{v}}_{x}},\varrho {{{v}}_{y}},\varrho {{{v}}_{z}},\varrho E){\kern 1pt} ',$
${\mathbf{F}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} {{{\alpha }_{1}}{{{v}}_{x}}}&{{{\alpha }_{1}}{{{v}}_{y}}}&{{{\alpha }_{1}}{{{v}}_{z}}} \\ \ldots & \ldots & \ldots \\ {{{\alpha }_{{N - 1}}}{{{v}}_{x}}}&{{{\alpha }_{{N - 1}}}{{{v}}_{y}}}&{{{\alpha }_{{N - 1}}}{{{v}}_{z}}} \\ {{{\varrho }_{1}}{{\alpha }_{1}}{{{v}}_{x}}}&{{{\varrho }_{1}}{{\alpha }_{1}}{{{v}}_{y}}}&{{{\varrho }_{1}}{{\alpha }_{1}}{{{v}}_{z}}} \\ \ldots & \ldots & \ldots \\ {{{\varrho }_{N}}{{\alpha }_{N}}{{{v}}_{x}}}&{{{\varrho }_{N}}{{\alpha }_{N}}{{{v}}_{y}}}&{{{\varrho }_{N}}{{\alpha }_{N}}{{{v}}_{z}}} \\ {\varrho {v}_{x}^{2} + p}&{\varrho {{{v}}_{x}}{{{v}}_{y}}}&{\varrho {{{v}}_{x}}{{{v}}_{z}}} \\ {\varrho {{{v}}_{y}}{{{v}}_{x}}}&{\varrho {v}_{y}^{2} + p}&{\varrho {{{v}}_{y}}{{{v}}_{z}}} \\ {\varrho {{{v}}_{z}}{{{v}}_{x}}}&{\varrho {{{v}}_{z}}{{{v}}_{y}}}&{\varrho {v}_{z}^{2} + p} \\ {(\varrho E + p){{{v}}_{x}}}&{(\varrho E + p){{{v}}_{y}}}&{(\varrho E + p){{{v}}_{z}}} \end{array}} \right),$
${\mathbf{b}} = ({{\alpha }_{1}}\nabla \cdot {\mathbf{v}}, \ldots ,{{\alpha }_{{N - 1}}}\nabla \cdot {\mathbf{v}},0, \ldots ,0,0,0,0,0){\kern 1pt} '.$

3. ОПИСАНИЕ ЧИСЛЕННОЙ СХЕМЫ

Пусть пространственная область разбита на произвольные выпуклые многогранники (ячейки) сплошным образом без пересечения. Любая грань разделяет только две ячейки, одна из которых обозначается индексом $P$, вторая – $N$. Все величины относятся к центрам ячеек.

Интегрирование системы (2) по объему $i$-й вычислительной ячейки и применение теоремы Остроградского–Гаусса дает следующую систему уравнений для каждой ячейки:

$\frac{{\partial {{{\left\langle {\mathbf{u}} \right\rangle }}_{i}}}}{{\partial t}} + \frac{1}{{{\text{|}}{{V}_{i}}{\kern 1pt} {\text{|}}}}\sum\limits_j \,\int\limits_{{{S}_{j}}} \,({\mathbf{F}}({\mathbf{u}}) \cdot {{{\mathbf{n}}}_{{i,j}}}){\kern 1pt} d{{S}_{j}} = {{\left\langle {\mathbf{b}} \right\rangle }_{i}},$
где ${{\left\langle {\mathbf{u}} \right\rangle }_{i}} \equiv \int_{{{V}_{i}}}^{} {{\mathbf{u}}dV{\text{/|}}{{V}_{i}}{\kern 1pt} {\text{|}}} $ – среднеинтегральное значение ${\mathbf{u}}$ по $i$-й ячейке, ${\text{|}}{{V}_{i}}{\kern 1pt} {\text{|}}$ – объем $i$-й ячейки, ${{{\mathbf{n}}}_{{i,j}}}$ – вектор внешней нормали к грани $j$ для ячейки $i$.

Поверхностные интегралы по граням ячеек и среднеинтегральные значения по ячейкам аппроксимируются со вторым порядком точности по формуле средней точки:

$\begin{gathered} \int\limits_{{{S}_{j}}} \,({\mathbf{F}}({\mathbf{u}}) \cdot {{{\mathbf{n}}}_{{i,j}}})d{{S}_{j}} \approx {{S}_{j}}({\mathbf{F}}{{({\mathbf{u}})}_{j}} \cdot {{{\mathbf{n}}}_{{i,j}}}) = {{S}_{j}}{{{\mathbf{f}}}^{n}}{{({\mathbf{u}})}_{{i,j}}}, \\ {{\left\langle {\mathbf{u}} \right\rangle }_{i}} \approx {{{\mathbf{u}}}_{i}},\quad {{\left\langle {\mathbf{b}} \right\rangle }_{i}} \approx {{{\mathbf{b}}}_{i}}, \\ \end{gathered} $
где ${{{\mathbf{f}}}^{n}}{{({\mathbf{u}})}_{{i,j}}}$ – нормальный поток в центре $j$-й грани для ячейки $i$, ${{S}_{j}}$ – площадь $j$-й грани. Поскольку ${{{\mathbf{f}}}^{n}}{{({\mathbf{u}})}_{{P,j}}} = - {{{\mathbf{f}}}^{n}}{{({\mathbf{u}})}_{{N,j}}}$, то далее индекс ячейки в обозначении потоков опускается. Аппроксимация ${{{\mathbf{f}}}^{n}}{{({\mathbf{u}})}_{j}} \approx {\mathbf{F}}_{j}^{n}$ дает общий вид полудискретной схемы:

$\frac{{\partial {{{\mathbf{u}}}_{i}}}}{{\partial t}} + \frac{1}{{{\text{|}}{{V}_{i}}{\kern 1pt} {\text{|}}}}\sum\limits_j \,{{S}_{j}}{\mathbf{F}}_{j}^{n} = {{{\mathbf{b}}}_{i}}.$

3.1. Вычисление потоков

Для аппроксимации нормальных потоков в Фокус используется тот или иной решатель Римана [6]. Стандартным подходом для того, чтобы воспользоваться выражениями для потока из одномерного решателя Римана в случае произвольной ориентации грани, является переход в локальную систему координат, связанную с гранью, так, чтобы одна из осей была сонаправлена с нормалью к грани. Далее вычисляется поток вдоль этой оси по одномерному решателю Римана, и затем этот поток переводится в глобальную систему координат. Избежать операций перехода в локальную систему координат и обратно, связанных с матрично-векторными произведениями можно, если получить выражение потока для случая произвольной ориентации оси, вдоль которой происходит распад разрыва.

Рассмотрим решатель Римана HLL [18], [6] для одномерной гиперболической системы законов сохранения

(3)
$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \frac{{\partial {{{\mathbf{f}}}^{x}}({\mathbf{u}})}}{{\partial x}} = 0.$
Численный поток HLL определяется в виде
(4)
${\mathbf{F}}_{{i + 1/2}}^{{x,HLL}} = \frac{{a_{{i + 1/2}}^{ + }{{{\mathbf{f}}}^{x}}({\mathbf{u}}_{{i + 1/2}}^{ - }) - a_{{i + 1/2}}^{ - }{{{\mathbf{f}}}^{x}}({\mathbf{u}}_{{i + 1/2}}^{ + })}}{{a_{{i + 1/2}}^{ + } - a_{{i + 1/2}}^{ - }}} + \frac{{a_{{i + 1/2}}^{ + }a_{{i + 1/2}}^{ - }}}{{a_{{i + 1/2}}^{ + } - a_{{i + 1/2}}^{ - }}}[{\mathbf{u}}_{{i + 1/2}}^{ + } - {\mathbf{u}}_{{i + 1/2}}^{ - }],$
где
${\mathbf{u}}_{{i + 1/2}}^{ - } = {{{\mathbf{p}}}_{i}}({{x}_{{i + 1/2}}}),\quad {\mathbf{u}}_{{i + 1/2}}^{ + } = {{{\mathbf{p}}}_{{i + 1}}}({{x}_{{i + 1/2}}})$
суть левосторонние и правосторонние реконструированные значения решения на грани $i + 1{\text{/}}2$, ${{{\mathbf{p}}}_{i}}(x)$ – реконструирующий многочлен в $i$-й ячейке,
$\begin{gathered} a_{{i + 1/2}}^{ + } = max\left\{ {{{\lambda }_{K}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{{i + 1/2}}^{ - })} \right),{{\lambda }_{K}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{{i + 1/2}}^{ + })} \right),0} \right\}, \\ a_{{i + 1/2}}^{ - } = min\left\{ {{{\lambda }_{1}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{{i + 1/2}}^{ - })} \right),{{\lambda }_{1}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{{i + 1/2}}^{ + })} \right),0} \right\} \\ \end{gathered} $
суть оценки для максимальной и минимальной скоростей распространения волн от распада произвольного разрыва на грани $i + 1{\text{/}}2$, $\partial {{{\mathbf{f}}}^{x}}{\text{/}}\partial {\mathbf{u}}$ – матрица Якоби системы (3) с собственными значениями ${{\lambda }_{1}} < ... < {{\lambda }_{K}}$. В случае системы уравнений газовой динамики ${{\lambda }_{1}} = {{v}_{x}} - c$, ${{\lambda }_{2}} = {{\lambda }_{3}} = ... = {{\lambda }_{{K - 1}}} = {{v}_{x}}$, ${{\lambda }_{K}} = {{v}_{x}} + c$, где $c$ – скорость звука.

Система уравнений газовой динамики (2) обладает свойством ротационной инвариантности [6], [19]:

${\mathbf{F}}({\mathbf{u}}) \cdot {\mathbf{n}} \equiv {{{\mathbf{T}}}^{{ - 1}}}{{{\mathbf{f}}}^{x}}({\mathbf{Tu}}),$
где ${\mathbf{T}}$ – тензор поворота глобальной системы координат к локальной системе координат грани, совмещающий ось ${\mathbf{x}}$ с ${\mathbf{n}}$. Пусть численный поток ${{{\mathbf{F}}}^{n}}{{({\mathbf{u}})}_{j}}$ обладает этим же свойством:
(5)
${{{\mathbf{F}}}^{n}}{{({\mathbf{u}})}_{j}} \equiv {{{\mathbf{T}}}^{{ - 1}}}{{{\mathbf{F}}}^{x}}{{({\mathbf{Tu}})}_{j}}.$
Подстановка (4) в (5) дает
$\begin{gathered} {\mathbf{F}}_{j}^{{n,HLL}} = \frac{{a_{j}^{ + }{{{\mathbf{T}}}^{{ - 1}}}{{{\mathbf{f}}}^{x}}({\mathbf{Tu}}_{j}^{P}) - a_{j}^{ - }{{{\mathbf{T}}}^{{ - 1}}}{{{\mathbf{f}}}^{x}}({\mathbf{Tu}}_{j}^{N})}}{{a_{j}^{ + } - a_{j}^{ - }}} + \frac{{a_{j}^{ + }a_{j}^{ - }}}{{a_{j}^{ + } - a_{j}^{ - }}}[{{{\mathbf{T}}}^{{ - 1}}}{\mathbf{Tu}}_{j}^{N} - {{{\mathbf{T}}}^{{ - 1}}}{\mathbf{Tu}}_{j}^{P}] = \\ \, = \frac{{a_{j}^{ + }{{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{P}) - a_{j}^{ - }{{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{N})}}{{a_{j}^{ + } - a_{j}^{ - }}} + \frac{{a_{j}^{ + }a_{j}^{ - }}}{{a_{j}^{ + } - a_{j}^{ - }}}[{\mathbf{u}}_{j}^{N} - {\mathbf{u}}_{j}^{P}], \\ \end{gathered} $
где
(6)
$\begin{gathered} {{{\mathbf{f}}}^{n}}({\mathbf{u}}) = {\mathbf{F}}({\mathbf{u}}) \cdot {\mathbf{n}} = ({{\alpha }_{1}}{{v}_{n}}, \ldots ,{{\alpha }_{{N - 1}}}{{v}_{n}},{{\rho }_{1}}{{\alpha }_{1}}{{v}_{n}}, \ldots ,{{\rho }_{N}}{{\alpha }_{N}}{{v}_{n}}, \\ \varrho {{v}_{x}}{{v}_{n}} + {{n}_{x}}p,\varrho {{v}_{y}}{{v}_{n}} + {{n}_{y}}p,\varrho {{v}_{z}}{{v}_{n}} + {{n}_{z}}p,(\varrho E + p){{v}_{n}}){\kern 1pt} {\text{'}}, \\ \end{gathered} $
${{v}_{n}} = {{n}_{x}}{{v}_{x}} + {{n}_{y}}{{v}_{y}} + {{n}_{z}}{{v}_{z}}$ – проекция скорости на нормаль к грани, ${\mathbf{u}}_{j}^{P}$ и ${\mathbf{u}}_{j}^{N}$ – реконструкции решения в центре $j$-й грани со стороны ячейки $P$ и $N$, соответственно,
$\begin{gathered} a_{j}^{ + } = max\left\{ {{{\lambda }_{K}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}({\mathbf{Tu}})}}{{\partial ({\mathbf{Tu}})}}({\mathbf{Tu}}_{j}^{P})} \right),{{\lambda }_{K}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}({\mathbf{Tu}})}}{{\partial ({\mathbf{Tu}})}}({\mathbf{Tu}}_{j}^{N})} \right),0} \right\}, \\ a_{j}^{ - } = min\left\{ {{{\lambda }_{1}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}({\mathbf{Tu}})}}{{\partial ({\mathbf{Tu}})}}({\mathbf{Tu}}_{j}^{P})} \right),{{\lambda }_{1}}\left( {\frac{{\partial {{{\mathbf{f}}}^{x}}({\mathbf{Tu}})}}{{\partial ({\mathbf{Tu}})}}({\mathbf{Tu}}_{j}^{N})} \right),0} \right\}. \\ \end{gathered} $
Поскольку собственные значения $\partial {{{\mathbf{f}}}_{n}}({\mathbf{u}}){\text{/}}\partial {\mathbf{u}}$ совпадают с собственными значениями $\partial {{{\mathbf{f}}}^{x}}({\mathbf{Tu}}){\text{/}}\partial ({\mathbf{Tu}})$ (см. [6]), то
(7)
$\begin{gathered} a_{j}^{ + } = max\left\{ {{{\lambda }_{K}}\left( {\frac{{\partial {{{\mathbf{f}}}_{n}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{j}^{P})} \right),{{\lambda }_{K}}\left( {\frac{{\partial {{{\mathbf{f}}}_{n}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{j}^{N})} \right),0} \right\},\quad a_{j}^{ - } = min\left\{ {{{\lambda }_{1}}\left( {\frac{{\partial {{{\mathbf{f}}}_{n}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{j}^{P})} \right),{{\lambda }_{1}}\left( {\frac{{\partial {{{\mathbf{f}}}_{n}}}}{{\partial {\mathbf{u}}}}({\mathbf{u}}_{j}^{N})} \right),0} \right\}, \\ {{\lambda }_{1}} = {{{v}}_{n}} - c,\quad {{\lambda }_{K}} = {{{v}}_{n}} + c,\quad c = \sqrt {\mathop {\left( {\frac{{\partial p}}{{\partial \varrho }}} \right)}\nolimits_T + \frac{{T\mathop {\left( {\tfrac{{\partial p}}{{\partial T}}} \right)}\nolimits_\varrho }}{{{{\varrho }^{2}}\mathop {\left( {\tfrac{{\partial e}}{{\partial T}}} \right)}\nolimits_\varrho }}} . \\ \end{gathered} $
Таким образом, HLL-аппроксимация нормального потока ${{{\mathbf{f}}}^{n}}{{({\mathbf{u}})}_{j}}$ в центре грани ячейки выражается следующим образом:
(8)
${{{\mathbf{f}}}^{n}}{{({\mathbf{u}})}_{j}} \approx {\mathbf{F}}_{j}^{{n,HLL}} = \frac{{a_{j}^{ + }{{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{P}) - a_{j}^{ - }{{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{N})}}{{a_{j}^{ + } - a_{j}^{ - }}} + \frac{{a_{j}^{ + }a_{j}^{ - }}}{{a_{j}^{ + } - a_{j}^{ - }}}[{\mathbf{u}}_{j}^{N} - {\mathbf{u}}_{j}^{P}],$
где $a_{j}^{ + }$ и $a_{j}^{ - }$ определяются согласно (7).

Аналогичным образом получается выражение для состояния HLL в центре грани в результате распада разрыва:

(9)
${\mathbf{u}}_{j}^{{*,HLL}} = \left\{ \begin{gathered} {\mathbf{u}}_{j}^{P},\quad {\text{если}}\quad a_{j}^{ - } > 0, \hfill \\ {\mathbf{u}}_{j}^{{HLL}},\,\;{\text{если}}\quad a_{j}^{ - } < = 0 < a_{j}^{ + }, \hfill \\ {\mathbf{u}}_{j}^{N},\quad {\text{если}}\quad a_{j}^{ + } < = 0, \hfill \\ \end{gathered} \right.$
где усредненное состояние

${\mathbf{u}}_{j}^{{HLL}} = \frac{{a_{j}^{ + }{\mathbf{u}}_{j}^{N} - a_{j}^{ - }{\mathbf{u}}_{j}^{P} + {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{P}) - {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{N})}}{{a_{j}^{ + } - a_{j}^{ - }}}.$

Как можно заметить, выражение потока HLL в (8) может быть получено путем применения метода HLL для координатного направления (4) к нормальному потоку (6). Это указывает на универсальный подход к получению формулировок других решателей Римана для произвольного направления: записать их применительно к (6).

Применим данный подход для получения решателя Римана HLLC для произвольной ориентации грани. Решатель HLLC является модификацией HLL c разделением серединного состояния ${{{\mathbf{u}}}^{{HLL}}}$ на два, соответствующие контактному разрыву [20]:

${\mathbf{F}}_{j}^{{n,HLLC}} = \left\{ \begin{gathered} {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{P}),\quad {\text{если}}\quad a_{j}^{ - } > 0, \hfill \\ \frac{{a_{j}^{*}(a_{j}^{ - }{\mathbf{u}}_{j}^{P} - {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{P})) + a_{j}^{ - }p_{j}^{*}{\mathbf{d}}_{j}^{*}}}{{a_{j}^{ - } - a_{j}^{*}}},\quad {\text{если}}\quad a_{j}^{ - } < = 0 < a_{j}^{*}, \hfill \\ \frac{{a_{j}^{*}(a_{j}^{ + }{\mathbf{u}}_{j}^{N} - {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{N})) + a_{j}^{ + }p_{j}^{*}{\mathbf{d}}_{j}^{*}}}{{a_{j}^{ + } - a_{j}^{*}}},\quad {\text{если}}\quad a_{j}^{*} < = 0 < a_{j}^{ + }, \hfill \\ {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{N}),\quad {\text{если}}\quad a_{j}^{ + } < = 0, \hfill \\ \end{gathered} \right.$
(10)
${\mathbf{u}}_{j}^{{*,HLLC}} = \left\{ \begin{gathered} {\mathbf{u}}_{j}^{P},\quad {\text{если}}\quad a_{j}^{ - } > 0, \hfill \\ \frac{{a_{j}^{ - }{\mathbf{u}}_{j}^{P} - {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{P}) + p_{j}^{*}{\mathbf{d}}_{j}^{*}}}{{a_{j}^{ - } - a_{j}^{*}}},\quad {\text{если}}\quad a_{j}^{ - } < = 0 < a_{j}^{*}, \hfill \\ \frac{{a_{j}^{ + }{\mathbf{u}}_{j}^{N} - {{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{N}) + p_{j}^{*}{\mathbf{d}}_{j}^{*}}}{{a_{j}^{ + } - a_{j}^{*}}},\quad {\text{если}}\quad a_{j}^{*} < = 0 < a_{j}^{ + }, \hfill \\ {\mathbf{u}}_{j}^{N},\quad {\text{если}}\quad a_{j}^{ + } < = 0, \hfill \\ \end{gathered} \right.$
$\begin{gathered} a_{j}^{*} = \frac{{{{p}^{N}} - {{p}^{P}} + {{\varrho }^{P}}{v}_{n}^{P}(a_{j}^{ - } - {v}_{n}^{P}) - {{\varrho }^{N}}{v}_{n}^{N}(a_{j}^{ + } - {v}_{n}^{N})}}{{{{\varrho }^{P}}(a_{j}^{ - } - {v}_{n}^{P}) - {{\varrho }^{N}}(a_{j}^{ + } - {v}_{n}^{N})}}, \\ p_{j}^{*} = \frac{1}{2}({{p}^{N}} + {{p}^{P}} + {{\varrho }^{P}}(a_{j}^{ - } - {v}_{n}^{P})(a_{j}^{*} - {v}_{n}^{P}) + {{\varrho }^{N}}(a_{j}^{ + } - {v}_{n}^{N})(a_{j}^{*} - {v}_{n}^{N})), \\ {\mathbf{d}}_{j}^{*} = (0, \ldots ,0,0, \ldots ,0,{{n}_{x}},{{n}_{y}},{{n}_{z}},a_{j}^{*}){\kern 1pt} ', \\ \end{gathered} $
где $a_{j}^{ + }$ и $a_{j}^{ - }$ определяются так же, как в решателе HLL. Подстановкой проверяется эквивалентность решателя HLLC, получаемого при использовании перехода в локальный базис грани, и (10).

Хотя использование записи решателя Римана для произвольной ориентации грани не дает заметного ускорения счета, однако упрощает алгоритм, поскольку не требуются отдельные этапы перехода в локальный базис и обратно, и сокращает количество арифметических операций с машинной точностью.

3.2. Реконструкция решения

В Фокус реконструкция решения на гранях ячеек проводится в примитивных переменных

${\mathbf{q}} = ({{\alpha }_{1}}, \ldots ,{{\alpha }_{{N - 1}}},{{\rho }_{1}}{{\alpha }_{1}}, \ldots ,{{\rho }_{N}}{{\alpha }_{N}},{{v}_{x}},{{v}_{y}},{{v}_{z}},p){\kern 1pt} '.$
Используются методы кусочно-линейной TVD реконструкции двух основных типов: квазиодномерная и многомерная [21]. В данной работе рассматривается многомерная реконструкция:
$u_{j}^{P} = {{u}_{P}} + {{\psi }_{P}}\nabla {{(u)}_{P}} \cdot ({{{\mathbf{C}}}_{j}} - {{{\mathbf{C}}}_{P}}),\quad u_{j}^{N} = {{u}_{N}} + {{\psi }_{N}}\nabla {{(u)}_{N}} \cdot ({{{\mathbf{C}}}_{j}} - {{{\mathbf{C}}}_{N}}),$
${{\psi }_{i}} = \mathop {min}\limits_j ({{\psi }_{{ij}}}),\quad {{\psi }_{{ij}}} = \left\{ \begin{gathered} \Phi \left( {\frac{{\delta u_{i}^{{\max }}}}{{u_{j}^{i} - {{u}_{i}}}}} \right),\quad {\text{если}}\quad u_{j}^{i} > {{u}_{i}}, \hfill \\ \Phi \left( {\frac{{\delta u_{i}^{{\min }}}}{{u_{j}^{i} - {{u}_{i}}}}} \right),\quad {\text{если}}\quad u_{j}^{i} < {{u}_{i}}, \hfill \\ 1,\quad {\text{если}}\quad u_{j}^{i} = {{u}_{i}}, \hfill \\ \end{gathered} \right.$
$\begin{gathered} \delta u_{i}^{{{\text{max}}}} = \mathop {max}\limits_k ({{u}_{k}} - {{u}_{i}}),\quad \delta u_{i}^{{{\text{min}}}} = \mathop {min}\limits_k ({{u}_{k}} - {{u}_{i}}), \\ {{u}_{k}} - {\text{значения}}\;{\text{в}}\;{\text{соседних}}\;{\text{ячейках}}, \\ \end{gathered} $
где ${{{\mathbf{C}}}_{P}}$, ${{{\mathbf{C}}}_{N}}$ и ${{{\mathbf{C}}}_{j}}$ – радиус-векторы центров ячейки $P$, ячейки $N$ и грани $j$ соответственно. В качестве функции-ограничителя используется $\Phi (x) = \tfrac{{{{x}^{2}} + 2x}}{{{{x}^{2}} + x + 2}}$ [22]. Для аппроксимации градиента в центре ячейки применяется метод, основанный на теореме Остроградского–Гаусса:
$\nabla {{(u)}_{i}} \approx \frac{{\sum\limits_j \,{{{\mathbf{n}}}_{j}}{{S}_{j}}{{u}_{j}}}}{{{\text{|}}{{V}_{i}}{\text{|}}}},$
где значения в центрах граней аппроксимируется как ${{u}_{j}} \approx {{w}_{j}}{{u}_{P}} + (1 - {{w}_{j}}){{u}_{N}}$, ${{w}_{j}} = \tfrac{{{{{\mathbf{n}}}_{j}} \cdot ({{{\mathbf{C}}}_{N}} - {{{\mathbf{C}}}_{j}})}}{{{{{\mathbf{n}}}_{j}} \cdot ({{{\mathbf{C}}}_{N}} - {{{\mathbf{C}}}_{P}})}}$.

Для реконструкции вектора скорости в Фокус применяется специальный алгоритм, поскольку известно, что простая покомпонентная реконструкция вектора скорости может приводить к несогласованному с течением результирующему вектору [23]–[27]. Например, в случае осесимметричных или сферически симметричных течений покомпонентно реконструированный вектор скорости может уже не удовлетворять типу течения и, как следствие, численное решение теряет симметрию. При реконструкции вектора скорости важно обеспечить инвариантность к ориентации координатных осей. Реализованный в Фокус метод является обобщением на трехмерный случай подхода [25], заключающегося в покомпонентной реконструкции вектора, но в локальном базисе для каждой ячейки, определяемом направлением течения среды.

Для реконструкции вектора скорости в $i$-й ячейке используется локальная декартовая система координат, базисные векторы которой определяются согласно

$\begin{gathered} {{\xi }_{1}} = ({{\xi }_{x}},{{\xi }_{y}},{{\xi }_{z}}){\kern 1pt} ',\quad {{\xi }_{2}} = ( - {{\xi }_{y}},{{\xi }_{x}},0){\kern 1pt} ',\quad {{\xi }_{3}} = {{\xi }_{1}} \times {{\xi }_{2}}, \\ {{\xi }_{x}} = {{v}_{x}}{\text{/|}}{{{v}}_{x}}{\text{|}},\quad {{\xi }_{y}} = {{{v}}_{y}}{\text{/|}}{{{v}}_{y}}{\text{|}},\quad {{\xi }_{z}} = {{{v}}_{z}}{\text{/|}}{{{v}}_{z}}{\text{|}}. \\ \end{gathered} $
Таким образом, ${{\xi }_{1}}$ сонаправлен с вектором скорости в $i$-й ячейке и ${{\xi }_{1}} \bot {{\xi }_{2}} \bot {{\xi }_{3}}$. Тензоры прямого, от глобальной системы к локальной, и обратного преобразований имеют вид
${\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {{{\xi }_{x}}}&{{{\xi }_{y}}}&{{{\xi }_{z}}} \\ { - {{\xi }_{y}}}&{{{\xi }_{x}}}&0 \\ { - {{\xi }_{x}}{{\xi }_{z}}}&{ - {{\xi }_{y}}{{\xi }_{z}}}&{\xi _{x}^{2} + \xi _{y}^{2}} \end{array}} \right),\quad {{{\mathbf{A}}}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} {{{\xi }_{x}}}&{ - {{\xi }_{y}}{\text{/|}}A{\text{|}}}&{ - {{\xi }_{x}}{{\xi }_{z}}{\text{/|}}A{\text{|}}} \\ {{{\xi }_{y}}}&{{{\xi }_{x}}{\text{/|}}A{\text{|}}}&{ - {{\xi }_{y}}{{\xi }_{z}}{\text{/|}}A{\text{|}}} \\ {{{\xi }_{z}}}&0&1 \end{array}} \right).$
Вектор скорости в локальном базисе выражается согласно
${\mathbf{w}} = {\mathbf{A}} \cdot {\mathbf{v}}.$
Тогда многомерная реконструкция вектора скорости определяется следующим образом:
${{\psi }_{i}} = \mathop {min}\limits_j ({{\psi }_{{ij}}}),\quad {{\psi }_{{ij}}} = \left\{ \begin{gathered} \Phi \left( {\frac{{\delta {\mathbf{w}}_{i}^{{{\text{max}}}}}}{{{\mathbf{w}}_{j}^{i} - {{{\mathbf{w}}}_{i}}}}} \right),\quad {\text{если}}\quad {\mathbf{w}}_{j}^{i} > {{{\mathbf{w}}}_{i}}, \hfill \\ \Phi \left( {\frac{{\delta {\mathbf{w}}_{i}^{{{\text{min}}}}}}{{{\mathbf{w}}_{j}^{i} - {{{\mathbf{w}}}_{i}}}}} \right),\quad {\text{если}}\quad {\mathbf{w}}_{j}^{i} < {{{\mathbf{w}}}_{i}}, \hfill \\ 1,\quad {\text{если}}\quad {\mathbf{w}}_{j}^{i} = {{{\mathbf{w}}}_{i}}, \hfill \\ \end{gathered} \right.$
$\begin{gathered} \delta {\mathbf{w}}_{i}^{{{\text{max}}}} = \mathop {max}\limits_k ({{{\mathbf{w}}}_{k}} - {{{\mathbf{w}}}_{i}}),\quad \delta {\mathbf{w}}_{i}^{{{\text{min}}}} = \mathop {min}\limits_k ({{{\mathbf{w}}}_{k}} - {{{\mathbf{w}}}_{i}}),\quad {{{\mathbf{w}}}_{k}} = {\mathbf{A}} \cdot {{{\mathbf{v}}}_{k}}, \\ {\mathbf{w}}_{j}^{i} = {\mathbf{A}} \cdot ({{{\mathbf{v}}}_{i}} + {{(\nabla {\mathbf{v}})}_{i}} \cdot ({{{\mathbf{C}}}_{j}} - {{{\mathbf{C}}}_{i}})), \\ {{\Psi }_{i}} = {{{\mathbf{A}}}^{{ - 1}}}{{\psi }_{i}}{\mathbf{A}},\quad {\mathbf{v}}_{j}^{i} = {{{\mathbf{v}}}_{i}} + ({{\Psi }_{i}} \cdot {{(\nabla {\mathbf{v}})}_{i}}) \cdot ({{{\mathbf{C}}}_{j}} - {{{\mathbf{C}}}_{i}}), \\ \end{gathered} $
где операции деления, применения функции ограничителя $\Phi $, определения максимума, минимума и сравнения для векторов производятся покомпонентно. Таким образом, в результате для каждой ячейки формируется тензор ограничителей для градиента вектора скорости.

3.3. Временная дискретизация

В рассматриваемой схеме для временной дискретизации используется явный метод Рунге–Кутты второго порядка (модифицированный метод Эйлера):

(11)
${\mathbf{u}}_{i}^{{l + 1}} = {\mathbf{u}}_{i}^{l} - \frac{{\Delta {{t}^{l}}}}{{{\text{|}}{{V}_{i}}{\text{|}}}}\sum\limits_j \,{{S}_{j}}{\mathbf{F}}_{j}^{{n,l + 1/2}} + \Delta {{t}_{l}}{\mathbf{b}}_{i}^{{l + 1/2}},$
где $l$ – номер временного слоя. Задача Римана решается для реконструированных состояний на временном слое $l + 1{\text{/}}2$: ${\mathbf{q}}_{j}^{{P,l + 1/2}}$ и ${\mathbf{q}}_{j}^{{N,l + 1/2}}$. Эти состояния вычисляются с использованием подхода Hancock [6]:
${\mathbf{q}}_{j}^{{P,l + 1/2}} = {\mathbf{q}}_{j}^{{P,l}} + {\mathbf{q}}_{P}^{{l + 1/2}} - {\mathbf{q}}_{P}^{l},\quad {\mathbf{q}}_{j}^{{N,l + 1/2}} = {\mathbf{q}}_{j}^{{N,l}} + {\mathbf{q}}_{N}^{{l + 1/2}} - {\mathbf{q}}_{N}^{l},$
где ${\mathbf{q}}_{P}^{{l + 1/2}}$ и ${\mathbf{q}}_{N}^{{l + 1/2}}$ определяются путем интегрирования системы на временном интервале $[{{t}^{l}},{{t}^{{l + 1/2}}}]$ без привлечения решения задачи Римана:
(12)
${\mathbf{u}}_{i}^{{l + 1/2}} = {\mathbf{u}}_{i}^{l} - \frac{{\Delta {{t}^{l}}}}{{2{\text{|}}{{V}_{i}}{\text{|}}}}\sum\limits_j \,{{S}_{j}}{{{\mathbf{f}}}^{n}}({\mathbf{u}}_{j}^{{i,l}}) + \frac{{\Delta {{t}^{l}}}}{2}{\mathbf{b}}_{i}^{l},\quad {\mathbf{u}}_{i}^{{l + 1/2}} \to {\mathbf{q}}_{i}^{{l + 1/2}},$
где ${\mathbf{u}}_{j}^{{i,l}}$ – реконструкция решения на временном слое $l$ на грани $j$ со стороны ячейки $i$. Дивергенция скорости в правой части (11) и (12) аппроксимируется с использованием формулы Остроградского–Гаусса:
$\nabla \cdot {{{\mathbf{v}}}_{i}} \approx \frac{{\sum\limits_j \,({{{\mathbf{v}}}_{j}} \cdot {{{\mathbf{n}}}_{j}}){{S}_{j}}}}{{{\text{|}}{{V}_{i}}{\text{|}}}},$
где в качестве ${{{\mathbf{v}}}_{j}}$ в (12) используется реконструированная скорость ${\mathbf{v}}_{j}^{{i,l}}$, а в (11) – скорость на грани из решения задачи Римана: (9) или (10).

Шаг по времени $\Delta {{t}^{l}}$ определяется из условия Куранта:

$\Delta {{t}^{l}}\mathop {max}\limits_i \left( {\frac{{\sum\limits_j \,({{S}_{j}}max({\kern 1pt} {\text{|}}a_{j}^{{ + ,l - 1/2}}{\text{|}},{\text{|}}a_{j}^{{ - ,l - 1/2}}{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{2{\text{|}}{{V}_{i}}{\kern 1pt} {\text{|}}}}} \right) \leqslant \mathbb{C},$
где $a_{j}^{{ + ,l - 1/2}}$, $a_{j}^{{ - ,l - 1/2}}$ вычисляются согласно (7) на временном слое $l - 1{\text{/}}2$, $\mathbb{C} < 1$ – число Куранта.

После расчета временного шага по схеме (11) давление ${{p}^{{l + 1}}}$ и внутренние энергии компонент $e_{k}^{{l + 1}}$ в каждой ячейке определяются путем итерационного решения алгебраической системы $N + 1$ уравнений:

${{e}^{{l + 1}}}{{\varrho }^{{l + 1}}} = \sum\limits_{k = 1}^N \,\alpha _{k}^{{l + 1}}\varrho _{k}^{{l + 1}}e_{k}^{{l + 1}},\quad {{p}^{{l + 1}}} = {{p}_{k}}(\varrho _{k}^{{l + 1}},e_{k}^{{l + 1}}),\quad k = 1, \ldots ,N.$

Распараллеливание численной схемы сделано на распределенной памяти с помощью библиотеки MPI в рамках подхода геометрической декомпозиции.

3.4. Граничные условия

В программе Фокус граница каждого фрагмента сетки, рассчитываемого отдельным MPI-процессом, разделена на части, соответствующие либо физической границе, либо межпроцессной.

На каждой части физической границы значения на гранях задаются, исходя из граничного условия задачи. В случае условия Дирихле, т.е. задания непосредственно значения величины на границе, это значение используется в качестве обоих реконструированных значений на грани. В случае условия фон Неймана, т.е. задания градиента величины на границе $\nabla {{u}^{\Gamma }}$, оно сводится к условию Дирихле:

$u_{j}^{\Gamma } = {{u}_{P}} + \nabla {{u}^{\Gamma }} \cdot ({{{\mathbf{C}}}_{j}} - {{{\mathbf{C}}}_{P}}),$
где ${{u}_{P}}$ – значение величины в центре приграничной ячейки, ${{{\mathbf{C}}}_{P}}$ и ${{{\mathbf{C}}}_{j}}$ – координатные векторы центров ячейки и грани соответственно.

На межпроцессных частях границы осуществляется MPI-обмен значениями реконструируемых величин и их градиентов в одном слое приграничных ячеек.

4. ТЕСТОВЫЕ РАСЧЕТЫ

Для демонстрации работы описанной численной схемы и ее элементов рассматриваются четыре тестовых задачи. Первая – плоская задача Римана о распаде начального разрыва с двумя компонентами, имеющими разные УРС, на трехмерной неструктурированной сетке. Вторая – сферическая задача Сода [6] на сферической сетке. Третья – моделирование турбулентной стадии неустойчивости Рихтмайера–Мешкова в постановке тета-группы [28]. Четвертая – расчет эксперимента на развитие неустойчивости Рэлея–Тейлора в волне разрежения.

4.1. Плоская задача Римана на трехмерной неструктурированной сетке

Расчетная область: $x \in (0,1)$, $y \in (0,0.1)$, $z \in (0,0.1)$, $t \in (0,0.2]$.

Начальные условия:

$({{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{1}}{{\varrho }_{1}},{{\alpha }_{2}}{{\varrho }_{2}},({{v}_{x}},{{v}_{y}},{{v}_{z}}),p) = \left\{ \begin{gathered} (1,\;0,\;1,\;0,\;( - 0.9014,\;0,\;0),\;1)\quad x \in (0,\;0.5), \hfill \\ ({\text{0,}}\;{\text{1,}}\;{\text{0,}}\;{\text{0}}{\text{.125}},\;( - 0.9014,\;0,\;0),\;0.1),\quad x \in [0.5,\;1). \hfill \\ \end{gathered} \right.$
Начальная скорость подобрана так, что после распада разрыва контактная граница газов становится неподвижной. Граничные условия: при $x = 0$, $x = 1$ – свободный выход (нулевой градиент всех величин), остальные границы – жесткие стенки со скольжением (нулевые градиенты всех величин кроме нормальной компоненты скорости, для которой нулевое само значение). УРС: идеальные газы с $\gamma = 1.4$, ${{с}_{v}} = 0.83$ для первой компоненты, $\gamma = 5{\text{/}}3$, ${{с}_{v}} = 0.36$ для второй. Расчетные сетки: трехмерные неструктурированные из тетраэдров и пирамид (см. фиг. 1) со средним линейным размером ячеек 0.04, 0.02, 0.01. Для удобства задания начального условия сетки построены так, чтобы исходно контактная граница проходила по граням ячеек. Число Куранта $\mathbb{C} = 0.8$.

Фиг. 1.

Плоская задача Римана. Фрагмент сетки $x \in (0,0.35)$, $y \in (0.05,0.1)$, $z \in (0,0.05)$ с распределением плотности на конечный момент времени.

На фиг. 1 приведен фрагмент сетки с распределением плотности в волне разрежения на конечный момент. Сравнение с аналитическим решением проводится вдоль серединного среза, параллельного оси х, с равномерным распределением точек на срезе. Значения в точках на срезе получаются линейной интерполяцией из значений в центрах ячеек. Как следует из фиг. 2, численное решение согласуется с аналитическим, при этом расчет с решателем Римана HLLC дает несколько меньшую численную диффузию на неподвижном контактном разрыве. При измельчении сетки погрешность численного решения в норме ${{L}_{1}}$ убывает.

Фиг. 2.

Плоская задача Римана. Распределение плотности вдоль оси x на серединном срезе на конечный момент времени (а) и зависимость погрешности плотности при измельчении сетки (б).

4.2. Сферическая задача Сода на сферической сетке

Цель данного однокомпонентного теста – определить влияние описанного выше специального алгоритма реконструкции вектора скорости на сохранение сферической симметрии. Для сравнения расчет задачи проводится также с простой покомпонентной реконструкцией скорости.

Расчетная область: $r = {{x}^{2}} + {{y}^{2}} + {{z}^{2}} < 1$, $t \in (0,0.15]$.

Начальные условия:

$(\varrho ,({{{v}}_{x}},{{{v}}_{y}},{{{v}}_{z}}),p) = \left\{ \begin{gathered} (1,(0,0,0),1),\quad r \in (0,0.5), \hfill \\ (0.125,(0,0,0),0.1),\quad r \in [0.5,1). \hfill \\ \end{gathered} \right.$
Граничные условия: при $r = 1$ – свободный выход, УРС: идеальный газ с $\gamma = 1.4$, ${{с}_{v}} = 0.83$. Расчетная сетка: сферическая из 100 листов со 100 ячейками по углу и 50 по радиусу в каждом листе (см. фиг. 3). Число Куранта $\mathbb{C} = 0.8$. Особенности схемы: используется решатель Римана HLL.

Фиг. 3.

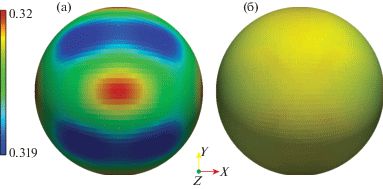
Сферическая задача Сода. Распределение плотности на конечный момент времени на четвертой части шара с сохранением топологии сетки.

На фиг. 3 приведено распределение плотности на конечный момент времени. Для проверки симметричности решения построено рапределение плотности на сфере радиуса $r = 0.51$. Как следует из фиг. 4, использование специального алгоритма реконструкции вектора скорости позволяет существенно лучше сохранять симметрию решения по сравнению с покомпонентной реконструкцией. При этом среднеквадратичное отклонение плотности на сфере радиуса $r = 0.51$ составило $2.9 \times {{10}^{{ - 5}}}$ и $2.6 \times {{10}^{{ - 3}}}$ соответственно.

Фиг. 4.

Сферическая задача Сода. Распределение плотности на сфере радиуса 0.51 на конечный момент времени. (а) – покомпонентная реконструкция, (б) – в локальном базисе.

4.3. Турбулентная стадия неустойчивости Рихтмайера–Мешкова

Турбулентная стадия неустойчивости Рихтмайера–Мешкова (НРМ) является важным для физики высоких плотностей энергии примером сжимаемого неустойчивого течения. Недавно было проведено масштабное численное исследование НРМ по восьми программам, в том числе Flamenco и NUT3D, в рамках сотрудничества ряда научных центров мира, названного тета-группой [28]. В результате работы тета-группы получено надежное эталонное решение для выбранной постановки задачи, которое позволяет верифицировать другие численные коды. Детали постановки задачи и описание анализируемых функционалов можно найти в [28].

Расчетная область: $x \in (0,2.8\pi )$, $y \in (0,2\pi )$, $z \in (0,2\pi )$, $t \in (0,0.5]$.

Начальные условия (см. фиг. 5):

$\begin{gathered} ({{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{1}}{{\varrho }_{1}},{{\alpha }_{2}}{{\varrho }_{2}},({{v}_{x}},{{v}_{y}},{{v}_{z}}),p) = \\ \, = \left\{ \begin{gathered} (1,\;0,\;6.37497,\;0,\;( - 61.48754,\;0,\;0),\;399995.9),\quad x \in (0,\;3), \hfill \\ (1,\;0,\;3,\;0,\;( - 291.575,\;0,\;0),\;{{10}^{5}}),\quad x \in [3,3.5 + f(y,z)), \hfill \\ ({\text{0,}}\;{\text{1,}}\;{\text{0,}}\;{\text{1}},\;( - 291.575,\;0,\;0),\;{{10}^{5}}),\quad x \in [3.5 + f(y,z),2.8\pi ), \hfill \\ \end{gathered} \right. \\ \end{gathered} $
где $f(y,z)$ – начальное полигармоническое возмущение. Граничные условия: при $x = 0$, $x = 2.8\pi $ – свободный выход, остальные границы – периодические. УРС: идеальный газ с $\gamma = 5{\text{/}}3$, ${{c}_{v}} = 312.4$. Расчетные сетки: кубические с количеством ячеек в поперечном направлении 256, 512, 1024 с общим количеством ячеек ≈23.5 млн, 188 млн, 1.5 млрд соответственно. Число Куранта $\mathbb{C} = 0.8$. Особенности схемы: используется решатель Римана HLLC с дополнительной низкомаховой коррекцией из [14].

Фиг. 5.

НРМ. Схематическое изображение начального условия.

На фиг. 6 с распределением объемной доли тяжелого газа в плоскости $z = 2\pi $ на моменты времени $0.1$ и $0.5$ с видно качественное согласие с результатом по коду Flamenco. Как следует из фиг. 7, такие характеристики перемешивания, как интегральные ширина зоны перемешивания и коэффициент гомогенного смешивания, согласуются с полученным по кодам Flamenco и NUT3D. Наблюдается сеточная сходимость данных функционалов.

Фиг. 6.

НРМ. Распределение объемной доли тяжелого газа в плоскости $z = 2\pi $ на моменты времени $0.1$ и $0.5$ с.

Фиг. 7.

НРМ. Зависимость безразмерной интегральной ширины зоны перемешивания (а) и интегрального коэффициента гомогенного смешивания (б) от времени.

Для расчета на сетке 512 использовалось в 8 раз больше MPI-фрагментов, чем на сеткe 256: в 2 раза больше по каждому направлению, т.е. на один MPI-фрагмент приходилось одинаковое количество ячеек. Счет на сетке 512 был в 1.13 раза дольше, чем на 256. Таким образом, эффективность слабого масштабирования здесь составила 88%.

4.4. Неустойчивость Рэлея–Тейлора в волне разрежения

Неустойчивость Рэлея–Тейлора (НРТ) – столь же важный для приложений вид гидродинамической неустойчивости, как и НРМ. Результаты проводимых экспериментов с НРТ служат для проверки и настройки численных кодов. В качестве последнего теста рассматривается моделирование по коду Фокус эксперимента, проведенного в РФЯЦ–ВНИИТФ, на развитие НРТ в волне разрежения [29]. На фиг. 8 показана схема экcперимента на ударной трубе. После устранения мембраны между отсеками с “вакуумом” и газом SF6 формируется волна разрежения (ВР), двигающаяся вверх к границе отсеков с SF6 и воздухом. Газы разделены жидкой мембраной, которая натянута на лески и имеет квазиодномерную гармоническую форму. Когда ВР достигает границы, жидкая мембрана разрушается и контактная граница газов начинает ускоряться вниз, что приводит к развитию НРТ. В постановке задачи используется система единиц СИ.

Фиг. 8.

НРТ в волне разрежения. (а) – схема эксперимента, (б) – фотоизображение рамки с жидкой разделительной мембраной.

Расчетная область: $x \in (0,0.138)$, $y \in (0,0.138)$, $z \in ( - 0.9,0.05)$, $t \in (0,0.01]$.

Начальные условия:

$\begin{gathered} ({{\alpha }_{{air}}},{{\alpha }_{{SF6}}},{{\alpha }_{{air}}}{{\varrho }_{{air}}},{{\alpha }_{{SF6}}}{{\varrho }_{{SF6}}},({{v}_{x}},{{v}_{y}},{{v}_{z}}),T) = \\ \, = \left\{ \begin{gathered} (1,0,0.02,0,(0,0,0),298),\quad z \in ( - 0.9, - 0.835), \hfill \\ (0,1,0,6.04,(0,0,0),298),\quad z \in [ - 0.835,f(x,y)), \hfill \\ (1,0,1.184,0,(0,0,0),298),\quad z \in [f(x,y),0.05), \hfill \\ \end{gathered} \right. \\ \end{gathered} $
где $f(x,y) = {{{\text{A}}}_{1}}cos\left( {\tfrac{{2\pi }}{\lambda }x} \right) + {{A}_{3}}cos\left( {\tfrac{{6\pi }}{\lambda }x} \right) + f{\kern 1pt} '(x,y),$ ${{A}_{1}} = 0.0037$, ${{A}_{3}} = 0.00012$, $\lambda = 0.0276$, $f{\kern 1pt} '(x,y)$ – случайная добавка с амплитудой 0.0004 для моделирования отклонения от гармонической формы контактной границы в эксперименте. Граничные условия: при $z = - 0.9$, $z = 0.05$ – свободный выход, остальные границы – жесткие стенки. УРС: идеальные газы с $\gamma = 1.4$ и ${{c}_{v}} = 717$ для воздуха, $\gamma = 1.0926$ и ${{c}_{v}} = 607$ для SF6. Расчетная сетка:
$\Delta z = 0.0005,\quad \Delta x,\Delta y = \left\{ \begin{gathered} 0.002,\quad z \in ( - 0.9, - 0.18), \hfill \\ 0.001,\quad z \in ( - 0.18, - 0.17), \hfill \\ 0.005,\quad z \in ( - 0.17,0.05). \hfill \\ \end{gathered} \right.$
Кубическая сетка размером 0.0005 сделана в области развития HPT, в остальной части системы применен переход на более грубую (в 4 раза) сетку по x, y для экономии ресурсов. Общее количество ячеек в сетке – 41.944 млн. Число Куранта $\mathbb{C} = 0.8$. Особенности схемы: используется решатель Римана HLLC.

Из фиг. 9 видно воспроизведение в расчете экспериментальной зависимости ширины зоны перемешивания газов от пройденного зоной пути. Ширина зоны в расчете вычислялась как $L = {{h}_{s}} - {{h}_{b}}$, где ${{h}_{s}}$ и ${{h}_{b}}$ – границы зоны, определенные по 0.03 и 0.97 объемной доле SF6, усредненной в плоскости $(x,y)$. Пройденный путь вычислен как $S = ({{h}_{s}} + {{h}_{b}}){\text{/}}2$. Основные структуры зоны в расчете качественно согласуются с экспериментом, см. фиг. 10.

Фиг. 9.

НРТ в волне разрежения. Зависимость ширины зоны перемешивания от пройденного пути.

Фиг. 10.

НРТ в волне разрежения. Сравнение распределения плотности в расчете в сечении $y = 0.069$ c экспериментальным шлирен-изображением. Черные полосы слева – реперы с координатами $z = - 0.0525$ и $z = - 0.1025$.

5. ЗАКЛЮЧЕНИЕ

В работе описана базовая эйлерова схема в программе Фокус для расчета многокомпонентных газодинамических течений на трехмерной неструктурированной сетке. Детально рассмотрены две особенности схемы: 1) формулировка решателей Римана HLL и HLLC без перехода в локальную систему координат каждой грани, 2) специальная TVD-реконструкция вектора скорости, учитывающая направление течения. Распараллеливание выполнено на распределенной памяти с помощью библиотеки MPI.

Работоспособность схемы показана на примере решения двукомпонентной задачи о распаде разрыва на трехмерной неструктурированной сетке. Эффективность специального алгоритма реконструкции вектора скорости продемонстрирована на задаче со сферически симметричным течением на сферической сетке. Проведено верификационное моделирование турбулентной стадии неустойчивости Рихтмайера–Мешкова в постановке тета-группы, на данной задаче проверена масштабируемость кода. Рассчитан эксперимент о развитии неустойчивости Рэлея–Тейлора в волне разрежения на сетке со статичной адаптацией в интересующей области течения.

Следует отметить, что приведенная схема обладает заметным недостатком – численной диффузией на контактных границах, свойственной эйлеровым схемам сквозного счета. Это может существенно снижать точность численного решения в задачах физики высоких плотностей энергии, влияя на качество моделирования дополнительных физических процессов, в том числе переноса излучения. Решение данной проблемы в программе Фокус будет рассмотрено в дальнейшем.

Авторы выражают благодарность сотрудникам РФЯЦ–ВНИИТФ М.И. Авраменко, М.Н. Чижкову за конструктивные обсуждения, Н.В. Глазыриной, С.Н. Щербаковой за помощь в проведении расчетов.

Список литературы

  1. Anuchina N., Volkov V., Gordeychuk V., Es’kov N., Ilyutina O., Kozyrev O. 3D Numerical simulation of Rayleigh-Taylor instability using MAX-3 code // Laser and Particle Beams. 2000. V. 18 (2). P. 175–181.

  2. Гуськов С.Ю., Демченко Н.Н., Змитренко Н.В., Кучугов П.А., Яхин Р.А. Сжатие и горение термоядерной мишени при зажигании фокусирующейся ударной волной в условиях нарушения симметрии облучения лазерными пучками // ЖЭТФ. 2020. Т. 157. Вып. 5. С. 889–900.

  3. Weber C.R., Clark D.S., Cook A.W., Busby L.E., Robey H.F. Inhibition of turbulence in inertial-confinement-fusion hot spots by viscous dissipation // Phys. Ref. E. 2014. V. 89. 053106.

  4. Clark D.S., Hinkel D.E., Eder D.C., Jones O.S., Haan S.W., Hammel B.A., Marinak M.M., Milovich J.L., Robey H.F., Suter L.J., and Town R.P.J. Detailed implosion modeling of deuterium-tritium layered experiments on the National Ignition Facility // Phys. Plasmas. 2013. V. 20. 056318.

  5. Годунов С.К. Разностный метод численного расчета разрывных решений гидродинамики // Мат. сборник. 1959. Т. 47 (89). № 3. С. 271–306.

  6. Toro E.F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction. Springer-Verlag Berlin Heidelberg, 2009. 624 p.

  7. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001. 608 с.

  8. Rudman M. Volume-tracking methods for interfacial flow calculations // Int. J. Numer. Meth. Fluids. 1997. V. 24. P. 671–691.

  9. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения в газовой динамике. М.: Наука, 1978. 688 с.

  10. Лебо И.Г., Тишкин В.Ф. Исследование гидродинамической неустойчивости в задачах лазерного термоядерного синтеза методами математического моделирования. М.: Физматлит, 2006. 304 с.

  11. Янилкин Ю.В., Колобянин В.Ю., Чистякова И.Н., Егужова М.Ю. Применение метода PPM в расчетах по методикам ЭГАК и ТРЭК // ВАНТ. Сер. Матем. моделирование физ. процессов. 2005. Вып. 4. С. 69–79.

  12. Marinak M.M., Kerbel G.D., Gentlie N.A., Jones O., Munro D., Polline S., Dittrich T.R., Haan S.W. Three-dimensional HYDRA simulations of National Ignition Facility targets // Phys. Plasmas. 2001. V. 8. № 5. P. 2275.

  13. Cook A.W. Artificial fluid properties for large eddy simulation of compressible turbulent mixing // Phys. of Fluids 2007. V. 19. 055103.

  14. Thornber B., Mosedale A., Drikakis D., Youngs D., Williams R.J.R. An improved reconstruction method for compressible flows with low Mach number features // J. Comput. Phys. 2008. V. 227. Issue 10. P. 4873–4894.

  15. Berger M.J., Colella P. Local Adaptive Mesh Refinement for Shock Hydrodynamics // J. Comput. Phys. 1989. V. 82. P. 64–84.

  16. Pember R.B., Bell J.B., Colella P., Crutchfield W.Y., Welcome M.L. An adaptive Cartesian grid method for unsteady compressible flow in irregular regions // J. Comput. Phys. 1995. V. 120. Issue 2. P. 278–304.

  17. Allaire G., Clerc S., Kokh S. A five-equation model for the simulation of interfaces between compressible fluids // J. Comp. Phys. 2002. V. 181. Issue 2. P. 577–616.

  18. Harten A., Lax P.D., van Leer B. On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws // SIAM Review 1983. V. 25. № 1. P. 35–61.

  19. Billett S.J., Toro E.F. On WAF-type schemes for multidimensional hyperbolic conservation // J. Comput. Phys. 1997. V. 130. Issue 1. P. 1–24.

  20. Toro E.F., Spruce M., Speares W. Restoration of the Contact Surface in the HLL-Riemann Solver // Shock Waves. 1997. V. 4. P. 25–34.

  21. Berger M., Aftosmis M.J., Murman S.M. Analysis of slope limiters on irregular grids // Paper presented at 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, United States. 2005. P. 2361–2382.

  22. Venkatakrishnan V. On the accuracy of limiters and convergence to steady state solutions // AIAA Paper. 1993. Technical Rep AIAA-93-0880.

  23. Матяш С.В. Новый метод использования принципа минимальных приращений в численных схемах второго порядка аппроксимации // Уч. зап. ЦАГИ. 2005. Т. 36. № 3–4. С. 42–51.

  24. Luttwak G., Falcovitz J. Slope limiting for vectors: A novel vector limiting algorithm // Int. J. Numer. Meth. Fluids. 2011. V. 65. P. 1365–1375.

  25. Maire P.-H., Loubere R., Vachal P. Staggered lagrangian discretization based on cell-centered Riemann solver and associated hydrodynamics scheme // Commun. Comput. Phys. 2011. V. 10. № 4. P. 940–978.

  26. Velechovsky J., Kucharik M., Liska R., Shashkov M. Symmetry-preserving momentum remap for ALE hydrodynamics // J. Physics: Conference Series. 2013. V. 454. 012003.

  27. Blueshields C.J., Weller H.G., Gasparini L., Reese J.M. Implementation of semi-discrete, non-staggered central schemes in a colocated, polyhedral, finite volume framework, for high-speed viscous flows // Int. J. Numer. Meth. in Fluids. 2009. V. 63. № 1. P. 1–21.

  28. Thornber B., Griffond J., Poujade O., Attal N., Varshochi H., Bigdelou P., Ramaprabhu P., Olson B., Greenough J., Zhou Y., Schilling O., Garside K.A., Williams R.J.R., Batha C.A., Kuchugov P.A., Ladonkina M.E., Tishkin V.F., Zmitrenko N.V., Rozanov V.B., Youngs D.L. Late-time growth rate, mixing and anisotropy in the multimode narrowband Richtmyer-Meshkov Instability: the Theta-Group Collaboron // Phys. of Fluids. 2017. V. 29. 105107.

  29. Tiaktev A.A., Pavlenko A.V., Piskunov Yu.A., Bugaenko I.L., Mokrushin S.S. Development of periodic pertubations at the gases interface under Rayleigh-Taylor instability // 16th Internat. Workshop on the Physics of Compressible Turbulent Mixing, Marseilles, France, 2018. www.iwpctm.org

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал