Журнал вычислительной математики и математической физики, 2021, T. 61, № 6, стр. 1034-1056
Математическое моделирование экономического положения домашних хозяйств в россии
М. В. Тарасенко 1, *, Н. В. Трусов 2, **, А. А. Шананин 2, 3, 4, ***
1 Высшая школа бизнеса МГУ
119234 Москва, Ленинские горы, 1, стр. 52, Россия
2 ВМК МГУ
119991 Москва, Ленинские горы, 1, стр. 52, Россия
3 ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 44, кор. 2, Россия
4 РУДН
117198 Москва, ул. Миклухо-Маклая, 6, Россия
* E-mail: tarasenko.m12@gmail.com
** E-mail: trunick.10.96@gmail.com
*** E-mail: alexshan@yandex.ru
Поступила в редакцию 18.08.2020
После доработки 18.08.2020
Принята к публикации 16.09.2020
Аннотация
Исследована задача оптимального управления, моделирующая экономическое поведение репрезентативного домашнего хозяйства. Доказана теорема о существовании решения, получены необходимые условия оптимальности в форме принципа максимума Понтрягина–Кларка и построен синтез оптимального управления. Модель идентифицирована по данным российской статистики. С ее помощью проанализирована проблема потребительского кредитования в России и влияния на экономическое положение домашних хозяйств в условиях пандемии COVID-19. Библ. 11. Фиг. 19. Табл. 2.
1. ВВЕДЕНИЕ
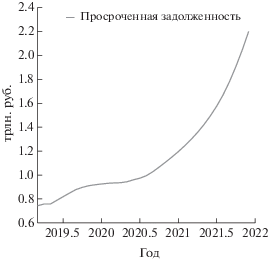
Потребительский кредит стал важным элементом экономических отношений в России XXI века. На фиг. 1 показана динамика отношения задолженности по потребительскому кредиту к ВВП.
В условиях низких реальных доходов основной части населения потребительский кредит стимулировал экономическую активность населения, поддерживал платежеспособный спрос домашних хозяйств и оказывал положительное влияние на темпы роста ВВП. В 2019 г. в активах консолидированного баланса коммерческих банков доля потребительского кредита, который является одним из самых доходных активов, достигла 18%. Около половины кредитной задолженности физических лиц составляет беззалоговый потребительский кредит. За период 2017–2019 гг. количество должников выросло с 34 до 40 млн человек и произошло увеличение отношения процентных требований банковской системы к совокупным доходам населения с 3 до 6%. Рост совокупной долговой нагрузки неравномерно распределен среди различных слоев населения. Имеющиеся исследования (см. [1], [2]) показывают, что различные показатели долговой нагрузки в среднем имеют наибольшие значения в первых 2-х, а также в 5-м и 6-м децилях распределения населения по доходам. Среди заемщиков из первых двух децилей преимущественно возникают просрочки по обслуживанию кредита, а в 5-м и 6-м децилях установилось высокое соотношение платежей по кредитам к доходу заемщиков. Также различна структура задолженности в различных регионах страны. В [3] был проведен пространственный анализ российских регионов через призму их кредитно-сберегательного поведения. В работе было отмечено, что склонность к заемному финансированию потребления характерна либо для регионов с высоким уровнем бедности, либо для регионов, чьи жители привыкли к высоким стандартам потребления в течение 2000-х годов. Среди регионов России второго типа отдельно выделяются Москва и Санкт-Петербург как регионы, в которых значительная часть населения имеет возможность совершать сбережения, а также поддерживать стандарты потребления, не подвергая себя излишней закредитованности.
Уже осенью 2019 г. в правительстве РФ (см. [4]) обсуждалась проблема потребительского кредита как актива коммерческих банков, а также меры по реструктуризации задолженности по потребительскому кредиту как условия дефолта физических лиц. Снижение реальных доходов населения, вызванные пандемией COVID-19, обостряют эту проблему. В данной работе на языке математических моделей анализируются различные аспекты этой проблемы и влияние на них кредитно-денежной политики.
2. МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ ДОМАШНЕГО ХОЗЯЙСТВА С ПОМОЩЬЮ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ РАМСЕЕВСКОГО ТИПА
Моделирование экономического поведения домашних хозяйств основывается на работе Ф. Рамсея (см. [5]). Модели рамсеевского типа в форме задач оптимального управления исследовались, например, в [6], [7].
Будем считать, что экономические решения, принимаемые типичным домашним хозяйством, являются ограниченно рациональными, т.е. домашнее хозяйство определяет потребительские расходы, сбережения и заимствования по потребительскому кредиту так, чтобы максимизировать дисконтированное потребление с учетом бюджетных ограничений. При этом предполагается, что домашнее хозяйство не может спрогнозировать изменения экономической конъюнктуры и принимает решения, считая, что темп инфляции, процентные ставки по депозитам и потребительскому кредиту будут оставаться на неизменном уровне. Будем предполагать, что в планах домашнего хозяйства предполагается, что его доходы $S$, исключая проценты по депозитам, описываются уравнением
где $t$ – момент времени, $\gamma $ – темп роста доходов (положительность $\gamma $ не предполагается), а индекс потребительских цен $p(t)$ растет с $j$ темпом, т.е. $p(t) = p{{e}^{{jt}}}$. Обозначим через $D(t)$ сбережения в форме депозитов под процентную ставку ${{r}_{D}}$, $L(t)$ – задолженность по потребительскому кредиту под процентную ставку ${{r}_{L}}$, $C(t)$ – потребление домашнего хозяйства, $p(t)$ – индекс потребительских цен, $M(t)$ – наличные деньги и счета до востребования. Запас денег ${{M}_{0}}(t)$, необходимый домашнему хозяйству для потребительских расходов $p(t)C(t)$, моделируется законом Фишера ${{M}_{0}}(t) = \theta p(t)C(t)$, где $1{\text{/}}\theta > 0$ – скорость обращения денег. Изменение запаса денег описывается балансовым уравнением Здесь ${{H}_{L}}(t)$ – заимствования по потребительскому кредиту, ${{H}_{D}}(t)$ – вложения в депозиты. Отметим, что отрицательность ${{H}_{L}}(t)$ означает платеж по кредитной задолженности, а отрицательность ${{H}_{D}}(t)$ – снятие денег с депозита. Изменение кредитной задолженности описывается уравнением Изменение сбережений в форме депозитов описывается уравнением Отсутствие арбитража на рынке сбережений и потребительского кредита предполагает, что ${{r}_{L}} > {{r}_{D}} > 0$, $L(t) \geqslant 0$, $D(t) \geqslant 0$. Финансовое состояние домашнего хозяйства задается величиной $X(t) = {{M}_{0}}(t) + D(t) - L(t)$. Рациональное использование финансовых возможностей предполагает, что$S + \left( {{{r}_{L}} - \gamma } \right){{x}_{0}} > 0$, $T - {{t}_{0}} > \mathop {\left\{ {\tfrac{1}{{{{r}_{L}}}}ln\left[ {\tfrac{S}{{S + \left( {{{r}_{L}} - \gamma } \right){{x}_{0}}}}} \right]} \right\}}\nolimits_ + $.
Таким образом, будем моделировать экономическое поведение домашнего хозяйства задачей оптимального управления
Теорема 1. Пусть
$S + ({{r}_{L}} - \gamma ){{x}_{0}} > 0$, $T > \mathop {\left\{ {\tfrac{1}{{{{r}_{L}}}}ln\left[ {\tfrac{S}{{S + \left( {{{r}_{L}} - \gamma } \right){{x}_{0}}}}} \right]} \right\}}\nolimits_ + $.
Тогда задача оптимального управления
(2)
$\frac{{dx}}{{dt}} = S - \gamma x - \frac{1}{\theta }M + {{r}_{D}}{{(x - M)}_{ + }} - {{r}_{L}}{{(M - x)}_{ + }},$Доказательство. При выполнении условий
$S + ({{r}_{L}} - \gamma ){{x}_{0}} > 0$, $T > \mathop {\left[ {\tfrac{1}{{{{r}_{L}}}}ln\left( {\tfrac{S}{{S + \left( {{{r}_{L}} - \gamma } \right){{x}_{0}}}}} \right)} \right]}\nolimits_ + $
управление $M(t) \equiv 0$ порождает в силу решения задачи Коши
траекторию $x(t)$, удовлетворяющую всем ограничениям задачи оптимального управления. Если ${{x}_{0}} \geqslant 0$, то из ограничений (2), (4) задачи оптимального управления следует, что По неравенству Гронуолла имеем оценкуОпределим фазовую траекторию $\left. {\{ {{x}_{{{\text{opt}}}}}(t)\,{\text{|}}\,t \in [0,T]} \right\}$, соответствующую управлению $\left. {\{ {{M}_{{{\text{opt}}}}}(t)\,{\text{|}}\,t \in [0,T]} \right\} \geqslant 0$, как решение задачи Коши
$\left\{ {\tfrac{1}{n}\sum\limits_{k = 1}^n \,{{M}_{{{{i}_{k}}}}}(t)\,{\text{|}}\,t \in [0,T]} \right\}$
и соответствующая ему фазовая траектория ${{\tilde {x}}_{n}}(t)$ удовлетворяют всем ограничениям (2)–(4) задачи оптимального управления.
По теореме Лебега о предельном переходе под знаком интеграла
Теорема 2. Если $\left\{ {x(t),M(t)\,{\text{|}}\,t \in [0,T]} \right\}$ – решение задачи оптимального управления (1)–(4), то $\left\{ {\varphi (t)\,|\,t \in [0,T]} \right\}$ – абсолютно непрерывная функция такая, что
1) если $\tfrac{{\alpha \theta }}{{1 + \theta {{r}_{L}}}} > {{x}^{{1 - \alpha }}}\varphi $, то $M = \mathop {\left[ {\tfrac{{\alpha \theta }}{{(1 + \theta {{r}_{L}})\varphi }}} \right]}\nolimits^{\tfrac{1}{{1 - \alpha }}} $ и
(5)
$\frac{{dx}}{{dt}} = S + ({{r}_{L}} - \gamma )x - \frac{{1 + \theta {{r}_{L}}}}{\theta }\mathop {\left[ {\frac{{\alpha \theta }}{{(1 + \theta {{r}_{L}})\varphi }}} \right]}\nolimits^{\tfrac{1}{{1 - \alpha }}} ,$2) если $\tfrac{{\alpha \theta }}{{1 + \theta {{r}_{L}}}} \leqslant {{x}^{{1 - \alpha }}}\varphi \leqslant \left( {\tfrac{{\alpha \theta }}{{1 + \theta {{r}_{D}}}}} \right)$, то $M(t) = x(t)$ и
(8)
$\frac{{d\varphi }}{{dt}} = [\delta + (1 - \alpha )\gamma - u(t)]\varphi ,\quad {{r}_{D}} \leqslant u(t) \leqslant {{r}_{L}},$3) если $\tfrac{{\alpha \theta }}{{1 + \theta {{r}_{D}}}} < {{x}^{{1 - \alpha }}}\varphi $, то $M = \mathop {\left[ {\tfrac{{\alpha \theta }}{{(1 + \theta {{r}_{D}})\varphi }}} \right]}\nolimits^{\tfrac{1}{{1 - \alpha }}} $ и
(9)
$\frac{{dx}}{{dt}} = S + ({{r}_{D}} - \gamma )x - \frac{{1 + \theta {{r}_{D}}}}{\theta }\mathop {\left[ {\frac{{\alpha \theta }}{{(1 + \theta {{r}_{L}})\varphi }}} \right]}\nolimits^{\tfrac{1}{{1 - \alpha }}} ,$Доказательство. Оптимальное решение задачи оптимального управления должно удовлетворять необходимым условиям принципа максимума Понтрягина в форме Ф. Кларка (см. [10, с. 115]), поскольку функция в правой части ограничения (2) является негладкой.
Функция Гамильтона имеет вид
Фазовый портрет на плоскости с координатами $(x,\varphi )$ состоит из трех областей, соответствующих трем различным режимам поведения домашнего хозяйства. В первой области: $\tfrac{{\alpha \theta }}{{1 + \theta {{r}_{L}}}} > {{x}^{{1 - \alpha }}}\varphi $, реализуется режим кредитования и моделируется домашнее хозяйство, которое использует потребительский кредит. Во второй области: $\tfrac{{\alpha \theta }}{{1 + \theta {{r}_{L}}}} \leqslant {{x}^{{1 - \alpha }}}\varphi \leqslant \tfrac{{\alpha \theta }}{{1 + \theta {{r}_{D}}}}$, реализуется автономный режим и моделируется домашнее хозяйство, не пользующееся потребительским кредитом и не сберегающее в форме депозитов. В третьей области: $\tfrac{{\alpha \theta }}{{1 + \theta {{r}_{D}}}} < {{x}^{{1 - \alpha }}}\varphi $, реализуется режим сбережения и моделируется домашнее хозяйство, сберегающее в форме депозитов. Траектория, определяемая оптимальным решением задачи (1)–(4), должна удовлетворять краевым условиям $x(0) = {{x}_{0}}$, $x(T) = 0$, и зависимость от значения параметров задачи ${{r}_{L}}$, ${{r}_{D}}$, $\gamma $, $\theta $, $\alpha $, $\delta $ может состоять из сочетания разных режимов. Зная траекторию, можно построить синтез оптимального управления. В пределе при $T \to + \infty $ синтез оптимального управления является стационарным, т.е. не зависит от времени. Опишем, как устроен синтез в зависимости от соотношения параметров.
Случай 1 (режим кредитования). Если ${{r}_{D}} < {{r}_{L}} < \delta - \tfrac{{1 - \alpha }}{\theta }$, то синтез оптимального управления задается функцией
Случай 2 (сочетание режима кредитования и автономного режима). Если ${{r}_{D}} < \delta - \tfrac{{1 - \alpha }}{\theta } < {{r}_{L}} < \delta + (1 - \alpha )\gamma $ ${{r}_{D}} < \delta - \tfrac{{1 - \alpha }}{\theta } < {{r}_{L}} < \delta + (1 - \alpha )\gamma $, то синтез оптимального управления задается функцией
Случай 3 (сочетание режимов кредитования, автономного и сбережений). Пусть $\delta - \tfrac{{1 - \alpha }}{\theta } < {{r}_{D}} < {{r}_{L}} < \delta + (1 - \alpha )\gamma $ $\delta - \tfrac{{1 - \alpha }}{\theta } < {{r}_{D}} < {{r}_{L}} < \delta + (1 - \alpha )\gamma $. Уравнение
Если $x \in \left[ {{{x}_{R}}({{r}_{L}},{{r}_{D}},\gamma ,\theta ,\alpha ,\delta ), + \infty } \right)$, то уравнение
Случай 4 (сочетание режимов кредитования и сбережения). Пусть ${{r}_{D}} < \delta + (1 - \alpha )\gamma < {{r}_{L}}$. Если $\tfrac{S}{{\gamma - {{r}_{L}}}} < x < \tfrac{{S\theta }}{{1 + \gamma \theta }}$, то уравнение
(12)
$x + \frac{S}{{{{r}_{L}} - \gamma }} = \frac{{S(1 + \theta {{r}_{L}})[\delta + (1 - \alpha )\gamma - {{r}_{L}}]}}{{(\delta - \alpha {{r}_{L}})(1 + \gamma \theta )({{r}_{L}} - \gamma )}}\mathop {\left[ {\frac{{{{M}_{2}}(1 + \gamma \theta )}}{{S\theta }}} \right]}\nolimits^{\tfrac{{(1 - \alpha )(\gamma - {{r}_{L}})}}{{(\delta + (1 - \alpha )\gamma - {{r}_{L}})}}} + \left[ {\frac{{(1 - \alpha )(1 + \theta {{r}_{L}})}}{{\theta (\delta - \alpha {{r}_{L}})}}} \right]{{M}_{2}}$Если $x > \tfrac{{S\theta }}{{1 + \gamma \theta }}$, то уравнение
(13)
$x + \frac{S}{{{{r}_{D}} - \gamma }} = \frac{{S(1 + \theta {{r}_{D}})[\delta + (1 - \alpha )\gamma - {{r}_{D}}]}}{{(\delta - \alpha {{r}_{D}})(1 + \gamma \theta )({{r}_{D}} - \gamma )}}\mathop {\left[ {\frac{{{{M}_{3}}(1 + \gamma \theta )}}{{S\theta }}} \right]}\nolimits^{\tfrac{{(1 - \alpha )(\gamma - {{r}_{D}})}}{{(\delta + (1 - \alpha )\gamma - {{r}_{D}})}}} + \left[ {\frac{{(1 - \alpha )(1 + \theta {{r}_{D}})}}{{\theta (\delta - \alpha {{r}_{D}})}}} \right]{{M}_{3}}$Тогда синтез оптимального управления задается функцией
Случай 5 (сочетание режимов кредитования и сбережения). Если $\delta + (1 - \alpha )\gamma < {{r}_{D}} < {{r}_{L}}$, то синтез оптимального управления задается функцией
Будем предполагать, что рациональное репрезентативное домашнее хозяйство принимает решение, ориентируясь на сложившуюся экономическую конъюнктуру и учитывая возможности ее изменения в значениях своих поведенческих параметров (коэффициента дисконтирования доходов, коэффициента отвращения к риску $(1 - \alpha )$, скорости обращения денег $1{\text{/}}\theta $). Построенный синтез оптимального управления $M\left( {x;{{r}_{L}},{{r}_{D}},\gamma ,\theta ,\alpha ,\delta } \right)$ позволяет моделировать по информации о динамике процентных ставок ${{r}_{L}}(t)$, ${{r}_{D}}(t)$ и доходах домашних хозяйств $\gamma (t)$ их экономическое поведение. Для этого нужно решать задачу Коши для дифференциального уравнения
Отметим, что при идентификации модели на больших интервалах времени порядка десяти лет поведенческие характеристики домашнего хозяйства $\theta $, $\delta $, $\alpha $ могут изменяться вследствие изменения экономической конъюнктуры.
3. ИДЕНТИФИКАЦИЯ И ВЕРИФИКАЦИЯ МОДЕЛИ ПО ДАННЫМ РОССИЙСКОЙ СТАТИСТИКИ
Модель экономического поведения домашних хозяйств, описанная выше, является незамкнутой моделью. Ее можно рассматривать как блок математической модели для среднесрочного анализа и прогнозирования динамики основных показателей экономики России. Входными переменными модели являются процентные ставки по депозитам ${{r}_{D}}$ и потребительским кредитам ${{r}_{L}}$, темп роста $\gamma $ доходов домашних хозяйств, темп инфляции потребительских цен $j$. Выходными параметрами являются денежный агрегат ${{M}_{0}}$ (наличные деньги на руках у населения и счета до востребования) и потребительские расходы домашних хозяйств, депозиты населения, задолженность по потребительским кредитам. Латентными параметрами модели, которые определяются при идентификации модели, являются коэффициенты дисконтирования $\delta $, параметр функции полезности $\alpha $ (параметр отвращения к риску), скорость обращения наличных денег $1{\text{/}}\theta $.
Для калибровки модели экономического поведения домашних хозяйств была использована статистика Российского мониторинга экономического положения и здоровья населения НИУ ВШЭ (РМЭЗ) и данные Росстата. На основе анализа данных РМЭЗ регионы России были разделены на две группы: богатую и бедную, в зависимости от особенностей распределения долговой нагрузки по децилям, а также в зависимости от показателей бедности и покупательной способности среднедушевого дохода. К богатой группе регионов были отнесены Москва, Московская область, Санкт-Петербург, Казань, Новая Москва. Остальные регионы Российской Федерации были отнесены к бедным группам регионов. В каждой группе регионов выделяются слои населения с высоким и низким уровнями доходов. Слои населения с низким уровнем доходов делятся на 3 группы: заемщиков необеспеченных кредитов (слой 1), не взаимодействующих с банками (слой 3) и сберегающих в форме депозитов (слой 4). При этом уровни доходов и расходов у слоев с низким уровнем доходов не сильно отличаются. Для слоя населения с высоким уровнем доходов (слой 2) характерны также высокие расходы. Домашние хозяйства, попадающие в данный слой, классифицируются как заемщики, которые берут обеспеченный кредит.
В табл. 1 и 2 приведены данные, описывающие слои населения в двух группах регионов. Использовались данные РМЭЗ (см. [11 ] ) за период 2015–2018 гг. Опрос домашних хозяйств РМЭЗ проводится один раз в год. Для качественной классификации были отобраны те домашние хозяйства, которые принимали участие в опросе на протяжении четырех лет (2015–2018 гг.). Домашние хозяйства отвечали на такие вопросы, как: сколько платили они по кредиту за последний месяц, удавалось ли им сберегать за последний месяц. Поскольку опрос является ежегодным, слои населения были сформированы по следующему принципу: домашние хозяйства, которые хотя бы один раз платили по кредиту в рассматриваемом периоде, классифицировались как домашние хозяйства, относящиеся к группе заемщиков. Среди оставшихся те домашние хозяйства, которые хотя бы один раз сберегали, классифицировались как домашние хозяйства, сберегающие в форме депозитов. Все остальные домашние хозяйства относились к слою населения, не взаимодействующему с банками.
Таблица 1.
Богатая группа регионов
| Характеристики социального слоя | $L > 0$ (59.6%) | $L > 0$ (40.4%) | $L = 0$, $D = 0$ | $L = 0$, $D > 0$ | Всего |
|---|---|---|---|---|---|
| Число д/х | 70 (17.24%) | 30 (7.39%) | 159 (39.16%) | 147 (36.21%) | 406 (100%) |
| Число человек | 241 (24.82%) | 76 (7.83%) | 364 (37.49%) | 290 (29.86%) | 971 (100%) |
| Средняя численность человек в д/х | 3.45 | 2.55 | 2.29 | 1.97 | 2.39 |
| Средний доход на человека в группе, руб. | 19 118 | 41 787 | 20 224 | 27 185 | 23 708 |
| Среднее потребление на человека в группе, руб. | 22 181 | 56 994 | 15 643 | 22 724 | 22 636 |
| Совокупные доходы группы по выборке РМЭЗ, руб. | $4.61 \times {{10}^{6}}$ (20.03%) | $3.18 \times {{10}^{6}}$ (13.81%) | $7.35 \times {{10}^{6}}$ (31.93%) | $7.88 \times {{10}^{6}}$ (34.23%) | $23.02 \times {{10}^{6}}$ (100%) |
| Совокупное потребление группы по выборке РМЭЗ, руб. | $5.35 \times {{10}^{6}}$ (24.34%) | $4.35 \times {{10}^{6}}$ (19.79%) | $5.69 \times {{10}^{6}}$ (25.89%) | $6.59 \times {{10}^{6}}$ (29.98%) | $21.98 \times {{10}^{6}}$ (100%) |
| Обозначение слоя населения | 1 | 2 | 3 | 4 |
Таблица 2.
Бедная группа регионов
| Характеристики социального слоя | $L > 0$ (52.3%) | $L > 0$ (47.7%) | $L = 0$, $D = 0$ | $L = 0$, $D > 0$ | Всего |
|---|---|---|---|---|---|
| Число д/х | 553 (25.3%) | 237 (10.84%) | 952 (43.55%) | 444 (20.31%) | 2186 (100%) |
| Число человек | 1816 (32.83%) | 601 (10.87%) | 2194 (39.67%) | 920 (16.63%) | 5531 (100%) |
| Средняя численность человек в д/х | 3.28 | 2.54 | 2.3 | 2.07 | 2.53 |
| Средний доход на человека в группе, руб. | 12 497 | 31 583 | 14 221 | 19 599 | 16 440 |
| Среднее потребление на человека в группе, руб. | 15 099 | 33 391 | 12 138 | 17 139 | 16 254 |
| Совокупные доходы группы по выборке РМЭЗ, руб. | $22.7 \times {{10}^{6}}$ (20.03%) | $18.99 \times {{10}^{6}}$ (20.88%) | $31.2 \times {{10}^{6}}$ (34.31%) | $18.04 \times {{10}^{6}}$ (19.85%) | $90.93 \times {{10}^{6}}$ (100%) |
| Совокупное потребление группы по выборке РМЭЗ, руб. | $27.42 \times {{10}^{6}}$ (30.05%) | $20.08 \times {{10}^{6}}$ (22.34%) | $26.63 \times {{10}^{6}}$ (29.62%) | $15.77 \times {{10}^{6}}$ (17.54%) | $89.9 \times {{10}^{6}}$ (100%) |
| Обозначение слоя населения | 1 | 2 | 3 | 4 |
Обратим внимание на типичный состав домашних хозяйств в различных слоях населения: самый большой по численности состав семьи наблюдается у заемщиков, берущих необеспеченный кредит. Напротив, самый маленький состав семьи наблюдается у сберегающего слоя населения. Можно предположить, что к заемщикам с необеспеченными кредитами относятся молодые семьи с детьми, а к сберегательному слою населения относятся люди старшего поколения. Не исключено, что домашние хозяйства, попавшие в разные слои населения, могут иметь родственные связи. Данное обстоятельство подразумевает возможность трансфертов между сберегающим слоем населения и кредитуемым слоем в случае, когда расходы кредитуемого слоя населения опускаются ниже прожиточного минимума.
На основании временны́х рядов доходов, потребления, сбережений и денежной массы в различных группах регионов была проведена первоначальная калибровка модели по данным за апрель 2009 г.–январь 2019 г. Для идентификации латентных параметров модели решаются обратные задачи. При этом допускается, что такая поведенческая характеристика, как коэффициент дисконтирования $\delta $, может изменяться под влиянием изменений экономической конъюнктуры (темпа инфляции потребительских цен, процентных ставок, темпа роста доходов). Построенные эконометрические регрессии приведены в приложении A. Отметим, что основным регрессором коэффициента дисконтирования у заемщиков является ставка по кредитам, а у сберегающего слоя населения – ставка по депозитам. Каждый слой населения характеризуется своими поведенческими параметрами, и поэтому моделировался отдельно. Для богатой группы регионов были выбраны следующие параметры: ${{\theta }_{1}} = 1$, ${{\theta }_{2}} = 2$, ${{\theta }_{4}} = 4$, ${{\alpha }_{1}} = 0.88$, ${{\alpha }_{2}} = 0.75$, ${{\alpha }_{4}} = 0.765$ (здесь и далее нижний индекс характеризует слой населения). Бедной группе регионов присущи параметры ${{\theta }_{1}} = 0.7$, ${{\theta }_{2}} = 2$, ${{\theta }_{4}} = 3$, ${{\alpha }_{1}} = 0.9$, ${{\alpha }_{2}} = 0.8$, ${{\alpha }_{4}} = 0.775$. Отметим, что коэффициент отвращения к риску больше у заемщиков с необеспеченными кредитами, чем у заемщиков с обеспеченными кредитами. Более того видно, что отвращение к риску у заемщиков в бедной группе регионов больше, чем у заемщиков в богатой группе регионов. Аналогичные замечания можно сделать для параметра, обратного к скорости обращения денег. Слой 3 населения, который не берет потребительский кредит и не сберегает, является значительным по численности. Баланс доходов и расходов слоя 3 и модель влияния экономической конъюнктуры на его поведенческую характеристику $\theta $ замыкают описания экономического поведения домашних хозяйств и позволяют качественно воспроизвести общую динамику расходов и денежной массы населения.
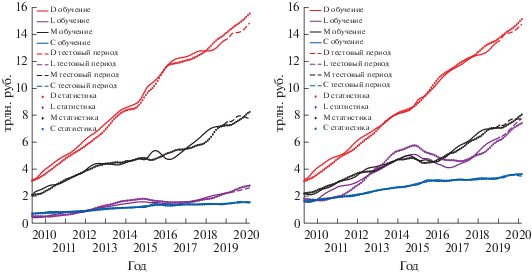
Для верификации модели на временнóм интервале февраль 2019 г.–февраль 2020 г. был построен прогноз, который позволил качественно оценить пригодность используемой модели. На фиг. 2 приведены результаты воспроизведения моделью статистических данных, а также их сравнение с прогнозом на периоде февраль 2019 г.–февраль 2020 г. Из фиг. 2 следует, что модель способна качественно воспроизвести данные, описывающие спрос на кредиты, денежную массу, потребление и объемы формируемых населением сбережений.
Фиг. 2.
Восстановление моделью фактической статистики потребления, задолженности, депозитов и денежной массы в первой (слева) и второй (справа) группах регионов. Точками обозначены фактические данные, линиями – модельные значения, пунктиром – значения прогноза. $D$ – депозиты, $M$ – денежная масса на руках у населения, $L$ – задолженность по потребительским кредитам, $C$ – потребление населения. Все значения даны в трлн. руб.
4. АНАЛИЗ ВЛИЯНИЯ COVID-19 НА ЭКОНОМИЧЕСКОЕ ПОЛОЖЕНИЕ ДОМАШНИХ ХОЗЯЙСТВ
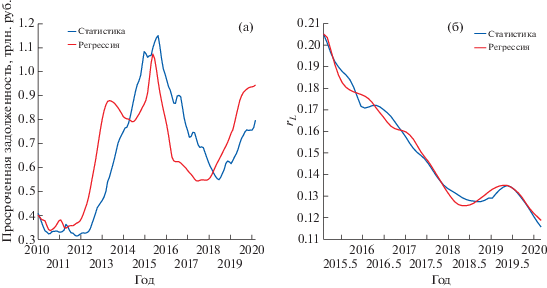
Для анализа и прогноза с помощью построенной модели кредитного поведения домашних хозяйств необходимо сформировать сценарии динамики доходов населения и процентных ставок по кредитам. Пандемия COVID-19 и карантинные меры, введенные в России в конце марта 2020 г., привели к значительному снижению реальных доходов населения. Так, по данным Росстата сезонно сглаженные номинальные доходы населения во втором квартале 2020 г. упали на 6.6% по отношению к первому кварталу 2020 г. Сокращение номинальных доходов было вызвано падением доходов от наемного труда, которые сократились на 4% по отношению к первому кварталу 2020 г. Значительная часть снижения доходов произошла в результате сжатия доходов от предпринимательской деятельности, которые сократились на 42% по отношению к первому кварталу в сезонно сглаженном выражении. В таких условиях представляется вероятным рост просроченной задолженности по кредитам из-за потери способности части населения обслуживать платежи по кредитам. Рост просроченной задолженности, в свою очередь, может приводить к повышению процентных ставок в том случае, если банки решат перенести риски кредитования в стоимость кредита. Для того чтобы учесть такую возможность, было проведено регресионное моделирование процентных ставок по кредитам в зависимости от величины просроченной задолженности по потребительскому кредиту, а также ключевой ставки Банка России. В то же время на величину просроченной задолженности непосредственно оказывает влияние стоимость кредитования, выражаемая через процентную ставку по кредитам, а также динамика необеспеченных, ненадежных кредитов, что было учтено с помощью построения дополнительной регрессии. Результаты ретроспективного моделирования изображены на фиг. 3.
Фиг. 3.
Фактические и модельные значения просроченной задолженности (а) и процентной ставки (б), полученные с помощью регрессии.
В условиях неопределенности относительно будущей траектории доходов населения рассмотрим несколько сценариев. Во всех этих сценариях ставки по кредитам моделируются с помощью регрессий, представленных в приложении A.
4.1. Сценарий 1. Ситуация отсутствия пандемии COVID-19
В этом сценарии предполагается рост номинальных доходов населения со средним темпом роста в 3.5% к соответствующему периоду прошлого года на всем прогнозном горизонте, а также сохранение ключевой ставки на уровне 6%, начиная с февраля 2020 г. В сценарии отсутствия пандемии и из-за незначительного роста доходов населения происходит рост задолженности населения в обеих группах регионов (фиг. 4). При этом в бедной группе регионов рост задолженности по необеспеченным кредитам носит гораздо более выраженный характер (фиг. 4б).
Фиг. 4.
Динамика потребительских задолженностей по обеспеченным (синяя линия) и необеспеченным (красная линия) кредитам богатой (а) и бедной (б) групп в условиях отсутствия карантинных мер и номинального роста доходов.

Крупными точками (фиг. 4б) отмечены временны́е периоды, когда нарушается фазовое ограничение $x \geqslant - \tfrac{S}{{{{r}_{L}} - \gamma }}$. Результаты моделирования показывают, что в условиях роста номинальных доходов и отсутствия карантинных мер необеспеченная задолженность в богатой группе регионов демонстрировала бы замедляющиеся темпы роста. Вместе с этим соразмерное замедление темпов роста в сегменте обеспеченного кредитования привело бы к фактической стагнации обеспеченной потребительской задолженности населения.
Результаты моделирования динамики потребительской задолженности для бедной группы регионов в условиях отсутствия падения доходов отличаются от результатов для богатой группы. В условиях растущих номинальных доходов произошло бы почти троекратное увеличение необеспеченной потребительской задолженности на прогнозируемом временнóм горизонте. Подобная динамика необеспеченной задолженности в бедной группе регионов в условиях стагнации реальных доходов фактически представляет из себя долговой пузырь.
В 2019 г. министр экономического развития М.С. Орешкин заявлял о рисках неограниченного роста потребительского кредитования. Согласно его утверждению (см. [4]), быстрые темпы роста необеспеченного кредитования привели бы к критическому росту перекредитованного населения к 2021 г., что привело бы к рецессии. Результаты моделирования подтверждают выводы бывшего министра.
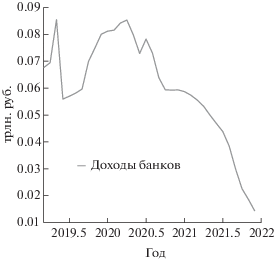
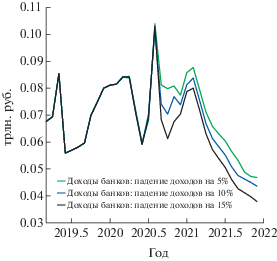
Помимо роста задолженности населения, интерес также представляют динамика просроченной задолженности и динамика доходов банков в условиях отсутствия пандемии. Доходы банков рассчитываются с помощью следующей формулы:
Постепенный рост просроченной задолженности к концу прогнозируемого периода, вызванный увеличением долгового бремени вследствие роста процентных ставок (фиг. 5), приводит к значительному снижению доходов банков от потребительского кредитования к концу прогнозируемого периода (фиг. 6).
4.2. Сценарий 2. Падение доходов населения при текущей ключевой ставке, равной 4.25%
Сценарий $1$ не учитывает произошедшего снижения доходов населения вследствие введения карантина в апреле–мае 2020 г. Сценарии, включающие падение доходов населения, были в первую очередь, основаны на различной динамике роста безработицы, а также имеющихся оценках падения выпуска в российской экономике в период карантина. Спектр роста безработицы включал в себя 5, 10 и 15% увеличения безработицы.
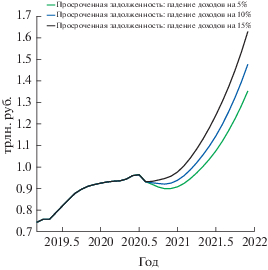
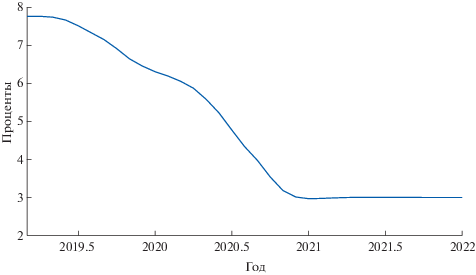
Различная динамика доходов населения, представленная на фиг. 7, оказывает значимое влияние на величину взятого кредита, а значит, и на величину просроченной задолженности в будущем. Просроченная задолженность, в свою очередь, оказывает прямое влияние на степень рискованности кредитования населения банками. В результате различные траектории динамики доходов подразумевают изменения в траектории процентных ставок по кредитованию, что отражено на фиг. 8.
Фиг. 8.
Динамика ставок по кредитам в зависимости от сценария падения доходов при неизменной ключевой ставке.

В условиях падения доходов рост потребительского кредитования наблюдается в бедной группе регионов (фиг. 9б), в которых спрос на потребительский кредит значительно превышает возможности коммерческих банков по его удовлетворению. Богатая группа регионов способна избежать значительного роста задолженности по потребительским кредитам (фиг. 9а).
Фиг. 9.
Динамика потребительских задолженности в бедной (а) и богатой (б) группах регионов при различных сценариях падения доходов при неизменной ключевой ставке: общая задолженность (слева), задолженности по необеспеченным и обеспеченным кредитам (справа).

Падение доходов, выражающееся в снижении возможностей домохозяйств к обслуживанию собственных обязательств, приводит к резкому снижению темпов обеспеченного кредитования. При этом происходит ускорение темпов роста необеспеченного кредитования, к концу прогнозируемого во всех сценариях, что обусловлено желанием домохозяйств поддержать сложившиеся стандарты потребления, а также необходимостью реструктуризации взятых ранее кредитов в условиях падения доходов. Высокие темпы падения доходов в условиях пандемии выражаются в большем росте необеспеченной задолженности, что и выражено в будущей динамике задолженности бедной группы регионов. Задолженность по необеспеченным кредитам в бедной группе регионов может удвоиться к концу 2021 г. и составить 9.8 трлн руб. в случае самого негативного сценария. Падение доходов в бедной группе регионов 2 приводит к значительному уменьшению способности домохозяйств к обслуживанию своих кредитов, что также отражается на ускоряющемся росте просроченной задолженности (фиг. 10). Отметим, что, несмотря на попытки банков сохранить собственную рентабельность путем увеличения ставок, ухудшение качества заемщиков приводит к более быстрому снижению доходов банков от кредитования физических лиц (фиг. 11).
4.3. Сценарий 3. Резкое снижение ключевой ставки до 3% при падении доходов населения
Рассмотрим сценарий с резким снижением процентной ставки до уровня в 3% в третьем квартале 2020 г. (фиг. 12). В этом сценарии останавливается рост задолженности по потребительским кредитам в богатой группе регионов (фиг. 13а) и по сравнению со сценарием 2 замедляется рост задолженности по потребительским кредитам в бедной группе регионов (фиг. 13б). Несмотря на снижение доходов населения, происходит значительное замедление темпов кредитования как в богатой, так и в бедной группах регионов. В бедной группе регионов задолженность по необеспеченным кредитам вырастает до $6.89$ трлн руб., а не до $9.8$ трлн руб., как в предыдущем сценарии. Просроченная задолженность (фиг. 14) и рентабельность банковской системы (фиг. 15) также демонстрируют более позитивную динамику по сравнению со сценарием 2.
Фиг. 13.
Динамика потребительских задолженностей в богатой (а) и бедной (б) группах регионов при различных сценариях падения доходов при резком снижении ключевой ставки до 3%: общая задолженность (слева), задолженности по необеспеченным и обеспеченным кредитам (справа).

4.4. Сценарий 4. Постепенное снижение ключевой ставки до 2% при падении доходов населения
Рассмотрим сценарий с постепенным снижением процентной ставки до уровня в 2% к концу 2021 г. (фиг. 16). В сценарии постепенного снижения ключевой ставки до уровня в 2% положительные результаты не так сильно выражены, как в сценарии с резким снижением ключевой ставки до 3%. Рост задолженности домохозяйств по-прежнему находится на более низкой траектории по сравнению с ситуацией отсутствия снижения ставки, однако замедление темпов кредитования носит менее выраженный характер (фиг. 17).
Фиг. 17.
Динамика потребительских задолженностей в богатой (а) и бедной (б) группах регионов при различных сценариях падения доходов при постепенном снижении ключевой ставки до 2%: общая задолженность (слева), задолженности по необеспеченным и обеспеченным кредитам (справа).

Уровень просроченной задолженности и доходы коммерческих банков от потребительского кредитования (фиг. 18, 19) также улучшаются по сравнению со сценарием 2 постоянной ключевой ставки 4.25%.
5. ВЫВОДЫ
Построение синтеза оптимального управления в модели рационального домашнего хозяйства позволило описать изменения экономического поведения при изменении конъюнктуры. Используя данные РМЭЗ НИУ ВШЭ (см. [11 ] ), были выделены репрезентативные типы домашних хозяйств. Модель идентифицирована по статистическим данным о доходах, расходах, потребительских кредитах и сбережениях домашних хозяйств России за апрель 2009 г.–январь 2019 г. Модель верифицирована по статистическим данным за февраль 2019 г.–февраль 2020 г. С помощью модели проанализирована актуальная проблема обеспеченности потребительских кредитов и связанных с ней рисков для коммерческих банков. Эта проблема остро обсуждалась в экономическом блоке правительства РФ в середине 2019 г. (см. [4]). Расчеты по модели показали обоснованность опасений о платежеспособности заемщиков в части регионов РФ. Анализ с помощью модели влияния пандемии COVID-19 показывает, что проблема платежеспособности заемщиков существенно обостряется из-за снижения доходов населения. Одним из основных источников, вызывающих рост долговой нагрузки на население, помимо падения доходов, является рост процентной ставки. В отличие от доходов населения, главным образом формирующихся в результате производственной деятельности в экономике, процентная ставка может быть оперативно отрегулирована государством с помощью изменения ключевой ставки Банка России, являющейся отправной точкой для банков при расчете ставки, по которой они готовы кредитовать экономику. Расчеты по модели показывают, что снижение ключевой ставки Банком России уменьшает долговую нагрузку на домашние хозяйства и долю неплатежеспособных заемщиков среди физических лиц. При этом эффективность снижения ключевой ставки существенно зависит от динамики снижения. Несмотря на явные преимущества сценария с резким снижением ключевой ставки, следует отметить, что резкое уменьшение ключевой ставки может привести к неожиданным негативным последствиям, таким как резкое ослабление курса рубля или значительное увеличение темпов инфляции.
Список литературы
Крупенский Н.А., Кузина О.Е. Перекредитованность россиян: миф или реальность? // Вопросы экономики. 2018. Т. 11. С. 85–104.
World Bank. Household Over-Indebtedness in Russia, 2020.
Зубаревич Н.В., Сафронов С.Г. Люди и деньги: доходы, потребление и финансовое поведение населения российских регионов в 2000–2017 гг. // Изв. РАН. Сер. географическая. 2019. Т. 5. С. 3–17.
Базанова Е. Минэкономразвития готово поддержать закредитованное население. Ведомости, 2019; https://www.vedomosti.ru/economics/articles/2019/07/2.
Ramsey F.P. A mathematical theory of savings // Economic J. 1928. V. 152. № 38. P. 543–559.
Рудева А.В., Шананин А.А. Синтез управления в модифицированной модели Рамсея с учетом ограничения ликвидности // Дифференц. ур-ния. 2009. Т. 45. № 12. С. 1799–1803.
Гималтдинов И.Ф. Исследование спроса на потребительские кредиты и наличные деньги // Матем. моделирование. 2012. Т. 24. № 2. С. 84–98.
Komlos J. A generalization of a problem of Steinhaus // Acta Math. Acad. Sci. Hungaricae. 1967. V. 18. P. 217–229.
Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений // М.: Изд-во иностр. лит., 1958. 474 с.
Кларк Ф. Оптимизация и негладкий анализ // М.: Наука, 1988. 280 с.
“Russia Longitudinal Monitoring survey, RLMS-HSE”, “Российский мониторинг экономического положения и здоровья населения НИУ ВШЭ (RLMS HSE)“, проводимый Национальным исследовательским университетом Высшая школа экономикии ООО Демоскоппри участии Центра народонаселения Университета Северной Каролины в Чапел Хилле и Института социологии Федерального научно-исследовательского социологического центра РАН.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики