Журнал вычислительной математики и математической физики, 2021, T. 61, № 7, стр. 1220-1232

2.1. Внутренние свойства модели

Транспортная сеть представляет собой связный ориентированный граф ${\mathbf{G}} = ({\mathbf{V}},{\mathbf{E}})$, где ${\mathbf{V}}$ – множество вершин, ${\mathbf{E}} = \{ (i,j)\} $ – множество ветвей графа. На граф также накладываются ограничения на максимальную и минимальную степень вершин $d(i)$: $min(d(i)) = 1$ и $max(d(i)) = 3$. Также $\forall i\,:d(i) > 1 \to \exists j,$ $l \in {\mathbf{V}}:(j,i),\;(i,l) \in {\mathbf{E}}$, т.е. не существует вершины, в которой только заканчиваются несколько ветвей, и не существует вершины, в которой только начинаются несколько ветвей.

Определим теперь все типы вершин графа в зависимости от их степеней.

1. $d(i) = 1$. В данном случае существует два варианта:

(a) $i\,:\exists (i,j) \in {\mathbf{E}}$. Такие вершины будем называть вершинами-въездами. Вершины-въезды образуют множество ${{{\mathbf{V}}}_{{{\text{in}}}}}$ и являются источниками автомобильно-транспортных средств(АТС) в рассматриваемой модели.

(б) $i\,:\exists (j,i) \in {\mathbf{E}}$. Такие вершины будем называть вершинами-съездами. Вершины-съезды образуют множество ${{{\mathbf{V}}}_{{{\text{out}}}}}$ и являются стоками автомобилей в рассматриваемой модели.

2. $d(i) = 2$. Это внутренние вершины модели, образующие множество ${{{\mathbf{V}}}_{{{\text{int}}}}}$.

3. $d(i) = 3$ – вершины-центры перекрестков дорожно-транспортной сети. Данные вершины также входят в множество ${{{\mathbf{V}}}_{{{\text{int}}}}}$, но образуют еще два подмножества.

(a) Если $\exists (i,j) \in {\mathbf{E}},$ $(i,k) \in {\mathbf{E}}\,:j \ne k$, то такие вершины образуют множество ${{{\mathbf{V}}}_{{{\text{sep}}}}}$ – вершины, в которых происходит разделение потоков в дорожно-транспортной сети.

(б) Если $\exists (j,i) \in {\mathbf{E}},$ $(k,i) \in {\mathbf{E}}\,:j \ne k$, то такие вершины образуют множество ${{{\mathbf{V}}}_{{{\text{mer}}}}}$ – вершины, в которых происходит слияние потоков в дорожно-транспортной сети.

Таким образом, ${\mathbf{V}} = {{{\mathbf{V}}}_{{{\text{int}}}}} \cup {{{\mathbf{V}}}_{{{\text{out}}}}} \cup {{{\mathbf{V}}}_{{{\text{in}}}}}$ – все вершины распределены по трем непересекающимся группам. Вершины же перекрестки с $d(i) = 3$ дополнительно разделены по типу перекрестка, причем ${{V}_{{{\text{sep}}}}} \cap {{V}_{{{\text{mer}}}}} = \not {0}$. Ввиду того, что в данной работе рассматриваются только автомагистрали, то вершины с $d(i) = 4$ и более не встречаются.

Разделим схожим образом ребра, инцидентные этим вершинам. Рассмотрим для этого некоторое ребро $(i,j)$.

1. Если $i \in {{{\mathbf{V}}}_{{{\text{in}}}}}$, то ребро $(i,j)$ – это ребро-въезд. Такие ребра образуют множество въездов ${{{\mathbf{E}}}_{{{\text{in}}}}}$.

2. Если $j \in {{{\mathbf{V}}}_{{{\text{out}}}}}$, то ребро $(i,j)$ – это ребро-съезд. Такие ребра образуют множество съездов ${{{\mathbf{E}}}_{{{\text{out}}}}}$.

3. Если $i \in {{{\mathbf{V}}}_{{{\text{int}}}}}$ и $j \in {{{\mathbf{V}}}_{{{\text{int}}}}}$, то ребро $(i,j)$ – это внутреннее ребро модели. Такие ребра образуют множество внутренних ребер модели ${{{\mathbf{E}}}_{{{\text{int}}}}}$.

Также как и с вершинами ${\mathbf{E}} = {{{\mathbf{E}}}_{{{\text{int}}}}} \cup {{{\mathbf{E}}}_{{{\text{out}}}}} \cup {{{\mathbf{E}}}_{{{\text{in}}}}}$ за исключением случая, когда модель представляет из себя одно ребро, который в этой работе не рассматривается.

Определим теперь понятие состояния модели в момент времени $t$. Для этого нам понадобится понятие автомобильной группы на ветви $(i,j){\kern 1pt} :\;{\mathbf{A}}_{k}^{t} = \{ \mathop {{\text{Pos}}}\nolimits_k ,{{V}_{k}},{{N}_{k}}\} $, обладающей следующими характеристиками:

1. $\mathop {{\text{Pos}}}\nolimits_k $ – позиция начала группы относительно начала ветви, на которой она расположена.

2. ${{V}_{k}}$ – скорость группы АТС.

3. ${{N}_{k}}$ – размер группы АТС из ${{\mathbb{R}}_{{ \geqslant 0}}} = {{\mathbb{R}}_{ + }}$.

Пусть теперь ${\mathbf{A}}_{{i,j}}^{t} = \{ {\mathbf{A}}_{k}^{t}\} $ – упорядоченное множество автомобильных групп на ветви $(i,j)$. Причем $\forall l,m:l < m \to {\text{Po}}{{{\text{s}}}_{l}} > {\text{Po}}{{{\text{s}}}_{m}}$ – группы не могут обгонять друг друга.

Таким образом, введем состояние системы в момент времени $t$ как ${{{\mathbf{A}}}^{t}} = \{ {\mathbf{A}}_{{i,j}}^{t}\} \cup \{ A_{{{\text{out}},i,j}}^{t}\} $, т.е. положение, скорость, размер и тип всех автомобильных групп на всех ветвях дорожно-транспортной сети. Группы АТС $\{ A_{{{\text{out}},i,j}}^{t}\} $ представляют собой специальные группы-буферы. Их особые свойства рассматриваются в разделе Общих свойств модели.

Для расчетов нам также понадобится понятие потенциала трансфера ${\text{Tr}}_{{(i,j),k}}^{t}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}})$ – число АТС, которые могут съехать с ветви $(i,j)$ на ветвь $(j,k)$ в интервал времени от $t - 1$ до $t$. Данная величина вычисляется заново на каждой временной итерации в зависимости от состояния системы.

2.2. Внешние свойства модели

Определим теперь свойства модели, задаваемые при ее инициализации.

Рассмотрим предварительно три ветви с $d(j) = 3{\kern 1pt} :\;(i,j),(j,{{k}_{1}}),(j,{{k}_{2}})$. В данной работе мы считаем $(j,{{k}_{1}})$ продолжением автомагистрали, а $(j,{{k}_{2}})$ – съездом с нее. Данное распределение полностью задается в момент инициализации модели.

Перечислим все внешние параметры модели для каждой ветви $(i,j) \in {\mathbf{E}}$ графа ${\mathbf{G}}$.

1. Длина ветви ${{l}_{{i,j}}}$.

2. Число полос, по которым разрешено движение автомобилей по данной ветви ${{n}_{{i,j}}}$.

3. ${{I}_{{i,j}}} = \{ 0,1\} $ – идентификатор того, является ветвь съездом или нет. Если является, то ${{I}_{{i,j}}} = 1$.

4. Функция скорости для данной ветви $V = {{f}_{{i,j}}}(\rho )$, ${{f}_{{i,j}}}:{{\mathbb{Q}}_{ + }} \to {{\mathbb{Q}}_{ + }}$, где $\rho \in {{\mathbb{R}}_{ + }}$ – плотность АТС. В данной работе рассматриваются только ограниченные, непрерывные, монотонно убывающие функции скорости. Процедура получения данной функции из экспериментальных данных детально описана в статье [17].

5. Матрица перемешивания в узле $j$ в момент времени $t$, задаваемая функцией ${{M}_{j}}(t)$. В случае если $j:\not {\exists }(j,k) \in {{{\mathbf{E}}}_{{{\text{out}}}}} \to \forall t:{{M}_{j}}(t) = 0$.

6. Интенсивность источника в узле $i$ в момент времени $t$, задаваемая функцией ${{F}_{i}}(t)$. Для всех $i\,:i \notin {{{\mathbf{V}}}_{{{\text{in}}}}} \to \forall t\,:{{F}_{i}}(t) = = 0$.

Также у каждой ветви есть буфер АТС $A_{{{\text{out}},i,j}}^{t} = \{ {\text{Po}}{{{\text{s}}}_{{{\text{out}},i,j}}},{{V}_{{{\text{out}},i,j}}},{{N}_{{{\text{out}},i,j}}}\} $, представляющий из себя группу АТС с ${\text{Po}}{{{\text{s}}}_{{{\text{out}},i,j}}} = {{l}_{{i,j}}},\;{{V}_{{{\text{out}},i,j}}} = 0$. Данная группа моделирует очередь на съезд с ребра $(i,j)$ – т.е. группу $(j,k)$ с ${{I}_{{i,j}}} = 1$. Работа с данной группой детально описана в разд. Алгоритмов перемещения и объединения групп АТС 3.

Будем считать, что в модели все автомобили имеют фиксированный размер ${{L}_{{{\text{ca}}{{{\text{r}}}^{{{\text{avg}}}}}}}}$. В дальнейшем, путем изменения этой величины можно также исследовать зависимость поведения автомагистрали от состава потока автомобилей. С его помощью получаем максимальное число автомобилей на ветви $(i,j)$ как $N_{{{\text{max}}}}^{{i,j}} = \tfrac{{{{l}_{{i,j}}} \cdot {{n}_{{i,j}}}}}{{L_{{{\text{car}}}}^{{{\text{avg}}}}}}$.

Введем также понятие динамического размера автомобилей ${{L}_{{{\text{car}}}}}(V) = L_{{{\text{car}}}}^{{{\text{avg}}}} + aV$, где $a = 0.504$. Данная величина отражает тот факт, что автомобили в среднем на определенной скорости не сближаются сильнее некоторого расстояния. Сама же константа $a$, как и данное приближение, взята из книги [19].

Таким образом, получаем, что все характеристики автомобильной группы ограничены сверху.

1. Положение $\mathop {{\text{Pos}}}\nolimits_k $ группы АТС длиной ветви, на которой группа находится.

2. Скорость ${{V}_{k}}$ ограничена максимальной скоростью на ветви, которую можно определить из функции скорости ${{f}_{{i,j}}}(\rho )$.

3. Максимальный размер ${{N}_{k}}$ ограничен максимальным числом автомобилей на ветви $N_{{{\text{max}}}}^{{i,j}}$.

Однако поскольку в нашей модели все группы АТС движутся так, как будто каждый автомобиль в группе обладает полным знанием обо всех других автомобилях, то это накладывает на группы логическое ограничение на их размер, так как сложно ожидать такого поведения у АТС в огромной группе. Мы в данной работе считаем разумным ограничение в ${{N}_{{{\text{max}}}}} = 20$ АТС.

Также нам понадобится величина среднего ускорения группы АТС ${{a}_{{{\text{avg}}}}}$ для ограничения увеличения скорости движения групп АТС по ветвям автомагистрали. В данной работе величина ускорения взята за константу и равна 2.2 м/с² (см. [20]).

3.1. Движение групп АТС по ветви

На каждой итерации алгоритма надо рассчитать новое положение групп АТС для каждой ветви. Перерасчет положения групп, а также их скорости производит функция ${\text{group\_mover}}({\mathbf{A}}_{{i,j}}^{t},k,(i,j),\tau ,t)$ по алгоритму 1. Расчеты по данному алгоритму сводятся к следующим шагам.

Шаг 1. Для выбранной группы АТС ${\mathbf{A}}_{k}^{t}$ на ветви $(i,j)$ рассчитываем ее скорость $V_{k}^{'}$ на основании плотности автомобилей на участке автодороги перед ней.

Шаг 2. Рассчитываем новое положение группы АТС.

Шаг 3. Если группа оказалась в конце ветви:

(а) рассчитать, сколько времени она ехала до конца ветви;

(б) в соответствии с матрицей перемешивания часть группы добавляется в буфер-группу $A_{{{\text{out}},i,j}}^{t}$;

(в) оставшаяся часть группы ${\mathbf{A}}_{k}^{t}$ пытается переехать на следующую для нее ветвь с ${{I}_{{j,{{m}_{1}}}}} = 0$;

(г) группа-буфер $A_{{{\text{out}},i,j}}^{t}$ пытается переехать на следующую для нее ветвь с ${{I}_{{j,{{m}_{1}}}}} = 1$.

Заметим, что функция group_transferrer алгоритм 3 вызывается тут с временным шагом $\tau {\kern 1pt} '$, что означает, что группа АТС при переезде на новую ветвь будет двигаться меньшее количество времени.

Алгоритм 1.  Алгоритм расчета положения и скорости группы АТС

Вход: ${\mathbf{A}}_{{i,j}}^{t}$ – множество характеристик автомобильных групп на ветви;

$k$ – индекс рассматриваемой автомобильной группы;

$(i,j)$ – рассматриваемая ветвь графа;

$\tau $ – временной шаг;

$t$ – текущий момент времени;

если $\mathop {{\text{Pos}}}\nolimits_k = {{l}_{{i,j}}}$, то

Если группа АТС уже в конце ветви, то она просто пытается переехать на следующую ветвь

Пусть $j{\kern 1pt} '{\kern 1pt} :\;(j,j{\kern 1pt} ') \in \widetilde {\mathbf{E}}$ – ветвь c ${{I}_{{j,j{\kern 1pt} '}}} = 0$

${\text{group\_transferrer}}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}},k,(i,j),(j,j{\kern 1pt} '),\tau {\kern 1pt} ')$ из Алгоритма 3

return 0

$\mathop {{\text{Pos}}}\nolimits_k + = {{V}_{k}} \cdot \tau $

Пусть $\rho = \tfrac{{\sum\nolimits_{m = k + 1}^{{\text{len}}({\mathbf{A}}_{{i,j}}^{t})} \,{{N}_{m}}}}{{{{l}_{{i,j}}} \cdot {{n}_{{i,j}}}}}$ – плотность АТС на участке ветви $(i,j)$ перед группой АТС $k$,

тогда $V_{k}^{'} = {{f}_{{i,j}}}(\rho )$ – новая скорость группы АТС.

если $V_{k}^{'} - {{V}_{k}} > {{a}_{{{\text{avg}}}}} \cdot \tau ,$ то

$V_{k}^{'} = {{V}_{k}} + {{a}_{{{\text{avg}}}}} \cdot \tau $

если ${\text{Po}}{{{\text{s}}}_{k}} \geqslant {{l}_{{i,j}}}$ и $k = 0,$ то

$\tau {\kern 1pt} ' = \tau \cdot \tfrac{{{\text{Po}}{{{\text{s}}}_{k}} - {{l}_{{i,k}}}}}{{{{V}_{k}} \cdot \tau }}$ – ’оставшееся’ время движения автомобильной группы

${\text{Po}}{{{\text{s}}}_{k}} = {{l}_{{i,k}}}$

Добавим АТС в группу-буфер ${\mathbf{A}}_{{{\text{out}},i,j}}^{t}$

${{N}_{{{\text{out}},i,j}}} + = {{N}_{k}} \cdot {{M}_{j}}(t)$

${{N}_{k}} = {{N}_{k}} \cdot (1 - {{M}_{j}}(t))$

Оставшиеся АТС должны продолжить движение по магистрали

Пусть $j{\kern 1pt} '\,:(j,j{\kern 1pt} ') \in \widetilde {\mathbf{E}}$ – ветвь c ${{I}_{{j,j{\kern 1pt} '}}} = 0$

${\text{group\_transferrer}}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}},k,(i,j),(j,j{\kern 1pt} '),\tau {\kern 1pt} ')$ по Алгоритму 3

Группа-буфер пытается съехать

Пусть $j{\kern 1pt} '{\kern 1pt} '\,:(j,j{\kern 1pt} '{\kern 1pt} ') \in \widetilde {\mathbf{E}}$ – ветвь c ${{I}_{{j,j{\kern 1pt} '{\kern 1pt} '}}} = 0$

${\text{group\_transferrer}}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}},k,(i,j),(j,j{\kern 1pt} '{\kern 1pt} '),\tau {\kern 1pt} ')$ по Алгоритму 3

иначе

если ${\text{Po}}{{{\text{s}}}_{k}} \geqslant {\text{Po}}{{{\text{s}}}_{{i,k - 1}}},$ то

${\text{Po}}{{{\text{s}}}_{k}} = {\text{Po}}{{{\text{s}}}_{{k - 1}}} - {{L}_{{{\text{car}}}}}({{V}_{{k - 1}}}) \cdot {{N}_{{k - 1}}}$

${\text{group\_union}}({{{\mathbf{A}}}_{{i,j}}},k,(i,j),t)$

Если группа АТС ${\mathbf{A}}_{k}^{t}$ все еще существует ${{V}_{k}} = V_{k}^{'}$

3.2. Объединение двух групп АТС

После изменения положения группы АТС на ветви нужно проверить, не может ли она быть объединена с какой-либо другой группой. Поскольку группы движутся только вперед и в нашей модели не могут обгонять друг друга, то проверка на возможность объединения идет только с группой перед рассматриваемой. То есть для группы АТС $j$ рассматривается возможность ее слияния с группой $j - 1$. За слияние групп отвечает функция ${\text{group\_union}}({\mathbf{A}}_{{i,j}}^{t},k,(i,j),t)$, работающая по алгоритму 2.

Алгоритм 2. Алгоритм объединения групп АТС

Вход: ${\mathbf{A}}_{{i,j}}^{t}$ – множество характеристик автомобильных групп на ветви;

$k$ – индекс рассматриваемой автомобильной группы;

$(i,j)$ – рассматриваемая ветвь графа;

$t$ – текущий момент времени;

если $k = 0$, то

Группу не с чем объединять, так как она самая первая

иначе

если ${\text{Po}}{{{\text{s}}}_{{k - 1}}} - {\text{Po}}{{{\text{s}}}_{k}} \leqslant {{L}_{{{\text{car}}}}}({{V}_{{k - 1}}}) \cdot {{N}_{{k - 1}}}$ и ${{N}_{{k - 1}}} + {{N}_{k}} \leqslant {{N}_{{{\text{max}}}}},$ то

Объединяем группы в одну

если $k - 1 = 0$ и $\operatorname{Pos} (k - 1) = {{l}_{{i,j}}},$ то

$N_{{{\text{exit}}}}^{j} + = {{N}_{k}} \cdot {{M}_{j}}(t)$

${{N}_{{k - 1}}} + = {{N}_{k}} \cdot (1 - {{M}_{j}}(t))$

иначе

${{N}_{{k - 1}}} + = {{N}_{k}}$

$\operatorname{del} {\mathbf{A}}_{k}^{t}$ – группа $k$ удаляется

3.3. Перемещение групп АТС между ветвями

Когда  группа  автомобилей  достигает  конца  ветви,  на  которой она находится, требуется определить,  какая  ее  часть  переедет на следующий сегмент автомагистрали и какое положение и скорость примет на новой ветви. За данные расчеты отвечает функция ${\text{group\_transferrer}}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}},k,(i,j),(j,j{\kern 1pt} '),\tau ,t)$ по алгоритму 3. Расчеты по данному алгоритму сводятся к следующим шагам.

Шаг 1. Определяем индекс новой группы АТС на ветви $(j,j{\kern 1pt} ')$.

Шаг 2. Определяем, может ли группа переехать на новую ветвь полностью. Если да:

(а) создаем новую группу АТС в конце ветви $(j,j{\kern 1pt} ')$ с ${{N}_{{k{\kern 1pt} '}}} = {{N}_{k}}$.

(б) Удаляем группу $k$ из ${\mathbf{A}}_{{i,j}}^{t}$.

Шаг 3. Если нет:

(а) создаем новую группу АТС в конце ветви $(j,j{\kern 1pt} ')$ с ${{N}_{{k{\kern 1pt} '}}} = N{\kern 1pt} '$, где $N'$ – число АТС, которые могут переехать.

(б) Уменьшаем размер группы $k$ на величину $N{\kern 1pt} '$.

Шаг 4. Вызываем функцию для перемещения новой группы по ветви $(j,j{\kern 1pt} ')$.

Алгоритм 3. Алгоритм перемещения группы АТС на новую ветвь

Вход: ${{{\mathbf{A}}}^{t}}$ – состояние системы в текущий момент времени;

${{{\mathbf{A}}}^{{t - 1}}}$ – состояние системы в предыдущий момент времени;

$k$ – индекс рассматриваемой автомобильной группы;

$(i,j)$ – ветвь, с которой хочет съехать группа АТС;

$(j,j{\kern 1pt} ')$ – ветвь, на которую хочет съехать группа АТС;

$\tau $ – временной шаг;

$t$ – текущий момент времени;

если ${{N}_{k}} \leqslant {\text{Tr}}_{{(i,j),j{\kern 1pt} '}}^{t}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}}),$ то

Группа полностью может переехать на новую ветвь

Пусть $k{\kern 1pt} ' = {\text{len}}({\mathbf{A}}_{{j,j{\kern 1pt} '}}^{t}) + 1$ – индекс новой группы АТС

Создаем новую группу АТС на ребре $(j,j{\kern 1pt} ')$ с индексом $k{\kern 1pt} '$ и характеристиками:

${\text{Po}}{{{\text{s}}}_{{k'}}} = 0,$ ${{V}_{{k{\kern 1pt} '}}} = {{f}_{{j,j{\kern 1pt} '}}}(\rho ),$ ${{N}_{{k{\kern 1pt} '}}} = {{N}_{k}}$

Удаляем группу $k$ из ${\mathbf{A}}_{{i,j}}^{t}$

${\text{group\_mover}}({\mathbf{A}}_{{j,j{\kern 1pt} '}}^{t},k{\kern 1pt} ',(j,j{\kern 1pt} '),\tau ,t)$

иначе

Только часть группы переезжает на новую ветвь

Пусть $k{\kern 1pt} ' = {\text{len}}({\mathbf{A}}_{{j,j{\kern 1pt} '}}^{t}) + 1$ – индекс новой группы АТС

Создаем новую группу АТС на ребре $(j,j{\kern 1pt} ')$ с индексом $k{\kern 1pt} '$ и характеристиками:

${\text{Po}}{{{\text{s}}}_{{k'}}} = 0,$ ${{V}_{{k{\kern 1pt} '}}} = {{f}_{{j,j{\kern 1pt} '}}}(\rho ),$ ${{N}_{{k{\kern 1pt} '}}} = {\text{Tr}}_{{(i,j),j{\kern 1pt} '}}^{t}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}})$

${{N}_{k}} - = {\text{Tr}}_{{(i,j),j{\kern 1pt} '}}^{t}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}})$

${\text{group\_mover}}({\mathbf{A}}_{{j,j{\kern 1pt} '}}^{t},k{\kern 1pt} ',(j,j{\kern 1pt} '),\tau ,t)$

4.1. Расчет потенциала трансфера

Для начала определим то, как в конце каждой итерации рассчитывается сколько АТС могут переехать с ветви $(i,j)$ на ветвь $(j,k)$. Особенностью является то, что алгоритм рассчитывает не потенциал трансфера для ветви $(i,j)$ на ветвь $(j,k)$, а все потенциалы трансфера $\forall i\,:(i,j) \in {\mathbf{E}} \to {\text{Tr}}_{{i,j}}^{k}$. То есть для ветви $(j,k)$ рассчитываются всевозможные ${\text{Tr}}_{{i,j}}^{k}$.

Данный расчет производит функция ${\text{Tr\_calculator}}({{{\mathbf{A}}}^{t}},{{{\mathbf{A}}}^{{t - 1}}},(j,k),\tau )$ по алгоритму 4. В процессе расчета нам также понадобятся величины $Q(i,j) = {\text{max}}(\rho \cdot {{f}_{{i,j}}}(\rho ))$ – максимальный поток АТС на ветви $(i,j)$, $N_{{{\text{max}}}}^{{i,j}}$ – максимальное число АТС на ветви $(i,j)$ и $N_{{i,j}}^{t} = \sum\nolimits_{m = 0}^{{\text{len}}({\mathbf{A}}_{{i,j}}^{t})} \,{{N}_{m}}$ – текущее число АТС на ветви $(i,j)$.

Процедура расчета сводится к определению двух величин:

1) ${{P}_{i}}$ – потенциальное количество АТС, которые могут доехать до конца ветви $(i,j)$, предшествующей $(j,k)$;

2) ${{N}_{{{\text{total}}}}}$ – сколько всего АТС может переехать на ветвь $(j,k)$ на основании ее вместимости и максимального потока на ней.

В итоге число АТС, которые могут переехать с ветви $(i,j)$ на ветвь $(j,k)$, определяется формулой ${{N}_{{{\text{total}}}}}\tfrac{{{{P}_{i}}}}{{\sum {{P}_{i}}}}$.

4.2. Процедура расчета

Процедура перехода от состояния системы ${{{\mathbf{A}}}^{{t - 1}}}$ к состоянию ${{{\mathbf{A}}}^{t}}$ происходит в соответствии со следующим циклом.

1. $\forall (i,j) \in {{{\mathbf{V}}}_{{{\text{out}}}}}$: удаляем все группы АТС, находящиеся на этой ветви, так как это ветви – стоки.

2. $\forall (i,j) \in {{{\mathbf{V}}}_{{{\text{in}}}}}$: формируем новую группу АТС $k{\kern 1pt} ' = {\text{len}}({\mathbf{A}}_{{i,j}}^{t}) + 1$ с $\mathop {{\text{Pos}}}\nolimits_{k{\kern 1pt} '} = 0,$ ${{V}_{{k{\kern 1pt} '}}} = {{f}_{{j,j{\kern 1pt} '}}}(\rho ),$ ${{N}_{{k{\kern 1pt} '}}} = {{F}_{i}}(t)$.

3. Пусть ${\mathbf{C}}$ – некоторое подмножество ветвей графа. Будем выполнять следующие действия пока оно не пусто:

(а) ${\mathbf{C}} = \{ (i,j)\} ,$ $(i,j) \in {{{\mathbf{V}}}_{{{\text{out}}}}}$.

(б) $\forall (i,j) \in {\mathbf{C}} \to \forall {\mathbf{A}}_{k}^{t} \in {\mathbf{A}}_{{i,j}}^{t} \to {\text{group\_mover}}({\mathbf{A}}_{{i,j}}^{t},k,(i,j),\tau ,t)$ – для каждой группы АТС рассчитываем ее новое положение. Причем расчет производится упорядоченно по убыванию величины $\mathop {{\text{Pos}}}\nolimits_k $, причем группы-буферы обсчитываются первыми.

(в) ${\mathbf{C}}{\kern 1pt} ' = \{ (k,i)\} :\exists j:(i,j) \in {\mathbf{C}}$ – формируем новое подмножество для расчетов.

(г) ${\mathbf{C}} = {\mathbf{C}}{\kern 1pt} '$.

4. $\forall (i,j) \in {\mathbf{E}} \to \forall {\mathbf{A}}_{k}^{t} \in {\mathbf{A}}_{{i,j}}^{t} \to {\text{group\_union}}({\mathbf{A}}_{{i,j}}^{t},k,(i,j),t)$ – объединяем группы АТС, если это возможно.

Таким образом, получаем состояние системы ${{{\mathbf{A}}}^{t}}$.

Алгоритм 4. Алгоритм расчета ${\text{Tr}}_{{i,j}}^{k}$

Вход: ${{{\mathbf{A}}}^{t}}$ – состояние системы в текущий момент времени;

${{{\mathbf{A}}}^{{t - 1}}}$ – состояние системы в предыдущий момент времени;

$(j,k)$ – ветвь, для которой проводится расчет;

$\tau $ – временной шаг;

Пусть ${\mathbf{I}} = \{ i:(i,j) \in {\mathbf{E}}\} $ – множество ветвей, предшествующих рассматриваемой

для всех $i \in {\mathbf{I}}$

${{P}_{i}} = 0$ – число АТС, которые теоретически могут достигнуть конца их ветви на следующей временной итерации

для всех $m = 0;$ $l \leqslant {\text{len}}({\mathbf{A}}_{{i,j}}^{t});$ $m + + $

если $\mathop {{\text{Pos}}}\nolimits_m + {{V}_{m}} \cdot \tau \geqslant {{m}_{{i,j}}},$ то

если $(j,k) \in {{{\mathbf{E}}}_{{{\text{int}}}}},$ то

${{P}_{i}} + = {{N}_{m}} \cdot (1 - {{M}_{j}}(t))$

иначе

${{P}_{i}} + = {{N}_{m}} \cdot {{M}_{j}}(t)$

Определим ${{N}_{{{\text{total}}}}}$ – сколько всего АТС может переехать на ветвь $(j,k)$

если $N_{{{\text{max}}}}^{{j,k}} - N_{{{\text{cur}}}}^{{j,k}} < {{Q}_{(}}j,k),$ то

${{N}_{{{\text{total}}}}} = N_{{{\text{max}}}}^{{j,k}} - N_{{{\text{cur}}}}^{{j,k}}$

иначе

${{N}_{{{\text{total}}}}} = {{Q}_{(}}j,k)$

для всех $i \in {\mathbf{I}}$

${\text{Tr}}_{{i,j}}^{k} = {{N}_{{{\text{total}}}}} \cdot \tfrac{{{{P}_{i}}}}{{\sum {{P}_{i}}}}$

6.1. Прямая дорога

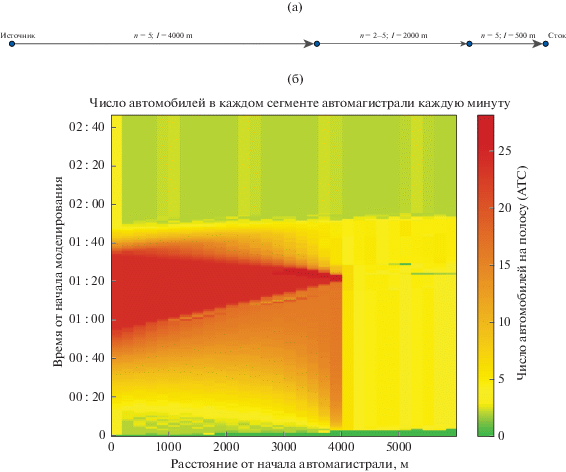
Для начала рассмотрим поведение модели для простой пятиполосной дороги длиной 6 километров без перекрестков с линейно нарастающим вплоть до 150 АТС/мин потоком изображенное на фиг. 1. В модели данная дорога представлена тремя ветвями по 2 километра. Данный эксперимент показывает, что в модели нет существенных краевых эффектов на стыке ветвей.

Фиг. 1.

(а) Схема простой дороги в модели состоит из 3 сегментов по 2 километра. (б) Тепловая карта автомобилей на простой дороге без перекрестков с линейно нарастающим вплоть до 150 АТС/мин потоком.

6.2. Прямая дорога с сужением и синусоидальным потоком

Для следующего эксперимента возьмем прямой участок пятиполосной дороги с сужением до двухполосной. В данном эксперименте с целью рассмотрения как процесса формирования затора, так и его исчезновения пустим на вход синусоидальный поток с периодом, равным времени моделирования, и амплитудой в 85 АТС/мин. Результат моделирования можно наблюдать на фиг. 2. На графике видно, что при уменьшении потока на сегменте, соответствующем двухполосной дороге, наблюдается разрыв потока АТС, который мы связываем с групповыми эффектами модели.

Фиг. 2.

(а) Схема дороги. (б) Тепловая карта автомобилей на пятиполосной дороге без перекрестков с сужением до двух полос и синусоидальным потоком на входе.

6.3. Прямая дорога с пропадающим сужением

Также рассмотрим ситуацию, когда при постоянном потоке в 100 АТС/мин на пятиполосной дороге с сужением до двухполосной данное сужение в середине моделирования пропадает. Такая ситуация может сложиться, например, при прекращении ремонтных работ или устранении аварии. Результаты моделирования можно наблюдать на фиг. 3.

Фиг. 3.

(а) Схема дороги. (б) Тепловая карта автомобилей на пятиполосной дороге без перекрестков с сужением до двух полос пропадающим в середине моделирования и постоянным потоком в 100 АТС/мин.

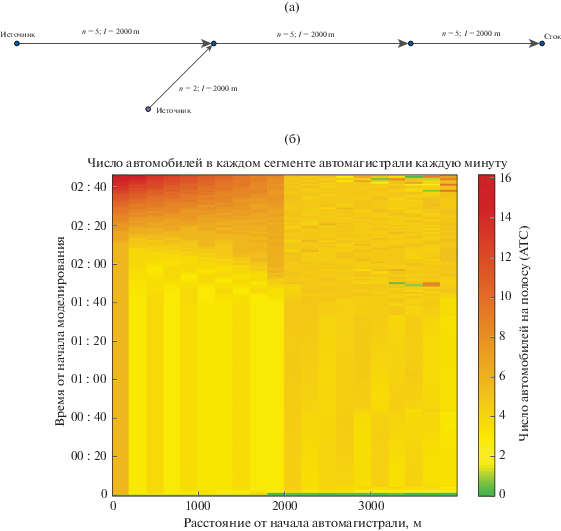
6.4. Перекресток со съездом

Промоделируем оба варианта перекрестков, возможных в предложенной модели. Перекресток со съездом и перекресток с въездом. В обоих случаях основная автомагистраль – пятиполосная. Въезд или съезд однополосные.

В эксперименте со съездом входной поток – 65 АТС/мин. Доля съезжающих автомобилей линейно растет с 20% до 60%. На фиг. 4 видно, что из-за недостаточной пропускной способности съезда на основной автомагистрали образуется пробка.

Фиг. 4.

(а) Схема дороги. (б) Тепловая карта автомобилей на пятиполосной дороге со съездом.

6.5. Перекресток с въездом

В эксперименте со въездом поток на автомагистрали – 140 АТС/мин, поток на въезде линейно растет от 20 до 50 АТС/мин. В данном случае также образуется пробка на основной автомагистрали, что видно на фиг. 5.

Фиг. 5.

(а) Схема дороги. (б) Тепловая карта автомобилей на пятиполосной дороге с въездом с постепенно нарастающим потоком с него.