1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 8, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 8, стр. 1336-1352

Метод характеристических штрафных функций для численного моделирования сжимаемых течений на неструктурированных сетках

И. В. Абалакин 1, *, О. В. Васильев 1, Н. С. Жданова 1, **, Т. К. Козубская 1

1 ИПМ им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

* E-mail: ilya.abalakin@gmail.com
** E-mail: nat.zhdanova@gmail.com

Поступила в редакцию 03.05.2020
После доработки 18.11.2020
Принята к публикации 09.04.2021

Полный текст (PDF)

Аннотация

В статье представлен метод характеристических штрафных функций для численного моделирования течений вязкого сжимаемого газа вблизи твердых тел с “погруженными” границами. В отличие от других методов погруженных границ на основе штрафных функций, характеристические штрафные функции обеспечивают корректную постановку условия Неймана и, в частности, адиабатического условия на поверхности обтекаемого тела. Дается подробное описание реализующего метод численного алгоритма, сочетающего конечно-объемный подход на основе EBR схем повышенной точности в зоне внешнего течения и конечно-разностный метод первого порядка внутри обтекаемого тела. Разработанный алгоритм обеспечивает возможность проведения расчета на сетках произвольной структуры, включая полностью неструктурированные. Эффективность метода характеристических штрафных функций и его реализации демонстрируется на примере тестовых задач об отражении ударной волны и акустического импульса от твердой стенки и задачи о течении Куэтта. Для сравнения даются решения тех же задач, полученные известным методом штрафных функций Бринкмана. Библ. 42. Фиг. 6. Табл. 4.

Ключевые слова: метод погруженных границ, метод характеристических штрафных функций, уравнения Навье–Стокса, условие Неймана.

ВВЕДЕНИЕ

Наиболее распространенный и ставший уже традиционным подход к численному моделированию граничных условий в задачах аэродинамического обтекания подразумевает использование согласованных с границей расчетных сеток, в которых поверхность раздела двух сред определяется сеточными узлами, а граничные условия задаются алгебраическими соотношениями в этих узлах. Если обтекаемое тело имеет сложную геометрическую форму, построение согласованной с поверхностью обтекаемого тела сетки представляет собой весьма ресурсоемкую задачу. Построение согласованных с границей сеток сильно усложняется для геометрии с движущимися или деформируемыми границами, так как требует непрерывной адаптации или построения новой сетки с интерполяцией решения со старой сетки на новую [1]. В этом случае более эффективным может оказаться альтернативный подход, основанный на методе погруженных границ. С помощью этого метода можно рассматривать задачу в односвязной области и обеспечивать выполнение граничного условия на поверхности тела без согласования сеточных узлов с границей. Этот подход существенным образом упрощает процедуру построения расчетной сетки, а также позволяет использовать методы динамической адаптации подвижной сетки к “погруженной” поверхности тела с сохранением сеточной топологии, что оказывается особенно полезным при моделировании течений вокруг движущихся объектов.

Методы погруженных границ могут быть разделены на два больших класса – дискретные и дифференциальные (объемные) методы. Дискретные подходы основаны на непосредственных преобразованиях дискретизированных уравнений, обеспечивающих выполнение тех или иных граничных условий, что делает их труднообобщаемыми ввиду прямой зависимости от методов дискретизации (см., например, [2]–[4]). Самыми большими недостатками дискретных методов погруженных границ являются отсутствие математических доказательств их сходимости и сложность контроля ошибки аппроксимации граничных условий. Дифференциальные методы погруженных границ (см., например, [5]–[7]) основаны на решении дифференциальных уравнений, модифицированных штрафными функциями в виде дополнительных сил или членов с обратной связью, обеспечивающих выполнение граничных условий.

Метод погруженных границ, как класс, был сформулирован Пескиным для численного моделирования сердечного клапана [8]. К настоящему времени разработано множество вариантов метода погруженных границ для вязких течений несжимаемой жидкости (см., например, [1]), среди которых можно выделить методы фиктивных ячеек (ghost-cells) [9], методы усеченных ячеек (cut-cell) [10], [11], метод свободной границы [12], методы штрафных функций [13], а также метод фиктивных областей [14].

Методы штрафных функций (МШФ) представляют отдельный подкласс дифференциальных методов погруженных границ, в которых эффект присутствия твердых тел сводится к добавлению источниковых членов в систему дифференциальных уравнений, определяющих математическую модель газодинамического процесса. Одним из таких методов является метод штрафных функций Бринкмана (МШФБ), который основан на идее моделирования обтекаемого твердого тела в приближении пористой среды с низкой проницаемостью. Для этого в уравнения моментов и энергии системы уравнений Навье–Стокса добавляются штрафные функции, отличные от нуля в области пористой среды. Преимуществом метода является возможность контроля ошибки через изменение значений штрафного параметра, при этом его математическое обоснование для течений несжимаемой жидкости основывается на доказанной сходимости решения системы уравнений Навье–Стокса со штрафными функциями к точному решению при стремлении штрафного параметра к нулю [15].

В отечественной литературе получило развитие независимое параллельное направление исследований дифференциального подкласса метода погруженных границ, широко известного как метод фиктивных областей (МФO) [14], основная идея которого заключается в решении приближенной задачи не в исходной сложной области ${{\Omega }_{E}}$, а в более простой области $\Omega $, включающей ${{\Omega }_{E}} \subset \Omega $. Вспомогательная задача в фиктивной (комплементарной) области ${{\Omega }_{B}} = \Omega {{\backslash }}{{\Omega }_{E}}$ формулируется таким образом, чтобы в ней присутствовал малый параметр η, определяющий величину разрыва коэффициентов уравнений на границе области $\partial {{\Omega }_{B}}$, и имела место сходимость приближенного решения параметризированной задачи к точному решению в области ${{\Omega }_{E}}$ при $\eta \to 0$. Детальный обзор литературы по истории развития и применению метода фиктивных областей можно найти в монографии Вабищевича [14]. Ниже приведено краткое обсуждение работ, связанных с развитием и использованием метода фиктивных областей для решения задач гидромеханики. Основополагающей работой в этом направлении можно назвать вышедшую в 1960 г. работу Вишика [16], в которой была сформулирована идея метода фиктивных областей о переходе к расширенной области. Впервые метод фиктивных областей как метод численного решения эллиптических задач со сложной геометрией был сформирован в работах Саульева [17], [18], в которых был разработан метод фиктивных областей с продолжением по старшим коэффициентам и получены оценки ошибки приближенного решения. Обобщение метода фиктивных областей с продолжением по младшим коэффициентам было предложено Лебедевым [19]. Расширения метода фиктивных областей для решения уравнений Навье–Стокса для несжимаемой жидкости были рассмотрены в многочисленных работах по численному моделированию как стационарных (см., например, [20]–[25]), так и нестационарных (см., например, [6], [26], [27]) течений. Отметим, что метод фиктивных областей с продолжением по младшим коэффициентам математически идентичен методу штрафных функций Бринкмана, и в западной литературе названия этих методов используются взаимозаменяемо (см., например, [13], [28], [29]) с более частым употреблением термина “метод штрафных функций”, несмотря на историческое первенство названия “метод фиктивных областей”. Ввиду математической эквивалентности двух подходов и для простоты обсуждения в данной работе все дифференциальные подклассы метода погруженных границ будут классифицироваться как метод штрафных функций.

Метод штрафных функций Бринкмана был впервые предложен в [30] и в дальнейшем успешно использовался при численном моделировании несжимаемых течений [31]–[34]. Существуют немногочисленные попытки адаптации метода штрафных функций Бринкмана к моделированию сжимаемых течений. Среди них можно выделить подход, предложенный в [35] и успешно использованный, например, в [36]. В [35], [36] показано, что предложенная модификация корректно описывает прохождение звуковых волн через пористую среду.

Практическое применение метода штрафных функций Бринкмана существенно ограничено возможностью определения на поверхности раздела двух сред лишь граничного условия Дирихле. Этот недостаток преодолен в методе характеристических штрафных функций, предложенном в [37]. Обеспечение возможности определения граничных условий Робина и Неймана в этом методе представляет интерес для исследования его практической применимости. Некоторые результаты такого исследования приведены в [37], где метод характеристических штрафных функций успешно применяется для численного моделирования ряда тестовых задач, среди которых процесс диффузии в одномерной постановке, отражение акустического импульса и ламинарное обтекание двумерного цилиндра. Метод численного решения разработан с помощью адаптивного вейвлетного коллокационного метода (Adaptive Wavelet Collocation Method, AWCM) для структурированных сеток [38], обеспечивающего активный контроль ошибки решения и необходимое локальное сеточное разрешение путем динамической адаптации сетки.

В настоящей работе уточняется формулировка метода характеристических штрафных функций и на ее основе строится конечно-объемный/конечно-разностный способ численного моделирования вязких сжимаемых течений на неструктурированных расчетных сетках. При этом для пространственной дискретизации используется EBR (Edge Based Reconstruction) схема [39], повышенная точность которой достигается за счет квазиодномерной реберно-ориентированной реконструкции потоковых переменных. Точность и корректность нового метода исследуются на примере численного моделирования задач с адиабатическим граничным условием: отражение акустического импульса, отражение ударной волны от стенки и течение Куэтта.

1. МЕТОД ХАРАКТЕРИСТИЧЕСКИХ ШТРАФНЫХ ФУНКЦИЙ

В качестве базовой математической модели для описания течений вязкой сжимаемой среды рассмотрим систему уравнений Навье–Стокса, записанную относительно физических переменных: плотности $\rho $, компонент вектора скорости ${{u}_{i}}$ и удельной внутренней энергии $\varepsilon $, следующим образом:

(1)
$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} = - \frac{{\partial \rho {{u}_{i}}}}{{\partial {{x}_{i}}}} = RH{{S}_{\rho }}, \\ \frac{{\partial {{u}_{i}}}}{{\partial t}} = - {{u}_{j}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} - \frac{1}{\rho }\frac{{\partial p}}{{\partial {{x}_{i}}}} + \frac{1}{\rho }\frac{{\partial {{P}_{{ij}}}}}{{\partial {{x}_{j}}}} = RH{{S}_{{{{u}_{i}}}}}, \\ \frac{{\partial \varepsilon }}{{\partial t}} = - {{u}_{i}}\frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}} - \frac{p}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}} + \frac{1}{\rho }D + \frac{1}{\rho }\frac{{\partial {{q}_{i}}}}{{\partial {{x}_{i}}}} = RH{{S}_{\varepsilon }}. \\ \end{gathered} $
Здесь и далее аббревиатура $RHS$ с нижним индексом используется для обозначения соответствующих физически обусловленных правых частей системы уравнений. Система уравнений (1) замыкается уравнением состояния идеального газа $p = \left( {\gamma - 1} \right)\rho \varepsilon $, где ${{\gamma }} = 1.4$ – показатель адиабаты. В системе (1) введены следующие обозначения:

• ${{P}_{{ij}}} = 2\mu {{S}_{{ij}}} - \frac{2}{3}\mu \frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}}{{\delta }_{{ij}}}$ – тензор вязких напряжений, ${{S}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right)$ – тензор скоростей деформации,

• $D = {{S}_{{ij}}}{{P}_{{ij}}}$ – диссипативная функция,

• ${{q}_{i}} = \frac{\gamma }{{\Pr }}\mu \frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}}$ – поток тепла, ${\text{Pr}} = 0.72$ – число Прандтля,

• $\mu $ – коэффициент молекулярной вязкости.

Здесь повторяющиеся индексы направления $i,j = 1, \ldots ,d$ предполагают операцию суммирования по направлениям, d – размерность задачи. При численном моделировании задачи внешнего обтекания твердого тела используются следующие обозначения:

• $\Omega $ – область определения задачи;

• ${{\Omega }_{B}}$ – внутренняя область твердого тела;

• $\partial {\kern 1pt} {{\Omega }_{B}}$ – граница твердого тела;

• ${{\Omega }_{E}} = \Omega {{\backslash }}({{\Omega }_{B}} \cup \partial {{\Omega }_{B}})$ – область, прилегающая к твердому телу;

• ${\mathbf{n}}$ – внутренняя нормаль к границе $\partial {{\Omega }_{B}}$.

На границе твердого тела, для рассматриваемых в работе тестовых задач, задаются граничные условия прилипания ${{\left. {\mathbf{u}} \right|}_{{\partial {{\Omega }_{B}}}}} = {\text{ }}{{{\mathbf{u}}}_{w}}$ и адиабатическое условие на поверхности ${{\left. {(\nabla \varepsilon ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = 0$, где ${{{\mathbf{u}}}_{w}}$ – вектор скорости движения твердого тела.

Согласно методу погруженных границ пространственное положение твердого тела определяется маркировочной функцией $\chi ({\mathbf{x}},t)$:

$\chi ({\mathbf{x}},t) = \left\{ \begin{gathered} 1,\quad {\mathbf{x}} \in {{{\bar {\Omega }}}_{B}}, \hfill \\ 0,\quad {\mathbf{x}} \notin {{{\bar {\Omega }}}_{B}}, \hfill \\ \end{gathered} \right.$
где ${{\bar {\Omega }}_{B}} = {{\Omega }_{B}} \cup \partial {{\Omega }_{B}}$.

Согласно методу характеристических штрафных функций, граничное условие прилипания для скорости обеспечивается добавлением штрафных функций в уравнения для компонент вектора скорости:

(2)
$\frac{{\partial {{u}_{i}}}}{{\partial t}} = (1 - \chi )RH{{S}_{{{{u}_{i}}}}} - \underbrace {\frac{\chi }{{{{\eta }_{b}}}}({{u}_{i}} - {{u}_{{w,}}}_{i})}_{{\text{штрафная}}\;{\text{функция}}} + \chi {{\nu }_{n}}\Delta {{u}_{i}}.$
Для условия прилипания вид штрафных функций такой же, как и в методе штрафных функций Бринкмана со штрафным параметром ${{\eta }_{b}} \ll 1$. Для обеспечения гладкости решения в области ${{\bar {\Omega }}_{B}}$ добавляется диффузионный член $\Delta {\kern 1pt} {\kern 1pt} {{u}_{i}},$ где ${{\nu }_{n}}$ – коэффициент искусственной вязкости, пропорциональный шагу сетки $h$. Этот член вводит искусственную вязкость явным образом. При использовании схем первого порядка по пространству роль искусственной вязкости играет схемная вязкость и в явном виде диффузию можно не добавлять. В работе [16] для обеспечения независимости ошибки численного решения от параметра ${{\eta }_{b}}$ предлагается выбирать коэффициент искусственной вязкости пропорционально величине ${{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} {{{\eta }_{b}}}}} \right. \kern-0em} {{{\eta }_{b}}}}$. Использование выражения $(1 - \chi )RH{{S}_{{{{u}_{i}}}}}$ в уравнении (2) означает исключение слагаемых конвективного и диффузного переноса из уравнений (1) в расчетных точках, находящихся внутри твердого тела. Это сделано для того, чтобы устранить их возможное влияние на процесс релаксации решения к требуемому граничному условию.

Граничное условие адиабатичности поверхности подразумевает постановку однородного граничного условия Неймана для внутренней энергии (или температуры).

В общем случае выполнение условия Неймана ${{\left. {(\nabla f,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = q({\mathbf{x}})$ по нормали к поверхности ${\mathbf{n}} = ({{n}_{1}}, \ldots ,{{n}_{d}})$, ориентированной внутрь препятствия, в методе характеристических штрафных функций обеспечивается решением следующего гиперболического уравнения со штрафным слагаемым:

(3)
$\frac{{\partial f}}{{\partial t}} = (1 - \chi )RH{{S}_{f}} - \underbrace {\frac{\chi }{{{{\eta }_{с}}}}\left( {{{n}_{k}}\frac{{\partial f}}{{\partial {{x}_{k}}}} - {{q}_{w}}({\mathbf{x}})} \right)}_{{\text{характеристическая}}\;{\text{штрафная}}\;{\text{функция}}},$
где ${{\eta }_{c}} \ll 1$ – малый штрафной параметр, в общем случае, отличный от штрафного параметра ${{\eta }_{b}}$ в уравнении (2).

В уравнении (3) штрафной источниковый член определяется по всему объему препятствия ${{\Omega }_{B}}$, а не только по его поверхности, поэтому определение нормали к поверхности $\partial {{\Omega }_{B}}$ обобщается на всю область ${{\Omega }_{B}}$ посредством взятия градиента от скалярной функции расстояния

${\mathbf{n}}({\mathbf{x}}) = \nabla \delta ({\mathbf{x}}),\quad {\mathbf{x}} \in {{\Omega }_{B}},$
где $\delta $ – расстояние до ближайшей точки границы

$\delta ({\mathbf{x}}) = \left\{ \begin{gathered} \mathop {\min }\limits_{y \in \partial {{\Omega }_{B}}} \left\| {x - y} \right\|,\quad {\mathbf{x}} \in \Omega {{\backslash }}{{\Omega }_{B}}, \hfill \\ - {\kern 1pt} \mathop {\min }\limits_{y \in \partial {{\Omega }_{B}}} \left\| {x - y} \right\|,\quad {\mathbf{x}} \in {{\Omega }_{B}}. \hfill \\ \end{gathered} \right.$

С математической точки зрения смысл уравнения (3) состоит в переносе решения во внутреннюю область препятствия ${{\Omega }_{B}}$ вдоль внутринаправленных характеристик, что обеспечивает выполнение требуемого значения производной функции f по направлению нормали n на границе тела $\partial {\kern 1pt} {{\Omega }_{B}}$. Это объясняется тем, что выбор параметра ${{\eta }_{c}} \ll 1$ приводит к тому, что уравнение (3) становится квазистационарным в пределах ${{\Omega }_{B}}$ на масштабе характерного времени решения уравнений гидродинамики ${{t}_{H}} = {L \mathord{\left/ {\vphantom {L {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}$ ($L$ – характерный размер препятствия, ${{U}_{0}}$ – характерная скорость течения около препятствия). В безразмерных переменных (со знаком “тильда”) уравнение (3) в области препятствия ${{\Omega }_{B}}$ можно записать в виде

(4)
$\frac{{{{t}_{R}}}}{{\mathop {{{t}_{H}}}\limits_{ \ll 1} }} \cdot \frac{{\partial{ \tilde {f}}}}{{\mathop {\partial t}\limits_{ \sim O\left( 1 \right)} }} = \underbrace {{{n}_{k}}\frac{{\partial{ \tilde {f}}}}{{\partial {{{\tilde {x}}}_{k}}}} - {{{\tilde {q}}}_{w}}({\mathbf{x}})}_{ \sim O\left( 1 \right)},$
где время релаксации ${{t}_{R}} = {{\eta }_{c}}L$. Так как при умеренных характерных скоростях обтекания ${{{{t}_{R}}} \mathord{\left/ {\vphantom {{{{t}_{R}}} {{{t}_{H}} = {{U}_{0}}{{\eta }_{c}} \ll 1}}} \right. \kern-0em} {{{t}_{H}} = {{U}_{0}}{{\eta }_{c}} \ll 1}}$, то из уравнения (4) следует, что граничное условие выполняется на масштабе времени O(tR), т.е.
$\frac{{\partial f}}{{\partial n}} \to {{q}_{w}}({\mathbf{x}})\quad {\text{при}}\quad {{\eta }_{c}} \to 0$
с асимптотической ошибкой порядка $O({{U}_{0}}{{\eta }_{c}})$. Таким образом, граничное условие адиабатичности поверхности обеспечивается добавлением характеристических штрафных функций в уравнение для удельной внутренней энергии

(5)
$\frac{{\partial \varepsilon }}{{\partial t}} = (1 - \chi )RH{{S}_{{{\kern 1pt} \varepsilon }}} - \frac{\chi }{{{{\eta }_{с}}}}{{n}_{k}}\frac{{\partial \varepsilon }}{{\partial {{x}_{k}}}}.$

Отметим, что течения с присоединенными пограничными слоями, такие как течения в приближении линейной акустики, удовлетворяют условию равенства нулю нормального градиента давления на границе ${{\left. {(\nabla p,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}}$. Для того, чтобы обеспечить выполнение уравнения состояния на адиабатической границе твердого тела, необходимо, чтобы нормальный градиент плотности на границе также был равен нулю, т.е. ${{\left. {(\nabla \rho ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = 0$, что можно считать дополнительным граничным условием на твердой поверхности для разностной системы уравнений Навье–Стокса.

В общем случае (например, течений с отрывами), когда ${{\left. {(\nabla \rho ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} \ne 0$, будем предполагать неоднородное граничное условие на производную плотности по направлению нормали n

(6)
${{\left. {(\nabla \rho ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = \Phi ({\mathbf{x}}).$
Тогда, в соответствии с общим определением (3) условий Неймана в методе характеристических штрафных функций, граничное условие (6) обеспечивается модификацией уравнения неразрывности
(7)
$\frac{{\partial \rho }}{{\partial t}} = (1 - \chi )RH{{S}_{{{\kern 1pt} \rho }}} - \underbrace {\frac{\chi }{{{{\eta }_{с}}}}\left( {{{n}_{k}}\frac{{\partial \rho }}{{\partial {{x}_{k}}}} - \Phi \left( {{\mathbf{x}},t} \right)} \right)}_{{\text{характеристическая}}\;{\text{штрафная}}\;{\text{функция}}}.$
Здесь $\Phi ({\mathbf{x}},t)$ – функция, удовлетворяющая решению следующей краевой задачи для уравнения переноса:
(8)
$\frac{{\partial \Phi }}{{\partial t}} = - \frac{\chi }{{{{\eta }_{с}}}}\frac{{\partial \Phi }}{{\partial n}},\quad {{\left. \Phi \right|}_{{\partial {{\Omega }_{B}}}}} = {{\left. {\frac{{\partial \rho }}{{\partial n}}} \right|}_{{\partial {{\Omega }_{B}}}}}.$
Согласно работе [40], решение задачи (8) можно интерпретировать как экстраполяцию граничного значения $\Phi $ внутрь области.

Пенализированные уравнения (2), (5), (7) и (8), записанные относительно физических переменных ${{(\rho ,{\mathbf{u}},\varepsilon )}^{Т}}$, при значении $\chi = 1$ определяют решение задачи внутри области ${{\Omega }_{B}}$, при этом обеспечивая выполнение граничного условия прилипания и отсутствия теплового потока на границе твердого тела.

Таким образом, система пенализированных уравнений (2), (5), (7) и (8), расширяющая систему уравнений Навье–Стокса (1) на всю область $\Omega $, определяет математическую модель обтекания твердого тела вязким сжимаемым газом, автоматически налагая граничные условия с помощью метода характеристических штрафных функций.

В работе [8] было показано, что асимптотическая ошибка при моделировании условия Дирихле методом штрафных функций Бринкмана имеет порядок $O(\eta _{b}^{{1/2}})$. Ошибка в представлении условий Неймана в методе характеристических штрафных функций имеет асимптотику порядка $O({{\eta }_{c}})$, установленную в работе [37] и проиллюстрированную в уравнении (4).

2. ЧИСЛЕННЫЙ МЕТОД

Система уравнений (2), (5), (7), записанная относительно вектора консервативных переменных ${{(\rho ,\rho {\mathbf{u}},E)}^{Т}}$, решается совместно с уравнением (8) путем численного интегрирования во всей области $\Omega $. Здесь переменная $E = {{\rho {{{\mathbf{u}}}^{2}}} \mathord{\left/ {\vphantom {{\rho {{{\mathbf{u}}}^{2}}} 2}} \right. \kern-0em} 2} + {p \mathord{\left/ {\vphantom {p {(\gamma - 1)}}} \right. \kern-0em} {(\gamma - 1)}}$ есть полная энергия, определяемая с учетом уравнения состояния идеального газа. Для интегрирования по времени применяется неявная схема интегрирования с линеаризацией по Ньютону.

Для пространственной дискретизации уравнений в области ${{\Omega }_{E}} = \Omega {{\backslash }}{{\bar {\Omega }}_{B}}$ (значение функции $\chi = 1$) применяется конечно-объемная EBR схема, повышенная точность которой обеспечивается за счет использования квазиодномерных реберно-ориентированных реконструкций потоковых переменных на неструктурированной сетке [39].

Численное интегрирование системы уравнений (2), (5), (7) в области ${{\bar {\Omega }}_{B}}$ проводится следующим образом.

Система уравнений (2), (5), (7) и (8), переписанная относительно консервативных переменных, принимает вид

$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} = - \frac{1}{{{{\eta }_{с}}}}\frac{{\partial \rho }}{{\partial n}} + \frac{1}{{{{\eta }_{с}}}}\Phi , \\ \frac{{\partial \rho u}}{{\partial t}} = - \frac{1}{{{{\eta }_{с}}}}u\frac{{\partial \rho }}{{\partial n}} + \frac{1}{{{{\eta }_{с}}}}u\Phi - \frac{1}{{{{\eta }_{b}}}}\rho (u - {{u}_{w}}) + \rho {{\nu }_{n}}\Delta u, \\ \end{gathered} $
(9)
$\begin{gathered} \frac{{\partial \rho v}}{{\partial t}} = - \frac{1}{{{{\eta }_{с}}}}v\frac{{\partial \rho }}{{\partial n}} + \frac{1}{{{{\eta }_{с}}}}v\Phi - \frac{1}{{{{\eta }_{b}}}}\rho (v - {{v}_{w}}) + \rho {{\nu }_{n}}\Delta v, \\ \frac{{\partial E}}{{\partial t}} = \frac{1}{{{{\eta }_{с}}}}\left[ { - ({{u}^{2}} + {{v}^{2}})\frac{{\partial \rho }}{{\partial n}} + u\frac{{\partial \rho u}}{{\partial n}} + v\frac{{\partial \rho v}}{{\partial n}} - \frac{{\partial E}}{{\partial n}}} \right] - \\ \end{gathered} $
$\begin{gathered} - \;\frac{1}{{{{\eta }_{b}}}}\left[ {\rho u(u - {{u}_{w}}) + \rho v(v - {{v}_{w}})} \right] + \frac{1}{{{{\eta }_{с}}}}\frac{E}{\rho }\Phi + \rho {{\nu }_{n}}(u\Delta u + v\Delta v), \\ \frac{{\partial \Phi }}{{\partial t}} = - \chi \frac{1}{{{{\eta }_{с}}}}\frac{{\partial \Phi }}{{\partial n}}. \\ \end{gathered} $
Отметим, что для аппроксимации производных по направлению нормали в системе (9) используется метод направленных разностей первого порядка, обладающий численной диффузией, пропорциональной шагу сетки. Поэтому члены с искусственной вязкостью ${{\nu }_{n}}\Delta {\kern 1pt} {\kern 1pt} {\mathbf{u}}$ в дальнейшем анализе опускаются.

Система (9) имеет следующее матрично-векторное представление:

(10)
$\frac{{\partial \operatorname{Q} }}{{\partial t}} = {\mathbf{A}}\frac{{\partial Q}}{{\partial n}} + {\mathbf{S}},$
где $Q = {{(\rho ,\;\rho u,\;\rho {v},\;E,\;\Phi )}^{Т}}$ – вектор консервативных переменных,
${\mathbf{A}} = \frac{1}{{{{\eta }_{с}}}}\left( {\begin{array}{*{20}{l}} { - 1}&0&0&0&0 \\ { - u}&0&0&0&0 \\ { - {v}}&0&0&0&0 \\ { - ({{u}^{2}} + {{{v}}^{2}})}&u&{v}&{ - 1}&0 \\ 0&0&0&0&{ - 1} \end{array}} \right),\quad {\mathbf{S}} = \left( {\begin{array}{*{20}{l}} {\frac{1}{{{{\eta }_{с}}}}\Phi } \\ { - \frac{1}{{{{\eta }_{b}}}}\rho (u - {{u}_{w}}) + \frac{1}{{{{\eta }_{с}}}}u\Phi } \\ { - \frac{1}{{{{\eta }_{b}}}}\rho ({v} - {{{v}}_{w}}) + \frac{1}{{{{\eta }_{с}}}}{v}\Phi } \\ { - \frac{1}{{{{\eta }_{b}}}}\left[ {\rho u(u - {{u}_{w}}) + \rho {v}({v} - {{{v}}_{w}})} \right] + \frac{1}{{{{\eta }_{с}}}}\frac{E}{\rho }\Phi } \\ 0 \end{array}} \right).$
Не ограничивая общности, будем считать, что область ${{\bar {\Omega }}_{B}}$ покрыта неструктурированной сеткой с треугольными элементами ${{T}_{j}}$ такая, что ${{\bar {\Omega }}_{B}} = \bigcup\nolimits_j^{} {{{T}_{j}}} $ и ${{T}_{j}} \cap {{T}_{i}} = \emptyset $ ${\text{(}}i \ne j{\text{)}}$. Отсюда следует, что все узлы ${{{\mathbf{x}}}_{i}} \in {{\bar {\Omega }}_{B}}$, где $i = 1, \ldots ,N$. Заметим, что сетка в области ${{\bar {\Omega }}_{B}}$ может состоять и из четырехугольных элементов, которые всегда представимы как объединение двух треугольников.

Для численного решения системы (10) строится неявная разностная схема:

(11)
$\frac{{Q_{i}^{{n + 1}} - Q_{i}^{n}}}{\tau } = {{{\mathbf{A}}}^{n}}\frac{{Q_{i}^{{n + 1}} - Q_{{i'}}^{{n + 1}}}}{{\Delta {{r}_{{ii'}}}}} + S_{i}^{{n + 1}}.$
Здесь производная в направлении внутренней нормали аппроксимируется односторонней разностью, при этом точка с индексом $i{\kern 1pt} '$ является ближайшей точкой пересечения внутренней нормали, исходящей из точки $i$, и ребра треугольного элемента. Значение ${{Q}_{{i'}}}$ находится посредством линейной интерполяции по значениям ${{Q}_{{{{i}_{1}}}}}$ и ${{Q}_{{{{i}_{2}}}}}$, где ${{i}_{1}}$ и ${{i}_{2}}$ – индексы узлов, образующих пересекаемую грань:
${{Q}_{{i'}}} = {{C}_{1}}{{Q}_{{{{i}_{1}}}}} + {{C}_{2}}{{Q}_{{{{i}_{2}}}}},$
где ${{C}_{1}}$ и ${{C}_{2}}$ суть коэффициенты линейной интерполяции, а $\Delta {{r}_{{ii'}}}$ – расстояние между точками с индексами $i$ и $i{\kern 1pt} '$.

Для решения нелинейного разностного уравнения (11) в рамках одного временного шага построим следующий итерационный процесс ($s$ – номер итерации) для нахождения приращения ${{\mathop {\Delta Q}\limits^{(s)} }_{i}} = \mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s + 1)} - \mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} $

$\begin{gathered} \frac{{{{{\mathop {\Delta Q}\limits^{(s)} }}_{i}}}}{\tau } = {\mathbf{A}}_{i}^{n}\frac{{{{{\mathop {\Delta Q}\limits^{(s)} }}_{i}} - {{C}_{1}}{{{\mathop {\Delta Q}\limits^{(s)} }}_{{{{i}_{1}}}}} - {{C}_{2}}{{{\mathop {\Delta Q}\limits^{(s)} }}_{{{{i}_{2}}}}}}}{{\Delta {{r}_{{ii'}}}}} + \mathop {{\mathbf{S}}_{{{\mathbf{Q}},i}}^{{n + 1}}}\limits^{(s)} {{\mathop {\Delta Q}\limits^{(s)} }_{i}} - \\ + \;{\mathbf{A}}_{i}^{n}\frac{{\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} - {{C}_{1}}\mathop {{\mathbf{Q}}_{{{{i}_{1}}}}^{{n + 1}}}\limits^{(s)} - {{C}_{2}}\mathop {{\mathbf{Q}}_{{{{i}_{2}}}}^{{n + 1}}}\limits^{(s)} }}{{\Delta {{r}_{{ii'}}}}} - \frac{{\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} - {\mathbf{Q}}_{i}^{n}}}{\tau } + \mathop {{\mathbf{S}}_{i}^{{n + 1}}}\limits^{(s)} , \\ \end{gathered} $
где ${{{\mathbf{S}}}_{{\mathbf{Q}}}}$ – матрица Якоби источникового слагаемого схемы (11)
${{{\mathbf{S}}}_{{\mathbf{Q}}}} = \frac{{\partial {\mathbf{S}}}}{{\partial {\mathbf{Q}}}} = ( - 1)\left( {\begin{array}{*{20}{c}} 0&0&0&0&{\frac{1}{{{{\eta }_{с}}}}} \\ { - \frac{{{{u}_{w}}}}{{{{\eta }_{b}}}} + \frac{u}{{{{\eta }_{c}}\rho }}\Phi }&{\frac{1}{{{{\eta }_{b}}}} + \frac{1}{{{{\eta }_{c}}\rho }}\Phi }&0&0&{ - \frac{1}{{{{\eta }_{с}}}}u} \\ { - \frac{{{{{v}}_{w}}}}{{{{\eta }_{b}}}} + \frac{{v}}{{{{\eta }_{c}}\rho }}\Phi }&0&{\frac{1}{{{{\eta }_{b}}}} + \frac{1}{{{{\eta }_{c}}\rho }}\Phi }&0&{ - \frac{1}{{{{\eta }_{с}}}}{v}} \\ { - \frac{1}{{{{\eta }_{b}}}}({{u}^{2}} + {{{v}}^{2}}) + \frac{E}{{{{\eta }_{c}}{{\rho }^{2}}}}\Phi }&{\frac{1}{{{{\eta }_{b}}}}(2u - {{u}_{w}})}&{\frac{1}{{{{\eta }_{b}}}}(2{v} - {{{v}}_{w}})}&{ - \frac{1}{{{{\eta }_{c}}\rho }}\Phi }&{ - \frac{1}{{{{\eta }_{с}}}}\frac{E}{\rho }} \\ 0&0&0&0&0 \end{array}} \right).$
В результате имеем систему линейных алгебраических уравнений (СЛАУ) для нахождения блочного вектора приращения $\mathop {\Delta Q}\limits^{(s)} = {{\left( {{{{\mathop {\Delta Q}\limits^{(s)} }}_{1}}, \ldots ,{{{\mathop {\Delta Q}\limits^{(s)} }}_{i}}, \ldots {{{\mathop {\Delta Q}\limits^{(s)} }}_{N}}} \right)}^{Т}}$
(12)
$\left( {\frac{1}{\tau }{\mathbf{I}} - {\mathbf{D}} - {\mathbf{M}}} \right)\mathop {\Delta Q}\limits^{(s)} = {\mathbf{M}}\mathop {{{{\mathbf{Q}}}^{{n + 1}}}}\limits^{(s)} - \frac{{\mathop {{{{\mathbf{Q}}}^{{n + 1}}}}\limits^{(s)} - {{{\mathbf{Q}}}^{n}}}}{\tau } + \mathop {{{{\mathbf{H}}}^{{n + 1}}}}\limits^{(s)} ,$
где ${\mathbf{I}}$ – единичная матрица размером $5N \times 5N$, ${\mathbf{D}}$, ${\mathbf{M}}$ – блочные (размер блока $5 \times 5$) матрицы размером $N \times N$, имеющими следующую структуру ($i$ – номер строки, ${{i}_{1}}$, ${{i}_{2}}$ – номера столбцов):

• ${\mathbf{D}} = \operatorname{diag} \left\{ {\mathop {{\mathbf{H}}_{{{\mathbf{Q}},i}}^{{n + 1}}}\limits^{(s)} } \right\}$ – диагональная матрица,

• ${\mathbf{M}} = \operatorname{diag} \{ {\mathbf{A}}_{i}^{n}\} + \operatorname{offdiag} \left\{ {{{{( - {{С}_{1}}{\mathbf{A}}_{i}^{n})}}_{{i{{i}_{1}}}}},{{{( - {{С}_{2}}{\mathbf{A}}_{i}^{n})}}_{{i{{i}_{2}}}}}} \right\}$ – матрица, имеющая в строке три ненулевых блока.

В результате решения системы (12) получаем значение вектора переменных на следующей итерации $\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s + 1)} = \mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} + {{\mathop {\Delta Q}\limits^{(s)} }_{i}}$. В качестве начального приближения $\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(0)} $ выбираются значения $Q_{i}^{n}$.

Таким образом, для уравнений (2), (5), (7) и (8) итерационный процесс интегрирования по времени может быть проведен единообразно для всей области $\Omega $. Зависимость переменных в областях $\Omega {{\backslash }}{{\bar {\Omega }}_{B}}$ и ${{\bar {\Omega }}_{B}}$ определяется шаблоном аппроксимации производных по направлению нормали в уравнениях (9), с одной стороны, и шаблоном реконструкции переменных в консервативной форме уравнений системы (1), с другой. На каждой итерации образуется единая система линейных алгебраических уравнений, которая решается стабилизированным методом бисопряженных градиентов (BiCGStab) [41] с предобуславливателем типа ILU0.

3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

В этом разделе рассмотрены результаты численного решения тестовых задач, имеющих точные решения.

Первые две одномерные тестовые задачи об отражении акустического импульса и ударной волны от твердой поверхности рассматриваются в двумерной постановке и невязком приближении. Решения этих начально-краевых задач для одномерной системы уравнений Эйлера хорошо известны и их можно использовать для проведения сравнения с численными результатами, полученными из двумерных расчетов с использованием системы уравнений Навье–Стокса при больших числах Рейнольдса (например, $\operatorname{Re} > {{10}^{6}}$) и определением на твердой стенке нулевого потока тепла (адиабатическая поверхность). Действительно, на твердой поверхности условие непротекания (равенства нулю нормальной к границе компоненты скорости) для уравнений Эйлера и условие прилипания для уравнения Навье–Стокса в одномерном случае совпадают ($u = 0$). Естественное условие для уравнений Эйлера – отсутствие потока энергии на твердой поверхности, обусловленное равенством нулю нормальной к границе компоненты скорости, выполняется и в случае уравнений Навье–Стокса при условии определения однородного граничного условия Неймана для температуры или внутренней энергии (${{\partial \varepsilon } \mathord{\left/ {\vphantom {{\partial \varepsilon } {\partial x}}} \right. \kern-0em} {\partial x}} = 0$). Таким образом, решения этих двух задач для системы уравнений Эйлера могут рассматриваться как решения системы уравнений Навье–Стокса с точностью $O\left( {{1 \mathord{\left/ {\vphantom {1 {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}} \right)$, а также использоваться для верификации граничного условия Неймана в методе характеристических штрафных функций. Отметим, что приведенная выше оценка справедлива только в одномерном случае. В многомерном случае при наличии твердой поверхности решение уравнений Навье–Стокса имеет асимптотику порядка $O(1{\text{/}}{{\operatorname{Re} }^{{1/2}}})$ .

В качестве третьей тестовой задачи рассмотрим течение Куэтта между двумя пластинами, позволяющее провести верификацию рассматриваемого метода характеристических штрафных функций при наличии касательного напряжения на твердой стенке, а также в случае подвижной поверхности (неоднородное условиe Дирихле). В постановке данной задачи предполагается отсутствие градиента давления и для получения нетривиального (отличного от “классического” линейного решения для профиля скорости) коэффициент вязкости выбирается отличным от константы, а именно обратно пропорциональным квадратному корню от температуры. В такой постановке и при условиях определения разных граничных условий (либо Неймана, либо Дирихле) на противоположных пластинах задача имеет точное решение (см. раздел документации на сайте https://github.com/bahvalo/ColESo).

Для более полного анализа приведены результаты моделирования тех же задач с применением известного метода штрафных функций Бринкмана. При проведении расчетов этим методом используются та же расчетная сетка, метод интегрирования по времени и пространственная дискретизация [42]. Отметим, что в методе штрафных функций Бринкмана отсутствуют явные средства (типа штрафных ограничений на производную температуры по направлению нормали), обеспечивающие выполнение условия адиабатичности на поверхности тела. Также обратим внимание на то, что в данной работе при применении метода штрафных функций Бринкмана не модифицировалось уравнение неразрывности, как в работе [35], и не вводилась пористость для контроля акустического импеданса внутри штрафной области и обеспечения незначительного проникновения и правильного отражения акустических волн.

3.1. Отражение одномерного акустического импульса

Рассмотрим двумерную постановку задачи в прямоугольной области $\Omega = \left[ { - 0.65,0.25} \right] \times \left[ {0,0.1} \right]$ с “погруженной” границей раздела $x = 0$ и штрафной областью ${{\bar {\Omega }}_{B}} = \left[ {0,0.25} \right] \times \left[ {0,0.1} \right]$. В области $\Omega $ построены структурированная сетка и последовательность сгущающихся (линейный размер элемента сетки уменьшается в два раза) неструктурированных квазиравномерных треугольных расчетных сеток. Также построена неравномерная треугольная сетка, с размером элемента около границы, равным размеру элемента подробной сетки, и дальнейшем разбегом (с коэффициентом 1.02) до размера элемента грубой сетки. Тип и размеры сеток приведены в табл. 1, а их вид на фиг. 1.

Таблица 1.  

Типы сеток и их характерные размеры

Название Тип Характерный размер элемента
ССП3 Прямоугольная структурированная 0.000244
СНТ1 Треугольная неструктурированная
Квазиравномерная 		0.001
СНТ2 Треугольная неструктурированная
Квазиравномерная 		0.0005
СНТ3 Треугольная неструктурированная
Квазиравномерная 		0.00025
СНТ4 Треугольная неструктурированная
с разбегом от линии x = 0 		0.00025–0.001
Фиг. 1.

Фрагменты неструктурированных треугольных сеток: СНТ1 (а) и СНТ2 (б), СНТ4 (в).

Пенализированная система уравнений (2), (5), (7) и (8), переписанная относительно консервативных переменных, решена для числа Рейнольдса $\operatorname{Re} = {{10}^{8}}$ и штрафных параметров ${{\eta }_{b}}$ = 10–6 и ${{\eta }_{c}}$ = 10–2.

На верхней и нижней границах расчетной области используются периодические граничные условия, а на левой и правой границах – условия Дирихле, определяемые невозмущенными параметрами среды.

Задача решается в безразмерных переменных. В качестве параметров обезразмеривания выбираются характерные параметры невозмущенной среды – скорость звука ${{c}_{0}}$ и плотность ${{\rho }_{0}}$. Давление обезразмеривается на величину ${{\rho }_{0}}c_{0}^{2}$.

В начальный момент времени задается одномерный акустический импульс

$\rho = 1 + \rho {\kern 1pt} ',\quad u = u{\kern 1pt} ',\quad p = \frac{1}{\gamma } + p{\kern 1pt} ',\quad - 0.45 \leqslant x \leqslant - 0.05,$
где
$\rho {\kern 1pt} ' = u{\kern 1pt} ' = p{\kern 1pt} ' = A{{\left( {\frac{{x + 0.25}}{{0.2}} - 1} \right)}^{4}}{{\left( {\frac{{x + 0.25}}{{0.2}} + 1} \right)}^{4}},\quad A = {{10}^{{ - 3}}}.$
Наличие малой амплитуды $A$ в начальном возмущении определяет решение линейной эволюционной задачи с использованием нелинейных уравнений.

Указанный импульс с течением времени движется слева направо, отражаясь от твердой поверхности и меняя направление движения.

На фиг. 2а приведены графики пульсаций давления вблизи стенки в момент времени $t = 0.25$ (время отражения от стенки), рассчитанных на различных сетках методом характеристических штрафных функций (МХШФ) и метода штрафных функций Бринкмана (МШФБ) в сравнении с аналитическим решением. Наблюдается хорошее согласование аналитического решения и решения, полученного МХШФ, даже на грубых сетках, в отличие от решения, полученного МШФБ, для которого заметны расхождения с точным решением и на подробной сетке. В момент времени $t = 0.5$ отраженная от твердой стенки акустическая волна имеет профиль скорости, показанный на фиг. 2б. Полученный в расчете МХШФ на грубой сетке СНТ1 профиль пульсаций скорости хорошо согласуeтся с точным решением, а в расчете МШФБ наблюдается небольшое расхождение в точке минимума с аналитическим решением.

Фиг. 2.

(а) – пульсации давления около стенки в момент отражения t = 0.25, (б) – пульсации скорости в момент времени t = 0.5 (отраженная волна).

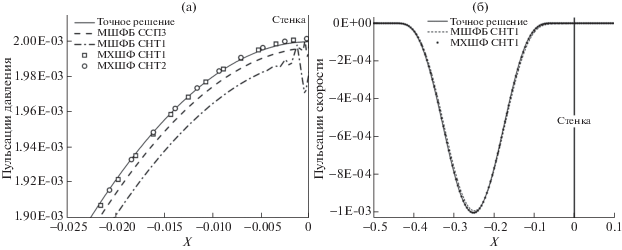
На фиг. 3 приведено сравнение профилей пульсаций давления, полученных МХШФ и МШФБ на сетке СНТ4 в окрестности экстремальной точки и вблизи стенки. Видно, что вблизи границы изнутри области ${{\bar {\Omega }}_{B}}$ в случае расчета МШФБ появляется всплеск давления, который приводит к слабому искажению профиля отраженной волны, связанному с уменьшением ее амплитуды. В отличие от метода штрафных функций Бринкмана метод характеристических штрафных функций определяет правильный нулевой поток энергии на границе, что позволяет сохранить профиль отраженной волны. Отметим, что неправильное отражение акустических волн при применении метода штрафных функций Бринкмана послужило мотивирующим фактором для обобщения МШФБ метода и включения пористости в уравнение наразрывности, как описано в работе [35].

Фиг. 3.

Пульсации давления отраженной волны в области максимума пульсаций и вблизи твердой границы.

Сеточная сходимость МХШФ и МШФБ показана в табл. 2 и 3, где приведены ошибки численного решения для пульсаций давления в среднеквадратичной норме, посчитанной в области физического определения решения $\Omega {{\backslash }}{{\Omega }_{B}}$, на моменты времени $t = 0.25$ и $t = 0.5$.

Таблица 2.  

Ошибка численного решения в норме ${{L}_{2}}$ на момент времени $t = 0.25$

Метод ССП3 СНТ1 СНТ2 СНТ3 СНТ4
МШФБ 4.43e–6 1.10e–5 6.43e–6 3.61e–6 4.59e–6
МХШФ 1.26e–6 2.83e–6 1.83e–6 5.79e–7 9.13e–7
Таблица 3.  

Ошибка численного решения в норме ${{L}_{2}}$ на момент времени $t = 0.5$

Метод ССП3 СНТ1 СНТ2 СНТ3 СНТ4
МШФБ 4.72e–6 1.33e–5 7.33e–6 3.71e–6 4.93e–6
МХШФ 9.82e–7 3.04e–6 1.67e–6 8.26e–7 7.20e–7

Из таблиц видно (см. столбцы СНТ1–СНТ3), что имеет место линейная сходимость (ошибка уменьшается приблизительно в два раза при измельчении сетки в два раза).

Расчет на неравномерной сетке СНТ4 дает результат, близкий к расчету на подробной сетке СНТ3. Это следует из того, что основной источник ошибки возникает в процессе отражения, а размеры элементов сетки СНТ3 и сетки СНТ4 около границы одинаковы.

Приведенные в таблицах нормы ошибок также показывают, что метод штрафных функций Бринкмана уступает по точности методу характеристических штрафных функций.

3.2. Отражение ударной волны

Рассмотрим задачу об отражении плоской ударной волны от твердой стенки. Фронт ударной волны движется слева направо вдоль оси $OX$ со скоростью, соответствующей числу Маха $\operatorname{M} = 2$. Задача решена в двумерной постановке в прямоугольной области $\Omega = \left[ {0,100} \right] \times \left[ {0,4} \right]$ с “погруженной” границей раздела $x = 80$ и штрафной областью ${{\bar {\Omega }}_{B}} = \left[ {80,100} \right] \times \left[ {0,4} \right]$. Как и в предыдущем примере, в области $\Omega $ построены три последовательно сгущающиеся квазиравномерные треугольные сетки с характерными размерами элементов – 1 (сетка СНТ1), 0.5 (сетка СНТ2), 0.25 (сетка СНТ3). Структура этих сеток аналогична структуре сеток, приведенных на фиг. 1.

Задача решена для следующих начальных кусочно-постоянных условий:

$\left( {\rho ,u,{v},p} \right) = \left\{ \begin{gathered} {{\left( {\rho ,u,{v},p} \right)}_{1}} = \left( {1,0,0,{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }} \right),\quad x \geqslant 30, \hfill \\ {{\left( {\rho ,u,{v},p} \right)}_{2}},\quad x < 30, \hfill \\ \end{gathered} \right.$
где состояние перед фронтом ударной волны ${{(\rho ,u,{v},p)}_{2}}$ определяется соотношениями Ренкина–Гюгонио. Здесь рассматриваются безразмерные переменные. В качестве параметров обезразмеривания выбираются параметры перед фронтом ударной волны – скорость звука ${{c}_{1}}$ и плотность ${{\rho }_{1}}$. Давление обезразмеривается на величину ${{\rho }_{1}}c_{1}^{2}$.

Пенализированная система уравнений (2), (5), (7) и (8), переписанная относительно консервативных переменных, решена для числа Рейнольдса $\operatorname{Re} = {{10}^{7}}$ и штрафных параметров ${{\eta }_{b}} = {{10}^{{ - 6}}}$ и ${{\eta }_{c}} = {{10}^{{ - 6}}}$. “Погруженная” поверхность твердой стенки ($x = 80$) моделируется методом погруженных границ при обеспечении граничного условия прилипания и адиабатичности.

Постановка задачи предполагает, что ударная волна отражается от поверхности и начинает двигаться справа налево. Профиль отраженной ударной волны в момент времени $t = 60$ приведен на фиг. 4, где также показаны результаты расчета методом штрафных функций Бринкмана и точное аналитическое решение задачи. Как видно из фигуры, численные решения, полученные МХШФ на подробной (СНТ3) и грубой (СНТ1) сетках, хорошо согласуются с аналитическим решением, в отличие от решения, полученного методом штрафных функций Бринкмана на тех же сетках. В последнем случае наблюдаются занижение амплитуды и фазовое отставание отраженной ударной волны, как и в предыдущей задаче при отражении акустической волны. Только в случае нелинейной задачи это занижение более существенно. Причина та же самая – неправильный поток энергии, моделируемый на границе при использовании метода штрафных функций Бринкмана. Заметим, что, как отмечалось в работе [37], в отличие от акустической волны, пористое расширение метода штрафных функций Бринкмана [35] не устраняет ошибку, связанную со скачкообразным изменением давления газа внутри штрафной области и последующим плавным уменьшением давления в результате просачивания. Расчет с применением метода характеристических штрафных функций дает правильный градиент давления на моделируемой твердой стенке, за счет корректного определения в “погруженной” области ${{\bar {\Omega }}_{B}}$ градиента плотности (экстраполируемого с поверхности $\partial {\kern 1pt} {{\Omega }_{B}}$) и градиента температуры (релаксирующего к нулю). Все это в совокупности приводит к нулевому потоку энергии на границе и, как следствие, правильному отражению ударной волны.

Фиг. 4.

Отраженная ударная волна в момент времени $t = 60$.

3.3. Течение Куэтта

Рассмотрим двумерное течение сжимаемого газа в канале, образованном двумя параллельными непроницаемыми пластинами. Одна пластина имеет заданную температуру (изотермическая поверхность) и неподвижна, другая пластина движется с постоянной скоростью и имеет адиабатическую поверхность. Рассматриваемая среда характеризуется переменным коэффициентом динамической вязкости в безразмерном виде: $\mu = {{{{{\left( {{T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right)}}^{{ - 1/2}}}} \mathord{\left/ {\vphantom {{{{{\left( {{T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right)}}^{{ - 1/2}}}} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$, где ${{T}_{0}}$ – температура пластины. Задача решена для числа Рейнольдса $\operatorname{Re} = 1$.

Численное решение получено при следующем выборе штрафных параметров МХШФ: ${{\eta }_{b}} = {{10}^{{ - 3}}}$ и ${{\eta }_{c}} = {{10}^{{ - 2}}}$. Задача определена в прямоугольной области $\Omega = \left[ { - 0.5,0.5} \right] \times \left[ {0,0.02} \right]$, где построены три последовательно сгущающиеся квазиравномерные треугольные сетки с характерными размерами элементов – 0.02 (сетка СНТ1), 0.01 (сетка СНТ2), 0.005 (сетка СНТ3). Пластины расположены перпендикулярно оси $OX$ и их границы пересекают эту ось в точках ${{x}_{L}} = - 0.5$ и ${{x}_{R}} = 0.2$. На левой границе расчетной области, совпадающей с поверхностью одной из пластин $(x = {{x}_{L}})$, задается температура ${{T}_{L}} = {3 \mathord{\left/ {\vphantom {3 \gamma }} \right. \kern-0em} \gamma }$ и условие прилипания ${{{v}}_{L}} = 0$. Правая пластина $(x = {{x}_{R}})$ движется со скоростью ${{{v}}_{P}} = 10$ и “погружена” в прямоугольную штрафную подобласть ${{\bar {\Omega }}_{B}} = \left[ {0.2,0.5} \right] \times \left[ {0,0.02} \right]$. Граничные условия на ее поверхности, такие как условие адиабатичности ${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0em} {\partial x}} = 0$ и условие прилипания ${{{v}}_{R}} = {{{v}}_{P}}$, моделируются с помощью метода характеристических штрафных функций.

Точное решение задачи для функции температуры дается выражением (см. раздел документации на сайте https://github.com/bahvalo/ColESo)

$\begin{gathered} T(x) = {{\tau }^{2}}(x), \\ \tau (x) = \sqrt {{{T}_{L}}} \frac{{\cos \left( {c({{x}_{R}} - x)} \right)}}{{\cos \left( {c({{x}_{R}} - {{x}_{L}})} \right)}},\quad c = \frac{1}{{({{x}_{R}} - {{x}_{L}})}}{\text{arctg}}\left( {\frac{{{{{v}}_{R}}}}{{\sqrt {{{T}_{L}}} }}{{{\left( {\frac{{\Pr ({{\gamma }} - 1)}}{{2{{\gamma }}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right), \\ \end{gathered} $
а решение для функции скорости определяется следующим соотношением:

${v}(x) = {{{v}}_{R}} - {{\left( {\frac{{\Pr ({{\gamma }} - 1)}}{{2{{\gamma }}}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sqrt {{{T}_{L}}} \frac{{\sin \left( {c({{x}_{R}} - x)} \right)}}{{\cos \left( {c({{x}_{R}} - {{x}_{L}})} \right)}}.$

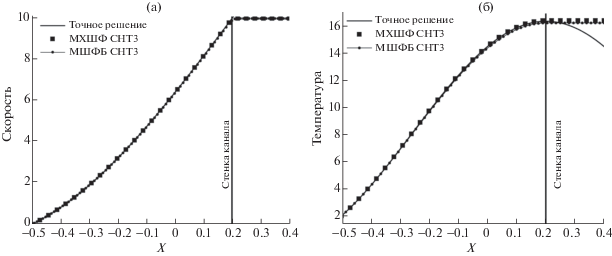
В процессе расчета получено численное стационарное решение задачи, не зависящее от координаты $y$. На фиг. 5а и фиг. 5б приведены распределения скорости и температуры вдоль оси $OX$, рассчитанные на подробной сетке СНТ3. Там же представлены соответствующие результаты моделирования с помощью метода штрафных функций Бринкмана и точное решение. Наблюдается хорошее согласование численных результатов с точным решением, за исключением окрестности правой границы. Далее на фиг. 6а и фиг. 6б приведены те же профили скоростей и температуры вблизи правой границы, полученные в расчетах на грубой (СНТ1) и подробной (СНТ3) сетках. Можно видеть, что расчеты с использованием метода характеристических штрафных функций дают более точные результаты, чем расчеты методом штрафных функций Бринкмана.

Фиг. 5.

Распределение характеристик течения Куэтта вдоль оси OX: (а) – поперечной скорости, (б) – температуры.

Фиг. 6.

Распределение характеристик течения Куэтта около правой границы: (а) – поперечной скорости, (б) – температуры.

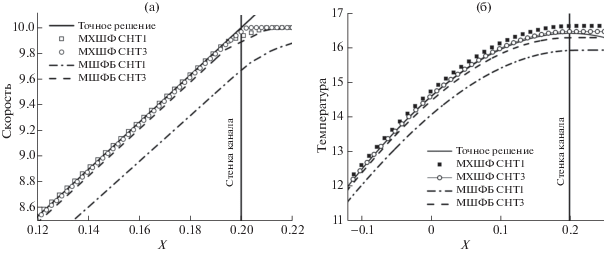
В табл. 4 показана сеточная сходимость метода характеристических штрафных функций, где приведены ошибки численного решения для температуры в среднеквадратичной норме, посчитанной в области физического определения решения ${\Omega \mathord{\left/ {\vphantom {\Omega {{{\Omega }_{B}}}}} \right. \kern-0em} {{{\Omega }_{B}}}}$. Можно видеть, что имеет место линейная сходимость при измельчении сетки, вызванная, как показaно в [37], доминированием ошибки численного метода по сравнению с ошибкой метода характеристических штрафных функций при заданных штрафных параметрах. Отметим, что в отличие от предыдущих тестовых задач, в данной задаче с помощью метода характеристических штрафных функций моделируется неоднородное граничное условие прилипания.

Таблица 4.  

Ошибка численного решения для температуры в норме ${{L}_{2}}$

СНТ1 СНТ2 СНТ3
1.07e–1 4.05e–2 1.83e–2

ЗАКЛЮЧЕНИЕ

В работе представлена методика численного моделирования задач аэродинамического обтекания на основе метода характеристических штрафных функций, являющегося разновидностью методов погруженных границ. В основе метода лежит качественно новый подход к реализации требуемых граничных условий на несогласованных с границей сетках. С одной стороны, он позволяет моделировать граничные условия различных типов (Дирихле, Неймана), а с другой, являясь методом штрафных функций, сохраняет относительную простоту численной реализации.

Разработанная методика использует математическую модель на основе системы уравнений Навье–Стокса для вязкой сжимаемой среды. В случае метода характеристических функций система Навье–Стокса дополняется еще одним уравнением для вычисления производной плотности по нормали к поверхности, которая присутствует в источниковых членах уравнений системы Навье–Стокса. Предложенный в статье численный метод решения такой системы предполагает одновременный расчет области течения и области, находящейся внутри препятствия. Таким образом, численное решение сводится к интегрированию единой СЛАУ, получаемой при дискретизации по времени по неявной схеме с использованием линеаризованного метода Ньютона.

Реализация в математической модели граничного условия Дирихле в методе характеристических штрафных функций соответствует способу, предлагаемому в методе штрафных функций Бринкмана. Однако в отличие от метода штрафных функций Бринкмана, методика характеристических штрафных функций позволяет обеспечить выполнение граничного условия Неймана.

С помощью разработанной методики на основе метода характеристических штрафных функций в работе проводится численное моделирование серии тестовых задач, имеющих аналитические решение: отражение акустического импульса, отражение ударной волны и течение Куэтта. Используемые математические модели включают граничные условия Дирихле и Неймана. Полученные результаты сравниваются как с аналитическим решением, так и с решением, полученным численно с помощью метода штрафных функций Бринкмана. Результаты, полученные методом характеристических штрафных функций, хорошо согласуются с аналитическими решениями. Показано, что в тестовых задачах этот метод обеспечивает более точный результат по сравнению с методом штрафных функций Бринкмана.

В целом полученные в работе результаты говорят об эффективности разработанной методики численного моделирования задач аэродинамического обтекания с использованием метода характеристических штрафных функций. Ее дальнейшее развитие связано с расширением применимости для трехмерных постановок, описывающих в том числе течения около движущихся тел.

Список литературы

  1. Iaccarino G., Verzicco R. Immersed boundary technique for turbulent flow simulations // Appl. Mech. Rev. 2003. V. 6. № 3. P. 331–347. https://doi.org/10.1115/1.1563627

  2. Lai M.C., Peskin C.S. An immersed boundary method with formal second order accuracy and reduced numerical viscosity // J. Comput. Phys. 2000. V. 160. № 2. P. 705–719. https://doi.org/10.1006/jcph.2000.6483

  3. Peskin C.S. The immersed boundary method // Acta Numerica. 2002. V. 11. P. 479–517. https://doi.org/10.1017/S0962492902000077

  4. Saiki E.M., Biringen S. Numerical simulation of a cylinder in uniform flow: Application of a virtual boundary method // J. Comput. Phys. 1996. V. 123. № 2. P. 450–465. https://doi.org/10.1006/jcph.1996.0036

  5. Бугров А.Н., Смагулов Ш.С. Метод фиктивных областей в краевых задачах для уравнений Навье–Стокса // В сб. науч. тр.: Математические модели течений жидкости. Новосибирск, ИТПМ СО АН СССР, 1978. С. 79–90.

  6. Вабищевич П.Н. Численная реализация метода фиктивных областей для нестационарных уравнений Навье–Стокса //Числен. методы механ. сплошной среды. 1985. Т. 16. № 6. С. 19–37.

  7. Goldstein D., Handler R., Sirovich L. Modeling a noslip flow boundary with an external force field // J. Comput. Phys. 1993. V. 105. № 2. P. 354–366. https://doi.org/10.1006/jcph.1993.1081

  8. Peskin C.S. Flow patterns around heart valves: A numerical method. // J. Comput. Phys. 1972. V. 10. № 2. P. 252–271. https://doi.org/10.1016/0021-9991(72)90065-4

  9. Fedkiw R. Coupling an eulerian fluid calculation to a lagrangian solid calculation with the ghost fluid method // J. Comput. Phys. 2002. V. 175. № 1. P. 200–224. https://doi.org/10.1006/jcph.2001.6935

  10. De Palma P., de Tullio M.D., Pascazio G., Napolitano M. An immersed-boundary method for compressible viscous flows // Comput. Fluids. 2006. V. 35. № 7. P. 693–702. https://doi.org/10.1016/j.compfluid.2006.01.004

  11. de Tullio M.D., Verzicco R., Iaccarino G. Immersed boundary technique for Large-Eddy Simulation / Large eddy simulation: Theory and applications /ed. by U. Piomelli & J.P.A.J. van Beeck. – VKI LS 2018-03. https://doi.org/10.35294/ ls201803.detullio

  12. Меньшов И.С., Корнев М.А. Метод свободной границы для численного решения уравнений газовой динамики в областях с изменяющейся геометрией // Матем. моделирование. 2014. Т. 26. № 5. С. 99–112. I.S. Menshov, M.A. Kornev. Free-boundary method for the numerical solution of gas-dynamic equations in domains with varying geometry // Math. Models Comput. Simul. 2014. V. 6. № 6. P. 612–621. https://doi.org/10.1134/S207004821406009X

  13. Khadra K., Parneix S., Angot P., Caltagirone J.P. Fictitious domain approach for numerical modelling of Navier–Stokes equations // Int. J. Numer. Meth. Fluids. 2000. V. 34. № 8. P. 651–684. https://doi.org/10.1002/1097-0363(20001230)34:8<651::AID-FLD61>3.0.CO;2-D

  14. Вабищевич П.Н. Метод фиктивных областей в задачах математической физики. М: Изд-во Московского университета, 1991.

  15. Carbou G., Fabrie P. Boundary layer for a penalization method for viscous incompressible flow // Adv. Differential Equations. 2003. V. 8. № 12. P. 1453–1480.

  16. Вишик М.И., Люстерник Л.А. Асимптотическое поведение решений линейных дифференциальных уравнений с большими или быстро меняющимися коэффициентами и граничными условиями // Успехи матем. наук. 1960. Т. 15. № 4. С. 27–95.

  17. Саульев В.К. Об одном методе автоматизации решения краевых задач на быстродействующих вычислительных машинах // Докл. АН СССР. 1962. Т. 144. № 3. С. 497–500.

  18. Саульев В.К. О решении некоторых краевых задач на быстродействующих вычислителных машинах методом фиктивных областей // Сибирский матем. ж. 1963. Т. 4. № 4. С. 912–925.

  19. Лебедев В.И. Разностные аналоги ортогональных разложений основных дифференциальных операторов и некоторых краевых задач математической физики. I // Ж. вычисл. матем. и матем. физ. 1964. Т. 4. № 3. С. 449–465.

  20. Бугров А.Н. Метод фиктивных областей в уравнениях относительно функции тока для вязкой несжимаемой жидкости: Препринт Института матем. СО АН СССР. Новосибирск, 1977.

  21. Вабищевич П.Н., Вабищевич Т.Н. Численное решение стационарных задач вязкой несжимаемой жидкости // Дифференц. ур-ния. 1983. Т. 19. № 5. С. 852–860.

  22. Вабищевич П.Н., Вабищевич Т.Н. Численное решение стационарных задач вязкой несжимаемой жидкости на основе метода фиктивных областей. В сб. Вычислительная математика и математическое обеспечение ЭВМ. М.: Изд-вo МГУ, 1985. С. 255–262.

  23. Мызникова Б.И., Тарунин Е.Л. Применение метода фиктивных областей для решения уравнений Навье–Стокса в переменных функциях тока и вихрь скорости В сб. Исследование тепловой конвекции и теплопередачи. Свердловск, УНЦ АН СССР, 1981. С. 45–57.

  24. Орунханов М.К., Смагулов Ш.С. Метод фиктивных областей для уравнения Навье–Стокса в терминах функции тока и вихря скоростей с неоднородными граничными условиями. В сб. Вычисл. технологии. Т. 5. Новосибирск. СО РАН, 2000. С. 46–53.

  25. Смагулов Ш.С. Метод фиктивных областей для краевой задачи уравнений Навье–Стокса: Препринт ВЦ СО АН СССР. Т. 68. Новосибирск, 1979.

  26. Аксенова А.Е., Вабищевич П.Н., Чуданов В.В. Численное моделирование свободно конвективной тепловыделяющей жидкости с фазовыми превращениями: Препринт NSI794. М.: Институт проблем безопасного развития атомной энергетики РАН, 1994.

  27. Вабищевич П.Н., Илиев О.П. Численное решение сопряженных задач тепло- и массопереноса с учетом фазового перехода // Дифференц. ур-ния. 1987. Т. 23. № 7. С. 1127–1132.

  28. Angot P. Analysis of singular perturbations on the Brinkman problem for fictitious domain models of viscous flows // Math. Meth. Appl. Sci. 1999. V. 22. № 16. P. 1395–1412. https://doi.org/10.1002/(SICI)1099-1476(19991110)22:16<1395::AID-MMA84>3.0.CO;2-3

  29. Ramière I., Angot P., Belliard M. A fictitious domain approach with spread interface for elliptic problems with general boundary conditions // Comput. Methods Appl. Mech. Engrg. 2007. V. 196. № 4–6. P. 766–781. https://doi.org/10.1016/j.cma.2006.05.012

  30. Angot P., Bruneau C.-H., Fabrie P. A penalization method to take into account obstacles in incompressible viscous flows // Numer. Math. 1999. V. 81. № 4. P. 497–520. https://doi.org/10.1007/s002110050401

  31. Bergmann M., Iollo A. Modeling and simulation of fish-like swimming // J. Comput. Phys. 2011. V. 230. № 2. P. 329–348. https://doi.org/10.1016/j.jcp.2010.09.017

  32. Kevlahan N., Ghidaglia J.-M. Computation of turbulent flow past an array of cylinders using a spectral method with Brinkman penalization // Eur. J. of Mech.- B/Fluids. 2001. V. 20. № 3. P. 333–350. https://doi.org/10.1016/S0997-7546(00)01121-3

  33. Vasilyev O., Kevlahan N. Hybrid wavelet collocation–Brinkman penalization method for complex geometry flows // Int. J. Num. Meth. Fluids. 2002. V. 40. № 3-4. P. 531–538. https://doi.org/10.1002/fld.307

  34. Spietz H.J., Hejlesen M.M., Walther J.H. Iterative Brinkman penalization for simulation of impulsively started flow past a sphere and a circular disc // J. Comput. Phys. 2017. V. 336. P. 261–274. https://doi.org/10.1016/j.jcp.2017.01.064

  35. Liu Q., Vasilyev O.V. Brinkman Penalization method for compressible flows in complex geometries // J. Comput. Phys. 2007. V. 227. № 2. P. 946–966. https://doi.org/10.1016/j.jcp.2007.07.037

  36. Komatsu R., Iwakami W., Hattori Y. Direct numerical simulation of aeroacoustic sound by volume penalization method // Comput. Fluids. 2016. V. 130. P. 24–36. https://doi.org/10.1016/j.compfluid.2016.02.016

  37. Brown-Dymkoski E., Kasimov N., Vasilyev O.V. A characteristic based volume penalization method for general evolution problems applied to compressible viscous flows // J. Comput. Phys. 2014. V. 262. P. 344–357. https://doi.org/10.1016/j.jcp.2013.12.060

  38. Nejadmalayeri A., Vezolainen A., Brown-Dymkoski E., Vasilyev O.V. Parallel Adaptive Wavelet Collocation Method for PDEs // J. Comput. Phys. 2015. V. 298. P. 237–253. https://doi.org/10.1016/j.jcp.2015.05.028

  39. Bakhvalov P., Abalakin I., Kozubskaya T. Edge-based reconstruction schemes for unstructured tetrahedral meshes // Int. J. Numer. Meth. Fluids. 2016. V. 81. № 6. P. 331–356. https://doi.org/10.1002/fld.4187

  40. Aslam T.D. A partial differential equation approach to multidimensional extrapolation // J. Comput. Phys. 2003. V. 193. № 1. P. 349–355. https://doi.org/10.1016/j.jcp.2003.08.001

  41. van der Vorst H.A. Bi-CGSTAB: A fast and smoothly converging variant of BI-CG for the solution of nonsymmetric linear systems // SIAM J. Sci. Stat. Comput. 1992. V. 13. № 2. P. 631–644. https://doi.org/10.1137/0913035

  42. Абалакин И.В., Горобец А.В., Жданова Н.С., Козубская Т.К. Применение метода Бринкмана штрафных функций для численного моделирования обтекания препятствий вязким сжимаемым газом: Препринт 011. M.: ИПМ им. М.В. Келдыша РАН, 2014. 14 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал