Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1447-1463

Идентификация коэффициента теплопроводности вещества в трехмерном случае путем решения соответствующей задачи оптимизации

А. Ф. Албу¹, В. И. Зубов^1, *

¹ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия

Поступила в редакцию 30.11.2020
После доработки 05.05.2021
Принята к публикации 12.05.2021

DOI: 10.31857/S0044466921090040

Аннотация

Рассматривается и исследуется обратная задача определения зависящего от температуры коэффициента теплопроводности вещества в параллелепипеде. Рассмотрение проводится на основе первой краевой задачи для трехмерного нестационарного уравнения теплопроводности. Обратная коэффициентная задача сводится к некоторой задаче оптимизации и решается численно с помощью градиентных методов минимизации функционала. На примере ряда нелинейных задач, коэффициенты которых зависят от температуры, показаны работоспособность и эффективность предложенного подхода. Библ. 17. Фиг. 9.

Ключевые слова: обратные коэффициентные задачи, нелинейные задачи, трехмерное уравнение теплопроводности, оптимальное управление, численные методы оптимизации, схемы переменных направлений.

ВВЕДЕНИЕ

В последнее время наблюдается потребность в создании новых материалов. Однако некоторые характеристики новых материалов бывают неизвестными, и для их определения прибегают к решению обратных задач. Довольно часто приходится встречаться с ситуацией, когда коэффициент теплопроводности вещества зависит только от температуры и эта зависимость неизвестна. В связи с этим возникает задача определения зависимости коэффициента теплопроводности вещества от температуры по результатам экспериментального наблюдения за динамикой температурного поля в исследуемом веществе (задача относится к классу задач идентификации параметров модели).

Задача определения коэффициента теплопроводности вещества представляет повышенный интерес и рассматривается довольно давно. Подтверждением этому может служить большое количество публикаций, посвященных указанному вопросу (см., например, [1]–[8]). Большое внимание в этих работах уделяется не только теоретическому исследованию обратных коэффициентных задач, но и разработке численных методов их решения.

Ранее обратная коэффициентная задача, посвященная вопросу идентификации зависящего от температуры коэффициента теплопроводности вещества, исследовалась авторами настоящей статьи в работах, опубликованных в этом журнале (№ 10, Т. 56; № 10, Т. 58; № 12, Т. 58). Рассмотрение проводилось на основе первой краевой задачи для одномерного и двумерного нестационарного уравнения теплопроводности. В качестве исследуемых объектов там выступали стержень и прямоугольная пластина.

В настоящей работе задача восстановления коэффициента теплопроводности решается в трехмерной постановке. Именно этот случай имеет наибольший интерес для практики, так как при сборе экспериментальных данных имеют дело с трехмерными объектами. При проведении экспериментальных исследований используют, как правило, образцы материала простой формы (обычно, это параллелепипед). Поэтому возникающую при этом обратную коэффициентную задачу в трехмерном случае разумно рассматривать также для объекта-параллелепипеда.

Рассмотренные ранее одномерный и двумерный варианты обратных коэффициентных задач представляют большой математический интерес и, безусловно, накопленный при их решении опыт оказался очень полезным при исследовании задачи в трехмерной постановке. Здесь, как и ранее, обратная задача сводится к вариационной задаче и решается численно с помощью градиентных методов минимизации функционала, а для вычисления градиента используется эффективная методология быстрого автоматического дифференцирования (БАД-методология, см. [9]).

Одна из сложностей, с которой приходится сталкиваться при решении задачи в трехмерной постановке, связана с решением прямой задачи. В отличие от одномерного и двумерного случаев, где можно однозначно указать эффективную разностную схему дискретизации уравнения теплопроводности, при решении задачи в трехмерной постановке необходимо проводить дополнительные исследования, касающиеся выбора разностной схемы в каждом конкретном случае.

В работе [10] поясняется, почему при решении обратной коэффициентной задачи для дискретизации уравнения теплопроводности целесообразно использовать одну из схем переменных направлений. В [10] на примере ряда нелинейных задач для трехмерного уравнения теплопроводности, коэффициенты которого зависят от температуры, проводится сравнительный анализ нескольких схем переменных направлений: локально-одномерной схемы ([11]), схемы Дугласа–Рекфорда (см. [12]) и схемы Писмена–Рекфорда (см. [13]). При сравнении методов принимались во внимание точность получаемого решения и время достижения требуемой точности на компьютере.

Основываясь на приведенных в работе [10] результатах исследований, авторы при решении практических задач рекомендуют реализовать все указанные выше схемы, чтобы на финальном этапе решения вариационной задачи проверить точность решения прямой задачи с помощью нескольких разностных схем. Схема Писмена-Рекфорда для трехмерного уравнения теплопроводности является условно устойчивой (см. [14]) и требует работы с мелким шагом по времени. Однако, как показали многочисленные расчеты и исследования (см. [10]), даже на грубых пространственных сетках при временном шаге, близком к максимально допустимому, эта схема позволяет получить высокую точность расчетов. Хочется отметить, что если реализована одна из схем переменных направлений, то на ее основе легко запрограммировать и остальные.

В настоящей работе задача идентификации параметров рассматриваемой трехмерной модели исследуется в следующей постановке: требуется найти такую зависимость коэффициента теплопроводности от температуры, при которой температурное поле, полученное в результате решения прямой задачи, мало отличается от данных, полученных экспериментально.

Сопряженные уравнения и формула для вычисления градиента целевого функционала, которые приводятся в настоящей работе, получены для случая использования локально-одномерной схемы, так как результаты проведенных численных экспериментов показали, что именно она оказалась наименее “капризной”. Для других разностных схем эти формулы можно получить аналогичным образом.

1. ПОСТАНОВКА ЗАДАЧИ

В работе [15] рассматриваемая обратная задача была сформулирована в общем, $n$-мерном случае. Здесь мы приводим краткую постановку задачи для трехмерного случая.

Пусть образец исследуемого вещества имеет форму прямого параллелепипеда длины $R$, ширины $E$ и высоты $H$. Температура $T$ этого параллелепипеда в начальный момент времени известна. Известно также, как изменяется во времени температура параллелепипеда на его гранях. Для математического описания процесса теплопроводности в параллелепипеде введем декартовы координаты $x,\;y$ и $z$. Точки $s = (x,y,z)$ параллелепипеда образуют область $Q = \left\{ {\,(0,R) \times (0,E) \times (0,H)\,} \right\}$ с границей $\Gamma = \partial Q$. Распределение температурного поля в параллелепипеде в каждый момент времени описывается решением следующей начально-краевой (смешанной) задачи:

(1.1)

$C(s)\frac{{\partial T(s,t)}}{{\partial t}} = {{\nabla }_{s}} \cdot \left( {K(T(s,t)) \cdot {{\nabla }_{s}}T(s,t)} \right),\quad (s,t) \in \left\{ {Q \times (0,\Theta )} \right\},$

(1.2)

$T(s,0) = {{w}_{0}}(s),\quad s \in \bar {Q},$

(1.3)

$T(s,t) = {{w}_{\Gamma }}(s,t),\quad s \in \Gamma ,\quad 0 \leqslant t \leqslant \Theta .$

Здесь $t$ – время; $T(s,t) \equiv T(x,y,z,t)$ – температура вещества в точке $s$ с координатами $(x,y,z)$ в момент времени $t$; $\;C(s)$ – объемная теплоемкость материала; $K(T)$ – коэффициент теплопроводности; ${{w}_{0}}(s)$ – заданная температура параллелепипеда в начальный момент времени $t = 0$; ${{w}_{\Gamma }}(s,t)$ – заданная температура на границе области. Объемная теплоемкость $\;C(s)$ считается известной функцией координат. При заданном коэффициенте теплопроводности $K(T)$ можно найти распределение температуры $T(s,t)$ в любой точке области $Q \times (0,\Theta )$, решив прямую задачу (1.1)–(1.3).

Обратная коэффициентная задача сводится к следующей вариационной задаче: требуется найти такую зависимость коэффициента теплопроводности вещества $K(T)$ от температуры $T$, при которой температурное поле $T(s,t)$, полученное в результате решения прямой задачи (1.1)–(1.3), мало отличается от температурного поля $Y(s,t)$, полученного экспериментально. В качестве меры отклонения этих функций рассматривается величина

(1.4)

$\Phi \left( {K(T)} \right) = \int\limits_0^\Theta {\int\limits_Q {\mu (s,t){{{\left[ {T(s,t) - Y(s,t)} \right]}}^{2}}ds} {\kern 1pt} dt} .$

Здесь $\mu (s,t) \geqslant 0$ – заданная весовая функция, $Y(s,t)$ – заданное температурное поле.

Таким образом, обратная задача идентификации функции $K(T)$ сводится к следующей задаче оптимального управления: определить оптимальное управление $K(T)$ и соответствующее решение $T(s,t)$ задачи (1.1)–(1.3), при котором целевой функционал (1.4) достигает минимального значения.

2. ВЫЧИСЛЕНИЕ ГРАДИЕНТА ЦЕЛЕВОГО ФУНКЦИОНАЛА

В работе [15] было получено аналитическое выражение для градиента целевого функционала в общей, $n$-мерной постановке сформулированной задачи оптимального управления. Однако использовать аналитическое выражение для градиента функционала при численном решении задачи практически невозможно в силу его сложности. Поэтому в предлагаемом алгоритме, как и ранее, для вычисления градиента функционала использовалась методология быстрого автоматического дифференцирования (БАД-методология).

Дискретная сопряженная задача, построенная на основе БАД-методологии, базируется на выбранной аппроксимации прямой задачи и согласованна с ней. Разностные схемы переменных направлений, которые мы рекомендуем для решения трехмерного уравнения теплопроводности, подробно описаны в [10]. В настоящей работе формула для вычисления градиента функционала получена для случая использования второго (итерационного) варианта локально-одномерной схемы при аппроксимации уравнения теплопроводности. Эти формулы могут быть использованы и в случае работы с явной локально-одномерной схемой, если полагать, что количество итераций равно единице.

Для дискретизации задачи в области $Q \times (0,\Theta )$ вводятся временнáя и пространственная сетки. Временнáя сетка задается набором узловых значений $\{ {{t}^{j}}\} _{{j = 0}}^{J}$, ${{t}^{0}} = 0$, ${{t}^{J}} = \Theta $ с шагом ${{\tau }^{{}}} = \Theta {\text{/}}J$. Пространственная сетка – множество точек $\left\{ {{{x}_{n}},{{y}_{i}},{{z}_{l}}} \right\}$, где $n = \overline {0,N} $, $i = \overline {0,I} $ и $l = \overline {0,L} $; $h_{n}^{x}$ – расстояние между опорными точками ${{x}_{n}}$ и ${{x}_{{n + 1}}}$, т.е. $h_{n}^{x} = {{x}_{{n + 1}}} - {{x}_{n}}$, $n = \overline {0,N - 1} $; аналогично: $h_{i}^{y} = {{y}_{{i + 1}}} - {{y}_{i}}$, $i = \overline {0,I - 1} $, $h_{l}^{z} = {{z}_{{l + 1}}} - {{z}_{l}}$, $l = \overline {0,L - 1} $ (подробнее см. [10]). В каждом узле $({{x}_{n}},{{y}_{i}},{{z}_{{l,}}}{{t}^{j}})$ расчетной области $Q \times (0,\Theta )$ все функции задаются своими значениями в этой точке (например, $T({{x}_{n}},{{y}_{i}},{{z}_{{l,}}}{{t}^{j}}) = T_{{nil}}^{j}$).

Границы отрезка $[a,b]$, на котором восстанавливается коэффициент теплопроводности $K(T)$, задавались как минимальное и максимальное значения функций ${{w}_{0}}(s)$ и ${{w}_{\Gamma }}(s,t)$. Отрезок $[\,a,b]$ разбивался точками ${{\tilde {T}}_{0}} = a$, ${{\tilde {T}}_{1}}$, ${{\tilde {T}}_{2}}$, …, ${{\tilde {T}}_{M}} = b$ на $M$ частей (они могут быть как равными, так и неравными). Каждой из точек ${{\tilde {T}}_{m}}$, $m = 0,...,M$, ставилось в соответствие число ${{k}_{m}} = K({{\tilde {T}}_{m}})$. Искомая функция $K(T)$ аппроксимировалась непрерывной кусочно-линейной функцией с узлами в точках $\{ ({{\tilde {T}}_{m}},{{k}_{m}})\} _{{m = 0}}^{M}$ так, как это показано в [15]. Если в процессе решения задачи температура в точке выходила за границы отрезка $[\,a,b]$, то для определения функции $K(T)$ использовалась линейная экстраполяция.

Целевой функционал (1.4) аппроксимировался функцией $F({{k}_{0}},{{k}_{1}},...,{{k}_{M}})$ конечного числа переменных следующим образом:

(2.1)

$\Phi \left( {K(T)} \right) \approx F = \tau \sum\limits_{j = 1}^J {\sum\limits_{l = 1}^{L - 1} {\sum\limits_{i = 1}^{I - 1} {\sum\limits_{n = 1}^{N - 1} {\left( {{{{(T_{{nil}}^{j} - \Upsilon _{{nil}}^{j})}}^{2}}\mu _{{nil}}^{j}h_{n}^{x}h_{i}^{y}h_{l}^{z}} \right)} } } } {\kern 1pt} .$

Согласно БАД-методологии, каждое уравнение выбранного дискретного варианта прямой задачи (итерационный вариант локально-одномерной схемы) записывается в так называемом каноническом виде:

$x$ – направление

$\begin{gathered} T_{{nil}}^{{j + 1/3}} = T_{{nil}}^{j} + {{a}_{{nil}}}\left( {K(T_{{n + 1,il}}^{{j + 1/3}})T_{{n + 1,il}}^{{j + 1/3}} + K(T_{{nil}}^{{j + 1/3}})T_{{n + 1,il}}^{{j + 1/3}} - K(T_{{n + 1,il}}^{{j + 1/3}})T_{{nil}}^{{j + 1/3}} - K(T_{{nil}}^{{j + 1/3}})T_{{nil}}^{{j + 1/3}}} \right) + \\ \, + {{b}_{{nil}}}\left( {K(T_{{n - 1,il}}^{{j + 1/3}})T_{{n - 1,il}}^{{j + 1/3}} + K(T_{{nil}}^{{j + 1/3}})T_{{n - 1,il}}^{{j + 1/3}} - K(T_{{n - 1,il}}^{{j + 1/3}})T_{{nil}}^{{j + 1/3}} - K(T_{{nil}}^{{j + 1/3}})T_{{nil}}^{{j + 1/3}}} \right) \equiv \psi _{{nil}}^{{j + 1/3}}, \\ \end{gathered} $

$y$ – направление

$\begin{gathered} T_{{nil}}^{{j + 2/3}} = T_{{nil}}^{{j + 1/3}} + {{c}_{{nil}}}\left( {K(T_{{n,i + 1,l}}^{{j + 2/3}})T_{{n,i + 1,l}}^{{j + 2/3}} + K(T_{{nil}}^{{j + 2/3}})T_{{n,i + 1,l}}^{{j + 2/3}} - K(T_{{n,i + 1,l}}^{{j + 2/3}})T_{{nil}}^{{j + 2/3}} - K(T_{{nil}}^{{j + 2/3}})T_{{nil}}^{{j + 2/3}}} \right) + \\ \, + {{d}_{{nil}}}\left( {K(T_{{n,i - 1,l}}^{{j + 2/3}})T_{{n,i - 1,l}}^{{j + 2/3}} + K(T_{{nil}}^{{j + 2/3}})T_{{n,i - 1,l}}^{{j + 2/3}} - K(T_{{n,i - 1,l}}^{{j + 2/3}})T_{{nil}}^{{j + 2/3}} - K(T_{{nil}}^{{j + 2/3}})T_{{nil}}^{{j + 2/3}}} \right) \equiv \psi _{{nil}}^{{j + 2/3}}, \\ \end{gathered} $

$z$ – направление

$\begin{gathered} T_{{nil}}^{{j + 1}} = T_{{nil}}^{{j + 2/3}} + {{e}_{{nil}}}\left( {K(T_{{ni,l + 1}}^{{j + 1}})T_{{ni,l + 1}}^{{j + 1}} + K(T_{{nil}}^{{j + 1}})T_{{ni,l + 1}}^{{j + 1}} - K(T_{{ni,l + 1}}^{{j + 1}})T_{{nil}}^{{j + 1}} - K(T_{{nil}}^{{j + 1}})T_{{nil}}^{{j + 1}}} \right) + \\ \, + {{f}_{{nil}}}\left( {K(T_{{ni,l - 1}}^{{j + 1}})T_{{ni,l - 1}}^{{j + 1}} + K(T_{{nil}}^{{j + 1}})T_{{ni,l - 1}}^{{j + 1}} - K(T_{{ni,l - 1}}^{{j + 1}})T_{{nil}}^{{j + 1}} - K(T_{{nil}}^{{j + 1}})T_{{nil}}^{{j + 1}}} \right) \equiv \psi _{{nil}}^{{j + 1}}, \\ \end{gathered} $

где

${{a}_{{nil}}} = \frac{\tau }{{6{{C}_{{nil}}}h_{n}^{x}(h_{n}^{x} + h_{{n - 1}}^{x})}},\quad {{b}_{{nil}}} = \frac{\tau }{{6{{C}_{{nil}}}h_{{n - 1}}^{x}(h_{n}^{x} + h_{{n - 1}}^{x})}},\quad {{c}_{{nil}}} = \frac{\tau }{{6{{C}_{{nil}}}h_{i}^{y}(h_{i}^{y} + h_{{i - 1}}^{y})}},$

${{d}_{{nil}}} = \frac{\tau }{{6{{C}_{{nil}}}h_{{i - 1}}^{y}(h_{i}^{y} + h_{{i - 1}}^{y})}},\quad {{e}_{{nil}}} = \frac{\tau }{{6{{C}_{{nil}}}h_{l}^{z}(h_{l}^{z} + h_{{l - 1}}^{z})}},\quad {{f}_{{nil}}} = \frac{\tau }{{6{{C}_{{nil}}}h_{{l - 1}}^{z}(h_{l}^{z} + h_{{l - 1}}^{z})}},$

$(n = \overline {1,N - 1,} \quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} ,\quad j = \overline {0,J - 1} ).$

БАД-методология позволяет формально записать систему сопряженных уравнений для используемой выше аппроксимации прямой задачи. Для более компактной записи этих соотношений введем следующие обозначения:

$D_{{nil}}^{j} = \frac{{dK(T)}}{{dT}}(T_{{ni}}^{j}) = \frac{{{{k}_{m}} - {{k}_{{m - 1}}}}}{{{{{\tilde {T}}}_{m}} - {{{\tilde {T}}}_{{m - 1}}}}},$

индекс $m$ здесь определяется условием ${{\tilde {T}}_{{m - 1}}} \leqslant T < {{\tilde {T}}_{m}}$,

$A_{{nil}}^{j} = \frac{{d\left( {K(T_{{nil}}^{j})T_{{nil}}^{j}} \right)}}{{dT_{{nil}}^{j}}} = D_{{nil}}^{j}T_{{nil}}^{j} + K(T_{{nil}}^{j}).$

Для тех индексов $(n,i,l,j)$, для которых

$(n < 0) \cup (n > N) \cup (i < 0) \cup (i > I) \cup (l < 0) \cup (L > I) \cup (j < 0) \cup (j > J),$

будем полагать $p_{{nil}}^{j} = 0$. Наконец, если в выражениях встречается слагаемое, представляющее собой произведение сопряженной переменной $p_{{nil}}^{j}$ на другие сеточные функции и эта $p_{{nil}}^{j} = 0$, то все слагаемое полагается равным нулю, несмотря на то, что другие сомножители могут быть в этой точке не определены.

Для того чтобы получить начальные условия для сопряженных переменных, необходимо на последнем временном слое $j = J$ для каждого $\;n = \overline {1,N - 1} $ и для каждого $\;i = \overline {1,I - 1} $ решить следующую систему линейных алгебраических уравнений относительно неизвестных $p_{{nil}}^{J}$:

(2.2)

$\begin{gathered} p_{{nil}}^{J} = \left[ {{{e}_{{nil}}}\left( {D_{{nil}}^{J}T_{{ni,l + 1}}^{J} - K(T_{{ni,l + 1}}^{J}) - A_{{nil}}^{J}} \right) + {{f}_{{nil}}}\left( {D_{{nil}}^{J}T_{{ni,l - 1}}^{J} - K(T_{{ni,l - 1}}^{J}) - A_{{nil}}^{J}} \right)} \right]p_{{nil}}^{J} - \\ - \;{{e}_{{ni,l - 1}}}\left( {D_{{nil}}^{J}T_{{ni,l - 1}}^{J} - K(T_{{ni,l - 1}}^{J}) - A_{{nil}}^{J}} \right)p_{{ni,l - 1}}^{J} - {{f}_{{ni,l + 1}}}\left( {D_{{nil}}^{J}T_{{ni,l + 1}}^{J} - K(T_{{ni,l + 1}}^{J}) - A_{{nil}}^{J}} \right)p_{{ni,l + 1}}^{J} + \frac{{\partial F}}{{\partial T_{{nil}}^{J}}}, \\ l = \overline {1,L - 1} . \\ \end{gathered} $

Далее сопряженная задача расщепляется на три подзадачи (по направлениям $y$, $x$ и $z$), причем такое расщепление автоматически дает БАД-методология:

$y$ – направление

(2.3)

$\begin{gathered} p_{{nil}}^{{j + 2/3}} = p_{{nil}}^{{j + 1}} + \left[ {{{c}_{{nil}}}\left( {D_{{nil}}^{{j + 2/3}}T_{{n,i + 1,l}}^{{j + 2/3}} - K(T_{{n,i + 1,l}}^{{j + 2/3}}) - A_{{nil}}^{{j + 2/3}}} \right)} \right. + \\ + \;\left. {{{d}_{{nil}}}\left( {D_{{nil}}^{{j + 2/3}}T_{{n,i - 1,l}}^{{j + 2/3}} - K(T_{{n,i - 1,l}}^{{j + 2/3}}) - A_{{nil}}^{{j + 2/3}}} \right)} \right]p_{{nil}}^{{j + 2/3}} - \\ - \;c_{{n,i - 1,l}}^{{}}\left( {D_{{nil}}^{{j + 2/3}}T_{{n,i - 1,l}}^{{j + 2/3}} - K(T_{{n,i - 1,l}}^{{j + 2/3}}) - A_{{nil}}^{{j + 2/3}}} \right)p_{{n,i - 1,l}}^{{j + 2/3}} - {{d}_{{n,i + 1,l}}}\left( {D_{{nil}}^{{j + 2/3}}T_{{n,i + 1,l}}^{{j + 2/3}} - K(T_{{n,i + 1,l}}^{{j + 2/3}}) - A_{{nil}}^{{j + 2/3}}} \right)p_{{n,i + 1,l}}^{{j + 2/3}}, \\ n = \overline {1,N - 1,} \quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} ,\quad j = \overline {J - 1,0} ; \\ \end{gathered} $

$x$ – направление

(2.4)

$\begin{gathered} p_{{nil}}^{{j + 1/3}} = p_{{nil}}^{{j + 2/3}} + \left[ {{{a}_{{nil}}}\left( {D_{{nil}}^{{j + 1/3}}T_{{n + 1,il}}^{{j + 1/3}} - K(T_{{n + 1,il}}^{{j + 1/3}}) - A_{{nil}}^{{j + 1/3}}} \right) + } \right. \\ + \;\left. {{{b}_{{nil}}}\left( {D_{{nil}}^{{j + 1/3}}T_{{n - 1,il}}^{{j + 1/3}} - K(T_{{n - 1,il}}^{{j + 1/3}}) - A_{{nil}}^{{j + 1/3}}} \right)} \right]p_{{nil}}^{{j + 1/3}} - \\ \, - {{a}_{{n - 1,il}}}\left( {D_{{nil}}^{{j + 1/3}}T_{{n - 1,il}}^{{j + 1/3}} - K(T_{{n - 1,il}}^{{j + 1/3}}) - A_{{nil}}^{{j + 1/3}}} \right)p_{{n - 1,il}}^{{j + 1/3}} - {{b}_{{n + 1,il}}}\left( {D_{{nil}}^{{j + 1/3}}T_{{n + 1,il}}^{{j + 1/3}} - K(T_{{n + 1,il}}^{{j + 1/3}}) - A_{{nil}}^{{j + 1/3}}} \right)p_{{n + 1,il}}^{{j + 1/3}}, \\ n = \overline {1,N - 1,} \quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} ,\quad j = \overline {J - 1,0} ; \\ \end{gathered} $

$z$ – направление

(2.5)

$\begin{gathered} p_{{nil}}^{j} = p_{{nil}}^{{j + 1/3}} + \left[ {{{e}_{{nil}}}\left( {D_{{nil}}^{j}T_{{ni,l + 1}}^{j} - K(T_{{ni,l + 1}}^{j}) - A_{{nil}}^{j}} \right) + {{f}_{{nil}}}\left( {D_{{nil}}^{j}T_{{ni,l - 1}}^{j} - K(T_{{ni,l - 1}}^{j}) - A_{{nil}}^{j}} \right)} \right]p_{{nil}}^{j} - \\ - \;{{e}_{{ni,l - 1}}}\left( {D_{{nil}}^{j}T_{{ni,l - 1}}^{j} - K(T_{{ni,l - 1}}^{j}) - A_{{nil}}^{j}} \right)p_{{ni,l - 1}}^{j} - {{f}_{{ni,l + 1}}}\left( {D_{{nil}}^{j}T_{{ni,l + 1}}^{j} - K(T_{{ni,l + 1}}^{j}) - A_{{nil}}^{j}} \right)p_{{ni,l + 1}}^{j} + \frac{{\partial F}}{{\partial T_{{nil}}^{j}}}, \\ n = \overline {1,N - 1,} \quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} ,\quad j = \overline {J - 1,1} . \\ \end{gathered} $

Полученные системы линейных алгебраических уравнений (2.2)–(2.5) решались с помощью метода прогонки (см. [16]).

Компоненты градиента целевой функции, в соответствии с БАД-методологией, вычисляются по формуле

(2.6)

$\begin{gathered} \frac{{\partial F}}{{\partial {\kern 1pt} {{k}_{m}}}} = \sum\limits_{g = 0}^J {\,\sum\limits_{r = 0}^L {\,\sum\limits_{q = 0}^I {\sum\limits_{s = 0}^N {\left( {{\rm X}_{{rqs}}^{g}\frac{{\partial K(T_{{rqs}}^{g})}}{{\partial {{k}_{m}}}}} \right)} } } } + \sum\limits_{g = 0}^{J - 1} {\,\sum\limits_{r = 0}^L {\,\sum\limits_{q = 0}^I {\sum\limits_{s = 0}^N {\left( {{\rm X}_{{rqs}}^{{g + 1/3}}\frac{{\partial K(T_{{rqs}}^{{g + 1/3}})}}{{\partial {{k}_{m}}}} + {\rm X}_{{rqs}}^{{g + \frac{2}{3}}}\frac{{\partial K(T_{{rqs}}^{{g + 2/3}})}}{{\partial {{k}_{m}}}}} \right)} } } } , \\ m = \overline {0,M} , \\ \end{gathered} $

где

$\begin{gathered} {\rm X}_{{rqs}}^{g} = \sum\limits_{j = 1}^J {\sum\limits_{l = 1}^{L - 1} {\sum\limits_{i = 1}^{I - 1} {\sum\limits_{n = 1}^{N - 1} {\left( {\frac{{\partial \psi _{{nil}}^{j}}}{{\partial K(T_{{rqs}}^{g})}}p_{{nli}}^{j} + \frac{{\partial \psi _{{nil}}^{{j - 1/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{nil}}^{{j - 1/3}} + \frac{{\partial \psi _{{nil}}^{{j - 2/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{nil}}^{{j - 2/3}}} \right)} } } } = \\ \, = \frac{{\partial \psi _{{rq,s - 1}}^{g}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rq,s - 1}}^{g} + \frac{{\partial \psi _{{rqs}}^{g}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rqs}}^{g} + \frac{{\partial \psi _{{rq,s + 1}}^{g}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rq,s + 1}}^{g} + \\ \end{gathered} $

$\begin{gathered} + \;\frac{{\partial \psi _{{rq,s - 1}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rq,s - 1}}^{{g + 1/3}} + \frac{{\partial \psi _{{rqs}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rqs}}^{{g + 1/3}} + \frac{{\partial \psi _{{rq,s + 1}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rq,s + 1}}^{{g + 1/3}} + \\ + \;\frac{{\partial \psi _{{rq,s - 1}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rq,s - 1}}^{{g + 2/3}} + \frac{{\partial \psi _{{rqs}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rqs}}^{{g + 2/3}} + \frac{{\partial \psi _{{rq,s + 1}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{g})}}p_{{rq,s + 1}}^{{g + 2/3}} = \\ \end{gathered} $

$\begin{gathered} = \left( {{{e}_{{rqs}}}(T_{{rq,s + 1}}^{g} - T_{{rqs}}^{g}) + {{f}_{{rqs}}}(T_{{rq,s - 1}}^{g} - T_{{rqs}}^{g})} \right)p_{{rqs}}^{g} + e_{{rq,s - 1}}^{{}}(T_{{rqs}}^{g} - T_{{rq,s - 1}}^{g})p_{{rq,s - 1}}^{g} + \\ \, + f_{{rq,s + 1}}^{{}}(T_{{rqs}}^{g} - T_{{rq,s + 1}}^{g})p_{{rq,s + 1}}^{g}, \\ \end{gathered} $

$\begin{gathered} {\rm X}_{{rqs}}^{{g + 1/3}} = \sum\limits_{j = 1}^J {\sum\limits_{l = 1}^{L - 1} {\sum\limits_{i = 1}^{I - 1} {\sum\limits_{n = 1}^{N - 1} {\left( {\frac{{\partial \psi _{{nil}}^{j}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{nli}}^{j} + \frac{{\partial \psi _{{nil}}^{{j - 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{nil}}^{{j - 1/3}} + \frac{{\partial \psi _{{nil}}^{{j - 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{nil}}^{{j - 2/3}}} \right)} } } } = \\ \, = \frac{{\partial \psi _{{rq,s - 1}}^{g}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rq,s - 1}}^{g} + \frac{{\partial \psi _{{rqs}}^{g}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rqs}}^{g} + \frac{{\partial \psi _{{rq,s + 1}}^{g}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rq,s + 1}}^{g} + \\ \end{gathered} $

$\begin{gathered} + \;\frac{{\partial \psi _{{rq,s - 1}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rq,s - 1}}^{{g + 1/3}} + \frac{{\partial \psi _{{rqs}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rqs}}^{{g + 1/3}} + \frac{{\partial \psi _{{rq,s + 1}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rq,s + 1}}^{{g + 1/3}} + \\ + \;\frac{{\partial \psi _{{rq,s - 1}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rq,s - 1}}^{{g + 2/3}} + \frac{{\partial \psi _{{rqs}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rqs}}^{{g + 2/3}} + \frac{{\partial \psi _{{rq,s + 1}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 1/3}})}}p_{{rq,s + 1}}^{{g + 2/3}} = \\ \end{gathered} $

$\begin{gathered} = \left( {{{a}_{{rqs}}}(T_{{r + 1,qs}}^{{g + 1/3}} - T_{{rqs}}^{{g + 1/3}}) + {{b}_{{rqs}}}(T_{{r - 1,qs}}^{{g + 1/3}} - T_{{rqs}}^{{g + 1/3}})} \right)p_{{rqs}}^{{g + 1/3}} + a_{{r - 1,qs}}^{{}}(T_{{rqs}}^{{g + 1/3}} - T_{{r - 1,qs}}^{{g + 1/3}})p_{{r - 1,qs}}^{{g + 1/3}} + \\ \, + {{b}_{{r + 1,qs}}}(T_{{rqs}}^{{g + 1/3}} - T_{{r + 1,qs}}^{{g + 1/3}})p_{{r + 1,qs}}^{{g + 1/3}}, \\ \end{gathered} $

$\begin{gathered} {\rm X}_{{rqs}}^{{g + 2/3}} = \sum\limits_{j = 1}^J {\sum\limits_{l = 1}^{L - 1} {\sum\limits_{i = 1}^{I - 1} {\sum\limits_{n = 1}^{N - 1} {\left( {\frac{{\partial \psi _{{nil}}^{j}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{nli}}^{j} + \frac{{\partial \psi _{{nil}}^{{j - 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{nil}}^{{j - 1/3}} + \frac{{\partial \psi _{{nil}}^{{j - 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{nil}}^{{j - 2/3}}} \right)} } } } = \\ \, = \frac{{\partial \psi _{{rq,s - 1}}^{g}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rq,s - 1}}^{g} + \frac{{\partial \psi _{{rqs}}^{g}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rqs}}^{g} + \frac{{\partial \psi _{{rq,s + 1}}^{g}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rq,s + 1}}^{g} + \\ \end{gathered} $

$\begin{gathered} + \;\frac{{\partial \psi _{{rq,s - 1}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rq,s - 1}}^{{g + 1/3}} + \frac{{\partial \psi _{{rqs}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rqs}}^{{g + 1/3}} + \frac{{\partial \psi _{{rq,s + 1}}^{{g + 1/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rq,s + 1}}^{{g + 1/3}} + \\ + \;\frac{{\partial \psi _{{rq,s - 1}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rq,s - 1}}^{{g + 2/3}} + \frac{{\partial \psi _{{rqs}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rqs}}^{{g + 2/3}} + \frac{{\partial \psi _{{rq,s + 1}}^{{g + 2/3}}}}{{\partial K(T_{{rqs}}^{{g + 2/3}})}}p_{{rq,s + 1}}^{{g + 2/3}} = \\ \end{gathered} $

$\begin{gathered} = \left( {{{c}_{{rqs}}}(T_{{r,q + 1,s}}^{{g + 2/3}} - T_{{rqs}}^{{g + 2/3}}) + {{d}_{{rqs}}}(T_{{r,q - 1,s}}^{{g + 2/3}} - T_{{rqs}}^{{g + 2/3}})} \right)p_{{rqs}}^{{g + 2/3}} + c_{{r,q - 1,s}}^{{}}(T_{{rqs}}^{{g + 2/3}} - T_{{r,q - 1,s}}^{{g + 2/3}})p_{{r,q - 1,s}}^{{g + 2/3}} + \\ \, + d_{{r,q + 1,s}}^{{}}(T_{{rqs}}^{{g + 2/3}} - T_{{r,q + 1,s}}^{{g + 2/3}})p_{{r,q + 1,s}}^{{g + 2/3}}. \\ \end{gathered} $

Множители $\frac{{\partial K(T_{{rqs}}^{g})}}{{\partial {{k}_{m}}}}$, присутствующие в формуле (2.6), вычисляются аналогично тому, как показано в работе [17]. Отметим, что значение градиента целевой функции $F({{k}_{0}},{{k}_{1}},...,{{k}_{M}})$, вычисленное по формуле (2.6), является точным для выбранной аппроксимации задачи оптимального управления.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Анализ результатов решения большого числа обратных коэффициентных задач в одномерном и двумерном случаях показал, что эти задачи могут иметь неединственное решение. Будет решение обратной задачи единственным или нет – существенно зависит от заданного экспериментального поля $Y(s,t)$, $s = (x,y,z)$. Ответ на вопрос, в каких случаях возможно появление неединственности решения сформулированной обратной коэффициентной задачи, может дать следующее утверждение.

Утверждение. Пусть функция $Y(s,t) \in C_{{s,t}}^{{2,1}}(G) \cap {{C}^{1}}(\bar {G})$ является решением прямой задачи (1.1)–(1.3) при двух допустимых коэффициентах теплопроводности ${{K}_{1}}(T) \in {{C}^{1}}\left( {[a,b]} \right)$ и ${{K}_{2}}(T) \in {{C}^{1}}\left( {[a,b]} \right)$. Тогда

а) найдется функция $R(T) \in C\left( {[a,b]} \right)$ такая, что ${{\Delta }_{s}}Y(s,t) = R\left( {Y(s,t)} \right) \cdot {{\left| {{{\nabla }_{s}}Y(s,t)} \right|}^{2}}$,

б) при такой функции $Y(s,t)$ решений $K(T)$ обратной задачи бесконечно много.

Доказательство этого утверждения аналогично тому, которое приведено в работе [17] для двумерного случая.

Условия указанного выше утверждения выполняются, например, в том случае, когда экспериментальное поле температур $Y(s,t)$ является достаточно гладкой монотонной функцией линейной комбинации пространственных координат и времени, т.е.

(3.1)

$\Upsilon (s,t) = \Upsilon (x,y,z,t) = f(\alpha x + \beta y + \gamma z + \lambda t),\quad где\quad {{\alpha }^{2}} + {{\beta }^{2}} + {{\gamma }^{2}} > 0.$

Сложности, с которыми приходится сталкиваться при решении задачи идентификации коэффициента теплопроводности в трехмерной постановке, связаны не только с выбором схемы дискретизации прямой задачи и с возможностью появления неединственности решения, но также с выбором расчетной сетки. Анализ полученных численных результатов показал, что если количество узлов пространственной сетки не меньше 20 по каждому направлению, то коэффициент теплопроводности восстанавливается с достаточно высокой точностью при условии, что грамотно выбран временной шаг (так как точность восстановления существенно зависит от выбора шага по времени).

Выбранная в настоящей работе локально-одномерная схема аппроксимации уравнения теплопроводности является устойчивой и позволяет работать с достаточно большим шагом по времени. Тем не менее для каждой используемой пространственной сетки необходимо проводить исследования, касающиеся выбора сетки по времени. Например, как показали расчеты, для пространственной сетки, у которой 25 узлов по каждому направлению (равномерная сетка), количество равных шагов по времени желательно брать не меньше 100. В случае использования более грубых сеток по времени коэффициенты теплопроводности могут восстанавливаться с большой погрешностью.

В приведенных примерах полагалось, что в целевом функционале (1.4) весовая функция $\mu (x,y,z,t) \equiv 1$, $(x,y,z) \in Q$. Минимизация целевой функции $F({{k}_{0}},{{k}_{1}},...,{{k}_{M}})$ проводилась численно с помощью градиентного метода. Отрезок $[a,b]$ разбивался на 80 интервалов, т.е. $M = 80$.

Хочется отметить, что для ускорения итерационного процесса спуска по градиенту во всех представленных здесь примерах использовался подход, предложенный в [17]. Он основан на последовательном увеличении числа $M$ разбиений отрезка $[\,a,b]$. Начинать процесс желательно с $M = 1$. После получения оптимального решения его следует использовать в качестве начального приближения для варианта с $M = 2$. Получив оптимальное решение для $M = 2$, использовать его в качестве начального приближения для $M = 4$, и т.д.

Для проверки работоспособности предложенного алгоритма было решено большое количество тестовых задач. Наиболее характерные из них представлены здесь в виде нескольких серий расчетов. В качестве “экспериментального” поля температур рассматривалось как “аналитическое” поле (аналитическое решение прямой задачи, спроектированное на расчетную сетку), так и “численное” поле, т.е. температурное поле, которое получено в результате численного решения прямой задачи с заданным коэффициентом теплопроводности.

Для оценки точности получаемых численных решений обратной задачи использовались два критерия:

(3.2)

${{\varepsilon }_{1}} = \mathop {\max }\limits_{0 \leqslant m \leqslant M} \frac{{\left| {{{K}_{{{\text{opt}}}}}({{{\tilde {T}}}_{m}}) - K({{{\tilde {T}}}_{m}})} \right|}}{{K{\kern 1pt} *}}$

(3.3)

${{\varepsilon }_{2}} = \frac{1}{{K{\kern 1pt} *}}\sqrt {\sum\limits_{m = 0}^M {\frac{{{{{\left( {{{K}_{{{\text{opt}}}}}({{{\tilde {T}}}_{m}}) - K({{{\tilde {T}}}_{m}})} \right)}}^{2}}}}{{M + 1}}} } ,$

где $K({{\tilde {T}}_{m}})$ – значения аналитического коэффициента теплопроводности, вычисленные в опорных точках отрезка температур, ${{K}_{{{\text{opt}}}}}({{\tilde {T}}_{m}})$ – значения коэффициента теплопроводности, полученного в результате решения оптимизационной задачи, а $K{\kern 1pt} *$ – некоторое характерное значение функции $K(T)$. В работе полагалось, что

$K{\kern 1pt} * = \frac{{\sum\limits_{m = 0}^M {K({{{\tilde {T}}}_{m}})} }}{{M + 1}}.$

Проведенные численные эксперименты показали, что качество восстановления коэффициента теплопроводности сильно зависит от распределения “экспериментального” температурного поля. Бывают случаи, когда на некоторых участках отрезка $[\,a,b]$ слишком мало данных, необходимых для идентификации коэффициента теплопроводности. Поэтому в каждом конкретном случае необходимо проанализировать распределение экспериментальных данных по интервалам интересующего нас отрезка температур.

3.1. Первая серия расчетов

В первой серии расчетов рассматривалась задача нахождения коэффициента теплопроводности вещества при следующих входных данных: в качестве начальной функции ${{w}_{0}}(x,y,z)$ и граничной функции ${{w}_{\Gamma }}(x,y,z,t)$ выбирались следы функции

(3.4)

$\Lambda (x,y,z,t) = x + y + z + \;3t + 0.5$

на параболической границе области $Q \times (0,\Theta ) = (0,1) \times (0,1) \times (0,1) \times (0,1)\,$. В этом случае функция (3.4) является решением смешанной задачи (1.1)–(1.3) при $C(s) = 1$ и $K(T) = T$. Температура на параболической границе рассматриваемой области изменяется от $a = {\text{0}}{\text{.5}}$ до $b = 6.{\text{5}}$.

Этот пример – простейший из всех рассмотренных. Целью первой серии расчетов являлась не только проверка работоспособности предложенного алгоритма, но и проверка корректности созданных машинных кодов, реализующих этот алгоритм. Если в качестве “экспериментального” поля температур использовалось “аналитическое” поле, то

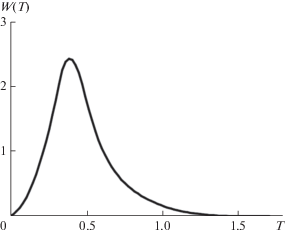
$\begin{gathered} Y_{{nil}}^{j} = \Lambda ({{x}_{n}},{{y}_{i}},{{z}_{{l,}}}{{t}^{j}}) = {{x}_{n}} + {{y}_{i}} + {{z}_{l}} + 3{{t}^{j}} + 0.5, \\ n = \overline {1,N - 1,} \quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} ,\quad j = \overline {1,J} . \\ \end{gathered} $

В качестве “численного экспериментального” поля выбиралось численное решение задачи (1.1)–(1.3) с указанными в этом примере входными данными и с $K(T) = T.$

Для анализа распределения экспериментальных данных по интервалам интересующего нас отрезка температур введем функцию ${{W}_{*}}(T)$ – относительную меру той подобласти области $Q \times (0,\Theta )$, в которой функция $\Lambda (x,y,z,t)$ удовлетворяет условию $\Lambda (x,y,z,t) < T$, а через $W(T)$ обозначим плотность распределения (производную) функции ${{W}_{*}}(T)$ по переменной $T$. На фиг. 1 представлено распределение функции $W(T)$ вдоль отрезка $[0.5,6.5]$.

Фиг. 1

Поведение этого распределения указывает на то, что могут возникнуть трудности с восстановлением коэффициента теплопроводности на концах отрезка $[0.5,6.5]$. Преодолевать эти трудности помогает подход (см. [17]), основанный на последовательном увеличении числа $M$ разбиений рассматриваемого отрезка.

Как нетрудно заметить, функция (3.4) имеет вид (3.1). Следовательно, обратная коэффициентная задача в этом случае может иметь неединственное решение, и все ее решения будут отличаться на константу, т.е. ${{K}_{{{\text{opt}}}}}(T) = T + {\text{Const}}$, где ${{K}_{{{\text{opt}}}}}(T)$ – решение оптимизационной задачи.

Рассматриваемая задача идентификации коэффициента теплопроводности решалась численно несколько раз, при этом в качестве начального приближения ${{K}_{{{\text{ini}}}}}(T)$ выбиралась новая функция. Также использовалось несколько расчетных сеток.

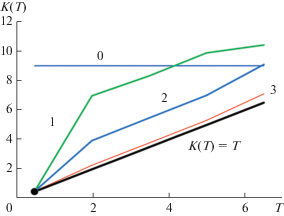
На фиг. 2 линия, помеченная как “$K(T) = T$”, представляет ожидаемое аналитическое решение поставленной задачи. Линии, отмеченные как “opt_1”, “opt_2” и “opt_3”, соответствуют разным решениям задачи оптимального управления. Они получены от начальных приближений ${{K}_{{{\text{ini}}}}}(T) = 9.0$, ${{K}_{{{\text{ini}}}}}(T) = 7.0$ и ${{K}_{{{\text{ini}}}}}(T) = 4.5$ соответственно. Приведенные результаты подтверждают правильность вывода о том, что решение задачи идентификации коэффициента теплопроводности в данном случае является неединственным.

Фиг. 2

Для выделения единственного решения сформулированной задачи оптимального управления предлагается дополнительно задавать точку ${{T}_{*}}$, в которой искомый коэффициент теплопроводности известен, т.е. ${{K}_{*}} = K({{T}_{*}})$. Многочисленные расчеты показали, что если на каждом шаге процесса минимизации целевого функционала приближенная функция $K(T)$ проходит через заданную точку $({{T}_{*}},{{K}_{*}})$, то решение обратной задачи будет единственным. На фиг. 3 проиллюстрировано, как в процессе минимизации функционала приближенные решения обратной задачи сходятся к точному решению $K(T) = T$. Здесь линия, отмеченная цифрой 0, соответствует начальному приближению ${{K}_{{{\text{ini}}}}}(T) = 9.0$ (оно не проходит через заданную точку). Далее приближения к решению задачи идентификации представлены через несколько итераций и отмечены возрастающими цифрами. Точка, помеченная кружком и имеющая координаты $({{T}_{*}},{{T}_{*}})$, принадлежит всем приближенным решениям.

Фиг. 3

Коэффициент теплопроводности идентифицировался с машинной точностью как в случае использования “аналитического” поля, так и в случае использования “численного” поля в функционале. Например, когда использовалось “аналитическое” поле и задача решалась на равномерной пространственной сетке с параметрами $N = 25$, $I = 25$, $L = 25$ (количество интервалов вдоль оси $x$, $y$ и $z$ соответственно) при $J = 100$ (количество интервалов вдоль оси $t$), значение целевого функционала изменилось от ${\text{8}}{\text{.6332}} \times {{10}^{{ - 5}}}$ на начальном приближении (${{K}_{{{\text{ini}}}}}(T) = 9.0$) к коэффициенту теплопроводности до ${\text{5}}{\text{.9142}} \times {{10}^{{ - 29}}}$ на финальном (оптимальном) приближении. Максимум модуля градиента целевого функционала изменился при этом от ${\text{4}}{\text{.0427}} \times {{10}^{{ - 6}}}$ до ${\text{2}}{\text{.4148}} \times {{10}^{{ - 18}}}$. Максимальное относительное отклонение полученного коэффициента теплопроводности от его аналитического значения $K(T) = T$ не превосходит ${\text{5}}{\text{.0981}} \times {{10}^{{ - 13}}}$.

3.2. Вторая серия расчетов

Во второй серии расчетов рассматривалась задача нахождения коэффициента теплопроводности при следующих входных данных: в качестве начальной функции ${{w}_{0}}(x,y,z)$ и граничной функции ${{w}_{\Gamma }}(x,y,z,t)$ выбирались следы функции

(3.5)

$\Lambda (x,y,z,t) = \sqrt {\frac{{{{x}^{2}} + {{y}^{2}} + {{z}^{2}}}}{{9 - 8t}}} $

на параболической границе области $Q \times (0,\Theta ) = (0,1) \times (0,1) \times (0,1) \times (0,1)\,$. Функция (3.5) является в этом случае решением смешанной задачи (1.1)–(1.3) при $C(s) = 1$ и $K(T) = {{T}^{2}}$. Температура на параболической границе рассматриваемой области изменяется от $a = {\text{0}}{\text{.0}}$ до $b = 1.{\text{732}}$.

Распределение экспериментальных данных вдоль отрезка температур $[0.0,\;1.732]$ представлено на фиг. 4 в виде зависимости функции $W(T)$ от температуры. Анализ этого распределения показывает, что правому концу отрезка $[0.0,\;1.732]$ соответствует слишком мало “экспериментальных” данных. Поэтому можно предположить, что там возникнут трудности с восстановлением коэффициента теплопроводности. Проведенные расчеты подтвердили это предположение: при равномерном разбиении отрезка температур на $M = 80$ интервалов последние две компоненты вектора управления не изменяются (там компоненты градиента равны нулю с машинной точностью).

Фиг. 4

Вариационная задача, к которой сводится задача идентификации коэффициента теплопроводности, для всех примеров решалась на нескольких расчетных сетках. Для каждой сетки расчеты были выполнены с использованием разных начальных приближений ${{K}_{{{\text{ini}}}}}(T)$.

Все проведенные расчеты второй серии можно разделить на две группы. В расчетах первой группы в качестве “экспериментального” поля температур использовалось “аналитическое” поле:

$Y_{{nil}}^{j} = \Lambda ({{x}_{n}},{{y}_{i}},{{z}_{{l,}}}{{t}^{j}}) = \sqrt {\frac{{x_{n}^{2} + y_{i}^{2} + z_{l}^{2}}}{{9 - 8{{t}^{j}}}}} ,\quad n = \overline {1,N - 1,} \quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} ,\quad j = \overline {1,J} .$

Расчеты этой группы выявили зависимость численного решения обратной задачи от точности решения прямой задачи. Все представленные ниже результаты расчетов первой группы получены при использовании равномерной пространственной сетки с параметрами $N = I = L = 25$. Количество $J$ интервалов разбиения отрезка $[0,\Theta ]$ по времени менялось.

1. Использовалась равномерная сетка по времени с количеством интервалов $J = 50$.

На фиг. 5а приведены начальное управление (Ini), функция $K(T) = {{T}^{2}}$ и оптимальные управления, полученные при $M = 1$, $M = 2$ и $M = 4$. Видно, что опорные точки кусочно-линейного оптимального управления, полученного при $M = 4$, почти лежат на линии $K(T) = {{T}^{2}}$.

Фиг. 5

Что касается оптимального управления, полученного при $M = 8$, то оно практически совпадает с функцией $K(T) = {{T}^{2}}$ (${{\varepsilon }_{1}} = {\text{6}}{\text{.7845}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{2}}}}}$ и ${{\varepsilon }_{2}} = {\text{3}}{\text{.8748}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{2}}}}}$).

Однако дальнейшее разбиение отрезка температур на более мелкие интервалы не приводит к желаемым результатам на выбранной пространственно-временной сетке. На фиг. 5б приведены функция $K(T) = {{T}^{2}}$ и оптимальное управление, полученные для $M = 80$. Видно, что в полученном решении присутствуют осцилляции. По-видимому, это связано с тем, что на используемой расчетной сетке решение прямой задачи определяется недостаточно точно. Использование небольшого количества разбиений (например, $M = 4$ или $M = 8$) отрезка температур в этом случае действует как сглаживающий фактор при решении задачи.

2. Использовалась равномерная сетка по времени с количеством интервалов $J = 100$.

Здесь в качестве начального приближения было выбрано управление ${{K}_{{{\text{ini}}}}}(T) \equiv 5.0$. В результате решения обратной задачи при $M = 80$ было получено гладкое решение, график которого практически совпадает с графиком функции $K(T) = T$. Небольшое отклонение от аналитического решения заметно лишь на правом конце, там, где, как показывает фиг. 4, намного меньше “экспериментальных” данных, чем на остальных подинтервалах температур.

В процессе решения оптимизационной задачи целевой функционал изменился от ${\text{7}}{\text{.8204}} \times {{10}^{{ - 4}}}$ до ${\text{1}}{\text{.4955}} \times {{10}^{{ - 7}}}$, максимум модуля градиента уменьшился от ${\text{1}}{\text{.4016}} \times {{10}^{{ - 5}}}$ до ${\text{8}}{\text{.2485}} \times {{10}^{{ - 10}}}$. Вычисленные по формулам (3.2) и (3.3) отклонения полученного коэффициента теплопроводности ${{K}_{{{\text{opt}}}}}(T)$ от его аналитического значения $K(T) = {{T}^{2}}$ составляют ${{\varepsilon }_{1}} = {\text{7}}{\text{.1707}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{2}}}}}$ и ${{\varepsilon }_{2}} = {\text{2}}{\text{.0082}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{2}}}}}$ соответственно.

3. Использовалась равномерная сетка по времени с количеством интервалов $J = 1000$.

Уменьшение временного шага в десять раз привело к тому, что точность идентификации коэффициента теплопроводности для разбиения отрезка температур на $M = 80$ частей улучшилась почти на два порядка по сравнению с предыдущим случаем. Целевой функционал упал до ${\text{1}}{\text{.9220}} \times {{10}^{{ - 9}}}$, максимум модуля градиента уменьшился до ${\text{1}}{\text{.6834}} \times {{10}^{{ - 10}}}$. Вычисленные по формулам (3.2) и (3.3) отклонения полученного коэффициента теплопроводности ${{K}_{{{\text{opt}}}}}(T)$ от его аналитического значения $K(T) = {{T}^{2}}$ составляют ${{\varepsilon }_{1}} = {\text{1}}{\text{.6252}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{3}}}}}$ и ${{\varepsilon }_{2}} = {\text{8}}{\text{.4366}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{4}}}}}$ соответственно. Графики функции ${{K}_{{{\text{opt}}}}}(T)$ и $K(T) = {{T}^{2}}$ полностью совпадают.

Следует также отметить, что для рассматриваемого примера мы не наблюдали неединственности решения обратной задачи. Расчеты, выполненные при разных начальных приближениях ${{K}_{{{\text{ini}}}}}(T)$, всегда приводили к одному и тому же решению.

В расчетах второй группы в качестве “экспериментального” температурного поля использовалось поле, полученное в результате численного решения задачи (1.1)–(1.3) с известным коэффициентом теплопроводности $K(T) = {{T}^{2}}$.

Для всех проведенных расчетов в данном случае коэффициент теплопроводности идентифицировался с высокой точностью. Даже при использовании равномерной пространственной сетки с параметрами $N = I = L = 25$ и количеством интервалов по времени $J = 25$ при $M = 80$ коэффициент теплопроводности восстанавливался без осцилляций и график полученной функции полностью накладывался на график функции $K(T) = {{T}^{2}}$ (см. п. 1 второй серии расчетов). Если же решать задачу при $N = I = L = 25$ и $J = 100$, то получаемые результаты превосходят результаты, описанные в п. 2 второй серии расчетов и полученные при $J = 1000$. Действительно, целевой функционал упал до ${\text{1}}.0894 \times {{10}^{{ - 16}}}$, максимум модуля градиента уменьшился до ${\text{7}}.7676 \times {{10}^{{ - 13}}}$, а для отклонений решения от теоретического получены оценки ${{\varepsilon }_{1}} = {\text{9}}.9378 \times {\text{1}}{{{\text{0}}}^{{ - {\text{5}}}}}$ и ${{\varepsilon }_{2}} = {\text{2}}.9106 \times {\text{1}}{{{\text{0}}}^{{ - {\text{5}}}}}$.

3.3. Третья серия расчетов

В третьей серии расчетов рассматривалась задача нахождения коэффициента теплопроводности при следующих входных данных: в качестве начальной функции ${{w}_{0}}(x,y,z)$ и граничной функции ${{w}_{\Gamma }}(x,y,z,t)$ выбирались следы функции

(3.6)

$\Lambda (x,y,z,t) = \frac{3}{{1.8{\kern 1pt} (5 - x - y - z - 1.8t)}}$

на параболической границе области $Q \times (0,\Theta ) = (0,1) \times (0,1) \times (0,1) \times (0,1)\,$. Функция (3.6) является решением смешанной задачи (1.1)–(1.3) при $C(s) = 1$ и $K(T) = \frac{1}{T}$. Температура на параболической границе рассматриваемой области изменяется от $a = {\text{0}}{\text{.33}}$ до $b = 8.{\text{33}}$.

На фиг. 6а представлено распределение экспериментальных данных по отрезку температур $[0.33,\;8.33]$ (функция $W(T)$), а на фиг. 6б – фрагмент фигуры 6а, который крупным планом показывает поведение функции $W(T)$ на правом конце отрезка. Анализируя представленные на этих фигурах графики, нетрудно увидеть, что на правом конце отрезка $[0.33,\;8.33]$ практически нет “экспериментальных” данных. Как показали проведенные расчеты этой серии, коэффициент теплопроводности на подотрезке $[6.0,\;8.33]$ не восстанавливается. При разбиении отрезка температур на $M = 80$ интервалов последние 23 компоненты градиента функционала всегда оказываются нулевыми (с машинной точностью). На этом участке коэффициент теплопроводности сохраняет определенный след выбранного начального приближения.

Фиг. 6

Кроме того, в этой серии расчетов мы опять сталкиваемся с неединственностью решения обратной задачи. Неединственность решения обусловлена экспериментальным полем

$\Lambda (x,y,z,t) = \frac{3}{{1.8{\kern 1pt} (5 - x - y - z - 1.8t)}},$

которое является функцией линейной комбинации пространственных координат и времени, т.е. имеет вид (3.1). Решения обратной коэффициентной задачи содержатся в семействе функций

${{K}_{{{\text{opt}}}}}(T) = \frac{1}{T} + \frac{{{\text{Const}}}}{{{{T}^{2}}}}.$

Для выделения единственного решения из этого семейства необходимо дополнительно задавать точку ${{T}_{*}}$, в которой искомый коэффициент теплопроводности известен.

В расчетах первой группы этой серии в качестве “экспериментального” поля температур рассматривалось “аналитическое” поле:

$\begin{gathered} Y_{{nil}}^{j} = T({{x}_{n}},{{y}_{i}},{{z}_{{l,}}}{{t}^{j}}) = \frac{3}{{1.8{\kern 1pt} (5 - {{x}_{n}} - {{y}_{i}} - {{z}_{l}} - 1.8{{t}^{j}})}}, \\ (n = \overline {1,N - 1,} \quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} ,\quad j = \overline {1,J} ). \\ \end{gathered} $

Задача оптимизации, к которой сводится рассматриваемая обратная коэффициентная задача, решалась при разных начальных приближениях ${{K}_{{{\text{ini}}}}}(T)$.

Первый расчет этой группы проводился без выделения и удержания какой-нибудь точки $\left( {{{T}_{*}},K({{T}_{*}})} \right)$. Использовалась равномерная пространственная сетка с параметрами $N = I = L = 25$ и количеством интервалов по времени $J = 100$. Отрезок $[0.33,\;8.33]$ разбивался на $M = 1,\,2,\,4\,,\,...\,,\,64$, и $M = 80$ подотрезков и для каждого разбиения решалась обратная задача. При росте числа $M$ наблюдалась сходимость численных решений обратной задачи к некоторой предельной функции, причем численные решения, полученные при $M = 32$ и $M = 80$ (оптимальное управление), практически не отличаются.

В качестве иллюстрации сказанного на фиг. 7 приведены функция $K(T) = \frac{1}{T}$, начальное управление – функция ${{K}_{{{\text{ini}}}}}(T) \equiv 2.5$, численные решения обратной задачи, полученное при $M = 8$ и $M = 80$. Видно, что на отрезке $[6.0,\;8.33]$ сохранился след выбранного начального приближения (здесь компоненты градиента практически нулевые). Наблюдаемое отличие оптимального управления от функции $K(T) = \frac{1}{T}$ в окрестности левого конца отрезка $[0.33,\;8.33]$ говорит о том, что получено некоторое решение обратной задачи из семейства

${{K}_{{{\text{opt}}}}}(T) = \frac{1}{T} + \frac{{{\text{Const}}}}{{{{T}^{2}}}}\quad {\text{с}}\quad {\text{Const}} \ne 0.$

Фиг. 7

Для получения ожидаемого аналитического решения $K(T) = \frac{1}{T}$ поставленной обратной задачи дополнительно зададим точку ${{T}_{*}}$, в которой искомый коэффициент теплопроводности известен, т.е. ${{K}_{*}} = K({{T}_{*}})$, и будем держать ее на каждом шаге процесса минимизации целевого функционала. В качестве такой точки была выбрана точка $\left( {0.33,\;1{\text{/}}0.33} \right)$.

На фиг. 8 приведены начальное управление (ini), функция $K(T) = \frac{1}{T}$ и оптимальные управления, полученные при $M = 8$ и $M = 16$. В этом расчете, как и в предыдущем, сохранился след выбранного начального приближения. Оптимальное управление ${{K}_{{{\text{opt}}}}}(T)$, полученное при разбиении отрезка температур на $M = 80$ интервалов, на фигуре не представлено, так как полностью совпадает с графиком функции $K(T) = \frac{1}{T}$ в точках, не принадлежащих указанному следу. Точка, помеченная кружком и имеющая координаты $\left( {{{T}_{*}},\frac{1}{{{{T}_{*}}}}} \right)$, принадлежит всем приближенным решениям. Следует также отметить, что коэффициент теплопроводности, полученный при $M = 16$, достаточно хорошо аппроксимирует теоретический коэффициент $K(T) = \frac{1}{T}$.

Фиг. 8

Если же в качестве начального приближения ${{K}_{{{\text{ini}}}}}(T)$ выбрать функцию, которая кроме левого конца отрезка температур проходит и через правый конец $T = 8.33$, то коэффициент теплопроводности $K(T) = \frac{1}{T}$ будет восстанавливаться на всем отрезке $[0.33,\;8.33]$. На фиг. 9 приведены начальное управление (ini), функция $K(T) = \frac{1}{T}$ и оптимальные управления, полученные при $M = 8$ и $M = 16$. Оптимальное управление ${{K}_{{{\text{opt}}}}}(T)$, полученное при разбиении отрезка температур на $M = 80$ интервалов, полностью совпадает с графиком функции $K(T) = \frac{1}{T}$. Точка, помеченная кружком и имеющая координаты $\left( {{{T}_{*}},\frac{1}{{{{T}_{*}}}}} \right)$, принадлежит всем приближенным решениям.

Фиг. 9

Что касается решения ${{K}_{{{\text{opt}}}}}(T)$, то здесь целевой функционал изменился от ${\text{7}}{\text{.7560}} \times {{10}^{{ - 5}}}$ до ${\text{8}}{\text{.9622}} \times {{10}^{{ - 10}}}$, максимум модуля градиента уменьшился от ${\text{8}}{\text{.6070}} \times {{10}^{{ - 5}}}$ до ${\text{3}}{\text{.1018}} \times {{10}^{{ - 12}}}$. Отклонения полученного коэффициента теплопроводности ${{K}_{{{\text{opt}}}}}(T)$ от его аналитического значения $K(T) = \frac{1}{T}$ составляют ${{\varepsilon }_{1}} = 9.3191 \times {\text{1}}{{{\text{0}}}^{{ - {\text{3}}}}}$ и ${{\varepsilon }_{2}} = 4.1455 \times {\text{1}}{{{\text{0}}}^{{ - {\text{3}}}}}$ соответственно.

В расчетах второй группы третьей серии в качестве “экспериментального” температурного поля рассматривалось численное решение задачи (1.1)–(1.3) с известным коэффициентом теплопроводности $K(T) = \frac{1}{T}$. Как и в предыдущем примере, для выделения единственного решения сформулированной задачи оптимального управления задавалась точка $\left( {{{T}_{*}},\frac{1}{{{{T}_{*}}}}} \right)$. Коэффициент теплопроводности идентифицировался в этом случае с высокой точностью. Так, целевой функционал на оптимальном решении упал до ${\text{2}}{\text{.2822}} \times {{10}^{{ - 17}}}$, максимум модуля градиента уменьшился до ${\text{7}}{\text{.3707}} \times {{10}^{{ - 13}}}$. Отклонения полученного коэффициента теплопроводности ${{K}_{{{\text{opt}}}}}(T)$ от его аналитического значения $K(T) = \frac{1}{T}$ составляют ${{\varepsilon }_{1}} = {\text{1}}{\text{.2985}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{3}}}}}$ и ${{\varepsilon }_{2}} = {\text{2}}{\text{.1873}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{4}}}}}$ соответственно.

Как показали многочисленные проведенные расчеты, предложенный алгоритм продемонстрировал свою устойчивость: небольшие отклонения в экспериментальных данных (~10%) приводят к погрешностям в решении того же порядка (~2–5%). При бóльших отклонениях в экспериментальных данных для получения устойчивого решения необходимо вводить регуляризатор.

ЗАКЛЮЧЕНИЕ

Проведенные исследования показали, что трехмерная задача идентификации коэффициента теплопроводности вещества существенно сложнее подобных задач в одномерном и двумерном случаях. Во-первых, решение трехмерных обратных задач требует огромных затрат ресурсов компьютера. Это приводит к необходимости проведения предварительных исследований, связанных с выбором эффективных разностных схем, аппроксимирующих рассматриваемую прямую задачу. Во-вторых, в трехмерном случае большое влияние оказывают те значения температуры, которые при решении прямой задачи достигаются на множестве малой меры. Коэффициент теплопроводности для таких значений температуры не идентифицируется регулярным способом. Поэтому для его определения в таких точках требуется проведение дополнительных исследований или введение дополнительных предположений.

Список литературы

Коздоба Л.А., Круковский П.Г. Методы решения обратных задач теплопереноса. Киев: Наук. Думка, 1982.
Алифанов О.М. Обратные задачи теплообмена. М.: Машиностр., 1988.
Вабищевич П.Н., Денисенко А.Ю. Численные методы решения коэффициентных обратных задач // Методы матем. моделирования и вычисл. диагностики. М.: Изд-во МГУ, 1990. С. 35–45.
Самарский А.А., Вабищевич П.Н. Разностные методы решения обратных задач математической физики // Фундаментальные основы матем. моделирования. М.: Наука, 1997. С. 5–97.
Марчук Г.И. Сопряженные уравнения и анализ сложных систем. М.: Наука, 1992.
Balazs Czel, Gyula Grof. Inverse identification of temperature-dependent thermal conductivity via genetic algorithm with cost function-based rearrangement of genes// Internat. Journal of Heat and Mass Transfer. 2012. V. 55. № 15. P. 4254–4263.
Miao Cui, Kai Yang, Xiao-liang Xu, Sheng-dong Wang, Xiao-wei Gao. A modified Levenberg-Marquardt algorithm for simultaneous estimation of multi-parameters of boundary heat flux by solving transient nonlinear inverse heat conduction problems// Internat. Journal of Heat and Mass Transfer.2016. V. 97. P. 908–916 .
Matsevityi Yu.M., Alekhina S.V., Borukhov V.T., Zayats G.M., Kostikova A.O. Identification of the thermal conductivity coefficient for quasi-stationary two-dimensional heat conduction equations// J. of Engineering Physics and Thermophysics. 2017. V. 90. № 6. P. 1295–1301.
Евтушенко Ю.Г. Оптимизация и быстрое автоматическое дифференцирование. М.: ВЦ им. А.А. Дородницына РАН, 2013. 144 с.
Албу А.Ф., Евтушенко Ю.Г., Зубов В.И. О выборе разностных схем при решении обратных коэффициентных задач // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 10. С. 1643–1655.
Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Едиториал УРСС, 2003.
Douglas J., Rachford H.H. On the numerical solution of heat conduction problems in two and three space variables // Trans. Amer. Math. Soc. 1956. V. 82. P. 421–439.
Peaceman D.W., Rachford H.H. The Numerical Solution of Parabolic and Elliptic Differential Equations // J. of the Society for Industrial and Appl. Math. 1955. V. 3. № 1. P. 28–41.
Gao Ch., Wang Y. A general formulation of Peaceman and Rachford ADI method for the N-dimensional heat diffusion equation // Int. Comm. Heat Mass Transfer1996. V. 23. № 6. P. 845–854.
Албу А.В., Зубов В.И. Опыт использования методологии Быстрого Автоматического Дифференцирования для решения обратных коэффициентных задач // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 1. С. 18–28.
Самарский А.А. Теория разностных схем. М.: Наука, 1977.
Албу A.Ф., Зубов В.И. О восстановлении коэффициента теплопроводности вещества по температурному полю // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 10. С. 1642–1657.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал