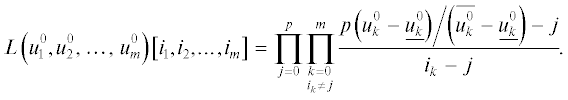1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 9, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1416-1430

Алгоритм адаптивной интерполяции с использованием tt-разложения для моделирования динамических систем с интервальными параметрами

В. Ю. Гидаспов 1, *, А. Ю. Морозов 1, 2, **, Д. Л. Ревизников 1, 2, ***

1 ФГБОУ ВО МАИ
125993 Москва, Волоколамское ш., 4, Россия

2 ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, к. 2, Россия

* E-mail: gidaspov@mai.ru
** E-mail: morozov@infway.ru
*** E-mail: reviznikov@mai.ru

Поступила в редакцию 03.12.2019
После доработки 19.03.2020
Принята к публикации 12.05.2021

Полный текст (PDF)

Аннотация

Задачи с неточно заданными данными возникают во многих практических областях и часто формулируются как задачи анализа динамических систем с интервальными параметрами. Для таких систем необходимо уметь получать интервальную оценку решения по интервальным значениям параметров. Основная идея алгоритма адаптивной интерполяции заключается в построении над множеством, образованным интервальными начальными условиями и параметрами задачи, адаптивной иерархической сетки на основе kd-дерева, в которой каждая ячейка содержит в себе интерполяционную сетку. Для каждого момента времени в зависимости от особенностей решения выполняется адаптивное перестроение разбиения. Результатом работы алгоритма на каждом шаге является кусочно-полиномиальная функция, которая интерполирует зависимость решения задачи от значений параметров с заданной точностью. С ростом числа интервальных параметров количество узлов, содержащихся в интерполяционной сетке, возрастает экспоненциально, что ограничивает область применения алгоритма. Для улучшения этой ситуации в работе предлагается использовать вместо многомерных массивов, в которых хранятся значения узлов интерполяционных сеток, их TT-разложение. На модельных задачах продемонстрирована эффективность данной модификации алгоритма. Выполнено моделирование горения водородно-кислородной смеси при наличии неопределенностей в константах скоростей химических реакций. Библ. 24. Фиг. 10. Табл. 4.

Ключевые слова: алгоритм адаптивной интерполяции, интервальные ОДУ, kd-дерево, тензорный поезд, TT-разложение, химическая кинетика.

ВВЕДЕНИЕ

Задачи с неточно заданными данными возникают во многих практических областях и обычно формулируются в виде динамических систем с интервальными параметрами [1], [2]. Для таких систем необходимо уметь получать интервальную оценку решения по интервальным значениям параметров. Традиционно подобные задачи формулируются в виде задачи Коши для системы обыкновенных дифференциальных уравнений (ОДУ) с интервальными начальными условиями или параметрами.

Зачастую сложность существующих методов является экспоненциальной относительно количества интервальных начальных условий или параметров, поэтому есть необходимость в эффективных способах уменьшения так называемого проклятия размерности.

Существуют подходы [3]–[8], позволяющие уменьшить вычислительную сложность задач за счет выявления скрытых структур и устранения избыточности. В работе рассматриваются вопросы ускорения алгоритма адаптивной интерполяции [9]–[12] с помощью применения ТТ-разложения [7]. Суть алгоритма адаптивной интерполяции заключается в построении динамической структурированной сетки на основе kd-дерева над множеством, образованным интервальными параметрами задачи. Каждая вершина дерева представляет собой регулярную интерполяционную сетку, соответствующую заданной степени интерполяционного многочлена. С каждым узлом сетки сопоставляется решение, найденное при параметрах, определяемых положением узла в пространстве. В процессе выполнения алгоритма на каждом шаге интегрирования исходной системы ОДУ строится кусочно-полиномиальная функция, которая интерполирует зависимость решения задачи от конкретных значений интервальных параметров.

В каждой вершине дерева хранится многомерный массив. В соответствии с используемой в работах [7], [8] терминологией далее под тензором будем подразумевать многомерный массив. Количество элементов в тензоре зависит от количества интервальных параметров как ${{(p + 1)}^{d}}$, где $p$ – степень интерполяционного полинома по каждому измерению, а $d$ – количество интервальных параметров задачи. Основная идея практического улучшения этой ситуации заключается в нахождении TT-разложения, которое можно построить с помощью алгоритма TT-cross [8], не вычисляя всех элементов тензора. Отметим, что ранее в работах [13], [14] разложение в тензорный поезд успешно применялось к приближению параметрических уравнений.

Важным свойством ТТ-разложения является то, что все арифметические (и не только) операции над тензорами можно выполнять в этом представлении. В процессе работы алгоритма над вершинами производятся следующие операции: интерполяция по сетке и разбиение вершины на две. В первом случае для каждой точки, в которой необходимо рассчитать приближенное значение, строится тензор, состоящий из значений базисных полиномов Лагранжа, в ТТ-формате. Далее полученный тензор поэлементно умножается на тензор, хранящийся в вершине, и в конце вычисляется сумма всех элементов. Во втором случае при разбиении вершины требуется применить одномерную интерполяцию по конкретному измерению, чтобы построить недостающие значения в узлах новых вершин. Данное действие тоже может быть представлено в виде композиций нескольких операций, доступных в TT-формате.

С использованием модифицированного алгоритма адаптивной интерполяции выполнено моделирование движения тел под действием гравитационных сил в условиях неопределенности начальных скоростей тел, а также моделирование горения водородно-кислородной смеси при наличии неопределенностей в константах скоростей химических реакций. Вторая задача имеет большую практическую значимость, так как кинетические механизмы, полученные разными исследователями, могут существенно различаться и при этом содержать сотни реакций.

Зачастую зависимость решения от параметров может быть вырожденной (например, большая часть смешанных производных тождественно равна нулю), при этом хранение всего тензора в чистом виде является нецелесообразным и избыточным. Использование ТТ-разложения в алгоритме адаптивной интерполяции позволяет расширить область его применения на случай большого числа интервальных параметров.

1. ТЕНЗОРНЫЙ ПОЕЗД

В основе подходов к уменьшению проклятия размерности лежит предположение о том, что исходные данные избыточны и могут быть представлены в более сжатом виде. Для матриц вопрос о компактном представлении является достаточно изученным и разработанным: существуют эффективные методы и алгоритмы [3]–[6]. Например, можно построить сингулярное разложение матрицы и столбцы и строки, соответствующие несущественным сингулярным числам, отбросить.

В случае большего количества измерений необходимо работать с многомерными массивами, с тензорами. Общая идея эффективного представления этих объектов основывается на разделении переменных. Существует несколько подходов: каноническое разложение [15], разложение Такера [16] и TT-разложение [7], [8] (tensor train, тензорный поезд). Для канонического разложения не существует надежных алгоритмов, а разложение Такера сложно применимо для большого числа измерений. ТТ-разложение появилось сравнительно недавно, и отличительной его особенностью является неподверженность проклятию размерности.

Пусть дан $n$-мерный тензор

$A \in {{\mathbb{R}}^{{{{p}_{1}} \times {{p}_{2}} \times ... \times {{p}_{n}}}}}.$
Его ТТ-разложение записывается следующим образом:
$\hat {A}({{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{n}}) = {{G}_{1}}({{i}_{1}}){{G}_{2}}({{i}_{2}})\; \ldots \;{{G}_{n}}({{i}_{n}}),$
где
${{G}_{k}} \in {{\mathbb{R}}^{{{{p}_{k}} \times {{r}_{{k - 1}}} \times {{r}_{k}}}}},\quad {{i}_{k}} = \overline {1,{{p}_{k}}} ,\quad k = \overline {1,n} ,\quad {{r}_{0}} = {{r}_{n}} = 1.$
Это есть произведение $n - 2$ трехмерных и 2 двухмерных тензоров (фиг. 1). Для вычисления значения конкретного элемента выполняется перемножение соответствующих матриц.

Фиг. 1.

Иллюстрация TT-разложения.

Построение TT-разложения сводится к обычным матричным разложениям. Выполняется переход от $n$ измерений к двум с помощью группировки индексов. Для матрицы вычисляется SVD-разложение. Строки и столбцы, соответствующие несущественным сингулярным числам, отбрасываются. Полученные матрицы превращаются обратно в тензоры меньшей размерности, для которых рекурсивно применяется алгоритм. Идея алгоритма TT-cross, позволяющего построить TT-разложение, не вычисляя всех элементов тензора, заключается в замене SVD-разложения на разложение с меньшей вычислительной стоимостью и не требующего полного знания всех элементов тензора [8].

2. АЛГОРИТМ АДАПТИВНОЙ ИНТЕРПОЛЯЦИИ

Рассматривается задача Коши с $m$ интервальными начальными условиями:

(1)
$\begin{gathered} \frac{{d{{u}_{i}}(t)}}{{dt}} = {{f}_{i}}({{u}_{1}}(t),{{u}_{2}}(t),\; \ldots ,\;{{u}_{n}}(t)),\quad i = \overline {1,n} , \\ {{u}_{i}}({{t}_{0}}) \in \left[ {\underline {u_{i}^{0}} ,\overline {u_{i}^{0}} } \right],\quad i = \overline {1,m} , \\ {{u}_{i}}({{t}_{0}}) = u_{i}^{0},\quad i = \overline {m + 1,n} , \\ t \in \left[ {{{t}_{0}},{{t}_{N}}} \right]. \\ \end{gathered} $

Если система ОДУ – не автономная или содержит параметры, то в систему добавляются фиктивные уравнения так, чтобы она приняла вид (1). Вектор-функция ${\mathbf{f}} = {{\left( {{{f}_{1}},{{f}_{2}},\; \ldots ,\;{{f}_{n}}} \right)}^{т}}$ удовлетворяет всем условиям, обеспечивающим единственность и существование решения при всех ${{u}_{1}}({{t}_{0}}) \in \left[ {\underline {u_{1}^{0}} ,\overline {u_{1}^{0}} } \right]$, ${{u}_{2}}({{t}_{0}}) \in \left[ {\underline {u_{2}^{0}} ,\overline {u_{2}^{0}} } \right]$, …, ${{u}_{m}}({{t}_{0}}) \in \left[ {\underline {u_{m}^{0}} ,\overline {u_{m}^{0}} } \right]$.

Цель алгоритма – для каждого момента времени ${{t}_{k}}$ построить кусочно-полиномиальную вектор-функцию ${{{\mathbf{P}}}^{k}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)$, где $u_{1}^{0} \in \left[ {\underline {u_{1}^{0}} ,\overline {u_{1}^{0}} } \right]$, $u_{2}^{0} \in \left[ {\underline {u_{2}^{0}} ,\overline {u_{2}^{0}} } \right]$, …, $u_{m}^{0} \in \left[ {\underline {u_{m}^{0}} ,\overline {u_{m}^{0}} } \right]$, которая интерполирует зависимость решения задачи от интервальных параметров с контролируемой точностью. При наличии функции ${{{\mathbf{P}}}^{k}}$ нахождение интервальной оценки решения (нахождение левой и правой границ интервалов) сводится к решению $2n$ задач условной оптимизации для явно заданной функции.

Суть алгоритма заключается в адаптивном иерархическом разбиении области неопределенности на прямоугольные подобласти с использованием kd-дерева. В каждой подобласти выполняется построение регулярной сетки и соответствующей полиномиальной функции, интерполирующей зависимость решения задачи от точечных значений интервальных параметров. Каждому узлу в сетке соответствует решение исходной неинтервальной задачи при значениях параметров, определяемых положением узла в пространстве.

Предположим, что в момент ${{t}_{k}}$ известно решение ${{{\mathbf{u}}}^{k}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)$. Над множеством, образованным интервальными начальными условиями, строится регулярная интерполяционная сетка, которая соответствует корневой вершине kd-дерева. Значения в узлах сетки формируют $(m + 1)$-мерный тензор $G_{0}^{k}$:

$\begin{gathered} G_{0}^{k}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}},j} \right] = u_{j}^{k}\left( {\underline {u_{1}^{0}} + \frac{{\overline {u_{1}^{0}} - \underline {u_{1}^{0}} }}{p}{{i}_{1}},\;\underline {u_{2}^{0}} + \frac{{\overline {u_{2}^{0}} - \underline {u_{2}^{0}} }}{p}{{i}_{2}},\;. \ldots ,\;\underline {u_{m}^{0}} + \frac{{\overline {u_{m}^{0}} - \underline {u_{m}^{0}} }}{p}{{i}_{m}}} \right), \\ {{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}} = \overline {0,p} ,\quad j = \overline {1,n} , \\ \end{gathered} $
где $p$ – степень интерполяционного многочлена по каждой переменной. Отметим, что требование равномерности сетки необязательно и используется здесь для сокращения записи. В каждом конкретном случае параметр $p$ подбирается из соображений точности и минимизации вычислительных затрат: увеличение $p$ приводит к повышению точности и увеличению количества вычислений в рамках одной вершины.

По $G_{0}^{k}$ выполняется построение $G_{0}^{{k + 1}}$, которое сводится к решению неинтервальных задач Коши для соответствующих элементов тензора:

(2)
$\begin{gathered} \frac{{d{{u}_{j}}(t)}}{{dt}} = {{f}_{j}}({{u}_{1}}(t),{{u}_{2}}(t),\; \ldots ,\;{{u}_{n}}(t)), \\ {{u}_{j}}({{t}_{k}}) = G_{0}^{k}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}},j} \right], \\ G_{0}^{{k + 1}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}},j} \right] = {{u}_{j}}({{t}_{{k + 1}}}),\quad j = \overline {1,n} , \\ t \in \left[ {{{t}_{k}},{{t}_{{k + 1}}}} \right]. \\ \end{gathered} $

Систему (2) можно рассматривать как некоторую функцию черного ящика, на вход которой подается $G_{0}^{k}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}}} \right]$, а на выходе получается $G_{0}^{{k + 1}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}}} \right]$. При использовании алгоритма TT-cross для построения $G_{0}^{{k + 1}}$ нет необходимости знать все элементы $G_{0}^{k}$.

По полученному тензору $G_{0}^{{k + 1}}$ строится интерполяционный полином ${{{\mathbf{P}}}^{{k + 1}}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right) = $ $ = {{\left( {P_{1}^{{k + 1}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right),\; \ldots ,\;P_{n}^{{k + 1}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)} \right)}^{т}}$ в форме Лагранжа:

$P_{j}^{{k + 1}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right) = \sum\limits_{{{i}_{1}},{{i}_{2}},...,{{i}_{m}} = 0}^p {L\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}}} \right]} {\kern 1pt} G_{0}^{{k + 1}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}},j} \right],\quad j = \overline {1,n} ,$
где $L\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)$ есть $m$-мерный тензор, состоящий из значений базисных полиномов Лагранжа:
Интерполяционный полином можно записать компактно в виде
$\begin{gathered} {{{\mathbf{P}}}^{{k + 1}}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right) = \hat {L}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)\mathop \odot \limits_{1,2,..,m} G_{0}^{{k + 1}}, \\ \hat {L}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}},ii} \right] = L\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}}} \right],\quad ii = \overline {1,n} , \\ \end{gathered} $
где операция $\mathop \odot \limits_{1,2,..,m} $ обозначает поэлементное перемножение и суммирование по измерениям $1,\;2,\; \ldots ,\;,m$. Операция $ \odot $ доступна для тензоров в TT-формате.

Если апостериорная погрешность интерполяции

(3)
$\operatorname{error} = \mathop {\max }\limits_{u_{1}^{0} \in \left[ {\underline {u_{1}^{0}} ,\overline {u_{1}^{0}} } \right],...,u_{m}^{0} \in \left[ {\underline {u_{m}^{0}} ,\overline {u_{m}^{0}} } \right]} \left\| {{{{\mathbf{u}}}^{{k + 1}}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right) - {{{\mathbf{P}}}^{{k + 1}}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)} \right\|$
больше некоторого заданного числа $\varepsilon $, то $G_{0}^{k}$ разбивается на две сетки: $G_{1}^{k}$ и $G_{2}^{k}$ таким образом, чтобы их оценка погрешности интерполяции была меньше $\operatorname{error} $. Для них выполняются все те же самые действия, что и для сетки $G_{0}^{k}$, и при необходимости они тоже разбиваются. Если ${{{\mathbf{u}}}^{{k + 1}}}\left( {u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}} \right)$ непрерывно дифференцируема $p + 1$ раз по $u_{1}^{0},u_{2}^{0},\; \ldots ,\;u_{m}^{0}$, то можно показать, что процесс дробления конечен [9]. В общем случае с теоретической точки зрения погрешность интерполяции оценивается сверху через старшие производные с коэффициентами пропорциональности, которые характеризуют интерполяционную сетку и ее размер. При каждом дроблении эти коэффициенты уменьшаются и, как следствие, уменьшается и погрешность интерполяции. На практике определяется минимальный размер ячейки, обычно сопоставимый с машинным эпсилоном, по достижении которого дробление дальше не происходит, а соответствующая область пространства помечается как “область разрыва”.

В результате на момент ${{t}_{{k + 1}}}$ будет получено kd-дерево и соответствующая ему кусочно-полиномиальная функция, интерполирующая решение с заданной точностью. Процесс построения kd-дерева проиллюстрирован на фиг. 2. Строить с нуля на каждом шаге kd-дерево нет необходимости, вместо этого используется дерево, полученное на предыдущем шаге, и в зависимости от оценки погрешности интерполяции оно перестраивается. Процесс дробления вершин всегда происходит на предыдущем шаге (пунктирные линии), потому что при создании новых вершин выполняется интерполяция связанных с их узлами значений, которую необходимо выполнять в момент, когда погрешность еще допустима. Если для вершины и всех ее потомков ошибка интерполяции становится приемлемой, то потомки удаляются и сама вершина становится листом.

Фиг. 2.

Иллюстрация работы алгоритма.

Оценка (3) на практике выполняется не для всех точек из области неопределенности, а только для некоторых (фиг. 3, выколотые точки). При создании вершины $G_{0}^{k}$ случайным образом создается тестовое множество точек:

$U_{0}^{k} = \left\{ {{{{\mathbf{u}}}^{k}}({{{\mathbf{x}}}^{0}})\,\left| {\,{{{\mathbf{x}}}^{0}} = {{{\left( {\operatorname{rand} \left[ {\underline {u_{1}^{0}} ,\overline {u_{1}^{0}} } \right],\;\operatorname{rand} \left[ {\underline {u_{2}^{0}} ,\overline {u_{2}^{0}} } \right],\; \ldots ,\;\operatorname{rand} \left[ {\underline {u_{m}^{0}} ,\overline {u_{m}^{0}} } \right]} \right)}}^{т}}} \right.} \right\}.$
По аналогии с построением $G_{0}^{{k + 1}}$ выполняется построение $U_{0}^{{k + 1}}$ по $U_{0}^{k}$ с помощью решения неинтервальных задач Коши, подобных (2).

Фиг. 3.

Тестовое множество точек в одной вершине (выколотые точки).

После этого апостериорная оценка погрешности интерполяции принимает следующий вид:

$\operatorname{error} = \mathop {\max }\limits_{\left( {{{{\mathbf{x}}}^{0}},{{{\mathbf{u}}}^{{k + 1}}}} \right) \in U_{0}^{{k + 1}}} \left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{P}}}^{{k + 1}}}({{{\mathbf{x}}}^{{\mathbf{0}}}})} \right\|.$
При этом тензор $L\left( {{{{\mathbf{x}}}^{0}}} \right)$, который участвует в вычислении ${{{\mathbf{P}}}^{{k + 1}}}({{{\mathbf{x}}}^{0}})$, строится единожды, сразу при создании тестового множества, так как он никак не зависит от $k$. На фиг. 4 показана геометрическая интерпретация погрешности интерполяции в евклидовой норме для одной вершины. Все линии получены путем интерполяции по закрашенным точкам и соответствуют линиям на фиг. 3.

Фиг. 4.

Геометрическая интерпретация погрешности интерполяции для одной вершины.

Рассмотрим один из возможных вариантов построения разбиения ${{G}_{0}}$ на две сетки: ${{G}_{1}}$ и ${{G}_{2}}$. Разбиение производится гиперплоскостью, перпендикулярной одной из координатных осей посередине. Выполняется перебор $m$ различных вариантов разбиения, из которых выбирается оптимальный с точки зрения погрешности интерполяции. Предположим, что ${{G}_{0}}$ разбивается гиперплоскостью, перпендикулярной координатной оси с номером $d$, тогда

(4)
$\begin{gathered} {{G}_{1}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{d}},\; \ldots ,\;{{i}_{m}},j} \right] = \sum\limits_{{{k}_{d}} = 0}^p {{{L}_{1}}\left[ {{{i}_{d}},{{k}_{d}}} \right]{{G}_{0}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{k}_{d}},\; \ldots ,\;{{i}_{m}},j} \right]} , \\ {{G}_{2}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{d}},\; \ldots ,\;{{i}_{m}},j} \right] = \sum\limits_{{{k}_{d}} = 0}^p {{{L}_{2}}\left[ {{{i}_{d}},{{k}_{d}}} \right]{{G}_{0}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{k}_{d}},\; \ldots ,\;{{i}_{m}},j} \right]} , \\ \end{gathered} $
где ${{L}_{1}}$и ${{L}_{2}}$ – матрицы, состоящие из значений базисных полиномов Лагранжа:
Запишем (4) в компактном виде:
${{G}_{1}} = {{\hat {L}}_{1}}\mathop \odot \limits_{(d + 1)} {{\hat {G}}_{0}},\quad {{G}_{2}} = {{\hat {L}}_{2}}\mathop \odot \limits_{(d + 1)} {{\hat {G}}_{0}},$
где
${{\hat {G}}_{0}}[{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{{d - 1}}},ii,{{i}_{d}},{{i}_{{d + 1}}},\; \ldots ,\;{{i}_{m}},j] = {{G}_{0}}[{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}},j],$
${{\hat {L}}_{1}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{{d - 1}}},ii,jj,{{i}_{{d + 1}}},\; \ldots ,\;{{i}_{m}},j} \right] = {{L}_{1}}\left[ {ii,jj} \right],$
${{\hat {L}}_{2}}\left[ {{{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{{d - 1}}},ii,jj,{{i}_{{d + 1}}},\; \ldots ,\;{{i}_{m}},j} \right] = {{L}_{2}}\left[ {ii,jj} \right],$
${{i}_{1}},{{i}_{2}},\; \ldots ,\;{{i}_{m}},\quad ii,jj = \overline {0,p} ,\quad j = \overline {1,n} .$
Тензоры ${{\hat {G}}_{0}}$, ${{\hat {L}}_{1}}$, ${{\hat {L}}_{2}}$ получаются путем произведения Кронекера ${{G}_{0}}$, ${{L}_{1}}$, ${{L}_{2}}$ на единичные тензоры с последующей перестановкой индексов.

В целом алгоритм адаптивной интерполяции состоит из трех элементов: перенос решений на следующий временной слой, оценка погрешности интерполяции для каждой вершины и разбиение вершин. Вместо явного хранения многомерных массивов в каждой вершине kd-дерева достаточно хранить только их TT-разложение: все необходимые действия в процессе работы алгоритма можно выполнять в рамках TT-формата.

3. РЕЗУЛЬТАТЫ

В данном разделе приводятся результаты решения двух систем ОДУ с интервальными параметрами и начальными условиями. Расчеты выполнены с помощью собственного разработанного программного обеспечения на языках программирования С++ и Python. При этом использовалась реализация тензорных поездов из пакета ttpy [17].

Для оценки апостериорной относительной погрешности ${{\operatorname{error} }_{g}}$ в начальный момент времени случайным образом генерируется тестовое множество точек из области неопределенности параметров системы и строятся соответствующие решения, с которыми выполняется сравнение. Для оценки вычислительных затрат используется критерий $I$, введенный в работе [9] и численно равный числу решенных неинтервальных систем (1) при точечных значениях интервальных параметров.

В качестве примера рассмотрим модельную задачу: движение тел с неопределенностями в начальных скоростях под действием сил гравитации. Вокруг массивного тела, расположенного в центре координат, двигаются по круговым орбитам шесть небольших тел, у которых начальные скорости даны в виде интервалов. Получающаяся область неопределенности имеет размерность, равную $6 \times 3 = 18$.

Система ОДУ в безразмерных переменных имеет следующий вид:

$\begin{gathered} \left( {{v}_{i}^{x}} \right)' = \sum\limits_{j = 1,j \ne i}^7 {{{m}_{j}}\frac{{{{x}_{j}} - {{x}_{i}}}}{{r_{{i,j}}^{3}}}} ,\quad \left( {{v}_{i}^{y}} \right){\text{'}} = \sum\limits_{j = 1,j \ne i}^7 {{{m}_{j}}\frac{{{{y}_{j}} - {{y}_{i}}}}{{r_{{i,j}}^{3}}}} ,\quad \left( {{v}_{i}^{z}} \right)' = \sum\limits_{j = 1,j \ne i}^7 {{{m}_{j}}\frac{{{{z}_{j}} - {{z}_{i}}}}{{r_{{i,j}}^{3}}}} , \\ x_{1}^{'} = {v}_{i}^{x},\quad y_{i}^{'} = {v}_{i}^{y},\quad z_{i}^{'} = {v}_{i}^{z},\quad i = \overline {1,7} ,\quad t \in \left[ {0.0,\;0.02} \right], \\ \end{gathered} $
(5)
$\begin{gathered} {{x}_{1}}(0) = {{y}_{1}}(0) = {{z}_{1}}(0) = {v}_{1}^{x}(0) = {v}_{1}^{y}(0) = {v}_{1}^{z}(0) = 0, \\ {{x}_{{2,3}}}(0) = \pm 1,\quad {{y}_{{2,3}}}(0) = {{z}_{{2,3}}}(0) = 0,\quad {{{v}}_{{2,3}}}(0) = {{\left( {\begin{array}{*{20}{c}} 0&{ \pm {\kern 1pt} {v}}&0 \end{array}} \right)}^{т}} + \Delta {v}_{{2,3}}^{т}, \\ \end{gathered} $
$\begin{gathered} {{y}_{{4,5}}}(0) = \pm 1,\quad {{x}_{{4,5}}}(0) = {{z}_{{4,5}}}(0) = 0,\quad {{{v}}_{{4,5}}}(0) = {{\left( {\begin{array}{*{20}{c}} 0&0&{ \pm {\kern 1pt} {v}} \end{array}} \right)}^{т}} + \Delta {v}_{{4,5}}^{т}, \\ {{z}_{{6,7}}}(0) = \pm 1,\quad {{x}_{{6,7}}}(0) = {{y}_{{6,7}}}(0) = 0,\quad {{{v}}_{{6,7}}}(0) = {{\left( { \pm {\kern 1pt} \begin{array}{*{20}{c}} {v}&0&0 \end{array}} \right)}^{т}} + \Delta {v}_{{6,7}}^{т}, \\ \end{gathered} $
где ${{r}_{{i,j}}} = \sqrt {{{{\left( {{{x}_{j}} - {{x}_{i}}} \right)}}^{2}} + {{{\left( {{{y}_{j}} - {{y}_{i}}} \right)}}^{2}} + {{{\left( {{{z}_{j}} - {{z}_{i}}} \right)}}^{2}}} $ – расстояние между двумя телами, ${v} = 316.23$° – начальная скорость тел, ${{m}_{1}} = {{10}^{5}}$, ${{m}_{{\overline {2,7} }}} = {{10}^{{ - 5}}}$ – массы тел, $\Delta {{{v}}_{{\overline {2,3} }}} = \left( {\left[ { - 2,\;2} \right],\left[ { - 6,\;6} \right],\left[ { - 2,\;2} \right]} \right)$, $\Delta {{{v}}_{{\overline {4,7} }}} = \left( {\left[ { - 2,\;2} \right],\left[ { - 2,\;2} \right],\left[ { - 2,\;2} \right]} \right)$ – интервальные неопределенности в скоростях тел.

Данная система является показательной, потому что неопределенность в скорости конкретного тела влияет в основном только на положение и скорость этого же тела, а на другие тела влияет слабо. Параметр $p = 4$, количество элементов в тензоре в каждой вершине равно ${{5}^{{18}}} \times 42 \approx {{10}^{{15}}}$. Число 42 соответствует количеству фазовых переменных. Использование алгоритма адаптивной интерполяции без применения TT-разложения привело бы к решению порядка ${{10}^{{12}}}$ систем ОДУ для каждой вершины, что потребовало бы колоссальных вычислительных мощностей.

В табл. 1 представлены результаты применения предлагаемого подхода к системе ОДУ (5) при разных значениях параметра $\varepsilon $. Во всех случаях значение критерия $I$, характеризующего вычислительные затраты, намного меньше, чем было бы при использовании классического варианта алгоритма ($I \approx {{10}^{{12}}}$). При $\varepsilon = {{10}^{{ - 3}}}$ решение фактически получено без kd-дерева (дерево состоит из одной корневой вершины). При уменьшении $\varepsilon $ становится необходимым выполнять уплотнение сетки, что приводит к росту дерева.

Таблица 1.  

Результаты интегрирования системы (5)

Параметр $\varepsilon = {{10}^{{ - 3}}}$ $\varepsilon = {{10}^{{ - 4}}}$ $\varepsilon = {{10}^{{ - 5}}}$
Максимальная высота kd-дерева 0 3 4
Максимальное количество вершин 1 9 31
$\max \left( {{{{\operatorname{error} }}_{g}}} \right)$ $3.9 \times {{10}^{{ - 4}}}$ $9.5 \times {{10}^{{ - 5}}}$ $8.8 \times {{10}^{{ - 6}}}$
Значение критерия $I$, $ \times {{10}^{6}}$ 0.5 8.3 29.4

На фиг. 5 показано kd-дерево в момент времени $t = 0.02$ при $\varepsilon = {{10}^{{ - 4}}}$. В каждой вершине дерева указан эффективный ранг соответствующего тензора, который характеризует средний размер получающихся ядер TT-разложения. Не листовые вершины дерева дополнительно помечены названием интервального параметра, по которому происходило разбиение области неопределенности. Ширина интервала $y$-компоненты начальной скорости второго и третьего тела больше, чем у остальных тел, поэтому уплотнение выполнялось в основном только по ${v}_{2}^{y}$ и ${v}_{3}^{y}$.

Фиг. 5.

Kd-дерево в конечный момент времени интегрирования системы (5).

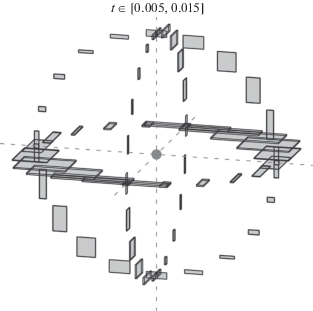
Решение задачи представлено на фиг. 6, прямоугольными параллелепипедами проиллюстрированы области неопределенности в пространстве для каждого тела в различные моменты времени.

Фиг. 6.

Неопределенности в положении тел в различные моменты времени.

Использование TT-разложения в алгоритме адаптивной интерполяции позволило успешно решить данную задачу на персональном компьютере, что говорит об эффективности предлагаемой модификации алгоритма.

Далее рассматривается прикладная задача: моделирование горения водород-кислородной смеси при наличии неопределенностей в константах скоростей химических реакций. Для моделирования газофазных химических превращений необходимо знать кинетический механизм и скорости протекающих реакций. Как правило, зависимости, которые описывают скорости, получают экспериментальными способами, зачастую дающими лишь приближенные значения [18]. Значения функций, аппроксимирующих скорость протекания одной и той же реакции, но полученных разными исследователями, могут различаться в десятки и в сотни раз. Естественно, для численного моделирования в этом случае необходимо применение интервальных методов, которые могут работать в условиях больших неопределенностей.

Многокомпонентная система переменного состава из $N$ веществ, в которой протекает ${{N}_{r}}$ реакций, имеет вид [19]:

$\sum\limits_{i = 1}^N {{\vec {v}}_{i}^{{(r)}}{{M}_{i}}} \;\mathop \rightleftarrows \limits_{{{{\overleftarrow W }}^{{(r)}}}}^{{{{\overrightarrow W }}^{{(r)}}}} \;\sum\limits_{i = 1}^N {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{v} }_{i}^{{(r)}}{{M}_{i}}} ,\quad {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {q} }^{{(r)}}} = \sum\limits_{i = 1}^N {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {v} }_{i}^{{(r)}}} ,\quad r = \overline {1,{{N}_{r}}} ,$
где $r$ – порядковый номер реакции, ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {v} }_{i}^{{(r)}}$ – стехиометрические коэффициенты, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {q} }^{{(r)}}}$ – молекулярность элементарных реакций, ${{M}_{i}}$ – символы молекул или атомов химических компонентов, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} }^{{(r)}}}$ – скорости $r$-й реакции в прямом и обратном направлении. Последняя величина определяет изменение концентрации компонентов с течением времени в единице объема смеси.

Скорость химической реакции ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} }^{{(r)}}}$ определяется как произведение объемных концентраций компонентов и константы скорости реакции ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {K} }^{{(r)}}}(T)$, зависящей от температуры:

${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} }^{{(r)}}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {K} }^{{(r)}}}(T)\prod\limits_i {{{{\left( {\rho {{\gamma }_{i}}} \right)}}^{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {v} }_{i}^{{(r)}}}}}} ,$
где $\rho $ – плотность, ${{\gamma }_{i}}$ – мольно-массовая концентрация $i$-го компонента.

Для аппроксимации температурной зависимости констант скоростей прямых реакций используется обобщенная формула Аррениуса:

$\vec {K}(T) = A{{T}^{n}}\exp \left( { - \frac{E}{T}} \right),$
где $A$, $n$, $E$ – некоторые постоянные величины, индивидуальные для каждой реакции. Именно в этих величинах и содержится неопределенность.

Константы скоростей обратных реакций для случая смеси совершенных газов вычисляются исходя из константы равновесия:

${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{K} }^{{(r)}}}(T) = {{\vec {K}}^{{(r)}}}(T)\exp \left[ {\sum\limits_i^N {\left( {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{v} }_{i}^{{(r)}} - {\vec {v}}_{i}^{{(r)}}} \right)\left( {\frac{{G_{i}^{0}(T)}}{{RT}} + \ln \frac{{RT}}{{{{P}_{0}}}}} \right)} } \right],$
где ${{P}_{0}} = 101\,325$ – стандартное давление, $R$ – универсальная газовая постоянная, $G_{i}^{0}(T)$ – стандартный молярный потенциал Гиббса $i$-го компонента, который задается с помощью полиномов из справочника [20].

Скорость образования $i$-го компонента имеет следующий вид:

${{W}_{i}} = \sum\limits_{r = 1}^{{{N}_{r}}} {\left( {{\vec {v}}_{i}^{{(r)}} - {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{v} }_{i}^{{(r)}}} \right)\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{W} }}^{{(r)}}} - {{{\vec {W}}}^{{(r)}}}} \right)} ,\quad i = \overline {1,N} .$

Для демонстрации неопределенностей, содержащихся в константах скоростей химических реакций, рассмотрим кинетические механизмы, приведенные в работах [21] (табл. 2) и [22] (табл. 3). Большая часть содержащихся в таблицах реакций не совпадает по направлению, поэтому для их сравнения воспользуемся константой равновесия. На фиг. 7 показаны зависимости некоторых констант скоростей от температуры для разных механизмов.

Таблица 2.  

Первый механизм горения смеси H2–O2

Реакция $A$, м моль с $n$ $E$, K
1. ${{{\text{O}}}_{2}}\, + \,{\text{H}} \to {\text{OH}}\, + \,{\text{O}}$ $2.0 \times {{10}^{8}}$ 0.0 8455
2. ${{{\text{H}}}_{2}}\, + \,{\text{O}} \to {\text{OH}}\, + \,{\text{H}}$ $5.06 \times {{10}^{{ - 2}}}$ 2.67 3163
3. ${{{\text{H}}}_{2}}\, + \,{\text{OH}} \to {{{\text{H}}}_{2}}{\text{O}}\, + \,{\text{H}}$ $1.0 \times {{10}^{2}}$ 1.6 1659
4. ${\text{OH}}\, + \,{\text{OH}} \to {{{\text{H}}}_{2}}{\text{O}}\, + \,{\text{O}}$ $1.5 \times {{10}^{3}}$ 1.14 50
5. ${\text{H}}\, + \,{\text{H}}\, + \,{\text{M}} \to {{{\text{H}}}_{2}}\, + \,{\text{M}}$ $1.8 \times {{10}^{6}}$ –1.0 0
6. ${\text{O}}\, + \,{\text{O}}\, + \,{\text{M}} \to {{{\text{O}}}_{2}}\, + \,{\text{M}}$ $2.9 \times {{10}^{5}}$ –1.0 0
7. ${\text{H}}\, + \,{\text{OH}}\, + \,{\text{M}} \to {{{\text{H}}}_{2}}{\text{O}}\, + \,{\text{M}}$ $2.2 \times {{10}^{{10}}}$ –2.0 0
Таблица 3.  

Второй механизм горения смеси H2–O2

Реакция $A$, м моль с $n$ $E$, K
1. ${{\operatorname{H} }_{2}}O\, + \,H \to \operatorname{OH} \, + \,{{H}_{2}}$ ${\text{8}}{\text{.4}} \times {\text{1}}{{{\text{0}}}^{7}}$ 0 10 116
2. ${{\operatorname{O} }_{2}}\, + \,H \to \operatorname{OH} \, + \,O$ ${\text{2}}{\text{.2}} \times {\text{1}}{{{\text{0}}}^{8}}$ 0 8455
3. ${{\operatorname{H} }_{2}}\, + \,O \to \operatorname{OH} \, + \,H$ $1.8 \times {{10}^{4}}$ 1 4480
4. ${{\operatorname{O} }_{2}}\, + \,M \to 2O\, + \,M$ $5.4 \times {{10}^{{12}}}$ –1 59 400
5. ${{\operatorname{H} }_{2}}\, + \,M \to 2H\, + \,M$ $2.2 \times {{10}^{8}}$ 0 48 300
6. ${{\operatorname{H} }_{2}}O\, + \,M \to \operatorname{OH} \, + \,H\, + \,M$ ${\text{1}}{{{\text{0}}}^{{18}}}$ –2.2 59 000
7. $\operatorname{HO} \, + \,M \to \operatorname{O} \, + \,H\, + \,M$ $8.5 \times {{10}^{{12}}}$ –1 50 830
8. ${{\operatorname{H} }_{2}}O\, + \,O \to 2OH$ ${\text{5}}{\text{.8}} \times {\text{1}}{{{\text{0}}}^{7}}$ 0 9059
Фиг. 7.

Сравнение различных механизмов горения смеси H2–O2.

В качестве интервального параметра выступает $a$ коэффициент суперпозиции значений констант скоростей реакций из разных механизмов:

$K(T) = (1 - a){{K}_{1}}(T) + a{{K}_{2}}(T),\quad a \in [0,\;1].$
Рассматривается  стехиометрическая смесь водорода и кислорода при начальной температуре $T = 1200$ K, постоянной плотности $\rho = 0.122$ кг/м3 и постоянной внутренней энергии $U = 1.48$ МДж/кг. Модель химической кинетики задается системой из шести компонентов (${{{\text{H}}}_{2}}{\text{O}}$, ${\text{OH}}$, ${{{\text{H}}}_{2}}$, ${{{\text{O}}}_{2}}$, ${\text{H}}$, ${\text{O}}$, в которой протекает восемь реакций (табл. 2 и 3).

Система ОДУ записывается следующим образом:

$\frac{{d{{\gamma }_{i}}}}{{dt}} = \frac{1}{\rho }\sum\limits_{r = 1}^8 {\left( {{\vec {v}}_{i}^{{(r)}} - {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{v} }_{i}^{{(r)}}} \right)\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{W} }}^{{(r)}}} - {{{\vec {W}}}^{{(r)}}}} \right)} ,\quad i = \overline {1,\;6} ,$
и дополняется уравнением сохранения внутренней энергии системы:
$U\left( {T,{\mathbf{\gamma }}} \right) = H\left( {T,\gamma } \right) - RT\sum\limits_{i = 1}^6 {{{\gamma }_{i}}} ,$
где $H\left( {T,{\mathbf{\gamma }}} \right)$ – энтальпия (калорическое уравнение):
$H\left( {T,{\mathbf{\gamma }}} \right) = \sum\limits_{i = 1}^N {{{\gamma }_{i}}\left( {G_{i}^{0}(T) - T\frac{{dG_{i}^{0}(T)}}{{dT}}} \right).} $
При каждом вычислении правой части системы ОДУ уравнение внутренней энергии разрешается относительно $T$ с помощью метода Ньютона. Начальные условия:

$\begin{gathered} {{\gamma }_{{{{\operatorname{H} }_{2}}}}} = {\text{55}}{\text{.50868}}\;\frac{{{\text{моль}}}}{{{\text{кг}}}},\quad {{\gamma }_{{{{\operatorname{O} }_{2}}}}} = {\text{27}}{\text{.75434 }}\frac{{{\text{моль}}}}{{{\text{кг}}}}{\text{,}} \\ {{\gamma }_{{{{\operatorname{H} }_{2}}O}}} = {{\gamma }_{{\operatorname{OH} }}} = {{\gamma }_{\operatorname{H} }} = {{\gamma }_{\operatorname{O} }} = 0\;\frac{{{\text{моль}}}}{{{\text{кг}}}}. \\ \end{gathered} $

Полученная система ОДУ является жесткой, и для интегрирования неинтервальных ОДУ в процессе работы алгоритма используется неявный метод Розенброка с заморозкой матрицы Якоби [23] (отметим, что здесь возможно использовать методы, представленные в работе [24]). Выполняется расчет при значении $p = 4$. На фиг. 8 представлены верхние и нижние оценки для концентраций всех компонентов смеси. Неопределенность в константах скоростей реакций приводит к неопределенности важного параметра — времени задержки воспламенения в диапазоне от 18 до 20 мкс.

Фиг. 8.

Зависимость мольно-массовых концентраций от времени.

Отметим, что для данной модели характерным является переход в равновесное состояние, которое никак не зависит от констант скоростей реакций, о чем свидетельствует совпадение верхних оценок концентраций с нижними оценками после определенного момента времени. Так же важным моментом является то, что решения, полученные с использованием каждого механизма в отдельности, содержатся внутри найденных оценок и при этом не совпадают с границами (т.е. для получения оценки не достаточно просто посчитать решения с разными механизмами).

Не все реакции оказывают существенное влияние на протекание газофазных химических превращений. Адаптивный учет этого влияния позволяет сократить вычислительные затраты при моделировании химических превращений. За счет использования TT-разложения среднее количество проинтегрированных неинтервальных систем ОДУ уменьшилось в 3–4 раза (табл. 4, критерий $I$). В случае применения алгоритма без использования kd-дерева значение относительной апостериорной погрешности возрастает и равно $0.04$, что дополнительно показывает эффективность предлагаемого подхода.

Таблица 4.

Результаты моделирования

Параметр Без kd-дерева $\varepsilon = {{10}^{{ - 3}}}$ $\varepsilon = {{10}^{{ - 4}}}$
Максимальная высота kd-дерева – 4 6
Максимальное количество вершин – 17 53
$\max \left( {{{{\operatorname{error} }}_{g}}} \right)$ 0.04 ${{10}^{{ - 3}}}$ $9.3 \times {{10}^{{ - 5}}}$
Значение критерия $I$ 6522 25 032 57 529
Значение критерия $I$ (классический вариант алгоритма) 78 125 105 469 170 703

На фиг. 9 показано kd-дерево в момент времени $t = 24$ мкс при значении $\varepsilon = {{10}^{{ - 3}}}$. В данный момент времени высота дерева является максимальной, это связано с тем, что при некоторых значениях параметров возгорание смеси уже произошло, а при некоторых еще нет, и в результате интерполируемая функция имеет резкие переходы, что требует уплотнения сетки. Отметим, что уплотнение в основном выполняется по измерениям, которые соответствуют первым трем реакциям в табл. 3.

Фиг. 9.

Kd-дерево в момент времени $t = 24$ мкс.

Для уменьшения вычислительных затрат обновление тензоров (перевычисление решений содержащихся в узлах сетки на текущий временной слой) происходит только для листовых вершин kd-дерева. В связи с этим приведенные значения эффективных рангов во внутренних узлах дерева актуальны только на момент разбиения соответствующей вершины.

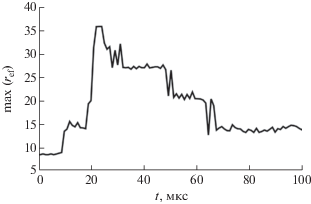
На фиг. 10 представлена зависимость максимального эффективного ранга от времени. Здесь наблюдается резкий рост максимального эффективного ранга в момент возгорания смеси, и дальнейшее постепенное его уменьшение, по мере перехода системы к равновесному состоянию.

Фиг. 10.

Зависимость максимального эффективного ранга от времени.

За счет использования TT-разложения в алгоритме адаптивной интерполяции требуемое вычислительное время для решения данной задачи сократилось в 3–4 раза.

4. ЗАКЛЮЧЕНИЕ

Алгоритм адаптивной интерполяции позволяет моделировать динамические системы с интервальными параметрами. В процессе работы алгоритма над множеством, образованным интервальными неопределенностями, строится регулярная сетка, в которой количество узлов зависит экспоненциально от количества интервальных параметров, что ограничивает область применения алгоритма. Зачастую зависимость решения задачи от совокупности параметров может быть вырожденной, при этом данные, которые содержатся в сетках, будут обладать существенной избыточностью. Использование ТТ-разложения в алгоритме адаптивной интерполяции позволяет устранить эту избыточность и расширить область его применения на случай большого числа интервальных параметров. Все действия над сетками, которые происходят в процессе выполнения алгоритма, осуществляются в рамках ТТ-формата. Эффективность рассмотренной модификации алгоритма подтверждена на задаче моделирования движения тел под действием гравитационных сил в условиях неопределенности начальных скоростей тел, а также на практически значимой задаче моделирования горения водородно-кислородной смеси при наличии неопределенностей в константах скоростей химических реакций.

Список литературы

  1. Moore R.E., Kearfott R.B., Cloud M.J. Introduction to Interval Analysis // SIAM, 2009.

  2. Shary S.P., Moradi B. Solving interval linear least squares problems by PPS-methods // Numerical Algorithms. 2020. https://doi.org/10.1007/s11075-020-00958-x

  3. Тыртышников Е.Е. Тензорные аппроксимации матриц, порожденных асимптотически гладкими функциями // Матем. сборник. 2003. Т. 194. № 6. С. 147–160.

  4. Тыртышников Е.Е., Щербакова Е.М. Методы неотрицательной матричной факторизации на основе крестовых малоранговых приближений // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 8. С. 1314–1330.

  5. Желтков Д.А., Тыртышников Е.Е. Параллельная реализация матричного крестового метода // Вычисл. методы и программирование. 2015. Т. 16. С. 369–375.

  6. Горейнов С.А., Замарашкин Н.Л., Тыртышников Е.Е. Псевдоскелетные аппроксимации при помощи подматриц наибольшего объема // Матем. заметки. 1997. Т. 62. Вып. 4. С. 619–623.

  7. Oseledets I.V. Tensor-train decomposition // SIAM Journal on Scientific Computing. 2011. V. 33. № 5. P. 2295–2317.

  8. Oseledets I., Tyrtyshnikov E. TT-cross approximation for multidimensional arrays // Linear Algebra and its Applications. 2010. V. 432. Iss. 1. P. 70–88.

  9. Морозов А.Ю., Ревизников Д.Л. Алгоритм адаптивной интерполяции на основе kd-дерева для численного интегрирования систем ОДУ с интервальными начальными условиями // Дифференц. ур-ния. 2018. Т. 54. № 7. С. 963–974. https://doi.org/10.1134/S0374064118070130

  10. Морозов А.Ю., Ревизников Д.Л., Гидаспов В.Ю. Алгоритм адаптивной интерполяции на основе kd-дерева для решения задач химической кинетики с интервальными параметрами // Матем. моделирование. 2018. Т. 30. № 12. С. 129–144. https://doi.org/10.31857/S023408790001940-8

  11. Morozov A.Yu., Zhuravlev A.A., Reviznikov D.L. Sparse Grid Adaptive Interpolation in Problems of Modeling Dynamic Systems with Interval Parameters // Mathematics. 2021. V. 9. № 4. 298. https://doi.org/10.3390/math9040298

  12. Morozov A.Yu., Reviznikov D.L. Modelling of Dynamic Systems with Interval Parameters on Graphic Processors // Programmnaya Ingeneria. 2019. V. 10. № 2. P. 69–76. https://doi.org/10.17587/prin.10.69-76

  13. Dolgov S.V., Kazeev V.A., Khoromskij B.N. Direct tensor-product solution of one-dimensional elliptic equations with parameter-dependent coefficients // Mathematics and Computers in Simulation. 2018. V. 145. P. 136–155. https://doi.org/10.1016/j.matcom.2017.10.009

  14. Olivier C., Ryckelynck D., Cortial J. Multiple Tensor Train Approximation of Parametric Constitutive Equations in Elasto-Viscoplasticity // Mathematical and Computational Applications. 2019. V. 24. № 1. 17. https://doi.org/10.3390/mca24010017

  15. Hitchcock F.L. The expression of a tensor or a polyadic as a sum of products // J. Math. Phys. 1927. V. 6. № 1. P. 164–189.

  16. Tucker L.R. Some mathematical notes on three-mode factor analysis // Psychometrika. 1966. V. 31. P. 279–311.

  17. ttpy [сайт]. URL: https://github.com/oseledets/ttpy (дата обращения: 07.03.2021)

  18. Вайтиев В.А., Мустафина С.А. Поиск областей неопределенности кинетических параметров математических моделей химической кинетики на основе интервальных вычислений // Вестник ЮУрГУ. Серия “Математическое моделирование и программирование”. 2014. Т. 7. № 2. С. 99–110.

  19. Гидаспов В.Ю., Северина Н.С. Элементарные модели и вычислительные алгоритмы физической газовой динамики. Термодинамика и химическая кинетика: Учебное пособие. М.: Факториал, 2014. 84 с.

  20. Глушко В.П., Гурвич Л.В., Вейц И.В. и др. Термодинамические свойства индивидуальных веществ. Т. 1. М.: Наука, 1978–2004.

  21. Варнатц Ю., Маас У., Диббл Р. Горение. Физические и химические аспекты, моделирование, эксперименты, образование загрязняющих веществ / Пер. с англ. Г.Л. Агафонова. Под ред. П.А. Власова. М.: Физматлит, 2003. 352 с.

  22. Старик А.М., Титова Н.С., Шарипов А.С., Козлов В.Е. О механизме окисления синтез-газа // Физ. горения и взрыва. 2010. Т. 46. № 5. С. 3–19.

  23. Новиков E.А., Голушко М.И. (m,3)-метод третьего порядка для жестких неавтономных систем ОДУ // Вычисл. технологии. 1998. Т. 3. № 3. С. 48–54.

  24. Васильев Е.И., Васильева Т.А. Мульти-неявные методы с автоматическим контролем погрешности в приложениях с химическими реакциями // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 9. С. 1570–1580.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал