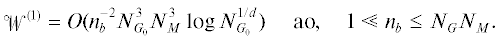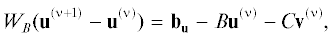Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1403-1415

ВВЕДЕНИЕ

Современное математическое моделирование физико-химических процессов в механике сплошных сред отличается применением сложных математических моделей, многообразных численных методов и различных суперкомпьютерных технологий. Сейчас уже вряд ли можно встретить специалиста, знакомого со всеми деталями современного вычислительного эксперимента. Поэтому основным направлением развития математического моделирования стало создание комплексов программ, устроенных по принципу “черного ящика”. Невозможность контроля пользователем построения сетки, аппроксимации уравнений математической модели и итерационного решения результирующей системы (не)линейных алгебраических уравнений на параллельном компьютере накладывает жесткие ограничения на численные методы для перспективных программных средств.

Как правило, математические модели стационарных физико-химических процессов в механике сплошных сред являются краевыми задачами для систем нелинейных дифференциальных уравнений в частных производных. Аппроксимация нелинейной краевой задачи на вычислительной сетке приводит к системе нелинейных алгебраических уравнений высокого порядка, численное решение которой требует огромных вычислительных усилий. Поэтому разработка эффективных методов численных решения подобных краевых задач имеет важное теоретическое и прикладное значение. Проблемы численного моделирования, связанные с разработкой и теоретическим обоснованием универсальных, эффективных и параллельных алгоритмов, не снимаются сами собой по мере появления все более мощных и дешевых компьютеров. Это связано, по меньшей мере, с двумя причинами: усложнением выдвигаемых как практикой, так и теорией, задач и необходимостью проведения большого числа серий вычислительных экспериментов для достаточно полного изучения объекта [1].

В середине 80-х годов прошлого века многосеточные методы, история которых начинается с пионерских работ выдающихся отечественных математиков Р.П. Федоренко, Н.С. Бахвалова и Г.П. Астраханцева, получили широкое распространение для решения прикладных задач. Кроме того, появились персональные компьютеры, достаточно мощные для проведения научно-технических расчетов. К вычислительной технике получили широкий доступ инженеры, физики, химики и специалисты из других проблемных областей, которые не обладали достаточной подготовкой в области вычислительной математики, но сталкивались с необходимостью решения прикладных задач, требующих большого объема вычислений. Поэтому с середины 80-х годов предпринимаются многочисленные попытки разработать вычислительные алгоритмы для программ, устроенных по принципу “черного ящика” (black box software).

К настоящему времени предложено труднообозримое количество различных алгоритмов для численного решения краевых задач, но наиболее значимыми являются только два из них.

1. Алгебраические многосеточные методы (АММ). В АММ вспомогательные системы линейных алгебраических уравнений (СЛАУ), необходимых для отыскания поправки, строят без привлечения геометрической информации о вычислительной сетке [2], [3]. АММ являются эффективными и высокоформализованными алгоритмами решения СЛАУ, полученных в результате аппроксимации линейных краевых задач на неструктурированных сетках. В нелинейном случае АММ применяют к решению СЛАУ, полученной в результате глобальной линеаризации дискретной краевой задачи. Помимо необходимости глобальной линеаризации исходной системы нелинейных алгебраических уравнений, остались проблемы, связанные с построением параллельных АММ.

2. Метод вспомогательного пространства (МВП или Auxiliary Space Method). Основная идея данного метода состоит в использовании вспомогательной задачи, решение которой проще, чем исходной [4]. Эффективность и параллелизм МВП определяется способом решения вспомогательной задачи.

Вычислительная сетка во многом определяет погрешность аппроксимации (начально-)краевых задач и трудоемкость итерационного алгоритма для решения результирующей системы (не)линейных алгебраических уравнений. Как правило, в области со сложной геометрией глобально-структурированную сетку построить гораздо сложнее, чем неструктурированную. Однако высокоэффективный и параллельный итерационный алгоритм для численного решения дискретных краевых задач проще разработать именно в случае использования глобально-структурированных сеток для аппроксимации (начально-)краевых задач. Очевидно, что вычислительная технология для перспективного программного обеспечения должна сочетать преимущества структурированных и неструктурированных сеток.

Целью данной работы является теоретическое исследование сходимости геометрических многосеточных методов на локально-структурированных (многоблочных) сетках в рамках классического многосеточного анализа, предложенного В. Хакбушем [5].

1. ЗАМЕЧАНИЯ О МЕТОДЕ ВСПОМОГАТЕЛЬНОГО ПРОСТРАНСТВА

Пусть $\Omega \in {{\mathbb{R}}^{3}}$ есть произвольная ограниченная область с границей $\partial \Omega $. Необходимо найти решение ${\mathbf{u}}({\mathbf{x}}) = {{({{u}^{{(1)}}}({\mathbf{x}}),{{u}^{{(2)}}}({\mathbf{x}}), \ldots ,{{u}^{{({{N}_{M}})}}}({\mathbf{x}}))}^{{\text{T}}}}$ 3D краевой задачи для системы линейных эллиптических дифференциальных уравнений в частных производных

Здесь ${\mathbf{x}} = {{({{x}_{1}},{{x}_{2}},{{x}_{3}})}^{{\text{T}}}}$, $\mathcal{L}_{\Omega }^{{(ij)}}$ и $\mathcal{L}_{{\partial \Omega }}^{{(ij)}}$ есть линейные эллиптические дифференциальные операторы, а $f_{\Omega }^{{(i)}}$ и $f_{{\partial \Omega }}^{{(i)}}$ – заданные функции в $\Omega $ и ее границе $\partial \Omega $ (${{N}_{M}} \leqslant {{N}_{B}}$). Для краткости будем обозначать данную краевую задачу как $\mathcal{L}{\mathbf{u}} = {\mathbf{f}}$ и полагать, что она имеет единственное решение ${\mathbf{u}} = {{\mathcal{L}}^{{ - 1}}}{\mathbf{f}}$.

Сначала сформулируем базовый односеточный алгоритм на основе метода Зейделя с блочным упорядочением неизвестных (Vanka-type smoother [6]) для численного решения краевой задачи (1). Использование метода Ванки означает совместное решение системы (1). Построим сетку ${{G}_{0}}$ с ${{N}_{{{{G}_{0}}}}}$ узлами, аппроксимируем некоторым образом краевую задачу (1) на сетке ${{G}_{0}}$ и запишем дискретный аналог (1) в матричной форме

где вектор неизвестных ${{\varphi }_{0}}$ аппроксимирует вектор ${\mathbf{u}}({\mathbf{x}})$. Базовый односеточный алгоритм представим в виде где ${{W}_{V}}$ есть матрица расщепления метода Ванки. Итерации (2) можно записать как

Базовый односеточный алгоритм 3 содержит следующие проблемно-зависимые компоненты:

а) матрица коэффициентов ${{A}_{0}}$ и вектор правых частей ${{{\mathbf{b}}}_{0}}$. В общем случае, матрица коэффициентов ${{A}_{0}}$ и вектор правых частей ${{{\mathbf{b}}}_{0}}$ зависят от способа и порядка аппроксимации исходной краевой задачи и упорядочения неизвестных;

б) упорядочение неизвестных;

в) критерий останова итераций.

Далее всегда будем полагать, что итерационный метод является вполне согласованным, т.е. решение СЛАУ $(I - {{S}_{V}}){{\varphi }_{0}} = W_{V}^{{ - 1}}{{{\mathbf{b}}}_{0}}$ совпадает с решением исходной СЛАУ ${{A}_{0}}{{\varphi }_{0}} = {{{\mathbf{b}}}_{0}}$, где ${{S}_{V}} = I - W_{V}^{{ - 1}}{{A}_{0}}$ есть матрица итераций [7]. Отсюда следует, что

Построим вычислительную сетку ${{G}_{A}}$ с ${{N}_{{{{G}_{A}}}}}$ узлами (${{N}_{{{{G}_{A}}}}} \approx {{N}_{{{{G}_{0}}}}}$), далее нижний индекс “A” (auxiliary) будет означать принадлежность к вспомогательной сетке. Итерации метода вспомогательного пространства, показанные на фиг. 1, могут быть записаны в виде

где матрица итераций линейного двухсеточного алгоритма имеет вид Здесь ${{\mathcal{R}}_{{0 \to A}}}$ есть оператор, проецирующий невязку ${{{\mathbf{b}}}_{0}} - {{A}_{0}}\varphi _{0}^{{(q)}}$ с исходной сетки ${{G}_{0}}$ на вспомогательную сетку ${{G}_{A}}$, ${{\mathcal{P}}_{{A \to 0}}}$ есть оператор, проецирующий поправку с исходной сетки ${{G}_{0}}$ на вспомогательную сетку ${{G}_{A}}$, $S_{0}^{\nu }$ – матрица итераций Ванки, $\nu $ – количество сглаживающих итераций, выполняемых на исходной сетке ${{G}_{0}}$. Матрица ${{A}_{A}}$ получена в результате аппроксимации линейного дифференциального оператора $\mathcal{L}$ на вспомогательной сетке методом контрольного объема, причем порядок аппроксимации не превышает 2.

Классический анализ сходимости линейного двухсеточного алгоритма основан на следующих утверждениях [5].

1. Свойство сглаживания: существует функция $\eta (\nu ):{{\mathbb{R}}_{ + }} \to {{\mathbb{R}}_{ + }}$ такая, что $\eta (\nu ) \to 0$ при $\nu \to \infty $ и

2. Свойство аппроксимации: для некоторой константы ${{C}_{A}} > 0$

Доказательство данных свойств является отдельной и очень трудной теоретической проблемой [8]. Наиболее значимые результаты были получены для симметричных положительно определенных матриц и точечного упорядочения неизвестных. В дальнейшем будем полагать, что свойства сглаживания и аппроксимации всегда выполнены. Тогда справедлива следующая оценка: Выполняя достаточное количество сглаживающих итераций $\nu $, можно добиться сходимости линейного двухсеточного алгоритма, т.е. ${\text{|}}{\kern 1pt} {\text{|}}M{\text{|}}{\kern 1pt} {\text{|}} \leqslant {{C}_{A}}\eta (\nu ) < 1$, причем из (3) следует оценка где ${{\rho }_{q}}$ есть коэффициент осредненного уменьшения нормы вектора невязки который показывает среднее за $q$ итераций уменьшение нормы вектора невязки $\left\| {{{{\mathbf{b}}}_{0}} - {{A}_{0}}\varphi _{0}^{{(q)}}} \right\|$ (см. [9]). Поскольку правая часть неравенства (8) не зависит от шага сетки, то количество межсеточных итераций также не зависит от шага сетки.

Фактически, линейный двухсеточный алгоритм можно рассматривать как способ построения предобуславливающей матрицы ${{P}^{{ - 1}}} = A_{0}^{{ - 1}}(I - M)$, т.е.

где матрица $M$ определена согласно (4).

Наиболее трудоемкой частью итерации двухсеточного алгоритма (3) является обращение матрицы ${{A}_{A}}$, т.е. решение соответствующей СЛАУ. Вычислительная стоимость сглаживающей итерации на исходной сетке ${{G}_{0}}$ составит арифметических операций (ао), где ${{N}_{{{{G}_{0}}}}}$ есть количество узлов исходной сетки ${{G}_{0}}$, ${{N}_{M}}$ есть количество уравнений в системе (1), а ${{n}_{b}}$ – количество блоков неизвестных $1 \ll {{n}_{b}} \leqslant {{N}_{G}}{{N}_{M}}$. Трудоемкость обращения матрицы ${{A}_{A}}$ не должна превышать 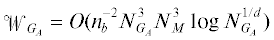ао, $1 \ll {{n}_{b}} \leqslant {{N}_{G}}{{N}_{M}}$. Поскольку ${{N}_{{{{G}_{0}}}}} \approx {{N}_{{{{G}_{A}}}}}$, то вычислительная стоимость одной итерации двухсеточного алгоритма составит

Рассмотренный линейный двухсеточный алгоритм можно рассматривать как разновидность известного вычислительного приема, называемого коррекцией дефекта [2]. Если выполнены свойства сглаживания (5) и аппроксимации (6), то основной объем вычислительной работы приходится на обращение матрицы ${{A}_{A}}$, а итерации (3) сходятся к ${{\varphi }_{0}} = A_{0}^{{ - 1}}{{{\mathbf{b}}}_{0}}$. Это позволяет гибко изменять способ и порядок аппроксимации системы (1).

Трудоемкость метода вспомогательного пространства определяется выбором итерационного метода для решения вспомогательной СЛАУ

где ${{{\mathbf{c}}}_{A}}$ есть поправка.

Численные методы решения краевых задач можно разделить на оптимизированные и робастные [5]. В оптимизированных алгоритмах необходимо адаптировать проблемно-зависимые компоненты к рассматриваемой проблеме, чтобы получить минимально возможную трудоемкость. Робастные алгоритмы пытаются построить так, чтобы компоненты не зависели от данной проблемы для единообразного решения большего класса задач. Основной областью применения робастных алгоритмов являются комплексы программ, устроенные по принципу “черного ящика” (black box software).

В конце 80-х годов прошлого века в теоретическом отделе лаборатории в Лос-Аламосе был описан многосеточный алгоритм (superconvergent multigrid), в котором несколько сеток использовано для отыскания поправки [10], [11]. Основная идея состояла в построении на грубых сетках более точной поправки для ускорения сходимости. В 90-м году аналогичный алгоритм (Robust Multigrid Technique) был предложен в Москве [12], но основная идея состояла в минимизации количества проблемно-зависимых компонентов для расширения класса задач, решаемых унифицированным образом [13]. Забавно, но дополнительные сетки были использованы для построения как оптимизированного, так и робастного алгоритмов.

Новизна предлагаемого подхода состоит в: 1) использовании вспомогательной структурированной сетки ${{G}_{A}}$ в методе вспомогательного пространства;

2) использовании универсальной многосеточной технологии (УМТ) для отыскания поправки на вспомогательной структурированной сетке ${{G}_{A}}$.

2. СГЛАЖИВАНИЕ НА ДВУХБЛОЧНЫХ СЕТКАХ

Пусть некоторая сетка ${{G}_{0}}$ образована ${{N}_{{{{G}_{0}}}}}$ узлами. Положим, что из сетки ${{G}_{0}}$ можно выделить подсетки ${{G}_{i}} \in {{G}_{0}}$, состоящие из ${{N}_{{{{G}_{i}}}}}$ узлов, такие, что

Будем говорить, что совокупность всех подсеток ${{G}_{i}}$, $i = 1,2, \ldots ,I$, образует сеточный уровень, причем а исходная сетка ${{G}_{0}}$ образует нулевой сеточный уровень. Возможны различные варианты построения подсеток ${{G}_{i}}$, однако нас будут интересовать только те из них, которые позволят аппроксимировать исходную краевую задачу на сетках ${{G}_{i}}$ с наименьшей погрешностью.

Определение 1. Вычислительная сетка $G_{1}^{0}$ называется глобально-структурированной, если ее подсетки $G_{k}^{l}$, $l = 1,2, \ldots ,{{L}^{ + }}$, $k = 1,2, \ldots ,K$, обладают следующими свойствами.

Свойство 1. Каждая сетка $G_{k}^{l}$ ($l \ne {{L}^{ + }}$, где ${{L}^{ + }}$ – уровень с самыми грубыми подсетками) представима в виде объединения $K$ соответствующих ей грубых подсеток уровня $l + 1$. Как следствие, исходная сетка $G_{1}^{0}$ представима в виде объединения всех подсеток одного уровня $l$:

Свойство 2. Подсетки одного уровня $l$ не имеют общих точек, т.е.

Свойство 3. Каждый конечный объем на подсетках $G_{k}^{l}$ представим в виде объединения $K$ конечных объемов на исходной сетке $G_{1}^{0}$.

Совокупность всех вычислительных сеток будем называть многосеточной структурой.

Построение глобально-структурированной сетки требует трудоемких действий, связанных либо с отображением области, либо с численным решением (начально-)краевых задач для дифференциальных уравнений в частных производных различных типов. Менее трудоемкими являются разделение области на подобласти более простой формы и построение структурированных сеток в каждой из подобластей. Такие сетки будем называть локально-структурированными или многоблочными. Блоки могут иметь общую границу (фиг. 2) или пересекаться (фиг. 3). В общем случае необходимо интерполировать приближение к решению исходной краевой задачи между блоками сеток, что приводит к снижению скорости сходимости итерационного алгоритма и затрудняет распараллеливание итераций. Способ интерполяции зависит от гладкости коэффициентов и решения. В дальнейшем интерполяцию между блоками сетки будем называть локальной.

Положим, что область $\Omega $ представима в виде объединения подобластей ${{\Omega }_{k}}$, в каждой из которых возможно построение структурированной сетки $G_{k}^{h}$, однако их объединение ${{G}^{h}} = \bigcup\nolimits_{k = 1}^K {G_{k}^{h}} $ не является глобально структурированной сеткой. Сетки данного типа будут называться локально-структурированными или многоблочными.

Далее будет рассмотрен простейший случай $K = 2$, характерный пример показан на фиг. 2: область $\Omega $ состоит из двух подобластей ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$, в каждой из которых построена равномерная структурированная сетка.

Рассмотрим линейную краевую задачу

Здесь ${\mathbf{x}} = {{({{x}_{1}}, \ldots ,{{x}_{d}})}^{{\text{T}}}}$ и $\Omega \in {{\mathbb{R}}^{d}}$ – заданная открытая область с границей $\partial \Omega $, ${{L}_{{{{\Omega }_{1}}}}}$ и ${{L}_{{{{\Omega }_{2}}}}}$ – эллиптические дифференциальные операторы, определенные в подобластях ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ соответственно, ${{f}_{{{{\Omega }_{1}}}}}$ и ${{f}_{{{{\Omega }_{2}}}}}$ обозначают данные функции на ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$. На внешней границе $\partial \Omega $ области $\Omega $ заданы граничные условия а на внутренней границе $\partial {{\Omega }_{2}}$ заданы условия сопряжения

Построим в каждой из областей ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ вычислительные сетки ${{G}_{1}}$ и ${{G}_{2}}$ с шагами ${{h}_{1}}$ и ${{h}_{2}}$. Аппроксимация исходной дифференциальной задачи на двухблочной сетке, образованной сетками ${{G}_{1}}$ и ${{G}_{2}}$, приводит к СЛАУ следующего вида:

где ${\mathbf{u}}$ и ${\mathbf{v}}$ суть дискретные аналоги функции $g$ на сетках ${{G}_{1}}$ и ${{G}_{2}}$ соответственно. Матрицы $C$ и $D$ в общем случае являются прямоугольными и ${{C}^{{\text{T}}}} \ne D$. Вид матриц $C$ и $D$ зависит от типа сеток ${{G}_{1}}$ и ${{G}_{2}}$, которые могут иметь общую границу или пересекаться.

Рассмотрим простейший итерационный метод для решения СЛАУ (10)

где ${{W}_{B}}$ и ${{W}_{F}}$ есть матрицы расщепления матриц $B$ и $F$.

Подставляя ${{{\mathbf{u}}}^{{(\nu + 1)}}}$ из (11а) в (11б), получаем

где Уравнение (12) можно записать в каноническом виде: где

Классический анализ сходимости многосеточных методов основан на свойствах сглаживания и аппроксимации [5]. К сожалению, наиболее изучен симметричный случай [8]. В несимметричном случае результаты получены лишь для сглаживателя с параметром [13]. Запишем (13) в виде

где $S(\omega )$ есть матрица сглаживающих итераций а $\omega \geqslant 0$ есть некоторый параметр.

В несимметричном случае доказательство сглаживающих свойств основано на следующей лемме.

Лемма 1. Пусть для матрицы $Q \in {{\mathbb{R}}^{{n \times n}}}$ выполнено ${\text{|}}{\kern 1pt} {\text{|}}Q{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}} \leqslant 1$ в некоторой операторной норме и $3 - 2\sqrt 2 \leqslant \omega \leqslant 3 + 2\sqrt 2 $. Тогда в той же норме справедливо

Доказательство леммы приведено в [13].

Тогда справедлива следующая лемма о сглаживающих свойствах.

Лемма 2. Пусть для матрицы сглаживающих итераций $S(0) \in {{\mathbb{R}}^{{n \times n}}}$ выполнено ${\text{|}}{\kern 1pt} {\text{|}}S(0){\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}} < 1$ и ${\text{|}}{\kern 1pt} {\text{|}}\tilde {W}{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}} \leqslant C{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}}A{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}}$ в некоторой операторной норме и $C$ есть некоторая константа. Тогда в той же норме при $3 - 2\sqrt 2 \leqslant \omega \leqslant 3 + 2\sqrt 2 $ справедливо:

а)

б)

где ${{r}^{{(\nu )}}} = {\mathbf{\tilde {b}}} - \tilde {A}{{\psi }^{{(\nu )}}}$ есть невязка $\nu $-го приближения ${{\psi }^{{(\nu )}}}$ к решению $\psi = {{\tilde {A}}^{{ - 1}}}{\mathbf{\tilde {b}}}$.

Доказательство. 1) с учетом (15) нетрудно получить

откуда следует (16);

2) для точного решения (14) справедливо

Откуда, домножая на матрицу $A$, следует, что Далее, учитывая (16), нетрудно получить (17).

Тем не менее традиционный подход к доказательству свойства сглаживания в несимметричном случае, основанный на оценках типа (15), является достаточно грубым: например, не симметризованный метод Зейделя обладает свойством сглаживания, что не следует из (16) при $\omega = 0$. Поэтому нужны дополнительные исследования случая $\omega \to 0$.

Данный подход легко обобщить на случай $K > 2$, т.е. если количество блоков сетки больше двух.

3. МНОГОСЕТОЧНЫЕ ИТЕРАЦИИ НА ДВУХБЛОЧНЫХ СЕТКАХ

Сходимость односеточной УМТ проще анализировать в предположении, что сглаживание осуществляют на многосеточной структуре – особой последовательности подсеток самой мелкой сетки [13]. На самом деле, многосеточная структура используется лишь для аппроксимации $\Sigma $-модифицированной краевой задачи (9) интегроинтерполяционным методом. Тогда разностная краевая задача может быть записана в матричной форме:

где матрица коэффициентов ${{A}_{l}}$ имеет вид Матрицы ${{B}_{l}}$, ${{C}_{l}}$, ${{D}_{l}}$ и ${{F}_{l}}$ имеют блочно диагональную форму, причем количество блоков на главной диагонали равно количеству сеток, образующих данный сеточный уровень – ${{3}^{{dl}}}$, d = 2, 3, l = = 0, 1, …, $L_{3}^{ + }$, где $L_{3}^{ + }$ есть номер сеточного уровня, состоящий из самых грубых сеток, построенных утроением шага. Векторы неизвестных ${{{\mathbf{c}}}_{{\mathbf{l}}}}$ и ${{{\mathbf{r}}}_{0}}$ имеют вид Здесь $q$ есть номер многосеточной итерации, ${\mathbf{c}}_{0}^{{\mathbf{u}}}$ и ${\mathbf{c}}_{0}^{{\mathbf{v}}}$ есть поправки к приближению к решению ${\mathbf{\hat {u}}}$ и ${\mathbf{\hat {v}}}$ на  сетках ${{G}_{1}}$  и ${{G}_{2}}$   соответственно.  Нижний индекс $l$ указывает на принадлежность к сеточному  уровню  $l$,  причем $l = 0$ есть самая мелкая сетка. 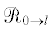Оператор сужения (restriction operator) проецирует вектор невязок ${{{\mathbf{r}}}_{0}}$ с самых мелких сеток ${{G}_{1}}$ и ${{G}_{2}}$ ($l = 0$) на сетки уровня $l = 0,1, \ldots ,L_{3}^{ + }$. Очевидно, что . Оператор сужения УМТ не зависит от решаемой задачи, а его конструкция однозначно определяется свойством аддитивности определенного интеграла относительно подобластей [13].

Сглаживающие итерации (13) на многосеточной структуре, порожденной двухблочной сеткой, могут быть записаны в виде

где

В УМТ используют пилообразный цикл (т.е. V-цикл без предварительного сглаживания [9]). После выполнения сглаживания на всех сетках уровня $l + 1$ осуществляют переход к более мелким сеткам уровня $l$

где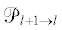 есть проблемно-независимый оператор пролонгации УМТ (перестановочная матрица), т.е. пролонгированное значение поправки с соседнего уровня с более грубыми сетками $l + 1$ принимают в качестве начального приближения для сглаживающих итераций на сетках уровня $l$ [13]. На уровне с самыми грубыми сетками $L_{3}^{ + }$ СЛАУ (18) решают точно.

Тогда из (19) нетрудно получить

где ${{{\mathbf{c}}}_{{\mathbf{l}}}} = A_{l}^{{ - 1}}{{\mathcal{R}}_{{0 \to l}}}{{{\mathbf{r}}}_{0}}$ есть точное значение поправки, а ${{d}_{l}}$ есть матрица вида Исследуя разность между точным и приближенным значением поправки на уровнях $l = L_{3}^{ + }, \ldots ,1,0$, получаем где матрица ${{Q}_{l}}$ определена реккурентным образом:

Значение поправки после выполнения многосеточной итерации УМТ составит

Тогда нетрудно получить новое приближение к решению т.е. матрица многосеточной итерации на многосеточной структуре, порожденной двухблочной сеткой, есть ${{Q}_{0}}{{\tilde {A}}_{0}}$.

Классический анализ сходимости многосеточных методов основан на следующих утверждениях [8].

1. Свойство сглаживания: существует функция $\eta ({{\nu }_{l}}):{{\mathbb{R}}_{ + }} \to {{\mathbb{R}}_{ + }}$ такая, что $\eta ({{\nu }_{l}}) \to 0$ при ${{\nu }_{l}} \to \infty $ и

2. Свойство аппроксимации: для некоторой константы ${{C}_{A}} > 0$

Заметим, что из (16) следует

Перепишем (22) в виде

Тогда справедлива следующая теорема о сходимости УМТ.

Теорема. Предположим, что выполнены свойства сглаживания (23) и аппроксимации (24), а так же $\left\| {I - \tilde {W}_{l}^{{ - 1}}{{A}_{l}}} \right\| < 1$, $\left\| {\mathcal{R}_{{0 \to l}}^{*}} \right\| \leqslant {{C}_{\mathcal{R}}}$ и $3 - 2\sqrt 2 \leqslant {{\omega }_{l}} \leqslant 3 + 2\sqrt 2 $. Тогда многосеточные итерации УМТ сходятся, причем

Доказательство. Из (21) следует оценка

Используя свойства сглаживания (23), (25) и аппроксимации (24), получаем Далее очевидно следующее неравенство: где ${{C}_{*}}$ есть некоторая константа. Тогда оценка (27), с учетом (28) и (29), принимает вид (26).

Доказанная теорема показывает, что сходимость УМТ не зависит ни от шага двухблочной сетки, а определяется только количеством сглаживающих итераций ${{\nu }_{l}}$, выполняемых на сетках уровней $l$. Выполняя достаточное количество сглаживающих итераций, можно добиться, что $\left\| {{{A}_{0}}{{Q}_{0}}} \right\| < 1$ (достаточное условие сходимости).

Полученные результаты легко обобщить на многоблочные сетки с количеством блоков больше двух.

4. ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ

В качестве модельной выбрана трехмерная задача Дирихле для уравнения Пуассона

в единичном кубе $\Omega $. Точное решение выбрано в виде Данное точное решение определяет правую часть $f$ и граничные условия.

Построим в области $\Omega $ равномерную сетку $G$. Разностный аналог исходной краевой задачи, полученный посредством аппроксимации на семиточечном шаблоне, запишем в матричной форме:

Первый тест предназначен для численного решения модельной краевой задачи в единичном кубе $\Omega $ (т.е. без разделения области на подобласти). После каждой многосеточной итерации $q$ вычислены норма вектора невязки $R = {{\left\| {{{{\mathbf{b}}}^{h}} - A{{{\mathbf{w}}}^{h}}} \right\|}_{\infty }}$ и ошибка численного решения $E = \mathop {max}\limits_{ijk} \left| {{{w}_{e}}({{x}_{i}},{{y}_{j}},{{z}_{k}}) - w_{{ijk}}^{h}} \right|$. Критерием останова многосеточных итераций выбрано условие $R < {{10}^{{ - 6}}}$. Результаты первого теста использованы для иллюстрации возможного уменьшения скорости сходимости многосеточных итераций УМТ, вызванного разбиением области $\Omega $ на две подобласти.

Второй тест предназначен для численного решения модельной краевой задачи на двухблочной сетке, построенной в единичном кубе $\Omega $. Равномерная сетка $G$ разделена на два блока ${{G}_{1}}$ и ${{G}_{2}}$ по плоскости $x = 0.5$. Пример разделения в 2D случае показан на фиг. 4. После каждой многосеточной итерации $q$ вычислены норма вектора невязки ${{R}_{{21}}} = {{\left\| {{{{\mathbf{b}}}^{h}} - \tilde {A}{{{\mathbf{w}}}^{h}}} \right\|}_{\infty }}$ и ошибка численного решения ${{E}_{{21}}} = \mathop {max}\limits_{ijk} \left| {{{w}_{e}}({{x}_{i}},{{y}_{j}},{{z}_{k}}) - w_{{ijk}}^{h}} \right|$ на сетке ${{G}_{1}}$, и ${{R}_{{22}}} = {{\left\| {{{{\mathbf{b}}}^{h}} - \tilde {A}{{{\mathbf{w}}}^{h}}} \right\|}_{\infty }}$ и ${{E}_{{22}}} = \mathop {max}\limits_{ijk} \left| {{{w}_{e}}({{x}_{i}},{{y}_{j}},{{z}_{k}}) - w_{{ijk}}^{h}} \right|$ на сетке ${{G}_{2}}$. Критерием останова многосеточных итераций выбрано условие ${\text{max}}({{R}_{{21}}};{{R}_{{22}}}) < {{10}^{{ - 6}}}$. Сглаживание осуществляется попеременно на подсетках сеток ${{G}_{1}}$ и ${{G}_{2}}$.

Третий тест отличается от второго только сглаживанием: сначала сглаживающие итерации выполняют на подсетках сетки ${{G}_{1}}$, потом на подсетках сетки ${{G}_{2}}$. После каждой многосеточной итерации $q$ вычислены норма вектора невязки ${{R}_{{31}}} = {{\left\| {{{{\mathbf{b}}}^{h}} - \tilde {A}{{{\mathbf{w}}}^{h}}} \right\|}_{\infty }}$ и ошибка численного решения ${{E}_{{31}}} = \mathop {max}\limits_{ijk} \left| {{{w}_{e}}({{x}_{i}},{{y}_{j}},{{z}_{k}}) - w_{{ijk}}^{h}} \right|$ на сетке ${{G}_{1}}$, и ${{R}_{{32}}} = {{\left\| {{{{\mathbf{b}}}^{h}} - \tilde {A}{{{\mathbf{w}}}^{h}}} \right\|}_{\infty }}$ и ${{E}_{{32}}} = \mathop {max}\limits_{ijk} \left| {{{w}_{e}}({{x}_{i}},{{y}_{j}},{{z}_{k}}) - w_{{ijk}}^{h}} \right|$ на сетке ${{G}_{2}}$. Критерием останова многосеточных итераций выбрано условие ${\text{max}}({{R}_{{31}}};{{R}_{{32}}}) < {{10}^{{ - 6}}}$.

В качестве сглаживателя выбран метод Зейделя с упорядочением неизвестных в блоки $3 \times 3 \times 3$. Вычисления проведены на сетках $101 \times 101 \times 101$ (${{h}_{x}} = {{h}_{y}} = {{h}_{z}} = 1{\text{/}}100$) и $301 \times 301 \times 301$ (${{h}_{x}} = {{h}_{y}} = {{h}_{z}} = 1{\text{/}}300$).

Результаты вычислительного эксперимента показаны на фиг. 5 и 6. При надлежащей организации сглаживания (второй тест) сходимость УМТ на двухблочной сетке практически не отличается от сходимости на моноблочной сетке (первый тест). Выполнение сглаживания последовательно на каждом блоке приводит к замедлению сходимости УМТ.

ЗАКЛЮЧЕНИЕ

Результаты выполненного теоретического анализа и проведенных вычислительных экспериментов показывают, что при надлежащей организации сглаживания количество многосеточных итераций не зависит ни от величины шага, ни от количества блоков сетки. Однако в теоретическом анализе сходимости многосеточных методов еще остаются пробелы, связанные, в частности, с доказательством свойства сглаживания для несимметричных итерационных методов, использующих блочное упорядочение неизвестных.