Журнал вычислительной математики и математической физики, 2022, T. 62, № 10, стр. 1740-1760
Численная модель многофазных течений на основе подсеточного разрешения контактных границ
И. С. Меньшов 1, 2, *, А. А. Серёжкин 1, **
1 Всероссийский научно-исследовательский институт автоматики
им. Н.Л. Духова
127030 Москва, Сущевская ул., 22, Россия
2 ИПМ им. М.В. Келдыша
125047 Москва, Миусская пл., 4, Россия
* E-mail: imen57@mail.ru
** E-mail: aaserezhkin@gmail.com
Поступила в редакцию 26.10.2021
После доработки 16.02.2022
Принята к публикации 23.04.2022
- EDN: JACQGC
- DOI: 10.31857/S0044466922090101
Аннотация
В статье рассматриваются вопросы численного моделирования сжимаемых многофазных течений с разрешением межфазных границ. Используется неравновесная по скорости, давлению и температуре релаксационная модель Байера-Нунзиато. Основными элементами предлагаемого подхода являются простая модель локальной подсеточной реконструкции межфазной границы в окрестности грани счетной ячейки и моделирование релаксационных процессов в смешанных ячейках с помощью решения составной задачи Римана. Предлагаются два приближенных решения этой задачи, учитывающие взаимодействие первичных и формирование вторичных волн в рамках приближенных решений типа HLL и HLLC. Метод не требует каких-либо специальных параметров релаксации и позволяет поддерживать фактически бездиффузионное разрешение межфазной границы, что демонстрируется на примерах расчетов ряда тестовых задач. Библ. 21. Фиг. 9. Табл. 2.
1. ВВЕДЕНИЕ
Рассматривается задача численного моделирования течения многофазной гетерогенной среды, состоящей из несмешивающихся материалов (фаз), разделенных контактными границами. Такие среды, с точки зрения сложившихся в современной науке подходов к моделированию, могут быть разделены на два класса, в зависимости от способа численного разрешения межфазной поверхности. Эта классификация является условной и определяется постановкой задачи и вычислительными ресурсами.
К первому классу относятся среды, в которых области, занимаемые конкретным материалом, имеют вид крупных структур, ограниченных поверхностью достаточно малой кривизны. Межфазные границы (интерфейсы) в этом случае разрешаются на расчетных сетках методами точного отслеживания их положения в пространстве (Sharp interface, immerseded boundary и др.), либо градиентом параметра объемной доли (VOF, THINC и др.) [1]–[5]. При этом большинство ячеек сетки не являются смешанными и содержат только одну фазу. Такого рода многофазные течения называются в литературе течениями с разрешаемым интерфейсом (interface resolved flows) [6]. Примером является развитие гидродинамической неустойчивости контактной поверхности [7], [8].
Ко второму классу относятся среды, в которых одна из фаз имеет вид мелких дисперсных структур (пузырьков, капель или частиц). Отслеживание границ таких структур на сеточном уровне требует слишком подробных сеток и для определенных задач нецелесообразно. Поэтому контактные границы не выделяются явным образом; неоднородность среды определяется параметром объемной доли фазы, принимающим значение между нулем и единицей. Примером подобных задач являются задачи динамики пылегазовых смесей, горения и детонации конденсированных ВВ, течения жидкости с пузырьками газа [9]–[11].
В настоящей работе рассматриваются многофазные течения, относящиеся к первому классу. Для численного моделирования таких многофазных (многоматериальных) гетерогенных сред разработан широкий класс моделей и методов численного решения систем уравнений математических моделей. В данной статье мы используем гидродинамическую модель 7 уравнений, основанную на полностью неравновесном подходе Баера-Нунзиато [9]. Этот подход базируется на представлении многофазной среды в виде множества взаимопроникающих и взаимодействующих континуумов, каждый из которых характеризуется своим вектором состояния, т.е. плотностью, скоростью, давлением и внутренней энергией. Параметры каждого континуума (фазы) связаны балансовыми уравнениями массы, импульса и энергии и уравнениями состояния. Объемное содержание фаз определяется параметром объемной доли. Взаимодействие фаз моделируется введением специальных переменных, характеризующих состояние среды на межфазных поверхностях, а также релаксационных параметров, определяющих скорость выравнивания давлений, скоростей и температур фаз в области контакта между фазами. Модели, использующие данный подход, являются строго гиперболическими и термодинамически согласованными. Как правило, модели семи уравнений применяются для расчетов течений сред, относящихся ко второму классу. В работе [12] показано, что как таковых ограничений на вид контактной поверхности для модели семи уравнений нет; аналогичные уравнения могут быть введены и для случая, когда контактная поверхность является разрешаемой на масштабах рассматриваемой задачи.
При моделировании сред, относящихся к первому классу, обычно используется упрощенный равновесный или частично равновесный подход, когда предполагается мгновенное выравнивание отдельных параметров течения фаз, например, скоростей, давлений или температур. Такие модели выводятся путем асимптотического анализа при стремлении параметров релаксации к нулю [10], [13], [14]. Однако переход к редуцированным моделям может приводить к нарушению гиперболичности и термодинамической согласованности. Этот недостаток исправляется выбором подходящих замыкающих соотношений на параметры межфазной границы, которые, как правило, не имеют физического обоснования. Кроме того, сокращение числа уравнений в этом случае требует дополнительных условий замыкания.
В силу вышесказанного имеет смысл рассмотреть моделирование течений сред, относящихся к первому классу, в рамках полностью неравновесных моделей. При этом возникает проблема выбора параметров релаксации. Надлежащий выбор этих параметров представляет собой отдельную проблему, и зачастую они, по сути, подгоняются под определенную задачу. С физической точки зрения релаксация параметров среды в малом объеме, содержащем контактную поверхность, является результатом гидродинамического взаимодействия фаз, что при искусственном выборе параметров релаксации игнорируется. В данной работе мы попытаемся полностью уйти от задания параметров релаксации путем замены релаксационного процесса моделированием гидродинамического взаимодействия на контакте.
Таким образом, формируется цель текущей работы – построение численной модели течений многофазных сред с разрешенным интерфейсом в рамках многоконтинуального неравновесного подхода с мгновенной механической релаксацией на контактной границе. Последнее подразумевает равенство скоростей и давлений на границе фаз, что обеспечивается за счет гидродинамического взаимодействия фаз на контактной границе. Для выполнения данной цели используются метод локального подсеточного восполнения границ и решение составной задачи Римана (Composite Riemann Problem – CRP), разработанные ранее для равновесной PT модели [6]. В настоящей статье рассматривается ее расширение WCRP для неравновесной модели.
Недостатком неравновесной модели является формальное вырождение системы уравнений в области, где одна из фаз отсутствует. Чтобы исключить его, предполагают, что отсутствующая в области фаза всегда представлена очень малым количеством, которое не оказывает влияния на рассматриваемый процесс, но позволяет избежать эффекта вырождения. В практической реализации считается, что в любой точке расчетной области присутствует весь набор фаз. Это, во-первых, увеличивает расчетное время, поскольку сложная система с малыми параметрами требует более сложных методов решения, приводящих к большим вычислительным затратам. Во-вторых, в случае жестких параметров релаксации и ввиду численных погрешностей методов, в фазах с малым объемным содержанием могут возникать физически невозможные состояния фаз (отрицательные плотности, давления, температуры). Несмотря на то что нефизичное состояние получается в малом объеме, и на течение оно не оказывает влияния, оно может привести к аварийной остановке счета. Численная методика, разрабатываемая в настоящей работе, позволяет обойти данную проблему.
Статья структурирована следующим образом. В первом разделе представлена математическая модель, которая будет использоваться для построения численной методики, показана связь системы уравнений с общеизвестными моделями. Во втором разделе описывается численный метод, включающий подсеточное восполнение контактной границы и аппроксимацию численных потоков, приводится постановка CRP и рассматриваются ее приближенные решения. В третьем разделе приводятся результаты численных расчетов. На примере задач конвективного переноса показывается основное преимущество предложенной методики – полное отсутствие численного размытия контактной границы. На примере задачи о распаде разрыва проводится сравнительный анализ численных результатов, полученных с использованием различных методов аппроксимации составной задачи Римана, и референсных решений по равновесной модели. Возможности предложенной методики демонстрируются на решениях двумерных задач: о схлопывании пузырька под воздействием ударной волны и тестовой задачи о тройной точке, известной в английской литературе как triple point problem.
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НЕРАВНОВЕСНОЙ МНОГОФАЗНОЙ СРЕДЫ
Построение модели и метода проводится для случая двух фаз. Мы используем описание среды в виде взаимопроникающих континуумов, что означает, что в любом сколь угодно малом объеме пространства находятся обе фазы с определенной объемной концентрацией. Это является математической абстракцией, так как физический объем нельзя сделать сколь угодно малым. Поэтому, говоря о континууме и о состоянии среды в точке, имеются в виду осредненные по малому физическому объему параметры течения. Таким образом, под понятием состояния среды в точке мы полагаем состояние, осредненное по некоторому малому объему, содержащему данную точку. Этот объем может включать как одну, так и обе фазы.
Рассмотрим некоторый достаточно малый объем пространства $\Omega $, произвольно разделенный гиперповерхностью ${{\partial }_{I}}\Omega $ ограниченной кривизны на две (не обязательно связные) области ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$. Положим, что каждая из областей заполнена сплошной средой, которая описывается гидродинамической моделью невязкой сжимаемой жидкости (модель Эйлера). Тогда, следуя выводу, предложенному в работе [12], получим систему уравнений, представляющую законы сохранения массы, импульса и энергии для каждой из фаз:
(1)
$\begin{gathered} \frac{{\partial {{\varphi }_{k}}{{\rho }_{k}}}}{{\partial t}} + \nabla \cdot ({{\varphi }_{k}}{{\rho }_{k}}{{{\mathbf{u}}}_{k}}) = 0, \\ \frac{{\partial {{\varphi }_{k}}{{\rho }_{k}}{{{\mathbf{u}}}_{k}}}}{{\partial t}} + \nabla \cdot ({{\varphi }_{k}}{{\rho }_{k}}{{{\mathbf{u}}}_{k}} \otimes {{{\mathbf{u}}}_{k}}) + \nabla ({{\varphi }_{k}}{{P}_{k}}) = \frac{1}{{V(\Omega )}}\int\limits_{{{\partial }_{I}}\Omega } {{P}_{I}}{{{\mathbf{n}}}_{k}}ds, \\ \frac{{\partial {{\varphi }_{k}}{{\rho }_{k}}{{E}_{k}}}}{{\partial t}} + \nabla \cdot ({{\varphi }_{k}}{{\rho }_{k}}{{E}_{k}}{{{\mathbf{u}}}_{k}}) + \nabla \cdot ({{\varphi }_{k}}{{P}_{k}}{{{\mathbf{u}}}_{k}}) = \frac{1}{{V(\Omega )}}\int\limits_{{{\partial }_{I}}\Omega } {{P}_{I}}({{{\mathbf{u}}}_{I}}{{{\mathbf{n}}}_{k}})ds. \\ \end{gathered} $(2)
$\frac{{\partial {{\varphi }_{k}}}}{{\partial t}} = \frac{1}{{V(\Omega )}}\int\limits_{{{\partial }_{I}}\Omega } ({{{\mathbf{u}}}_{I}}{{{\mathbf{n}}}_{k}})ds.$Предполагаем, что осредненные параметры фаз удовлетворяют уравнениям состояния: ${{e}_{k}} = {{e}_{k}}({{\rho }_{k}},{{P}_{k}})$, где ${{e}_{k}} = {{E}_{k}} - 0.5({{{\mathbf{u}}}_{k}}{{{\mathbf{u}}}_{k}})$.
Система уравнений (1) и (2) имеет недивергентную форму, поскольку включает интегральные члены в правых частях, зависящие от значений интерфейсных параметров. Стандартный подход к упрощению модели состоит в том, чтобы аппроксимировать интерфейсные величины ${{P}_{I}}$ и ${{{\mathbf{u}}}_{I}}$ осредненными величинами ${{\bar {P}}_{I}}$ и ${{{\mathbf{\bar {u}}}}_{I}}$, постоянными по объему $\Omega $, и предположить, что зависимость формы и площади поверхности ${{\partial }_{I}}\Omega $ от времени мала. В этом случае система уравнений (1) и (2) примет вид:
(3)
$\begin{gathered} \frac{{\partial {{\varphi }_{k}}{{\rho }_{k}}}}{{\partial t}} + \nabla \cdot ({{\varphi }_{k}}{{\rho }_{k}}{{{\mathbf{u}}}_{k}}) = 0, \\ \frac{{\partial {{\varphi }_{k}}{{\rho }_{k}}{{{\mathbf{u}}}_{k}}}}{{\partial t}} + \nabla \cdot ({{\varphi }_{k}}{{\rho }_{k}}{{{\mathbf{u}}}_{k}} \otimes {{{\mathbf{u}}}_{k}}) + \nabla ({{\varphi }_{k}}{{P}_{k}}) = {{{\bar {P}}}_{I}}\nabla {{\varphi }_{k}}, \\ \frac{{\partial {{\varphi }_{k}}{{\rho }_{k}}{{E}_{k}}}}{{\partial t}} + \nabla \cdot ({{\varphi }_{k}}{{\rho }_{k}}{{E}_{k}}{{{\mathbf{u}}}_{k}}) + \nabla \cdot ({{\varphi }_{k}}{{P}_{k}}{{{\mathbf{u}}}_{k}}) = {{{\bar {P}}}_{I}}{{{{\mathbf{\bar {u}}}}}_{I}}\nabla {{\varphi }_{k}}, \\ \frac{{\partial {{\varphi }_{k}}}}{{\partial t}} = - {{{{\mathbf{\bar {u}}}}}_{I}}\nabla {{\varphi }_{k}}. \\ \end{gathered} $Определение средних величин ${{\bar {P}}_{I}}$ и ${{{\mathbf{\bar {u}}}}_{I}}$ может быть введено разными способами. В классической модели Баера-Нунзиато [9] выделяется одна более плотная фаза (твердая) и одна менее плотная фаза (газ), и в качестве ${{P}_{I}}$ берется давление газовой фазы, а в качестве ${{{\mathbf{u}}}_{I}}$ – скорость твердой фазы.
В модели Сауреля и Абграля [15] используется среднее по динамическим импедансам,
(4)
${{\bar {P}}_{I}} = \frac{{{{\rho }_{1}}{{C}_{1}}{{P}_{2}} + {{\rho }_{2}}{{C}_{2}}{{P}_{1}}}}{{{{\rho }_{1}}{{C}_{1}} + {{\rho }_{2}}{{C}_{2}}}},$(5)
${{{\mathbf{\bar {u}}}}_{I}} = \frac{{{{\rho }_{1}}{{C}_{1}}{{{\mathbf{u}}}_{1}} + {{\rho }_{2}}{{C}_{2}}{{{\mathbf{u}}}_{2}}}}{{{{\rho }_{1}}{{C}_{1}} + {{\rho }_{2}}{{C}_{2}}}} - {\text{sgn}}\left( {\nabla {{\varphi }_{1}}{{{\mathbf{n}}}_{1}}} \right)\frac{{{{P}_{1}} - {{P}_{2}}}}{{{{\rho }_{1}}{{C}_{1}} + {{\rho }_{2}}{{C}_{2}}}}.$В работе [12] предлагается модель интерфейсных параметров, основанная на предположении о связности областей, занимаемых фазами в $\Omega $. Если обе области связные, давление ${{\bar {P}}_{I}}$ является решением квадратного уравнения:
(6)
$\frac{{{{P}_{1}} - {{{\bar {P}}}_{I}}}}{{{{T}_{1}}}}{{\varphi }_{1}}{{\rho }_{2}}C_{{2I}}^{2} + \frac{{{{P}_{2}} - {{{\bar {P}}}_{I}}}}{{{{T}_{2}}}}{{\varphi }_{2}}{{\rho }_{1}}C_{{1I}}^{2} = 0$(7)
${{{\mathbf{\bar {u}}}}_{I}} = \frac{{{{\varphi }_{2}}{{\rho }_{1}}C_{{1I}}^{2}{{{\mathbf{u}}}_{1}} + {{\varphi }_{1}}{{\rho }_{2}}C_{{2I}}^{2}{{{\mathbf{u}}}_{2}}}}{{{{\varphi }_{2}}{{\rho }_{1}}C_{{1I}}^{2} + {{\varphi }_{1}}{{\rho }_{2}}C_{{2I}}^{2}}}.$(8)
$C_{{kI}}^{2} = \frac{{{{{\bar {P}}}_{I}}{\text{/}}\rho _{k}^{2} + \partial {{e}_{k}}{\text{/}}\partial {{\rho }_{k}}}}{{\partial {{e}_{k}}{\text{/}}\partial {{P}_{k}}}}.$Если область фазы 1 связная, а фазы 2 несвязная, давление и скорость на контакте равны ${{\bar {P}}_{I}} = {{P}_{1}}$, ${{{\mathbf{\bar {u}}}}_{I}} = {{{\mathbf{u}}}_{2}}$. Если наоборот (2 – связная, 1 – несвязная), значения параметров на контактной границе берутся соответственно: ${{\bar {P}}_{I}} = {{P}_{2}}$, ${{{\mathbf{\bar {u}}}}_{I}} = {{{\mathbf{u}}}_{1}}$.
В настоящей работе в качестве интерфейсных значений ${{\bar {P}}_{I}}$ и ${{{\mathbf{\bar {u}}}}_{I}}$ берутся их значения, получающиеся непосредственно из решения задачи о распаде разрыва на контактной поверхности. Задача состоит в том, каким образом определить положение контактной поверхности и параметры взаимодействующих на ней фаз. В п. 3.2 этот вопрос рассматривается на основе специального алгоритма подсеточного восполнения межфазной границы.
Система уравнений (1)–(2) может быть записана в векторной форме:
(9)
$\frac{{\partial {\mathbf{Q}}}}{{\partial t}} + \frac{{\partial {{{\mathbf{F}}}_{x}}}}{{\partial x}} + \frac{{\partial {{{\mathbf{F}}}_{y}}}}{{\partial y}} + \frac{{\partial {{{\mathbf{F}}}_{z}}}}{{\partial z}} = \frac{1}{{V(\Omega )}}\int\limits_{{{\partial }_{I}}\Omega } {\mathbf{G}}ds.$(10)
${\mathbf{Q}} = \left( {\begin{array}{*{20}{c}} {{{\varphi }_{1}}{{\rho }_{1}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{{\mathbf{u}}}_{{1x}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{{\mathbf{u}}}_{{1y}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{{\mathbf{u}}}_{{1z}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{E}_{1}}} \\ {{{\varphi }_{1}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{{\mathbf{u}}}_{{2x}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{{\mathbf{u}}}_{{2y}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{{\mathbf{u}}}_{{2z}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{E}_{2}}} \\ {{{\varphi }_{2}}} \end{array}} \right).$Вектора ${{F}_{x}}$, ${{F}_{y}}$, ${{F}_{z}}$ определяют консервативные потоки по направлениям $x,\;y,\;z$:
(11)
${{{\mathbf{F}}}_{x}} = \left( {\begin{array}{*{20}{c}} {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1x}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1x}}}{{u}_{{1x}}} + {{\varphi }_{1}}{{P}_{1}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1y}}}{{u}_{{1x}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1z}}}{{u}_{{1x}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{E}_{1}}{{u}_{{1x}}} + {{\varphi }_{1}}{{P}_{1}}{{u}_{{1x}}}} \\ 0 \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2x}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2x}}}{{u}_{{2x}}} + {{\varphi }_{2}}{{P}_{2}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2y}}}{{u}_{{2x}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2z}}}{{u}_{{2x}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{E}_{2}}{{u}_{{2x}}} + {{\varphi }_{2}}{{P}_{2}}{{u}_{{2x}}}} \\ 0 \end{array}} \right),\quad {{{\mathbf{F}}}_{y}} = \left( {\begin{array}{*{20}{c}} {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1y}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1x}}}{{u}_{{1y}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1y}}}{{u}_{{1y}}} + {{\varphi }_{1}}{{P}_{1}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1z}}}{{u}_{{1y}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{E}_{1}}{{u}_{{1y}}} + {{\varphi }_{1}}{{P}_{1}}{{u}_{{1y}}}} \\ 0 \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2y}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2x}}}{{u}_{{2y}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2y}}}{{u}_{{2y}}} + {{\varphi }_{2}}{{P}_{2}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2z}}}{{u}_{{2y}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{E}_{2}}{{u}_{{2y}}} + {{\varphi }_{2}}{{P}_{2}}{{u}_{{2y}}}} \\ 0 \end{array}} \right),\quad {{{\mathbf{F}}}_{z}} = \left( {\begin{array}{*{20}{c}} {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1z}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1x}}}{{u}_{{1z}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1y}}}{{u}_{{1z}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{u}_{{1z}}}{{u}_{{1z}}} + {{\varphi }_{1}}{{P}_{1}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{E}_{1}}{{u}_{{1z}}} + {{\varphi }_{1}}{{P}_{1}}{{u}_{{1z}}}} \\ 0 \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2z}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2x}}}{{u}_{{2z}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2y}}}{{u}_{{2z}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{u}_{{2z}}}{{u}_{{2z}}} + {{\varphi }_{2}}{{P}_{2}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{E}_{2}}{{u}_{{2z}}} + {{\varphi }_{2}}{{P}_{2}}{{u}_{{2z}}}} \\ 0 \end{array}} \right).$Вектор ${\mathbf{G}}$ определяет неконсервативную часть системы:
(12)
${\mathbf{G}} = \left( {\begin{array}{*{20}{c}} 0 \\ {{{P}_{I}}{{n}_{{1x}}}} \\ {{{P}_{I}}{{n}_{{1y}}}} \\ {{{P}_{I}}{{n}_{{1z}}}} \\ {{{P}_{I}}{{u}_{{Ix}}}{{n}_{{1x}}} + {{P}_{I}}{{u}_{{Iy}}}{{n}_{{1y}}} + {{P}_{I}}{{u}_{{Iz}}}{{n}_{{1z}}}} \\ {{{u}_{{Ix}}}{{n}_{{1x}}} + {{u}_{{Iy}}}{{n}_{{1y}}} + {{u}_{{Iz}}}{{n}_{{1z}}}} \\ 0 \\ {{{P}_{I}}{{n}_{{2x}}}} \\ {{{P}_{I}}{{n}_{{2y}}}} \\ {{{P}_{I}}{{n}_{{2z}}}} \\ {{{P}_{I}}{{u}_{{Ix}}}{{n}_{{2x}}} + {{P}_{I}}{{u}_{{Iy}}}{{n}_{{2y}}} + {{P}_{I}}{{u}_{{Iz}}}{{n}_{{2z}}}} \\ {{{u}_{{Ix}}}{{n}_{{2x}}} + {{u}_{{Iy}}}{{n}_{{2y}}} + {{u}_{{Iz}}}{{n}_{{2z}}}} \end{array}} \right).$Заметим, что в областях ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ система уравнений (9) удовлетворяется. Значения объемных долей принимают значения $0$ или $1$, интеграл в правой части берется по пустому множеству и равен нулю. Часть уравнений вырождается, и система (9) сводится к системе Эйлера для одной из фаз. Параметр объемной доли служит здесь индикаторной функцией фазы. Данное замечание является ключевым в построении численного метода для решения системы (9).
3. ЧИСЛЕННЫЙ МЕТОД
3.1. Схема расчета нового временного слоя
Построение численного метода рассмотрим сначала для одномерного случая, а потом приведем обобщение на многомерный случай.
Пусть имеется одномерная эйлерова сетка с постоянным шагом $\Delta l$, в которой ячейка $i$ является смешанной (фиг. 1). Рассмотрим одномерный аналог системы уравнений (9), где $\Omega $ соответствует интервалу $\Delta l$, и проинтегрируем ее по времени на шаге $\Delta t$ и по ячейке $i$. В результате получим следующее уравнение для перехода сеточных значений консервативного вектора ${\mathbf{Q}}$ с одного временного слоя на другой:
(13)
$({{{\mathbf{Q}}}_{i}}({{t}_{0}} + \Delta t) - {{{\mathbf{Q}}}_{i}}({{t}_{0}}))\Delta l = \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{F}}({{x}_{{i - 1/2}}})dt - \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{F}}({{x}_{{i + 1/2}}})dt + \int\limits_{{{\partial }_{I}}} \,{\mathbf{G}}dt,$(14)
$\int\limits_{{{\partial }_{I}}} {\kern 1pt} {\mathbf{G}}dt = - \int\limits_{{{\partial }^{ - }}} {\kern 1pt} ({\mathbf{Q}}{{u}_{I}} - {\mathbf{F}})dt + \int\limits_{{{\partial }^{ + }}} {\kern 1pt} ({\mathbf{Q}}{{u}_{I}} - {\mathbf{F}})dt,$(15)
$\begin{gathered} ({{{\mathbf{Q}}}_{i}}({{t}_{0}} + \Delta t) - {{{\mathbf{Q}}}_{i}}({{t}_{0}}))\Delta l = - \left[ {\int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{F}}({{x}_{{i + 1/2}}})dt - \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} ({\mathbf{Q}}(x_{c}^{ + }(t)){{u}_{I}} - {\mathbf{F}}(x_{c}^{ + }(t)))dt} \right] + \\ \, + \left[ {\int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{F}}({{x}_{{i - 1/2}}})dt - \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} ({\mathbf{Q}}(x_{c}^{ - }(t)){{u}_{I}} - {\mathbf{F}}(x_{c}^{ - }(t)))dt} \right], \\ \end{gathered} $(16)
${{{\mathbf{Q}}}_{i}}({{t}_{0}} + \Delta t) = {{{\mathbf{Q}}}_{i}}({{t}_{0}}) - \frac{1}{{\Delta l}}({{{\mathbf{F}}}_{{i + 1/2}}} - {{{\mathbf{F}}}_{{i - 1/2}}}),$(18)
$\begin{gathered} {{\Phi }_{{i + 1/2}}} = \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{F}}({{x}_{{i + 1/2}}})dt,\quad {{\Phi }_{{i - 1/2}}} = \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{F}}({{x}_{{i - 1/2}}})dt, \\ \Phi _{{i + 1/2}}^{'} = \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{Q}}(x_{c}^{ \pm }){{u}_{I}} - {\mathbf{F}}(x_{c}^{ \pm })dt,\quad \Phi _{{i - 1/2}}^{'} = \int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} {\mathbf{Q}}(x_{c}^{ \pm }){{u}_{I}} - {\mathbf{F}}(x_{c}^{ \pm })dt, \\ \end{gathered} $Заметим, что если контактная граница в течение рассматриваемого промежутка времени выходит за границы ячейки, то схема (16) учитывает интеграл неконсервативной части системы уравнений только по той части кривой ${{\partial }_{I}}$, которая соответствует нахождению контактной границы внутри ячейки; оставшаяся часть должна учитываться в расчете соседней ячейки. Аппроксимация потоков ${{{\mathbf{F}}}_{{i \pm 1/2}}}$ выполняется по методу С.К. Годунова на основе решения составной задачи Римана. Ниже вопрос аппроксимации потока рассматривается более подробно.
Рассмотренная схема обобщается на многомерный случай в предположении локальной одномерности течения вблизи каждой грани счетной ячейки. В общем случае схема принимает следующий вид:
(19)
${{{\mathbf{Q}}}_{i}}({{t}_{0}} + \Delta t) = {{{\mathbf{Q}}}_{i}}({{t}_{0}}) - \frac{1}{{V(\Omega )}}\int\limits_{{{t}_{0}}}^{{{t}_{0}} + \Delta t} \left( {\sum\limits_{{{\Psi }^{k}}} \left( {\int\limits_{{{\Psi }_{k}}} {{\Phi }_{n}}ds - \int\limits_{{{\Psi }_{k}}} \Phi _{n}^{'}ds} \right)} \right)dt,$3.2. Подсеточная реконструкция контактной границы
Для подсеточного восполнения контактной границы используется метод, предложенный в работе [6], [8]. Реконструкция границы внутри ячейки производится локально около каждой грани ${{\Psi }^{i}}$ ячейки $\Omega $ ($i = 1,2,...$, $\partial \Omega = {{\Psi }^{1}} \cup {{\Psi }^{2}} \cup ...$). с помощью определенного паттерна, выбор которого определяется в зависимости от объемного содержания фаз в текущей ячейке и в соседней с ней через рассматриваемую грань.
Допустим, в одной из рассматриваемых ячеек ${{\Omega }^{1}}$ содержится только одна фаза, например, фаза 1 (будем называть ячейку чистой), а в другой ячейке ${{\Omega }^{2}}$ содержится две фазы $1$ и $2$ с объемными долями ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ (будем называть такую ячейку смешанной). Тогда подсеточная реконструкция поверхности определяется паттерном плоскости, параллельной грани $\Psi $, фиг. 2а. Расстояние от грани до границы $\delta $ определяется объемной долей фаз в смешанной ячейке,
здесь и далее $S(\Psi )$ – площадь грани $\Psi $. Другой случай – это когда обе соседствующие ячейки являются смешанными с объемным содержанием фаз $\varphi _{1}^{1}$ и $\varphi _{2}^{1}$ в первой и $\varphi _{1}^{2}$ и $\varphi _{2}^{2}$ во второй. Подсеточная реконструкция поверхности в этом случае производится с помощью паттерна типа ступенька, схематически представленного на фиг. 2б,в. Параметры этого паттерна определяются площадями ${{S}_{1}}$ и ${{S}_{2}}$, занятыми фазами 1 и 2, соответственно. В случае, если $\nabla {{\varphi }_{1}}{{{\mathbf{n}}}^{1}} < 0$, где ${{{\mathbf{n}}}^{1}}$ – внешняя по отношению к ${{\Omega }^{1}}$ нормаль к грани $\Psi $, реконструкция производится по паттерну, изображенному на фиг. 2б, и значения его параметров определяются следующим образом:(21)
$\frac{{{{S}_{2}}}}{{{{S}_{2}} + {{S}_{1}}}} = \left\{ \begin{gathered} \frac{{\varphi _{2}^{1}}}{{\varphi _{1}^{2} + \varphi _{2}^{1}}},\quad {\text{если}}\quad \varphi _{1}^{2} < \varphi _{2}^{2}, \hfill \\ \frac{{\varphi _{2}^{2}}}{{\varphi _{1}^{1} + \varphi _{2}^{2}}},\quad {\text{если}}\quad \varphi _{1}^{2} > \varphi _{2}^{2}, \hfill \\ \end{gathered} \right.\quad {{S}_{1}} + {{S}_{2}} = S(\Psi ),$(22)
${{\delta }^{1}} = \frac{{\varphi _{2}^{1}V({{\Omega }^{1}})}}{{{{S}_{2}}}},\quad {{\delta }^{2}} = \frac{{\varphi _{1}^{2}V({{\Omega }^{2}})}}{{{{S}_{1}}}}.$Фиг. 2.
Восполнение контактной поверхности при расчете составной задачи Римана на границе между чистой и смешанной ячеек (а) и двух смешанных ячеек (б, в).

В случае если $\nabla {{\varphi }_{1}}{{{\mathbf{n}}}^{1}} > 0$, подсеточная реконструкция строится по паттерну, представленному на фиг. 2в, значения параметров определяются следующим образом:
(23)
$\frac{{{{S}_{1}}}}{{{{S}_{2}} + {{S}_{1}}}} = \left\{ \begin{gathered} \frac{{\varphi _{1}^{1}}}{{\varphi _{1}^{1} + \varphi _{2}^{2}}},\quad {\text{если}}\quad \varphi _{1}^{1} < \varphi _{1}^{2}, \hfill \\ \frac{{\varphi _{1}^{2}}}{{\varphi _{2}^{1} + \varphi _{1}^{2}}},\quad {\text{если}}\quad \varphi _{1}^{1} > \varphi _{1}^{2}, \hfill \\ \end{gathered} \right.\quad {{S}_{1}} + {{S}_{2}} = S(\Psi ),$(24)
${{\delta }^{1}} = \frac{{\varphi _{1}^{1}V({{\Omega }^{1}})}}{{{{S}_{1}}}},\quad {{\delta }^{2}} = \frac{{\varphi _{2}^{2}V({{\Omega }^{2}})}}{{{{S}_{2}}}}.$Расчет численных потоков на грани двух смешанных ячеек разбивается на две локально одномерные задачи вычисления потока через грань, разделяющую чистую и смешанную ячейки. Аппроксимация потока строится на основе решения составной задачи Римана (CRP). Полный поток определяется взвешенной с весами $\frac{{{{S}_{1}}}}{{{{S}_{1}} + {{S}_{2}}}}$ и $\frac{{{{S}_{2}}}}{{{{S}_{1}} + {{S}_{2}}}}$ суммой потоков, полученных решением двух локально одномерных CRP.
3.3. Аппроксимация численного потока
3.3.1. Приближенные решения автомодельной задачи Римана. Кратко опишем методы HLL и HLLC для приближенной аппроксимации решения задачи Римана. С помощью этих решений затем будут строиться решение составной задачи Римана и аппроксимация численного потока. Пусть имеются две полубесконечные области слева и справа от плоскости начального разрыва, в которых заданы равномерные распределения векторов состояния ${{{\mathbf{Q}}}_{L}}$ и ${{{\mathbf{Q}}}_{R}}$ и соответствующие векторы консервативных потоков в нормальном к плоскости направлении ${{{\mathbf{F}}}_{L}}$ и ${{{\mathbf{F}}}_{R}}$. Не теряя общности, положим, что нормальное направление к плоскости начального разрыва совпадает с осью x. Задача является автомодельной, и возмущения от начального разрыва распространяются вдоль характеристик в плоскости $(x,t)$. Приближенные решения задачи Римана строятся на основе предположений о структуре решения и условия выполнения соотношений Рэнкина–Гюгонио на сильном разрыве, $[{\mathbf{F}} - s{\mathbf{Q}}] = 0$, где $s$ – скорость разрыва.
Структура решения в HLL-аппроксимации решения задачи Римана представляется возмущенной областью, ограниченной характеристиками со скоростями ${{s}_{L}}$ и ${{s}_{R}}$. Вектор состояния ${\mathbf{Q}}{\kern 1pt} *$ возмущенной области определяется из соотношений Рэнкина–Гюгонио на характеристиках и имеет следующий вид:
(25)
${\mathbf{Q}}{\kern 1pt} * = \frac{{{{{\mathbf{Q}}}_{R}}{{s}_{R}} - {{{\mathbf{Q}}}_{L}}{{s}_{L}} + {{{\mathbf{F}}}_{L}} - {{{\mathbf{F}}}_{R}}}}{{{{s}_{R}} - {{s}_{L}}}}.$Соответствующий вектор потока в возмущенной области определяется выражением
(26)
${\mathbf{F}}{\kern 1pt} * = \frac{{{{s}_{R}}{{{\mathbf{F}}}_{L}} - {{s}_{L}}{{{\mathbf{F}}}_{R}} + {{s}_{L}}{{s}_{R}}({{{\mathbf{Q}}}_{R}} - {{{\mathbf{Q}}}_{L}})}}{{{{s}_{R}} - {{s}_{L}}}},$Аппроксимация HLL для решения задачи Римана является универсальной и может применяться к любой гиперболической системе дифференциальных уравнений; знание структуры вектора состояния ${\mathbf{Q}}$ при этом не требуется. Недостатком этой аппроксимации является то, что она не позволяет разрешать внутреннюю структуру возмущенной зоны. В частности, не определяет положение контактного разрыва. Для того, чтобы выделить внутри возмущенной зоны положение контактного разрыва, разработана HLLC аппроксимация [18]. Данная аппроксимация строится исключительно для случая, когда среда слева и справа от начального разрыва является чистой и содержит только одну фазу. Фазы слева и справа, вообще говоря, могут отличаться.
Аппроксимация HLLC использует особенности структуры векторов состояния ${\mathbf{Q}}$ и вектора консервативного потока ${\mathbf{F}}$. Введем для простоты понимания следующие обозначения для компонент векторов состояния и консервативного потока. Обозначим компоненту плотности $i$-й фазы среды через ${\mathbf{Q}} \cdot {{\rho }_{i}}$, импульс $i$-й фазы в направлении $x$ обозначим ${\mathbf{Q}} \cdot {{u}_{i}}$, энергию $i$-й фазы обозначим ${\mathbf{Q}} \cdot {{E}_{i}}$. Также обозначим компоненту потока массы $i$-й фазы среды через ${\mathbf{F}} \cdot {{\rho }_{i}}$, поток импульса $i$-й фазы в направлении $x$ обозначим ${\mathbf{F}} \cdot {{u}_{i}}$, поток энергии $i$-й фазы обозначим ${\mathbf{F}} \cdot {{E}_{i}}$. Поскольку слева и справа от начального разрыва среда однофазная, отождествим в принятых обозначениях компонент индексы $i$ и $L$, $R$. То есть, например, ${\mathbf{F}} \cdot {{\rho }_{L}}$ будет означать компоненту потока массы той фазы, что изначально находилась слева от разрыва.
Положим, что возмущенная зона ограничена характеристиками со скоростями ${{s}_{L}}$ и ${{s}_{R}}$. Эти скорости определяются в соответствии с работой [19] следующим образом:
(27)
${{s}_{L}} = \min (0,\min ({{u}_{L}} - {{a}_{L}},\bar {u} - \bar {a})),\quad {{s}_{R}} = \max (0,\max ({{u}_{R}} + {{a}_{R}},\bar {u} + \bar {a})),$Возмущенная зона разделяется характеристикой, распространяющейся со скоростью $C$, ${{s}_{L}} < C < {{s}_{R}}$, которая аппроксимирует контактный разрыв, т.е. фаза в области $[{{s}_{L}},C]$ совпадает с фазой слева от начального разрыва, фаза в области $[C,{{s}_{R}}]$ совпадает с фазой справа от начального разрыва. Скорость этой характеристики определим по аналогии с [18]:
(28)
$C = \frac{{{{\rho }_{L}}{{u}_{L}}{{s}_{L}} - {\mathbf{F}} \cdot {{u}_{L}} - {{\rho }_{R}}{{u}_{R}}{{s}_{R}} + {\mathbf{F}} \cdot {{u}_{R}}}}{{{{\rho }_{L}}{{s}_{L}} - {\mathbf{F}} \cdot {{\rho }_{L}} - {{\rho }_{R}}{{s}_{R}} + {\mathbf{F}} \cdot {{\rho }_{R}}}}.$Предполагая, что скорости фаз в возмущенной зоне слева и справа от контактного разрыва совпадают и равны $C$. Плотности фаз в возмущенной зоне определяются следующим образом:
(29)
$\rho _{L}^{*} = {{\rho }_{L}}\frac{{{{s}_{L}} - {{u}_{L}}}}{{{{s}_{L}} - C}},\quad \rho _{R}^{*} = {{\rho }_{R}}\frac{{{{s}_{R}} - {{u}_{R}}}}{{{{s}_{R}} - C}}.$Давление в возмущенной области определяются соотношением:
(30)
$P_{L}^{*} = {\mathbf{F}} \cdot {{u}_{L}} - C{\mathbf{F}} \cdot {{\rho }_{L}} - {{\rho }_{L}}({{u}_{L}} - C){{s}_{L}},\quad P_{R}^{*} = {\mathbf{F}} \cdot {{u}_{R}} - C{\mathbf{F}} \cdot {{\rho }_{R}} - {{\rho }_{R}}({{u}_{R}} - C){{s}_{R}}.$Заметим, что из уравнений (28), (29) и (30) следует $P_{L}^{*} = P_{R}^{*}$. Полная энергия в возмущенной области слева и справа от контактного разрыва после этого находится из условия сохранения энергии:
(31)
$({{\rho }_{L}}{{E}_{L}}){\kern 1pt} * = \frac{{{{\rho }_{L}}{{E}_{L}}{{s}_{L}} - {\mathbf{F}} \cdot {{E}_{L}} - P_{L}^{*}C}}{{{{s}_{L}} - C}},\quad ({{\rho }_{R}}{{E}_{R}}){\kern 1pt} * = \frac{{{{\rho }_{R}}{{E}_{R}}{{s}_{R}} - {\mathbf{F}} \cdot {{E}_{R}} - P_{R}^{*}C}}{{{{s}_{R}} - C}}.$Таким образом, компоненты векторов состояния в возмущенной зоне имеют вид:
(32)
$\begin{gathered} {\mathbf{Q}}_{L}^{*} \cdot {{\rho }_{L}} = \rho _{L}^{*},\quad {\mathbf{Q}}_{L}^{*} \cdot {{u}_{L}} = \rho _{L}^{*}C,\quad {\mathbf{Q}}_{L}^{*} \cdot {{E}_{L}} = ({{\rho }_{L}}{{E}_{L}}){\kern 1pt} *,\quad {\mathbf{Q}}_{L}^{*} \cdot {{\varphi }_{L}} = 1, \\ {\mathbf{Q}}_{R}^{*} \cdot {{\rho }_{R}} = \rho _{R}^{*},\quad {\mathbf{Q}}_{R}^{*} \cdot {{u}_{R}} = \rho _{R}^{*}C,\quad {\mathbf{Q}}_{R}^{*} \cdot {{E}_{R}} = ({{\rho }_{R}}{{E}_{R}}){\kern 1pt} *,\quad {\mathbf{Q}}_{R}^{*} \cdot {{\varphi }_{R}} = 1. \\ \end{gathered} $Остальные компоненты векторов состояния (касательные компоненты импульса) определяются в форме:
(33)
${\mathbf{Q}}_{L}^{*} \cdot \bullet = \frac{{{{s}_{L}} - C}}{{{{s}_{L}} - {{u}_{L}}}}{{{\mathbf{Q}}}_{L}} \cdot \bullet ,\quad {\mathbf{Q}}_{R}^{*} \cdot \bullet = \frac{{{{s}_{R}} - C}}{{{{s}_{R}} - {{u}_{R}}}}{{{\mathbf{Q}}}_{R}} \cdot \bullet .$Зная векторы состояния в возмущенных зонах, из условий Рэнкина–Гюгонио можно определить соответствующие потоковые векторы:
(34)
${\mathbf{F}}_{L}^{*} = {{{\mathbf{F}}}_{L}} + {{s}_{L}}({\mathbf{Q}}_{L}^{*} - {{{\mathbf{Q}}}_{L}}),\quad {\mathbf{F}}_{R}^{*} = {{{\mathbf{F}}}_{R}} + {{s}_{R}}({\mathbf{Q}}_{R}^{*} - {{{\mathbf{Q}}}_{R}}){\kern 1pt} {\kern 1pt} .$Заметим, что если ${{{\mathbf{F}}}_{L}} = {\mathbf{F}}({{{\mathbf{Q}}}_{L}})$ и ${{{\mathbf{F}}}_{R}} = {\mathbf{F}}({{{\mathbf{Q}}}_{R}})$, то выражения для компонент векторов состояния в точности совпадают с методом HLLC аппроксимации решения задачи о газодинамическом распаде начального разрыва [18].
3.3.2. W-аппроксимация решения составной задачи Римана. Как уже отмечалось выше, для реализации численной схемы необходимо построить методику расчета численного потока на границе двух ячеек, одна из которых является чистой, другая – смешанной. Контактная граница предполагается плоской, параллельной границе между ячейками и находящейся на расстоянии $\delta $ от нее. Примем для определенности, что левая ячейка смешанная, содержит фазы $1$ и $2$, а правая чистая содержит только фазу $1$. Состояние в левой ячейке описывается вектором ${{{\mathbf{Q}}}_{L}}$, состояние в правой – вектором ${{{\mathbf{Q}}}_{R}}$.
Расщепим вектор ${{{\mathbf{Q}}}_{L}}$ на два вектора, которые будут описывать состояния фаз слева и справа от контактной границы:
(35)
${{{\mathbf{Q}}}_{L}} = \left( {\begin{array}{*{20}{c}} {{{\varphi }_{1}}{{\rho }_{1}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{{\mathbf{u}}}_{{1x}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{{\mathbf{u}}}_{{1y}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{{\mathbf{u}}}_{{1z}}}} \\ {{{\varphi }_{1}}{{\rho }_{1}}{{E}_{1}}} \\ {{{\varphi }_{1}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{{\mathbf{u}}}_{{2x}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{{\mathbf{u}}}_{{2y}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{{\mathbf{u}}}_{{2z}}}} \\ {{{\varphi }_{2}}{{\rho }_{2}}{{E}_{2}}} \\ {{{\varphi }_{2}}} \end{array}} \right) = {{\varphi }_{2}}\left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {{{\rho }_{2}}} \\ {{{\rho }_{2}}{{{\mathbf{u}}}_{{2x}}}} \\ {{{\rho }_{2}}{{{\mathbf{u}}}_{{2y}}}} \\ {{{\rho }_{2}}{{{\mathbf{u}}}_{{2z}}}} \\ {{{\rho }_{2}}{{E}_{2}}} \\ 1 \end{array}} \right) + {{\varphi }_{1}}\left( {\begin{array}{*{20}{c}} {{{\rho }_{1}}} \\ {{{\rho }_{1}}{{{\mathbf{u}}}_{{1x}}}} \\ {{{\rho }_{1}}{{{\mathbf{u}}}_{{1y}}}} \\ {{{\rho }_{1}}{{{\mathbf{u}}}_{{1z}}}} \\ {{{\rho }_{1}}{{E}_{1}}} \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}} \right).$Обозначим данные векторы как ${{{\mathbf{Q}}}_{{LL}}}$ и ${{{\mathbf{Q}}}_{{LR}}}$, ${{{\mathbf{Q}}}_{L}} = {{\varphi }_{2}}{{{\mathbf{Q}}}_{{LL}}} + {{\varphi }_{1}}{{{\mathbf{Q}}}_{{LR}}}$. Задача Коши с начальными данными: ${{{\mathbf{Q}}}_{{LL}}}$ при $x < - \delta $, ${{{\mathbf{Q}}}_{{LR}}}$ при $ - \delta < x < 0$, ${{{\mathbf{Q}}}_{R}}$ при $x > 0$, носит название составной задачи Римана [6]. Решение составной задачи Римана представляет собой результат взаимодействия возмущений от распада разрыва на контактной поверхности внутри ячейки и от распада разрыва на границе между ячейками. Это решение может быть достаточно сложным из-за большого количества волн, возникающих из-за взаимодействия возмущенных зон от двух начальных разрывов. Поэтому предлагается рассмотреть приближенное решение составной задачи Римана, учитывающее только основные стадии взаимодействия и основывающееся на рассмотренных выше HLL и HLLC аппроксимациях решения автомодельной задачи Римана.
Ниже мы рассмотрим два приближения для решения CRP. Одно – W-аппроксимация – учитывает первичное взаимодействие волн, образование вторичных волн и взаимодействие их с контактным разрывом с образованием семейства третичных волн. Волновая диаграмма для W‑аппроксимации изображена на фиг. 3.
Здесь начальные разрывы CRP обозначены цифрами $0$ и $1$, вторичный разрыв – $2$ и третичный – $3$. Возмущенная область имеет W-форму и состоит, в общем случае, из шести подобластей, ограниченных соответствующими характеристиками начальных, первичного и вторичного разрывов. Вторичный разрыв $2$ возникает как результат взаимодействия крайних характеристик HLL-решения начального разрыва $0$ и HLLC-решения начального разрыва $1$ (фиг. 3). Этот разрыв порождает возмущенную область, которая взаимодействует с контактной границей, порождая третичный разрыв $3$.
Возмущенные области разрывов $0$ и $2$ мы приближенно описываем решением HLL, а возмущенные области разрывов $1$ и $3$ – приближенным решением HLLC. При такой аппроксимации решения CRP возмущенная область в общем случае состоит из шести подобластей (фиг. 3):
• A ограничена характеристиками $s_{L}^{0}$, $s_{R}^{0}$, $s_{R}^{2}$, вектор состояния ${\mathbf{Q}}_{R}^{*}$;
• B ограничена характеристиками $s_{L}^{1}$, ${{C}^{1}}$, и $s_{L}^{3}$ вектор состояния ${\mathbf{Q}}_{{LL}}^{*}$;
• C ограничена характеристиками $s_{R}^{1}$, ${{C}^{1}}$, $s_{L}^{2}$ вектор состояния ${\mathbf{Q}}_{{LR}}^{*}$;
• D ограничена характеристиками $s_{R}^{2}$, $s_{L}^{2}$, $s_{R}^{3}$ вектор состояния ${\mathbf{Q}}_{R}^{{**}}$;
• E ограничена характеристиками $s_{L}^{3}$, ${{C}^{3}}$ вектор состояния ${\mathbf{Q}}_{{LL}}^{{**}}$;
• F ограничена характеристиками ${{C}^{3}}$, $s_{R}^{3}$ вектор состояния ${\mathbf{Q}}_{{LR}}^{{**}}$.
Здесь скорости характеристик $s_{L}^{0}$, $s_{R}^{0}$, ${{C}^{1}}$ и т.д. и векторы возмущенных состояний ${\mathbf{Q}}_{R}^{*}$, ${\mathbf{Q}}_{{LL}}^{*}$, ${\mathbf{Q}}_{{LR}}^{*}$, … определяются приближенными солверами HLL и HLLC, описанными выше.
Подобласть A является возмущенной областью HLL решения для разрыва $0$, подобласть $B$ и $C$ – левая и правая возмущенные области HLLC решения для разрыва $1$, D – возмущенная область HLL решения для разрыва $2$, E и F – возмущенные области HLLC решения для разрыва $3$. Таким образом, параметры, определяющие W-аппроксимацию решения CRP, определяются в соответствии с табл. 1.
Таблица 1.
W-аппроксимация решения CRP
| Начальные данные | Солвер | Решение |
|---|---|---|
| ${{{\mathbf{Q}}}_{{LR}}}$, ${{{\mathbf{Q}}}_{R}}$, ${\mathbf{F}}({{{\mathbf{Q}}}_{{LR}}})$, ${\mathbf{F}}({{{\mathbf{Q}}}_{R}})$, | HLL | $s_{L}^{0}$, $s_{R}^{0}$, ${\mathbf{Q}}_{R}^{*}$ |
| ${{{\mathbf{Q}}}_{{LL}}}$, ${{{\mathbf{Q}}}_{{LR}}}$, ${\mathbf{F}}({{{\mathbf{Q}}}_{{LL}}})$, ${\mathbf{F}}({{{\mathbf{Q}}}_{{LR}}})$ | HLLC | $s_{L}^{1}$, ${{C}^{1}}$, $s_{R}^{1}$, ${\mathbf{Q}}_{{LL}}^{*}$, ${\mathbf{Q}}_{{LR}}^{*}$ |
| ${\mathbf{Q}}_{{LR}}^{*}$, ${\mathbf{Q}}_{R}^{*}$, ${\mathbf{F}}_{{LR}}^{*}$, ${\mathbf{F}}_{R}^{*}$ | HLL | $s_{L}^{2}$, $s_{R}^{2}$, ${\mathbf{Q}}_{R}^{{*{\kern 1pt} *}}$ |
| ${\mathbf{Q}}_{{LL}}^{*}$, ${\mathbf{Q}}_{R}^{{*{\kern 1pt} *}}$, ${\mathbf{F}}_{{LL}}^{*}$, ${\mathbf{F}}_{R}^{{*{\kern 1pt} *}}$ | HLLC | $s_{L}^{3}$, ${{C}^{3}}$, $s_{R}^{3}$, ${\mathbf{Q}}_{{LL}}^{{*{\kern 1pt} *}}$, ${\mathbf{Q}}_{{LR}}^{{*{\kern 1pt} *}}$ |
Соответствующие потоковые векторы в подобластях определяются из соотношений Рэнкина–Гюгонио:
(36)
$\begin{gathered} {\mathbf{F}}_{R}^{*} = {\mathbf{F}}({{{\mathbf{Q}}}_{R}}) + s_{R}^{0}({\mathbf{Q}}_{R}^{*} - {{{\mathbf{Q}}}_{R}})\quad {\mathbf{F}}_{{LL}}^{*} = {\mathbf{F}}({{{\mathbf{Q}}}_{{LL}}}) + s_{L}^{1}({\mathbf{Q}}_{{LL}}^{*} - {{{\mathbf{Q}}}_{{LL}}}), \\ {\mathbf{F}}_{{LR}}^{*} = {\mathbf{F}}({{{\mathbf{Q}}}_{{LR}}}) + s_{R}^{1}({\mathbf{Q}}_{{LR}}^{*} - {{{\mathbf{Q}}}_{{LR}}}),\quad {\mathbf{F}}_{R}^{{**}} = {\mathbf{F}}_{R}^{*} + s_{R}^{2}({\mathbf{Q}}_{R}^{{**}} - {\mathbf{Q}}_{R}^{*}), \\ {\mathbf{F}}_{{LL}}^{{**}} = {\mathbf{F}}_{{LL}}^{*} + s_{L}^{3}({\mathbf{Q}}_{{LL}}^{{**}} - {\mathbf{Q}}_{{LL}}^{*}),\quad {\mathbf{F}}_{{LR}}^{{**}} = {\mathbf{F}}_{R}^{{**}} + s_{R}^{3}({\mathbf{Q}}_{{LR}}^{{**}} - {\mathbf{Q}}_{R}^{{**}}). \\ \end{gathered} $Следует отметить, что рассмотренная W-аппроксимация решения CRP имеет место в предположении, что правосторонние характеристики $s_{R}^{0}$, $s_{R}^{2}$, $s_{R}^{3}$, так же как и левосторонние характеристики $s_{L}^{1}$ и $s_{L}^{3}$, не пересекаются между собой. В противном случае возникают дополнительные разрывы и волны, рассмотрение которых сильно усложняет задачу. Чтобы избежать эту ситуацию, в случае пересечения характеристик можно скорректировать выбор скоростей характеристик, назначив для правосторонних одинаковую скорость, равную ${\text{max}}(s_{R}^{0},s_{R}^{2},s_{R}^{3})$, а для левосторонних – $\min (s_{L}^{1},s_{L}^{3})$.
Численный поток, который определяет изменение консервативного вектора на шаге по времени $\Delta t$, состоит из двух частей (17). Один, $\Phi $, связан с консервативной частью уравнений и определяет потоки массы, импульса и энергии через грань ячейки. Другой, $\Phi {\kern 1pt} '$, определяет поток, связанный с контактной границей (18). Имея рассмотренную W-аппроксимацию решение CRP, указанные потоки могут быть вычислены следующим образом:
(37)
$\Phi = {\mathbf{F}}_{R}^{*}{{t}_{1}} + {\mathbf{F}}_{R}^{{**}}({{t}_{4}} - {{t}_{1}}) + {\mathbf{F}}_{{LR}}^{{**}}({{t}_{5}} - {{t}_{4}}) + {\mathbf{F}}_{{LL}}^{{**}}(\Delta t - {{t}_{5}}),$(38)
$\Phi {\kern 1pt} ' = ({\mathbf{F}}_{{LR}}^{*} - {{C}^{1}}{\mathbf{Q}}_{{LR}}^{*}){{t}_{3}} + ({\mathbf{F}}_{{LR}}^{{**}} - {{C}^{3}}{\mathbf{Q}}_{{LR}}^{{**}})({{t}_{5}} - {{t}_{3}}).$(39)
$\begin{gathered} {{t}_{1}} = \frac{{s_{R}^{2} - s_{L}^{0}}}{{s_{R}^{2}}}{{t}_{2}},\quad {{t}_{2}} = \frac{\delta }{{s_{R}^{1} - s_{L}^{0}}},\quad {{t}_{3}} = \frac{{\delta + (s_{L}^{0} - s_{L}^{2}){{t}_{2}}}}{{{{C}^{1}} - s_{L}^{2}}}, \\ {{t}_{4}} = \frac{{s_{R}^{3}{{t}_{3}} - s_{L}^{2}({{t}_{2}} - {{t}_{3}}) - s_{L}^{0}{{t}_{2}}}}{{s_{R}^{3}}},\quad {{t}_{5}} = \frac{{{{C}^{3}}{{t}_{3}} - s_{L}^{2}({{t}_{2}} - {{t}_{3}}) - s_{L}^{0}{{t}_{2}}}}{{{{C}^{3}}}}. \\ \end{gathered} $Формулы (37) и (38) верны при условии наиболее полной волновой конфигурации на шаге времени $\Delta t$, когда ${{t}_{1}} \in [0,\Delta t]$, ${{t}_{2}} \in [0,\Delta t]$, ${{t}_{3}} \in [{{t}_{2}},\Delta t]$, ${{t}_{4}} \in [{{t}_{3}},\Delta t]$, ${{t}_{5}} \in [{{t}_{4}},\Delta t]$. Если эти условия не выполняются, волновая конфигурация упрощается, и выражения для потоков модифицируются следующим образом:
• ${{t}_{2}} \notin [0,\Delta t]$ $ \Rightarrow $ возмущение от разрывов $0$ и $1$ не взаимодействует:
• ${{t}_{2}} \in [0,\Delta t]$ и ${{t}_{3}} \notin [{{t}_{2}},\Delta t]$ $ \Rightarrow $ третичный распад $3$ возникает за пределами временного шага:
• ${{t}_{3}} \in [0,\Delta t]$, а ${{t}_{4}} \notin [{{t}_{3}},\Delta t]$ или ${{t}_{5}} \notin [{{t}_{3}},\Delta t]$ $ \Rightarrow $ третичный распад $3$ возникает в пределах временного шага, но не все возмущения от него выходят на грань:
Полученные выше потоки $\Phi $ и $\Phi {\kern 1pt} '$ используются для расчета консервативного вектора в текущей ячейке. При этом поток $\Phi {\kern 1pt} '$, определяющий вклад контактной границы, учитывает ту сторону контактной границы, которая направлена к грани ячейки . Вклад от противоположной стороны определяется при рассмотрении противоположной грани ячейки. Если реализуется случай ${{t}_{3}} \in [0,\Delta t]$, то траектория контактной границы меняется. Это изменение обусловлено влиянием соседней ячейки и близостью контактной границы к грани ячейки. В силу курантовского условия устойчивости траектория контактной границы не будет меняться при вычислении потоков на противоположной грани ячейки. Поэтому стороны ${{\partial }^{ - }}$ и ${{\partial }^{ + }}$ контактной границы в расчете окажутся рассогласованы, что приведет к потере консервативности схемы.
Чтобы устранить этот недостаток, предлагается простая модификация потока $\Phi {\kern 1pt} '$. Суть сводится к тому, что суммарный эффект контактной границы при расчете смешанной ячейки, т.е. суммарный вклад сторон ${{\partial }^{ - }}$ и ${{\partial }^{ + }}$, определяется волновой конфигурацией той грани ячейки, где возникает искривление контактной границы. Эта модификация вводится следующим образом. Если ${{t}_{3}} \in [0,\Delta t]$:
(40)
$\Phi {\kern 1pt} ' \leftarrow \Phi {\kern 1pt} '\; + ({\mathbf{F}}_{{LL}}^{*} - {{C}^{1}}{\mathbf{Q}}_{{LL}}^{*})(\Delta t - {{t}_{3}}) - ({\mathbf{F}}_{{LL}}^{{**}} - {{C}^{3}}{\mathbf{Q}}_{{LL}}^{{**}})({{t}_{5}} - {{t}_{3}}).$Если ${{t}_{5}} \in [0,\Delta t]$, то контактная граница пересекает грань ячейки и проходит в соседнюю ячейку. Таким образом, соседняя ячейка меняет на временном шаге свой статус на смешанную. Чтобы учесть эффект появления контактной границы в соседней ячейке, необходимо модифицировать численный поток, который будет вычитаться при расчете этой ячейки. Поток для соседней ячейки корректируется следующим образом:
(41)
$\Phi \leftarrow \Phi + (\Delta t - {{t}_{5}})(({\mathbf{F}}_{{LR}}^{{**}} - {{C}^{3}}{\mathbf{Q}}_{{LR}}^{{**}}) - ({\mathbf{F}}_{{LL}}^{{**}} - {{C}^{3}}{\mathbf{Q}}_{{LL}}^{{**}})).$На гранях чистых ячеек численный поток определяется методом HLL. С целью уменьшения схемной вязкости на гранях между чистыми ячейками можно рассчитывать численные потоки, используя точные решения задачи Римана [20] или методом HLLC, учитывающим в волновой структуре контактный разрыв.
3.3.3. Метод V-аппроксимации решения составной задачи Римана. Рассмотренная в п. 3.3.2 W‑аппроксимация решения составной задачи Римана допускает упрощение, которое заключается в том, что начиная со второй стадии взаимодействия мы не будем рассматривать неравномерность в распределении параметров состояния справа от контактного разрыва. Схема решения представлена на фиг. 4, вторая стадия взаимодействия имеет стандартную V-образную форму, поэтому назовем данное решение V-аппроксимацией CRP.
Первичная стадия взаимодействия рассматривается аналогично предыдущему случаю до момента пересечения правой характеристики для распада разрыва 1 (внутри ячейки) и левой характеристики для распада разрыва 0 (на грани между ячейками) ${{t}_{1}} = \frac{\delta }{{s_{R}^{1} - s_{L}^{0}}}$. Для этого, прежде чем рассмотреть вторичный распад разрыва, сгладим распределение в возмущенной зоне справа от контактного разрыва в момент времени ${{t}_{1}}$:
(42)
${\mathbf{Q}}_{R}^{{**}} = \frac{{(s_{R}^{1} - {{C}^{1}}){\mathbf{Q}}_{{LR}}^{*} + (s_{R}^{0} - s_{L}^{0}){\mathbf{Q}}_{R}^{*}}}{{s_{R}^{1} - {{C}^{1}} + s_{R}^{0} - s_{L}^{0}}}.$Будем использовать величины ${\mathbf{Q}}_{{LL}}^{*}$ и ${\mathbf{Q}}_{R}^{{**}}$ в качестве начальных значений слева и справа для аппроксимации вторичного распада разрыва на контактной поверхности (фиг. 4). Аппроксимация вторичного распада разрыва производится по методу HLLC, в качестве векторов потока слева и справа рассматривается ${\mathbf{F}}({\mathbf{Q}}_{{LL}}^{*})$ и ${\mathbf{F}}({\mathbf{Q}}_{R}^{{**}})$. Взаимодействие левой и правой волны, распространяющихся со скоростями $s_{L}^{2}$ и $s_{R}^{2}$, с волнами с первичного распада разрыва не рассматриваются.
Возмущенная область при рассмотрении V-аппроксимации состоит из следующего набора областей (фиг. 4):
• A ограничена характеристиками $s_{L}^{0}$, $s_{R}^{0}$ и прямой $t = {{t}_{1}}$, вектор состояния ${\mathbf{Q}}_{R}^{*}$;
• B ограничена характеристиками $s_{L}^{1}$, ${{C}^{1}}$ и прямой $t = {{t}_{1}}$, вектор состояния ${\mathbf{Q}}_{{LL}}^{*}$;
• C ограничена характеристиками $s_{R}^{1}$, ${{C}^{1}}$ и прямой $t = {{t}_{1}}$ вектор состояния ${\mathbf{Q}}_{{LR}}^{*}$;
• D ограничена характеристиками $s_{L}^{2}$, ${{C}^{2}}$ вектор состояния ${\mathbf{Q}}_{{LL}}^{{**}}$;
• E ограничена характеристиками ${{C}^{2}}$, $s_{R}^{2}$ вектор состояния ${\mathbf{Q}}_{{LR}}^{{**}}$.
Параметры, определяющие V-аппроксимацию решения CRP, определяются в соответствии с табл. 2.
Таблица 2.
V-аппроксимация решения CRP
| Начальные данные | Солвер | Решение |
|---|---|---|
| ${{{\mathbf{Q}}}_{{LR}}}$, ${{{\mathbf{Q}}}_{R}}$, ${\mathbf{F}}({{{\mathbf{Q}}}_{{LR}}})$, ${\mathbf{F}}({{{\mathbf{Q}}}_{R}})$ | HLL | $s_{L}^{0}$, $s_{R}^{0}$, ${\mathbf{Q}}_{R}^{*}$ |
| ${{{\mathbf{Q}}}_{{LL}}}$, ${{{\mathbf{Q}}}_{{LR}}}$, ${\mathbf{F}}({{{\mathbf{Q}}}_{{LL}}})$, ${\mathbf{F}}({{{\mathbf{Q}}}_{{LR}}})$ | HLLC | $s_{L}^{1}$, ${{C}^{1}}$, $s_{R}^{1}$, ${\mathbf{Q}}_{{LL}}^{*}$, ${\mathbf{Q}}_{{LR}}^{*}$ |
| ${\mathbf{Q}}_{{LL}}^{*}$, ${\mathbf{Q}}_{R}^{{*{\kern 1pt} *}}$, ${\mathbf{F}}_{{LL}}^{*}$, ${\mathbf{F}}({\mathbf{Q}}_{R}^{{*{\kern 1pt} *}})$ | HLLC | $s_{L}^{2}$, ${{C}^{2}}$, $s_{R}^{2}$, ${\mathbf{Q}}_{{LL}}^{{*{\kern 1pt} *}}$, ${\mathbf{Q}}_{{LR}}^{{*{\kern 1pt} *}}$ |
Соответствующие потоковые векторы на первичной стадии взаимодействия определяются из соотношений Рэнкина–Гюгонио:
(43)
${\mathbf{F}}_{R}^{*} = {\mathbf{F}}({{{\mathbf{Q}}}_{R}}) + s_{R}^{0}({\mathbf{Q}}_{R}^{*} - {{{\mathbf{Q}}}_{R}}),\quad {\mathbf{F}}_{{LL}}^{*} = {\mathbf{F}}({{{\mathbf{Q}}}_{{LL}}}) + s_{L}^{1}({\mathbf{Q}}_{{LL}}^{*} - {{{\mathbf{Q}}}_{{LL}}}),\quad {\mathbf{F}}_{{LR}}^{*} = {\mathbf{F}}({{{\mathbf{Q}}}_{{LR}}}) + s_{R}^{1}({\mathbf{Q}}_{{LR}}^{*} - {{{\mathbf{Q}}}_{{LR}}}).$На вторичной стадии взаимодействия потоковые векторы определяются соотношениями:
(44)
${\mathbf{F}}_{{LL}}^{{**}} = {\mathbf{F}}_{{LL}}^{*} + s_{L}^{2}({\mathbf{Q}}_{{LL}}^{{**}} - {\mathbf{Q}}_{{LL}}^{*}),\quad {\mathbf{F}}_{{LR}}^{{**}} = {\mathbf{F}}_{R}^{{**}} + s_{R}^{2}({\mathbf{Q}}_{{LR}}^{{**}} - {\mathbf{Q}}_{R}^{{**}}).$В качестве потока ${\mathbf{F}}_{R}^{{**}}$ рассмотрим его прямое выражение от величины осредненного состояния ${\mathbf{F}}_{R}^{{**}} = ({\mathbf{F}}_{Q}^{{**}})$.
Метод V-аппроксимации наиболее близок к методу решения составной задачи Римана для равновесной модели [16]. Главное отличие состоит в том, что на первой стадии рассматривается взаимодействие на контактной поверхности в смешанной ячейке.
Преимущество V-аппроксимации состоит еще в том, что рассматривается меньшее количество взаимодействий, что ускоряет расчет и упрощает код вычислительной программы. Более того, при расчете вторичных распадов разрыва на второй стадии можно использовать и более точные методы решения задачи Римана, например, использовать точное решение, если оно может быть получено аналитически.
Расчет численных потоков в случае V-аппроксимации решения составной задачи Римана аналогичен случаю W-аппроксимации. Полный численный поток, согласно схеме (16), является суммой потоков $\Phi $ на грани между ячейками и на контактной границе $\Phi {\kern 1pt} '$.
(45)
$\Phi = {\mathbf{F}}_{R}^{*}{{t}_{1}} + {\mathbf{F}}_{R}^{{**}}({{t}_{2}} - {{t}_{1}}) + {\mathbf{F}}_{{LR}}^{{**}}({{t}_{3}} - {{t}_{2}}) + {\mathbf{F}}_{{LL}}^{{**}}(\Delta t - {{t}_{3}}),$(46)
$\Phi {\kern 1pt} ' = ({\mathbf{F}}_{{LR}}^{*} - {{C}^{1}}{\mathbf{Q}}_{{LR}}^{*}){{t}_{1}} + ({\mathbf{F}}_{{LR}}^{{**}} - {{C}^{2}}{\mathbf{Q}}_{{LR}}^{{**}})({{t}_{3}} - {{t}_{1}}).$(47)
${{t}_{2}} = {{t}_{1}} + \frac{{{{\delta }_{1}}}}{{s_{R}^{2}}},\quad {{\delta }_{1}} = \delta - {{C}^{1}}\Delta {{t}_{1}},\quad {{t}_{3}} = {{t}_{1}} + \frac{{{{\delta }_{1}}}}{{{{C}^{2}}}}.$В случае возникновения вторичного возмущения, аналогично методике W-аппроксимации, необходима модификация потока $\Phi {\kern 1pt} '$ для устранения рассогласованности потоков на поверхностях ${{\partial }^{ - }}$ и ${{\partial }^{ - }}$. Модификация представляется следующим образом, если ${{t}_{1}} \in [0,\Delta t]$:
(48)
$\Phi {\kern 1pt} ' \leftarrow \Phi {\kern 1pt} '\; + ({\mathbf{F}}_{{LL}}^{*} - {{C}^{1}}{\mathbf{Q}}_{{LL}}^{*})(\Delta t - {{t}_{1}}) - ({\mathbf{F}}_{{LL}}^{{**}} - {{C}^{2}}{\mathbf{Q}}_{{LL}}^{{**}})({{t}_{3}} - {{t}_{1}}).$Если ${{t}_{3}} \in [0,\Delta t]$, контактная граница пересекает грань ячейки и проходит в соседнюю ячейку. В этом случае, аналогично методике W-аппроксимации, необходима коррекция потока для правой ячейки:
(49)
$\Phi \leftarrow \Phi + (\Delta t - {{t}_{3}})(({\mathbf{F}}_{{LR}}^{{**}} - {{C}^{2}}{\mathbf{Q}}_{{LR}}^{{**}}) - ({\mathbf{F}}_{{LL}}^{{**}} - {{C}^{2}}{\mathbf{Q}}_{{LL}}^{{**}})).$Таким образом аппроксимируется процесс течения и проводится расчет численных потоков в результате двойного распада разрыва (CRP). Изначально составная задача Римана ставится для равновесной модели, это означает, что внутри смешанной ячейки результатом распада разрыва является только движение контактной границы. В данной работе предлагается постановка для полностью неравновесной модели. Вследствие того, что аппроксимация картины распада двойного разрыва похожа формой на букву $W$, назовем данный метод $WCRP$. Далее проведем численные расчеты с целью апробации и верификации рассмотренной методики.
4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ
В данном разделе приводятся результаты численных расчетов некоторых задач течения многофазных сред. Рассматриваются следующие задачи: одномерная задача переноса, движение контактной границы, задача о распаде начального разрыва, задача о схлопывании воздушного пузырька в воде под действием ударной волны, задача о тройной точке (triple point). Расчет этих задач проводится на равномерных стационарных декартовых сетках.
4.1. Движение контактной границы
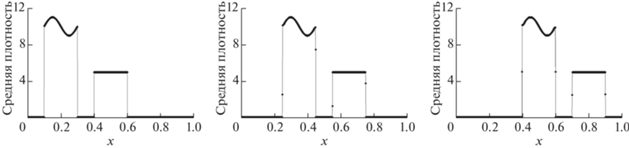
Основное преимущество метода CRP, как уже отмечалось в работе [6], это точное описание контактной границы, с устранением эффекта численной диффузии. На одномерных задачах контактная граница воспроизводится с точностью до одной ячейки. Предложенная методика WCRP наследует это свойство и также качественно описывает движение контактной границы. Приведем здесь результаты одномерного расчета следующей задачи. Пусть имеется одномерная область длиной $1$. Отрезок $[0.1;0.3]$ занимает фаза $2$ с распределением плотности ${{\rho }_{2}} = 10 + \sin (\pi (10x - 1))$. Отрезок $[0.4;0.6]$ занимает фаза $2$ с распределением плотности ${{\rho }_{2}} = 5$. Остальное пространство занимает фаза $1$ с плотностью $0.1$. Скорости и давления в фазах равны ${{P}_{1}} = {{P}_{2}}{{ = 10}^{5}}$, ${{u}_{{x1}}} = {{u}_{{x2}}} = 299.5$. Уравнения состояния фаз рассматриваются в форме:
Для фазы $1$ показатель адиабаты равен ${{\gamma }_{1}} = 1.4$, для фазы $2$ показатель адиабаты рассмотрим равным ${{\gamma }_{2}} = 2.5$. В расчетной области задана равномерная сетка из 1000 ячеек, на левой и правой границе накладываются периодические граничные условия. Расчет ведется до момента времени $0.001$. Скорость движения среды намеренно выбрана нецелой, чтобы в конечный момент времени координата межфазной границы приходилась на середину ячейки.
На фиг. 5 показано распределение средней плотности $\rho = {{\varphi }_{1}}{{\rho }_{1}} + {{\varphi }_{2}}{{\rho }_{2}}$ на моменты времени $0$, $0.0005$ и $0.001$. Маркеры на фиг. 5 соответствуют значениям в ячейках. Как видно, несмотря на достаточно большое количество шагов (11 865), методика удерживает размытие контактной границы в пределах одной ячейки.
4.2. Задача о распаде разрыва
В данном разделе рассмотрим одномерную задачу распада разрыва для системы уравнений Эйлера. С помощью предложенной методики будем отслеживать положение контактного разрыва. Целью данного теста является проверка аппроксимации динамики контактного разрыва при использовании схем с V-аппроксимацией и с W-аппроксимацией решения составной задачи Римана. Для сравнения приводится стандартное решение методом конечного объема с аппроксимацией задачи Римана по методу HLLC.
Рассмотрим две различные постановки, использованные в [9] для тестирования численных схем. В постановке 1 состояние слева от разрыва характеризуется параметрами $\rho = 1.0$, $u = 0.0$, $P = 1.0$ состояние справа от разрыва характеризуется параметрами $\rho = 0.125$, $u = 0.0$, $P = 0.1$. В постановке 2 состояние слева от разрыва характеризуется параметрами $\rho = 1.0$, $u = 0.0$, $P = 1000.0$ состояние справа от разрыва характеризуется параметрами $\rho = 1.0$, $u = 0.0$, $P = 0.01$. Состояние среды удовлетворяет уравнению состояния идеального газа $P = (\gamma - 1)\rho e$ с параметром адиабаты $\gamma = 1.4$. Расчетная область представляет собой отрезок $[0.0,1.0]$, начальное положение разрыва находится в точке $x = 0.5$. В области задана равномерная сетка, для первой постановки количество ячеек составляет 250 и 1000, для второй постановки – 500 и 2000.
Эта задача может решаться стандартным методом Годунова первого порядка с аппроксимацией численного потока методом HLLC, без выделения контактного разрыва. В рамках рассматриваемого подхода материал фазы слева может быть рассмотрен как материал 1, материал фазы справа может быть рассмотрен как материал 2, несмотря на то, что по сути это два одинаковых материала. Тогда задача может решаться с помощью системы уравнений (1), параметры объемной доли слева от начального разрыва ${{\alpha }_{1}} = 1.0$, ${{\alpha }_{2}} = 0.0$ справа ${{\alpha }_{1}} = 0.0$, ${{\alpha }_{2}} = 1.0$.
На фиг. 6 и фиг. 7 приведены результаты численного моделирования. На приведенных графиках распределений давления, скорости и плотности черными кривыми представлены результаты стандартного решения методом HLLC, синими кривыми – результаты решения с использованием методики W-аппроксимации, красными кривыми – результаты решения с использованием методики V-аппроксимации. Пунктирные кривые означают расчет на более грубой сетке, сплошные – на более подробной сетке. Зеленым показано аналитическое решение. Из приведенных результатов видно, что в расчетах с использованием предложенной методики подсеточного восполнения на контактном разрыве скорости и давления справа и слева выравниваются, несмотря на отсутствие в системе уравнений релаксационных членов, и хорошо согласуются с результатами стандартного решения методом HLLC.
Фиг. 6.
Результаты моделирования задачи о распаде разрыва в постановке 1. Распределения параметров давления (а), скорости (б), плотности (в, г) в момент времени 0.25. Черным показаны результаты, посчитанные с использованием HLLC схемы, синим – с использованием W схемы, красным – с использованием V схемы. Зеленая кривая на распределении плотности справа снизу – аналитическое решение.

Фиг. 7.
Результаты моделирования задачи о распаде разрыва в постановке 2. Распределения параметров давления (а), скорости (б), плотности (в, г) в момент времени 0.012. Черным показаны результаты, посчитанные с использованием HLLC схемы, синим – с использованием W схемы, красным – с использованием V схемы. Зеленая кривая на распределении плотности справа снизу – аналитическое решение.

Заметим, что в задаче 1 решения с использованием методик W-аппроксимации и V-аппроксимации дают примерно одинаковые результаты. Контактная граница разрешается точно, с точностью до одной расчетной ячейки, без численного размытия контакта, которое присутствует в стандартном решении. В то же время в задаче 2, где взаимодействие соседних ячеек гораздо интенсивнее, чем в задаче 1, результаты, полученные с использованием W-аппроксимации, лучше соответствуют точному аналитическому решению, чем результаты, полученные с использованием V-аппроксимации.
4.3. Задача схлопывания пузырька
Рассмотрим далее задачу взаимодействия воздушного пузырька в воде с ударной волной. В задаче предполагается два материала – воздух, назовем его материал 1, и вода, назовем его материал 2. Ударная волна формируется набеганием слева потока воды, движущегося со скоростью 1000 м/с. Целью моделирования является численное описание деформации границы пузырька.
Расчетная область представляет квадрат $[0,0.012$ м$] \times [0,0.012$ м$]$, центр пузырька радиусом $0.003$ м находится в точке $(0.006,0.006)$. На границе области ставится условие нулевого сноса, $(\nabla {\mathbf{Q}},{\mathbf{n}}) = {\mathbf{0}}$. В области задана равномерная декартова сетка $1200 \times 1200$ ячеек.
Начальные условия ставятся следующим образом. В области
находится воздух с плотностью ${{\rho }_{1}} = 1.16$ кг/м3, давлением ${{P}_{1}}{{ = 10}^{5}}$ Па, скоростью, равной нулю. Область $x < 0.002$ м занята водой с плотностью ${{\rho }_{2}} = 1000$ кг/м3, давлением ${{P}_{2}}{{ = 10}^{5}}$ Па, скоростью вдоль оси $x$, равной ${{u}_{{2x}}} = 1000$ м/с. В остальной области находится вода с плотностью ${{\rho }_{2}} = 1000$ кг/м3, давлением ${{P}_{2}}{{ = 10}^{5}}$ Па, скоростью, равной нулю. Изначально все ячейки чистые, т.е. заполнены каким-либо одним материалом. Тип материала в ячейке определяется попаданием центра ячейки в обозначенные в постановке области.Уравнение состояния воды и воздуха рассматривается в двухпараметрической форме:
Величины параметров для воздуха: ${{\gamma }_{1}} = 1.4$, ${{P}_{0}} = 0$, для воды: $\gamma = 4.4$, ${{P}_{0}} = 6 \times {{10}^{8}}$ Па. На фиг. 8 представлены результаты распределения объемной доли воздуха, ${{\varphi }_{1}}$, с шагом $0.43 \times {{10}^{{ - 6}}}$ с, начиная с момента времени $0.86 \times {{10}^{{ - 6}}}$ с. Видно, что предложенный метод позволяет поддерживать разрешения контактной границы с точностью до нескольких счетных ячеек.
4.4. Задача о тройной точке
Эта задача, известная в литературе как triple point, ставится в форме расчета распада разрыва в точке контакта трех материалов с различными начальными значениями параметров. В стандартной постановке задача подразумевает расчет точки контакта трех материалов. Предлагаемая в настоящей работе методика на данный момент разработана для расчета контакта только двух материалов. Поэтому рассмотрим слегка упрощенную постановку, в которой два из трех материалов рассматриваются одинаковыми.
Задача рассматривается в безразмерных переменных. Расчетная область представляет собой прямоугольник размером $7$ по оси $x$ и $3$ по оси $y$. В части расчетной области $x < 1$ находится материал $1$ с плотностью ${{\rho }_{1}} = 1$, давлением ${{P}_{1}} = 1$ и скоростью ${{{\mathbf{u}}}_{1}} = {\mathbf{0}}$. В части расчетной области, определяемой неравенствами $x > 1$ и $y > 1.5$, находится материал $1$ с плотностью ${{\rho }_{1}} = 0.125$, давлением ${{P}_{1}} = 0.1$ и скоростью ${{{\mathbf{u}}}_{1}} = {\mathbf{0}}$. В части расчетной области, определяемой неравенствами $x > 1$ и $y < 1.5$, находится материал $2$ с плотностью ${{\rho }_{2}} = 1.0$, давлением ${{P}_{2}} = 0.1$ и скоростью ${{{\mathbf{u}}}_{2}} = {\mathbf{0}}$. Состояние материала $1$ удовлетворяет уравнению состояния идеального газа (50) с показателем адиабаты ${{\gamma }_{1}} = 1.4$, состояние материала $2$ удовлетворяет уравнению состояния идеального газа (50) с показателем адиабаты ${{\gamma }_{2}} = 1.5$. В расчетной области задана равномерная декартова сетка $2100 \times 900$ ячеек. Граничные условия на всех границах ставятся в форме недеформируемой непроницаемой преграды, или непротекания, определяемые соотношениями $({\mathbf{un}}) = 0$.
На фиг. 9 представлены распределения параметра ${{\varphi }_{2}}$, по сути являющегося индикатором присутствия второго материала, в моменты времени $0$, $1$, $2$, $3$, $4$ и $5$. Из результатов видны развитие завихрения на контактной границе и развитие неустойчивости Кельвина–Гельмгольца, возникающей из-за разности скоростей фаз в касательном к контактной поверхности направлении. В результате развития неустойчивости мелкомасштабная структура материала $2$ в области завихренности распадается на отдельные фрагменты. Предложенная численная модель многофазных течений позволяет адекватно воспроизвести деформацию контактной границы в этом сложном нестационарном процессе.
5. ЗАКЛЮЧЕНИЕ
В настоящей работе была предложена методика численного моделирования сжимаемых многофазных течений с разрешением межфазных границ. Математическая модель основана на полностью неравновесной модели Баера-Нунзиато. Для сквозного расчета движения межфазной границы (интерфейса) на эйлеровых сетках рассмотрен алгоритм, основанный на частичном локально-одномерном паттерне геометрии интерфейса вблизи грани смешанной ячейки. С использованием паттерна интерфейса релаксационный процесс в смешанной ячейке моделируется с помощью решения составной задачи Римана. Построены два приближенных решения этой задачи, учитывающие взаимодействие первичных и формирование вторичных волн в рамках приближенных решений типа HLL и HLLC. Предложенный метод не требует каких-либо специальных параметров релаксации и позволяет поддерживать фактически бездиффузионное разрешение межфазной границы, что продемонстрировано на примерах расчетов ряда тестовых задач.
Методика разработана для расчетов задач, включающих только два различных материала. Расширение методики для расчета задач, подразумевающих контакт трех и более материалов, допустимо и стоит в ближайших планах авторов статьи. Кроме того, методика может быть расширена для возможности учета упругопластических свойств материалов.
Список литературы
Greenough J.A., Beckner V., Pember R.B., Crutchfield W.Y., Bell J.B., Colella P. An adaptive multi_uid interface-capturing method for compressible flow in complex geometries // AIAA Paper. 1995. V. 95. P. 1718.
Xiao F., Honma Y., Kono T. A simple algebraic interface capturing scheme using hyperbolic tangent function // Int. J. Numer. Meth. Fluids. 2005. 48. P. 1023–1040.
Terashima H., Tryggvason G. A front-tracking/ghost-fluid method for fluid interfaces in compressible flows // J. Comput. Phys. 2009. V. 228. P. 4012–4037.
Fedkiw R.P., Aslam T., Merriman B., Osher S. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method) // J.Comput. Phys. 1999. V. 152. P. 457–494.
Shukla R.K., Pantano C., Freund J.B. An interface capturing method for the simulation of multi-phase compressible flows // J. Comput. Phys. 2010. V. 229. P. 7411–7439.
Menshov I., Zakharov P. On the composite Riemann problem for multi-material fluid flows // International Journal for Numerical Methods in Fluids. 2014. V. 76. № 2. P. 109–127.
Gorodnichev K., Zakharov P., Kuratov S., Menshov I., Gorodnichev E. Theoretical and numerical analysis of density perturbation development inducted by high velocity impact // Physics of fluids. 2020. V. 32. № 034101. P. 1–13.
Городничев К.Е., Захаров П.П., Куратов С.Е., Меньшов И.С., Серёжкин А.А. Развитие возмущений при ударном воздействии неоднородной по плоности среды // Матем. моделирование. 2017. 29. № 3. С. 95–112.
Baer M., Nunziato J. A two-phase mixture theory for the deflagration-to-detonation transition (ddt) in reactive granular materials // International journal of multiphase flow. 1986. V. 12. P. 861–889.
Ambroso A., Chalons C., Raviart P.A. A Godunov-type method for the sevenequation model of compressible two-phase flow // Comput. Fluids. 2012. V. 54. P. 67–91.
Menshov I., Serezhkin A. A generalized Rusanov method for the Baer-Nunziato equations with application to DDT process in condensed porous explosives // Int J Numer Meth Fluids. 2017. P. 1–19.
Serezhkin A. Mathematical modeling of wide-range compressible two-phase flows // Computers and mathematics with applications. 2019. V. 78. № 2. P. 517–540.
Grove J.W. Pressure-velocity equilibrium hydrodynamic models // Acta Math. Sci. 2010. V 30B. № 2. P. 563–594.
Saurel R., Chinnayya A., Carmouze Q. Modelling compressible dense and dilute twophase flows // Physics of Fluids. 2017. V. 29. P. 063301.
Saurel R., Abgrall R. A multiphase Godunov method for compressible multifluid and multiphase flows // J. Comput. Phys. 1999. V. 150. P. 425–467.
Zhang C., Menshov I. Using the composite Riemann problem solution for carturing interfaces in compressible two-phase flows // Applied Mathematics and Computation. 2019. V. 363. P. 124610.
Harten A., Lax P.D., Leer B.V. On upstream differencing and godunov-type schemes for hyperbolic conservation laws // SIAM review. 1983. V. 25. P. 35–61.
Toro E.F., Spruce M., Speares W. Restoration of the contact surface in the hll-riemann solver // Shock waves. 1994. V. 4. P. 25–34.
Einfeltd B. On Godunov-type methods for gas dynamics // SIAM J. Numer. Anal. 1988. V. 25 № 2. P. 294–318.
Godunov S. A finite difference method for the computation of discontinuous solutions of the equations of fluid dynamics // Sbornik: Mathematics. 1959. V. 89. P. 271–306.
Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. Berlin. Springer, 2009.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики