1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 10, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 10, стр. 1723-1739

Численное моделирование турбулентных потоков на основе современных моделей турбулентности

М. Э. Мадалиев 1, *, З. М. Маликов 2, **

1 Ферганский политехнический институт
150107 Фергана, ул. Фергана, 86, Узбекистан

2 Институт механики и сейсмостойкости сооружений АН Республики Узбекистан
100007 Ташкент, ул. Дурман, 5, Узбекистан

* E-mail: Madaliev.ME2019@mail.ru
** E-mail: malikov.z62@mail.ru

Поступила в редакцию 10.10.2021
После доработки 17.05.2022
Принята к публикации 08.06.2022

Полный текст (PDF)

Аннотация

Проводится сравнение новой двухжидкостной модели турбулентности с другими RANS-моделями для различных турбулентных потоков: смешение двух потоков, течение в плоском диффузоре и осесимметричная несжимаемая дозвуковая струя. В качестве RANS-моделей рассмотрены наиболее популярные модели, способные адекватно описывать сложные турбулентные течения. Сравнения моделей проводятся не только по точности полученных результатов, но и по расходу вычислительных ресурсов для реализации этих моделей. Поэтому вычислительный алгоритм для всех моделей был одинаковым и для достижения стационарных решений использован метод установления, т.е. интегрирования нестационарных уравнений. Для численной реализации систем гидродинамических уравнений использована конечно-разностная схема, где вязкостные члены аппроксимировались центральной разностью неявным образом, а для конвективных членов использовалась явная схема против потока второго порядка точности. На каждом временном шаге коррекция для скоростей проводилась через давление по процедуре SIMPLE. Для оценки адекватности полученные численные результаты сопоставлены с известными экспериментальными данными. Сравнения численных результатов показали, что двухжидкостная модель проста в реализации, требует меньше вычислительных ресурсов, чем другие RANS-модели, и способна с большой точностью предсказывать турбулентные течения. Библ. 33. Фиг. 9.

Ключевые слова: уравнения Навье–Стокса, диффузор, отрывное течение, двухжидкостная модель, метод контрольного объема.

1. ВВЕДЕНИЕ

В настоящее время высокопроизводительные компьютеры позволяют инженерам изучать сложные течения потока путем численного решения уравнений гидродинамики с использованием одного из существующих вычислительных методов. Подобные исследования имеют большое значение для изучения аэро- или гидродинамических процессов, а также для проектирования различных устройств. Известно, что в подавляющем большинстве случаев потоки имеют турбулентный характер. На сегодняшний день турбулентность имеет большое значение для изучения не только жидкостей и газа, но и наножидкостей. Например, в [1]–[7] математические модели турбулентности используются для изучения турбулентного теплообмена в наножидкостях. Поэтому для изучения таких потоков в качестве инструмента необходимо использовать надежную математическую модель турбулентности. В мире существует более 120 различных моделей. Однако каждая модель способна адекватно описать только определенный класс турбулентных течений. Таким образом, до сих пор не существует универсальной модели турбулентности, и создание надежной математической модели турбулентности является одной важной проблемой гидродинамики.

В настоящее время существует несколько подходов к построению математических моделей турбулентности. Первый подход – это гипотеза о применимости уравнений Навье–Стокса для описания турбулентности. Все модели, построенные на основе данного подхода, называются методами прямого моделирования (DNS) и крупных вихрей (LES). Однако для реализации этих методов необходимо решать нестационарные уравнения с расчетными ячейками менее колмогоровского масштаба в трехмерной постановке и необходимо выполнять интегрирование на очень малых временных шагах. В этой связи требуется использование мощных суперкомпьютеров, а их широкое практическое применение, по оценкам специалистов, может начаться лишь в конце этого века.

Второй подход для описания турбулентности – это подход Рейнольдса. В основе данного подхода лежит так называемое уравнение Навье–Стокса, осредненное по Рейнольдсу (RANS). Вывод данного уравнения основан на предположении, что в турбулентном режиме течения скорость потока состоит из осредненных ($\bar {u},\;\bar {v},\;\bar {w}$) и пульсационных ($u{\kern 1pt} ',\;v{\kern 1pt} ',\;w{\kern 1pt} '$) скоростей. При таком подходе в уравнениях гидродинамики после осреднения по времени возникают напряжения Рейнольдса, которые необходимо определить. Следовательно, полученная система уравнений является незамкнутой, и все модели, направленные на замыкания данной системы, называются полуэмпирическими RANS-моделями. В свое время большим шагом в решении проблемы замыкания систем уравнений Рейнольдса была гипотеза Буссинеска (см. [8]), в которой зависимость турбулентных напряжений от осредненной скорости имеет вид

(1)
$ - \overline {u_{i}^{'}u_{j}^{'}} = {{\nu }_{t}}\left( {\partial {{{\bar {u}}}_{i}}{\text{/}}\partial {{x}_{j}} + \partial {{{\bar {u}}}_{j}}{\text{/}}\partial {{x}_{i}}} \right) - 2{\text{/}}3k{{\delta }_{{ij}}},$
где ${{\nu }_{t}}$ – турбулентная вязкость, $k$ – кинетическая энергия пульсации.

Однако, как видно из выражения (1), возникает так называемая неизвестная турбулентная вязкость. Поэтому последующие исследования были направлены на поиск этой турбулентной вязкости. Большие достижения в этом направлении сделаны в работах Колмогорова (см. [9]), Прандтля (см. [10]), Кармана (см. [11]) и т.д.

В базе данных NASA по турбулентности приведен сравнительный анализ различных полуэмпирических моделей. Из этого анализа можно заключить, что высокие рейтинги имеют такие модели, как модели Спаларта–Аллмараса (см. [12]) и Ментера k–ω SST (см. [13], [14]). На сегодняшний день с помощью этих моделей получены численные решения многих важных практических задач. Однако данные модели не дают удовлетворительных результатов при отрывах, вращении и при обтекании тел с большой кривизной. Это объясняется тем, что в основе моделей лежит гипотеза Буссинеска, которая справедлива для изотропных турбулентных течений, а в течениях с отрывом и с сильной закруткой возникает анизотропная турбулентность. Поэтому для течений с анизотропной турбулентностью разработаны модели без привлечения гипотезы Буссинеска, например, модели напряжений Рейнольдса. Недостатком моделей напряжений Рейнольдса является необходимость решать не менее семи уравнений турбулентности, что требует больших вычислительных ресурсов. Кроме того, необходимо использовать специальные средства для улучшения устойчивости и сходимости, нет строгих физических оснований при постановке граничных условий для напряжений на свободных границах.

Еще одним подходом к решению проблемы турбулентности является двухжидкостный подход Сполдинга (см. [15], [16]). Суть данного подхода в том, что турбулентный поток делится на две жидкости по некоторым отличительным признакам потока. Однако двухжидкостной подход Сполдинга не получил дальнейшего развития. Причина в том, что для замыкания систем уравнений, как в RANS-моделях, привлекались еще дополнительные уравнения на основе различных гипотез. В результате число решаемых уравнений удваивалось по сравнению с RANS-моделями, что увеличивало вычислительное время. Данный подход после достаточно долгого периода получил развитие в [17]–[19]. В этих работах показано, что турбулентный поток можно представить в виде гетерогенной смеси двух жидкостей с различными скоростями и температурами. Такая возможность математически доказывается на основе первой гипотезы Рейнольдса (скорость турбулентного потока состоит из осредненной и флуктуирующей скоростей) и молярного движения в турбулентном течении. В [17] на примере различных экспериментально хорошо изученных задач турбулентности показано, что двухжидкостная модель имеет высокую точность, проста в реализации и способна описывать сложные анизотропные турбулентные течения. В [19] приведена методика использования двухжидкостного подхода для моделирования переноса тепла. В этой работе для моделирования турбулентного переноса не использована обобщенная гипотеза Буссинеска и не вводится турбулентное число Прандтля. Вместо них использованы более понятные параметры с точки зрения физики. Поэтому в настоящей работе поставлена цель показать, что разработанная двухжидкостная модель обладает универсальностью и способна с большой точностью описывать различные сложные турбулентные течения. Работа построена следующим образом. Предлагаемая модель турбулентности является сравнительно новой, поэтому в п. 2.1 дается ее описание. В п. 2.2 на основе двухжидкостной модели рассматривается численное исследование турбулентного смешения двух потоков в канале. В п. 2.3 обсуждаются полученные численные результаты. Для наглядности приводятся также опытные данные и результаты моделей SA и SST. В п. 2.4 проводится численное исследование турбулентного потока в плоском диффузоре. В п. 2.5 обсуждаются результаты и проводится сравнение с моделью рейнольдсовых напряжений RSM. В п. 2.6 рассматривается другой тип турбулентности – свободная струя. В п. 2.7 обсуждаются полученные результаты и сравниваются с известными опытными данными, а также с результатами моделей SA и SST.

2. ФИЗИКО-МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧ

2.1. Описание двухжидкостной модели

Рассмотрим течение неоднородной смеси двух жидкостей с разными скоростями. На фиг. 1 показано течение такой смеси в плоскости, перпендикулярной к направлению i. Здесь серым цветом обозначена жидкость I и светлым цветом – жидкость II. Обозначим через ${{V}_{1}},\,\,{{V}_{2}}$ их скорости. Будем считать их плотности одинаковыми и равными ρ. Пусть $\Delta {{S}_{i}}$ – неподвижная элементарная площадь, а $\Delta {{S}_{{1i}}}$ – площадь, занимаемая жидкостью I и $\Delta {{S}_{{2i}}}$ – жидкостью II. Очевидно, что

(2)
$\Delta {{S}_{i}} = \Delta {{S}_{{1i}}} + \Delta {{S}_{{2i}}}.$
Фиг. 1

Определим суммарную массу жидкостей, проходящих через элементарную площадку$\Delta {{S}_{i}}$ за время $\Delta t$:

(3)
$\Delta m = \rho {{V}_{{1i}}}\Delta {{S}_{{1i}}}\Delta t + \rho {{V}_{{2i}}}\Delta {{S}_{{2i}}}\Delta t.$

С другой стороны, данную массу через скорость смеси ${{V}_{i}}$ запишем в виде

(4)
$\Delta m = \rho {{V}_{i}}\Delta {{S}_{i}}\Delta t.$

Приравнивая правые части (3) и (4), а также учитывая (2), найдем скорость гетерогенной смеси двух жидкостей

(5)
${{V}_{i}} = \frac{{\Delta {{S}_{{1i}}}}}{{\Delta {{S}_{i}}}}{{V}_{{1i}}} + \left( {1 - \frac{{\Delta {{S}_{{1i}}}}}{{\Delta {{S}_{i}}}}} \right){{V}_{{2i}}}.$

Очевидно, что

(6)
$0 < \frac{{\Delta {{S}_{{1i}}}}}{{\Delta {{S}_{i}}}} < 1.$

Жидкости состоят из отдельных объемов. Поэтому элементарная площадь $\Delta {{S}_{i}}$ может быть полностью внутри жидкостей I или II в промежутке времени $\tau \approx l{\text{/}}\left| {\mathbf{V}} \right|$, где $l$ – характерный размер объемов жидкостей. Если данный размер существенно меньше, чем характерный размер течения, т.е. $l \ll L$, то и время τ тоже будет существенно меньше, чем характерное время течения. Следовательно, параметр ${{\alpha }_{i}} = \Delta {{S}_{{1i}}}{\text{/}}\Delta {{S}_{i}}$ имеет флуктуирующий характер. Параметр ${{\alpha }_{i}}$ можно интерпретировать как поверхностную долю первой жидкости в элементарной площадке. Следовательно, соотношение (5) можно представить в виде

(7)
${{V}_{i}} = {{\alpha }_{i}}{{V}_{{1i}}} + (1 - {{\alpha }_{i}}){{V}_{{2i}}}.$

Рассмотрим теперь турбулентный поток для несжимаемой жидкости, поэтому флуктуациями плотности можно пренебречь. Следуя гипотезе Рейнольдса, скорость турбулентного потока представим в виде суммы осредненной ${{\bar {V}}_{i}}$ и флуктуирующей $\vartheta _{i}^{'}$ скоростей:

(8)
${{V}_{i}} = {{\bar {V}}_{i}} + \vartheta _{i}^{'}.$

Осреднение скорости здесь проводится по способу Рейнольдса:

(9)
${{\bar {V}}_{i}} = \frac{1}{T}\int\limits_{t - T/2}^{t + T/2} {{{V}_{i}}d\tau .} $
Здесь $T$ – период интегрирования. Введем непульсирующую скорость ${{\vartheta }_{i}}$, для которой выполняется условие $\left| {{{\vartheta }_{i}}} \right| = {{\left| {{{\vartheta }_{i}}} \right|}_{{\max }}}$ в промежутке времени $t - T{\text{/}}2 < \tau < t + T{\text{/}}2$. Флуктуирующую скорость представим в виде
(10)
${{\vartheta }_{i}} = \frac{{\vartheta _{i}^{'}}}{{{{\vartheta }_{i}}}}{{\vartheta }_{i}} = {{\varphi }_{i}}{{\vartheta }_{i}},$
где ${{\varphi }_{i}} = \vartheta _{i}^{'}{\text{/}}{{\vartheta }_{i}}$ – флуктуирующая безразмерная функция, которая меняется во времени в пределах $ - 1 < {{\varphi }_{i}} < 1$. Таким образом, скорость $\left| {{{\vartheta }_{i}}} \right|$ можно интерпретировать как амплитуду флуктуирующей скорости. Введем еще один параметр: ${{\gamma }_{i}} = ({{\varphi }_{i}} + 1){\text{/}}2$. Тогда (10) можно записать в виде

(11)
$\vartheta _{i}^{'} = (2{{\gamma }_{i}} - 1){{\vartheta }_{i}}.$

Осредненное по времени значение флуктуирующей скорости должно быть равно нулю, т.е.

(12)
$\bar {\vartheta }_{i}^{'} = (2{{\bar {\gamma }}_{i}} - 1){{\vartheta }_{i}} = 0.$

Отсюда следует ${{\bar {\gamma }}_{i}} = 0.5$. Таким образом, выражение (8) можно представить в виде

(13)
${{V}_{i}} = {{\gamma }_{i}}({{\bar {V}}_{i}} + {{\vartheta }_{i}}) + (1 - {{\gamma }_{i}})({{\bar {V}}_{i}} - {{\vartheta }_{i}}).$

Опытные наблюдения показывают, что в турбулентном потоке жидкость распадается на отдельные объемы – моли, которые совершают относительное движение. Следовательно, турбулентный поток можно представить как гетерогенную смесь. Поэтому, сравнивая выражения (13) и (7), получим, что турбулентный поток можно представить в виде гетерогенной смеси из двух жидкостей со скоростями

(14)
${{V}_{{1i}}} = {{\bar {V}}_{i}} + {{\vartheta }_{i}},\quad {{V}_{{2i}}} = {{\bar {V}}_{i}} - {{\vartheta }_{i}}.$
и поверхностная доля первой жидкости

(15)
${{\alpha }_{i}} = \Delta {{S}_{{1i}}}{\text{/}}\Delta {{S}_{i}} = {{\gamma }_{i}}.$

Следовательно,

(16)
${{\bar {\alpha }}_{i}} = {{\bar {\gamma }}_{i}} = 0.5.$

Из соотношений (14) следует, что первая жидкость является более “быстрой”, а вторая жидкость – более “медленной”, скорость ${{v}_{i}}$ можно рассматривать как относительную скорость жидкостей. Таким образом, флуктуирующий характер скорости в турбулентном потоке вызван относительным движением двух жидкостей и случайным изменением их поверхностных долей во времени. Следовательно, в турбулентном потоке флуктуирующим параметром являются их поверхностные доли, а не скорости жидкостей. Потому что не существует такой силы, под действием которой объемы жидкостей (моли) могут иметь флуктуирующие скорости.

Для дальнейшего исследования введем объемную долю первой жидкости:

(17)
$\varepsilon = \frac{{\Delta {{\Omega }_{1}}}}{{\Delta \Omega }}.$
Здесь $\Delta \Omega $ – элементарный объем, $\Delta {{\Omega }_{1}}$ – объем, занимаемый первой жидкостью.

Теперь определим массовую плотность первой жидкости в элементарном объеме:

(18)
${{\rho }_{1}} = \frac{{\rho \Delta {{\Omega }_{1}}}}{{\Delta \Omega }} = \varepsilon \rho .$

Масса первой жидкости, прошедшей через элементарную площадку $\Delta {{S}_{i}}$ за время T, определяется интегралом

(19)
$\Delta {{m}_{1}} = \int\limits_{t - T/2}^{t + T/2} {\rho {{V}_{{1i}}}\Delta {{S}_{{1i}}}d\tau = \rho {{V}_{{1i}}}\Delta {{S}_{i}}\int\limits_{t - T/2}^{t + T/2} {{{\alpha }_{i}}d\tau = T{{{\bar {\alpha }}}_{i}}} \rho {{V}_{{1i}}}\Delta {{S}_{i}}.} $

С другой стороны, данная масса определяется интегралом

(20)
$\Delta {{m}_{1}} = \int\limits_{t - T/2}^{t + T/2} {{{\rho }_{1}}{{V}_{{1i}}}\Delta {{S}_{i}}d\tau = \rho {{V}_{{1i}}}\Delta {{S}_{i}}\int\limits_{t - T/2}^{t + T/2} {\varepsilon d\tau = T\bar {\varepsilon }} \rho {{V}_{{1i}}}\Delta {{S}_{i}}.} $

Сопоставляя правые части (19) и (20), получим

(21)
$\bar {\varepsilon } = {{\bar {\alpha }}_{i}} = 0.5.\,$

Таким образом, представляя турбулентное течение как смесь двух потоков, уравнения неразрывности для каждой жидкости запишем в виде

(22)
$\frac{{\partial \varepsilon \rho }}{{\partial t}} + \frac{{\partial \rho {{\alpha }_{j}}{{V}_{{1j}}}}}{{\partial {{x}_{j}}}} = J,\quad \frac{{\partial (1 - \varepsilon )\rho }}{{\partial t}} + \frac{{\partial \rho (1 - {{\alpha }_{j}}){{V}_{{2j}}}}}{{\partial {{x}_{j}}}} = - J.$
Здесь $J$ – интенсивность обмена массой между жидкостями. После подстановки в уравнение (22) скорости из соотношения (14) и осреднения по времени получим уравнения

(23)
$\frac{{\partial 0.5\rho ({{{\bar {V}}}_{j}} + {{\vartheta }_{j}})}}{{\partial {{x}_{j}}}} = \bar {J},\quad \frac{{\partial 0.5\rho ({{{\bar {V}}}_{j}} - {{\vartheta }_{j}})}}{{\partial {{x}_{j}}}} = - \bar {J}.$

При этом учитывалось соотношение (21), а также несжимаемость потока. Из систем уравнений (23) несложно получить

(24)
$\frac{{\partial \rho {{{\bar {V}}}_{j}}}}{{\partial {{x}_{j}}}} = 0,\quad \frac{{\partial \rho {{\vartheta }_{j}}}}{{\partial {{x}_{j}}}} = 2\bar {J}.$

Аналогично запишем для каждой жидкости уравнение движения (см. [12]):

(25)
$\begin{gathered} \frac{{\partial \varepsilon \rho {{V}_{{1i}}}}}{{\partial t}} + \frac{{\partial {{\alpha }_{j}}(\rho {{V}_{{1j}}}{{V}_{{1i}}} + {{\delta }_{{ij}}}p - {{\sigma }_{{1ji}}})}}{{\partial {{x}_{j}}}} = {{f}_{i}}, \\ \frac{{\partial (1 - \varepsilon )\rho {{V}_{{2i}}}}}{{\partial t}} + \frac{{\partial (1 - {{\alpha }_{j}})(\rho {{V}_{{2j}}}{{V}_{{2i}}} + {{\delta }_{{ij}}}p - {{\sigma }_{{2ji}}})}}{{\partial {{x}_{j}}}} = - {{f}_{i}}. \\ \end{gathered} $

Согласно гипотезе Рейнольдса, давление жидкости представим в виде суммы осредненного и пульсационного давлений: $p = \bar {p} + p{\kern 1pt} '$. Тогда после осреднения по времени получим

(26)
$\begin{gathered} \frac{{\partial 0.5\rho {{V}_{{1i}}}}}{{\partial t}} + \frac{{\partial 0.5(\rho {{V}_{{1j}}}{{V}_{{1i}}} + {{\delta }_{{ij}}}\bar {p} - {{\sigma }_{{1ji}}})}}{{\partial {{x}_{j}}}} = {{{\bar {f}}}_{i}}, \\ \frac{{\partial 0.5\rho {{V}_{{2i}}}}}{{\partial t}} + \frac{{\partial 0.5(\rho {{V}_{{2j}}}{{V}_{{2i}}} + {{\delta }_{{ij}}}\bar {p} - {{\sigma }_{{2ji}}})}}{{\partial {{x}_{j}}}} = - {{{\bar {f}}}_{i}}. \\ \end{gathered} $
Здесь
(27)
$\begin{gathered} {{{\bar {f}}}_{i}} = \frac{1}{T}\int\limits_{t - T/2}^{t + T/2} {({{f}_{i}} - {{\alpha }_{i}}p{\kern 1pt} ')d\tau ,} \\ {{\sigma }_{{1ij}}} = \mu \left( {\frac{{\partial {{V}_{{1i}}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{V}_{{1j}}}}}{{\partial {{x}_{i}}}}} \right),\quad {{\sigma }_{{2ij}}} = \mu \left( {\frac{{\partial {{V}_{{2i}}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{V}_{{2j}}}}}{{\partial {{x}_{i}}}}} \right), \\ \end{gathered} $
где $\mu $ – коэффициент динамической вязкости жидкости.

Подставим скорости молей из (14) в (26), затем сложим эти уравнения. В итоге получим уравнение импульса для осредненного потока

(28)
$\frac{{\partial \rho {{{\bar {V}}}_{i}}}}{{\partial t}} + \frac{{\partial (\rho {{{\bar {V}}}_{j}}{{{\bar {V}}}_{i}} + {{\delta }_{{ij}}}\bar {p})}}{{\partial {{x}_{j}}}} = \frac{{\partial ({{\Pi }_{{ji}}} - \rho {{\vartheta }_{j}}{{\vartheta }_{i}})}}{{\partial {{x}_{j}}}},$
где

${{\Pi }_{{ji}}} = \mu \left( {\frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{\bar {V}}}_{j}}}}{{\partial {{x}_{i}}}}} \right).$

Теперь, если в системе (26) вычтем из первого уравнения второе, получим уравнение для относительной скорости

(29)
$\begin{gathered} \frac{{\partial \rho {{\vartheta }_{i}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{j}}}}(\rho {{{\bar {V}}}_{j}}{{\vartheta }_{i}} + \rho {{\vartheta }_{j}}{{{\bar {V}}}_{i}} - {{\pi }_{{ji}}}) = 2{{{\bar {f}}}_{i}}, \\ {{\pi }_{{ji}}} = \mu \left( {\frac{{\partial {{\vartheta }_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{\vartheta }_{j}}}}{{\partial {{x}_{i}}}}} \right). \\ \end{gathered} $

Таким образом, систему уравнений для осредненных величин турбулентного потока можно записать следующим образом:

(30)
$\begin{gathered} \frac{{\partial \rho {{{\bar {V}}}_{j}}}}{{\partial {{x}_{j}}}} = 0,\quad \frac{{\partial \rho {{v}_{j}}}}{{\partial {{x}_{j}}}} = 2\bar {J}, \\ \frac{{\partial \rho {{{\bar {V}}}_{i}}}}{{\partial t}} + \frac{{\partial (\rho {{{\bar {V}}}_{j}}{{{\bar {V}}}_{i}} + {{\delta }_{{ji}}}\bar {p})}}{{\partial {{x}_{j}}}} = \frac{{\partial ({{\Pi }_{{ji}}} - \rho {{\vartheta }_{j}}{{\vartheta }_{i}})}}{{\partial {{x}_{j}}}},\quad \frac{{\partial \rho {{\vartheta }_{i}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{j}}}}(\rho {{{\bar {V}}}_{j}}{{\vartheta }_{i}} + \rho {{\vartheta }_{j}}{{{\bar {V}}}_{i}} - {{\pi }_{{ji}}}) = 2{{{\bar {f}}}_{i}}, \\ {{\Pi }_{{ji}}} = \mu \left( {\frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{\bar {V}}}_{j}}}}{{\partial {{x}_{i}}}}} \right),\quad {{\pi }_{{ji}}} = \mu \left( {\frac{{\partial {{\vartheta }_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{\vartheta }_{j}}}}{{\partial {{x}_{i}}}}} \right). \\ \end{gathered} $

Система (30) – это основные уравнения нового двухжидкостного подхода к математическому описанию турбулентности. Как видно из (30), уравнение движения для осредненного потока имеет вид, очень похожий на осредненное уравнение Рейнольдса. Однако в уравнениях Рейнольдса турбулентные напряжения являются неизвестными. Следовательно, уравнения Рейнольдса являются незамкнутыми, и для замыкания необходимо привлечь различные гипотезы. Что же касается нового двухжидкостного подхода, то он дает замкнутую систему уравнений (30).

В упомянутой работе [17] подробно описаны методики определения сил взаимодействия между жидкостями${{\bar {f}}_{i}}$. Поэтому здесь приведем только их окончательный вид:

(31)
$\begin{gathered} 2{{{\bar {f}}}_{i}} = 2{{{\bar {V}}}_{i}}\bar {J} + {{F}_{{si}}} + {{F}_{{fi}}} + {{F}_{{mi}}}, \\ {{{\mathbf{F}}}_{s}} = \rho {{C}_{s}}\operatorname{rot} {\mathbf{\bar {V}}} \times \vartheta ,\quad {{{\mathbf{F}}}_{i}} = - \rho {{K}_{f}}\vartheta ,\quad {{F}_{{mi}}} = 2\frac{\partial }{{\partial {{x}_{j}}}}\left[ {\rho {{\nu }_{{ji}}}\left( {\frac{{\partial {{\vartheta }_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{\vartheta }_{j}}}}{{\partial {{x}_{i}}}}} \right)} \right], \\ {{\nu }_{{ji}}} = 3\nu + 2\left| {\frac{{{{\vartheta }_{i}}{{\vartheta }_{j}}}}{{\operatorname{def} ({\mathbf{\bar {V}}})}}} \right|\quad {\text{для}}\quad i \ne j,\quad {{\nu }_{{ii}}} = 3\nu + \frac{1}{{\operatorname{div} {\mathbf{v}}}}\left| {\frac{{{{\vartheta }_{k}}{{\vartheta }_{k}}}}{{\operatorname{def} ({\mathbf{\bar {V}}})}}} \right|\frac{{\partial {{\vartheta }_{k}}}}{{\partial {{x}_{k}}}}. \\ \end{gathered} $
Здесь $2{{\bar {V}}_{i}}\bar {J}$ – сила, вызванная обменом массой между жидкостями, ${{F}_{{si}}}$ – поперечная сила Сефмена (см. [20]), обусловленная сдвиговым полем скорости, ${{F}_{{fi}}}$ – сила трения, ${{F}_{{mi}}}$ – сила, возникающая в результате относительного молярного движения жидкостей, ${\text{def}}({\mathbf{\bar {V}}}) = \sqrt {2{{S}_{{ij}}}} {{S}_{{ij}}},$ ${{S}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{\bar {V}}}_{j}}}}{{\partial {{x}_{i}}}}} \right)$ – скорость деформации. Подставляя выражения (31) в систему уравнений (30), получим окончательный вид системы уравнений для турбулентного потока в новом двухжидкостном подходе:
(32)
$\begin{gathered} \frac{{\partial \rho {{{\bar {V}}}_{j}}}}{{\partial {{x}_{j}}}} = 0,\quad \frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial t}} + {{{\bar {V}}}_{j}}\frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial{ \bar {p}}}}{{\rho \partial {{x}_{i}}}} = \frac{\partial }{{\partial {{x}_{j}}}}\left[ {\nu \left( {\frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{\bar {V}}}_{j}}}}{{\partial {{x}_{i}}}}} \right) - {{\vartheta }_{j}}{{\vartheta }_{i}})} \right], \\ \frac{{\partial {{\vartheta }_{i}}}}{{\partial t}} + {{{\bar {V}}}_{j}}\frac{{\partial {{\vartheta }_{i}}}}{{\partial {{x}_{j}}}} = - \rho {{v}_{j}}\frac{{\partial{ \bar {V}}}}{{\partial {{x}_{j}}}} + \frac{\partial }{{\partial {{x}_{j}}}}\left[ {{{\nu }_{{ji}}}\left( {\frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{\bar {V}}}_{j}}}}{{\partial {{x}_{i}}}}} \right)} \right] + \frac{{{{F}_{{si}}}}}{\rho } + \frac{{{{F}_{{fi}}}}}{\rho }, \\ {{\nu }_{{ji}}} = 3\nu + 2\left| {\frac{{{{\vartheta }_{i}}{{\vartheta }_{j}}}}{{\operatorname{def} ({\mathbf{\bar {V}}})}}} \right|\quad {\text{для}}\quad i \ne j,\quad {{\nu }_{{ii}}} = 3\nu + \frac{{{{\vartheta }_{k}}{{\vartheta }_{k}}{{J}_{k}}}}{{\operatorname{def} ({\mathbf{\bar {V}}})\sum {{{J}_{n}}} }},\quad {{J}_{k}} = \left| {\frac{{\partial {{\vartheta }_{k}}}}{{\partial {{x}_{k}}}}} \right|, \\ {{{\mathbf{F}}}_{f}} = - \rho {{K}_{f}}\vartheta ,\quad {{{\mathbf{F}}}_{s}} = \rho {{C}_{s}}\operatorname{rot} \overline {\mathbf{V}} \times \vartheta . \\ \end{gathered} $
Здесь ${{K}_{f}}$ – коэффициент трения:

(33)
${{K}_{f}} = {{C}_{1}}{{\lambda }_{{\max }}} + {{C}_{2}}\frac{{\left| {{\mathbf{d}} \cdot \vartheta } \right|}}{{{{d}^{2}}}}.$

В данном выражении $d$ – ближайшее расстояние до твердой стенки, ${{\lambda }_{{\max }}}$ – наибольший корень характеристического уравнения

(34)
$\det (A - \lambda E) = 0,$
где $A$ – матрица
$A = \left| {\begin{array}{*{20}{c}} { - \frac{{\partial {{{\bar {V}}}_{1}}}}{{\partial {{x}_{1}}}}}&{ - \frac{{\partial {{{\bar {V}}}_{1}}}}{{\partial {{x}_{2}}}} - {{C}_{s}}{{\zeta }_{3}}}&{ - \frac{{\partial {{{\bar {V}}}_{1}}}}{{\partial {{x}_{3}}}} + {{C}_{s}}{{\zeta }_{2}}} \\ { - \frac{{\partial {{{\bar {V}}}_{2}}}}{{\partial {{x}_{1}}}} + {{C}_{s}}{{\zeta }_{3}}}&{ - \frac{{\partial {{{\bar {V}}}_{2}}}}{{\partial {{x}_{2}}}}}&{ - \frac{{\partial {{{\bar {V}}}_{2}}}}{{\partial {{x}_{3}}}} - {{C}_{s}}{{\zeta }_{1}}} \\ { - \frac{{\partial {{{\bar {V}}}_{3}}}}{{\partial {{x}_{1}}}} - {{C}_{s}}{{\zeta }_{2}}}&{ - \frac{{\partial {{{\bar {V}}}_{3}}}}{{\partial {{x}_{2}}}} + {{C}_{s}}{{\zeta }_{1}}}&{ - \frac{{\partial {{V}_{3}}}}{{\partial {{x}_{3}}}}} \end{array}} \right|$
и $\zeta = \operatorname{rot} {\mathbf{V}}$.

В тестовых задачах показано, что хорошие результаты получаются при ${{C}_{1}} = 0.7825,$ ${{C}_{2}} = 0.306,$ ${{C}_{s}} = 0.2$.

2.2. Смешение двух турбулентных потоков

Смешение двух параллельных потоков является важной фундаментальной проблемой в турбулентных потоках. Проблема имеет отношение ко многим промышленным применениям и природным явлениям, таким как распыление воздуха в системах впрыска топлива и разрушение волн в океане. В данной работе моделируется турбулентное смешение двух потоков с разными скоростями (см. [21]).

Схема течения представлена на фиг. 2. Торец пластины расположен в точке х = 0, а два потока жидкости с разными скоростями сливаются ниже по потоку от этого места. Общая длина канала равна х =1800 мм. В эксперименте скорость на входе верхнего потока равна ${{U}_{1}} = 41.54\,$ м/с, а нижнего – ${{U}_{2}} = 22.4\,$ м/с.

Фиг. 2.

Смешивание слоев.

Для численной реализации системы уравнений (32) ниже для всех задач используется метод контрольного объема. При этом вязкостные члены аппроксимировались центральной разностью, а для конвективных членов использовалась схема второго порядка точности. Для одномерного случая данная схема имеет вид

$U\frac{{\partial U}}{{\partial x}} = \left| \begin{gathered} {{U}_{i}}\frac{{3{{U}_{i}} - 4{{U}_{{i - 1}}} + {{U}_{{i - 2}}}}}{{2\Delta x}},\quad {{U}_{i}} > 0 \hfill \\ {{U}_{i}}\frac{{ - {{U}_{{i + 2}}} + 4{{U}_{{i + 1}}} - 3{{U}_{i}}}}{{2\Delta x}},\quad {{U}_{i}} < 0 \hfill \\ \end{gathered} \right|.$

Связь между давлением и скоростями осуществлялась по процедуре SIMPLE (см. [22]). Таким образом, общая схема дает второго порядка точности по пространству и первого по времени.

Система уравнений (32) была приведена к безразмерному виду путем соотнесения всех скоростей со средней скоростью на входе к верхнему потоку, а пространственные размеры – к высоте общего канала. Число Рейнольдса было равно ${{\operatorname{Re} }_{H}} = 870\,000$. Для численной реализации систем уравнений (32) в качестве начального условия задавались скорости несмешивающихся потоков. На входе также задавались начальные безразмерные относительные скорости $u = 0.01$, $\vartheta = 0$. На стенках ставились условия прилипания. На выходе x = 1200 мм задавались условия экстраполяции второго порядка точности (см. [23]).

Для получения более точных результатов проведено преобразование центра координат по Y0 = 0, сгущение сетки по Y:

$x = \bar {x},\quad \bar {y} = B + \frac{1}{\tau }{\text{arsh}}\left[ {\left( {\frac{y}{{{{y}_{c}}}} - 1} \right){\text{sh}}\left( {\tau B} \right)} \right].$
Здесь
$B = \frac{1}{{2\tau }}\ln \left[ {\frac{{1 + ({{e}^{\tau }} - 1)({{y}_{c}}{\text{/}}h)}}{{1 + ({{e}^{{ - \tau }}} - 1)({{y}_{c}}{\text{/}}h)}}} \right],\quad 0 < \tau < \infty ,$
где τ = 0.9 – параметр растяжения, который изменяется от нуля до больших значений, ${{y}_{c}}$ = 0 – координаты сгущающейся области сетки.

После преобразования система уравнений (32) имеет следующий вид:

(35)
$\begin{gathered} \frac{{\partial U}}{{\partial t}} + U\frac{{\partial U}}{{\partial{ \bar {x}}}} + U\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial U}}{{\partial{ \bar {y}}}} + V\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial U}}{{\partial{ \bar {y}}}} + \frac{{\partial p}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial p}}{{\partial{ \bar {y}}}} = \\ = \frac{1}{{\operatorname{Re} }}\left( {\frac{{\partial U}}{{\partial {{{\bar {x}}}^{2}}}} + 2\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{{{\partial }^{2}}U}}{{\partial{ \bar {x}}\partial{ \bar {y}}}} + {{{\left( {\frac{{\partial{ \bar {y}}}}{{\partial x}}} \right)}}^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{{\bar {y}}}^{2}}}} + \frac{{{{\partial }^{2}}\bar {y}}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{2}}U}}{{\partial {{{\bar {y}}}^{2}}}} + {{{\left( {\frac{{\partial{ \bar {y}}}}{{\partial y}}} \right)}}^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{{\bar {y}}}^{2}}}}} \right) - \frac{{\partial uu}}{{\partial{ \bar {x}}}} - \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial uu}}{{\partial{ \bar {y}}}} - \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial u\vartheta }}{{\partial{ \bar {y}}}}; \\ \frac{{\partial V}}{{\partial t}} + U\frac{{\partial V}}{{\partial{ \bar {x}}}} + U\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial V}}{{\partial{ \bar {y}}}} + V\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial V}}{{\partial{ \bar {y}}}} + \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial p}}{{\partial{ \bar {y}}}} = \\ = \frac{1}{{\operatorname{Re} }}\left( {\frac{{\partial V}}{{\partial {{{\bar {x}}}^{2}}}} + 2\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{{{\partial }^{2}}V}}{{\partial{ \bar {x}}\partial{ \bar {y}}}} + {{{\left( {\frac{{\partial{ \bar {y}}}}{{\partial x}}} \right)}}^{2}}\frac{{{{\partial }^{2}}V}}{{\partial {{{\bar {y}}}^{2}}}} + \frac{{{{\partial }^{2}}\bar {y}}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{2}}V}}{{\partial {{{\bar {y}}}^{2}}}} + {{{\left( {\frac{{\partial{ \bar {y}}}}{{\partial y}}} \right)}}^{2}}\frac{{{{\partial }^{2}}V}}{{\partial {{{\bar {y}}}^{2}}}}} \right) - \frac{{\partial \vartheta u}}{{\partial{ \bar {x}}}} - \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial \vartheta u}}{{\partial{ \bar {y}}}} - \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial \vartheta \vartheta }}{{\partial{ \bar {y}}}}; \\ \frac{{\partial u}}{{\partial t}} + U\frac{{\partial u}}{{\partial{ \bar {x}}}} + U\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial u}}{{\partial{ \bar {y}}}} + V\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial u}}{{\partial{ \bar {y}}}} = - \left( {u\frac{{\partial U}}{{\partial{ \bar {x}}}} + u\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial U}}{{\partial{ \bar {y}}}} + \vartheta \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial U}}{{\partial{ \bar {y}}}}} \right) + \\ + \;{{C}_{s}}\left( { - \left( {\frac{{\partial V}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial V}}{{\partial{ \bar {y}}}} - \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial U}}{{\partial{ \bar {y}}}}} \right)\vartheta } \right) + \frac{\partial }{{\partial{ \bar {x}}}}\left( {2v_{{xx}}^{'}\left( {\frac{{\partial u}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial u}}{{\partial{ \bar {y}}}}} \right)} \right) + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{\partial }{{\partial{ \bar {y}}}}\left( {2v_{{xx}}^{'}\left( {\frac{{\partial u}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial u}}{{\partial{ \bar {y}}}}} \right)} \right) + \\ + \;\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{\partial }{{\partial{ \bar {y}}}}\left( {v_{{xy}}^{'}\left( {\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial u}}{{\partial{ \bar {y}}}} + \frac{{\partial \vartheta }}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial \vartheta }}{{\partial{ \bar {y}}}}} \right)} \right) - {{C}_{r}}u; \\ \frac{{\partial \vartheta }}{{\partial t}} + U\frac{{\partial \vartheta }}{{\partial{ \bar {x}}}} + U\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial \vartheta }}{{\partial{ \bar {y}}}} + V\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial \vartheta }}{{\partial{ \bar {y}}}} = - \left( {u\frac{{\partial V}}{{\partial{ \bar {x}}}} + u\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial V}}{{\partial{ \bar {y}}}} + \vartheta \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial V}}{{\partial{ \bar {y}}}}} \right) + \\ + \;{{C}_{s}}\left( {\left( {\frac{{\partial V}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial V}}{{\partial{ \bar {y}}}} - \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial U}}{{\partial{ \bar {y}}}}} \right)u} \right) + \frac{\partial }{{\partial{ \bar {x}}}}\left( {v_{{xy}}^{'}\left( {\frac{{\partial \vartheta }}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial \vartheta }}{{\partial{ \bar {y}}}} + \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial u}}{{\partial{ \bar {y}}}}} \right)} \right) + \\ + \;\frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{\partial }{{\partial{ \bar {y}}}}\left( {v_{{xy}}^{'}\left( {\frac{{\partial \vartheta }}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial \vartheta }}{{\partial{ \bar {y}}}} + \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial u}}{{\partial{ \bar {y}}}}} \right)} \right) + \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{\partial }{{\partial{ \bar {y}}}}\left( {2{{{v'}}_{{yy}}}\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial \vartheta }}{{\partial{ \bar {y}}}}} \right) - {{C}_{r}}\vartheta ; \\ \frac{{\partial U}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial U}}{{\partial{ \bar {y}}}} + \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial V}}{{\partial{ \bar {y}}}} = 0. \\ \end{gathered} $
Здесь

$\begin{gathered} {{\nu }_{{xx}}} = {{\nu }_{{yy}}} = \frac{3}{{\operatorname{Re} }} + 2\frac{S}{{\left| {\operatorname{def} U} \right|}},\quad {{\nu }_{{xy}}} = \frac{3}{{\operatorname{Re} }} + 2\left| {\frac{{u\vartheta }}{{\operatorname{def} U}}} \right|,\quad S = \frac{{{{u}^{2}}{{J}_{x}} + {{\vartheta }^{2}}{{J}_{y}}}}{{{{J}_{x}} + {{J}_{y}}}},\quad {{J}_{x}} = \left| {\frac{{\partial u}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial u}}{{\partial{ \bar {y}}}}} \right|, \\ {{J}_{y}} = \left| {\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial \vartheta }}{{\partial{ \bar {y}}}}} \right|,\quad \left| {\operatorname{def} \bar {U}} \right| = \sqrt {2\left( {{{{\left( {\frac{{\partial U}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial U}}{{\partial{ \bar {y}}}}} \right)}}^{2}} + {{{\left( {\frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial V}}{{\partial{ \bar {y}}}}} \right)}}^{2}}} \right) + {{{\left( {\frac{{\partial V}}{{\partial{ \bar {x}}}} + \frac{{\partial{ \bar {y}}}}{{\partial x}}\frac{{\partial V}}{{\partial{ \bar {y}}}} + \frac{{\partial{ \bar {y}}}}{{\partial y}}\frac{{\partial U}}{{\partial{ \bar {y}}}}} \right)}}^{2}}} {{C}_{s}} = 0.2, \\ {{C}_{r}} = {{C}_{1}}{{\lambda }_{{\max }}} + {{C}_{2}}\frac{{\left| {d \cdot \vartheta } \right|}}{{{{d}^{2}}}}. \\ \end{gathered} $

Для численного расчета используется сетка 120 × 300 со сгущением в центре канала. Таким образом, поперечный шаг равен Δy = 1/300, а продольный – Δx = 1/30. Интегрирование проводилось шагом по времени Δt = 0.005.

2.3. Результаты расчетов и их обсуждение для задачи смешивания двух потоков

На фиг. 3 представлены графики в различных сечениях канала для безразмерной продольной скорости по результатам моделей турбулентности. Для сравнения приведены экспериментальные данные из базы данных NASA. Здесь U1= 22.40 м/с, ∆U = 19.14 м/с и (а) – δw = 13.771 мм при x = 200 мм, (б) – δw = 35.894 мм при x = 650 мм, (в) – δw = 50.547 мм при x = 950 мм.

Фиг. 3.

Профили безразмерной осевой скорости на различных участках канала: (а) – x = 200 мм, (б) – x = 650 мм, (в) – x = 950 мм.

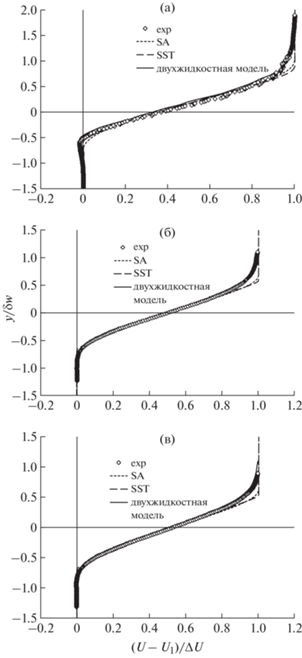
Из фиг. 3 следует, что результаты двухжидкостной модели имеют наибольшее согласие с экспериментальными данными.

На фиг. 4 представлены профили турбулентного напряжения в различных сечениях канала.

Фиг. 4.

Профили турбулентных напряжений при различных поперечных сечениях канала: (а) – x = 200 мм, (б) – x = 650 мм, (в) – x = 950 мм.

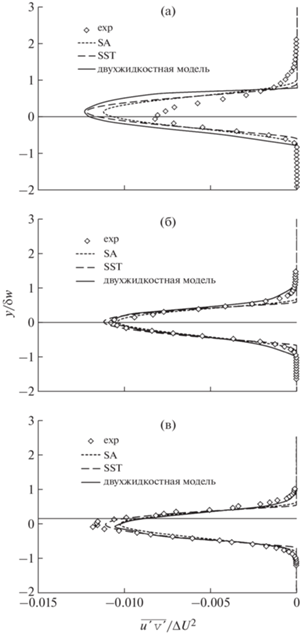
Из фиг. 4 следует, что все модели дают приблизительно одинаковые результаты. Однако при интегрировании для устойчивости модели SA требовался шаг по времени Δt = 0.001, для SST – Δt = 0.0001, а для двухжидкостной модели – Δt = 0.005. Таким образом, для реализации двухжидкостной модели требуется меньше вычислительных ресурсов, чем для RANS-моделей.

2.4. Асимметричный плоский диффузор

Явление отрыва имеет большое значение как в теоретическом, так и в практическом плане. Поэтому в этом направлении проведено много исследований. Одной из первых работ, где проведен расчет точки разделения в несжимаемых турбулентных потоках, является работа Себечи и др. [24]. В [25] Оби и др. экспериментально и вычислительно изучили разделение в асимметричном плоском диффузоре, и их работа привлекла широкое внимание. Аналогичное исследование проведено Клистафани (см. [26]) и Торнбломом (см. [27]). Результаты этих работ согласуются с результатами Оби.

В [28], [29] проведен сравнительный анализ различных RANS-моделей применительно для расчета асимметричного диффузора. В настоящей работе делается вывод, что наиболее точные результаты для профиля продольной скорости дает метод напряжений Рейнольдса.

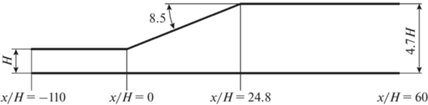
В данном исследовании геометрия рассматриваемого двухмерного асимметричного плоского диффузора показана на фиг. 5. Для сопоставления численных результатов размер геометрии диффузора соответствует диффузору из работы Байса и Итона [30], где представлены экспериментальные данные.

Фиг. 5.

Схема вычислительной области в осесимметричном плоском диффузоре.

В работе турбулентная жидкость в асимметричном диффузоре исследуется на основе двухжидкостной модели и метода турбулентных напряжений ERASM (см. [31]). Для двухжидкостной модели используется система уравнений (35) и выполняется преобразование координат $(x,y) \to (\bar {x},\bar {y})$, приводящее к равномерной прямоугольной вычислительной области (см. [11]):

$\begin{gathered} \bar {x} = \frac{x}{H},\quad \bar {y} = \frac{y}{H},\quad - 110 < \frac{x}{H} < 0, \\ \bar {x} = \frac{x}{H},\quad \bar {y} = \frac{y}{{H\left( {1 + 3.7\frac{{x{\text{/}}H}}{{24.8}}} \right)}},\quad 0 < \frac{x}{H} < 24.8, \\ \bar {x} = \frac{x}{H},\quad \bar {y} = \frac{y}{{4.7H}},\quad 24.8 < \frac{x}{H} < 60. \\ \end{gathered} $

Система уравнений (35) приводилась к безразмерному виду путем соотнесения всех скоростей к средней скорости на входе, а пространственные размеры – к высоте H. На входе были заданы следующие условия:

$U = 1,\quad V = 0,\quad u = 0.01,\quad \vartheta = 0.$

На стенках задавались условия прилипания. На выходе использовались условия экстраполяции. Число Рейнольдса было равно ${{\operatorname{Re} }_{H}} = 20\,000$. В работе использована сетка 500 × 100. Исследование сходимости сеток показало, что увеличение числа сеток в 2 раза в поперечном направлении привело к изменениям численных результатов не более, чем на 3%. Поэтому оптимальный поперечный шаг был Δy = 0.01, а продольный – Δx = 0.3896. Интегрирование проводилось с шагом по времени Δt = 0.005.

2.5. Результаты расчетов и их обсуждение для задачи асимметричного плоского диффузора

На фиг. 6 и 7 приведены графики сравнения расчетных и экспериментальных данных. На фиг. 6 показаны профили продольной скорости в различных сечениях диффузора. Здесь также представлены и численные результаты по EARSM.

Фиг. 6.

Профили аксиальной ($10U{\text{/}}{{U}_{0}} + x{\text{/}}H$) компоненты скорости: кружки – эксперимент из [24], сплошные линии – двухжидкостная модель, штриховые – EARSM из [25].

Фиг. 7.

Профили турбулентных напряжений $\left( {500\overline {u{\kern 1pt} 'u{\kern 1pt} '} {\text{/}}U_{0}^{2} + x{\text{/}}H} \right)$: (a) – $\overline {u{\kern 1pt} 'u{\kern 1pt} '} $, (б) – $\overline {v{\kern 1pt} 'v{\kern 1pt} '} $, (в) – $\overline {u{\kern 1pt} 'v{\kern 1pt} '} $, в различных сечениях канала: кружки – эксперимент, сплошные линии – двухжидкостная модель, штриховые – EARSM.

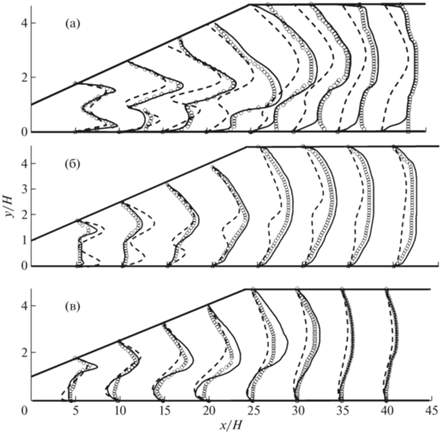
Из фиг. 6 следует, что обе модели удовлетворительно предсказывают профиль продольной скорости, но наиболее близкое совпадение наблюдается у двухжидкостной модели.

На фиг. 7 представлены профили турбулентных напряжений $\overline {u{\kern 1pt} 'u{\kern 1pt} '} ,$ $\overline {v{\kern 1pt} 'v{\kern 1pt} '} ,$ $\overline {u{\kern 1pt} 'v{\kern 1pt} '} $ в различных сечениях.

Из фиг. 7 следует, что и в этом случае двухжидкостная модель предсказывает турбулентные напряжения более адекватно, чем достаточно сложная модель EARSM.

2.6. Осесимметричная дозвуковая струя

Во многих случаях при движении жидкости и газа возникают так называемые поверхности тангенциального разрыва. Течение жидкости в окрестности такой поверхности называется струей. Тангенциальный разрыв допустим по таким параметрам, как скорость течения, температура и концентрация примеси. При этом распределение статического давления оказывается непрерывным. Как известно, на поверхности тангенциального разрыва в связи с ее неустойчивостью возникают вихри, беспорядочно движущиеся вдоль и поперек потока, вследствие этого происходит молярный поперечный перенос количества движения, тепла и примесей. В результате на границе двух струй формируется область конечной толщины с непрерывным распределением скорости, температуры и концентрации примеси, которая называется струйным турбулентным пограничным слоем. Наиболее изученным видом турбулентной струи является струя, распространяющаяся в покоящейся среде, такая струя называется затопленной (см. [32]).

Рассматриваемая задача имеет большое значение для авиационной и ракетно-космической техники. В [17] на основе новой двухжидкостной модели проведено исследование затопленной струи. При этом использовалась упрощенная, параболизованная система уравнений, т.е. давление предполагалось постоянным. Однако не во всех струйных течениях давление можно считать постоянным. Например, во многих технических устройствах струя может протекать в ограниченных пространствах. Поэтому целью настоящей работы является апробация двухжидкостной модели для затопленной струи при использовании полной системы уравнений турбулентности. Описание данной задачи представлено в базе данных NASA (см. [33]).

Система уравнений несжимаемой турбулентной струи в двухжидкостной модели в цилиндрических координатах имеет следующий вид (см. [18], [23]):

(36)
$\begin{gathered} \frac{{\partial U}}{{\partial t}} + U\frac{{\partial U}}{{\partial x}} + V\frac{{\partial U}}{{\partial r}} + \frac{{\partial p}}{{\rho \partial x}} = \nu \left( {\frac{{{{\partial }^{2}}U}}{{\partial {{r}^{2}}}} + \frac{{\partial U}}{{r\partial r}} + \frac{{{{\partial }^{2}}U}}{{\partial {{x}^{2}}}}} \right) - \frac{{\partial r\vartheta u}}{{r\partial r}} - \frac{{\partial uu}}{{\partial x}}, \\ \frac{{\partial V}}{{\partial t}} + U\frac{{\partial V}}{{\partial x}} + V\frac{{\partial V}}{{\partial r}} + \frac{{\partial p}}{{\rho \partial r}} = \nu \left( {\frac{{{{\partial }^{2}}V}}{{\partial {{r}^{2}}}} + \frac{{\partial V}}{{r\partial r}} + \frac{{{{\partial }^{2}}V}}{{\partial {{x}^{2}}}}} \right) - \frac{{\partial r\vartheta \vartheta }}{{r\partial r}} - \frac{{\partial u\vartheta }}{{\partial x}}, \\ \frac{{\partial u}}{{\partial t}} + U\frac{{\partial u}}{{\partial x}} + V\frac{{\partial u}}{{\partial r}} = - \frac{{\partial U}}{{\partial x}}u - \frac{{\partial U}}{{\partial r}}\vartheta + {{C}_{s}}\left( {\frac{{\partial U}}{{\partial r}} - \frac{{\partial V}}{{\partial x}}} \right)\vartheta + \\ + \;\frac{\partial }{{\partial x}}\left( {2{{\nu }_{{xx}}}\frac{{\partial u}}{{\partial x}}} \right) + \frac{\partial }{{r\partial r}}\left( {{{\nu }_{{xr}}}r\left( {\frac{{\partial u}}{{\partial r}} + \frac{{\partial \vartheta }}{{\partial x}}} \right)} \right) - {{K}_{f}}u, \\ \frac{{\partial \vartheta }}{{\partial t}} + U\frac{{\partial \vartheta }}{{\partial x}} + V\frac{{\partial \vartheta }}{{\partial r}} = - \frac{{\partial V}}{{\partial r}}\vartheta - \frac{{\partial V}}{{\partial x}}u - {{C}_{s}}\left( {\frac{{\partial U}}{{\partial r}} - \frac{{\partial V}}{{\partial x}}} \right)u + \\ + \;\frac{\partial }{{\partial x}}\left( {{{\nu }_{{xr}}}\left( {\frac{{\partial \vartheta }}{{\partial x}} + \frac{{\partial u}}{{\partial r}}} \right)} \right) + \frac{\partial }{{r\partial r}}\left( {2{{\nu }_{{rr}}}r\frac{{\partial \vartheta }}{{\partial r}}} \right) - 2{{\nu }_{{rr}}}r\frac{\vartheta }{{{{r}^{2}}}} - {{K}_{f}}\vartheta , \\ \frac{{\partial U}}{{\partial x}} + \frac{{\partial rV}}{{r\partial r}} = 0, \\ \end{gathered} $
где

$\begin{gathered} {{\nu }_{{xx}}} = {{\nu }_{{rr}}} = 3\nu + 2\frac{S}{{\operatorname{def} ({\mathbf{V}})}},\quad {{\nu }_{{xr}}} = 3\nu + 2\left| {\frac{{u\vartheta }}{{\operatorname{def} ({\mathbf{V}})}}} \right|,\quad \operatorname{def} ({\mathbf{V}}) = \sqrt {{{{\left( {\frac{{\partial U}}{{\partial r}} + \frac{{\partial V}}{{\partial x}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial U}}{{\partial x}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial V}}{{\partial r}}} \right)}}^{2}}} , \\ S = \frac{{{{u}^{2}}{{J}_{x}} + {{\vartheta }^{2}}{{J}_{r}}}}{{{{J}_{x}} + {{J}_{r}}}},\quad {{J}_{x}} = \left| {\frac{{\partial u}}{{\partial x}}} \right|,\quad {{J}_{r}} = \left| {\frac{{\partial \vartheta }}{{\partial r}}} \right|,\quad {{C}_{s}} = 0.2,\quad {{K}_{f}} = {{C}_{1}}{{\lambda }_{{\max }}} + {{C}_{2}}\frac{{\left| {d\vartheta } \right|}}{{{{d}^{2}}}}. \\ \end{gathered} $

Для численной реализации система уравнений (36) приводилась к безразмерному виду путем соотнесения всех скоростей к средней скорости струи на выходе из сопла ${{U}_{0}}$, а линейные размеры – к радиусу сопла R. Исследование проводилось для струи с числом Рейнольдса $\operatorname{Re} = \rho R{{U}_{0}}{\text{/}}\mu $ = 5600. Для получения стационарного решения систем уравнений (36) и в этом случае использовался метод установления. При интегрировании уравнений использовалась прямоугольная сетка 200 × 100, безразмерные шаги интегрирования были равны $\Delta t = 0.005$, $\Delta x = 0.2$, $\Delta r = 0.1$. В качестве начального условия рассматривалась идеальная струя без расширения. Условия на выходе из сопла имели вид $U = 1$, $V = 0$, $u = 0.005$, $\vartheta = 0.028{{r}^{{1/2}}}$.

2.7. Результаты расчетов и их обсуждение для осесимметричной дозвуковой струи

На фиг. 8 приведены численные результаты для безразмерной осевой продольной скорости в зависимости от расстояния до сопла. Здесь для сравнения представлены результаты моделей SA и SST, а также опытные данные из [24]. Из фиг. 8 следует, что двухжидкостная модель существенно лучше совпадает с экспериментальными данными, чем RANS-модели.

Фиг. 8.

Безразмерная осевая продольная скорость в зависимости от расстояния до сопла.

На фиг. 9 представлены профили турбулентного напряжения в различных сечениях струи. Эта фигура также демонстрируют, что двухжидкостная модель точнее описывает турбулентные характеристики свободной струи, чем известные RANS-модели.

Фиг. 9.

Профиль турбулентного напряжения: (a) – x/DJet = 2, (б) – x/DJet = 5, (в) – x/DJet = 10, (г) – x/DJet = 15, (д) – x/DJet = 20.

3. ВЫВОДЫ

В работе представлены численные результаты принципиально различных моделей турбулентности для различных течений турбулентности: турбулентное смешивание двух потоков, турбулентное течение в плоском диффузоре и осесимметричная дозвуковая струя. Сравнения двухжидкостной модели с другими популярными полуэмпирическими моделями показали, что она имеет неоспоримые преимущества. Во-первых, точность двухжидкостной модели, по крайней мере, не хуже, чем известных моделей. Во-вторых, двухжидкостная модель проста в реализации и требует гораздо меньших вычислительных ресурсов. Поэтому двухжидкостную модель можно рекомендовать для решения практических работ, где возникает анизотропная турбулентность, обусловленная такими сложными явлениями, как отрыв и рециркуляция потока.

Список литературы

  1. Bahmani M.H. et al. Investigation of turbulent heat transfer and nanofluid flow in a double pipe heat exchanger // Advanced Powder Technology. 2018. V. 29. P. 273–282. https://doi.org/10.1016/j.apt.2017.11.013

  2. Goodarzi M. et al. Numerical Study of Entropy Generation due to Coupled Laminar and Turbulent Mixed Convection and Thermal Radiation in an Enclosure Filled with a Semitransparent Medium // Hindawi Publishing Corporation the Scientific World Journal Volume 2014, Article ID 761745, 8 p. https://doi.org/10.1155/2014/761745

  3. Mohammad R.S. et al. Heat Transfer and Pressure Drop in Fully Developed Turbulent Flows of Graphene Nanoplatelets–Silver/Water Nanofluids // Fluids. 2016. 1. P. 20. https://doi.org/10.3390/?uids1030020

  4. Gheynani A.R., Akbari O.A., Zarringhalam M., Shabani G.A.Sh., Alnaqi A.A., Goodarzi M., Toghraie D. Investigating the effect of nanoparticles diameter on turbulent flow and heat transfer properties of non-Newtonian carboxymethyl cellulose/CuO fluid in a microtube // Inter. J. Numer. Meth. Heat&Fluid Flow. 2019. V. 29. Iss. 5. P. 1699–1723. https://doi.org/10.1108/HFF-07-2018-0368

  5. Tian Zhe et al. Turbulent flows in a spiral double-pipe heat exchanger Optimal performance conditions using an enhanced genetic algorithm // Inter. J. Numer. Meth. Heat&Fluid Flow. 2020. V. 30. № 1. P. 39–53. https://doi.org/10.1108/HFF-04-2019-0287

  6. Togun H. et al. Numerical simulation of laminar to turbulent nanofluid flow and heat transfer over a backward-facing step // Appl. Math. Comput. 2014. V. 239. P. 153–170. https://doi.org/10.1016/j.amc.2014.04.051

  7. Safaei R., Togun H., Vafai K., Kazi S.N., Badarudin A. Investigation of Heat Transfer Enhancement in a Forward-Facing Contracting Channel Using FMWCNT Nanofluids, Numerical Heat Transfer, Part A: Applications // Inter. J. Comput. Methodolog. 2014. V. 66. № 12. P. 1321–1340. https://doi.org/10.1080/10407782.2014.916101

  8. Boussinesk J. Essai sur la théorie des eaux courantes. Paris: Mémoires présentées par diverses savants à l’Acad. D. Sci., 1877. V. 23.

  9. Kolmogorov A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. // Dokl. USSR Acad. of Sci. 1941. V. 30. № 4. P. 299.

  10. Prandtl L. Untersuchungen zur ausgebildete Turbulenz // Zeitschr. f. Angew. Math. u. Mech. 1925. V. 5.

  11. Karman Th. Mechanische Ahnlichkeit und Turbulenz. Nachr. d. Gesellsch. d. Wissen. Zu Gottingen, Math. Phys. Kl., 1930.

  12. Spalart P.R., Allmaras S.R. A one-equation turbulence model for aerodynamic flows // AIAA Paper 1992-0439.

  13. Menter F.R. Zonal two-equation k-ω turbulence models for aerodynamic flows // AIAA Paper 1993-2906.

  14. Menter F.R., Kuntz M., Langtry R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbulence, Heat and Mass Transfer 4, ed: K. Hanjalic, Y. Nagano, M. Tummers, Begell House, Inc., 2003. P. 625–632.

  15. Spalding D.B. Chemical reaction in turbulent fluids // J. Physico-Chemical Hydrodyn. 1983. V. 4. P. 323–336.

  16. Spalding D.B. A turbulence model for buoyant and combusting flows. 4th Int. Conf. on Numer. Meth. in Thermal Problems, Swansea, 15–18 July 1984. Also, as Imperial College Report CFD/86/4 (1984).

  17. Malikov Z.M. Mathematical model of turbulence based on the dynamics of two fluids // Appl. Math. Model. 2020. V. 82. P. 409–436.

  18. Malikov Z.M., Madaliev M.E. Numerical simulation of two-phase flow in a centrifugal separator // Fluid Dynam. 2020. V. 55. № 8. P. 1012–1028.

  19. Malikov Z.M. Mathematical model of turbulent heat transfer based on the dynamics of two fluids // Appl. Math. Model. 2021. V. 91. P. 186–213. https://orcid.org/0000-0001-9038-5407

  20. Saffman P.G. The lift on a small sphere in a slow shear flow // J. Fluid. Mech. 1965. V. 22. P. 385–400.

  21. Fernholz H.H., Fiedler H.E. Proceedings of the Second European Turbulence Conference, Berlin, Aug 30–Sept 2, 1988, Springer Verlag, Berlin, 1989. P. 251–256.

  22. Patankar S.V. Numerical Heat Transfer and Fluid Flow. Taylor&Francis. ISBN 978-0-89116-522-4, 1980.

  23. Erkinjon son M.M. Numerical calculation of an air centrifugal separator based on the SARC turbulence model // J. Appl. Comput. Mech. 2020. V. 6. P. 1133–1140. https://doi.org/10.22055/JACM.2020.31423.1871

  24. Cebeci T., Mosinskis G.J., Smith A.M.O. Calculation of separation points in incompressible turbulent flows // J. Aircraft. V. 9. № 9. P. 618–624.

  25. Obi S., Aoki K., Masuda S. Experimental and computational study of turbulent separating flow in an asymmetric plane diffuser. In Ninth Symp. on Turbulent Shear Flows, Hyoto, Japan, (1993): 305-1.

  26. Klistafani Y. Experimental and Numerical Study of Turbulent Flow Characteristics in Asymmetric Diffuser. Inter. Conf. ADRI – 5 Sci. Publ. towards Global Competitive Higher Education, 2017. P. 285–291.

  27. Törnblom O. Experimental and computational studies of turbulent separating internal flows. PhD diss., KTH, 2006.

  28. Reid A.B. Turbulent flow through an asymmetric plane diffuser, Purdue Univer., April-2011.

  29. Muhammad T.H., Mahmud M.J., Umar S.U., Aisha S. Numerical study of flow in asymmetric 2D plane diffusers with different inlet channel lengths // CFD Lett. 2019. V. 11. Iss. 5. P. 1–21.

  30. Buice C.U., Eaton J.K. Experimental investigation of flow through an asymmetric plane diffuser // J. of Fluids Engineering-transactions of the Asme, 1995.

  31. Wallin S., Johansson A.V. An explicit algebraic model of Reynolds stresses for incompressible and compressible turbulent flows // Fluid Mech. 2000. V. 403. P. 89–132.

  32. Madaliev M.E. Numerical study of axisymmetric jet flows based on the turbulent model vt-92 // Vestnik SUSU. Ser.: Comput. Math. and Comput. Sci. 2020. V. 9. № 4. P. 67–78. (in Russian)https://doi.org/10.14529 / cmse200405

  33. Cristopher R. Responsible NASA official. Turbulence modeling Resource. NASA Langley Research Center. http://turbmodels.larc.nasa.gov. (04.04.2019)

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал