Журнал вычислительной математики и математической физики, 2022, T. 62, № 10, стр. 1662-1681
Конечные ряды Фурье в гиперболических начально-краевых задачах для областей с криволинейными границами
В. Л. Леонтьев *
Санкт-Петербургский политехнический университет Петра Великого, Научный центр мирового уровня “Передовые цифровые технологии”
195251 Санкт-Петербург, ул. Политехническая, 29, Россия
* E-mail: leontiev_vl@spbstu.ru
Поступила в редакцию 10.01.2022
После доработки 10.01.2022
Принята к публикации 08.06.2022
- EDN: OQOLHC
- DOI: 10.31857/S0044466922100088
Аннотация
Метод Фурье, связанный с применением ортогональных сплайнов, применяется при решении линейной гиперболической начально-краевой задачи для области с криволинейной границей. Теоретические исследования и решения задач о свободных колебаниях мембран с криволинейными границами показывают, что формируемая алгоритмом метода последовательность конечных рядов Фурье в каждый момент времени сходится к точному решению задачи – бесконечному ряду Фурье. Структура этих конечных рядов Фурье, каждый из которых связан с конкретной сеткой в рассматриваемой области, аналогична структуре соответствующих частичных сумм бесконечного ряда Фурье – точного решения задачи. При увеличении числа узлов сетки в области с криволинейной границей имеет место сходимость приближенных собственных значений и функций краевой задачи к точным собственным значениям и функциям, определяющая сходимость конечных рядов Фурье к точному решению начально-краевой задачи. Метод Фурье, связанный с ортогональными сплайнами, дает сколь угодно точные приближенные аналитические решения начально-краевой задачи для области с криволинейной границей в форме конечных обобщенных рядов Фурье, по структуре аналогичных частичным суммам точного решения, и имеет расширенную область своего применения. Библ. 15. Фиг. 13. Табл. 1.
1. ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ
Метод разделения переменных (метод Фурье) позволяет находить решения краевых и начально-краевых задач для уравнений в частных производных, допускающих разделение переменных. Метод связан с задачей Штурма–Лиувилля и при ее решении в некоторых случаях со специальными функциями. Метод Фурье позволяет получать решения широких классов задач, но его реализация для задач многих типов, в том числе для задач, постановки которых содержат нерегулярные граничные условия, даже тогда, когда все участки границы области являются координатными линиями или поверхностями, встречается со значительными трудностями. Одно из направлений расширения области применения метода Фурье – решение сопутствующих методу математических проблем, связанных с характером граничных условий [1]. Специальные функции появляются в алгоритме метода при решении задачи Штурма–Лиувилля в цилиндрической или сферической системах координат для областей, все участки границ которых – координатные линии или поверхности. В общем случае задач для областей с криволинейными границами применение специальных функций является неэффективным. Метод Фурье целесообразен при решении краевых и начально-краевых задач для областей классической формы, что отмечается, например, в [2] при решении контактных задач для упругих тел с криволинейными границами. Решения, полученные методом Фурье, приводятся, в частности, в статьях [3], [4], применение метода рассматривается во многих книгах, например, в [5]. Направления совершенствования математических инструментов решения задач для областей с криволинейными границами связаны также, во-первых, с созданием и развитием других методов, например, конечно-разностных методов и методов конечных элементов [6]–[8], и, во-вторых, с модификацией самого метода Фурье. Использование конечно-разностных методов, методов конечных элементов для решения задачи Штурма–Лиувилля не позволяет получать решения в форме рядов Фурье в рамках процедуры метода Фурье. Данная статья направлена на расширение области применения метода Фурье, определяемое применением ортогональных сплайнов [9] и связанных с ними конечных обобщенных рядов Фурье [9], [10] при решении задачи Штурма–Лиувилля, а также на демонстрацию эффективности используемого алгоритма метода при решении конкретных задач для областей с криволинейными границами. Такой алгоритм метода Фурье позволяет получать сходящиеся к точному решению последовательности конечных обобщенных рядов Фурье.
Ортогональные сплайны (см. [9]) разработаны и исследованы в работах автора данной статьи и его учеников, начиная с 1993 г. Созданное при этом направление теории сплайнов, а также алгоритмы вариационно-сеточных (ВСМ) и проекционно-сеточных методов (ПСМ), связанных с применением ортогональных сплайнов, содержатся в книге [9]. Ортогональные сплайны [9] строятся на каждой сетке с помощью двух процедур ортогонализации неортогональных сплайнов – функций с конечными носителями (финитных функций). Бесконечные последовательности сеточных наборов ортогональных сплайнов, порождаемые сгущением сеток, образуют базисы в пространствах Соболева. Эти процедуры ортогонализации формируют на каждой сетке набор ортогональных сплайнов и, в отличие от процедуры ортогонализации Грама–Шмидта, не приводят к изменению конечных носителей сеточных функций и к утрате сеточными базисными функциями свойства финитности, которое является важнейшим свойством для алгоритмов сеточных методов, поскольку позволяет радикально улучшить обусловленность глобальных систем сеточных уравнений. Появляющееся после применения предложенных процедур ортогонализации [9] свойство ортогональности сплайнов открывает возможность построения на каждой сетке обобщенных конечных рядов Фурье, а конечные носители сплайнов, совместно со свойством ортогональности, позволяют получать решения начально-краевых задач для областей с криволинейными границами с помощью метода Фурье. В статье используются сеточные наборы тензорных произведений непрерывных кусочно-линейных ортогональных сплайнов [9] на двумерных прямоугольных сетках. Непрерывные кусочно-линейные ортогональные сплайны на трехмерных и n-мерных прямоугольных сетках, на треугольных и тетраэдральных сетках, а также непрерывные кусочно-квадратичные ортогональные сплайны на треугольных сетках, определяются и исследуются в [9], там же приводятся примеры их применения в ВСМ и ПСМ. Показывается (см. [9]), что применение ортогональных сплайнов в ВСМ, основанных на смешанных вариационных принципах, например, на вариационном принципе Рейсснера [9], и характеризующихся совместной и независимой аппроксимацией как основной функции (например, температуры или вектора перемещений), так и ее частных производных (соответственно, потока тепла или деформаций, напряжений), устраняет основной недостаток таких методов. Этот недостаток вызывается увеличением в несколько раз числа узловых неизвестных величин на той же сетке по сравнению с ВСМЛ, основанным на вариационном принципе Лагранжа и связанным с аппроксимацией только основной функции. Ортогональные сплайны дают возможность исключения, причем в аналитической форме, узловых неизвестных для частных производных из глобальной системы сеточных уравнений до начала ее решения на компьютере. Таким образом, объемы вычислительных операций для смешанного ВСМ и для ВСМЛ оказываются величинами одного порядка, при этом в смешанном ВСМ гладкость решений для основной функции и для ее частных производных одинакова, а их точность – одного порядка. Гладкость и точность решения ВСМЛ, например, для потока тепла ниже, чем для основной функции – температуры.
Здесь в алгоритме метода разделения переменных используется свойство ортогональности сплайнов [9], [10], приводящее к расширению области применения этого метода и к рациональному алгоритму метода. Представленные здесь решения различных задач показывают эффективность такого алгоритма метода разделения переменных и сходимость последовательностей конечных обобщенных рядов Фурье, получаемых с помощью этого метода в начально-краевых задачах для областей с криволинейными границами.
2. ПОСТАНОВКА ЗАДАЧИ. МЕТОД ФУРЬЕ, СВЯЗАННЫЙ С ОРТОГОНАЛЬНЫМИ СПЛАЙНАМИ
Рассматривается линейная гиперболическая начально-краевая задача
(2.1)
$\begin{gathered} L[U] = {{a}^{2}}\Delta U(x,y,t) = {{a}^{2}}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}}} \right) = \frac{{{{\partial }^{2}}U}}{{\partial {{t}^{2}}}}\quad \forall (x,y) \in S,\quad \forall t \geqslant 0; \\ {{\left. U \right|}_{{t = 0}}} = {{f}_{1}}(x,y),\quad {{\left. {\frac{{\partial U}}{{\partial t}}} \right|}_{{t = 0}}} = {{f}_{2}}(x,y)\quad \forall (x,y) \in S; \\ {{\left. U \right|}_{{\partial S}}} = 0\quad \forall t \geqslant 0; \\ \end{gathered} $Решение задачи (2.1) разыскивается в виде произведения двух функций
подстановка которого в дифференциальное уравнение (2.1) и разделение переменных приводят к(2.3)
$\frac{{L[u(x,y)]}}{{u(x,y)}} = \frac{1}{{v(t)}}\frac{{{{\partial }^{2}}v(t)}}{{\partial {{t}^{2}}}} = - \lambda = \operatorname{const} (x,y,t) < 0$(2.4)
$L[u] + \lambda u = {{a}^{2}}\Delta u + \lambda u = 0\;\;(S),\quad {{\left. u \right|}_{{\partial S}}} = 0,$Область $S$ с криволинейной границей $\partial S$ вписывается в прямоугольную область $G = \{ a \leqslant x \leqslant b;\,\,c \leqslant y \leqslant d\} $, в которой строится равномерная сетка $\{ a = {{x}_{1}} < {{x}_{2}} < ... < {{x}_{N}} = b;$ $c = {{y}_{1}} < {{y}_{2}} < ... < {{y}_{M}} = d\} $ с шагами ${{h}_{1}},\;{{h}_{2}}$ соответственно по осям $x,\;y$. Нетривиальные решения краевой задачи (2.4) ищутся в виде
(2.6)
${{u}_{N}}(x,y) = \sum\limits_{i = 1}^N {\sum\limits_{j = {{M}_{1}}(i)}^{{{M}_{2}}(i)} {{{a}_{{ij}}}{{\varphi }_{i}}(x){{\varphi }_{j}}(y)} } .$После нормирования сплайнов одного аргумента
сумма (2.6) переписывается в виде(2.7)
${{u}_{N}}(x,y) = \sum\limits_{i = 1}^N {\sum\limits_{j = {{M}_{1}}(i)}^{{{M}_{2}}(i)} {{{b}_{{ij}}}{{\Phi }_{i}}(x){{\Phi }_{j}}(y)} } ,$(2.8)
${{u}_{N}}(x,y) = \sum\limits_{i = {{N}_{1}}}^{{{N}_{2}}} {\sum\limits_{j = {{m}_{1}}(i)}^{{{m}_{2}}(i)} {{{b}_{{ij}}}{{\Phi }_{i}}(x){{\Phi }_{j}}(y),} } $(2.9)
$({{b}_{{n + 1,m}}} - 2{{b}_{{nm}}} + {{b}_{{n - 1,m}}}){\text{/}}h_{1}^{2} + ({{b}_{{n,m + 1}}} - 2{{b}_{{nm}}} + {{b}_{{n,m - 1}}}){\text{/}}h_{2}^{2} + \lambda {{b}_{{nm}}} = 0.$Сумма
Общие решения дифференциальных уравнений (2.5) после подстановки в них приближенных собственных значений ${{\lambda }_{p}}$ имеют вид
Следовательно, сумма
удовлетворяет уравнению (2.4) в вариационной форме, уравнению (2.5), а также граничному условию (2.4). Ее подстановка в первое начальное условие (2.1) дает и затем, после умножения обеих частей на $u_{N}^{{(r)}}(x,y)$, интегрирования по области $S$ и учета ортогональности собственных функций приводит к формуле(2.11)
${{A}_{p}} = \frac{1}{{{{{\left\| {u_{N}^{{(p)}}} \right\|}}^{2}}}}\iint\limits_S {{{f}_{1}}(x,y)u_{N}^{{(p)}}(x,y)dS}.$(2.12)
${{B}_{p}} = \frac{1}{{\sqrt {{{\lambda }_{p}}} {{{\left\| {u_{N}^{{(p)}}} \right\|}}^{2}}}}\iint\limits_S {{{f}_{2}}(x,y)u_{N}^{{(p)}}(x,y)dS}.$(2.13)
${{U}^{{(K)}}}(x,y,t) = \sum\limits_{p = 1}^K {\left[ {({{A}_{p}}\cos \sqrt {{{\lambda }_{p}}} t + {{B}_{p}}\sin \sqrt {{{\lambda }_{p}}} t)\sum\limits_{i = {{N}_{1}}}^{{{N}_{2}}} {\sum\limits_{j = {{m}_{1}}(i)}^{{{m}_{2}}(i)} {b_{{ij}}^{{(p)}}{{\Phi }_{i}}(x){{\Phi }_{j}}(y)} } } \right]} ,$Для проведения расчетов на компьютере в удобной форме и для анализа получаемых результатов, далее выполняется переход от системы уравнений (2.9) и (2.5), явно содержащей приближенные собственные значения ${{\lambda }_{p}}$, к системе сеточных уравнений, явно не содержащей собственные значения. Имеем, используя ортогональность сплайнов, с учетом того, что в каждое уравнение (2.9) входит ${{\lambda }_{p}}{{b}_{{nm}}}$ и ${{b}_{{nm}}} = {{u}_{{nm}}}$,
(2.14)
$[({{u}_{{n + 1,m}}} - 2{{u}_{{nm}}} + {{u}_{{n - 1,m}}}){\text{/}}h_{1}^{2} + ({{u}_{{n,m + 1}}} - 2{{u}_{{nm}}} + {{u}_{{n,m - 1}}}){\text{/}}h_{2}^{2}]{\text{/}}{{u}_{{nm}}} = - {{\lambda }_{p}},$(2.15)
$\frac{1}{{{{v}^{l}}}}({{v}^{{l + 1}}} - 2{{v}^{l}} + {{v}^{{l - 1}}}){\text{/}}{{(\Delta t)}^{2}} = - {{\lambda }_{p}}.$(2.16)
$(U_{{n + 1,m}}^{l} - 2U_{{nm}}^{l} + U_{{n - 1,m}}^{l}){\text{/}}h_{1}^{2} + (U_{{n,m + 1}}^{l} - 2U_{{nm}}^{l} + U_{{n,m - 1}}^{l}){\text{/}}h_{2}^{2} = (U_{{nm}}^{{l + 1}} - 2U_{{nm}}^{l} + U_{{nm}}^{{l - 1}}){\text{/}}{{(\Delta t)}^{2}}.$Совместно с системой уравнений (2.14), (2.15) или (2.16) задаются начальные условия, соответствующие (2.1), на первых двух слоях (по времени) узлов сетки, а также граничное условие (2.1).
При решении системы уравнений (2.14), (2.15), без исключения собственных значений, вначале решается система уравнений (2.14) с учетом граничного условия, а затем, после подстановки найденных приближенных значений ${{\lambda }_{p}}$ в уравнения системы уравнений (2.15), определяется для узлов сетки в области $S$ закон изменения во времени узловых значений искомого решения. Система конечно-разностных уравнений (2.16) содержит в себе исходную систему вариационно-разностных уравнений (2.14) задачи Штурма–Лиувилля, поэтому неявно определяемые при решении системы сеточных уравнений (2.16) собственные значения и собственные векторы остаются такими же, как для (2.14). Дополнительная погрешность сеточных решений, имеющая второй порядок малости, порождаемая конечно-разностной аппроксимацией (2.15) производных по времени, снижает точность приближенных решений, получаемых в расчетах на компьютере. Поэтому приближенные решения – конечные ряды Фурье, получаемые с помощью уравнений (2.16) метода Фурье с неявным присутствием собственных значений и векторов, дают оценки приближенных решений в форме конечных рядов Фурье, получаемых не только с помощью (2.16), но и с помощью системы уравнений (2.9) и (2.5) без исключения собственных значений и без конечно-разностной аппроксимации второй производной по времени.
3. О СХОДИМОСТИ МЕТОДА
Условие стационарности функционала
(3.1)
$\left| {\Phi ({{u}^{{(p)}}})} \right| = \mathop {\min }\limits_{\forall \,w\, \in H} \left| {\Phi (w)} \right| = 0.$Поэтому (3.1) сводится к задаче
В [9], [11] показано, что при увеличении числа узлов сетки в области $S$, т.е. при увеличении числа ортогональных сплайнов, приближенные собственные частоты ${{\lambda }_{p}}$ сходятся к соответствующим по номерам точным собственным частотам краевой задачи (2.4). Сходимость ${{\lambda }_{p}}$ определяется также сходимостью $u_{N}^{{(p)}}(x,y)$ к ${{u}^{{(p)}}}(x,y)$, которой не может быть без сходимости ${{\lambda }_{p}}$. При этом неограниченно возрастает число собственных значений и собственных функций краевой задачи в вариационной форме, а следовательно, сумма по $k$ от $1$ до $K$ в пределе переходит в бесконечный ряд по $k$ от $1$ до $\infty $, который при всяком значении $t > 0$ является бесконечным рядом Фурье. Такой ряд является единственным решением задачи (2.1), что следует из теоремы Стеклова [12]. Отличие данного метода решения начально-краевых задач для областей с криволинейными границами от других методов, например, от метода конечных элементов [8], состоит в том, что в данном методе определяемая его алгоритмом последовательность конечных рядов Фурье в каждый фиксированный момент времени сходится к соответствующему бесконечному ряду Фурье, сформированному на основе точных собственных функций ${{u}^{{(p)}}}(x,y)$ и представляющему собой существующее точное решение задачи (2.1), которое в случае криволинейной границы не удается определить. Следовательно, эти конечные ряды Фурье представляют собой аналитические приближенные решения задачи (2.1) для области с криволинейной границей, которые при увеличении числа узлов сетки неограниченно близко подходят к точному решению этой задачи – бесконечному ряду Фурье, не только по количественным критериям, но по своей аналитической структуре. Метод дает в форме ортогональных рядов – конечных рядов Фурье, сколь угодно точные приближенные аналитические решения задачи (2.1) для областей с криволинейной границей, структуры которых аналогичны структуре точного решения.
4. О СХОДИМОСТИ МЕТОДА В ЗАДАЧЕ ДЛЯ КВАДРАТНОЙ ОБЛАСТИ
Решение задачи (2.1) и соответственно задачи Штурма–Лиувилля (2.4) для области $\bar {S}$, граница $\partial S$ которой является квадратом со стороной $l = \pi $, получается с помощью уравнений (2.14) и (2.5) без перехода к (2.16) и без аппроксимации в (2.5) второй производной по времени конечной разностью.
Используется прямоугольная равномерная сетка с шагами ${{h}_{1}} = {{h}_{2}} = h$, узлы которой имеют координаты $({{x}_{i}} = ih,{{y}_{j}} = jh) \in \bar {S},$ $0 \leqslant i,j \leqslant N.$ Разностные уравнения (2.14), записанные для внутренних узлов $(1 \leqslant i,j \leqslant N - 1)$ с учетом граничных условий (2.4), дают однородную систему разностных уравнений, нетривиальными точными решениями которой в случае $l = \pi $ являются собственные функции (см. [13])
соответствующие точным собственным значениям этой системы разностных уравнений [13](4.1)
${{U}^{{(N)}}}(x,y,t) = \sum\limits_{s = 1}^{N - 1} {\sum\limits_{r = 1}^{N - 1} {({{A}_{{sr}}}\cos \sqrt {{{\lambda }_{{sr}}}} t + } } {{B}_{{sr}}}\sin \sqrt {{{\lambda }_{{sr}}}} t)u_{N}^{{(sr)}},$Точное решение задачи Штурма–Лиувилля (2.4) для случая ${{a}^{2}} = 1$ и квадратной области $\bar {S}$ определяется собственными функциями и собственными значениями [12]: ${{\Phi }_{{sr}}}(x,y) = \sin (sx)\sin (ry)$, ${{\omega }_{{sr}}} = {{s}^{2}} + {{t}^{2}}.$ Основанное на решении задачи (2.4) точное решение задачи (2.1) имеет вид [12]
(4.2)
$U(x,y,t) = \sum\limits_{s = 1}^\infty {\sum\limits_{r = 1}^\infty {({{C}_{{sr}}}\cos \sqrt {{{\omega }_{{sr}}}} t + } } {{D}_{{sr}}}\sin \sqrt {{{\omega }_{{sr}}}} t)\sin (sx)\sin (ty).$5. О СХОДИМОСТИ МЕТОДА В ЗАДАЧЕ О КОЛЕБАНИЯХ СПЛОШНОЙ КРУГЛОЙ МЕМБРАНЫ
Решение задачи (2.1) в случае ${{a}^{2}} = 1$ на отрезке времени $[0;1.8]$ и соответствующей задачи Штурма–Лиувилля (2.4) для области $\bar {S}$, граница $\partial S$ которой является окружностью радиуса $R = 1$, находится с помощью уравнений (2.16) после предварительной аппроксимации в (2.5) второй производной по времени конечной разностью.
На квадратной области ${{\bar {S}}_{1}} = \{ - 1 \leqslant x \leqslant 1;\; - {\kern 1pt} 1 \leqslant y \leqslant 1\} $, в которую вписана круглая область $\bar {S}$ сплошной мембраны, используется квадратная сетка с шагами ${{h}_{1}} = {{h}_{2}} = h$, ее узлы имеют координаты $({{x}_{i}} = - 1 + ih,\;{{y}_{j}} = - 1 + jh) \in \bar {S},$ $0 \leqslant i,$ $j \leqslant N$. Решения системы уравнений (2.16) с учетом однородного граничного условия (2.1) на окружности $\partial S$, соответствующего закреплению мембраны на ее границе, а также с учетом двух начальных условий (2.1), в которых функциями
Таблица 1 содержит величины прогиба центра мембраны ($r = 0;\;x = y = 0$) в различные моменты времени на отрезке $[0;1.8]$: $U$ – решение в рядах, ${{U}_{1}},\;{{U}_{2}},\;{{U}_{3}}$ – приближенные решения, полученные на сетках, соответственно, при $N = 18$, 80, 200. Величина шага по времени была согласована с величинами шагов по координатам для обеспечения устойчивости алгоритма решения системы уравнений (2.16) совместно с граничным и начальными условиями. Погрешности ${{E}_{i}}\;(i = 1,2,3)$ соответствующих приближенных значений прогибов подсчитаны в процентах относительно $1.4084$ – модуля максимального значения прогиба в центре мембраны на отрезке времени $[0;\;1.8]$. Погрешности в основном своем числе являются очень малыми даже на самой редкой сетке при $N = 18$, максимальное значение погрешности ${{E}_{1}} = 2.68\% $ на такой сетке проявляется только в окрестности экстремума функциональной зависимости прогиба в центре мембраны от времени. Но величины прогиба мембраны и в этой окрестности снижаются до ${{E}_{2}} = 0.72\% $ на более густой сетке и до ${{E}_{3}} = 0.35\% $ на сетке для $N = 220$.
Таблица 1
| $t$ | $U$ | ${{U}_{1}}$ | ${{E}_{1}}$ | ${{U}_{2}}$ | ${{E}_{2}}$ | ${{U}_{3}}$ | ${{E}_{3}}$ |
|---|---|---|---|---|---|---|---|
| 0.06 | 0.9331 | 0.9329 | 0.01 | 0.9329 | 0.01 | 0.9329 | 0.01 |
| 0.12 | 0.8523 | 0.8524 | 0.01 | 0.8524 | 0.01 | 0.8524 | 0.01 |
| 0.18 | 0.7591 | 0.7590 | 0.01 | 0.7591 | 0.00 | 0.7591 | 0.00 |
| 0.24 | 0.6540 | 0.6539 | 0.01 | 0.6540 | 0.00 | 0.6540 | 0.00 |
| 0.30 | 0.5380 | 0.5378 | 0.02 | 0.5380 | 0.00 | 0.5380 | 0.00 |
| 0.36 | 0.4119 | 0.4117 | 0.02 | 0.4119 | 0.00 | 0.4119 | 0.00 |
| 0.42 | 0.2766 | 0.2763 | 0.02 | 0.2766 | 0.00 | 0.2766 | 0.00 |
| 0.48 | 0.1329 | 0.1326 | 0.02 | 0.1329 | 0.00 | 0.1329 | 0.00 |
| 0.54 | –0.0182 | –0.0185 | 0.02 | –0.0182 | 0.00 | –0.0182 | 0.00 |
| 0.60 | –0.1760 | –0.1764 | 0.03 | –0.1760 | 0.00 | –0.1760 | 0.00 |
| 0.66 | –0.3395 | –0.3400 | 0.04 | –0.3395 | 0.00 | –0.3395 | 0.00 |
| 0.72 | –0.5080 | –0.5087 | 0.05 | –0.5080 | 0.00 | –0.5080 | 0.00 |
| 0.78 | –0.6804 | –0.6817 | 0.09 | –0.6804 | 0.00 | –0.6804 | 0.00 |
| 0.84 | –0.8561 | –0.8579 | 0.13 | –0.8561 | 0.00 | –0.8561 | 0.00 |
| 0.90 | –1.0339 | –1.0337 | 0.02 | –1.0339 | 0.00 | –1.0340 | 0.01 |
| 0.96 | –1.2135 | –1.1991 | 1.02 | –1.2110 | 0.18 | –1.2131 | 0.03 |
| 1.02 | –1.3725 | –1.3348 | 2.68 | –1.3624 | 0.72 | –1.3676 | 0.35 |
| 1.08 | –1.4084 | –1.4149 | 0.46 | –1.4119 | 0.25 | –1.4132 | 0.34 |
| 1.14 | –1.3813 | –1.4186 | 2.65 | –1.3817 | 0.03 | –1.3844 | 0.22 |
| 1.20 | –1.3139 | –1.3468 | 2.34 | –1.3163 | 0.17 | –1.3142 | 0.02 |
| 1.26 | –1.2181 | –1.2268 | 0.62 | –1.2177 | 0.03 | –1.2170 | 0.08 |
| 1.32 | –1.1017 | –1.0952 | 0.46 | –1.1066 | 0.35 | –1.1031 | 0.10 |
| 1.38 | –0.9700 | –0.9701 | 0.01 | –0.9647 | 0.38 | –0.9719 | 0.14 |
| 1.44 | –0.8277 | –0.8408 | 0.93 | –0.8312 | 0.25 | –0.8300 | 0.16 |
| 1.50 | –0.6780 | –0.6887 | 0.76 | –0.6814 | 0.24 | –0.6776 | 0.03 |
| 1.56 | –0.5242 | –0.5164 | 0.55 | –0.5275 | 0.23 | –0.5263 | 0.15 |
| 1.62 | –0.3684 | –0.3481 | 1.44 | –0.3701 | 0.12 | –0.3701 | 0.12 |
| 1.68 | –0.2132 | –0.1995 | 0.97 | –0.2050 | 0.58 | –0.2146 | 0.10 |
| 1.74 | –0.0600 | –0.0588 | 0.09 | –0.0601 | 0.01 | –0.0616 | 0.11 |
| 1.80 | 0.0889 | 0.0933 | 0.31 | 0.0838 | 0.36 | 0.0883 | 0.04 |
На фиг. 1–6 находятся изображения мембраны в случае редкой и густой сеток для трех моментов времени, взятых на характерных этапах рассматриваемого цикла свободных колебаний мембраны. При решении задачи используется сетка в декартовой, а не в полярной, системе координат, потому, что рассматриваемый алгоритм ориентирован на решение начально-краевых задач для областей с криволинейными границами общего вида, не состоящих из координатных линий некоторой криволинейной ортогональной системы координат. Зависимости от радиуса $r$ приближенных решений для прогиба при сгущении сетки приближаются к соответствующему графику решения в рядах для прогиба. Погрешности приближенных решений, характеризующих перемещение мембраны как вблизи экстремума зависимости прогиба от времени, так и при наличии нескольких экстремумов и точки перегиба на графике прогиба по радиусу, больше, чем погрешности на других этапах свободных колебаний мембраны, но погрешности на всех этапах колебаний снижаются при увеличении числа узлов сетки. Это показали результаты расчетов, выполненных не только на сетках для значений $N = 18$, 80, 220, но и на других сетках, а также анализ результатов, полученных на всех шагах по времени.
Фиг. 1.
Прогиб мембраны ${{U}_{1}}$ $(N = 18)\,$ (a) и зависимость ${{U}_{1}}$ от радиуса (б), $t = 0.12.$

Фиг. 3.
Прогиб мембраны ${{U}_{1}}$ $(N = 18)\,$ (a) и зависимость ${{U}_{1}}$ от радиуса (б), $t = 0.54.$

Фиг. 5.
Прогиб мембраны ${{U}_{1}}$ $(N = 18)\,$ (a) и зависимость ${{U}_{1}}$ от радиуса (б), $t = 1.62.$

Таким образом, получена последовательность наборов конечных обобщенных рядов Фурье (2.8), характеризующих прогиб мембраны. Коэффициенты ${{b}_{{ij}}}$ рядов равны соответствующим узловым значениям прогиба ${{u}_{{ij}}}$, полученным при решении системы уравнений (2.16) совместно с граничным условием и двумя начальными условиями. Каждый набор конечных рядов соответствует определенной сетке, конечные ряды одного набора получены для различных моментов времени. Таким образом, показано, что последовательность конечных обобщенных рядов Фурье сходится при сгущении сетки к известному решению в рядах.
6. О СХОДИМОСТИ МЕТОДА В ЗАДАЧЕ О КОЛЕБАНИЯХ КРУГЛОЙ МЕМБРАНЫ С КРУГЛЫМ ОТВЕРСТИЕМ
Рассматривается задача (2.1) в случае ${{a}^{2}} = 4$ на отрезке времени $[0;1.8]$ для области $\bar {S}$, представляющей собой круг радиуса $R = 1$, из которого вырезан круг радиуса ${{R}_{1}} = 0.12$ с центром, находящимся на оси $Ox$ в точке с координатой ${{x}_{0}} = 0.66.$ Граница $\partial S$ области состоит из двух окружностей радиусов $R = 1,$ ${{R}_{1}} = 0.12$. Мембрана в недеформированном состоянии располагается на плоскости $Oxy$ в области $\bar {S}$.
На квадратной области ${{\bar {S}}_{1}} = \{ - 1 \leqslant x \leqslant 1;\; - {\kern 1pt} 1 \leqslant y \leqslant 1\} $, в которую вписана область $\bar {S}$ мембраны с круглым вырезом, строится квадратная равномерная сетка с шагами ${{h}_{1}} = {{h}_{2}} = h$, ее узлы имеют координаты $({{x}_{i}} = - 1 + ih,$ ${{y}_{j}} = - 1 + jh) \in \bar {S},$ $0 \leqslant i,j \leqslant N.$ Используется система уравнений (2.16) совместно, во-первых, с однородным граничным условием (2.1) на $\partial S$, соответствующим закреплению мембраны на всей ее границе – на двух окружностях, и, во-вторых, совместно с двумя начальными условиями (2.1), в которых функциями
Фигуры 7–13 содержат часть результатов расчетов, которые проводились с помощью программы MatLab. Прогибы мембраны, полученные при $N = 100$ и отраженные на фиг. 7, 8, 9а,б,г,д, согласуются с соответствующими прогибами аналогичной мембраны с такими же параметрами в случае 2, рассмотренном в [15]. Трехмерные изображения прогибов, показанные на фиг. 7, 8, 9, дополняются здесь изображениями линий уровней. Кроме того, на фиг. 9в,е, 10, 11, 12, 13 даются прогибы круглой мембраны, имеющей отверстие, на отрезке времени в три раза более длинном, чем в задаче из статьи [15]. При этом фиг. 12, 13 показывают сгущение приближенных решений – конечных обобщенных рядов Фурье (2.8), при возрастании числа узлов сетки, т.е. демонстрируют характер сходимости этих рядов.
Фиг. 7.
Прогиб мембраны: (a) начальный прогиб, t = 0; (б) $t = 0.10875;$ (в) $t = 0.18375.$ (г), (д), (е) – соответствующие линии уровня.

Фиг. 8.
Прогиб мембраны: (a) $t = 0.25875;$ (б) $t = 0.33375;$ (в) $t = 0.40875.$ (г), (д), (е) – соответствующие линии уровня.

Фиг. 9.
Прогиб мембраны: (a) $t = 0.55875;$ (б) $t = 0.59625;$ (в) $t = 0.82125.$ (г), (д), (е) – соответствующие линии уровня.

Фиг. 10.
Прогиб мембраны: (a) $t = 0.93375;$ (б) $t = 1.2712;$ (в) $t = 1.3837.$ (г), (д), (е) – соответствующие линии уровня.

Фиг. 11.
Прогиб мембраны: (a) $t = 1.4962;$ (б) $t = 1.5337;$ (в) $t = 1.7212.$ (г), (д), (е) – соответствующие линии уровня.
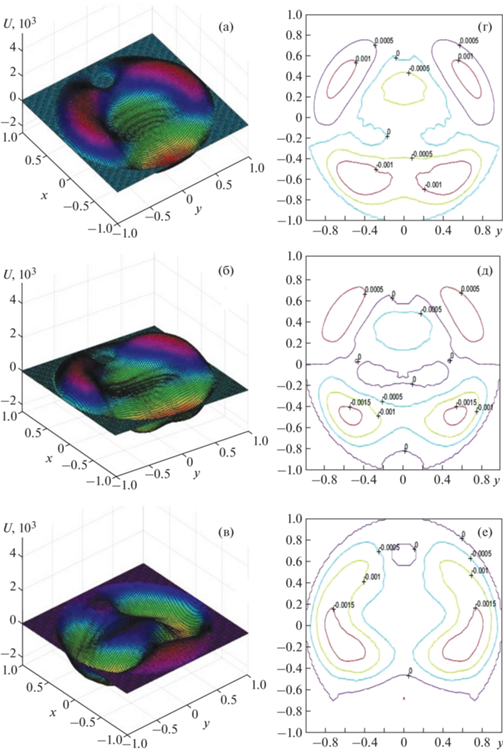
Фиг. 12.
Линии уровня прогиба мембраны при $t = 1.6838$: (a) $N = 100$, (б) $N = 200$, (в) $N = 250;$ а также при $t = 1.7588$: (г) $N = 100$.

Сходимость решений задачи – конечных рядов Фурье, показали результаты расчетов, выполненных не только на сетках для $N = 100$, 200, 250, но также и на других сетках, а также анализ результатов, полученных на всех шагах по времени.
7. ЗАКЛЮЧЕНИЕ
Возможности ортогональных сплайнов и метода конечных разностей приводят в рамках метода Фурье к аналитическим решениям начально-краевых задач для областей с криволинейными границами. Эти решения, имеющие форму конечных обобщенных рядов Фурье, качественно и с высокой точностью соответствуют частичным суммам бесконечных рядов Фурье – точных решений этих задач. Конечные ряды Фурье, полученные для последовательности значений времени в задачах о свободных колебаниях сплошной круглой мембраны и круглой мембраны с круглым отверстием с помощью системы уравнений (2.16), могут находиться также посредством системы уравнений (2.14) и (2.15). При этом вначале определяются из системы уравнений (2.14), рассматриваемой совместно с граничным условием, собственные значения и векторы. Затем для каждого известного собственного значения находится решение системы уравнений (2.15) совместно с начальными условиями, приводящее к приближенному функциональному закону изменения прогиба во времени. В итоге формируется ряд вида (2.13), из которого после подстановки в него определенных значений времени получаются конечные обобщенные ряды Фурье, представляющие собой линейные комбинации конечных рядов Фурье – собственных функций задачи Штурма–Лиувилля. Эти ряды совпадут, если не учитывать погрешности округлений при вычислениях, с конечными рядами Фурье, полученными с помощью системы уравнений (2.16). При этом объем арифметических операций в варианте алгоритма, связанном с (2.16) и возможном благодаря ортогональности сплайнов, меньше, чем в варианте алгоритма, связанном с (2.14) и (2.15), т.е. алгоритм, ориентированный на (2.16), является более рациональным. В случае алгоритма метода Фурье, связанного с (2.9) и (2.5) без аппроксимации производной по времени, решения (2.13) будут характеризоваться более высокой точностью по сравнению с теми решениями, которые получаются в задачах о колебаниях круглых мембран после проведения в (2.5) аппроксимации производной по времени и позволяют на их основе оценивать эффективность и сходимость рассматриваемого метода. Здесь показано, что использование ортогональных сплайнов в методе Фурье приводит к расширению области его эффективного применения и к рациональному алгоритму метода.
Список литературы
Гасымов Э.А., Гусейнова А.О., Гасанова У.Н. Применение обобщенного метода разделения переменных к решению смешанных задач с нерегулярными граничными условиями // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 7. С. 1335–1339.
Савичев И.С., Чернышев А.Д. Применение метода угловых суперпозиций для решения контактной задачи о сжатии упругого цилиндра // Изв. РАН. Механ. твердого тела. 2009. № 3. С. 151–162.
Малов Ю.И., Мартинсон Л.К., Павлов К.Б. Решение некоторых смешанных краевых задач гидродинамики проводящих сред методом разделения переменных // Ж. вычисл. матем. и матем. физ. 1972. Т. 12. № 3. С. 627–638.
Исраилов М.Ш. Дифракция акустических и упругих волн на полуплоскости при разнотипных граничных условиях // Изв. РАН. Механ. твердого тела. 2013. № 3. С. 121–134.
Vretblad A. Fourier Analysis and its Applications. New York, Berlin, Heidelber: Springer-Verlag, 2003. P. 272.
Усов А.Б. Конечно-разностный метод решения уравнений Навье–Стокса в переменной области с криволинейными границами // Ж. вычисл. матем. и матем. физ. 2008. Т. 48. № 3. С. 491–504.
Крутицкий П.А. Первая начально-краевая задача для уравнения гравитационно-гироскопических волн в многосвязной области // Ж. вычисл. матем. и матем. физ. 1997. Т. 37. № 1. С. 117–128.
Strang G., Fix G.J. An Analysis of the Finite Element Method. Prentice-Hall, Inc., Englewood Cliffs, 1973, P. 306.
Леонтьев В.Л. Ортогональные сплайны и специальные функции в методах вычислительной механики и математики. С-Пб.: ПОЛИТЕХ-ПРЕСС, 2021. С. 466.
Leontiev V.L. Fourier Method in Initial Boundary Value Problems for Regions with Curvilinear Boundaries // Math. and Statistics. 2021. V. 9. № 1. P. 24–30.
Леонтьев В.Л. Вариационно-сеточный метод решения задач о собственных колебаниях упругих трехмерных тел, связанный с использованием ортогональных финитных функций // Изв. РАН. Механ. твердого тела. 2002. № 3. С. 117–126.
Арсенин В.Я. Методы математической физики и специальные функции. М.: Физматлит,1974. С. 432.
Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Физматлит, 1978. С. 592.
Араманович И.Г., Левин В.И. Уравнения математической физики. М.: Физматлит, 1969. С. 288.
Alsahlani A., Mukherjee R. Dynamics of a circular membrane with an eccentric circular areal constraint: Analysis and accurate simulations // Simulat. Modelling Practice and Theory. 2013. V. 31. P. 149–168.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики






