Журнал вычислительной математики и математической физики, 2022, T. 62, № 11, стр. 1763-1803

1. ВВЕДЕНИЕ

В работе [1], широко известной в связи со схемой распада разрыва, было введено понятие монотонности численной схемы и показано, что среди линейных двухслойных по времени схем нет монотонных схем повышенного порядка аппроксимации. Дальнейшее развитие теории численных методов сквозного счета для гиперболических систем законов сохранения было направлено на преодоление этого запрета Годунова. В результате были разработаны различные классы конечно-разностных, конечно-объемных и проекционных схем, в которых повышенный порядок аппроксимации на гладких решениях и монотонность достигались за счет нелинейной коррекции потоков, приводящей к нелинейности этих схем при аппроксимации линейного уравнения переноса. Перечислим основные классы таких схем, которые будем сокращенно называть NFC (Nonlinear Flux Correction) схемами: MUSCL (см. [2]), TVD (см. [3]), ENO (см. [4]), CU (Central Upwind) (см. [5]), WENO (см. [6], [7]), DG (Discontinuous Galerkin) (см. [8]), CABARET (см. [9]), MBiC (Monotonized BiCompact) (см. [10], [11]). Основное достоинство этих схем заключается в том, что они с высокой точностью локализуют ударные волны при отсутствии существенных нефизических осцилляций на их фронтах.

При построении NFC-схем повышенный порядок аппроксимации понимается в смысле тейлоровского разложения на гладких решениях, что не гарантирует аналогичного повышения точности при расчете разрывных решений. Несмотря на это, в течение длительного времени преобладала ошибочная точка зрения, что эти схемы должны сохранять повышенную точность (соответствующую порядку их классической аппроксимации) во всех гладких частях рассчитываемых обобщенных решений. Способствовало распространению этого ошибочного мнения то, что в подавляющем числе работ тестирование разностных схем сквозного счета в значительной степени проводится на различных вариантах задачи Римана о распаде разрыва, точное решение которой представляет собой набор простых волн, соединенных областями постоянных течений (причем тестирование обычно ограничивается графическим сравнением численного решения с точным). Такое тестирование позволяет эффективно оценить разрешимость схемой сильных и слабых разрывов, а именно, ширину их размазывания и наличие или отсутствие осцилляций на фронтах ударных волн. Однако оно не может дать достаточной информации о реальной точности схемы в областях влияния ударных волн, поскольку точное решение за их фронтами является постоянным. Кроме того, эту точность нельзя оценить при расчете ударных волн, возникающих при решении скалярного закона сохранения, поскольку в этом случае область влияния устойчивой ударной волны совпадает с линией ее фронта.

Для корректного определения точности схемы в областях влияния ударных волн необходимо рассчитывать разрывные решения квазилинейных систем законов сохранения с ударными волнами, за фронтами которых формируется непостоянное решение. Такое решение для систем законов сохранения, как правило, не описывается точными формулами, и для определения скорости сходимости к нему разностного решения необходимо проведение серии расчетов на последовательности сжимающихся сеток. В [12]–[15] указанным способом было показано, что различные типы NFC-схем имеют не более чем пеpвый поpядок локальной сходимости в областях влияния удаpных волн и, тем самым, по существу схемами повышенной точности не являются. Такое снижение порядков сходимости свидетельствует о том, что в этих схемах происходит потеря точности при передаче условий Гюгонио через размазанные фронты ударных волн. Однако свидетельствует опосредованно.

Для непосредственной оценки точности передачи схемой условий Гюгонио необходимо исследовать сходимость интегралов от разностного решения по областям, содержащим фронт ударной волны. Причем эти интегралы должны допускать потенциальную возможность получения повышенного (как минимум, второго) порядка сходимости для схем сквозного счета, в силу чего такая сходимость не может быть сильной, например, в нормах ${{L}_{1}}$ или ${{L}_{2}}$. Связано это с тем, что в схемах сквозного счета в нескольких узлах в окрестности фронта ударной волны отсутствует локальная сходимость разностного решения к точному, и поэтому порядок сходимости разностного решения в сильной норме, содержащей линию разрыва, в принципе не может быть выше первого.

В этой связи в [16] для TVD-схемы Хартена из [3], в [17] для различных вариантов WENO-схемы из [7], в [18] для DG-метода Кокбурна из [8], в [19] для монотонной модификации схемы CABARET из [9], в [20] для CU-схемы из [5] и в [21] для MBiC-схемы из [11] точность передачи схемой условий Гюгонио через фронт ударной волны оценивается путем определения порядка сходимости интеграла от разностного решения, что соответствует сходимости в соответствующей негативной норме. В [16]–[21] показано, что в рассмотренных NFC-схемах такой порядок интегральной сходимости снижается до первого на интервалах интегрирования, одна или обе границы которых находятся в области влияния ударной волны. Одна из причин такого снижения точности заключается в том, что коррекция потоков, характерная для этих схем, приводит к снижению гладкости разностных потоков, что в свою очередь приводит к снижению порядка аппроксимации $\varepsilon $-условий Гюгонио на фронтах ударных волн (см. [22]). В то же время, как показано в [15], [16], некоторые немонотонные схемы повышенной точности (в частности, схема Русанова из [23] и компактная схема из [15]), имеющие аналитические функции численных потоков и, как следствие, с повышенной точностью аппроксимирующие $\varepsilon $-условия Гюгонио, сохраняют повышенный порядок сходимости в негативной норме при интегрировании по областям, содержащим сильные разрывы. Эти немонотонные схемы, в отличие от NFC-схем, сохраняют повышенный порядок сходимости в областях влияния ударных волн, несмотря на заметные схемные осцилляции на их фронтах. Далее для таких немонотонных схем повышенной точности мы будем использовать аббревиатуру HASIA (High Accuracy Shock Influence Area).

В результате в теории численных схем сквозного счета сложилась следующая альтернатива: невозможно одновременно с высокой точностью локализовать сильные разрывы и сохранить повышенный порядок сходимости в областях их влияния. При этом на практике NFC-схемы (особенно схемы WENO и DG) широко применяются при численном моделировании сложных газо- и гидродинамических течений с большим числом ударных волн различной амплитуды, в силу чего все такие расчеты имеют лишь первый порядок точности. Первая попытка решения этой проблемы была связана с применением методики построения гибридных схем (см. [24]–[28]), при которой на каждом временном слое численное решение сначала строится с помощью внешней немонотонной HASIA-схемы, имеющей заметные осцилляции на ударной волне. После этого в окрестности фронта ударной волны численное решение стандартным образом корректируется с помощью одной из NFC-схем, и на новом временном слое получается монотонизированное численное решение без заметных нефизических осцилляций. Однако тестовые расчеты показали, что в построенной таким образом гибридной схеме теряется основное преимущество внешней HASIA-схемы – ее повышенная точность в областях влияния ударных волн; эта точность снижается приблизительно так же, как и в стандартных NFC-схемах.

Данный недостаток как NFC-схем, так и гибридных схем, непосредственно связан с их главным преимуществом – монотонной локализацией фронтов ударных волн, поскольку любая конечная сумма ряда Фурье для разрывной функции не является монотонной. С учетом этого осцилляции, возникающие на фронтах ударных волн в немонотонных HASIA-схемах, несут информацию о волновой структуре фурье-разложения разрывной функции в окрестности сильного разрыва, что позволяет этим схемам с повышенной точностью передавать условия Гюгонио и, как следствие, сохранять повышенную точность в областях влияния ударных волн. NFC-схемы и гибридные схемы в результате искусственного сглаживания численных ударных волн эту информацию теряют, что приводит к снижению их точности при аппроксимации условий Гюгонио.

В [29] была предложена методика построения принципиально нового класса численных методов сквозного счета (получивших название комбинированные схемы), которые сочетают достоинства как NFC-схем, так и немонотонных HASIA-схем, а именно, монотонно локализуют фронты ударных волн и одновременно сохраняют повышенную точность в областях их влияния. В комбинированной схеме применяется базисная немонотонная HASIA-схема, по которой разностное решение строится во всей расчетной области. В окрестностях больших градиентов, где это решение имеет нефизические осцилляции, оно корректируется путем численного решения внутренних начально-краевых задач по одной из NFC-схем. Причем внутренняя NFC-схема (в отличие от случая гибридных схем) не влияет на решение, получаемое по базисной схеме, что позволяет комбинированной схеме сохранять повышенную точность в областях влияния ударных волн. В [29] была рассмотрена комбинированная схема, в которой в качестве базисной H-ASIA-схемы использовалась компактная схема третьего порядка слабой аппроксимации (см. [15]), а в качестве внутренней NFC-схемы – монотонная модификация схемы CABARET (см. [9]) второго порядка точности на гладких решениях. Далее для компактной схемы из [15] будем использовать аббревиатуру CWA (Compact Weak Approximation), а для схемы CABARET, предложенной в [30], будем применять аббревиатуру CABARETM.

Недостаток комбинированной схемы, построенной в [29], заключался в том, что соответствующие ей базисная и внутренняя схемы имели существенно различные типы: базисная CWA-схема являлась неявной и трехслойной по времени, в то время как внутренняя схема CABARETM – явной и двухслойной по времени, что приводило к определенным сложностям при численной реализации такого алгоритма. Поэтому в [31] был предложен новый вариант комбинированной разностной схемы, в которой как немонотонная базисная HASIA-схема, так и внутренняя NFC-схема являлись явными и двухслойными по времени. А именно, в качестве базисной была использована схема Русанова третьего порядка (см. [23]), а в качестве внутренней – схема CABARETM второго порядка (см. [30]). В [29] и [31] приведены тестовые расчеты разрывных решений с ударными волнами, демонстрирующие существенные преимущества построенных в них комбинированных разностных схем по сравнению со схемой WENO5 из [7] пятого порядка по пространству и третьего порядка по времени.

Следующий этап в развитии теории комбинированных схем был связан с разработкой согласованных численных алгоритмов, в которых базисная и внутренняя схемы являются схемами одного класса, а именно, внутренняя схема получается из базисной схемы в результате применения соответствующей NFC-процедуры. В [32] такая комбинированная схема была построена на основе DG-метода из [8], при этом в качестве базисной схемы использовался немонотонный вариант DG-метода третьего порядка без применения NFC-процедуры, а в качестве внутренней схемы использовался монотонный вариант этого метода, в котором коррекция потоков осуществлялась с помощью ограничителя Кокбурна (см. [8]). Построенная комбинированная DG-схема показала существенные преимущества по сравнению со стандартной NFC-схемой DG-метода при расчете нестационарных ударных волн.

В [33] согласованная комбинированная схема была построена на основе бикомпактных разностных схем. В качестве внутренней схемы применялась бикомпактная схема четвертого порядка аппроксимации по пространству с интегрированием по времени неявным методом Эйлера. Эта схема устойчива при любых соотношениях шагов сетки и монотонна при числах Куранта, не меньших $1{\text{/}}4$. В отличие от работ [29], [31], [32] вычисления по внутренней схеме велись во всей пространственно-временной расчетной области. Решение базисной схемы определялось посредством глобальной (пассивной в терминологии [34]) экстраполяции Ричардсона второго порядка по решениям внутренней схемы, рассчитанным на двух вложенных сетках. Локальные немонотонности у решения базисной схемы устранялись с помощью процедуры, близкой по своей сути к гибридной схеме из [10]. Однако эта процедура имела характер пост-обработки, т.е. применялась лишь после завершения вычислений по базисной и внутренней схемам, а не при каждом переходе со слоя на слой. Комбинированная бикомпактная схема из [33] продемонстрировала высокий порядок точности, который не достигается MBiC-схемой (см. [11]).

В настоящей работе более детально излагаются теория комбинированных схем, методы их построения и результаты тестовых расчетов, демонстрирующие преимущества этого нового класса схем по сравнению со стандартными NFC-схемами. В разд. 2 описываются методы оценки точности схем сквозного счета, аппроксимирующих гиперболическую систему законов сохранения. В разд. 3 приводится основная тестовая задача для уравнений теории мелкой воды, в результате численного решения которой проводится сравнительный анализ точности изучаемых схем. В разд. 4 описываются численные алгоритмы разностных схем Русанова, CWA, CABARETM и WENO5, а в разд. 5 приводятся результаты расчетов по этим схемам основной тестовой задачи, из которых следует, что HASIA-схемы Русанова и CWA имеют существенно более высокую точность в областях влияния ударных волн, чем NFC-схемы CABARETM и WENO5. В разд. 6 излагается общая методика построения гибридных численных схем и изучаются две гибридные схемы, в которых в качестве базисной используется схема Русанова или CWA-схема, а в качестве внутренней применяется схема CABARETM. Тестовые расчеты показали, что в этих гибридных схемах теряется основное преимущество исходных HASIA-схем – повышенная точность в областях влияния ударных волн, которая становится сравнимой с точностью NFC-схем.

В разд. 7 описывается методика построения комбинированных схем, которые монотонно локализуют фронты ударных волн и одновременно сохраняют повышенную точность в областях их влияния. Построены и протестированы две комбинированные схемы, в которых базисной является схема Русанова или CWA-схема, а внутренней – схема CABARETM. В разд. 8 изучаются согласованные комбинированные схемы, в которых базисная и внутренняя схемы являются схемами одного класса, а именно, внутренняя схема получается из базисной HASIA-схемы в результате применения соответствующей NFC-процедуры. В п. 8.1 такая комбинированная схема построена на основе DG-метода из [8], а в п. 8.2 – на основе бикомпактных разностных схем из [10]. В разд. 9 проведен сравнительный анализ точности комбинированных разностных схем, построенных в разд. 7, со схемой WENO5 при численном моделировании задачи о многократном взаимодействии ударных волн. В разд. 10 построена двумерная комбинированная бикомпактная схема, которая при расчете пространственно двумерных разрывных решений обеспечивает второй порядок локальной сходимости в областях влияния ударных волн. В разд. 11 дается общая характеристика полученных результатов, приводится их сравнение с современным мировым уровнем данного научного направления и формулируются основные перспективные направления дальнейшего развития теории комбинированных схем.

2. МЕТОДЫ ОЦЕНКИ ТОЧНОСТИ СХЕМ СКВОЗНОГО СЧЕТА

Рассмотрим квазилинейную строго гиперболическую систему законов сохранения (см. [35], [36])

Явные численные схемы, аппроксимирующие задачу (2.1), (2.2), будем строить на равномерной прямоугольной сетке

Для приближенной оценки порядков локальной сходимости численного решения ${{{\mathbf{v}}}_{h}}$, построенного на равномерной сетке (2.3), зафиксируем на этой сетке некоторый узел $({{x}_{{j + \alpha }}},{{t}_{n}})$, где $n \geqslant 1$, и введем для него новое обозначение $(\tilde {x},\tilde {t})$, где $\tilde {x} = (j + \alpha )h$ и $\tilde {t} = n\tau > 0$. Рассмотрим последовательность сгущающихся сеток

В случае дискретных конечно-разностных и конечно-объемных схем, для которых численное решение определено в целых или в полуцелых пространственных узлах численной сетки (2.3), для приближенного определения порядков интегральной сходимости численного решения к точному зададим целое число $N \geqslant 2$ и момент времени $T = N\tau = N{{\tau }_{i}}{{k}^{{i - 1}}} > 0$, для которого путем линейной или квадратичной (параболической) интерполяции доопределим дискретные численные решения ${{{\mathbf{v}}}_{{{{h}_{i}}}}}(x_{{j + \alpha }}^{i},t_{n}^{i})$ до непрерывных по $x$ функций ${{{\mathbf{v}}}_{{{{h}_{i}}}}}(x,T)$. В случае проекционной схемы DG-метода [8] численное решение на сетке (2.5) строится как функция ${{{\mathbf{v}}}_{{{{h}_{i}}}}}(x,t_{n}^{i})$, зависящая от непрерывно изменяющегося аргумента $x$, которая в пространственных узлах $x_{j}^{i}$ в общем случае имеет сильные разрывы. Поэтому для DG-метода соответствующая функция ${{{\mathbf{v}}}_{{{{h}_{i}}}}}(x,T)$ непосредственно получается из самого численного решения.

Зафиксируем отрезок $[a,b]$ на оси $x$ и зададим интегралы

Если интегралы ${{{\mathbf{V}}}_{{{{h}_{i}}}}}(t,a,b)$ в случае дискретных схем вычисляются по формуле трапеций (которая имеет второй порядок точности на гладких функциях), то порядок интегральной сходимости в общем случае удовлетворяет условию $\rho \leqslant 2$; если эти интегралы вычисляются по формуле парабол (которая имеет четвертый порядок точности на гладких функциях), то в общем случае $\rho \leqslant 4$. Для DG-метода указанное ограничение на порядок интегральной сходимости отсутствует и при расчете гладких решений этот порядок будет совпадать с формальным порядком аппроксимации DG-метода. При расчете разрывных решений порядок интегральной сходимости на отрезках $[a,b]$, содержащих ударные волны, может снижаться за счет потери точности при передаче схемой условий Гюгонио через размазанные фронты ударных волн.

Поскольку в рассматриваемых далее тестовых задачах Коши (2.1), (2.2) точное решение ${\mathbf{u}}$ заранее неизвестно, то для приближенного вычисления порядков сходимости разностного решения мы не можем непосредственно воспользоваться формулами (2.7) и (2.9), которые зависят от этого точного решения. Это затруднение можно преодолеть двумя различными способами. При первом способе точное решение ${\mathbf{u}}$ в формулах (2.7) и (2.9) заменяется на некоторое квазиточное численное решение ${{{\mathbf{v}}}_{{{{h}_{*}}}}}$, получаемое по одной из схем повышенной точности на равномерной сетке с пространственным шагом ${{h}_{*}} \ll h$, где $h$ – пространственный шаг базисной сетки (2.3). При втором способе необходимо выполнить три численных расчета на сетках (2.5) с пространственными шагами ${{h}_{1}} = h$, ${{h}_{2}} = h{\text{/}}k$ и ${{h}_{3}} = h{\text{/}}{{k}^{2}}$. Вычитая из первой формулы (2.6) эту же формулу, в которой индекс $i$ заменен на $i + 1$, получаем

Следует отметить, что первый способ вычисления порядков сходимости, использующий квазиточное численное решение, формально является более точным, но и существенно более трудоемким по сравнению со вторым способом, при котором применяются формулы (2.12) и (2.13). Поэтому в приводимых далее расчетах порядки сходимости в основном определяются с помощью второго способа, корректность которого предварительно проверяется путем сравнения на контрольных тестах с результатами, получаемыми на основе первого способа. Численные расчеты показывают (см. [12], [15]), что порядки локальной сходимости, вычисляемые по формуле (2.12), могут сильно осциллировать в областях влияния ударных волн, особенно у NFC-схем, что не позволяет с необходимой точностью определить значения этих порядков; в [15], [18], [19] для подавления таких осцилляций перед применением формулы (2.12) использовались различные методы локального осреднения получаемого разностного решения. Поэтому в данной работе мы в основном будем приводить порядки интегральной сходимости (2.13), позволяющие оценить точность, с которой численное решение аппроксимирует условия Гюгонио на фронте ударной волны.

Пусть $w = w({\mathbf{u}})$ – гладкая скалярная функция векторного решения ${\mathbf{u}}$, точность вычисления которой необходимо оценить. Для этого так же, как при определении порядков сходимости численного решения, можно применять два различных способа. При использовании квазиточного численного решения ${{{\mathbf{v}}}_{{{{h}_{*}}}}}$ сразу получается формула

В приводимых далее тестовых расчетах применяются обе формулы (2.14) и (2.17). При этом на графиках мы будем показывать относительные дисбалансы вычисления функции $w$, определяемые по формуле

3. ОСНОВНАЯ ТЕСТОВАЯ ЗАДАЧА

В качестве конкретной гиперболической системы законов сохранения выберем систему уравнений первого приближения теории мелкой воды (см. [38]), дивергентная форма записи которой в случае прямоугольного горизонтального русла без учета влияния донного трения имеет вид (2.1), где

Фиг. 1.

Начальные значения скорости жидкости $v$ и глубины жидкости $H$, задаваемые формулами (3.2).

В точном решении задачи (2.1), (3.1), (3.2) в момент времени $t \approx 0.54$ в результате градиентных катастроф формируется последовательность изолированных ударных волн, которые распространяются друг за другом с одинаковыми скоростями в положительном направлении оси $x$, в силу чего расстояние между соседними ударными волнами остается постоянным и равным длине периода $X$. На фиг. 2 на отрезке $[0,X]$ длины периода штриховой линией показана начальная глубина жидкости, задаваемая второй формулой (3.2), а сплошными линиями изображены квазиточные профили глубины, получаемые в результате численного расчета по схеме CABARETM из [30] на достаточно мелкой сетке в моменты времени $t = 0.5$, $t = 1$ и $t = 2.5$. К моменту времени $t = 0.5$ в точном решении начинают формироваться области больших градиентов, но решение еще остается гладким (линия 1 на фиг. 2). Ударные волны, которые в момент времени $t \approx 0.54$ возникают как сильные разрывы первоначально бесконечно малой амплитуды, в момент времени $t = 1$ имеют конечную амплитуду (линия 2 на фиг. 2), но область их влияния, расположенная внутри интервала $(4,9) \subset [0,X]$, еще не заполняет всю расчетную область. К моменту времени $t = 2.5$ ударные волны проходят расстояние, большее длины периода $X$, и вся расчетная область становится их областью влияния. С учетом этого сильный разрыв, расположенный на линии 3 фиг. 2, соответствует ударной волне, которая сформировалась при $t \approx 0.54$ внутри интервала $[ - X,0]$.

Фиг. 2.

Глубины жидкости $H$ в квазиточном решении задачи Коши (2.1), (3.1), (3.2), получаемые в моменты времени $t = 0$ (штриховая линия), $t = 0.5$ (линия 1), $t = 1$ (линия 2) и $t = 2.5$ (линия 3).

4. ЧИСЛЕННЫЕ СХЕМЫ РУСАНОВА, CWA, CABARETM И WENO5

В данном разделе приводятся численные алгоритмы схем Русанова из [23], CWA из [15], CABARETM из [30] и WENO5 из [7], аппроксимирующих гиперболическую систему (2.1). Результаты тестовых расчетов по этим схемам задачи Коши (2.1), (3.1), (3.2), приведенные в следующем разд. 5, лежат в основе методики построения комбинированных схем. Отметим, что в схемах Русанова, CWA и WENO5 численные решения определяются в целых пространственных узлах ${{x}_{j}} = jh$ базисной сетки (2.3), в силу чего, наряду с ${{{\mathbf{v}}}_{h}}$, мы будем использовать для них сокращенные обозначения ${\mathbf{v}}_{j}^{n} = {{{\mathbf{v}}}_{h}}({{x}_{j}},{{t}_{n}})$.

5. РЕЗУЛЬТАТЫ РАСЧЕТА ОСНОВНОЙ ТЕСТОВОЙ ЗАДАЧИ ПО СХЕМАМ РУСАНОВА, CWA, CABARETM И WENO5

В этом разделе на три момента времени $t = 0.5,\;1,\;2.5$ приведены результаты численных расчетов основной тестовой задачи (2.1), (3.1), (3.2) по схемам Русанова (4.1)–(4.3), CWA (4.4)–(4.7), CABARETM (4.8)–(4.12) и WENO5 (4.13)–(4.21), проведенные на равномерной сетке (2.3) с коэффициентом запаса $z = 0.45$, что обеспечивает выполнение условия устойчивости (2.4). На фиг. 3–6 результаты расчетов по схеме Русанова показаны кружками, по CWA-схеме – квадратиками, по схеме CABARETM – точками и по схеме WENO5 – крестиками.

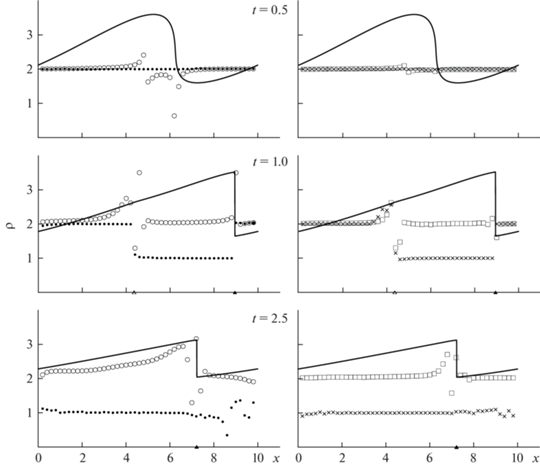
Фиг. 3.

Глубины жидкости $H$, получаемые при численном решении задачи Коши (2.1), (3.1), (3.2) по схемам Русанова (кружки), CWA (квадратики), CABARETM (точки) и WENO5 (крестики). Cплошными линиями изображены квазиточные значения глубины.

Фиг. 4.

Порядки интегральной сходимости $\rho $, получаемые по схемам Русанова (кружки), CWA (квадратики), CABARETM (точки) и WENO5 (крестики). Cплошными линиями изображены квазиточные значения глубины.

Фиг. 5.

Относительные локальные дисбалансы $\Delta {{w}_{{1h}}}({{x}_{j}},t)$ вычисления инварианта ${{w}_{1}} = v - 2c$, получаемые по схемам Русанова (кружки), CWA (квадратики), CABARETM (точки) и WENO5 (крестики).

Фиг. 6.

Относительные локальные дисбалансы $\Delta {{w}_{{2h}}}({{x}_{j}},t)$ вычисления инварианта ${{w}_{2}} = v + 2c$, получаемые по схемам Русанова (кружки), CWA (квадратики), CABARETM (точки) и WENO5 (крестики).

На фиг. 3 приведены значения глубины жидкости, получаемые при численном расчете на сетке (2.3) с пространственным шагом $h = 0.25$. Cплошными линиями на этой фигуре изображены квазиточные  профили глубины,  получаемые  в результате численного расчета по схеме CABARETM на достаточно мелкой сетке. Из фиг. 3 следует, что, в отличие от NFC-схем CABARETM и WENO5, схемы Русанова и CWA имеют заметные осцилляции в окрестностях ударных волн. Следует также отметить, что схема CABARETM заметно меньше размазывает фронт ударной волны, чем схема WENO5 более высокого порядка аппроксимации.

На фиг. 4 показаны порядки интегральной сходимости $\rho ({{x}_{j}},X,t)$, определяемые по формуле (2.13), в которой интегралы ${{{\mathbf{V}}}_{{{{h}_{i}}}}}$ вычисляются по формуле трапеций, а на фиг. 5 и 6 – относительные локальные дисбалансы $\Delta {{w}_{{ih}}}({{x}_{j}},t)$ вычисления инвариантов ${{w}_{i}}$, задаваемые формулами (2.17) и (2.18); причем в формуле (2.13) для схем Русанова, CWA и WENO5 параметр $k = 2$, а для схемы CABARETM параметр $k = 3$. Расчеты для фиг. 4–6 проводились на базисной сетке (2.3) с пространственным шагом $h = 0.005$, что соответствует 2000 пространственным ячейкам сетки на отрезке $[0,X]$ длины периода; результаты этих расчетов показаны для каждого 40-го пространственного узла $j = 40i$ численной сетки. На фиг. 4–6 при $t = 1,\;2.5$ темными треугольниками на оси $x$ обозначены положения фронтов ударных волн, а при $t = 1$ светлым треугольником показана левая граница области влияния ударной волны.

Из фиг. 4 следует, что в момент времени $t = 0.5$, когда точное решение является гладким, и ударная волна еще не сформировалась, все схемы имеют приблизительно второй порядок интегральной сходимости ${{\rho }_{j}}$ почти на всех отрезках $[{{x}_{j}},X] \in [0,X]$. Заметные колебания порядков интегральной сходимости, получаемых по схеме Русанова в окрестности области больших градиентов точного решения, свидетельствуют о том, что эта схема более тонко реагирует на начальный этап формирования ударной волны. При $t = 1,\;2.5$ из фиг. 4 следует, что в отличие от немонотонных HASIA-схем Русанова и CWA, обеспечивающих повышенный порядок интегральной сходимости, схемы CABARETM и WENO5 имеют приблизительно первый порядок интегральной сходимости на интервалах $[{{x}_{j}},X]$, левая граница которых лежит в области влияния ударной волны. В момент времени $t = 2.5$, когда вся расчетная область становится областью влияния ударной волны, порядки интегральной сходимости NFC-схем CABARETM и WENO5 также снижаются приблизительно до первого порядка почти во всей расчетной области.

Из фиг. 5 и 6 следует, что вне области влияния ударной волны точность вычисления инвариантов во всех схемах является различной и согласуется с порядком их аппроксимации на гладких решениях. Однако в области влияния ударной волны, где порядок интегральной сходимости NFC-схем CABARETM и WENO5 снижается до первого, точность вычисления инвариантов по этим схемам резко падает, становится сравнимой и на несколько порядков меньшей, чем в HASIA-схемах Русанова и CWA, сохраняющих второй порядок интегральной сходимости. При этом значения функций $\Delta {{w}_{{ih}}}({{x}_{j}},t)$, получаемые по NFC-схемам, заметно осциллируют (у схемы CABARETM существенно больше, чем у схемы WENO5 формально более высокого порядка), что связано с мелкомасштабными колебаниями численного решения в областях влияния ударных волн, характерными для NFC-схем. Следует также отметить, что в момент времени $t = 1$, когда области влияния ударных волн еще не заполнили всю расчетную область, во всех схемах точность вычисления в этих областях инварианта ${{w}_{2}} = v + 2c$, приходящего в них из гладких частей точного решения, существенно выше, чем инварианта ${{w}_{1}} = v - 2c$, приходящего с фронта ударной волны и приносящего информацию о точности, с которой схема аппроксимирует условия Гюгонио. Причем максимальное снижение точности вычисления инварианта ${{w}_{1}}$ происходит не на правой границе области влияния, которая примыкает к фронту ударной волны, а в окрестности ее левой границы, где точное решение является достаточно гладким.

Из результатов численных расчетов, приведенных на фиг. 3–6, следует, что в теории численных схем сквозного счета сложилась следующая альтернатива: NFC-схемы, монотонно локализующие фронты ударных волн, теряют свою точность в областях их влияния, в то время как немонотонные HASIA-схемы, имеющие заметные нефизические осцилляции на фронтах ударных волн, в областях их влияния сохраняют повышенную точность.

6. ГИБРИДНЫЕ СХЕМЫ

Первая попытка построения численных схем, которые монотонно локализуют фронты ударных волн и одновременно сохраняют повышенную точность в областях их влияния, была связана с применением методики построения гибридных схем (см. [24]–[28]), при которой на каждом временном слое численное решение сначала строится с помощью внешней немонотонной HASIA-схемы, имеющей заметные осцилляции на ударной волне. После этого в окрестности фронта ударной волны численное решение стандартным образом корректируется с помощью одной из NFC-схем, и на новом временном слое получается монотонизированное численное решение без заметных нефизических осцилляций. Опишем эту методику более детально при аппроксимации гибридной схемой задачи Коши (2.1), (2.2).

Предположим, что численное решение ${\mathbf{v}}_{j}^{n}$ гибридной схемы, определяемое в целых узлах базисной сетки (2.3), известно на первых $n$ временных слоях этой сетки. Численное решение ${\mathbf{v}}_{j}^{{n + 1}}$ на $(n + 1)$-м временном слое находится следующим образом. По внешней немонотонной H-ASIA-схеме строится предварительное решение ${\mathbf{\hat {v}}}_{j}^{{n + 1}}$ во всей однослойной расчетной области

Из предыдущего раздела, в котором приведены результаты численного решения задачи Коши (2.1), (3.1), (3.2) для системы уравнений мелкой воды, следует, что схема CABARETM, имеющая компактный шаблон, с наибольшей точностью локализует фронты ударных волн (фиг. 3), в то время как HASIA-схемы Русанова и CWA, второго порядка интегральной сходимости (фиг. 4), имеют существенно более высокую точность в областях влияния ударных волн (фиг. 5, 6) по сравнению с NFC-схемами CABARETM и WENO5. С учетом этого возникает идея построения гибридных схем, в которых внешней схемой является одна из HASIA-схем Русанова или CWA, а в качестве внутренней NFC-схемы применяется схема CABARETM; далее для этих гибридных схем будем использовать аббревиатуры HR-схема (Hybrid Rusanov scheme) и HC-схема (Hybrid Сompact scheme). В схемах HR и HC подобласть $S_{{n + 1}}^{*}$, в которой применяется схема CABARETM, выделяется простейшим градиентным методом, предложенным в [29], [31]. В рамках этого метода

На фиг. 7, 8 показаны относительные локальные дисбалансы $\Delta {{w}_{{ih}}}({{x}_{j}},t)$ вычисления инвариантов ${{w}_{i}}$, полученные при расчете основной тестовой задачи (2.1), (3.1), (3.2) по схемам HR, HC, CABARETM и WENO5 на равномерной сетке (2.3) с коэффициентом запаса $z = 0.45$. Эти дисбалансы определялись по формулам (2.17) и (2.18), в которых ${{h}_{i}} = h{\text{/}}{{k}^{{i - 1}}}$, где $k = 3$ для схем HR, HC, CABARETM и $k = 2$ для схемы WENO5. Расчеты для фиг. 7, 8 проводились на базисной сетке (2.3) с пространственным шагом $h = 0.005$, и их результаты показаны для каждого 40-го пространственного узла $j = 40i$ численной сетки.

Фиг. 7.

Относительные локальные дисбалансы $\Delta {{w}_{{1h}}}({{x}_{j}},t)$ вычисления инварианта ${{w}_{1}} = v - 2c$, получаемые по схемам HR (кружки), HC (квадратики), CABARETM (точки) и WENO5 (крестики).

Фиг. 8.

Относительные локальные дисбалансы $\Delta {{w}_{{2h}}}({{x}_{j}},t)$ вычисления инварианта ${{w}_{2}} = v + 2c$, получаемые по схемам HR (кружки), HC (квадратики), CABARETM (точки) и WENO5 (крестики).

Из результатов расчетов, приведенных на фиг. 7, 8, следует, что гибридные схемы HR и HC теряют основное преимущество исходных HASIA-схем Русанова и CWA – повышенный порядок интегральной сходимости на интервалах $[{{x}_{j}},X]$, левая граница которых лежит в области влияния ударной волны. Это приводит к снижению точности схем HR и HC в областях влияния ударных волн, которая становится сравнимой с точностью NFC-схем CABARETM и WENO5 и существенно более низкой, чем в схемах Русанова и CWA. Поскольку алгоритм гибридизации (6.1), (6.2) в схемах HR и HC начинает работать в момент времени $t \approx 0.3$, т.е. раньше, чем возникают ударные волны в точном решении, то снижение точности этих схем происходит в областях влияния больших градиентов численного решения, которые содержат внутри себя и заметно превосходят области влияния ударных волн.

7. ПЕРВЫЕ КОМБИНИРОВАННЫЕ СХЕМЫ

Из результатов предыдущего раздела следует, что гибридные схемы, в которых в качестве внешней применяется  одна из HASIA-схем, не сохраняют основного преимущества этих HASIA-схем – повышенную точность в областях влияния ударных волн. Данный недостаток как NFC-схем, так и гибридных схем, непосредственно связан с их главным преимуществом – монотонной локализацией фронтов ударных волн, поскольку любая конечная сумма ряда Фурье для разрывной функции не является монотонной. С учетом этого осцилляции, возникающие на фронтах ударных волн в немонотонных HASIA-схемах, несут информацию о волновой структуре фурье-разложения разрывной функции в окрестности сильного разрыва, что позволяет этим схемам с повышенной точностью передавать условия Гюгонио и, как следствие, сохранять повышенную точность в областях влияния ударных волн. NFC-схемы и гибридные схемы в результате искусственного сглаживания численных ударных волн эту информацию теряют, что приводит к снижению их точности при аппроксимации условий Гюгонио.

В [29], [31] была предложена методика построения комбинированных схем, которые сочетают достоинства как NFC-схем, так и немонотонных HASIA-схем, а именно, монотонно локализуют фронты ударных волн и одновременно сохраняют повышенную точность в областях их влияния. В комбинированной схеме применяется базисная немонотонная HASIA-схема, по которой численное решение ${\mathbf{\hat {v}}}_{j}^{n}$ задачи Коши (2.1), (2.2) строится во всей расчетной области $S$, задаваемой формулой (2.3). В подобласти $S{\kern 1pt} * \subset S$, где решение ${\mathbf{\hat {v}}}_{j}^{n}$ имеет большие градиенты, приводящие к нефизическим осцилляциям, оно корректируется путем построения численного решения $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} _{j}^{n}$ внутренней начально-краевой задачи по одной из NFC-схем с начальными и граничными условиями, получаемыми на границе области $S{{\backslash }}S{\kern 1pt} *$ из решения ${\mathbf{\hat {v}}}_{j}^{n}$. В результате решение комбинированной схемы в расчетной области (2.3) определяется по формуле

На фиг. 9 приведены значения глубины жидкости, получаемые при численном расчете задачи Коши (2.1), (3.1), (3.2) по схемам CR (кружки), CCWA (квадратики), CABARETM (точки) и WENO5 (крестики) на сетке (2.3) с пространственным шагом $h = 0.25$. Из фиг. 9 следует, что в комбинированных схемах CR и CCWA эффективно подавляются нефизические осцилляции, присущие базисным HASIA-схемам Русанова и CWA на фронтах ударных волн (фиг. 3). Поскольку внутренней схемой для данных комбинированных схем является схема CABARETM, с высокой точностью локализующая ударные волны, то схемы CR и CCWA (подобно схеме CABARETM) заметно меньше размазывают фронт ударной волны по сравнению со схемой WENO5 более высокого порядка аппроксимации. Так как внутренняя схема CABARETM не влияет на решения базисных схем Русанова и CWA в области $S{{\backslash }}S{\kern 1pt} *$, то комбинированные схемы CR и CCWA (в отличие от гибридных схем HR и HCWA) сохраняют повышенную точность вычисления инвариантов в областях влияния ударных волн, которая вне области (7.1) совпадает с точностью вычисления инвариантов по схемам Русанова и CWA (фиг. 5, 6), имеющих повышенный порядок интегральной сходимости (фиг. 4).

Фиг. 9.

Глубины жидкости $H$, получаемые при численном решении задачи Коши (2.1), (3.1), (3.2) по схемам CR (кружки), CCWA (квадратики), CABARETM (точки) и WENO5 (крестики). Cплошными линиями изображены квазиточные значения глубины.

8. СОГЛАСОВАННЫЕ КОМБИНИРОВАННЫЕ СХЕМЫ

Основной недостаток комбинированных схем CR и CCWA, построенных в предыдущем разделе, заключается в том, что соответствующие им базисная и внутренняя схемы имеют существенно различный тип, что приводит к определенным сложностям при реализации численного алгоритма на границе внутренней расчетной области (7.1). Поэтому следующий этап в развитии теории комбинированных схем был связан с разработкой согласованных численных алгоритмов, в которых базисная и внутренняя схемы являются схемами одного класса, а именно, внутренняя схема получается из базисной схемы в результате применения соответствующей NFC-процедуры. В [32] такая комбинированная схема была построена на основе DG-метода из [8], а в [33] – на основе бикомпактных разностных схем (см. [10]).

8.1. Комбинированная схема DG-метода

В отличие от описанных в разд. 4 конечно-разностных схем, DG-схема представляет собой (см. [8]) проекционно-разностный метод (проекционный по пространственной переменной $x$ и разностный по временной переменной $t$), в котором численное решение ищется в виде кусочно-полиномиальной разрывной функции относительно пространственной переменной $x$. Впервые предложенный в [66] и детально изученный в [8], DG-метод в настоящее время активно развивается (см. [67]–[70]) и применяется для решения сложных многомасштабных задач математической физики (см. [71]–[75]). Одним из основных достоинств данного метода является компактность пространственного шаблона, что позволяет обеспечить повышенный порядок аппроксимации на многомерных неструктурированных сетках с произвольной формой ячеек (см. [71]–[77]). Для монотонизации численного решения в окрестностях сильных разрывов в DG-схемах применяются различные методы коррекции потоков (см. [68], [73], [76], [78], [79]); наиболее распространенными из них являются NFC-лимитеры (см. [8], [70], [76], [77], [80], [81], которые, однако, могут приводить к снижению точности получаемого численного решения (см. [18]). При этом DG-метод показал (см. [82]) заметные преимущества по сравнению с MUSCL-схемами из [2] при численном расчете различных тестовых задач как на декартовых сетках, так и на неподвижных и движущихся сетках Вороного.

Поскольку применение DG-схемы для расчета многомерных прикладных задач требует выполнения большего числа достаточно громоздких вычислений, то эффективное использование этой схемы связано с применением всех возможностей современной вычислительной техники (см. [83], [84]), что диктует необходимость создания программных комплексов, достаточно легко адаптируемых для работы на различных (в том числе гибридных) параллельных компьютерных архитектурах. С учетом этого при решении DG-методом многомерных уравнений Навье–Стокса был разработан новый сеточно-операторный подход к программированию задач математической физики (см. [74]), позволяющий единообразно компактно записывать и эффективно вычислять сложные математические формулы на разных типах сеток и для различных вычислительных архитектур, в том числе для графических ускорителей CUDA (см. [84], [85]).

Далее в этом разделе приводятся результаты работы [32], в которой исследуется точность различных модификаций пространственно-одномерной DG-схемы, заданной на равномерной численной сетке (2.3). Рассмотрим сначала проекционно-дифференциальную форму записи DG-схемы (проекционную по $x$ и дифференциальную по $t$), в рамках которой численное решение ${{{\mathbf{v}}}_{h}}(x,t)$ в каждой пространственной ячейке $[{{x}_{j}},{{x}_{{j + 1}}})$ сетки (2.3) представляет собой полином степени не выше $p$ относительно переменной $x$:

(8.1)

${{{\mathbf{v}}}_{h}}(x,t) = {{{\mathbf{v}}}_{{hj}}}(x,t) = \sum\limits_{i = 0}^p \,{{{\mathbf{v}}}_{{ji}}}(t){{\varphi }_{{hji}}}(x),\quad x \in [{{x}_{j}},{{x}_{{j + 1}}}),$

где ${{{\mathbf{v}}}_{{ji}}}(t)$ – искомые вектор-функции,

(8.2)

${{\varphi }_{{hji}}}(x) = {{\left( {\frac{{x - {{x}_{{j + 1/2}}}}}{h}} \right)}^{i}}$

есть базисные многочлены. В приводимых далее формулах индекс $h$ у функций ${{{\mathbf{v}}}_{{hj}}}$ и ${{\varphi }_{{hji}}}$ для краткости опускается.

При аппроксимации DG-схемой гиперболической системы (2.1) каждая функция ${{{\mathbf{v}}}_{j}}(x,t)$ удовлетворяет векторному дифференциальному уравнению (см. [8])

(8.3)

$\frac{d}{{dt}}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {{{\mathbf{v}}}_{j}}{{\varphi }_{{jk}}}dx = {{\Psi }_{{jk}}},$

в котором

(8.4)

${{\Psi }_{{jk}}} = \int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {\mathbf{f}}({{{\mathbf{v}}}_{j}})\varphi _{{jk}}^{'}dx - {{{\mathbf{F}}}_{{j + 1}}}{{\varphi }_{{jk}}}({{x}_{{j + 1}}}) + {{{\mathbf{F}}}_{j}}{{\varphi }_{{jk}}}({{x}_{j}}),$

где

(8.5)

${{{\mathbf{F}}}_{j}} = \frac{{{\mathbf{f}}({{{\mathbf{v}}}_{{j - 1}}}({{x}_{j}},t)) + {\mathbf{f}}({{{\mathbf{v}}}_{j}}({{x}_{j}},t))}}{2} - \frac{{{{a}_{j}}\left( {{{{\mathbf{v}}}_{j}}({{x}_{j}},t) - {{{\mathbf{v}}}_{{j - 1}}}({{x}_{j}},t)} \right)}}{2}$

есть численные потоки, определяемые по формуле Русанова–Лакса–Фридрихса,

${{a}_{j}} = \mathop {\max }\limits_m \mathop {\max }\limits_{} \left( {{\text{|}}{{\lambda }_{m}}({{{\mathbf{v}}}_{{j - 1}}}({{x}_{j}},t)){\kern 1pt} {\text{|}},{\text{|}}{{\lambda }_{m}}({{{\mathbf{v}}}_{j}}({{x}_{j}},t)){\kern 1pt} {\text{|}}} \right),$

${{\lambda }_{m}}$ – собственные значения матрицы Якоби ${{{\mathbf{f}}}_{{\mathbf{u}}}}$ системы (2.1). С учетом формулы (8.1)

$\frac{d}{{dt}}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {{{\mathbf{v}}}_{j}}{{\varphi }_{{jk}}}dx = \sum\limits_{i = 0}^p \,a_{{ki}}^{j}\frac{{d{{{\mathbf{v}}}_{{ji}}}}}{{dt}},\quad a_{{ki}}^{j} = \int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {{\varphi }_{{jk}}}{{\varphi }_{{ji}}}dx,$

где матрицы ${{A}_{j}} = \left( {a_{{ki}}^{j}} \right)$ являются невырожденными, векторное уравнение (8.3) эквивалентно следующей системе векторных уравнений:

(8.6)

$\frac{{d{{{\mathbf{v}}}_{{ji}}}}}{{dt}} = \sum\limits_{k = 0}^p \,b_{{ik}}^{j}{{\Psi }_{{jk}}},\quad i = \overline {0,p} ,$

в которой ${{B}_{j}} = \left( {b_{{ik}}^{j}} \right)$ – матрица, обратная к ${{A}_{j}}$.

Следуя [32], мы будем рассматривать DG-метод (8.1)–(8.6), для которого $p = 1$, в силу чего численное решение (8.1) ищется в виде кусочно-линейной по $x$ вектор-функции

(8.7)

${{{\mathbf{v}}}_{h}}(x,t) = {{{\mathbf{v}}}_{{j0}}}(t) + \frac{{x - {{x}_{{j + 1/2}}}}}{h}\;{{{\mathbf{v}}}_{{j1}}}(t)\;,\quad \quad x \in [{{x}_{j}},{{x}_{{j + 1}}}).$

Для такого DG-метода будем использовать аббревиатуру DG1. Поскольку DG1-метод (8.1)–(8.7) имеет не менее, чем второй порядок точности на гладких решениях, и не принадлежит классу NFC-схем, то получаемое на его основе численное решение может иметь заметные нефизические осцилляции на фронтах ударных волн. Для подавления этих осцилляций применим ограничитель Кокбурна (см. [8]), который каждую компоненту ${{{v}}_{{j1}}}$ векторной функции ${{{\mathbf{v}}}_{{j1}}}$, входящей в формулу (8.7), заменяет на величину

(8.8)

${{w}_{{j1}}} = M\left( {{{v}_{{j1}}},\alpha ({{v}_{{j + 1,0}}} - {{v}_{{j0}}}),\alpha ({{v}_{{j0}}} - {{v}_{{j - 1,0}}})} \right),$

где $\alpha \in [1,2]$ – эвристический параметр, ${{v}_{{l0}}}$ – соответствующие компоненты векторов ${{{\mathbf{v}}}_{{l0}}}$,

(8.9)

$M\left( {{{v}_{1}},{{v}_{2}},{{v}_{3}}} \right) = s\min \left( {\left| {{{v}_{1}}} \right|,\left| {{{v}_{2}}} \right|,\left| {{{v}_{3}}} \right|} \right)$

есть стандартный оператор minmod, в котором $s = {\text{sign}}({{{v}}_{i}})$ при условии, что все числа ${{{v}}_{i}}$, входящие в соотношение (8.9), имеют одинаковый знак, и $s = 0$, если это условие не выполнено. Для DG1-методов, коррекция которых по формуле (8.8) происходит при параметрах $\alpha = 1$ и $\alpha = 2$, будем использовать обозначения DG1A1 и DG1A2 соответственно.

Для DG-схемы (8.1)–(8.9) полудискретное численное решение ${{{\mathbf{v}}}_{h}}(x,n\tau )$ получается путем решения системы обыкновенных дифференциальных уравнений (8.6) методом Рунге–Кутты третьего порядка по формулам, аналогичным (4.13). При этом тестовые расчеты показывают, что увеличение параметра $\alpha $, входящего в оператор коррекции (8.8), приводит к уменьшению схемной вязкости, что может вызвать возникновение небольших осцилляций на фронтах ударных волн. В то же время уменьшение параметра $\alpha $, связанное с увеличением схемной вязкости, будет приводить к более сильному размазыванию фронтов ударных волн. С учетом этого метод DG1A1 полностью подавляет численные осцилляции, возникающие на фронтах ударных волн в DG1-методе, в то время как метод DG1A2 подавляет эти осцилляции лишь частично.

На фиг. 10–12 приведены результаты численных расчетов основной тестовой задачи (2,1), (3.1), (3.2) по трем DG-схемам: DG1, DG1A1 и DG1A2, проведенные на равномерной сетке (2.3) с коэффициентом запаса $z = 0.45$, что обеспечивает выполнение условия устойчивости (2.4); результаты расчетов по схеме DG1 показаны кружками, по схеме DG1A1 – точками и по схеме DG1A2 – крестиками. При $t = 1,{\kern 1pt} 2.5$ темными треугольниками на оси $x$ обозначены положения фронтов ударных волн, а при $t = 1$ светлым треугольником показана левая граница области влияния ударной волны. Cплошными линиями на фиг. 10 и 12 изображены квазиточные профили глубины, получаемые в результате численного расчета по схеме DG1A1 на достаточно мелкой сетке. На фиг. 10 показаны численные значения глубины жидкости $H({{x}_{{j + 1/2}}},t)$ и порядки интегральной сходимости $\rho ({{x}_{j}},X,t)$, определяемые по формуле (2.13), в которой $k = 3$, а на фиг. 11 – относительные локальные дисбалансы $\Delta {{w}_{{ih}}}({{x}_{{j + 1/2}}},t)$, вычисления инвариантов ${{w}_{i}}$, задаваемые формулами (2.17) и (2.18). Глубины жидкости $H$ вычислялись на сетке (2.3) с пространственным шагом $h = 0.25$, а величины $\rho $ и $\Delta {{w}_{{ih}}}$ были вычислены на базисной сетке (2.3) с шагом $h = 0.005$ и показаны для каждой 40-й ячейки этой сетки.

Фиг. 10.

Глубины жидкости $H$ и порядки интегральной сходимости $\rho $, получаемые при численном решении задачи Коши (2.1), (3.1), (3.2) по схемам DG1 (кружки), DG1A1 (точки) и DG1A2 (крестики). Cплошными линиями изображены квазиточные значения глубины.

Фиг. 11.

Относительные локальные дисбалансы $\Delta {{w}_{{ih}}}({{x}_{{j + 1/2}}},t)$ вычисления инвариантов ${{w}_{i}}$, получаемые по схемам DG1 (кружки), DG1A1 (точки) и DG1A2 (крестики).

Фиг. 12.

Глубины жидкости $H$, получаемые при численном решении задачи Коши (2.1), (3.1), (3.2) по схемам DG1 (кружки), DG1A1 (точки) и CDG (квадратики). Cплошными линиями изображены квазиточные значения глубины.

На графиках, приведенных слева на фиг. 10, видно, что в отличие от NFC-схем DG1A1 и DG1A2, схема DG1 имеет заметные осцилляции в окрестностях ударных волн; при этом схемы DG1 и DG1A2 заметно меньше размазывают фронт ударной волны, чем схема DG1A1. Из графиков, показанных справа на фиг. 10, следует, что немонотонная схема DG1, несмотря на нефизические осцилляции на фронте ударной волны, обеспечивает второй порядок интегральной сходимости на отрезках $[{{x}_{j}},X]$, левая граница которых расположена внутри области влияния ударной волны. Схемы DG1A1 и DG1A2, полученные путем монотонизации схемы DG1, подобно конечно-разностным NFC-схемам, снижают скорость этой сходимости приблизительно до первого порядка, что приводит к заметному снижению их точности по сравнению со схемой DG1 при вычислении инвариантов в области влияния ударной волны (фиг. 11).

На графиках, приведенных справа на фиг. 10, видно, что при $t = 0.5,\;1$ схемы DG1 и DG1A2 имеют третий порядок интегральной сходимости на интервалах $[{{x}_{j}},X]$, левая граница которых лежит вне области влияния ударной волны, в то время как схема DG1A1 имеет на этих интервалах второй порядок интегральной сходимости. Объясняется это тем, что схема DG1 обеспечивает третий порядок локальной аппроксимации на гладких решениях и коррекция потоков в схеме DG1A2 этот порядок сохраняет, в то время как более сильная коррекция потоков в схеме DG1A1 снижает точность этой аппроксимации до второго порядка. В результате вне области влияния ударной волны инварианты вычисляются по схеме DG1A1 с существенно более низкой точностью, чем по схемамам DG1 и DG1A2 (фиг. 11).

Проведенный анализ точности схем DG1 и DG1A1 позволяет использовать их для построения методом, изложенным в разд. 7, комбинированной схемы разрывного метода Галеркина, в которой в качестве базисной HASIA-схемы применяется немонотонная схема DG1, а в качестве внутренней NFC-схемы – схема DG1A1. Для получаемой таким образом комбинированной DG-схемы будем использовать аббревиатуру CDG-схема (Combined Discontinuous Galerkin scheme). На фиг. 12 при $t = 1,\;2.5$ приведены значения глубины жидкости $H({{x}_{{j + 1/2}}},t)$, получаемые при численном расчете задачи Коши (2.1), (3.1), (3.2) по схемам CDG (квадратики), DG1 (кружки) и DG1A1 (точки) на сетке (2.3) с пространственным шагом $h = 0.25$. На фиг. 12 видно, что в комбинированной CDG-схеме эффективно подавляются нефизические осцилляции на фронтах ударных волн, присущие базисной DG1-схеме (фиг. 10). Поскольку внутренняя схема DG1A1 не влияет на решение базисной схемы DG1 вне многосвязной области (7.1), внутри которой расположены ударные волны, то комбинированная CDG-схема сохраняет повышенную точность вычисления инвариантов в областях влияния ударных волн, которая совпадает с точностью вычисления инвариантов по схеме DG1 (фиг. 11), имеющей повышенный порядок интегральной сходимости (фиг. 10).

8.2. Бикомпактные комбинированные схемы

Определяющей чертой бикомпактных схем является высокоточная компактная аппроксимация пространственных производных на шаблоне, который размещается в одной ячейке сетки. По каждому пространственному направлению этот шаблон включает в себя лишь два целых узла сетки, что и дало название этому классу схем. Высокий четный порядок аппроксимации по пространству в бикомпактных схемах достигается за счет введения дополнительных искомых сеточных функций, определенных на множестве либо уже имеющихся целых, либо вспомогательных дробных узлов. Для отыскания этих дополнительных функций привлекаются дифференциальные следствия аппроксимируемых уравнений. Преимущество бикомпактных схем заключается в сочетании нескольких положительных свойств: это слабые ограничения по устойчивости (благодаря неявности временной дискретизации), экономичная реализация, совпадение числа граничных условий в разностной и дифференциальной постановках задачи (благодаря минимальности шаблона), высокое спектральное разрешение (см. [86], [87]).

Применительно к нестационарным уравнениям в частных производных бикомпактные схемы были впервые построены: для одномерного линейного уравнения теплопроводности в [88], для одномерного линейного уравнения переноса в [10], для одномерных гиперболических систем законов сохранения в [89]. В дальнейшем бикомпактные схемы получили обобщение на различные многомерные уравнения и системы уравнений: гиперболические уравнения (см. [90]) и системы (см. [28], [91]), уравнения Эйлера для многокомпонентных химически реагирующих газов (см. [92]), линейное уравнение конвекции-диффузии (см. [93]), уравнения Навье–Стокса для несжимаемой жидкости (см. [94]). Для эффективной реализации многомерных бикомпактных схем было предложено применять локально-одномерное расщепление (см. [95]) и метод итерируемой приближенной факторизации (см. [96]). В работах [86], [87] были исследованы диссипативные и дисперсионные свойства бикомпактных схем. Было показано в [86], что бикомпактные схемы имеют лучшее спектральное разрешение по сравнению с классическими компактными схемами такого же порядка аппроксимации по пространству. В [11] был предложен метод консервативной монотонизации бикомпактных схем, в котором устранен главный недостаток метода гибридной схемы (см. [10], [28], [89]–[91]) – нарушение свойства консервативности. Вопросы точности бикомпактных схем в областях влияния ударных волн и построения комбинированных бикомпактных схем рассматривались в [21], [33], [97]. В настоящем разделе дается обзор результатов из [21], [33].

Простейшая бикомпактная схема, аппроксимирующая систему (2.1), имеет вид

(8.10)

$\begin{gathered} \frac{1}{\tau }A_{0}^{x}({\mathbf{v}}_{{j + 1/2}}^{*} - {\mathbf{v}}_{{j + 1/2}}^{n}) + \Lambda _{1}^{x}{{{\mathbf{f}}}^{ + }}({\mathbf{v}}_{{j + 1/2}}^{*}) = {\mathbf{0}},\quad \frac{1}{\tau }A_{0}^{x}({\mathbf{v}}_{{j + 1/2}}^{{n + 1}} - {\mathbf{v}}_{{j + 1/2}}^{*}) + \Lambda _{1}^{x}{{{\mathbf{f}}}^{ - }}({\mathbf{v}}_{{j + 1/2}}^{{n + 1}}) = {\mathbf{0}}, \hfill \\ \frac{1}{\tau }\Lambda _{1}^{x}({\mathbf{v}}_{{j + 1/2}}^{{n + 1}} - {\mathbf{v}}_{{j + 1/2}}^{*}) + \Lambda _{2}^{x}{{{\mathbf{f}}}^{ - }}({\mathbf{v}}_{{j + 1/2}}^{{n + 1}}) = {\mathbf{0}};\quad \frac{1}{\tau }\Lambda _{1}^{x}({\mathbf{v}}_{{j + 1/2}}^{*} - {\mathbf{v}}_{{j + 1/2}}^{n}) + \Lambda _{2}^{x}{{{\mathbf{f}}}^{ + }}({\mathbf{v}}_{{j + 1/2}}^{*}) = {\mathbf{0}}; \hfill \\ \end{gathered} $

где искомые функции ${\mathbf{v}}_{j}^{n}$ и ${\mathbf{v}}_{{j + 1/2}}^{n}$, так же как в схеме CABARETM, вычисляются в целых и полуцелых пространственных узлах однородной разностной сетки (2.3), действие сеточных операторов $A_{0}^{x},\;\Lambda _{1}^{x},\;\Lambda _{2}^{x}$ определяется формулами

$A_{0}^{x}{\mathbf{v}}_{{j + 1/2}}^{n} = \frac{{{\mathbf{v}}_{j}^{n} + 4{\mathbf{v}}_{{j + 1/2}}^{n} + {\mathbf{v}}_{{j + 1}}^{n}}}{6},\quad \Lambda _{1}^{x}{\mathbf{v}}_{{j + 1/2}}^{n} = \frac{{{\mathbf{v}}_{{j + 1}}^{n} - {\mathbf{v}}_{j}^{n}}}{h},\quad \Lambda _{2}^{x}{\mathbf{v}}_{{j + 1/2}}^{n} = \frac{{4({\mathbf{v}}_{j}^{n} - 2{\mathbf{v}}_{{j + 1/2}}^{n} + {\mathbf{v}}_{{j + 1}}^{n})}}{{{{h}^{2}}}},$

а функции ${{{\mathbf{f}}}^{ \pm }}({\mathbf{u}})$ порождаются глобальным расщеплением потоков Лакса–Фридрихса

(8.11)

${{{\mathbf{f}}}^{ \pm }}({\mathbf{u}}) = \frac{1}{2}{\mathbf{f}}({\mathbf{u}}) \pm {{C}_{2}}{\mathbf{u}},\quad {{C}_{2}} = \frac{{1 + 2\delta }}{2}\mathop {\max }\limits_{k,{\kern 1pt} j,{\kern 1pt} \alpha } \left| {{{\lambda }_{k}}({\mathbf{v}}_{{j + \alpha }}^{n})} \right|,$

в котором параметр $\delta > 0$ отвечает за запас положительной либо отрицательной определенности матриц Якоби ${{A}^{ \pm }}({\mathbf{u}}) = {\mathbf{f}}_{{\mathbf{u}}}^{ \pm }({\mathbf{u}})$. Бикомпактная схема (8.10) является консервативной и безусловно устойчивой, имеет четвертый порядок аппроксимации по пространству и первый порядок аппроксимации по времени, поскольку в этой схеме для дискретизации по времени применяется неявный метод Эйлера первого порядка. При аппроксимации линейного уравнения переноса схема (8.10) монотонна при числах Куранта, не меньших $1{\text{/}}4$.

Далее мы рассматриваем три бикомпактные схемы на основе (8.10): MBiC, NFC-схему формально третьего порядка аппроксимации по времени (см. [11]); RBiC, HASIA-схему с пассивной (в терминологии [34]) или глобальной экстраполяцией Ричардсона (см. [21]) второго порядка по времени; CBiC, комбинированную схему второго порядка аппроксимации по времени (см. [33]).

Дадим краткое описание схемы MBiC. Ее построение начинается с того, что порядок аппроксимации схемы (8.10) по времени повышается до третьего. Для этого временные производные аппроксимируются не разностями назад, а диагонально-неявным методом Рунге–Кутты соответствующего порядка из работы [98]:

$\begin{array}{*{20}{c}} a&\vline & a&{}&{} \\ {{{a}_{{21}}} + a}&\vline & {{{a}_{{21}}}}&a&{} \\ 1&\vline & {{{a}_{{31}}}}&{{{a}_{{32}}}}&a \\ \hline {}&\vline & {{{a}_{{31}}}}&{{{a}_{{32}}}}&a \end{array},\quad a = 1 + \sqrt 2 \cos \left( {\frac{{4\pi }}{3} + \frac{1}{3}\arccos \frac{{2\sqrt 2 }}{3}} \right),$

${{a}_{{21}}} = - \frac{{a - 1{\text{/}}3}}{{2({{a}^{2}} - 2a + 1{\text{/}}2)}},\quad {{a}_{{32}}} = - \frac{{2({{a}^{2}} - 2a + 1{\text{/}}{{{2)}}^{2}}}}{{a - 1{\text{/}}3}},\quad {{a}_{{31}}} = 1 - a - {{a}_{{32}}}.$

Добавим, что данный метод является жестко-точным и $L$-устойчивым. Полученную таким образом бикомпактную схему третьего порядка аппроксимации по времени будем называть схемой $B$. По теореме Годунова из [1] схема $B$ является немонотонной. Генерируемые ею нефизические осцилляции подавляются с помощью метода консервативной монотонизации, предложенного в [11]. Его конструкция предполагает использование второй схемы – монотонной схемы $A$. Последняя не обязана быть бикомпактной и может быть выбрана исходя из любых нужных критериев (экономичность, устойчивость, количество аппроксимационной вязкости). В качестве схемы $A$ возьмем схему (8.10) .

Рассмотрим переход со слоя ${{t}_{n}}$ на слой ${{t}_{{n + 1}}}$ по схеме MBiC. Искомое решение ${\mathbf{v}}_{h}^{{n + 1}}$ находится в три этапа. На первом этапе по схемам $A$ и $B$ вычисляются два решения на слое ${{t}_{{n + 1}}}$: ${\mathbf{v}}_{h}^{A}$ и ${\mathbf{v}}_{h}^{B}$ соответственно. Общим промежуточным начальным условием для обеих схем полагается решение ${\mathbf{v}}_{h}^{n}$. На втором этапе решение ${\mathbf{v}}_{h}^{B}$ ограничивается локально в каждой ячейке ${{K}_{{j + 1/2}}} = [{{x}_{j}},{{x}_{{j + 1}}}]$ около своего интегрального среднего ${\mathbf{\bar {v}}}_{{j + 1/2}}^{B} = A_{0}^{x}{\mathbf{v}}_{{j + 1/2}}^{B}$:

(8.12)

${{\tilde {v}}_{h}}(x;{{K}_{{j + 1/2}}}) = \bar {v}_{{j + 1/2}}^{B} + {{\beta }_{{j + 1/2}}}[v_{h}^{B}(x) - \bar {v}_{{j + 1/2}}^{B}],\quad x = {{x}_{j}},{{x}_{{j + 1/2}}},{{x}_{{j + 1}}},$

где

(8.13)

${{\beta }_{{j + 1/2}}} = \frac{1}{{1 + d_{{j + 1/2}}^{2}}},\quad {{d}_{{j + 1/2}}} = \frac{{{{C}_{1}}\mathop {\max }\limits_{x = {{x}_{j}},{{x}_{{j + 1/2}}},{{x}_{{j + 1}}}} \left| {v_{h}^{A}(x) - v_{h}^{B}(x)} \right|}}{{\mathop {\max }\limits_{x = {{x}_{j}},{{x}_{{j + 1/2}}},{{x}_{{j + 1}}}} \left| {v_{h}^{A}(x)} \right|}}.$

Формулы (8.12), (8.13) применяются покомпонентно, т.е. $v \equiv {{v}^{i}}$, $\beta \equiv {{\beta }^{i}}$, $d = {{d}^{i}}$, $i = \overline {1,m} $. На третьем этапе устраняется многозначность решения ${{{\mathbf{\tilde {v}}}}_{h}}$ на границах между ячейками, после чего мы получаем результирующее решение на слое ${{t}_{{n + 1}}}$:

(8.14)

${{{\mathbf{v}}}_{h}}({{x}_{j}},{{t}_{{n + 1}}}) = \frac{{{{{{\mathbf{\tilde {v}}}}}_{h}}({{x}_{j}};{{K}_{{j - 1/2}}}) + {{{{\mathbf{\tilde {v}}}}}_{h}}({{x}_{j}};{{K}_{{j + 1/2}}})}}{2},\quad {{{\mathbf{v}}}_{h}}({{x}_{{j + 1/2}}},{{t}_{{n + 1}}}) = {{{\mathbf{\tilde {v}}}}_{h}}({{x}_{{j + 1/2}}};{{K}_{{j + 1/2}}}).$

Число ${{C}_{1}}\; \geqslant \;0$ является параметром метода консервативной монотонизации (см. [11]).

Суть формул (8.12)–(8.14) сводится к следующему. В областях гладкости точного решения

$\left| {v_{h}^{A}(x) - v_{h}^{B}(x)} \right| = O(\tau ),\quad {{d}_{{j + 1/2}}} = O(\tau ),\quad \left| {{{\beta }_{{j + 1/2}}} - 1} \right| = O({{\tau }^{2}})$

и решение ${\mathbf{v}}_{h}^{B}$ корректируется лишь на величину $O({{h}^{3}})$. Вблизи сильных разрывов точного решения

$\left| {v_{h}^{A}(x) - v_{h}^{B}(x)} \right| = O(1),\quad {{d}_{{j + 1/2}}} = O(1),\quad \left| {{{\beta }_{{j + 1/2}}} - 1} \right| = O(1)$

и решение ${\mathbf{v}}_{h}^{B}$ сглаживается на величину $O(1)$. Из формул (8.12) и (8.13) следует, что монотонизация тем интенсивнее, чем больше параметр ${{C}_{1}}$; в предельном случае при ${{C}_{1}} = 0$ монотонизация отсутствует.

Перейдем к схеме RBiC и основанной на ней комбинированной схеме CBiC. Чтобы построить решение по схеме RBiC, необходимо сначала провести полный расчет задачи по бикомпактной схеме (8.10) на двух сетках: с шагами ${{h}_{1}} = h$, ${{\tau }_{1}} = \tau $ и шагами ${{h}_{2}} = h{\text{/}}2$, ${{\tau }_{2}} = \tau {\text{/}}2$. Затем на любом слое $t_{n}^{1}$ по двум полученным решениям с помощью пассивной экстраполяции Ричардсона второго порядка вычисляется искомое решение

(8.15)

${{{\mathbf{v}}}_{{{{h}_{1}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};B) = 2{{{\mathbf{v}}}_{{{{h}_{2}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};A) - {{{\mathbf{v}}}_{{{{h}_{1}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};A),$

где ради краткости мы обозначили схему (8.10) буквой $A$ (как в MBiC), а схему RBiC – буквой $B$. Подчеркнем, что пассивная (глобальная) экстраполяция Ричардсона, в отличие от активной (локальной), реализуется не при каждом переходе со слоя на слой (подобно стадиям методов Рунге–Кутты), а только после полного завершения счета.

Решение, задаваемое формулой (8.15), содержит осцилляции, однако их количество невелико, и они локализованы в окрестностях ударных волн. Поскольку схема RBiC реализуется пассивно, эти осцилляции разумно устранять некоторой простой пост-обработкой. Применяя для этого формулы, аналогичные формулам гибридной схемы из [10], мы приходим к комбинированной схеме CBiC из [33]:

(8.16)

$\begin{array}{*{20}{c}} {{{v}_{h}}(x_{{j + \alpha }}^{1},t_{n}^{1};{\text{CBiC}}) = {{v}_{{{{h}_{1}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};B) + {{\omega }_{{j + \alpha }}}{{D}_{{j + \alpha }}},} \\ {{{D}_{{j + \alpha }}} = {{v}_{{{{h}_{2}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};A) - {{v}_{{{{h}_{1}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};B),\quad {{\omega }_{{j + \alpha }}} = \left\{ \begin{gathered} 0\quad {\text{при}}\quad \left| {{{D}_{{j + \alpha }}}} \right|\;\leqslant \;{{d}_{*}}Q, \hfill \\ 1 - \frac{{{{d}_{*}}Q}}{{\left| {{{D}_{{j + \alpha }}}} \right|}}\quad {\text{иначе,}} \hfill \\ \end{gathered} \right.} \\ {Q = \mathop {\max }\limits_{j,\alpha } {{v}_{{{{h}_{2}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};A) - \mathop {\min }\limits_{j,\alpha } {{v}_{{{{h}_{2}}}}}(x_{{j + \alpha }}^{1},t_{n}^{1};A),} \end{array}$

где ${{d}_{*}}\; \geqslant \;0$ – входной параметр схемы CBiC. Как и формулы (8.12)–(8.14), формула (8.16) применяется покомпонентно. В комбинированной схеме CBiC базисной HASIA-схемой является схема RBiC (схема $B$), а внутренней монотонной схемой – схема (8.10) (схема $A$). Отметим, что для реализации комбинированной схемы CBiC не нужно явного выделения фронтов ударных волн вида (6.1), (6.2) и последующего решения внутренних начально-краевых задач. Обратим внимание на одно важное свойство базисной схемы RBiC. Предположим, что ударная волна большой амплитуды распространяется по фону, близкому к границам области применимости данной физической модели. Например, в случае уравнений мелкой воды такой границей является нулевая глубина жидкости ($H = 0$), в случае уравнений газовой динамики – нулевые плотность, температура и давление газа. При сквозном расчете такого процесса по какой-либо HASIA-схеме может возникнуть осцилляция, которая выведет решение в область физически недопустимых значений, что, в свою очередь, приведет к аварийному завершению счета. В схеме же RBiC такая ситуация исключена, так как решение этой базисной схемы строится пассивно из монотонных решений внутренней бикомпактной схемы (8.10) .

Обсудим результаты расчетов основной тестовой задачи, описанной в разд. 3, по бикомпактным схемам MBiC, RBiC и CBiC. Укажем значения параметров схем: во всех схемах $\delta = 0.2$; в схеме MBiC $\tau {\text{/}}h = 0.09$ и ${{C}_{1}} = 10$; в схемах RBiC и CBiC $\tau {\text{/}}h = 0.05$, в схеме CBiC ${{d}_{ * }} = 0.01$.

На фиг. 13 показаны численные значения глубины жидкости $H$, а также порядки локальной сходимости $r$, определяемые по формуле (2.7) при $k = 2$, и порядки интегральной сходимости $\rho $, определяемые по формуле (2.9), в которой $k = 2$ и интегралы ${{{\mathbf{V}}}_{{{{h}_{i}}}}}$ вычисляются по формуле парабол. Порядки интегральной сходимости приводятся в том случае (графики слева на фиг. 13 при $t = 1,{\kern 1pt} 2.5$), когда порядки локальной сходимости разностных решений сильно осциллируют и не дают необходимой информации о точности этих решений. На фиг. 14 приведены относительные локальные дисбалансы $\Delta {{w}_{{ih}}}$ вычисления инвариантов ${{w}_{i}}$, задаваемые формулами (2.14) и (2.18). Глубины жидкости $H$ определялись на сетке (2.3) с пространственным шагом $h = 0.25$, а величины $r$, $\rho $ и $\Delta {{w}_{{ih}}}$ были вычислены на базисной сетке (2.3) с шагом $h = 0.005$ и показаны для каждой 40-й ячейки этой сетки. В качестве квазиточного решения в формулах (2.7) и (2.9) использовалось численное решение, полученное по схеме Русанова на достаточно мелкой сетке.

Фиг. 13.

Глубины жидкости $H$, порядки локальной сходимости $r$ и интегральной сходимости $\rho $, получаемые по схемам MBiC (кружки полые и закрашенные), CBiC (квадратики полые и закрашенные) и RBiC (крестики). Cплошными линиями изображены квазиточные значения глубины.

Фиг. 14.

Относительные локальные дисбалансы $\Delta {{w}_{{ih}}}({{x}_{j}},t)$ вычисления инвариантов ${{w}_{i}}$, получаемые по схемам MBiC (кружки), CBiC (квадратики), RBiC (косые крестики) и WENO5 (прямые крестики).

Из фиг. 13 следует, что профили глубины, рассчитанные по схемам MBiC и CBiC, практически не отличаются друг от друга. Разница между схемами проявляется только к моменту времени $t = 2.5$: NFC-схема MBiC размазывает фронт ударной волны на две ячейки, а комбинированная схема CBiC – на три. Немонотонность HASIA-схемы RBiC заметна при $t = 1.0,\;2.5$. Как уже было отмечено выше, осцилляции численного решения локализованы непосредственно перед и за фронтом ударной волны. В комбинированной схеме CBiC эти осцилляции отсутствуют. Из фиг. 13 также следует, что бикомпактная схема MBiC, как и другие NFC-схемы, снижает свою точность в области влияния ударной волны: порядок сходимости снижается с третьего до первого. Комбинированная бикомпактная схема CBiC имеет второй порядок локальной сходимости во всей расчетной области, за исключением некоторых окрестностей ударных волн. Это означает, что бикомпактная схема RBiC с пассивной экстраполяцией Ричардсона по времени является HASIA-схемой.

Из фиг. 14 следует, что при $t = 0.5$, когда начинают формироваться области больших градиентов, но  решение еще остается гладким, схемы RBiC и CBiC предсказуемо проигрывают NFC-схемам MBiC и WENO5 по реальной точности. Это объясняется более низким, вторым порядком аппроксимации по времени у схем RBiC и CBiC. Однако при $t = 1.0$ в области влияния ударной волны схемы RBiC и CBiC, наоборот, превосходят NFC-схемы MBiC и WENO5: погрешности инвариантов для первой пары схем в среднем на порядок меньше. Тем не менее схемы MBiC и WENO5 по-прежнему демонстрируют лучшую точность вне области влияния. По мере расширения этой области данное преимущество исчезает. К моменту времени $t = 2.5$, когда область влияния ударной волны занимает всю расчетную область, схемы RBiC и CBiC оказываются в среднем на порядок точнее всюду, кроме относительно небольших окрестностей ударных волн. При этом схемы MBiC и WENO5, будучи по существу разными схемами, имеют примерно одну и ту же точность в области влияния ударной волны.

9. ЗАДАЧА О МНОГОКРАТНОМ ВЗАИМОДЕЙСТВИИ УДАРНЫХ ВОЛН

В этом разделе приводятся результаты работы [99], в которой проведен сравнительный анализ точности комбинированных разностных схем CR и CCWA, построенных в разд. 7, со схемой WENO5 при численном моделировании задачи о многократном взаимодействии ударных волн на равномерной сетке (2.3) с коэффициентом запаса $z = 0.45$ в условии устойчивости (2.4).

Рассмотрим для системы уравнений мелкой воды (2.1), (3.1) задачу Коши (2.2) с периодическими начальными данными

Фиг. 15.

Глубины жидкости $H$, получаемые при численном решении задачи Коши (2.1), (3.1), (9.1) в моменты времени $t = 0$ (штриховая линия), $t = 0.5$ (линия 1), $t = 1$ (линия 2), $t = 2$ (линия 3) и $t = 3$ (линия 4). Кружками показаны результаты численного расчета по CR-схеме, квадратиками – по CCWA-схеме и крестиками – по схеме WENO5.

На фиг. 15 в моменты времени $t = 1,\;2,\;3$ приведены глубины жидкости, получаемые в результате численных расчетов задачи (2.1), (3.1), (9.1) по схемам CR, CCWA и WENO5 с пространственным шагом $h = 1{\text{/}}15$. Поскольку эти разностные решения (так же, как и точное решение) симметричны относительно точки $x = X{\text{/}}2$, то на фиг. 15 каждое из них в фиксированный момент времени приводится на одном из отрезков $[0,X{\text{/}}2]$ или $[X{\text{/}}2,X]$ длины полупериода. Из фиг. 15 следует, что комбинированные схемы CR и CCWA размазывают фронт ударной волны существенно меньше, чем схема WENO5. Это объясняется тем, что в этих комбинированных схемах в качестве внутренней используется схема CABARETM, которая с высокой точностью локализует фронты ударных волн.

На фиг. 16 в моменты времени $t = 0.5,{\kern 1pt} \;1,\;2,\;3$ показаны относительные локальные дисбалансы $\Delta {{w}_{{1h}}}({{x}_{j}},t)$, вычисления инварианта ${{w}_{1}} = v - 2c$, задаваемые формулами (2.14) и (2.18) при $h = 0.02$, в которых квазиточное значение инварианта ${{w}_{1}}$ моделируется расчетом по CR-схеме при $h = 0.0002$. В силу симметрии начальных данных (9.1) графики относительных локальных дисбалансов $\Delta {{w}_{{2h}}}({{x}_{j}},t)$ вычисления инварианта ${{w}_{2}} = v + 2c$ получаются из графиков, приведенных на фиг. 16, путем их отражения относительно вертикальной прямой $x = X{\text{/}}2$. Из фиг. 16 при $t = 0.5,\;1$ следует, что на интервалах, которые не входят в области влияния ударных волн, точность вычисления инвариантов в схеме WENO5 существенно выше, чем в комбинированных схемах; это объясняется более высокой точностью схемы WENO5 на гладких решениях. Однако на интервалах, расположенных между расходящимися ударными волнами, на фиг. 16 при $t = 1$ точность схемы WENO5 резко падает и становится ниже, чем в комбинированных схемах. С течением времени, когда вся расчетная область становится областью влияния взаимодействующих ударных волн (фиг. 16 при $t = 2,\;3$), точность вычисления инвариантов в комбинированных схемах становится существенно выше, чем в схеме WENO5, везде за исключением малых окрестностей ударных волн, где сходимость разностного решения к точному отсутствует. Отметим также, что CCWA-схема, в которой базисной является компактная схема (4.4)–(4.7) , демонстрирует более высокую точность, чем CR-схема, в которой базисной является схема Русанова (4.1)–(4.3). Это объясняется тем, что компактная схема (4.4)–(4.7) имеет третий порядок как классической аппроксимации на гладких решениях, так и слабой аппроксимации на разрывных решениях, в то время как схема Русанова третьего порядка классической аппроксимации имеет лишь первый порядок слабой аппроксимации.

Фиг. 16.

Относительные локальные дисбалансы $\Delta {{w}_{{1h}}}({{x}_{j}},t)$ вычисления инварианта ${{w}_{1}} = v - 2c$, получаемые при численном решении задачи Коши (2.1), (3.1), (9.1) по схемам Русанова (кружки), CWA (квадратики) и WENO5 (крестики).

10. ПРИМЕНЕНИЕ КОМБИНИРОВАННОЙ БИКОМПАКТНОЙ СХЕМЫ ДЛЯ РАСЧЕТА ДВУМЕРНЫХ ГИДРОДИНАМИЧЕСКИХ ТЕЧЕНИЙ

В этом разделе приводятся результаты работы [97], в которой комбинированная бикомпактная схема, предложенная в [33], обобщается на многомерный случай.

Двумерные уравнения первого приближения теории мелкой воды в случае плоского горизонтального дна без учета влияния донного трения имеют вид

Фиг. 17.

Начальные значения скоростей жидкости ${{v}_{x}}$, ${{v}_{y}}$ и глубины жидкости $H$, задаваемые формулами (10.3) и (10.4).

Комбинированная бикомпактная схема CBiC, аппроксимирующая задачу (10.1)–(10.4) и представляющая собой двумерный вариант схемы $A$ из п. 8.2, строится на равномерной прямоугольной разностной сетке

Применяя методы локально-одномерного расщепления из [95] и глобального расщепления потоков Лакса–Фридрихса, представим систему (10.1) в виде суммы четырех одномерных систем

Рассмотрим результаты расчетов задачи Коши (10.1)–(10.4) по комбинированной бикомпактной схеме CBiC, которые выполнялись при параметрах $\delta = 0.2$, $\tau {\text{/}}{{h}_{x}} = \tau {\text{/}}{{h}_{y}} = 0.04$ и ${{d}_{ * }} = 0.01$. На фиг. 18 в моменты времени $t = 0.5,\;1.0$ приведены графики глубины жидкости, получаемые при расчете на сетке (10.6) с пространственными шагами ${{h}_{x}} = {{h}_{y}} = 0.025$, и графики порядков локальной сходимости, определяемые по формуле, аналогичной (2.7), в которой $k = 2$ и в качестве базисной сетки используется разностная сетка (10.6) при ${{h}_{x}} = {{h}_{y}} = 0.05$. Из фиг. 18 следует, что в решении, получаемом по комбинированной схеме CBiC, отсутствуют нефизические осцилляции в окрестностях ударных волн, а порядки локальной сходимости $r \approx 2$ почти во всей расчетной области, как при $t = 0.5$, когда ударные волны только начинают формироваться, так и при $t = 1$, когда области влияния ударных волн занимают всю расчетную область. Отклонение от второго порядка сходимости происходит только в малых окрестностях ударных волн, где отсутствует локальная сходимость разностного решения к точному.

Фиг. 18.

Глубины жидкости $H$ и порядки локальной сходимости $r$, получаемые при численном решении по комбинированной схеме CBiC двумерной задачи Коши (10.1)–(10.4).

11. ЗАКЛЮЧЕНИЕ

Рассмотренные в данной работе комбинированные схемы сквозного счета: CR (Combined Rusanov), CCWA (Combined Сompact Weak Approximation), CDG (Combined Discontinuous Galerkin) и CBiC (Combined BiСompact), при численном расчете основной тестовой задачи (2.1), (3.1), (3.2) обеспечивают существенно более высокую точность в областях влияния ударных волн по сравнению со стандартными NFC-схемами (MUSCL, TVD, CU, WENO5, DG1A2, CABARETM, MBiC), которые в настоящее время широко применяются при численном моделировании прикладных задач математической физики. Причем, как показали тестовые расчеты, точность комбинированных схем при расчете разрывных решений может быть на несколько порядков выше точности NFC-схем (независимо от формального порядка аппроксимации этих схем на гладких решениях), в силу чего изложенные в данной работе результаты заметно превосходят современный мировой уровень развития данного научного направления и, по нашему мнению, в значительной степени будут определять дальнейшее развитие этого научного направления. Поэтому безусловно актуальной представляется необходимость дальнейшего всестороннего развития теории комбинированных схем сквозного счета и изучение возможностей применения этих схем для численного расчета различных многомерных прикладных задач. Сформулируем основные перспективные направления развития теории комбинированных схем.

В комбинированных схемах CR, CCWA и CDG в качестве базисных применяются HASIA-схемы третьего порядка, в то время как в комбинированной бикомпактной схеме CBiC базисной является HASIA-схема второго порядка. В результате точность вычисления инвариантов в области влияния ударных волн по схеме CBiC приблизительно на порядок выше, чем в NFC-схеме WENO5 (фиг. 14), но одновременно приблизительно на порядок ниже, чем в схемах CR, CCWA и CDG (фиг. 5, 6, 11). Поэтому несомненный интерес представляет разработка новых комбинированных бикомпактных схем, в которых в качестве базисных будут использованы бикомпактные HASIA-схемы не ниже третьего порядка, что позволит существенно повысить точность этих комбинированных схем, по сравнению со схемой CBiC.

К настоящему времени преимущества комбинированных схем были продемонстрированы на тестах, связанных с расчетом разрывных решений системы уравнений мелкой воды, представляющей собой простейшую сильно нелинейную гиперболическую систему законов сохранения (см. [35]), не имеющую контактных разрывов и допускающую запись в форме инвариантов. Поэтому в дальнейшем предполагается провести изучение точности комбинированных схем при расчете разрывных решений гиперболических систем законов сохранения общего вида, в частности, законов сохранения неизоэнтропической газовой динамики (см. [36]), допускающих контактные разрывы.

В данной работе при построении комбинированных схем область расчета по внутренней NFC-схеме определяется простейшим градиентным методом (6.2), что затрудняет применение этих схем для моделирования более сложных (в том числе многомерных) задач, в которых происходит многократное взаимодействие сильных разрывов. В то же время в рамках теории построения гибридных схем (см. [24]–[28]) разработаны более эффективные методы выделения областей, внутри которых сосредоточены основные особенности рассчитываемого точного решения. Наиболее распространенными являются методы, использующие коэффициенты фурье-разложения (см. [24]) или вейвлет-разложения (см. [25]) разностного решения, основанные на определении численного производства энтропии (см. [26]), а также использующие слабую локальную невязку разностного решения, получаемую путем подстановки непрерывного аналога этого решения в аппроксимируемую систему законов сохранения, записанную в слабо интегральной форме (см. [27]). С учетом этого в дальнейшем планируется разработать новые классы комбинированных схем сквозного счета, в которых для выделения областей больших градиентов, где расчет проводится по внутренней NFC-схеме, будут применены наиболее эффективные методы, развитые в теории гибридных схем.