Журнал вычислительной математики и математической физики, 2022, T. 62, № 12, стр. 2090-2104

3.1. Прогнозируемые типы солитонных решений

Быстрая магнитозвуковая ветвь имеет точку перегиба при $k > 0$ в случае $\theta < {{\theta }_{c}}$ (см. [4]), $\theta \in [0,\pi {\text{/}}2]$, где $\theta = {\text{arctg}}[(B_{y}^{2} + B_{z}^{2}{{)}^{{1/2}}}{\text{/}}{{B}_{x}}]$, ${{\theta }_{c}}(b)$ – некоторое критическое значение, и пересечение при $k > 0$ с прямой касательной к этой ветви в начале координат. При $\theta > {{\theta }_{c}}$ точек перегиба и пересечения нет. В случае медленных магнитозвуковых волн всегда имеется аналогичное пересечение с альвеновской ветвью. В [4] методом исследования нормальных форм в случае отсутствия пересечения доказано существование солитонных решений с малой амплитудой волн. При наличии пересечения возможны обобщенные уединенные волны, т.е. комбинации уединенной и периодической волн. В обоих случаях для малых амплитуд волны могут быть описаны уравнением Кортевега–де Вриза. Может быть также получено приближенное решение типа уединенной волны в виде ряда. Аппроксимация по амплитуде волны при этом может быть достигнута выше любого алгебраического порядка. Для быстрых магнитозвуковых волн доказывалось существование так называемых 1 : 1 уединенных волн, наличие которых связано с существованием прямой, проходящей через начало координат и касающейся дисперсионной ветви при $k > 0$. Для медленных магнитозвуковых волн предполагается существование обобщенных уединенных волн. Отметим, что несовпадение точного решения (обобщенная уединенная волна) с приближенным (уединенная волна) по определению означает отсутствие сходимости приближения в виде ряда. Ниже будут описаны численные методики, корректные для нахождения симметричных уединенных волн в случае, когда прямая, соответствующая скорости волны, не пересекает дисперсионные ветви при $k > 0$, и для нахождения обобщенных уединенных волн в случае, когда имеется одно такое пересечение. Малости амплитуд волн при этом не предполагается. Под корректностью здесь понимается совпадение числа доступных варьируемых параметров с числом неизвестных, которые нужно приравнять к нулю для поиска решения. В случае наличия пересечения число варьируемых параметров меньше числа обнуляемых неизвестных, обычные и 1 : 1 уединенные волны могут быть только в специальных случаях.

Для полноты анализа солитонных решений исследуем альвеновские волны колебательного типа, описываемые дисперсионным соотношением (2.3). В зависимости от значений $\theta $ и $b$ возможно пересечение касательной в начале координат с быстрой магнитозвуковой ветвью при $\theta < {{\theta }_{{{\text{cam}}}}}$, $b < 1$, отсутствие пересечений при ${{\theta }_{{{\text{cam}}}}} < \theta < {{\theta }_{{{\text{caa}}}}}$ или ${{\theta }_{{{\text{cam}}}}} < \theta $, ${{b}^{2}}\rho < 1$, пересечение с альвеновской ветвью при $\theta > {{\theta }_{{{\text{caa}}}}}$ или $b > 1$. Здесь ${{\theta }_{{{\text{cam}}}}}$ и ${{\theta }_{{{\text{caa}}}}}$ – некоторые критические значения, соответствующие возникновению пересечения с быстрой магнитозвуковой ветвью и пересечения с альвеновской ветвью при $k > 0$ (в соответствии с введенной здесь системой обозначений, упомянутое выше ${{\theta }_{c}}$ можно было бы обозначить через ${{\theta }_{{{\text{cmm}}}}}$), определяемые формулами, получаемые исследованием соотношения (2.3):

3.2. Уравнения бегущих волн

Рассматриваются уравнения волн, бегущих со скоростью $V$, в недиссипативном случае

Подставим ${{({v}{\kern 1pt} ',w{\kern 1pt} ',B_{y}^{'},B_{x}^{'})}^{{\text{T}}}} = {\mathbf{k}}\exp \lambda x$ и найдем собственные векторы ${{{\mathbf{k}}}_{{1,2,3,4}}}$ и собственные значения ${{\lambda }_{{1,2,3,4}}}$. В зависимости от угла $\theta $ и параметра скорости $V$ может быть четыре действительных собственных значения: ${{\lambda }_{1}} = - {{\lambda }_{3}} > 0$, ${{\lambda }_{2}} = - {{\lambda }_{4}} > 0$, четыре комплексных: ${{\lambda }_{{1,2,3,4}}} = \pm r \pm is$, $r > 0$, два мнимых и два действительных: ${{\lambda }_{{1,3}}} = \pm r$, ${{\lambda }_{{2,4}}} = \pm is$. В последнем случае могут быть только решения типа обобщенной уединенной волны.

Метод 1. В случае действительных значений ищем классические (обычные) уединенные волны, используя начальные данные в виде

Метод 2. В случае комплексных значений ищем 1 : 1 уединенные волны и мультисолитоны, используя начальные данные вида

Эти волны имеют колебания, затухающие на бесконечности. Имеются базовая волна и мультисолитоны, которые можно интерпретировать как сумму базовых волн, сдвинутых на некоторые расстояния относительно друг друга. Структуры разрывов с излучением, т.е. переходы между однородным и периодическим состояниями, можно найти как пределы последовательностей 1 : 1 уединенных волн.

Метод 3. В случае, когда амплитуда периодической компоненты обобщенной уединенной волны мала по сравнению с амплитудой солитонной части, начальные данные берутся такими:

При использовании методов 1–3 решаем численно уравнения (3.1) и выбираем все значения ${{x}_{*}}$, при которых ${{B}_{z}} = 0$. Здесь используется метод Рунге–Кутты второго порядка. Методы высокого порядка более шумные, при уменьшении шага вычислительный хаос за счет машинного округления начинается раньше. Получаем ветви некоторых кривых на плоскости $(\varphi ,w)$. Затем, исследуя поточечные графики, выбираем значение $\varphi $ так, чтобы $w = 0$. В связи с большим количеством таких значений и мультисолитонов при применении методов 2 и 3 лучше воздержаться от автоматического, программного определения таких значений, поскольку анализ графиков расположения ветвей дает возможность систематического анализа мультисолитонных решений. Симметризуя/антисимметризуя решение относительно точки ${{x}_{*}}$ для $u$, $n$, ${v}$, ${{B}_{y}}{\text{/}}w$, ${{B}_{z}}$, получаем уединенную волну.

Метод 4. Периодические симметричные решения (однопериодные и двоякопериодические) ищем следующим образом. Находим состояние равновесия, выбираем симметризуемую возмущаемую величину, например, ${{B}_{y}} = {{B}_{{y0}}} + Z$. Выбираем ${{x}_{{*p}}}$ такое, что антисимметризуемая величина, например $w$, обращается в нуль $p$ раз. Далее варьируем другую величину, например, ${v} = {{{v}}_{0}} + Y$ так, чтобы вторая антисимметризуемая величина ${{B}_{z}}$ приняла значение нуль. Симметризуя/антисимметризуя решение относительно ${{x}_{{*p}}}$, находим периодическое решение на периоде. Заметим, что здесь симметричные и антисимметричные переменные могут быть определены и противоположным способом, наоборот, но при исследовании предельных солитонных решений предпочтительнее первый вариант. Назовем график $Z(Y)$ при заданном значении $p$ ветвью периодического решения. Ветви желательно изображать разным цветом. Одно и то же решение может отображаться при разных значениях $p$, ищем для него минимальное значение $p$, обозначим его через $q$. Для этого вначале строятся графики с большим значением $p$, а затем – с меньшим. По этому значению можно судить об отношении периодов волн двоякопериодического решения. Для уточнения строятся графики решений для различных неизвестных, а также проводится анализ расположения ветвей линеаризованных решений с тем, чтобы выявить закономерности и продолжить их на нелинейные. Обычные 1 : 1 и обобщенные уединенные волны ищутся как предельные решения для периодических волн (см. [8]). Обычная уединенная волна находится как предельное решение на конце одноволновой ветви. Таким способом можно находить и приближенные решения типа уединенных волн, если точного решения не существует, а также находить решения в особом случае, когда уединенная волна существует, несмотря на наличие действительных и мнимых собственных значений. В случае 1 : 1 уединенных волн выявляются спиральные ветви, ищутся предельные решения, соответствующие центру спиралей, ему соответствует гребень 1 : 1 уединенной волны. В случае обобщенных уединенных волн рассматриваются последовательности ветвей, сходящиеся к некоторому участку одноволновой ветви. Анализ числа пересечений прямой $V = \omega {\text{/}}k$ с дисперсионными ветвями в данном методе не обязателен, при двух пересечениях ожидаются двоякопериодические решения, при одном пересечении – однопериодные (двоякопериодические возможны), но при отсутствии пересечений те и другие тоже могут быть.

4.1. Быстрые магнитозвуковые уединенные волны

На фиг. 1 показано расположение областей решений различных типов на плоскости $(\cos \theta ,{{\mu }^{{1/2}}})$ при ${{b}^{2}} = 0.5$, $0 < \theta < 1.57 \approx \pi {\text{/}}2$ в случае быстрых магнитозвуковых волн. Использовались методы 1–3. Дополнительно те же кривые показаны при ${{b}^{2}} = 0.001$ пунктирной линией, т.е. фактически для холодной плазмы. Здесь 1 – область существования обычных уединенных волн, 2 – область существования 1 : 1 уединенных волн. В области 3 нет обычных или обобщенных уединенных волн, определяемых методами 1–3. Но обобщенные уединенные волны, определяемые методом 3, есть при $\mu < 0$, $\theta < {{\theta }_{c}}$. Выше кривой ${{L}_{1}}$ обычных уединенных волн нет. На кривой ${{L}_{3}}$ происходит переход от обычных уединенных волн к 1 : 1 уединенным волнам. Кривая ${{L}_{4}}$ соответствует появлению слабонелинейных 1 : 1 уединенных волн. Кривые ${{L}_{3}}$ и ${{L}_{4}}$ пересекаются при $\mu = 0$, $\theta = {{\theta }_{c}}$.

Фиг. 1

Кривые ${{L}_{1}}$ и ${{L}_{2}}$ соответствуют волне с острым гребнем. На фиг. 2а (${{b}^{2}} = 0.5$, $\theta = 1.55$, $\mu = 0.2675$) показана 1 : 1 уединенная волна, соответствующая кривой ${{L}_{2}}$. Заметим, что волны на воде обладают аналогичным свойством. Когда увеличивается амплитуда уединенной волны, то образуется волна с острым гребнем, уединенных волн с большими амплитудами нет, значит, волны большой амплитуды опрокидываются.

Фиг. 2

Было обнаружено, что при $\theta > {{\theta }_{c}}$ вид 1 : 1 уединенной волны, соответствующей области 2, подобен виду обычных уединенных волн. Для $(\theta ,\mu )$ вблизи ${{L}_{3}}$ в области 2 $\operatorname{Im} \lambda $ стремится к нулю, поэтому колебания не наблюдаемы из-за большой длины их волны в сравнении с длиной уединенной волны (обычно длина уединенной волны определяется на уровне половины ее амплитуды), ассоциированной со значением ${\text{Re}}\lambda $. Колебания экспоненциально убывают, и их амплитуда уменьшается при удалении от точки симметрии, они не видны. Для $(\theta ,\mu )$ вблизи ${{L}_{2}}$ амплитуда горба уединенной волны существенно больше амплитуды осцилляций, они также не наблюдаются. Для $\theta < {{\theta }_{c}}$ и $\mu $ чуть выше значения на ${{L}_{4}}$ 1 : 1 уединенная волна аналогична солитону огибающей нелинейного уравнения Шрёдингера. На кривой ${{L}_{4}}$ фазовая скорость волн совпадает с групповой. В случае $(\theta ,\mu )$ далеко от ${{L}_{4}}$ такое приближение может применяться только формально, график прогнозируемого решения близок к обычной уединенной волне, поскольку длина волны солитона огибающей мала по сравнению с длиной волны осцилляций.

Ниже на фиг. 2б показаны 1 : 1 уединенные волны возвышения (сплошная линия) в точке симметрии и понижения (штриховая линия), похожие на решения нелинейного уравнения Шрёдингера и переходящие в них при приближении к ${{L}_{4}}$; $\theta = 1.52$, $\mu = 0.16$. Анализ бифуркаций ветвей мультисолитонных решений показывает, что волна понижения является 1 : 1 бисолитоном. Это также легко видеть на фиг. 2б. В окрестности кривой ${{L}_{3}}$ число мультисолитонов при одном и том же значении $(\theta ,\mu )$ стремится к бесконечности, а график первичной 1 : 1 уединенной волны качественно не отличается от графика обычной уединенной волны. В окрестности кри-вой ${{L}_{4}}$ есть только две уединенные волны: повышения и понижения, аналогичные показанным на фиг. 2б. Отметим, что утверждения о числе уединенных волн в окрестности кривых ${{L}_{3}}$ и ${{L}_{4}}$ основаны на исследовании системы бегущих волн уравнения Кортевега–де Вриза с производной пятого порядка (см. [13]) (это уравнение является модельным уравнением для быстрых магнитозвуковых волн, см. [3]). Наличие двух волн в окрестности ${{L}_{4}}$ следует также из [4], где исследовались решения для ЭМГД методом нормальных форм, позволяющим утверждать, что иных решений нет.

На фиг. 2в–д показаны несколько 1 : 1 уединенных волн, одновременно существующих при одних и тех же значениях $\theta $ и $\mu $ из области 2 ($\theta = 1.55$, $\mu = 0.1$). Это 1-солитон (в), 2-солитон (г), 3-солитон (д), образующие начальные элементы последовательности, стремящейся к структуре разрыва с излучением.

Обобщенные уединенные волны – это двухпараметрические решения, параметрами служат амплитуды солитонной и периодической составляющей (в некоторых работах обобщенной уединенной волной называются волны с минимально возможной амплитудой периодической составляющей, а волны с произвольной амплитудой названы волнами с рябью, см. [4]). Численный анализ с помощью метода 4 показал, что для фиксированного $\mu $ амплитуда периодической компоненты $a$ может варьироваться в некотором интервале $({{a}_{{{\text{min}}}}},{{a}_{{{\text{max}}}}})$, ${{a}_{{{\text{max}}}}}$ соответствует чисто периодической волне. Есть синфазные и противофазные решения в том смысле, что в одном случае максимум волн периодической составляющей совпадает с максимумом солитонной компоненты, а в другом случае максимум солитонной компоненты совпадает с минимумом периодической составляющей. Эти понятия вводятся по аналогии с линейными волнами в результате исследования двоякопериодических волн (см. п. 4.2). При достижении минимальной амплитуды периодической составляющей синфазное и противофазное решения совпадают. Можно предполагать, что, как и в случае уравнения Кортевега–де Вриза с производной пятого порядка (см. [14]), ${{a}_{{{\text{min}}}}}$ экспоненциально мало по $\mu $. Обнаруживаются также обобщенные мультисолитоны. Ниже на фиг. 3 ($\theta = 1.52$, $\mu = - 0.1$) показаны двухсолитонные и пятисолитонные обобщенные уединенные волны, упорядоченного типа, т.е. с почти одинаковыми расстояниями между солитонными элементами, эти расстояния во всех решениях разные (анализ см. п. 4.2). Получены методом 3. Величина амплитуды периодической составляющей здесь равна $1.538{{a}_{{{\text{min}}}}}$. Проводилось исследование на поиск 2-солитонов с минимальным числом периодов короткой волны между ними (см. п. 4.2) путем вариации параметра $a$, при дальнейшем его увеличении больше сблизить их не удается.

Фиг. 3

Проблемы взаимодействия уединенных волн здесь не рассматриваются, понятия солитон и уединенная волна – синонимы.

Были проведены также расчеты решений уравнений (2.1), описывающие эволюцию локализованных начальных данных при $\theta > {{\theta }_{c}}$. Использовались данные в виде быстрой магнитозвуковой 1 : 1 уединенной волны, растянутой вдоль оси $x$ в 10 раз. Амплитуда была взята близкой к максимально допустимой. Использовалась численная схема с центральными разностями для пространственных переменных и аппроксимацией временных производных методом Рунге–Кутты четвертого порядка. Эта схема была исследована в [12], было показано, что она сама способна устранять опрокидывание магнитозвуковых волн за счет схемной дисперсии. В расчете со временем происходили рост амплитуды и распад на последовательность уединенных волн. Амплитуда первой волны цуга волн оказалась больше максимально допустимой, т.е. опрокидывание устранено численной схемой. Амплитуды других волн допустимые, часть из них со временем соответствует 1 : 1 уединенным волнам, а часть – обычным. Принципиальных отличий в поведении этих двух типов уединенных волн в случае эволюции локализованных начальных данных не было. При уменьшении амплитуды начальных данных первая волна имела допустимую амплитуду.

Отметим, что скорость первой, схемной волны была заметно больше скорости последующих волн и она начинала отделяться от них. Это один из способов визуально выявить опрокидывание волны при численных расчетах с использованием данной численной схемы, не делая расчеты с разным пространственным шагом (длина схемных волн коррелирует с пространственным шагом схемы). Поэтому при расчетах для систем с дисперсией задачи о распаде разрыва в случае расширяющихся структур солитонного типа при схемной коррекции опрокидывания может возникать огибающая волновых зон неестественного вида с уменьшением угла наклона вблизи границы за счет конкуренции схемной дисперсии и дисперсии уравнений, что также позволяет заподозрить опрокидывание.

4.2. Структуры разрывов быстрых магнитозвуковых волн

Основной задачей данной работы является анализ возможных бездиссипативных структур разрывов. Учитывая, что структуры разрывов можно получить как предельные последовательности уединенных волн, на фиг. 1 качественно можно ориентироваться и при оценке существования структур разрывов при условии, что правая часть этих структур в случае волн, бегущих вправо, ассоциирована с состоянием равновесия 1. Так, область 1 можно считать точной областью структур солитонного типа. Область 2 – приблизительно областью структур разрывов с излучением, но кривая ${{L}_{3}}$ определяет границу этой области точно. Структура с излучением возникает сразу в области выше кривой ${{L}_{3}}$ при $\theta > {{\theta }_{c}}$, поскольку при переходе через эту кривую возникает сразу бесконечно много 1 : 1 уединенных волн. В окрестности же кривой ${{L}_{4}}$ есть только две 1 : 1 уединенные волны, поэтому структура с излучением возникает при больших значениях $\mu $, чем на этой кривой. На фиг. 1 условно показана кривая ${{L}_{5}}$, ограничивающая область этих структур. Наличие таких структур подтверждается также расчетами задачи о распаде начального разрыва для исходных уравнений в частных производных, где эти структуры являются локальными элементами расширяющихся со временем бездиссипативных структур. В области 3, а также в области 2 вблизи кривой ${{L}_{4}}$ при расчетах исходных уравнений без диссипации возникает нестационарная хаотическая структура. При этом в случае включения диссипации в области 3 при не слишком больших значениях $\mu $ наблюдаются стационарные решения, которые можно интерпретировать как решения с внутренними структурами типа перехода между периодическим и двоякопериодическим состоянием.

При анализе методом 4 для заданного значения скорости разрыва можно рассматривать две равноценные точки равновесия, связанные соотношениями (2.2) (верно как в случае быстрого магнитозвукового разрыва, так и медленного). В связи с этим при $\theta < {{\theta }_{c}}$ и $\mu > 0$ можно выявить таким способом обобщенные быстрые магнитозвуковые уединенные волны и структуры разрывов с исходной точкой равновесия 1, ассоциированной с двухпериодными линейными волнами, а в случае $\mu < 0$ – с однопериодными. При использовании метода 3 непосредственно доступны только обобщенные уединенные волны, у которых подошва ассоциирована с исходной точкой равновесия 1. Используя (2.2), можно найти и вторую точку равновесия, применить к ней метод 3 и найти соответствующие решения при $\mu > 0$. Именно они представляют интерес, когда рассматриваются расширяющиеся со временем бездиссипативные структуры быстрых магнитозвуковых волн, бегущих вправо, если правая сторона ассоциируется с точкой равновесия 1. Заметим также, что ориентируясь на вторую точку равновесия, можно найти методами 1–3 обычные и 1 : 1 уединенные волны при $\mu < 0$. В области $\mu < 0$ можно построить кривые $L_{{1 - 4}}^{'}$, аналогичные ${{L}_{{1 - 4}}}$, ограничивающие области $1{\kern 1pt} '{\kern 1pt} - {\kern 1pt} 3{\kern 1pt} '$. Причем при малых значениях ${\text{|}}\mu {\kern 1pt} {\text{|}}$ их можно построить зеркальным отражением относительно оси $\theta $.

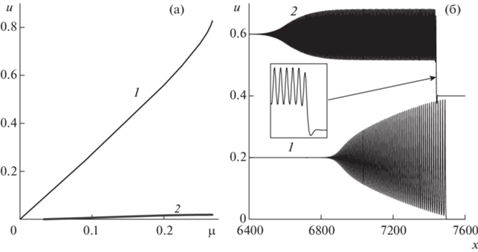
Ранее было установлено (см. [7]), что так называемая бездиссипативная структура разрыва с излучением (переход между однородным и периодическим состояниями) может быть найдена как предельное решение последовательности мультисолитонных решений при увеличении числа солитонов. Три мультисолитонных решения из этой последовательности (односолитонное, двухсолитонное и трехсолитонное) показаны на фиг. 2в–д. Графики на фиг. 3 соответствуют односолитонному и двухсолитонному решениям из этой последовательности. Нет существенной разницы для максимального значения $u$ для односолитонного, двухсолитонного и трехсолитонного решений. Нет также существенной разницы для минимального значения $u$ в области между гребнями в случае двухсолитонного решения с близко расположенными гребнями и трехсолитонного решения (см. фиг. 2г). На фиг. 4a показана зависимость от $\mu $ амплитуды на гребне волны (кривая 1) в случае обычной или 1 : 1 уединенной волны и амплитуда в центре симметрии (кривая 2) для двухсолитонного решения с близко расположенными гребнями (см. фиг. 2в,г), $\theta = 1.55 > {{\theta }_{c}}$. Поэтому, используя фиг. 4а, мы можем определить зависимость от $\mu $ амплитуды уединенной волны в солитонной структуре на начальном интервале значений $\mu $ и зависимость от $\mu $ для максимального (кривая 1) и минимального (кривая 2) значений $u$ для периодического состояния в случае структуры разрыва с излучением. Мы можем определить также максимальное значение $\mu $, при котором такое решение существует. На фиг. 4б показаны расширяющиеся со временем бездиссипативные структуры с локальной структурой с излучением на границе волновой зоны при $\theta = 1.55$ (кривая 1) и $\theta = 1.53$ (кривая 2, смещена по вертикали), $t = 2500$. Начальные данные брались в виде сглаженной ступеньки. В первом случае структура близка к солитонной, поскольку минимальное значение $u$ в периодическом состоянии, согласно фиг. 4а, невелико. Во втором случае четко виден однородный периодический участок и затухающие при увеличении $x$ колебания справа. Эти колебания хорошо заметны для 1 : 1 мультисолитонов при $\theta < {{\theta }_{c}}$, пределом последовательности которых является данная структура.

Фиг. 4

Как ясно из фиг. 1, структуры разрывов солитонного типа и с излучением существуют только для ограниченных значений $\mu $. Эти результаты соответствуют результатам работы [12], где было обнаружено, что из-за исчезновения дисперсии для коротких волн (${{\partial }^{2}}\omega {\text{/}}\partial {{k}^{2}} \to 0$ при $k \to \infty $) классическое решение рассматриваемых уравнений существует не при всех начальных данных, и может иметь место опрокидывание волны, требующее рассмотрения обобщенного решения или включения газодинамической или магнитной вязкостей.

В [8] детально исследовалось расположение ветвей периодических решений в случае уравнения Кортевега–де Вриза с производной пятого порядка, являющегося модельным для описания слабонелинейных быстрых магнитозвуковых волн вблизи ${{\theta }_{c}}$. Исследования для ЭМГД подтвердили, что расположение ветвей аналогично их расположению в [8]. На фиг. 5а показан пример расположения ветвей периодических решений для $\theta = 1.52$, $\mu = - 0.1$. Точки с $p = 1$ сделаны более жирными. Отрицательное значение $\mu $ взято для удобства применения метода 3 для получения обобщенных уединенных волн с малой амплитудой периодической компоненты, при положительном $\mu $ картина расположения ветвей аналогичная, только начало координат в другой точке равновесия. Решения в виде обобщенных уединенных волн при методе 4 получаются несколько смещенными относительно решений, получаемых методом 3 при одних и тех же значениях $\mu $ и $\theta $, состоянию 1 соответствуют гребни или впадины периодических решений, но при малых амплитудах периодической компоненты это не существенно. На ветви различного типа указывают стрелки с обозначениями. Из точки равновесия выходят эллипсообразная коротковолновая ($1S$) и длинноволновая ($1L$) ветви. Длинноволновая состоит из нескольких частей, ее пересекают ветви с рациональным соотношением длин волн (резонансные ветви). Ветви с целым отношением периодов обозначены по образцу $1{\text{/}}n{\kern 1pt} \pm $, $n$ – целое число, обозначающее отношение длин волн, знак плюс обозначает, что расположение волн синфазное, а минус – противофазное, $1{\text{/}}\infty {\kern 1pt} \pm $ – предельные ветви обобщенных уединенных волн. Длинноволновая ветвь может рваться при пересечении ее с ветвью с целым соотношением длин волн. При $\mu \to 0$ значение $n$ для первого разрыва ветви стремится к бесконечности. При увеличении ${\text{|}}\mu {\kern 1pt} {\text{|}}$, как и в случае уравнения Кортевега–де Вриза с производной пятого порядка (см. [8]), наступает момент, когда исчезает пересечение в точке равновесия $1L$ и $1S$ ветвей и возникают спиральные ветви, указывающие на наличие 1 : 1 уединенных волн.

Фиг. 5

Можно допустить, что существует переход (структура разрыва) между ветвями с целым отношением длин волн и коротковолновой ветвью. Тогда, если такой переход существует в точке разрыва ветви, то как в диссипативном, так и слабодиссипативном случае можно построить решение усредненных уравнений, описывающее решение с длинноволновой и коротковолновой волновыми зонами. При включении слабой, но конечной диссипации в расчетах задачи о распаде разрыва действительно можно наблюдать такие структуры внутри слабодиссипативной стационарной структуры разрыва при расчете уравнений в частных производных. Переход в таких решениях соответствует точке сочленения длинноволновой ветви с коротковолновой с целым отношением периодов, поскольку графики решений, соответствующие длинноволновой ветви вблизи точки перехода к резонансной ветви выглядят как двоякопериодические. Поэтому внутри стационарной слабодиссипативной структуры может возникать бездиссипативная структура типа перехода между периодическим и двоякопериодическим состояними с минимальным значением амплитуды периодического состояния. По мере уменьшения ${\text{|}}\mu {\kern 1pt} {\text{|}}$ отношение периодов волн в двоякопериодическом состоянии увеличивается. При этом в зависимости от начальных данных могут наблюдаться структуры с разным отношением периодов. В случае отсутствия диссипации наблюдается решение стохастического типа. При уменьшении диссипации может наблюдаться промежуточное нестационарное решение с периодическими колебаниями.

Объясним, в чем причина такого поведения на примере расположения ветвей, показанного на фиг. 5а. Длинноволновая ветвь, исходящая из точки равновесия, рвется при резонансе $1{\text{/}}4{\kern 1pt} - $, и переходит в резонансную противофазную двухволновую ветвь. Ветвь называется неустойчивой, если при небольшом возмущении начальных данных возможен значительный уход от периодического или двоякопериодического решений. Переход на коротковолновую ветвь возможен только для неустойчивых ветвей. Синфазная ветвь с резонансом $1{\text{/}}4{\kern 1pt} - $ оказалась неустойчивой, $1{\text{/}}4{\kern 1pt} + $ – устойчивой. Противофазная ветвь $1{\text{/}}5{\kern 1pt} - $ неустойчивая, как и более удаленные ветви, но уединенных волн с участком, как-то аппроксимирующим волны этой ветви, обнаружено не было. Для синфазной ветви $1{\text{/}}5{\kern 1pt} + $ и противофазной $1{\text{/6}}{\kern 1pt} - $ выявлен только 2-солитон (фиг. 4а, сплошная и штриховая линии), у которого область между гребнями аппроксимирует волны этой ветви. А для синфазной $1{\text{/6}}{\kern 1pt} + $ ветви и противофазной $1{\text{/}}7{\kern 1pt} - $ выявлены уже 5-солитоны (2-, 3-, 4-солитоны тоже есть), аппроксимирующие структуры перехода между периодическим и двоякопериодическим состояниями (фиг. 4б, сплошная и штриховая линии). Можно предположить, что существуют и точные решения для соответствующих структур разрывов. Таким образом, наличие разрыва длинноволновой ветви не согласовано с наличием соответствующей структуры перехода между длинноволновой и коротковолновой зонами. Наличие диссипации компенсирует это, возникает решение, в котором такая структура может рассматриваться лишь как приближенная. Соответственно в чисто бездиссипативном случае построить решение усредненных уравнений невозможно и возникает нестационарное решение. На фиг. 6б показаны графики $u$ (кривая 1) и ${{B}_{z}}$ (кривая 2, смещена по вертикали) для стационарного решения (2.1) при $\mu = 0.1$ и начальными данными, согласно (2.2), с использованием магнитной вязкости ${{\nu }_{m}} = 0.02$. Решение получено методом установления: скорость по обе стороны разрыва в начальных данных уменьшалась на величину $V$, на фиг. 5б скорость $u$ увеличена на $V$ по сравнению с расчетной. Соотношение длин волн на внутренней структуре разрыва здесь оценивается как $1{\text{/}}5{\kern 1pt} - $. При меньших значениях вязкости становятся заметны периодические колебания амплитуды волны слева. Соотношение длин волн в нестационарном бездиссипативном решении близко к $1{\text{/}}6{\kern 1pt} - $.

Фиг. 6

На фиг. 6 показан пример возникновения для ветви $1{\text{/}}4{\kern 1pt} - $ уединенной волны огибающей фазовых колебаний двухволнового решения как результат развития неустойчивости, но возможен и уход к бесконечным значениям величин. Можно предположить, что существует и точное аналогичное солитонное решение (не солитон огибающей) подобно тому, как в окрестности кривой ${{L}_{4}}$ есть точные решения в виде 1 : 1 солитонов, приближенно описываемые как уединенные волны огибающей нелинейного уравнения Шрёдингера. Отметим, что уединенные волны огибающей двухволновых решений с фазовыми колебаниями для обыкновенных дифференциальных уравнений рассматривались ранее (см. [15]). В [16] для исследования резонансных двоякопериодических решений применялся метод усреднения, позволяющий утверждать, что среди таких решений возможны и структуры перехода между одним значением фазового сдвига к другому значению (среди решений усредненных уравнений есть переходы от одного гиперболического состояния равновесия к другому). Можно в принципе допустить по аналогии с обычными солитонными расширяющимися структурами и существование расширяющихся нестационарных структур фазовых колебаний солитонного типа или аналогичных стационарных слабодиссипативных решений.

4.3. Медленные магнитозвуковые и альвеновские колебательные волны

Для медленных магнитозвуковых волн можно допустить наличие обобщенных уединенных волн и структур разрывов типа переходов между периодическим и двоякопериодическим состояниями. В расчетах уравнений в частных производных они не наблюдались (см. [12]), не было также излучения коротких колебательных альвеновских волн на медленных магнитозвуковых разрывах. В случае медленных магнитозвуковых волн метод 3 показывает отсутствие обобщенных уединенных волн. Для уточнения было предпринято исследование методом 4. В процессе исследования проводились расчеты с постепенным увеличением значения $\mu $, $\mu > 0$. Если имеется пересечение прямой, соответствующей фазовой скорости, с альвеновской дисперсионной ветвью, то выявляется наличие одноволновой ветви альвеновских колебательных волн, проходящей через точку равновесия. Амплитуда этих волн ограничена. На концах ветви не было обнаружено солитонных решений или заострения гребней волн. Тем не менее альвеновские колебательные волны нелинейные, поскольку ветвь все же отличается от прямой линии. Кроме того, имеются еще комбинированные двухволновые ветви, соответствующие резонансу медленных магнитозвуковых и альвеновских колебательных волн. Согласно проведенному исследованию, ветвь медленных магнитозвуковых волн практически доходит до точки равновесия при умеренных значениях $\mu $, поэтому можно получить решение, почти неотличимое от солитонного. При увеличении $\mu $ выявляется его критическое значение (${{\mu }_{*}} \approx 0.73$ при $\theta = 1.525$), при котором медленных магнитозвуковых волн нет, остается только альвеновская ветвь. Только при значениях $\mu $, близких к критическому значению, становится заметно, что вблизи точки равновесия есть только колебательная альвеновская ветвь, и одноволновая медленная магнитозвуковая ветвь отделена от альвеновской, а точке на медленной магнитозвуковой ветви, максимально приближенной к точке равновесия, соответствует двоякопериодическое решение, похожее на обобщенную уединенную волну. На фиг. 7а показаны соответствующие решения при $\mu = 0.65$ (кривая 1) и $\mu = 0.72$ (кривая 2), $\theta = 1.525$. Кривая 2 на самом деле состоит из множества коротких альвеновских колебаний, сливающихся в жирную линию, фактически видны только огибающие сверху и снизу. Каждое альвеновское колебание детально рассчитывалось, на него приходится порядка 150–300 пространственных шагов методом Рунге–Кутты второго порядка. При рассмотрении графика величины $w$ (на графиках ${v}$ и $w$ колебаний практически нет) четко видно, что при $\mu = 0.72$ это не уединенная, а периодическая волна. Если допустить, что и при малых значениях $\mu $ медленная магнитозвуковая ветвь и резонансные ветви отделены от точки равновесия, то точного решения в виде обычной или обобщенной уединенной волны при малых значениях $\mu $ нет, если же обобщенная уединенных волн существует, то минимальная амплитуда ее периодической компоненты настолько мала, что ее невозможно определить численно.

Фиг. 7

Отметим также, что на некотором диапазоне значений $\mu $, помимо приближенного медленного магнитозвукового солитонного решения, выявляется еще одно приближенное солитонное решение с нетипичным профилем (фиг. 8 б), $\mu = 0.575$ (при меньших значениях $\mu $ такого решения нет, при увеличении $\mu $ решение принимает вид двоякопериодической волны, как и на фиг. 8a , кривая 2) на графике ${{B}_{y}}$ два максимума и один минимум (кривая 1), график величины $u$ (кривая 2) имеет вид солитон–яма, а не солитон–горб, как на фиг. 8 а. Наличие двух солитонных решений с одними состоянием у подошвы одновременно возможно, если есть три точки равновесия, как, например, у модифицированного уравнения Кортевега–де Вриза с кубической нелинейностью (см. [7]). В связи с тем, что такое решение наблюдалось только при большой нелинейности, соотнести его с какими-либо волнами, описываемыми линейным дисперсионным соотношением, невозможно, судя по длине волны, оно скорее имеет отношение к медленным магнитозвуковым волнам. Дополнительным аргументом в пользу этого утверждения может служить то, что анализ бифуркаций решений (2.2) при изменении $\mu $ показывает, что эта уединенная волна связана с состоянием равновесия, ответвляющимся при $\mu \approx 0.875$ от состояния, ассоциированного с медленными магнитозвуковыми разрывами в МГД. Вообще же выявляется до четырех состояний равновесия системы (3.1), не всегда они физически реальные, бывают и с $n < 0$.

Эти исследования показывают, что малое значение минимальной амплитуды коротковолновой периодической составляющей не обязательно связано с малой амплитудой солитонной или длинноволновой компоненты. Это связано с малым отношением длин. Длину уединенной волны можно определить по уровню половины от амплитуды. Но приближение к значениям амплитуды, при которых могло бы быть заострение гребня уединенной волны, приводит к росту коротковолновой составляющей в разложении Фурье для медленной магнитозвуковой компоненты и соответственно к увеличению минимальной амплитуды альвеновской составляющей.

В случае дальнейшего увеличения скорости, $V > {{V}_{a}} = \cos \theta $, и возникновения двукратного пересечения при $k > 0$ прямой, соответствующей фазовой скорости, с альвеновской дисперсионной ветвью, выявляются коротковолновая и длинноволновая, а также двоякопериодические резонансные ветви альвеновских колебательных волн, их амплитуда ограничена. После прохождения значения $V$, где $\omega {\text{/}}k = \partial \omega {\text{/}}\partial k$ при $k > 0$, альвеновские волны исчезают.