Журнал вычислительной математики и математической физики, 2022, T. 62, № 12, стр. 1943-1980

1. ВВЕДЕНИЕ

1.1. Вводные замечания

Как известно, основной трудностью, возникающей при использовании интеграла Кристоффеля–Шварца для построения конформного отображения канонической области на многоугольник, является проблема параметров этого интеграла (об этом см., например, [1]–[8]).

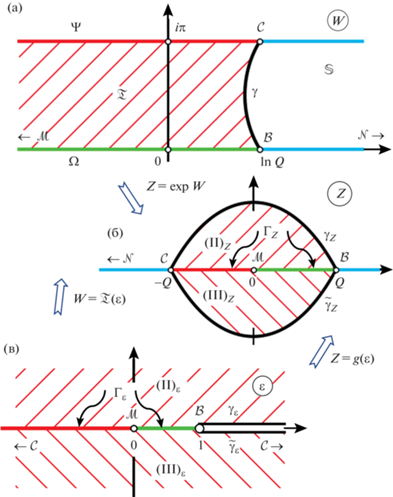
Для рассматриваемого в работе отображения $w = f(\zeta )$ полуплоскости $\mathbb{H}: = \{ \operatorname{Im} \zeta > 0\} $ на симметричную $L$-образную область (на фиг. 1 заштриховано дополнение к областям) с соответствием точек

данную проблему, по существу, составляет нахождение только одного параметра – прообраза ${{\zeta }_{3}}$ вершины ${{w}_{3}}$, обозначенного через $\tau $. Прообразы остальных вершин, фигурирующие в интеграле Кристоффеля–Шварца для рассматриваемой области $\mathbb{L}(\beta ,A,h)$, определяемой параметрами заданы так, как показано на фиг. 1. Такое отображение, эквивалентное отображению первого квадранта $\{ \zeta :\operatorname{Re} \zeta > 0,\;\operatorname{Im} \zeta > 0\} $ на четырехугольник $\mathbb{L}(\beta ,A,h) \cap \{ {\text{Im}}\,w > 0\} $ с переводом точек $0,\;1,\;\infty $ соответственно в вершины ${{w}_{1}},\;{{w}_{2}},\;{{w}_{4}}$ существует и единственно.

Уравнение, связывающее величину $\tau $ с геометрическими параметрами области $\mathbb{L}(\beta ,A,h)$, составляемое, как обычно [2], [3], на основе (осуществляемого отображением $f$) соответствия между точками плоскостей $\zeta $ и $w$, записывается в виде

с подстановкой сюда отображения $f(\zeta )$, выраженного через интеграл Кристоффеля–Шварца. После некоторых преобразований (см. п. 2.5) и введения вместо $\tau $ и относительной длины (см. фиг. 1а) новых переменных – соответственно $\varepsilon $ и $W$ – по формулам где $Q$ явным образом определяется через $\beta $ (см. п. 2.4), уравнение (3) преобразуется к виду в котором $\mathcal{F}$ выражается через гипергеометрическую функцию Гаусса (об этой специальной функции см. [9], [10], а о более общих гипергеометрических функциях см. [11]). Величину $\varepsilon $ будем называть модифицированным прообразом.

Замечательный факт, служащий ключом к получению аналитического решения уравнения (6), состоит в том, что если переменным $\varepsilon $ и $W$ придавать комплексные значения, то функция $W = \mathcal{F}(\varepsilon )$ будет осуществлять конформное отображение полуплоскости $\mathbb{H}$ на некоторый круговой треугольник (этот факт для интеграла Кристоффеля–Шварца, соответствующего произвольному четырехугольнику, установлен в [3]). Для нашего случая такой круговой треугольник на плоскости $W$, обозначенный через $\mathfrak{T}$, на фиг. 2а заштрихован.

Поскольку область $\mathfrak{T}$, очевидно, представляет собой деформированную полосу

а отображение полуплоскости на полосу осуществляет $\ln \varepsilon $, то согласно результатам о конформном отображении сингулярно деформированных областей [12], [13], отображение $W = \mathcal{F}(\varepsilon )$ может быть представлено в виде суперпозиции логарифма и ряда Тейлора: где коэффициенты ${{\lambda }_{k}}$ определяются только через показатель $\beta $ по явным формулам, получаемым из упомянутого выше представления отображения $\mathcal{F}(\varepsilon )$ через гипергеометрическую функцию. Обращая зависимость (8), получаем для обратного отображения $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ ряд по натуральным степеням переменной ${{e}^{W}}$. Записывая эту переменную с помощью второй формулы (5) через $Q$ и параметр в виде ${{e}^{W}} = Q\delta $, получаем функцию $\varepsilon = G(\delta ): = {{\mathcal{F}}^{{ - 1}}} \circ \ln (Q\delta )$, выражающую искомый модифицированный прообраз $\varepsilon $ через геометрические параметры области $\mathbb{L}(\beta ,A,h)$ в виде следующего ряда: по степеням параметра $\delta $ с коэффициентами ${{B}_{k}}$, зависящими только от показателя $\beta $ (так называют величину угла, деленную на $\pi $).

Параметр $\delta $, как видно из его определения (9), быстро убывает при возрастании величины $A{\text{/}}h$ – относительной длины полки области $\mathbb{L}(\beta ,A,h)$; полкой называют вписанный в область $\mathbb{L}(\beta ,A,h)$ прямоугольник с вершинами ${{w}_{2}}$, ${{w}_{3}}$, ${{w}_{4}}$ и четвертой, лежащей на стороне , см. фиг. 1а. В разд. 2 установлено, что ряд (10) сходится при всех значениях $\beta \in (1,2)$ и всех значениях относительной длины $A{\text{/}}h \in (0,\infty )$, а его вещественные коэффициенты ${{B}_{k}}$ выражаются через $\beta $ по явным формулам.

Это и дает аналитическое решение проблемы параметров для рассматриваемого интеграла Кристоффеля–Шварца. Такой способ отличается от известных подходов, предлагающих находить требуемые параметры либо из нелинейных трансцендентных уравнений, аналогичных (6), применяя к ним итерационные методы типа Ньютона [2]–[8], [14]–[16], либо из системы нелинейных обыкновенных дифференциальных уравнений [17]–[19] с помощью численных методов.

1.2. Проблема кроудинга

С проблемой параметров интеграла Кристоффеля–Шварца тесно связано явление кроудинга (от английского “to crowd” – толпиться, скучиваться), т.е. чрезвычайно близкое расположение соседних прообразов. Его исследованию и преодолению вызываемых им вычислительных трудностей посвящены многие работы (см., например, [5]–[8], [11], [15], [20]–[24] и приведенную там библиографию).

Для отображения $w = f(\zeta )$, определенного в п. 1.1, это явление заключается в том, что при возрастании относительной длины $A{\text{/}}h$ полки резко сокращается расстояние $\tau - 1$ между прообразами ${{\zeta }_{3}}$ и ${{\zeta }_{2}}$ (см. фиг. 1б). Этот факт находит отражение в виде следующей асимптотики:

согласующейся с (10) и первой формулой (5). Здесь параметр $\delta $, определяемый формулой (9), быстро уменьшается с ростом относительной длины $A{\text{/}}h$; действительно, $\delta = 4.32 \times {{10}^{{ - 2}}}$ при $A = h$ и $\delta = 1.51 \times {{10}^{{ - 7}}}$ при $A = 5h$, а зависимость асимптотики (11) от показателя входящего угла β осуществляется через параметр $Q$, значение которого для наиболее часто встречающегося показателя $\beta = 3{\text{/}}2$ составляет $Q = 6.65$.

Если же рассмотреть отображение $w = {{f}_{\mathbb{U}}}(\xi )$ другой канонической области, единичного круга $\mathbb{U}: = \{ {\kern 1pt} {\text{|}}\xi {\kern 1pt} {\text{|}} < 1\} $, на область $\mathbb{L}(\beta ,A,h)$ с однозначно определяющей его нормировкой (см. фиг. 3б, 3в),

(${{w}_{0}}$ лежит на середине отрезка ), то для такого отображения кроудинг возникает не только при увеличении, но и при укорочении относительной длины $A{\text{/}}h$. Последний проявляется в быстром приближении прообраза ${{\xi }_{5}}: = f_{\mathbb{U}}^{{ - 1}}({{w}_{5}}) = {{e}^{{i\theta }}}$ к прообразу ${{\xi }_{4}}: = f_{\mathbb{U}}^{{ - 1}}({{w}_{4}}) = 1$ при $A{\text{/}}h \to 0$ (одновременно симметрично приближается к точке ${{\xi }_{4}}$ и прообраз ${{\xi }_{3}} = {{e}^{{ - i\theta }}}$), что описывается следующей асимптотикой для углового расстояния $\theta $ между ${{\xi }_{5}}$ (или ${{\xi }_{3}}$) и прообразом ${{\xi }_{4}}$, см. фиг. 3б: выражение для фигурирующего здесь коэффициента ${{\mathcal{P}}_{1}}$, зависящего только от $\beta $, дано в разд. 4. Его значение для наиболее часто встречающегося показателя $\beta = 3{\text{/}}2$ составляет ${{\mathcal{P}}_{1}} = 9.5785359$.

1.3. Численная реализация

В работе осуществлена численная реализация отображения полуплоскости на $L$-образную область, т.е. ${{\widetilde f}_{\mathbb{H}}}:\mathbb{H}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{L}(\beta ,A,h)$, с модифицированной по сравнению с приведенной в п. 1.1 нормировкой:

где точки ${{w}_{0}}$, ${{w}_{6}}$, ${{w}_{\infty }}$ указаны на фиг. 4. Результаты численной реализации построенного отображения ${{\widetilde f}_{\mathbb{H}}}(\zeta )$ представлены в виде образа декартовой сетки полуплоскости, изображенного на фиг. 4; более подробный вид фрагмента этого образа в окрестности вершины входящего угла дан на фиг. 5.

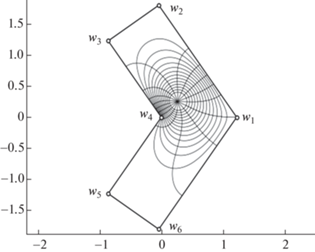
Построено также отображение круга на $L$-образную область, т.е. ${{\widetilde f}_{\mathbb{U}}}:\mathbb{U}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{L}(\beta ,A,h)$, переводящее центр круга $\xi = 0$ в ${{w}_{0}}$, а граничную точку $\xi = 1$ в ${{w}_{1}}$. На фиг. 6 представлена численная реализация этого отображения в виде образа полярной сетки для случая несимметричного расположения точки ${{w}_{0}}$. Сама полярная сетка в $\mathbb{U}$ изображена на фиг. 7.

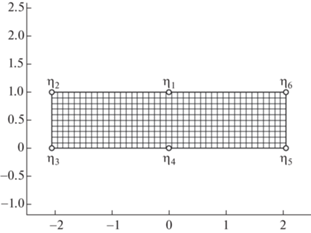
В работе рассмотрено отображение $w = {{f}_{\mathbb{P}}}(\eta )$ еще одной области, прямоугольника

на область $\mathbb{L}(\beta ,A,h)$ со следующим соответствием граничных точек (легко усматриваемым из фиг. 3а, 3в): где ${{w}_{k}}$ – вершины шестиугольника $\mathbb{L}(\beta ,A,h)$. При этом ширина полки (как и в других примерах) полагалась равной $h = 1$, а заранее неизвестная длина $A$ полки $L$-образной области находилась из трансцендентного уравнения, указанного в разд. 4. Численная реализация этого отображения продемонстрирована на фиг. 8 в виде образа декартовой сетки прямоугольника, изображенной на фиг. 9; более подробный вид фрагмента этого образа в окрестности вершины входящего угла дан на фиг. 10.

Развернутое описание численных результатов приведено в разд. 4.

Необходимо отметить, что, в отличие от традиционного подхода (как, например, в [5]–[8], [16], [22] для вычисления интеграла Кристоффеля–Шварца в настоящей работе не использовались квадратурные формулы. Расчет этого интеграла осуществлялся на основе полученного для него набора разложений (по степеням некоторых функций) вблизи некоторых граничных точек или отрезков границы. Коэффициенты разложений выписаны явно, а сами разложения допускают обращение, что дает представления для обратных отображений вблизи некоторых вершин многоугольника и торцов его полок. При этом множества сходимости представлений для отображения полуплоскости на многоугольник покрывают в совокупности замыкание полуплоскости, а множества сходимости представлений для обратного отображения покрывают замыкание всего многоугольника.

1.4. Заключительные замечания

Некоторые использованные в работе подходы и отдельные результаты были в краткой форме изложены в работах [23], [25] с приложением к проблемам физики плазмы, а также в работах [26]–[28], где они были применены – в сочетании с аналитическим методом Треффца [29], [30] – к решению задачи о кручении призматических стержней с полигональным поперечным сечением, включая получение явных аналитичнских формул для коэффициентов интенсивности во входящих углах сечения.

Следует отметить, что развернутые исследования вычислительных аспектов конформного отображения многоугольников продолжаются, в том числе и в связи с расширяющимся кругом их приложений к различным проблемам прикладной и вычислительной математики, механики и других преметных областей [24], [31]–[36].

2. ИНТЕГРАЛ КРИСТОФФЕЛЯ–ШВАРЦА И ЕГО ПАРАМЕТРЫ

2.1. Отображение на L-образную область

Рассматриваемая $L$-образная область $\mathbb{L}(\beta ,A,h)$ задается на комплексной плоскости $w$ как симметричный (относительно вещественной оси) шестиугольник, изображенный на фиг. 1а, с вершинами

Углы в вершинах ${{w}_{1}}$ и ${{w}_{4}}$ равны соответственно $\pi (2 - \beta )$ и $\pi \beta $, где показатель $\beta $ входящего угла рассматриваемой области подчинен включению а в остальных вершинах углы прямые.

Конформное отображение $w = f(\zeta )$ верхней полуплоскости $\mathbb{H}: = \{ {\text{Im}}\,\zeta > 0\} $ на область $\mathbb{L}(\beta ,A,h)$, которое строится в работе, подчинено нормировке (1), где прообразы ${{\zeta }_{k}}$ вершин ${{w}_{k}}$ указаны на фиг. 1, причем прообраз $\tau $ вершины ${{w}_{3}}$ заранее неизвестен (это отмечалось в п. 1.1); согласно принципу соответствия границ [37], он удовлетворяет неравенству

Указанная нормировка отображения $w = f(\zeta )$ с учетом симметричности области, принципа симметрии Римана–Шварца [37] и следующего из него равенства обеспечивает существование и единственность этого отображения.

В соответствии с теорией конформного отображения многоугольников [3], [6], [37] записываем рассматриваемое отображение в виде интеграла Кристоффеля–Шварца

где, кроме прообраза $\tau $, неизвестным и подлежащим нахождению является еще коэффициент $\mathcal{K} > 0$.

2.2. Параметры отображения

Для вычисления величин $\tau $ и $\mathcal{K}$ составим с помощью традиционного подхода (изложенного, например, в [2]–[4], [6], [37]) систему уравнений, приравнивая заданные стороны многоугольника $\mathbb{L}(\beta ,A,h)$, рассматриваемые как векторы, их выражениям через интеграл (20). Для сторон и имеем (порядок букв в обозначении граничных дуг соответствует такому направлению обхода области, когда она остается слева):

Подставляя в (21), (22) представление (20) для $f(\zeta )$, получаем систему Проведя в первом из этих интегралов замену переменной ${{x}^{2}} = t$, а во втором – замену ${{x}^{2}} = 1 + ({{\tau }^{2}} - 1)t$, $t \in [0,1]$, и воспользовавшись интегральным представлением Эйлера [9] для гипергеометрической функции Гаусса $F(a,b;c;z)$, выразим через нее интегралы в системе (23). В результате она приобретет вид Перейдем далее вместо $\tau $ к переменной а для гипергеометрической функции в уравнении (26) поменяем местами первый и второй параметры (что допустимо), а также выполним аналитическое продолжение функции Гаусса по формуле (6) из [9, с. 116], имеющей вид: Тогда система (25), (26) переписывается следующим образом: а из неравенства (18) находим, что областью определения искомого прообраза $\varepsilon $ является интервал

Деля левые части уравнений (29), (30) друг на друга, и учитывая известное равенство ${{\Gamma }^{2}}\left( {\frac{1}{2}} \right) = \pi $, получим уравнение, содержащее только одну искомую величину $\varepsilon $; после умножения на $( - 1)$ оно примет вид:

Если решение $\varepsilon $ этого уравнения найдено, то прообраз $\tau $ находится по формуле следующей из равенства (27), а второй неизвестный параметр интеграла (20) – величина $\mathcal{K}$ – по формуле легко следующей из равенства (27) и уравнения (30).

Таким образом, проблему параметров интеграла Кристоффеля–Шварца для рассматриваемого отображения $w = f(\zeta )$, как это и говорилось в п. 1.1, по существу, составляет получение только одного параметра – прообраза $\tau $, что в силу (27) эквивалентно нахождению величины $\varepsilon $.

2.3. Преобразование функции Гаусса

Проведем преобразования уравнения (32) с помощью известных положений теории гипергеометрической функции Гаусса, изложенных, например, в [9], [10].

Заметим, что функции $F(a,b;c;z)$ и $F(a,\;b;a + b + 1 - c;1 - z)$ также называют решениями Куммера ${{u}_{1}}(z)$ и ${{u}_{2}}(z)$ гипергеометрического уравнения

или рядами Куммера (они линейно независимы).

Принимая функцию Гаусса в знаменателе левой части (32) в качестве ${{u}_{1}}(\varepsilon )$, а функцию Гаусса в числителе – в качестве ${{u}_{2}}(\varepsilon )$, видим, что значения параметров $a$, $b$, $c$ в нашем случае суть

Так как функция ${{u}_{1}}(\varepsilon )$ отвечает условию $c\not { = }0, - 1, - 2...$, то она с учетом (36) представляется в окрестности точки $\varepsilon = 0$ в виде гипергеометрического ряда где ${{(a)}_{k}}$ – символ Похгаммера [9], выражаемый в виде произведений или через гамма-функцию $\Gamma (a)$ по формуле ${{(a)}_{k}}: = \Gamma (a + k){\text{/}}\Gamma (a)$.

Чтобы найти в окрестности той же точки $\varepsilon = 0$ аналогичное представление для функции ${{u}_{2}}(\varepsilon )$, фигурирующей в числителе (32), учтем, что для нее имеет место логарифмический случай (поскольку у нее третий параметр равен сумме первых двух), и воспользуемся формулой аналитического продолжения функции $F\left( {a,b;a + b;z} \right)$ в окрестность точки $z = 1$, т.е. формулой (14) из [9], с. 117. После подстановки в эту формулу значений параметров $a$ и $b$ из (36) и замены $z = 1 - \varepsilon $ получаем искомое представление для ${{u}_{2}}(\varepsilon )$ в окрестности начала координат:

где берется ветвь логарифма $\ln \varepsilon $, принимающая вещественные значения при положительных значениях аргумента $\varepsilon $, т.е. Коэффициенты ${{q}_{k}}$ в формуле (38) определяются через логарифмическую производную $\psi (\alpha ) = \Gamma {\kern 1pt} '(\alpha ){\text{/}}\Gamma (\alpha )$ гамма-функции следующим образом: В частности, коэффициент ${{q}_{0}}$ дается равенством отметим, что при $\beta = 3{\text{/}}2$ он составляет ${{q}_{0}} = \pi {\text{/}}2 + 5\ln 2$. Остальные ${{q}_{k}}$, соответствующие $k = 1,2...$, могут быть вычислены с помощью (41) и рекуррентных соотношений легко следующих из равенства $\psi (z + 1) = \psi (z) + \frac{1}{z}$ для пси-функции (см. [9]).

Заменяя в числителе уравнения (32) функцию Гаусса на ${{u}_{2}}(\varepsilon )$ из (38), а в знаменателе – на ${{u}_{1}}(\varepsilon )$ из (37), прибавляя к обеим частям уравнения величину ${{q}_{0}}$ и используя соотношения для пси-функции из [9]:

где ${\mathbf{c}} = - \psi (1) = 0.57721 \ldots $ – постоянная Эйлера, приводим уравнение (32) к виду

2.4. Проблема параметров и отображение кругового треугольника

Уравнение (43) определяет некоторую связь между модифицированным прообразом $\varepsilon $ и геометрическими параметрами $\beta $ и $\frac{A}{h}$ области $\mathbb{L}(\beta ,A,h)$. Для выяснения смысла этой связи как конформного отображения, о чем говорилось в п. 1.1, будем использовать некоторые известные результаты теории аналитических функций, приведенные в [9], [38], [39].

Как установил Г.А. Шварц [40], отношение $\Phi (z)$ двух линейно независимых решений гипергеометрического уравнения (35), например, ${{u}_{1}}(z){\text{/}}{{u}_{2}}(z)$, – или комбинация этого отношения с любой дробно-линейной функцией – осуществляет конформное отображение полуплоскости $\mathbb{H}$ на некоторый круговой треугольник. Его вершины представляют собой образы при отображении $\Phi (z)$ особых точек $0,1,\infty $ уравнения (35), а углы в этих вершинах (с точностью до знака) соответственно равны $\pi {{\alpha }_{1}}$, $\pi {{\alpha }_{2}}$, $\pi {{\alpha }_{3}}$, где

Сама же отображающая функция $\Phi (z)$ удовлетворяет уравнению Шварца Его левая часть, называемая шварцианом и обозначаемая через $\{ \Phi ,z\} $, как известно, инвариантна относительно дробно-линейных преобразований, т.е. (${{\sigma }_{l}},l = \overline {1,4} $, – постоянные). Правая же часть уравнения (45) не изменяется при замене некоторых ${{\alpha }_{m}}$ на $ - {{\alpha }_{m}}$, поскольку они входят в это уравнение в квадратах. Знаки показателей ${{\alpha }_{m}}$ выбираются так, чтобы в конечных вершинах углы были неотрицательны, а в бесконечных – неположительны.

Возвращаясь к рассматриваемому уравнению (43), обозначим его левую часть через

а правую – через где величина $\delta $ определена по формуле (9), а величина $Q$ – по следующей формуле: где, напомним, через $\psi (x)$ обозначена пси-функция, а через ${\mathbf{c}}$ – постоянная Эйлера. Величина $Q$ зависит только от показателя $\beta $, причем при его изменении в заданном диапазоне (2), т.е. при возрастании $\beta $ от $1$ до $2$, величина $Q$ монотонно убывает от $16$ до $4$; отметим, что для важного случая $\beta = 3{\text{/}}2$ она составляет $Q = \exp (5\ln 2 - \pi {\text{/}}2) = 6.652146443 \ldots $.

Таким образом, уравнение (43) переписывается в виде $W = \mathcal{F}(\varepsilon )$. Для отыскания его решения будем (как уже говорилось выше) придавать входящим в него переменным $\varepsilon $ и $W$ комплексные значения, а функцию $\mathcal{F}(\varepsilon )$ рассматривать как конформное отображение.

Обратимся для этого к выражению (47) для $\mathcal{F}$. Фигурирующие в нем ряды Куммера ${{u}_{1}}(\varepsilon )$ и ${{u}_{2}}(\varepsilon )$, определяемые соответственно равенствами (37) и (38), составляют, как известно, пару линейно независимых решений гипергеометрического уравнения (35) с подставленными в него значениями параметров (36) и заменой $z$ на $\varepsilon $. Отсюда с учетом изложенного в данном пункте материала следует, что функция $W = \mathcal{F}(\varepsilon )$, отличающаяся от отношения ${{u}_{1}}(\varepsilon ){\text{/}}{{u}_{2}}(\varepsilon )$, как видно из (47), лишь на дробно-линейное преобразование, осуществляет конформное отображение полуплоскости $\mathbb{H}$ на некоторый круговой треугольник $\mathfrak{T}$, расположенный на плоскости $W$; его вид установлен в п. 2.5.

Вершины этого треугольника, являющиеся образами – при рассматриваемом отображении $W = \mathcal{F}(\varepsilon )$ – особых точек $\varepsilon = 0,1,\infty $ уравнения (35), обозначим соответственно через

Прообразы этих вершин будем обозначать теми же буквами, что и сами вершины.

Углы в вершинах $\mathcal{M},\;\mathcal{B},\;\mathcal{C}$ обозначаем, как и выше, соответственно через $\pi {{\alpha }_{1}}$, $\pi {{\alpha }_{2}}$, $\pi {{\alpha }_{3}}$, где согласно (36) и (44), показатели углов (с точностью до знака) равны

Знаки в этих формулах выберем после вычисления (в п. 2.5) координат этих вершин в зависимости от того, является ли вершина конечной или бесконечной.

2.5. Вид кругового треугольника

Выясним вид кругового треугольника $\mathfrak{T}$ на плоскости $W$. Подставив разложения (37) и (38) соответственно для ${{u}_{1}}(\varepsilon )$ и ${{u}_{2}}(\varepsilon )$ в выражение (47) для отображающей функции $W = \mathcal{F}(\varepsilon )$ и выполнив деление, приходим к следующему представлению для $\mathcal{F}(\varepsilon )$ вблизи точки $\varepsilon = 0$, являющейся прообразом вершины $\mathcal{M}$ треугольника $\mathfrak{T}$:

где берется ветвь логарифма, отвечающая условию (39). Отсюда с учетом равенства получаемого из (42), вытекает асимптотика означающая, что вершина $\mathcal{M}$ расположена в бесконечности, а значит, выходящие из нее стороны и треугольника $\mathfrak{T}$ должны быть прямолинейными лучами, причем, поскольку они являются образами соответственно интервалов $(0,1)$ и $( - \infty ,0)$ вещественной оси на плоскости $W$, то из (53) следует, что эти стороны определяются формулами где ${{\sigma }_{5}}$ и ${{\sigma }_{6}}$ – некоторые вещественные числа, определяемые ниже.

Вычислим координату вершины $\mathcal{B}$ – образа точки $\varepsilon = 1$ при отображении $W = \mathcal{F}(\varepsilon )$. Для этого найдем значение решений Куммера ${{u}_{1}}(\varepsilon )$ и ${{u}_{2}}(\varepsilon )$, входящих в представление (47), при $\varepsilon = 1$. Из равенства (38) получаем

Для вычисления значения ${{u}_{1}}(\varepsilon )$ при $\varepsilon = 1$ воспользуемся формулой (46) из [9], с. 112: Заметим, что для функции ${{u}_{1}}(\varepsilon )$, представляемой равенством (37), выполняются требуемые для состоятельности этой формулы условия $c\not { = }0, - 1, - 2 \ldots $ и $\operatorname{Re} c > \operatorname{Re} (a + b)$; последнее неравенство вытекает из выражений для параметров (36) и условия $\beta > 1$, см. (17). Тогда из (37) и (58) находим: Подставляя величины (57) и (59) в представление (47), устанавливаем Используя, наконец, равенство ${{\Gamma }^{2}}\left( {\frac{1}{2}} \right) = \pi $ и свойство $\Gamma $-функции (см. [9, с. 18]) получаем из (60), что требуемая координата вершины $\mathcal{B}$ (очевидно, совпадающая с ${{\sigma }_{5}}$ из (55)) дается формулой $\mathcal{B} = \mathcal{F}(1) = {{q}_{0}} + \pi {\kern 1pt} {\kern 1pt} {\text{ctg}}{\kern 1pt} {\kern 1pt} (\pi \beta {\text{/}}2)$, которая с учетом (49) переписывается в виде отметим, что для $\beta = 3{\text{/}}2$ имеем $\mathcal{B} = 5\ln 2 - \frac{\pi }{2} = 1.894939576$.

Найдем теперь координату вершины $\mathcal{C}$ треугольника $\mathfrak{T}$, являющейся образом точки $\varepsilon = \infty $ при рассматриваемом отображении $W = \mathcal{F}(\varepsilon )$. Для аналитического продолжения гипергеометрической функции нам понадобится формула (34) из [9, с. 115], вида

(справедливая для всех значений $a,\;b,\;c$, для которых $\Gamma $-множители в числителях конечны), где ${{u}_{3}}(z)$ и ${{u}_{4}}(z)$ определяются равенствами Заменив в формуле (63) переменную $z$ на $1 - \varepsilon $, применим формулу (63) к функции ${{u}_{2}}(\varepsilon )$ из числителя (47), определяемой равенством (38), и устремим $\varepsilon \to \infty $ при условии ${\text{Im}}\,\varepsilon > 0$. Поскольку для рассматриваемой области $\mathbb{L}(\beta ,A,h)$ выполняется неравенство $\beta > 1$, то для множителей при гипергеометрических функциях в правой части (65) справедливо соотношение Отсюда, учитывая, что гипергеометрические функции в правой части равенства (65) стремятся к единице при $\varepsilon \to \infty $, получаем из этого равенства следующую оценку: Применив теперь формулу (63) к функции ${{u}_{1}}(\varepsilon ) = F\left( {\frac{1}{2},1 - \frac{\beta }{2};1;\varepsilon } \right)$ из знаменателя (47), находим Аналогично предыдущему, учитывая неравенство $\beta > 1$, убеждаемся, что множители при гипергеометрических функциях в правой части (68) отвечают при $\varepsilon \to \infty $ оценке а сами эти функции стремятся к единице. Отсюда получаем асимптотику Подставим полученные асимптотики (67) и (70) в представление (47) для отображения $W = \mathcal{F}(\varepsilon )$ и устремим $\varepsilon \to \infty $ при $\operatorname{Im} \varepsilon > 0$, учитывая при этом формулу (61), равенство и выражение (49). Тогда получаем искомую координату третьей вершины треугольника $\mathfrak{T}$, тогда для величины ${{\sigma }_{6}}$ из (56) получаем

Поскольку вершины $\mathcal{B}$ и $\mathcal{C}$, согласно равенствам (62), (71), конечны, то выбирая в форму-ле (51) положительные знаки в соответствии с замечанием, сделанным после этой формулы, находим значения показателей углов в вершинах области $\mathfrak{T}$,

причем для $\alpha $ выполняется включение вытекающее из заданного в (2) условия $\beta \in (1,2)$.

Тогда из формул (54)–(56), (62), (71)–(73) следует вид кругового треугольника $\mathfrak{T}$, изображенного на фиг. 2а.

2.6. Представления для основных функций

Таким образом, установлено, что функция $\mathcal{F}$, фигурирующая в уравнении для $\varepsilon $,

выполняет отображение где $\mathfrak{T}$ – круговой треугольник, построенный в п. 2.5.

Подставляя в уравнение (75) формулу (48) для $W$, получаем соотношение $\mathcal{F}(\varepsilon ) = \ln (Q\delta )$, где $\delta $ и $Q$ выражаются через $\beta $ и $A{\text{/}}h$ по формулам (9) и (49). Обращая указанное соотношение, видим, что искомую зависимость величины $\delta $ от геометрических параметров $\beta $ и $A{\text{/}}h$ области $\mathbb{L}(\beta ,A,h)$ осуществляет функция

Построение этой функции дает в итоге решение проблемы параметров интеграла Кристоффеля–Шварца для исходного отображения $w = f(\zeta )$ полуплоскости на область $\mathbb{L}(\beta ,A,h)$.

В приводимой ниже теореме 1 даны представления для отображения (76) и для искомой функции $\varepsilon = G(\delta )$; в ней также установлена связь между коэффициентами этих представлений и получены оценки для коэффициентов.

Отметим, что обратное отображение ${{\mathcal{F}}^{{ - 1}}}:\mathfrak{T}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{H}$ обеспечивает соответствие

вытекающие из равенств (54), (62), (71) и фиг. 2а, 2в.

Введем для сторон треугольника $\mathfrak{T}$ обозначения:

а для объединения двух последних сторон – обозначение ; таким образом, $\partial{ \mathfrak{T}} = \Gamma \cup \gamma $. Введем еще обозначения для круга полукруга, и для полуполосы, а также напомним, что полоса $\mathbb{S}$ определяется равенством (7), а функция осуществляет ее отображение со следующим соответствием точек: (см. фиг. 2а, 2б), где учтены выражения (62), (71) для $\mathcal{B}$ и $\mathcal{C}$. Напомним еще, что $\beta $ – показатель входящего угла исходной области $\mathbb{L}(\beta ,A,h)$, связанный с показателем $\alpha $ углов треугольника $\mathfrak{T}$ формулой (73). Дугу $\mathcal{L}$ без концевых точек обозначаем через ${\text{int}}\mathcal{L}$, а комплексную плоскость – через $\mathbb{C}$.

Теорема 1. Справедливы следующие утверждения.

1. Для отображения (76) имеет место представление

где выбрана ветвь логарифма, принимающая вещественные значения при положительных значениях аргумента; в представлении (85) ряд сходится в полукруге ${{\mathbb{U}}_{ + }}$, а его коэффициенты ${{\lambda }_{k}}$ вещественны и отвечают оценке

2. Для функции $\varepsilon = G(\delta )$, определяемой равенством (77), справедливо представление

где ряд с вещественными коэффициентами ${{B}_{m}}$ сходится в единичном круге $\mathbb{U}$ при всех $\beta \in (1,2)$, а величина $Q$ дается формулой (49).

3. При $\beta \in [3{\text{/}}2,2)$ коэффициенты ряда (87) удовлетворяют оценке

4. Коэффициенты ${{B}_{m}}$ выражаются через коэффициенты ${{\lambda }_{k}}$ ряда (85) по формуле

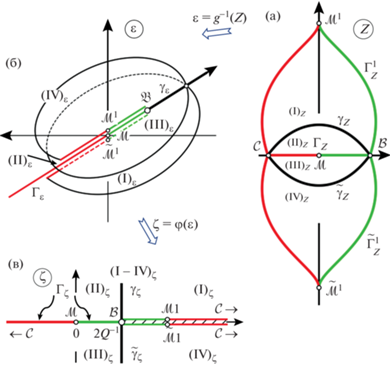
где сумма берется по всем разбиениям $\mathfrak{P}(m - 1)$ числа $(m - 1)$, т.е. по всем решениям $({{n}_{1}},{{n}_{2}}, \ldots ,{{n}_{{(m - 1)}}})$ в неотрицательных целых числах уравненияа число $n$ равно $n = {{n}_{1}} + {{n}_{2}} + \ldots + {{n}_{{(m - 1)}}}$.

Доказательство. 1. Из фиг. 2а видно, что треугольник $\mathfrak{T}$ представляет собой подобласть полосы $\mathbb{S}$, а $\Gamma : = \Psi \cup \Omega $ является общей дугой границ $\partial{ \mathfrak{T}}$ и $\partial \mathbb{S}$. Тогда, принимая во внимание соотношения (84), а также принципы сохранения области и соответствия границ [41], находим, что образом треугольника $\mathfrak{T}$ при отображении $Z = \exp {\kern 1pt} {\kern 1pt} (W)$ служит область

(см. фиг. 2б) с границей, состоящей из двух дуг, первой из которых является отрезок ${{\Gamma }_{Z}}$ вещественной оси, а вторая, ${{\gamma }_{Z}}$, расположена (кроме концевых точек) в верхней полуплоскости; на фиг. 2а, 2б для областей $\mathfrak{T}$ и ${{({\text{II}})}_{Z}}$ дана штриховка с наклоном вправо. Таким образом,

Исходя из соотношений (78) для отображения $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$, видим, что образом треугольника $\mathfrak{T}$ при этом отображении будет верхняя полуплоскость $\mathbb{H}$, которую переобозначим через ${{({\text{II}})}_{\varepsilon }}$; для нее на фиг. 2в также дана штриховка с наклоном вправо. Ее граница состоит из двух отрезков вещественной оси, $\partial {{({\text{II}})}_{\varepsilon }} = {{\Gamma }_{\varepsilon }} \cup {{\gamma }_{\varepsilon }}$, где

Таким образом,

Тогда из выражений (93), (95) следует, что функция $Z = g(\varepsilon )$, определенная в виде суперпозиции

осуществляет (однолистное) отображение переводящее согласно (92), (94) отрезок ${{\Gamma }_{\varepsilon }}$ в отрезок ${{\Gamma }_{Z}}$ и оставляющее на месте начало координат, последнее равенство следует из вторых формул (78) и (84).

Поэтому, согласно принципу симметрии Римана–Шварца [41], функция (96) может быть аналитически продолжена через ${{\Gamma }_{\varepsilon }}$ с помощью инверсии относительно этого отрезка, т.е. по правилу (об инверсии, симметрии или зеркальном отражении см. [6], [37], [41])

в нижнюю полуплоскость ${{({\text{III}})}_{\varepsilon }} = \{ \operatorname{Im} \varepsilon < 0\} $, см. фиг. 2б, 2в. Продолженная функция конформно отображает ${{({\text{III}})}_{\varepsilon }}$ на область ${{({\text{III}})}_{Z}}$, симметричную области ${{({\text{II}})}_{Z}}$ относительно ${{\Gamma }_{Z}}$, с границей $\partial {{({\text{III}})}_{Z}} = {{\Gamma }_{Z}} \cup {{\tilde {\gamma }}_{Z}}$, где ${{\tilde {\gamma }}_{Z}}$ – зеркальный образ дуги ${{\gamma }_{Z}}$ $($отметим, что для областей ${{({\text{III}})}_{\varepsilon }}$ и ${{({\text{III}})}_{Z}}$ на фиг. 2б, 2в дана штриховка с наклоном влево$)$. Тогда, введя обозначения видим, что функция (96) вместе с ее продолжением осуществляет отображение являющееся однолистным в силу условия (99) его построения и однолистности исходного отображения (97).

Поскольку область ${{({\text{II}},{\text{III}})}_{\varepsilon }}$ представляет собой плоскость с разрезом $[1, + \infty )$ по вещественной оси, то эта область содержит единичный круг $\mathbb{U}$, в котором функция $Z = g(\varepsilon )$ регулярна и однолистна, а значит, представима сходящимся в нем рядом Тейлора по степеням ${{\varepsilon }^{k}}$ с коэффициентами ${{\lambda }_{k}}$, причем ${{\lambda }_{0}} = 0$ в силу равенства (98), а ${{\lambda }_{1}} = 1$ в силу соотношений (53), (96). Функцию с такими свойствами называют (см. [38], [42]) принадлежащей классу $S$. Для нашей функции $g(\varepsilon )$, кроме того, коэффициенты ${{\lambda }_{k}}$ вещественны в силу соотношения (99). Тогда требуемое неравенство (86) представляет собой установленную в работах [43], [44], [45] оценку для функций класса $S$ с вещественными коэффициентами Тейлора. (Заметим, что эта оценка составляет широко известную гипотезу Бибербаха (см. [6], [38], [42], [46]), доказанную Луи де Бранжем [47] для не обязательно вещественных коэффициентов Тейлора).

Таким образом, продолженная функция $Z = g(\varepsilon )$ представима в круге $\mathbb{U}$ в виде сходящегося разложения

а значит, отображение (97) представимо в полукруге ${{\mathbb{U}}_{ + }}$ в виде этого разложения. Понимая левую часть равенства (102) как такое отображение и учитывая вид (96) представления для $g(\varepsilon )$, подействуем на обе части равенства (102) функцией $\ln Z$, у которой выбрана ветвь, указанная в формулировке теоремы; эта ветвь логарифма однозначно определена в области ${{({\text{II}})}_{Z}}$, изображенной на фиг. 2б. В результате получим представление (85), где ряд сходится в ${{\mathbb{U}}_{ + }}$, а коэффициенты ${{\lambda }_{k}}$ вещественны и удовлетворяют оценке (86). Первое утверждение теоремы доказано.

2. Обратимся к доказательству второго утверждения теоремы. Образ множества на плоскости W при его инверсии относительно дуги $\gamma $, $\Psi $ или $\Omega $ будем обозначать тем же символом, добавляя к нему соответственно верхний индекс $1,2$ или $3$. Те же индексы приписываются и при инверсии относительно зеркальных отражений указанных дуг, а также при многократном отражении, так что может возникать индекс из нескольких указанных цифр.

Поскольку функция $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$, отображающая треугольник $\mathfrak{T}$ на верхнюю полуплоскость ${{({\text{II}})}_{\varepsilon }}$ (обе области на фиг. 11а и фиг. 11б заштрихованы с наклоном вправо), переводит дугу окружности $\gamma $ в прямолинейный отрезок ${{\gamma }_{\varepsilon }}$, определямый из (94), то по принципу симметрии эта функция может быть аналитически продолжена через $\gamma $ в симметричный круговой треугольник ${{\mathfrak{T}}^{1}}$.

Две вершины нового треугольника расположены в тех же точках $\mathcal{B} = \ln Q$ и $\mathcal{C} = \ln Q + i\pi $, что и у исходного $\mathfrak{T}$, с тем же показателем углов $\alpha $, т.к. преобразование инверсии сохраняет углы, а третья вершина ${{\mathcal{M}}^{1}}$, симметричная $\mathcal{M} = \infty $ относительно $\gamma $ и имеющая (как и $\mathcal{M}$) нулевой угол, дается формулой, получаемой с использованем (62):

Сторонами треугольника ${{\mathfrak{T}}^{1}}$, кроме $\gamma $, являются еще ${{\Psi }^{1}}$ и ${{\Omega }^{1}}$, симметричные соответственно лучам $\Psi $ и $\Omega $ относительно $\gamma $ (см. фиг. 11б). Обозначим ${{\Gamma }^{1}}: = {{\Psi }^{1}} \cup {{\Omega }^{1}}$.

Продолженная функция $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ отображает ${{\mathfrak{T}}^{1}}$ на нижнюю полуплоскость ${{({\text{I}})}_{\varepsilon }}$. Она является другим, отличным от ${{({\text{III}})}_{\varepsilon }}$, экземпляром полуплоскости (см. фиг. 11а), поскольку последняя получена отражением ${{({\text{II}})}_{\varepsilon }}$ относительно ${{\Gamma }_{\varepsilon }}$, а ${{({\text{I}})}_{\varepsilon }}$ – отражением ${{({\text{II}})}_{\varepsilon }}$ относительно ${{\gamma }_{\varepsilon }}$ $($на фиг. 11а и фиг. 11б области ${{\mathfrak{T}}^{1}}$ и ${{({\text{I}})}_{\varepsilon }}$ заштрихованы с наклоном влево$)$.

По принципу симметрии функция $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ вместе с продолжением отображает область

являющуюся круговым четырехугольником с границей $\partial ({{\mathfrak{T}}^{1}},\mathfrak{T}) = \Gamma \cup {{\Gamma }^{1}}$, на область представляющую собой плоскость с разрезом $( - \infty ,1]$ (см. фиг. 11а и фиг. 11б), т.е. где ${{\Gamma }_{\varepsilon }}$ – верхний, а $\Gamma _{\varepsilon }^{1}$ – нижний берег указанного разреза (см. фиг. 11а). Образы вершин $\mathcal{M}$ и ${{\mathcal{M}}^{1}}$ четырехугольника при этом отображении будут (геометрически) расположены в одной и той же точке $\varepsilon = 0$, но на разных – верхнем и нижнем – берегах указанного разреза. (Более точно, $\mathcal{M}$ и ${{\mathcal{M}}^{1}}$ являются разными простыми концами (см. [38], [41], [48]) области ${{({\text{I}},{\text{II}})}_{\varepsilon }}$).

Показатели углов в вершинах $\mathcal{B}$ и $\mathcal{C}$ четырехугольника (104) равны $2\alpha $. Поэтому, если выполняется условие

которое, согласно (73), соответствует включению $\beta \in [3{\text{/}}2,2)$ для показателя входящего угла области $\mathbb{L}(\beta ,A,h)$, то четырехугольник (104) содержит полуполосу ${{\mathbb{S}}_{ + }}(\ln Q)$, определенную по формуле (82), и сам содержится в полосе $\mathbb{S}$. Тем самым, доказано

Предложение 1. При условии $\beta \in [3{\text{/}}2,2)$ функция $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ может быть аналитически продолжена в четырехугольник $({{\mathfrak{T}}^{1}},\mathfrak{T})$, отвечающий соотношениям

и осуществляет отображение (106).

Если же $\alpha $ лежит в дополнительном к (107) диапазоне, т.е. выполняется включение

соответствующее значениям $\beta \in (1,3{\text{/}}2)$ показателя входящего угла, то в этом случае углы четырехугольника $({{\mathfrak{T}}^{1}},\mathfrak{T})$ в вершинах $\mathcal{B}$ и $\mathcal{C}$ оказываются меньшими $\pi {\text{/}}2$, вследствие чего стороны ${{\Psi }^{1}}$ и ${{\Omega }^{1}}$ пересекают торец полуполосы ${{\mathbb{S}}_{ + }}(\ln Q)$, и, таким образом, она не содержится целиком в нашем четырехугольнике (см. фиг. 11б).

Тем не менее и в случае (109) можно построить область аналитичности функции $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$, охватывающую всю полуполосу ${{\mathbb{S}}_{ + }}(\ln Q)$.

Для этого, применяя принцип симметрии, расширим построенную область аналитичности $({{\mathfrak{T}}^{1}},\mathfrak{T})$, присоединив к ней новые треугольники ${{\mathfrak{T}}^{{12}}}$ и ${{\mathfrak{T}}^{{13}}}$, симметричные ${{\mathfrak{T}}^{1}}$, а также открытые дуги ${\text{int}}\,{{\Psi }^{1}}$, ${\text{int}}\,{{\Omega }^{1}}$, лежащие между $({{\mathfrak{T}}^{1}},\mathfrak{T})$ и новыми треугольниками, затем – присоединив симметричные им треугольники ${{\mathfrak{T}}^{{121}}}$, ${{\mathfrak{T}}^{{123}}}$, ${{\mathfrak{T}}^{{131}}}$, ${{\mathfrak{T}}^{{132}}}$ и соответствующие открытые дуги, далее продолжая подобный процесс (см. фиг. 12). В результате мы получим область аналитичности продолженной функции $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ в виде некоторого кругового многоугольника $\mathfrak{M}$, причем $\partial{ \mathfrak{M}} \supset \Gamma $.

Образом многоугольника $\mathfrak{M}$ при отображении ${{\mathcal{F}}^{{ - 1}}}$ является риманова поверхность $\Re $, которую получаем путем последовательного присоединения к первоначальной полуплоскости ${{({\text{II}})}_{\varepsilon }}$ полуплоскостей, являющихся образами присоединяемых треугольников, и интервалов вещественной оси – образов открытых дуг, через которые выполняется присоединение. При этом дуга $\Gamma $ границы $\partial{ \mathfrak{M}}$ переходит в дугу ${{\Gamma }_{\varepsilon }}$, представляющую собой отрезок $[ - \infty ,1]$ вещественной оси, лежащий на границе римановой поверхности $\Re $.

Для любого из присоединяемых треугольников два его угла будут равны $\pi \alpha $, а третий – нулю. Сторонами треугольников являются дуги окружностей, причем их центры лежат на вертикальной прямой

проходящей через точку ${{\mathcal{M}}^{1}}$. Это утверждение вытекает из того, что, во-первых, центры дуг $\gamma $, ${{\Psi }^{1}}$, ${{\Omega }^{1}}$, очевидно (см. фиг. 12), лежат на $\mathcal{A}$, во-вторых, все стороны новых треугольников получаются отражением дуг $\gamma $, ${{\Psi }^{1}}$, ${{\Omega }^{1}}$ друг от друга (либо от их зеркальных образов), а в-третьих, это следует из того общего положения, что центр зеркального образа одной окружности относительно другой всегда лежит на прямой, соединяющей центры первых двух. Из установленного утверждения следует еще, что для всех присоединяемых треугольников вершины с нулевыми углами лежат на прямой $\mathcal{A}$.

Рассмотрим теперь вершины треугольников с углами $\pi \alpha $. Каждая такая вершина получена из вершины с углом $\pi \alpha $, принадлежащей некоторому треугольнику с предыдущего шага процесса, путем инверсии относительно противолежащей дуги, имеющей центр на $\mathcal{A}$, причем вершина–прообраз находится снаружи от окружности инверсии, а вершина–образ – внутри нее и, тем самым, расположена ближе к прямой $\mathcal{A}$. Поскольку каждая из рассматриваемых вершин получена через цепочку инверсий из $\mathcal{B}$ или из $\mathcal{C}$, то все они лежат не дальше от $\mathcal{A}$, чем точки $\mathcal{B}$ и $\mathcal{C}$, т.е. принадлежат прямоугольнику

На первом шаге описываемого процесса мы к исходной области $({{\mathfrak{T}}^{1}},\mathfrak{T})$ присоединяем множество $\{ {{\mathfrak{T}}^{{12}}}$, ${{\mathfrak{T}}^{{121}}}$, ${{\mathfrak{T}}^{{1212}}}, \ldots \} $, состоящее из

треугольников (символ $\left\lceil a \right\rceil $ означает наименьшее целое число, большее или равное $a$) с общей вершиной $\mathcal{B}$, и множество $\{ {{\mathfrak{T}}^{{13}}}$, ${{\mathfrak{T}}^{{131}}}$, ${{\mathfrak{T}}^{{1313}}}, \ldots \} $ из $N$ треугольников с общей вершиной $\mathcal{C}$, а также множество из $2N$ открытых круговых дуг, каждая из которых является общей стороной пары смежных треугольников, симметричных относительно этой дуги и содержащихся в указанных множествах.

В результате мы получаем область аналитичности продолженной функции $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ в виде некоторого кругового многоугольника ${{\mathfrak{M}}_{1}}$. Углы в его вершинах $\mathcal{B}$ и $\mathcal{C}$ равны $\pi {{\alpha }_{0}}$, где величина

больше или равна $1{\text{/}}2$, а выходящие из них стороны многоугольника ${{\mathfrak{M}}_{1}}$ выпуклы внутрь него. Отсюда следует, что этот многоугольник покрывает некоторые окрестности точек $\mathcal{B}$ и $\mathcal{C}$ в полуполосе ${{\mathbb{S}}_{ + }}(\ln Q)$, но при этом не выходит за пределы полосы $\mathbb{S}$.

Вместе с тем многоугольник ${{\mathfrak{M}}_{1}}$ не обязательно содержит в себе всю полуполосу ${{\mathbb{S}}_{ + }}(\ln Q)$, поскольку его стороны, т.е. дуги, соединяющие соседние вершины, могут не принадлежать целиком прямоугольнику $\Pi $, даже если оба конца лежат внутри $\Pi $. В то же время все эти дуги выпуклы внутрь многоугольника, что позволяет продолжить описанный процесс аналитического продолжения, получая на $j$-м шаге область аналитичности функции ${{\mathcal{F}}^{{ - 1}}}(W)$ в виде кругового многоугольника ${{\mathfrak{M}}_{j}}$, причем ${{\mathfrak{M}}_{j}} \supset {{\mathfrak{M}}_{{j - 1}}}$, но вместе с тем ${{\mathfrak{M}}_{j}} \subset \mathbb{S}$. Через некоторое конечное число описанных шагов мы получим область аналитичности $\mathfrak{M}$, которая содержит всю полуполосу ${{\mathbb{S}}_{ + }}(\ln Q)$; сама же она содержится в полосе $\mathbb{S}$. При этом допускается любое $\alpha \in (0,1{\text{/}}4)$, что эквивалентно $\beta \in (1,3{\text{/}}2)$.

Учитывая еще предложение 1, устанавливаем

Предложение 2. Для любого $\beta \in (1,2)$ существует круговой многоугольник $\mathfrak{M}$, отвечающий соотношению

а функция $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ осуществляет его отображениепричем дуга $\Gamma \subset \partial{ \mathfrak{M}}$ переходит в отрезок ${{\Gamma }_{\varepsilon }} = [ - \infty ,1]$ границы $\partial \Re $.

Продолжим доказательство утверждения 2 теоремы. Используя включение (113) и свойства (84) отображения $Z = \exp {\kern 1pt} {\kern 1pt} (W)$, находим, что образом многоугольника $\mathfrak{M}$ при этом отображении является подобласть ${{\mathfrak{M}}_{Z}} = \exp {\kern 1pt} {\kern 1pt} (\mathfrak{M})$ верхней полуплоскости $\mathbb{H}$, содержащая полукруг ${{\mathbb{U}}_{ + }}(Q)$, т.е.

причем дуга $\Gamma \subset \partial{ \mathfrak{M}}$ переходит в отрезок ${{\Gamma }_{Z}} = [ - Q,Q]$ границы $\partial {{\mathfrak{M}}_{Z}}$. Отсюда для обратного отображения получаем

Введя по формуле

функцию, обратную к (96), убеждаемся с помошью соотношений (114), (116), что она осуществляет отображение переводящее отрезок ${{\Gamma }_{Z}}$ в отрезок ${{\Gamma }_{\varepsilon }}$ границы $\partial \Re $. Тогда по принципу симметрии функция (117) может быть аналитически продолжена через отрезок ${{\Gamma }_{Z}}$ по правилу Определив область по формуле где – многоугольник, симметричный ${{\mathfrak{M}}_{Z}}$ относительно ${{\Gamma }_{Z}}$, а также определив область $\widehat \Re $ по формуле где $\widetilde \Re $ – область, симметричная $\Re $ относительно ${{\Gamma }_{\varepsilon }}$, находим, что функция $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ вместе с продолжением осуществляет отображение

Согласно соотношению (115) область ${{\mathfrak{M}}_{Z}}$ содержит полукруг ${{\mathbb{U}}_{ + }}(Q)$, поэтому построенная по формулам (119), (120) область содержит круг $\mathbb{U}(Q)$. В нем (продолженная) функция $\varepsilon = {{\mathcal{F}}^{{ - 1}}}(W)$ аналитична, поэтому представима сходящимся в нем рядом Тейлора по степеням $Z$. Коэффициенты ${{\Lambda }_{m}}$ этого ряда вещественны в силу соотношения (119), нулевой коэффициент ${{\Lambda }_{0}} = 0$ в силу равенства (98), а первый коэффициент ${{\Lambda }_{1}} = 1$, поскольку единице равен первый коэффициент ${{\lambda }_{1}}$ ряда Тейлора (102) для обратной функции, а эти коэффициены связаны формулой ${{\Lambda }_{1}} = 1{\text{/}}{{\lambda }_{1}}$. Таким образом, для функции $\varepsilon = {{g}^{{ - 1}}}(Z)$ имеем сходящийся в $\mathbb{U}(Q)$ ряд:

Применяя здесь вытекающую из (77) и (117) связь $G(\delta ) = {{g}^{{ - 1}}}(Q\delta )$ и производя замены

соответствующие выражениям (48), (83), получаем из разложения (123) требуемое представление (87) для функции $\varepsilon = G(\delta )$, где ряд с вещественными коэффициентами ${{B}_{k}}$ сходится в единичном круге $\mathbb{U}$. Утверждение 2 теоремы доказано.

3. Докажем теперь третье утверждение теоремы, полагая, что выполненяется условие (107), указанное в предложении 1; при этом мы частично будем переносить приведенные выше рассуждения на более узкий случай, соответствующий замене $\mathfrak{M}$ на $({{\mathfrak{T}}^{1}},\mathfrak{T})$ и другим аналогичным заменам, вытекающим из условия (107).

Используя соотношение (108) и свойства (84) отображения $Z = \exp (W)$, находим, что образом четырехугольника $({{\mathfrak{T}}^{1}},\mathfrak{T})$ при данном отображении служит область

с границей $\partial {{({\text{I}},{\text{II}})}_{Z}} = {{\Gamma }_{Z}} \cup \Gamma _{Z}^{1}$. Здесь область ${{({\text{II}})}_{Z}}$ и дуги ${{\Gamma }_{Z}}$, ${{\gamma }_{Z}}$ определены в (91), (92), область ${{({\text{I}})}_{Z}}: = \exp ({{\mathfrak{T}}^{1}})$, а дуга $\Gamma _{Z}^{1}: = \exp ({{\Gamma }^{1}})$ лежит, кроме концевых точек, в $\mathbb{H}$. При этом выполняется включение (для областей ${{\mathfrak{T}}^{1}}$, ${{({\text{I}})}_{\varepsilon }}$ и ${{({\text{I}})}_{Z}}$ на фиг. 11б, фиг. 11а, фиг. 11в дана штриховка с наклоном влево). Таким образом,

Из соотношений (106) и (127) следует, что определенная по формуле (117) функция $\varepsilon = {{g}^{{ - 1}}}(Z)$ осуществляет отображение

переводящее отрезок ${{\Gamma }_{Z}}$ в отрезок ${{\Gamma }_{\varepsilon }}$ (см. фиг. 11в, фиг. 11а). Тогда, согласно принципу симметрии, функция (117) может быть аналитически продолжена через отрезок ${{\Gamma }_{Z}}$ по правилу (119) в область где ${{({\text{III}})}_{Z}}$, ${{({\text{IV}})}_{Z}}$ и $\operatorname{int} {{\tilde {\gamma }}_{Z}}$ симметричны соответственно областям ${{({\text{II}})}_{Z}}$, ${{({\text{I}})}_{Z}}$ и (открытой) дуге $\operatorname{int} {{\gamma }_{Z}}$; дуга $\widetilde \Gamma _{Z}^{1}$ и точка суть зеркальные образы соответственно $\Gamma _{Z}^{1}$ и ${{\mathcal{M}}^{1}}$ относительно ${{\Gamma }_{Z}}$ (см. фиг. 11в).

Продолженная функция $\varepsilon = {{g}^{{ - 1}}}(Z)$ отображает ${{({\text{III}},{\text{IV}})}_{Z}}$ на область ${{({\text{III}},{\text{IV}})}_{\varepsilon }}$, симметричную области ${{({\text{I}},{\text{II}})}_{\varepsilon }}$ относительно ${{\Gamma }_{\varepsilon }}$, т.е. представляющую собой плоскость с разрезом $[ - \infty ,1]$ по вещественной оси (см. фиг. 11г). Она получена соединением нижней полуплоскости ${{({\text{III}})}_{\varepsilon }}$ с верхней ${{({\text{IV}})}_{\varepsilon }}$ через интервал $(1, + \infty )$; подчеркнем, что ${{({\text{IV}})}_{\varepsilon }}$ представляет собой иной, нежели ${{({\text{II}})}_{\varepsilon }}$ экземпляр верхней полуплоскости (для областей ${{({\text{IV}})}_{\varepsilon }}$ и ${{({\text{IV}})}_{Z}}$ на фиг. 11в, фиг. 11г дана штриховка с наклоном вправо).

Обозначим через

область, изображенную на фиг. 11в и фиг. 13а. Затем, соединив два экземпляра, ${{({\text{I}},{\text{II}})}_{\varepsilon }}$ и ${{({\text{III}},{\text{IV}})}_{\varepsilon }}$, плоскости с разрезом $( - \infty ,1]$ путем склейки верхнего берега первой области с нижним берегом второй (на фиг. 11а, фиг. 11г эти берега изображены штриховыми линиями), образуем двулистную риманову поверхность ${{({\text{I}}{\kern 1pt} - {\kern 1pt} {\text{IV}})}_{\varepsilon }}$; ее схематическое изображение дано на фиг. 13б. Тогда видим, что функция (117) вместе с ее продолжением осуществляет отображение

Поскольку, согласно (126), область ${{({\text{I}},{\text{II}})}_{Z}}$ содержит полукруг ${{\mathbb{U}}_{ + }}(Q)$, то область ${{({\text{I}}{\kern 1pt} - {\kern 1pt} {\text{IV}})}_{Z}}$ содержит круг $\mathbb{U}(Q)$, т.е.

Продолженная функция $\varepsilon = {{g}^{{ - 1}}}(Z)$ в нем регулярна, а значит, как и было установлено аналогичным образом в более общем случае (при доказательстве утверждения 2), она представима в $\mathbb{U}(Q)$ сходящимся рядом (123) с вещественными коэффициентами ${{\Lambda }_{m}}$, откуда (как и в упомянутом доказательстве) для функции $\varepsilon = G(\delta )$ следует представление (87), где ряд с вещественными коэффициентами ${{B}_{m}}$ сходится в единичном круге $\mathbb{U}$.

Запишем представление (87) для функции $\varepsilon = G(\delta )$ в следующем виде:

Заметим, что функция отвечает условиям и конформно отображает риманову поверхность ${{({\text{I}}{\kern 1pt} - {\kern 1pt} {\text{IV}})}_{\varepsilon }}$ на область представляющую собой внешность разреза $[2{{Q}^{{ - 1}}}, + \infty )$ по вещественной оси (см. фиг. 13в), т.е. Отсюда и из (130) получаем, что суперпозиция $\zeta = \varphi \circ {{g}^{{ - 1}}}(Z)$ функций (117) и (133) однолистно отображает область ${{({\text{I}}{\kern 1pt} - {\kern 1pt} {\text{IV}})}_{Z}}$, определенную в (129), на внешность разреза, задаваемую форму-лой (135). При этом подобласти ${{({\text{I}})}_{Z}}$, ${{({\text{II}})}_{Z}}$, ${{({\text{III}})}_{Z}}$ и ${{({\text{IV}})}_{Z}}$, составляющие область ${{({\text{I}}{\kern 1pt} - {\kern 1pt} {\text{IV}})}_{Z}}$, переходят соответственно в подобласти ${{({\text{I}})}_{\zeta }}$, ${{({\text{II}})}_{\zeta }}$, ${{({\text{III}})}_{\zeta }}$ и ${{({\text{IV}})}_{\zeta }}$ области ${{({\text{I}}{\kern 1pt} - {\kern 1pt} {\text{IV}})}_{\zeta }}$, т.е. на первую, вторую, третью и четвертую четверти (квадранты), на которые прямые $\{ \operatorname{Im} \zeta = 0\} $ и $\{ \operatorname{Re} \zeta = 2{{Q}^{{ - 1}}}\} $ разбивают область ${{({\text{I}}{\kern 1pt} - {\kern 1pt} {\text{IV}})}_{\zeta }}$, а также и саму плоскость $\zeta $ (см. фиг. 13в).

Из сказанного вытекает, что функция

регулярна и, с учетом (131), однолистна в единичном круге $\mathbb{U}$, а значит, представима в нем рядом Тейлора по степеням $\delta $ с коэффициентами ${{D}_{k}}$. Из разложения (132) для $\varepsilon = G(\delta )$ и свойств (134) функции $\zeta = \varphi (\varepsilon )$ следует, что коэффициенты ${{D}_{k}}$ этого ряда вещественны, причем ${{D}_{0}} = 0$, а ${{D}_{1}} = 1$. Таким образом, функция (137) разлагается в ряд и принадлежит классу $S$ с вещественными коэффициентами (о котором сказано выше при доказательстве утверждения 1 теоремы), а значит, коэффициенты этого ряда удовлетворяют неравенству

Чтобы получить требуемую оценку для коэффициентов ${{B}_{k}}$ из разложения (132), подставим выражение (133) и формулу $\varepsilon = G(\delta )$ в представление (137). Тогда после простых выкладок найдем

возводя обе части этого равенства в квадрат, подставляя представление (132) вместо $G(\delta )$ и разложение (138) вместо $\Phi (\delta )$, получим после возвышения последнего ряда в квадрат и упрощений следующее равенство: Приравнивая здесь коэффициенты при одинаковых степенях ${{\delta }^{k}}$, находим следующую связь между ${{B}_{k}}$ и ${{D}_{k}}$: Оценивая ${{B}_{k}}$ по модулю на основе (141) с использованием неравенства (139) и формул получаем и окончательно

Таким образом, установлено, что при условии $\beta \in [3{\text{/}}2,2)$ коэффициенты ${{B}_{k}}$ ряда (87) для функции $\varepsilon = G(\delta )$ удовлетворяют оценке (88). Третье утверждение теоремы доказано.

4. Докажем четвертое утверждение теоремы. Для этого прежде всего заметим, что связь между коэффициентами ${{\lambda }_{k}}$ и ${{\Lambda }_{m}}$ соответственно рядов (102) и (123), представляющих взаимно обратные функции $g(\varepsilon )$ и ${{g}^{{ - 1}}}(Z)$, может быть найдена с помощью формулы Бюрмана–Лагранжа [10], [37]:

Запишем функцию в квадратных скобках в (143), обозначив ее через $A(t)$, в виде суперпозиции

функций $a(t)$ и $b(u)$, которые определим в соответствии с (102), (144), а последнюю разложим в биномиальный ряд по формулам Тогда из (143) видим, что коэффициент ${{\Lambda }_{m}}$ выражается через производную ${{A}_{{m - 1}}}$ функции $A(t)$ в виде ${{\Lambda }_{m}} = (1{\text{/}}m!){{A}_{{m - 1}}}$, а учитывая связь (124) между ${{\Lambda }_{m}}$ и ${{B}_{m}}$, выводим для последнего выражение

Применяя для нахождения фигурирующей здесь ${{A}_{{m - 1}}}$ формулу Фаа ди Бруно [49], [50] для производной сложной функции, находим

где $n = {{n}_{1}} + {{n}_{2}} + \ldots + {{n}_{{(m - 1)}}}$, а суммирование выполняется по всем разбиениям $\mathfrak{P}(m - 1)$ числа $(m - 1)$, т.е. всем решениям $({{n}_{1}},{{n}_{2}}, \ldots ,{{n}_{{(m - 1)}}})$ в неотрицательных целых числах уравнения (90). Подставляя в полученное выражение (148) значения ${{a}_{k}}$ из (145) и ${{b}_{n}}$ из (146), а результат – в равенство (147), получаем после простых выкладок выражение (89) для ${{B}_{m}}$ через коэффициенты ${{\lambda }_{k}}$. Четвертое утверждение и теорема в целом доказаны.

2.7. Получение коэффициентов ${{\lambda }_{k}}$ в представлении для $\mathcal{F}(\varepsilon )$

Итак, коэффициенты ${{B}_{m}}$ разложения (87) функции $G(\delta )$ выражены в виде формулы (89) через коэффициенты ${{\lambda }_{k}}$ представления (85) функции $\mathcal{F}(\varepsilon )$. Остается найти выражение для ${{\lambda }_{k}}$.

Для этого, разделив друг на друга ряды, помещенные в квадратные скобки в выражении (52) для функции $\mathcal{F}(\varepsilon )$, приведем эту функцию к виду

с коэффициентами $\lambda _{k}^{'}$, вычисляемыми по следующим рекуррентным формулам:

Чтобы преобразовать (149) к виду (85), приравняем эти представления друг другу, а результат пропотенцируем; тогда после упрощений получим соотношение

здесь левую часть первого равенства будем рассматривать как некоторую функцию $A(\varepsilon )$, а сумму ряда в скобках в его правой части – как функцию, обозначаемую через $b(\varepsilon )$. Тогда коэффициент ${{\lambda }_{k}}$ будет представлять собой $(k - 1)$-ю производную при $\varepsilon = 0$ функции $A(\varepsilon ) = \exp \circ b(\varepsilon )$, деленную на $(k - 1)!$ Вычисляя эту производную с помощью формулы Фаа ди Бруно (которая уже использовалась выше), находим где суммирование выполняется по всем разбиениям $\mathfrak{P}(k - 1)$ числа $(k - 1)$, т.е. всем решениям $({{j}_{1}},{{j}_{2}}, \ldots ,{{l}_{{(k - 1)}}})$ в неотрицательных целых числах уравнения ${{j}_{1}} + 2{{j}_{2}} + \ldots + (k - 1){{j}_{{(k - 1)}}} = k - 1$.

Таким образом, чтобы прийти к итоговым формулам для коэффицентов ${{B}_{m}}$, нужно в равенство (89), представляющее ${{B}_{m}}$ через ${{\lambda }_{k}}$, подставить формулу (152), выражающую ${{\lambda }_{k}}$ через коэффициенты $\lambda _{k}^{'}$, предварительно получив последние из рекуррентных соотношений (150).

2.8. Аналитическое решение проблемы параметров

Описанный метод дает коэффиценты ${{B}_{m}}$ разложения (87) функции $\varepsilon = G(\delta )$ в виде аналитических формул, выражающих ${{B}_{m}}$ в явном виде через показатель $\beta $ входящего угла области $\mathbb{L}(\beta ,A,h)$. В частности, для нескольких первых коэффициентов разложения (87) получаем следующие выражения:

где (напомним) величина $Q$ определяется через $\beta $ по формуле (49). Вывод подобных выражений для ${{B}_{m}}$ осуществлялся (на основе указанных выше формул) с помощью программы символьных преобразований, входящей в пакет компьютерной алгебры Maple-18.

Для нахождения таким способом первых 50 коэффициентов ${{B}_{m}}$ на процессоре средней производительности Intel Core i3 потребовалось время порядка ${{10}^{{ - 3}}}$ с. Получив эти формулы один раз и подставив их в ряд (87) для функции $\varepsilon = G(\delta )$, можно использовать его для вычисления модифицированного прообраза $\varepsilon $ при различных значениях геометрических параметров $\beta $ и $\delta $ области $\mathbb{L}(\beta ,A,h)$.

Поскольку ряд (87) сходится практически с экспоненциальной скоростью, то погрешность вычисления на его основе величины $\varepsilon $ равна по порядку величины первому отброшенному члену, равному ${{\delta }^{{K + 1}}}$, где $K$ – длина используемой частичной суммы ряда (87). Для удобства в табл. 1 приведены численные значения параметра $\delta $ при различных значениях относительной длины полки $A{\text{/}}h$.

Отметим, что была также проведена проверка соответствия формул для ${{B}_{m}}$ оценке (88) путем непосредственного сопоставления с ней численных значений коэффициентов ${{B}_{m}}$, вычисленных по формулам типа (153) для различных значений показателя $\beta $. Сопоставление показало, что для $\beta \in [3{\text{/}}2,2)$ неравенство (88) выполняется, тогда как для $\beta < 3{\text{/}}2$ оно нарушается. Этот численный эксперимент подтвердил утверждение 3 теоремы 1.

Очевидно, что для описанного метода вычисления $\varepsilon $ сравнительно неблагоприятным является случай короткой полки, т.е. когда $A < h$, например, $A{\text{/}}h = 0.5$. Но и в этом случае метод оказывается достаточно эффективным. Действительно, чтобы для случая $A{\text{/}}h = 0.5$ обеспечить вычисления $\varepsilon $ с относительной точностью ${{10}^{{ - 20}}}$, необходимо, согласно указанной выше оценке, использовать частичную сумму ряда (87) длиной $29$ членов. Такое вычисление на указанном процессоре заняло около ${{10}^{{ - 3}}}$ с, что и подтверждает высокую эффективность изложенного метода вычисления величины $\varepsilon $.

Если модифицированный прообраз $\varepsilon $ известен, то искомые параметры рассматриваемого интеграла (20), т.е. прообраз $\tau $ и предынтегральный множитель $\mathcal{K}$ выражаются через $\varepsilon $ соответственно по формулам (34) и (27). Это и дает явное аналитическое решение проблемы параметров интеграла Кристоффеля–Шварца (20).

Таблица значений прообраза $\tau $ для некоторых величин показателя $\beta $ входящего угла и относительной длины полки $A{\text{/}}h$ приведена в разд. 4. Заметим, что ширина полки $h$ области $\mathbb{L}(\beta ,A,h)$ фигурирует в качестве множителя в выражении (20) для отображения $f(\zeta )$.

3. ПРЕДСТАВЛЕНИЯ ДЛЯ ПРЯМОГО И ОБРАТНОГО ОТОБРАЖЕНИЙ

3.1. Предварительные замечания

Численная реализация функции $w = f(\zeta )$, дающей конформное отображение

(см. фиг. 1) и записанной в виде интеграла Кристоффеля–Шварца (20), выполнена в работе с помощью набора из четырех разложений, представляющих эту функцию вблизи точек ${{\zeta }_{1}} = 0$ и ${{\zeta }_{4}} = \infty $, а также вблизи отрезков $[1,\tau ]$ и $[ - \tau , - 1]$ вещественной оси $\{ \operatorname{Im} \zeta = 0\} $. Области сходимости этих разложений покрывают в совокупности множество , т.е. всю замкнутую верхнюю полуплоскость.

С помощью обращения этих разложений получены четыре представления для обратной функции $\zeta = {{f}^{{ - 1}}}(w)$. Области их сходимости покрывают в совокупности всю замкнутую область, т.е. . Вид областей сходимости получаемых представлений для прямого $w = f(\zeta )$ и обратного $\zeta = {{f}^{{ - 1}}}(w)$ отображений вытекает из теории конформного отображения сингулярно деформируемых областей [12], [13].

3.2. Представление для отображения $f(\zeta )$ вблизи прообраза ${{\zeta }_{1}} = 0$

Переписывая интеграл (20) в виде

и подставляя в него вместо биномов их биномиальные разложения, перемножая их и интегрируя результат, получаем

Приведем это представление к виду

Для этого, приравнивая (156) и (158) и возвышая получаемое равенство после упрощений в степень $1{\text{/}}(2 - \beta )$, приходим к соотношению: Рассматривая его правую часть как некоторую функцию $A(\zeta )$, а сумму ряда в скобках в его левой части – как функцию $b(\zeta )$, видим, что коэффициент ${{c}_{j}}$ представляет собой деленную на $(2j)!$ производную $(2j)$-го порядка функции при $\zeta = 0$. Вычисляя эту производную с помощью формулы Фаа ди Бруно с учетом разложения находим коэффициенты ${{c}_{j}}$: где $p = {{p}_{1}} + {{p}_{2}} + \ldots + {{p}_{j}}$, а суммирование выполняется по всем разбиениям $\mathfrak{P}(j)$ числа $(j)$, т.е. всем решениям $({{p}_{1}},{{p}_{2}}, \ldots ,{{p}_{j}})$ в неотрицательных целых числах уравнения

Таким образом, построено искомое представление (158) для отображения (154) с коэффициентами (159), сходящееся в полукруге ${{\mathbb{U}}_{ + }}$.

3.3. Представление для обратного отображения ${{f}^{{ - 1}}}(w)$ вблизи вершины ${{w}_{1}}$

Вводя вспомогательную переменную

приводим представление (158) к виду

Тогда для обратной к ${{V}_{1}} = \xi (\zeta )$ функции $\zeta = \Xi ({{V}_{1}})$ записываем разложение

где коэффициенты ${{C}_{m}}$ выражаются через функцию $\xi (\zeta )$ согласно формуле Бюрмана–Лагранжа (уже использовавшейся выше): Повторяя приемы, использованные при выводе формул (144)–(148), находим где суммирование выполняется по всем разбиениям $\mathfrak{P}(2m + 1)$ числа $(2m + 1)$, т.е. всем решениям $({{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{{2m + 1}}})$ в неотрицательных целых числах уравнения ${{k}_{1}} + 2{{k}_{2}} + \ldots + (2m + 1){{k}_{{2m + 1}}} = 2m + 1$.

Подставляя в правую часть разложения (162) формулу $\zeta = {{f}^{{ - 1}}}(w)$, а в левую ${{V}_{1}} = {{V}_{1}}(w)$, получим искомое представление для обратного отображения:

Здесь ${{V}_{1}}(w)$ дается формулой (160), а коэффициенты ${{C}_{m}}$ – формулой (164); это представление сходится в секторе

3.4. Представление для отображения $f(\zeta )$ вблизи прообраза ${{\zeta }_{4}} = \infty $

Переписывая интеграл (20) в виде

и подставляя для множителей внутри интеграла их разложения, перемножая их и интегрируя, получаем

Действуя аналогично п. 3.2, приводим это представление к виду

где коэффициенты ${{e}_{n}}$ даются формулой Здесь индексы $p,{{p}_{1}},{{p}_{2}}, \ldots {{p}_{n}}$, возникающие при использовании разбиения, определены аналогично вышеприведенному.

Таким образом, получено требуемое представление (169) для отображения $w = f(\zeta )$ с коэффициентами (170); это представление сходится на множестве $\mathbb{H}{{\backslash }}{{\mathbb{U}}_{ + }}(\tau )$, т.е. в замкнутой полуплоскости с выброшенным полукругом.

3.5. Представление для обратного отображения ${{f}^{{ - 1}}}(w)$ вблизи вершины ${{w}_{4}}$

Вводя переменную

приводим представление (169) к виду

Тогда для обратной к ${{V}_{4}} = \omega (\zeta )$ функции $\zeta = \Omega ({{V}_{4}})$ записываем разложение

где коэффициенты ${{E}_{m}}$ выражаются через функцию $\omega (\zeta )$ согласно формуле типа Бюрмана–Лагранжа [13]: Повторяя приемы, использованные при выводе формул (144)–(148), находим где суммирование выполняется по всем разбиениям $\mathfrak{P}(m)$ числа $m$, т.е. по всем решениям $({{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{m}})$ в неотрицательных целых числах уравнения ${{k}_{1}} + 2{{k}_{2}} + \ldots + m{{k}_{m}} = m$.

Таким образом, получено представление (173) для ${{f}^{{ - 1}}}(w)$, где ${{V}_{4}}(w)$ дается формулой (171), а коэффициенты ${{E}_{m}}$ – формулой (175); это представление сходится в секторе

3.6. Представление для отображения $f(\zeta )$ вблизи отрезка $\zeta \in [1,\tau ]$

Выполнив преобразование полуплоскости на себя,

проведя замену переменной (176) в интеграле Кристоффеля–Шварца (20) и обозначив модифицированный интеграл через $\widehat f(u): = f \circ \nu (u)$, получим для него представление

Разложив содержащиеся под знаком интеграла (177) биномы в биномиальные ряды по степеням $\xi $, перемножив их и проинтегрировав полученное разложение, приходим к следующему представлению для отображения $w = \widehat f(u)$:

выражение для коэффициентов ${{\hat {s}}_{n}}$, получаемое указанным стандартным способом, здесь опущено ввиду его громоздкости.

Приведем представление (179) к виду

Для этого, приравнивая соотношения (179) и (180), а также проводя простые преобразования, приходим к соотношению: Подействовав теперь на обе части этого равенства функцией ${\text{ch}}$ и использовав свойства приведем его к виду

С помощью приемов, использованных в п. 3.2, включая формулу Фаа ди Бруно, выводим выражение для коэффициентов ${{s}_{k}}$:

Фигурирующие здесь индексы $n$, ${{n}_{1}}$, ${{n}_{2}}, \ldots ,{{n}_{k}}$ связаны с разбиваемым номером $k$ по правилам, применявшимся выше.

Возвращаясь к исходному отображению $f(\zeta )$ с помощью обратной к (176) замены

получаем для отображения $f(\zeta )$ искомое представление вблизи отрезка $\zeta \in [1,\tau ]$, имеющее вид $f(\zeta ) = \widehat f \circ {{\nu }^{{ - 1}}}(\zeta )$, где $\widehat f$ дается формулой (180) с коэффициентами (183), а ${{\nu }^{{ - 1}}}(\zeta )$ – формулой (184).

Используя соотношение

получаем из равенства (180) искомое представление для отображения (154): где ${{\nu }^{{ - 1}}}(\zeta )$ дается формулой (184), а коэффициенты ${{s}_{k}}$ – формулой (183); это представление сходится в полукруге

3.7. Представление для обратного отображения ${{f}^{{ - 1}}}(w)$ вблизи торца

Выполнив сдвиг и поворот плоскости $w$,

и проведя замену переменной (186) в соотношении (180), получим из него следующее представление для функции $v = \mu \circ \widehat f(u)$Подействовав на обе части равенства (187) функцией ${\text{ch}}$ и обозначив $\Phi = {\text{ch}}(v)$, получаем для функции $\Phi = \mathfrak{V}(u): = {\text{ch}} \circ \mu \circ \widehat f(u)$ разложение

Тогда разложение для обратной функции записывается как

где коэффициенты ${{S}_{m}}$ выражаются через функцию $\mathfrak{V}$ по формуле Бюрмана–Лагранжа, указанной выше. Повторяя приемы, использованные при выводе формул (144)–(148), находим: где суммирование выполняется по всем разбиениям $\mathfrak{P}(m - 1)$ числа $(m - 1)$, т.е. по всем решениям $({{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{{m - 1}}})$ в неотрицательных целых числах уравнения

Для того чтобы вывести искомое представление для обратного отображения $\zeta = {{f}^{{ - 1}}}(w)$, подставим $\Phi = \mathfrak{V}(u): = {\text{ch}} \circ \mu (w)$ в разложение (189) и подействуем на обе части получаемого равенства функцией $\zeta = \nu (u)$. В результате получим требуемое представление

где $\nu (u)$ и $\mu (w)$ – линейные преобразования (176) и (186), а коэффициенты ${{S}_{m}}$ определяются из (190). Это представление сходится в области являющейся полкой отображаемой $L$-образной области.

4. КРОУДИНГ И ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

4.1. Асимптотика расстояния между прообразами при длинной и короткой полке

Во введении было отмечено, что при удлинении или укорочении относительной длины полки (величины $A{\text{/}}h$) расстояния между некоторыми прообразами быстро сокращаются. Явление скучивания прообразов вершин (или других характерных точек отображаемых областей), называемое кроудингом, носит довольно общий характер и часто возникает при конформном отображении (см., например, [5]–[8], [20]–[23]).

Для рассматриваемого в работе отображения $f:\mathbb{H}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{L}(\beta ,A,h)$ с нормировкой (1) при увеличении относительной длины полки $A{\text{/}}h$ резко сокращается расстояние $\tau - 1$ между прообразами вершин ${{w}_{3}}$ и ${{w}_{2}}$. Для получения асимптотики расстояния $\tau - 1$ при $A{\text{/}}h \to \infty $, т.е. при $\delta = \exp \left( { - \pi \tfrac{A}{h}} \right) \to 0$, подставим разложение (87) в биномиальный ряд для $\tau = (1 - \varepsilon {{)}^{{ - 1/2}}}$ с учетом формул (153); в результате получим

Для отображения другой канонической области, круга $\mathbb{U}$ на $L$-образную область, т.е. для отображения ${{f}_{\mathbb{U}}}(\xi ):\mathbb{U}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{L}(\beta ,A,h)$ с нормировкой (12) возникает сближение прообразов ${{\xi }_{3}}$ и ${{\xi }_{5}}$ к прообразу ${{\xi }_{4}}$ (см. фиг. 3б) при укорочении полки, т.е. при $A{\text{/}}h \to 0$.

Чтобы получить соответствующую асимптотику, прежде всего представим это отображение в виде суперпозиции ${{f}_{\mathbb{U}}}(\xi ) = f \circ \Upsilon (\xi )$. Здесь $w = f(\zeta )$ – исходное отображение, а $\zeta = \Upsilon (\xi )$ – отображение круга на полуплоскость

где (чисто мнимая величина) ${{\zeta }_{0}}$ – прообраз точки ${{w}_{0}}$ при отображении $w = f(\zeta )$.

Используя интегральное представление (20) для отображения $w = f(\zeta )$, получим уравнения для длин $h$ и $A$ области $\mathbb{L}(\beta ,A,h)$, проинтегрировав в этом представлении соответственно от $\zeta = 1$ до $\zeta = \tau $ и от $\zeta = \tau $ до $\zeta = \infty $. В результате получим систему уравнений для $\mathcal{K}$ и $\tau $. Разделив второе уравнение на первое, находим (после анализа, аналогичного проведенному в п. 2.2) асимптотики для $\tau $ и $\mathcal{K}$ при $A{\text{/}}h \to 0$:

Для получения прообраза ${{\zeta }_{0}}$ проинтегрируем (20) от $\zeta = 0$ до $\zeta = {{\zeta }_{0}}$ и приравняем результат к $ - h\operatorname{cosec} (\pi \beta {\text{/}}2){\text{/}}2$. Подставив найденную ${{\zeta }_{0}}$ и асимптотику (194) для $\tau $ в выражение (193) для функции ${{\Upsilon }^{{ - 1}}}( - \tau )$, найдем асимптотику для ${{\xi }_{5}} = {{e}^{{i\theta }}}$. Это дает

Для частного случая $\beta = 3{\text{/}}2$ эта асимптотика принимает вид:

4.2. Численные результаты

Для вычисления искомых параметров $\tau $ и $\mathcal{K}$ интеграла Кристоффеля–Шварца (20) вначале находится модифицированный прообраз $\varepsilon $ с помощью ряда (87) по степеням $\delta $. Коэффициенты ${{B}_{m}}$ этого ряда получаются по формулам (89), (150), (152), а величина $Q$ – по формуле (49). Значения величины $Q$ для некоторых $\beta $ приведены в табл. 3, а значения параметра $\delta $ для некоторых $A{\text{/}}h$ – в табл. 1.

В п. 2.8 была отмечена высокая эффективность численной реализации такого способа вычисления величины $\varepsilon $: для ее получения с относительной точностью ${{10}^{{ - 20}}}$ на процессоре средней производительности Intel Core i3 потребовалось время порядка ${{10}^{{ - 3}}}$ с.

По найденному $\varepsilon $ искомый прообраз $\tau $ и множитель $\mathcal{K}$ вычисляются с помощью равенств (33), (34). Значения прообраза $\tau $ для некоторых $\beta $ и $A{\text{/}}h$ даны в табл. 2.

Необходимо подчеркнуть высокую вычислительную эффективность изложенного в разд. 3 метода построения отображений $w = f(\zeta )$ и $\zeta = {{f}^{{ - 1}}}(w)$. Так, для вычисления функции $f(\zeta )$ в любой точке полуплоскости $\mathbb{H}$ или функции ${{f}^{{ - 1}}}(w)$ в любой точке области $\mathbb{L}(\beta ,A,h)$ с относительной точностью ${{10}^{{ - 10}}}$ на процессоре Intel Core i3 требовалось время порядка ${{10}^{{ - 3}}}$ с.

Численная реализация отображения $w = f(\zeta )$ полуплоскости на область $\mathbb{L}(\beta ,A,h)$ была продемонстрирована на примерах ее сочетания с дробно-линейным отображением либо с эллиптическим синусом. Отметим, что во всех примерах полка $L$-образной области бралась единичной ширины, поэтому мы полагали $h = 1$.

1. В качестве первого примера рассмотрена область $\mathbb{L}(\beta ,A,1)$ с параметрами $\pi \beta = 310^\circ $, $A = 0.45$, а в качестве отображения взята суперпозиция

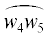функции $f$ с дробно-линейной функцией $\widetilde \Upsilon $, выполняющей автоморфизм верхней полуплоскости. Суперпозиция (198) осуществляет отображение ${{\widetilde f}_{\mathbb{H}}}:\mathbb{H}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{L}(\beta ,A,1)$ и обеспечивает нормировку (14). Фигурирующие в этой нормировке точки ${{w}_{0}}$ и ${{w}_{\infty }}$ заданы соответственно на сторонах и 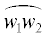, а их прообразы $f({{\zeta }_{0}})$ и $f({{\zeta }_{\infty }})$, присутствующие в (198), находятся по формулам алгоритм вычисления используемой здесь функции $\zeta = {{f}^{{ - 1}}}(w)$ приведен в разд. 3. На фиг. 4 даны результаты численной реализации отображения $w = {{\widetilde f}_{\mathbb{H}}}(\widetilde \zeta )$ в виде образа декартовой сетки полуплоскости $\widetilde \zeta $. Картина этой сетки в увеличенном масштабе вблизи вершины входящего угла приведена на фиг. 5.

2. В качестве второго примера рассмотрена область $\mathbb{L}(\beta ,A,1)$ с параметрами $\pi \beta = 250^\circ $, $A = 1.5$, а в качестве отображения взята суперпозиция

функции $f$ с дробно-линейной функцией $\Phi $, выполняющей отображение единичного круга на верхнюю полуплоскость. Суперпозиция (201) осуществляет отображение ${{\widetilde f}_{\mathbb{U}}}:\mathbb{U}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{L}(\beta ,A,1)$ и обеспечивает нормировку Здесь прообраз ${{\zeta }_{0}}$ на плоскости $\zeta $ точки ${{w}_{0}}$, заданной в области $\mathbb{L}(\beta ,A,1)$, находится по формуле ${{\zeta }_{0}} = {{f}^{{ - 1}}}({{w}_{0}})$, где функция ${{f}^{{ - 1}}}(w)$, как и в предыдущем примере, строится с помощью метода, изложенного в разд. 3. На фиг. 6 построен образ полярной сетки круга, а сама полярная сетка дана на фиг. 7.

3. В качестве третьего примера рассмотрено отображение прямоугольника

единичной ширины и длины $l = 4.1$ на область $\mathbb{L}(\beta ,A,1)$ со входящим углом $\pi \beta = 290^\circ $ и с полкой такой длины $A$, что выполняются условия нормировки (15). Введем полные эллиптические интегралы $K(k)$ и $K{\kern 1pt} '{\kern 1pt} (k)$, соответствующие модулю $k$ эллиптического синуса ${\text{sn}}(z;k)$ (см. [14], [37]) и выразим их через функцию Гаусса: Тогда, как можно убедиться, требуемое отображение ${{f}_{\mathbb{P}}}(\eta ):\mathbb{P}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{L}(\beta ,A,1)$, обеспечивающее предписанную нормировку (15), представляется в виде суперпозиции исходной функции $f$ с функцией, выражающейся через эллиптический синус При этом модуль $k$ находится из уравнения Тогда, подставив $\tau = 1{\text{/}}k$ в (27), а найденное $\varepsilon $ в формулу (32), получаем из нее искомую длину полки $A$. Для рассматриваемого примера вычисления дали $A = 1.7281235849$.