Журнал вычислительной математики и математической физики, 2022, T. 62, № 12, стр. 1981-2001

ВВЕДЕНИЕ

Численные методы решения задач газовой динамики относятся к основным в вычислительной математике. Им посвящена обширная литература (см. [1]–[4] и цитированную там литературу). Большой теоретический и прикладной интерес представляют условия устойчивости таких методов, в том числе явных по времени.

Среди этих численных методов существует класс методов, основанных на предварительной регуляризации уравнений газовой динамики. К ним относятся явные методы с симметричной аппроксимацией по пространству, основанные на так называемых квазигазодинамической и квазигидродинамической (КГидД) регуляризациях, которые были успешно использованы для решения широкого круга прикладных задач (см. [5]–[8]). В том числе такие методы применялись для разнообразных задач в баротропной постановке (см., например, [9]–[12]). При этом всегда использовались схемы на неразнесенных сетках, где основные искомые функции определены на одной и той же сетке по пространству. Анализ условий ${{L}^{2}}$-диссипативности таких схем в линеаризованной баротропной постановке был недавно выполнен в [13]–[16]. Отметим, что в последние годы развито немало других подходов к построению численных методов решения уравнений газовой динамики, основанных на их различных регуляризациях (см. в том числе [17]–[20]).

Схемы на разнесенных сетках также хорошо известны в вычислительной гидродинамике (см. [21]), и спектральный анализ устойчивости, включая условие фон Неймана, для подобных схем был дан в [22]–[24]. Недавно в [25] впервые была построена и успешно апробирована явная схема на разнесенных сетках с КГидД регуляризацией для 3D уравнений Навье–Стокса–Кана–Хилларда. Позже в [26] выведен в том числе критерий (необходимое и достаточное условие) ${{L}^{2}}$-диссипативности такой схемы, линеаризованной на постоянном решении в случае 1D баротропных уравнений Эйлера и Навье–Стокса сжимаемого газа при нулевом фоновом числе Маха $M = 0$. Однако этот результат применим на практике только при малых $M$.

В настоящей работе изучается ${{L}^{2}}$-диссипативность линеаризованной на постоянном решении схемы на разнесенных сетках из [25] для указанных 1D систем уравнений, но в существенно более сложном случае любого M. Используется спектральный метод (см., например, [3], [27]), но анализируются не собственные значения несамосопряженной матрицы-символа соответствующего оператора перехода со слоя на слой, а матричные неравенства, содержащие символы симметричных матриц конвективных и регуляризующих слагаемых. Критерий ${{L}^{2}}$-диссипативности выглядит слишком громоздко, и основное внимание уделяется выводу более простых близких друг к другу необходимых условий и достаточных условий (отличающихся не более чем в 4 и ровно в 2 раза). Возможность получения не только достаточных, но и необходимых условий является важным достоинством спектрального метода. При этом как вывод результатов, так и их формулировки оказываются заметно более сложными, чем в случае схем на неразнесенных сетках (см. [14], [15]). Выполненный анализ дает указание на выбор параметров схемы, позволяющий брать максимальный шаг по времени. Для случая уравнений Навье–Стокса (без использования искусственной вязкости) впервые указаны формулы для выбора шага по времени при $M \ne 0$. Существенно, что разработанная техника анализа достаточно общая и применима и в случае регуляризаций другого типа (в качестве примера см. [28]).

Естественность анализа именно свойства ${{L}^{2}}$-диссипативности схемы связана с тем, что оно соответствует важному с точки зрения качества КГидД регуляризации свойству, доказанному в линеаризованной дифференциальной постановке [29], и его выполнение обеспечивает не только устойчивость в ${{L}^{2}}$-норме, но и лучшее качество численного решения. Спектральное условие устойчивости фон Неймана служит для этого свойства лишь необходимым условием и само по себе не гарантирует устойчивости в какой-либо норме. В работе выясняется, что оно заметно грубее критерия ${{L}^{2}}$-диссипативности уже в случае $M = 0$. К тому же выполненные численные эксперименты в исходной нелинейной постановке показывают, что ${{L}^{2}}$-диссипативность является более тонким инструментом по сравнению с условием фон Неймана для того, чтобы добиться устранения или существенного уменьшения осцилляций решения.

1. РЕГУЛЯРИЗОВАННЫЕ УРАВНЕНИЯ И РАЗНОСТНАЯ СХЕМА НА РАЗНЕСЕННЫХ СЕТКАХ

КГидД 1D баротропная система уравнений движения вязкого сжимаемого газа без учета внешних сил состоит из следующих уравнений баланса массы и импульса:

где $\rho > 0$ и $u$ – искомые плотность и скорость газа, зависящие от $(x,t)$, $x \in \mathbb{R}$, $t \geqslant 0$, а ${{\partial }_{t}} = \partial {\text{/}}\partial t$, ${{\partial }_{x}} = \partial {\text{/}}\partial x$. Также $p(\rho )$ – давление, $p(\rho ) \in {{C}^{2}}(0, + \infty )$, $p{\kern 1pt} '(\rho ) > 0$.

Регуляризованный поток массы $j$, регуляризующая скорость $\hat {w}$ и вязкое напряжение $\Pi $ задаются формулами

Здесь $\mu {{\partial }_{x}}u$ и ${{\Pi }^{\tau }}$ – вязкие типа Навье–Стокса и регуляризующее напряжения, $\tau = \tau (\rho ,u) > 0$ – параметр регуляризации, $\mu = {{\mu }_{{{\text{ph}}}}} + {{\mu }_{{{\text{art}}}}}$, ${{\mu }_{{{\text{ph}}}}}$ и ${{\mu }_{{{\text{art}}}}} = \tau {{\alpha }_{s}}\rho p{\kern 1pt} '(\rho )$ – соответственно коэффициенты полной, физической (суммарной динамической и объемной) и искусственной вязкости, которые могут зависеть от $\rho $ и $u$. Кроме того, ${{\alpha }_{s}} \geqslant 0$ – число Шмидта; его можно использовать и как параметр численного метода. Пусть $\nu = \mu {\text{/}}\rho = {{\nu }_{{{\text{ph}}}}} + \tau {{\alpha }_{s}}p{\kern 1pt} '(\rho )$ и ${{\nu }_{{{\text{ph}}}}} = {{\mu }_{{{\text{ph}}}}}{\text{/}}\rho $ – соответствующие коэффициенты кинематической вязкости.

Введем сетку ${{\omega }_{h}}$ с узлами ${{x}_{k}} = kh$ и сдвинутую сетку $\omega _{h}^{*}$ с узлами ${{x}_{{k - 1/2}}} = (k - 1{\text{/}}2)h$, $k \in \mathbb{Z}$, с шагом $h > 0$, а также сетку ${{\bar {\omega }}^{{\Delta t}}}$ с узлами ${{t}_{m}} = m\Delta t$, $m \geqslant 0$ и шагом $\Delta t > 0$.

Введем операторы на функциях $v$, $w$, $y$, заданных на сетках ${{\omega }_{h}}$, $\omega _{h}^{*}$, ${{\bar {\omega }}^{{\Delta t}}}$ соответственно:

где ${{v}_{k}} = v({{x}_{k}})$, ${{w}_{{k - 1/2}}} = w({{x}_{{k - 1/2}}})$, ${{y}^{m}} = y({{t}_{m}})$. Отметим, что и .

Введем известную первообразную функцию – энтальпию:

где ${{r}_{0}} > 0$ (см. ее подробное обсуждение в [30]). В [25] была построена явная двухслойная по времени 3D разностная схема с КГидД регуляризацией на разнесенных сетках, принимающая в 1D постановке (1), (2) вид на ${{\bar {\omega }}^{{\Delta t}}}$. Здесь $\rho $ и $u$ заданы по пространству на разнесенных сетках $\omega _{h}^{*}$ и ${{\omega }_{h}}$ соответственно. Отметим, что нестандартная аппроксимация типа ${{\partial }_{x}}p(\rho ) \approx (s{\kern 1pt} *{\kern 1pt} \rho )\delta {\kern 1pt} *{\kern 1pt} {{P}_{1}}(\rho )$ была предложена в [30, c. 62] для неразнесенных сеток. В данной схеме пространственная дискретизация неконсервативна по импульсу, зато диссипативна по полной энергии (см. [25]).

2. КРИТЕРИЙ ${{L}^{2}}$-ДИССИПАТИВНОСТИ ЛИНЕАРИЗОВАННОЙ СХЕМЫ И ДОПОЛНИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ

Выписанную схему линеаризуем на постоянном решении ${{\rho }_{*}} = {\text{const}} > 0$, ${{u}_{*}} = {\text{const}}$. Для этого запишем ее решение в виде $\rho = {{\rho }_{*}} + {{\rho }_{*}}\tilde {\rho }$, $u = {{u}_{*}} + {{c}_{*}}\tilde {u}$, подставим в уравнения схемы, отбросим слагаемые второго порядка малости по отношению к обезразмеренным возмущениям $\tilde {\rho }$, $\tilde {u}$ и получим линеаризованную схему

где ${{\tau }_{*}} = {{\tau }_{*}}({{\rho }_{*}},{{u}_{*}})$, ${{c}_{*}} = \sqrt {p{\kern 1pt} '({{\rho }_{*}})} $, ${{\nu }_{*}} = {{\nu }_{{{\text{ph}}*}}} + {{\tau }_{*}}{{\alpha }_{s}}c_{*}^{2}$ и ${{\nu }_{{{\text{ph}}*}}}$ – фоновые параметр регуляризации, скорость звука и кинематические вязкости. Заметим, что линеаризованная схема не меняется при замене слагаемого $\delta {\kern 1pt} *{\kern 1pt} {{P}_{1}}(\rho )$ на более стандартное ${{(s{\kern 1pt} *{\kern 1pt} \rho )}^{{ - 1}}}\delta {\kern 1pt} *{\kern 1pt} p(\rho )$ в (3), (4). Ниже тильды над возмущениями $\tilde {\rho }$, $\tilde {u}$ отбросим для упрощения обозначений.

Пусть $H(\omega )$ – гильбертово пространство комплекснозначных функций, определенных и суммируемых в квадрате на сетке $\omega $. Введем также гильбертово пространство пар функций $(\rho ,u) \in {\mathbf{H}}: = H(\omega _{h}^{*}) \times H({{\omega }_{h}})$ с обычными скалярным произведением и нормой

где * означает комплексное сопряжение.

Перепишем схему (6), (7) в рекуррентном виде

с безразмерными величинами $M: = {{u}_{*}}{\text{/}}{{c}_{*}}$ и ${{\tilde {\nu }}_{*}}: = {{\nu }_{*}}{\text{/}}({{\tau }_{*}}c_{*}^{2}) = {{\nu }_{{{\text{ph}}*}}}{\text{/}}({{\tau }_{*}}c_{*}^{2}) + {{\alpha }_{s}}$; при этом ${\text{|}}M{\kern 1pt} {\text{|}}$ – фоновое число Маха.

Поставим вопрос об условиях выполнения для решения схемы (8), (9) оценки

Изучать их достаточно естественно, поскольку соответствующая оценка доказана для решения задачи Коши для линеаризованной системы уравнений (1) (см. [29]). Более того, напомним, что оценка (10) означает, что $\mathop {\sup }\limits_{m \geqslant 0} {{\left\| {{{{\mathbf{G}}}^{m}}} \right\|}_{{{\mathbf{H}} \to {\mathbf{H}}}}} \leqslant 1$, где ${\mathbf{G}} = {\mathbf{I}} - \Delta t{{c}_{*}}{\mathbf{B}} + \Delta t{{\tau }_{*}}c_{*}^{2}{\mathbf{A}}$ – оператор перехода со слоя на слой c действующими в ${\mathbf{H}}$ единичным оператором ${\mathbf{I}}$ и операторами конвективных и вязких слагаемых ${\mathbf{B}}$ и ${\mathbf{A}}$ такими, что Эквивалентно, ${{\left\| {\mathbf{G}} \right\|}_{{{\mathbf{H}} \to {\mathbf{H}}}}} \leqslant 1$. Поэтому, в свою очередь, оценка (10) эквивалентна важному свойству ${{L}^{2}}$-диссипативности схемы

Замечание 1. Для более полного анализа устойчивости нетрудно рассмотреть неоднородный вариант схемы (6), (7) с заменой нулей в ее правых частях на заданные функции ${{f}_{\rho }},\;{{f}_{u}}$ соответственно. А именно, при ${{\left\| {\mathbf{G}} \right\|}_{{{\mathbf{H}} \to {\mathbf{H}}}}} \leqslant 1$ верна оценка

Пусть $\Delta t$ и ${{\tau }_{*}}$ задаются стандартными формулами (см. [6], [7]):

с параметрами $\beta > 0$ и $\alpha > 0$. В данном разделе дается необходимое и достаточное условие на $\beta $ в зависимости от $\alpha $ для выполнения оценки (10) в случае ${{\mu }_{{{\text{ph}}}}} = 0$.

Для этого в соответствии со спектральным подходом (см., например, [3], [27]) подставим в уравнения (8), (9) частное решение вида

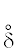где ${\mathbf{i}}$ – мнимая единица и $\xi \in [0,2\pi ]$ – параметр. Функция ${{e}^{{{\mathbf{i}}k\xi }}}$ является собственной для операторов и $ - \delta {\kern 1pt} *{\kern 1pt} \delta $, а ${{e}^{{{\mathbf{i}}(k - 1/2)\xi }}}$ – операторов и $ - \delta \delta {\kern 1pt} *$, и они отвечают соответственно одним и тем же собственным значениям ${\mathbf{i}}{{h}^{{ - 1}}}\sin \xi = {\mathbf{i}}2{{h}^{{ - 1}}}{{s}_{\xi }}{{c}_{\xi }}$ и $4{{h}^{{ - 2}}}s_{\xi }^{2}$, где ${{s}_{\xi }} = \sin (\xi {\text{/}}2)$ и ${{c}_{\xi }} = \cos (\xi {\text{/}}2)$. Кроме того, имеем Использовав эти формулы и (11), получим рекуррентные формулы

Введем вектор-столбец ${\mathbf{w}} = ({{w}_{\rho }},{{w}_{u}}{{)}^{{\text{T}}}}$ и перейдем к матричной форме записи

при ${{\mu }_{{{\text{ph}}}}} = 0$. Ее удобно переписать в компактном виде: с использованием $2 \times 2$ матриц где $G(q)$ – символ оператора ${\mathbf{G}}$, $B(q)$ и $A(q)$ пропорциональны символам операторов ${\mathbf{B}}$ и ${\mathbf{A}}$, $I$ – единичная матрица 2-го порядка, $q = q(\xi ) = {{M}^{2}}{{\cos }^{2}}(\xi {\text{/}}2)$, $\sigma = {{\sin }^{2}}(\xi {\text{/}}2)$, причем $\sigma = 1 - q{\text{/}}{{M}^{2}}$ при $M \ne 0$, а $ \pm = (sgnM)\operatorname{sgn} \cos (\xi {\text{/}}2)$.

Теорема 1. Пусть ${{\mu }_{{{\text{ph}}}}} = 0$ и $M \ne 0$. Для ${{L}^{2}}$-диссипативности схемы (6), (7) необходимо и достаточно выполнение матричного неравенства

для всех $0 \leqslant q \leqslant {{M}^{2}}$, где $Q(q)$ – эрмитова матрица, $Q(q) \geqslant 0$ при $0 \leqslant q \leqslant {{M}^{2}}$, а $[A,B] = AB - BA$ . При $M = 0$ (т.е. ${{u}_{*}} = 0$) результат сохраняет силу с заменой параметра $0 \leqslant q \leqslant {{M}^{2}}$ на $0 \leqslant \sigma \leqslant 1$.

Доказательство. Согласно [26, лемма 1], свойство диссипативности (10) эквивалентно спектральной оценке

где ${{\lambda }_{{\max }}}(C)$ – максимальное собственное значение эрмитовой матрицы $C$.

Подобно [15, теорема 1], эта оценка эквивалентна матричному неравенству $G{\kern 1pt} *{\kern 1pt} G \leqslant I$, т.е. неравенству $\beta F{\kern 1pt} *{\kern 1pt} F \leqslant F + F{\kern 1pt} *$, при всех $0 \leqslant q \leqslant {{M}^{2}}$. Для $F = {{F}_{R}} + {\mathbf{i}}{{F}_{I}}$ с эрмитовыми матрицами ${{F}_{R}} = 4\alpha \sigma A(q)$ и ${{F}_{I}} = 2\sqrt \sigma B(q)$ оно принимает вид

и после сокращения на $8\alpha \sigma $ при $\sigma \ne 0$ (т.е. $q \ne {{M}^{2}}$) переходит в (14) с $Q = (8\alpha \sigma {{)}^{{ - 1}}}F{\kern 1pt} *{\kern 1pt} F \geqslant 0$. По непрерывности (14) выполняется и при $q = {{M}^{2}}$.

В случае $M = 0$ имеем $q = 0$, и за параметр следует взять $0 \leqslant \sigma \leqslant 1$.

Укажем для дальнейшего, что верны формулы

По свойствам спектральной нормы матриц имеем

Поскольку ${\text{|}}\lambda (G){\kern 1pt} {\text{|}} \leqslant {{\left\| G \right\|}_{2}}$ для собственных значений $\lambda (G)$ любой матрицы $G$, то спектральное условие устойчивости фон Нейманаследует из спектральной оценки (15) и поэтому служит лишь необходимым условием ${{L}^{2}}$-диссипативности. При этом оно не гарантирует устойчивость схемы в какой-либо норме. Хотя условия типа (18) широко используются в литературе (см. в том числе для разнесенных сеток [22], [24]), убедимся, что здесь оно оказывается слишком грубым в сравнении с (15) даже в относительно простом частном случае $M = 0$.

Теорема 2. Пусть ${{\mu }_{{{\text{ph}}}}} = 0$ и $M = 0$. Спектральное условие устойчивости фон Неймана (18) для схемы (6), (7) выполнено, если и только если

Доказательство. В условиях теоремы $q = 0$ и согласно формулам (12), (13) матрицу $G$ можно записать в виде

Аналогичная матрица изучалась в [14, теорема 1], где показано, что при ${{\alpha }_{s}}\omega _{1}^{2} + \omega _{2}^{2} > 0$ условие (18) для нее сводится к выполнению двух неравенств: Если же ${{\alpha }_{s}}\omega _{1}^{2} + \omega _{2}^{2} = 0$, то ${{\omega }_{2}} = 0$, $\sigma = 0$, ${{\omega }_{1}} = 0$, и тогда $G = I$, а последние неравенства выполнены. Таким образом, должны выполняться неравенства

Неравенство (20) приводит к условию

В случае ${{\alpha }_{s}} > 0$ в неравенстве (21) вершина квадратного трехчлена ${{r}_{2}}(\sigma )$ такова: Свойство ${{\sigma }_{{v}}} > 1$ эквивалентно неравенству $\beta < ({{\alpha }_{s}} + 1)\alpha {\text{/}}(4{{\alpha }_{s}}{{\alpha }^{2}} + 0.5)$, выполненному в силу (22). Поэтому ${{r}_{2}}(\sigma )$ убывает на $[0,1]$, и неравенство (21) сводится к неравенству В случае ${{\alpha }_{s}} = 0$ неравенство (21) упрощается до $\beta (2\alpha - \beta )\sigma \leqslant 1$ для всех $0 \leqslant \sigma \leqslant 1$, а поскольку здесь $\beta \leqslant \alpha $ в силу (22), то и до неравенства $\beta (2\alpha - \beta ) \leqslant 1$, совпадающего с (23) при ${{\alpha }_{s}} = 0$.

Детерминант квадратного трехчлена относительно $\beta $ в левой части неравенства (23) равен $4[({{\alpha }_{s}} - {{1)}^{2}}{{\alpha }^{2}} - 1]$, а его вершина совпадает с правой частью (22). Поэтому с учетом условия (22) неравенство (23) означает, что

В сочетании с (22) это приводит к условию (19).

Проанализировав максимумы каждой из функций в (19), можно показать, что ${{\beta }_{{{v}N}}} \leqslant 1$.

При $M = 0$ в [26] был дан критерий ${{L}^{2}}$-диссипативности схемы (6), (7) , имеющий вид

Учитывая, что $({{\alpha }_{s}} + 1)\; - \;{\text{|}}{{\alpha }_{s}} - 1{\text{|}} = 2\min \{ {{\alpha }_{s}},1\} $, легко видеть, что ${{\beta }_{{{\text{cr}}}}} < {{\beta }_{{{v}N}}}$ при всех ${{\alpha }_{s}} \geqslant 0$, ${{\alpha }_{s}} \ne 1$ либо ${{\beta }_{{{\text{cr}}}}} = {{\beta }_{{vN}}}$ при ${{\alpha }_{s}} = 1$ (для всех $\alpha > 0$) (см. также фиг. 1). В том числе при ${{\alpha }_{s}} = 0$ имеем ${{\beta }_{{{\text{cr}}}}} = 0$ и ${{L}^{2}}$-диссипативность отсутствует, тогда как ${{\beta }_{{vN}}} = \alpha - \sqrt {\max \{ {{\alpha }^{2}} - 1,0\} } > 0$. Для схем с регуляризациями на неразнесенных сетках различие между условиями, соответствующими (19) и (24), было установлено в (14). Однако здесь для схемы на разнесенных сетках оно более существенно, а поведение ${{\beta }_{{{v}N}}}$ заметно сложнее.

Указанное совпадение при ${{\alpha }_{s}} = 1$ не случайно. В этом частном случае матрица $G = G(q)$ обладает свойством $G{\kern 1pt} *{\kern 1pt} G = GG{\kern 1pt} *$, т.е. является нормальной, поэтому она унитарно подобна диагональной матрице, и максимальный из ${\text{|}}\lambda (G){\kern 1pt} {\text{|}}$ равен ${{\left\| G \right\|}_{2}}$. Свойство $G{\kern 1pt} *G = GG{\kern 1pt} *$ эквивалентно свойству $F{\kern 1pt} *{\kern 1pt} F = F{\kern 1pt} *$ и далее $[A,B] = AB - BA = 0$ (при $\sigma \ne 0$) (см. (17)).

Пусть ${\text{|}}A{\kern 1pt} {\text{|}}$ – детерминант матрицы $A$, а $z = {{z}_{R}} + {\mathbf{i}}{{z}_{I}}$ – стандартная запись числа $z \in \mathbb{C}$. Ниже для применения теоремы 1 существен следующий алгебраический критерий.

Лемма 1. Рассмотрим произвольные вещественную симметричную и комплексную эрмитову матрицы

с любым $q \in \mathbb{C}$. Пусть также $A > 0$, $Q \geqslant 0$. Неравенство $\zeta A \geqslant Q$ с параметром $\zeta \geqslant 0$ выполнено, если и только еслигде $b: = {{a}_{1}}{{q}_{2}} + {{a}_{2}}{{q}_{1}} - 2a{{q}_{R}}$. В этом неравенстве ${{b}^{2}} \geqslant 4\left| A \right|\left| Q \right|$, а $b > 0$ при $Q \ne 0$.

Доказательство. По критериям Сильвестра положительной определенности и неотрицательной определенности матриц имеем

При $Q = 0$ неравенство (25) просто означает, что $\zeta \geqslant 0$. Пусть ниже $Q \ne 0$, тогда ${{q}_{1}} > 0$ либо ${{q}_{2}} > 0$.

По второму из упомянутых критериев неравенство $\zeta A - Q \geqslant 0$ эквивалентно системе неравенств

С использованием введенной выше величины $b$ их можно переписать в виде

Вычислим величину

при ${{q}_{1}} > 0$. Аналогично проверяется формула при ${{q}_{2}} > 0$. Отсюда следует, что квадратный трехчлен ${{p}_{2}}(\zeta )$ имеет корень ${{\zeta }_{1}} > 0$, и поэтому его детерминант ${{b}^{2}} - 4\left| A \right|\left| Q \right| \geqslant 0$. Более того, второй корень ${{\zeta }_{2}}$ тоже положителен при ${\text{|}}Q{\kern 1pt} {\text{|}} > 0$ либо равен 0 при ${\text{|}}Q{\kern 1pt} {\text{|}} = 0$ (так как ${\text{|}}A{\kern 1pt} {\text{|}}{{\zeta }_{1}}{{\zeta }_{2}} = {\text{|}}Q{\kern 1pt} {\text{|}}$). Тем самым $b = {\text{|}}A{\kern 1pt} {\kern 1pt} {\text{|}}({{\zeta }_{1}} + {{\zeta }_{2}}) > 0$.

Теперь квадратное неравенство (27) в сочетании с (26) приводит к условию (25), где справа стоит бóльший из корней ${{\zeta }_{1}}$, ${{\zeta }_{2}}$.

Замечание 2. Как правило, $\Delta : = {{b}^{2}} - 4\left| A \right|\left| Q \right| > 0$ при $Q \ne 0$, за исключением специального случая. А именно, $\Delta = 0$ при $Q \ne 0$ означает, что ${{\zeta }_{1}} = {{\zeta }_{2}}$. Тогда при ${{q}_{1}} = 0$ либо ${{q}_{2}} = 0$ имеем $\Delta = {{b}^{2}} > 0$, откуда ${{q}_{1}} > 0$ и ${{q}_{2}} > 0$. Тогда в силу (28) имеем ${{p}_{2}}({{q}_{1}}{\text{/}}{{a}_{1}}) = 0$, и поэтому $a{\text{/}}{{a}_{1}} = {{q}_{R}}{\text{/}}{{q}_{1}}$ и ${{q}_{I}} = 0$. Аналогично, в силу (29) имеем $a{\text{/}}{{a}_{2}} = {{q}_{R}}{\text{/}}{{q}_{2}}$, и далее ${{q}_{R}}({{a}_{1}}{\text{/}}{{q}_{1}} - {{a}_{2}}{\text{/}}{{q}_{2}}) = 0$. Если ${{q}_{R}} \ne 0$, то ${{a}_{1}}{\text{/}}{{q}_{1}} - {{a}_{2}}{\text{/}}{{q}_{2}} = 0$. Если ${{q}_{R}} = 0$, то $a = 0$ и $\Delta = ({{a}_{1}}{{q}_{2}} + {{a}_{2}}{{q}_{1}}{{)}^{2}} - 4{{a}_{1}}{{a}_{2}}{{q}_{1}}{{q}_{2}} = ({{a}_{1}}{{q}_{2}} - {{a}_{2}}{{q}_{1}}{{)}^{2}}$, и при $\Delta = 0$ опять ${{a}_{1}}{\text{/}}{{q}_{1}} - {{a}_{2}}{\text{/}}{{q}_{2}} = 0$. Эквивалентно, ${{a}_{2}}{\text{/}}{{a}_{1}} = {{q}_{2}}{\text{/}}{{q}_{1}} = \theta > 0$. Таким образом, приходим к матрицам

(здесь $A > 0$ и $Q \geqslant 0$ при ${{a}_{1}} > 0$, $\theta > 0$, ${\text{|}}q{\kern 1pt} {\text{|}} < \sqrt \theta {{q}_{1}}$). Для таких матриц имеем

Следствие 1. В условиях леммы 1 для выполнения неравенства $\zeta A \geqslant Q$ с $\zeta \geqslant 0$ необходимо, чтобы $\zeta \geqslant b{\text{/}}(2{\kern 1pt} {\text{|}}A{\kern 1pt} {\text{|}}{\kern 1pt} )$, и достаточно, чтобы $\zeta \geqslant b{\text{/|}}A{\kern 1pt} {\text{|}}$. В эти условия не входит ${\text{|}}Q{\kern 1pt} {\text{|}}$.

В самом деле, в силу свойств ${{b}^{2}} - 4\left| A \right|\left| Q \right| \geqslant 0$, $\left| A \right|\left| Q \right| \geqslant 0$ и $b \geqslant 0$ результат следует из оценок $b \leqslant b + \sqrt {{{b}^{2}} - 4\left| A \right|\left| Q \right|} \leqslant 2b$.

3. НЕОБХОДИМЫЕ УСЛОВИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ L²-ДИССИПАТИВНОСТИ

Следующий результат можно считать основным в данной работе.

Теорема 3. Пусть ${{\mu }_{{{\text{ph}}}}} = 0$, ${{\alpha }_{s}} > 0$ и $M \ne 0$. Для ${{L}^{2}}$-диссипативности схемы (6), (7) необходимо выполнение неравенства

и достаточно выполнение неравенствагде

Доказательство. В силу теоремы 1 и леммы 1 в применении к матрицам $A(q)$ и $Q(q)$, введенным в (13) и (14), для ${{L}^{2}}$-диссипативности схемы (6), (7) необходимо и достаточно, чтобы выполнялось неравенство

где $b = {{a}_{{11}}}{{q}_{{22}}} + {{a}_{{22}}}{{q}_{{11}}} - 2{{a}_{{12}}}{{q}_{{12{\kern 1pt} R}}}$ и учтено, что ${\text{|}}A(q){\kern 1pt} {\text{|}} = {{\alpha }_{s}}$.   Из формул (13) и (16) следует, что с квадратными трехчленами относительно $q$ (зависящими также от ${{\alpha }_{s}}$ и $M$)

По следствию 1 необходимым условием выполнения критерия (34) служат неравенства

Корнями квадратного трехчлена ${{b}_{1}}(q)$ являются $q = - {{\alpha }_{s}} - 1$ и $q = {{M}^{2}}$. Он является вогнутой функцией по $q$ и ${{b}_{1}}(0) = {{\alpha }_{s}} + 1$. Его вершиной является ${{q}_{{1v}}} = 0.5{{M}^{2}}[1 - ({{\alpha }_{s}} + 1){\text{/}}{{M}^{2}}]$, и Поскольку ${{q}_{{1v}}} \geqslant 0$ при ${{M}^{2}} \geqslant {{\alpha }_{s}} + 1$, то верна формула (32).

Имеем ${{b}_{2}}(q) = {{q}^{2}} + ({{\alpha }_{s}} - 2)q + ({{\alpha }_{s}} + 1)$. Его вершиной служит ${{q}_{{2{v}}}} = 1 - {{\alpha }_{s}}{\text{/}}2$. В случае ${{\alpha }_{s}} \geqslant 2$ данный ${{b}_{2}}(q)$ возрастает по $q \geqslant 0$, и поэтому ${{\bar {b}}_{2}} = {{b}_{2}}({{M}^{2}}) = ({{M}^{2}} - {{1)}^{2}} + {{\alpha }_{s}}({{M}^{2}} + 1)$. В случае ${{\alpha }_{s}} < 2$ имеем ${{q}_{{2v}}} > 0$, и тем самым ${{\bar {b}}_{2}} = {{b}_{2}}(0) = {{\alpha }_{s}} + 1$ при ${{M}^{2}} \leqslant 2{{q}_{{2v}}}$ либо ${{\bar {b}}_{2}} = {{b}_{2}}({{M}^{2}})$ при ${{M}^{2}} \geqslant 2{{q}_{{2v}}}$. В итоге это приводит к формуле (33).

Достаточное условие (31) выполнения критерия (34) вытекает из следствия 1 и оценки $\mathop {\max }\limits_{0 \leqslant q \leqslant {{M}^{2}}} b{\text{/}}{{\alpha }_{s}} \leqslant 2{{\bar {b}}_{1}}\alpha + {{\bar {b}}_{2}}{\text{/}}(2{{\alpha }_{s}}\alpha )$.

Замечание 3. При $M = 0$ имеем $q = 0$ и ${{b}_{1}} = \sigma ({{\alpha }_{s}} + 1)$ и ${{b}_{2}} = {{\alpha }_{s}} + 1$. В этом случае следует брать максимум по $0 \leqslant \sigma \leqslant 1$, и теорема сохраняет силу, более того, необходимое условие можно усилить до

Функции ${{\beta }_{{{\text{nec}}}}}$ и ${{\beta }_{{{\text{suf}}}}}$ непрерывны в октанте $\alpha > 0$, ${{\alpha }_{s}} \geqslant 0$, ${{M}^{2}} \geqslant 0$, не возрастают по ${{M}^{2}}$ (так как по определению ${{\bar {b}}_{1}}$ и ${{\bar {b}}_{2}}$ не убывают по ${{M}^{2}}$) и стремятся к 0 при $\alpha \to + 0$ и $\alpha \to + \infty $. Существенно, что в силу указанного невозрастания выполнение условий (30) или (31) при некотором $M = {{M}_{0}} > 0$ влечет их выполнение при всех $0 \leqslant {\text{|}}M{\kern 1pt} {\text{|}} \leqslant {{M}_{0}}$ (при фиксированных $\alpha $ и ${{\alpha }_{s}}$). Обратим внимание на то, что $0.25{{\beta }_{{{\text{nec}}}}} \leqslant {{\beta }_{{{\text{suf}}}}} \leqslant 0.5{{\beta }_{{{\text{nec}}}}}$.

На фиг. 2 даны типичные графики ${{\beta }_{{{\text{nec}}}}}$ и ${{\beta }_{{{\text{suf}}}}}$ в зависимости от $\alpha $ и ${\text{|}}M{\kern 1pt} {\text{|}}$ при трех характерных значениях ${{\alpha }_{s}}$.

Выполненные численные эксперименты в целом неплохо соотносятся с приведенным выше теоретическим анализом. Для линеаризованной задачи при $M = 0$ уже простые эксперименты показывают, что даже небольшое нарушение условия устойчивости фон Неймана обычно приводит к разрушению численного решения. С другой стороны, они подтверждают, что это условие не обеспечивает ${{L}^{2}}$-диссипативности, как и предсказывает теория (детали для краткости опускаем). Последнее не столь критично для линеаризованной задачи. Тем не менее выполнение этого свойства оказывается важным в исходной нелинейной постановке для обеспечения лучшего качества численных решений с целью устранения или существенного уменьшения численных осцилляций, хотя обычно лишь достаточно сильные из них приводят к полному разрушению решений.

В нелинейной постановке возьмем $p(\rho ) = {{\rho }^{\gamma }}$ с $\gamma = 1.4$. Пусть

подобно (11). Рассмотрим две задачи Римана. В примере 1 выберем начальные данные и численно решим задачу до момента времени ${{t}_{{{\text{fin}}}}} = 0.04$. Тогда число Маха ${\text{|}}M{\kern 1pt} {\text{|}}$ варьируется от 0 до $ \approx 0.1777$ и тем самым невелико.

Возьмем $\alpha = 0.25$, $\hat {\beta } = 0.05$ и $h = 1{\text{/}}150$. На фиг. 3 даны графики решения $\rho $ и $u$ по пространству при $t = {{t}_{{{\text{fin}}}}}$ и график по времени его полной пространственной вариации

При ${{\alpha }_{s}} = 1$ численное решение не имеет видимых осцилляций, а $V(\rho ,u)$ является лишь слабо немонотонной и стремится к пределу. Отметим, что в этом случае ${{\beta }_{{{\text{suf}}}}} = 0.2$. Но при ${{\alpha }_{s}} = 0$ осцилляции $\rho $, $u$, $V(\rho ,u)$ заметны, и несмотря на то, что $\hat {\beta } = 0.05$ много меньше ${{\beta }_{{vN}}} = 0.25$ (см. (19)), качество численного решения низкое.

В примере 2 используем другие начальные данные:

и прежнее ${{t}_{{{\text{fin}}}}}$. Здесь в расчете число Маха варьируется от 0 до $0.5$ и уже не мало.

Возьмем прежние ${{\alpha }_{s}}$, $h$, а $\hat {\beta } = 0.3$. На фиг. 4б при ${{\alpha }_{s}} = 1$ у $\rho $, $u$ нет осцилляций, а $V(\rho ,u)$ возрастает и стремится к пределу. Напротив, на фиг. 4а при ${{\alpha }_{s}} = 0$ все величины $\rho ,\;u,\;V(\rho ,u)$ осциллируют, и поэтому этот выбор ${{\alpha }_{s}}$ намного хуже, что и предсказывает данный выше анализ диссипативности в контрасте с условием фон Неймана (см. фиг. 1a).

Также в ряде численных экспериментов с ударными волнами нами было отмечено, что значение $\beta = {{\beta }_{{{\text{suf}}}}}$ позволяет неплохо разделять слабо- или неосциллирующие решения от осциллирующих; детали для краткости опускаем.

В доказательстве теоремы 3 можно было найти $\mathop {\max }\limits_{0 \leqslant q \leqslant {{M}^{2}}} b$ и тем самым несколько уточнить результат, сблизив необходимое и достаточное условия подобно [15]. Однако соответствующее выражение зависит от $\alpha $ более сложным образом, и приводимая ниже теорема оказывается более громоздкой.

Теорема 4. Пусть ${{\mu }_{{{\text{ph}}}}} = 0$, ${{\alpha }_{s}} > 0$ и $M \ne 0$. Для ${{L}^{2}}$-диссипативности схемы (6), (7) необходимо, чтобы $\beta \leqslant \beta _{{{\text{nec}}}}^{{(0)}}$, и достаточно, чтобы $\beta \leqslant \beta _{{{\text{suf}}}}^{{(0)}}: = 0.5\beta _{{{\text{nec}}}}^{{(0)}}$, где

с $\unicode{230} : = 4{{\alpha }_{s}}{\text{/}}{{M}^{2}}$. Множества ${{D}_{{\text{I}}}}$–${{D}_{{{\text{III}}}}}$ включают точки с положительными координатами $({{\alpha }^{2}},{{\alpha }_{s}},{{M}^{2}})$. В ${{D}_{{\text{I}}}}$ это: 1) $\unicode{230} {{\alpha }^{2}} < 1$, $({{M}^{2}} - {{\alpha }_{s}} - 1)\unicode{230} {{\alpha }^{2}} + {{\alpha }_{s}} - 2 < 0$ и $({{\alpha }_{s}} + 1)\unicode{230} {{\alpha }^{2}} \geqslant {{M}^{2}} + {{\alpha }_{s}} - 2$; 2) $\unicode{230} {{\alpha }^{2}} = 1$ и ${{M}^{2}} \leqslant 3$; 3) $\unicode{230} {{\alpha }^{2}} > 1$ и $({{M}^{2}} - {{\alpha }_{s}} - 1)\unicode{230} {{\alpha }^{2}} + {{\alpha }_{s}} - 2 \leqslant 0$.

В ${{D}_{{{\text{II}}}}}$ это: 1) $\unicode{230} {{\alpha }^{2}} < 1$ и $({{M}^{2}} - {{\alpha }_{s}} - 1)\unicode{230} {{\alpha }^{2}} + {{\alpha }_{s}} - 2 \geqslant 0$; 2) $\unicode{230} {{\alpha }^{2}} < 1$, $({{M}^{2}} - {{\alpha }_{s}} - 1)\unicode{230} {{\alpha }^{2}} + {{\alpha }_{s}} - 2 < 0$ и $({{\alpha }_{s}} + 1)\unicode{230} {{\alpha }^{2}} \leqslant {{M}^{2}} + {{\alpha }_{s}} - 2$; 3) $\unicode{230} {{\alpha }^{2}} = 1$ и ${{M}^{2}} \geqslant 3$; 4) $\unicode{230} {{\alpha }^{2}} > 1$, $({{M}^{2}} - {{\alpha }_{s}} - 1)\unicode{230} {{\alpha }^{2}} + {{\alpha }_{s}} - 2 > 0$ и $({{M}^{2}} + {{\alpha }_{s}} + 1)\unicode{230} {{\alpha }^{2}} \leqslant 2{{M}^{2}} + {{\alpha }_{s}} - 2$.

В ${{D}_{{{\text{III}}}}}$ это $\unicode{230} {{\alpha }^{2}} > 1$, $({{M}^{2}} - {{\alpha }_{s}} - 1)\unicode{230} {{\alpha }^{2}} + {{\alpha }_{s}} - 2 > 0$ и $({{M}^{2}} + {{\alpha }_{s}} + 1)\unicode{230} {{\alpha }^{2}} \geqslant 2{{M}^{2}} + {{\alpha }_{s}} - 2$.

Доказательство. Вернемся к началу доказательства теоремы 3. Верны формулы

Обозначим через ${{q}_{*}}$ (любую) точку максимума ${{s}_{2}}(q)$ на $[0,{{M}^{2}}]$. При $\unicode{230} {{\alpha }^{2}} \ne 1$ ясно, что ${{s}_{2}}(q)$ – квадратный трехчлен с вершиной ${{q}_{{v}}} = - {{a}_{1}}{\text{/}}(2a)$.

В случае $\unicode{230} {{\alpha }^{2}} < 1$ имеем ${{a}_{0}} > 0$, и при ${{a}_{1}} \geqslant 0$ получаем, что ${{q}_{v}} \leqslant 0$ и ${{s}_{2}}(q)$ возрастает при $q \geqslant 0$, и поэтому ${{q}_{*}} = {{M}^{2}}$. При ${{a}_{1}} < 0$ имеем ${{q}_{v}} > 0$, и поэтому ${{q}_{*}} = 0$ для ${{M}^{2}} \leqslant 2{{q}_{v}}$ (эквивалентно, $({{\alpha }_{s}} + 1)\unicode{230} {{\alpha }^{2}} \geqslant {{M}^{2}} + {{\alpha }_{s}} - 2$) либо ${{q}_{*}} = {{M}^{2}}$ для ${{M}^{2}} \geqslant 2{{q}_{v}}$.

В случае $\unicode{230} {{\alpha }^{2}} = 1$ имеем ${{a}_{0}} = 0$, ${{s}_{2}}(q)$ – аффинная функция, поэтому ${{q}_{*}} = 0$ при ${{a}_{1}} \leqslant 0$ (эквивалентно, ${{M}^{2}} \leqslant 3$) либо ${{q}_{*}} = {{M}^{2}}$ для ${{M}^{2}} \geqslant 3$.

В случае $\unicode{230} {{\alpha }^{2}} > 1$ имеем ${{a}_{0}} < 0$, и при ${{a}_{1}} \leqslant 0$ получаем, что ${{s}_{2}}(q)$ убывает при $q \geqslant 0$, и поэтому ${{q}_{*}} = 0$. При ${{a}_{1}} > 0$ имеем ${{q}_{v}} > 0$, и поэтому ${{q}_{*}} = {{M}^{2}}$ для ${{M}^{2}} \leqslant {{q}_{v}}$ (эквивалентно, $({{M}^{2}} + {{\alpha }_{s}} + 1)\unicode{230} {{\alpha }^{2}} \leqslant 2{{M}^{2}} + {{\alpha }_{s}} - 2$) либо ${{q}_{*}} = {{q}_{v}}$ для ${{M}^{2}} \geqslant {{q}_{{v}}}$.

При этом верны формулы

Переупорядочив результаты согласно этим значениям, завершим доказательство.

Функция $\beta _{{{\text{nec}}}}^{{(0)}}$ непрерывна в октанте $\alpha > 0$, ${{\alpha }_{s}} > 0$, ${{M}^{2}} > 0$, не возрастает по ${{M}^{2}}$ и, как нетрудно проверить, стремится к 0 при $\alpha \to + 0$ и $\alpha \to + \infty $. Кроме того, она не зависит от $M$ на ${{D}_{{\text{I}}}}$ и возрастает по $\alpha $ на ${{D}_{{{\text{II}}}}}$. На фиг. 5 представлены графики $\beta _{{{\text{nec}}}}^{{(0)}}$ в зависимости от $\alpha $ и ${\text{|}}M{\kern 1pt} {\text{|}}$ при трех характерных значениях ${{\alpha }_{s}}$. На всех трех графиках имеются участки, относящиеся ко всем множествам ${{D}_{{\text{I}}}}$–${{D}_{{{\text{III}}}}}$, и они помечены разной штриховкой.

На фиг. 6 даны графики $\beta _{{{\text{nec}}}}^{{(0)}}$ в зависимости от $\alpha $ и ${{\alpha }_{s}}$ при двух характерных значениях ${\text{|}}M{\kern 1pt} {\text{|}} = 1$ и 2. В силу указанного свойства невозрастания выполнение условий теоремы с $\beta _{{{\text{nec}}}}^{{(0)}}$ при некотором $M = {{M}_{0}} > 0$ влечет их выполнение при всех $0 \leqslant {\text{|}}M{\kern 1pt} {\text{|}} \leqslant {{M}_{0}}$ (при фиксированных $\alpha $ и ${{\alpha }_{s}}$), тем самым график на фиг. 6а представляет интерес для всей дозвуковой области ${\text{|}}M{\kern 1pt} {\text{|}} \leqslant 1$, а график на фиг. 6б – также и для транс- и сверхзвуковых областей ${\text{|}}M{\kern 1pt} {\text{|}} \leqslant 2$. На них фигурируют участки, относящиеся только ко множествам ${{D}_{{\text{I}}}}$ и ${{D}_{{{\text{II}}}}}$.

Вернемся к теореме 3. Оптимальное значение $\alpha $, при котором достигаются максимальные значения ${{\beta }_{{{\text{nec}}}}}$ и ${{\beta }_{{{\text{suf}}}}}$ (это происходит одновременно) и тем самым – максимальный шаг по времени, определяется из простого уравнения ${{\bar {b}}_{1}}\alpha = {{\bar {b}}_{2}}{\text{/}}(4{{\alpha }_{s}}\alpha )$. Эти значения $\alpha $, ${{\beta }_{{{\text{nec}}}}}$ и ${{\beta }_{{{\text{suf}}}}}$ даются формулами

Конкретизируем их. Неравенства на ${{\alpha }_{s}}$ и ${{M}^{2}}$, входящие в выражения для ${{\bar {b}}_{1}}$ и ${{\bar {b}}_{2}}$, порождают разбиение квадранта параметров $({{\alpha }_{s}},{{M}^{2}})$ на четыре подобласти (фиг. 7). В области ${{\Omega }_{{\text{I}}}}$ имеем ${{M}^{2}} \leqslant \min \{ {{\alpha }_{s}} + 1,2 - {{\alpha }_{s}}\} $ (здесь $0 < {{\alpha }_{s}} \leqslant 2$), и необходимое условие (30) принимает вид Только в ней оптимальные значения $\alpha $ и ${{\beta }_{{{\text{nec}}}}}$ задаются формулами, не зависящими от $M$: Максимум ${{\bar {\beta }}_{{{\text{nec}}}}}$ достигается при ${{\alpha }_{s}} = 1$ и равен 1.

Как нетрудно убедиться, сечения ${{D}_{{\text{I}}}}$ любой плоскостью ${{\alpha }^{2}} = {\text{const}} > 0$ содержат ${{\Omega }_{I}}$. Поэтому теорема 4 позволяет в (36) и (37) улучшить $1{\text{/}}{{\beta }_{{{\text{nec}}}}}$ и ${{\bar {\beta }}_{{{\text{nec}}}}}$ до соответственно $({{\alpha }_{s}} + 1)[\alpha + 1{\text{/}}(4{{\alpha }_{s}}\alpha )] = 1{\text{/}}(2{{\beta }_{{{\text{suf}}}}})$ и $\sqrt {{{\alpha }_{s}}} {\text{/}}({{\alpha }_{s}} + 1)$.

В ${{\Omega }_{{{\text{II}}}}}$ имеем ${{\alpha }_{s}} + 1 \leqslant {{M}^{2}} \leqslant 2 - {{\alpha }_{s}}$ (здесь $0 < {{\alpha }_{s}} \leqslant 0.5$), и необходимое условие можно записать в виде

Оптимальные значения $\alpha $ и ${{\beta }_{{{\text{nec}}}}}$ задаются формулами

В ${{\Omega }_{{{\text{III}}}}}$ имеем $\max \{ {{\alpha }_{s}} + 1,2 - {{\alpha }_{s}}\} \leqslant {{M}^{2}}$, и необходимое условие принимает вид

Оптимальные значения $\alpha $ и ${{\beta }_{{{\text{nec}}}}}$ задаются формулами где асимптотическое поведение указано при ${\text{|}}M{\kern 1pt} {\text{|}} \to \infty $ и фиксированном ${{\alpha }_{s}}$. Отметим линейный рост ${{\alpha }_{{{\text{opt}}}}}$ и, к сожалению, быстрое убывание ${{\bar {\beta }}_{{{\text{nec}}}}}$ с ростом ${\text{|}}M{\kern 1pt} {\text{|}}$.

В ${{\Omega }_{{{\text{IV}}}}}$ имеем $2 - {{\alpha }_{s}} \leqslant {{M}^{2}} \leqslant {{\alpha }_{s}} + 1$ (здесь ${{\alpha }_{s}} \geqslant 0.5$), и необходимое условие таково:

Оптимальные значения $\alpha $ и ${{\beta }_{{{\text{nec}}}}}$ задаются формулами

На фиг. 8 представлены графики ${{\alpha }_{{{\text{opt}}}}}$ и ${{\bar {\beta }}_{{{\text{nec}}}}}$ в зависимости от ${{\alpha }_{s}},{{M}^{2}} \in (0,3]$. На них разной штриховкой отмечены участки, относящиеся к разным областям ${{\Omega }_{{\text{I}}}}$–${{\Omega }_{{{\text{IV}}}}}$.

При $M = 0$ формулы (38), (39) переходят в (37). Для сравнения отметим, что согласно критерию (24) значение ${{\alpha }_{{{\text{opt}}}}}$ такое же, как в (37), а оптимальное значение ${{\bar {\beta }}_{{{\text{cr}}}}}$ следующее:

При этом асимптотическое поведение ${{\bar {\beta }}_{{{\text{cr}}}}}$ и ${{\bar {\beta }}_{{{\text{suf}}}}}$ (но не ${{\bar {\beta }}_{{{\text{nec}}}}}$) при ${{\alpha }_{s}} \to + 0$ и $ + \infty $ одинаковое. Графики трех величин из последних неравенств даны на фиг. 9.

4. СЛУЧАЙ КГидД РЕГУЛЯРИЗАЦИИ УРАВНЕНИЙ НАВЬЕ–СТОКСА БЕЗ ИСКУССТВЕННОГО КОЭФФИЦИЕНТА ВЯЗКОСТИ

Рассмотрим теперь бегло другой важный на практике случай, когда ${{\mu }_{{{\text{art}}}}} = 0$ (т.е. ${{\alpha }_{s}} = 0$), а ${{\mu }_{{{\text{ph}}}}} > 0$, использованный в том числе в [10], [12], [25]. Он существенно отличается от предыдущего, поскольку теперь используется регуляризация баротропных уравнений Навье–Стокса, а не Эйлера, и уравнение импульса относительно $u$ имеет уже параболический тип вместо гиперболического 1-го порядка. При этом весьма важно то, что благодаря рассмотрению выше любых значений ${{\alpha }_{s}} > 0$, новый анализ не требуется, ибо его можно свести к уже выполненному посредством замен

где параметр $d$ имеет размерность времени. Следуя [26], теперь формулы (11) не используются и работа идет непосредственно с ${{\tau }_{*}}$ и $\Delta t$; это связано и с тем, что выбор $\tau $ здесь априори не очевиден, и более того, его желательно выяснить в ходе анализа устойчивости. Ниже для краткости опускаем индекс * у ${{\nu }_{{{\text{ph}}*}}}$ и ${{\tau }_{*}}$.

Указанные замены в теореме 3 приводят к следующему результату.

Теорема 5. Пусть ${{\mu }_{{{\text{art}}}}} = 0$ и $d > 0$. Для ${{L}^{2}}$-диссипативности схемы (6), (7) необходимо выполнение неравенства

и достаточно выполнение неравенства где

Переформулировка теоремы 4 выполняется аналогично; для краткости ее опускаем.

Введем безразмерный параметр ${{\theta }_{h}} = {{c}_{*}}h{\text{/}}{{\nu }_{{{\text{ph}}}}}$. В области ${{\Omega }_{{\text{I}}}}$, где ${{M}^{2}} \leqslant \min \{ {{\tau }^{{ - 1}}}d + 1,2 - {{\tau }^{{ - 1}}}d\} $ (здесь $0 < {{\tau }^{{ - 1}}}d \leqslant 2$, а ${{M}^{2}} \leqslant 3{\text{/}}2$), необходимое условие (40) с учетом теоремы 4, как указано в предыдущем разделе, можно уточнить как

а достаточное условие (41) принимает вид $\Delta t \leqslant \Delta {{t}_{{{\text{suf}}}}} = 0.5\Delta t_{{{\text{nec}}}}^{{(0)}}$. Верны двусторонние оценки Соответствующее оптимальное значение параметра $\tau $, при котором как необходимое, так и достаточное условия на $\Delta t$ наиболее широкие, таково: Обратим внимание на то, что ${{\tau }_{{{\text{opt}}}}}$ в двух из трех указанных случаев не зависит от $h$, что принципиально отличается от предыдущей формулы (11) для $\tau $; подобное относится и к оценкам (43), а также имеет место ниже и в случае областей ${{\Omega }_{{{\text{II}}}}}$–${{\Omega }_{{{\text{IV}}}}}$. В оставшемся третьем случае ${{\tau }_{{{\text{opt}}}}}$ совпадает с (11) при $\alpha = 0.5$ и не зависит от $M$. Расчеты в [25] были выполнены с параметрами, попадающими в последний случай и в основном с таким ${{\tau }_{{{\text{opt}}}}}$, при малых числах Маха. Для них $\Delta t_{{{\text{nec}}}}^{{(0)}} \approx 4d$ в формуле (42), что достаточно хорошо согласуется с $\Delta t$, найденным экспериментально в [25]. Подчеркнем, что до сих пор никаких формул типа (42) для выбора $\Delta t$ для схем на разнесенных или неразнесенных сетках с регуляризацией при ${{\mu }_{{{\text{art}}}}} = 0$ в литературе предложено не было (исключая [26] при $M = 0$).

Отметим, что при $2{\text{/}}{{\theta }_{h}} \leqslant {{M}^{2}} - 1$ и ${\text{|}}M{\kern 1pt} {\text{|}} \to 1 + 0$ имеем ${{\tau }_{{{\text{opt}}}}} \to + \infty $; это является признаком того, что данная регуляризация при таких параметрах едва ли удовлетворительна. Подобное наблюдается при ${\text{|}}M{\kern 1pt} {\text{|}} \to 1$ или ${\text{|}}M{\kern 1pt} {\text{|}} \to \sqrt 2 $ и в аналогичных формулах ниже.

Замечание 4. В теореме 5 необходимое условие (40) в ${{\Omega }_{{\text{I}}}}$

не очень существенно отличается от (42). Однако оно приводит к другой формуле для оптимального значения $\tau $, которая представляется менее адекватной:

Для сравнения отметим, что в ${{\Omega }_{{\text{I}}}}$ при $M = 0$ получаем

где значение ${{\tau }_{{{\text{opt}},{\text{cr}}}}} = d$ получено на основе критерия (24) (см. [26]).

В области ${{\Omega }_{{{\text{II}}}}}$, где $1 + {{\tau }^{{ - 1}}}d \leqslant {{M}^{2}} \leqslant 2 - {{\tau }^{{ - 1}}}d$ (здесь $0 < {{\tau }^{{ - 1}}}d \leqslant 0.5$, а $1 < {{M}^{2}} < 2$), достаточное условие (41) таково:

и оно приводит к следующему оптимальному значению $\tau $:

В области ${{\Omega }_{{{\text{III}}}}}$, где $\max \{ {{\tau }^{{ - 1}}}d + 1,2 - {{\tau }^{{ - 1}}}d\} \leqslant {{M}^{2}}$ (здесь ${{M}^{2}} \geqslant 3{\text{/}}2$), достаточное условие (41) имеет вид

и приводит к следующему оптимальному значению $\tau $: где $r(M,{{\theta }_{h}}): = ({{M}^{2}} + 1){\text{/}}\sqrt {1 + ({{M}^{2}} + 1){{M}^{2}}\theta _{h}^{2}} $.

В области ${{\Omega }_{{{\text{IV}}}}}$, где $2 - {{\tau }^{{ - 1}}}d \leqslant {{M}^{2}} \leqslant {{\tau }^{{ - 1}}}d + 1$ (здесь ${{\tau }^{{ - 1}}}d > 0.5$), достаточное условие (41) таково:

и оно приводит к следующему оптимальному значению $\tau $: В случае ${{M}^{2}} \leqslant 1 - \varepsilon $ с $0 < \varepsilon < 1$ справедливы аналогичные (43), (44) оценки

При $M = 0$ в ${{\Omega }_{{{\text{IV}}}}}$ получаем ${{\tau }_{{{\text{opt}}}}} = \min \{ h{\text{/}}(2{{c}_{*}}),d{\text{/}}2\} $ и по-прежнему ${{\tau }_{{{\text{opt}},{\text{cr}}}}} = d$.