1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 2, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 2, стр. 289-304

Быстрый алгоритм решения трехмерной обратной многочастотной задачи скалярной акустики с данными в цилиндрической области

А. Б. Бакушинский 1, 2, *, А. С. Леонов 3, **

1 ИСА ФИЦ ИУ РАН
117312 Москва, пр-т 60-летия Октября, 9, Россия

2 МарГУ
424000 Йошкар-Ола, пл. Ленина, 1, Республика Марий Эл, Россия

3 НИЯУ “МИФИ”
115409 Москва, Каширское ш., 31, Россия

* E-mail: bakush@isa.ru
** E-mail: asleonov@mephi.ru

Поступила в редакцию 10.03.2021
После доработки 10.03.2021
Принята к публикации 04.08.2021

Полный текст (PDF)

Аннотация

Предлагается новый алгоритм устойчивого решения трехмерной скалярной обратной задачи акустического зондирования неоднородной среды в цилиндрической области. Данными для ее решения является комплексная амплитуда волнового поля, измеряемая вне области акустических неоднородностей в цилиндрическом слое. Обратная задача сводится с помощью преобразования Фурье и рядов Фурье к решению совокупности одномерных интегральных уравнений Фредгольма I рода, к последующему вычислению комплексной амплитуды волнового поля в области неоднородности и далее к нахождению искомого поля скоростей звука в этой области. Алгоритм позволяет решать обратную задачу на персональном компьютере средней производительности для достаточно мелких трехмерных сеток за десятки секунд. Проведено численное исследование точности предлагаемого алгоритма для решения модельных обратных задач на различных частотах и исследованы вопросы устойчивости алгоритма по отношению к возмущениям данных. Библ. 28. Фиг. 8.

Ключевые слова: трехмерное волновое уравнение, обратная коэффициентная задача, регуляризующий алгоритм, быстрое преобразование Фурье.

1. ВВЕДЕНИЕ

Пусть скалярная функция $p({\mathbf{x}},t)$ определяет акустическое волновое поле, зависящее от координат ${\mathbf{x}} = (x,y,z)$ и времени $t \geqslant 0$ в области $Q \subset {{\mathbb{R}}^{3}}$. Область $Q$ есть бесконечный цилиндр вида $Q = \{ (x,y,z)\,:{{x}^{2}} + {{y}^{2}} \leqslant {{b}^{2}},\;z \in \mathbb{R}\} $. Поле создается источниками, локализованными в известной области $S$. Среда характеризуется локальной фазовой скоростью звука $c({\mathbf{x}})$ и имеет постоянную плотность. При этом известно, что $c({\mathbf{x}}) = {{c}_{0}} = {\text{const}}$ вне заданной области $X \subset Q$, удовлетворяющей условию $X \cap S = \emptyset $. В самой области $X$ функция $c({\mathbf{x}})$ может быть переменной, и это интерпретируется как расположение там акустических неоднородностей. В этом случае для гармонического источника вида $f({\mathbf{x}},\omega ){{e}^{{i\omega t}}}$ с известной частотой $\omega $ поле $p({\mathbf{x}},t)$ в рамках приближения линейной акустики может быть найдено в форме $p({\mathbf{x}},t) = u({\mathbf{x}},\omega ){{e}^{{i\omega t}}}$, где комплексная амплитуда $u({\mathbf{x}},\omega )$ удовлетворяет уравнению

(1.1)
$\Delta u({\mathbf{x}},\omega ) + k_{0}^{2}u({\mathbf{x}},\omega ) = f({\mathbf{x}},\omega ) + {{\omega }^{2}}\xi ({\mathbf{x}})u({\mathbf{x}},\omega ),\quad {\mathbf{x}} \in Q.$
Здесь ${{k}_{0}} = \tfrac{\omega }{{{{c}_{0}}}}$, а $\xi ({\mathbf{x}}) = c_{0}^{{ - 2}} - {{c}^{{ - 2}}}({\mathbf{x}})$. Будем считать, что выполнено также граничное условие
$\mathop {\left. {l[u]} \right|}\nolimits_{\partial Q} = \mathop {\left( {\frac{{\partial u}}{{\partial n}} + \sigma ({\mathbf{x}})u} \right)}\nolimits_{\partial Q} = 0$
с известной функцией $\sigma ({\mathbf{x}})$ и условие излучения по координате $z$. Не вдаваясь в детализацию условий на коэффициенты $\sigma ({\mathbf{x}})$ и $f({\mathbf{x}},\omega )$, мы сделаем

Предположение 1. Функция $\xi ({\mathbf{x}})$ непрерывна с компактным носителем в $X$ и соответствующая задача (1.1) с указанными дополнительными условиями имеет при каждом рассматриваемом $\omega $ единственное решение $u({\mathbf{x}},a) \in {{H}_{1}}(Q)$.

Нахождение такой функции $u({\mathbf{x}},\omega )$ составляет прямую задачу. Нас интересует следующая обратная задача для уравнения (1.1) с указанными дополнительными условиями: зная для некоторого набора частот $\omega $ комплексную амплитуду поля $u({\mathbf{x}},\omega )$ в области $Y$ ($Y \subset Q$, $Y \cap X = \emptyset $, $Y \cap S = \emptyset $) найти коэффициент $\xi ({\mathbf{x}})$, т.е. функцию $c({\mathbf{x}})$, определяющую акустические неоднородности в области $X$.

Вводя функцию Грина $G({\mathbf{x}},{\mathbf{x}}{\text{'}},\omega )$ для уравнения Гельмгольца в области $Q$ для нерезонансных величин $\omega $, можно при определенных предположениях о гладкости функций $u({\mathbf{x}},\omega )$, $f({\mathbf{x}},\omega )$, $c({\mathbf{x}})$ (см., например, [1]–[4] и др.) свести обратную задачу к нелинейной относительно неизвестных $u({\mathbf{x}}{\text{'}},\omega )$, $\xi ({\mathbf{x}}{\text{'}})$, ${\mathbf{x}}{\text{'}} \in X$, системе интегральных уравнений:

(1.2)
$\begin{gathered} u({\mathbf{x}},\omega ) = {{u}_{0}}({\mathbf{x}},\omega ) + {{\omega }^{2}}\int\limits_X G ({\mathbf{x}},{\mathbf{x}}{\text{'}},\omega )\xi ({\mathbf{x}}{\text{'}})u({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}},\quad {\mathbf{x}} \in X, \\ {{\omega }^{2}}\int\limits_X G ({\mathbf{x}},{\mathbf{x}}{\text{'}},\omega )\xi ({\mathbf{x}}{\text{'}})u({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}} = w({\mathbf{x}},\omega ),\quad {\mathbf{x}} \in Y. \\ \end{gathered} $
Входящие в (1.2) функции
${{u}_{0}}({\mathbf{x}},\omega ) = \int\limits_X G ({\mathbf{x}},{\mathbf{x}}{\text{'}},\omega )f({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}},\quad w({\mathbf{x}},\omega ) = u({\mathbf{x}},\omega ) - {{u}_{0}}({\mathbf{x}},\omega ),\quad {\mathbf{x}} \in Y,$
суть известные (вычислимые) функции, а величины $u({\mathbf{x}}{\text{'}},\omega )$, $\xi ({\mathbf{x}}{\text{'}})$, ${\mathbf{x}}{\text{'}} \in X$, подлежат определению.

Задача (1.2) достаточно хорошо исследована теоретически: изучены вопросы существования и единственности ее решения в различных областях $Q$, $X$, $Y$ (см., например, [2]–[5] и др.), вопросы ее устойчивости по отношению к возмущениям данных и т.д. Например, известно, что для единственности решения такой обратной задачи в общем случае необходимо использовать по меньшей мере счетное число частот. Однако на практике реализовать это невозможно, и приходится ограничиваться сравнительно небольшим их числом, теоретически теряя единственность решения. Анализ этой проблемы дан, например, в [4]. Тем не менее такое изучение акустических рассеивателей на сравнительно небольшом числе частот часто встречается на практике. Для получения в этом случае определенного решения обратной задачи необходимо использовать дополнительные априорные ограничения для него, сужающие множество возможных решений.

Отметим, что цель этой статьи – не теоретическое исследование свойств обратной задачи (1.2). Мы лишь предлагаем в рамках рассматриваемой модели (1.2) эффективный с точки зрения быстродействия на достаточно “мелких” сетках численный метод ее решения в случае цилиндрических областей $Q$, $X$, $Y$. Предположение цилиндричности является принципиальным: именно оно определяет структуру метода и в конечном итоге его быстродействие. Имея в виду такие акценты, мы не проводим детальную редукцию обратной задачи к системе (1.2) с указанием всех требований к коэффициентам, а сделаем лишь

Предположение 2. Редукция обратной задачи к системе (1.2) возможна для данной функции ${{u}_{0}}({\mathbf{x}},\omega ) \in {{L}_{2}}(Q)$. Система (1.2) разрешима и для всех рассматриваемых $\omega $ определяет некоторое решение обратной задачи: непрерывную функцию $\xi ({\mathbf{x}})$ с компактным носителем в $X$ и функцию $u({\mathbf{x}},\omega ) \in {{L}_{2}}(X)$.

Подчеркнем, что при таких предположениях система (1.2) может иметь неединственное решение. Выделение единственного решения требует дополнительных предположений о его характере, и это будет сделано ниже.

Во многих работах рассмотрены разнообразные численные методы решения задач типа (1.2) в двумерной и трехмерной постановках. Так, в [3] система (1.2) сводится к нелинейному операторному уравнению, которое затем решается специальным итерационным методом. При этом явно не учитывается, что это уравнение является некорректно поставленной задачей и итерационный метод не регуляризируется. Тем не менее метод работает для модельных “рассеивателей средней силы” [3, с. 101–105]. В работе [5] для решения системы уравнений (1.2) в трехмерном аксиально-симметричном случае использован регуляризованный метод Гаусса–Ньютона. В работе [6] для аналогичной задачи были применены специальный градиентный метод и метод Флетчера–Ривса. Другие градиентные методы были использованы в [7], [8]. Обзор этих и подобных подходов можно найти, например, в [4].

Отметим, что имеются и альтернативные подходы в решении обратной задачи акустического зондирования, не связанные с системой типа (1.2). В частности, оригинальный метод граничного управления, позволяющий решать трехмерные задачи типа (2), был предложен и развит в работах [9], [10]. В [11] для решения двумерной обратной задачи рассеяния был применен известный метод Р.Г. Новикова [12], а в последующей работе [13] проведен сравнительный анализ разновидности этого метода и некоторых других функционально-аналитических методов решения двумерных обратных задач акустического рассеяния (см. также [4]). Весьма многообещающими при обработке реальных экспериментальных данных оказались методы М.В. Клибанова, суммированные в монографии [14], а также методы из монографии [15]. Большой интерес представляют также недавние работы [16], [17].

Все упомянутые методы решения обратной задачи акустического зондирования требуют в трехмерной постановке значительных вычислительных ресурсов и, прежде всего, – большого времени решения. Поэтому здесь актуально создание быстродействующих алгоритмов. В связи с этим отметим статьи [18]–[20]. В них рассматривались не задачи (1.1) и (1.2), а трехмерное интегральное уравнение Фредгольма I рода

$\int\limits_X {\frac{{\zeta (x{\text{'}})dx{\text{'}}}}{{\left| {x - x{\text{'}}} \right|}}} = {{U}^{{(0)}}}(x) - U(x),\quad x \in Y,$
к которому в различных областях $X$ сводится обратная коэффициентная задача для волнового уравнения. Правая часть этого уравнения содержит специальные интегралы ${{U}^{{(0)}}}(x)$, $U(x)$ от регистрируемого в $Y$ волнового поля, а искомая функция $\zeta (x)$ связана с $\xi (x)$. Принципиальной в этих статьях является область регистрации этого поля – плоский или цилиндрический тонкий слой. В результате предложенные в этих статьях методы решения интегрального уравнения оказались очень эффективным численно, и позволили решать трехмерные обратные задачи для достаточно мелких сеток на персональном компьютере (ПК) даже без распараллеливания за несколько минут. В дальнейшем мы применили в работе [21] аналогичный, но не тождественный, метод для решения уже другой задачи – задачи (1.2) в бесконечном пространстве с использованием плоских слоев $X,\;Y$. В предлагаемой теперь работе мы модифицируем метод решения указанного интегрального уравнения из [20] для его приложения к обратной задачe (2) в цилиндрической области, и в итоге получаем весьма быстродействующий алгоритм ее решения.

В статье мы придерживаемся следующей схемы решения нелинейной системы (1.2) как обратной задачи для каждой используемой частоты $\omega $:

1) решаем второе уравнение (линейное интегральное уравнение Фредгольма I рода), записанное в виде

(1.3)
${{\omega }^{2}}\int\limits_X G ({\mathbf{x}},{\mathbf{x}}{\text{'}},\omega ){v}({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}} = w({\mathbf{x}},\omega ),\quad {\mathbf{x}} \in Y,$
относительно функции ${v}({\mathbf{x}}{\text{'}},\omega ) = \xi ({\mathbf{x}}{\text{'}})u({\mathbf{x}}{\text{'}},\omega ),\;{\mathbf{x}}{\text{'}} \in X$;

2) вычисляем функцию $u({\mathbf{x}},\omega )$, ${\mathbf{x}} \in X$, из первого равенства системы (1.2), записанного в форме

(1.4)
$u({\mathbf{x}},\omega ) = {{u}_{0}}({\mathbf{x}},\omega ) + {{\omega }^{2}}\int\limits_X G ({\mathbf{x}},{\mathbf{x}}{\text{'}},\omega ){v}({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}},\quad {\mathbf{x}} \in X;$

3) находим функцию $\xi ({\mathbf{x}})$ из уравнения ${v}({\mathbf{x}},\omega ) = \xi ({\mathbf{x}})u({\mathbf{x}},\omega )$, ${\mathbf{x}} \in X$, используя найденные функции ${v}({\mathbf{x}},\omega )$, $u({\mathbf{x}},\omega )$.

Эта схема будет конкретизирована ниже. Близкий подход использовался и ранее. Например, он реализован в работе [22]. Однако там для решения некорректной задачи – трехмерного уравнения, аналогичного (1.3), не применялись методы регуляризации, а решение обратной задачи искалось на достаточно узком классе функций с “кусочно-постоянным током”. В итоге, для решения такой трехмерной обратной задачи на сравнительно мелких сетках также требуется значительное время.

Мы предлагаем численный алгоритм решения обратной задачи (1.2), основанный на схеме 1 )–3) и специализированный для цилиндрических областей $X$, $Y$, $Q$. В этом смысле алгоритм не является универсальным. Однако используемая в нем геометрия области решений $X$ и области регистрации данных $Y$ приемлема в определенной мере для ряда технических систем. Ниже мы продемонстрируем быстродействие полученного алгоритма. Этот новый алгоритм решения обратной задачи (1.2) в цилиндрической области, основанный на схеме 1 )–3), и его численное исследование являются основными результатами данной работы.

2. ИСПОЛЬЗУЕМАЯ ГЕОМЕТРИЧЕСКАЯ СХЕМА И СВЕДЕНИЕ ОБРАТНОЙ ЗАДАЧИ К ОДНОМЕРНЫМ ИНТЕГРАЛЬНЫМ УРАВНЕНИЯМ

Везде далее области $X$, $Y$ имеют вид цилиндров: область решения $X = {\text{\{ }}0 \leqslant r \leqslant a{\text{\} }} \times {{\mathbb{R}}_{z}}$, $r = \sqrt {{{x}^{2}} + {{y}^{2}}} $, и область наблюдения $Y = {\text{\{ }}{{r}_{0}} \leqslant r \leqslant b{\text{\} }} \times {{\mathbb{R}}_{z}}$. На фиг. 1 представлена схема расположения этих областей. Там же условно показано и возможное положение источников. Мы считаем цилиндры бесконечными по переменной $z$: $z \in ( - \infty , + \infty )$, имея в виду финитность искомой функции $\xi $ и по этой переменной в частности. В дальнейшем будем обозначать через ${{X}_{{xy}}}$, ${{Y}_{{xy}}}$ сечения цилиндрических областей $X$, $Y$ плоскостью, перпендикулярной оси $Oz$.

Фиг. 1.

Геометрическая схема регистрации данных обратной задачи: $X$ – область рассеивателей волнового поля, $Y$– область регистрации данных, звездочки – условные положения источников.

Будем далее считать, что $\sigma ({\mathbf{x}}) = \sigma = {\text{const}} \geqslant 0$. Функция Грина для задачи (1.1) с указанными дополнительными условиями в цилиндрической области $Q$ хорошо известна (см., например, [23, с. 615]), и здесь мы не будем выписывать ее явно. Отметим важную особенность этой функции: в цилиндрических координатах ${\mathbf{x}} = (r,\varphi ,z)$, ${\mathbf{x}}{\text{'}} = (r{\text{'}},\varphi {\text{'}},z{\text{'}})$ она имеет форму:

$\begin{gathered} G({\mathbf{x}},{\mathbf{x}}{\text{'}},\omega ) = G\left( {\sqrt {{{r}^{2}} + {{r}^{{'2}}} - 2rr{\text{'}}cos(\varphi - \varphi {\text{'}}) + \mathop {(z - z{\text{'}})}\nolimits^2 } ;\omega } \right) = \\ = \;{{G}_{0}}(r,r{\text{'}},\varphi - \varphi {\text{'}},z - z{\text{'}};\omega ), \\ \end{gathered} $
а вид функции ${{G}_{0}}$ можно найти, например, в [23]. В этих же координатах представим функции $u({\mathbf{x}},\omega ) = u(r,\varphi ,z,\omega )$, ${v}({\mathbf{x}},\omega ) = {v}(r,\varphi ,z,\omega )$. Тогда уравнения (1.3), (1.4) можно записать в виде
(2.1)
${{\omega }^{2}}\int\limits_0^a {\int\limits_0^{2\pi } {\int\limits_{ - \infty }^{ + \infty } {{{G}_{0}}} } } (r,r{\text{'}},\varphi - \varphi {\text{'}},z - z{\text{'}};\omega ){v}(r{\text{'}},\varphi {\text{'}},z{\text{'}};\omega )r{\text{'}}dr{\text{'}}d\varphi {\text{'}}dz{\text{'}} = w(r,\varphi ,z;\omega ),\quad r \in [{{r}_{0}},b],$
(2.2)
$\begin{gathered} u(r,\varphi ,z;\omega ) - {{u}_{0}}(r,\varphi ,z;\omega ) = \\ = \;{{\omega }^{2}}\int\limits_0^a {\int\limits_0^{2\pi } {\int\limits_{ - \infty }^{ + \infty } {{{G}_{0}}} } } (r,r{\text{'}},\varphi - \varphi {\text{'}},z - z{\text{'}};\omega ){v}(r{\text{'}},\varphi {\text{'}},z{\text{'}};\omega )r{\text{'}}dr{\text{'}}d\varphi {\text{'}}dz{\text{'}},\quad r \in [0,a], \\ \end{gathered} $
при $\varphi \in [0,2\pi ]$, $z \in \mathbb{R}$. Здесь ${v}(r{\text{'}},\varphi {\text{'}},z{\text{'}};\omega ) = \xi (r{\text{'}},\varphi {\text{'}},z{\text{'}})u(r{\text{'}},\varphi {\text{'}},z{\text{'}};\omega )$.

Введем преобразования Фурье

${{F}_{z}}[{\kern 1pt} \cdot {\kern 1pt} ] = \int\limits_{ - \infty }^{ + \infty } {[{\kern 1pt} \cdot {\kern 1pt} ]} {\kern 1pt} {{e}^{{i\Omega z}}}dz$
по переменной $z$ (или $z{\text{'}}$) для функций ${{G}_{0}}$, ${v}$, $u$, ${{u}_{0}}$, $w$ как элементов пространства ${{L}_{2}}$ (см. предположение 2):
$\begin{array}{*{20}{c}} {\tilde {G}(r,r{\text{'}},\varphi ,\Omega ;\omega ) = {{F}_{z}}\left[ {{{G}_{0}}(r,r{\text{'}},\varphi ,z;\omega )} \right](\Omega ),\quad \tilde {w}(r,\varphi ,\Omega ;\omega ) = {{F}_{z}}\left[ {w(r,\varphi ,z;\omega )} \right](\Omega ),} \\ {\tilde {u}(r,\varphi ,\Omega ;\omega ) = {{F}_{z}}\left[ {u(r,\varphi ,z;\omega )} \right](\Omega ),\quad {{{\tilde {u}}}_{0}}(r,\varphi ,\Omega ;\omega ) = {{F}_{z}}\left[ {{{u}_{0}}(r,\varphi ,z;\omega )} \right](\Omega ).} \end{array}$
Тогда по теореме о свертке равенства (2.1), (2.2) можно записать в виде
(2.3)
${{\omega }^{2}}\int\limits_0^a {\int\limits_0^{2\pi } {\tilde {G}} } (r,r{\text{'}},\varphi - \varphi {\text{'}},\Omega ;\omega ){\tilde {v}}(r{\text{'}},\varphi {\text{'}},\Omega ;\omega )r{\text{'}}dr{\text{'}}d\varphi {\text{'}} = \tilde {w}(r,\varphi ,\Omega ;\omega ),\quad r \in [{{r}_{0}},b],$
(2.4)
$\begin{gathered} \tilde {u}(r,\varphi ,\Omega ;\omega ) - {{{\tilde {u}}}_{0}}(r,\varphi ,\Omega ;\omega ) = \\ = \;{{\omega }^{2}}\int\limits_0^a {\int\limits_0^{2\pi } {\tilde {G}} } (r,r{\text{'}},\varphi - \varphi {\text{'}},\Omega ;\omega ){\tilde {v}}(r{\text{'}},\varphi {\text{'}},\Omega ;\omega )r{\text{'}}dr{\text{'}}d\varphi {\text{'}},\quad r \in [0,a], \\ \end{gathered} $
где ${\tilde {v}}(r{\text{'}},\varphi {\text{'}},\Omega ;\omega ) = {{F}_{z}}\left[ {{v}(r{\text{'}},\varphi {\text{'}},z{\text{'}};\omega )} \right](\Omega ) = {{F}_{z}}\left[ {\xi (r{\text{'}},\varphi {\text{'}},z{\text{'}})u(r{\text{'}},\varphi {\text{'}},z{\text{'}};\omega )} \right]$. Введем также разложения функций $\tilde {G}$, ${\tilde {v}}$, $\tilde {u}$, ${{\tilde {u}}_{0}}$, $\tilde {w}$ по системе $\{ {{e}^{{in\varphi }}}\} $, $n \in \mathbb{Z}$, в пространстве ${{L}_{2}}(0,2\pi )$:
$\begin{array}{*{20}{c}} {\tilde {G}(r,r{\text{'}},\varphi ,\Omega ;\omega ) = \sum\limits_n {{{G}_{n}}} (r,r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi }}},\quad {\tilde {v}}(r{\text{'}},\varphi {\text{'}},\Omega ;\omega ) = \sum\limits_n {{{{v}}_{n}}} (r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi {\text{'}}}}},} \\ {\tilde {u}(r,\varphi ,\Omega ;\omega ) = \sum\limits_n {{{u}_{n}}} (r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi }}},\quad {{{\tilde {u}}}_{0}}(r,\varphi ,\Omega ;\omega ) = \sum\limits_n {{{u}_{{0n}}}} (r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi }}};} \\ {\tilde {w}(r,\varphi ,\Omega ;\omega ) = \sum\limits_n {{{w}_{n}}} (r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi }}};\quad \varphi ,\varphi {\text{'}} \in [0,2\pi ]} \end{array}$
с коэффициентами
$\begin{array}{*{20}{c}} {{{G}_{n}}(r,r{\text{'}},\Omega ;\omega ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\tilde {G}} (r,r{\text{'}},\varphi ,\Omega ;\omega ){{e}^{{ - in\varphi }}}d\varphi ,} \\ {{{{v}}_{n}}(r{\text{'}},\Omega ;\omega ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{\tilde {v}}} (r{\text{'}},\varphi {\text{'}},\Omega ;\omega ){{e}^{{ - in\varphi {\text{'}}}}}d\varphi {\text{'}},\quad {{w}_{n}}(r,\Omega ;\omega ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\tilde {w}} (r,\varphi ,\Omega ;\omega ){{e}^{{ - in\varphi }}}d\varphi ,} \\ {{{u}_{n}}(r,\Omega ;\omega ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\tilde {u}} (r,\varphi ,\Omega ;\omega ){{e}^{{ - in\varphi }}}d\varphi ,\quad {{u}_{{0n}}}(r,\Omega ;\omega ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{{\tilde {u}}}_{0}}} (r,\varphi ,\Omega ;\omega ){{e}^{{ - in\varphi }}}d\varphi .} \end{array}$
Тогда соотношения (2.3), (2.4) можно свести к следующей системе равенств, справедливой для любых $n \in \mathbb{Z}$, $\Omega \in \mathbb{R}$ и всех рассматриваемых $\omega $:
(2.5)
${{\omega }^{2}}\int\limits_0^a {{{G}_{n}}} (r,r{\text{'}},\Omega ;\omega ){{{v}}_{n}}(r{\text{'}},\Omega ;\omega )r{\text{'}}dr{\text{'}} = \frac{1}{{2\pi }}{{w}_{n}}(r,\Omega ;\omega ),\quad r \in [{{r}_{0}},b];$
(2.6)
При этом
(2.7)
$\begin{gathered} {{{v}}_{n}}(r{\text{'}},\Omega ;\omega ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{F}_{z}}} \left[ {{v}(r{\text{'}},\varphi ,z;\omega )} \right]{{e}^{{ - in\varphi }}}d\varphi = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{F}_{z}}} \left[ {\xi (r{\text{'}},\varphi ,z)u(r{\text{'}},\varphi ,z;\omega )} \right]{{e}^{{ - in\varphi }}}d\varphi = \\ = \;\frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{F}_{z}}} \left[ {\xi (r{\text{'}},\varphi ,z)\sum\limits_m {{{u}_{m}}} (r{\text{'}},\Omega ;\omega ){{e}^{{im\varphi }}}} \right]{{e}^{{ - in\varphi }}}d\varphi . \\ \end{gathered} $
Соотношения (2.5), (2.6) являются уравнениями для неизвестных функций ${{{v}}_{n}}(r{\text{'}},\Omega ;\omega )$ и ${{u}_{n}}(r,\Omega ;\omega )$ одной переменной $r{\text{'}}$ или $r$. Другие аргументы этих функций, т.е. $\Omega $, $\omega $, играют роль параметров.

3. АЛГОРИТМЫ РЕШЕНИЯ ПРЯМОЙ И ОБРАТНОЙ ЗАДАЧИ ДЛЯ ЦИЛИНДРИЧЕСКОЙ ОБЛАСТИ

3.1. Прямая задача

Рассматриваемая ниже прямая задача заключается в нахождении из равенств (2.1), (2.2) функции $w\left( {r,\varphi ,z,\omega } \right)$, $r \in [{{r}_{0}},b]$, $\varphi \in [0,2\pi ]$, $z \in \mathbb{R}$, по известной финитной функции $\xi (r{\text{'}},\varphi {\text{'}},z{\text{'}})$ и заданной функции источников ${{u}_{0}}(r,\varphi ,z;\omega )$ для рассматриваемого конечного набора частот $\omega $. Для этого равенства (2.1), (2.2) сводятся к системе (2.3), (2.4) и далее к системе соотношений (2.5)–(2.7). Тогда вычисление функции $w$ можно представить в виде следующего алгоритма.

Алгоритм 1

Шаг 1. Для набора рассматриваемых частот $\omega $ вычисляем преобразования Фурье по $z$ известных функций ${{G}_{0}}$, ${{u}_{0}}$:

$\tilde {G}(r,r{\text{'}},\varphi ,\Omega ;\omega ) = {{F}_{z}}\left[ {{{G}_{0}}(r,r{\text{'}},\varphi ,z;\omega )} \right](\Omega ),\quad {{\tilde {u}}_{0}}(r,\varphi ,\Omega ;\omega ) = {{F}_{z}}\left[ {{{u}_{0}}(r,\varphi ,z;\omega )} \right](\Omega )$
и раскладываем полученные функции в ряды Фурье по $\varphi $:
$\tilde {G}(r,r{\text{'}},\varphi ,\Omega ;\omega ) = \sum\limits_n {{{G}_{n}}} (r,r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi }}},\quad {{\tilde {u}}_{0}}(r,\varphi ,\Omega ;\omega ) = \sum\limits_n {{{u}_{{0n}}}} (r,r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi }}}.$
Обе эти процедуры реализуются с применением быстрого дискретного преобразования Фурье (БПФ).

Шаг 2. Для каждого из параметров $\omega $, $\Omega $ реализуем следующий итерационный процесс решения уравнений (2.6), (2.7) относительно набора функции ${\text{\{ }}{{u}_{n}}(r,\Omega ;\omega ){\text{\} }}$:

(3.1)
${v}_{n}^{{(k)}}(r{\text{'}},\Omega ;\omega ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{F}_{z}}} \left[ {\xi (r{\text{'}},\varphi ,z)\sum\limits_m {u_{m}^{{(k)}}} (r{\text{'}},\Omega ;\omega ){{e}^{{im\varphi }}}} \right]{{e}^{{ - in\varphi }}}d\varphi ,\quad r{\text{'}} \in [0,a],$
(3.2)
$\begin{gathered} u_{n}^{{(k + 1)}}(r,\Omega ;\omega ) = {{u}_{{0n}}}(r,\Omega ;\omega ) + 2\pi {{\omega }^{2}}\int\limits_0^a {{{G}_{n}}} (r,r{\text{'}},\Omega ;\omega ){v}_{n}^{{(k)}}(r{\text{'}},\Omega ;\omega )r{\text{'}}dr{\text{'}},\quad r \in [0,a], \\ k = 0,1,2, \ldots , \\ \end{gathered} $
с начальным приближением в виде набора функций $\{ u_{n}^{{(0)}}(r,\Omega ;\omega )\} = \{ {{u}_{{0n}}}(r,\Omega ;\omega )\} $.

Шаг 3. Останавливаем процесс по некоторому правилу на итерации номер $\nu $ и получаем приближенное решение $\{ u_{n}^{{(\nu )}}(r,\Omega ;\omega )\} $ системы (2.6), (2.7) и соответствующие функции $\{ {v}_{n}^{{(\nu )}}(r,\Omega ;\omega )\} $.

Шаг 4. Согласно (2.5) вычисляем приближенный набор величин $\left\{ {{{w}_{n}}(r,\Omega ;\omega )} \right\}$:

(3.3)
$w_{n}^{{(\nu )}}(r,\Omega ;\omega ) = 2\pi {{\omega }^{2}}\int\limits_0^a {{{G}_{n}}} (r,r{\text{'}},\Omega ;\omega ){v}_{n}^{{(\nu )}}(r{\text{'}},\Omega ;\omega )r{\text{'}}dr{\text{'}},\quad r \in [{{r}_{0}},b],$
и принимаем функцию
(3.4)
$\mathop {\tilde {w}}\nolimits^{(\nu )} (r,\varphi ,\Omega ;\omega ) = \sum\limits_n {w_{n}^{{(\nu )}}} (r{\text{'}},\Omega ;\omega ){{e}^{{in\varphi }}}$
(или ее обратное преобразование Фурье) как приближенное решение прямой задачи.

Мы не будем здесь проводить теоретический анализ сходимости алгоритма 1, так как формально он не используется нами при решении обратной задачи. Он нужен нам лишь для генерации ее модельных данных, и это лишь один из способов получения таких данных. Отметим лишь, что, как следует из общей теории решения интегральных уравнений II рода (см., например, [25]), алгоритм будет быстро сходиться по крайней мере для малых $\omega $. Ниже будут продемонстрированы численные примеры, подтверждающие это положение.

3.2. Обратная задача

Она состоит в нахождении решения $\xi (r{\text{'}},\varphi {\text{'}},z{\text{'}})$ из системы (2.1), (2.2) по заданной функции $w\left( {r,\varphi ,z,\omega } \right)$, $r \in [{{r}_{0}},b]$, $\varphi \in [0,2\pi ]$, $z \in \mathbb{R}$, и заданной функции источников ${{u}_{0}}(r,\varphi ,z;\omega )$ для каждой рассматриваемой частоты $\omega $. Для этого мы сводим задачу (2.1), (2.2) к системе (2.5)–(2.7), считая заданными (вычисленными) наборы функций $\left\{ {{{w}_{n}}(r,\Omega ;\omega )} \right\}$, $\left\{ {{{u}_{{0n}}}(r,\Omega ;\omega )} \right\}$, и по этим наборам находим функцию $\xi $. Процедура решения представлена в виде следующего алгоритма.

Алгоритм 2

Шаг 1. Для всех рассматриваемых параметров $\omega $, $\Omega $ и всех рассматриваемых $n$ решаем одномерные интегральные уравнения I рода, соответствующие равенствам (2.5):

(3.5)
${{\omega }^{2}}\int\limits_0^a {{{G}_{n}}} (r,r{\text{'}},\Omega ;\omega ){{{v}}_{n}}(r{\text{'}},\Omega ;\omega )r{\text{'}}dr{\text{'}} = \frac{1}{{2\pi }}{{w}_{n}}(r,\Omega ;\omega ),\quad r \in [{{r}_{0}},b].$
При этом используется подходящий метод регуляризации (регуляризующий алгоритм, РА) этих некорректно поставленных задач. В итоге получается набор приближенных решений $\{ {{{v}}_{n}}(r{\text{'}},\Omega ;\omega )\} $.

Шаг 2. По найденному набору $\{ {{{v}}_{n}}(r{\text{'}},\Omega ;\omega )\} $ вычисляем, используя равенства (2.6), набор функций $\{ {{u}_{n}}(r,\Omega ;\omega )\} $:

(3.6)
${{u}_{n}}(r,\Omega ;\omega ) = {{u}_{{0n}}}(r,\Omega ;\omega ) + 2\pi {{\omega }^{2}}\int\limits_0^a {{{G}_{n}}} (r,r{\text{'}},\Omega ;\omega ){{{v}}_{n}}(r{\text{'}},\Omega ;\omega )r{\text{'}}dr{\text{'}},\quad r \in [0,a].$

Шаг 3. Восстанавливаем по наборам $\{ {{{v}}_{n}}(r{\text{'}},\Omega ;\omega )\} $ и $\{ {{u}_{n}}(r,\Omega ;\omega )\} $ функции ${v}(r,\varphi ,z)$, $u(r,\varphi ,z)$, $r{\text{'}},r \in [0,a]$, $\varphi \in [0,2\pi ]$, $z \in \mathbb{R}$, суммируя соответствующие ряды Фурье.

Шаг 4. Находим решение $\xi (r,\varphi ,z)$ из уравнения $u(r,\varphi ,z,\omega )\xi (r,\varphi ,z) = {v}(r,z,\omega )$ для каждой точки $(r,\varphi ,z) \in X$. Это можно сделать для каждого рассматриваемого $\omega $, и результат будет, вообще говоря, зависеть от $\omega $. Такая процедура соответствует исследованию акустических неоднородностей раздельно на каждой частоте. Далее можно, например, усреднить результаты тем или иным методом по величине $\omega $. Альтернативный вариант – решить для каждой точки $(r,\varphi ,z) \in X$ систему уравнений для всех рассмотренных $\omega $: $u(r,\varphi ,z,\omega )\xi (r,\varphi ,z) = {v}(r,z,\omega )$, используя метод наименьших квадратов. Это также будет определенным усреднением по $\omega $ получаемых решений.

Шаг 5. Вычисляем функцию $c(r,\varphi ,z)$ из равенства $\xi (r,\varphi ,z) = c_{0}^{{ - 2}} - {{c}^{{ - 2}}}(r,\varphi ,z)$.

Сделаем некоторые замечания об алгоритме 2.

Замечание 1. Для реализации ш. 1 необходимо детализировать предположения о функциях ${v}$, $w$. Используя предположение 2, мы считаем, что справедливы включения ${v}({\mathbf{x}},\omega ) \in {{L}_{2}}(X)$, $w({\mathbf{x}},\omega ) \in {{L}_{2}}(Y)$ для каждой рассматриваемой частоты $\omega $. Первое включение вытекает из финитности функции $\xi $, а второе постулируется. В этом случае для уравнений (3.5) применимы известные методы решения линейных некорректно поставленных задач в гильбертовых пространствах (см., например, [5], [6], [26]–[28] и др.).

Замечание 2. В используемой схеме решения обратной задачи уравнение (1.3) (т.е. (2.1)) и порождаемые им уравнения (3.5)) могут иметь неединственное решение для используемого конечного набора частот $\omega $. Поэтому важно установить связь решений этих уравнений. Эту связь обосновывают следующие утверждения.

Теорема 1. 1. Пусть $w(r,\varphi ,z;\omega ) \in {{L}_{2}}(Y)$ при каждом $\omega $. Тогда всякое решение уравнения (2.1) ${v}(r,\varphi ,z;\omega ) \in {{L}_{2}}(X)$ представимо в виде

(3.7)
${v}(r,\varphi ,z;\omega ) = F_{\Omega }^{{ - 1}}\left[ {\sum\limits_n {{{{v}}_{n}}} (r,\Omega ;\omega ){{e}^{{in\varphi }}}} \right](z),\quad (r,\varphi ,z) \in X,$
где функции ${{{v}}_{n}}(r,\Omega ;\omega ) \in {{L}_{2}}\left\{ {[0,a] \times {{\mathbb{R}}_{\Omega }}} \right\}$ удовлетворяют интегральным уравнениям (2.5) при каждом $\omega $. Обратно, если ${{{v}}_{n}}(r,\Omega ;\omega ) \in {{L}_{2}}\left\{ {[0,a] \times {{\mathbb{R}}_{\Omega }}} \right\}$ – решения уравнений (2.5) такие, что $\sum\nolimits_n {\mathop {\left\| {{{{v}}_{n}}(r,\Omega ;\omega )} \right\|}\nolimits_{{{L}_{2}}\left\{ {[0,a] \times {{\mathbb{R}}_{\Omega }}} \right\}}^2 } < \infty $ при каждом $\omega $, то функция вида (3.7) есть решение уравнения (2.1).

2. Для каждого $\omega $ справедливо равенство

(3.8)
$\mathop {\left\| {{v}(r,\varphi ,z;\omega )} \right\|}\nolimits_{{{L}_{2}}(X)}^2 = \sum\limits_n {\mathop {\left\| {{{{v}}_{n}}(r,\Omega ;\omega )} \right\|}\nolimits_{{{L}_{2}}\{ [0,a] \times {{\mathbb{R}}_{\Omega }}\} }^2 } .$
Здесь $F_{\Omega }^{{ - 1}}[{\kern 1pt} \cdot {\kern 1pt} ]$ – обратное преобразование Фурье по переменной $z$.

Следствие 1. Пусть функции ${{{\bar {v}}}_{n}}(r,\Omega ;\omega ) \in {{L}_{2}}\{ [0,a] \times {{\mathbb{R}}_{\Omega }}\} $ – нормальные решения уравнений (2.5) (решения с минимальной нормой). Тогда функция

${\bar {v}}(r,\varphi ,z;\omega ) = F_{\Omega }^{{ - 1}}\left[ {\sum\nolimits_n {{{{{\bar {v}}}}_{n}}} (r,\Omega ;\omega ){{e}^{{in\varphi }}}} \right](z)$, $(r,\varphi ,z) \in X$,

есть единственное нормальное решение уравнения (2.1).

Доказательства этих утверждений проводятся так же, как в работе [18]. Там аналогичные утверждения доказывались для решений другого интегрального уравнения I рода, схожего с (2.1) по виду и свойствам и отличающегося ядром и правой частью. Для краткости мы опускаем повторение этих доказательств, заметив, что интегральное уравнение из [18] не имеет прямого отношения к обратной задаче, рассматриваемой в данной статье.

Замечание 3. В используемой схеме решения обратной задачи и в алгоритме 2 процедура обращения фактически используется только при решении уравнений I рода (2.5) (или (3.5)), которые представляют собой некорректно поставленные задачи. Для уравнения вида (2.5) применимы многие устойчивые методы решения линейных некорректно поставленных задач (например, [5], [6], [26]–[28] и др.). В силу возможной неединственности решений этих уравнения мы применяем для реализации ш. 1 алгоритма методы, ориентированные на поиск нормальных решений (тихоновская регуляризация, метод TSVD). В случае неединственного решения уравнения (2.1), т.е неединственных решений уравнений (3.5), такой подход выделяет из всех возможных решений то, которое имеет минимальную норму “вторичных источников” ${v}(r,z,\omega ) = u(r,\varphi ,z,\omega )\xi (r,\varphi ,z)$ (см. [4]), и это теоретически позволяет исключить или ослабить появления ложных акустических неоднородностей.

В случае единственности решения оно будет совпадать с вычисленным нормальным решением. Указанные методы регуляризации обоснованы и апробированы в ряде работ (например, в [18], [19] при решении другой обратной задачи). Отметим, что ш. 1 алгоритма является наиболее трудоемким пунктом при использовании алгоритма 2.

4. КОНЕЧНОМЕРНАЯ АППРОКСИМАЦИЯ И РЕШЕНИЕ МОДЕЛЬНЫХ ЗАДАЧ

Везде далее полагается, что уравнения (1.3), (1.4) и их следствия записаны в безразмерном виде с ${{c}_{0}} = 1$, так что ${{k}_{0}} = \omega $. Модельные области имеют вид

$\begin{gathered} Q = \{ (x,y,z)\,:{{x}^{2}} + {{y}^{2}} \leqslant {{4}^{2}},\;\left| z \right| \leqslant 2\} ,\quad X = \{ (x,y,z)\,:{{x}^{2}} + {{y}^{2}} \leqslant 1,\left| z \right| \leqslant 2\} , \\ Y = \{ (x,y,z)\,:{{3}^{2}} \leqslant {{x}^{2}} + {{y}^{2}} \leqslant {{4}^{2}},\left| z \right| \leqslant 2\} . \\ \end{gathered} $
Cчитается также, что $\sigma ({\mathbf{x}}) = 0$ и модельные источники задаются в форме
$f({\mathbf{x}}) = \sum\limits_{m = 1}^{{{M}_{s}}} {{{A}_{m}}} \delta ({\mathbf{x}} - {{{\mathbf{x}}}_{m}}),$
где ${{{\mathbf{x}}}_{m}}$ – координаты точечных $\delta $-образных источников. Тогда
${{u}_{0}}({\mathbf{x}},\omega ) = \sum\limits_{m = 1}^{{{M}_{s}}} {{{A}_{m}}} {{G}_{0}}({\mathbf{x}},{\mathbf{x}}_{m}^{'},\omega ),$
и преобразование Фурье этой функции, ${{\tilde {u}}_{0}}(r,\varphi ,\Omega ;\omega )$, можно заранее вычислить. Мы не ставили себе целью оптимизировать число, положения и амплитуды источников. Во всех расчетах считалось, что ${{M}_{s}} = 8$, ${{A}_{m}} = 1$, ${{{\mathbf{x}}}_{m}} = ({{r}_{m}},{{\varphi }_{m}},{{z}_{m}})$, где ${{r}_{m}} = 4.01$ и
${{\varphi }_{m}} = \left[ {0,\;\frac{\pi }{2},\; - \,\frac{\pi }{2},\;\pi ,\;0,\;\frac{\pi }{2},\; - \,\frac{\pi }{2},\;\pi } \right],\quad {{z}_{m}} = [ - 1,\; - {\kern 1pt} 1,\; - {\kern 1pt} 1,\; - {\kern 1pt} 1,\;1,\;1,\;1,\;1].$
Для численного исследования предлагаемых алгоритмов рассмотрены две прямые и обратные модельные задачи.

Задача 1. Задача имеет решение $\xi (x,y,z)$ вида

$\begin{gathered} \xi (x,y,z) = {{\xi }_{1}}(x,y,z) + {{\xi }_{2}}(x,y,z),\quad (x,y,z) \in Q; \\ {{\xi }_{1}}(x,y,z) = \{ {{A}_{0}}exp\{ - 30{{R}_{1}}(x,y,z)\} ,\;(x,y,z) \in {{Q}_{1}};\;0,\;(x,y,z) \in Q{{\backslash }}{{Q}_{1}}\} , \\ {{\xi }_{2}}(x,y,z) = \{ 2{{A}_{0}}exp\{ - 30{{R}_{2}}(x,y,z)\} ,\;(x,y,z) \in {{Q}_{2}};\;0,\;(x,y,z) \in Q{{\backslash }}{{Q}_{2}}\} , \\ \end{gathered} $
где
$\begin{gathered} {{R}_{1}}(x,y,z) = 5{{(x - 0.4)}^{2}} + 5{{y}^{2}} + 0.125{{(z + 0.1)}^{2}}, \\ {{R}_{2}}(x,y,z) = 5{{(x + 0.4)}^{2}} + 5{{(y - 0.4)}^{2}} + 0.125{{(z - 0.2)}^{2}} \\ \end{gathered} $
и
$\begin{gathered} {{Q}_{1}} = \{ (x,y,z)\,:{{(x - 0.4)}^{2}} + {{y}^{2}} + 0.125{{(z + 0.1)}^{2}} \leqslant {{1.3}^{2}}\} , \\ {{Q}_{2}} = \{ (x,y,z)\,:{{(x + 0.4)}^{2}} + {{(y - 0.4)}^{2}} + 0.125{{(z - 0.2)}^{2}} \leqslant {{0.5}^{2}}\} . \\ \end{gathered} $
Эта функция моделирует небольшие локальные неоднородности среды, положение которых и соответствующие им распределения скоростей нужно найти. Именно на поиск таких неоднородностей “настраивается” алгоритм 2.

Величина ${{A}_{0}}$ определяет контраст

$\frac{{\Delta c}}{{{{c}_{0}}}} = {\mathbf{x}}max\left\{ {\frac{1}{{\sqrt {1 - c_{0}^{2}\xi ({\mathbf{x}})} }}} \right\} - 1$
искомого решения. В расчетах использовалось значение ${{A}_{0}} = 0.545$, которое соответствует контрасту 15.95. По классификации из [3, с. 33] такой рассеиватель можно считать “сильным”, учитывая его характерные размеры $l \sim 0.2$ (см. фиг. 4а) и значения ${{c}_{0}} = 1$, $\omega = 3$: $\tfrac{{\Delta c}}{{{{c}_{0}}}} \gg \tfrac{{{{c}_{0}}}}{{l\omega }}$. Подобные рассеиватели достаточно часто встречаются на практике. Вторая модельная задача будет описана ниже.

Исходные уравнения (1.3), (1.4) аппроксимировались в областях $X$, $Y$ конечно-разностным методом на равномерных сетках по переменным $r$, $r{\text{'}}$, $\varphi $, $z$. Размеры сеток определяются числами ${{N}_{r}}$, ${{N}_{{r'}}}$, ${{N}_{\varphi }}$, ${{N}_{z}}$. В области $X$ сетка имеет размер ${{N}_{{r'}}} \times {{N}_{\varphi }} \times {{N}_{z}}$, а в области $Y$ размер ${{N}_{r}} \times {{N}_{\varphi }} \times {{N}_{z}}$. Конкретные размеры будут указаны ниже для каждого примера. Дискретные аналоги функций $\tilde {G}(r,r{\text{'}},\varphi ,\Omega ;\omega )$, ${{\tilde {u}}_{0}}(r,\varphi ,\Omega ;\omega )$, использующиеся в алгоритмах 1 и 2, вычислялись для рассматриваемых частот $\omega $ по известным величинам ${{G}_{0}}\left( {r,r{\text{'}},\varphi ,z;\omega } \right)$, ${{u}_{0}}(r,\varphi ,z;\omega )$ с помощью быстрого преобразования Фурье с сеткой $\{ {{\Omega }^{{(m)}}}\} _{{m = 1}}^{{{{N}_{z}}}}$ по переменной $\Omega $. Разложения в ряды Фурье реализовывались также с помощью БПФ с $n \in [0,{{N}_{\varphi }} - 1]$. Детали этих хорошо известных стандартных вычислений даны, например, в [26].

4.1. Получение модельных данных для решения обратной задачи с помощью алгоритма 1

Приведем типичные результаты численного исследования итерационного процесса (3.1), (3.2) для получения данных первой обратной задачи на сетках размера ${{N}_{r}} = 32$, ${{N}_{{r{\text{'}}}}} = 33$, ${{N}_{\varphi }} = 90$, ${{N}_{z}} = 64$. На фиг. 2 показаны в сравнении скорости сходимости процесса для различных величин $\omega = {{k}_{0}}$.

Фиг. 2.

Скорость сходимости итераций (3.1), (3.2) для разных $\omega = {{k}_{0}}$.

Останов итераций производился по величине

${{\Delta }_{k}}(\omega ) = \mathop {\left\{ {\sum\limits_n {\mathop {\left\| {u_{n}^{{(k)}}\left( {r,\Omega ;\omega } \right) - u_{n}^{{(k - 1)}}\left( {r,\Omega ;\omega } \right)} \right\|}\nolimits_{{{L}_{2}}\{ \Pi \} }^2 } } \right\}}\nolimits^{1/2} \mathop {\left\{ {\sum\limits_n {\mathop {\left\| {u_{n}^{{(0)}}\left( {r,\Omega ;\omega } \right)} \right\|}\nolimits_{{{L}_{2}}\{ \Pi \} }^2 } } \right\}}\nolimits^{ - 1/2} ,$
когда для номера итерации $\nu $ выполнялось условие ${{\Delta }_{\nu }}(\omega ) \leqslant {{10}^{{ - 13}}}$. Здесь $\Pi = \left\{ {(r,\Omega ) \in [0,a] \times {{\mathbb{R}}_{\Omega }}} \right\}$. После этого по найденному набору функций $\{ u_{n}^{{(\nu )}}(r,\Omega ;\omega )\} $ по формуле (3.1) c $k = \nu $ вычислялись функции $\{ {v}_{n}^{{(\nu )}}(r{\text{'}},\Omega ;\omega )\} $, затем по формуле (3.3) находились функции $\{ w_{n}^{{(\nu )}}(r,\Omega ;\omega )\} $, которые далее преобразовывались, согласно (3.4), в функции ${{\tilde {w}}^{{(\nu )}}}(r,\varphi ,\Omega ;\omega )$. Обратное преобразование Фурье последней функции по переменной $z$, ${{w}^{{(\nu )}}}(r{\text{'}},\varphi ,z;\omega )$, представляет данные для решения обратной задачи. Вид этой функции, найденной для $\omega = {{k}_{0}} = 3$, показан на фиг. 3 для сечения $z = 0$.

Фиг. 3.

Типичные данные ${{w}^{{(\nu )}}}(r,\varphi ,0;\omega = 3)$ для решения обратной задачи.

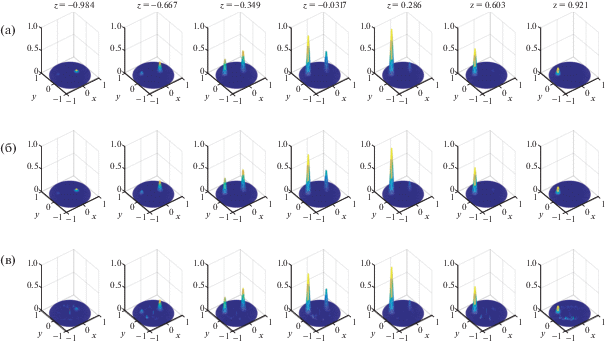
Фиг. 4.

Качественное сравнение точного решения ${{\xi }_{{{\text{exact}}}}}(x,y,z)$ и вычисленных приближенных решений ${{\xi }_{{{\text{appr}}}}}(x,y,z)$ обратной задачи в различных сечениях $z = {\text{const}}$; (а) – точное решение; (б) – приближенное решение, полученное для точных данных по алгоритму 2; (в) – приближенное решение для возмущенных данных с $\delta = {{10}^{{ - 8}}}$.

Данные для решения обратной задачи задавались с некоторой ошибкой, которая интерпретируется как ошибка измерения. В наших расчетах это моделировалось наложением на функцию ${{w}^{{(\nu )}}}(r,\varphi ,z;\omega )$ аддитивной нормально распределенной псевдослучайной помехи с нулевым средним так, что получаемая в итоге приближенная функция $w_{\delta }^{{(\nu )}}(r,\varphi ,z;\omega )$ удовлетворяла бы условию

$\mathop {\left\| {w_{\delta }^{{(\nu )}}(r,\varphi ,z;\omega ) - {{w}^{{(\nu )}}}(r,\varphi ,z;\omega )} \right\|}\nolimits_{{{L}_{2}}(Y)} \leqslant \delta {{\left\| {{{w}^{{(\nu )}}}(r,\varphi ,z;\omega )} \right\|}_{{{{L}_{2}}(Y)}}}\mathop = \limits^{{\text{def}}} {{\delta }_{0}}.$
Это соответствует приближенному заданию данных с относительной точностью $\delta $.

4.2. Реализация алгоритма 2

Первый шаг алгоритма 2 – решение уравнений I рода (3.5) методами регуляризации – обсуждался в работах [18], [19] в связи с решением другого интегрального уравнения, отличающегося видом  ядра и  правой части. В этих работах отмечено, что для каждой рассматриваемой частоты $\omega $ используемая дискретизация приводит уравнения (3.5) к системе линейных алгебраических уравнений (СЛАУ) вида $A_{n}^{{(m)}}V_{n}^{{(m)}} = W_{n}^{{(m)}}$ для каждого $n \in [0,{{N}_{\varphi }} - 1]$, $m \in [1,{{N}_{z}}]$. Здесь $A_{n}^{{(m)}} = [{{\mu }_{{ij}}}{{G}_{n}}({{r}_{i}},r_{j}^{'},{{\Omega }^{{(m)}}};\omega )]_{{i = 1,j = 1}}^{{{{N}_{r}},{{N}_{{r{\text{'}}}}}}}$ – матрица системы, получаемая дискретизацией ядра уравнения (3.5) на рассматриваемой сетке размера ${{N}_{r}} \times {{N}_{{r{\text{'}}}}}$, ${{\Omega }^{{(m)}}}$ – точки сетки величин $\Omega $, а ${{\mu }_{{ij}}}$ – квадратурные коэффициенты для вычисления интегралов в (3.5). Правые части

$W_{n}^{{(m)}} = \frac{1}{{2\pi {{\omega }^{2}}}}[{{w}_{n}}({{r}_{i}},{{\Omega }^{{(m)}}};\omega )]_{{i = 1}}^{{{{N}_{r}}}}$
системы суть вектор-столбцы высоты ${{N}_{r}}$, а искомый вектор-столбец $V_{n}^{{(m)}}$ содержит неизвестные ${{{v}}_{n}}(r_{j}^{'},{{\Omega }^{{(m)}}};\omega )$. Таким образом, при выполнении ш. 1 алгоритма 2 для каждого $\omega $ необходимо решить ${{N}_{\varphi }} \times {{N}_{z}}$ систем линейных уравнений с матрицами размера ${{N}_{r}} \times {{N}_{{r{\text{'}}}}}$.

Мы решали указанные СЛАУ с помощью различных вариантов метода регуляризации А.Н. Тихонова [26], [27] и с помощью метода TSVD [28]. Обоснование применения этих методов дано с общих позиций теории регуляризации некорректных задач в [18], [19] для аналогичного интегрального уравнения, и здесь мы не повторяем это обоснование. Наилучшие результаты в расчетах получились для метода TSVD с “обрезанием” (см. [28]) сингулярных чисел матриц $A_{n}^{{(m)}}$ по уровню $\delta _{0}^{{2/3}}$. Эти результаты мы и будем приводить в дальнейшем.

Шаг 2 алгоритма 2 не вызывает сложностей для дискретизированной задачи, так как сводится к матричному умножению дискретных величин ${{G}_{n}}$, ${{{v}}_{n}}$ и сложению результата с дискретным аналогом функции ${{u}_{{0n}}}$. Шаг 3 выполнялся с помощью обратного БПФ. Наконец, шаг 4 при решении обратной задачи для каждой из рассматриваемых частот $\omega $ реализовывался с помощью следующей процедуры нахождения нормального псевдорешения уравнения $u\xi = {v}$ в каждой точке $(r{\text{'}},\varphi {\text{'}},z) \in X$ по методу TSVD: $\xi = \left\{ {\frac{{v}}{u},\left| u \right| > {\text{tol}};\;0,\;\left| u \right| \leqslant {\text{tol}}} \right\}$ с ${\text{tol}} = {{10}^{{ - 12}}}$. Далее, при необходимости нетрудно пересчитать функцию $\xi ({\mathbf{x}})$ в $c({\mathbf{x}})$. В приводимых ниже примерах мы для краткости этого не делаем, представляя на рисунках непосредственно величину $\xi ({\mathbf{x}})$.

4.3. Результаты решения обратной задачи

Первая серия экспериментов связана с решением с помощью предлагаемого алгоритма 2 первой модельной обратной задачи на сетках размера ${{N}_{r}} = 32$, ${{N}_{{r{\text{'}}}}} = 33$, ${{N}_{\varphi }} = 90$, ${{N}_{z}} = 64$ при $\omega = {{k}_{0}} = 3$. Задачи решались с точными (вычисленными по алгоритму 1) данными и приближенными данными с различным уровнем возмущения $\delta $. На фиг. 4 представлены для качественного сравнения точное ${{\xi }_{{{\text{exact}}}}}(x,y,z)$ и приближенные решения ${{\xi }_{{{\text{appr}}}}}(x,y,z)$ обратной задачи в различных сечениях по $z$. Точное решение показано в первой строке рисунка. Во второй строке приведено приближенное решение обратной задачи для точных данных. В третьей строке изображено решение для возмущенных данных с $\delta = {{10}^{{ - 8}}}$. Рисунок демонстрирует достаточно высокую чувствительность приближенных решений к возмущениям данных. Более детальная информация о точности решения обратной задачи, т.е. о величине относительной ошибки

${{\Delta }_{{{{L}_{2}}}}}(z) = \frac{{\mathop {\left\| {{{\xi }_{{{\text{appr}}}}}(x,y,z) - {{\xi }_{{{\text{exact}}}}}(x,y,z)} \right\|}\nolimits_{{{L}_{2}}({{X}_{{xy}}})} }}{{zmax\mathop {\left\| {{{\xi }_{{{\text{exact}}}}}(x,y,z)} \right\|}\nolimits_{{{L}_{2}}({{X}_{{xy}}})} }}$
приближенного решения ${{\xi }_{{{\text{appr}}}}}(x,y,z)$ в слое $z = {\text{const}}$ от величины $z$ при разных уровнях погрешности данных $\delta $ представлены на фиг. 5. Для сравнения на фиг. 6 приведены точности приближенных решений, полученных при разных $\delta $ для модельных задач с $\omega = 1$ и $\omega = 2$. Очевидно улучшение точности с возрастанием $\omega $.

Фиг. 5.

Первая модельная задача. Относительная точность ${{\Delta }_{{{{L}_{2}}}}}(z)$ приближенных решений для различных $z$ при разных уровнях возмущения данных $\delta $ для $\omega = 3$.

Фиг. 6.

Первая модельная задача. Относительная точность ${{\Delta }_{{{{L}_{2}}}}}(z)$ приближенных решений для различных $z$ при разных уровнях возмущения данных $\delta $; (а) – для $\omega = 1$; (б) – для $\omega = 2$.

При решении рассматриваемой обратной задачи весьма важно, насколько точно алгоритм позволяет определять положения изучаемых локальных рассеивателей. Для иллюстрации была решена

Задача 2. Задача отличается от первой лишь выражениями для ${{\xi }_{1}}(x,y,z)$ и ${{\xi }_{2}}(x,y,z)$:

$\begin{gathered} {{\xi }_{1}}(x,y,z) = \{ {{A}_{0}};\;(x,y,z) \in {{Q}_{1}};\;0,\;(x,y,z) \in Q{{\backslash }}{{Q}_{1}}\} , \\ {{\xi }_{2}}(x,y,z) = \{ 2{{A}_{0}};\;(x,y,z) \in {{Q}_{2}};\;0,\;(x,y,z) \in Q{{\backslash }}{{Q}_{2}}\} ,\quad {{A}_{0}} = 0.2. \\ \end{gathered} $
Это соответствует двум рассеивателям эллипсоидальной формы, лежащим в области $X$ и заполненным веществом с различными показателями преломления. Фигура 7 показывает качественно влияние возмущения данных задачи на определение положения и геометрии неоднородностей. Контраст точного решения здесь равен 0.291. Видно, что положения могут быть достаточно уверенно определены в случае $\delta = {{10}^{{ - 9}}}$, а при использовании подходящей фильтрации шумов в найденном решении и для $\delta = {{10}^{{ - 8}}}$.

Фиг. 7.

Вторая модельная задача с $\omega = 3$. Качественное сравнение положений и геометрии восстанавливаемой неоднородности $\xi ({\mathbf{x}})$ для различных $\delta $.

5. НЕКОТОРЫЕ СВОЙСТВА АЛГОРИТМА 2

Все вычисления проводились в системе МАТЛАБ на ПК с процессором Intel (R) Core (TM) i7-7700 CPU 3.60 GHz, ОЗУ 16 Гб (без распараллеливания). Алгоритм 2 решения обратной задачи оказался достаточно быстрым. Приведем данные соответствующих численных экспериментов для решения первой обратной задачи на частоте $\omega = 2$. В экспериментах считалось, что сетка по $z$ фиксирована (${{N}_{z}} = 64$), а меняются только размеры ${{N}_{r}}$, ${{N}_{\varphi }}$ сеток по $r$ и $\varphi $. Кроме того, полагалось, что ${{N}_{{r'}}} = {{N}_{r}} + 1$. Тогда время решения обратной задачи есть функция вида ${{T}_{{IP}}}({{N}_{r}},{{N}_{\varphi }})$. Эта зависимость приведена на фиг. 8. При изменении размера сетки по $z$ время ${{T}_{{IP}}}({{N}_{r}},{{N}_{\varphi }})$ меняется пропорционально числу ${{N}_{z}}$, так как оно определяется решением ${{N}_{z}} \times {{N}_{\varphi }}$ уравнений вида (3.5).

Фиг. 8.

Время решения обратной задачи ${{T}_{{IP}}}({{N}_{r}},{{N}_{\varphi }})$ для различных ${{N}_{r}}$, ${{N}_{\varphi }}$.

Еще раз отметим, что решаемая обратная задача весьма чувствительна к ошибкам входных данных. При решении интегрального уравнения (1.3) с двойной точностью внесение в правую часть эквивалентной системы уравнения (3.5) случайных ошибок с амплитудой порядка ${{10}^{{ - 8}}}$ приводит к серьезным искажениям решения при использовании и метода TSVD, и метода регуляризации. Это связано с весьма быстрым убыванием сингулярных чисел матриц $A_{n}^{{(m)}}$ для СЛАУ, решаемых на ш. 1 алгоритма 2, и такое убывание является специфической особенностью решаемой обратной задачи, а точнее, интегрального уравнения (1.3). Аналогичное свойство обратной коэффициентной задачи для волнового уравнения отмечалось ранее в работах [18], [19]. Подтверждающие это соответствующие теоретические оценки устойчивости при различных априорных предположениях на точное решение можно найти в [5], [6].

6. ВЫВОДЫ

В этой работе мы не стремились построить наилучший по всем характеристикам численный алгоритм решения обратной задачи (1.2). В рамках именно этой модели, с учетом цилиндрической геометрии областей решений и наблюдений, мы предложили некоторый алгоритм, который позволяет быстро решать обратную задачу на достаточно мелких сетках. Исследуя свойства алгоритма в численных экспериментах, представленных в работе, мы можем сделать следующие выводы.

1. Рассматриваемая трехмерная обратная задача скалярной акустики в цилиндрической области может быть решена численно с помощью предлагаемого алгоритма для достаточно мелких сеток за время порядка десятков секунд на ПК средней производительности даже без распараллеливания. Для этого следует использовать указываемую в статье схему регистрации данных обратной задачи в цилиндрическом слое. Предлагаемый алгоритм легко распараллеливается.

2. Исходная обратная задача, рассматриваемая для конечного набора частот, имеет, вообще говоря, неединственное решение. Для выделения определенного решения обратной задачи в нашем алгоритме используется поиск нормального решения интегрального уравнения (1.3). В случае, когда уравнение (1.3) имеет единственное решение при рассматриваемом наборе частот, это решение совпадает с найденным нормальным.

3. Рассматриваемая обратная задача, основанная на уравнениях (1.2) и решаемая раздельно на каждой частоте, сама по себе весьма чувствительна к возмущениям данных: для получения детального приближенного решения требуются данные, измеренные с большой точностью. Эта особенность задачи связана с видом ядра интегрального уравнения (1.3), его сингулярными числами и не зависит от используемого алгоритма решения этого уравнения. Устойчивость исходной обратной задачи можно повышать, вводя дополнительные априорные ограничения на решения.

4. Алгоритм 2 позволяет достаточно надежно определять положения и форму небольших локальных неоднородностей акустической среды при данных с малыми ошибками.

Авторы благодарны А.Г. Яголе за полезные замечания.

Список литературы

  1. Ramm A.G. Multidimensional Inverse Scattering Problems. Pitman Monogr. Surv. Pure Appl. Math. 51. Harlow: Longman Scientific & Technical, 1992.

  2. Colton D., Kress R. Inverse Acoustic and Electromagnetic Scattering Theory. 2nd ed. Appl. Math. Sci. 93. Berlin: Springer, 1998.

  3. Горюнов А.А., Сасковец А.В. Обратные задачи рассеяния в акустике. М.: Изд-во МГУ, 1989.

  4. Буров В.А., Румянцева О.Д. Обратные волновые задачи акустической томографии. Ч. 2. Обратные задачи акустического рассеяния. М.: ЛЕНАНД, 2020.

  5. Bakushinsky A., Goncharsky A. Ill-Posed Problems: Theory and Applications. Dordrecht: Kluwer Academic Publishers, 1994.

  6. Bakushinsky A.B., Kokurin M.Yu. Iterative methods for approximate solution of inverse problems. Mathematics and Its Applications. Dordrecht: Kluwer Academic Publishers, 2004.

  7. Гончарский А.В., Романов С.Ю. О двух подходах к решению коэффициентных обратных задач для волновых уравнений // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 2. С. 263–269.

  8. Гончарский А.В., Романов С.Ю. Суперкомпьютерные технологии в разработке методов решения обратных задач в УЗИ-томографии // Вычисл. методы и программирование: новые вычисл. технологии. 2012. Т. 13. № 1. С. 235–238.

  9. Belishev M.I. Recent progress in the boundary control method // Inverse Problems. 2007. V. 23. № 5. P. 1–67.

  10. Пестов Л.Н., Болгова В.М., Данилин А.Н. Численная реконструкция трехмерной скорости звука методом граничного управления // Вестн. Югорского государственного университета. 2011. Вып. 3. С. 92–98.

  11. Буров В.А., Алексеенко Н.В., Румянцева О.Д. Многочастотное обобщение алгоритма Новикова для решения обратной двумерной задачи рассеяния // Акустический ж. 2009. Т. 55. № 6. С. 784–798.

  12. Новиков P.Г. Восстановление двумерного оператора Шредингера по амплитуде рассеяния при фиксированной энергии // Функцион. анализ и его прил. 1986. Т. 20. № 3. С. 90–91.

  13. Буров В.А., Вечерин С.Н., Морозов С.А., Румянцева О.Д. Моделирование точного решения обратной задачи акустического рассеяния функциональными методами // Акустический ж. 2010. Т. 56. № 4. С. 516–536.

  14. Beilina L., Klibanov M.V. Approximate Global Convergence and Adaptivity for Coefficient Inverse Problems. New York: Springer, 2012.

  15. Kabanikhin S.I., Satybaev A.D., Shishlenin M.A. Direct Methods of Solving Multidimensional Inverse Hyperbolic Problems. Utrecht: VSP, 2004.

  16. Klibanov M.V., Kolesov A.E. Convexification of a 3D coefficient inverse scattering problem // Computers and Mathematics with Applications. 2019. V. 77. P. 1681–1702.

  17. Klibanov M.V., Kolesov A.E., Nguyen Dinh-Liem. Convexification method for an inverse scattering problem and its performance for experimental backscatter data for buried targets // SIAM J. Imaging Sciences. 2019. V. 12. № 1. P. 576–603.

  18. Bakushinsky A.B., Leonov A.S. Fast numerical method of solving 3D coefficient inverse problem for wave equation with integral data // J. of Inverse and Ill-Posed Problems. 2018. V. 26. Issue 4. P. 477–492.

  19. Бакушинский А.Б., Леонов А.С. Экономичный численный метод решения коэффициентной обратной задачи для волнового уравнения в трехмерном пространстве // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 4. С. 561–574.

  20. Бакушинский А.Б., Леонов А.С. Численное решение трехмерной коэффициентной обратной задачи для волнового уравнения с интегральными данными в цилиндрической области // Сиб. ж. вычисл. матем. 2019. Т. 22. № 4. С. 381–396.

  21. Бакушинский А.Б., Леонов А.С. К численному решению обратной многочастотной задачи скалярной акустики // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 6. С. 1013–1026.

  22. Евстигнеев Р.О., Медведик М.Ю., Смирнов Ю.Г., Цупак А.А. Обратная задача восстановления неоднородностей тела для ранней диагностики заболеваний с помощью микроволновой томографии // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. 2017. Т. 44. № 4. С. 3–17.

  23. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. М.: Наука, 1972.

  24. Владимиров В.С. Обобщенные функции в математической физике. М.: Наука, 1976.

  25. Рисс Ф., Сëкефальви-Надь Б. Лекции по функциональному анализу. М.: Мир, 1979.

  26. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука, 1990.

  27. Леонов А.С. Решение некорректно поставленных обратных задач: Очерк теории, практические алгоритмы и демонстрации в МАТЛАБ. Изд. 2. М.: Либроком, 2013.

  28. Engl H.W., Hanke M., Neubauer A. Regularization of Inverse Problems. Dordrecht: Kluwer Academic Publishers, 1996.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал