Журнал вычислительной математики и математической физики, 2022, T. 62, № 2, стр. 270-288

Математическое моделирование опасных явлений природного характера в мелководном водоеме

А. М. Атаян^1, 2, А. В. Никитина^{1, 2, 3, 4, *}, А. И. Сухинов¹, А. Е. Чистяков^1, 2

¹ Донской государственный технический университет
344000 Ростов-на-Дону, пл. Гагарина, 1, Россия

² Научно-технологический университет “Сириус”
347900 Сочи, Олимпийский пр-т, 1, Россия

³ Южный федеральный университет
344006 Ростов-на-Дону, Большая Садовая ул., 105/42, Россия

⁴ Научно-исследовательский центр супер-ЭВМ и нейрокомпьютеров
347900 Таганрог, пер. Итальянский, 106, Россия

^* E-mail: nikitina.vm@gmail.com

Поступила в редакцию 15.02.2021
После доработки 17.07.2021
Принята к публикации 04.08.2021

EDN: WXANGN
DOI: 10.31857/S0044466921120048

Полный текст (PDF)

Аннотация

Работа посвящена построению и исследованию взаимосвязанных математических моделей гидрофизики и биологической кинетики, используемых для прогнозирования опасных явлений природного характера, возникающих в мелководных водоемах. На распространение и трансформацию гидробионтов влияют такие физические факторы, как пространственно-трехмерное движение водной среды с учетом адвективного переноса и микротурбулентной диффузии, пространственно-неоднородное распределение температуры, солености и кислорода. Биогенные загрязняющие вещества вызывают рост водорослей, в том числе, токсичных и вредоносных, их массовое развитие может приводить к возникновению опасных явлений в водоеме, включая эвтрофикацию и заморные явления. Построена и исследована трехмерная математическая модель гидродинамики, используемая в работе для расчета поля скоростей водного потока. Для исследования опасных явлений мелководного водоема, связанных с заморными явлениями в нем, разработана пространственно-неоднородная трехмерная ихтиологическая модель динамики промысловой рыбы. Рассмотрены модели наблюдений, параметризованные на основе стехиометрических соотношений, законов Моно, Михаэлиса–Ментен и Митчерлиха–Бауле, описывающие потребление, накопление планктоном и промысловыми рыбами-детритофагами питательных веществ, а также рост гидробионтов в зависимости от пространственного распределения солености и температуры, кислородного режима. Для калибровки и верификации разработанных моделей использовались постоянно пополняемые базы экологических данных, полученные, в том числе, и с помощью экспедиционных исследований Азовского моря и Таганрогского залива. Для повышения точности прогнозного моделирования натурные данные были отфильтрованы на основе алгоритма Калмана. При решении задачи обработки гидрологической информации получены изолинии солености и температуры в поверхностном слое, для чего применен алгоритм распознавания. С помощью алгоритма интерполяции и путем наложения границ области получены более подробные карты глубин, солености и температуры Азовского моря. Разработаны численные методы решения поставленных задач, использующие конечно-разностные схемы, учитывающие степень заполненности контрольных ячеек расчетной области, реализованные на высокопроизводительных вычислительных системах, позволяющие уменьшить погрешность численного решения задачи и сократить время расчетов в несколько раз. На основе численной реализации разработанных моделей проведена реконструкция опасных явлений природного характера, возникающих в мелководном водоеме (связанных с распространением вредных загрязняющих веществ), эвтрофикацию, “цветение водорослей”, вызывающее заморные явления в водоеме. Библ. 21. Фиг. 12. Табл. 1.

Ключевые слова: математическая модель, гидродинамика, биологическая кинетика, планктон, промысловая рыба, программный комплекс, высокопроизводительная вычислительная система, опасные явления, мелководный водоем.

ВВЕДЕНИЕ

Решение многих задач водной экологии начинается с расчета гидрофизических параметров. Гидродинамические характеристики водоемов (поле скоростей водного потока, функция возвышения уровня) используются в качестве входных данных для расчета концентраций загрязняющих веществ и изучения развития всего живого в водной среде, начиная от микроорганизмов, фито-, зоопланктона и заканчивая млекопитающими.

Для изучения процессов гидродинамики и биологической кинетики широко используются методы и подходы математического моделирования, позволяющие значительно расширить возможности исследователя, разработать предупредительные меры по локализации, устранению и уменьшению вреда опасных явлений, периодически возникающих в водных экосистемах в результате воздействия природных и техногенных факторов.

Изучению динамических процессов, ответственных за формирование циркуляции атмосферы и океана, посвящены работы Г.И. Марчука, В.П. Дымникова. В этих работах на основе последовательной разработки и анализа математических моделей исследуются процессы переноса примесей в атмосфере и океане, нелинейная передача энергии по спектру в квазидвумерном и квазигеострофическом приближениях, динамика крупномасштабных волн и их устойчивость, формирование пограничных струйных течений. Даны оценки точности аппроксимаций задач на базе использования неявных разностных аппроксимаций метода расщепления. Доказана абсолютная устойчивость разностных схем и установлены балансные соотношения в форме квадратичных функционалов. Введены в рассмотрение сопряженные уравнения гидродинамики и сформулирована теория возмущений, на основе которой делаются выводы о предсказуемости метеорологических элементов (см. [1]).

Для выявления общих свойств сложных пространственных течений широко используются численные методы (см. [2]). Известно, что сложно получить достаточно точное решение физической задачи, связанное с нахождением гидродинамических характеристик, если граничные условия не заданы адекватным образом. Уравнения Навье–Стокса и неразрывности представляют собой дифференциальные уравнения, описывающие удивительно широкий класс разнообразных течений, которые при изменении условий на границе могут отличаться друг от друга не только количественно, но и качественно.

В публикациях авторов R. Ansorge, T. Sonar представлены математические модели, включающие уравнения Навье–Стокса, Эйлера, уравнения пограничного слоя, модели турбулентности с целью получения качественного, а также количественного представления о процессах потоковых явлений (см. [3]).

Работа B. Roux и др. [4] посвящена изучению нелинейных гидродинамических процессов на основе 3D-модели RANS в широкой полузамкнутой лагунной экосистеме, а также условий восстановления погруженной водной растительности.

Изучению процессов биологической кинетики посвящен ряд работ Е.В. Якушева (см. [5]), Д.О. Логофета (см. [6]), Ю.В. Тютюнова(см. [7]), В.Г. Ильичева, занимающихся изучением влияния различных факторов как внешних природных, так и биотических, включая таксис, межвидовую конкуренцию, механизм эктокринной регуляции, на динамику изучаемых продукционно-деструкционных процессов.

Интерес к численному решению класса таких задач не ослабевает – в последние десятилетия появилось множество программных комплексов и отдельных модулей, которые широко используются для изучения гидрофизических процессов. В институте ИПМ им. М.В. Келдыша РАН Б.Н. Четверушкиным, В.А. Гасиловым, С.В. Поляковым, М.В. Якобовским и др. разработан пакет прикладных программ GIMM для решения задач гидродинамики на многопроцессорных вычислительных системах (см. [8]).

Модуль Вычислительная гидродинамика, расширяющий возможности среды численного моделирования COMSOL Multiphysics, разработанный сотрудниками кампании COMSOL, основанной еще в 1986 г. в Стокгольме (Швеция), объединяет несколько офисов и дистрибьюторскую сеть, раскинувшуюся по всему миру. Разработанное программное обеспечение может быть применимо для численного анализа систем (в которых гидродинамические процессы сопровождаются другими физическими явлениями), содержит инструменты для создания ключевых моделей течений, описывающих несжимаемые и сжимаемые среды, ламинарные и турбулентные течения, однофазные и многофазные потоки, течения в свободной и пористой среде, а также в открытых областях, течения в тонких пленках. Эти возможности реализованы в структурированных гидродинамических интерфейсах, предназначенных для постановки, решения и анализа стационарных и нестационарных задач в двумерных, двумерных осесимметричных и трехмерных областях. В модуле реализованы алгоритмы решения задач о течении неньютоновских жидкостей, течении во вращающемся оборудовании и течении при высоких числах Маха. Возможность описать в модели сразу несколько физических явлений является ценной при анализе гидродинамических процессов. С помощью модуля можно строить модели сопряженной теплопередачи и химически-реагирующих потоков. Имеются дополнительные мультифизические возможности, включая расчет взаимодействия потоков с механическими конструкциями. Несмотря на большое количество публикаций по данной проблематике часть вопросов, связанных с изучением механизмов возникновения опасных явлений в водных экосистемах, до сих пор остается открытой, прикладные задачи гидрофизики и биологической кинетики зачастую не рассматриваются в комплексе.

Существующие пакеты и программные комплексы нередко сложно настроить на конкретную водную экосистему ввиду существенного различия в гидрофизических параметрах и видовом составе гидробионтов. Требуемая высокая точность расчетов накладывает дополнительные условия на метод дискретизации исходных нелинейных непрерывных задач. Кроме того, возникает необходимость в обработке и фильтрации входных данных. Большой объем вычислительной работы по реализации рассматриваемых задач в реальных областях сложной формы при ограниченном времени построения прогнозов изменения экологической обстановки в водоеме, например, при возникновении в нем опасного явления, требует разработки эффективных алгоритмов, ориентированных на супервычислительные системы с распределенной памятью.

2. ОСНОВНЫЕ УРАВНЕНИЯ МОДЕЛЕЙ ГИДРОДИНАМИКИ И БИОЛОГИЧЕСКОЙ КИНЕТИКИ

Для описания процессов гидродинамики и биологической кинетики в мелководном водоеме, таком как Азовское море, характеризующимся значительным перепадом глубин, а также построения прогнозов изменения состояния водных экосистем при возникновении в них опасных явлений природного характера, к которым можно отнести штормовые нагоны, явления аноксии и гипоксии, в данной работе предложено использовать математические модели гидродинамики и биологической кинетики.

Гидродинамическая модель движения водной среды предназначена для расчета поля вектора скорости водного потока водоема со сложной батиметрией, к такому типу можно отнести мелководный водоем – Азовское море. Модель учитывает пространственно-трехмерную структуру движения водной среды, стоки рек, сгонно-нагонные явления, сложную геометрию рельефа дна и береговой линии.

Модель биологической кинетики представляет собой систему “фитопланктон–зоопланктон–биогенное вещество–детрит–рыба”, учитывает следующие физические процессы: движение водного потока, микротурбулентную диффузию, температуру, соленость, пространственное распределение кислорода и загрязняющих биогенных веществ, включая соединения азота, фосфора и кремния, их взаимодействие и осаждение, влияние на продукционно-деструкционные процессы водоема; нелинейное взаимодействие гидробионтов, включая фито-, зоопланктон и промысловую рыбу, межвидовую конкуренцию, вылов, таксис, механизм наружно-гормонального регулирования и аллелопатическое воздействие.

2.1. Модель гидродинамики

В основу разрабатываемой модели расчета трехмерных полей вектора скорости движения водной среды, температуры и солености положена математическая модель гидродинамики мелководных водоемов, учитывающая транспорт тепла и солей (см. [9]):

– уравнение движения (Навье–Стокса)

(1)

$u_{t}^{'} + uu_{x}^{'} + vu_{y}^{'} + wu_{z}^{'} = - \frac{1}{\rho }P_{x}^{'} + (\mu u_{x}^{'})_{x}^{'} + (\mu u_{y}^{'})_{y}^{'} + (\nu u_{z}^{'})_{z}^{'} + 2{{\Omega }}(v\sin \vartheta - w\cos \vartheta ),$

(2)

$v_{t}^{'} + uv_{x}^{'} + vv_{y}^{'} + wv_{z}^{'} = - \frac{1}{\rho }P_{y}^{'} + (\mu v_{x}^{'})_{x}^{'} + (\mu v_{y}^{'})_{y}^{'} + (\nu v_{z}^{'})_{z}^{'} + 2{{\Omega }}u\sin \vartheta ,$

(3)

$w_{t}^{'} + uw_{x}^{'} + vw_{y}^{'} + ww_{z}^{'} = - \frac{1}{\rho }P_{z}^{'} + (\mu w_{x}^{'})_{x}^{'} + (\mu w_{y}^{'})_{y}^{'} + (\nu w_{z}^{'})_{z}^{'} + 2{{\Omega }}u\cos \vartheta + g,$

– уравнение неразрывности в случае переменной плотности

(4)

$\rho _{t}^{'} + (\rho u)_{x}^{'} + (\rho v)_{y}^{'} + (\rho w)_{z}^{'} = 0,$

– уравнение транспорта тепла

(5)

$T_{t}^{'} + uT_{x}^{'} + vT_{y}^{'} + wT_{z}^{'} = (\mu T_{x}^{'})_{x}^{'} + (\mu T_{y}^{'})_{y}^{'} + (\nu T_{z}^{'})_{z}^{'} + {{f}_{T}},$

– уравнение транспорта солей

(6)

$S_{t}^{'} + uS_{x}^{'} + vS_{y}^{'} + wS_{z}^{'} = ({{\mu }}S_{x}^{'})_{x}^{'} + ({{\mu }}S_{y}^{'})_{y}^{'} + (\nu S_{z}^{'})_{z}^{'} + {{f}_{S}}$,

где V = {u, $v$, w} – компоненты вектора скорости, P – полное гидродинамическое давление, S и T – соленость и температура водной среды, ρ – плотность водной среды, μ, ν – горизонтальная и вертикальная составляющие коэффициента турбулентного обмена, ${\mathbf{\Omega }} = \Omega \times (\cos \vartheta \times {\mathbf{j}} + \sin \vartheta \times {\mathbf{k}})$ – угловая скорость вращения Земли, $\vartheta $ – широта места, g – ускорение свободного падения,${{f}_{T}}$, ${{f}_{S}}$ – источники тепла и соли (находятся на границе области).

Для мелководных водоемов из полного гидродинамического давления условно можно выделить две составляющие: функцию давления столба жидкости и гидродинамическую часть:

$P(x,y,z,t) = p(x,y,z,t) + {{\rho }_{0}}gz,$

где $p$ – гидростатическое давление невозмущенной жидкости, ${{\rho }_{0}}$ – плотность пресной воды при нормальных условиях.

Уравнение состояния для плотности

$\rho = \tilde {\rho } + {{\rho }_{0}},$

где ${{\rho }_{0}}$ – плотность пресной воды при нормальных условиях, $\tilde {\rho }$ определяется уравнением, рекомендованным UNESCO:

(7)

$\begin{gathered} \tilde {\rho } = {{{\tilde {\rho }}}_{w}} + (8.24493 \times {{10}^{{ - 1}}} - 4.0899 \times {{10}^{{ - 3}}}T + 7.6438 \times {{10}^{{ - 5}}}{{T}^{2}} - 8.2467 \times {{10}^{{ - 7}}}{{T}^{3}} + 5.3875 \times \\ \times \;{{10}^{{ - 9}}}{{T}^{4}})S + ( - 5.72466 \times {{10}^{{ - 3}}} + 1.0227 \times {{10}^{{ - 4}}}T - 1.6546 \times {{10}^{{ - 6}}}{{T}^{2}}){{S}^{{3/2}}} + 4.8314 \times {{10}^{{ - 4}}}{{S}^{2}}, \\ \end{gathered} $

где ${{\tilde {\rho }}_{w}}$ – плотность пресной воды, задаваемая полиномом

$\begin{gathered} {{{\tilde {\rho }}}_{w}} = 999.842594 + 6.793952 \times {{10}^{{ - 2}}}T - 9.095290 \times {{10}^{{ - 3}}}{{T}^{2}} + \\ + \;1.001685 \times {{10}^{{ - 4}}}{{T}^{3}} - 1.120083 \times {{10}^{{ - 6}}}{{T}^{4}} + 6.536332 \times {{10}^{{ - 9}}}{{T}^{5}}. \\ \end{gathered} $

Уравнение (7) применимо для солености в диапазоне 0–42‰ и температуры от –2 до 40°C.

Система уравнений (1)–(7) рассматривается при следующих краевых условиях:

– на входе (устья рек Дон и Кубань)

${\mathbf{V}} = {{{\mathbf{V}}}_{1}},\quad P_{{\mathbf{n}}}^{'} = 0,\quad T = {{T}_{1}},\quad S = {{S}_{1}},$

– донная граница

${{\rho }_{v}}\mu ({{{\mathbf{V}}}_{{\mathbf{\tau }}}})_{{\mathbf{n}}}^{'} = - {\mathbf{\tau }},\quad {{{\mathbf{V}}}_{{\mathbf{n}}}} = 0,\quad P_{{\mathbf{n}}}^{'} = 0,\quad T_{{\mathbf{n}}}^{'} = 0,\quad S_{{\mathbf{n}}}^{'} = 0,\quad {{f}_{T}} = 0,\quad {{f}_{S}} = 0,$

– боковая граница

$({{{\mathbf{V}}}_{{\mathbf{\tau }}}})_{{\mathbf{n}}}^{'} = 0,\quad {\mathbf{V}}_{{\mathbf{n}}}^{'} = 0,\quad P_{{\mathbf{n}}}^{'} = 0,\quad T_{{\mathbf{n}}}^{'} = 0,\quad S_{{\mathbf{n}}}^{'} = 0,\quad {{f}_{T}} = 0,\quad {{f}_{S}} = 0,$

– верхняя граница

$\begin{gathered} {{\rho }_{v}}\mu ({{{\mathbf{V}}}_{{\mathbf{\tau }}}})_{{\mathbf{n}}}^{'} = - {\mathbf{\tau }},\quad w = - \omega - P_{t}^{'}{\text{/}}\rho g,\quad P_{{\mathbf{n}}}^{'} = 0,\quad T_{{\mathbf{n}}}^{'} = 0,\quad S_{{\mathbf{n}}}^{'} = 0, \\ {{f}_{T}} = k({{T}_{a}} - T),\quad {{f}_{S}} = \frac{\omega }{{{{h}_{z}} - {{h}_{\omega }}}}S, \\ \end{gathered} $

– на выходе (Керченский пролив)

$P_{{\mathbf{n}}}^{'} = 0,\quad {\mathbf{V}}_{{\mathbf{n}}}^{'} = 0,\quad T_{{\mathbf{n}}}^{'} = 0,\quad S_{{\mathbf{n}}}^{'} = 0,\quad {{f}_{T}} = 0,$

где ω – интенсивность испарения жидкости, ${{{\mathbf{V}}}_{{\mathbf{n}}}}$, ${{{\mathbf{V}}}_{{\mathbf{\tau }}}}$ – нормальная и тангенциальная составляющие вектора скорости, τ = {τ_x, τ_y, τ_z} – вектор тангенциального напряжения, $\rho $ – плотность водной среды, ${{\rho }_{{v}}}$ – плотность взвеси, T_a – температура атмосферы, k – коэффициент передачи тепла между атмосферой и водной средой, ${{h}_{z}}$ – шаг расчетной сетки по глубине, ${{h}_{\omega }} = \omega \tau $ – слой жидкости, который испаряется за время $\tau $.

Вектор тангенциального напряжения для свободной поверхности рассчитывается по формуле

$\tau = {{\rho }_{a}}C{{d}_{s}}\left| W \right|{\mathbf{W}},$

где ${\mathbf{W}}$ – вектор скорости ветра относительно воды, ρ_a – плотность атмосферы, Cd_s –безразмерный коэффициент поверхностного сопротивления, который зависит от скорости ветра и находится в диапазоне 0.0016–0.0032 (см. [5]).

Вектор тангенциального напряжения для дна имеет вид

$\tau = \rho C{{d}_{b}}\left| V \right|V,$

где Cd_b = gk²/h^1/3, k – групповой коэффициент шероховатости в формуле Мэннинга, рассматривается в диапазоне 0.025–0.2, в процессе моделирования использовалось значение 0.025, обусловленное преимущественным покрытием дна Азовского моря илистыми отложениями, h = = H + η – глубина акватории, H – глубина до невозмущенной поверхности, η – высота свободной поверхности относительно геоида (уровень моря).

Система уравнений (1)–(7) рассматривается при начальных условиях

${\mathbf{V}} = {{{\mathbf{V}}}_{0}},\quad T = {{T}_{0}},\quad S = {{S}_{0}}.$

Турбулентная вязкость ν определяется средним значением скорости диссипации энергии турбулентности ε, приходящейся на единицу объема: $\nu \sim {{\varepsilon }^{{1/3}}}{{\Delta }^{{4/3}}},$ где ∆ – характерный масштаб сетки (для расчета коэффициента турбулентного обмена по вертикали $\Delta \equiv {{h}_{z}}$). Скорость диссипации $\bar {s}$ может быть выражена через среднюю скорость деформации ячеечного масштаба: $\bar {s} = 2{{\bar {s}}_{{ij}}}{{\bar {s}}_{{ij}}}$, где ${{\bar {s}}_{{ij}}}$ – осредненный тензор скоростей деформации, $\bar {s}$: ${{\varepsilon }^{{2/3}}}{{\Delta }^{{ - 4/3}}}$. Выражение для турбулентной вязкости имеет вид

(8)

$\nu = C_{s}^{2}{{\Delta }^{2}}{{\bar {s}}^{{1/2}}},$

где ${{C}_{S}}$ – безразмерная эмпирическая константа, значение которой определяется на основе расчета процесса затухания однородной изотропной турбулентности. Выбранное значение постоянной ${{C}_{S}}$ должно обеспечивать соответствие с экспериментальными измерениями.

2.2. Модель биологической кинетики

Многовидовая математическая модель взаимодействия промысловой рыбы-детритофага, фито- и зоопланктона основана на системе нестационарных уравнений конвекции–диффузии–реакции параболического типа с нелинейными функциями источников и младшими производными, вид которых для каждого модельного блока ${{S}_{i}}$определяется следующим образом:

$\frac{{\partial {{S}_{i}}}}{{\partial t}} + {\text{div}}({\mathbf{v}}{{S}_{i}}) = \mu {}_{i}\Delta {{S}_{i}} + \frac{\partial }{{\partial z}}\left( {{{\nu }_{i}}\frac{{\partial {{S}_{i}}}}{{\partial z}}} \right) + {{\psi }_{i}},\quad {{\psi }_{1}} = {{g}_{1}}({{S}_{1}},{{S}_{3}}) - {{\delta }_{1}}{{S}_{1}}{{S}_{2}} - {{\lambda }_{1}}{{S}_{1}} - {{\sigma }_{1}}{{S}_{1}}{{S}_{5}},$

(9)

${{\psi }_{2}} = {{g}_{2}}({{S}_{1}},{{S}_{2}}) - {{\lambda }_{2}}{{S}_{2}} - {{\delta }_{2}}{{S}_{2}},\quad {{\psi }_{3}} = {{\gamma }_{3}}{{\lambda }_{4}}{{S}_{4}} - {{g}_{3}}({{S}_{1}},{{S}_{3}}) + B({{\tilde {S}}_{3}} - {{S}_{3}}) + f,$

${{\psi }_{4}} = {{\lambda }_{1}}{{S}_{1}} + {{\lambda }_{2}}{{S}_{2}} - {{\lambda }_{4}}{{S}_{4}} - {{g}_{4}}({{S}_{4}},{{S}_{5}}),\quad {{\psi }_{5}} = {{g}_{5}}({{S}_{1}},{{S}_{4}},{{S}_{5}}) - {{\lambda }_{5}}{{S}_{5}} - {{\delta }_{5}}{{S}_{5}},$

где ${{S}_{i}}$ – концентрация i-й компоненты, $i = \overline {1,5} $; ${{\psi }_{i}}$ – химико-биологический источник (сток) или член, описывающий агрегирование (слипание-разлипание), если соответствующая компонента является взвесью, $i$ – вид субстанции, $i = \overline {1,5} $: 1 – концентрации фитопланктона (Coscinodiscus) $\left( P \right)$, 2 – зоопланктона (Copepoda) (Z), 3 – биогенного вещества $(M)$, 4 – детрита (D), 5 – промысловой рыбы-детритофага (F); ${\mathbf{v}} = {\mathbf{V}} + {{{\mathbf{V}}}_{{0i}}}$ – скорость конвективного переноса вещества; ${{{\mathbf{V}}}_{{0i}}}$ – скорость осаждения $i$-й субстанции под действием силы тяжести, $i \in \overline {1,4} $, ${{g}_{i}}$ – трофические функции для субстанций $i \in \overline {1,5} $, ${{\tilde {S}}_{3}}$ – предельно возможная концентрация биогенного вещества; $f = f(t,x,y,z)$ – функция источника загрязнения; B – удельная скорость поступления загрязняющего вещества; ${{\lambda }_{2}}$, ${{\lambda }_{5}}$ – коэффициенты элиминации (смертности) $Z$, $F$ соответственно. Положим ${{g}_{1}}({{S}_{1}},{{S}_{3}}) = {{\gamma }_{1}}{{\alpha }_{3}}{{\phi }_{1}}{{S}_{1}}{{S}_{3}}$, ${{g}_{2}}({{S}_{1}},{{S}_{2}}) = {{\gamma }_{2}}{{\phi }_{2}}{{\delta }_{1}}{{S}_{1}}{{S}_{2}}$, ${{g}_{3}}({{S}_{1}},{{S}_{3}}) = {{\alpha }_{3}}{{S}_{1}}{{S}_{3}}$, ${{g}_{4}}({{S}_{4}},{{S}_{5}}) = {{\beta }_{4}}{{S}_{4}}{{S}_{5}}$, ${{g}_{5}}({{S}_{1}},{{S}_{4}},{{S}_{5}}) = ({{\gamma }_{5}}{{\beta }_{4}}{{S}_{4}} + {{\xi }_{5}}{{\sigma }_{1}}{{S}_{1}}){{\phi }_{5}}{{S}_{5}}$; ${{\alpha }_{3}}$ – коэффициент потребления биогенного вещества фитопланктоном; ${{\gamma }_{1}}$_{, ${{\gamma }_{2}}$,}${{\gamma }_{5}}$ – передаточные коэффициенты трофических функций; ${{\gamma }_{3}}$ – доля питательного вещества, находящегося в биомассе фитопланктона; ${{\lambda }_{1}}$ – коэффициент, учитывающий смертность и метаболизм $P$; ${{\delta }_{1}}$ – убыль фитопланктона за счет выедания зоопланктоном; ${{\delta }_{2}}$ – убыль зоопланктона за счет выедания рыбами; ${{\delta }_{5}}$ – убыль рыбы за счет вылова; ${{\lambda }_{4}}$ – коэффициент разложения детрита; ${{\beta }_{4}}$ – скорость потребления органических остатков рыбой; ${{\sigma }_{1}}$ – коэффициент убыли фитопланктона в результате потребления его рыбой; ${{\xi }_{5}}$ – передаточный коэффициент роста концентрации рыбы за счет фитопланктона; ${{\mu }_{i}},$ ${{\nu }_{i}}$ – диффузионные коэффициенты в горизонтальном и вертикальном направлениях $i$-й субстанции, $i \in \overline {1,5} $; $\Delta $ – двумерный оператор Лапласа.

При параметризации системы (9) использовались модели наблюдений, представляющие собой функциональные зависимости, параметризованные на основе стехиометрических соотношений, законов Моно, Михаэлиса–Ментен и Митчерлиха–Бауле, описывающие потребление, накопление планктоном и промысловыми рыбами-детритофагами питательных веществ, а также рост гидробионтов в зависимости от пространственного распределения солености и температуры, кислородного режима(см. [5]–[7]).

Функции зависимости скорости роста гидробионтов от температуры и солености задавались следующим образом:

${{\phi }_{m}} = \exp \left[ { - {{\alpha }_{m}}{{{\left( {\frac{{T - {{T}_{{{\text{opt}}}}}}}{{{{T}_{{{\text{opt}}}}}}}} \right)}}^{2}}} \right]\exp \left[ { - {{\beta }_{m}}{{{\left( {\frac{{S - {{S}_{{{\text{opt}}}}}}}{{{{S}_{{{\text{opt}}}}}}}} \right)}}^{2}}} \right],\quad m \in \left\{ {1,2,5} \right\},$

где ${{T}_{{{\text{opt}}}}}$, ${{S}_{{{\text{opt}}}}}$ – температура и соленость, оптимальные для данного вида планктона и рыб; ${{\alpha }_{m}} > 0$, ${{\beta }_{m}} > 0$ – коэффициенты ширины интервала толерантности планктона к температуре и солености соответственно.

Расчетная область $\bar {G}$ (Азовское море) представляет собой замкнутую область, ограниченную невозмущенной поверхностью водоема ${{\Sigma }_{0}}$, дном ${{\Sigma }_{H}} = {{\Sigma }_{H}}(x,y)$ и боковой цилиндрической поверхностью $\sigma $ для временного промежутка $0 < t \leqslant {{T}_{0}}$; $\sum $ – кусочно-гладкая граница области $G$, $\sum = {{\sum }_{0}} \cup {{\sum }_{H}} \cup \;\sigma $; ${\mathbf{n}}$ – вектор внешней нормали к поверхности; ${{{\mathbf{v}}}_{{\mathbf{n}}}}$ – нормальная по отношению к $\sum $ составляющая вектора скорости водного потока.

Начальные условия

(10)

${{\left. {{{S}_{i}}} \right|}_{{t = 0}}} = S_{{i0}}^{{}}(x,y,z),\quad i = \overline {1,5} .$

Граничные условия

(11)

$\begin{gathered} {{S}_{i}} = 0\;\;на\;\;\sigma ,\quad если\quad {{{\mathbf{v}}}_{{\mathbf{n}}}} < 0;\quad \frac{{\partial {{S}_{i}}}}{{\partial {\mathbf{n}}}} = 0\;\;на\;\;\sigma ,\quad если\quad {{{\mathbf{v}}}_{{\mathbf{n}}}} \geqslant 0,\quad i = \overline {1,5} ; \\ \frac{{\partial {{S}_{i}}}}{{\partial z}} = - {{\varepsilon }_{i}}{{S}_{i}}\;\;на\;\;{{\Sigma }_{H}};\quad \frac{{\partial {{S}_{i}}}}{{\partial z}} = \varphi ({{S}_{i}})\;\;на\;\;{{\Sigma }_{0}};\quad \varphi ({{S}_{i}}) = \left\{ \begin{gathered} {{k}_{i}}{{S}_{i}},\quad i = 3; \hfill \\ 0,\quad i \ne 3, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

где ${{\varepsilon }_{1}}$, ${{\varepsilon }_{2}}$, ${{\varepsilon }_{3}}$, ${{\varepsilon }_{4}}$, ${{\varepsilon }_{5}}$ – неотрицательные постоянные; ${{\varepsilon }_{1}}$, ${{\varepsilon }_{3}}$, ${{\varepsilon }_{5}}$ – учитывают опускание планктона и рыб на дно и их затопление; ${{\varepsilon }_{2}}$, ${{\varepsilon }_{4}}$ – учитывают поглощение биогенного вещества и детрита донными отложениями; ${{k}_{3}}$ –удельная скорость поступления загрязняющего биогенного вещества из воздушной среды.

Будем учитывать влияние кормового таксиса на функционирование системы “фитопланктон–зоопланктон–биогенное вещество–детрит–рыба”, для этого к системе (9)–(11) добавим следующие уравнения:

(12)

$\frac{{\partial {{{\mathbf{v}}}_{5}}}}{{\partial t}} + \operatorname{div} ({{{\mathbf{V}}}_{5}} \otimes {{{\mathbf{v}}}_{5}}) = {{\mu }_{u}}\Delta {{{\mathbf{v}}}_{5}} + \frac{\partial }{{\partial z}}\left( {{{\nu }_{u}}\frac{{\partial {{{\mathbf{v}}}_{5}}}}{{\partial z}}} \right) - {{\alpha }_{u}}{{{\mathbf{v}}}_{5}} + {{k}_{1}}\operatorname{grad} {{S}_{1}} + {{k}_{4}}\operatorname{grad} {{S}_{4}},$

где ${{{\mathbf{v}}}_{5}} = {\mathbf{V}} + {{{\mathbf{V}}}_{5}}$ – скорость конвективного переноса рыбы; ${{{\mathbf{V}}}_{5}}$ – скорость движения рыбы относительно воды; ${{k}_{1}}$, ${{k}_{4}}$ – коэффициенты таксиса; ${{\mu }_{u}}$, ${{\nu }_{u}}$ – коэффициенты горизонтальной и вертикальной составляющей диффузии скорости таксиса; ${{\alpha }_{u}}$ – коэффициент инерционного движения рыбы; $ \otimes $ – тензорное произведение векторов.

Поскольку рассматриваемый вид рыбы является детритофагом, то им перерабатывается значительное количество отложений органических илов – отмерших остатков планктона, рыб, бентосных животных, разложение которых в летний период при достаточном прогреве водной толщи вызывает нехватку кислорода в воде и приводит к заморным явлениям в экосистеме. Для учета распределения концентрации кислорода в водоеме к системе (9)–(12) добавим следующее уравнение:

(13)

$C = {{C}_{0}} - m{{S}_{4}},\quad {{\left. C \right|}_{{t = 0}}} = \theta (x,y,z)\quad \forall (x,y,z) \in \bar {G},$

где ${{C}_{0}}$ – концентрация кислорода при отсутствии органических примесей; $m$ – количество кислорода, необходимое для окисления детрита в толще водоема; $\theta $ – заданная функция.

3. МЕТОД РЕШЕНИЯ ЗАДАЧИ ГИДРОДИНАМИКИ

Согласно методу поправки к давлению, исходная модель гидродинамики разбивается на три подзадачи (см. [9]). Первая подзадача представлена уравнением диффузии–конвекции–реакции, с помощью которого вычисляются компоненты поля вектора скорости водного потока на промежуточном временном слое (см. [10]):

(14)

$\frac{{\tilde {u} - u}}{\tau } + u\bar {u}{{_{x}^{'}}_{{}}} + v\bar {u}{{_{{}}^{'}}_{y}} + w\bar {u}_{z}^{'} = (\mu \bar {u}_{x}^{'})_{x}^{'} + (\mu \bar {u}_{y}^{'})_{x}^{'} + (\nu \bar {u}_{z}^{'})_{z}^{'} + 2\Omega (v\sin \theta - w\cos \theta ),$

(15)

$\frac{{\tilde {v} - v}}{\tau } + u\bar {v}_{x}^{'} + v\bar {v}_{y}^{'} + w\bar {v}{{_{{}}^{'}}_{z}} = (\mu \bar {v}_{x}^{'})_{x}^{'} + (\mu \bar {v}_{y}^{'})_{y}^{'} + (\nu \bar {v}_{z}^{'})_{z}^{'} - 2\Omega u\sin \theta ,$

(16)

$\frac{{\tilde {w} - w}}{\tau } + u\bar {w}_{x}^{'} + v\bar {w}_{y}^{'} + w\bar {w}_{z}^{'} = (\mu \bar {w}_{x}^{'})_{x}^{'} + (\mu \bar {w}_{y}^{'})_{y}^{'} + (\nu \bar {w}_{z}^{'})_{z}^{'} + 2\Omega u\cos \theta + g\left( {\frac{{{{\rho }_{0}}}}{\rho } - 1} \right),$

где $u$, $v$, $w$ – значения компонент вектора скорости на предыдущем слое по времени, $\tilde {u}$, $\tilde {v}$, $\tilde {w}$ – значения компонент вектора скорости на промежуточном слое по времени, $\bar {u} = \sigma \tilde {u} + \left( {1 - \sigma } \right)u$, $\bar {v} = \sigma \tilde {v} + (1 - \sigma )v$, $\bar {w} = \sigma \tilde {w} + (1 - \sigma )w$, $\sigma \in \left[ {0,\;1} \right]$ – вес схемы.

Следует отметить, что слагаемое $g({{\rho }_{0}}{\text{/}}\rho - 1)$ описывает плавучесть (силу Архимеда). Многочисленными экспериментами по моделированию движения среды в мелководных водоемах, подобных Азовскому морю установлено, что данное слагаемое вносит незначительный вклад в решение задачи и им можно пренебречь. Для аппроксимации уравнения диффузии–конвекции–реакции по времени использованы схемы с весами. Здесь $\bar {u} = \sigma \tilde {u} + (1 - \sigma )u$, $\sigma \in \left[ {0,\;1} \right]$ – вес схемы.

Расчет распределения давлений (вторая подзадача) базируется на уравнении Пуассона

(17)

$p_{{xx}}^{{''}} + p_{{yy}}^{{''}} + p_{{zz}}^{{''}} = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } - \rho }}{{{{\tau }^{2}}}} + \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \tilde {u})_{x}^{'}}}{\tau } + \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \tilde {v})_{y}^{'}}}{\tau } + \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \tilde {w})_{z}^{'}}}{\tau }.$

Значение поля скорости водного потока на верхней границе (поверхности водоема) задается следующим образом:$w = - \omega - p_{t}^{'}{\text{/}}\rho g$. При данном условии уравнение (17) запишется в виде

(18)

${{\left( {\frac{{p_{t}^{'}}}{{\tau g{{h}_{z}}}}} \right)}_{k}} = \frac{{{{{(p_{{xx}}^{{''}} + p_{{yy}}^{{''}})}}_{k}}}}{2} + \frac{{{{p}_{{k + 1}}} - {{p}_{k}}}}{{h_{z}^{2}}} - \frac{1}{2}{{\left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } - \rho }}{{{{\tau }^{2}}}} + \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \tilde {u}z)_{x}^{'}}}{\tau } + \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \tilde {v})_{y}^{'}}}{\tau }} \right)}_{k}} - \frac{{{{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } \tilde {w})}}_{{k + 1/2}}} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } }}_{k}}\omega }}{{\tau {{h}_{z}}}},$

где $k$ – индекс расчетной сетки по вертикальному координатному направлению.

В качестве начального приближения для данной задачи используется упрощенная гидростатическая модель движения водной среды, что значительно уменьшает время расчета.

Третья подзадача позволяет по явным формулам определить распределение скоростей водного потока на следующем временном слое:

(19)

$\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} - \tilde {u}}}{\tau } = - \frac{1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } }}p_{x}^{'},\quad \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} - \tilde {v}}}{\tau } = - \frac{1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } }}p_{y}^{'},\quad \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} - \tilde {w}}}{\tau } = - \frac{1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rho } }}p_{z}^{'},$

где $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} $, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} $, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} $ – значения компонент вектора скорости водного потока на текущем слое по времени.

Для программной реализации трехмерной математической модели гидродинамики вводится равномерная сетка. Обозначим через ${{o}_{{i,\,j,k}}}$ степень “заполненности” ячейки $(i,j,k)$. Степень заполненности ячейки задается давлением водного столба на дно данной ячейки. В общем случае степень заполненности ячеек рассчитывается, исходя из выражения (см. [11])

(20)

${{o}_{{i,j,k}}} = \frac{{{{P}_{{i,j,k}}} + {{P}_{{i - 1,j,k}}} + {{P}_{{i,j - 1,k}}} + {{P}_{{i - 1,j - 1,k}}}}}{{4\rho g{{h}_{z}}}}.$

Аппроксимация задачи расчета поля скорости движения водной среды по пространственным переменным выполнена на основе метода баланса с учетом коэффициентов заполненности контрольных областей.

3.1. Разностные схемы для операторов диффузии и конвекции, учитывающие функцию заполненности ячеек

Для построения и тестирования разностных схем операторов диффузии и конвекции, учитывающих функцию заполненности ячеек, вводится равномерная сетка:

${{w}_{h}} = \{ {{t}^{n}} = n\tau ,\;{{x}_{i}} = i{{h}_{x}},\;{{y}_{j}} = j{{h}_{y}};\;n = \overline {0,{{N}_{t}}} ,\;i = \overline {0,{{N}_{x}}} ,\;j = \overline {0,{{N}_{y}}} ;\;{{N}_{t}}\tau = T,\;{{N}_{x}}{{h}_{x}} = {{l}_{x}},\;{{N}_{y}}{{h}_{y}} = {{l}_{y}}\} ,$

где $\tau $ – шаг по времени, ${{h}_{x}}$, ${{h}_{y}}$ – шаги по пространству, ${{N}_{t}}$ – наибольшее число шагов по времени, ${{N}_{x}}$, ${{N}_{y}}$ – количество шагов пространственной сетки по направлению Ох и Оу соответственно.

Дискретные аналоги операторов конвективного $u{{c'}_{x}}$ и диффузионного $(\mu c_{x}^{'})_{x}^{'}$ переноса в случае частичной заполненности ячеек с граничными условиями III рода $c_{n}^{'}(x,z,t) = {{\alpha }_{n}}c + {{\beta }_{n}}$ могут быть записаны в следующем виде (см. [11]):

${{({{q}_{0}})}_{{i,j}}}uc_{x}^{'} \simeq {{({{q}_{1}})}_{{i,j}}}{{u}_{{i + 1/2,j}}}\frac{{{{c}_{{i + 1,j}}} - {{c}_{{i,\,j}}}}}{{2{{h}_{x}}}} + {{({{q}_{2}})}_{{i,j}}}{{u}_{{i - 1/2,j}}}\frac{{{{c}_{{i,j}}} - {{c}_{{i - 1,j}}}}}{{2{{h}_{x}}}},$

${{({{q}_{0}})}_{{i,j}}}(\mu c_{x}^{'})_{x}^{'} \simeq {{({{q}_{1}})}_{{i,j}}}{{\mu }_{{i + 1/2,j}}}\frac{{{{c}_{{i + 1,j}}} - {{c}_{{i,j}}}}}{{h_{x}^{2}}} - {{({{q}_{2}})}_{{i,j}}}{{\mu }_{{i - 1/2,j}}}\frac{{{{c}_{{i,j}}} - {{c}_{{i - 1,j}}}}}{{h_{x}^{2}}} - \left| {{{{({{q}_{1}})}}_{{i,j}}} - {{{({{q}_{2}})}}_{{i,j}}}} \right|{{\mu }_{{i,j}}}\frac{{{{\alpha }_{x}}{{c}_{{i,j}}} + {{\beta }_{x}}}}{{{{h}_{x}}}},$

где ${{q}_{0}}$, ${{q}_{1}}$, ${{q}_{2}}$ – коэффициенты заполненности контрольных областей.

Тестирование разностных схем, учитывающих функцию заполненности ячеек, выполнено на основе численного решения задачи расчета течения вязкой жидкости между двумя соосными полуцилиндрами (течения Куэтта–Тейлора). Для данной задачи исследованы погрешности численного решения на сетках, учитывающих “заполненность” ячеек (случай гладкой границы), и на сетках со ступенчатой аппроксимацией границы. При использовании сеток, учитывающих “заполненность” ячеек, погрешность численного решения модельной задачи гидродинамики не превосходят 6%, а в случае ступенчатой аппроксимацией границы может достигать 70% от решения задачи. В табл. 1 представлены значения погрешностей численного решения задачи течения жидкости между двумя соосными полуцилиндрами, полученные на последовательности сгущающихся расчетных сеток размерами 11 × 21, 21 × 41, 41 × 81 и 81 × 161 узлов в случаях гладкой и ступенчатой аппроксимации границы.

Таблица 1.

Погрешность решения задачи течения жидкости между двумя цилиндрами

Размеры сетки	11 × 21	21 × 41	41 × 81	81 × 161
Максимальное значение погрешности в случае гладкой границы, м/с	0.053	0.052	0.058	0.056
Среднее значение погрешности в случае гладкой границы, м/с	0.023	0.012	0.006	0.003
Максимальное значение погрешности в случае ступенчатой границы, м/с	0.272	0.731	0.717	0.75
Среднее значение погрешности в случае ступенчатой границы, м/с	0.165	0.132	0.069	0.056

Анализ результатов расчетов погрешности численного решения задачи течения жидкости между двумя цилиндрами на последовательности сгущающихся сеток, представленных в табл. 1, позволяет сделать вывод об эффективности использования разностных схем, учитывающих заполненность ячеек. При решении модельной задачи дробление сетки в 8 раз по каждому из пространственных направлений не приводит к повышению точности, которой обладают решения, полученные на сетках, учитывающих заполненность ячеек.

3.2. Метод решения задачи восстановления донной поверхности

Для получения функции рельефа дна используем решение уравнения диффузии, к которому сводится уравнение Сен-Венана, описывающее транспорт донных материалов (см. [12]). Решение задачи диффузии на длительные интервалы времени сводится к решению уравнения Лапласа

(21)

$\Delta H = 0,$

где $H$ – глубина водоема.

Данный подход обладает существенным недостатком, связанным с отсутствием гладкости в точках, где задаются значения поля глубин. Для устранения данной проблемы можно использовать решения следующего уравнения:

(22)

${{\Delta }^{2}}H = 0.$

К недостаткам этого подхода относят большие выбросы (отклонение от линейной функции). С помощью первых двух подходов можно получать функции, которые не обладают выделенностью направлений, но каждый из подходов обладает недостатками.

Для получения гладкой функции рельефа дна также можно использовать решение уравнения, применяемого для получения схем повышенного порядка точности для уравнения Лапласа:

(23)

$\Delta H - \frac{{{{h}^{2}}}}{{12}}{{\Delta }^{2}}H = 0.$

Заметим, что оператор для третьей задачи можно записать как линейную комбинацию операторов для первой и второй задачи.

Фундаментальной системой решений уравнения (21) являются функции

(24)

${{H}_{1}}(x) = 1,\quad {{H}_{2}}(x) = x;$

уравнения (22) –

(25)

${{H}_{1}}(x) = 1,\quad {{H}_{2}}(x) = x,\quad {{H}_{3}}(x) = {{x}^{2}},\quad {{H}_{4}}(x) = {{x}^{3}};$

уравнения (23) –

(26)

${{H}_{1}}(x) = 1,\quad {{H}_{2}}(x) = x,\quad {{H}_{3}}(x) = ch(kx),\quad {{H}_{4}}(x) = sh(kx),\quad k = \sqrt {12} {\text{/}}h.$

В первом случае интерполяция осуществляется отрезками прямых, проходящих через соседние точки. Во втором случае интерполяция выполняется на основе кубических сплайнов. В третьем случае – на основе сплайнов функции (26). Ниже описан алгоритм, предназначенный для одномерной интерполяции на основе функции (26), и проведено сравнение предложенных подходов. Результат работы предложенного алгоритма приведен на фиг. 1.

Фиг. 1.

Результат интерполяции: 1 – линейная интерполяция, 2 – кубический сплайн, 3 – на основе предложенного алгоритма.

Из фиг. 1 видно, что интерполяция, полученная на основе предложенного алгоритма, имеет меньшее отклонение от линейной интерполяции по сравнению с кубическим сплайном и обладает достаточной степенью гладкости в точках склейки функций.

3.3. Модифицированный попеременно-треугольный итерационный метод

После получения разностных схем исходные задачи сводятся к решению систем сеточных уравнений, которые могут быть записаны в матричном виде. В конечномерном гильбертовом пространстве H рассматривается задача отыскания решения операторного уравнения(см. [13]–[15])

(27)

$Ax = f,\quad A:H \to H,$

где A – линейный, положительно-определенный оператор ($A > 0$). Для нахождения решения задачи (27) будем использовать неявный итерационный процесс

(28)

$B\frac{{{{x}^{{m + 1}}} - {{x}^{m}}}}{\tau } + A{{x}^{m}} = f,\quad B:H \to H,$

где m – номер итерации, τ – итерационный параметр (τ > 0), а B – некоторый обратимый оператор. Обращение оператора B в (28) должно быть существенно проще, чем непосредственное обращение исходного оператора A в (27). При построении B будем исходить из аддитивного представления оператора ${{A}_{0}}$ – симметричной части оператора А:

(29)

${{A}_{0}} = {{R}_{1}} + {{R}_{2}},\quad {{R}_{1}} = R_{2}^{*},$

где ${{R}_{1}}$, ${{R}_{2}}$ – нижне- и верхнетреугольные операторы.

Также здесь и далее будем использовать кососимметричную часть оператора А:

${{A}_{1}} = \frac{{A - A{\kern 1pt} {\text{*}}}}{2}.$

В силу (29) $(Ay,y) = ({{A}_{0}}y,y) = 2({{R}_{1}}y,y) = 2({{R}_{2}}y,y)$. Поэтому в (29) ${{R}_{1}} > 0$, ${{R}_{2}} > 0$. Пусть в (28)

(30)

$B = (D + \omega {{R}_{1}}){{D}^{{ - 1}}}(D + \omega {{R}_{2}}),\quad D = D* > 0,\quad \omega > 0,\quad y \in H,$

где $D$ – некоторый оператор (например, диагональная часть оператора A).

Поскольку ${{A}_{0}} = A_{0}^{*} > 0$, то вместе с (29) это дает $B = B* > 0$. Соотношения (28)–(30) задают модифицированный попеременно-треугольный метод (МПТМ) решения задачи, если определены операторы ${{R}_{1}}$, ${{R}_{2}}$ и указаны способы определения параметров $\tau $, $\omega $ и оператора $D$.

Алгоритм нахождения решений системы сеточных уравнений МПТМ вариационного типа запишется в виде

${{r}^{m}} = A{{x}^{m}} - f,\quad B({{\omega }_{m}}){{w}^{m}} = {{r}^{m}},\quad {{\tilde {\omega }}_{m}} = \sqrt {\frac{{(D{{w}^{m}},{{w}^{m}})}}{{({{D}^{{ - 1}}}{{R}_{2}}{{w}^{m}},{{R}_{2}}{{w}^{m}})}}} ,$

(31)

$s_{m}^{2} = 1 - \frac{{{{{({{A}_{0}}{{w}^{m}},{{w}^{m}})}}^{2}}}}{{({{B}^{{ - 1}}}{{A}_{0}}{{w}^{m}},{{A}_{0}}{{w}^{m}})(B{{w}^{m}},{{w}^{m}})}},\quad k_{m}^{2} = \frac{{({{B}^{{ - 1}}}{{A}_{1}}{{w}^{m}},{{A}_{1}}{{w}^{m}})}}{{({{B}^{{ - 1}}}{{A}_{0}}{{w}^{m}},{{A}_{0}}{{w}^{m}})}},$

${{\theta }_{m}} = \frac{{1 - \sqrt {\frac{{s_{m}^{2}k_{m}^{2}}}{{(1 + k_{m}^{2})}}} }}{{1 + k_{m}^{2}(1 - s_{m}^{2})}},\quad {{\tau }_{{m + 1}}} = {{\theta }_{m}}\frac{{({{A}_{0}}{{w}^{m}},{{w}^{m}})}}{{({{B}^{{ - 1}}}{{A}_{0}}{{w}^{m}},{{A}_{0}}{{w}^{m}})}},\quad {{x}^{{m + 1}}} = {{x}^{m}} - {{\tau }_{{m + 1}}}{{w}^{m}},\quad {{\omega }_{{m + 1}}} = {{\tilde {\omega }}_{m}},$

где ${{r}^{m}}$ – вектор невязки, ${{w}^{m}}$ – вектор поправки, ${{s}_{m}}$ – скорость сходимости метода, $\,{{k}_{m}}$ – отношение нормы кососимметричной части оператора к норме симметричной части.

Скорость сходимости метода равна

(32)

$\rho \leqslant \frac{{\nu {\text{*}} - 1}}{{\nu {\text{*}} + 1}},$

где $\nu * = \nu {{(\sqrt {1 + {{k}^{2}}} + k)}^{2}}$, где $\nu $ – число обусловленности матрицы ${{C}_{0}}$, ${{C}_{0}} = {{B}^{{ - 1/2}}}{{A}_{0}}{{B}^{{ - 1/2}}}$.

Значение $\omega $ оптимально, если

$\omega = \sqrt {\frac{{(D{{w}^{m}},{{w}^{m}})}}{{({{D}^{{ - 1}}}{{R}_{2}}{{w}^{m}},{{R}_{2}}{{w}^{m}})}}} $

и имеет место оценка числа обусловленности матрицы ${{C}_{0}}$

$\nu = \mathop {\max }\limits_{y \ne 0} \left( {\frac{1}{2} + \frac{{\sqrt {(Dy,y)({{D}^{{ - 1}}}{{R}_{2}}y,{{R}_{2}}y)} }}{{({{A}_{0}}y,y)}}} \right) \leqslant \frac{1}{2}\left( {1 + \sqrt {\frac{\Delta }{\delta }} } \right) = \frac{{1 + \sqrt \xi }}{{2\sqrt \xi }},$

где $\xi = \frac{\delta }{\Delta }$, $D \leqslant \frac{1}{\delta }{{A}_{0}}$, ${{R}_{1}}{{D}^{{ - 1}}}{{R}_{2}} \leqslant \frac{\Delta }{4}{{A}_{0}}$.

4. ЭКСПЕДИЦИОННЫЕ ИССЛЕДОВАНИЯ АЗОВСКОГО МОРЯ И ОБРАБОТКА НАТУРНЫХ ДАННЫХ

Исследования проводились на 17 станциях в центрально-восточной части Азовского моря на научно-исследовательском судне “Денеб” Южного научного центра РАН (фиг. 2). В процессе реализации расчета структуры течений в водоемах с различной батиметрией самая часто возникающая проблема – это параметризация процесса турбулентного обмена. Поскольку именно турбулентная структура течения водного потока определяет интенсивность и характер протекания таких процессов, как транспорт наносов и перенос различных загрязняющих примесей, размыв дна.

Фиг. 2.

Экспедиция в Азовском море: (а) – маршрут экспедиции, (б) – научно-исследовательское судно “Денеб”.

В ходе экспедиции были получены данные о пульсациях скоростей водного потока в некоторых точках мелководных систем на основе зонда ADCP (Acoustic Doppler Current Profiler) WHS600 Sentinel. Профилограф работает на доплеровском эффекте, передавая акустический сигнал на фиксированной частоте и принимая отраженный на неоднородностях водной среды сигнал в расположенной под излучателем (начиная с зоны чувствительности) толще водного столба. Изучено влияние изменения значений коэффициента вертикального турбулентного обмена на содержание растворенного кислорода в придонном слое мелководного водоема. Примерно на глубине 3 м и ниже значения коэффициента вертикального турбулентного обмена близки к нулю, что означает пониженный турбулентный обмен по вертикали в данной области и объясняет явление гипоксии в придонном слое центрально-восточной части Азовского моря в летний период. В качестве входных данных при решении задачи фильтрации поступают исходные данные о скоростях потоков течения водной среды. Исходные данные для решения поставленной задачи следующие: количество элементов разрешения по глубине составляло 128, шаг измерения по глубине был взят 10 см, период измерений 1 с, количество измерений на каждой станции менялось в пределах от 200 до 1000. Для решения задачи построения модели фильтрации за основу был взят двухэтапный алгоритм Калмана. На фиг. 3 представлен тестовый пример работы программного обеспечения, предназначенного для устранения зашумленности экспедиционных измерений одной из составляющих вектора скорости водного потока.

Фиг. 3.

Применение фильтра Калмана для устранения зашумленности данных в двумерном случае: (а) – исходные данные с погрешностью измерительного прибора, (б) – данные, полученные после применения алгоритма фильтрации.

По вертикальной оси отмечена глубина водоема, по горизонтали – время. Цветом выделена скорость водного потока в мм/с в соответствии с приведенной на фиг. 3 шкалой.

Турбулентность напрямую рассчитывается непосредственно из уравнений Навье–Стокса и находится естественным путем при численном моделировании, если вертикальное разрешение сетки позволяет воспроизвести все механизмы до масштабов вязкой диссипации очень мелких вихрей.

Выполненные численные эксперименты на основе нескольких подходов для всех точек позволили получить распределение коэффициента вертикального турбулентного обмена в Азовском море (фиг. 4).

Фиг. 4.

Коэффициент вертикального турбулентного обмена в точках 1, 2, 3, 12.

Основываясь на результатах экспедиционных измерений параметров водной среды, проведенных авторами в акватории Азовского моря, можно утверждать, что в его центрально-восточной части существует область, в которой происходят заморные явления биоты. Причем появление этой области носит сезонный характер.

На фиг. 5 представлены результаты натурных измерений профиля температуры, солености и растворенного кислорода, полученные с помощью гидрофизического зонда “Sea Bird Electronics 19 Plus” на одной из экспедиционных станций.

Фиг. 5.

Профили растворенного кислорода, солености и температуры.

На фиг. 5 продемонстрирован тот факт, что содержание кислорода в контрольной точке Азовского моря на глубине более 6.5 м близко к нулевой отметке. На данной станции можно было наблюдать явление аноксии. Явление аноксии периодически, преимущественно в летний период, (не каждый год) возникает в Азовском море, но сопровождается катастрофическими последствиями, связанными с массовой гибелью рыбы на обширной территории. Известно, что механизмы возникновения аноксии для мелководных и глубоководных морей различны.

5. ОПИСАНИЕ ПРОГРАММНОГО КОМПЛЕКСА И РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ ПО РЕКОНСТРУКЦИИ ЭКОЛОГИЧЕСКИХ КАТАСТРОФ

При решении задачи обработки гидрологической информации получены изолинии солености и температуры в поверхностном слое, для чего применен алгоритм распознавания. С помощью алгоритма интерполяции получены карты солености и температуры Азовского моря в летний период (фиг. 6, 7 ) на основе имеющихся гидрологических данных (изолинии уровня, значения полей в отдельных точках). Данная информация является входной для моделей гидродинамики.

Фиг. 6.

Восстановленное поле солености Азовского моря.

Фиг. 7.

Восстановленное поле температуры Азовского моря.

Программная реализация математических моделей учитывает силу Кориолиса, ветровые течения и трение о дно, турбулентный обмен, испарение, стоки рек, а также сложную геометрию дна и береговой линии. Расчетная область соответствует физическим размерам Азовского моря: длина 355 км, ширина 233 км, максимальная глубина 13.2 м, шаг по пространству в горизонтальном направлении 1000 и 0.5 м по вертикали, шаг по времени 6 мин.

Для реконструкции экологической катастрофы была численно реализована трехмерная математическая модель вида (1)–(8), описывающая гидрофизические процессы, происходящие в мелководных водоемах на примере Азовского моря. На фиг. 8 приведены результаты численного моделирования движения водной среды (водные потоки) в акватории Азовского моря на основе программного комплекса “Azov3d”. Рассмотрена задача на установление течений в Азовском море при восточном ветре интенсивностью 5 м/с. Изначально жидкость находилась в состоянии покоя. Расчетный интервал составлял 24 ч. На мелководье водные потоки преимущественно направлены вдоль ветра. В глубоководных участках Азовского моря, вследствие разности уровней водной среды, в толще водоема поток направлен против ветра. Для изучения полей течений в Азовском море удобно использовать интегральные характеристики: $U = \int_\eta ^H {udz} $, $V = \int_\eta ^H {vdz} .$ На фиг. 8 приведен пример расчета полей течений водного потока Азовского моря. Шкала справа отражает интегральную характеристику водного потока $\left( {U,V} \right)$.

Фиг. 8.

Результаты математического моделирования движения водной среды.

В восточной части Азовского моря можно наблюдать область с вихревой структурой течений (природной ловушкой), в которой может находиться достаточно большое количество отмершей органики, ранее вовлеченной в движение водотока. Предположительно, данные явления привели к экологической катастрофе в июле 2001 г. в Азовском море, когда на площади более 1000 кв. км возникла зона анаэробного (сероводородного) заражения и наблюдалась массовая гибель ихтиофауны.

Проведенные комплексные экспедиционные измерения параметров водной среды в акватории Азовского моря и Таганрогского залива позволили обновить базы данных многолетних наблюдений за состоянием их водной среды. На фиг. 9 приведены профили горизонтальных составляющих вектора скорости водного потока (красная тонкая линия – результаты численных экспериментов, толстая синяя линия – натурных). Относительное отклонение расчетных гидрофизических параметров, полученных в результате моделирования и натурных опытов, находится в пределах от 15 до 20%.

Фиг. 9.

Профили горизонтальной компоненты вектора скорости: (а) – составляющая вектора скорости, направленная с запада на восток (u), (б) – с севера на юг (${v}$).

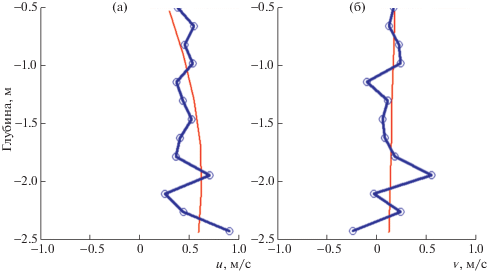
Дальнейшее повышение точности модели осложнено тем, что результаты натурных экспериментов при одних и тех же условиях по некоторым параметрам могут значительным образом отличаться от среднего значения.

Натурные исследования позволили провести калибровку и верификацию разработанной математической модели гидродинамики.

6. ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ ПО МОДЕЛИРОВАНИЮ ПРОЦЕССОВ БИОЛОГИЧЕСКОЙ КИНЕТИКИ

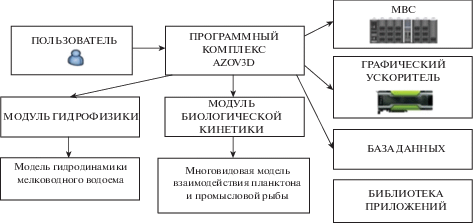
Для решения поставленной задач гидродинамики (1)–(8) и биологической кинетики вида (9)–(11) были разработаны модули, входящие в программный комплекс (ПК) “Azov3D”, реализованные на высокопроизводительных вычислительных системах: МВС и графическом ускорителе (см. [16]–[18]). ПК включает следующие блоки: блок управления, океанологические и метеорологические базы данных, библиотека прикладных программ для решения задач гидробиологии; осуществляется интеграция с различными геоинформационными системами (ГИС), глобальной базой данных с ресурсами для геотаггинга и доступа к системам сбора спутниковых данных, базой данных реанализа NCEP/NCAR (фиг. 10).

Фиг. 10.

Схема программного комплекса.

Использование ГИС предоставляет дополнительные возможности для более качественного и сложного пространственного анализа, а решения на его основе являются более точными.

На фиг. 11 представлены результаты расчета концентрации загрязняющего биогенного вещества и фитопланктона, усредненных по глубине, для модели биологической кинетики.

Фиг. 11.

Распределение концентраций: (а) – загрязняющих биогенных веществ в начальный момент времени $\left( {{{S}_{3}}} \right)$; (б) – с течением времени, $T = 28$ дней; (в) – распределение концентрации фитопланктона $\left( {{{S}_{1}}} \right)$ в начальный момент времени; (г) – с течением времени, $T = 64$ дня.

Значения коэффициентов: ${{\mu }_{3}} = 5 \times {{10}^{{ - 10}}}$; ${{\nu }_{3}} = {{10}^{{ - 10}}}$; $B = 0.001$; ${{\tilde {S}}_{3}} = 1$; $f = 3$; ${{\tau }_{i}} = 0.1$; $i \in \left\{ {1,\;5} \right\}$; ${{\lambda }_{2}} = 0.8$; ${{\mu }_{1}} = 5 \times {{10}^{{ - 11}}}$; ${{\nu }_{1}} = {{10}^{{ - 11}}}$; $N$ – номер итерации (начальное распределение полей течений водного потока для северного ветра). Начальные данные для модели биологической кинетики были получены на основе экспедиционных данных, литературных источников, электронного атласа, подготовленного ЮНЦ РАН 2018 г., экологического атласа Черного и Азовского морей, подготовленного в 2019 г. Для калибровки и верификации разработанных моделей гидрофизики, входящих в ПК, использовались данные портала Единой государственной системы информации об обстановке в Мировом океане “ЕСИМО”, портала “Аналитические ГИС”, разработанного Институтом проблем передачи информации РАН (Москва). В качестве входных данных для моделирования гидрофизических процессов, помимо экспедиционных данных и литературных источников, использовались данные НИЦ “Планета”, данные Азовского научно-исследовательского института рыбного хозяйства (“АзНИИРХ”), ФГУ “Азовморинформцентра”, экспедиционные исследования.

С использованием разработанного комплекса программ был изучен механизм опасного явления – образования заморных зон в мелководном водоеме. На фиг. 12 представлены результаты моделирования возможных сценариев развития экосистемы Азовского моря (изменения концентрации популяции промысловой рыбы-детритофага пиленгас) (начальное распределение полей течений водного потока, полученное в результате натурного эксперимента, задано для северного направления ветра). Белым цветом выделены максимальные значения концентраций рыбы и детрита, начальное распределение полей течений в Азовском море при северном ветре. Значения коэффициентов: ${{\mu }_{4}} = 3 \times {{10}^{{ - 11}}}$; ${{\nu }_{4}} = {{10}^{{ - 11}}}$; ${{\varepsilon }_{4}} = 1.9 \times {{10}^{{ - 5}}}$; ${{\beta }_{4}} = 0.1$; ${{\lambda }_{4}} = 0.4$; ${{\mu }_{5}} = 1.5 \times {{10}^{{ - 3}}}$; ${{\nu }_{5}} = 1.6 \times {{10}^{{ - 3}}}$; ${{\gamma }_{5}} = 0.125$; ${{\lambda }_{5}} = 1.16 \times {{10}^{{ - 3}}}$; ${{\xi }_{5}} = 0.8$; ${{\varepsilon }_{5}} = 0.47$; ${{\delta }_{5}} = 0.05$.

Фиг. 12.

Распределение концентраций: (а) – детрита, временной интервал T = 62 дня; (б) – промысловой рыбы, временной интервал T = 76 дней.

Представленные результаты численного эксперимента, проведенного на основе сценарного подхода, позволяют исследовать возможный сценарий зарыбления акватории Азовского моря пеленгасом, участвующим в донной мелиорации мест скопления детрита. При значении временного интервала, начиная с 61-го дня, согласно представленным результатам, наблюдается снижение концентрации детрита, а значит, и концентрации донных отложений в центрально-восточной части Азовского моря, что в конечном счете приведет к уменьшению площадей заморных зон и улучшению качества вод в изучаемом водоеме.

С помощью разработанного программного комплекса можно исследовать пластичность пищевого режима и вопросы акклиматизации рыб-детритофагов в новых по экологическому режиму условиях, оценить специфику условий водоема, используемого для выпуска молоди, что позволит избежать непредвиденных отрицательных технологических влияний и планировать улучшение процессов воспроизводства промысловых рыб, активно участвующих в процессах самоочищения и донной мелиорации экосистемы. Анализ полученных результатов позволил сделать выводы о свойствах математической модели детрит–промысловая рыба и возможностях управления качеством вод мелководных водоемов, таких как Азовское море, с помощью методов и средств математического моделирования.

ЗАКЛЮЧЕНИЕ

Разработаны взаимосвязанные математические пространственно-трехмерные модели гидродинамики и биологической кинетики мелководного водоема, характеризующегося значительными перепадами глубин и солености, сложным распределением температуры водной среды и кислородным режимом. Результаты расчетов с помощью пространственно-трехмерной модели гидродинамики, учитывающей физические свойства водной среды, используются в качестве входных данных для разработки сценариев динамики процессов транспорта и трансформации загрязняющих биогенных элементов в водоеме, влияющих на развитие биоты, включая фито-, зоопланктон и рыбные популяции (см. [19]–[21]).

Построена и исследована трехмерная математическая модель динамики планктона и промысловых рыб для мелководного водоема, учитывающая конвективный и диффузионный переносы, поглощение и выделение питательных веществ фито- и зоопланктоном, соленость, температуру, кислородный режим, пространственное распределение детрита, нелинейное взаимодействие гидробионтов, таксис и др. Разработка численных методов решения поставленных модельных задач, использующих конечно-разностные схемы с учетом степени заполненности контрольных ячеек расчетной области, позволила уменьшить погрешность и сократить время расчетов в десятки раз. Задачи гидродинамики и биологической кинетики были решены с использованием высокопроизводительных вычислительных систем, способных выполнять большое количество сложных расчетов и обрабатывать огромные объемы данных за ограниченное время, что является актуальным при построении оперативных прогнозов изменения состояния водной экосистемы при возникновении в ней опасных явлений природного характера.

На основе разработанного программного комплекса проведена реконструкция опасных явлений мелководного водоема (природного и техногенного характеров), связанных с распространением вредных загрязняющих веществ, эвтрофикацией, “цветением водорослей”, вызывающим возникновение заморных зон, характеризующихся пониженной концентрацией кислорода. Изучение подобных ПК водоемов показало, что в результате его разработки удалось повысить точность прогнозов изменения концентраций планктона и промысловых рыб на 10–15% в зависимости от решаемой модельной задачи биологической кинетики. Мониторинг водной акватории, проводимый на регулярной основе, позволил разработать математические модели процессов гидрофизики и биологической кинетики, предназначенные для прогнозирования возможных сценариев развития экосистемы Азовского моря, а также изучения механизмов возникновения областей анаэробного заражения и принятия своевременных мер, направленных на их локализацию и уменьшение возможных негативных последствий.

Список литературы

Марчук Г.И., Дымников В.П., Залесный В.Б., Лыкосов В.Н., Бобылева И.М., Галин В.Я., Перов В.Л. Математическая модель общей циркуляции атмосферы и океана // Докл. АН СССР. 1980. Т. 253. № 3. С. 577–581.
Самарский А.А., Вабищевич П.Н. Численные методы решения задач конвекции–диффузии. М.: URSS, 2009. 248 с.
Ansorge R., Sonar Th. Mathematical models of fluid dynamics: modelling, theory, basic numerical facts –an introduction, 2nd, Updated Edition. ISBN: 978-3-527-62797-4. 2009. 242 p.
Alekseenko E., Roux B., Sukhinov A.I., Kotarba R., Fougere D. Coastal hydrodynamics in a windy lagoon // Computers and Fluids. 2013. V. 77. P. 24–35.
Yakushev E.V., Lukashev Yu.F., Skirta A.Yu., Sorokin P.Yu., Soldatova E.V., Yakubenko V.G., Sukhinov A.I., Sergeev N.E., Fomin S.Yu., Sapozhnikov F.V. Comprehensive oceanological studies of the sea of Azov during cruise 28 of r/v Akvanavt (july–august 2001) // Oceanology. 2003. V. 43. № 1. P. 39–47.
Logofet D.O. Stronger-than-Lyapunov notions of matrix stability, or how “flowers” help solve problems in mathematical ecology // Linear Algebra and its Appl. 2005. V. 398. P. 75–100.
Tyutyunov Yu.V., Titova L.I., Senina I.N. Prey-taxis destabilizes homogeneous stationary state in spatial Gause–Kolmogorov-type model for predator-prey system // Ecological Complexity. 2017. V. 31. P. 170–180.
Четверушкин Б.Н., Гасилов В.А., Поляков С.В., Карташева Е.Л., Якобовский М.В., Абалакин И.В., Бобков В.Г., Болдарев А.С., Болдырев С.Н., Дьяченко С.В., Кринов П.С., Минкин А.С., Нестеров И.А., Ольховская О.Г., Попов И.В., Суков С.А. Пакет прикладных программ GIMM для решения задач гидродинамики на многопроцессорных вычислительных системах // Матем. моделирование. 2005. Т. 17. № 6. С. 58–74.
Давыдов А.А., Четверушкин Б.Н., Шильников Е.В. Моделирование течений несжимаемой жидкости и слабосжимаемого газа на многоядерных гибридных вычислительных системах // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 12. С. 2275–2284.
Четверушкин Б.Н. Пределы детализации и формулировка моделей уравнений сплошных сред // Матем. моделирование. 2012. Т. 24. № 11. С. 33–52.
Сухинов А.И., Чистяков А.Е., Шишеня А.В., Тимофеева Е.Ф. Предсказательное моделирование прибрежных гидрофизических процессов на многопроцессорной системе с использованием явных схем // Матем. моделирование. 2018. Т. 30. № 3. С. 83–100.
Петров И.Б., Фаворская А.В., Санников А.В., Квасов И.Е. Сеточно-характеристический метод с использованием интерполяции высоких порядков на тетраэдральных иерархических сетках с кратным шагом по времени // Матем. моделирование. 2013. Т. 25. № 2. С. 42–52.
Белоцерковский О.М., Опарин А.М., Чечеткин В.М. Турбулентность. Новые подходы. М.: Наука, 2003. 286 с.
Коновалов А.Н. Метод скорейшего спуска с адаптивным попеременно-треугольным переобусловливателем // Дифференц. ур-ния. 2004. Т. 40. № 7. С. 953–963.
Sukhinov A.I., Nikitina A.V., Chistyakov A.E., Semenov I.S. Mathematical modeling of conditions for the formation of locks in shallow water reservoirs on a multiprocessor computer system // Comput. Meth. and Programming: New Comput. Technolog. 2013. V. 14. № 1. P. 103–112.
Никитина А.В. Модели биологической кинетики, стабилизирующие экологическую систему Таганрогского залива // Изв. ЮФУ. 2009. № 8 (97). С. 130–134.
Никитина А.В., Семенов И.С. Параллельная реализация модели динамики токсичной водоросли в Азовском море с применением многопоточности в операционной системе Windows // Изв. ЮФУ. Технические науки. 2013. № 1 (138). С. 130–135.
Sukhinov A.I., Chistyakov A.E., Ugol’nitskii G.A., Usov A.B., Nikitina A.V., Puchkin M.V., Semenov I.S. Game-theoretic regulations for control mechanisms of sustainable development for shallow water ecosystems // Automat. and Remote Control. 2017. V. 78 (6). P. 1059–1071.
Sukhinov A.I., Chistyakov A.E., Nikitina A.V., Belova Yu.V., Sumbaev V.V., Semenyakina A.A. Supercomputer modeling of hydrochemical condition of shallow waters in summer taking into account the influence of the environment // Comm. in Computer and Informat. Sci. 2018. V. 910. P. 336–351.
Nikitina A.V., Kravchenko L., Semenov I., Belova Y., Semenyakina A. Modeling of production and destruction processes in coastal systems on a supercomputer // MATEC Web of Conferences, 2018, 226, 04025. https://doi.org/10.1051/matecconf/201822604025
Гущин В.А., Никитина А.В., Семенякина А.А., Сухинов А.И., Чистяков А.Е. Модель транспорта и трансформации биогенных элементов в прибрежной системе и ее численная реализация // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 8. С. 120–137.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал