Журнал вычислительной математики и математической физики, 2022, T. 62, № 2, стр. 255-269

ВВЕДЕНИЕ

Задача настоящей работы, которая решалась и решается, – это создание оптимизированного математического описания кинетики зарождения, роста и агрегирования частиц по их экспериментальным функциям распределения по свойствам.

Структуру статьи определяет следующая основная идея математического описания результатов экспериментов. Сначала возникает постановка задачи: определяются параметры функции распределения. На этом этапе экспериментаторы предлагают параметры, которые они могут измерить, т.е. какие параметры выбирать для модели. Затем первый шаг математического моделирования – это создание априорной модели, содержащей неизвестные функции как параметры, подлежащие в дальнейшем определению. Априорная модель – это написание правильных (физико-химически обоснованных) уравнений, содержащих неизвестные параметры. Модель должна отвечать на вопросы: каковы условия эксперимента, как и в каком диапазоне их следует менять, и что следует определять в эксперименте, чтобы получить эти неизвестные функции априорной модели. Мы отвечаем на эти вопросы для нашей задачи. На основе экспериментов эти неизвестные функции определяются: возникает апостериорная модель. Так получается математическое описание экспериментов. После того исследование предполагается повторить, расширив перечень и интервалы варьирования учитываемых условий. Цель – предсказывать, как синтезировать новые материалы с наибольшей экологической безопасностью и с наименьшими энергетическими затратами.

Поэтому возникает вопрос: какую информацию о кинетике элементарных процессов сохраняет тело к моменту завершения процесса? Частичный ответ на этот вопрос дают данные о зависимости формы тел и некоторых других их свойств от условий синтеза, которую стали рассматривать как память тел (морфологическая память) о том, как они образовались. Это свойство тел, которое было названо морфологической памятью, можно результативно использовать при разработке технологий.

1. ПОСТАНОВКА ЗАДАЧИ

В работах Дж.К. Максвелла (см. [1]), Л. Больцмана (см. [2]) и др. исследователей кинетики различных процессов исследуется функция распределения по скоростям и координатам, зависящая от времени. В [2] Больцманом впервые была рассмотрена теорема, о которой мы будем неоднократно говорить в настоящей работе. Теперь же возникает многопараметрическое описание, которое связано с тем, что оно стало доступно для экспериментального наблюдения. Задача состоит в том, чтобы написать уравнения на функцию распределения частиц по этим многим параметрам.

В настоящей статье мы продолжаем линию работ [3], [4] и др., посвященных математическому моделированию зарождения и роста иерархических структур с помощью кинетического подхода.

Типичная структура представляет собой иерархическую структуру. Виды тел, отличающиеся уровнем иерархической структуры (номером поколения), будем обозначать параметром $k \in N$: частицы каждого $k$-го поколения укрупняются путем присоединения частиц всех $j < k$ видов, причем, как показывает эксперимент, происходит парное взаимодействие частиц.

При описании образования тел целесообразно различать несколько стадий процесса. Сначала зарождаются и растут первичные частицы, далее наступает стадия агрегации – образование агломератов из первичных частиц в результате их столкновений друг с другом, а затем происходит и образование агрегатов из них. Несмотря на то что все стадии идут одновременно, сначала преобладает процесс образования первичных частиц, потом – их агрегатов, т.е. вторичных агломератов, затем – агрегатов из вторичных агломератов и т.д. Итак, образование дисперсного вещества происходит стадийно, и каждая стадия вносит вклад в структуру образовывающегося вещества. Этот факт используется при моделировании.

Чтобы создать наноструктуру (и вообще, какую-то структуру) с нужными свойствами, используют явления образования и распада зародышей первичных наночастиц, их роста и растворения, появления и ликвидации ростовых дефектов, захвата и выброса захваченных примесей, агрегации и разрушения агрегатов, перекристаллизации и топохимических реакций спекания и керамизации (см. [3]). При описании данных явлений учитываются свойства ${\mathbf{X}}$ каждой частицы: внутренние и внешние. Внешние параметры состояния частицы характеризуют ее вещественно-энергетический обмен со средой, а внутренние – перераспределение вещества и энергии внутри частицы.

На всех стадиях процесса рассматриваемая система неоднородна, причем на каждом ее участке присутствуют молекулы, агрегаты молекул, укрупняющиеся за счет присоединения молекул, агрегаты второго поколения и т.д. В первом приближении можно считать, что стенки и мешалка обеспечивают однородность среды и фазообразующего вещества. В континуальном приближении каждый участок характеризуется собственной функцией распределения частиц по свойствам:

Здесь ${{\Psi }_{k}}\left( {{\mathbf{X}},t} \right)$ – функция распределения частиц поколения $k$; ${{N}_{{k,{\mathbf{X}}}}}$ – локальная концентрация частиц $k$-вида, у которых параметры состояния меньше соответствующих компонент вектора ${\mathbf{X}}$; ${{{\mathbf{X}}}_{0}}$ – минимально возможное значение свойства ${\mathbf{X}}$. Вектор ${\mathbf{X}}$ не включает пространственные координаты частиц, которые отождествляются с координатами участка.

Для решения нашей задачи (выписывания корректных уравнений с коэффициентами, подлежащих в дальнейшем определению на основе эксперимента) нам понадобится выразить функцию от многих параметров ${{\Psi }_{k}}\left( {{\mathbf{X}},t} \right)$ через однопараметричные функции распределения. Нам понадобится следующая

Лемма. Пусть функция $f\left( {{{x}_{1}},{{x}_{2}}} \right) > 0$ такая, что $\int {f\left( {{{x}_{1}},{{x}_{2}}} \right)d{{x}_{2}}} $ конечен. Тогда функция $f$ может быть представлена единственным способом в следующем виде:

где $\int {{{g}_{2}}\left( {{{x}_{1}},{{x}_{2}}} \right)d{{x}_{2}}} = 1$.

Доказательство. Пусть ${{g}_{1}}\left( {{{x}_{1}}} \right) \equiv \int {f\left( {{{x}_{1}},{{x}_{2}}} \right)d{{x}_{2}}} $. Тогда ${{g}_{2}}\left( {{{x}_{1}},{{x}_{2}}} \right) = \frac{1}{{{{g}_{1}}\left( {{{x}_{1}}} \right)}}f\left( {{{x}_{1}},{{x}_{2}}} \right)$.

Такое представление приводит к теоретико-вероятностному описанию второй переменной ${{x}_{2}}$ как случайной величины: ${{g}_{2}}\left( {{{x}_{1}},{{x}_{2}}} \right)$ как функции распределения величины ${{x}_{2}}$ при условии ${{x}_{1}}$, и записывается в теории вероятностей как ${{g}_{2}}\left( {\left. {{{x}_{2}}} \right|{{x}_{1}}} \right)$.

Это представление допускает обобщение на произвольное число переменных. Пусть $f\left( {{{x}_{1}},...,{{x}_{r}}} \right) > 0$ и все интегралы ($k = 0, \ldots ,s - 2$) существуют. Тогда разложение $f = {{g}_{1}}\left( {{{x}_{1}}} \right) \ldots {{g}_{k}}\left( {{{x}_{1}}, \ldots ,{{x}_{k}}} \right) \ldots {{g}_{r}}\left( {{{x}_{1}}, \ldots ,{{x}_{r}}} \right)$, где , определяется единственным способом. Такие формулы в теории вероятностей называются формулами Байеса (см. [5]), а кинетическая теория придает смысл сокращенного описания, как отмечалось в [3].

Пример 1 (см. [1], [2]). В кинетической теории вводят функцию $f\left( {{\mathbf{v}},{\mathbf{x}},t} \right)$ распределения молекул по скоростям ${\mathbf{v}} \in {{R}^{3}}$ и пространству ${\mathbf{x}} \in {{R}^{3}}$ в момент времени $t$. Обычно считают величину ${\mathbf{v}}$ вероятностной переменной, и происходит сокращение описания в результате столкновений до локально максвелловского распределения частиц массы $M$:

где $n\left( {{\mathbf{x}},t} \right) \equiv {{\psi }_{1}}\left( {{\mathbf{x}},t} \right)$ – концентрация частиц массы $M$, $T\left( {{\mathbf{x}},t} \right)$ – температура, ${{\kappa }_{{\text{B}}}}$ – постоянная Больцмана, ${\mathbf{V}}\left( {{\mathbf{x}},t} \right)$ – значение средней скорости частиц с массой $M$.

Основной параметр функции распределения частиц каждого из $k$ видов определяется как первый параметр в приведенном ниже разложении. Целесообразно брать число молекул $n$, составляющих частицу, в качестве основного параметра: ${{x}_{1}} = n$, и тогда

где ${{\psi }_{k}}\left( {n,t} \right)$ – функция распределения частиц по числу $n$, составляющих их молекул, ${{f}_{{k,i}}}\left( {{{x}_{i}}\,|\,n,{{x}_{2}}, \ldots ,{{x}_{{i - 1}}};t} \right)$, где $i = 2, \ldots ,s$, – это плотности распределений частиц по свойству ${{x}_{i}}$ при условии, что параметры, выписанные после $|$, фиксированы: .

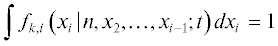В силу того, что число молекул $n$, составляющих частицу, – основной параметр, в первую очередь, представляет интерес рассмотрение функций распределения по этому параметру.

Пример 1 мы привели в качестве классического примера. Рассмотрим еще пример распределения (1.1) из [6].

Пример 2 (см. [1], [2], [6]). Пример распределения (1.1) дает максвелловская функция распределения частиц с массой ${{M}_{n}} = nM$, где $M$ – масса одной молекулы фазообразующего вещества (см. [6]):

где ${\mathbf{p}} \in {{R}^{3}}$ – значение импульса частицы с массой ${{M}_{n}}$.

Более точно, масса в (1.1) должна быть представлена как

где ${{M}_{0}}$ и ${{M}_{L}}$ – массы отдельных молекул вещества, образующего твердую фазу, и среды системы, ${{n}_{L}}$ – количество молекул среды, захваченных в объеме и на поверхности частицы.

Тогда

где $\nu $ – объем частицы, ${{\nu }_{0}}$ и ${{\nu }_{{0L}}}$ – объемы, занимаемые отдельными молекулами вещества, образующего твердую фазу, и среды системы внутри частицы. В рамках оценочной модели целесообразно предположить, что объем и площадь поверхности каждой частицы могут быть представлены как функции эффективного размера: где ${{\gamma }_{1}}$, ${{\gamma }_{2}}$ и ${{\gamma }_{3}}$ – параметры формы, ${{l}_{M}}$ – максимальное расстояние между точками на поверхности частицы. Ряд закономерностей в поведении частицы можно выявить, если предположить, что ее форма близка к шару (${{\gamma }_{1}} = 1$, ${{\gamma }_{2}} = \pi $, ${{\gamma }_{3}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$) или кубу (${{\gamma }_{1}} = \sqrt 3 $, ${{\gamma }_{2}} = 6$, ${{\gamma }_{3}} = 1$). Для более точного моделирования необходимо использовать параметры формы, определяемые экспериментально.

Если частицы имеют форму пластины, то целесообразно полагать, что $\nu = hs$, где $h$ – эффективная толщина частицы. Если частицы представляют собой цепочки, тогда $\nu = {{h}^{2}}{{l}_{M}}$. Поэтому в общем случае, если $\nu \gg {{n}_{L}}{{\nu }_{{0L}}}$, то из (1.4) и (1.5) получаем

где ${{\nu }_{0}}$ – объем одной молекулы фазообразующего вещества, $\delta = 1$ для цепочек из молекул, $\delta = 2$ для пластин, $\delta = 3$ для объемов. Мы также предполагаем, что параметры формы ${{\gamma }_{\delta }}$ не зависят от $l$.

Число молекул $n$, составляющих частицу, является основным параметром, и поэтому в первую очередь представляет интерес для функций распределения дисперсного вещества по нему. В эксперименте мы получаем интегральную функцию распределения в зависимости от размера частиц $l$, у которой измерен дискретный набор значений. Интегральные функции распределения агрегатов поколения $k$, моделирующие (аппроксимирующие) экспериментальное дискретное распределение, будем обозначать через ${{\theta }_{k}}\left( l \right)$.

Мы рассматриваем систему, которая является двухкомпонентной и состоит из растворителя или газа-носителя и кристаллообразующего вещества: пересыщенного раствора или пара.

Частотные функции для частиц, которые являются объемами из молекул, могут быть пропорциональны ${{n}^{{1/3}}}$, ${{n}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}$ или не зависеть от $n$. Первый случай означает, что активные центры представляют собой одномерную структуру, второй – то, что число активных центров пропорционально площади поверхности, а последний, что число активных центров – фиксированное число. Например, один или два активных центра возникают в случае цепочек из полимерных молекул. Энергия активации $\varepsilon $ рассчитывается по уравнению Аррениуса (см. [6]–[8]): частота присоединения или отрыва молекулы (или более крупной частицы) от другой частицы пропорциональна $\exp \left( {{{ - \varepsilon } \mathord{\left/ {\vphantom {{ - \varepsilon } {kT}}} \right. \kern-0em} {kT}}} \right)$, где $\varepsilon $ – энергия активации объединения или распада. Ее определяют экспериментально, согласно (1.3), по частотным функциям объединения и распада.

Мы будем рассматривать только два параметра, характеризующие частицу: ее массу и потенциальную энергию, которую мы учтем в коэффициентах уравнений.

Цель нашего исследования – определить коэффициенты уравнений на функцию распределения по тем, которые получаются в экспериментах. Поэтому первая задача – это получение этих уравнений, вторая – рассмотрение классов функций распределения частиц, хорошо аппроксимирующих данные, получаемые в эксперименте, а третья – получение соотношений между параметрами таких функций и коэффициентами уравнений.

Первая задача, которая возникает, – получение правильных уравнений, описывающих кинетику дисперсного вещества и, следовательно, вывод одних уравнений из других: рассмотрение связи между дискретными и континуальными уравнениями, переход от многопараметрического описания к сокращенному (например, вывод уравнений на функцию распределения частиц по размерам из обобщенных уравнений типа Больцмана на функцию распределения тел по размерам и скоростям их центра масс). Вторая задача начала рассматриваться в [6], а третья – в [9], и мы также будем ее обсуждать в следующем разделе. Рассматривается дискретная функция распределения, и получаются уравнения на нее.

В разд. 2 формулируются дискретные уравнения баланса первичных частиц, учитывающие возможность их укрупнения и распада, и показывается, как из дискретного описания получаются континуальные уравнения типа Фоккера–Планка. В теории вероятностей такое уравнение называют дифференциальным уравнением Эйнштейна–Колмогорова (см. [10]). В силу параболического вида полученного уравнения оно также называется диффузным приближением.

В разд. 3 мы обсудим параметры и классы функций распределения, хорошо аппроксимирующие данные, получаемые в эксперименте.

В разд. 4 рассмотрено точное решение диффузного приближения, которое в каждый момент времени совпадает с предложенными новыми аппроксимирующими функции распределения, и получены другие классы моделирующих функций на основе анализа этого уравнения и соотношения между параметрами аппроксимирующих функций и коэффициентами уравнений, описывающих кинетику дисперсного вещества.

2. ПЕРЕХОД К КОНТИНУАЛЬНОМУ ОПИСАНИЮ

Уравнения коагуляции частиц были впервые выведены и изучены для случая растворов Смолуховским (см. [11]) (без учета фрагментации – случай Смолуховского). Эта система уравнения, конечно, не учитывала разделение частиц на агрегаты различных поколений.

Первая стадия агрегирования описывается так называемыми уравнениями Беккера–Дёринга (см. [12]) – это случай, когда только одна молекула может присоединяться или отделяться от другой частицы.

Выпишем систему уравнений объединения–фрагментации с учетом различия поколений агрегатов. Она получается похожей на систему уравнений Смолуховского (см. [11]), которая в случае учета фрагментации называется системой коагуляции– дробления (см. [13, с. 56, и ссылки в ней]). В правой части такой системы возникает суммирование по числу молекул, составляющих частицу. А у нас (см. [3], [4]) возникает двойное суммирование, так как мы учитываем, что частицы представляют собой иерархические структуры и различаются по поколениям $k$ (соответствующий индекс суммирования $l$):

для $n = {{n}_{{p,0}}},{{n}_{{p,0}}} + 1, \ldots ,{{m}_{p}}$, где ${{n}_{{p,0}}}$ и ${{m}_{p}}$ – соответственно минимально и максимально возможные числа молекул в частице поколения $p$. В (2.1) ${{N}_{k}}\left( {n,t} \right)$ – число частиц поколения $k$, состоящих из $n$ молекул; ${{\alpha }_{{k,p}}}\left( {n,c} \right)$ – частотная функция (сечение) объединения частицы поколения $k$, состоящих из $n$ молекул, с частицей вида $p$, состоящей из $c$ молекул; ${{\beta }_{{k,p}}}\left( {n,d} \right)$ – частота распада частицы вида $k$, состоящей из $n$ молекул, на частицу того же поколения, состоящую из $\left( {n - d} \right)$ молекул, и на частицу вида $p$, состоящую из $d$ молекул; ${{\Omega }_{k}}\left( {n,t} \right)$ означает, что число частиц вида $k$ может также меняться в результате объединения двух частиц поколения $k - 1$ или процесса, обратного данному, вследствие объединения частицы вида $k$ с частицами поколения, большего либо равного $k$, и вследствие отпада частицы вида $k$ от частиц поколения, большего либо равного $k$.

Однако эксперименты и вычисления на компьютере требуют системы дискретных уравнений с шагом по времени $\Delta t$:

Здесь $\Delta {{N}_{k}}\left( {n,t,\Delta t} \right)$ – изменение числа частиц ${{N}_{k}}\left( {n,t} \right)$ поколения $k$, состоящих из $n$ молекул, за интервал времени $\Delta t$. Мы должны определить $\Delta {{N}_{k}}\left( {n,t,\Delta t} \right)$ через $N\left( {n,t} \right)$. Если $\Delta N\left( {n,t,\Delta t} \right) \equiv N\left( {n,t + \Delta t} \right) - N\left( {n,t} \right)$, то мы имеем явную дискретизацию системы обыкновенных дифференциальных уравнений (2.1). Система уравнений (2.1) принадлежит классу систем уравнений физико-химической кинетики (см. [14]), потому для нее $H$-теорема выполняется при выполнении условия динамического равновесия (the complex balance condition) (см. [15]–[17]), а для (2.1) с явной дискретизацией по времени она не верна в этом случае: в [17], [18] доказано, что  $H$-теорема не выполняется в случае, когда рассматриваются только отдельные молекулы и   димеры. Но она справедлива для неявной дискретизации по времени: когда $\Delta N\left( {n,t,\Delta t} \right) \equiv N\left( {n,t} \right) - N\left( {n,t - \Delta t} \right)$ (см. [19], [21]). И поэтому не следует использовать явную дискретизацию по времени для компьютерного моделирования.

Простая континуальная аналогия системы уравнений (2.1) имеет вид

для $n \in \left[ {{{n}_{{k,0}}},{{m}_{k}}} \right]$. Здесь вместо суммирования по $с$ и $d$ мы можем написать интегралы.

Уравнения (2.3) обосновываются тем, что подстановка суммы $\delta $-функций

${{\psi }_{k}}\left( {n,t} \right) = \sum\nolimits_{i = {{n}_{{k,0}}}}^{{{m}_{k}}} {{{N}_{k}}\left( {i,t} \right)~\delta \left( {n - i} \right)} $

для каждого номера поколения $k$ дает (2.1). Действительно, подставляя в (2.3) сумму $\delta $-функций и интегрируя для каждого натурального $n \in \left[ {{{n}_{{k,0}}},{{m}_{k}}} \right]$ обе части полученного уравнения на интервале, содержащем только одно целое значение $n$, мы получаем (2.1) для этого $n$.

Перепишем (2.3) в виде

разложим приращения функций в этом уравнении в ряды Тейлора и рассмотрим только два первых члена в разложениях в ряды Тейлора. Мы можем пренебречь остальными членами, если размер частиц поколений меньших $k$ достаточно мал по сравнению с размерами агрегатов вида $k$. Тогда мы получаем уравнения типа Фоккера–Планка на функции ${{\psi }_{k}} = {{\psi }_{k}}\left( {n,t} \right)$, которые имеют вид где $J\left( {n,t} \right) = G\left( {n,t} \right){{\psi }_{k}} - \frac{\partial }{{\partial n}}\left( {D\left( {n,t} \right){{\psi }_{k}}} \right)$,

В (2.5), (2.6) получилась линейная зависимость коэффициентов уравнения типа Фоккера–Планка (2.4) от ${{N}_{l}}\left( {c,t} \right)$, $l < k$. Так получилось из-за того, что мы предполагали в (2.1) парность взаимодействия частиц, что, вообще говоря, верно только для разреженных газов.

Итак, мы получили уравнения типа Фоккера–Планка (2.4) с источником или стоком ${{\Omega }_{k}}\left( {n,t} \right)$.

Наша дальнейшая цель – определить коэффициенты уравнения типа Фоккера–Планка (2.4) по функциям распределения.

3. МОДЕЛИРУЮЩИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

В настоящем и следующих разделах мы будем опускать в обозначениях функций распределения нижний индекс $k$, определяющий номер поколения частицы.

Дисперсный состав порошков описывают с помощью дифференциальных функций распределения $\varphi \left( l \right)$ или $\psi \left( n \right)$, связь между которыми проявляется в интегральной функции распределения

$\theta \left( {l,t} \right) \equiv \frac{1}{{N\left( t \right)}}\int_{{{l}_{0}}}^l {\varphi \left( {l{\kern 1pt} ',t} \right)dl{\kern 1pt} '} = \frac{1}{{N\left( t \right)}}\int_{{{n}_{0}}}^{n\left( l \right)} {\psi \left( {n{\kern 1pt} ',t} \right)dn{\kern 1pt} '} $,

где ${{l}_{0}} = {{l}_{0}}\left( t \right)$ – минимальный размер ($\varphi = 0$ при $l < {{l}_{0}}$),

$N\left( t \right) \equiv \int_{{{l}_{0}}}^{ + \infty } {\varphi \left( {l{\kern 1pt} ',t} \right)dl{\kern 1pt} '} = \int_{{{n}_{0}}}^{ + \infty } {\psi \left( {n,t} \right)dn} $

есть полное число частиц, $n\left( l \right)$ – число молекул фазообразующего вещества в частице размера $l$ (см. (1.6)), ${{n}_{0}} \equiv n\left( {{{l}_{0}}} \right)$ – минимальное значение числа таких молекул. На практике в основном применяются четыре формулы:

– Гордена–Андреева $\theta \left( l \right) = A{{l}^{q}}$(см. [21], [22]),

– Розина–Раммлера–Беннета $\theta \left( l \right) = 1 - \exp ( - A{{l}^{q}})$ (см. [21], [23]),

– нормальное (см. [23], [25], [29]) или

– логарифмически нормальное (см. [24]–[29]) распределения.

В [24], [28], [29] рассматривался вопрос о недостаточности двухпараметричных распределений. В [27], [30] возникают распределения с несколькими модами: разные моды соответствуют разным поколениям агрегатов.

Оказалось, что существует наименьший размер частиц ${{l}_{0}}$, меньше которого агрегатов не наблюдается. Поэтому использование указанных распределений с минимальным размером ${{l}_{0}} = 0$ является нецелесообразным. Кроме того, формулы Розана–Раммлера–Беннета (1934 г.) и Гордена–Андреева (1951 г.) (которая является первыми двумя членами разложения в ряд Маклорена первой из них) содержат, вообще говоря, дробный показатель степени $q$. Обобщение этих формул на случай ${{l}_{0}} > 0$ было рассмотрено в [4]. Но чтобы избежать дробности, можно рассматривать линейные комбинации с целыми показателями степени. Целые значения $q$ соответствовали бы размерности пространства или процесса, согласно (1.2).

Для описания полимерных частиц, представляющих собой поверхности с фиксированным числом активных центров присоединения и распада, оказалось целесообразным использовать следующий класс функций:

Здесь ${{a}_{1}}$, ${{a}_{2}}$, ${{s}_{0}}$ – параметры функции распределения, $s = {{l}^{2}}$ – площадь изображения частицы нанодисперсного вещества, ${{s}_{0}} = {{l}_{0}}^{2}$. В одномерном случае (для цепочек из молекул) площадь изображения пропорциональна $l$. Уравнение (3.1) хорошо аппроксимирует функции распределения частиц, являющихся поверхностями из исходных частиц (с фиксированным числом активных центров). В этом случае $\delta = 2$ в (1.6), и можно переписать (3.1) в следующем виде:

Поэтому, согласно (1.6), мы имеем классы функций

где $\delta = 1,2,3$ соответственно для цепочек, поверхностей и объемов из исходных частиц.

4. СООТНОШЕНИЯ МЕЖДУ ПАРАМЕТРАМИ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ И КОЭФФИЦИЕНТАМИ УРАВНЕНИЯ ТИПА ФОККЕРА–ПЛАНКА

Теперь мы попытаемся, по возможности, связать простые феноменологические формулы из разд. 3 с уравнениями типа Фоккера–Планка из разд. 2 настоящей работы.

Уравнение типа Фоккера–Планка имеет вид

Уравнение (4.1) рассматривается в замкнутой области $n \in \left[ {{{n}_{0}}\left( t \right), + \infty } \right)$, $t \in \left[ {{{t}_{0}}, + \infty } \right)$. Минимальное число составляющих частицу молекул ${{n}_{0}}$ может зависеть от времени, например, через зависимость ${{n}_{0}}$ от температуры: при различных температурах значения ${{n}_{0}}$ могут различаться. При $n < {{n}_{0}}\left( t \right)$ функция распределения обращается в нуль.

Пусть

Для $h\left( n \right)$ мы возьмем выражение

Уточним возможные значения показателя $\sigma $ в (4.3).

Активные центры (места на поверхности частицы, где присоединяются молекулы) представляют собой либо одномерную структуру, либо число активных центров пропорционально площади поверхности, либо число активных молекул на поверхности тела фиксировано. В последнем случае $\sigma = 0$. Для цепочек из молекул, для поверхностей из молекул и для объемных тел может реализовываться этот случай. Кроме того, в случае поверхностей из молекул активные центры могут представлять собой одномерную структуру, тогда $\sigma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$. А для объемных тел, кроме случая $\sigma = 0$, возможно, что $\sigma = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$, когда активные центры представляют собой одномерную структуру, или что $\sigma = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$, когда число активных центров пропорционально площади поверхности.

Во всех случаях $h\left( n \right)$ таково, что для достаточно больших $n$

Уравнение (4.1) с учетом (4.2) перепишем в виде

Сделаем замену переменных

Тогда для функции $\tilde {\psi }\left( {z,\tau } \right) = \psi \left( {n,t} \right)$ получим, что

Подставляя (4.7)–(4.9) в (4.5), имеем уравнение на функцию $\tilde {\psi }\left( {z,\tau } \right) = \psi \left( {n,t} \right)$. Воспользовавшись условиями (4.4) и пренебрегая производными от $h\left( n \right)$, получим существенно более простое уравнение

В случае, когда $\sigma = 0$, замена (4.6) имеет вид

и в точности приводит исходное уравнение (4.1) к уравнению (4.10) (см. [31, с. 309]).

Возьмем следующее решение уравнения (4.10) (см. [31, с. 233]):

и получим выражение для интегральной функции распределения

Итак, мы рассматриваем решение не исходного уравнения (4.1), (4.2), а уравнения, которое имеет простой вид (4.10) в переменных $\tau $, $z$. В исходных переменных (4.10) дает громоздкое (в случае $\sigma \ne 0$) уравнение вида

коэффициенты которого определяются, согласно замене (4.6). Оно дает уравнение (4.1), (4.2) существенно более простого вида, если пренебречь производными от $h\left( n \right)$. Важно отметить, что в случае, когда $\sigma = 0$, мы в точности решаем уравнение (4.1).

Пусть

Тогда

В силу (4.11), (4.6) и (4.12) имеем, что

Учитывая (4.3), перейдем в (4.14) к следующему виду:

где

Поскольку $\tau > 0$, то из (4.6) получаем $h\left( n \right)a + A > 0$. Следовательно, $a > 0$ в силу (4.3) и поэтому $A > - h\left( n \right)a$. Откуда имеем, что

Так как $z \geqslant 0$, то, согласно (4.6) и (4.3), получаем, что

$h\left( n \right)\left( {{{{{n}_{0}}} \mathord{\left/ {\vphantom {{{{n}_{0}}} {h\left( {{{n}_{0}}} \right)}}} \right. \kern-0em} {h\left( {{{n}_{0}}} \right)}} - \int_{{{t}_{0}}}^t {g\left( x \right)dx} + b} \right) + B \geqslant 0$.

Следовательно, в силу (4.3)

$b \geqslant \int_{{{t}_{0}}}^t {g\left( x \right)dx} - {{{{n}_{0}}} \mathord{\left/ {\vphantom {{{{n}_{0}}} {h\left( {{{n}_{0}}} \right)}}} \right. \kern-0em} {h\left( {{{n}_{0}}} \right)}}$,      $B \geqslant h\left( {{{n}_{0}}} \right)\int_{{{t}_{0}}}^t {g\left( x \right)dx} - h\left( {{{n}_{0}}} \right)b - {{n}_{0}}$.

Откуда имеем, что

Если $\sigma = 0$, то, обозначая

из (4.15) получаем

Если возьмем ${{a}_{1}} \equiv - {{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} {\left( {2{{d}_{1}}} \right)}}} \right. \kern-0em} {\left( {2{{d}_{1}}} \right)}}$, ${{a}_{1}}{{a}_{2}} \equiv {1 \mathord{\left/ {\vphantom {1 {\left( {4{{d}_{1}}} \right)}}} \right. \kern-0em} {\left( {4{{d}_{1}}} \right)}}$, то получим функцию распределения (3.2) и

Причем, согласно (4.17)–(4.19), (4.21), имеем ${{a}_{1}}\left( t \right) > 0$ и ${{a}_{2}}\left( t \right) > 0$.

В силу (4.12), (4.13), (4.16), (4.19), (4.21) мы получаем связь между частотными функциями уравнения типа Фоккера–Планка и параметрами моделирующей функции распределения (3.2) в случае $\sigma = 0$:

В общем случае, когда $\sigma $ необязательно равно нулю, получается целесообразным использовать неупрощенную аппроксимирующую функцию распределения (4.15), для которой параметры связаны с частотными функциями уравнения типа Фоккера–Планка (4.1), (4.2) соотношениями

Полученные формулы (4.22), (4.23) связывают феноменологию разд. 5 с уравнением типа Фоккера–Планка разд. 2 настоящей работы.

Согласно определениям (2.5) и (2.6) функций $G$ и $D$, они зависят от времени $t$ только через температуру $T\left( t \right)$ и числа частиц поколений $l$, меньших $k$: ${{N}_{l}}\left( {c,t} \right)$, $l < k$. Если $T\left( t \right)$ и ${{N}_{l}}\left( {c,t} \right)$ постоянны или их изменениями в течение интервала времени $\left[ {t,t + \Delta t} \right]$ можно пренебречь, то, согласно (4.23) (или (4.22) в случае $\sigma = 0$), по двум измерениям в моменты времени $t$ и $t + \Delta t$ мы можем найти значения функций $g$ и $d$ для заданной температуры $T$ и для чисел частиц ${{N}_{l}}\left( {c,t} \right)$: $g = {{n}_{0}}{{\left( {{{c}_{2}}\left( {t + \Delta t} \right) - {{c}_{2}}\left( t \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{c}_{2}}\left( {t + \Delta t} \right) - {{c}_{2}}\left( t \right)} \right)} {\Delta t}}} \right. \kern-0em} {\Delta t}}$, $d = {{n}_{0}}^{2}{{\left( {{{c}_{1}}\left( {t + \Delta t} \right) - {{c}_{1}}\left( t \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{c}_{1}}\left( {t + \Delta t} \right) - {{c}_{1}}\left( t \right)} \right)} {\Delta t}}} \right. \kern-0em} {\Delta t}}$.

Меняя условия системы: рассматривая различные значения $T$ и ${{N}_{l}}\left( {c,t} \right)$, и вычисляя в каждом случае значения функций $g$ и $d$, мы можем получить сами эти функции как зависимости от $T$ и проверить линейность зависимости $G$ и $D$ от ${{N}_{l}}\left( {c,t} \right)$ в (2.5) и (2.6).

5. ОЦЕНКИ ДЛЯ ПАРАМЕТРОВ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ

Для вычисления оптимальных значений параметров на компьютере нужно задать априорный диапазон изменения параметров.

В разд. 4 мы получили, что для функции (3.2) (или (3.1))

а для параметров функции (4.15) имеют место оценки (4.17), (4.18).

В настоящем разделе мы уточним (улучшим) оценки (5.1).

Итак, рассмотрим функцию (3.2) (или (3.1)):

и обозначим через ${{Z}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ медиану, т.е. точку, где она принимает значение ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, т.е. половина всех частиц дает значение $Z$ меньшее, чем ${{Z}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, а половина – большее: Из (5.3) находим, что

Пусть мы имеем оценку для ${{Z}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$:

$Z_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{\min }}$ можно взять равным, например, ${{{{s}_{m}}} \mathord{\left/ {\vphantom {{{{s}_{m}}} {\left( {2{{s}_{0}}} \right)}}} \right. \kern-0em} {\left( {2{{s}_{0}}} \right)}}$, где ${{s}_{m}}$ – площадь изображения одной молекулы, а $Z_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{\max }}$ оценить, например, значением ${{10}^{2}}$: медианное значение площади частицы не превосходит минимальное значение больше, чем в сто раз. Более точные значения $Z_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{\min }}$ и $Z_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{\max }}$ можно получить из рассматриваемых экспериментальных данных.

В силу (5.4) и (5.5) имеем

Из формул (5.6), (5.7) видно, что проще и лучше рассматривать получение оценок в переменных ${{a}_{1}}$, ${{a}_{1}}{{a}_{2}}$: в этих переменных все неравенства задают полуплоскости.

Из неравенств (5.1), (5.6) получаются следующие оценки параметров:

Неравенство (5.7) не улучшает полученных оценок.

Обозначим через $\tilde {Z}$ точку перегиба функции (5.2), ее значение определяется равенством ${{{{\partial }^{2}}\theta } \mathord{\left/ {\vphantom {{{{\partial }^{2}}\theta } {\partial {{Z}^{2}}}}} \right. \kern-0em} {\partial {{Z}^{2}}}} = 0$:

Точка перегиба может быть у функции (5.2), когда $\tilde {Z} > 0$ или

или отсутствовать при $\tilde {Z} \leqslant 0$ или

В случае (5.9) имеем следующие улучшенные оценки:

А в случае (5.10) имеем

Аналогично, можно получить оценки параметров и для функции (4.15).

6. СРАВНЕНИЕ ТЕОРИИ С ЭКСПЕРИМЕНТОМ

В [32] анализ эффекта теплового разброса средних размеров наночастиц ниосом (представляющих собой поверхностно-активные вещества) обнаружил тенденцию к уменьшению их диаметра при увеличении температуры. Ниосомы (поверхностно активные частицы, нерастворимые в воде), которые подвергли тепловой обработке, становились более устойчивыми и сохраняли средний размер частиц около 100 нм (фиг. 1 и 2). Этот подход может быть рекомендован для дальнейшего улучшения методов приготовления и хранения лекарственных форм.

Мы аппроксимировали экспериментальные данные из [32] (точки на фиг. 1 и 2) интегральными функциями распределения (3.3) или (4.15) c $\sigma = 0$ при $\delta = 3$ (фиг. 1) и (4.15) c $\sigma = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ при $\delta = 3$ (фиг. 2). Во втором случае мы пренебрегли отличием ${{C}_{1}}\left( t \right)$ и ${{C}_{2}}\left( t \right)$ от нуля, чтобы не увеличивать число параметров в (4.15) по сравнению с (3.3). Значения остальных параметров представлены в табл. 1. В первом случае мы получили плохую аппроксимацию, а во втором – хорошую. Это соответствует тому, что ниосомы представляют собой поверхностно-активные вещества. Итак, мы получили для этих экспериментальных данных, что коэффициенты уравнения типа Фоккера–Планка зависят не только от времени, но и от числа молекул $n$, составляющих частицы.

Оказалось, что доступными для определения стали трехпараметрические функции типа (4.15), (4.20), которые более информативны, чем обычно используемые нормальное и логнормальное распределения, а также распределения Розана–Раммлера–Беннета и Гордена–Андреева. На доступность трехпараметрических функций распределения указывают, в частности, опубликованные в [32] данные об изменении свойств нановезикул–ниосом при их нагревании до разных температур. Обработка этих данных показала, что изученные ниосомы были распределены по размеру (фиг. 2) в соответствии с функцией распределения (4.15) с $\delta = 3$ и $\sigma = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$.

ЗАКЛЮЧЕНИЕ И ОБСУЖДЕНИЕ

В разд. 2 мы осуществили переход от дискретных уравнений к континуальному уравнению баланса числа частиц, учитывающему возможность их укрупнения и распада.

В разд. 3 мы рассмотрели основные известные и новые моделирующие (аппроксимирующие) функции распределения и их параметры. Такие функции, получаемые в экспериментах, не являются стационарными решениями рассматриваемой системы уравнений. Поэтому в разд. 4 мы нашли точные решения уравнения типа Фоккера–Планка, которые в каждый момент времени дают функции распределения частиц дисперсного вещества из разд. 3, и научились находить частотные функции по параметрам моделирующих функций распределения.

В разд. 5 получены оценки для параметров аппроксимирующих функций распределения. Они нужны для того, чтобы вычислить оптимальные значения параметров на компьютере, поскольку для этого требуется задать априорный диапазон изменения параметров.

Отметим, что рассмотрение H-теоремы для нелинейных систем с дискретным временем, в частности, даже для дискретных моделей уравнения Больцмана (см. [33], [34]) и для системы уравнений Беккера–Дёринга, является крайне важной задачей, поскольку компьютерное моделирование играет принципиальную роль при решении проблемы создания новых материалов. В линейном случае переход от непрерывного времени к дискретному дает переход от марковского процесса к марковской цепи, и H-теорема выполняется и изучена в этом случае (см. [35] и ссылки в ней, [37]). В нелинейном случае для явной дискретизации по времени она выполняется в редких случаях (см. [17], [18]), а для неявной она исследована в [17], [19], [37]. Диффузное приближение широко используется для моделирования процессов кристаллизации (см. [3], [4]). Однако мы доказали, что для рассматриваемого нелинейного уравнения типа Фоккера–Планка (2.4)–(2.6) H-теорема, вообще говоря, неверна (см. [37]). Но уравнения типа Фоккера–Планка (2.4)–(2.6), тем не менее, хорошо описывают эксперименты, поскольку в них функция распределения сдвигается и расплывается в пространстве свойств. Для расчетов на компьютере лучше использовать их дискретные аналоги, о которых мы говорили и для которых H-теорема исследована, как обсуждалось в настоящей работе (см. [18]–[20], [37]). Однако в эксперименте не удается измерить дискретную функцию распределения. Именно поэтому уравнения типа Фоккера–Планка так любят использовать химики. А надо использовать уравнения на гистограммные дискретные функции распределения, аналогичные c точностью до коэффициентов, рассмотренным дискретным аналогам, но это, возможно, тема для отдельной небольшой статьи.

Характерные особенности, которые возникли при решении задачи, обсуждаемой в настоящей работе, – это (1) существование минимального размера и (2) самоподобие функций распределения дисперсного вещества независимо от того, эволюция какого типа агрегатов рассматривается. Первый пункт мы учли, когда предлагали новые моделирующие функции распределения. Оба этих пункта нуждаются в обосновании.

В настоящей работе во всех разделах мы обобщаем результаты обзорной статьи [38].