1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 3, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 3, стр. 437-441

Задача Авалос–Триггиани для линейной системы Осколкова и системы волновых уравнений

Г. А. Свиридюк 1, *, Т. Г. Сукачева 2, 1, **

1 ЮУрГУ (НИУ)
454080 Челябинск, пр-т В.И. Ленина, 76, Россия

2 НовГУ им. Ярослава Мудрого
173003 Великий Новгород, ул. Большая Санкт-Петербургская, 41, Россия

* E-mail: ridyu@mail.ru
** E-mail: tamara.sukacheva@novsu.ru

Поступила в редакцию 20.05.2021
После доработки 20.05.2021
Принята к публикации 12.10.2021

Полный текст (PDF)

Аннотация

Исследуется задача Авалос–Триггиани для системы волновых уравнений и линейной системы Осколкова. На основе метода, предложенного авторами указанной задачи, доказана теорема существования единственного решения задачи Авалос–Триггиани. Математическая модель содержит линейную систему Осколкова, описывающую течение несжимаемой вязкоупругой жидкости Кельвина–Фойгта нулевого порядка, и волновое векторное уравнение, соответствующее некоторой структуре, погруженной в указанную жидкость. Библ. 17. Фиг. 1.

Ключевые слова: задача Авалос–Триггиани, несжимаемая вязкоупругая жидкость, линейная система Осколкова.

1. ВВЕДЕНИЕ

А.П. Осколковым изучались начально-краевые задачи для уравнений, описывающих движение вязкоупругих жидкостей, “которые способны к релаксации напряжений при деформировании или проявляют феномен задержанного развития деформаций после снятия напряжений” [1]. Связь тензора напряжений $\sigma $ и тензора скоростей деформаций $D$ определяет тип жидкости. Соотношение между $\sigma $ и $D,$ называемое определяющим или реологическим, имеет вид

$\left( {1 + \sum\limits_{l = 1}^L \,{{\lambda }_{l}}\frac{{{{\partial }^{l}}}}{{\partial {{t}^{l}}}}} \right)\sigma = 2\nu \left( {1 + \sum\limits_{m = 1}^M \,{{\kappa }_{m}}{{\nu }^{{ - 1}}}\frac{{{{\partial }^{m}}}}{{\partial {{t}^{m}}}}} \right)D - pE,$
где $\{ {{\lambda }_{l}}\} ,\;l = 1, \ldots ,L$ – времена релаксаций, $\{ {{\kappa }_{m}}\} ,\;m = 1, \ldots ,M$ – времена запаздывания, $p$ – давление жидкости.

Простейшими из них являются жидкости Максвелла $(L = 1,\;M = 0),$ жидкости Кельвина–Фойгта $(L = 0,\;M = 1)$ и жидкости Олдройта $(L = M = 1).$ В жидкостях Максвелла напряжения после прекращения движения уменьшаются как $exp( - t\mathop {{{\lambda }_{1}}}\nolimits^{ - 1} ),$ в жидкостях Кельвина–Фойгта при снятии напряжений скорость деформации уменьшается как $exp( - t\mathop {{{\kappa }_{1}}}\nolimits^{ - 1} ),$ а в жидкостях Олдройта наблюдается как экспоненциальное релаксирование напряжений, так и экспоненциальное запаздывание деформаций.

Подстановкой соответствующего реологического соотношения в уравнения движения несжимаемой жидкости

${{u}_{t}} + (u \cdot \nabla )u = \nabla \sigma + f,\quad \nabla \cdot u = 0,$
в [2] получена система, представляющая собой обобщение знаменитой системы уравнений Навье–Стокса [3], в которую она переходит при $L = M = 0.$

А.П. Осколков (см. [4], [5]) исследовал разрешимость в гёльдеровых и соболевских пространствах начально-краевой задачи в цилиндре $\Omega \times (0,T)$

$u(x,0) = {{u}_{0}}(x),\quad x \in \Omega ,\quad u(x,t) = 0,\quad (x,t) \in \partial \Omega \times (0,T),$
для линейного уравнения
$(\lambda - {{\nabla }^{2}}){{u}_{t}} = \nu {{\nabla }^{2}}u - \nabla p + f,\quad \nabla \cdot u = 0.$
Здесь $\nu $ – положительный параметр, $\lambda > - {{\lambda }_{1}}$ (${{\lambda }_{1}}$ – наименьшее собственное число спектральной задачи $ - {{\nabla }^{2}}{v} + \nabla p = \lambda {v},$ $\nabla \cdot {v} = 0,$ ${v} = 0$ на $\partial \Omega $).

В [2], [4] исследована разрешимость в пространстве ${{L}^{2}}(\Omega )$ начально-краевой задачи для “квазилинейной” системы уравнений

$(\lambda - {{\nabla }^{2}}){{u}_{t}} = \nu {{\nabla }^{2}}u - (u \cdot \nabla )u - \nabla p + f,\quad \nabla \cdot u = 0,$
в цилиндре $\Omega \times (0,T),$ $n = 2,3,4$ при $\lambda > - {{\lambda }_{1}}.$

Далее А.П. Осколков вместе с учениками (см., например, [6]) построил теорию глобальной разрешимости на $[0,\infty ]$ начально-краевых задач для течений жидкостей Олдройта ($n = 2$) и жидкостей Кельвина–Фойгта ($n = 3$), на основе которой возникла теория аттракторов и динамических систем, порождаемых этими начально-краевыми задачами. Ими были получены глобальные априорные оценки на полуоси для решений уравнений движения жидкостей Олдройта и жидкостей Кельвина–Фойгта.

В [7] уравнение движения жидкостей Кельвина–Фойгта сводится к операторному уравнению

для которого исследуется ряд нелокальных проблем.

Ранее авторами с помощью метода фазового пространства исследовалась первая начально-краевая задача для полученных Осколковым уравнений, описывающих движение вязкоупругих несжимаемых жидкостей Кельвина–Фойгта различного порядка. Основы таких исследований в автономном случае были заложены в статье [8], а в неавтономном случае в [9]. Эти работы явились основополагающими для построения теории разрешимости задачи Коши для полулинейного автономного и неавтономного уравнения соболевского типа. В качестве приложений этих теорий были изучены начально-краевые задачи для уравнений, полученных А.П. Осколковым. Поэтому такие уравнения мы называем “уравнениями Осколкова”. Начально-краевые задачи для порожденных уравнениями Осколкова уравнений магнитогидродинамики в автономном случае исследовались в [10], а в неавтономном в [11].

Заметим, что все указанные модели изучались в рамках теории разрешимости задачи Коши для уравнений соболевского типа. И в настоящее время теория таких уравнений развивается во многих направлениях, что подтверждают, например, работы [14]–[16]. В данной работе для вязкоупругой жидкости Кельвина–Фойгта, движение которой описывается соответствующей системой уравнений Осколкова, исследуется задача Авалос–Триггиани [12], [13].

В этих работах авторы получили теорему существования единственного решения для системы волновых уравнений и линейной системы Навье–Стокса. Мы изучаем указанную задачу Авалос–Триггиани с заменой в ней вязкой жидкости на вязкоупругую жидкость Кельвина–Фойгта. Рассматриваемая задача ставится и исследуется впервые. Перейдем теперь к постановке задачи.

2. ПОСТАНОВКА ЗАДАЧИ

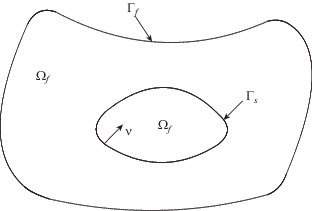
Пусть $\Omega $ – ограниченная область в ${{R}^{n}},\;n = 2,3,$ с достаточно гладкой границей $\partial \Omega .$ Пусть $u = \operatorname{col} ({{u}_{1}},{{u}_{2}},...,{{u}_{n}})$ есть n-мерный вектор скорости $n = 2,3$, скалярная функция $p$ – давление, а вектор $w = {\text{col}}({{w}_{1}}.{{w}_{2}},...,{{w}_{n}})$ – вектор смещения тела, занимающего область ${{\Omega }_{s}},$ и погруженного в жидкость, занимающую область ${{\Omega }_{f}}.$

Таким образом, $\Omega = {{\Omega }_{s}} \cup {{\Omega }_{f}},$ ${{\bar {\Omega }}_{s}} \cup {{\bar {\Omega }}_{f}} = \partial {{\Omega }_{s}} \equiv {{\Gamma }_{s}},$ – общая граница ${{\Omega }_{s}}$ и ${{\Omega }_{f}}$. Внешнюю границу области ${{\Omega }_{f}}$ обозначим через ${{\Gamma }_{f}}$ (см. фиг. 1).

Фиг. 1.

Физическая модель.

Наша цель: исследовать задачу Авалос–Триггиани [12], [13] для случая, когда жидкость в ${{\Omega }_{f}}$ является несжимаемой вязкоупругой жидкостью Кельвина–Фойгта нулевого порядка [5]. Рассматриваемая математическая модель определяется системой

(1)
$(1 - \kappa {{\nabla }^{2}}){{u}_{t}} - \nu {{\nabla }^{2}}u + \nabla p = 0\quad \forall (t,x) \in (0,T) \times {{\Omega }_{f}},$
(2)
$\nabla \cdot u = 0\quad \forall (t,x) \in (0,T) \times {{\Omega }_{f}},$
(3)
${{w}_{{tt}}} - {{\nabla }^{2}}w + w = 0\quad \forall (t,x) \in (0,T) \times {{\Omega }_{s}}$
с краевыми условиями
(4)
${{\left. u \right|}_{{{{\Gamma }_{f}}}}} \equiv 0\quad \forall (t,x) \in (0,T) \times {{\Gamma }_{f}},$
(5)
$u \equiv {{w}_{t}}\quad \forall (t,x) \in (0,T) \times {{\Gamma }_{s}},$
(6)
$\frac{{\partial u}}{{\partial \nu }} - \frac{{\partial w}}{{\partial \nu }} = p\nu \quad \forall (t,x) \in (0,T) \times {{\Gamma }_{s}}$
и начальным условием
(7)
$(w(0, \cdot ),{{w}_{t}}(0, \cdot ),u(0, \cdot )) = ({{w}_{0}},{{w}_{1}},{{u}_{0}}) \in {\mathbf{H}},$
где ${\mathbf{H}} = {{({{H}^{1}}({{\Omega }_{s}}))}^{n}} \times {{({{L}^{2}}({{\Omega }_{s}}))}^{n}} \times {{\mathcal{H}}_{f}}$ и ${{\mathcal{H}}_{f}} = \{ f \in {{({{L}^{2}}({{\Omega }_{s}}))}^{n}}:\nabla \cdot f = 0$ в ${{\Omega }_{f}}$ и ${{\left. {[f \cdot \nu ]} \right|}_{{{{\Gamma }_{f}}}}} = 0\} .$

В системе (1) параметры $\kappa $ и $\nu $ характеризуют упругие и вязкие свойства жидкости соответственно. В случае $\kappa = 0$ задача (1)–(3) исследовалась в работах [12], [13]. Случай $\kappa \ne 0$ рассматривается впервые.

3. РЕДУКЦИЯ К АБСТРАКТНОЙ ЗАДАЧЕ КОШИ

Следуя [12], [13], будем считать, что $p(t)$ удовлетворяет следующей эллиптической задаче:

(8)
$\begin{array}{*{20}{c}} {\Delta p = 0\quad {\text{в}}\quad {{\Omega }_{f}},} \\ {p = \frac{{\partial u}}{{\partial \nu }} \cdot \nu - \frac{{\partial w}}{{\partial \nu }} \cdot \nu \quad {\text{на}}\quad {{\Gamma }_{s}},} \\ {\frac{{\partial p}}{{\partial \nu }} = \Delta u \cdot \nu \quad {\text{на}}\quad {{\Gamma }_{f}}.} \end{array}$

Тогда давление $p$ может быть представлено в виде

$p(t) = {{D}_{s}}\left\{ {{{{\left( {\frac{{\partial u(t)}}{{\partial \nu }} \cdot \nu - \frac{{\partial w(t)}}{{\partial \nu }} \cdot \nu } \right)}}_{{{{\Gamma }_{s}}}}}} \right\} + {{N}_{f}}(\mathop {(\Delta u(t) \cdot \nu )}\nolimits_{{{\Gamma }_{f}}} )\quad {\text{в}}\quad {{\Omega }_{f}};$
где отображение Дирихле (“Dirichlet” map) ${{D}_{s}}$ определяется соотношениями
$h = {{D}_{s}}(g) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\Delta h = 0\quad {\text{в}}\quad {{\Omega }_{f}},} \\ {h = g\quad {\text{на}}\quad {{\Gamma }_{s}},} \\ {\frac{{\partial h}}{{\partial \nu }} = 0\quad {\text{на}}\quad {{\Gamma }_{f}},} \end{array}} \right.$
а отображение Неймана (“Neumann” map) ${{N}_{f}}$ определяется соотношениями
$h = {{N}_{f}}(g) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\Delta h = 0\quad {\text{в}}\quad {{\Omega }_{f}},} \\ {h = 0\quad {\text{на}}\quad {{\Gamma }_{s}},} \\ {\frac{{\partial h}}{{\partial \nu }} = g\quad {\text{на}}\quad {{\Gamma }_{f}}.} \end{array}} \right.$
Тогда исходная система (1)–(3), описывающая взаимодействие жидкости и тела, погруженного в нее, примет вид
(9)
$(1 - \kappa {{\nabla }^{2}}){{u}_{t}} - \nu {{\nabla }^{2}}u + {{G}_{1}}w + {{G}_{2}}w = 0\quad \forall (t,x) \in (0,T) \times {{\Omega }_{f}},$
(10)
$\nabla \cdot u = 0\quad \forall (t,x) \in (0,T) \times {{\Omega }_{f}},$
(11)
${{w}_{{tt}}} - {{\nabla }^{2}}w + w = 0\quad \forall (t,x) \in (0,T) \times {{\Omega }_{s}}$
с краевыми условиями
(12)
${{\left. u \right|}_{{{{\Gamma }_{f}}}}} \equiv 0\quad \forall (t,x) \in (0,T) \times {{\Gamma }_{f}},$
(13)
$u \equiv {{w}_{t}}\quad \forall (t,x) \in (0,T) \times {{\Gamma }_{s}},$
где

${{G}_{1}}u \equiv \nabla \left\{ {{{D}_{s}}\left\{ {{{{\left( {\frac{{\partial w(t)}}{{\partial \nu }} \cdot \nu } \right)}}_{{{{\Gamma }_{s}}}}}} \right\}} \right\},$
${{G}_{2}}u \equiv - \nabla \left\{ {{{D}_{s}}\left\{ {{{{\left( {\frac{{\partial u(t)}}{{\partial \nu }} \cdot \nu } \right)}}_{{{{\Gamma }_{s}}}}}} \right\} + {{N}_{f}}(\mathop {(\Delta u(t) \cdot \nu )}\nolimits_{{{\Gamma }_{f}}} )} \right\}.$

Задачу (9)–(13), в которой исключено давление, запишем в виде абстрактной задачи Коши,

(14)
$L\dot {v} = Mv,\quad v(0) = {{v}_{0}},$
где операторы $L$ и $M$ определяются матрицами
$L: = \left( {\begin{array}{*{20}{c}} I&O&O \\ O&I&O \\ O&O&{{{A}_{\kappa }}} \end{array}} \right),$
$M: = \left( {\begin{array}{*{20}{c}} O&I&O \\ {\Delta - I}&O&O \\ {{{G}_{1}}}&O&{\nu \Delta + {{G}_{2}}} \end{array}} \right).$
Здесь ${v} = \operatorname{col} (w,{{w}_{t}},u),$ ${{A}_{\kappa }} = 1 - \kappa {{\nabla }^{2}},$ $I$ – единичный оператор, область определения которого ясна из контекста. При условии обратимости оператора $L$ задача (14) сводится к абстрактной задаче Коши:
(15)
${\dot {v}} = A{v},\quad {v}(0) = {{{v}}_{0}},$
где оператор $A = {{L}^{{ - 1}}}M.$

К задаче (15) применимы все результаты, полученные в [12], [13].

В заключение отметим, что в [17] и других работах О.А. Олейник построена математическая теория уравнений пограничного слоя для двумерных стационарных и нестационарных течений несжимаемой вязкой жидкости. Причем предложенные автором методы применимы также в случае сжимаемой жидкости и для трехмерных течений. Доказаны теоремы существования решений основных задач теории пограничного слоя, теоремы единственности, исследована устойчивость решений при разного типа возмущениях, указаны простые способы построения приближенных решений и доказана их сходимость к точным решениям.

Список литературы

  1. Осколков А.П. О нестационарных течениях вязкоупругих жидкостей // Тр. матем. ин-та АН СССР. 1983. № 159. С. 101–130.

  2. Осколков А.П. О некоторых нестационарных линейных и квазилинейных системах, встречающихся при изучении движения вязких жидкостей // Зап. науч. семин. ЛОМИ АН СССР. 1976. Т. 59. С. 133–177

  3. Ладыженская О.А. Математические вопросы динамики вязкой несжимаемой жидкости. М.: Наука, 1970. 288 с.

  4. Осколков А.П. К теории жидкостей Фойгта // Зап. науч. сем. ЛОМИ. 1980. Т. 96. С. 233–236.

  5. Осколков А.П. Начально-краевые задачи для уравнений движения жидкостей Кельвина–Фойгта и Олдройта // Тр. Матем. ин-та АН СССР. 1988. Т. 179. С. 126–164.

  6. Осколков А.П., Ахматов М.М., Котсиолис А.А. Об уравнениях движения линейных вязкоупругих жидкостей и уравнениях фильтрации жидкостей с запаздыванием // Зап. науч. семин. ЛОМИ АН СССР. 1987. Т. 163. С. 132–136.

  7. Осколков А.П. Нелокальные проблемы для одного класса нелинейных операторных уравнений, возникающих в теории уравнений типа С.Л. Соболева // Зап. науч. семин. ЛОМИ. 1991. Т. 198. С. 31–48.

  8. Свиридюк Г.А., Сукачева Т.Г. Фазовые пространства одного класса операторных уравнений // Дифференц. ур-ния. 1990. Т. 26. № 2. С. 250–258.

  9. Свиридюк Г.А., Сукачева Т.Г. О разрешимости нестационарной задачи динамики несжимаемой вязкоупругой жидкости // Матем. заметки. 1998. Т. 63. № 3. С. 442–450.

  10. Кондюков А.О., Сукачева Т.Г. Фазовое пространство начально-краевой задачи для системы Осколкова ненулевого порядка // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 5. С. 823–829.

  11. Kondyukov A.O., Sukacheva T.G. A Non-stationary Model of the Incompressible Viscoelastic Kelvin-Voigt Fluid of Non-zero Order in the Magnetic Field of the Earth // Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software. 2019. V. 12. № 3. P. 42–51.

  12. Avalos G., Lasiecka I., Triggiani R. Higher regularity of a coupled parabolic-hyperbolic fluid-structure interactive system // Georgian Mathematical Journal. 2008. V. 15 . № 3. P. 403–437.

  13. Avalos G., Triggiani R. J.Backward uniqueness of the s.c. semigroup arising in parabolic–hyperbolic fluid–structure interaction // Differential Equations. 2008. V. 245. P. 737–761.

  14. Vasyuchkova K.V., Manakova N.A., Sviridyuk G.A. Some Mathematical Models with a Relatively Bounded Operator and Additive “White Noise” // Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software. 2017. T. 10. № 4. C. 5–14.

  15. Sviridyuk G.A., Zamyshlyaeva A.A., Zagrebina S.A. Multipoint Initial-Final Value for one class of Sobolev Type Models of Higher Order with Additive “White Noise” // Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software. 2018. T. 11. № 3. C. 103–117.

  16. Favini A., Zagrebina S.A., Sviridyuk G.A. Multipoint Initial-Final Value Problems for Dinamical Sobolev-Type Equations in the Space of Noises // Electronic Journal of Differential Equations. 2018. V. 2018. № 128, pp. 1–10. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu https://ejde.math.txstate.edu/Volumes/2018/128/favini.pdf

  17. Олейник О.А. О системе уравнений теории пограничного слоя // Ж. вычисл. матем. и матем. физ. 1963. Т. 3. № 3. С. 489–507. U.S.S.R. Comput. Math. Math. Phys., 3:3 (1963), 650–673.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал