Журнал вычислительной математики и математической физики, 2022, T. 62, № 5, стр. 742-756
Алгоритм разделения матричного спектра относительно угла
Э. А. Бибердорф *
Институт математики им. С.Л. Соболева СО РАН
630090 Новосибирск, пр-т Акад. Коптюга, 4, Россия
* E-mail: biberdorf@ngs.ru
Поступила в редакцию 21.09.2021
После доработки 12.11.2021
Принята к публикации 14.01.2022
- EDN: RPZLUI
- DOI: 10.31857/S0044466922050027
Аннотация
Представлен алгоритм разделения спектра относительно кусочно-гладкой кривой, а именно относительно угла. В работе дано полное описание задачи и ее решения, начиная от постановки и краткого изложения теоретических основ базовых алгоритмов дихотомии и заканчивая численными примерами использования алгоритма дихотомии матричного спектра относительно угла. Библ. 29. Фиг. 4. Табл. 1.
ВВЕДЕНИЕ
В данной работе предлагается алгоритм для решения задачи о расположении спектра относительно некоторого угла. Эта проблема связана с исследованиями так называемых секториальных операторов, спектр которых находится внутри определенного сектора комплексной плоскости. В частности, к секториальным относятся многие дифференциальные операторы (см. [1]). Параметрами сектора определяется скорость роста или убывания в зависимости от времени решений уравнений с оператором такого типа [2].
Структура работы следующая. В первом разделе обсуждаются особенности различных постановок спектральных задач для несимметричных матриц, связанные с чувствительностью собственных значений к возмущению матрицы. В разд. 2 приведен ряд фактов, на которых основаны простейшие алгоритмы дихотомии. Далее, в разд. 3 описаны способы решения вспомогательных задач и введены необходимые обозначения. В разд. 4 дано обоснование алгоритма дихотомии относительно угла. Затем (разд. 5) приведены примеры его использования. В частности, показано применение алгоритма к спектральной задаче для оператора Орра-Зоммерфельда для плоскопараллельного течения Пуазейля.
1. ПОСТАНОВКИ СПЕКТРАЛЬНЫХ ЗАДАЧ
1.1. Роль псевдоспектра при решении прикладных задач
Информация о спектрах линейных операторов необходима для решения большого круга прикладных задач. Постановки многих из них (например, задач устойчивости) обладают общими специфическими свойствами. В частности, для решения таких задач не требуется определения каждого собственного значения в отдельности. Вместо этого нужна информация о расположении групп собственных значений в определенных областях комплексной плоскости (например, областях устойчивости и неустойчивости).
Другое общее свойство прикладных задач связано с тем, что модуль непрерывности собственных значений несимметричных операторов ведет себя непредсказуемым образом. Для его исследования вводится понятие ε-спектра или псевдоспектра ${{\Lambda }_{\varepsilon }}(A)$ (см. [1], [3]). По определению к ε-спектру $n \times n$ матрицы A относятся те комплексные числа λ, для которых матрица $A - \lambda {{I}_{n}}$ “почти вырождена”
где ${{I}_{n}}$ – единичная матрица, ${{\sigma }_{{\min }}}$ – минимальное сингулярное число.Визуализировать структуру $\varepsilon $-спектра можно, изображая график функции
например, с помощью линий уровня (см. примеры в разд. 5).Размеры пятен ε-спектра определяют, насколько могут отличаться собственные значения $\left| {{{\lambda }_{j}}(A) - {{\lambda }_{j}}(A + \Delta A)} \right|$ исходной и возмущенной матриц, $\left\| A \right\| \leqslant \varepsilon $. Расположением пятен объясняются на первый взгляд парадоксальные примеры, когда решения системы $y{\text{'}} = Ay$ устойчивы, а возмущенной системы $y{\text{'}} = (A + \Delta A)y$ – неустойчивы. Этим же объясняется тот факт, что решения устойчивых систем могут на начальных временных интервалах показывать большой рост (“практическая” неустойчивость), что на практике может приводить к разрушениям инженерных конструкций, развитию турбулентности течений и т.д. [4].
Таким образом, для решения прикладных задач знания расположения точек спектра недостаточно, необходима информация о расположении и параметрах спектральных пятен. Нетрудно заметить, что спектральная задача в классической постановке ориентирована именно на вычисление отдельных собственных значений. То есть с точки зрения приложений она с одной стороны избыточна, а с другой стороны – недостаточна.
1.2. Исследования псевдоспектра и критерии расположения спектра в заданной области
Движение в сторону альтернативных постановок задач можно видеть во многих работах. Так, целый ряд статей посвящен методам изображения псевдоспектра. С точки зрения вычислений это весьма затратная процедура. Поэтому предпринимаются попытки создать более быстрые алгоритмы для вычисления некоторого приближения к функции (1.1) (см., например, [5]). Авторы других работ концентрируются на конкретных операторах и численно исследуют, какие из собственных значений наименее устойчивы к возмущению матрицы [6]. Заметим, что изображение псевдоспектра матрицы не гарантирует, что на нем будут видны все собственные значения, лежащие в данной области. Некоторые пятна ε-спектра могут быть настолько небольшими, что их легко пропустить при вычислении значений функции (1.1) даже на сетке с довольно мелкой ячейкой.
Другой подход может быть связан с подбором некоторого численного критерия (или критериев), который определенным образом характеризует часть спектра, находящуюся в фиксированной области в целом. В качестве известного примера можно привести теорему Раусса-Гурвица о том, что все корни полинома с вещественными коэффициентами лежат строго в левой полуплоскости тогда и только тогда, когда положительны все главные миноры матрицы Гурвица [7]. Этот факт является одним из многих результатов, связывающих расположение корней полиномов и свойства определенных матриц и знакопеременных квадратичных форм, собранных в подробном обзоре [8]. В частности, там упоминается работа [9] о расположении всех корней полинома в угловой области $ - \theta < {\text{arg}}\;x < \theta $.
Для конструирования других критериев можно использовать свойства некоторых интегралов по контуру $\gamma $, ограничивающему заданную область. Например, нетрудно установить, что матрица
является проектором на инвариантное подпространство матрицы A, соответствующее собственным значениям ${{\lambda }_{j}}(A)$, лежащим внутри контура γ. Причем след проектора равен числу этих собственных значений с учетом кратности [1]. Можно сказать, что этот факт является матричным вариантом принципа аргумента.Однако при вычислении перечисленных критериев также могут возникать проблемы вплоть до ложного результата, связанные с расположением пятен псевдоспектра вблизи границы области.
1.3. Задача дихотомии матричного спектра
К конструктивному решению проблемы новой постановки спектральной задачи подошла научная группа под руководством С.К. Годунова. Ими была сформулирована задача о дихотомии матричного спектра. Суть ее состоит в том, чтобы определить
1) есть ли на заданной кривой точки спектра матрицы,
2) если на кривой отсутствуют точки спектра, определить базисы инвариантных подпространств матрицы, соответствующие собственным значениям, находящимся по разные стороны от кривой, и привести матрицу к клеточно-диагональному виду.
Заметим, что сходство названия задачи с ε-дихотомией пространства решений дифференциальных уравнений, описанной в [10], неслучайно, так как и в том и в другом случае производится разделение пространства на прямую сумму подпространств.
При этом критерием дихотомии и ответом на первый вопрос задачи является (возможно, с дополнительной нормировкой) интеграл
(1.3)
$H = \oint\limits_\gamma {{{{(\lambda {{I}_{n}} - A)}}^{{ - 1}}}} {{\left( {\bar {\lambda }{{I}_{n}} - A{\kern 1pt} *} \right)}^{{ - 1}}}d\lambda ,$Несмотря на то что в основе метода лежат контурные интегралы, для их определения не используется численное интегрирование. Вместо этого алгоритм представляет собой последовательность итераций, состоящих из QR-разложения и других матричных операций. Сходимость итераций связана с величиной H и зависит от тех спектральных пятен, которые пересекают границу области. А значит, в процессе выполнения алгоритма диагностируется ситуация, когда псевдоспектр может критически повлиять на результат. Подробнее см. в следующем разделе.
В данный момент разработаны алгоритмы дихотомии относительно окружности и мнимой оси, которые можно назвать базовыми, так как они являются основной составляющей частью всех других алгоритмов дихотомии [12]–[17]. Кроме того, существуют алгоритмы дихотомии относительно кривых второго порядка [18]–[20] и алгоритм дихотомии корней полинома относительно окружности [21]. Более подробный обзор алгоритмов дихотомии и их приложений представлен в статье [22].
2. БАЗОВЫЕ АЛГОРИТМЫ
2.1. Математическая основа
В данном разделе мы представим обоснование алгоритма дихотомии относительно единичной окружности, опираясь исключительно на свойства решений краевых задач для линейных разностных уравнений
(2.1)
$\begin{gathered} {{U}_{{j + 1}}} = A{{U}_{j}} + {{f}_{j}},\quad \left\| {{{f}_{j}}} \right\| \leqslant C < \infty , \\ \left\| {{{U}_{j}}} \right\| \leqslant C < \infty ,\quad - \infty < j < \infty \\ \end{gathered} $(2.2)
$\begin{gathered} {{G}_{{k + 1}}} = A{{G}_{k}},\quad k \ne 0, \\ {{G}_{1}} = A{{G}_{0}} + {{I}_{n}}, \\ \left\| {{{G}_{k}}} \right\| \leqslant C \leqslant \infty ,\quad - \infty < k < \infty . \\ \end{gathered} $Заметим, что утверждения, которые будут приведены ниже, в известной степени аналогичны утверждениям о разрешимости краевой задачи для системы линейных обыкновенных дифференциальных уравнений, заданной на бесконечном интервале (см. [14], [23]–[25]), правда, в последнем случае спектр разделяется относительно мнимой оси.
В первую очередь поставим вопрос об условиях единственности решений (2.1) и (2.2). Для ответа на него используется следующая лемма о разрешимости однородной задачи:
Лемма 1. Однородная краевая задача
(2.3)
$\begin{gathered} U_{{j + 1}}^{{[{\text{од}}]}} = AU_{j}^{{[{\text{од}}]}}, \\ \left\| {U_{j}^{{[{\text{од}}]}}} \right\| \leqslant C < \infty ,\quad - \infty < j < \infty , \\ \end{gathered} $Доказательство следует из представления общего решения однородных разностных уравнений в виде $U_{j}^{{[{\text{од}}]}} = {{A}^{j}}U_{0}^{{[{\text{од}}]}}.$ Решение уравнения из (2.1) будет нетривиальном в случае $\left\| {U_{0}^{{[{\text{од}}]}}} \right\| \ne 0$ и ограниченным, если вектор $U_{0}^{{[{\text{од}}]}}$ является линейной комбинацией собственных векторов, соответствующих собственным значениям $\left| {\lambda (A)} \right| = 1$. В противном случае нетривиальных решений однородной задачи нет.
Следующее утверждение определяет условия единственности решений задач (2.1) и (2.2).
Лемма 2. Решения краевых задач (2.1) и (2.2) единственны тогда и только тогда, когда собственные значения матрицы $A$ не лежат на единичной окружности
Теперь рассмотрим вопрос о существовании решений. Заметим, что если спектр матрицы A делится единичной окружностью на два непересекающихся множества, то с помощью подобного преобразования она может быть приведена к блочно-диагональной форме (см., например, [1]):
(2.5)
$A = T\left[ {\begin{array}{*{20}{c}} {{{\Lambda }_{0}}}&0 \\ 0&{{{\Lambda }_{\infty }}} \end{array}} \right]{{T}^{{ - 1}}},\quad \left| {{{\lambda }_{i}}({{\Lambda }_{0}})} \right| < 1,\quad \left| {{{\lambda }_{i}}({{\Lambda }_{\infty }})} \right| > 1.$Лемма 3. Если выполнено условие (2.4), то решение задачи (2.2) существует и может быть представлено в явном виде
(2.6)
${{G}_{k}} = \left\{ {\begin{array}{*{20}{c}} {T\left[ {\begin{array}{*{20}{c}} {\Lambda _{0}^{{k - 1}}}&0 \\ 0&0 \end{array}} \right]{{T}^{{ - 1}}},\quad k > 0,} \\ {T\left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&{ - \Lambda _{\infty }^{k}} \end{array}} \right]{{T}^{{ - 1}}},\quad k \leqslant 0.} \end{array}} \right.$То, что заданная в (2.6) функция ${{G}_{k}}$ является решением задачи (2.2), проверяется непосредственной подстановкой.
Замечание. Если у матрицы A есть собственные значения, лежащие на единичной окружности, то представления, аналогичные (2.5) и (2.6), отличающиеся только нестрогими неравенствами для спектров подматриц ${{\Lambda }_{0}}$ или ${{\Lambda }_{\infty }}$, также имеют место. Однако условия ограниченности решения (2.2) и/или его единственности при этом нарушаются.
Лемма 4. Если выполнено условие (2.4), то решение задачи (2.2) существует и может быть представлено в виде
Сходимость ряда в формуле (2.7) для любой ограниченной разностной функции правой части ${{f}_{k}}$ является следствием леммы 3. Справедливость представления (2.7) для решения задачи (2.1) может быть проверена непосредственной подстановкой.
Приведенные выше леммы 1–4 представляют собой отдельные этапы доказательства следующей теоремы.
Теорема 1. Для существования и единственности решения задачи (2.1) необходимо и достаточно выполнение условия (2.4).
Рассмотрим величину
и заметим, что этот ряд также как и (2.7) сходится только при условии (2.4). А значит, можно сформулировать следующий критерий разделения спектра матрицы $A$ единичной окружностью как следствие теоремы (1).Утверждение 1. Условие (2.4) выполняется тогда и только тогда, когда $\left\| H \right\| < \infty $.
Обратим внимание, что матрица ${{P}_{{{\text{in}}}}} = {{G}_{1}}$ является проектором на инвариантное подпространство матрицы A, соответствующее собственным значениям, лежащим внутри единичной окружности. Проектор на подпространство, соответствующее собственным значениям, лежащим вне окружности, имеет вид ${{P}_{{{\text{out}}}}} = {{I}_{n}} - {{P}_{{{\text{in}}}}}$. Размерность инвариантных подпространств вычисляется по формулам ${{n}_{{{\text{in}}}}} = {\text{tr}}\;{{P}_{{{\text{in}}}}}$, ${{n}_{{{\text{out}}}}} = {\text{tr}}\;{{P}_{{{\text{out}}}}}$. C помощью сингулярного разложения (см., в частности, [1])
Обобщая вышесказанное на случай матричных пучков $A - \lambda B$, можно сформулировать следующее
Утверждение 2. На единичной окружности отсутствуют собственные значения пучка $A - \lambda B$ и возможно представление
(2.9)
$\begin{gathered} A{{G}_{{k + 1}}} - B{{G}_{k}} = 0,\quad k \ne 0, \\ {{G}_{1}} - {{G}_{0}} = {{I}_{n}}, \\ \left\| {{{G}_{k}}} \right\| \leqslant C < \infty ,\quad - \infty < k < \infty . \\ \end{gathered} $Причем численным критерием качества дихотомии спектра $A - \lambda B$ является величина (2.8).
Таким образом, задача о разделении матричного спектра единичной окружностью сводится к решению краевой задачи (2.9), которая имеет постоянные матричные коэффициенты и может быть эффективно решена с использованием метода удвоений и ортогональных исключений.
2.2. Дихотомия единичной окружностью и мнимой осью
Приведенные выше факты лежат в основе алгоритма дихотомии единичной окружностью, который, в свою очередь, является ключевой частью алгоритмов дихотомии относительно остальных кривых. Существует несколько вариантов этого алгоритма. Однако основной цикл каждого из них представляет собой метод удвоений, т.е. переход от уравнений ${{A}_{k}}{{U}_{j}} - {{B}_{k}}{{U}_{{j + {{2}^{k}}}}} = 0$ к уравнениям ${{A}_{{k + 1}}}{{U}_{j}} - {{B}_{{k + 1}}}{{U}_{{j + {{2}^{{k + 1}}}}}} = 0$ путем исключения промежуточного слагаемого при помощи QR-разложения соответствующей матрицы.
Заметим также, что условия сходимости основного цикла могут быть сформулированы по-разному. Можно следить за абсолютной сходимостью, как это сделано ниже, или за относительной. В условие можно также включать сходимость проектора ${{P}_{k}}$. Кроме того, существуют оценки, позволяющие априорно оценить число итераций, необходимых для сходимости алгоритма при условии $\left\| H \right\| \leqslant {{\omega }_{{{\text{max}}}}}$. Эту оценку также можно использовать в качестве верхней границы числа итераций. При этом нужно принимать во внимание, что она, как правило, очень завышена, так как в обычной ситуации для сходимости с высокой точностью достаточно нескольких итераций.
Алгоритм дихотомии матричного спектра относительно единичной окружности
Дано: матричный пучок ${{A}_{0}} - \lambda {{B}_{0}}$, ${{\varepsilon }_{{it}}}$ – требуемая точность итерационного процесса, ${{\omega }_{{{\text{max}}}}}$, ${{\mu }_{{{\text{max}}}}}$ – максимальные значения критерия дихотомии и числа обусловленности матрицы.
Если ${\text{cond}}({{A}_{0}} - {{B}_{0}}) > {{\mu }_{{{\text{max}}}}}$,
то дихотомия невозможна, конец расчетов.
иначе вычисляется начальное приближение матричного критерия дихотомии H
Цикл пока$\left\| {{{H}_{k}} - {{H}_{{k - 1}}}} \right\| > {{\varepsilon }_{{it}}}$
Если $\left\| {{{H}_{k}}} \right\| \geqslant {{\omega }_{{{\text{max}}}}}$ или ${\text{cond}}({{A}_{k}} + {{B}_{k}}) > {{\mu }_{{{\text{max}}}}}$,
то дихотомия невозможна, конец расчетов.
иначе вычисляются вспомогательные матрицы ${{V}_{{k + 1}}} = ({{A}_{k}} + {{B}_{k}}{{)}^{{ - 1}}}{{A}_{k}}$, ${{U}_{{k + 1}}} = {{I}_{n}} - {{V}_{{k + 1}}},$
приближение матричного критерия дихотомии $H$ ${{H}_{{k + 1}}} = {{U}_{{k + 1}}}{{H}_{k}}U_{{k + 1}}^{*} + {{V}_{{k + 1}}}{{H}_{k}}V_{{k + 1}}^{*},$
преобразование матричного пучка $qr\left( {\left[ {\begin{array}{*{20}{c}} { - {{B}_{k}}}&{{{A}_{k}}}&0 \\ {{{A}_{k}}}&0&{ - {{B}_{k}}} \end{array}} \right]} \right) = \left[ {\begin{array}{*{20}{c}} *&*&* \\ 0&{{{A}_{{k + 1}}}}&{ - {{B}_{{k + 1}}}} \end{array}} \right],$
приближение матрицы проектора ${{P}_{{{\text{in}}}}}$ ${{P}_{k}} = - {{({{A}_{{k + 1}}} - {{B}_{{k + 1}}})}^{{ - 1}}}{{B}_{{k + 1}}}.$
Конец цикла.
Алгоритм дихотомии спектра матрицы A относительно мнимой оси основан на свойствах экспоненциального отображения, которое переводит левую полуплоскость в единичный круг. Таким образом, его отличие от дихотомии относительно окружности заключается в том, что в качестве начального матричного пучка используется ${{A}_{0}} - \lambda {{B}_{0}} = {{e}^{{\tau A}}} - \lambda {{I}_{n}}$. Параметр τ выбирается так, чтобы обеспечить быструю сходимость при вычислении матричной экспоненты, например, $\tau \approx 1{\text{/}}2\left\| A \right\|$. Однако в случае матриц с большой нормой, например, аппроксимирующих дифференциальные операторы, такой выбор τ может приводить к ложным результатам. Поэтому для матриц с большой нормой используется прием, описанный в [17], заключающийся в выборе τ в виде степени двойки $\tau {{ = 2}^{{ - K}}}$ и последующем применении K дополнительных итераций.
3. ОБОЗНАЧЕНИЯ И ВСПОМОГАТЕЛЬНЫЕ АЛГОРИТМЫ
В данном разделе приводятся алгоритмы, которые войдут в качестве составной части в алгоритм дихотомии относительно угла. Кроме этого, здесь будет определен ряд обозначений, которые будут использоваться в основном алгоритме.
3.1. Используемые обозначения
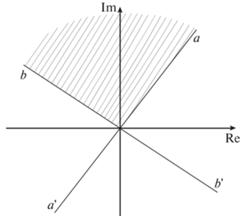
Основными математическими объектами, которые будут рассматриваться далее, являются лучи (или полупрямые) на комплексной плоскости $\mathbb{C}$, начало которых будет находиться в точке 0. Обозначать лучи будем малыми буквами $a,\;b,\;c,\; \ldots $ . Угол, который образуют два луча a и b, будем обозначать $ab$ или $\angle ab$ (см. фиг. 1). Положительный отсчет меры угла будет направлен против часовой стрелки. Тогда, очевидно, верно равенство для сопряженных углов $\angle ab = 2\pi - \angle ba$.
Прямые, проходящие через точку $(0,\;0)$, будем обозначать двумя буквами $aa{\text{'}}$, где a и $a{\text{'}}$ – лучи с началом в точке (0, 0), составляющие вместе данную прямую. Такое двойное обозначение позволяет отождествлять прямую $aa{\kern 1pt} '$ и развернутый угол $aa{\text{'}}$. Кроме того, по аналогии с вещественной и мнимой осью для каждой прямой будем задавать направление. То есть один из лучей будем называть положительным, другой – отрицательным. Эти направления можно задавать или полностью произвольно, или исходя из удобства выкладок. При обозначениях мы будем учитывать направление прямой следующим образом: у прямой $aa{\text{'}}$ полупрямая a будет положительной, а полупрямая $a{\text{'}}$ – отрицательной. Так как основным инструментом для решения основной задачи будет являться дихотомия матричного спектра мнимой осью, которая делит плоскость на правую и левую полуплоскости, то по аналогии мы определим правые и левые полуплоскости для всех прямых, у которых мы определим направление. Правой назовем полуплоскость, в которой находится угол $a{\text{'}}a$ (от отрицательного направления $a{\text{'}}$ прямой $aa{\text{'}}$ к положительному a), и обозначим через $\mathbb{C}_{{aa'}}^{r}$. Соответственно вторую полуплоскость, в которой находится угол $aa{\text{'}}$ (от положительного направления к отрицательному), будем называть левой и обозначать через $\mathbb{C}_{{aa'}}^{l}$. В этих обозначениях часть плоскости внутри угла $ab$ является пересечением левой полуплоскости относительно прямой $aa{\text{'}}$ и правой полуплоскости относительно прямой $bb'$: $\mathbb{C}_{{aa'}}^{l} \cap \mathbb{C}_{{bb'}}^{r}$.
3.2. Дихотомия спектра матрицы произвольной прямой
Для того, чтобы исследовать расположение спектра матрицы $A$ относительно произвольной прямой $aa{\text{'}}$, проходящей через начало координат, необходимо совершить поворот комплексной плоскости на угол φ между прямой $aa{\text{'}}$ и мнимой осью $\xi = {{e}^{{i\varphi }}}\lambda $. При таком преобразовании прямая $aa{\text{'}}$ перейдет в мнимую ось, а исходная спектральная задача $Av = \lambda v$ в задачу для нового спектрального параметра ${{A}_{\varphi }}v = \xi v$, где ${{A}_{\varphi }} = {{e}^{{i\varphi }}}A$. Из этих равенств видно, что собственные векторы, а значит, и инвариантные подпространства у матриц A и ${{A}_{\varphi }}$ совпадают, а собственные значения отличаются на угол φ. А значит, дихотомия спектра ${{A}_{\varphi }}$ относительно мнимой оси позволит определить проекторы ${{P}^{r}}$ и ${{P}^{l}}$ на инвариантные подпространства матрицы A, соответствующие собственным значениям, лежащим в правой $\mathbb{C}_{{aa'}}^{r}$ и левой $\mathbb{C}_{{aa{\text{'}}}}^{l}$ полуплоскостях. С помощью сингулярного разложения получаем ортогональные базисы ${{U}^{r}}$, ${{U}^{l}}$в инвариантных подпространствах, после чего можем представить матрицу в клеточно-диагональном виде:
3.3. Проверка наличия собственных значений матрицы на луче
Стороны угла являются лучами, поэтому проверка отсутствия собственных значений заданной матрицы A на сторонах угла сводится к вопросу о нахождении собственных значений на луче.
Обозначим через a луч с началом в точке (0, 0), а угол между ним и вещественной положительной полуосью $\alpha $. Причем отсчет угла производим от луча a к полуоси против часовой стрелки. Тогда задача о локализации спектра $n \times n$ матрицы A на заданном луче a при помощи поворота сводится к вопросу о расположении спектра матрицы ${{A}_{\alpha }} = {{e}^{{i\alpha }}}A$ на вещественной положительной полуоси.
Далее заметим, что среди собственных значений матрицы ${{A}_{\alpha }}$ отсутствуют положительные вещественные числа тогда и только тогда, когда среди собственных значений матричного пучка ${{A}_{\alpha }} - {{\xi }^{2}}{{I}_{n}}$, квадратичного относительно спектрального параметра ξ, нет вещественных чисел. Из равенства определителей
И, наконец, очевидно, что наличие собственных значений матрицы A на вещественной оси эквивалентно наличию собственных значений матрицы $i{\mathbf{A}}$ на мнимой оси.
Итак, для того чтобы определить наличие или отсутствие точек спектра матрицы A на луче a, нужно вычислить критерий дихотомии относительно мнимой оси для матрицы $i{\mathbf{A}}$. Заметим, что вычисления проекторов в данном случае не происходит, так как луч не разделяет плоскость на две непересекающиеся области.
4. ЗАДАЧА О ДИХОТОМИИ ОТНОСИТЕЛЬНО УГЛА
4.1. Формулировка задачи
На комплексной плоскости задан угол с вершиной в начале координат, образованный лучами a, b (см. фиг. 1). Задача заключается в том, чтобы разделить спектр заданной матрицы A на две части в зависимости от расположения относительно угла $ab$. Для этого нужно будет определить, лежат ли на сторонах угла $ab$ собственные значения матрицы A. В случае, если стороны угла свободны от точек спектра, нужно вычислить проекторы на инвариантные подпространства матрицы, соответствующие собственным значениям, лежащим, соответственно, внутри и вне угла $ab$, определить базисы этих инвариантных подпространств и привести матрицу A к клеточно-диагональному виду.
Так как угол состоит из двух лучей, то для того, чтобы определить критерий дихотомии спектра углом, нужно определить численный критерий отсутствия точек спектра на каждом луче отдельно (см. разд. 3). Если определены значения $\omega (a)$ и $\omega (b)$ для обеих сторон угла, то в качестве критерия дихотомии углом можно взять их сумму:
Далее нужно вычислить проекторы ${{P}_{{{\text{in}}}}}$ и ${{P}_{{{\text{out}}}}} = {{I}_{n}} - {{P}_{{{\text{in}}}}}$ на инвариантные подпространства, соответствующие собственным значениям, лежащим внутри и вне угла $ab$ соответственно, а также привести подобным преобразованием матрицу A к клеточно-диагональному виду
(4.1)
$A = T\left[ {\begin{array}{*{20}{l}} {{{A}_{{{\text{in}}}}}}&{} \\ {}&{{{B}_{{{\text{out}}}}}} \end{array}} \right]{{T}^{{ - 1}}}.$Здесь собственные значения подматрицы ${{A}_{{{\text{in}}}}}$ лежат внутри угла $ab$, а собственные значения ${{B}_{{{\text{out}}}}}$ – вне угла.
4.2. Дихотомия прямыми $aa{\text{'}}$ и $bb{\text{'}}$
Для выделения части спектра, лежащей внутри угла $ab$, можно использовать алгоритм дихотомии прямыми, являющимися продолжением сторон угла. Обозначим соответствующие прямые через $aa{\text{'}}$ и $bb{\text{'}}$.
Случай 1. На обеих прямых $aa{\text{'}}$ и $bb{\text{'}}$ отсутствуют собственные значения матрицы $A$. В этой ситуации алгоритм решения задачи дихотомии максимально прост, но, очевидно, неприменим в общем случае. Решение сводится к последовательному выполнению дихотомии спектра A относительно обеих прямых с вычислением проекторов $P_{{bb'}}^{l}$ и $P_{{aa{\text{'}}}}^{r}$. Тогда проектор на инвариантное подпространство, соответствующее собственным значениям, находящимся внутри угла $ab$, представляет собой произведение ${{P}_{{{\text{in}}}}} = P_{{bb{\text{'}}}}^{l}P_{{aa{\text{'}}}}^{r}$. Сингулярное разложение проекторов ${{P}_{{{\text{in}}}}}$ и ${{I}_{n}} - {{P}_{{{\text{in}}}}}$ позволяет получить базисы инвариантных подпространств и привести матрицу $A$ к клеточно-диагональному виду.
Случай 2. На прямой $aa{\text{'}}$ нет собственных значений матрицы A. Произведем дихотомию спектра односительно этой прямой (см. разд. 3). В результате чего множество всех собственных значений разделится на два непересекающихся подмножества, лежащих в полуплоскостях $\mathbb{C}_{{aa'}}^{l}$ и $\mathbb{C}_{{aa'}}^{r}$, разделенных прямой $aa{\text{'}}$. При этом будут вычислены проекторы
на инвариантные подпространства матрицы A размерности ${{n}_{1}} = {\text{tr}}\;{{P}_{1}}$ и $n - {{n}_{1}}$, соответствующих собственным значениям, лежащим в полуплоскостях, разделенных прямой $aa{\kern 1pt} '$, базисы в данных инвариантных подпространствах $U_{{aa'}}^{l}$, $U_{{aa{\text{'}}}}^{r}$ и матрицу перехода приводящую матрицу A к клеточно-диагональному виду:(4.4)
$A = {{T}_{1}}\left[ {\begin{array}{*{20}{l}} {{{A}_{1}}}&{} \\ {}&{{{B}_{1}}} \end{array}} \right]T_{1}^{{ - 1}}.$Здесь спектр подматрицы ${{A}_{1}}$ полностью лежит в левой полуплоскости $\mathbb{C}_{{aa'}}^{l}$, а спектр ${{B}_{1}}$ – в правой $\mathbb{C}_{{aa'}}^{r}$
Луч $b$ лежит в левой полуплоскости $\mathbb{C}_{{aa'}}^{l}$ прямой $aa{\text{'}}$, тогда как его продолжение $b{\text{'}}$ лежит в правой полуплоскости. А внутренняя часть угла $ab$ представляет собой пересечение полуплоскостей $\mathbb{C}_{{aa'}}^{l} \cap \mathbb{C}_{{bb'}}^{r}$. Следовательно, для завершения решения задачи необходимо разделить спектр матрицы ${{A}_{1}}$ относительно прямой $bb{\text{'}}$. В результате применения метода дихотомии матричного спектра прямой будут получены проекторы
базисы $U_{{bb{\text{'}}}}^{r}$, $U_{{bb{\text{'}}}}^{l}$ и матрица перехода приводящую матрицу ${{A}_{1}}$ к клеточно-диагональному виду:(4.7)
${{A}_{1}} = {{T}_{2}}\left[ {\begin{array}{*{20}{l}} {{{A}_{2}}}&{} \\ {}&{{{B}_{2}}} \end{array}} \right]T_{2}^{{ - 1}},$Случай 3. На прямой $bb{\text{'}}$ отсутствуют собственные значения матрицы A. Если при этом критерий дихотомии спектра прямой $aa{\text{'}}$ бесконечен, то порядок действий поменяется. Сначала нужно провести дихотомию прямой $bb{\text{'}}$. Результат этого действия: проекторы
на инвариантные подпространства матрицы $A$, соответствующих собственным значениям, лежащим в полуплоскостях, разделенных прямой $bb{\text{'}}$, базисы в данных инвариантных подпространствах $U_{{bb'}}^{r}$, $U_{{bb'}}^{l}$ и матрицу перехода приводящую матрицу A к клеточно-диагональному виду (4.4), причемДалее производится дихотомия спектра подматрицы ${{A}_{1}}$ относительно прямой $aa{\text{'}}$. Будут получены: проекторы
базис $U_{{aa'}}^{l}$, $U_{{aa'}}^{r}$ и матрица перехода такая, что имеет место представление (4.7), гдеИтоговые матрицы проекторов и матричные разложения будут иметь следующий вид:
(4.12)
${{P}_{{{\text{in}}}}} = {{P}_{1}}{{T}_{1}}\left[ {\begin{array}{*{20}{l}} {{{P}_{2}}}&{} \\ {}&{{{0}_{{n - {{n}_{1}}}}}} \end{array}} \right]T_{1}^{{ - 1}} = {{T}_{1}}\left[ {\begin{array}{*{20}{l}} {{{P}_{2}}}&{} \\ {}&{{{0}_{{n - {{n}_{1}}}}}} \end{array}} \right]T_{1}^{{ - 1}}{{P}_{1}},\quad {{P}_{{{\text{out}}}}} = {{I}_{n}} - {{P}_{{{\text{in}}}}},$(4.13)
$T = {{T}_{1}}\left[ {\begin{array}{*{20}{l}} {{{T}_{2}}}&{} \\ {}&{{{I}_{{n - {{n}_{1}}}}}} \end{array}} \right],\quad {{A}_{{{\text{in}}}}} = {{A}_{2}},\quad {{B}_{{{\text{out}}}}} = \left[ {\begin{array}{*{20}{l}} {{{B}_{2}}}&{} \\ {}&{{{B}_{1}}} \end{array}} \right].$Здесь символом ${{0}_{{n - {{n}_{1}}}}}$ обозначена квадратная нулевая матрица размера $(n - {{n}_{1}}) \times (n - {{n}_{1}})$.
Упрощенный алгоритм дихотомии углом
Дано: матрица A, угол $ab$ на комплексной плоскости с вершиной в точке $(0,\;0)$, максимально допустимое значение критерия дихотомии ${{\omega }_{{\max }}}$.
Шаг 1. Проверка наличия собственных значений матрицы на лучах a и b.
Если $\omega (ab) < {{\omega }_{{\max }}}$, то выполняются шаги 2, 3.
Шаг 2. Если $\omega (aa{\text{'}}) < {{\omega }_{{\max }}}$, то вычисляются матрицы (4.2), (4.3), (4.5), (4.6). Если $\omega (aa{\text{'}}) \geqslant {{\omega }_{{\max }}}$, но $\omega (bb{\text{'}}) < {{\omega }_{{\max }}}$, то вычисляются матрицы (4.8), (4.9), (4.10), (4.11).
Шаг 3. Построение матриц (4.12), (4.13), участвующих в разложении (4.1).
Результат. Значение критерия дихотомии $\omega $, проекторы ${{P}_{{{\text{in}}}}}$, ${{P}_{{{\text{out}}}}}$ и разложение (4.1), если на сторонах угла $ab$ собственных значений матрицы A нет, $\omega = {{\omega }_{{\max }}}$ в случае пересечения сторонами угла $ab$ пятен ε-спектра матрицы при малых значениях ε.
4.3. Случай невозможности дихотомии прямыми $aa{\text{'}}$ и $bb{\text{'}}$
Более сложной является ситуация, когда на обоих лучах $a{\text{'}}$ и $b{\text{'}}$, продолжающих стороны угла $ab$, находятся собственные значения матрицы A. В этом случае в алгоритм вводится дополнительный этап, целью которого является приведение исходной матрицы к такому клеточно-диагональному виду
(4.14)
$A = {{T}_{0}}\left( {\begin{array}{*{20}{l}} {{{A}_{0}}}&{} \\ {}&{{{B}_{0}}} \end{array}} \right)T_{0}^{{ - 1}},$Разделим угол $b{\text{'}}a$ на равные части лучами ${{c}_{1}},{{c}_{2}},\; \ldots ,\;{{c}_{{n - 1}}}$. Так как у матрицы $A$ всего $n$ собственных значений с учетом кратности, и на прямых $aa{\text{'}}$ и $bb{\text{'}}$ по предположению находятся собственные значения, то найдется прямая ${{c}_{k}}c_{k}^{'}$, на которой точки спектра матрицы A будут отсутствовать. Здесь $c_{k}^{'}$ – луч, продолжающий луч ${{c}_{k}}$, при этом внутренность угла $ab$ лежит в левой полуплоскости $\mathbb{C}_{{{{c}_{k}}c_{k}^{'}}}^{l}$. Таким образом, дополнительным этапом алгоритма является дихотомия спектра матрицы $A$ прямой ${{c}_{k}}c_{k}^{'}$. Результатом этого этапа являются матрицы проекторов
Далее к матрице ${{A}_{0}}$ применяется упрощенный алгоритм. В итоге будут получены следующие матрицы:
(4.16)
${{P}_{{{\text{in}}}}} = {{P}_{0}}\left[ {\begin{array}{*{20}{l}} {{{P}_{1}}}&{} \\ {}&{{{0}_{{n - {{n}_{0}}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{P}_{2}}}&{} \\ {}&{{{0}_{{n - {{n}_{1}}}}}} \end{array}} \right],\quad {{P}_{{{\text{out}}}}} = {{I}_{n}} - {{P}_{{{\text{in}}}}},$(4.17)
$T = {{T}_{0}}\left[ {\begin{array}{*{20}{l}} {{{T}_{1}}}&{} \\ {}&{{{I}_{{n - {{n}_{0}}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{T}_{2}}}&{}&{} \\ {}&{{{I}_{{n - {{n}_{1}}}}}}&{} \end{array}} \right],\quad {{A}_{{{\text{in}}}}} = {{A}_{2}},\quad {{B}_{{{\text{out}}}}} = \left[ {\begin{array}{*{20}{l}} {{{B}_{2}}}&{}&{} \\ {}&{{{B}_{1}}}&{} \\ {}&{}&{{{B}_{0}}} \end{array}} \right],$Алгоритм дихотомии углом
Дано: матрица A, угол $ab$ на комплексной плоскости с вершиной в точке $(0,\;0)$, максимально допустимое значение критерия дихотомии ${{\omega }_{{\max }}}$.
Шаг 1. Проверка наличия собственных значений матрицы на лучах a и b. Если $\omega (ab) < {{\omega }_{{\max }}}$, то выполняются шаги 2, 3.
Шаг 2. Проверка наличия собственных значений матрицы A на прямых $aa{\text{'}}$, $bb{\text{'}}$.
Если $\omega (aa{\text{'}}) < {{\omega }_{{\max }}}$ или $\omega (bb{\text{'}}) < {{\omega }_{{\max }}}$, то ${{A}_{0}} = A$, ${{T}_{0}} = {{I}_{n}}$ и выполняется шаг 4.
Если $\omega (aa{\text{'}}) \geqslant {{\omega }_{{\max }}}$ и $\omega (bb{\text{'}}) \geqslant {{\omega }_{{\max }}}$, то выполняется шаг 3.
Шаг 3. Строятся лучи ${{c}_{1}},\; \ldots \;{{c}_{{n - 1}}}$, делящие угол $b{\text{'}}a$ на равные части.
В цикле находится прямая ${{c}_{k}}c_{k}^{'}$, для которой $\omega ({{c}_{k}}c_{k}^{'}) < {{\omega }_{{\max }}}$. Производится дихотомия спектра матрицы A этой прямой и вычисляется разложение (4.14) с приводящей матрицей (4.15).
Шаг 4. Применение упрощенного алгоритма к матрице ${{A}_{0}}$.
Результат. Значение критерия дихотомии ω, проекторы ${{P}_{{{\text{in}}}}}$, ${{P}_{{{\text{out}}}}}$ (см. формулы (4.16), (4.17)) и разложение (4.1), если на сторонах угла $ab$ собственных значений матрицы A нет, $\omega = {{\omega }_{{\max }}}$ в случае пересечения сторонами угла $ab$ пятен ε-спектра матрицы при малых значениях ε.
5. ПРИМЕРЫ
5.1. Определение сектора дифференциального оператора
В качестве первого примера мы рассмотрим спектральную задачу для уравнения Орра–Зоммерфельда для плоскопараллельного течения Пуазейля вязкой несжимаемой жидкости. Изучению спектральных характеристик оператора Орра–Зоммерфельда посвящено множество работ, например, уже упоминавшиеся [4], [6], [17]. В статье [26] реализована идея разложения собственных функций в ряды в граничных точках, а обширный список литературы, приведенный в этой работе, содержит ссылки на разносторонние исследования оператора Орра–Зоммерфельда. Среди них можно отдельно отметить [27]. Изложенный в данной работе подход перекликается с задачей дихотомии, так как алгоритм применяется к точкам границы области с некоторым шагом, а позволяет сделать вывод о числе собственных значений, лежащих внутри области.
С одной стороны, спектральная задача для уравнения Орра–Зоммерфельда имеет важное прикладное значение с точки зрения исследования развития турбулентности. С другой – это содержательный пример несамосопряженного дифференциального оператора, и исследование его спектра представляет собой нетривиальную, но при этом хорошо изученную задачу. Таким образом, оператор Орра–Зоммерфельда является идеальным объектом для апробации новых вычислительных методов.
Рассмотрим матричный пучок $A - \lambda B$, являющийся дискретной аппроксимацией оператора Орра–Зоммефельда [28], [29]
Здесь ${{D}_{2}}$, ${{D}_{4}}$ – матрицы коллокационных производных второго и четвертого порядков, учитывающие однородные условия Дирихле и Неймана, I – единичная матрица, α и ${{\kappa }^{2}} = {{\alpha }^{2}} + {{\beta }^{2}}$ – спектральные параметры, Re – число Рейнольдса, $U(y) = 1 - {{y}^{2}}$, $ - 1 \leqslant y \leqslant 1$ – профиль основного течения Пуазейля, ${\text{diag}}(U)$ – диагональная матрица, на диагонали которой стоят значения функции U в точках Гаусса-Лобатто ${{y}_{j}} = \cos \pi {\text{/}}n$. Далее будем полагать $n = 100$, ${\text{Re}} = 6000$, $\alpha = 1.02$, $\beta = 0$.
Часть $\varepsilon $-спектра матрицы $\mathcal{A} = {{B}^{{ - 1}}}A$ изображена на фиг. 2 в виде линий уровня функции $f(\lambda ) = \mathop {\log }\nolimits_{10} {{\sigma }_{{\min }}}(\mathcal{A} - \lambda I)$. Цифрами обозначены значения, которые принимает функция $f(\lambda )$ на данном контуре.
Пусть стороны угла $ab$ образуют с положительной вещественной полуосью углы $5\pi {\text{/}}4$ и $7\pi {\text{/}}4$. Рассмотрим семейство ломаных ${{a}_{t}}{{b}_{t}}$, полученных из угла $ab$ переносом его вершины вдоль мнимой оси в точку $(0,\;t)$ (см. фиг. 2). Очевидно, что дихотомия спектра матрицы $\mathcal{A}$ относительно угла ${{a}_{t}}{{b}_{t}}$ равносильна дихотомии спектра матрицы $\mathcal{A} - itI$ относительно угла $ab$. Для каждого t из заданного интервала вычислим критерий дихотомии $\omega ({{a}_{t}}{{b}_{t}})$ и проектор ${{P}_{{{\text{in}}}}}({{a}_{t}}{{b}_{t}})$ на инвариантное подпространство, соответствующее собственным значениям матрицы $\mathcal{A}$, находящимся внутри угла ${{a}_{t}}{{b}_{t}}$.
На фиг. 3a изображен график функции $g(t) = \mathop {\log }\nolimits_{10} \omega ({{a}_{t}}{{b}_{t}})$, значения которой конечны, если на сторонах угла ${{a}_{t}}{{b}_{t}}$ нет точек спектра матрицы $\mathcal{A}$, и бесконечны в обратном случае. То есть “пики” графика $g(t)$ указывают на значения t, при которых собственные значения $\mathcal{A}$ оказываются на стороне угла ${{a}_{t}}{{b}_{t}}$.
Фиг. 3.
График критерия дихотомии относительно угла ${{a}_{t}}{{b}_{t}}$ (а), след проектора на инвариантное подпространство матрицы $\mathcal{A}$, соответствующее собственным значениям внутри угла ${{a}_{t}}{{b}_{t}}$ (б).

На фиг. 3б изображен график кусочно-постоянной функции $h(t) = {\text{tr}}\;{{P}_{{{\text{in}}}}}({{a}_{t}}{{b}_{t}})$. Значения этой функции совпадают с числом собственных значений матрицы $\mathcal{A}$, находящихся внутри угла ${{a}_{t}}{{b}_{t}}$. При прохождении стороны угла ${{a}_{t}}{{b}_{t}}$ через точки спектра функция меняет значение на величину, равную числу собственных значений, оказавшихся в этот момент на стороне угла. На представленном графике величина каждого такого изменения равна двум. Это согласуется с тем фактом (см., например, [28]), что кратность собственных значений на ветви P (группа собственных значений, для которых ${\text{Re}}\lambda \to 1$) равна двум, каждому из них соответствуют две собственные функции – четная и нечетная. Кроме того, при $t > {{t}_{0}} = 0.9284$ функция $h(t)$ тождественно равна размерности матрицы $n = 100$. Это означает, что сектор с вершиной в точке $(0,\;t)$, $t > {{t}_{0}}$, и углом полураствора $\pi {\text{/}}4$ содержит все собственные значения матрицы $\mathcal{A}$.
5.2. Случай дугообразного спектрального пятна
Описанный в предыдущем разделе алгоритм даст ложноотрицательный результат, если пятно ε-спектра матрицы для достаточно малого ε имеет вид дуги, охватывающей вершину угла. В этом случае может оказаться, что при конечном значении критерия дихотомии $\omega (ab)$ предварительное разделение спектра любой прямой $cc{\text{'}}$ невозможно, а значит, невозможно выполнение алгоритма в целом.
Для того, чтобы решить эту проблему, можно произвести предварительное разделение спектра (шаг 3 алгоритма) относительно какой-то выпуклой кривой, охватывающей вершину угла, но полностью лежащей внутри спектральной дуги.
Рассмотрим пример двухдиагональной матрицы A размера $n \times n$, на главной диагонали которой стоят числа
Зафиксируем угол $ab$, стороны которого образуют с положительной вещественной полуосью углы $3\pi {\text{/}}4$ и $5\pi {\text{/}}4$, и применим алгоритм из разд. 4 дихотомии относительно угла $ab$ к этим матрицам. При этом положим ${{\omega }_{{\max }}} = {{10}^{{16}}}$. Результаты вычислений представлены в строках 1–5 табл. 1.
Таблица 1
| Размерность $n$ | Критерий дихотомии углом $\log \omega (ab)$ | Критерий дополнительной дихотомии | Точность проектора $\log \left\| {{{P}^{2}} - P} \right\|$ | Точность проектора $\log \left\| {PA - AP} \right\|$ | |
|---|---|---|---|---|---|
| 1 | 10 | 2.5 | 4.0 | –13.9 | –21.9 |
| 2 | 20 | 5.2 | 8.5 | –11.4 | –20.6 |
| 3 | 30 | 7.9 | 13.2 | –8.7 | –17.4 |
| 4 | 35 | 9.3 | 15.6 | –7.6 | –15.7 |
| 5 | 40 | 10.6 | >16 | – | – |
| 6 | 40 | 10.6 | 13.3 | –9.6 | –12.3 |
Значения, приведенные в последних двух столбцах, говорят о том, что проекторы вычисляются с большой точностью.
В строке 5 табл. 1 мы видим, что при $n = 40$ $\omega (ab) < {{\omega }_{{\max }}}$, т.е. спектральные пятна достаточно хорошо разделены сторонами угла. Однако вспомогательная дихотомия относительно одной из прямых ${{c}_{k}}c_{k}^{'}$ невозможна, так как $\omega ({{c}_{k}}c_{k}^{'}) \geqslant {{\omega }_{{\max }}}$. Пробелы в последних двух ячейках этой строки говорят о том, что при $\omega \geqslant {{\omega }_{{\max }}}$ дальнейшие вычисления не проводились.
Однако дихотомия спектра при $n = 40$ может быть осуществлена, если для дополнительной дихотоми вместо прямой выбрать окружность. В данном конкретном случае это окружность радиуса $R = 3$ с центром в точке (–3, 0). Результаты вычислений см. в табл. 1, строка 6.
6. ЗАКЛЮЧЕНИЕ
Данная работа продолжает серию публикаций, посвященных новой постановке спектральной задачи – дихотомии матричного спектра относительно заданной кривой. Впервые поставлена задача разделения спектра относительно кусочно-гладкой кривой, а именно относительно угла, и представлен алгоритм для ее решения. Очевидно, что идея этого метода может быть использована при решении широкого круга задач о разделении спектра матрицы относительно кусочно-гладких кривых, состоящих из дуг кривых второго порядка и отрезков прямых.
Список литературы
Годунов С.К. Современные аспекты линейной алгебры. Новосибирск: Научная книга, 1997. С. 388.
Годунов С.К. Дихотомия спектра и критерий устойчивости для секториальных операторов // Сиб. мат. журн. 1995. Т. 36. № 6. С. 1328–1335.
Trefethen L.N., Embree M. Spectra and Pseudospectra. Princeton University Press, 2005. P. 606.
Trefethen L.N., Trefethen A.E., Satish C.R., Tobin A. Hydrodynamic Stability without Eigenvalues // Science, New Series. 1993. V. 261. № 5121. P. 578–584.
Toh K.-Ch., Trefethen L. Calculation of Pseudospectra by the Arnoldi Iteration // SIAM J. Sci. Comput. 1999. V. 17. № 1. P. 1–15.
Reddy S.C., Schmid P.J., Henningson D.S. Pseudospectra of the Orr–Sommerfeld Operator // SIAM J. on Applied Mathematics. 1993. V. 53. № 1. P. 15–47.
Постников М.М. Устойчивые многочлены. М.: Наука, 1981. С. 176.
Крейн М.Г., Неймарк М.А. Метод симметрических и эрмитовых форм в теории отделения корней алгебраических уравнений. Харьков: ГНТИ Украины, 1936. С. 40.
Fujiwara M. Über die Nullstellen der ganzen Funktionen vom Geschlecht Null und Eins // Tôhoku Math. J. 1925. V. 25. P. 29.
Далецкий Ю.Г., Крейн М.Г. Устойчивость решений дифференциальных уравнений в банаховом пространстве. М.: Наука, 1970. С. 534.
Бибердорф Э.А. Гарантированная точность в прикладных задачах линейной алгебры. Новосибирск: РИЦ НГУ, 2008. С. 145.
Годунов С.К. Круговая дихотомия матричного спектра // Сиб. матeм. журн. 1986. Т. 27. № 5. С. 24–37.
Булгаков А.Я., Годунов С.К. Круговая дихотомия матричного спектра // Сиб. матeм. журн. 1988. Т. 29. № 5. С. 59–70.
Малышев А.Н. Введение в вычислительную линейную алгебру. Новосибирск: Наука, Сибирское отделение. 1991. С. 228.
Godunov S.K., Sadkane M. Spectral Analysis of Symplectic Matrices with Application to the Theory of Parametric Resonance // SIAM J. on Matrix Analysis and Applications. 2006. V. 28. № 4. C. 1083–1096.
Буньков В.Г., Годунов С.К., Курзин В.Б., Садкане М. Применение нового математического аппарата “Одномерные спектральные портреты матрицы” к решению проблемы аэроупругих колебаний решеток лопастей // Ученые записки ЦАГИ. 2009. Т. 40. № 6. С. 3–13.
Бибердорф Э.А., Блинова М.А., Попова Н.И. Модификации метода дихотомии матричного спектра и их применение к задачам устойчивости // Сиб. ж. вычисл. матем. 2018. Т. 21. № 2. С. 139–153.
Godunov S.K., Sadkane M. Elliptic dichotomy of a matrix spectrum // Linear Algebra and its Applications. 1996. V. 248. P. 205–232.
Malyshev A.N., Sadkane M. On parabolic and elliptic spectral dichotomy // SIAM Journal on Matrix Analysis and its Applications. 1997. V. 18. P. 265–278.
Блинова М.А., Попова Н.И., Бибердорф Э.А. Приложение дихотомии матричного спектра к исследованию устойчивости течений // Марчуковские научные чтения – 2017. Труды Международной научной конференции. 2017. С. 106–112.
Бибердорф Э.А. Критерий дихотомии корней полинома единичной окружностью // Сиб. журн. индустр. матем. 2000. Т. 3. № 1. С. 16–32.
Biberdorf E. Development of the matrix spectrum dichotomy method // Continuum mechanics, applied mathematics and scientific computing: Godunov’s legacy – A liber amicorum to Professor Godunov; Book series: Advanced Structured Materials. 2020. P. 37–43.
Демиденко Г.В., Матвеева И.И. Обыкновенные дифференциальные уравнения в задачах. Новосибирск: ИПЦ НГУ, 2021. С. 246.
Годунов С.К. Обыкновенные дифференциальные уравнения с постоянными коэффициентами. Новосибирск: Изд. НГУ, 1994. С. 263.
Фадеев С.И., Когай В.В. Линейные и нелинейные краевые задачи для систем обыкновенных дифференциальных уравнений. Новосибирск: ИПЦ НГУ, 2018. С. 290.
Скороходов С.Л. Численный анализ спектра задачи Орра–Зоммерфельда // Ж. вычисл. матем. и матем. физ. 2007. Т. 47. № 10. С. 1672–1691.
Курочкин С.В. Метод выявления неустойчивости и поиска неустойчивых собственных значений в задаче Орра–Зоммерфельда // Ж. вычисл. матем. и матем. физ. 2001. Т. 41. № 1. С. 86–94.
Бойко А.А., Грек Г.Р., Довгаль А.В., Козлов В.В. Физические механизмы перехода к турбулентности в открытых течениях. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2006. С. 301.
Trefethen L.N. Spectral Methods in MATLAB. SIAM. Philadelphia. 2000. P. 163.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики