Журнал вычислительной математики и математической физики, 2022, T. 62, № 5, стр. 790-808

1. ВВЕДЕНИЕ

Диагонально-неявные методы Рунге–Кутты (DIRK, см. [1]–[18]) относятся к неявным методам, которые наиболее просто реализуются. Благодаря этому методы DIRK широко применяются в прикладных вычислениях. Они используются для решения жестких ОДУ, ДАУ индексов 2 и 3 (см. [3], [4], [10]–[12], [14]), уравнений в частных производных (см. [15], [19]–[21]), а также входят в состав явно‑неявных аддитивных методов (см. [21], [22]). Методы DIRK реализованы в программных продуктах MATLAB и SimInTech (см. [23]).

Один шаг метода DIRK при решении задачи Коши

выполняется согласно формулам где h – размер шага, s – число стадий, Y_i и F_i – стадийные значения и их производные. Таблица коэффициентов (таблица Бутчера) метода DIRK имеет вид (нулевые элементы матрицы A обычно опускают).

Практическое применение нашли однократно диагонально-неявные методы Рунге–Кутты (SDIRK – Singly DIRK) и аналогичные методы с явной первой стадией (ESDIRK – Explicit first stage SDIRK). Методы SDIRK имеют ${{a}_{{ii}}}\, = \gamma ,i = 1,...,s$, а методы ESDIRK имеют a₁₁ = 0, a_ii = γ, $i = 2,...,s$. В [1] исследовалась сходимость методов SDIRK при решении жесткого уравнения Протеро–Робинсона (см. [24]). В результате был сделан вывод о преимуществе методов, имеющих ${{b}_{i}} = {{a}_{{si}}},i = 1, \ldots ,s$ (такие методы Рунге–Кутты называют жестко точными).

Большое значение при решении жестких ОДУ и ДАУ высших индексов имеет также стадийный порядок – наибольшее целое q, для которого выполняются равенства

(здесь и далее предполагаем покомпонентное выполнение операций возведения вектора в степень и умножения векторов). Стадийный порядок методов SDIRK не может быть выше 1-го, а методов ESDIRK – выше 2-го.

Простейший тест для методов решения ОДУ – уравнение Далквиста $y' = \lambda y$. Один шаг решения этого уравнения методом Рунге–Кутты запишется в виде ${{y}_{{n + 1}}} = R\left( {h\lambda } \right){{y}_{n}}$, где R(z) – функция устойчивости, вычисляемая по формуле

Метод называется A(α)-устойчивым, если $\left| {R\left( z \right)} \right| \leqslant 1$ при $\left| {\arg ( - z)} \right| \leqslant \alpha $, и A-устойчивым, если α = 90°. Если при этом $R\left( \infty \right) = 0$, то метод называется L(α)-устойчивым либо L-устойчивым (при α = 90°). Жестко точные методы SDIRK удовлетворяют условию $R\left( \infty \right) = 0$. Потребуем выполнения этого условия также и для методов ESDIRK. Требование L-устойчивости часто является завышенным, поэтому будем рассматривать также и L(α)-устойчивые методы при значении α, близком к 90°.

Согласно [25], метод называется L-затухающим порядка μ > 0, если его функция устойчивости удовлетворяет соотношению $\left| {R\left( z \right)} \right| = O({{z}^{{ - \mu }}})$ при z → ∞. L(α)-устойчивый метод с порядком L-затухания μ > 1 будем обозначать как Lμ(α)‑устойчивый. На основании численных экспериментов мы убедились, что повышенный порядок L‑затухания (μ > 1) не дает преимущества при решении жестких задач. Действительно, любой L(α)‑устойчивый метод обеспечит порядок L-затухания μ, если принять μ шагов за один шаг. Однако L2(α)-устойчивый метод позволяет реализовать эффективный контроль ошибки при решении ДАУ индекса 3. Поэтому наряду с L(α)-устойчивыми методами рассмотрим также и L2(α)-устойчивый метод.

Тестовое сравнение методов SDIRK и ESDIRK было выполнено в [7]–[10], [14], где показано преимущество методов ESDIRK при решении жестких ОДУ и ДАУ индексов 2 и 3. Это преимущество объясняется более высоким стадийным порядком и наличием дополнительных коэффициентов матрицы A при таком же числе неявных стадий. Поэтому мы рассматриваем жестко точные L(α)-устойчивые методы ESDIRK 2-го стадийного порядка, и в дальнейшем под методами ESDIRK подразумеваем именно такие методы.

Простейший метод ESDIRK, обладающий перечисленными свойствами, имеет 2-й порядок и задается таблицей Бутчера

Этот метод можно интерпретировать как последовательное применение правила трапеций (TR) и формулы дифференцирования назад 2-го порядка (BDF2), поэтому он получил название TR‑BDF2. Благодаря простым расчетным формулам и высокой эффективности, этот метод широко применяется в практических вычислениях, и ему посвящено множество работ, среди которых [17], [18]. Однако метод TR‑BDF2 эффективен только при вычислениях с низкой точностью, а для получения более точного результата следует использовать методы более высоких порядков.

Четырехстадийный метод ESDIRK 3-го порядка можно получить, задав γ равным одному из корней многочлена $1 - 9\gamma + 18{{\gamma }^{2}} - 6{{\gamma }^{3}}$. Задав γ = 0.4358…, получаем L-устойчивый метод, а задав γ = 0.1589…, получаем более точный, но L(75.6°)-устойчивый метод. Такие методы рассматривались в [4]–[7]. Последующие исследования показали, что можно построить более эффективные методы, увеличив число стадий. Поэтому в настоящей статье рассматриваются пяти- и шестистадийные методы порядков 3 и 4.

2. ФУНКЦИЯ УСТОЙЧИВОСТИ

Построение метода ESDIRK обычно начинается с выбора значения диагонального элемента γ. Пусть r = s – 1 – число неявных стадий, а p – порядок метода. Примем p = r – 1 и $R\left( \infty \right) = 0$, тогда функция устойчивости метода ESDIRK однозначно определяется значением γ и имеет вид

Функция (2.1) аппроксимирует экспоненту с порядком p = r – 1. Разложив выражение ${{e}^{z}} - R\left( z \right)$ в ряд Тейлора, получаем

где коэффициенты C_r и ${{C}_{{r + 1}}}$ совпадают с одними из коэффициентов погрешности метода. Заметим, что при γ = 0, r ≤ 5 получаем функцию устойчивости явного p-стадийного метода порядка p = r – 1, тогда ${{C}_{r}} = {{C}_{{r + 1}}} = 1$.

При выборе подходящих значений γ исходим из того, что метод должен иметь достаточно большой сектор устойчивости (примем α > 75°). Это требование задает ограничение величины γ снизу. Кроме того, должна обеспечиваться достаточно высокая точность решения уравнения Далквиста (зададим ограничения $\left| {{{C}_{r}}} \right| < 1$, $\left| {{{C}_{{r + 1}}}} \right| < 1$, т.е. точность должна быть заведомо выше, чем у явного метода порядка r – 1, полученного при γ = 0). Из условия $0 \leqslant {{c}_{i}} \leqslant 1$ получаем также γ ≤ 0.5. Эти требования ограничивают величину γ сверху. Исходя из перечисленных требований, получаем ограничения значения γ для пятистадийных методов в виде 0.117 < γ < 0.263, а для шестистадийных методов – в виде 0.143 < γ < 0.289.

Исследуем зависимости угла α и коэффициентов C_r, ${{C}_{{r + 1}}}$ от γ. Для пятистадийных методов (r = 4) с функцией устойчивости (2.1) получаем

На фиг. 1а приведены графики зависимостей α, С₄ и С₅ от γ. В общем случае при выборе соответствующих коэффициентов такие методы имеют 3-й порядок. А если задать γ равным одному из 4 значений, удовлетворяющих условию C₄ = 0, то метод может иметь 4-й порядок. Наилучшая точность обеспечивается при наименьшем из этих значении (γ = 0.1064…), но такой метод не является даже L(0)-устойчивым. Таким образом, выбор γ  сводится к компромиссу между точностью и устойчивостью.

В первых пяти строках табл. 1 приведены характеристики функции устойчивости для некоторых значений γ, пригодных для построения пятистадийных L(α)-устойчивых методов 3-го порядка. Значение γ = 0.125 примерно соответствует локальному максимуму зависимости α(γ). Близкое к этому значение γ = 0.1288… (один из корней многочлена $1 - 12\gamma + 36{{\gamma }^{2}} - 24{{\gamma }^{3}}$) обеспечивает 2-й порядок L-затухания. Метод будет L-устойчивым, если 0.2236… ≤ γ ≤ 0.5728… (см. [2]). Значение γ = 0.225 близко к левой границе этого интервала и использовалось в двух методах из [13]. А значение γ = 0.5728… (правая граница интервала) является единственным, при котором метод L-устойчив и имеет 4-й порядок. В результате сравнения характеристик мы выбрали значение γ = 0.2204…, при котором метод имеет 4-й порядок (см. строку 1 в табл. 2). Метод с таким значением γ был предложен в [7] и является наиболее эффективным среди пятистадийных L(α)-устойчивых методов. Он не является L-устойчивым, но ниже будет показано, что даже при решении жесткой задачи с чисто мнимым спектром матрицы Якоби он показывает приемлемые результаты. В табл. 1 (строки 3, 4, 6, 7) приведены также значения γ  методов, построенных в разд. 4, 5 и удовлетворяющих дополнительным условиям порядка для ДАУ индексов 2 и 3.

Рассмотрим теперь функцию R(z) шестистадийных методов 4-го порядка. В этом случае коэффициенты погрешности в (2.2) находим по формулам

На фиг. 1б приведены графики зависимостей α, C₅ и C₆ от γ на интересующем нас интервале, а в строках 2–5 табл. 2 приведены характеристики функции устойчивости при некоторых значениях γ. В пределах этого интервала метод будет L-устойчивым при γ ≥ 0.2479… (см. [2]). Наиболее удобно близкое к граничному значение γ = 0.25, которое использовалось при построении методов 4‑го порядка в [2], [7]–[10], [13], [14], [21]. В [2] рекомендовалось также значение γ = 4/15 = 0.2666…, при котором ${{C}_{5}}$ и ${{C}_{6}}$ малы. Отметим, что при 0.164 ≤ γ ≤ 0.191 коэффициенты погрешности невелики, а α > 89.9°. Значение γ = 1/ 6 – наиболее удобное из этого интервала. Методы с таким γ предлагались в [9], [10], [14]. Близкое к этому значение γ = 0.1744… (один из корней многочлена $1 - 20\gamma + 120{{\gamma }^{2}} - 240{{\gamma }^{3}} + 120{{\gamma }^{4}}$) обеспечивает 2-й порядок L-затухания.

3. ТОЧНОСТЬ

Главным показателем точности методов численного решения ОДУ является порядок аппроксимации. Условия, обеспечивающие порядок p метода Рунге–Кутты, можно представить в виде

где e(T_ij) – коэффициенты погрешности метода; T_ij – корневые деревья порядка i, соответствующие этим коэффициентам; ${{\nu }_{i}}$ – число различных деревьев порядка i. Для i ≤ 6 имеем ${{\nu }_{1}} = {{\nu }_{2}} = 1$, ${{\nu }_{3}} = 2$, ${{\nu }_{4}} = 4$, ${{\nu }_{5}} = 9$, ${{\nu }_{6}} = 20$. Условия порядка до 5-го включительно вместе с соответствующими деревьями приведены в [14], [26].

В общем случае все коэффициенты погрешности различны, но если стадийный порядок больше 1, то число различных коэффициентов сокращается. Для методов 2‑го стадийного порядка справедливы равенства

Для методов ESDIRK из условия 1-го стадийного порядка получаем

Коэффициенты a_i1 не входят во все остальные условия, поэтому их вычисляют в последнюю очередь. Из условия 2-го стадийного порядка имеем

Остальные коэффициенты находим исходя из условий порядка (3.1) для 2 < i ≤ p, необходимого условия L(α)-устойчивости $R\left( \infty \right) = 0$ и некоторых дополнительных условий (например, условий порядка для ДАУ индексов 2 и 3).

Основная трудность при построении методов высоких порядков (4 и выше) заключается в необходимости обеспечить выполнение большого числа алгебраических условий. Учет диагональной формы матрицы A позволяет упростить эти условия, в результате они становятся не сложнее, чем для явных методов. Упрощенные условия порядка для методов ESDIRK до 5-го порядка включительно приведены в [9], [14]. Пусть выполняются условия 2-го стадийного порядка (3.2), (3.3). Тогда для обеспечения 3-го порядка метода дополнительно должно выполняться условие

а для обеспечения 4-го порядка должны выполняться также и условия

Кроме выполнения условий порядка потребуем выполнения необходимого условия L(α)-устойчивости, которое запишется в виде

где

При p = s – 1 выполнение этого условия обеспечивается, если γ – корень многочлена D_p(γ), а при p = s – 2 условие (3.6) приводится к виду

Точность решения ОДУ методом порядка p зависит, прежде всего, от размера шага и от коэффициентов погрешности $e\left( {{{T}_{{p + 1,i}}}} \right)$. Используя свободные коэффициенты метода как оптимизируемые параметры, можно повысить точность метода, минимизировав коэффициенты погрешности. Такой подход является обычным при построении методов Рунге–Кутты.

При решении жестких ОДУ реальный порядок метода может быть ниже классического порядка, что приводит к заметному снижению точности решения. Для исследования этого явления, которое получило известность как феномен снижения порядка, Протеро и Робинсон (см. [24]) исследовали уравнение

с точным решением y(t) = φ(t). Используя разложение φ(t) в ряд Тейлора, получаем локальную ошибку метода стадийного порядка q в виде где ${{e}_{i}}\left( z \right) = z{{{\mathbf{b}}}^{{\text{{\rm T}}}}}{{\left( {{\mathbf{I}} - z{\mathbf{A}}} \right)}^{{ - 1}}}({{{\mathbf{c}}}^{i}} - i{\mathbf{A}}{{{\mathbf{c}}}^{{i - 1}}}) + (1 - i{{{\mathbf{b}}}^{{\text{T}}}}{{{\mathbf{c}}}^{{i - 1}}})$ – предложенные в [7] функции погрешности. Глобальная ошибка выражается формулой где δ_{n+ 1} – локальная ошибка на (n + 1)-м шаге. Для жестко точных методов с явной 1-й стадией функции погрешности можно представить в виде

В [8], [9], [11], [14] были рассмотрены также функции погрешности e_ij(z), полученные при анализе ошибок решения простейших модельных уравнений, отличных от уравнения Протеро–Робинсона. Но при этом для всех j имеем ${{e}_{{q + 1,j}}}\left( z \right) \equiv {{e}_{{q + 1}}}\left( z \right)$. Таким образом, функция ${{e}_{{q + 1}}}\left( z \right)$ задает главный член погрешности при решении жестких модельных уравнений, поэтому далее будем рассматривать только функцию e₃(z).

Анализ ошибки численного решения уравнения (3.8) в зависимости от величины z = hλ показал важность понятий жесткой точности и стадийного порядка для эффективного решения жестких задач. Жесткая точность обеспечивает малую ошибку при больших по модулю значениях z, а высокий стадийный порядок ограничивает ошибку при умеренных z. Снижение точности и порядка тем заметнее, чем больше разность между классическим порядком p и стадийным порядком q. Можно ограничить снижение точности, если минимизировать функцию ${{e}_{3}}\left( z \right)$. Методы ESDIRK с минимизированной функцией погрешности предлагались в [7]–[9], [14]. В [9], [14], [27] были рассмотрены также методы, имеющие ${{e}_{3}}\left( z \right) \equiv 0$, но они требуют выполнения двух дополнительных стадий.

Обсудим теперь точность решения ДАУ методами ESDIRK. Системы ДАУ индекса 1 имеют вид

где матрица ${{{\mathbf{g}}}_{{\mathbf{z}}}} = {{\partial {\mathbf{g}}\left( {{\mathbf{y}},{\mathbf{z}}} \right)} \mathord{\left/ {\vphantom {{\partial {\mathbf{g}}\left( {{\mathbf{y}},{\mathbf{z}}} \right)} {\partial {\mathbf{z}}}}} \right. \kern-0em} {\partial {\mathbf{z}}}}$ обратима в окрестности решения. Жестко точные методы, к которым относятся ESDIRK, обеспечивают точное выполнение алгебраического соотношения, поэтому порядки сходимости дифференциальных и алгебраических компонент совпадают с порядком метода: ${{p}_{y}} = {{p}_{z}} = p$.

Систему ДАУ индекса 2 можно привести к виду

где матрица g_yf_z обратима в окрестности решения. Как следствие теоремы 5.2 из [28], порядки сходимости соответствующих компонент при решении таких задач методами ESDIRK (при p ≥ 3, q = 2) следующие: ${{p}_{y}} = \min (p,\;q + 1) = 3$, ${{p}_{z}} = q = 2$.

Систему ДАУ индекса 3 можно представить в виде

где матрица g_yf_zk_u обратима в окрестности решения. В [29] получены порядки сходимости компонент y, z, u при решении таких задач методами с обратимой матрицей A. Для методов с явной 1-й стадией аналогичных результатов мы не нашли, но численные эксперименты с методами ESDIRK давали оценки порядков ${{\tilde {p}}_{y}} = {{\tilde {p}}_{z}} = 2$, ${{\tilde {p}}_{u}} = 1$.

В [10], [11], [14] для исследования сходимости решения ДАУ индексов 2 и 3 использовались простые модельные уравнения, позволившие получить дополнительные условия, необходимые для повышения порядков сходимости различных компонент ДАУ. Для методов ESDIRK при R(∞) = 0, q = 2 эти условия имеют вид

В табл. 3 приведены необходимые условия сходимости с заданным порядком для компонент ДАУ, где необходимое условие для каждой компоненты отмечено знаком +. Эти условия являются необходимыми для рассмотренных в [10], [11], [14] модельных уравнений, а значит, и для уравнений более общего вида. На ряде тестовых задач мы убедились, что выполнение этих условий действительно обеспечивает указанные порядки, но у нас нет доказательства, что эти условия являются также и достаточными.

4. ПЯТИСТАДИЙНЫЕ МЕТОДЫ

Чтобы различать рассматриваемые методы, условимся обозначать их в виде ESDIRKsp(γ), где s – число стадий, p – порядок, γ – диагональный элемент.

Пятистадийный метод 4-го порядка должен удовлетворять условиям (3.3)–(3.5), из которых получаем

после чего коэффициенты a_i1 находим из (3.2). Такой метод будет иметь R(∞) = 0, если γ – корень многочлена ${{D}_{4}}\left( \gamma \right)$. Мы выбрали значение которое считаем наиболее подходящим (тогда метод L(89.55°)-устойчив и имеет малые значения двух из девяти коэффициентов погрешности 5-го порядка: $e\left( {{{T}_{{58}}}} \right) = e\left( {{{T}_{{59}}}} \right) = 0.135$). Альтернативное значение γ = 0.5728… обеспечивает L-устойчивость, но тогда $e\left( {{{T}_{{58}}}} \right) = e\left( {{{T}_{{59}}}} \right) = - 3.27$ и ${{c}_{2}} > 1$.

У нас остались два свободных параметра – ${{c}_{3}}$ и ${{c}_{4}}$. Их подбором можно минимизировать остальные коэффициенты погрешности, но это приводит к большим значениям коэффициентов метода, что нежелательно. Более заметный эффект получим, минимизировав функцию погрешности. При p = r = s – 1 функция ${{e}_{3}}\left( z \right)$ метода ESDIRK зависит только от γ и c₃ и имеет вид

В [9], [14] было показано, что неравенство $c_{3}^{ * } \leqslant {{c}_{3}} \leqslant c_{3}^{ * } + \gamma $ задает множество всех (Парето-оптимальных) значений c₃, изменяя которые невозможно уменьшить функцию $\left| {{{e}_{3}}\left( z \right)} \right|$ сразу во всех точках левой полуплоскости. Отметим также, что значение ${{c}_{3}} = c_{3}^{ * }$ обеспечивает выполнение равенства (3.9).

При заданном значении γ (4.2) интервал оптимальных значений c₃ получаем в виде $0.701\, \leqslant \,{{c}_{3}}\, \leqslant \,0.921$. Мы выбрали

Эти значения обеспечивают попадание c₃ в оптимальный интервал, а также L-устойчивость 3-й и 4-й стадий, тогда

Метод, задаваемый формулами (4.1)–(4.4), был предложен в [7], численные значения его коэффициентов приведены в [7], [9], [14]. Обозначим его через ESDIRK54(0.220).

Рассмотрим теперь построение пятистадийных методов, обладающих повышенной точностью при решении ДАУ индексов 2 и 3. Методы 4-го порядка не подходят для этого вследствие недостаточного числа свободных коэффициентов. Поэтому снизим порядок до 3-го и используем условия (3.2)–(3.4), (3.7), (3.9)–(3.11). В этом случае число алгебраических условий совпадает с числом коэффициентов метода. Мы нашли 12 методов, которые удовлетворяют этим условиям. Они разбиваются на 3 группы в зависимости от значений b₂ и b₃: 1) ${{b}_{2}} = 0,\;\;{{b}_{3}} \ne 0$ – 6 методов; 2) ${{b}_{2}} = 0,\;\;{{b}_{3}} = 0$ – 3 метода; 3) ${{b}_{2}} \ne 0,\;\;{{b}_{3}} \ne 0$ – 3 метода. Для всех методов ${{c}_{3}}$ задается формулой

Из всех 12 методов только два удовлетворяют нашим требованиям. Первый из них принадлежит 1-й группе, в которой γ – один из корней многочлена $1 - 24\gamma + 186{{\gamma }^{2}} - 600{{\gamma }^{3}} + 828{{\gamma }^{4}} - 432{{\gamma }^{5}}$ + + 72γ⁶. Его коэффициенты находим по формулам (3.2), (3.3), (4.5),

Обозначим этот метод через ESDIRK53(0.182).

Второй метод принадлежит 2-й группе, в которой γ – один из трех вещественных корней многочлена $2 - 36\gamma + 201{{\gamma }^{2}} - 432{{\gamma }^{3}} + 360{{\gamma }^{4}} - 72{{\gamma }^{5}}$ (два других корня – комплексно-сопряженные). Его коэффициенты находим по формулам (3.2), (3.3), (4.5),

Обозначим этот метод через ESDIRK53(0.216).

5. ШЕСТИСТАДИЙНЫЕ МЕТОДЫ

При построении шестистадийных методов 4-го порядка часто используют значение γ = 1/4, которое обеспечивает L-устойчивость и малые коэффициенты погрешности. В [13] при таком значении γ свободные параметры метода выбирались из условий L-устойчивости внутренних стадий и минимизации коэффициентов погрешности. Построенный метод ESDIRK4(3)6L [2]SA (см. [13], табл. 16) “is recommended as a good default method for solving stiff problems at moderate error tolerances”. В наших обозначениях это метод ESDIRK64(1/4).

В [10], [14] рассматривались шестистадийные методы ESDIRK 4-го порядка, удовлетворяющие условиям (3.9)–(3.12). При γ = 1/6 такие методы образуют однопараметрическое семейство со свободным параметром c₄. Из этого семейства мы выбрали метод, имеющий c₄ = 2/3 и таблицу Бутчера

Обозначим этот метод через ESDIRK64(1/6).

Рассмотрим также шестистадийные методы 3-го порядка, удовлетворяющие условиям (3.9)–(3.11). С уменьшением порядка появились дополнительные свободные параметры, которые позволили обеспечить удобную и эффективную реализацию методов с контролем ошибки. Приведем два таких метода.

Первый метод является L2(88.91°)-устойчивым (см. строку 6 в табл. 1) и имеет таблицу коэффициентов

Обозначим его через ESDIRK63(1/6).

Второй метод является L-устойчивым (см. строку 7 в табл. 1). При его построении мы старались минимизировать функцию e₃(z). Полученный метод ESDIRK63(1/5) имеет таблицу коэффициентов

Основные характеристики рассмотренных методов приведены в табл. 4, где

6. РЕЗУЛЬТАТЫ РАСЧЕТОВ С ПОСТОЯННЫМ РАЗМЕРОМ ШАГА

Чтобы обеспечить одинаковые условия для всех методов, задаем размер шага таким, чтобы на всем интервале было выполнено заданное число неявных стадий Nr. В этом случае будет выполнено N = Nr/r шагов размером h = T/N. На каждой неявной стадии выполняем достаточно большое число итераций, заведомо обеспечивающее сходимость.

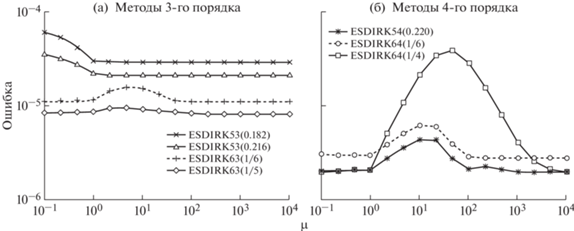
Посмотрим сначала, как влияет жесткость задачи на точность решения. Для этого используем задачу

решение которой ${{y}_{1}}\left( t \right) = \sin \;t$, ${{y}_{2}}\left( t \right) = \cos \;t$, а собственные числа матрицы Якоби равны –1 и –μ. Задаем Nr = 120 и вычисляем максимальное значение евклидовой нормы ошибки на всем интервале интегрирования. Полученные результаты (зависимости ошибки от μ) приведены на фиг. 2. Большой “горб” кривой для ESDIRK64(1/4) объясняется поведением функции погрешности e₃(z), которая у жестко точных методов достигает максимального значения при умеренных значениях z. У других методов такой горб проявляется значительно меньше или совсем отсутствует, что объясняется меньшими значениями функции погрешности и меньшей разностью p – q у методов 3-го порядка.

Вторая задача – тест PLATE (ее описание дано в [2]). Она содержит 80 переменных и имеет комплексный спектр матрицы Якоби. Интегрирование выполняем на интервале [0, 7] с размерами шага ${{h}_{1}} = {7 \mathord{\left/ {\vphantom {7 N}} \right. \kern-0em} N}$ и ${{h}_{2}} = 0.1{{h}_{1}}$, где $N = {{280} \mathord{\left/ {\vphantom {{280} r}} \right. \kern-0em} r}$. Точность решения оцениваем величиной

где y_i – точное, а ${{\tilde {y}}_{i}}$ – численное решение по i-й компоненте в конце интервала интегрирования. Величина scd (significant correct digits) показывает число правильных значащих цифр численного решения. Результаты приведены в табл. 5. Видно, что порядок метода практически не влияет на точность решения этой задачи, и лучшие результаты показывают методы, имеющие малые нормы функции погрешности (см. табл. 4). Такие результаты характерны для умеренно жестких задач, а также для задач с распределенным спектром матрицы Якоби, к которым относится PLATE.

Еще две задачи – ДАУ индексов 2 и 3. Задача индекса 2 задается уравнениями

и имеет решение ${{y}_{1}}\left( t \right) = \sin \left( {\sin t} \right)$, ${{y}_{2}}\left( t \right) = \cos \left( {\sin t} \right)$, $z\left( t \right) = \cos t$. Задаем Nr = 200 и вычисляем e_y и e_z – максимальные ошибки соответствующих компонент на всем интервале (для вектора ${\mathbf{y}} = {{\left( {{{y}_{1}},\;{{y}_{2}}} \right)}^{{\text{T}}}}$ используем евклидову норму ошибки). Вычисляем также оценки порядков сходимости ${{\tilde {p}}_{y}}$ и ${{\tilde {p}}_{z}}$ по соответствующим компонентам (для этого используем ошибки, полученные при размерах шага h и h/2). Результаты приведены в табл. 6.

Задача индекса 3 задается уравнениями

и имеет решение ${{y}_{1}}\left( t \right) = \sin \left( {\sin t} \right)$, ${{y}_{2}}\left( t \right) = \cos \left( {\sin t} \right)$, ${{z}_{1}}\left( t \right) = \cos \left( {\sin t} \right) \cdot \cos t$, z₂(t) = –sin(sint) · cost, $u\left( t \right) = {{\cos }^{2}}t$. Задаем Nr = 1000, и аналогично предыдущей задаче вычисляем ошибки и оценки порядков сходимости. Результаты приведены в табл. 7.

Из приведенных результатов следует, что методы ESDIRK53(0.220) и ESDIRK64(1/4), которые не удовлетворяют условиям (3.9)–(3.11), уступают остальным методам, для которых эти условия выполняются. Аналогичные результаты были получены и при решении других задач индексов 2 и 3.

7. РЕАЛИЗАЦИЯ МЕТОДОВ С КОНТРОЛЕМ ОШИБКИ

Для  реализации  с  переменным  размером  шага  были  выбраны  методы 3-го порядка ESDIRK63(1/6) и ESDIRK63(1/5) (как более удобные для реализации) и все три метода 4-го порядка. Используем экономичную схему реализации с двухшаговым прогнозом (см. [14], [30], [31]). Рассмотрим эту схему применительно к системе ДАУ

Формулы (n + 1)-го шага решения этой системы методом ESDIRK запишутся в виде

где выполнение неявных стадий сводится к решению нелинейных алгебраических уравнений.

Обозначим через f_y, f_z, g_y и g_z соответствующие матрицы частных производных, вычисленные в некоторой точке численного решения (предполагается, что эти матрицы не изменяются в течение нескольких шагов). Итерации метода Ньютона при реализации i-й стадии запишутся в виде

где m – число итераций.

Перед началом итераций нужно задать начальные значения $\Delta {\mathbf{Y}}_{i}^{0} = {\mathbf{Y}}_{i}^{0} - {{{\mathbf{y}}}_{n}}{\kern 1pt} $, $\Delta {\mathbf{Z}}_{i}^{0} = \,{\mathbf{Z}}_{i}^{0} - {{{\mathbf{z}}}_{n}}$, ${\mathbf{F}}_{i}^{0}$, ${\mathbf{G}}_{i}^{0}$. Для уменьшения числа итераций применяем двухшаговый прогноз, задаваемый в виде

где ${{{\mathbf{\bar {Y}}}}_{j}}$, ${{{\mathbf{\bar {Z}}}}_{j}}$ – стадийные значения предыдущего шага (на 1-м шаге принимаем ${{{\mathbf{\bar {Y}}}}_{j}} = {{{\mathbf{y}}}_{0}}$, ${{{\mathbf{\bar {Z}}}}_{j}} = {{{\mathbf{z}}}_{0}}$). Значения ${\mathbf{F}}_{i}^{0}$ и ${\mathbf{G}}_{i}^{0}$ обычно вычисляют как правые части в (7.1) при ${\mathbf{y}} = {\mathbf{Y}}_{i}^{0}$, ${\mathbf{z}} = {\mathbf{Z}}_{i}^{0}$. В экономичной схеме вместо этого используем такой же прогноз, как для переменных, в результате получаем

После выполнения итераций следует вычислить значение F_i, которое будет использовано на последующих стадиях. Определяем его из формулы вычисления Y_i в (7.2), откуда

Использование (7.3), (7.4) позволяет сэкономить одно вычисление правой части на каждой неявной стадии, а для жестких задач (как показали эксперименты) дает более точный результат по сравнению со стандартной схемой.

Остановимся на формулах прогноза. Для методов ESDIRK прогноз 2-го порядка формируем как значение интерполяционного многочлена, построенного по уже вычисленным трем стадийным значениям. Пусть для формирования прогноза используются два стадийных значения предыдущего шага: ${{{\mathbf{\bar {Y}}}}_{i}}$ и ${{{\mathbf{\bar {Y}}}}_{j}}$ (мы задаем i = 1 и  j – наибольшее значение, при котором $0.5 \leqslant {{c}_{j}} < 1$). Принимаем также $w = {h \mathord{\left/ {\vphantom {h {\bar {h}}}} \right. \kern-0em} {\bar {h}}}$, где $\bar {h}$ – размер предыдущего шага. Формулы прогноза на стадиях 2, 3, 4 запишутся в виде

На 5-й стадии имеет смысл формировать прогноз 3-го порядка в виде

где коэффициенты ${{\beta }_{{52}}}$, ${{\beta }_{{53}}}$, ${{\beta }_{{54}}}$ находим из уравнений (под порядком прогноза понимают порядок аппроксимации стадийного значения формулой прогноза).

На 6-й стадии к условиям порядка можно добавить условие L-сходимости прогноза. Для методов ESDIRK64(1/6) и ESDIRK64(1/4) такой прогноз 3-го порядка принимаем в виде

где ${{\beta }_{{62}}},\; \ldots ,\;{{\beta }_{{65}}}$ находим из системы линейных уравнений

Для метода ESDIRK63(1/6) принимаем ${\mathbf{Y}}_{6}^{0} = {{\left( {{{{\mathbf{Y}}}_{4}} + 2{{{\mathbf{Y}}}_{5}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\mathbf{Y}}}_{4}} + 2{{{\mathbf{Y}}}_{5}}} \right)} 3}} \right. \kern-0em} 3}$, что обеспечивает L-сходимость прогноза, а для ESDIRK63(1/5) принимаем ${\mathbf{Y}}_{6}^{0} = {{{\mathbf{Y}}}_{5}}$.

Формулу прогноза последней стадии используем также и для формирования нормированной оценки ошибки, которую принимаем в виде

где Rtol – допустимая относительная ошибка, Atol – допустимая абсолютная ошибка. Такая оценка соответствует применению вложенной формулы, записанной в виде ${{{\mathbf{\hat {y}}}}_{{n + 1}}} = {{{\mathbf{y}}}_{{n + 1}}} - \delta {\mathbf{y}}$. Принимаем следующие значения коэффициента K: ESDIRK54(0.220) – K = 0.5, ESDIRK64(1/6) – K = 0.125, ESDIRK64(1/4) – K = 0.0712123 (это значение эквивалентно вложенной формуле в [13], табл. 16), ESDIRK63(1/6) и ESDIRK63(1/5) – K = 0.25. Шаг считаем успешным, если err ≤ 1. Размер следующего шага принимаем в виде ${{h}_{{{\text{new}}}}} = fac \times er{{r}^{{ - {1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0em} p}}}}h$, где fac = 0.7 для методов 3-го порядка и fac = 0.75 для методов 4-го порядка.

Сходимость итерационных схем решения задачи Коши исследовалась в [32], [33]. При определенных условиях каждая итерация с неточной матрицей Якоби повышает порядок схемы на 1 до тех пор, пока не будет достигнут порядок метода. Численные эксперименты показали, что при использовании экономичной схемы и приведенных формул прогноза для решения жестких ОДУ достаточно выполнить две итерации, первая из которых не требует вычисления правой части. На последней стадии добавляем 3-ю итерацию, которая позволяет получить оценку сходимости итераций в виде $\theta = {{{{\delta }_{3}}} \mathord{\left/ {\vphantom {{{{\delta }_{3}}} {{{\delta }_{2}}}}} \right. \kern-0em} {{{\delta }_{2}}}}$, где ${{\delta }_{i}}$ – норма приращения стадийных значений на i-й итерации. Перерасчет матрицы Якоби выполняем, если θ > 0.1 и при этом ${{\delta }_{3}}$ не очень мало – это позволяет исключить перерасчет при незначительном изменении матрицы.

При решении ДАУ высших индексов сходимость итераций более медленная, поэтому следует предусмотреть возможность выполнения большего числа итераций. В этом случае усложняется также контроль ошибки для переменных высших индексов. Исследуем точность этих компонент на примере системы

где переменная z имеет индекс 2, а переменная u – индекс 3. Глобальные ошибки решения этих уравнений запишутся в виде где ${{\alpha }_{0}} = R\left( \infty \right)$, ${{\alpha }_{1}} = \mathop {\lim }\limits_{z \to \infty } z\left( {R\left( z \right) - {{\alpha }_{0}}} \right)$, ${{\alpha }_{2}} = \mathop {\lim }\limits_{z \to \infty } z\left[ {z\left( {R\left( z \right) - {{\alpha }_{0}}} \right) - {{\alpha }_{1}}} \right]$, $\delta {{y}_{{n + 1}}}$, $\delta {{z}_{{n + 1}}}$, $\delta {{u}_{{n + 1}}}$ – локальные ошибки соответствующих компонент. Для жестко точных методов ${{y}_{n}} = {{\varphi }_{n}}$ и $\delta {{y}_{{n + 1}}} = 0$.

Аналогичные выражения получаем для вложенной формулы (заменяем α_i, $\delta {{y}_{{n + 1}}}$, $\delta {{z}_{{n + 1}}}$, $\delta {{u}_{{n + 1}}}$ соответствующими значениями ${{\hat {\alpha }}_{i}}$, $\delta {{\hat {y}}_{{n + 1}}}$, $\delta {{\hat {z}}_{{n + 1}}}$, $\delta {{\hat {u}}_{{n + 1}}}$ вложенного метода). Из приведенных выражений следует, что в оценке ошибки появляются составляющие, пропорциональные h^–1, а также составляющие, пропорциональные только глобальной ошибке. В результате размер шага может уменьшаться до нуля, что приводит к аварийной остановке численного решения. Чтобы этого не происходило, в [34] предлагалось специальным образом масштабировать либо игнорировать оценки ошибки для переменных высших индексов.

Заметим, что если ${{\hat {\alpha }}_{0}} = {{\alpha }_{0}}$, ${{\hat {\alpha }}_{1}} = {{\alpha }_{1}}$ и при этом ${{\alpha }_{0}} = {{\alpha }_{1}} = 0$, то глобальные ошибки будут равны локальным ошибкам. В этом случае можно применять обычный контроль ошибки для всех переменных, не опасаясь аварийной остановки. Вложенная пара такого типа была построена на основе метода ESDIRK63(1/6), в который добавлена еще одна (6-я) стадия специально для оценивания ошибки. Эта же стадия используется как прогноз ${\mathbf{Y}}_{7}^{0} = {{{\mathbf{Y}}}_{6}}$ для заключительной стадии. Полученный метод имеет таблицу Бутчера

Здесь основной шестистадийный метод (5.1) и вложенная формула образуют семистадийный метод, который обозначим через ESDIRK73(1/6).

Аналогичным образом на основе метода ESDIRK63(1/5) построен метод ESDIRK73(1/5), 6-я стадия которого является вложенной формулой для оценивания ошибки и имеет коэффициенты

(но в этом случае ${{\hat {\alpha }}_{1}} = {{\alpha }_{1}} \ne 0$). Численные эксперименты показали, что методы (вложенные пары) ESDIRK73(1/6) и ESDIRK73(1/5) более эффективны, чем соответствующие методы (пары) ESDIRK63(1/6) и ESDIRK63(1/5), поэтому далее приводим результаты методов ESDIRK73(1/6) и ESDIRK73(1/5).

8. РЕЗУЛЬТАТЫ РАСЧЕТОВ С ПЕРЕМЕННЫМ РАЗМЕРОМ ШАГА

При реализации всех методов используем одинаковое число итераций и одинаковые условия обновления матрицы Якоби. При решении ОДУ выполняем две итерации экономичной схемы на предварительных стадиях и три итерации на последней стадии. Для решения ДАУ индекса 3 такого числа итераций оказалось недостаточно, в этом случае выполняем три итерации на каждой стадии и вычисляем матрицу Якоби на каждом шаге. Вложенные формулы (6-е стадии) в методах ESDIRK73(1/6) и ESDIRK73(1/6) реализуем, делая одну итерацию (без вычисления правой части) при решении ОДУ и две итерации при решении ДАУ.

Для решения с переменным шагом были выбраны четыре жестких теста: VDPOL, HIRES, PLATE и BEAM, подробные описания которых приведены в [2], [35]. Интервалы интегрирования и размеры начального шага берем, как в [35], [36]. Для всех задач принимаем Rtol = Atol = Tol, где Rtol – относительная допустимая ошибка, Atol – абсолютная допустимая ошибка. Как и в [35], [36] точность решения оцениваем значениями scd (6.1) и

где ${{y}_{i}}$ – точное, а ${{\tilde {y}}_{i}}$ – численное решение по i-й компоненте в конце интервала интегрирования. При решении задачи BEAM значение scd вычисляем для первых 40 (из 80) переменных, поскольку “they refer to the physically important quantities” [35]. Каждую задачу решаем при двух значениях Tol: 10^–3 и 10^–4, но если при Tol = 10^–3 точность решения низкая (scd < 1), то приводим результаты при Tol = 10^–4, 10^–5. Вычислительные затраты оцениванием числом вычислений правой части Nf и числом вычислений матрицы Якоби NJ. Результаты расчетов приведены в табл. 8–11. Приводим также некоторые результаты решателя RADAU5, взятые из [36]. Результаты решения этих задач другими известными методами приведены в [35], [36].

Приведенные результаты подтверждают высокую эффективность методов ESDIRK при решении жестких задач с умеренной точностью. Задача BEAM имеет чисто мнимый спектр матрицы Якоби. По этой причине многие известные методы требуют большого объема вычислений при решении этой задачи даже с невысокой точностью (см. [35], [36]). Рассмотренные методы ESDIRK (в том числе и L(α)-устойчивые) успешно решают эту задачу с малыми вычислительными затратами. Этот факт показывает, что строгое соблюдение условия L-устойчивости не является необходимым при построении эффективных методов, достаточно, чтобы метод был L(α)-устойчивым при α, близком к 90°.

В табл. 12 приведены результаты решения системы ДАУ индекса 3 (6.3). Задаем Rtol = Tol, Atol = 10^–4Tol, ${{h}_{0}} = Tol$ и вычисляем ошибки по соответствующим компонентам. Из всех методов только ESDIRK73(1/6) обеспечил устойчивое управление размером шага при контроле ошибки по всем компонентам. Поэтому в методах ESDIRK64(1/6), ESDIRK64(1/4) и ESDIRK73(1/5) контроль ошибки выполняем по y- и z-компонентам, а в методе ESDIRK54(0.220) – только по y-компоненте (в отличие от других методов, вложенная формула в ESDIRK54(0.220) имеет ${{\hat {\alpha }}_{0}} \ne 0$). Чтобы  получить  приемлемые  результаты, пришлось уменьшить значение Tol для метода ESDIRK54(0.220) на 2 порядка и для ESDIRK64(1/4) на порядок. Три других метода оказались более эффективными, при этом для решения задач индекса 3 удобнее всего использовать метод ESDIRK73(1/6), позволяющий осуществлять контроль ошибки по всем переменным.