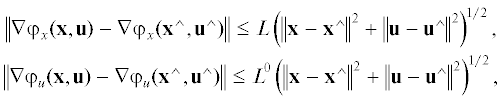Журнал вычислительной математики и математической физики, 2022, T. 62, № 5, стр. 777-789
Непрерывный проекционный обобщенный экстраградиентный квазиньютоновский метод второго порядка для решения седловых задач
В. Г. Малинов *
УлГУ
432000 Ульяновск, ул.Толстого, 42, Россия
* E-mail: vgmalinov@mail.ru
Поступила в редакцию 16.09.2020
После доработки 04.10.2021
Принята к публикации 14.01.2022
- EDN: LMNXKR
- DOI: 10.31857/S0044466922050088
Аннотация
Исследуется указанный метод решения седловых задач для выпукло-вогнутых гладких функций с липшицевыми частными градиентами на выпуклом замкнутом подмножестве конечномерного евклидова пространства. Средствами выпуклого анализа доказаны сходимость и экспоненциальная скорость сходимости метода. Библ. 11.
1. ВВЕДЕНИЕ
1.1. Известны множество методов оптимизации и меньшее число методов для решения седловых задач (см. [1]–[11]); последние предназначены для отыскания седловых точек или точек равновесия. Напомним, точку (x*, u*) ∈ Q × U ⊂ En × Em, называют седловой точкой всякой функции φ(x, u), ${\mathbf{x}} \in Q \subset {{E}^{n}}$, ${\mathbf{u}} \in U \subset {{E}^{m}}$, с непустыми множествами $Q \subset {{E}^{n}}$, $U \subset {{E}^{m}}$, в евклидовых пространствах ${{E}^{n}}$ и ${{E}^{m}}$, если эта точка есть решение системы неравенств:
(1.1)
$\varphi ({\mathbf{x}}*,{\mathbf{u}}) \leqslant \varphi ({\mathbf{x}}*,{\mathbf{u}}*) \leqslant \varphi ({\mathbf{x}},{\mathbf{u}}*)\quad \forall {\mathbf{x}} \in Q,\quad {\mathbf{u}} \in U.$Существуют непрерывные проекционные методы отыскания седловых точек (НПМОСТ) и минимизации (НПММ), и итеративные для соответствующих математических моделей (ММ) исследуемых процессов. К разработке новых методов решения этих задач приводят экстремальные задачи теории игр, математической экономики, математической физики, оптимального управления [1]–[10]. В связи с наличием все более сложных ММ, приводящих к седловым задачам, и небогатым разнообразием методов их решения, актуальна задача исследования новых НПМОСТ [1]–[3], [7], [10], [11].
В работах [3], [10] детально рассмотрены применения седловых методов, в [10] седловые задачи охарактеризованы “как мостик, через который можно попытаться перенести развитую технику решения задач оптимизации для решения игровых задач”, исследованы управляемые (обратными связями по производной, по невязке и смешанными) НПМОСТ второго порядка. Разработана методика преобразования седловых задач и методов к равновесным. В [11] построены и изучены не исследованные в [10] равновесные методы второго порядка на основе управляемого (дифференциального) НПМОСТ второго порядка. В [3] исследовано, наряду с другими, несколько перспективных игровых равновесных методов. Здесь предлагается и исследуется базовый НПМОСТ второго порядка с переменной метрикой, на основе которого можно построить частные методы решения конкретных случаев седловых и равновесных задач в перечисленных науках.
Рассматриваемые НПМОСТ соответствуют задаче Коши для обыкновенных дифференциальных уравнений (ОДУ), описывающих динамические процессы. Существенно одно из благоприятных свойств дифференциальных моделей — возможность использования численных методов вычислительной математики, для решения ОДУ в алгоритмах численной реализации НПМОСТ и НПММ [3]–[6].
Седловые задачи для конкретных математических моделей решаются при своих требованиях (к пространствам, множествам и функциям), выражающихся в постановке задачи и влияющих на метод ее решения. В этой работе предлагается и исследуется НПМОСТ для решения задачи в следующей постановке.
1.2. Постановка задачи
Требуется решить задачу об отыскании седловой точки $\left( {{\mathbf{x}}*,{\mathbf{u}}*} \right)$ ∈ $Q \times U$ ⊂ ${{E}^{n}} \times {{E}^{m}}$ функции $\varphi ({\mathbf{x}},{\mathbf{u}})$.
Предполагаем следующее: а) множества $Q \subset {{E}^{n}}$, $U \subset {{E}^{m}}$, $Q \times U$ ⊂ ${{E}^{n}} \times {{E}^{m}}$ непустые выпуклые замкнутые; б) выпукло-вогнутая функция $\varphi ({\mathbf{x}},{\mathbf{u}})$ с овражными гиперповерхностями уровней определена в окрестности подмножества $W \subset Q \times U$ ⊂ ${{E}^{n}} \times {{E}^{m}}$, выпукла по ${\mathbf{x}} \in Q \subset {{E}^{n}}$ и вогнута по ${\mathbf{u}} \in U \subset {{E}^{m}}$, т.е. для всех фиксированных ${\mathbf{u}} \in U$ функция $g({\mathbf{x}}) = \varphi ({\mathbf{x}},{\mathbf{u}})$ выпукла на $Q \subset {{E}^{n}}$, а $\forall \;{\mathbf{x}} \in Q$ фиксированного функция $h({\mathbf{u}}) = \varphi ({\mathbf{x}},{\mathbf{u}})$ вогнута на $U \subset {{E}^{m}}$; в) множество седловых точек $\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right)$ функции $\varphi ({\mathbf{x}},{\mathbf{u}})$ на $W \subset {{E}^{n}} \times {{E}^{m}}$ непустое, ${{W}_{*}}$ = ${{Q}_{*}} \times U* \ne \emptyset $; г) частные градиенты функции $\varphi ({\mathbf{x}},{\mathbf{u}})$ липшицевы на $Q \times U$,
где $L > 0$, ${{L}^{0}} > 0$ – константы Липшица. В терминах оператора проектирования седловая точка $\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right) \in {{W}_{*}}$ задачи (1.1) характеризуется равенствами(1.3)
${\mathbf{x}}* = {{P}_{Q}}\left[ {{\mathbf{x}}{\kern 1pt} * - \;\tau \nabla {{\varphi }_{x}}\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right)} \right],\quad {\mathbf{u}}* = {{P}_{U}}\left[ {{\mathbf{u}}{\kern 1pt} * + \;\tau \nabla {{\varphi }_{u}}\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right)} \right],\quad \tau > 0,$1.3. Траектории не всех НПМОСТ сходятся к седловой точке. Например, сходимость на седловых задачах простейшего итеративного метода проекции градиента седлового [1] доказана лишь при весьма ограничительных предположениях сильной выпукло-вогнутости, что не выполняется для многих нужных классов седловых задач [2]. Поэтому предложено несколько способов устранения этого недостатка. Таковым является и изменение самого НПМОСТ: построением экстраградиентного метода (ЭГМ) [2]; включением в ОДУ управления с помощью прогноза и обратных связей [3], приводящим к ЭГМ. Успешный способ улучшения сходимости воплощен в НПМОСТ, использующих прогноз и, аналогично методам минимизации [4]–[6], операторы переменной метрики.
Цель данной работы в широком смысле — распространение подхода к построению методов минимизации из работ [4]–[6] на НПМОСТ; точнее, обоснование НПМОСТ второго порядка с лучшими свойствами, построенного на основе синтеза идеи и теории: НПММ переменной метрики [4], проекционного обобщенного двухточечного экстраградиентного метода минимизации квазиньютоновского (ПОДЭМК) [5], непрерывного проекционного обобщенного экстраградиентного квазиньютоновского метода минимизации (НПОЭКМ) второго порядка [6], итеративного ПОДЭМК седлового из [7]. Наша цель в узком смысле — исследование предложенного НПОЭКМ седлового (НПОЭКМС) второго порядка.
Последнее включает обоснование вспомогательных утверждений, доказательство сходимости НПОЭКМС и оценки скорости его сходимости для выпукло-вогнутых функций.
2. ПРЕДЛАГАЕМЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ
2.1. Предлагается для решения задачи (1.1)–(1.3) НПОЭКМС второго порядка, обычно записываемый в виде задачи Коши для системы ОДУ:
(2.1)
$\begin{gathered} \alpha (t){\mathbf{u}}{\kern 1pt} ''(t) + \beta (t){\mathbf{u}}{\kern 1pt} '(t) + {\mathbf{u}}(t) = {{P}_{U}}[{\mathbf{v}}(t) + \lambda (t){{{\mathbf{G}}}^{{ - 1}}}({\mathbf{v}}(t))\nabla {{\varphi }_{u}}({\mathbf{y}}(t),{\mathbf{v}}(t))], \\ {\mathbf{y}}(t) = {\mathbf{x}}(t) - \sigma (t){\mathbf{x}}{\kern 1pt} '(t),\quad {\mathbf{v}}(t) = {\mathbf{u}}(t) - \theta (t){\mathbf{u}}{\kern 1pt} '(t),\quad t \geqslant 0, \\ \end{gathered} $В частности, этим условиям удовлетворяют такие параметры−функции НПОЭКМС (2.1): $\alpha (t) = {{\alpha }_{0}} + \tfrac{1}{{1 + t}}$, $\beta (t) = {{\beta }_{0}} + \frac{1}{{2 + t}}$, $\gamma (t) = {{\gamma }_{0}} + \frac{1}{{3 + t}}$, $\lambda (t) = {{\lambda }_{0}} + \frac{1}{{3 + t}}$, $\sigma (t) = {{\sigma }_{0}} + \frac{1}{{t + 1}}$, $\theta (t) = {{\theta }_{0}} + \frac{1}{{t + 1}}$.
Операторы ${\mathbf{B}}({\mathbf{x}}):{{E}^{n}} \to {{E}^{n}}$ $\forall {\mathbf{x}} \in {{E}^{n}}$ фиксированного и ${\mathbf{G}}({\mathbf{u}}):{{E}^{m}} \to {{E}^{m}}$ $\forall {\mathbf{u}} \in {{E}^{m}}$ фиксированного — положительно-определенные самосопряженные линейные, изменяющие метрику пространства; они в (2.1) таковы, что
(2.2)
$m{{\left\| {\mathbf{v}} \right\|}^{2}} \leqslant ({\mathbf{B}}({\mathbf{x}}){\mathbf{v}},{\mathbf{v}}) \leqslant M{{\left\| {\mathbf{v}} \right\|}^{2}},\quad 0 < m \leqslant M,\quad {\mathbf{v}},{\mathbf{x}} \in {{E}^{n}},$(2.3)
$m{{\left\| {\mathbf{v}} \right\|}^{2}} \leqslant ({\mathbf{G}}({\mathbf{u}}){\mathbf{v}},{\mathbf{v}}) \leqslant M{{\left\| {\mathbf{v}} \right\|}^{2}},\quad 0 < m \leqslant M,\quad {\mathbf{v}},{\mathbf{u}} \in {{E}^{m}}.$Обратные операторы таковы, что
(2.4)
$\begin{gathered} {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}M \leqslant ({{{\mathbf{B}}}^{{ - 1}}}({\mathbf{x}}){\mathbf{v}},{\mathbf{v}}) \leqslant {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}m,\quad {\mathbf{v}},{\mathbf{x}} \in {{E}^{n}}, \\ {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}M \leqslant ({{{\mathbf{G}}}^{{ - 1}}}({\mathbf{u}}){\mathbf{v}},{\mathbf{v}}) \leqslant {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}m,\quad {\mathbf{v}},{\mathbf{u}} \in {{E}^{m}}. \\ \end{gathered} $2.2. Для метода (2.1)−(2.4) характеристики вида (1.3) седловой точки $\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right)$ имеют следующий вид:
(2.5)
${\mathbf{x}}* = {{P}_{Q}}\left[ {{\mathbf{x}}{\kern 1pt} * - \;\gamma (t){{{\mathbf{B}}}^{{ - 1}}}({\mathbf{x}}*)\nabla {{\varphi }_{x}}\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right)} \right],\quad \gamma > 0,$(2.6)
${\mathbf{u}}* = {{P}_{U}}\left[ {{\mathbf{u}}{\kern 1pt} * + \;\lambda (t){{{\mathbf{G}}}^{{ - 1}}}({\mathbf{u}}*)\nabla {{\varphi }_{u}}\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right)} \right],\quad \lambda > 0.$2.3. Замечание. Отметим следующее.
1. В этой работе для простоты обозначены через $\nabla {{\varphi }_{x}}$ − частный градиент по первому аргументу, а $\nabla {{\varphi }_{u}}$ – по второму.
2. Поскольку в (2.1) операторы проектирования в исходной метрике, критерии проекций ${\mathbf{w}} = {{P}_{Q}}({\mathbf{v}})$ по первой и ${\mathbf{s}} = {{P}_{U}}({\mathbf{v}})$ по второй переменным будут по исходной метрике (см. [8, с. 189]):
(2.7)
$({\mathbf{w}} - {\mathbf{v}},{\mathbf{x}} - {\mathbf{w}}) \geqslant 0,\quad {\mathbf{x}} \in Q,\quad ({\mathbf{s}} - {\mathbf{v}},{\mathbf{u}} - {\mathbf{s}}) \geqslant 0,\quad {\mathbf{u}} \in U.$3. Имеются и непрерывные, и итеративные, проекционные методы с операторами проектирования: ${{P}_{Q}}(.)$, ${{P}_{U}}(.)$ – в исходной метрике; $P_{Q}^{{{\mathbf{G}}({\mathbf{v}}(t))}}$, $P_{U}^{{{\mathbf{G}}({\mathbf{u}}(t))}}$ – в новой метрике.
3. ВСПОМОГАТЕЛЬНЫЕ УТВЕРЖДЕНИЯ
Приведем неравенства, дополняющие необходимый для обоснования сходимости и оценки скорости сходимости методов математический аппарат.
3.1. Лемма 1. Если для (2.1) при любом фиксированном ${\mathbf{u}} \in U \in {{E}^{m}}$ выпуклая функция ${{g}_{1}}\left( {\mathbf{x}} \right) \in {{C}^{{1,1}}}(Q)$ такова, что $\nabla {{g}_{1}}({\mathbf{x}}) = {{{\mathbf{B}}}^{{ - 1}}}({\mathbf{x}})\nabla {{\varphi }_{x}}\left( {{\mathbf{x}},{\mathbf{u}}} \right)$,
(3.1)
$\left( {\nabla {{g}_{1}}\left( {{\mathbf{x}}{\kern 1pt} *} \right),{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right) \geqslant 0,\quad {\mathbf{x}} \in Q.$Доказательство. Из характеристического свойства (2.5) седловой точки, критерия проекции ${\mathbf{w}} = {{P}_{Q}}({\mathbf{v}})$, ${\mathbf{v}} \in {{H}_{Q}}$ из (2.7), и равенства из условия леммы 1, имеем
(3.1a)
$({\mathbf{x}}{\kern 1pt} * - \;{\mathbf{x}}{\kern 1pt} * - \;\gamma {{{\mathbf{B}}}^{{ - 1}}}({\mathbf{x}}*)\nabla {{\varphi }_{x}}\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right),{\mathbf{x}} - {\mathbf{x}}*) = \gamma (\nabla {{g}_{1}}({\mathbf{x}}*),{\mathbf{x}} - {\mathbf{x}}*) \geqslant 0,$3.2. Лемма 2. Если для (2.1) при любом фиксированном ${\mathbf{x}} \in Q \subset {{E}^{n}}$ вогнутая функция ${{h}_{1}}\left( {\mathbf{u}} \right) \in {{C}^{{1,1}}}(U)$ такова, что $\nabla {{h}_{1}}\left( {\mathbf{u}} \right)$ = ${{{\mathbf{G}}}^{{ - 1}}}({\mathbf{u}})\nabla {{\varphi }_{u}}\left( {{\mathbf{x}},{\mathbf{u}}} \right)$,
(3.2)
$(\nabla {{h}_{1}}\left( {{\mathbf{u}}{\kern 1pt} *} \right),{\mathbf{u}}{\kern 1pt} * - \;{\mathbf{u}}) \geqslant 0,\quad {\mathbf{u}} \in U.$Доказательство проведено для работы [7].
4. ОБОСНОВАНИЕ СХОДИМОСТИ НПОЭКМС (2.1)
Теорема 1. Пусть выполнены предположения а)−г) о задаче и функции $\varphi ({\mathbf{x}},{\mathbf{u}})$ из разд.1 и функциях-параметрах из п. 2.1; неравенства (2.2)−(2.7); леммы 1 и 2; параметры метода (2.1), функции $\alpha (t),\beta (t),\gamma (t),\sigma (t),\theta (t)$ таковы, что
(4.1)
$\begin{gathered} 0 < \gamma (t) < (\beta + 2\sigma ){\text{/}}[K(\beta + \sigma )],\quad 0 < \sigma < 3\beta {\text{/}}2, \\ 0 < \lambda < \min \left\{ {\frac{{2\beta (\beta + \theta ) - 2\alpha }}{{R(\beta + \theta )(\beta + \theta )}};\frac{{3 - 2\beta - 2\theta }}{{2R}}} \right\},\quad \beta + \sigma < 3{\text{/}}2, \\ \end{gathered} $Тогда НПОЭКМС (2.1), (4.1) $\forall \left( {{{{\mathbf{x}}}^{0}},{{{\mathbf{u}}}^{0}}} \right) \in {{E}^{n}} \times {{E}^{m}}$ по норме сходится к седловой точке $\left( {{\mathbf{x}}*,{\mathbf{u}}{\kern 1pt} *} \right)$ ∈ ∈ ${{Q}_{*}} \times U{\kern 1pt} *$ функции $\varphi ({\mathbf{x}},{\mathbf{u}})$,
(4.2)
$\begin{gathered} \int\limits_0^{ + \infty } {\left[ {{{{\left\| {{\mathbf{x}}{\text{(}}s{\text{)}} - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}{\kern 1pt} '{\kern 1pt} {\text{(}}s{\text{)}}} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}{\kern 1pt} ''{\kern 1pt} {\text{(}}s{\text{)}}} \right\|}}^{2}}} \right]ds} < + \infty , \\ \left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\| + \left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\| + \left\| {{\mathbf{x}}{\kern 1pt} ''(t)} \right\| \to 0,\quad t \to \infty , \\ \end{gathered} $(4.3)
$\begin{gathered} \int\limits_0^{ + \infty } {\left[ {{{{\left\| {{\mathbf{u}}{\text{(}}s{\text{)}} - {\mathbf{u}}{\kern 1pt} *} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}{\kern 1pt} '{\text{(}}s{\text{)}}} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}{\kern 1pt} ''{\kern 1pt} {\text{(}}s{\text{)}}} \right\|}}^{2}}} \right]ds} < + \infty , \\ \left\| {{\mathbf{u}}(t) - {\mathbf{u}}{\kern 1pt} *} \right\| + \left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\| + \left\| {{\mathbf{u}}{\kern 1pt} ''(t)} \right\| \to 0,\quad t \to \infty , \\ \end{gathered} $Доказательство. Представим первые два уравнения НПОЭКМС (2.1), пользуясь (2.7), в виде вариационных неравенств
(4.4)
$\begin{gathered} \left( {{\mathbf{w}}(t) - {\mathbf{y}}(t) + \gamma (t){{{\mathbf{B}}}^{{ - 1}}}({\mathbf{y}}(t))\nabla {{\varphi }_{x}}\left( {{\mathbf{y}}(t),{\mathbf{u}}(t)} \right),a - {\mathbf{w}}(t)} \right) \geqslant 0,\quad a \in Q, \\ \left( {{\mathbf{s}}(t) - {\mathbf{v}}(t) - \lambda (t){{{\mathbf{G}}}^{{ - 1}}}({\mathbf{v}}(t))\nabla {{\varphi }_{u}}\left( {{\mathbf{y}}(t),{\mathbf{v}}(t)} \right),b - {\mathbf{s}}(t)} \right) \geqslant 0,\quad b \in U, \\ \end{gathered} $Неравенства (4.4) преобразуем, пользуясь свойствами скалярного произведения, неравенством Коши–Буняковского, нерасширяющим свойством оператора проектирования (см. [8, с. 190]), а также (2.1), (4.1), леммами 1 и 2.
В первом неравенстве (4.4) положим $a = {\mathbf{x}}{\kern 1pt} *$, пользуясь леммой 1, неравенство (3.1) умножим на $\gamma > 0$, примем ${\mathbf{x}} = {\mathbf{w}}(t)$, полученные неравенства сложим и получим
(4.5)
$\left( {{\mathbf{w}}(t) - {\mathbf{y}}(t),{\mathbf{w}}(t) - {\mathbf{x}}{\kern 1pt} *} \right) \leqslant \gamma (t)\left( {\nabla {{g}_{1}}({\mathbf{y}}(t)) - \nabla {{g}_{1}}({\mathbf{x}}*),{\mathbf{x}}{\kern 1pt} * - \;{\mathbf{w}}(t)} \right),\quad t \geqslant 0.$Преобразуем (4.5). Для левой части, пользуясь (2.1), последовательно получаем
(4.6)
$ = \left( {\alpha {\mathbf{x}}{\kern 1pt} ''\; + \beta {\mathbf{x}}{\kern 1pt} ',{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right) + {{\left\| {\alpha {\mathbf{x}}{\kern 1pt} ''\; + \beta {\mathbf{x}}{\kern 1pt} '} \right\|}^{2}} + \sigma \left( {{\mathbf{x}}{\kern 1pt} ',{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right) + \alpha \sigma \left( {{\mathbf{x}}{\kern 1pt} ',{\mathbf{x}}{\kern 1pt} ''} \right) + \beta \sigma {{\left\| {{\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} = $Правую часть (4.5) оценим с помощью следующего неравенства (см. [8, с. 175])
Подставив эту оценку и (4.6) в (4.5), получим
(4.7)
$\alpha (t)\left( {{\mathbf{x}}{\kern 1pt} '',{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right) + {{a}_{1}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} ''{\kern 1pt} } \right\|}^{2}} + {{a}_{2}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} + {{a}_{3}}(t)\left( {{\mathbf{x}}{\kern 1pt} ',{\mathbf{x}}{\kern 1pt} ''} \right) + {{a}_{4}}(t)\left( {{\mathbf{x}}{\kern 1pt} ',{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right) \leqslant 0,\quad t \geqslant 0,\quad {\mathbf{x}}* \in {{Q}_{*}},$Неравенство (4.7) преобразуем с помощью тождеств
(4.8)
$\begin{gathered} 2({\mathbf{x}}{\kern 1pt} ''(t),{\mathbf{x}}{\kern 1pt} '(t)) = \frac{d}{{dt}}{{\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\|}^{2}};\quad 2({\mathbf{x}}{\kern 1pt} '(t),{\mathbf{x}}(t) - {\mathbf{x}}*) = \frac{d}{{dt}}{{\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}}; \\ ({\mathbf{x}}{\kern 1pt} '',{\mathbf{x}} - {\mathbf{x}}*) = \frac{{{{d}^{2}}}}{{d{{t}^{2}}}}{{\left\| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}}{\text{/}}2 - {{\left\| {{\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}},\quad t \geqslant 0, \\ \end{gathered} $(4.9)
${{a}_{1}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} ''{\kern 1pt} } \right\|}^{2}} + {{a}_{{21}}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} '} \right\|}^{2}} + {{a}_{{31}}}(t)\frac{d}{{dt}}{{\left\| {{\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} + \alpha (t)\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}{{\left\| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}}{\text{/}}2 + {{a}_{{41}}}(t)\frac{d}{{dt}}{{\left\| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}} \leqslant 0,\quad t \geqslant 0,$Проинтегрировав (4.9) на отрезке $[\xi ,t]$, $t > \xi \geqslant 0$, придем к неравенству
(4.10)
$ + \;{{a}_{{23}}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\|}^{2}} + {{a}_{{43}}}(t){{\left\| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}}{\text{/}}2 + \alpha (t)\frac{d}{{dt}}{{\left\| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}}{\text{/}}2 \leqslant {{C}_{1}}(\xi ,{\mathbf{x}}*),$Умножим это неравенство на
Отсюда с учетом производной $e{\kern 1pt} '(t) = {{a}_{{43}}}(t)e(t){\text{/}}\alpha (t)$, имеем
Проинтегрировав его на $[\xi ,t]$ и умножив полученное неравенство на ${{e}^{{ - 1}}}(t)$, получим
(4.11)
$\begin{gathered} {{\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}} \leqslant \frac{{2{{C}_{1}}(\xi ,{\mathbf{x}}*)}}{{\alpha e(t)}}\int\limits_\xi ^t {e(s)ds} + \frac{{e(\xi ){{{\left\| {{\mathbf{x}}(\xi ) - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}}}}{{e(t)}} \leqslant 2{{C}_{1}}(\xi ,{\mathbf{x}}*)p(t),\quad t > \xi \geqslant 0, \\ p(t) = \frac{1}{{{{\alpha }_{0}}e(t)}}\int\limits_\xi ^t {e(s)ds} + \frac{{e(\xi ){{{\left\| {{\mathbf{x}}(\xi ) - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}}}}{{2e(t)}}C_{1}^{{ - 1}}(\xi ,{\mathbf{x}}*),\quad \alpha (t) \geqslant {{\alpha }_{0}} > 0,\quad \mathop {\lim }\limits_{t \to \infty } p(t) = \alpha _{0}^{{ - 1}}. \\ \end{gathered} $Из (4.11) следует
(4.12)
$\mathop {\overline {\lim } }\limits_{t \to \infty } {{\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}} \leqslant 2{{C}_{1}}(\xi ,{\mathbf{x}}*){\text{/}}{{\alpha }_{0}},\quad t > \xi \geqslant 0,\quad {\mathbf{x}}* \in {{Q}_{*}}.$Оценим второе и третье слагаемые для второго соотношения из (4.2) с помощью неравенств (4.10) и (4.7). Учитывая (4.1) и (4.8), существование чисел $r > 0$ (пусть $r = {{\beta }_{0}}{{\gamma }_{0}}{{\sigma }_{0}}{{\theta }_{0}}$) и $\eta \geqslant 0$ таких, что для $s > \eta \geqslant \xi \geqslant 0$ коэффициенты подынтегральных слагаемых в (4.10) ${{a}_{1}}(s) \geqslant r > 0$, ${{a}_{{22}}}(s) \geqslant r > 0$, ${{a}_{{42}}}(s) \geqslant r > 0$, из (4.10) получим
(4.13)
$\begin{gathered} r\int\limits_\xi ^t {\left\{ {{{{\left\| {{\mathbf{x}}{\kern 1pt} ''(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}{\kern 1pt} '(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}(s) - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}}} \right\}ds} + {{a}_{{43}}}(t){{\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}}{\text{/}}2 + \\ + \;\alpha (t)({\mathbf{x}}{\kern 1pt} '(t),{\mathbf{x}}(t) - {\mathbf{x}}*) + {{a}_{{23}}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant {{C}_{1}}(\xi ,{\mathbf{x}}{\kern 1pt} *),\quad t > \xi \geqslant \eta \geqslant 0. \\ \end{gathered} $В (4.13) третье слагаемое оценим с помощью известного неравенства
(4.14)
$2\left| {ab} \right| \leqslant \varepsilon {{a}^{2}} + {{\varepsilon }^{{ - 1}}}{{b}^{2}}\quad \forall a,b,\varepsilon > 0$Тогда из (4.13) следует
(4.15)
$ + \;[{{a}_{{41}}}(t) - \alpha {\kern 1pt} '(t){\text{/}}2 - \alpha (t){\text{/}}(2\beta )]{{\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}} \leqslant {{C}_{1}}(\xi ,{\mathbf{x}}*),$(4.15а)
$\int\limits_\xi ^t {\left[ {{{{\left\| {{\mathbf{x}}{\kern 1pt} ''(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}{\kern 1pt} '(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}(s) - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}}} \right]ds} \leqslant {{C}_{1}}(\xi ,{\mathbf{x}}*){\text{/}}r,$(4.15б)
${{\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant 4{{C}_{1}}(\xi ,{\mathbf{x}}*){{(\alpha \beta )}^{{ - 1}}},\quad t > \eta \geqslant \xi \geqslant 0.$Из (4.15а) и (4.15б) с учетом условий (4.1) при $t \to \infty $ следует
(4.16)
$\int\limits_0^\infty {\left( {{{{\left\| {{\mathbf{x}}(s) - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}{\kern 1pt} '(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}{\kern 1pt} ''(s)} \right\|}}^{2}}} \right)ds} < + \infty \quad \forall {\mathbf{x}}* \in {{Q}_{*}},$(4.17)
$\mathop {\overline {\lim } }\limits_{t \to \infty } {{\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant 4{{C}_{1}}(\xi ,{\mathbf{x}}*){{({{\alpha }_{0}}{{\beta }_{0}})}^{{ - 1}}},\quad t > \eta \geqslant \xi \geqslant 0.$Далее оценим $\left\| {{\mathbf{x}}{\kern 1pt} ''(t)} \right\|$, исходя из (4.7) и пользуясь (4.14). Неравенства
(4.18а)
$a_{{11}}^{1}(t){{\left\| {{\mathbf{x}}{\kern 1pt} ''} \right\|}^{2}} \leqslant {{a}_{{24}}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} + {{a}_{{44}}}(t){{\left\| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}},\quad t \geqslant 0,\quad {\mathbf{x}}* \in {{Q}_{*}}.$В (4.18а) оценим коэффициенты при квадратах норм при условиях (4.1):
Учитывая эти оценки, из (4.18а) получаем
(4.18б)
${{a}_{{11}}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} ''{\kern 1pt} } \right\|}^{2}} \leqslant {{a}_{{25}}}(t){{\left\| {{\mathbf{x}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} + {{a}_{{45}}}(t){{\left\| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}},\quad t \geqslant 0,\quad {\mathbf{x}}* \in {{Q}_{*}}.$Из (4.18б) с учетом оценок (4.11), (4.15б) имеем
(4.18)
${{\left\| {{\mathbf{x}}{\kern 1pt} ''{\kern 1pt} } \right\|}^{2}} \leqslant {{[{{a}_{{11}}}(t)]}^{{ - 1}}}\left( {2{{C}_{1}}(\xi ,{\mathbf{x}}*)[2{{a}_{{25}}}(t){{{(\alpha \beta )}}^{{ - 1}}} + {{a}_{{45}}}(t)p(t)]} \right).$С учетом условий (4.1), а также соотношений (4.12), (4.17), из (4.18) следует
(4.19)
$\mathop {\overline {\lim } }\limits_{t \to \infty } {{\left\| {{\mathbf{x}}{\kern 1pt} ''(t)} \right\|}^{2}} \leqslant {{C}_{2}}(\xi ,{\mathbf{x}}*),\quad t > \eta \geqslant \xi \geqslant 0,\quad {\mathbf{x}}* \in {{Q}_{*}},$Асимптотическую устойчивость траектории системы (2.1) и единственность предельной точки траектории можно показать по аналогии с работами [3]–[6].
Из (4.11), (4.12) следует, что траектория x(t) ограничена, а в силу (4.16) имеем
(4.20а)
$\mathop {\underline {\lim } }\limits_{t \to \infty } \left[ {{{{\left\| {{\mathbf{x}}{\kern 1pt} ''(t)} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\|}}^{2}} + {{{\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}}} \right] = 0\quad \forall {\mathbf{x}}* \in {{Q}_{*}}$(4.20б)
$\left\| {{\mathbf{x}}{\kern 1pt} ''({{t}_{i}})} \right\| \to 0,\quad \left\| {{\mathbf{x}}{\kern 1pt} '({{t}_{i}})} \right\| \to 0,\quad \left\| {{\mathbf{x}}({{t}_{i}}) - {\mathbf{x}}{\kern 1pt} *} \right\| \to 0,\quad i \to \infty ,\quad {\mathbf{x}}* \in {{Q}_{*}}.$Если в ${{C}_{1}}(\xi ,{\mathbf{x}}*)$ из (4.10) положим $t = {{t}_{i}}$, учтем (4.9) и для ${{t}_{i}} \geqslant {{t}_{1}}$ обозначим
(4.21)
${{C}_{1}}({{t}_{i}},{\mathbf{x}}*) \to 0,\quad i \to \infty ,\quad {\mathbf{x}}* \in {{Q}_{*}}.$Тогда с учетом (4.21) из (4.15а), (4.16) следует первое доказываемое соотношение из (4.2), а из (4.12), (4.17), (4.19), (4.20б), (4.21) следует второе соотношение из (4.2).
Из второго неравенства (4.4) при $b = {\mathbf{u}}{\kern 1pt} *$, с учетом (3.2) из леммы 2, имеем
(4.22)
$\begin{gathered} \left( {{\mathbf{s}}(t) - {\mathbf{v}}(t),{\mathbf{s}} - {\mathbf{u}}{\kern 1pt} *} \right) \leqslant - \lambda (t)\left( {\nabla {{h}_{1}}({\mathbf{v}}(t)),{\mathbf{u}}{\kern 1pt} * - \;{\mathbf{s}}(t)} \right),\quad {\mathbf{u}}* \in U* \subset U, \\ {\mathbf{s}}(t) = \alpha (t){\mathbf{u}}{\kern 1pt} ''(t) + \beta (t){\mathbf{u}}{\kern 1pt} '(t) + {\mathbf{u}}(t),\quad {\mathbf{v}}(t) = {\mathbf{u}}(t) - \theta (t){\mathbf{u}}'(t),\quad t \geqslant 0, \\ \end{gathered} $(4.23)
$ - \left( {\nabla {{h}_{1}}({\mathbf{v}}(t)),{\mathbf{u}}{\kern 1pt} * - \;{\mathbf{s}}(t)} \right) = - \left( {\nabla {{h}_{1}}({\mathbf{v}}(t)),{\mathbf{u}}{\kern 1pt} * - \;{\mathbf{v}}(t)} \right) - \left( {\nabla {{h}_{1}}({\mathbf{v}}(t)),{\mathbf{v}}(t - {\mathbf{s}}(t)} \right).$Слагаемые в правой части (4.23) преобразуем с помощью неравенства для вогнутой функции (см. [9, § 2.4, с. 44]),
(4.23а)
$ - (\nabla {{h}_{1}}\left( {\mathbf{v}} \right),{\mathbf{u}}{\kern 1pt} * - \;{\mathbf{s}}) \leqslant {{h}_{1}}\left( {\mathbf{s}} \right) - {{h}_{1}}\left( {{\mathbf{u}}{\kern 1pt} *} \right) + \frac{R}{2}{{\left\| {{\mathbf{v}} - {\mathbf{s}}} \right\|}^{2}} \leqslant \frac{R}{2}{{\left\| {{\mathbf{v}} - {\mathbf{s}}} \right\|}^{2}},$(4.24)
$\left( {{\mathbf{s}}(t) - {\mathbf{v}}(t),{\mathbf{s}} - {\mathbf{u}}{\kern 1pt} *} \right) \leqslant \frac{{R\lambda }}{2}{{\left\| {{\mathbf{v}}(t) - {\mathbf{s}}(t)} \right\|}^{2}}.$В (4.24) подставим разложения для левой части и квадрата нормы в правой части
После их подстановки из (4.24) следует
(4.25)
$\begin{gathered} {{b}_{1}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} ''{\kern 1pt} } \right\|}^{2}} + b_{{21}}^{a}(t){{\left\| {{\mathbf{u}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} + {{b}_{{31}}}(t)\left( {{\mathbf{u}}{\kern 1pt} ',{\mathbf{u}}{\kern 1pt} ''} \right) + \\ + \;\alpha \left( {{\mathbf{u}}{\kern 1pt} '',{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right) + (\beta + \theta )\left( {{\mathbf{u}}{\kern 1pt} ',{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right) \leqslant 0,\quad t \geqslant 0, \\ \end{gathered} $Справедливы аналогичные (4.8) тождества
(4.8а)
$\begin{gathered} 2({\mathbf{u}}{\kern 1pt} ''(t),{\mathbf{u}}{\kern 1pt} '(t)) = \frac{d}{{dt}}{{\left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\|}^{2}};\quad 2({\mathbf{u}}{\kern 1pt} '(t),{\mathbf{u}}(t) - {\mathbf{u}}*) = \frac{d}{{dt}}{{\left\| {{\mathbf{u}}(t) - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}}; \\ ({\mathbf{u}}{\kern 1pt} '',\;{\mathbf{u}} - {\mathbf{u}}*) = \frac{{{{d}^{2}}}}{{d{{t}^{2}}}}{{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}}{\text{/}}2 - {{\left\| {{\mathbf{u}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}},\quad t \geqslant 0. \\ \end{gathered} $Преобразуем (4.25) с помощью тождеств (4.8a), тогда получим
(4.26)
${{b}_{1}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} ''{\kern 1pt} } \right\|}^{2}} + {{b}_{{22}}}{{\left\| {{\mathbf{u}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} + {{b}_{3}}(t)\frac{d}{{dt}}{{\left\| {{\mathbf{u}}{\kern 1pt} '{\kern 1pt} } \right\|}^{2}} + \alpha (t)\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}{{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}}{\text{/}}2 + {{b}_{{41}}}\frac{d}{{dt}}{{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} \leqslant 0,\quad t \geqslant 0,$Проинтегрировав (4.26), на отрезке $[\xi ,t]$, $t > \xi \geqslant 0$, получим
(4.27)
$ + \;{{b}_{3}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\|}^{2}} + {{b}_{{43}}}(t){{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} + \alpha (t)\frac{d}{{dt}}{{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*),$(4.28)
$\frac{{\alpha (t)}}{{{{b}_{{43}}}(t)}}\frac{d}{{dt}}{{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} + {{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*){\text{/}}{{b}_{{43}}}(t),\quad t > \xi \geqslant 0,\quad {\mathbf{u}}* \in U{\kern 1pt} *{\kern 1pt} .$Умножим (4.28) на
Отсюда с учетом производной $g{\kern 1pt} '(t) = {{b}_{{43}}}(t)g(t){\text{/}}\alpha (t)$ имеем
(4.29)
$\frac{d}{{dt}}[g(t){{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}}] \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*)g(t){\text{/}}\alpha ,\quad t > \xi \geqslant 0.$Проинтегрировав (4.29) на $[\xi ,t]$ и умножив полученное неравенство на ${{g}^{{ - 1}}}(t)$, получим
(4.30а)
$\begin{gathered} {{\left\| {{\mathbf{u}}(t) - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} \leqslant \frac{{{{C}_{3}}(\xi ,{\mathbf{u}}*)}}{{\alpha g(t)}}\int\limits_\xi ^t {g(s)ds} + \frac{{g(\xi ){{{\left\| {{\mathbf{u}}(\xi ) - {\mathbf{u}}{\kern 1pt} *} \right\|}}^{2}}}}{{g(t)}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*)q(t),\quad t > \xi \geqslant 0, \\ q(t) = \frac{1}{{{{\alpha }_{0}}g(t)}}\int\limits_\xi ^t {g(s)ds} + \frac{{g(\xi ){{{\left\| {{\mathbf{u}}(\xi ) - {\mathbf{u}}{\kern 1pt} *} \right\|}}^{2}}}}{{{{C}_{3}}(\xi ,{\mathbf{u}}*)g(t)}},\quad \alpha (t) \geqslant {{\alpha }_{0}} > 0,\quad \mathop {\lim }\limits_{t \to \infty } q(t) = \alpha _{0}^{{ - 1}}. \\ \end{gathered} $Отсюда имеем
(4.30)
$\mathop {\overline {\lim } }\limits_{t \to \infty } {{\left\| {{\mathbf{u}}(t) - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*){\text{/}}{{\alpha }_{0}},\quad t > \xi \geqslant 0,\quad {\mathbf{u}}* \in U{\kern 1pt} *{\kern 1pt} .$Оценим второе и третье слагаемые во втором соотношении из (4.3) с помощью неравенств (4.8а) и (4.14). Учитывая (4.1) и то, что существуют числа $r > 0$ и $\eta \geqslant 0$ такие, что для $s > \eta \geqslant \xi \geqslant 0$ коэффициенты подынтегральных слагаемых в (4.27) ${{b}_{1}}(s) \geqslant r > 0$, ${{b}_{{21}}}(s) \geqslant r > 0$, ${{b}_{{42}}}(s) \geqslant r > 0$, и применяя (4.8а), из (4.27) получаем
(4.31)
$ + 2\alpha (t)({\mathbf{u}}{\kern 1pt} '(t),{\mathbf{u}}(t) - {\mathbf{u}}*) + {{b}_{3}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*),$В (4.31) третье слагаемое оценим с помощью неравенства (4.14) при $\varepsilon = \beta $, $a = {\mathbf{u}}{\kern 1pt} '(t)$, $b = {\mathbf{u}}(t) - {\mathbf{u}}{\kern 1pt} *$, т.е.
Тогда верно
(4.32)
$\begin{gathered} r\int\limits_\xi ^t {\left\{ {{{{\left\| {{\mathbf{u}}{\kern 1pt} ''(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}{\kern 1pt} '(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}(s) - {\mathbf{u}}{\kern 1pt} *} \right\|}}^{2}}} \right\}ds} + {{b}_{{32}}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\|}^{2}} + {{b}_{{44}}}(t){{\left\| {{\mathbf{u}}(s) - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*), \\ t > \eta \geqslant \xi \geqslant 0, \\ \end{gathered} $Неравенство (4.32) эквивалентно системе
(4.33а)
$\int\limits_\xi ^t {\left[ {{{{\left\| {{\mathbf{u}}{\kern 1pt} ''(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}{\kern 1pt} '(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}(s) - {\mathbf{u}}{\kern 1pt} *} \right\|}}^{2}}} \right]ds} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*){\text{/}}r,$(4.34a)
${{\left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*){\text{/}}{{b}_{{32}}}(t),\quad t > \eta \geqslant \xi \geqslant 0.$Из (4.33а), (4.34а), с учетом $\lim {{b}_{{32}}}(t) = {{\alpha }_{0}}{{\beta }_{0}} + \frac{3}{2}{{\alpha }_{0}}{{\theta }_{0}} = b_{{32}}^{0}$ при $t \to \infty $, и условий (4.1) для параметров метода, следует
(4.33)
$\int\limits_0^\infty {\left( {{{{\left\| {{\mathbf{u}}(s) - {\mathbf{u}}{\kern 1pt} *} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}{\kern 1pt} '(s)} \right\|}}^{2}} + {{{\left\| {{\mathbf{u}}{\kern 1pt} ''(s)} \right\|}}^{2}}} \right)ds} < + \infty \quad \forall {\mathbf{u}}* \in U{\kern 1pt} *{\kern 1pt} ,$(4.34)
$\mathop {\overline {\lim } }\limits_{t \to \infty } {{\left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant {{C}_{3}}(\xi ,{\mathbf{u}}*){\text{/}}b_{{32}}^{0},\quad t > \eta \geqslant \xi \geqslant 0.$Оценку для $\left\| {{\mathbf{u}}{\kern 1pt} ''(t)} \right\|$ получим из (4.25) с помощью (4.8a) и (4.14). С учетом оценок
(4.35)
$b_{{11}}^{1}(t){{\left\| {{\mathbf{u}}{\kern 1pt} ''} \right\|}^{2}} \leqslant {{b}_{{24}}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} '} \right\|}^{2}} + {{b}_{{44}}}(t){{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}},\quad t \geqslant 0,\quad {\mathbf{u}}* \in {{Q}_{*}},$С учетом этих оценок и (4.30а), (4.34а), из (4.35) получим
(4.36а)
$\begin{gathered} {{b}_{{11}}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} ''} \right\|}^{2}} \leqslant {{b}_{{25}}}(t){{\left\| {{\mathbf{u}}{\kern 1pt} '} \right\|}^{2}} + {{b}_{{45}}}(t){{\left\| {{\mathbf{u}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}},\quad t \geqslant 0,\quad {\mathbf{u}}* \in {{Q}_{*}}, \\ {{\left\| {{\mathbf{u}}{\kern 1pt} ''} \right\|}^{2}} \leqslant {{[{{b}_{{11}}}(t)]}^{{ - 1}}}\left( {{{C}_{3}}(\xi ,{\mathbf{u}}*)[{{b}_{{25}}}(t){{{[{{b}_{{32}}}(t)]}}^{{ - 1}}} + {{b}_{{45}}}(t)q(t)]} \right). \\ \end{gathered} $С учетом (4.30), (4.34) из (4.36а) следует
(4.36б)
$\mathop {\overline {\lim } }\limits_{x \to \infty } {{\left\| {{\mathbf{u}}{\kern 1pt} ''(t)} \right\|}^{2}} \leqslant {{C}_{4}}(\xi ,{\mathbf{u}}*),\quad {\mathbf{u}}* \in U{\kern 1pt} *{\kern 1pt} ,$Далее, в силу (4.30а), (4.30) траектория ${\mathbf{u}}(t)$ ограничена, а в силу (4.33) имеем
(4.37)
$\left\| {{\mathbf{u}}{\kern 1pt} ''({{t}_{i}})} \right\| \to 0,\quad \left\| {{\mathbf{u}}{\kern 1pt} '({{t}_{i}})} \right\| \to 0,\quad \left\| {{\mathbf{u}}({{t}_{i}}) - {\mathbf{u}}{\kern 1pt} *} \right\| \to 0,\quad i \to \infty ,\quad {\mathbf{u}}* \in U{\kern 1pt} *{\kern 1pt} .$Если в (4.10) положим $t = {{t}_{i}}$, учтем (4.9) и для ${{t}_{i}} \geqslant {{t}_{1}}$ обозначим
Тогда с учетом (4.37) из (4.33) следует третье доказываемое соотношение из (4.3), а из (4.30), (4.34), (4.36), (4.37) следует четвертое соотношение из (4.3).
Теорема 1 доказана.
5. ОЦЕНКА СКОРОСТИ СХОДИМОСТИ НПОЭКМС (2.1)
Получим оценки скорости сходимости метода (2.1), (4.1) для выпукло-вогнутой функции.
Теорема 2. Пусть выполнены все условия теоремы 1, включая (4.1)−(4.3), леммы 1 и 2. Тогда траектория $\left\{ {{\mathbf{x}}(t);{\mathbf{u}}(t)} \right\}$ НПОЭКМС (2.1), (4.1)−(4.3) сходится к седловой точке $\left( {{\mathbf{x}}*;{\mathbf{u}}{\kern 1pt} *} \right) \in {{Q}_{*}} \times U{\kern 1pt} *$ задачи (1.1) $\forall t \geqslant 0$ с экспоненциальной скоростью с оценками:
(5.1)
$\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\| \leqslant {{\left\{ {2{{C}_{{21}}}{{p}_{2}}(t)} \right\}}^{{1/2}}},$(5.2)
$\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\| \leqslant 2{{\left( {{{C}_{{21}}}{{{(\alpha (t)\beta (t))}}^{{ - 1}}}} \right)}^{{1/2}}},$(5.3)
$\left\| {{\mathbf{x}}{\kern 1pt} ''{\kern 1pt} } \right\| \leqslant {{[{{a}_{{11}}}(t)]}^{{ - 1/2}}}{{\left\{ {2{{C}_{{21}}}[2{{a}_{{25}}}(t){{{(\alpha \beta )}}^{{ - 1}}} + {{a}_{{45}}}(t){{p}_{2}}(t)]} \right\}}^{{1/2}}},$(5.4)
$\left\| {{\mathbf{u}}(t) - {\mathbf{u}}{\kern 1pt} *} \right\| \leqslant {{\left[ {{{C}_{{31}}}{{q}_{2}}(t)} \right]}^{{1/2}}},$(5.5)
$\begin{gathered} \left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\| \leqslant {{\left( {{{C}_{{31}}}{\text{/}}{{b}_{{32}}}(t)} \right)}^{{1/2}}}, \\ \left\| {{\mathbf{u}}{\kern 1pt} ''(t)} \right\| \leqslant {{[{{b}_{{11}}}(t)]}^{{ - 1/2}}}{{\left\{ {{{C}_{{31}}}[{{b}_{{25}}}(t){{{({{b}_{{32}}}(t))}}^{{ - 1}}} + {{b}_{{45}}}(t){{q}_{2}}(t)]} \right\}}^{{1/2}}}, \\ \end{gathered} $(5.6)
$\begin{gathered} {{C}_{{21}}} = {{a}_{{31}}}(0){{\left\| {{{{\mathbf{x}}}^{1}}} \right\|}^{2}} + \alpha (0)({{{\mathbf{x}}}^{1}},{{{\mathbf{x}}}^{0}} - {\mathbf{x}}*) + ({{a}_{{41}}}(0) - \frac{1}{2}\alpha {\kern 1pt} '(0)){{\left\| {{{{\mathbf{x}}}^{0}} - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}}, \\ {{C}_{{31}}} = {{b}_{3}}(0){{\left\| {{{{\mathbf{u}}}^{1}}} \right\|}^{2}} + 2\alpha (0)({{{\mathbf{u}}}^{1}},{{{\mathbf{u}}}^{0}} - {\mathbf{u}}*) + {{b}_{{43}}}(0){{\left\| {{{{\mathbf{u}}}^{0}} - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}}, \\ \end{gathered} $Доказательство. Заметим, что при выполнении всех условий теоремы 2, выкладки и результаты теоремы 1 о сходимости метода (2.1) справедливы (обозначения коэффициентов, совпадающих с полученными в теореме 1, сохраняем; новые коэффициенты ${{C}_{{21}}}$, ${{C}_{{31}}}$ приведены в формулировке теоремы 2). Проведя аналоги выкладок из теоремы 1 от (4.4), но теперь при $\xi = 0$, получим аналог (4.11)
(5.7)
${{\left\| {{\mathbf{x}}(t) - {\mathbf{x}}{\kern 1pt} *} \right\|}^{2}} \leqslant \frac{{2{{C}_{{21}}}}}{{\alpha e(t)}}\int\limits_0^t {e(s)ds} + \frac{{e(0){{{\left\| {{{{\mathbf{x}}}^{0}} - {\mathbf{x}}{\kern 1pt} *} \right\|}}^{2}}}}{{e(t)}} \leqslant 2{{C}_{{21}}}{{p}_{2}}(t),\quad t \geqslant 0.$Из (5.7) следует оценка (5.1).
Проведем выкладки, аналогичные проведенным в теореме 1 от (4.13) до (4.15б), только при $\xi = 0$, тогда аналог (4.15б) имеет вид
(5.8)
${{\left\| {{\mathbf{x}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant 4{{C}_{{21}}}{{(\alpha (t)\beta (t))}^{{ - 1}}},\quad t \geqslant 0.$Из (5.8) следует оценка (5.2).
Для получения (5.3) вычислим аналоги (4.16)−(4.18) для $\xi = 0$, тогда (сохраняя из теоремы 1 и обозначения, за исключением ${{p}_{2}}(t)$ и ${{q}_{2}}(t)$), с учетом (5.7), (5.8) получим
(5.9)
${{\left\| {{\mathbf{x}}{\kern 1pt} ''{\kern 1pt} } \right\|}^{2}} \leqslant {{[{{a}_{{11}}}(t)]}^{{ - 1}}}\left( {2{{C}_{{21}}}[2{{a}_{{25}}}(t){{{(\alpha \beta )}}^{{ - 1}}} + {{a}_{{45}}}(t){{p}_{2}}(t)]} \right),\quad t \geqslant 0,$Теперь проведем аналоги выкладок из теоремы 1 по ${\mathbf{u}}(t)$, но при $\xi = 0$. Вычислив аналоги для (4.26)−(4.29), затем получим аналог неравенства (4.30а)
(5.10)
${{\left\| {{\mathbf{u}}(t) - {\mathbf{u}}{\kern 1pt} *} \right\|}^{2}} \leqslant \frac{{{{C}_{{31}}}}}{{\alpha g(t)}}\int\limits_0^t {e(s)ds} + \frac{{g(0){{{\left\| {{{{\mathbf{u}}}^{0}} - {\mathbf{u}}{\kern 1pt} *} \right\|}}^{2}}}}{{g(t)}} \leqslant {{C}_{{31}}}{{q}_{2}}(t),\quad t \geqslant 0.$Из неравенства (5.10) следует оценка (5.4).
Далее получим оценку (5.5). Проведем аналоги выкладок из теоремы 1 после (4.30) до получения неравенства (4.34а), только при $\xi = 0$, с учетом неравенства (5.10), оценок коэффициентов, получим
(5.11)
${{\left\| {{\mathbf{u}}{\kern 1pt} '(t)} \right\|}^{2}} \leqslant {{C}_{{31}}}{\text{/}}{{b}_{{32}}}(t),\quad t > 0.$Из (5.11) следует оценка (5.5).
Для вычисления оценки (5.6) продолжим аналоги выкладок из теоремы 1 после (4.34) до получения (4.36а), только при $\xi = 0$; с учетом неравенств (5.10), (5.11) получим
(5.12)
${{\left\| {{\mathbf{u}}{\kern 1pt} ''(t)} \right\|}^{2}} \leqslant {{[{{b}_{{11}}}(t)]}^{{ - 1}}}\left\{ {{{C}_{{31}}}[{{b}_{{25}}}(t){{{({{b}_{{32}}}(t))}}^{{ - 1}}} + {{b}_{{45}}}(t){{q}_{2}}(t)]} \right\},\quad t > 0,$Теорема 2 доказана.
6. ВЫВОДЫ
Исследованный в данной работе НПОЭКМС (2.1) продолжает на непрерывные проекционные ЭГМ второго порядка для решения седловых задач идею использования операторов переменной метрики, впервые воплощенную в НПММ первого порядка в работе [4]. НПОЭКМС (2.1) обладает достоинствами, присущими и НПММ, и методам переменной метрики; он имеет лучшую точность и скорость сходимости в окрестности седловой точки.
Список литературы
Эрроу К.Дж., Гурвиц Л., Удзава Х. Исследования по линейному и нелинейному программированию. М.: Изд-во иностр. лит., 1962.
Корпелевич Г.М. Экстраполяционные градиентные методы и их связь с модифицированными функциями Лагранжа // Экономика и матем. методы. 1983. Т. 19. Вып. 4. С. 694−703.
Антипин А.С. Градиентный и экстраградиентный подходы в билинейном и равновесном программировании. М.: Изд-во ВЦ РАН, 2002.
Антипин А.С., Васильев Ф.П. О непрерывном методе минимизации в пространствах с переменной метрикой // Известия вузов. Математика. 1995. № 12(403). С. 3−9.
Малинов В.Г. О проекционном квазиньютоновском обобщeнном двухшаговом методе минимизации и оптимизации траектории летательного аппарата // Ж. Средневолжского матем. общества. 2010. Т. 12. № 4. С. 37−48.
Малинов В.Г. Версия непрерывного проекционного метода минимизации второго порядка с переменной метрикой // Ж. Средневолжского матем. общества. 2014. Т. 16. № 1. С. 121−134.
Малинов В.Г. О версии обобщенного экстраградиентного квазиньютоновского метода решения седловых и других задач // IX Московская международная конференция по исследованию операций (ORM2018): Москва. 22–27 октября 2018 г.: Труды. В двух томах. Том II. М.: МАКС ПРЕСС, 2018. С. 124−126.
Васильев Ф.П. Численные методы решения экстремальных задач. М.: Наука, 1988.
Карманов В.Г. Математическое программирование. М.: Наука, 1975.
Антипин А.С., Хамраева З.С. Управляемые седловые дифференциальные градиентные методы 2-го порядка. М.: Вычислительный Центр РАН, 1996.
Антипин А.С. Управляемые дифференциальные градиентные методы второго порядка для решения равновесных задач // Дифференц. ур-ния. 1999. Т. 35. № 5. С. 590–599.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики